Machine Learning Tools Applied for Training Optimization in Handball

Analytics have become increasingly popular among sports in recent years, providing valuable information regarding physical and mental health. Many athletes have found that analytics during training can help to improve their performance, reduce the risk of injury, and enhance their overall well-being. This paper aims to improve the results of handball players by applying a method for measuring the influence of different trials on aggregate performance calculated per each athlete in order to qualify for the Olympic Games. By separating the isolated action of each trial, the result is an additional influence caused by the interaction of factors or the simultaneous action. That might explain why the neuromuscular feedback loop is utterly necessary to perform handball motor actions. Further on, the ML analysis can help identify areas for improvement, optimize training programs, and enhance overall team performance.

Keywords:

Subject: Social Sciences - Tourism, Leisure, Sport and Hospitality

1. Introduction

For measuring the influence of factors like these we propose a formula to calculate their proportional influence that may determine the modification of an aggregate performance indicator for human activity, for example in handball.

By applying substitution on symbolic constants, based on a lexicographic method, we shall use the Tanagra ML (Machine Learning) system to generate the C-RT decision tree and find out which factor is the most important for qualifying athletes for the World Cup. Decision trees can analyze large datasets to extract meaningful insights and improve performance over time [1]. For this purpose, we have applied the method of separating the isolated action of each factor (acceleration, aerobic fitness, jumping) based on a weighting system that uses a basic comparison of quantitative indicators even if it leads to the amplification of the volume of calculations, especially for more than three factors. The result is an additional influence that is caused by the interaction of factors or the simultaneous action of factors, accordingly to the recurrence relationship between absolute changes for three factors, after [2]:

Δ = a₁b₁c₁ – a₀b₀c₀ = Δ^(a)+ Δ^(b)+ Δ^(c)+ Δ^(a)(b)+ Δ^(a)(c)+ Δ^(b)(c)+ Δ^(a)(b)(c),

(1)

where a, b, and c are influence factors.

Machine learning was used previously to analyze and predict mental health problems among higher education students [3]. The objective of our research was to find analysis methods and improve handball performance athletes, by using technology. ML can be used in various aspects of handball, including player performance analysis, referee decision-making, and coaching assistance. We implemented to choose the best athletes for the competition based on the ML analysis of 3 factors acceleration, aerobic fitness, and jumping. These factors were chosen based on an exploratory factor analysis in SPSS that reflected the factors with the higher importance for the competition. Our method method contributes uniquely to sports analytics, as in handball no similar ML analysis was done.

2. Important items to be analyzed in handball athletes

For top athletes to train and compete as well as the avoidance of potential sports injuries, workload monitoring is essential. New technologies have been made available for the evaluation of external load in sports teams, assisting coaches in individualized training and playing system optimization. We have to examine the physical requirements placed on a top handball team over the course of an entire sporting season. For each position in this physically demanding team activity involving body contact, novel facts are given [4].

In the handball game, there are some important items to be analyzed: acceleration, aerobic fitness, jumping, ball throwing speed, number of sprints, number of decelerations, handgrip strength, anthropometric variables, ventilation of the lungs, absolute intake of oxygen, and oxygen consumption at the three points-lactate limit, breath by breath. [5,6,7,8,9]

The rate at which an object's velocity alters over time is referred to as acceleration. Acceleration is frequently equated with explosive force and the capacity to achieve high speeds quickly when discussing physical fitness or athletic performance. It is crucial for tasks that call for sudden bursts of speed, such as sprinting, sharp turns, or acceleration in sports like handball, basketball, or soccer. Acceleration's impact may be crucial for raising performance in these areas.

Performance metrics such as playing time, total distance traveled while moving at various running rates, and acceleration factors are frequently tracked [4]. Other authors consider that the number of decelerations, number of sprints, accelerations interspersed with a maximum of 30s between them (RAS30s), and the heart rate (HR) are other variables that can provide important information regarding athletes' performance [5]. Other authors attempt to offer a workable and affordable approach to calculate the throwing velocity in handball using wrist acceleration signals [9]. Standard handball athletes achieved better flying sprint performance, whereas elite players demonstrated higher acceleration potential and jump ability. There was no difference in throwing velocity across the various standard levels [6,7].

The ability of the body to use oxygen effectively while engaging in prolonged exercise is referred to as aerobic fitness. It is frequently assessed using parameters like VO2 max, which represents the maximum amount of oxygen the body can use during strenuous exercise. For activities requiring endurance, like long-distance running, cycling, or swimming, aerobic fitness is crucial. It affects the body's capacity to withstand sustained physical effort. Some researchers compared the physiological characteristics used to determine cardiorespiratory fitness measured through the multistage treadmill endurance (TR) test and the 30-15 interrupted fitness (30-15(IFT)) test. The findings demonstrated that VO2 max and peak speed of running (V) for the 30-15 (IFT) testing were significantly greater than those achieved for the TR test. Additionally, it was discovered that the initiation of blood accumulation of lactate was considerably earlier at 30-15 (IFT) than during TR for each of the following measures: VO2 max, running speed, and maximal heart rate [8].

To enhance athletic performance, optimizing % of body fat should be taken into account as an objective when planning workouts and nutrition [10]. Plyometric exercises and high-intensity interval training (HIIT) can help young handball players strengthen their physical fitness skills, which are very important for them [11].

An evaluation of a person's lower-body strength and explosive power can be measured through their ability to jump. It applies to sports like basketball and volleyball as well as some jumps like the long jump and high jump. Muscle power, strength, and technique are all aspects that affect a jumper's ability. Enhancing leaping ability can improve performance in sports that call for fast upward movements or vertical leaps. The drop jump is a well-liked plyometric exercise that is frequently done to improve countermovement jump height. Despite being widely used, drop jump training frequently has unpredictable results on countermovement jump height. These discrepancies could be caused by discrepancies in the drop-jump method used. The countermovement drop jump and the bounce drop jump are two well-known types of drop jumps, and the current study looked at how eight weeks of practice with these drop jump methods affected countermovement jump height. When it comes to increasing countermovement leap height, the countermovement drop jump can be superior to the bounce drop jump [12,13]. A credible, trustworthy, and practical tool for determining leap height is ADR-Jumping [14]. Also, the Wheeler Jump Sensor is a trustworthy tool that gives researchers and experts accurate data regarding fluctuations in players' athletic abilities [15]. In handball, jumping is influenced by strength. When evaluating jump-related strength in handball players, it is crucial to use tests that focus on performance-relevant neuromuscular features. Maximum strength and impulse at about 60% 1RM did not seem to adequately capture the capacities associated with jump height [16].

In handball, there is a standard procedure to evaluate the performance of players. A handball match involves a lot of accelerations, sprints, twists, and hops, as well as direct contact with the opposition. Both on defense and on offense, there is a significant amount of sprinting and maximal leaping. Additionally, flexibility, throwing velocity, agility, and coordinative skills are essential for effectively handling game circumstances [17]. Strong aerobic capacity assures a delayed onset of exhaustion and quicker recovery, whereas anaerobic capacity is what allows for endurance during high-intensity, repeated activity [18]. The data collected from players were introduced into SPSS software where Exploratory factor analysis was designed. The result of the Eigenvalue and rotated component matrix showed that acceleration, aerobic fitness, and jumping are the factor with greater importance that has to be introduced into our analysis.

3. Methodology

Before an official competition of a national team, the coach organizes training sessions with certain players, evaluated based on the results of the team they work for, the percentage of goals scored and missed throws, the way of scoring a goal (collective or individual, counterattack or positional).

To take part in this study, the following inclusion criteria were specified: (i) to be enrolled in the national handball team (ii) taking part in and routinely attending international contests; (iii) providing informed consent to participate in the study is step iii. (iv) completing the exam so that data may be collected. The athletes were also made aware that they might stop taking part in the study whenever they wanted. One of the researchers physically gathered the data. Before taking part, each person in the study provided their consent. The University of Brasov's Ethics Committee accepted the study, which was carried out in conformity with the Declaration of Helsinki.

For our study, there have been recorded the outcomes of the three athletic probes important in handball players: acceleration, aerobic exercise, and jumping. The aim is to acquire more detailed knowledge of what is meant by "influence" and the context in which these factors are being taken into account to calculate the proportional influence of three factors acceleration, aerobic fitness, and jumping.

During the verification camp, for confirmation, the coaches perform these tests with the players, tests that have been completed by the players at their home clubs. Following the test results, the players are selected for competition from 85 trials.

After the proportional distribution of the changes caused by the interaction of the factors with the changes calculated by the isolated substitution of each factor, according, to equation (1), the factorial influences expressed in absolute figures for the influence of the factor "A" are (2):

I_A = Δ_Ab₀c₀ + Δ_Ab₀c₀/(Δ_Ab₀c₀+a₀Δ_Bc₀+a₀b₀Δ_C) · Δ_AΔ_BΔ_C + Δ_Ab₀c/(Δ_Ab₀c+a₀Δ_Bc₀) · Δ_AΔ_Bc₀ + Δ_Ab₀c₀/(Δ_Ab₀c + a₀b₀ Δ_C) · Δ_Ab₀Δ_C,

(2)

where Δ_A = a₁-a₀, Δ_B = b₁-b₀, and Δ_C = c₁-c₀ thus resulting the following (3):

I_A/Δ_Ab₀c₀ = 1 + 1/(1 + a₀Δ_Bc₀ + a₀b₀ Δ_C) · Δ_AΔ_BΔ_C + 1/(1+ a₀Δ_Bc₀) · Δ_AΔ_Bc₀ + 1/(1+ a₀b₀ Δ_C) · Δ_Ab₀Δ_C,

(3)

resulting in the recurrence relationship being of combinatorial type depending on the number of factors (4):

\sum_{i, j} \frac{p X_{i, j}}{\sum_{i} P a_{i} - P a_{i}}

(4)

for i, j = 1, 2, ..., n, and n = 3, where pX is the vector of linear permutations of two and three factors, and Pa is the vector of linear permutations related to each factor. For the pseudo-code related to the recurrence formula, see Appendix A.

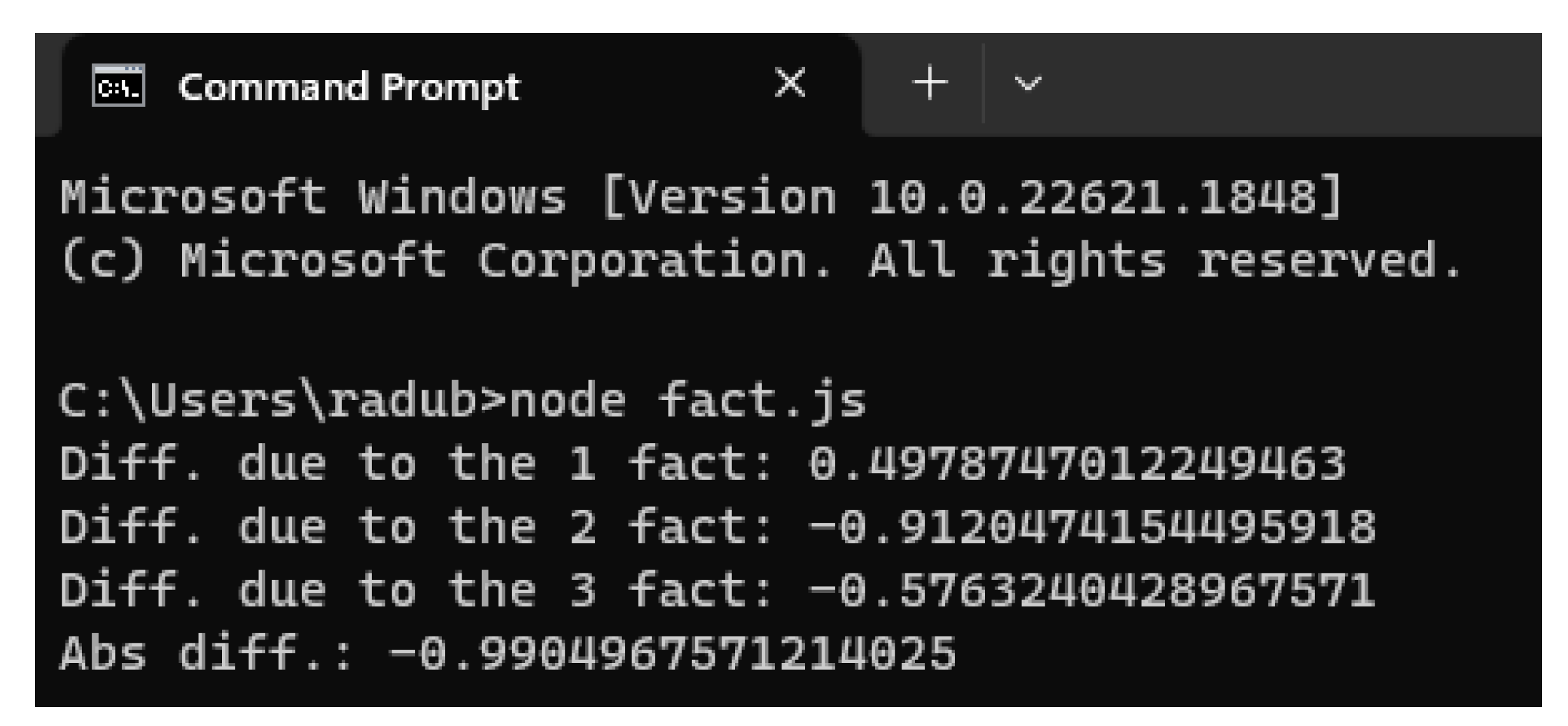
We directly implemented the algorithm in the Javascript language, see Appendix B, obtaining the value 0.4978 for the influence of the factor 'a' in an iterative way, as follows (Figure 1):

In conclusion, applying equation (5) we obtained a value quite close to the initial estimate. We continued the development of the program for determining the influence of factors b and c, the deviation obtained being reasonable/negligible.

iA = Pa [0] ×(1 + 1/sum_Pa × pA [0] + 1/(sum_Pa - Pa [1]) × pA [1] + 1/(sum_Pa - Pa [2]) × pA [2]),

(5)

A special fact is that the calculation formula for all influence factors (a, b, and c) is identical, as it results from the program code, see Appendix B, only the second type of linear permutation vector (pX) changes after each influence factor (pA, pB and pC), as follows (6, 7, 8):

p_A ={ Δ_A· Δ_B·Δ_C, Δ_A·Δ_B·c₀, Δ_A·b₀·Δ_C },

(6)

p_B={ Δ_A·Δ_B·Δ_C, Δ_A·Δ_B·c₀, a₀·Δ_B·Δ_C },

(7)

p_C={ Δ_A·Δ_B·Δ_C, Δ_A·b₀·Δ_C, a₀·Δ_B·Δ_C },

(8)

where Δ_A= (a₁-a₀), Δ_B= (b₁-b₀), and Δ_C= (c₁-c₀).

Consequently, the squad of players who performed these tests was 25 players, and participants in the official competitions of the national team were 13 players (7 players on the field and 6 kept reserved in the stand (in case of injury to a player or suspension for 1 or 2 stages of a player, he can be replaced by a reserve)

4. Materials

According to [19], fundamental changes are required for programming methodologies and paradigms to utilize the existing computing power:

The limitations of producing a faster clock rate Central Processing Unit (CPU);
The growing number of interconnected devices;
The demand for more computing power.

Different programming paradigms have been proposed and applied to solve different problems such as Object-Oriented Programming (OOP), Functional Programming (FP), Imperative Languages (IL), Symbolic Programming, etc., following Table 1:

Starting with the ES5 version, Javascript functional features were improved considerably from an object-oriented language to a hybrid one. Even from the earlier versions, JS functions were first-class citizens, so the function itself replaced the class concept used for gathering variables and methods alike, adopting even a constructor.

One of the first functional features adopted in JS was the pure functions that ensure no side effects. This way data is safely transformed by value via one primitive or composed function into another, as seen in Figure 2:

Our program calculates the Inf and Tot values based on the given arrays and constants. For this purpose, it defines several arrays and constants, including iB, iC, Pa, pA, pB, pC, pX, Inf, Tot, Sum, and iA. The N variable represents the number of elements in the arrays, and iB and iC represent arrays of length N containing integer values. The other variables are initialized to 0.0.

The calculatePa, calculatepA, calculatepB, calculatepC, calculatepX, and calculateInfAndTot functions are defined to calculate the values of these arrays and constants, as below:

The calculatePa function calculates the Pa array based on the values of iB and iC. The Pa array is an array of products of the differences between the corresponding elements of iC and iB and the other elements of iB;
The calculatepA, calculatepB, and calculatepC functions calculate the pA, pB, and pC arrays based on the values of iB and iC. These arrays are also products of the differences between the corresponding elements of iC and iB and the other elements of iB, but with different combinations of elements;
The calculatepX function calculates the pX array based on the values of pA, pB, and pC. The pX array is a 2D array with 3 rows and N columns. The first row of pX is the pA array, the second row is the pB array, and the third row is the pC array.

The calculateInfAndTot function calculates the Inf and Tot values based on the values of Pa and pX, as follows:

The Inf value is calculated for each element of Pa using a nested loop using the formula (1 + Sum) × Pa[k], where Sum is the sum of the pX values for the corresponding row and column;
The Tot value is the sum of all Inf values.
Finally, the calculatePa, calculatepA, calculatepB, calculatepC, calculatepX, and calculateInfAndTot functions are called to calculate the Inf and Tot values.

5. Results

We started the analysis with a nationwide selection elite focus group of 5 athletes. Their results served as a training data set for the Bayesian analysis conducted on 20 non-elite athletes. The output based on the larger data set confirmed the elite athletes based on the weighted factor hierarchies established at faze one of the analyses (C-RT decision tree method).

There have been recorded the following results on three probes: acceleration, aerobic, and jumping. To determine the proportional influence of three factors, it is necessary to have more specific information about what is meant by "influence" and the context in which these factors are being considered. For this purpose, we provide some general insights about these factors:

The proportional influence of these factors will vary depending on the specific activity or sport in question. For example, in a sprinting event, acceleration may have a higher proportional influence compared to aerobic fitness or jumping ability. On the other hand, in endurance events like long-distance running, aerobic fitness will play a more dominant role. Similarly, in sports that heavily rely on jumping, such as basketball, jumping ability will be a significant factor.

Each of the athletes had been given several trials on which we took into consideration the first and the last trial, for example, L.P. obtained the following results, see Table 2:

It's important to note that these factors are interconnected, and improving one aspect can have positive effects on others.

Acceleration refers to the rate at which an athlete's velocity changes over time. In the context of physical fitness or sports performance, acceleration is often associated with explosive power and the ability to quickly reach high speeds. It plays a significant role in activities that require bursts of speed, such as sprinting, changing directions rapidly, or accelerating in sports like basketball or soccer. The influence of acceleration can be important for improving performance in these areas [21,22].

Aerobic fitness refers to the body's ability to use oxygen efficiently during prolonged exercise. It is typically measured by factors such as VO2 max, which is the maximum amount of oxygen the body can utilize during intense exercise. Aerobic fitness is important for activities that require endurance, such as long-distance running, cycling, or swimming. It influences the body's ability to sustain physical effort over extended periods [21,22].

Jumping ability is a measure of an individual's explosive power and lower-body strength. It is relevant in activities like basketball, volleyball, or certain athletic events such as the long jump or high jump. Jumping ability is influenced by factors like muscle strength, power, and technique. Improving jumping ability can enhance performance in sports that require vertical leaps or quick upward movements [21,22].

The analysis shows us the following:

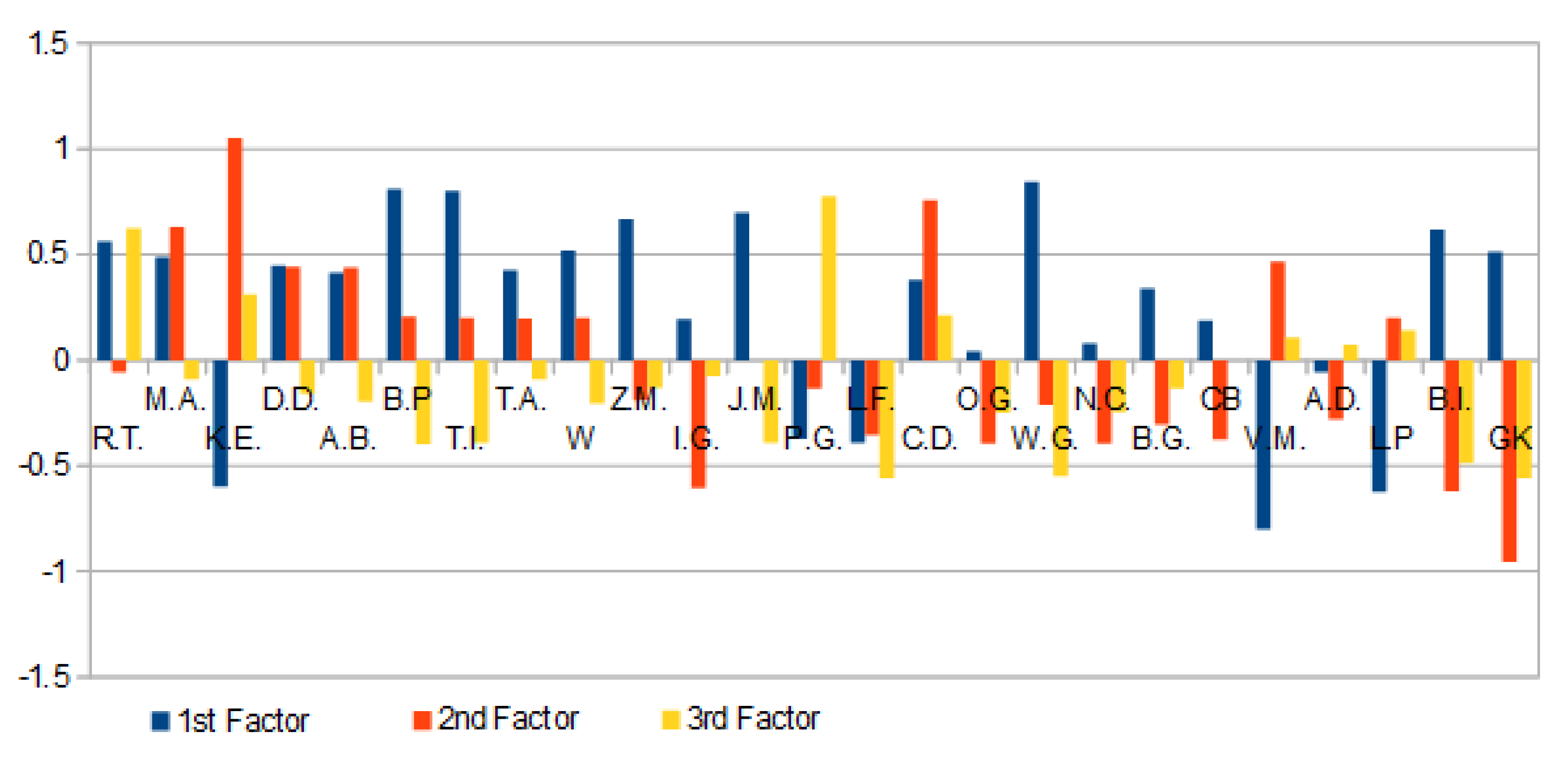
For the L.P. athlete, the aggregate performance (-0.28) was diminished mainly by the acceleration trial (-0.62), the better performances achieved at aerobics (0.20), and jumping (0.15) respectively hadn’t been enough to compensate the results of the first trial.

For the W. athlete, the overall performance was improved considerably (0.5) based mainly on the acceleration trial (0.51), then on the aerobics trial (0.20). The jumping trial performance (-0.20) might reflect fatigue or even some minor accident so we recommend reversing the trial order for this particular athlete to record better results.

For the B.P. athlete, the situation is similar to the W athlete (0.61 absolute difference), based mostly on the acceleration trial (0.81) and diminished only by the jumping trail (0.4). It also applies the reversal order of trials for better results as previously.

The results of the C.B. athlete were inconclusive, due to the number of trials taken (only two!).

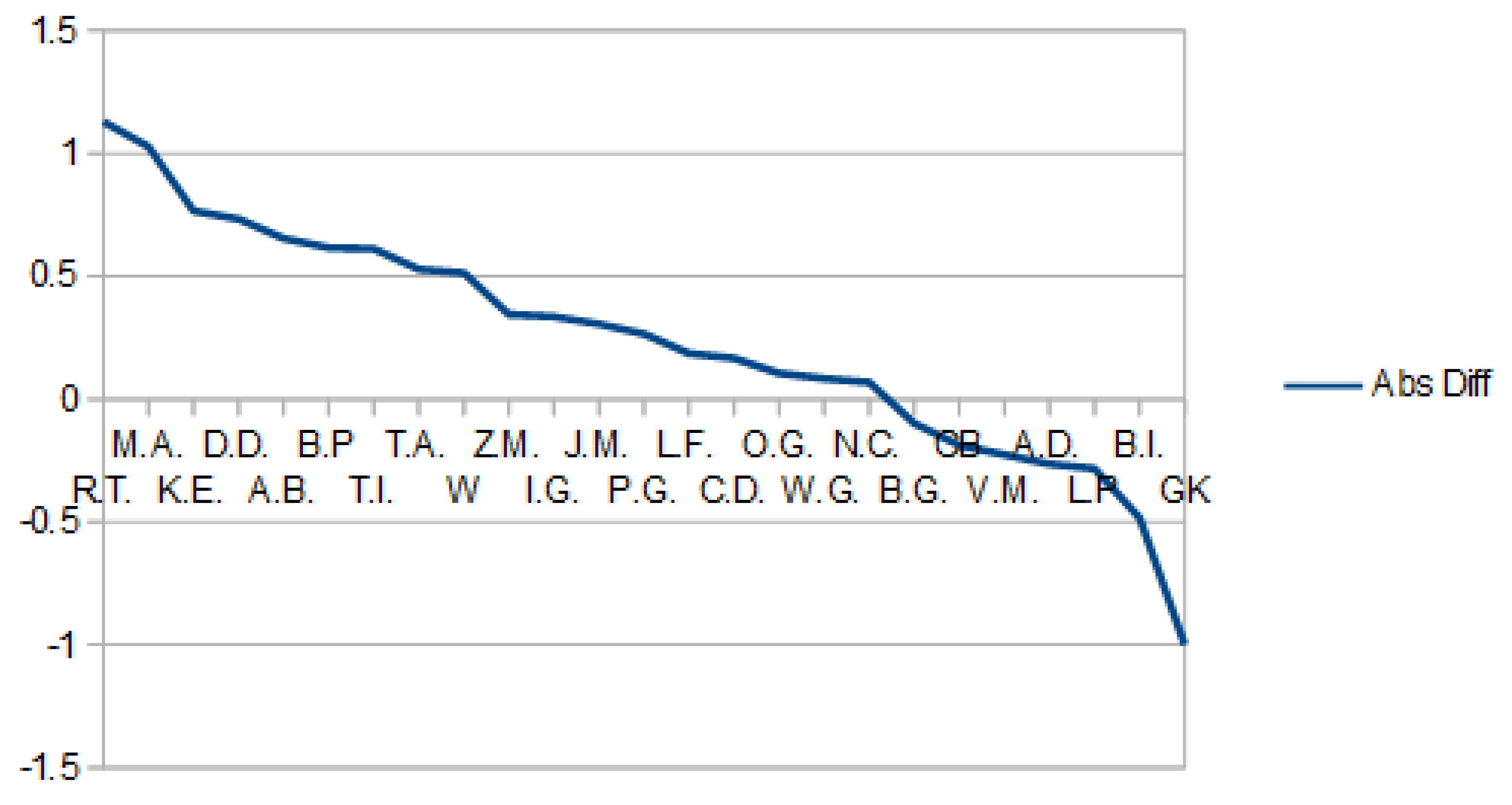
For the G.K. athlete the probability of some accident occurring is high, please see Figure 4, so the aerobics and jumping trials are poorly represented by -0.91 and -0.57, respectively (Figure 3):

The performance results per athlete may be seen in the next figure (Figure 4), based on the absolute modification due to the trial results in proportional influences:

To confirm the results of our research, we used the C-RT algorithm on our dataset with the athletes' results to generate a decision tree classifying and ordering the training factors based on their importance, and for this purpose, we will use the TanagraML system. Tanagra is open-source software for data mining that can be used for free for learning and research, being created by a professor (R. Rakotomalala,) at the University of Lyon, France.

Tanagra can only work with one database at a time, and it must be in the format of a text file containing on the first line the names of the database attributes, separated by the tab, and on the next lines the values of those attributes, one line for each record, as may be seen in Table 3:

The last column stands for the classifier parameter Class that takes True/Yes for the qualifying athletes and False/No for the athletes that failed the qualify for the World Cup. In TANAGRA almost all operations require defining the attributes to be used and how they will be used. This is done using the Define status operation, like in our example below (Table 4):

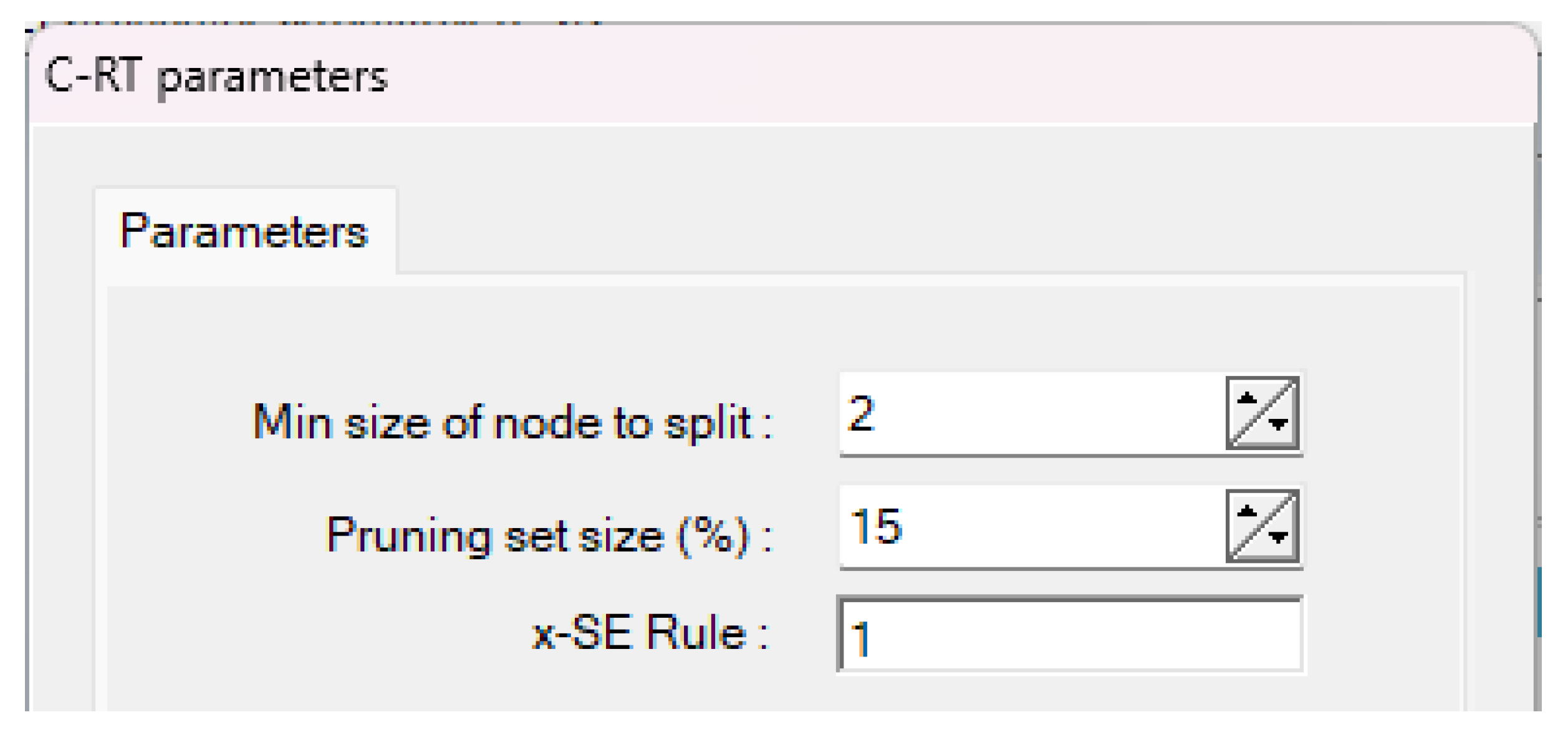
We want to generate the decision tree and calculate the classifier error rate on the test crowd, performing the following steps:

1. Choose from SPV learning operator C-RT;

2. Choose min size of the node to split=2;

3. Set the parameter Pruning size = 15%, as in the figure below (Figure 5):

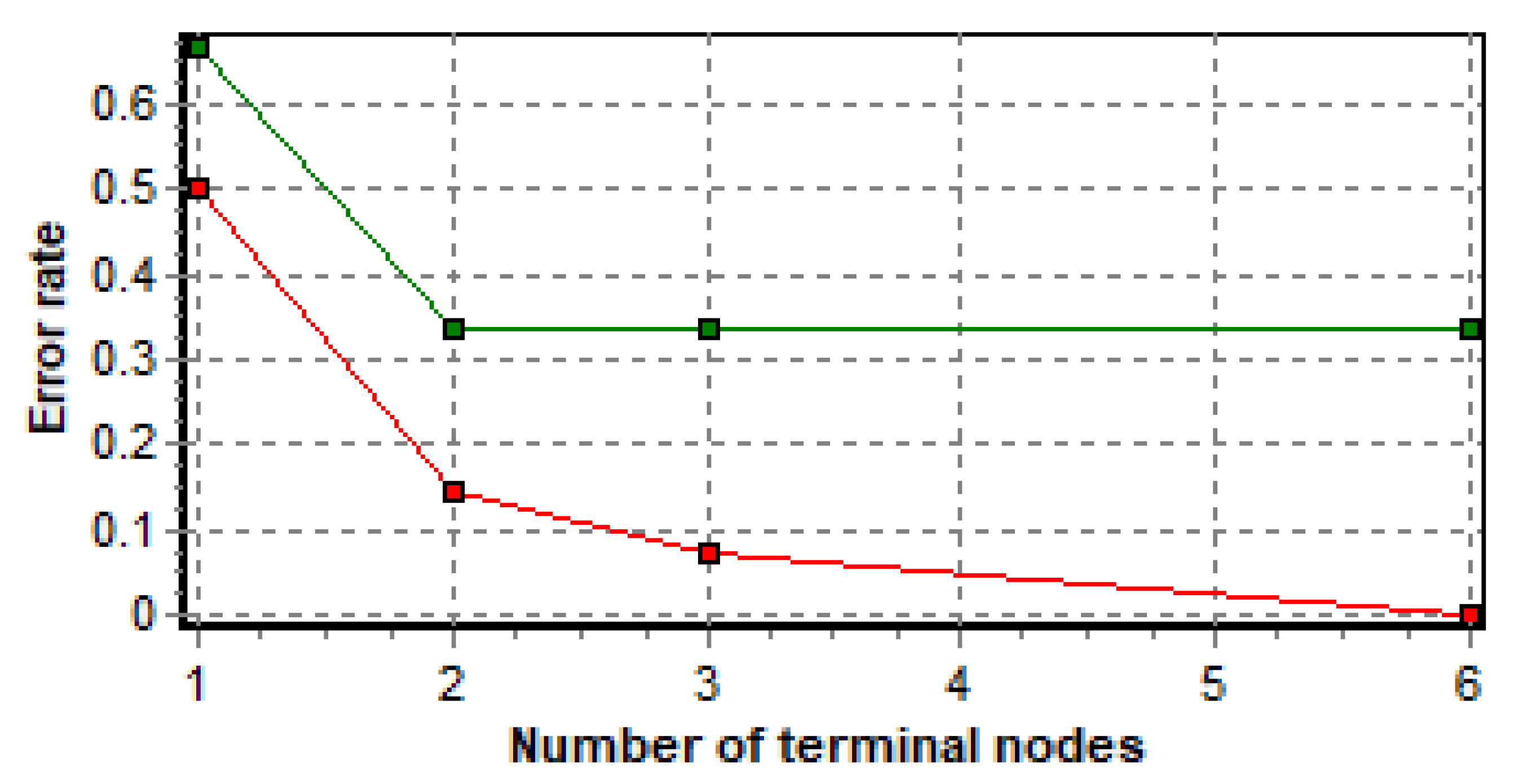
We obtained an error on the test set = 0.1765 that we consider negligible for the size of the result set, according to Table 5 and Figure 6:

It follows that for a length of less than 2.18m in the jumping probe none of the athletes qualifies, or Jumping < 2.1850 then Class = N (100% of 5 examples), according to Tanagra. Qualify for the World Cup approx. 8 out of 10 athletes who jump more than 2.18m, i.e.Jumping>= 2.1850 then Class = Y (77.78% of 9 examples).

To apply the results for the whole team of athletes (25), we choose Bayesian analysis. For this purpose, we need discrete values instead of continuous data for trials and we used the Quartile function for each attribute in this respect.

We set the first 17 records as training data set in Tanagra and we obtained the same error (0.1765) for classifier performance, so the loss in information due to the discretization of values is negligible.

Then we set the next 20 records for testing the classification error based on the training data set. This time, the error was significant (0.4) based mostly on the fact that we set the Play values to N by default, see Table 6:

We now have all the data classified so we can export the records to observe the qualified athletes (Table 7):

We could see that the results for athletes like Z.M., J.M., B.P., and T.I. seem to be inconclusive (2xY & 2xN), indicating that these athletes require further trials to qualify for the World Cup or that we should just maintain them as reserves.

To confirm the selected players, trial games are organized with national or international teams. If there are players who do not meet the selection criteria from the squad selected after all the tests, the squad will be reunited with other players selected but placed in the "reserve".

Handball is a complex game that requires players to adopt and develop aerobic and anaerobic capacities and several motor skills such as sprinting, jumping, flexibility, and acceleration, all of them being important parameters of the game and contribute to the high performance of the player and the team [20,21]. Only W. and B.P. athletes seem ready for a World competition, the rest of them needing more training and/or medical assistance. A well-rounded training program would typically incorporate exercises and activities to develop all three factors in a balanced manner, based on the specific goals and requirements of the individual.

6. Discussion

Beginning with the ES5 version, Javascript functional features increased significantly as it transitioned from an object-oriented language to a hybrid one. JS functions were first-class citizens even in previous versions, thus the function itself superseded the class notion used for gathering variables and methods alike, adopting even a constructor in that respect.

Pure functions, which assure no side effects, were one of the first functional features accepted in JS. Data is securely converted by value in this manner by one primitive or composite function into another.

The paper demonstrates how Javascript functional features and our statistical method can be utilized to analyze large amounts of data to uncover relevant information for athletes, trainers, and sports management about the athletes' competitiveness.

Handball is an intricate sport that necessitates athletes to develop their aerobic and anaerobic capacities, as well as a variety of motor abilities such as running jumping, mobility, and acceleration, all of which are important parameters of the game and contribute to the player's and team's high performance [21,22]. Essentially, the algorithm assists us in determining which competitors are ready for a sporting event and which require further preparation and/or medical care. A well-rounded workout regimen would normally include activities that seek to develop all three components equitably, based on the individual's objectives and needs.

7. Conclusions

ML analytics have grown in popularity across several sports in recent years since they give essential information about mental as well as physical wellness. A lot of athletes have discovered that using statistics throughout training may help them improve their athletic ability, lower their risk of trauma, and increase their general well-being. This study proposes to enhance handball players' performances by using a mechanism for assessing the effect of various tests on cumulative performance determined for every participant to be eligible for the World Cup.

When each action of each experiment is separated, the outcome is an extra impact created by the interplay of components or the concurrent action. That might explain why the neuro-muscular feedback loop is so important in handball motor motions.

Successful application of ML in handball requires access to quality data, appropriate algorithms, and expertise in implementing these technologies. Moreover, human judgment and expertise remain crucial in using AI as a supportive tool in handball rather than replacing human decision-making entirely.

8. Limitations

Certain limitations concerning the implemented code regarding the user’s platform, browser, and hardware are why we tried to keep it as simple and portable as possible, due to future adaptations that might be necessary. Our code was tested on several browsers (Chrome, IE, and Microsoft Edge) and Node execution environment, but to avoid any inconvenient, we recommend taking into consideration the following possible failures and coding improvements before installing and/or using our software, see (Table 8),:

Author Contributions

Conceptualization, L-G.T. and V.M.; methodology, V.M.; software, R.B.M.T.; validation, L-G.T., S.P.S., and R.B.M.T.; formal analysis, V.M.; investigation, R.B.M.T.; resources, L-G.T.; data curation, V.M.; writing—original draft preparation, R.B.M.T.; writing—review and editing, R.B.M.T.; visualization, V.M.; supervision, S.P.S; project administration, V.M. All authors have read and agreed to the published version of the manuscript.

Funding

"This research received no external funding”

Institutional Review Board Statement

"The study was conducted by the Declaration of Helsinki”

Informed Consent Statement

“Informed consent was obtained from all subjects involved in the study”

Conflicts of Interest

Declare conflicts of interest or state “The authors declare no conflict of interest.”

Appendix A

BEGIN

READ(a0,b0,c0,...,n0, a1,b1,c1,...,n1);

INT i = 0, n;

DOUBLE Sum = 0.0, iA = 0.0, iB = 0.0, iC = 0.0,..., iN = 0.0;

DOUBLE Pa[n], PA[n];

Sum = Sum + 1/(1 + (Pa.SUM()-Pa[i])*PA[i])

IF(i>0)

Sum = Sum + 1/(1 + (Pa.SUM()-Pa[i]-Pa[n-1])*PA[i])

i = i + 1;

WHILE(i<n)

iA = (1 + Sum) * Pa [0];

iB = (1 + Sum) * Pb [0];...

WRITE(iA);

...

END

Appendix B

const fs = require('fs');

const N = 3;

var iB = [];

var iC = [];

[...Array(3).keys()].map(x=>{iB.push(process.argv[x+2])});

[...Array(3).keys()].map(x=>{iC.push(process.argv[x+5])});

var Pa = [], pA = [], pB = [], pC = [], pD = [], pX = [[], [], []];

/**

* Calculates the Pa array

Pa [0] = (iC [0] - iB [0]) * iB [1] * iB [2];

Pa [1] = iB [0] * (iC [1] - iB [1]) * iB [2];

Pa [2] = iB [0] * iB [1] * (iC [2] - iB [2]);

/**

* Calculates the sum of the Pa array {sumPa}

let sumPa = [...Array(N).keys()].map(x=>Pa[x]).reduce((x,y)=>x+y);

/**

* Calculates the pA array

pA [0] = (iC [0] - iB [0]) * (iC [1] - iB [1]) * (iC [2] - iB [2]);

pA [1] = (iC [0] - iB [0]) * (iC [1] - iB [1]) * iB [2];

pA [2] = (iC [0] - iB [0]) * iB [1] * (iC [2] - iB [2]);

/**

* Calculates the pB array

pB [0] = (iC [0] - iB [0]) * (iC [1] - iB [1]) * (iC [2] - iB [2]);

pB [1] = (iC [0] - iB [0]) * (iC [1] - iB [1]) * iB [2];

pB [2] = iB [0] * (iC [1] - iB [1]) * (iC [2] - iB [2]);

/**

* Calculates the pC array

pC [0] = (iC [0] - iB [0]) * (iC [1] - iB [1]) * (iC [2] - iB [2]);

pC [1] = (iC [0] - iB [0]) * iB [1] * (iC [2] - iB [2]);

pC [2] = iB [0] * (iC [1] - iB [1]) * (iC [2] - iB [2]);

/**

* Calculates the pX array

[...Array(N).keys()].map(j=>

{

pX [0][j] = pA[j];//linia 1

pX [1][j] = pB[j];//linia 2

pX [2][j] = pC[j];//...

});

/**

* Calculates the Inf and Tot values

var Tot = 0.0;

[...Array(N).keys()].map(k=> {

let Sum = 0.0;

[...Array(N).keys()].map(l=> {

(l == 0) ? Sum += 1/sumPa * pX[k][l] : Sum += 1/(sumPa - Pa[l]) * pX[k][l];

});

let Inf = (1 + Sum) * Pa[k];

Tot += Inf;

console.log(`Diff. due to the ${k + 1} fact: ${Inf}`);

fs.appendFile('test.txt', Inf + '\t', function(err) {

if(err) {

return console.log(err);

}

});

console.log(`Abs diff.: ${Tot}`);

fs.appendFile("test.txt", Tot + '\n', function(err) {

if(err) {

return console.log(err);

}

});

References

Kuleto, V., Ilić, M., Dumangiu, M., Ranković, M., Martins, O.M.D., Păun, D., Mihoreanu, L.; Exploring Opportunities and Challenges of Artificial Intelligence and Machine Learning in Higher Education Institutions; Sustainability 2021, 13, 10424. [CrossRef]
Mihailescu, Nicolae.; Statisticasibazelestatistice ale econometriei, editia a 6-a; Ed. Transversal, 2021; ISBN:9786066051187.
Nor Safika Mohd Shafiee, Sofianita Mutalib. " Prediction of Mental Health Problems among Higher Education Student Using Machine Learning ", International Journal of Education and Management Engineering (IJEME), Vol.10, No.6, pp.1-9, 2020. [CrossRef]
Font, Roger et al.; Monitoring external load in elite male handball players depending on playing positions; Biology of sport vol. 38,3 (2021): 475-481. [CrossRef]
Ortega-Becerra, Manuel, et al.; Physical and Physiological Demands During Handball Matches in Male Adolescent Players; Journal of human kinetics vol. 72 253-263. 31 Mar. 2020, . [CrossRef]
Lemos a, Luís et al.; Sport-Specific Skills Differentiate Performance Levels Better Than Anthropometric or Physiological Factors in Beach Handball; Research quarterly for exercise and sport vol. 93,4 (2022): 682-687. [CrossRef]
Lemos b, Luís F, et al.; Physical fitness profile in elite beach handball players of different age categories; The Journal of sports medicine and physical fitness vol. 60,12 (2020): 1536-1543. [CrossRef]
Mohoric, U; Sibila, M.; Strumbelj, B.; Positional differences in some physiological parameters obtained by the incremental field endurance test among elite handball players; Kinesiology; Volume 53, Issue 1, Page3-11, 2021 . [CrossRef]
Skejø, Sebastian D et al.; Estimating Throwing Speed in Handball Using a Wearable Device; Sensors (Basel, Switzerland) vol. 20,17 4925. 31 Aug. 2020, . [CrossRef]
Hermassi, Souhail, et al.; Body Fat Is a Predictor of Physical Fitness in Obese Adolescent Handball Athletes; International Journal of Environmental Research and Public Health vol. 17,22 8428. 14 Nov. 2020, . [CrossRef]
Hammami, M et al.; Effects of high-intensity interval training and plyometric exercise on the physical fitness of junior male handball players; European review for medical and pharmacological sciences vol. 25,23 (2021): 7380-7389. [CrossRef]
Marshall, Brendan Michael, and Kieran Andrew Moran; Which drop jump technique is most effective at enhancing countermovement jump ability, "countermovement" drop jump or "bounce" drop jump?; Journal of sports sciences vol. 31,12 (2013): 1368-74. [CrossRef]
Ketterer, Jakob, et al.; Biomechanicalagreement between different imitation jumps and hill jumps in ski jumping; Scandinavian Journal of medicine & science in sports vol. 31,1 (2021): 115-123. [CrossRef]
Gonzalez-Conde, A.; Gonzalez-Devesa, D.; Suarez-Iglesias, D.; Ayan, C.; The validity and reliability of a portable device (ADR-Jumping) to estimate vertical jump performance; Proceedings of the Institution of Mechanical Engineers Part P - Journal of Sports, Engineering and Technology;2022. [CrossRef]
Patino-Palma, BE; Wheeler-Botero, CA; Ramos-Parraci, CA.; Validation and Reliability of The Wheeler Jump Sensor for the Execution of the Countermovement Jump; Apunts Educacion Fisicay Deportes, Issue 149m, Page37-44. [CrossRef]
McGhie, David, et al.; Strength Determinants of Jump Height in the Jump Throw Movement in Women Handball Players; Journal of strength and conditioning research vol. 34,10 (2020): 2937-2946. [CrossRef]
Galal El-Din, H., Zapartidis, I., & Ibrahim, H. A comparative study between talented young Greek and German Handball players in some physical and anthropometric characteristics. Biology of Sport, 28, (2011). 245-248.
Bělka, Jan, et al. Analysis of the Fitness Level in Elite Handball Players (U16 and U18) between 2003 and 2013. Journal of physical education and sport 16 (2016): 1381.
19. Abdullah Khanfor, Ye Yang; An Overview of Practical Impacts of Functional Programming Conference Paper; December 2017; URL: https://www.researchgate.net/publication/323714122. [CrossRef]
Fogus, M.; Functional JavaScript: Introducing Functional Programming with Underscore.js; O'Reilly Media; 1st edition (July 2, 2013); ISBN: 9781449360726.
Oxyzogloun, H.D., Oxyzoglou, N., Hatzimanouil, D., Iconomou, C., Ioannidis, T., Lazaridis, S., &Papadopoulus, K.; Evaluation of high-level handball players in morphological characteristics and various motor abilities by playing position; European Journal of Sports Medicine; 1(2), 21-28, (2014).
Swartz, E., & Bruce, L.; Balance Training for Neuromuscular Control and Performance Enhancement: A Call for More Research; Athletic Training and Sports Health Care; 3(4), 71-173; 2011. [CrossRef]
Code Explainer | CodePal - The Ultimate Coding Companion; URL: https://codepal.ai/code-explainer; (accessed on 6/19/2023).

Figure 1. The influence of the factor 'a'.

Figure 2. Functional data transformation in React, after [20].

Figure 3. The representation of the results obtained for trials by each athlete.

Figure 4. The aggregate influence of trial results on each athlete.

Figure 5. Supervised C-RT parameters in Tanagra.

Figure 6. Error rate according to the tree complexity.

Table 1. Suitability for programming languages in parallel distributed systems, after [19].

	Weak points	Strong points
OOP	verbosity	the simplicity eases the representation of many problems
		the numerous OOP tool suites
		a large number of programmers familiar with OOP
FP	purely FP only on large-scale software	writing programs using functional languages increases the security
	the lack of expert developers in this paradigm	mitigates security risks by forbidding the state changes
	the complexity and the cost of software design tasks	higher-order functions encourage and promote the reuse
	small changes may require an extensive restructuring of the program to meet these change	recursive calls promote the reuse of codes and functions
	a sophisticated module system	using frameworks
		immutable data structure results in an advantage for distributed systems
		no side effects.
IL	tend to be longer in lines of code
	the software cost and effort estimations
	mutable data structure -> changing of the semantics and the result of the execution

Table 2. Trials for Trials(85) for the 25 athletes.

Athlete	Acceleration	Aerobic fitness	Jumping
L.P.	1.98	1.75	1.96
	1.91	1.85	1.84
	1.81	1.8	2
W.	1.7	1.85	2.28
	1.7	1.95	2.3
	1.8	1.85	2.3
	1.83	1.95	2.19
	1.82	1.9	2.21
B.P.	1.74	1.8	2.21
	1.71	1.75	2.23
	1.98	1.8	2.22
	1.94	1.85	2.04
C.B.	1.8	1.8	2.21
C.B.	1.85	1.7	2.21
G.K.	1.91	1.75	2.18
	1.96	1.9	2.09
	2.01	1.55	2.02
V.M.	1.97	1.76	1.98
	1.95	1.84	1.84
	1.8	1.9	2.02
T.A.	1.7	1.85	2.24
	1.71	1.95	2.27
	1.8	1.75	2.3
	1.82	1.95	2.19
	1.8	1.9	2.21
T.I.	1.73	1.8	2.2
	1.7	1.75	2.23
	1.96	1.8	2.15
	1.93	1.85	2.04
O.G.	1.81	1.9	2.18
O.G.	1.82	1.8	2.21
B.I.	1.9	1.65	2.15
	1.94	1.8	2.09
	1.99	1.55	2.04
K.E.	1.97	1.65	1.96
	1.9	1.7	1.84
	1.81	1.85	2.04
M.A.	1.71	1.8	2.24
	1.73	1.95	2.3
	1.79	1.85	2.28
	1.81	1.9	2.19
	1.82	1.95	2.21
J.M.	1.74	1.8	2.2
	1.71	1.75	2.23
	1.98	1.85	2.15
	1.93	1.8	2.04
N.C.	1.81	1.85	2.22
N.C.	1.83	1.75	2.24
D.D.	1.9	1.75	2.15
	1.95	1.9	2.07
	2.01	1.85	2.1
P.G.	1.98	1.75	1.9
	1.9	1.85	1.84
	1.83	1.7	2.03
A.B.	1.72	1.8	2.28
	1.69	1.95	2.3
	1.76	1.85	2.2
	1.83	1.95	2.19
	1.81	1.9	2.21
W.G.	1.73	1.9	2.25
	1.75	1.85	2.15
	1.91	1.8	2.22
	1.94	1.85	2.04
A.D.	1.81	1.9	2.19
A.D.	1.79	1.8	2.21
B.G.	1.89	1.75	2.15
	1.91	1.8	2.09
	1.98	1.65	2.1
L.F.	1.96	1.8	1.97
	1.9	1.85	1.97
	1.84	1.7	2.02
R.T.	1.69	1.75	2.26
	1.7	1.85	2.3
	1.81	1.75	2.29
	1.83	1.85	2.19
	1.82	1.9	2.24
Z.M.	1.77	1.9	2.19
	1.72	1.75	2.23
	1.95	1.8	2.2
	1.94	1.85	2.15
I.G.	1.8	1.9	2.15
I.G.	1.85	1.75	2.24
C.D.	1.91	1.7	2.15
	1.93	1.85	2.09
	2.01	1.75	2.2

Table 3. Data source with the athletes' results for Tanagra ML System.

Athlete	1st Factor	2nd Factor	3rd Factor	Abs Diff
R.T.	0.561602	-0.05826	0.625511	1.128853
M.A.	0.487373	0.63038	-0.090031	1.027722
K.E.	-0.598061	1.0521	0.312252	0.766291
D.D.	0.448212	0.442453	-0.157728	0.732937
A.B.	0.413087	0.438226	-0.196942	0.654371
B.P	0.810156	0.20482	-0.398658	0.616318
T.I.	0.802255	0.201242	-0.391879	0.611617
T.A.	0.424977	0.196204	-0.092288	0.528893
W	0.518689	0.201253	-0.206124	0.513818
Z.M.	0.667222	-0.189027	-0.132534	0.345662
I.G.	0.195191	-0.605435	-0.074391	0.335854
J.M.	0.69768	0	-0.391994	0.305686
P.G.	-0.374326	-0.135353	0.775285	0.265606
L.F.	-0.390401	-0.353777	-0.558167	0.186011
C.D.	0.378511	0.756183	0.211294	0.166378
O.G.	0.040734	-0.394745	-0.248836	0.105175
W.G.	0.842533	-0.210876	-0.547741	0.083917
N.C.	0.079517	-0.394469	-0.246881	0.068071
B.G.	0.339526	-0.303481	-0.134463	-0.098418
CB	0.18785	-0.3757	0	-0.18785
V.M.	-0.800864	0.467144	0.107894	-0.225826
A.D.	-0.058101	-0.279109	0.072912	-0.264297
L.P	-0.623581	0.199601	0.141088	-0.282892
B.I.	0.618561	-0.620952	-0.485936	-0.483545
GK	0.512436	-0.954111	-0.55831	-0.999985

Table 4. Define the status table for parameters in Tanagra.

Attribute	Target	Input
Acceleration	–	yes
Aerobic fitness	–	yes
Jumping	–	yes
Class	yes	–

Table 5. Classifier performances in Tanagra.

Error rate			0.1765
Values prediction			Confusion matrix
Values	Recall	1-Precision		N	Y	Sum
N	0.75	0.1429	N	6	2	8
Y	0.8889	0.2	Y	1	8	9
			Sum	7	10	17

Table 6. pred_SpvInstance classifier performance.

Error rate			0.4000
Values prediction			Confusion matrix
Values	Recall	1-Precision		N	Y	Sum
N	0.5714	0.0588	N	32	24	56
Y	0.7778	0.7742	Y	2	7	9
			Sum	34	31	65

Table 7. The results after applying the Bayesian classification method.

Athlete	Acceleration	Aerobic	Jumping	Play	Type	pred
Athlete	Acceleration	Aerobic	Jumping	Play	Type	SpvInstance
L.P	fast	weak	short	N	training	N
L.P	fast	better	short	N	training	N
L.P	slow	good	short	N	training	N
W	slow	better	longer	Y	training	Y
W	slow	best	longest	Y	training	Y
W	slow	better	longest	Y	training	Y
W	fast	best	long	Y	training	Y
W	slow	better	long	Y	training	Y
B.P	slow	good	long	Y	training	Y
B.P	slow	weak	longer	Y	training	Y
B.P	fast	good	long	Y	training	N
B.P	fast	better	short	Y	training	N
CB	slow	good	long	N	training	Y
CB	fast	weak	long	N	training	N
GK	fast	weak	short	N	training	N
GK	fast	better	short	N	training	N
GK	fastest	weak	short	N	training	N
V.M.	fast	weak	short	N	test	N
V.M.	fast	good	short	N	test	N
V.M.	slow	better	short	N	test	N
T.A.	slow	better	longer	N	test	Y
T.A.	slow	best	longer	N	test	Y
T.A.	slow	weak	longest	N	test	Y
T.A.	slow	best	long	N	test	Y
T.A.	slow	better	long	N	test	Y
T.I.	slow	good	long	N	test	Y
T.I.	slow	weak	longer	N	test	Y
T.I.	fast	good	short	N	test	N
T.I.	fast	better	short	N	test	N
O.G.	slow	better	short	N	test	N
O.G.	slow	good	long	N	test	Y
B.I.	fast	weak	short	N	test	N
B.I.	fast	good	short	N	test	N
B.I.	fast	weak	short	N	test	N
K.E.	fast	weak	short	N	test	N
K.E.	fast	weak	short	N	test	N
K.E.	slow	better	short	N	test	N
M.A.	slow	good	longer	N	new	Y
M.A.	slow	best	longest	N	new	Y
M.A.	slow	better	longer	N	new	Y
M.A.	slow	better	long	N	new	Y
M.A.	slow	best	long	N	new	Y
J.M.	slow	good	long	N	new	Y
J.M.	slow	weak	longer	N	new	Y
J.M.	fast	better	short	N	new	N
J.M.	fast	good	short	N	new	N
N.C.	slow	better	long	N	new	Y
N.C.	fast	weak	longer	N	new	N
D.D.	fast	weak	short	N	new	N
D.D.	fast	better	short	N	new	N
D.D.	fastest	better	short	N	new	N
P.G.	fast	weak	short	N	new	N
P.G.	fast	better	short	N	new	N
P.G.	fast	weak	short	N	new	N
A.B.	slow	good	longer	N	new	Y
A.B.	slow	best	longest	N	new	Y
A.B.	slow	better	long	N	new	Y
A.B.	fast	best	long	N	new	Y
A.B.	slow	better	long	N	new	Y
W.G.	slow	better	longer	N	new	Y
W.G.	slow	better	short	N	new	N
W.G.	fast	good	long	N	new	N
W.G.	fast	better	short	N	new	N
A.D.	slow	better	long	N	new	Y
A.D.	slow	good	long	N	new	Y
B.G.	fast	weak	short	N	new	N
B.G.	fast	good	short	N	new	N
B.G.	fast	weak	short	N	new	N
L.F.	fast	good	short	N	new	N
L.F.	fast	better	short	N	new	N
L.F.	fast	weak	short	N	new	N
R.T.	slow	weak	longer	N	new	Y
R.T.	slow	better	longest	N	new	Y
R.T.	slow	weak	longer	N	new	Y
R.T.	fast	better	long	N	new	Y
R.T.	slow	better	longer	N	new	Y
Z.M.	slow	better	long	N	new	Y
Z.M.	slow	weak	longer	N	new	Y
Z.M.	fast	good	long	N	new	N
Z.M.	fast	better	short	N	new	N
I.G.	slow	better	short	N	new	N
I.G.	fast	weak	longer	N	new	N
C.D.	fast	weak	short	N	new	N
C.D.	fast	better	short	N	new	N
C.D.	fastest	weak	long	N	new	N

Table 8. Possible bugs and future improvements, after [23].

Possible bugs	Future improvements
The code assumes that iB and iC arrays have the same length.	Add input validation to ensure that the arrays and constants are valid.
The code may throw an error if calculateSumPa() returns 0.	Refactor the code to use more descriptive variable names.
The code assumes that N is equal to the length of iB and iC.	Add comments to explain the purpose of each function and variable.
If the iB and iC arrays do not have the same length, the code will throw an error.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer