Prerpints.org logo
Preprint
Article

Double-Constrained Consensus Clustering with Application to Online Anti-Counterfeiting

Altmetrics

Downloads

96

Views

28

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

01 August 2023

Posted:

03 August 2023

You are already at the latest version

Alerts
Abstract
Semi-supervised consensus clustering is a promising strategy to compensate for the subjectivity of clustering and its sensitivity to design factors, with various techniques being recently proposed to integrate domain knowledge and multiple clustering partitions. In this article we present a new approach that makes double use of domain knowledge, namely to build the initial partitions as well as to combine them. In particular, we show how to model and integrate must-link and cannot-link constraints into the objective function of a generic consensus clustering (??) framework that maximizes the similarity between the consensus partition and the input partitions, which have, in turn, been enriched with the same constraints. In addition, borrowing from the theory of functional dependencies, the integrated framework exploits the notions of deductive closure and minimal cover to take full advantage of the logical implication between constraints. Using standard UCI benchmarks, we found that the resulting algorithm, termed ??? (double-Constrained Consensus Clustering), was more effective than plain ?? at combining base constrained partitions. We then argue that ??? is especially well-suited to profiling counterfeit e-commerce websites, because constraints can be acquired by leveraging specific domain features, and demonstrate its potential for detecting affiliate marketing programs. Taken together, our experiments suggest that ??? makes the process of clustering more robust and able to withstand changes in clustering algorithms, datasets, and features, with a remarkable improvement of average performance.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Today, after many years of research, there are specialized clustering algorithms that can find groupings with complex contiguous shapes in data that were previously impossible to identify. However, it is well known that no single algorithm is suitable for all datasets because the groups may be similar or dissimilar for very different reasons. The diversity of approaches reflects the difficulty of providing a formal definition of clustering ([1,2]). This phenomenon has been concisely described with the expression `clustering is in the eye of the beholder’. The subjectivity issue is compounded by sensitivity to design factors. When clustering a dataset, we are confronted with a number of choices: the clustering algorithm family (e.g., hierarchical agglomerative clustering, k-means, spectral, density-based), the clustering family instance (e.g., the linkage method for hierarchical agglomerative clustering), the setting of clustering instance parameters (e.g., cutoff threshold), and the data features used for clustering. A change in any of these factors often results in large overall performance variations. The user must thus grupple with the dilemma of selecting appropriate techniques, parameters, and features, given the dataset to be investigated.
These inherent limitations have spurred explorations of ways to add other sources of evidence to the clustering process, beyond the paradigm of a single unsupervised algorithm. One line of research, termed ensemble clustering (or consensus clustering), has focused on merging multiple clustering partitions into a consensus partition that shares their common characteristics and is more robust than individual methods to changes and errors [3]. Another area of research, termed semi-supervised clustering, has investigated the use of a limited amount of domain knowledge such as cannot-link and must-link constraints in the clustering process, to find a solution that is more aligned with the user’s preferences (e.g., [4], with a focus on semi-supervised k-means algorithms, and [5], covering several clustering families ). While the two lines of research arose independently, in recent years we have seen several attempts to combine them, in an effort to retain the main advantages of each.
The semi-supervised ensemble clustering algorithms that have been proposed so far, reviewed in [6], exploit various combination strategies. Constraints have been used to create or select better ensemble members prior to their merging, or to find a better consensus partition from unenhanced given partitions, or to refine the consensus partition after its generation. However, constraints are usually employed to improve only one of the steps involved in the semi-supervised ensemble clustering process. Moreover, most approaches use constraints as is, without trying to infer more knowledge from them.
Our work was inspired by a desire to make the most of constraints, extending their use and understanding in the semi-supervised ensemble clustering process. In the proposed framework, the role played by constraints is twofold. First, they are used to enhance the generation of the base partitions. Second, the same constraints are used again to combine the enhanced base partitions. This combination strategy is depicted in Figure 1.
In this article we do not dwell on the generation of constrained base partitions. We assume that the base clustering algorithm or algorithms are equipped with a constraint-enhanced version and that their results are provided as an input. Our focus is on the merging of such results, aided by constraints, and on the benefits of the double use of constraints.
Building on the consensus clustering framework introduced in [7], which maximizes the similarity (based on the Probabilistic Rand Index) between a consensus partition and a set of given partitions,1 we modify its objective function to incorporate must-link and cannot-link constraints. Compliance with the given constraints is expressed in terms of the percentage of constraints that are satisfied by the consensus partition, modeling the logical implication between constraints by means of a deductive closure concept derived from the theory of functional dependencies. The resulting optimization problem is solved using a simple stochastic hill-climbing strategy, preceded by an ad hoc procedure for computing the deductive closure of the input constraints. The overall algorithm is termed CCC, which stands for (double-)Constrained Consensus Clustering. We also define a procedure to build a minimal cover for a set of constraints, useful for evaluation purposes.
We then present two experimental studies. In the first, conducted with standard UCI datasets, we found that using CCC was a marked improvement over merging the constrained base partitions with plain consensus clustering (CC). We also observed that the performance of CCC, measured as a function of the main clustering factors, was not only clearly better than the average performance of the base constrained partitions but also almost on par with their best performance, achievable for a specific combination of clustering feature and constrained base clustering algorithm on each dataset.
The second experimental study looked at web anti-counterfeiting. We applied CCC to the problem of detecting affiliate marketing programs behind fraudulent e-commerce websites. We argue that the interesting feature of this application domain is that constraints can be partly acquired in an automatic manner, thus making the overall approach more appealing and useful. The potential of CCC for discovering affiliate programs is demonstrated using a new test collection made available for re-use.
The main contributions of this article are the following.
  • We define a novel framework for semi-supervised consensus clustering that exploits constraints both to build the base partitions and to combine them through an optimization-based constrained consensus clustering algorithm. The framework has been implemented into a system named CCC.
  • We offer an analysis of the logical implications between constraints that helps optimize their use not only in CCC but in any clustering algorithm making use of must- and cannot-links constraints.
  • We present an experimental evaluation with the UCI datasets showing that the re-utilization of constraints within the consensus function that combines base constrained partitions is more effective than using unenhanced consensus clustering.
  • We demonstrate the potential of using CCC to analyze counterfeit web shops and detect affiliate programs. This is done through a comprehensive approach starting from raw data and including the automatic generation of constraints and experimentation with a new test collection made available for use.
The remainder of the paper is organized as follows. We first introduce the double-constrained consensus clustering framework: after providing some notation and background information, we formalize it as an optimization problem that exploits the logical implications between constraints, and provide a heuristic solution. In the next section, we describe the study conducted with UCI datasets, detailing its design, preparation, and findings. We then present the application of CCC to anti-counterfeiting activities on the web, involving experimental goals, the construction of the ground truth dataset, the selection of clustering features and base clustering algorithms, the automatic acquisition of constraints, and an analysis of findings. Next, we discuss related work, splitted into two main themes: semi-supervised ensemble clustering and clustering fraudulent websites. In the last section, we offer some conclusions.

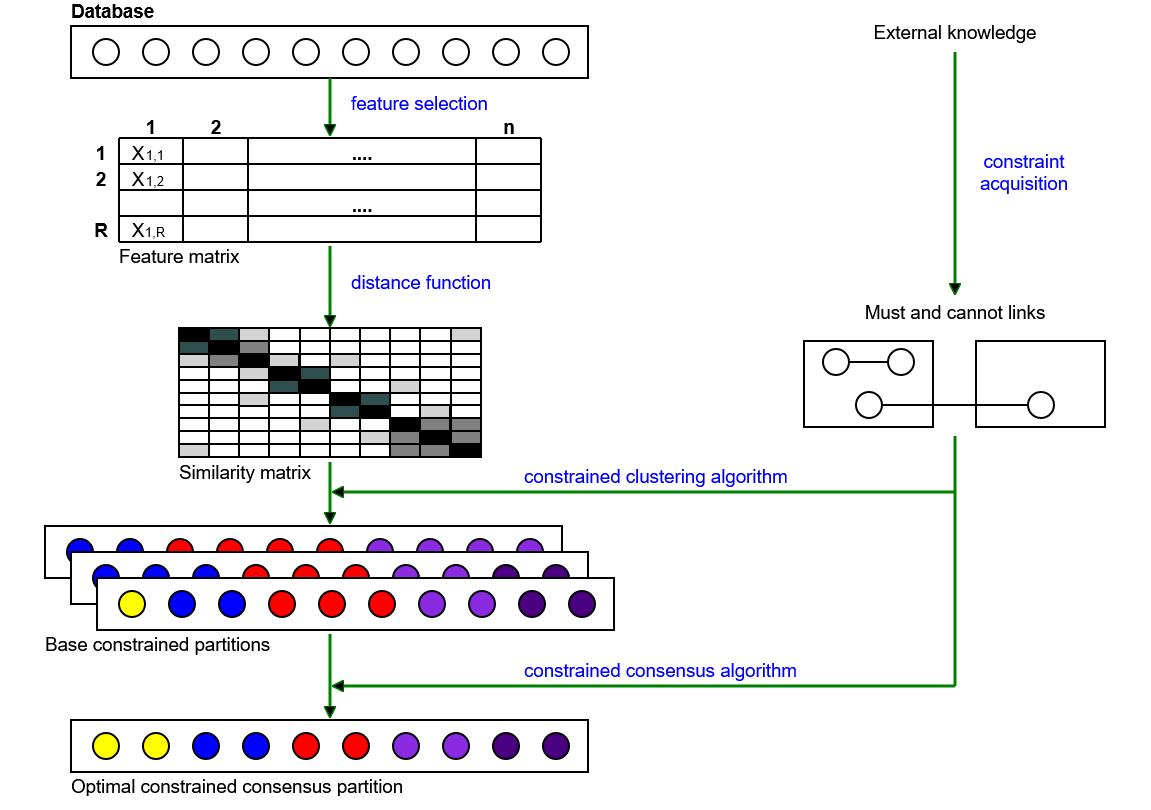
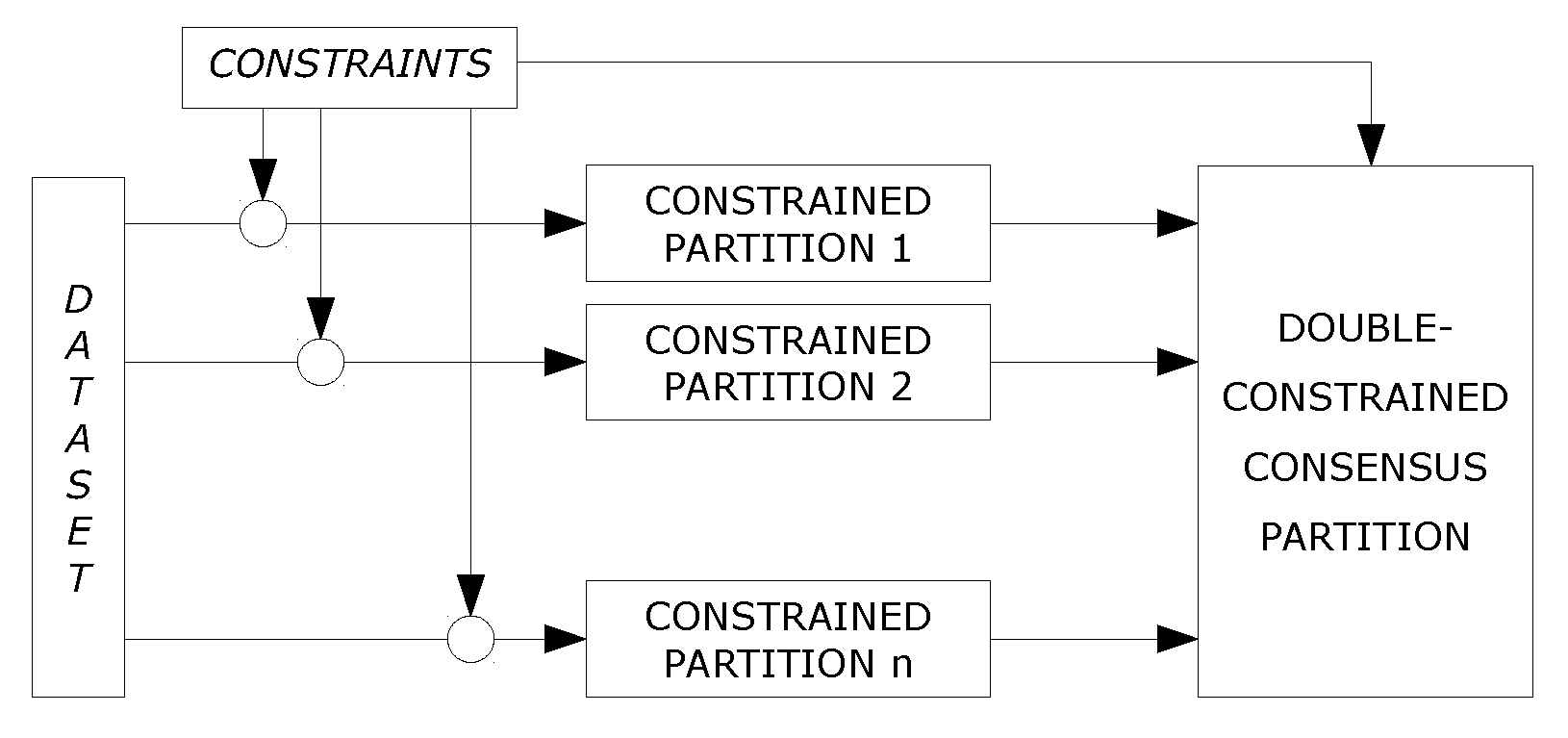
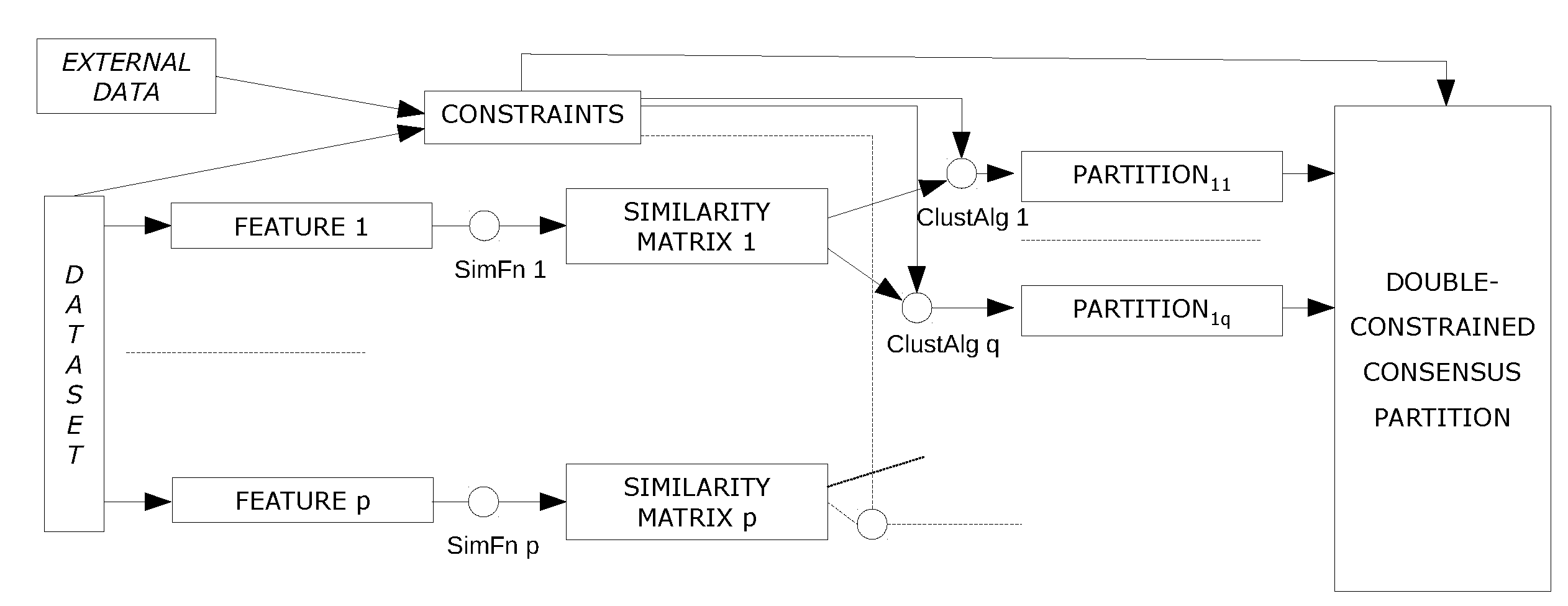
2. Double-constrained consensus clustering framework

2.1. Notation and background

Given a set O of n objects O = { o 1 , . . . o n } , a partition Π = { π 1 , . . . π m } of O is a grouping of the elements of O into m non-empty subsets (or clusters), in such a way that every element is included in one and only one of the subsets; i.e, ⋃ i = 1 m π i = O and π i ∩ π j = ∅ , for 1 ≤ i ≠ j ≤ m .
The similarity between two different partitions is key to consensus clustering. One of the best-known similarity strategies is the Rand index [8], which measures the agreement among the decisions made by the two partitions on individual pairs of objects. Given two partitions of O to compare, Π 1 = { π 1 , 1 , . . . π 1 , m 1 } and Π 2 = { π 2 , 1 , . . . π 2 , m 2 } , the Rand index ( R I ) is defined as:
R I = n 11 + n 00 n 00 + n 01 + n 10 + n 11 = n 11 + n 00 n 2
where
  • n 11 : number of pairs of objects that are in the same cluster in both Π 1 and Π 2 ,
  • n 00 : number of pairs of objects that are in different clusters in both Π 1 and Π 2 ,
  • n 10 : number of pairs of objects that are in the same cluster in Π 1 but in different clusters in Π 2 ,
  • n 01 : number of pairs of objects that are in different clusters in Π 1 but in the same cluster in Π 2 .
Intuitively, one can think of n 11 + n 00 as the number of agreements between Π 1 and Π 2 , and n 10 + n 01 as the number of disagreements between Π 1 and Π 2 . The Rand index has a value between 0 (i.e., no agreement on any pair of objects, which happens only when one partition consists of a single cluster while the other consists only of clusters containing single objects) and 1 (i.e., when the two partitions coincide).
The problem with Rand and other pair counting-based indices such as the Adjusted Rand Index [9] is that the individual contribution of the different types of agreements and disagreements to the overall similarity is the same, even when there is a high probability that they occurred by chance. The Probabilistic Rand Index (PRI), introduced in [7], further analyzed in [10], and recently made available for use at https://github.com/gianniromano8/Probabilistic-Rand-Index is based on the observation that as the number of cluster grows, the likelihood for a pair of objects being placed in the same cluster decreases, while at the same time the likelihood of being placed in different clusters increases. Using the PRI, agreements and disagreements are inversely weighted with the probability of their occurring by chance:
P R I = w 11 · n 11 + w 00 · n 00 w 00 · n 00 + w 01 · n 01 + w 10 · n 10 + w 11 · n 11
In Equation 2, the weights are estimated with the self information (i.e., w 11 = − log 2 p 11 , w 00 = − log 2 p 00 , ...) and the probabilities are expressed as a function of the number of clusters in each partition:
  • p 11 = 1 m 1 · 1 m 2 ,
  • p 00 = m 1 − 1 m 1 · m 2 − 1 m 2 ,
  • p 10 = 1 m 1 · m 2 − 1 m 2 ,
  • p 01 = m 1 − 1 m 1 · 1 m 2 .

2.2. Constrained consensus clustering as an optimization problem

A very common and general approach to consensus clustering consists of casting it as an optimization problem, where the objective is to find a consensus partition Π o p t such that the similarity Ψ between Π o p t and q base partitions Π 1 , Π 2 , . . . , Π q built by q base clustering algorithms is maximal:
Π o p t = arg max Π Ψ ( Π , Π 1 , . . . , Π q )
The objective function Ψ can be defined in terms of a pairwise similarity measure:
Ψ ( Π , Π 1 , Π 2 , . . . , Π q ) = 1 q ∑ r = 1 q P R I ( Π , Π r )
Here we use the PRI because it is more reliable than the RI, especially when, as in many domains of interest including online anti-counterfeiting, the number of clusters to find may be high. Following [11], we now assume that background knowledge is given in the form of pairwise constraints that indicate whether two objects should be in the same cluster or not. This form of supervision is more realistic than providing class labels in many applications, and is also more general: a set of classified points implies an equivalent set of pairwise constraints, but not vice versa [12]. Specifically, we assume that we are given a set of must-link constraints M L , where ( i , j ) ∈ M L indicates that objects o i and o j should be in the same cluster. Similarly, we are given a set of cannot-link constraints C L , where ( i , j ) ∈ C L indicates that objects o i and o j should be in different clusters. By Π ( i ) = k and Π ( i ) ∉ k , we denote, respectively, that in partition Π object o i is, or is not, an element of cluster π k . The two sets of constraints may be exploited by the base clustering algorithms to generate constrained base partitions as an input. This is our reference scenario, but the consensus clustering framework can also be applied to unconstrained base partitions.
We can then use the provided constraints to modify our objective function. One possibility is to require that the consensus partition should strictly respect the constraints, which would lead to the following optimization problem:
Maximize 1 q ∑ r = 1 q P R I ( Π , Π r ) s u b j e c t t o Π ( i ) = Π ( j ) , ∀ ( i , j ) ∈ M L ; Π ( i ) ≠ Π ( j ) , ∀ ( i , j ) ∈ C L
However, this formulation does not allow for exceptions: all the constraints must be satisfied. Such a requirement is, in general, not the best choice [13], and in our case it may further complicate the search for an admissible consensus partition because the input partitions do not necessarily satisfy the given constraints. It seems more convenient to use soft constraints, where compliance is rewarded but violation is still allowed. Maximizing both the similarity to the input partitions and the compliance with constraints naturally leads to the following form of objective function, where the second addend is the percentage of the given constraints that are satisfied by the (constrained) consensus partition :
1 q ∑ r = 1 q P R I ( Π , Π r ) + ∑ ( i , j ) ∈ M L I [ Π ( i ) = Π ( j ) ] + ∑ ( i , j ) ∈ C L I [ Π ( i ) ≠ Π ( j ) ] | M L | + | C L |
In the above expression, I is an indicator function having the value 1 if the enclosed expression is true and 0 otherwise, while M L and C L refer to the constraints provided as an input. We now have to consider the fact that constraints are not independent. In a set of given constraints, some of them may be logically implied by others, while there may also be constraints not in the set that can be derived from those in the set. This issue affects the actual compliance of the consensus partition with the initial constraints, extending their usefulness in the clustering process through implicit constraints. In the next section we will see how to refine the second addend in expression 6, based on the logical properties of constraints.

2.3. Analysis of constraints

First of all, consider the number of constraints associated with n objects and m partitions. There may be at most n ( n − 1 ) 2 constraints, one for each possible pair of objects (this bound is independent of m). Let us denote this set with C. By analogy with the theory of functional dependencies, the logical implication between constraints can be characterized by two axioms (or inference rules):
transitivity
if Π ( i ) = Π ( j ) and Π ( j ) = Π ( l ) , then Π ( i ) = Π ( l )
composition
if Π ( i ) = Π ( j ) and Π ( j ) ≠ Π ( l ) , then Π ( i ) ≠ Π ( l )
The deductive closure of a set of constraints is then the complete set of all possible constraints that can be derived from the given set using the inference rules. We can now modify the second addend in expression 6 to take into account all the constraints provided as an input, whether explicitly or implicitly. It suffices to compute the deductive closure of the input constraints, denoted by D e d ( { M L } ∪ { C L } ) , and then use all the constraints in it to compute the numerator and the denominator in expression 6. The objective function to be maximized becomes:
Ψ c ( Π , Π 1 , . . . , Π q , M L , C L ) = 1 q ∑ r = 1 q P R I ( Π , Π r ) + ∑ ( i , j ) ∈ M L * I [ Π ( i ) = Π ( j ) ] + ∑ ( i , j ) ∈ C L * I [ Π ( i ) ≠ Π ( j ) ] | D e d ( { M L } ∪ { C L } ) |
where by M L * and C L * we indicate, respectively, the set of must-link and cannot-link constraints in D e d ( { M L } ∪ { C L } ) .
An optimal constrained consensus partition Π c o p t is then given by:
Π c o p t = arg max Π Ψ c
The dependencies between constraints also naturally leads to the definition of minimal cover, which will be useful to characterize the behavior of clustering algorithms as the number of constraints varies. A minimal cover M of C is a set of constraints such that: (i) M is equivalent to C (i.e., it is possible to generate C from M by means of repeatedly applying the axioms to constraints in M), and (ii) we cannot remove any constraint from M and still have a set of constraints that are equivalent to C.
A minimal cover of the whole set of constraints associated with n objects partitioned into m clusters can be easily constructed using the following procedure. For each cluster in the partition, we need to express two properties. The first is that all objects in the cluster are coclustered (this requires by transitivity as many must-link constraints as the number of objects in the cluster minus one). The second is that the objects in the cluster cannot be coclustered with the objects in each of the remaining clusters (this requires, by composition, as many cannot links as all the possible pairs of m clusters). This minimal cover has thus a size of n − m + m ( m − 1 ) 2 = n + m ( m − 3 ) 2 . Different minimal covers of the same size can be constructed by choosing the objects involved in the n − m must-link and m ( m − 1 ) 2 cannot-link constraints in alternative ways. These are the smallest minimal covers associated with n objects partitioned into m clusters.
As an illustration, consider a set of five objects { o 1 , o 2 , o 3 , o 4 , o 5 } with three input constraints: Π ( 1 ) = Π ( 2 ) , Π ( 2 ) = Π ( 3 ) , and Π ( 3 ) ≠ Π ( 4 ) . We can derive three logically implied constraints: Π ( 1 ) = Π ( 3 ) , by transitivity, and Π ( 1 ) ≠ Π ( 4 ) , Π ( 2 ) ≠ Π ( 4 ) , by composition. This situation is depicted in Table 1, where the symbols 1 and -1 indicate, respectively, must-link and cannot-link constraints, and the implied constraints are shown in bold. The six constraints are the deductive closure of the three input constraints. Now we turn to the minimal cover associated with a partition. There are two possible partitions of the five objects consistent with the given constraints: Π 1 = { ( o 1 , o 2 , o 3 ) , ( o 4 ) , ( o 5 ) } , Π 2 = { ( o 1 , o 2 , o 3 ) , ( o 4 , o 5 ) } . According to the constructive procedure described above, a (smallest) minimal cover for Π 1 is given by two must-link constraints associated with its first cluster (e.g., Π ( 1 ) = Π ( 2 ) , Π ( 2 ) = Π ( 3 ) ) and by one cannot-link constraint for any pair of the three clusters in the partition; e.g., Π ( 1 ) ≠ Π ( 4 ) for clusters one and two, Π ( 1 ) ≠ Π ( 5 ) for clusters one and three, and Π ( 4 ) ≠ Π ( 5 ) for clusters two and three. In all, we get 5 constraints. A different minimal cover for Π 1 , among many others, is given for instance by { Π ( 1 ) = Π ( 2 ) , Π ( 1 ) = Π ( 3 ) , Π ( 2 ) ≠ Π ( 4 ) , Π ( 2 ) ≠ Π ( 5 ) }. As for Π 2 , a minimal cover can be produced by taking, in addition to two must-link constraints associated with its first cluster, one must-link constraint associated with its second cluster and one cannot-link constraint for the (sole) pair of clusters in the partition. In this case, we get a minimal cover of size 4. One possible minimal cover for P2 is Π ( 1 ) = Π ( 2 ) , Π ( 2 ) = Π ( 3 ) , Π ( 4 ) = Π ( 5 ) , Π ( 1 ) ≠ Π ( 4 ) .
We would like to highlight that these remarks on the logical implication of constraints are not limited to the CCC framework: they hold true for any clustering algorithm making use of must-link and cannot-link constraints. Finding a minimal cover has also a practical importance for designing well-founded performance evaluation of constrained clustering algorithms, as will be seen later, because it allows us to experiment with a small set of constraints encoding all the available information, while at the same time ensuring that there are no implicit redundancies with constraints already seen. To our knowledge, this aspect has been neglected so far in experimental studies involving constraints. Finally, it is worth noting that in the experiments described later we ended up generating a (larger) minimal cover of C in a more realistic manner than the deterministic selection of constraints, namely by incrementally adding new randomly chosen constraints that are non-redundant to the set of current constraints.

2.4. A heuristic solution

The input of the algorithm is a set of objects, a set of constrained partitions of the objects, and two sets of constraints (must-links and cannot-links). Its output is an optimal double-constrained consensus partition of the objects. Note that, unlike most semi-supervised ensemble clustering algorithms, the input partitions may have a different number of clusters and CCC does not require the number of clusters in the consensus partition as an input parameter.
The first step of the algorithm is the computation of the deductive closure of the input constraints, based on the inference rules introduced in Section 2.3. We examine one constraint at a time and incrementally update the current set of holding constraints. If the new constraint is a must-link between objects iand j, then we create a new must-link between any object coclustered with i and any object coclustered with j and, in addition, we create a cannot-link between any object that cannot be coclustered with i and any object that cannot be coclustered with j. If the new constraint is a cannot-link between objects iand j, then we create a cannot-link between any object co-clustered with i and any object coclustered with j. With the deductive closure, it is possible to calculate the value of the objective function (expression 7) for any set of partitions and constraints. The next step is to find an optimal partition.
We used a simple, efficient stochastic hill-climbing strategy, as done in [14] and [7] for similar objective functions not enriched with constraints. It consists of starting with a partition and iteratively moving a single object to a different (possibly empty) cluster until the objective function (expression 7) associated with the newly created partition and with the given set of constraints increases. This procedure is very efficient and experimentally generates good approximate solutions. We checked that using alternative meta-heuristic optimization strategies [15] that are, in principle, more powerful to avoid local optima, such as simulated and quantum annealing, did not produce better results. These findings are analogous to those reported in [14] and [7].
In the implementation made for the CCC algorithm, the seed (initial) partition is the input partition with the highest similarity value with the given partitions, successors are selected randomly, and the computation is halted after testing all possible n m successors for the current partition. These choices were made after extensive experimentation with other possible ways of choosing the seed partition, such as emphasizing its compliance with constraints, as well as with different termination criteria, such as random-restart hill climbing. The full algorithm is described in Table 2.

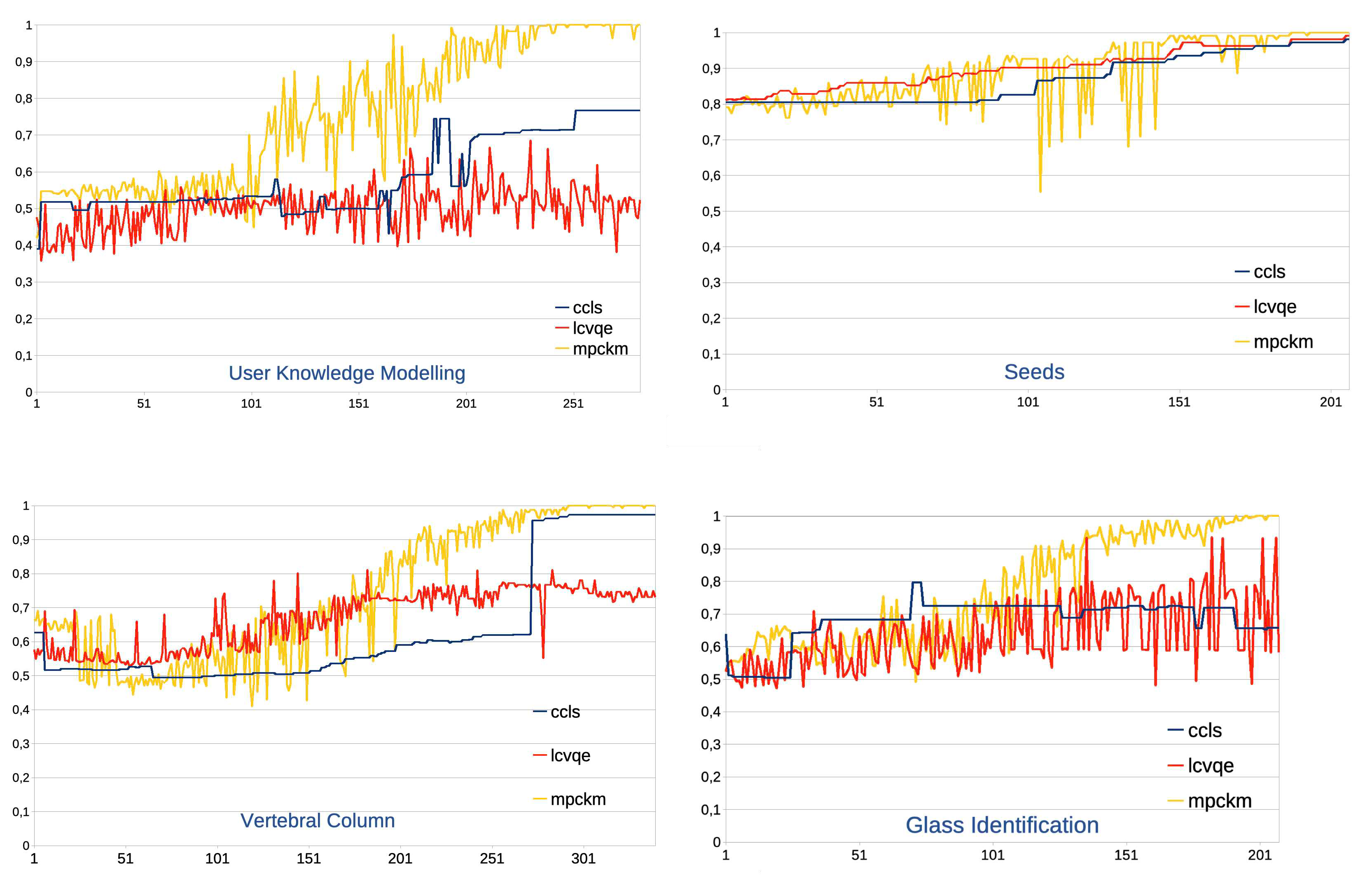
3. Experimenting with UCI datasets

3.1. Design and preparation

The goal of the first experimental study was to evaluate the performance of CC and CCC when applied to a set of constrained clustering algorithms, in comparison to the performance of the single constrained clustering algorithms. We use standard algorithms and datasets. For the choice of algorithms, we relied on the k-means family, partly because it is well understood and commonly used, and partly because the constrained versions of its members have been made available online. We selected three semi-supervised k-means algorithms in the conclust R package:2 lcvqe [16], mpckm [12], and ccls [17]. All of them accept a list of objects, the number of clusters, and two lists of must-link and cannot-link constraints as input, and they output a partition of the objects using specific clustering models. The package contains a fourth algorithm, ckmeans [11], but we did not include it in the set of base algorithms because it could not process the UCI datasets used for the experiments and described below.
For the datasets, the aim was to experiment with a varying number of objects, attributes, and classes. However, our choice of data was also determined by the characteristics of the three base clustering algorithms, which require integer or real attributes and do not support extensive experimentation with a large number of objects and attributes, due to their inherent computational complexity. We selected four classical UCI datasets (Glass Identification, Seeds , User Knowledge Modeling, and Vertebral Column). Each dataset was then enriched with an ordered set of pairs of constraints, as detailed below. Each pair in the set contains a must-link and a cannot-link constraint, such that they cannot be deduced from the links in the preceding pairs. The set of constraints was built incrementally: at each step we added a pair not implied by the current set of constraints, through iterative random selection of must-links and cannot-links from the dataset. The procedure halts when it is not possible to find new non-redundant links, eventually producing a cover of the whole set of constraints associated with the dataset. It is worth noting that implication rules rarely apply at the beginning of this process. For instance, during the construction of the cover for the User Knowledge Modeling dataset, the first implied must-link constraint occurred in position 15.
Table 3 shows the main features of each dataset and also reports the number of must-links and cannot-links in the cover, as well as the total number of must-links and cannot-links generated by the cover. Note that the sum of the total number of must-links and cannot-links is equal to the total number of constraints given by all possible pairs of objects in the dataset. For instance, the cover of Glass Identification contains 208 must-links and 208 cannot-links (in this case there are as many must-links as cannot-links, but the number of must-links and cannot-links present in a cover will, in general, not coincide), from which it is possible to generate 5921 must-links and 16870 cannot-links. Their sum (i.e., 22791) is equal to the total number of constraints associated with the objects in the dataset (i.e., 214 ( 214 − 1 ) 2 ), while the size of the smallest minimal cover (see Section 2.3) is 214 + 6 ( 6 − 3 ) 2 = 223 .
In order to assess how good the five clustering algorithms (i.e., the three base algorithms plus C C and C C C ) were at recovering the classes of the UCI datasets, we used the well-known F measure, thoroughly discussed in [18] together with related cluster validity metrics. The F measure is the harmonic mean of precision and recall:
F = 2 P x R P + R
with
P = T P T P + F P , R = T P T P + F N
where TP, FP, and FN are, respectively, the number of true-positives (i.e., two objects of the same class assigned to the same cluster), false-positives (i.e., two objects of different classes assigned to the same cluster), and false-negatives (i.e., two objects of the same class assigned to different clusters).

3.2. Results

We first studied the behavior of the single base clustering algorithms with respect to the number of constraints. For each dataset, we ran the three algorithms using the set of constraint pairs associated with the dataset (produced as described in the preceding section). More specifically, growing subsets of pairs were provided as an input to each algorithm, by taking the pairs in their order until the last pair in the set. We consider the full spectrum of constraints rather than only a small percentage, as usually reported in earlier studies, because this results in a better understanding of potential and limitations of constraints to aid in the clustering process. Clustering effectiveness was measured with the F measure.
The results are shown in Figure 2. There are four charts, one for each dataset. Each point on the x axis of a chart refers to a set of constraint pairs, from the set with one pair (containing one must-link and one cannot-link) to the set that is as large as the cover of the specific dataset of the chart, as detailed in Table 3. The four charts thus have different X-axis scales. It is worth noting that the point with zero constraints is not depicted because the three clustering algorithms used were not run with an empty set of constraints.
Figure 2 suggests that, in general, performance increases as more constraints are seen, although with frequent ample oscillations and with modest overall gains in performance for some combinations of clustering algorithms and datasets. These findings are consistent with those reported in [19] for a restricted percentage of constraints. However, rather surprisingly, even applying 100% of constraints, only one algorithm achieves the maximum performance in all datasets, with the other two algorithms not performing particularly well on some datasets. The likely explanation is that at least some of these algorithms disregard the implication issue, thus not taking full advantage of constraints.
Aside from absolute results, we are interested in the relative performance of the three algorithms. Figure 2 shows that it is deeply affected by the specific dataset and by the number of constraints used. In detail, mpckm generally performed best with a very large number of constraints, while with fewer constraints it achieved the worst results for many data points on Seeds and Vertebral Column due to its ample oscillations. Also, lcvqe got very good results (without dropping spikes) on Seeds and, for a more limited range of constraints, on Vertebral Column, but it performed badly for most data points on User Knowledge Modeling and Glass Identification. Finally, ccls struck a better balance between good and bad results due to its greater stability, although it got the best results only for some data points on Glass Identification.
Having seen that there is no single best algorithm across different datasets and sets of constraints, the question arises as to whether it is possible to mitigate the inherent lack of robustness of individual algorithms and to improve their average effectiveness through consensus clustering techniques. We will now address this issue.
For each dataset and for each set of constraint pairs associated with it, we computed the three (constrained) partitions generated by the clustering algorithms, then used them as an input to both C C and, together again with constraints, to C C C . In all, we computed 5 x ( 208 + 207 + 282 + 340 ) = 5 , 185 partitions. Figure 3 shows the performance of CC and CCC as a function of the number of constraints. To make the results across datasets with different constraint sizes comparable, the X axis is the number of constraints expressed as a percentage.
Our first observation is that C C is between the mean and the maximum of the base algorithms. It outperformed the base algorithm mean (except for one data point, with 20% of constraints), often by a clear margin, but it did noticeably worse than the maximum performance of base algorithms no matter the set of constraints, especially for a large number of them. This is consistent with the findings reported in [7], because in this case we have, at least for a large number of constraints, two similar base clusterings (according to PRI) with lower effectiveness (i.e., ccls and lcvqe) and one dissimilar base clustering with higher effectiveness (i.e., mpckm).
Apart from the behavior of C C , the main finding indicated in Figure 3 is the superior performance of C C C . Not only did it consistently outperform C C (and thus than the mean performance of base algorithms), with spectacular improvements on almost all data points, but it was also almost on par with the maximum performance of the base algorithms. In particular, it achieved very similar results to that of the best base algorithm for most data points, while it was worse for 20% and 50% and (slightly) better for 40%. We also conducted a paired-t-test to see the statistical significance of the difference of the means for each of the 40 entries (i.e., 10 constraint sizes by 4 datasets) that had values from the five algorithms. This analysis confirmed that the difference between C C C and C C was statistically significant, while the difference between the maximum performance of the base algorithms and C C C was not statistically significant.
These findings suggest that C C C performs similarly, on average, to that obtained by choosing the best algorithm for each data point individually (characterized by a specific dataset and number of constraints), without advance knowledge of the relative performance of the available clustering algorithms in each experimental setting. C C C was thus an effective way of increasing the robustness of constrained clustering with respect to the choice of clustering algorithms and datasets, across the full spectrum of input constraint sizes. It is also important to highlight that the gains achieved by C C C were obtained from a strong baseline with semi-supervised base algorithms, thus yielding a notable absolute performance of the overall constrained clustering process.
If we look at the improvement of C C C over C C , we see that the use of constraints made it possible to overcome one main limitation of C C , namely its inability to properly handle a set of base algorithms in which there is one very effective algorithm that is dissimilar to the other base algorithms. Consider the objective function of expression 7 in this situation: as more and more constraints are seen, the small-valued inter-similarity addend of a candidate partition similar to the spurious base clustering can be counterbalanced by its large-valued performance addend, thus promoting the partition. This is yet another advantage of using the constraints in the consensus clustering function, beyond their utilization in the base algorithms.

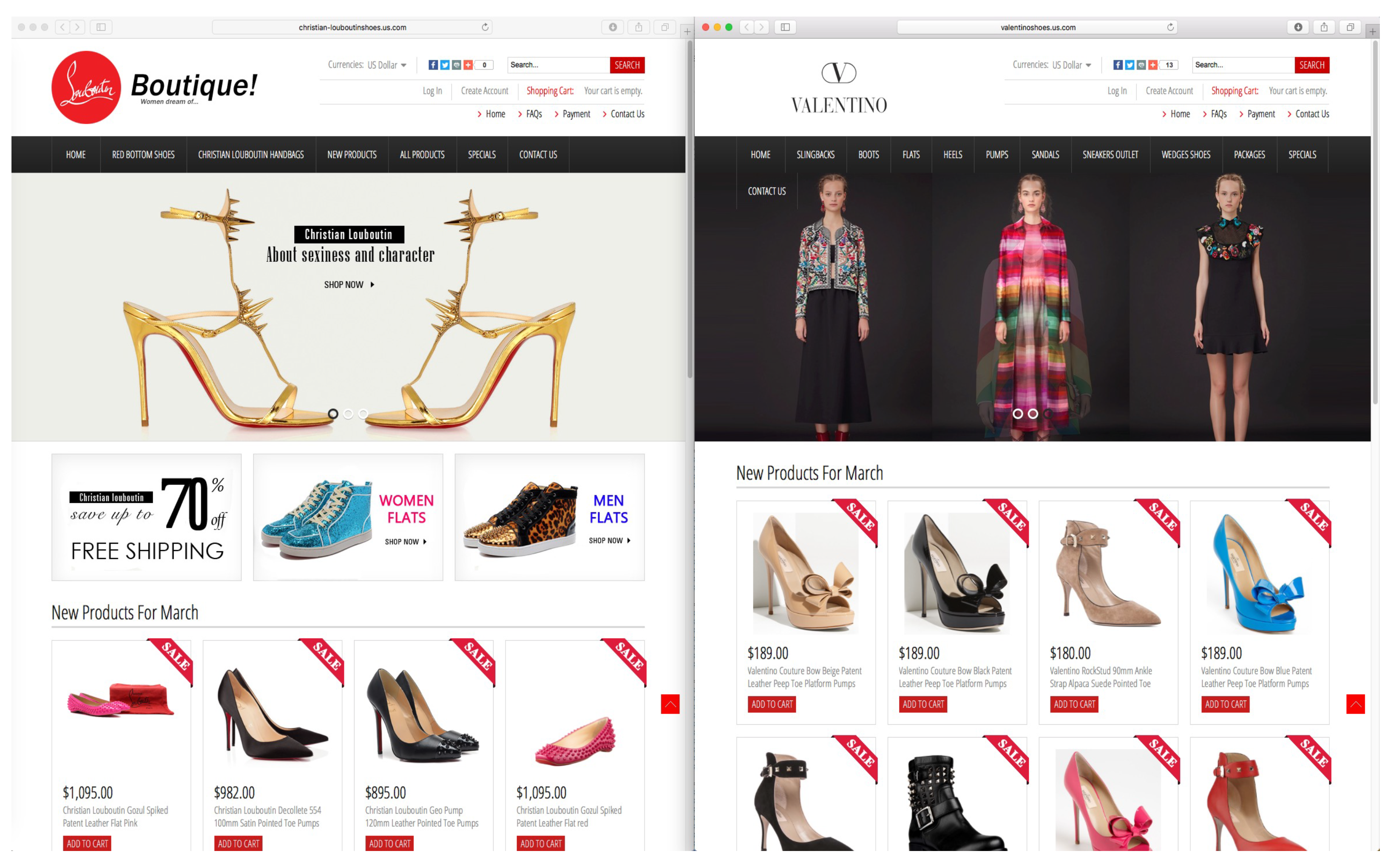
4. Experimenting with counterfeit web shops

4.1. Motivation and approach overview

Counterfeiting occurs in several channels of online sales, including marketplaces and social media. One widespread illegal activity consists of selling unauthorized goods on specialized fake websites, luring customers with cheap, inferior versions of brand-name products. To increase visibility, such websites are often optimized to appear among the results returned by web search engines in response to a query containing the brand name. Also, for reasons of scale and economy, multiple fake websites are often managed by a single criminal entity. The research on automating web anti-counterfeiting efforts has thus a twofold aim: (i) detecting fake web shops, especially among web search results, and (ii) identifying the affiliate marketing programs behind fake web shops.
The latter problem is conceptually different from the former because it is addressed by clustering techniques, as opposed to classification techniques, and relies on different types of learning features. Whereas classification features are common characteristics of illicit web shops that are generally not shared by legitimate web shops (e.g., large discounts, a lack of contact information, and the use of untraceable payment methods), clustering features need to model the process by which multiple counterfeit websites are created and managed by the same entity. The assumption is that web shops belonging to the same network share similarities in terms of their structure, content, and network, since making truly unique versions of each site does not scale well. However, web shops under the same criminal entity may render very differently, especially if they sell entirely different products, while there may be seemingly similar web shops that are actually unrelated, posing a challenge to clustering algorithms.
While the ability to automatically distinguish between fake and genuine web shops has been well studied (e.g., [20,21]) and continues to be actively investigated ([22,23,24]), the subsequent task of recognizing affiliate programs among the detected fake web shops has been less researched to date, although it allows enforcement at scale and brings long-lasting results. One notable exception is [25], where the authors make use of a conventional clustering algorithm together with a few clustering features, mainly extracted from the HTML and the URLs of the websites. However, they reported limited success. Single or combined clustering algorithms have also been recently applied to find networks of malicious websites in several other domains leveraging similar or novel clustering features (e.g., [26,27,28,29,30,31]. Our work expands on previous research by integrating constraints and multiple clustering algorithms in the process of grouping fraudulent websites into connected networks and by showing how such constraints can be partly acquired in an automatic manner.
One practical difficulty of clustering fraudulent websites is that there are no available datasets with associated feature matrices and therefore base partitions must be constructed from raw data. In addition, the features of interest are heterogeneous and must be treated individually. Assuming the use of distance-based clustering algorithms (although other choices would be possible, such as density-based or spectral), this task can be addressed through a three-step pipeline consisting of feature selection, construction of a similarity matrix, and application of several clustering algorithms (or multiple variants of the same clustering algorithm, or the same variant with multiple features). For the last step, we will use both multiple algorithms and multiple features, thus extending the experimental setting commonly adopted in earlier studies. In this way, we will be able to consider a wider range of variables when measuring the performance of double-constrained consensus clustering for web anti-counterfeiting efforts. The specialized double-constrained consensus clustering architecture is shown in Figure 4. The partitions are generated from each of the p clustering features by q base clustering algorithms, and they are next merged through the C C C framework. Compared to Figure 1, we have highlighted the generation of the base partitions and the automatic acquisition of constraints from the input dataset and external data.

4.2. Experiment design and preparation

In this section, we will describe, in turn, the goals of our experiment, the construction of a ground truth dataset, the choice of clustering features and corresponding distance matrices, the selection of base clustering algorithms, and the acquisition of constraints.

4.2.1. Goals

The experiments that we have conducted on grouping illicit web shops had two main objectives. The first was to gain a deeper understanding of the combined effect of features and algorithms on the overall clustering effectiveness, because little work has been done in this domain on evaluating the relative performance of clustering algorithms and features. Most studies use a specific clustering algorithm with a specific combination of features. By contrast, we have analyzed and compared the behavior of individual features across a range of algorithms, and, dually, the behavior of individual algorithms across a range of features. The second goal was to evaluate the effectiveness of plain consensus clustering and constrained consensus clustering for web anti-counterfeiting, which has not been explored so far. This requires computing the base clusterings from the raw set of counterfeit web shops, instead of assuming that the clustering features are known (as in the UCI experiments).

4.2.2. Construction of the ground truth dataset

To the best of our knowledge, there are no available test collections of this kind. The first step was to generate a suitable set of counterfeit websites that holds potential for revealing affiliate programs. We relied on RI.SI.CO. [23], a machine learning system that can detect fake web shops in search engine results generated in response to brand search queries. The procedure was as follows. We first selected 20 famous luxury brands that are known to be targeted by counterfeiters [23]. The corresponding (`complicit’) queries, formed by adding `replica’ and `cheap’ to the brand name, were given as an input to RI.SI.CO., which submitted them to three web search engines, collected 6,043 search results (about 100 for each query), and then identified 1,076 suspicious e-commerce webpages in the set of results. These 1,076 webpages were hosted on 302 distinct websites, We next selected one webpage per website as a representative, removing the redundant items. We also deleted the webpages that were no longer accessible (e.g., due to trademark infringement), with 217 items remaining. The automatic classification performed by RI.SI.CO. is mostly accurate but there may be false positives in the set of webpages labeled as fake. To increase the reliability of the results, we had a few web anti-counterfeiting experts manually remove from the remaining webpages those that had been misclassified by RI.SI.CO., eventually ending up with a set of truly illegitimate webpages containing 203 items.
The next step was to group the 203 webpages (websites) in homogeneous clusters, which was performed by the same experts. Their task was facilitated by extracting a set of unique features associated with each counterfeit network (see Section 4.2.5), which were used to form initial seeds, prior to manual inspection. Given the limited number of items, this effort required on the whole a non negligible but reasonable amount of time. Other strategies to complement manual inspection in the identification of affiliate programs from a larger set of fake web shops have been proposed, such as the heuristic pattern-matching of html content in [32], and the formulation of the problem as a classification task (with labeled data) in [25]. The clusters with one or very few elements were then removed by our experts, thus resulting in a set of 121 websites partitioned in six clusters.
A few clusters accounting for the majority of items is a confirmation of the presence of affiliate fake web shops in brand search results, at least for heavily targeted brands and complicit queries. We checked that affiliate web shops were both mono-brand and multi-brand for a specific type of product (e.g., shoes) or even for different types of products (e.g., shoes and jackets). As an illustration, Figure 5 shows the homepages of two fake web shops with top-selling shoe brands (i.e., Louboutin and Valentino) that were grouped together.
Given the limited lifespan of counterfeit websites, it is essential to get a snapshot of all the relevant information associated with them when they are still functional. In the final step, a set of clustering features (see Section 4.2.3) was extracted for each domain. The set of 121 domain names with associated clustering features and group information form a ground truth dataset termed CAP (Counterfeit Affiliate Programs).3 We believe that CAP, although small in size, fills a gap in the research on online anti-counterfeiting.

4.2.3. Clustering features and distance matrices

Various clustering features have been proposed for this or related tasks, usually associated with the structure ([25,27,28,33]), content ([26,29,30,31]), and visual appearance of malicious websites ([26,34]), or with information about their registration or network infrastructure ([25,26,31]). We followed two main criteria to select the features for the experiments: that they were representative of main feature categories, and that they were present and easily acquirable for almost all web shops in CAP. For instance, we did not use any feature related to website registration because the WHOIS service available to us covered only a small fraction of the sample. Also, unlike [25], we did not include network features such as name servers or autonomous system numbers because we found that they were very weak clustering signals, while the IP address can be regarded as a very strong signal and used to acquire constraints, as is discussed in Section 4.2.5. The selected raw features, along with the actual clustering features extracted from them and the similarity function associated with each, are described below.
As a structural feature, we relied on the DOM tree associated with each of the webpages. Following [33], we encoded the structure of each DOM tree in CAP as a bit string through SimHash fingerprinting, and then computed the pairwise similarities with the Hamming distance. As a visual feature, we chose the website header of the web shops. We created five visual clustering features from the homepage screenshot, corresponding to website headers with a variable number of rows (from 30 to 150, with a step of 30). The similarity matrix for a selected header was found by first extracting, for each website in CAP, an image tensor containing the HSV value of the pixels in the region of interest associated with that header, and by successively computing the Chi-Square distance between the HSV histograms of any pair of elements in CAP. We finally used two novel clustering features related to the specific content items of web shops, namely privacy policy and shipping policy. The rationale is that policies between affiliated fake web shops can be reused to reduce the effort involved in website authorship, often with only minor adjustments, e.g., the name of the site owner. We did not use other possible, and probably relevant, policies (e.g., `payment methods’ and `returns and refunds’) because these pieces of information were not provided in the majority of the elements in CAP. For both features, we extracted the textual content of the policies from each website in CAP, and then measured the pairwise similarity based on the number of shared sentences.

4.2.4. Base clustering algorithms

Moving on to the selection of base clusterings, first of all we would like to note that constrained clustering algorithms available online that accept a user-defined similarity matrix are very rare. As this was an essential prerequisite in the domain at hand, we decided to use base clustering algorithms that cannot take advantage of constraints (unlike former experiments with UCI datasets). On the other hand, it should be noted that the potentially unfair use of constraints in the consensus clustering framework (for the purpose of performance comparison to clustering without constraints) is mitigated by the fact that, as we shall see, in web anti-counterfeiting constraints can be partly acquired automatically.
We relied on the h c l u s t package in the R statistical programming language. It provides a set of eight distinct agglomerative hierarchical clustering algorithms, with the additional facility that users can define their own similarity matrix (which is, in fact, a `dissimilarity structure’ and requires a a suitable transformation of the format of the similarity matrix). The algorithms differ in the procedure used to select which clusters are to be merged at each step, and will in general produce very different results. The algorithms, described in more detail in the package documentation,4 are: Average, Centroid, Complete, Mcquitty, Median, Single, Ward.D, and Ward.02. The output of these algorithms in R is a dendrogram. To find the corresponding partition, we then cut each dendrogram into six disjoint subtrees (as the number of clusters in CAP).

4.2.5. Automatic acquisition of constraints

We now turn to the acquisition of constraints. While the clustering features introduced above are only indicative of membership (i.e., two domains sharing a same feature may or may not belong to an affiliate program), in the web anti-counterfeiting field it is sometimes possible to state that two different web domains are in fact linked to the same entity by leveraging certain registration and network information as well as specific content on their websites. The latter type of information can be seen as high-confidence but infrequent features, as opposed to the frequent yet lower-confidence features used as proper clustering features in Section 4.2.3. In particular, a must-link constraint between two domain names can be created with some certainty when one of the following properties is satisfied.
- Redirection. Some fake websites redirect the visitor from the initial web domain to one or more additional sites, ultimately resolving the final web page [32]. This is done either by URL redirection, whereby a fake web page is made available in parallel under more than one URL address, or by search-redirection, in which fake websites hack high ranking websites to redirect to their store based on the user’s search query [35]. If two fake websites share the same final domain after redirection, they almost certainly belong to one affiliate marketing network.
- Same IP address. Multiple websites can be hosted on one web server. If two fake websites have the same resolved IP address for their domain names, then it is very likely that they were created by the same entity [36].
- Same WHOIS Registrant data. Although domain name registrant information (name, email, address) as provided by databases like WHOIS are largely incomplete due to several issues (including privacy regulations), shared registrant data is a clear indication that two fake websites should be linked together because it means that they have been registered by the same legal person (juridical or natural).
- Same website contact information. Fake websites try to resembles genuine websites to increase visitor trust. This includes providing reassuring contact information such as an email address or telephone number, but also a physical address and links to the web pages of physical stores. If two fake websites share that data then they probably belong to one affiliate marketing program.
- Same Google analytics ID. Third-party analytics services are used by many ecommerce websites to better understand their customers. If two fake websites contain the same analytics ID within their source code, it means that they are reporting to the same analytics account and presumably are part of one affiliation program. Finding matching Google analytics IDs has been used to group illicit websites into connected campaigns [37].
We automatically acquired the features necessary to assess the abovementioned properties (when available) for any of the 121 websites in CAP, and then, through pairwise comparison, we generated 53 must-links, 32 of which were non-redundant. This is a small fraction of the total number of must-links, but it may be enough to drive the process of constrained consensus clustering and significantly improve performance improvement, as is shown in the next section.

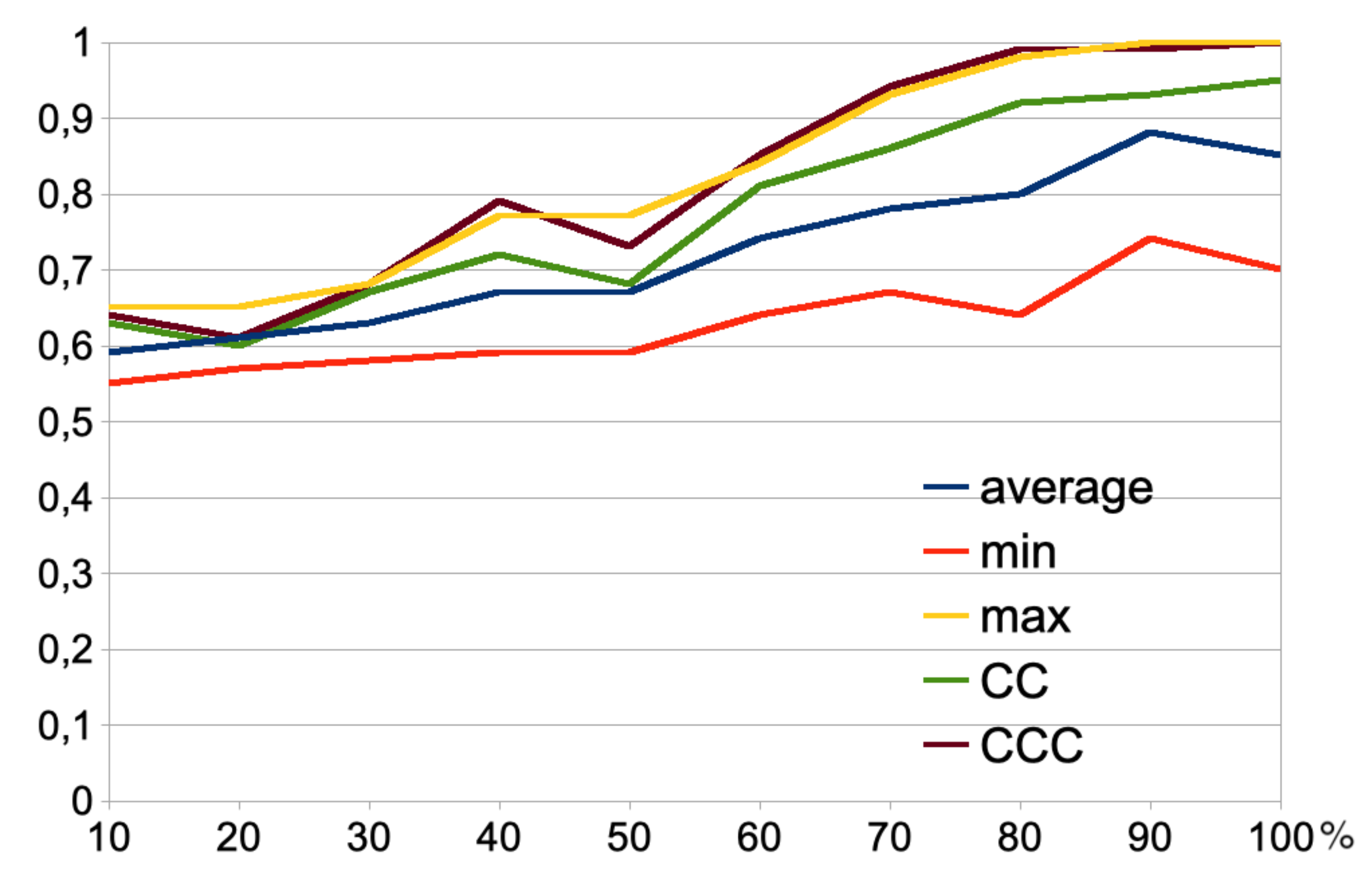
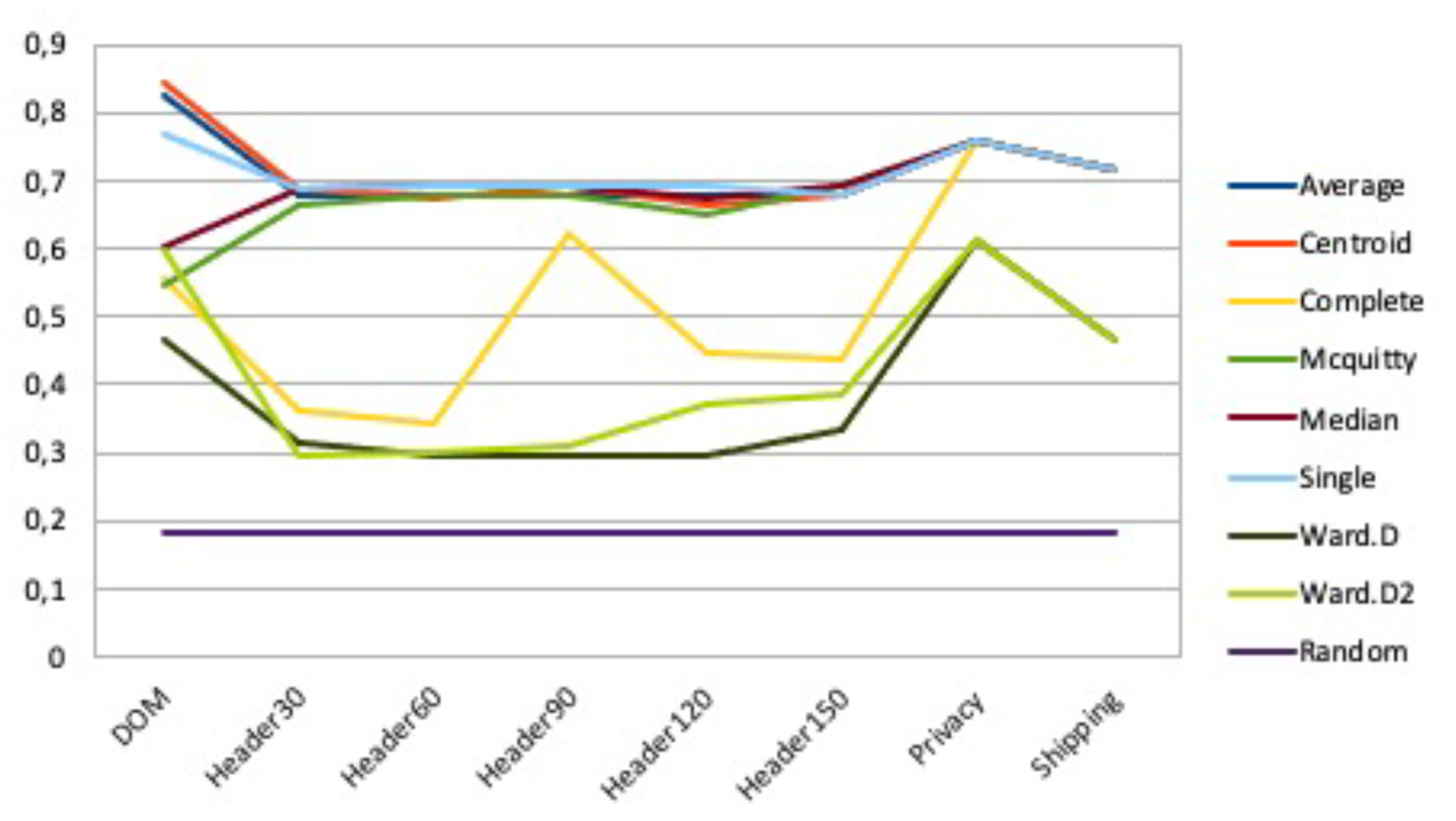
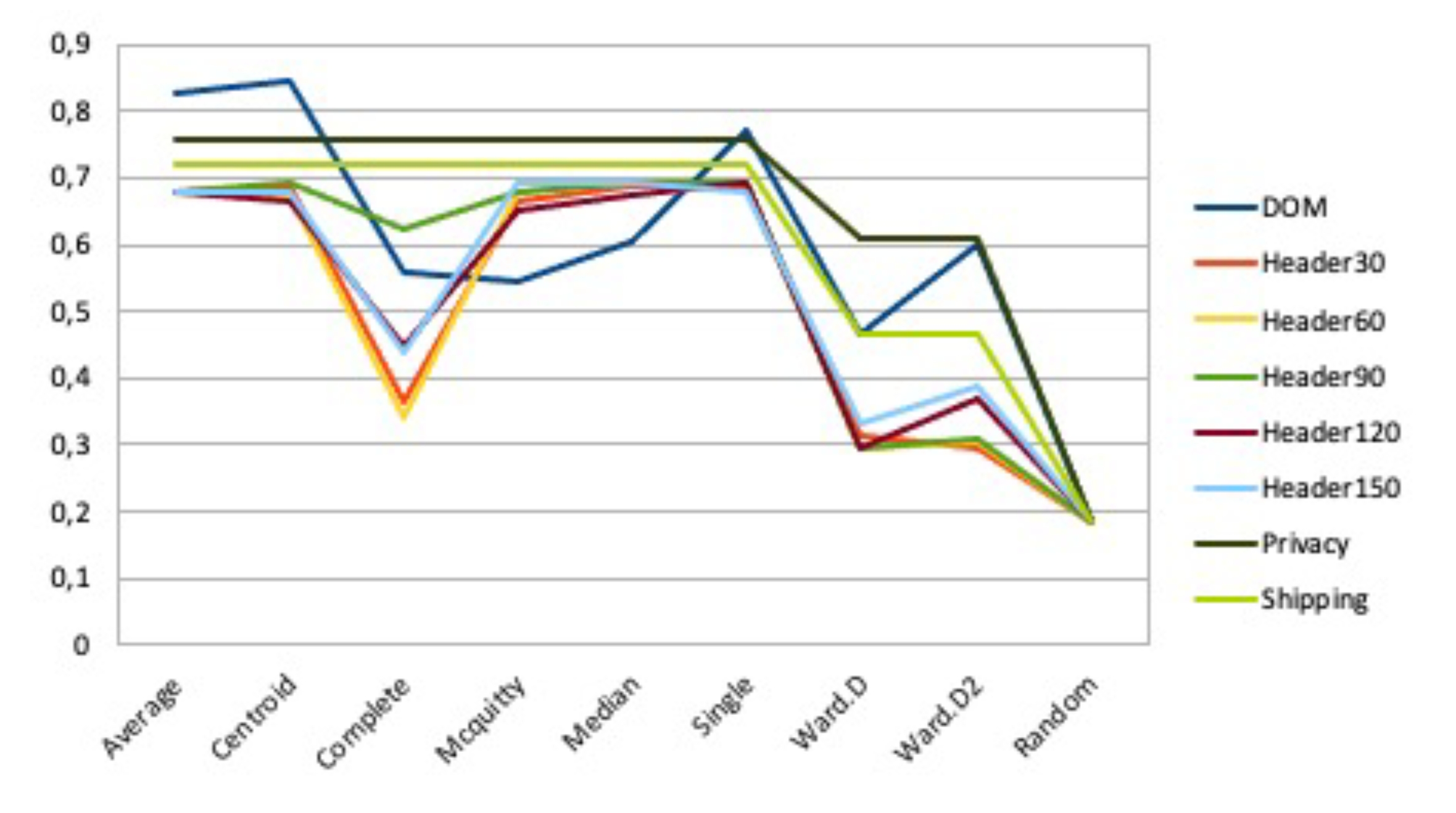
4.3. Results

We tested 64 combinations of clustering methods and features (8x8), and measured the performance of each by F measure. For the ease of interpretation, the results are shown in two distinct charts, rather than a table. Figure 6 reports the performance of each of the eight clustering methods across the eight clustering features. We also included the performance of a random partition (independent of feature), for the sake of comparison. The figure clearly suggests that the result of individual methods may change to a great extent as features vary, and that there is no best method across all features, consistent with the observation that any clustering method is not inherently better or worse than another one. More specifically, Complete had the largest performance range (from 0.36 to 0.76), while Centroid, Average, Single, Median, and Mcquitty were relatively more stable with change of features (except for feature DOM), with Ward.D and Ward.02 exhibiting intermediate behavior. Looking at the relative performance of clustering methods, Centroid, Average, Single, Median, and Mcquitty obtained more comparable and higher results than Complete, Ward.02, and Ward.D (in that order). Finally, any clustering method was markedly better than the random partition for any clustering feature.
Figure 7 reports the performance of each of the eight clustering features across the eight clustering methods, including the random partition again. Analogous to the behavior of clustering methods, the result of individual features changes as clustering methods vary, and there is no best feature across all methods. Feature Header120 has the largest performance range, from 0.30 a 0.69, with the other visual features exhibiting similar variations. DOM was also very unstable, while the two features pertaining to textual content were relatively more stable across clustering methods. In terms of feature comparison, Privacy and Shipping usually achieved good results. By contrast, visual features were in general less effective (although Header90 performed well for some methods), while DOM was comparatively inferior for some methods but it also achieved the best overall results for three methods.
Figure 6 and Figure 7 show that the performance of all possible combinations of methods and features varies across a very wide interval, from a minimum of 0.30 to a maximum of 0.85. As there is no way to know in advance which combination will perform better, it is important to find ways to improve the average expected behavior for the set of methods and features at hand. Using consensus clustering and constrained consensus clustering may be an effective strategy, as we will now expound on.
To evaluate CC and CCC, the procedure was as follows. For each clustering feature, we used the partitions generated by the eight clustering algorithms as base partitions and computed the CC partition. We then added the constraints and computed the corresponding CCC partitions. We used a growing set of constraints, from 10 to 80 (with a step of 10). The full set of 80 constraints used in the experiments was obtained by completing the constraints acquired automatically as described in Section 4.2.5 with those extracted from CAP using the same method as with UCI datasets. In all, we generated 8 x 8 x 8 = 512 partitions. Finally, we evaluated the performanceof each with F measure.
The results are reported in Table 4. For each clustering feature (listed in the first column), we first show the minimum, maximum, and average performance value obtained by the eight hclust algorithms for that feature. In the subsequent columns, we report the performance of CCC using the eight hclust algorithms (with that feature) as an input to CCC, as the number of constraints grows from 0 to 80. In particular, CCC with zero constraints is equivalent to using unconstrained consensus clustering (i.e., CC). We also show, in parenthesis, the percentage of improvement of CCC over the average performance of the eight base methods (for each single feature). Finally, the last row reports the mean performance value (averaged over the set of features) of minimum, maximum, average (and thus means of means), and CCC (relative to the eight basis algorithms and for any set of constraints, including unconstrained CC).
The are two main findings. The first is that CC works well, with improved performance over the average result of basis clustering methods ranging from 8% to 26%, depending on which clustering feature we consider. The average improvement over all methods and features was 17% (last row, CC column). Not only are the CC results better than the average results of the basis methods for all the features, but very often they are also equal or close to those obtained by the the best basis method. In particular, CC matches the best result for the Header30, Header90, Privacy, and Shipping features, while it is very slightly inferior to the best method for Header60, Header120, Header150. These observations confirm the effectiveness of CC for the domain at hand.
The second main finding is that the use of constraints within CC was very effective. Table 4 shows that the results of CCC were better than the average performance of the eight basis algorithms for any set of constraints and for any feature, with a peak of 59% improvement over a single feature and 45% improvement over average performance, reached with 80 constraints. Also, and more importantly, CCC soon outperformed the best basis method. For instance, with 30 constraints, CCC performed better than the best basis method seven times out of eight. Comparing CCC to CC, we see that with a small number of constraints, CCC was slightly worse than CC, while with 30+ constraints on CCC was systematically better than CC both on average and for individual features. In this range of constraints, the improvement of CCC over CC grew monotonically, gaining up to 24% with 80 constraints (from 0.7 to 0.87).
Before concluding this section, we would like to note that, besides using clustering algorithms with individual features, we also tried to combine the single features into one overall feature, by normalizing the distance matrices and taking their mean, as was done in [38], for instance. The results were unsatisfying, probably due to the different distribution of the values produced by each feature.

5. Related work

In this section we review two main related areas, namely the earlier approaches to semi-supervised ensemble clustering and the application of clustering techniques to detect connected networks behind fraudulent websites of various types with varied content.

5.1. Semi-supervised ensemble clustering

In their survey on ensemble learning [6] which includes semi-supervised ensemble clustering the authors point out that existing semi-supervised ensemble clustering algorithms make an unsatisfying use of constraint information and encourage more research on this issue. We have addressed it from two perspectives, as described below.
Previous work on semi-supervised ensemble clustering can be described according to the strategy used for combining constraints and consensus clustering. The most common approach consists of using constraints prior to ensemble clustering to identify better base partitions. Yu et al. [39] use constraints to eliminate redundant ensemble members from a larger set generated by the random subspace method [40], where member selection is driven by an objective function that incorporates constraints and similarity of attributes in the subspaces. Selection of ensemble members is also pursued in [41] and [42], building again on the the random subspace method. In [41], constraints are used to transform features after their random generation, while in [42] constraints are projected onto the subspaces and weighted. Two other different example of the first combination strategy are [43] and [44]. In [43], constraints are used within a specific clustering algorithm (i.e., semi-supervised spectral clustering [45]) to build constrained base partitions before their merging by an unconstrained consensus algorithm. This is similar to the first step of our double-constrained framework. In [44], confidence scores are assigned to each ensemble member based on its compliance with constraints, and the weighted partitions are then merged through a consensus matrix.
The second main strategy is to incorporate domain knowledge directly within the construction of the clustering ensemble, rather than using it as a pre-processing technique. In [46] and [47], constraints are used to modify the graph-based consensus function of Chameleon [48], to make more informed decisions when merging or splitting subgraphs. In [49], constraints are integrated into a consensus function based on frequent closed itemset mining; similar to CCC, the number of clusters in the consensus partition does not need to be specified. In [50], constraints are used to compute the similarity matrix associated with the ant colony clusterings, modifying the pick-up and drop-down probabilities.
A third, little explored combination strategy is to refine the clustering ensemble by constraints after its generation. In [51], an initial consensus partition is modified to strictly satisfy the constraints while changing as little as possible. The cluster similarity is modeled through anchors, (i.e., sets of data points that are representative of clusters) and the optimization framework is cast as an integer linear programming problem.
Compared to earlier works, our combination strategy is different because constraints are used in two distinct phases of the semi-supervised ensemble clustering process, namely for generating ensemble members and for merging them. To our knowledge, this is novel. While it can be argued that other existing (single) constrained consensus clustering algorithms may, in principle, be applied to constraint-enhanced rather than unconstrained base partitions (thus turning into double-constrained approaches), so far this hypothesis has neither been explicitly considered nor been experimentally evaluated.
Aside from combination strategy, a few earlier works have focused on the treatment of constraints, in an attempt to extract additional knowledge from them. Building on [52], Yu et al. [39] generate a constraint matrix in which supervised information is propagated from labeled to unlabeled pairs of objects by means of q-nearest neighbor graphs. Another approach consists of propagating pairwise information to logically implied constraints through transitive closure. The basic idea of the latter study is the same as in our work, but Yu et al. [53] in their formulation fail to make an explicit link to the theory of functional dependencies. In addition, more importantly, we introduce a novel notion of minimal cover of the set of constraints associated with a partition, providing constructive procedures and showing its usefulness to evaluate the performance of semi-supervised consensus clustering algorithms.
Another research issue is based on the observation that not all constraints are equally informative or useful for a given dataset. Indeed, constraints may even affect the results negatively, as is also highlighted in our experiments. Yu et al. [42] weigh constraints according to their importance in each random subspace of features. It would also be possible to weigh constraints according to the probability of their occurring by chance, analogous to PRI. In this article we have not explored this approach, leaving it for future research work.
Finally, some works have focused on the use of other types of information sources, beyond pairwise constraints. A uniform representation of pairwise constraints and label constraints is provided in [54] These two types of constraints have been used to build hybrid enhanced base partitions through specific clustering algorithms that use either constraint [43]. Another type of constraint, termed triplet constraints, is defined in [51], namely `object A is closer to object B than to object C’.

5.2. Clustering fraudulent websites

Although counterfeit web shops are perhaps the best-known category of fraudulent websites, there have been very few works on clustering them. The approach proposed in [25] relies on two types of features: HTML features, encoded as a bag-of-word in which each word is a tag-attribute-value triplet, and network features, extracted from the address and name server records of web shops. The authors then used the k-means algorithm with these features on a large dataset containing 44 affiliate programs. They reported that the resulting partitions were useful to identifying the largest affiliate programs but exhibited a high error rate for the other programs, because large programs tended to swallow up the smaller ones. Their somewhat disappointing results highlighted the difficulty of this task, although they may have been influenced by the characteristics of the specific clustering algorithm used, given that k-means has trouble clustering data when the clusters are of varying sizes.
In our paper, we use a more comprehensive set of features and, more importantly, a much more sophisticated clustering algorithm – semi-supervised ensemble clustering – with the additional desirable property that the background knowledge in this domain can be acquired automatically. We believe that this is a step ahead towards the timely and accurate identification of large-scale counterfeit networks, which is key to effective enforcement efforts yet still largely unsolved. Furthermore, in contrast to previous work, we study the behavior of algorithms and features when intersected rather than experimenting with a specific clustering method on a whole fixed set of features, and we also ensure the results are replicable by sharing the ground truth dataset.
The use of clustering techniques to analyze the content and the infrastructure of fraudulent websites has been recently investigated to combat other malicious online activities carried out across a variety of website categories. A few examples are the following: acquisition of cryptocurrency funds from unsuspecting investors with the false promise of gaining more cryptocurrency or accessing to a service [30], sale and delivery of fictitious pets through scam websites [29], monetization of parked domain names through hosting ads [27], distribution of exploit kits through malicious websites [28], fake escrow services and high-yield investment programs [26], video piracy [31], and phishing websites [34]. Analogous to anti-counterfeiting, studies in these fields report that a limited number of entities are running multiple instances of similar scams. All these studies were conducted using a particular clustering algorithm on a whole (domain-specific) set of features. One partial exception is [26], where a hierarchical agglomerative clustering algorithm was run on all possible combinations of individual features. However, this approach requires labelled training data to select the top performing combination. Previous work on clustering fraudulent websites did not explore the use of consensus clustering or constrained clustering, let alone of constrained consensus clustering. Since the automatic acquisition of constraints seems possible even in the abovementioned domains, the application of CCC to other types of fraudulent websites is an avenue for future research.

6. Conclusions and future work

We have presented a novel approach to semi-supervised ensemble clustering that makes double use of pairwise constraints, on the ground that they can be exploited both to generate better base partitions and to improve the combination of such partitions. The first step is carried out through constraint-enriched single clustering algorithms, while the merging is achieved by incorporating compliance with constraints into an objective function that maximizes the PRI similarity between the consensus partition and the constrained base partitions. The compliance with constraints also takes into account their logical properties, thus helping optimize their use. The effectiveness of the proposed framework is suggested by the fact that re-using the constraints in the consensus function produced much better results than combining the constrained base partitions with the unenhanced consensus function.
We have also argued that the proposed framework can be used to combat web counterfeiting, because constraints can be partly acquired in an automatic manner, and have shown its utility for detecting affiliate marketing programs behind fraudulent e-commerce websites present in search engine results. From a practical point of view, our research confirms that semi-supervised ensemble clustering is generally a viable strategy to address the inherent limitations of single unsupervised clustering algorithms, while offering new insights into the increased robustness that can be achieved when changing the dataset to be clustered, the clustering technique, and the clustering features.
There are two main directions for future research. Methodologically, we plan to extend the objective function from constraint counting to constraint weighting, as hinted at in the article. In addition, we would like to explore different optimization methods to compute the constrained consensus partition. The second research direction concerns applications. One goal is to apply CCC to the sector of counterfeit auto and moto parts, which we are currently investigating with the support of industrial and institutional partners. Also, we plan to experiment with types of fraudulent websites that support illicit activities other than counterfeiting, as reported in the article. We believe that our approach has great potential because it goes beyond the paradigm of the single unconstrained clustering algorithm, adopted so far, and also because the constraints can potentially be acquired automatically, similar to the web anti-counterfeiting scenario.

Acknowledgments

We would like to thank Andrea Bernardini and Federica Mangiatordi for their help in assembling the CAP test collection and extracting the DOM and visual features used by the website clustering algorithms.

References

  1. Kleinberg, J. An impossibility theorem for clustering. In Proceedings of the Proceedings of the 15th International Conference on Neural Information Processing Systems (NIPS’02), Vancouver, British Columbia, Canada, 2002, pp.; pp. 463–470.
  2. Estivill-Castro, V. Why so many clustering algorithms: a position paper. SIGKDD Explorations 2002, 4, 65–75. [Google Scholar] [CrossRef]
  3. Boongoen, T.; Iam-On, N. Cluster ensembles: A survey of approaches with recent extensions and applications. Computer Science Review 2018, 28, 1–25. [Google Scholar] [CrossRef]
  4. Bair, E. Semi-supervised clustering methods. Wiley Interdisciplinary Reviews: Computational Statistics 2013, 5, 349–361. [Google Scholar] [CrossRef]
  5. Taha, K. Semi-supervised and un-supervised clustering: A review and experimental evaluation. Information Systems 2023, 114. [Google Scholar] [CrossRef]
  6. Xibin Dong, Zhiwen Yu, W. C.Y.S.; Ma, Q. A survey on ensemble learning. Frontiers of Computer Science 2020, 14, 241–2585. [Google Scholar] [CrossRef]
  7. Carpineto, C.; Romano, G. Consensus Clustering Based on a New Probabilistic Rand Index with Application to Subtopic Retrieval. IEEE Transactions on Pattern Analysis and Machine Intelligence 2012, 34, 2315–2326. [Google Scholar] [CrossRef]
  8. Rand, W.M. Objective criteria for the evaluation of clustering methods. Journal of American Statistical Association 1971, 66, 846–850. [Google Scholar] [CrossRef]
  9. Hubert, L.; Arabie, P. Comparing partitions. Journal of Classification 1985, 2, 193–218. [Google Scholar] [CrossRef]
  10. Rovetta, S.; Masulli, F.; Cabri, A. The Probabilistic Rand Index: A Look from Some Different Perspectives. In Neural Approaches to Dynamics of Signal Exchanges: Smart Innovation, Systems and Technologies; Esposito, A.; Faundez-Zanuy, M.; Morabito, F.C.; Pasero, E., Eds.; 2019; Vol. 151, pp. 95–105.
  11. Wagstaff, K.; Cardie, C.; Rogers, S.; Scrödl, S. Constrained K-means Clustering with Background Knowledge. In Proceedings of the Proceedings of the 18th International Conference on Machine Learning, Williamstown, MA, USA.; Morgan Kaufmann, 2001; pp. 577–584.
  12. Bansal, N.; Blum, A.; Chawla, S. Integrating constraints and metric learning in semi-supervised clustering. In Proceedings of the Proceedings of the twenty-first international conference on Machine learning (ICML ’04), Banff, Alberta, Canada.; ACM, 2004; pp. 81–88.
  13. Ghasemi, Z.; Khorshidi, H.A.; Aickelin, U. A survey on Optimisation-based Semi-supervised Clustering Methods. In Proceedings of the 2021 IEEE International Conference on Big Knowledge (ICBK), Auckland, New Zealand. IEEE; 2021; pp. 477–482. [Google Scholar]
  14. Carpineto, C.; Romano, G. Optimal meta search results clustering. In Proceedings of the Proceedings of SIGIR 2010, Geneva, Switzerland.; ACM Press, 2010; pp. 170–177.
  15. Luke, S. Essentials of Metaheuristics; 2009. available at. Available online: http://cs.gmu.edu/∼sean/book/metaheuristics/.
  16. Pelleg, D.; Baras, D. K-Means with Large and Noisy Constraint Sets. In Proceedings of the Proceedings of 2007 European Conference on Machine Learning, Warsaw, Poland, 2007, pp.; pp. 6747–682.
  17. Hiep, T.K.; Duc, N.M.; Trung, B.Q. Local search approach for the pairwise constrained clustering problem. In Proceedings of the SoICT ’16: Proceedings of the 7th Symposium on Information and Communication Technology (SoICT ’16), Ho Chi Minh City, Vietnam.; AC, 2016; pp. 107–118.
  18. Manning, C.D.; Raghavan, P.; Schütze, H. Introduction to Information Retrieval; Cambridge University Press, 2008.
  19. Craenendonck, T.V.; Blockeel, H. Constraint-based clustering selection. Machine Learning 2017, 106, 1497–1521. [Google Scholar] [CrossRef]
  20. Wadleigh, J.; Drew, J.; Moore, T. The E-Commerce Market for "Lemons": Identification and Analysis of Websites Selling Counterfeit Goods. In Proceedings of the Proceedings of the 24th International Conference on World Wide Web (WWW ’15), 2015, pp.; pp. 1188–1197.
  21. Carpineto, C.; Romano, G. Learning to detect and measure fake ecommerce websites in search-engine results. In Proceedings of the Proceedings of 2017 IEEE/WIC/ACM International Conference on Web Intelligence (WI 2017), Leipzig, Germany, 2017, pp.; pp. 403–410.
  22. Beltzung, L.; Lindley, A.; Dinica, O.; Hermann, N.; Lindner, R. Real-Time Detection of Fake-Shops through Machine Learning. In Proceedings of the Proceedings of 2020 IEEE International Conference on Big Data.; IEEE, 2020; pp. 2254–2263.
  23. Carpineto, C.; Romano, G. An Experimental Study of Automatic Detection and Measurement of Counterfeit in Brand Search Results. ACM Transactions on the Web 2020, 14, 1–35. [Google Scholar] [CrossRef]
  24. Gopal, A.R.D.; Hojati, A.; Patterson, R.A. Analysis of third-party request structures to detect fraudulent websites. Decision Support Systems 2022, 154, Issue C.
  25. Der, A.M.F.; Saul, L.K.; Savage, S.; Voelker, G.M. Knock it off: profiling the online storefronts of counterfeit merchandise. In Proceedings of the Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining.; ACM, 2014; pp. 1759–1768.
  26. Drew, J.M.; Moore, T. Optimized combined-clustering methods for finding replicated criminal websites. EURASIP Journal on Information Security 2014, 14, 1–13. [Google Scholar] [CrossRef]
  27. Geraci, F. Identification of Web Spam through Clustering of Website Structures. In Proceedings of the Proceedings of the 23th international conference on World Wide Web (Companion Volume).; ACM, 2015; pp. 1447–1452.
  28. Nagai, T.; Kamizono, M.; Shiraishi, Y.; Xia, K.; Mohri, M.; Takano, Y.; Morii, M. A Malicious Web Site Identification Technique Using Web Structure Clustering. IEICE Transactions on Information and Systems 2019, E102.D, 1665–1672. [Google Scholar] [CrossRef]
  29. Price, B.; Edwards, M. Resource networks of pet scam websites. In Proceedings of the Proceedings of 2020 APWG Symposium on Electronic Crime Research (eCrime), 2005, pp.; pp. 1–10.
  30. Phillips, R.; Wilder, H. Tracing Cryptocurrency Scams: Clustering Replicated Advance-Fee and Phishing Websites. In Proceedings of the Proceedings of 2020 IEEE International Conference on Blockchain and Cryptocurrency (ICBC); 2020. [Google Scholar]
  31. Wang, A.C.; Yu, Y.; Pu, A.; Shi, F.; Huang, C. Spotlight on Video Piracy Websites: Familial Analysis Based on Multidimensional Features. In Proceedings of the Proceedings of 15th International Conference on Knowledge Science, Engineering and Management, 2022, pp.; pp. 272–288.
  32. Levchenko, K.; Pitsillidis, A.; Chachra, N.; Enright, B.; Felegyhazi, M.; Grier, C.; Halvorson, T.; Kanich, C.; Kreibich, C.; Liu, H.; et al. Click Trajectories: End-to-End Analysis of the Spam Value Chain. In Proceedings of the Proceedings of 2011 IEEE Symposium on Security and Privacy, 2011, pp.; pp. 431–446.
  33. Bernardini, A. Extending domain name monitoring. Identifying potential malicious domains using hash signatures of DOM elements. In Proceedings of the Proceedings of ITASEC 2018, Italian Conference on Cybersecurity, 2018. [Google Scholar]
  34. Prettejohn, N. Phishing Website Identification through Visual Clusteringe. PhD thesis, Department of Computing Imperial College London, London, UK, 2016.
  35. Leontiadis, N.; Moore, T.; Christin, N. Measuring and analyzing search-redirection attacks in the illicit online prescription drug trade. In Proceedings of the Proceedings of 20th USENIX Security Symposium (USENIX Security 11).
  36. Wei, C.; Sprague, A.; Warner, G.; Skjellum, A. Clustering Spam Domains and Destination Websites: Digital Forensics with Data Mining. Journal of Digital Forensics, Security and Law (JDFSL) 2010, 5. [Google Scholar] [CrossRef]
  37. Starov, O.; Zhou, Y.; Zhang, X.; Miramirkh, N.; Nikiforakis, N. Document Clustering With Committees. In Proceedings of the Proceedings of the 2018 World Wide Web Conference.; ACM Press, 2018; pp. 227–236.
  38. Navarro-Arribas, G.; Torra, V.; Erola, A.; Castellà-Roca, J. User k-anonymity for privacy preserving data mining of query logs. Information Processing & Management 2019, 48, 476–487. [Google Scholar]
  39. Yu, Z.; Luo, P.; You, J.; Wong, H.S.; Leung, H.; Wu, S.; Zhang, J.; Han, G. Incremental Semi-Supervised Clustering Ensemble for High Dimensional Data Clustering. IEEE Transactions on Knowledge and Data Engineering 2015, 28, 701–714. [Google Scholar] [CrossRef]
  40. Ho, T.K. The Random Subspace Method for Constructing Decision Forests. IEEE Transactions on Pattern Analysis and Machine Intelligence 1998, 20, 832–844. [Google Scholar]
  41. Luo, R.; Yu, Z.; Cao, W.; Liu, C.; Won, H.S.; Chen, C.L.P. The Random Subspace Method for Constructing Decision Forests. IEEE Access 2019, 8, 17926–17934. [Google Scholar] [CrossRef]
  42. Yu, Z.; Luo, P.; Liu, J.; Wong, H.S.; You, J.; Han, G.; Zhang, J. Semi-Supervised Ensemble Clustering Based on Selected Constraint Projection. IEEE Transactions on Knowledge and Data Engineering 2018, 30, 2394–2407. [Google Scholar] [CrossRef]
  43. Wei, S.; Li, Z.; Zhang, C. Combined constraint-based with metric-based in semi-supervised clustering ensemble. International Journal of Machine Learning and Cybernetics 2017, 9, 1085–1100. [Google Scholar] [CrossRef]
  44. Yu, Z.; Wongb, H.S.; You, J.; Yang, Q.; Liao, H. Knowledge based cluster ensemble for cancer discovery from biomolecular data. IEEE Transactions on Nanobioscience 2011, 10, 76–85. [Google Scholar] [PubMed]
  45. Ding, S.; Jia, H.; Zhang, L.; Jin, F. Research of semi-supervised spectral clustering algorithm based on pairwise constraints. Neural Computing and Applications 2014, 24, 211–219. [Google Scholar] [CrossRef]
  46. Xiao, W.; Yang, Y.; Wang, H.; Li, T.; Xing, H. Semi-supervised hierarchical clustering ensemble and its application. Neurocomputing 2016, 173, 1362–1376. [Google Scholar] [CrossRef]
  47. Ma, T.; Zhang, Z.; Guo, L.; Wang, X.; Qian, Y.; Al-Nabhan, N. Semi-supervised Selective Clustering Ensemble based on constraint information. Neurocomputing 2021, 462, 412–425. [Google Scholar] [CrossRef]
  48. Karypis, G.; Han, E.H.; Kumar, V. Chameleon: hierarchical clustering using dynamic modeling. IEEE Computer 1999, 32, 68–75. [Google Scholar] [CrossRef]
  49. Yang, T.; Pasquier, N.; Precioso, F. Semi-supervised consensus clustering based on closed patterns. Knowledge-Based Systems 2022, 235. [Google Scholar] [CrossRef]
  50. Yang, Y.; Teng, F.; Li, T.; Wang, H.; Wang, H.; Zhang, Q. Parallel Semi-Supervised Multi-Ant Colonies Clustering Ensemble Based on MapReduce Methodology. IEEE Transactions on Cloud Computing 2015, 6. [Google Scholar] [CrossRef]
  51. Guilbert, M.; Vrain, C.; Dao, T.B.H.; de Souto, M.C.P. Anchored Constrained Clustering Ensemble. In Proceedings of the Proceedings of 2022 International Joint Conference on Neural Networks.; IEEE; p. 2022.
  52. Lu, Z.; Ip, H.H.; Peng, Y. Exhaustive and Efficient Constraint Propagation: A Semi-Supervised Learning Perspective and Its Applications. In Proceedings of the arXiv:1109.4684 [cs.AI]; 2011. [Google Scholar]
  53. Yu, Z.; Kuang, Z.; Liu, J.; Chen, H.; Zhang, J.; You, J.; Wong, H.S.; Han, G. Adaptive Ensembling of Semi-Supervised Clustering Solutions. IEEE Transactions on Knowledge and Data Engineering 2017, 29, 1577–1599. [Google Scholar] [CrossRef]
  54. Bai, L.; Liang, J.; of Computer, F.C.S.; Information Technology, Shanxi University, T. S.C. Semi-Supervised Clustering With Constraints of Different Types From Multiple Information Sources. IEEE Transactions on Pattern Analysis and Machine Intelligence 2020, 43, 3247–3268. [Google Scholar] [CrossRef]
1
The terms partition and clustering will be used interchangeably throughout the paper.
2
https://cran.r-project.org/web/packages/conclust/index.htm
3
CAP is available at https://www.kaggle.com/datasets/claudiocarpineto/counterfeit-affiliate-programs/code.
4
https://www.rdocumentation.org/packages/stats/versions/3.6.2/topics/hclust
Preprints 81271 g001
Figure 1. Overview of the architecture of double-constrained consensus clustering.
Figure 1. Overview of the architecture of double-constrained consensus clustering.
Preprints 81271 g001
Preprints 81271 g002
Figure 2. Performance of base clustering algorithms as a function of the number of constraints.
Figure 2. Performance of base clustering algorithms as a function of the number of constraints.
Preprints 81271 g002
Preprints 81271 g003
Figure 3. Mean performance of CC and CCC (averaged over the four datasets) as a function of the number of constraints, compared to minimum, average, and maximum performance of base algorithms.
Figure 3. Mean performance of CC and CCC (averaged over the four datasets) as a function of the number of constraints, compared to minimum, average, and maximum performance of base algorithms.
Preprints 81271 g003
Preprints 81271 g004
Figure 4. A specialized double-constrained consensus clustering architecture for web anti-counterfeiting, including generation of base constrained partitions and automatic acquisition of constraints.
Figure 4. A specialized double-constrained consensus clustering architecture for web anti-counterfeiting, including generation of base constrained partitions and automatic acquisition of constraints.
Preprints 81271 g004
Preprints 81271 g005
Figure 5. An example of two fake webshops grouped in a same cluster.
Figure 5. An example of two fake webshops grouped in a same cluster.
Preprints 81271 g005
Preprints 81271 g006
Figure 6. Performance of clustering algorithms as a function of clustering features.
Figure 6. Performance of clustering algorithms as a function of clustering features.
Preprints 81271 g006
Preprints 81271 g007
Figure 7. Performance of clustering features as a function of clustering algorithms.
Figure 7. Performance of clustering features as a function of clustering algorithms.
Preprints 81271 g007
Table 1. Example database with explicit and implicit (in bold) constraints.
Table 1. Example database with explicit and implicit (in bold) constraints.
o 1 o 2 o 3 o 4 o 5
o 1
o 2 1
o 3 1 1
o 4 -1 -1 -1
o 5
Table 2. The (double-)Constrained Consensus Clustering (CCC) algorithm.
Table 2. The (double-)Constrained Consensus Clustering (CCC) algorithm.
Input:
A set O of n objects
A set SP of q (constrained) partitions { Π 1 , . . . , Π q } o f O
A set ML of must-link constraints
A set CL of cannot-link constraints
Output:
A partition Π c of O
1. Find D e d ( { M L } ∪ { C L } ) .
2. Set Π c to the input partition with the highest Ψ c similarity with SP.
3. Assign an object in Π c to a different (possibly empty) cluster such that
the newly created partition Π ′ has a higher Ψ c similarity with SP than Π c .
4. Update Π c to Π ′ .
5. Iterate between (3) and (4) until no partition with a higher Ψ c has been found.
6. Return Π c .
Table 3. Features and constraints of the four UCI datasets: Glass Identification (GI), Seeds (S), User Knowledge Modeking (UKM), Vertebral Column (VC).
Table 3. Features and constraints of the four UCI datasets: Glass Identification (GI), Seeds (S), User Knowledge Modeking (UKM), Vertebral Column (VC).
Dataset objects attributes classes must-links cannot-links must-links cannot-links
in the cover in the cover (total no.) (total no.)
GI 214 10 6 208 208 5921 16870
S 210 7 3 207 207 7245 14700
UKM 258 5 4 254 282 9460 23693
VC 310 6 3 307 340 17895 30000
Table 4. Performance of CCC on the eight hclust algorithms for each clustering feature (first column) as the number of constraints grows from 0 to 80.
Table 4. Performance of CCC on the eight hclust algorithms for each clustering feature (first column) as the number of constraints grows from 0 to 80.
feature min max avg 0 (CC) 10 20 30 40 50 60 70 80
Dom 0.47 0.85 0.65 0.70 0.65 0.72 0.72 0.77 0.78 0.79 0.79 0.91
(8%) (0%) (11%) (11%) (18%) (20%) (22%) (22%) (40%)
Header30 0.30 0.69 0.55 0.69 0.68 0.62 0.71 0.72 0.76 0.81 0.82 0.87
(25%) (24%) (13%) (29%) (31%) (38%) (47%) (49%) (58%)
Header60 0.30 0.69 0.54 0.68 0.68 0.68 0.71 0.72 0.75 0.80 0.81 0.86
(26%) (26%) (26%) (31%) (33%) (39%) (48%) (50%) (59%)
Header90 0.30 0.69 0.58 0.69 0.73 0.71 0.70 0.72 0.75 0.81 0.82 0.85
(19%) (26%) (22%) (21%) (24%) (29%) (40%) (41%) (47%)
Header120 0.29 0.69 0.56 0.66 0.67 0.65 0.72 0.70 0.73 0.79 0.81 0.85
(18%) (20%) (16%) (29%) (25%) (30%) (41%) (45%) (52%)
Header150 0.33 0.69 0.57 0.68 0.66 0.62 0.72 0.72 0.75 0.80 0.81 0.86
(19%) (16%) (9%) (26%) (26%) (32%) (40%) (42%) (51%)
Privacy 0.61 0.76 0.72 0.76 0.74 0.76 0.80 0.80 0.80 0.84 0.85 0.87
(6%) (3%) (6%) (11%) (11%) (11%) (17%) (18%) (21%)
Shipping 0.47 0.72 0.65 0.72 0.72 0.73 0.75 0.77 0.76 0.79 0.80 0.87
(11%) (11%) (12%) (15%) (18%) (17%) (22%) (23%) (34%)
avg 0.38 0.72 0.60 0.70 0.69 0.69 0.73 0.74 0.76 0.80 0.81 0.87
(17%) (15%) (15%) (22%) (23%) (27%) (33%) (35%) (45%)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated