Submitted:
28 July 2023
Posted:
01 August 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
1.1. Radiational energy loss in vacuum
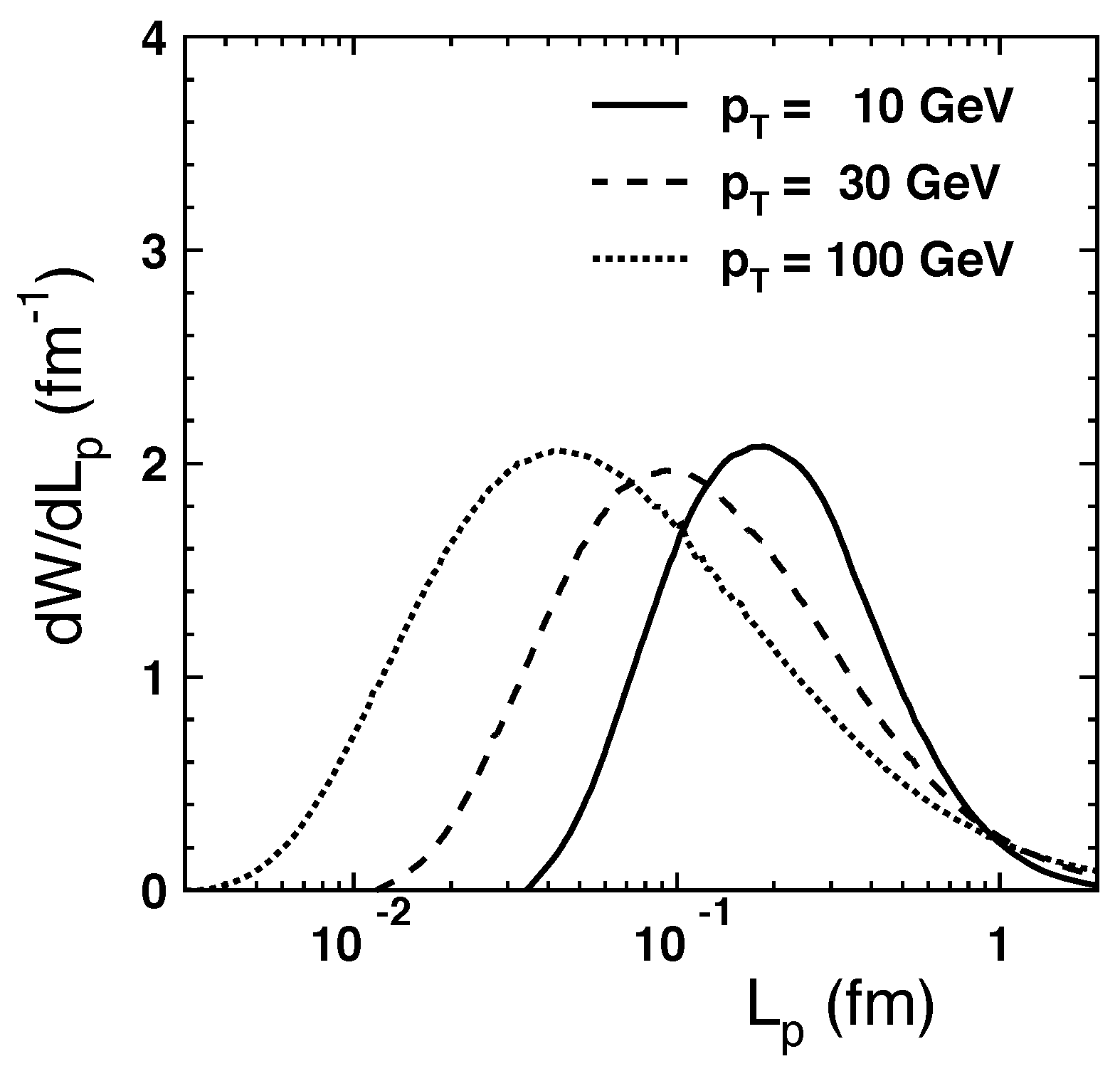
2. Production length
3. Fragmentation in a dense medium
3.1. Formation length of a meson
3.2. Attenuation of dipoles propagating in a dense medium
3.3. Medium modified production rate
3.4. Data analysis
4. Summary
- Heavy and light quarks originated from hard collisions radiate differently. The former is subject to the dead-cone effect, suppressing radiation of low- gluons. Consequently heavy quarks regenerate their color field much faster than light ones and radiate a significantly smaller fraction of the initial energy. The heavier is a quark, the less it radiates.
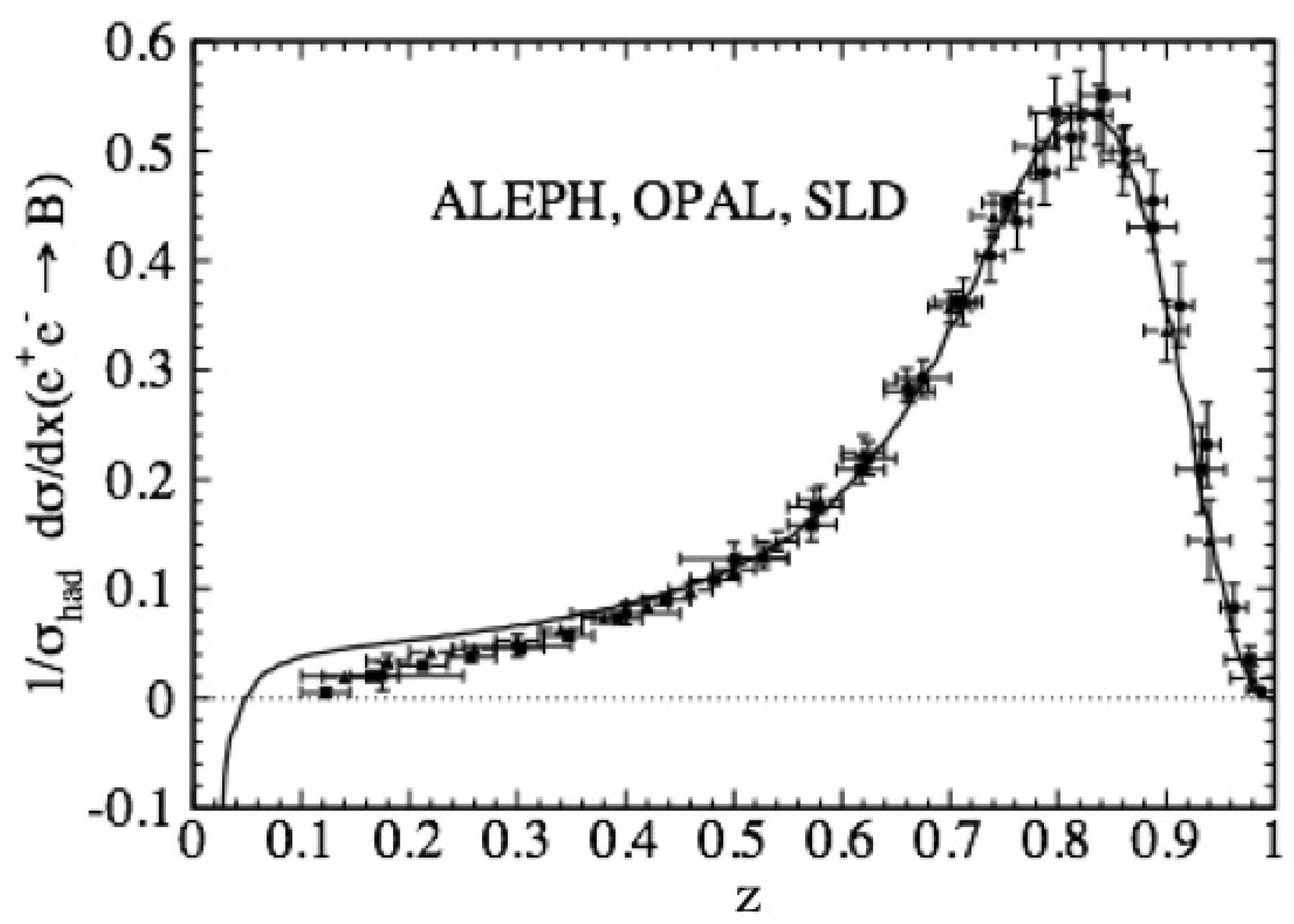
- The fragmentation function usually depends on two variables , fractional light-cone momentum of produced meson, and the scale . However, we consider here the case of "maximal" scale, when the jet energy and the hard scale coincide. This happens e.g. in annihilation, or high- jet production at Feynman .
- The dead-cone effect suppressing bremsstrahlung of heavy quarks, explains the unusual shape of the fragmentation function of heavy quarks , observed at LEP and SLAC. It peaks at large fractional momentum z, i.e. the produced heavy-light mesons, B or D, carry the main fraction of the jet momentum. On the contrary, the fragmentation function of light quarks is falling steadily with z towards .
- Differently from propagation of a small dipole, which survives in the medium due to color transparency, a dipole promptly expands to a large transverse size, controlled by the small mass of the light quark. Such a big dipole has no chance to remain intact in a hot medium. On the other hand, a breakup of such a dipole hardly affects the production rate of mesons.
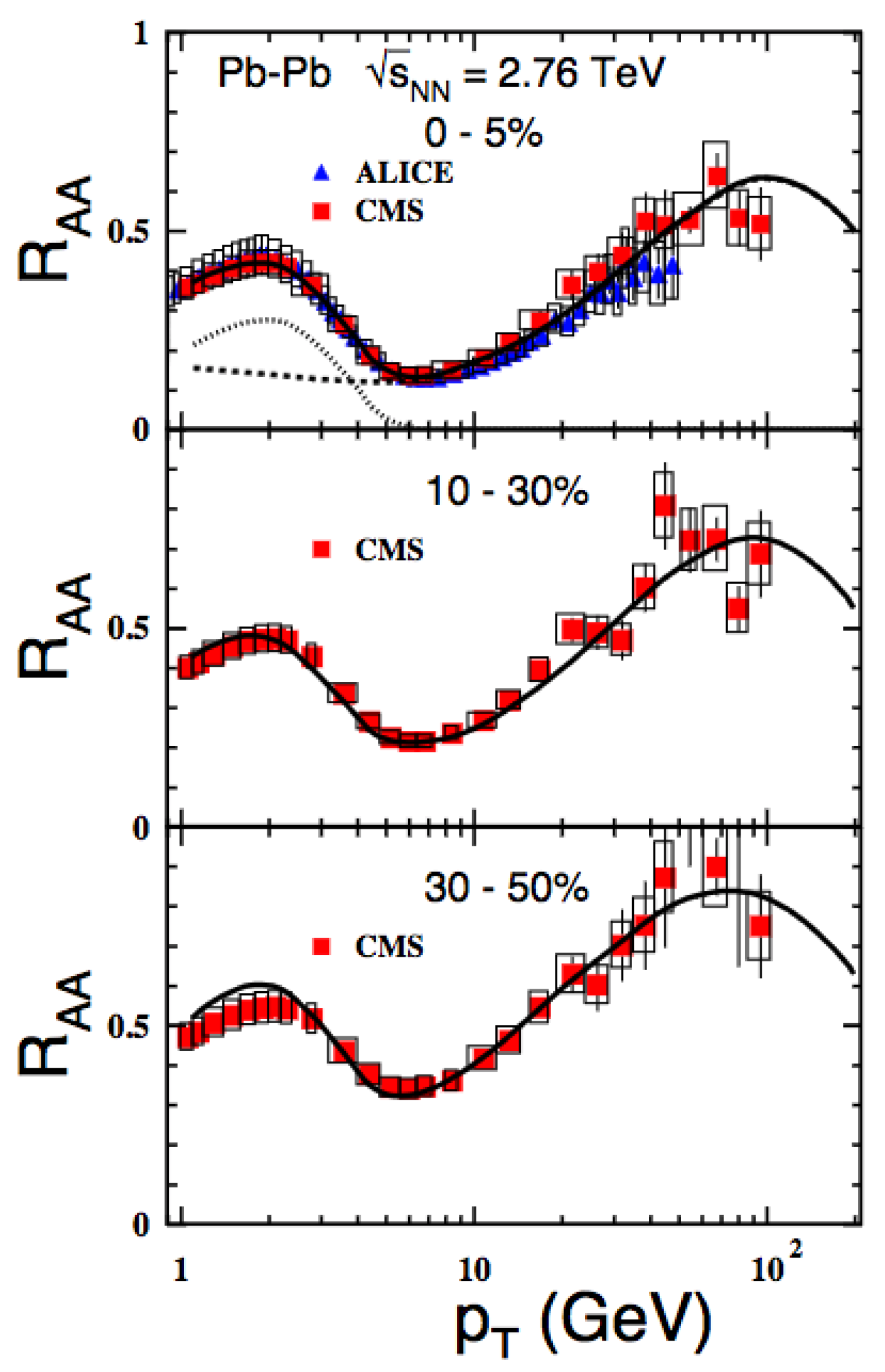
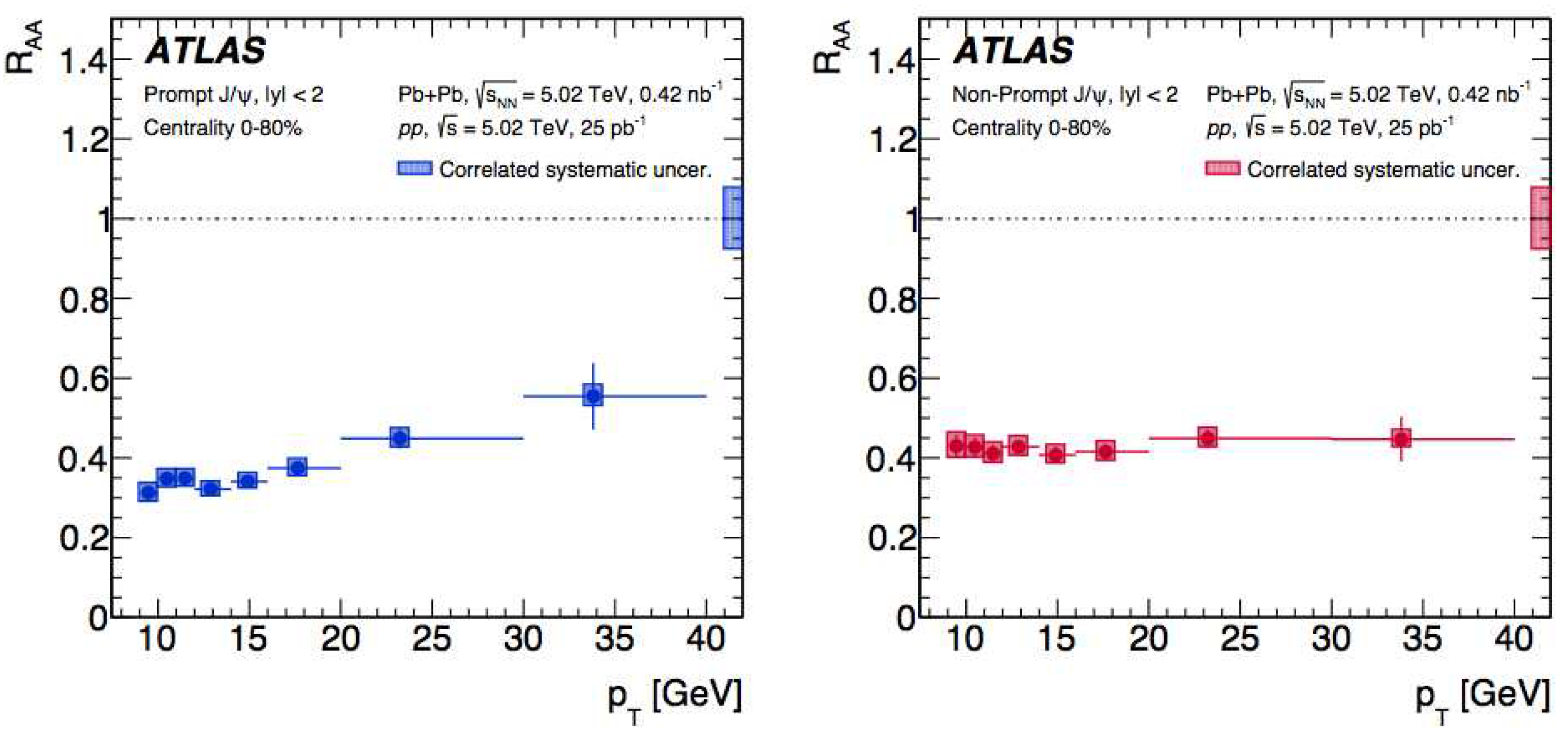
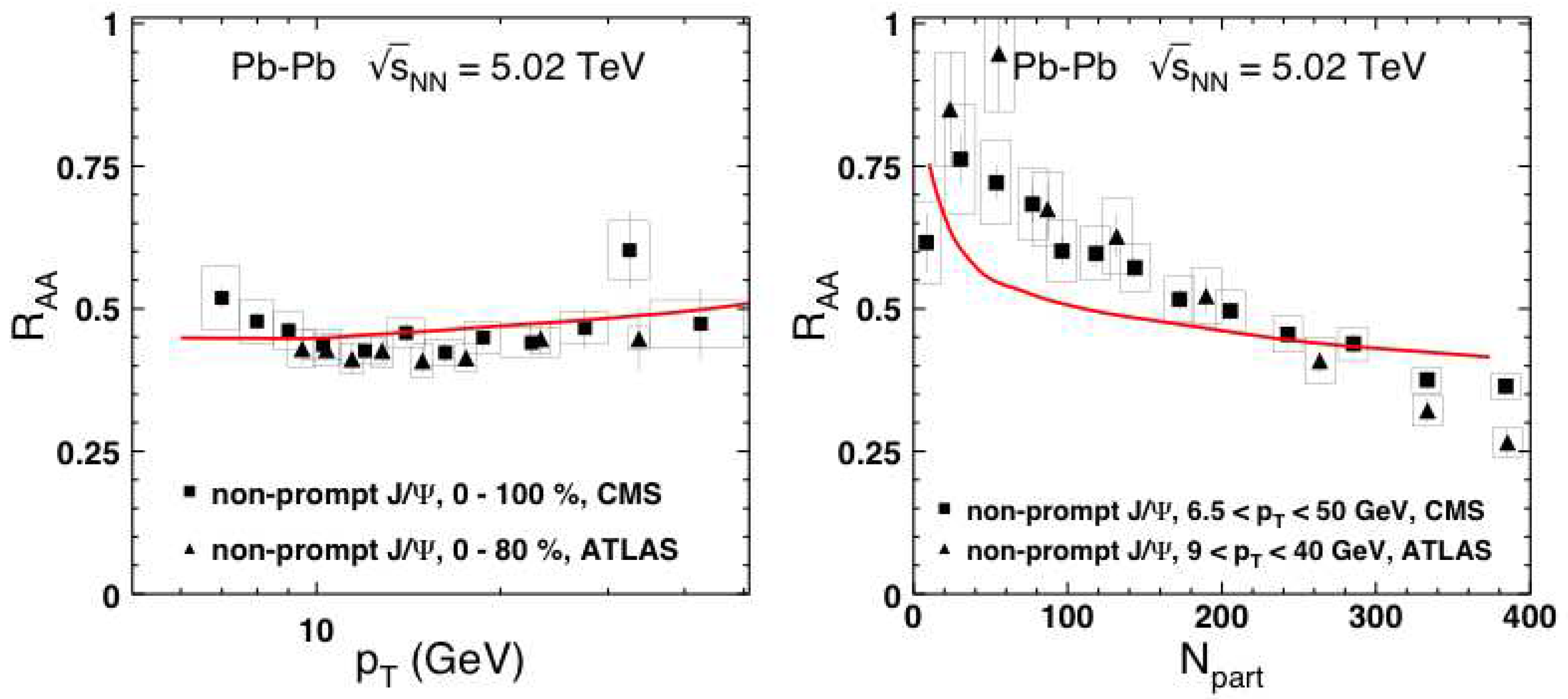
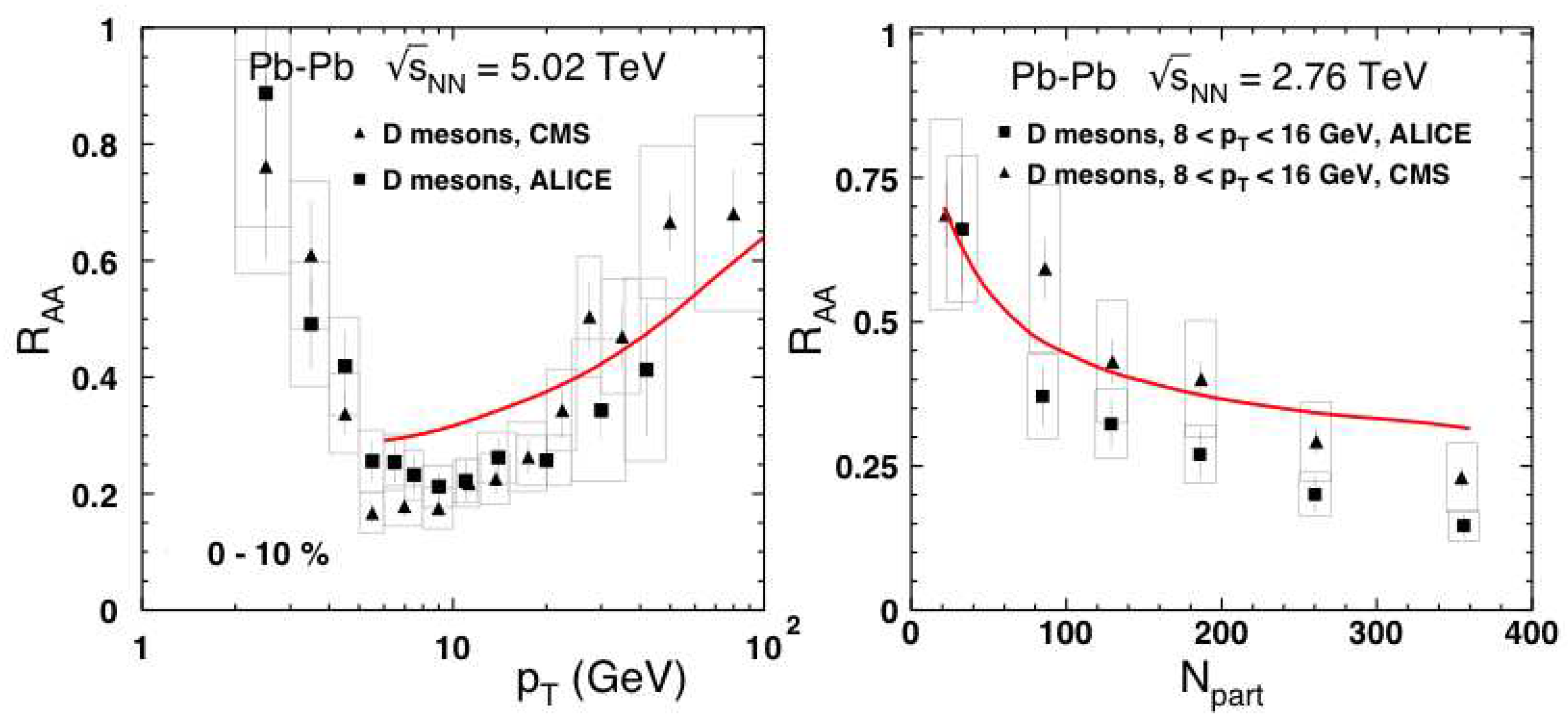
- We successfully described data on and centrality dependence of the production rate of B and D mesons in heavy ion collisions. The only unavoidable parameter of such analyses is the broadening rate (usually called transport coefficient) of the quark in the medium. Its maximal value was found , and for b, c and light quarks respectively. Such hierarchy of the broadening rates is related to the same dead-cone effect.Suppression of bremsstrahlung leads to a considerable reduction of broadening.
Acknowledgments
References
- Landau, L.D.; Pomeranchuk, I. Limits of applicability of the theory of bremsstrahlung electrons and pair production at high-energies, Dokl. Akad. Nauk Ser. Fiz., 1953, 92, 535.
- Dokshitzer, Y.L.; Khoze, V.A.; Troian, S.I. On specific QCD properties of heavy quark fragmentation (’dead cone’). J. Phys. G 1991, 17, 1602–1604. [Google Scholar] [CrossRef]
- Kopeliovich, B.Z.; Potashnikova, I.K.; Schmidt, I. Why heavy and light quarks radiate energy with similar rates. Phys. Rev. C 2010, 82, 037901–037904. [Google Scholar] [CrossRef]
- Kniehl, B.A.; Kramer, G; Schienbein, I.; Spiesberger, H. Finite-mass effects on inclusive B meson hadroproduction. Phys. Rev. D 2008, 77, 014011-014038. [CrossRef]
- Kneesch, T.; Kniehl, B.A.; Kramer, G; Schienbein, I. Charmed-meson fragmentation functions with finite-mass corrections, Nucl. Phys. B 2008, 799, 34-69. [CrossRef]
- Kopeliovich, B.Z.; Pirner, H.-J.; Potashnikova, I.K.; Schmidt, I.; Tarasov, A.V. Perturbative fragmentation, Phys. Rev. D 2008, 77, 054004–054014. [Google Scholar] [CrossRef]
- Hwang, C.W. Charge radii of light and heavy mesons, Eur. Phys. J. C 2002, 23, 585–596. [Google Scholar] [CrossRef]
- Aaboud, M.; Aad, G.; Abbott, B.; et al. Prompt and non-prompt J/ψ and ψ(2S) suppression at high transverse momentum in 5.02 TeV Pb+Pb collisions with the ATLAS experiment, Eur. Phys. J. C 2018, 78, 762-797,.
- Dokshitzer, Y.L.; Kharzeev, D.E. Heavy quark colorimetry of QCD matter, Phys. Lett. B 2001, 519, 199–214. [Google Scholar] [CrossRef]
- Toki, H.; Sasaki, S.; Ichie, H.; Suganuma, H. Chiral symmetry breaking in the dual Ginzburg-Landau theory, Austral. J. Phys. 1997, 50, 199–206. [Google Scholar] [CrossRef]
- Kopeliovich, B.Z.; Schäfer, A.; Tarasov, A.V. Bremsstrahlung of a quark propagating through a nucleus, Phys. Rev. C 1999, 59, 1609–1619. [Google Scholar] [CrossRef]
- Kopeliovich, B.Z.; Schäfer, A.; Tarasov, A.V. Nonperturbative effects in gluon radiation and photo-production of quark pairs, Phys. Rev. D 2000, 62, 054022–054080. [Google Scholar] [CrossRef]
- Chen, X.F.; Greiner, C.; Wang, E.; Wang, X.N.; Xu, Z. Bulk matter evolution and extraction of jet transport parameter in heavy-ion collisions at RHIC,’ Phys. Rev. C 2010, 81, 064908–064921. [Google Scholar] [CrossRef]
- Sirunyan, A.M.; et al. Measurement of the B± Meson Nuclear Modification Factor in Pb-Pb Collisions at =5.02TeV, Phys. Rev. Lett. 2017, 119, no.15, 152301-152305. [CrossRef]
- Acharya, S.; et al. Measurement of D0, D+, D*+ and Ds+ production in Pb-Pb collisions at =5.02TeV, JHEP 2018, 1810, 174-209. [CrossRef]
- Sirunyan, A.M.; et al. Nuclear modification factor of D0 mesons in PbPb collisions at =5.02TeV, Phys. Lett. B 2018, 782, 474-496. [CrossRef]
- Baier, R.; Dokshitzer, Y.L.; Mueller, A.H.; Peigne, S.; Schiff, D. Radiative energy loss and p(T) broadening of high-energy partons in nuclei, Nucl. Phys. B 1997, 484, 265–283. [Google Scholar] [CrossRef]
- Kopeliovich, B.Z.; Pirner, H.-J.; Potashnikova, I.K.; Schmidt, I. Mutual boosting of the saturation scales in colliding nuclei, Phys. Lett. B, 2011, 697, 333-344. [CrossRef]
- Johnson, M.B.; Kopeliovich, B.Z.; Tarasov, A.V. Broadening of transverse momentum of partons propagating through a medium, Phys. Rev. C 2001, 63, 035203–035230. [Google Scholar] [CrossRef]
- Kopeliovich, B.Z.; Potashnikova, I.K.; Povh, B.; Schmidt, I. Evidences for two scales in hadrons, Phys. Rev. D 2007, 76, 094020–094035. [Google Scholar] [CrossRef]
- Kopeliovich, B.Z.; Nemchik, J; Potashnikova, I.K.; Schmidt, I. Quenching of high-pT hadrons: Energy Loss vs Color Transparency, Phys. Rev. C 2012, 86, 054904-054921. [CrossRef]
- Nemchik, J.; Karpenko, I.A.; Kopeliovich, B.Z.; Potashnikova, I.K.; Sinyukov, Y.M., High-pT hadrons from nuclear collisions: Unifying pQCD with hydrodynamics, 2013, Proceedings, 15th conference on Elastic and Diffractive scattering (EDS Blois 2013), 9-13 September 2013. Saariselka, Lapland, Finland [arXiv:1310.3455].
- Abelev, B.; et al. Centrality dependence of charged particle production at large transverse momentum in Pb-Pb collisions at =2.76TeV, Phys. Lett. B 2013, 720, 52-62. [CrossRef]
- Lee, Y.-J.; (for the CMS Collaboration), Quarkonia Measurements by the CMS Experiment in pp and Pb-Pb Collisions, J. Phys. G 2011, 38, 124015-124023. [CrossRef]
- Yoon, A.S.; (for the CMS Collaboration), Centrality and pT dependence of charged particle RAA in Pb-Pb collisions at =2.76TeV, J. Phys. G 2011, 38, 124116-124122. [CrossRef]

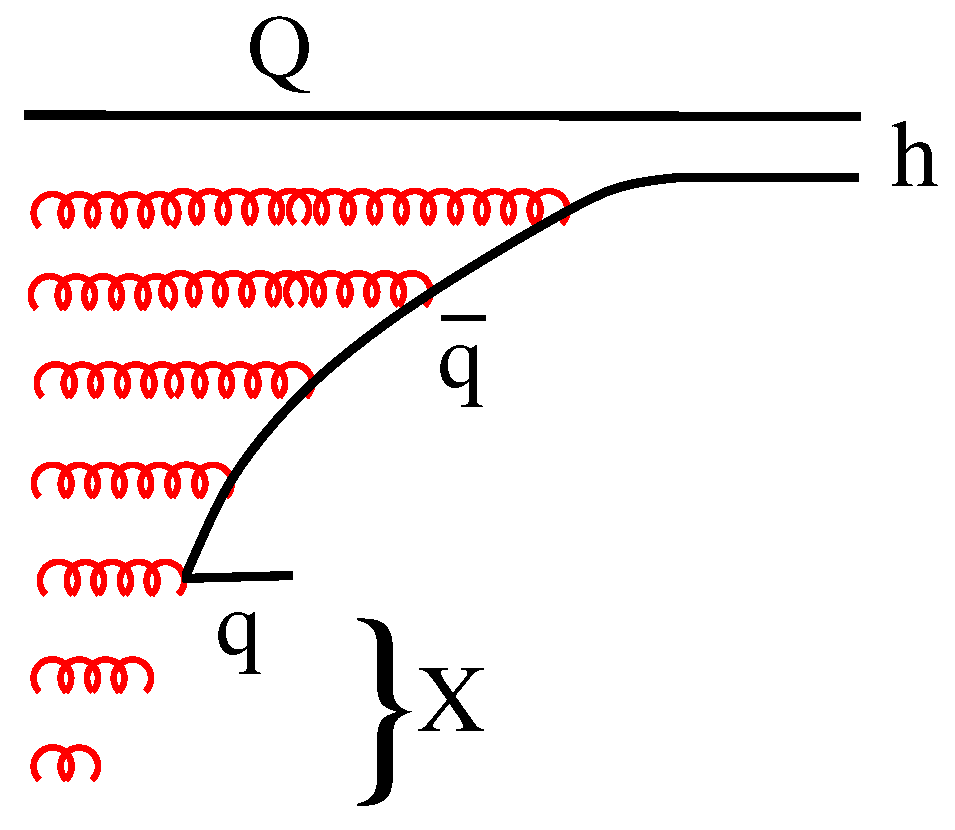
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).