Single Photon Superadiance and Subradiance as Collective Emission from Symmetric and Anti-Symmetric States

Preprint

Article

Single Photon Superadiance and Subradiance as Collective Emission from Symmetric and Anti-Symmetric States

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

27 July 2023

Posted:

28 July 2023

You are already at the latest version

Alerts

Abstract

Recent works have shown that collective single photon spontaneous emission from an ensemble of N resonant two-level atoms is a rich field of study. Superradiance describes emission from a completely symmetric state of N atoms, with a single excited atom prepared with a given phase, for instance imprinted by an external laser. Instead, subradiance is associated with the emission from the remaining N−1 asymmetric states, with a collective decay rate less than the single-atom value. Here, we discuss the properties of the orthonormal basis of symmetric and asymmetric states and the entanglement properties of superradiant and subradiant states.

Keywords:

Subject: Physical Sciences - Quantum Science and Technology

1. Introduction

Cooperative light scattering by a system of N two-level atoms has been a topic studied since many years [1]. Many studies in the past have been focused on a diffusive regime dominated by multiple scattering [2], where light travels over distances much larger than the mean free path. More recently, it has been shown that light scattering in dilute systems induces a dipole-dipole interaction between atom pairs, leading to a different regime dominated by single scattering of photons by many atoms. The transition between single and multiple scattering is controlled by the optical thickness parameter

b (Δ) = b_{0} / (1 + 4 Δ^{2} / Γ^{2})

[3,4], where

b_{0}

is the resonant optical thickness,

Δ

is the detuning of the laser frequency from the atomic resonance frequency and

Γ

is the single atom decay rate. A different cooperative emission is provided by superradiance and subradiant, both originally predicted by Dicke in 1954 [5] in fully inverted system. Whereas Dicke superradiance is based on constructive interference between many emitted photons, subradiance is a destructive interference effect leading to the partial trapping of light in the system. Dicke states have been considered for an assembly of N two-level systems, realized, e.g., by atoms [6] or quantum dots [7]. In contrast to an initially fully inverted system with N photons stored by N atoms, states with at most one single excitation have attracted increasing attention in the context of quantum information science [8,9,10], where the accessible Hilbert space can be restricted to single excitations by using, e.g., the Rydberg blockade [11,12,13]. A particular kind of single-excitation superradiance has been proposed by Scully and coworkers [14,15,16], in a system of N two-level atoms prepared by the absorption of a single photon (Timed Dicke state). A link between this single-photon superradiance and the more classical process of cooperative scattering of an incident laser by N atoms has been proposed by a series of theoretical and experimental papers [17,18,19,20,21]. In such systems of driven cold atoms subradiance has been also predicted [22] and then observed [23], after that the laser is abruptly switched off and the emitted photons detected in a given direction. Subradiance, by itself, has attracted a large interest of its application in the quantum optics as a possible method to control the spontaneous emission, storing the excitation for a relatively long time. A crucial point is to determine if such subradiant states are entangled or not, in view of a possible application as quantum memories.

The aim of this paper is to provide a mathematical description of the single-excitation states in terms of superradiant and subradiant states, i.e. separating the fully symmetric state by the remaining antisymmetric ones. Symmetric and subradiant excited states are distinguished by their decay rates, once populated by a classical external laser and observed after that the laser is switched off: the symmetric state has a superradiant decay rate proportional to

N Γ

, where

Γ

is the single-atom decay, whereas the antisymmetric states have a decay rate slower than

Γ

. Once characterized the time evolution of these states, we will apply the criteria of the spin squeezing inequalities introduced by Tóth [24] to detect entanglement in the superradiant and subradiant states. We outline that we limit our study to the linear regime, where the excitation amplitude is proportional to the driving incident electric field. In this linear regime, we must consider the entanglement criteria which are independent on the value of the driving field, i.e. abandoning these criteria which lead to expressions which depend nonlinearly from the driving field, as it will be discussed in the following.

The paper is organized as follow. In Section 2 we present the Hamiltonian describing the dynamics of N two-level atoms interacting with the driving field and write the equation of motion in the linear regime. Then we calculate the decay rate and the transition rates between different elements of the so-called Timed-Dicke basis with its symmetric and antisymmetric states. Section 3 introduces the collective spin operator and the formalism of the spin-squeezing inequalities to assess entanglement. Conclusions are eventually drawn in Section 4.

2. The model

We consider

N ≫ 1

two-level atoms with the same atomic transition frequency

ω_{a}

, linewidth

Γ

and dipole d (polarization effects are neglected). The atoms are driven by a monochromatic plane wave with electric field

E_{0}

, frequency

ω_{0}

and wave vector

k_{0}

, detuned from the atomic transition by

Δ_{0} = ω_{0} - ω_{a}

. If

| g_{j} 〉

and

| e_{j} 〉

are the ground and excited states, respectively, of the j-th atom,

j = 1, \dots, N

, which is placed at position

r_{j}

, the dynamics of the whole system is described by the effective Hamiltonian

\hat{H} = {\hat{H}}_{0} - i {\hat{H}}_{eff}

, where [25]

\begin{matrix} {\hat{H}}_{0} = - ℏ Δ_{0} \sum_{j = 1}^{N} {\hat{σ}}_{j}^{†} {\hat{σ}}_{j} + \frac{ℏ Ω_{0}}{2} \sum_{j = 1}^{N} ({\hat{σ}}_{j} e^{- i k_{0} \cdot r_{j}} + {\hat{σ}}_{j}^{†} e^{i k_{0} \cdot r_{j}}) \end{matrix}

(1)

\begin{matrix} {\hat{H}}_{eff} = \frac{ℏ Γ}{2} \sum_{j, m} G_{j m} {\hat{σ}}_{j}^{†} {\hat{σ}}_{m} . \end{matrix}

(2)

Here

Ω_{0} = d E_{0} / ℏ

is the Rabi frequency,

{\hat{σ}}_{j} = | g_{j} 〉 〈 e_{j} |

and

{\hat{σ}}_{j}^{†} = | e_{j} 〉 〈 g_{j} |

are the lowering and raising operators and

G_{j m} = \{\begin{matrix} Γ_{j m} - i Ω_{j m} & i f j \neq m, \\ 1 & i f j = m, \end{matrix}

(3)

where

Γ_{j m} = \frac{sin (k_{0} r_{j m})}{k_{0} r_{j m}} and Ω_{j m} = \frac{cos (k_{0} r_{j m})}{k_{0} r_{j m}} .

(4)

In this paper we consider the case in which only one atom among N can be found in the excited states, whereas all the others are in their ground state. Therefore, we have a

(N + 1)

-dimensional Hilbert space and a generic state

| Ψ 〉

of the our system can be written as [14,26]

| Ψ 〉 = α | g 〉 + \sum_{j = 1}^{N} β_{j} e^{i k_{0} \cdot r_{j}} | j 〉

(5)

where

| g 〉 = | g_{1}, \dots, g_{N} 〉

and

| j 〉 = | g_{1}, \dots, e_{j}, \dots, g_{N} 〉

j = 1, \dots, N

. Starting from the Schrödinger equation

i ℏ \frac{\partial | Ψ 〉}{\partial t} = ({\hat{H}}_{0} - i {\hat{H}}_{eff}) | Ψ 〉 .

(6)

and assuming

α \approx 1

in the linear regime of weak excitation, we obtain the following equations for the coefficients

β_{j}

of the state (5):

\begin{matrix} {\dot{β}}_{j} & = (i Δ_{0} - \frac{Γ}{2}) β_{j} - \frac{i Ω_{0}}{2} - \frac{Γ}{2} \sum_{m \neq j} {\tilde{G}}_{j m} β_{m} (t), (j = 1, \dots, N) \end{matrix}

(7)

where

{\dot{β}}_{j}

refers to the time derivative of the coefficient

β_{j}

and

{\tilde{G}}_{j m} = G_{j m} e^{- i k_{0} \cdot (r_{j} - r_{m})}

The use of the bare basis

{| g 〉, | j 〉}

has the advantage that Eq. (7) can be easily solved numerically. However, it does not distinguish between symmetric and anti-symmetric states, that play a relevant role in our investigation. For this reason we introduce the Timed-Dicke (TD) basis with a single excitation [15,27]:

\{{| g 〉, | + 〉}_{k_{0}} {, | 1 〉}_{k_{0}}, \dots, {| N - 1 〉}_{k_{0}}\},

(8)

where

| g 〉

has been introduced above, whereas

{| + 〉}_{k_{0}} = \frac{1}{\sqrt{N}} \sum_{j = 1}^{N} e^{i k_{0} \cdot r_{j}} | j 〉

(9)

is the symmetric Timed–Dicke (STD) state and

{| s 〉}_{k_{0}} = \frac{1}{\sqrt{s (s + 1)}} \{\sum_{j = 1}^{s} e^{i k_{0} \cdot r_{j}} | j 〉 - s e^{i k_{0} \cdot r_{s + 1}} | s + 1 〉\}, (s = 1, \dots, N - 1)

(10)

are the anti-symmetric ones. The advantage of using the TD basis is that

{| s 〉}_{k_{0}}

are collective states involving

s + 1

atoms. It is easy to verify that, within the considered Hilbert space, the TD basis is complete, namely:

{| g 〉 〈 g | + | + 〉}_{k_{0}} 〈 + | + \sum_{s = 1}^{N - 1} {| s 〉}_{k_{0}} 〈 s | = \hat{I}

(11)

and orthonormal, since

{〈 g | + 〉}_{k_{0}} = {〈 g | s 〉}_{k_{0}} =_{k_{0}} {〈 + | s 〉}_{k_{0}} = 0

, and

_{k_{0}} {〈 s | s^{'} 〉}_{k_{0}} = δ_{s, s^{'}}

To highlight the physical meaning of the TD states, it is useful to evaluate the following transition rates between the basis elements. On the one hand we find

\begin{matrix} _{k_{0}} 〈 + | {\hat{H}}_{0} {| + 〉}_{k_{0}} = - ℏ Δ_{0} and_{k_{0}} 〈 + | {\hat{H}}_{eff} {| + 〉}_{k_{0}} = \frac{ℏ Γ_{+}}{2} - i ℏ Ω_{+} \end{matrix}

(12)

with

{\hat{H}}_{0}

and

{\hat{H}}_{eff}

given in Eqs. (1) and (), respectively, and

\begin{matrix} Γ_{+} & = Γ (1 + \frac{1}{N} \sum_{j = 1}^{N} \sum_{\binom{m = 1}{(m \neq j)}}^{N} {\tilde{Γ}}_{j m}), \end{matrix}

(13)

\begin{matrix} Ω_{+} & = \frac{Γ}{N} \sum_{j = 1}^{N} \sum_{\binom{m = 1}{(m \neq j)}}^{N} {\tilde{Ω}}_{j m} \end{matrix}

(14)

where

{\tilde{Γ}}_{j m} = Γ_{j m} cos [k_{0} \cdot (r_{j} - r_{m})] and {\tilde{Ω}}_{j m} = Ω_{j m} cos [k_{0} \cdot (r_{j} - r_{m})]

(15)

and

Γ_{j m}

and

Ω_{j m}

have been introduced in Eq. (4). For a cloud of cold atoms with a Gaussian distribution with parameter

σ_{r}

, one can prove that

Γ_{+} \approx Γ (1 + b_{0} / 12)

[18,25], where

b_{0} = 3 N / σ^{2}

is the resonant optical thickness, with

σ = k_{0} σ_{r}

. Thus we can conclude that

{| + 〉}_{k_{0}}

is a superradiant state for very large

b_{0}

[15,16].

On the other hand, the transition rates for the states

{| s 〉}_{k_{0}}

s = 1, \dots, N - 1

, read

\begin{matrix} _{k_{0}} 〈 s | {\hat{H}}_{0} {| s 〉}_{k_{0}} = - ℏ Δ_{0} and_{k_{0}} 〈 s | {\hat{H}}_{eff} {| s 〉}_{k_{0}} = \frac{ℏ Γ_{s}}{2} - i ℏ Ω_{s} \end{matrix}

(16)

with

\begin{matrix} Γ_{s} = Γ [1 + \frac{1}{s + 1} (\frac{1}{s} \sum_{j = 1}^{s} \sum_{\binom{m = 1}{(m \neq j)}}^{s} {\tilde{Γ}}_{j m} - 2 \sum_{j = 1}^{s} {\tilde{Γ}}_{j, s + 1})], \end{matrix}

(17)

\begin{matrix} Ω_{s} = \frac{Γ}{2 (s + 1)} (\frac{1}{s} \sum_{j \neq m = 1}^{s} {\tilde{Ω}}_{j m} - 2 \sum_{j = 1}^{s} {\tilde{Ω}}_{j, s + 1}) . \end{matrix}

(18)

In this case the decay rates

Γ_{s}

are less than the single-atom decay rate

Γ

and the states

{| s 〉}_{k_{0}}

turn out to be subradiant [26].

Now we focus on the state (5), that in the TD basis reads

| Ψ 〉 = α | g 〉 + β_{+} {| + 〉}_{k_{0}} + \sum_{s = 1}^{N - 1} γ_{s} {| s 〉}_{k_{0}},

(19)

with

\begin{matrix} β_{+} & =_{k_{0}} 〈 + | Ψ 〉 = \frac{1}{\sqrt{N}} \sum_{j = 1}^{N} β_{j}, \end{matrix}

(20)

\begin{matrix} γ_{s} & =_{k_{0}} 〈 s | Ψ 〉 = \frac{1}{\sqrt{s (s + 1)}} (\sum_{j = 1}^{s} β_{j} - s β_{s + 1}) . \end{matrix}

(21)

Thanks to the considerations made above about the properties of the TD states, we can easily find the probability to find our state in a superradiant, i.e. STD, and subradiant state, that is:

P_{+} = {| β_{+} |}^{2}

(22)

and

P_{sub} = \sum_{s = 1}^{N - 1} {| γ_{s} |}^{2},

(23)

respectively. Moreover, from the normalization of the state

| Ψ 〉

it follows that

\begin{matrix} \sum_{j = 1}^{N} {| β_{j} |}^{2} & = | β_{+} |^{2} + \sum_{s = 1}^{N - 1} {| γ_{s} |}^{2} = P_{+} + P_{sub} . \end{matrix}

(24)

Finally, the superradiant fraction of excited atoms is given by

f_{SR} = \frac{P_{+}}{P_{+} + P_{sub}} = \frac{{|\bar{β}|}^{2}}{\bar{{| β |}^{2}}}

(25)

where we introduced the mean quantities:

\begin{matrix} \bar{{| β |}^{2}} = \frac{1}{N} \sum_{j = 1}^{N} {| β_{j} |}^{2} \end{matrix}

(26)

\begin{matrix} |\bar{β}| = \frac{1}{N} |\sum_{j = 1}^{N} β_{j}| . \end{matrix}

(27)

and, in turn, the subradiant fraction is

f_{sub} = 1 - f_{SR}

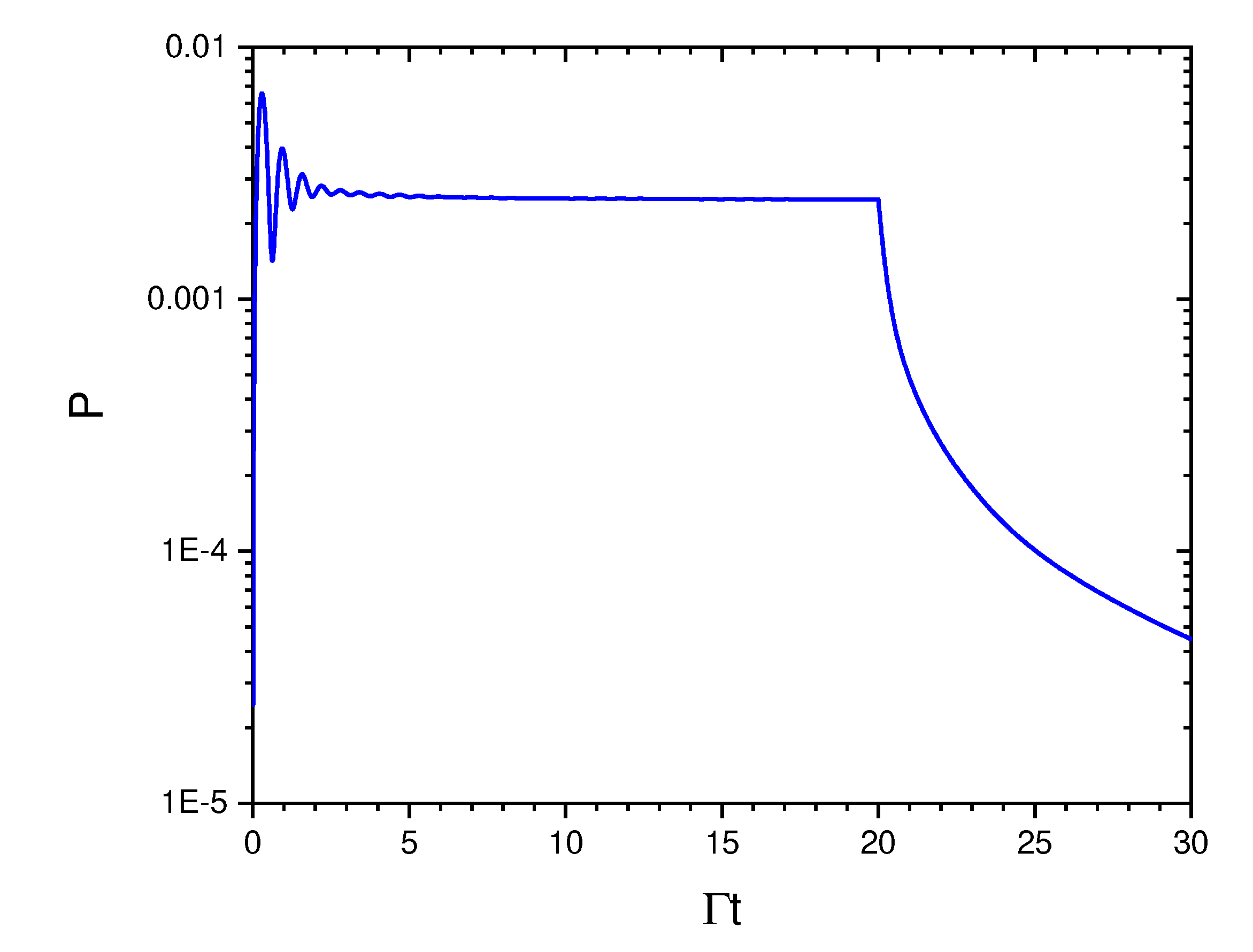
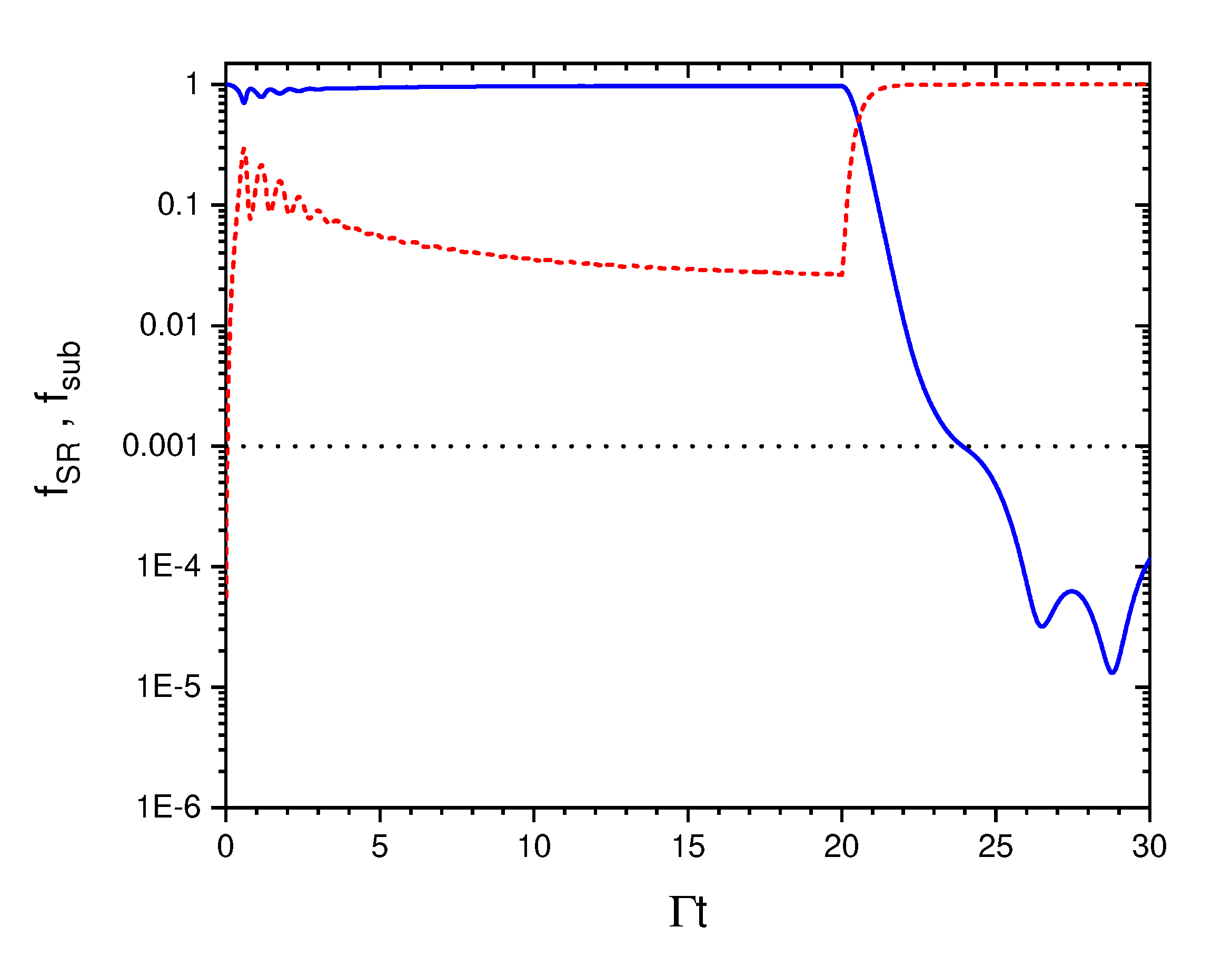
3. Entanglement properties of the superradiant and subradiant collective states

As the system we are investigating it this paper consists in a large number of atoms,

N ≫ 1

, we cannot asses its entanglement properties by individually addressing the single particles. Nevertheless, it is known that spin squeezing can be used to create large scale entanglement [28]. Therefore, here we consider suitable generalized spin squeezing inequalities [24] based only on collective quantities that are accessible and can be measured experimentally.

Given N two-level atoms, we start defining the following collective angular momentum operators:

{\hat{J}}_{k} = \frac{1}{2} \sum_{j = 1}^{N} {\hat{σ}}_{j}^{(k)}, (k = x, y, z)

(28)

where

{\hat{σ}}_{j}^{(k)}

are the Pauli matrices associated with the j-th atom. If we assume the state given by Eq. (5), we can calculate the expectation values of the first and second moments of

{\hat{J}}_{k}

using the result of the previous section (see Appendix A for the details):

\begin{matrix} 〈 {\hat{J}}_{x} 〉 & = ℜ e [α^{*} \sum_{j = 1}^{N} β_{j}], \end{matrix}

(29)

\begin{matrix} 〈 {\hat{J}}_{y} 〉 & = - ℑ m [α^{*} \sum_{j = 1}^{N} β_{j}], \end{matrix}

(30)

\begin{matrix} 〈 {\hat{J}}_{z} 〉 & = - N (\frac{1}{2} - \bar{{| β |}^{2}}), \end{matrix}

(31)

and

\begin{matrix} 〈 {\hat{J}}_{x}^{2} 〉 = 〈 {\hat{J}}_{y}^{2} 〉 = \frac{N}{2} (\frac{1}{2} + N {|\bar{β}|}^{2} - \bar{{| β |}^{2}}), \end{matrix}

(32)

\begin{matrix} 〈 {\hat{J}}_{z}^{2} 〉 = N [\frac{N}{4} - (N - 1) \bar{{| β |}^{2}}], \end{matrix}

(33)

β_{j}

being the solutions of Eq. (7) and

\bar{{| β |}^{2}}

and

|\bar{β}|

are given in Eqs. (26) and (27), respectively. One can also straightforwardly evaluate the corresponding variances

{(Δ {\hat{J}}_{k})}^{2} = 〈 {\hat{J}}_{k}^{2} 〉 - {〈 {\hat{J}}_{k} 〉}^{2}

k = x, y, z

In Ref. [24], G. Tóth and co-workers proved that a sufficient condition to have entanglement is the violation of suitable inequalities involving the first and second moments of the

{\hat{J}}_{k}

operators evaluated above. Though they proposed four inequalities, in our case only one of them is relevant to our system, namely:

{(Δ {\hat{J}}_{x})}^{2} + {(Δ {\hat{J}}_{y})}^{2} + {(Δ {\hat{J}}_{z})}^{2} \geq \frac{N}{2},

(34)

since the other three:

\begin{matrix} 〈 {\hat{J}}_{x}^{2} 〉 + 〈 {\hat{J}}_{y}^{2} 〉 + 〈 {\hat{J}}_{z}^{2} 〉 & \leq \frac{N (N + 2)}{4}, \end{matrix}

(35a)

\begin{matrix} 〈 {\hat{J}}_{k}^{2} 〉 + 〈 {\hat{J}}_{l}^{2} 〉 - \frac{N}{2} & \leq (N - 1) {(Δ {\hat{J}}_{m})}^{2}, \end{matrix}

(35b)

\begin{matrix} (N - 1) [{(Δ {\hat{J}}_{k})}^{2} + {(Δ {\hat{J}}_{l})}^{2}] & \geq 〈 {\hat{J}}_{m}^{2} 〉 + \frac{N (N - 2)}{4} \end{matrix}

(35c)

where

k, l, m

take all the possible permutations of

x, y, z

, are not useful, as the first and the third are never violated, whereas the second one leads to a condition on the

β_{j}

going beyond the linear regime assumed to solve Eq. (6), as shown in Appendix B.

The inequality (34) is more interesting. Its l.h.s. can be rewritten as a function of the superradiant fraction (25), that is:

\begin{matrix} {(Δ {\hat{J}}_{x})}^{2} + {(Δ {\hat{J}}_{y})}^{2} + {(Δ {\hat{J}}_{z})}^{2} & = \frac{N}{2} + N^{2} \bar{{| β |}^{2}} (N | \bar{β} |^{2} - \bar{{| β |}^{2}}) \end{matrix}

(36)

\begin{matrix} = \frac{N}{2} + N^{2} {(\bar{{| β |}^{2}})}^{2} (N f_{SR} - 1), \end{matrix}

(37)

which can be solved within the linear regime assumed throughout the paper. Hence, the Ineq. (34) is violated when the superradiant fraction is

f_{S R} < 1 / N

, then highlighting the entanglement of the collective atomic state. This will occur when the driving laser is cut and the superradiant component decays faster than the subradiant one, until the subradiant fraction becomes larger than

1 - 1 / N

Figure 1 and Figure 2 present a typical result. We evaluate numerically the values of

β_{j}

solving the linear equations (7) for

N = 10^{3}

Δ_{0} = 10 Γ

and a Gaussian distribution with

σ = k_{0} σ_{R} = 10

. The laser is cut off after

Γ t = 20

. Figure 1 shows

P = (1 / N) \sum_{j} {| β_{j} |}^{2}

vs time. Figure 2 shows the superradiant and subradiant fractions,

f_{S R}

(continuous blue line) and

f_{s u b}

(dashed red line), as defined by Eq. (25). The dotted black line is the value

1 / N

. We observe that when the laser is on, the subradiant fraction is only about the

3 %

of the total excitation. As soon as the laser is cut off, the superradiant fraction decays fast and the subradiant fraction increases, becoming dominating for

Γ t > 20.5

. The atoms become entangled when

f_{S R} < 1 / N

, at time larger than

Γ t > 24

4. Conclusions

We have discussed the symmetry properties of the state of N two-level atoms with positions

r_{j}

(with

j = 1, \dots, N

), where only one is excited among N. The single-excitation Hilbert space can be spanned by a completely symmetric, state (the ’Symmetric Timed Dicke state’) and

N - 1

asymmetric ones, where the first has a superradiant decay rate proportional to N, while the others have a subradiant decay rates less than the single-atom value. Remarkably, the projection on the symmetric and asymmetric states allows to calculate the superradiant and subradiant fractions of the ensemble.

One open question is whether the atoms in the superradiant and subradiant fraction are entangled or not. To address this problem, we studied the relevant case of an ensemble of N atoms driven by an external, uniform laser. In the framework of the linear regime, the probability amplitude of excitation is proportional to the incident electric field, and the superradiant fraction is largely dominant, with only a small fraction of atoms in the subradiant states. However, when the laser is cut off, the superradiant fraction rapidly decays to zero, leaving only the subradiant one, as it has been observed in the experiments of Ref. [23].

In order to investigate the entanglement properties of the atomic ensemble, we exploited the spin squeezing inequalities introduced by G. Tóth and cowokers [24], based on the first and the second order moments of collective spin operators. We have found that one of these inequalities is violated when the superradiant fraction decreases below the value

1 / N

. Therefore, to have entanglement the probability of finding N atoms in the superradiant state must be less than the average probability per atom to be in the excited state. Conversely, when the superradiant fraction is larger than

1 / N

no entanglement can be detected by measuring the moments of the collective spin operators.

Author Contributions

All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A. Calculation of the first and second moments of ${\hat{J}}_{k}$

In this appendix we explicitly calculate the first and second moments of the collective angular momentum operators used in the text, namely:

{\hat{J}}_{k} = \frac{1}{2} \sum_{j = 1}^{N} {\hat{σ}}_{j}^{(k)}, (k = x, y, z)

(A1)

where

{\hat{σ}}_{j}^{(k)}

are the Pauli matrices associated with the j-th atom. It is useful introducing the identities

{\hat{σ}}_{j}^{†} = ({\hat{σ}}_{j}^{(x)} + i {\hat{σ}}_{j}^{(y)}) / 2

and

{\hat{σ}}_{j} = ({\hat{σ}}_{j}^{(x)} - i {\hat{σ}}_{j}^{(y)}) / 2

, that are the raising and lowering operators appearing in Eqs. (1) and (2), and

σ_{j}^{(z)} = | e_{j} 〉 〈 e_{j} | - | g_{j} 〉 〈 g_{j} |

. We define

\begin{matrix} {\tilde{σ}}_{j}^{†} = e^{i k_{0} \cdot r_{j}} {\hat{σ}}_{j}^{†}, {\tilde{σ}}_{j} = e^{- i k_{0} \cdot r_{j}} {\hat{σ}}_{j} \end{matrix}

(A2)

and the collective operators:

\begin{matrix} {\hat{J}}_{-} = \sum_{j = 1}^{N} {\tilde{σ}}_{j}, {\hat{J}}_{+} = \sum_{j = 1}^{N} {\tilde{σ}}_{j}^{†} a n d {\hat{J}}_{z} = \frac{1}{2} \sum_{j = 1}^{N} {\hat{σ}}_{j}^{(z)} \end{matrix}

(A3)

with commutation relations:

\begin{matrix} [{\hat{J}}_{+}, {\hat{J}}_{-}] = 2 {\hat{J}}_{z}, [{\hat{J}}_{z}, {\hat{J}}_{\pm}] = \pm 2 {\hat{J}}_{\pm} . \end{matrix}

(A4)

We can now apply the formalism of Ref. [24], calculating the first and second order moments of the collective operators

{\hat{J}}_{x} = ({\hat{J}}_{+} + {\hat{J}}_{-}) / 2

and

{\hat{J}}_{y} = ({\hat{J}}_{+} - {\hat{J}}_{-}) / (2 i)

. Explicitly,

\begin{matrix} 〈 {\hat{J}}_{x} 〉 & = & \frac{1}{2} \{〈 {\hat{J}}_{+} 〉 + 〈 {\hat{J}}_{-} 〉\}, \end{matrix}

(A5)

\begin{matrix} 〈 {\hat{J}}_{y} 〉 & = & \frac{1}{2 i} \{〈 {\hat{J}}_{+} 〉 - 〈 {\hat{J}}_{-} 〉\}, \end{matrix}

(A6)

\begin{matrix} 〈 {\hat{J}}_{x}^{2} 〉 & = & \frac{1}{4} \{〈 {\hat{J}}_{+} {\hat{J}}_{-} 〉 + 〈 {\hat{J}}_{-} {\hat{J}}_{+} 〉 + 〈 {\hat{J}}_{+}^{2} 〉 + 〈 {\hat{J}}_{-}^{2} 〉\}, \end{matrix}

(A7)

\begin{matrix} 〈 {\hat{J}}_{y}^{2} 〉 & = & \frac{1}{4} \{〈 {\hat{J}}_{+} {\hat{J}}_{-} 〉 + 〈 {\hat{J}}_{-} {\hat{J}}_{+} 〉 - 〈 {\hat{J}}_{+}^{2} 〉 - 〈 {\hat{J}}_{-}^{2} 〉\}, \end{matrix}

(A8)

where the expectations are evaluated using the

β_{j}

as evaluated from the Eq. (7) (see Sec. 2). Since:

\begin{matrix} {\tilde{σ}}_{j} | Ψ 〉 & = β_{j} | g 〉, \end{matrix}

(A9)

\begin{matrix} {\tilde{σ}}_{j}^{†} | Ψ 〉 & = α e^{i k_{0} \cdot r_{j}} | j 〉, \\ {\hat{σ}}_{j}^{(z)} | Ψ 〉 & = - α | g 〉 + β_{j} e^{i k_{0} \cdot r_{j}} | j 〉 - \sum_{m = 1}^{N} (1 - δ_{j m}) β_{m} e^{i k_{0} \cdot r_{m}} | m 〉 \end{matrix}

(A10)

\begin{matrix} = - | Ψ 〉 + 2 β_{j} e^{i k_{0} \cdot r_{j}} | j 〉, \end{matrix}

(A11)

we derive

\begin{matrix} 〈 {\hat{J}}_{-} 〉 & = \sum_{j = 1}^{N} 〈 {\tilde{σ}}_{j} 〉 = α^{*} \sum_{j = 1}^{N} β_{j}, \end{matrix}

(A12)

\begin{matrix} 〈 {\hat{J}}_{+} 〉 & = \sum_{j = 1}^{N} 〈 {\tilde{σ}}_{j}^{†} 〉 = α \sum_{j = 1}^{N} β_{j}^{*}, \end{matrix}

(A13)

\begin{matrix} 〈 {\hat{J}}_{z} 〉 & = \frac{1}{2} \sum_{j} 〈 {\hat{σ}}_{j}^{(z)} 〉 = - \frac{N}{2} + \sum_{j} {| β_{j} |}^{2}, \end{matrix}

(A14)

\begin{matrix} 〈 {\hat{J}}_{x} 〉 & = ℜ e [α^{*} \sum_{j = 1}^{N} β_{j}], \end{matrix}

(A15)

\begin{matrix} 〈 {\hat{J}}_{y} 〉 & = - ℑ m [α^{*} \sum_{j = 1}^{N} β_{j}] . \end{matrix}

(A16)

Recalling that the system has a single excitation, we have

{\tilde{σ}}_{j} {\tilde{σ}}_{m}^{†} | Ψ 〉 = 0

and

{\tilde{σ}}_{j}^{†} {\tilde{σ}}_{m}^{†} | Ψ 〉 = 0

, and we get:

〈 {\hat{J}}_{-}^{2} 〉 = 〈 {\hat{J}}_{+}^{2} 〉 = 0 .

(A17)

Furthermore,

\begin{matrix} 〈 {\hat{J}}_{+} {\hat{J}}_{-} 〉 & = \sum_{j, m} 〈 {\tilde{σ}}_{j}^{†} {\hat{σ}}_{j} 〉 \\ = \sum_{j, m} β_{j}^{*} β_{m} = {|\sum_{j = 1}^{N} β_{j}|}^{2} \end{matrix}

(A18)

and, using the commutation rule (A4) and Eqs. (A14) and (A18), we find

\begin{matrix} 〈 {\hat{J}}_{-} {\hat{J}}_{+} 〉 & = 〈 {\hat{J}}_{+} {\hat{J}}_{-} 〉 - 2 〈 {\hat{J}}_{z} 〉 \\ = N + {|\sum_{j = 1}^{N} β_{j}|}^{2} - 2 \sum_{j = 1}^{N} {| β_{j} |}^{2} . \end{matrix}

(A19)

From these results, we can calculate the expectations of

〈 {\hat{J}}_{k}^{2} 〉

k = x, y, z

, namely:

\begin{matrix} 〈 {\hat{J}}_{x}^{2} 〉 & = 〈 {\hat{J}}_{y}^{2} 〉 = \frac{N}{4} + \frac{1}{2} {|\sum_{j = 1}^{N} β_{j}|}^{2} - \frac{1}{2} \sum_{j = 1}^{N} {| β_{j} |}^{2}, \end{matrix}

(A20)

\begin{matrix} 〈 {\hat{J}}_{z}^{2} 〉 & = \frac{N^{2}}{4} - (N - 1) \sum_{j = 1}^{N} {| β_{j} |}^{2} . \end{matrix}

(A21)

It is remarkable that the second order moments do not depend on

α

, which appears only in the expression for

〈 {\hat{J}}_{x, y} 〉

We are now ready to evaluate also the variances of the collective angular momentum operators. Defining

{(Δ \hat{A})}^{2} = 〈 {\hat{A}}^{2} 〉 - {〈 \hat{A} 〉}^{2}

, we have:

\begin{matrix} {(Δ {\hat{J}}_{x})}^{2} & = \frac{N}{4} + \frac{1}{2} {|\sum_{j = 1}^{N} β_{j}|}^{2} - \frac{1}{2} \sum_{j = 1}^{N} {| β_{j} |}^{2} - {\{ℜ e [α^{*} \sum_{j = 1}^{N} β_{j}]\}}^{2} \end{matrix}

(A22)

\begin{matrix} {(Δ {\hat{J}}_{y})}^{2} & = \frac{N}{4} + \frac{1}{2} {|\sum_{j = 1}^{N} β_{j}|}^{2} - \frac{1}{2} \sum_{j = 1}^{N} {| β_{j} |}^{2} - {\{ℑ m [α^{*} \sum_{j = 1}^{N} β_{j}]\}}^{2} \end{matrix}

(A23)

\begin{matrix} {(Δ {\hat{J}}_{z})}^{2} & = (\sum_{j = 1}^{N} {| β_{j} |}^{2}) (1 - \sum_{j = 1}^{N} {| β_{j} |}^{2}) . \end{matrix}

(A24)

Notice that:

\begin{matrix} {(Δ {\hat{J}}_{x})}^{2} + {(Δ {\hat{J}}_{y})}^{2} = \frac{N}{2} - (\sum_{j = 1}^{N} {| β_{j} |}^{2}) (1 - {|\sum_{j = 1}^{N} β_{j}|}^{2}) \end{matrix}

(A25)

which is independent of

α

All the previous results can be simplified introducing the mean quantities

\bar{{| β |}^{2}}

and

|\bar{β}|

given in Eqs. (26) and (27), respectively. The corresponding expressions are directly reported in Sec. 3.

Appendix B. Considerations on Ineqs. (35b) and (35c)

In this appendix we show that, in our case, Ineqs. (35a), (35b) and (35c) cannot lead to useful conclusions.

In our case the l.h.s. of the Ineq. (35a) reads:

〈 {\hat{J}}_{x}^{2} 〉 + 〈 {\hat{J}}_{y}^{2} 〉 + 〈 {\hat{J}}_{z}^{2} 〉 = \frac{N (N + 2)}{4} - N^{2} σ_{β}^{2}

(A26)

where we defined the particle variance

\begin{matrix} σ_{β}^{2} & = \bar{{| β |}^{2}} - {|\bar{β}|}^{2}, \end{matrix}

(A27)

\begin{matrix} = \frac{1}{N} \sum_{s = 1}^{N - 1} {| γ_{s} |}^{2} . \end{matrix}

(A28)

As one may expect, the Ineq. (35a) is true and the equality sign holds for all the symmetric states, with

σ_{β} = 0

or, equivalently,

f_{SR} = 1

Concerning the Ineq. (35b), if we study the following expression (similar results can be obtained for the other combination of the involved expectations):

〈 {\hat{J}}_{x}^{2} 〉 + 〈 {\hat{J}}_{y}^{2} 〉 - \frac{N}{2} \leq (N - 1) {(Δ {\hat{J}}_{z})}^{2},

(A29)

we derive:

\begin{matrix} {|\bar{β}|}^{2} & \leq \bar{{| β |}^{2}} [1 - (N - 1) \bar{{| β |}^{2}}] \end{matrix}

(A30)

or, equivalently:

σ_{β} \geq \sqrt{N - 1} (| \bar{β} |^{2} + σ_{β}^{2}),

(A31)

where

σ_{β}^{2} = \bar{{| β |}^{2}} - {|\bar{β}|}^{2}

is the particle variance and

\bar{{| β |}^{2}}

and

|\bar{β}|

given in Eqs. (26) and (27), respectively. We can clearly see that these inequalities are nonlinear in

\bar{{| β |}^{2}}

. Recalling Eqs. (26) and (27), we conclude that they cannot lead to useful conditions, since the solution of (A30) or (A31) depends on the

β_{j}^{2}

and, thus on

Ω_{0}^{2}

, whereas the

β_{j}

have been obtained in the framework of the linear regime with respect

Ω_{0}

, see Eq. (7).

Ineq. (35c) is never violated for our system. In fact, for instance, we have:

\begin{matrix} (N - 1) [{(Δ {\hat{J}}_{x})}^{2} + {(Δ {\hat{J}}_{y})}^{2}] \geq 〈 {\hat{J}}_{z}^{2} 〉 + \frac{N (N - 2)}{4} \end{matrix}

(A32)

which, using Eqs. (A25) and (A20), yields

\begin{matrix} N^{2} \bar{{| β |}^{2}} {|\bar{β}|}^{2} > 0 . \end{matrix}

(A33)

References

Lehmberg, R.H. Radiation from an N-Atom System. I. General Formalism. Physical Review A 1970, 2, 883–888. [Google Scholar] [CrossRef]
van der Mark, M.B.; van Albada, M.P.; Lagendijk, A. Light scattering in strongly scattering media: Multiple scattering and weak localization. Phys. Rev. B 1988, 37, 3575–3592. [Google Scholar] [CrossRef] [PubMed]
Labeyrie, G.; Vaujour, E.; Mueller, C.A.; Delande, D.; Miniatura, C.; Wilkowski, D.; Kaiser, R. Slow diffusion of light in a cold atomic cloud. Physical review letters 2003, 91, 223904. [Google Scholar] [CrossRef] [PubMed]
Guerin, W.; Rouabah, M.; Kaiser, R. Light interacting with atomic ensembles: collective, cooperative and mesoscopic effects. Journal of Modern Optics 2017, 64, 895–907. [Google Scholar] [CrossRef]
Dicke, R.H. Coherence in Spontaneous Radiation Processes. Physical Reveiw 1954, 93, 99–100. [Google Scholar] [CrossRef]
Gross, M.; Haroche, S. Superradiance: An essay on the theory of collective spontaneous emission. Physics Reports 1982, 93, 301–396. [Google Scholar] [CrossRef]
Lodahl, P.; Floris van Driel, A.; Nikolaev, I.S.; Irman, A.; Overgaag, K.; Vanmaekelbergh, D.; Vos, W.L. Controlling the dynamics of spontaneous emission from quantum dots by photonic crystals. Nature 2004, 430, 654–657. [Google Scholar] [CrossRef]
Brandes, T. Coherent and collective quantum optical effects in mesoscopic systems. physics reports 2005, 408, 315–474. [Google Scholar] [CrossRef]
Karasik, R.I.; Marzlin, K.P.; Sanders, B.C.; Whaley, K.B. Multiparticle decoherence-free subspaces in extended systems. Physical Review A 2007, 76, 012331. [Google Scholar] [CrossRef]
Pedersen, L.H.; Mølmer, K. Few qubit atom-light interfaces with collective encoding. Physical Review A 2009, 79, 012320. [Google Scholar] [CrossRef]
Tong, D.; Farooqi, S.; Stanojevic, J.; Krishnan, S.; Zhang, Y.; Côté, R.; Eyler, E.; Gould, P. Local blockade of Rydberg excitation in an ultracold gas. Physical Review Letters 2004, 93, 063001. [Google Scholar] [CrossRef] [PubMed]
Urban, E.; Johnson, T.A.; Henage, T.; Isenhower, L.; Yavuz, D.; Walker, T.; Saffman, M. Observation of Rydberg blockade between two atoms. Nature Physics 2009, 5, 110–114. [Google Scholar] [CrossRef]
Gaëtan, A.; Miroshnychenko, Y.; Wilk, T.; Chotia, A.; Viteau, M.; Comparat, D.; Pillet, P.; Browaeys, A.; Grangier, P. Observation of collective excitation of two individual atoms in the Rydberg blockade regime. Nature Physics 2009, 5, 115–118. [Google Scholar] [CrossRef]
Scully, M.; Fry, E.; Ooi, C.; Wodkiewicz, K. Directed Spontaneous Emission from an Extended Ensemble of N Atoms: Timing Is Everything. Physical Review Letters 2006, 96, 010501. [Google Scholar] [CrossRef]
Svidzinsky, A.A.; Chang, J.T.; Scully, M.O. Dynamical Evolution of Correlated Spontaneous Emission of a Single Photon from a Uniformly Excited Cloud of N Atoms. Physical Review Letters 2008, 100, 160504. [Google Scholar] [CrossRef]
Svidzinsky, A.A.; Chang, J.T.; Scully, M.O. Cooperative spontaneous emission of N atoms: Many-body eigenstates, the effect of virtual Lamb shift processes, and analogy with radiation of N classical oscillators. Physical Review A 2010, 81, 053821. [Google Scholar] [CrossRef]
Courteille, P.W.; Bux, S.; Lucioni, E.; Lauber, K.; Bienaimé, T.; Kaiser, R.; Piovella, N. Modification of radiation pressure due to cooperative scattering of light. The European Physical Journal D 2010, 58, 69–73. [Google Scholar] [CrossRef]
Bienaimé, T.; Bux, S.; Lucioni, E.; Courteille, P.; Piovella, N.; Kaiser, R. Observation of a Cooperative Radiation Force in the Presence of Disorder. Physical Review Letters 2010, 104, 183602. [Google Scholar] [CrossRef]
Bienaimé, T.; Bachelard, R.; Piovella, N.; Kaiser, R. Cooperativity in light scattering by cold atoms. Fortschritte der Physik 2013, 61, 377–392. [Google Scholar] [CrossRef]
Chabé, J.; Rouabah, M.T.; Bellando, L.; Bienaimé, T.; Piovella, N.; Bachelard, R.; Kaiser, R. Coherent and incoherent multiple scattering. Physical Review A 2014, 89, 043833. [Google Scholar] [CrossRef]
Bachelard, R.; Piovella, N.; Guerin, W.; Kaiser, R. Collective effects in the radiation pressure force. Physical Review A 2016, 94. [Google Scholar] [CrossRef]
Bienaimé, T.; Piovella, N.; Kaiser, R. Controlled Dicke Subradiance from a Large Cloud of Two-Level Systems. Physical Review Letters 2012, 108, 123602. [Google Scholar] [CrossRef] [PubMed]
Guerin, W.; Araújo, M.O.; Kaiser, R. Subradiance in a Large Cloud of Cold Atoms. Physical Review Letters 2016, 116, 083601. [Google Scholar] [CrossRef] [PubMed]
Tóth, G.; Knapp, C.; Gühne, O.; Briegel, H.J. Optimal spin squeezing inequalities detect bound entanglement in spin models. Physical Review Letters 2007, 99, 250405. [Google Scholar] [CrossRef]
Bienaimé, T.; Petruzzo, M.; Bigerni, D.; Piovella, N.; Kaiser, R. Atom and photon measurement in cooperative scattering by cold atoms. Journal of Modern Optics 2011, 58, 1942–1950. [Google Scholar] [CrossRef]
Scully, M.O. Single photon subradiance: quantum control of spontaneous emission and ultrafast readout. Physical Review Letters 2015, 115, 243602. [Google Scholar] [CrossRef]
Scully, M.O.; Svidzinsky, A.A. The Lamb Shift—Yesterday, Today, and Tomorrow. Science 2010, 328, 1239–1241. [Google Scholar] [CrossRef]
Kitagawa, M.; Ueda, M. Squeezed spin states. Phys. Rev. A 1993, 47, 5138–5143. [Google Scholar] [CrossRef]

Figure 1.

P = (1 / N) \sum_{j} {| β_{j} |}^{2}

vs time, obtained solving Eq. (7) for

N = 10^{3}

Δ_{0} = 10 Γ

and a Gaussian distribution with

σ = k_{0} σ_{R} = 10

. The laser is cut off after

Γ t = 20

Figure 1.

P = (1 / N) \sum_{j} {| β_{j} |}^{2}

vs time, obtained solving Eq. (7) for

N = 10^{3}

Δ_{0} = 10 Γ

and a Gaussian distribution with

σ = k_{0} σ_{R} = 10

. The laser is cut off after

Γ t = 20

Figure 2. superradiant and subradiant fractions,

f_{S R}

(continuous blue line) and

f_{s u b}

(dashed red line), for the same parameters of Figure 1. The dotted black line is the value

1 / N

Figure 2. superradiant and subradiant fractions,

f_{S R}

(continuous blue line) and

f_{s u b}

(dashed red line), for the same parameters of Figure 1. The dotted black line is the value

1 / N

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Single Photon Superadiance and Subradiance as Collective Emission from Symmetric and Anti-Symmetric States

Abstract

1. Introduction

2. The model

3. Entanglement properties of the superradiant and subradiant collective states

4. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

Appendix A. Calculation of the first and second moments of J ^ k

Appendix B. Considerations on Ineqs. (35b) and (35c)

References

MDPI Initiatives

Important Links

Subscribe

Appendix A. Calculation of the first and second moments of ${\hat{J}}_{k}$