1. Introduction

2. Results and discussions

2.1. Application of the Klein-Gordon equation

As you know that a non-relativistic quantum mechanical system is described by Schrödinger equation involving a Hamiltonian with second derivatives of 3D-space i.e. the Laplace operator. Klein [17] and Gordon [18] have extended the equation for a relativistic context by the inclusion of time as the 4^th dimension in non-Euclidian Minkovski space where the Laplace operator is replaced by a 4D-operator so called the D’Alembartian operator given as

$${⧠}^2{=\nabla }^2-\frac{1}{c^2}\frac{{\partial }^2}{\partial t^2}$$

(1)

where ${\nabla }^2$is the Laplace operator and $c$ the speed of light. The first ever relativistic version of Schrödinger equation is called the Klein-Gordon equation which has opened a new gateway in sorting out the quantum fields in particle physics especially after the advancement of it by the Dirac equation [19] with the involvement of electromagnetic interaction and fermions.

Now, let us think that we are neither living in Schrödinger’s non-relativistic quantum world nor in Klein, Gordon and Dirac’s relativistic one, we are living in one dimensional space of time approximated from the case of the conditions at the singularity of a Schwarzschild black hole where general relativity and Galilean relativity collapse. In other words, we assume the conditions at which the 3D-space swaps with the 1D-time. Then the question arises; how would Schrödinger write his equation for a free particle with a mass of m in the 1D-time world? Using only the time derivative term of the D’Alembartian operator in Eq.1, one can probably write it as

$$\frac{{\hslash }^2}{2m{c}^2}\frac{d^2\psi \left(t\right)}{d{t}^2}=i\hslash \frac{d\psi \left(t\right)}{dt}$$

(2)

where ℏ is the reduced Planck constant and $\psi \left(t\right)$ the particle wave function in $t$ dimension. One should notice the fact that partial differentiation is not used here, because time is considered to be the only dimension. We ignore the presence of the other spatial dimensions at all, as we ignore the presence of the time dimension in conventional Schrödinger equations. This is neither a non-relativistic ordinary Schrödinger equation nor Klein-Gordon’s relativistic one. This is a unique equation adopted from the Schrödinger equation for a particle at a point in time, $t$, considering space is simultaneous for all frames of references but only time is relativistic. We can probably call this situation as singularity of time. This is a kind of reverse conjuncture to the situation in Galilean space where time is simultaneous but normal 3D-space differs. The overall layout of the circumstances is summarized and tabulated in Table 1.

Table 1. The summary of circumstances predicted in, respectively, Galilean relativity, general relativity and this study. .

Table 1. The summary of circumstances predicted in, respectively, Galilean relativity, general relativity and this study. .

Circumstance	Galilean relativity	General relativity	Present work
Relativity	Non-relativistic	relativistic	?
Dimensions	$3D-\left(xyz\right)$	$4D-\left(xyzt\right)$	$1D-\left(t\right)$
Wave equation	Schrödinger equation	Klein-Gordon and Dirac Equations	Eq.2
Wave operator	Laplace Operator, ${\nabla }^2$	D’Alembartian operator, ${\nabla }^2-{\partial }_t^2/c^2$	$-{\partial }_t^2/c^2$

We now focus on the situation of a particle with a rest mass of $m$ under the effect of ultra-high gravity of a Schwarzschild black hole with a mass of $M$. We can rewrite Eq.2 with the inclusion of the potential term [20].

$$\left[\frac{{\hslash }^2}{2m{c}^2}\frac{d^2}{d{t}^2}-G\frac{Mm}{r}\right]\psi \left(t\right)=i\hslash \frac{d\psi \left(t\right)}{dt}$$

(3)

where $G$ is the gravitational constant and $r$ the Schwarzschild radius, considering the particle near the edge of the event-horizon. Form the definition of the Schwarzschild radius as

$$c=\sqrt{G\frac{M}{r}}$$

(4)

we can rearrange Eq.3 as

$$\left[\frac{{\hslash }^2}{2m{c}^2}\frac{d^2}{d{t}^2}-m{c}^2\right]\psi \left(t\right)=i\hslash \frac{d\psi \left(t\right)}{dt}$$

(5)

or in much simplified notation, using the natural units where $\hslash =c=1$

$$\left({{\partial }_t}^2/2-i{m\partial }_t-m^2\right)\psi \left(t\right)=0$$

(6)

This is entirely time dependent wave equation of a particle with a mass of $m$ and can be considered stationary in terms of ordinary (xyz) positions, just as normal Schrödinger equation of an atom is considered to be stationary in terms of time. A solution of Eq.6 gives rise to

$$\psi \left(t\right)=C{e}^{i\omega t}[e^{\tau \omega t}+e^{-\tau \omega t}]$$

(7)

where $C$ is a probability constant smaller than unity applied in both positive and negative $t$-directions since we consider that the situation is rather symmetrical around the edge of the event horizon. It can be calculated from the normalization condition over time. The angular frequency, $\omega$ can simply be calculated from the equivalent mass energy of the particle, provided $E=\hslash \omega =m{c}^2$. $\tau$ appears as a dimensionless factor bigger than unity in the wave function solution, acting like an emerging factor which is going to be discussed later on. Time, $t$ represents all the points in time dimension, ranging from $-\infty$ to $+\infty$. However, there is a limit of time range within which the described wave equations given by Eqs.5 and 6, and corresponding wave function given by Eq.7 is valid. Out of this limited time range, the effect of ultra-high gravity eventually weakens and normal relativistic quantum mechanical wave equations become applicable where the particle is considered to be in 4D-spacetime.

The conceptual descriptions of black holes given by scientists such as Hawking and Penrose [21] and Schwarzschild [22] brought about some important issues, such as the fact that noting (even light) can escape from a black hole, which contradicts with fundamental observations and principles of quantum mechanics. Some other scientists such as Zeldovich and Starobinsky [23] raised the question that it is impossible due to the fact that the black hole has a certain absolute temperature, even though it is too small, and this should have caused a black body radiation at long wavelength range. As a result of these discussions, Hawking came up with a quantum mechanical model [3] of black holes, describing a kind of black hole evaporation named after him—the Hawking radiation.

It is considered in Hawking’s quantum mechanical model that there always exists a possibility of virtual particles (virtual positron-electron pairs) of the quantum fluctuations becoming a real particle by separation at the edge of the event horizon zone. One of the partners of the particle pair goes out traveling forward in time, and the other stay in traveling backward in time, at the boundary between the event horizon and infinity. Ingoing partner is called the Hawking partner, and outgoing the Hawking particle, released to the infinity according to Hawking’s quantum mechanical approach [3]. It is described by Hawking [3] that the first has to move in negative and the latter in positive t-direction. Eq.7 shows the possibility of the particle moving in both directions which is in agreement with the predictions of Hawking.

In order to briefly understand time can change in both directions near the event horizon, let us draw attention to the following discussion. According to general relativity time flows slower on a planet then it does in free space. The time, $t_1$ on a planet measured from a reference time is behind the time $t_2$ in free space. Therefore, we can apparently assume that time flows normally in free space while it is stopped at the edge of the event-horizon of the black hole. It is consequently right to assume that time originates from the edge of the event-horizon being positive towards free space and so, being negative towards the singularity.

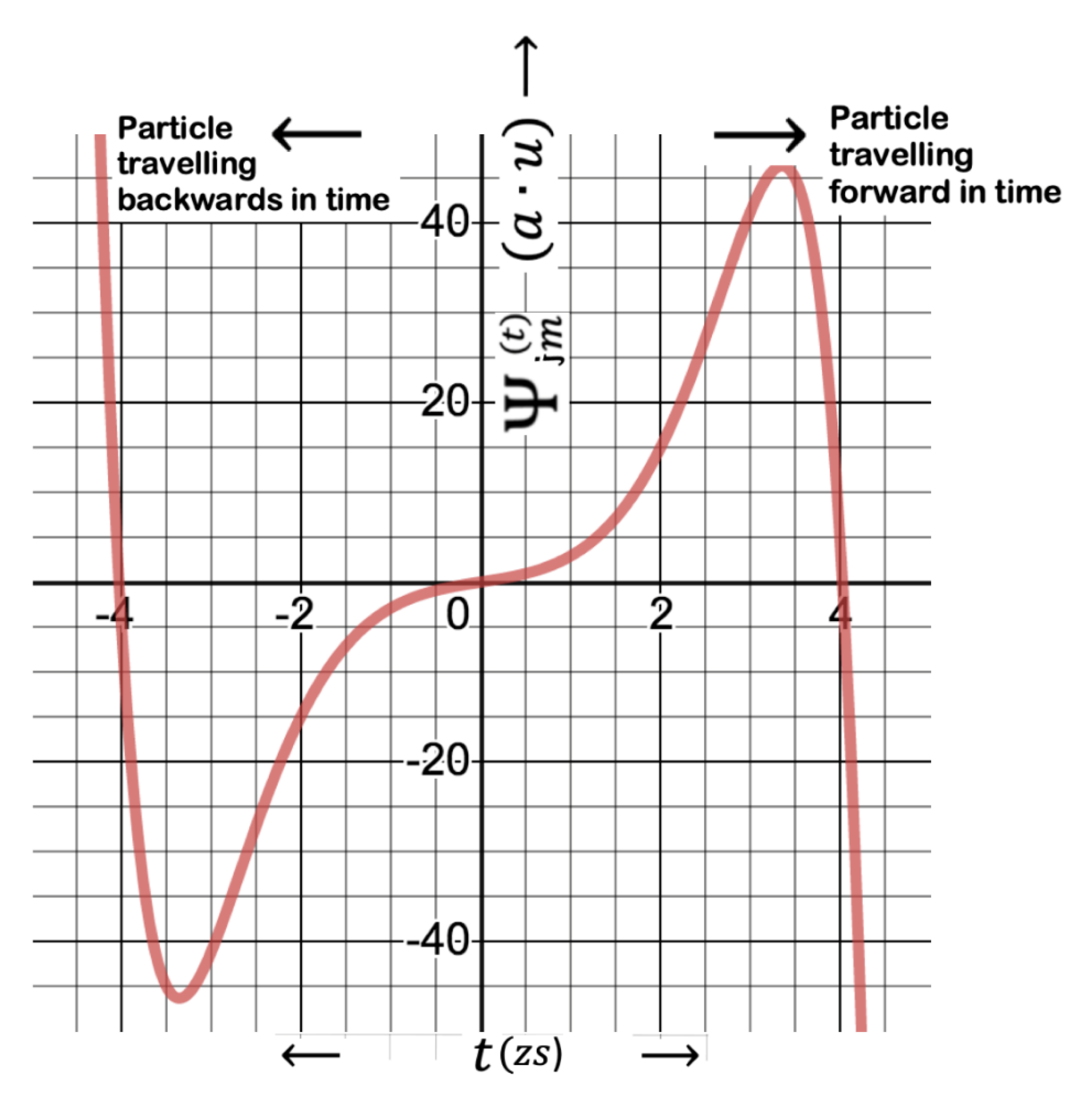
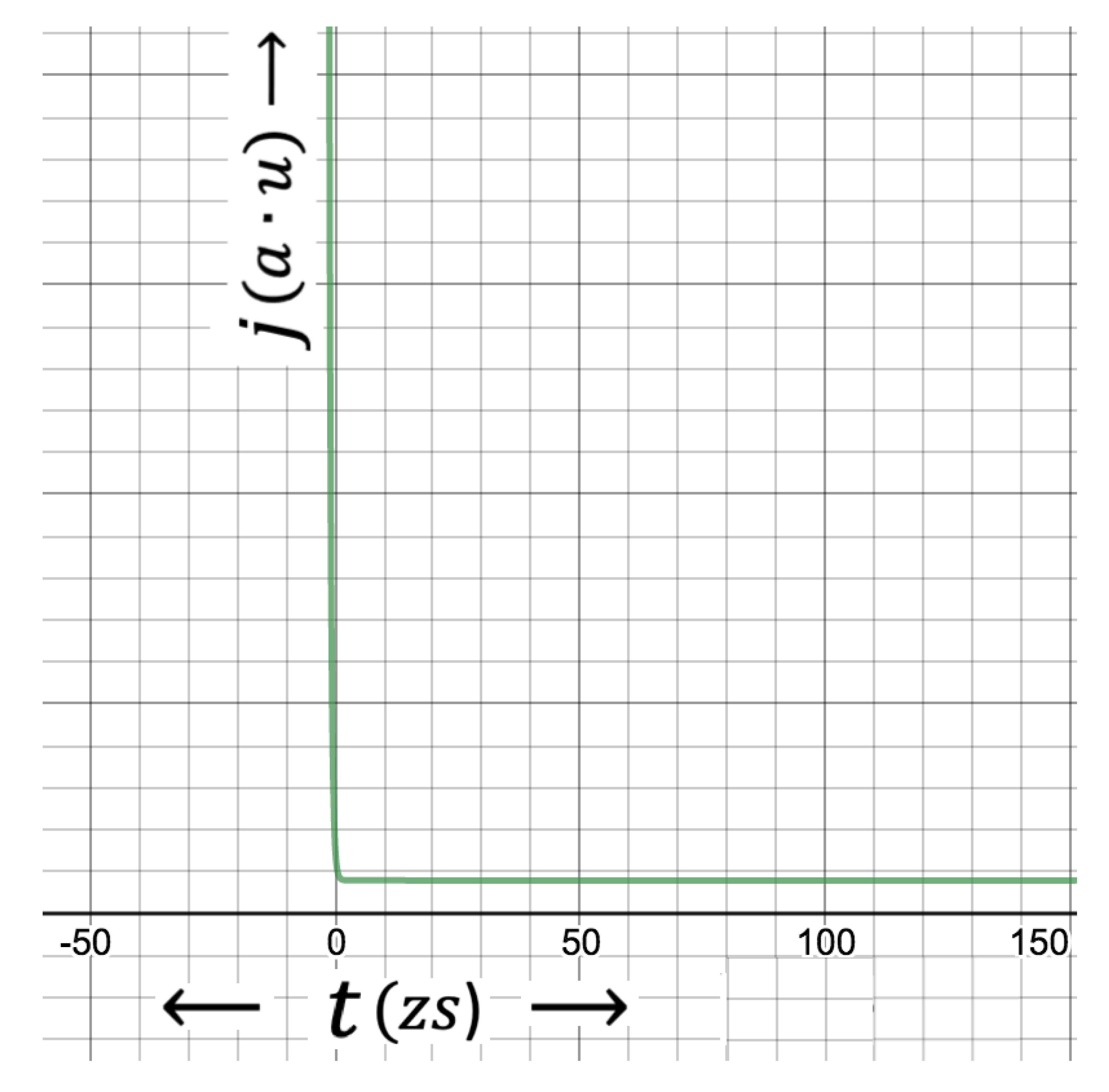
Figure 1 and Figure 2 respectively show the distribution of wave function given by Eq.7 and its absolute square i.e. the probability function. They are drawn for an electron or positron for which $\omega =7.8\times {10}^{20}$rad/s, calculated from the equivalent mass energy of an electron or a positron. As can be seen, wave function and corresponding probability distributions are respectively antisymmetric and symmetric for the particles moving in and out. It has been quantum mechanically shown by the wave function in Eq.7 and by these corresponding figures that there exist real particles on the edge of the event-horizon moving either reverse or forward in time with the same possibility. It is to show that there is a possibility of particle escaping the infinite gravity of black hole which is impossible to accept in classical theory. This is the reconfirmation of Hawking radiation theory, once again quantum mechanically proved in this study. The wave function of the particle in Figure 1 is antisymmetric, meaning that particle spin changes sign in both sides of the event horizon; that is, ψ(t) = −ψ(-t), where the variables t and -t respectively correspond to the particle moving forward and backward in time as described by the Hawking quantum model of black holes, preserving the angular momenta. Since the absolute value is not changed by a sign swap, this corresponds to equal probabilities. It is true of the fact that once the virtual pairs of the quantum fluctuations are separated into real particles at the boundary of the event horizon, they only have one of the choices of being inside or outside.

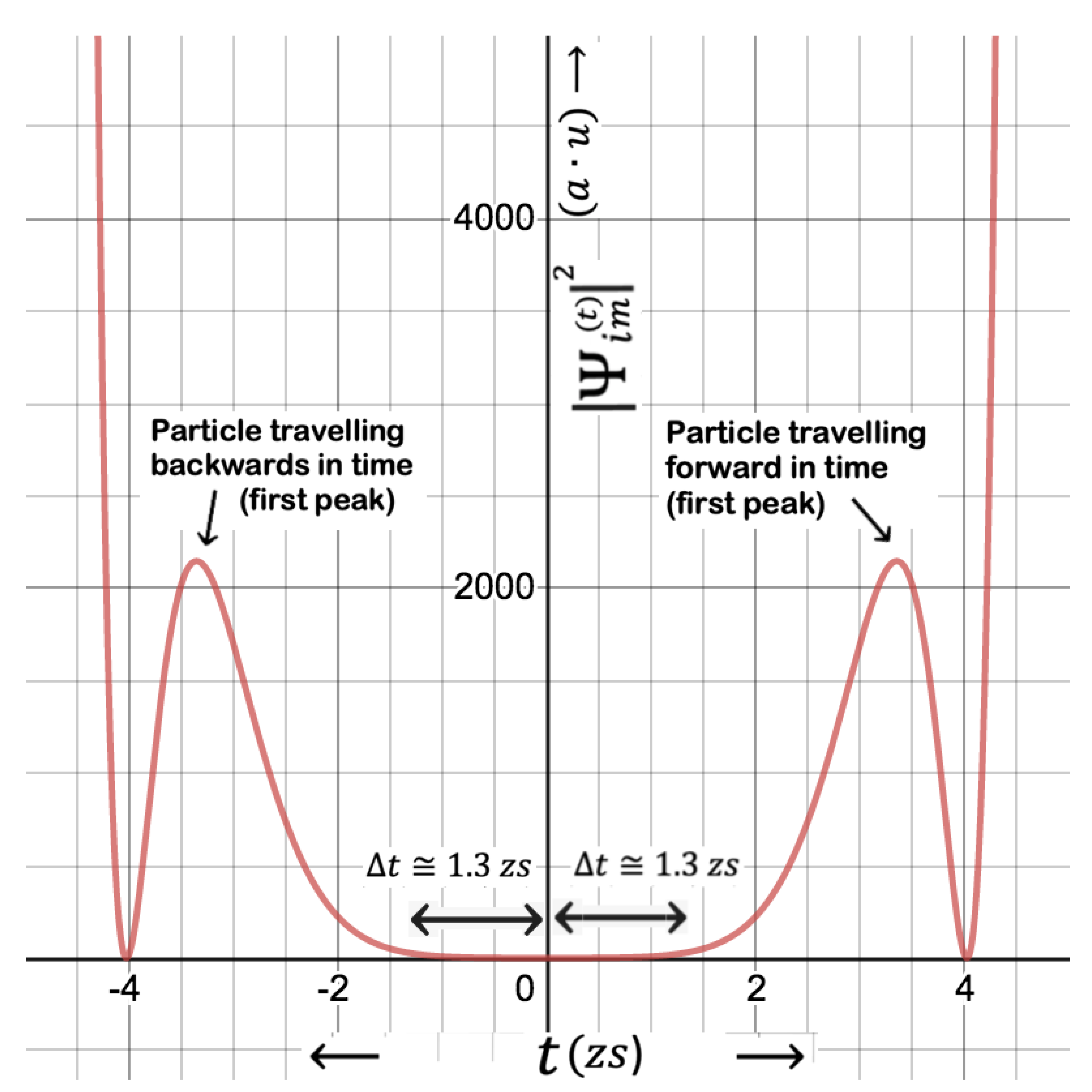
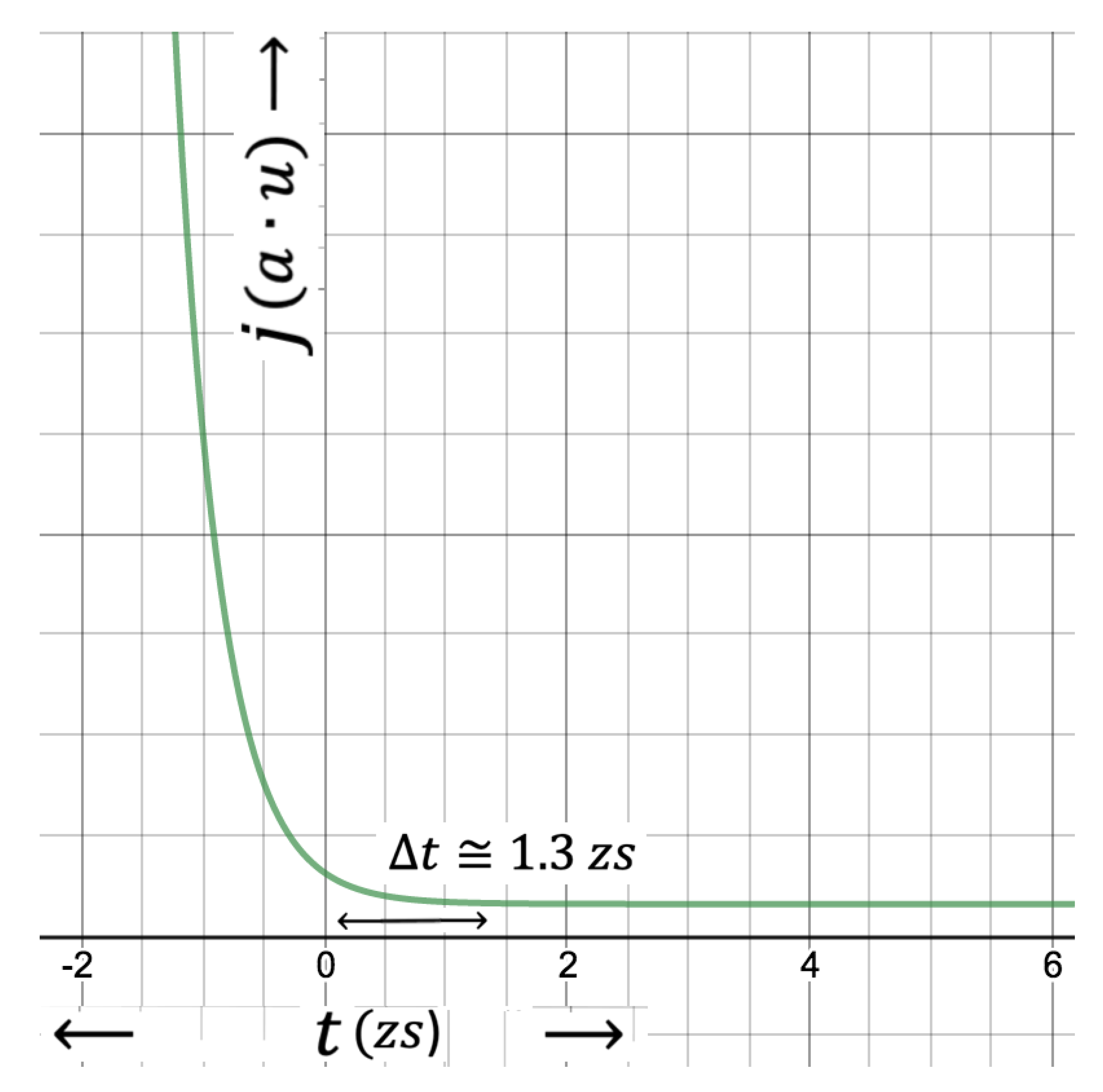
As seen in Figure 1 and Figure 2, the first peak appears at $t=3.36zepto-second\left(zs\right)\left({1zs=10}^{-21}s\right)$, which is comparable with the uncertainty in time, $∆t=1.3zs$, calculated from the energy-time version of the Heisenberg Uncertainty Principle (HUP). $∆t$ can be considered to be the average lifetime until the virtual electron-positron pairs of an electron field annihilate in accordance with the standard model of particle physics [24,25,26]. This is to say that escape of one of the partners of the virtual electron-positron pairs is only possible, if they live about twice as much longer than the average lifetime of the virtual electron-positron pairs. This reduces the amplitude of the cumulative distribution function (CDF) as time increases in positive direction, which will be discussed in the next section 2.2.

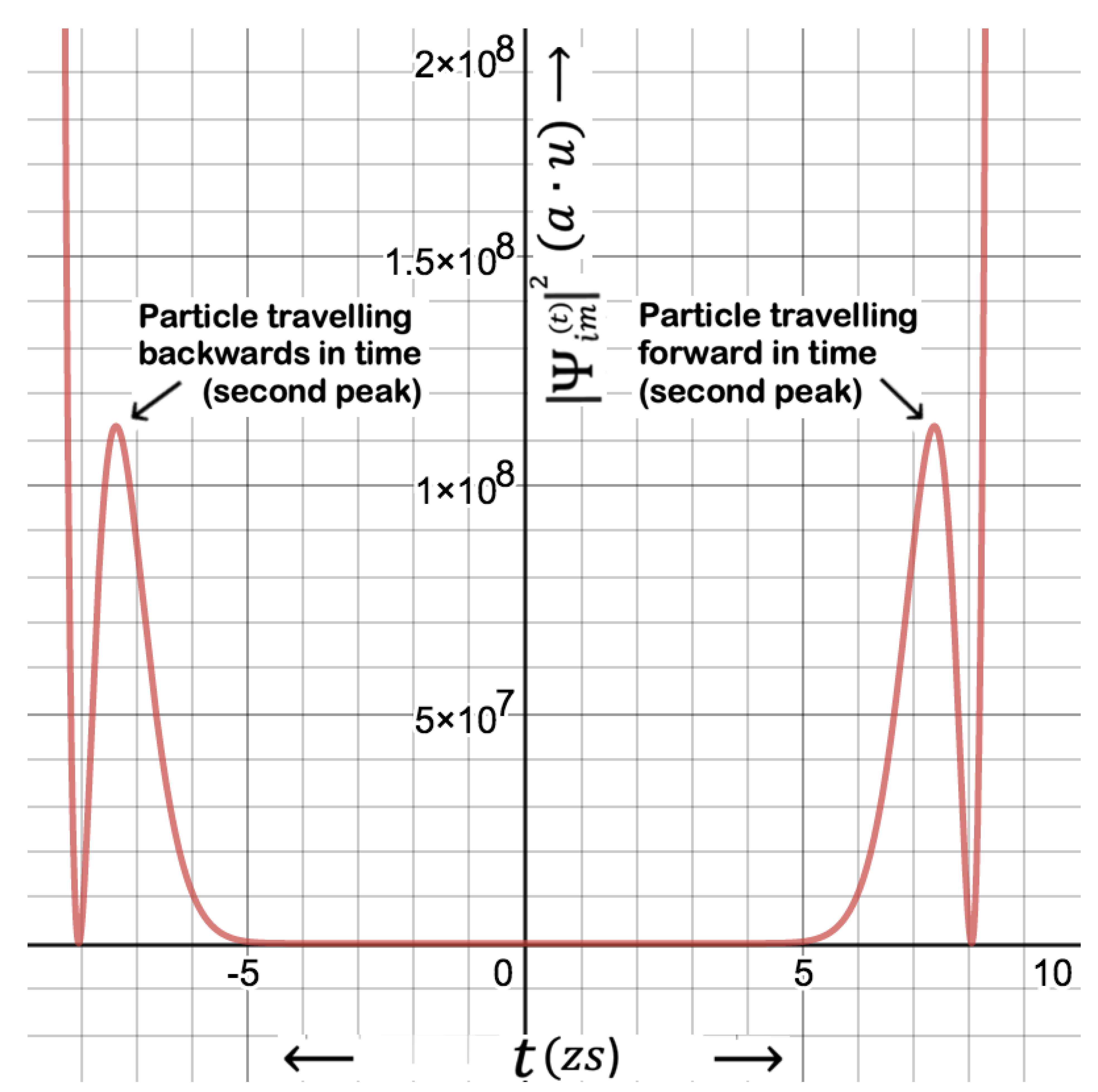
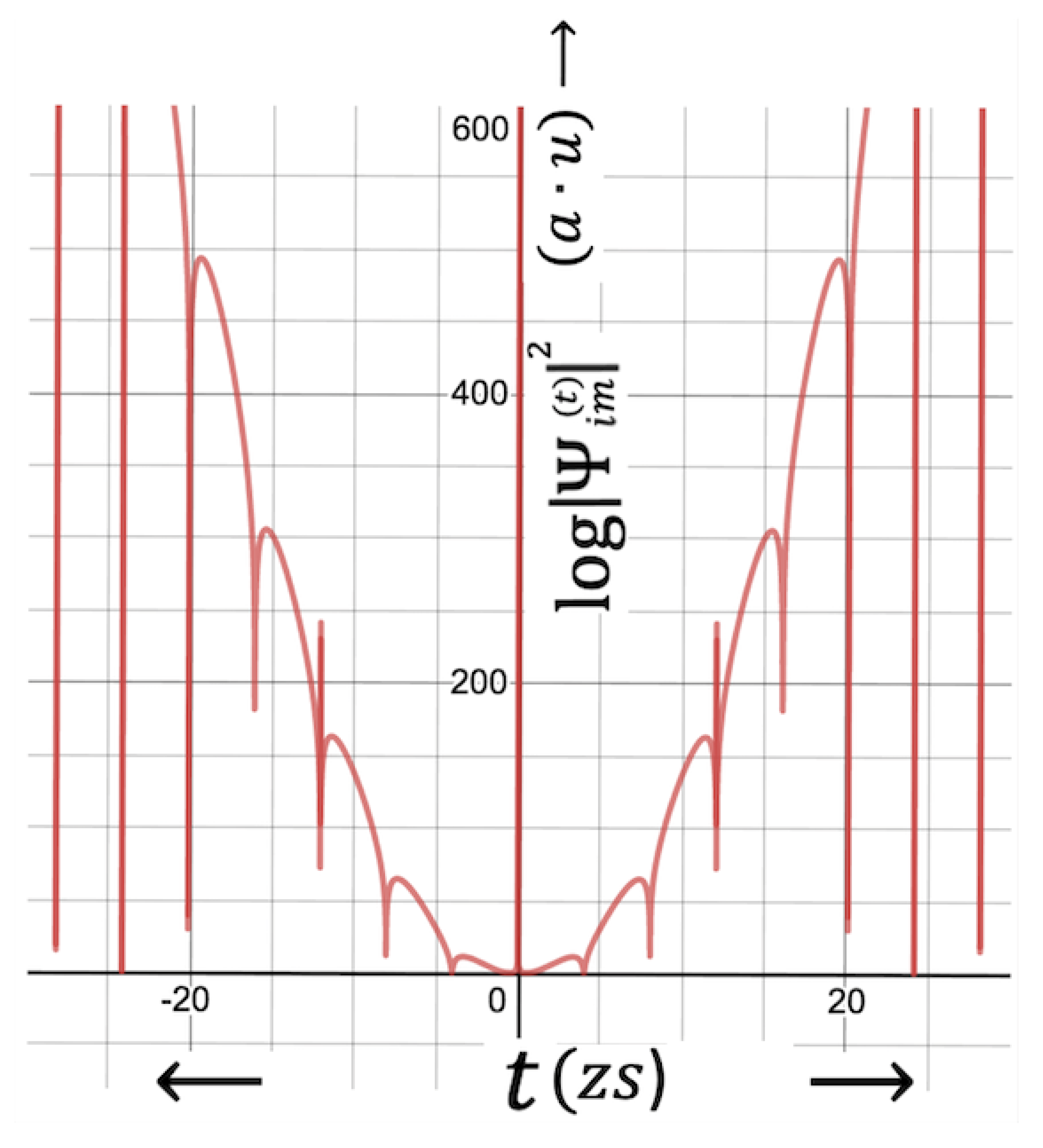
The second peak is illustrated in Figure 3. As the Hawking particle move away from the event horizon, it is more likely to survive from the event-horizon as the second and third peaks appear at respectively $7.38zs$ and $11.4zs$ s. This is because of the fact that the probability function exponentially increase as can be seen from the logarithmic version of the probability function shown in Figure 4. However, number of virtual particles that live longer than the average lifetime rather exponentially reduces, resulting in low probability current densities discussed later. Dimensionless coefficient $\tau$ appears to be 1.73 in Eq.7, and somehow act as an emerging factor that helps increase the probability of particle emission and backdate the peaks, without which particle emission seems to be impossible, since the first peak would have appeared as late as at $7.05zs$, if $\tau$ was unity for instance.

On the other hand, the peaks appearing by certain intervals are the possible indication for the quantization of time. The time intervals between the subsequent peaks increase as the time goes on, meaning that the gaps between the peaks enlarge and the uncertainty in time becomes low in comparison to the gaps. Analogical analyses between the uncertainty in time ($∆t$) and uncertainty in space ($∆x)$ mean that $∆t$ should be similar to the quantum steps of the particle along t-dimension, as $∆x$ likens to be the quantum steps corresponding to the de Broglie wavelength of a certain quantum mechanical particle in normal ordinary space. The fact that time intervals increase as the time increases further away from the event-horizon, the possibility of the particle jumping from one peak to the other so weakens that the theory presented here become invalid, after which the relativistic 4D Klein-Gordon or Dirac equations should be applied. Exact value of the time at which particle appears to have an escape possibility will be given after the calculations of the probability current density (PCD) along time dimension.

Before we move on these calculations, let us have a look at the shapes of wave and corresponding probability functions. As can be seen in Figure 1, Figure 2, Figure 3 and Figure 4 the peaks are broader when they emerge and steeper when they descent. This is a kind of similarity that appears in the Franck-Hertz experiment which is one of the first demonstrations of energy quantization of atoms. This similarity shows that the predicted time quantization probably occurs in a similar manner. In t-dimension, transition from an upper peak to the lower would probably result in the emission of a particle just as in the case of the transition of an electron from higher energy states, resulting in photon emission due to atomic quantization of energy levels. In the case of possible time quantization, transition from one peak to the other will probably result in either an absorption or emission of gravitation particle, hypothetically introduced as gravitons. The time intervals between the peaks along time dimension would be an important measure in absorption or dissipation of gravitational energy, hypothesizing that time also has energy.

3. Conclusions

Acknowledgement:

Conflict of Interst

References

1. G. ‘t Hooft, On the quantum structure of a black hole, Nuclear Physics B. 256, 727 (1985). [CrossRef]
2. Hawking, S.W. Particle creation by black holes. Commun. Math. Phys. 1975, 43, 199–220,. [CrossRef]
3. Hawking, S.W. The Quantum Mechanics of Black Holes. Sci. Am. 1977, 236, 34–41,. [CrossRef]
4. Hawking, S.W. Information loss in black holes. Phys. Rev. D 2005, 72, 084013,. [CrossRef]
5. S. B. Giddings, Black holes, quantum information and the foundations of physics, Physics Today, 30 (2013). [CrossRef]
6. Carroll, B.W.; Ostlie, D.A.; Friedlander, M. An Introduction to Modern Astrophysics. Phys. Today 1997, 50, 66–67,. [CrossRef]
7. M. Wittemer, F. Hakelberg, P. Kiefer, J.-P. Schröder, C. Fey, R. Schützhold, U. Warring and T. Schaetz, Particle pair creation by inflation of quantum vacuum fluctuations in an ion trap, arXiv:1903.05523v1 [quant-ph] (2019). [CrossRef]
8. Q.-Q. Jiang, S.-Q. Wu, X. Cai, Hawking radiation as tunneling from the Kerr and Kerr-Newman black holes, Phys. Rev. D. 73, 069902 (2006). [CrossRef]
9. Hotta, M.; Schützhold, R.; Unruh, W.G. Partner particles for moving mirror radiation and black hole evaporation. Phys. Rev. D 2015, 91, 124060,. [CrossRef]
10. W. G. Tifft, A Brief History of Quantized Time, Mercury 25, 12, (1995).
11. G. Wendel, L. Martinez and M. Bojowald, Phys. Rev. Lett. 124, 241301 (2020). [CrossRef]
12. Khrennikov, A. Quantum Randomness as a Result of Random Fluctuations at the Planck Time Scale?. Int. J. Theor. Phys. 2007, 47, 114–124,. [CrossRef]
13. D. Finkelstein, Space-Time Code, Phys. Rev. 184, 1261 (1969). [CrossRef]
14. Janis, A.I.; Newman, E.T.; Winicour, J. Reality of the Schwarzschild Singularity. Phys. Rev. Lett. 1968, 20, 878–880,. [CrossRef]
15. Regge, T.; Wheeler, J.A. Stability of a Schwarzschild Singularity. Phys. Rev. 1957, 108, 1063–1069,. [CrossRef]
16. Virbhadra, K.S.; Ellis, G.F.R. Schwarzschild black hole lensing. Phys. Rev. D 2000, 62, 084003,. [CrossRef]
17. O. Klein, Quantentheorie und fünfdimensionale Relativitätstheorie, Z. Phys 37(12), 895 (1926). [CrossRef]
18. Von W. Gordon, Der comptoneffekt nach der schrödingerschen theorie, Z. Phys 40(1-2), 117 (1926). [CrossRef]
19. P. A. M. Dirac, Proc. of Royal Society A. 117(778), 610 (1928).
20. Dolan, S.; Doran, C.; Lasenby, A. Fermion scattering by a Schwarzschild black hole. Phys. Rev. D 2006, 74, 064005,. [CrossRef]
21. S. W. Hawking, R. Penrose, Singularities of gravitational collapse and cosmology, Proceedings of the Royal Society of London Series A-Mathematical and Physical Sciences. 314(1519), 529 (1970). [CrossRef]
22. K. Schwarzschild, Original: Uber das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie, Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin, Phys.-Math. Klasse, 189 (1916), Translation: On the gravitational field of a mass point according to Einstein's theory, General Relativity and Gravitation. 35(5), 951 (2003).
23. Y. B. Zeldovich and A. A. Starobinsky, Particle production and vacuum polarization in an anisotropic gravitational-field, Soviet Physics Jetp-USSR 34(6), 1159 (1972). [CrossRef]
24. Tüzemen, S. A Possible Microscopic Model for Gravitational Interaction. Phys. Sci. Int. J. 2016, 9, 1–6,. [CrossRef]
25. S. Tüzemen, Approaching to Gravity? Journal of Physics: Conference Series 707, 012003 (2016). [CrossRef]
26. S. Tüzemen, The Quantum and Cosmic Codes of the Universe, Cambridge Scholars Publishing, 124 (2020).
27. R. M. Wald, The Thermodynamics of Black Holes, Living Reviews in Relativity. 4, 6 (2001). ttps://doi.org/10.12942/lrr-2001-6.
28. J. D. Bekenstein, Black Holes and Entropy, Phys. Rev. D. 7, 2333 (1973). [CrossRef]
29. C. D. Anderson, The Positive Electron, Phys. Rev. 43, 491 (1933). [CrossRef]