Submitted:
24 July 2023
Posted:
26 July 2023
You are already at the latest version
Abstract
Keywords:
Introduction
1. Structure of the Lax Operator for a Quadratic Spectral Bundle
2. The Monodromy Matrix
3. Conservation Laws
4. Integrable Nonlinear Evolutionary Equations
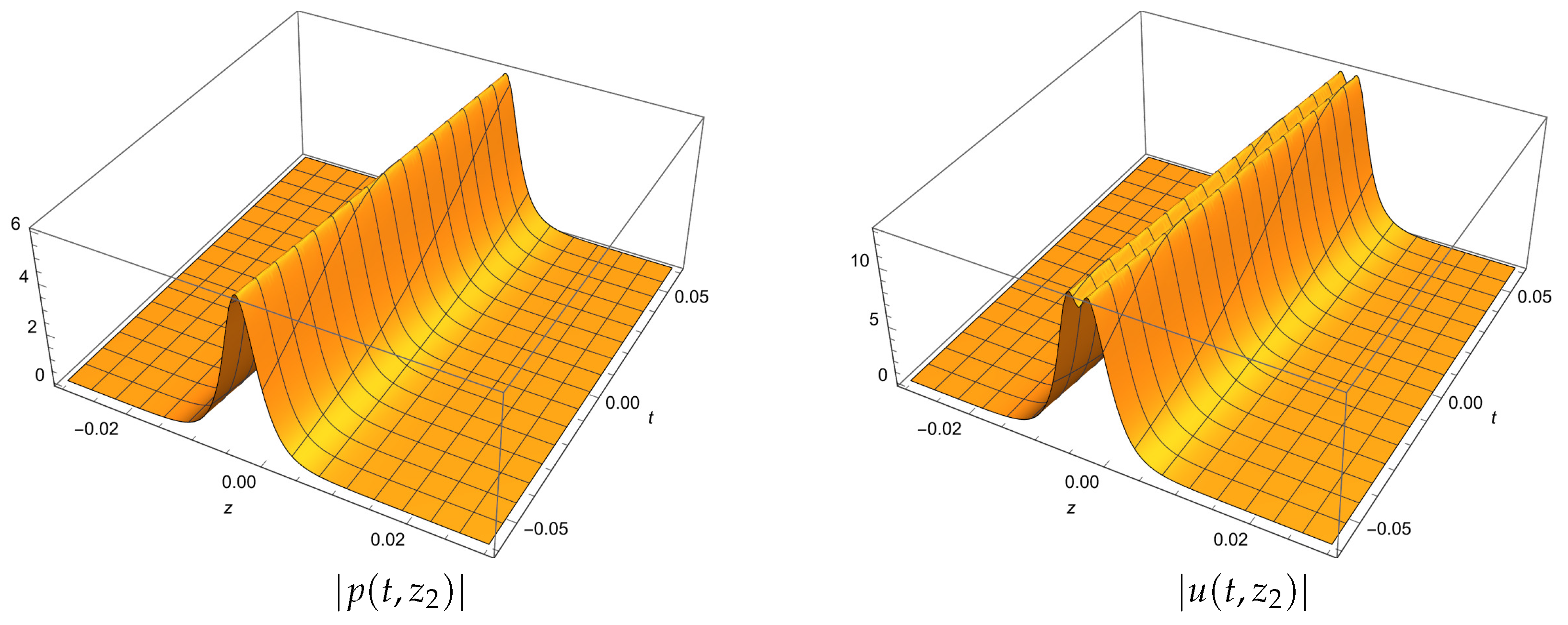
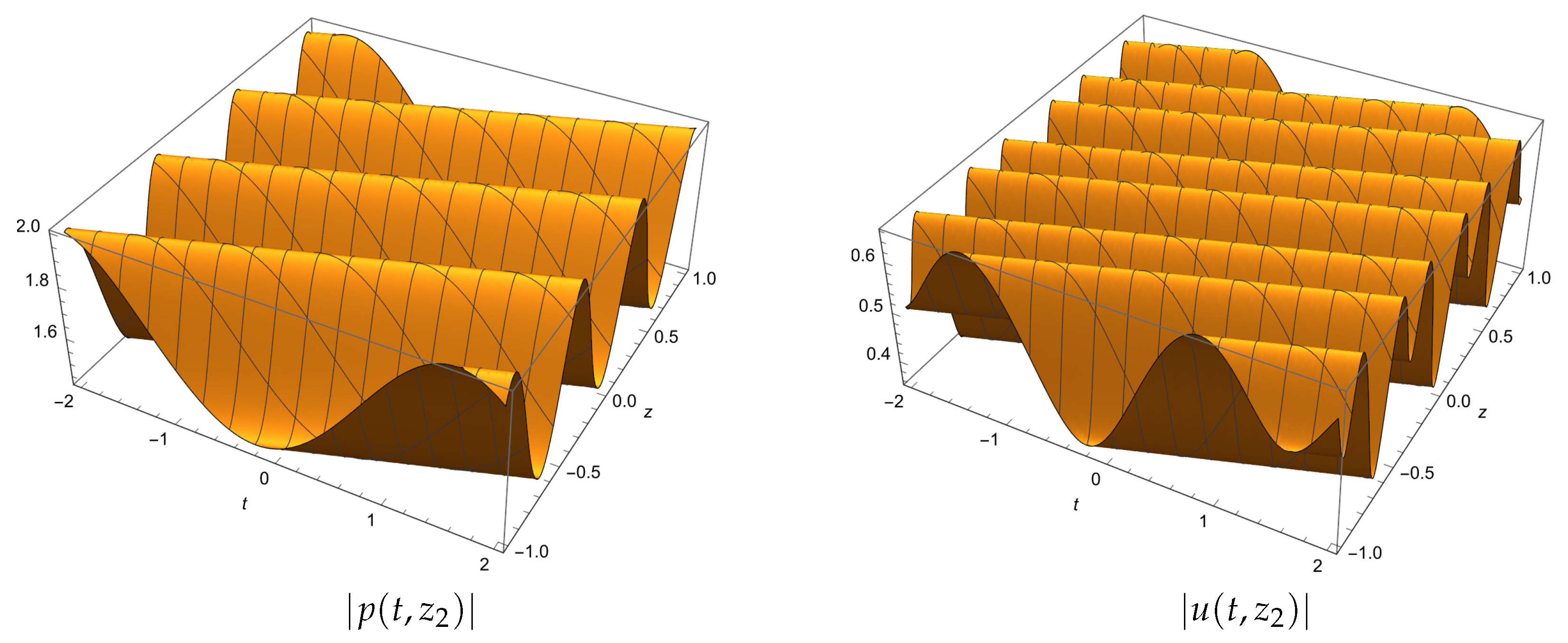
5. One-Phase Solutions
Concluding Remarks
Funding
Conflicts of Interest
References
- Akhmediev, N.N.; Ankiewicz, A. Solitons, Nonlinear Pulses and Beams; CHAPMAN & HALL, 1997; p. 336. [Google Scholar]
- Ablowitz, M.J.; Segur, H. Solitons and the inverse scattering transform; SIAM: Philadelpphia, 1981; p. 425. [Google Scholar]
- Dodd, R.; Eilbeck, J.C.; Gibbon, J.D.; Morris, H.C. Solitons and nonlinear wave equations; Academic Press, Inc., 1982; p. 648. [Google Scholar]
- Calogero, F.; Degasperis, A. Spectral transform and solitons: tools to solve and investigate nonlinear evolution equations; North-Holland Publ. Comp.: Amsterdam, New York, Oxford, 1982; p. 516. [Google Scholar]
- Zakharov, V.E.; Manakov, S.V.; Novikov, S.P.; Pitaevskii, L.P. Theory of solitons. The inverse scattering method; Plenum, N.Y., 1984; p. 276. [Google Scholar]
- Faddeev, L.D.; Takhtajan, L.A. Hamiltonian Methods in the Theory of Solitons; Springer Ser. Classics in Mathematics, Springer, 2007; p. 585. [Google Scholar]
- Hirota, R. Exact envelope-soliton solutions of a nonlinear wave equation. J. Math. Phys. 1973, 14, 805–809. [Google Scholar] [CrossRef]
- Dai, C.Q.; Zhang, J.F. New solitons for the Hirota equation and generalized higher-order nonlinear Schrödinger equation with variable coefficients. J. Phys. A 2006, 39, 723–737. [Google Scholar] [CrossRef]
- Ankiewicz, A.; Soto-Crespo, J.M.; Akhmediev, N. Rogue waves and rational solutions of the Hirota equation. Phys. Rev. E 2010, 81, 046602. [Google Scholar] [CrossRef]
- Li, L.; Wu, Z.; Wang, L.; He, J. High-order rogue waves for the Hirota equation. Ann. Phys. 2013, 334, 198–211. [Google Scholar] [CrossRef]
- Wang, L.H.; Porsezian, K.; He, J.S. Breather and rogue wave solutions of a generalized nonlinear Schrödinger equation. Phys. Rev. E 2013, 87, 053202. [Google Scholar] [CrossRef]
- Ankiewicz, A.; Akhmediev, N. High-order integrable evolution equation and its soliton solutions. Phys. Lett. A 2014, 378, 358–361. [Google Scholar] [CrossRef]
- Chowdury, A.; Krolikowski, W.; Akhmediev, N. Breather solutions of a fourth-order nonlinear Schrödinger equation in the degenerate, soliton, and rogue wave limits. Phys. Rev. E 2017, 96, 042209. [Google Scholar] [CrossRef]
- Chowdury, A.; Kedziora, D.J.; Ankiewicz, A.; Akhmediev, N. Breather solutions of the integrable quintic nonlinear Schrödinger equation and their interactions. Phys. Rev. E 2015, 91, 022919. [Google Scholar] [CrossRef] [PubMed]
- Kaup, D.J.; Newell, A.C. An exact solution for a Derivative Nonlinear Schrödinger equation. J. Math. Phys. 1978, 19, 798–801. [Google Scholar] [CrossRef]
- Kamchatnov, A.M. New approach to periodic solutions of integrable equations and nonlinear theory of modulational instability. Physics Reports 1997, 286, 199–270. [Google Scholar] [CrossRef]
- Geng, X.G.; Li, Z.; Xue, B.; Guan, L. Explicit quasi-periodic solutions of the Kaup-Newell hierarchy. J. Math. Anal. Appl. 2015, 425, 1097–1112. [Google Scholar] [CrossRef]
- Arshed, S.; Biswas, A.; Abdelaty, M.; Zhou, Q.; Moshokoa, S.P.; Belic, M. Sub pico-second chirp-free optical solitons with Kaup-Newell equation using a couple of strategic algorithms. Optik 2018, 172, 766–771. [Google Scholar] [CrossRef]
- Jawad, A.J.M.; Al Azzawi, F.J.I.; Biswas, A.; Khan, S.; Zhou, Q.; Moshokoa, S.P.; Belic, M.R. Bright and singular optical solitons for Kaup-Newell equation with two fundamental integration norms. Optik 2019, 182, 594–597. [Google Scholar] [CrossRef]
- Smirnov, A.O.; Filimonova, E.G.; Matveev, V.B. The spectral curve method for the Kaup-Newell hierarchy. IOP Conf. Ser.: Mat. Sci. Eng. 2020, 919, 052051. [Google Scholar] [CrossRef]
- Ahmed, H.M.; Rabie, W.B.; Ragusa, M.A. Optical solitons and other solutions to Kaup-Newell equation with Jacobi elliptic function expansion method. Analysis and Math. Phys. 2021, 11, 23. [Google Scholar] [CrossRef]
- Chen, H.H.; Lee, Y.C.; Liu, C.S. Integrability of nonlinear Hamiltonian systems by inverse scattering method. Special issue on solitons in physics. Physica Scripta 1979, 20, 490–492. [Google Scholar] [CrossRef]
- Guo, B.; Ling, L.; Liu, Q.P. High-Order Solutions and Generalized Darboux transformations of derivative nonlinear Schrödinger equations. Studies in Appl. Math. 2013, 130, 317–344. [Google Scholar] [CrossRef]
- Yang, B.; Zhang, W.-G., Z. H.Q.; Pei, S.B. Generalized Darboux transformation and rational soliton solutions for Chen–Lee–Liu equation. Appl. Math. Comput. 2014, 242, 863–876. [Google Scholar]
- Zhang, Y.S.; Guo, L.J.; He, J.S.; Zhou, Z.X. Darboux transformation of the second-type derivative nonlinear Schrödinger equation. Lett. Math. Phys. 2015, 105, 853–891. [Google Scholar] [CrossRef]
- Peng, W.; Pu, J.; Chen, Y. PINN deep learning for the Chen-Lee-Liu equation: Rogue wave on the periodic background. Commun. Nonlinear Sci. Numer. Simul. 2022, 105, 106067. [Google Scholar] [CrossRef]
- Gerdjikov, V.S.; Ivanov, M.I. The quadratic bundle of general form and the nonlinear evolution equations. I. Expansions over the “squared” solutions are generalized Fourier transforms. Bulgarian J. Phys. 1983, 10, 13–26. [Google Scholar]
- Gerdjikov, V.S.; Ivanov, M.I. A quadratic pencil of general type and nonlinear evolution equations. II. Hierarchies of Hamiltonian structures. Bulgarian J. Phys. 1983, 10, 130–143. [Google Scholar]
- He, J.; Xu, S. The rogue wave and breather solution of the Gerdjikov-Ivanov equation. J. Math. Phys. 2012, 53, 03507. [Google Scholar]
- Guo, L.; Zhang, Y.; Xu, S.; Wu, Z.; He, J. The higher order Rogue Wave solutions of the Gerdjikov-Ivanov equation. Phys. Scripta 2014, 89, 035501. [Google Scholar] [CrossRef]
- Kundu, A. Landau-Lifshitz and higher-order nonlinear systems gauge generated from nonlinear Schrödinger-type equations. J. Math. Phys. 1984, 25, 3433–3438. [Google Scholar] [CrossRef]
- Xu, S.; He, J.; Wang, L. The Darboux transformation of the derivative nonlinear Schrödinger equation. J. Phys. A 2011, 44, 305203. [Google Scholar] [CrossRef]
- Smirnov, A.O. Spectral curves for the derivative nonlinear Schrödinger equations. Symmetry 2021, 13, 1203. [Google Scholar] [CrossRef]
- Kundu, A. Integrable Hierarchy of Higher Nonlinear Schrodinger Type Equations. SIGMA 2006, 2, 078. [Google Scholar] [CrossRef]
- Calogero, F.; Eckhaus, W. Nonlinear evolution equations, rescalings, model PDEs and their integrability: I. Inverse Problems 1987, 3, 229–262. [Google Scholar] [CrossRef]
- Zhang, C.; Li, C.; He, J. Darboux transformation and Rogue waves of the Kundu-nonlinear Schrödinger equation. Mathematical Methods in the Applied Sciences 2015, 38, 2411–2425. [Google Scholar] [CrossRef]
- Goossens, J.V.; Yousefi, M.I.; Jaouën, Y.; Haffermann, H. Polarization-Division Multiplexing Based on the Nonlinear Fourier Transform. Optic Express 2017, 25, 26437–26452. [Google Scholar] [CrossRef]
- Gaiarin, S.; Perego, A.M.; da Silva, E.P.; Da Ros, F.; Zibar, D. Dual polarization nonlinear Fourier transform-based optical communication system. Optica 2018, 5, 263–270. [Google Scholar] [CrossRef]
- Civelli, S.; Turitsyn, S.K.; Secondini, M.; Prilepsky, J.E. Polarization-multiplexed nonlinear inverse synthesis with standard and reduced-complexity NFT processing. Optic Express 2018, 26, 17360–17377. [Google Scholar] [CrossRef] [PubMed]
- Gaiarin, S.; Perego, A.M.; da Silva, E.P.; Da Ros, F.; Zibar, D. Experimental demonstration of nonlinear frequency division multiplexing transmission with neural network receiver. Journal of Lightwave Technology 2020, 38, 6465–6473. [Google Scholar] [CrossRef]
- Gerdjikov, V.S.; Smirnov, A.O.; Matveev, V.B. From generalized Fourier transforms to spectral curves for the Manakov hierarchy. I. Generalized Fourier transforms. Eur. Phys. J. Plus 2020, 135, 659. [Google Scholar] [CrossRef]
- Smirnov, A.O.; Gerdjikov, V.S.; Matveev, V.B. From generalized Fourier transforms to spectral curves for the Manakov hierarchy. II. Spectral curves for the Manakov hierarchy. Eur. Phys. J. Plus 2020, 135, 561. [Google Scholar] [CrossRef]
- Yousefi, M.I.; Kschischang, F.R. Information transmission using the nonlinear Fourier transform, part I: Mathematical tools. IEEE Trans. Inf. Theory 2014, 60, 4312–4328. [Google Scholar] [CrossRef]
- Yousefi, M.I.; Kschischang, F.R. Information transmission using the nonlinear Fourier transform, part II: Numerical methods. IEEE Trans. Inf. Theory 2014, 60, 4329–4345. [Google Scholar] [CrossRef]
- Yousefi, M.I.; Kschischang, F.R. Information transmission using the nonlinear Fourier transform, part III: Spectrum modulation. IEEE Trans. Inf. Theory 2014, 60, 4346–4369. [Google Scholar] [CrossRef]
- Le, S.T.; Prilepsky, J.E.; Turitsyn, S.K. Nonlinear inverse synthesis for high spectral efficiency transmission in optical fibers. Opt. Express 2014, 22, 26720–26741. [Google Scholar] [CrossRef]
- Goossens, J.W.; Haffermann, H.; Yousefi, M.I.; Jaouën, Y. Nonlinear Fourier trasform in optical communications. Optic InfoBase Conference Papers, 2017. Part F82-CLEO_Europe 2017.
- Matveev, V.B.; Smirnov, A.O. Solutions of the Ablowitz-Kaup-Newell-Segur hierarchy equations of the “rogue wave” type: a unified approach. Theor. Math. Phys. 2016, 186, 156–182. [Google Scholar] [CrossRef]
- Matveev, V.B.; Smirnov, A.O. AKNS hierarchy, MRW solutions, Pn breathers, and beyond. J. Math. Phys. 2018, 59, 091419. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Kaup, D.J.; Newell, A.C.; Segur, H. The Inverse Scattering Transform-Fourier Analysis for Nonlinear Problems. Studies in Appl. Math. 1974, 53, 249–315. [Google Scholar] [CrossRef]
- Manakov, S.V. On the theory of two-dimensional stationary self-focussing of electromagnetic waves. Sov. Phys. JETP 1974, 38, 248–253. [Google Scholar]
- Eilbeck, J.C.; Enol’skii, V.Z.; Kostov, N.A. Quasiperiodic and periodic solutions for vector nonlinear Schrödinger equations. J. Math. Phys. 2000, 41, 8236. [Google Scholar] [CrossRef]
- Christiansen, P.L.; Eilbeck, J.C.; Enol’skii, V.Z.; Kostov, N.A. Quasi-periodic and periodic solutions for coupled nonlinear Schrödinger equations of Manakov type. Proc. R. Soc. Lond. Ser A 2000, 456, 2263–2281. [Google Scholar] [CrossRef]
- Elgin, J.N.; Enol’skii, V.Z.; Its, A.R. Effective integration of the nonlinear vector Schrödinger equation. Physica D 2007, 225, 127–152. [Google Scholar] [CrossRef]
- Woodcock, T.; Warren, O.H.; Elgin, J.N. Genus two finite gap solutions to the vector nonlinear Schrödinger equation. J. Phys. A 2007, 40, F355–F361. [Google Scholar] [CrossRef]
- Warren, O.H.; Elgin, J.N. The vector nonlinear Schrödinger hierarchy. Physica D 2007, 228, 166–171. [Google Scholar] [CrossRef]
- Morris, H.C.; Dodd, R.K. The two component derivative nonlinear Schrödinger equation. Physica Scripta 1979, 20, 505. [Google Scholar] [CrossRef]
- Xu, T.; Tian, B.; Zhang, C.; Meng, X.H.; Lu, X. Alfvén solitons in the coupled derivative nonlinear Schrödinger system with symbolic computation. J. Phys. A. 2009, 42, 415201. [Google Scholar] [CrossRef]
- Ling, L.; Liu, Q.P. Darboux transformation for a two-component derivative nonlinear Schrödinger equation. J. Phys. A. 2010, 43, 434023. [Google Scholar] [CrossRef]
- Chan, H.N.; Malomed, B.A.; Chow, K.W.; Ding, E. Rogue waves for a system of coupled derivative nonlinear Schrödinger equations. Phys. Rev. E. 2016, 93, 012217. [Google Scholar] [CrossRef] [PubMed]
- Guo, L.; Wang, L.; Cheng, Y.; He, J. Higher-order rogue waves and modulation instability of the two-component derivative nonlinear Schrödinger equation. Commun. Nonlinear Sci. Numer. Simulat. 2019, 79, 104915. [Google Scholar] [CrossRef]
- Kibler, B.; Fatome, J.; Finot, C.; Millot, G.; Dias, F.; Genty, G.; Akhmediev, N.; Dudley, J.M. The Peregrine soliton in nonlinear fibre optics. Nature physics 2010, 6, 790–795. [Google Scholar] [CrossRef]
- Kibler, B.; Fatome, J.; Finot, C.; Millot, G.; Genty, G.; Wetzel, B.; Akhmediev, N.; Dias, F.; Dudley, J.M. Observation of Kuznetsov-Ma soliton dynamics in optical fibre. Scientific Reports 2012, 2, 463. [Google Scholar] [CrossRef] [PubMed]
- Randoux, S.; Suret, P.; Chabchoub, A.; Kibler, B.; El, G. Nonlinear spectral analysis of Peregrine solitons observed in optics and in hydrodynamic experiments. Phys. Rev. E 2018, 98, 022219. [Google Scholar] [CrossRef]
- He, Y.; Suret, P.; Chabchoub, A. Phase evolution of the Time- and Space-like Peregrine breather in a baboratory. Fluids 2021, 6, 308. [Google Scholar] [CrossRef]
- Smirnov, A.O.; Caplieva, A.A. The vector form of Kundu-Eckhaus equation and its simplest solutions. Preprint, arXiv:2211.12895, 2022. 20p. arXiv:2211.12895, 2022. 20p.
- Clarkson, P.A.; Cosgrove, C.M. Painleve analysis of the nonlinear Schrödinger family of equations. J. Phys. A 1987, 20, 2003–2024. [Google Scholar] [CrossRef]
- Tsuchida, T.; Wadati, M. Complete integrability of derivative nonlinear Schrödinger-type equations. Inverse Problems 1999, 15, 1363–1373. [Google Scholar] [CrossRef]
- Yang, B.; Chen, J.; Yang, J. Rogue Waves in the Generalized Derivative Nonlinear Schrödinger Equations. Journal of Nonlinear Science 2020, 30, 3027–3056. [Google Scholar] [CrossRef]
- Wadati, M.; Sogo, K. Gauge transformations in soliton theory. J. Phys. Soc. Jpn. 1983, 52, 394–398. [Google Scholar] [CrossRef]
- Kundu, A. Exact solutions to higher-order nonlinear equations through gauge transformation. Physica D 1987, 25, 399–406. [Google Scholar] [CrossRef]
- Zhang, G.; Yan, Z. The derivative nonlinear Schrödinger equation with zero/nonzero boundary conditions: Inverse scattering transforms and N-double-pole solutions. Journal of Nonlinear Science 2020, 30, 3089–3127. [Google Scholar] [CrossRef]
- Dubrovin, B.A. Matrix finite-zone operators. J. Soviet Math. 1985, 28, 20–50. [Google Scholar] [CrossRef]
- Smirnov, A.; Frolov, E. On a method for constructing solutions to equations of nonlinear optics. Wave Electronics and Its Application in Information and Telecommunication Systems 2022, 5, 448–451. [Google Scholar]
- Akhiezer, N.I. Elements of the theory of elliptic functions; American Mathematical Society: Providence, RI, 1990; Translated from the second Russian edition by H. H. McFaden. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. (Eds.) Handbook of mathematical functions with formulae, graphs and mathematical tables; Willey-Interscience: New York, 1972; p. 1045. [Google Scholar]
- Smirnov, A.O.; Pavlov, M.V.; Matveev, V.B.; Gerdjikov, V.S. Finite-gap solutions of the Mikhalëv equation. Proceedings of Symposia in Pure Mathematics. 2021, 103.1, 429–450. [Google Scholar]
- Gerdjikov, V.S.; Smirnov, A.O. On the elliptic null-phase solutions of the Kulish–Sklyanin model. Chaos, Solitons and Fractals 2023, 166, 112994. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).