CNN-LSTM Hybrid Model to Promote Signal Processing of Ultrasonic Guided Lamb Waves for Damage Detection of Metallic Pipelines

Preprint

Article

CNN-LSTM Hybrid Model to Promote Signal Processing of Ultrasonic Guided Lamb Waves for Damage Detection of Metallic Pipelines

Altmetrics

Downloads

137

Views

Comments

A peer-reviewed article of this preprint also exists.

Hong Pan^*,

Hong Pan^*,

This version is not peer-reviewed

Submitted:

13 July 2023

Posted:

14 July 2023

You are already at the latest version

Alerts

Abstract

Ultrasonic-guided lamb wave approach is an effective non-destructive testing (NDT) method used for detecting localized mechanical damage, corrosion, and welding defects experienced in metallic pipelines. Signal processing of the guided waves is often challenged due to the complexity of operational conditions and environments in the pipelines. Machine learning approaches in recent years, including convolutional neural networks (CNN) and long short-term memory (LSTM), have exhibited their advantages to overcome these challenges for signal process and data classification of complex systems, thus great potential for damage detection of critical oil/gas pipeline structures. In this study, a CNN-LSTM hybrid model is utilized for decoding ultrasonic guided waves for damage detection of metallic pipelines, and twenty-nine features are extracted as input to classify different types of defects from metallic pipes. The prediction capacity of the CNN-LSTM model is assessed by comparing it to the CNN and LSTM. The results demonstrate that the CNN-LSTM hybrid model exhibits much higher accuracy, with 94.8%, as compared to those of CNN and LSTM. Interestingly, the results also reveal that predetermined features, including time-, frequency-, and time-frequency domains, could significantly improve the robustness of the deep learning approaches, even though the deep learning approaches are often believed they include automated feature extraction, without the hand-crafted steps as the shallow learning do. Furthermore, the CNN-LSTM model displays higher performance when the noise level is relatively low (e.g., SNR=9 or higher), as compared to the other two models, but its prediction drops gradually with the increase of the noise.

Keywords:

Subject: Engineering - Civil Engineering

1. Introduction

Onshore transmission/distribution oil/gas pipelines are major energy systems to transport and deliver energy to power communities and other end users. These pipeline structures are vulnerable to mechanical damage, corrosion, and other threats when subjected to aging and different stressors. Different NDT-based sensors and inline inspection tools, including the ultrasonic-guided lamb wave approach, have been used to monitor, detect, and locate potential defects in pipelines.

Besides the physics-based signal process, data-driven approaches have been accepted in the recent decade for data process, including the use of artificial neural networks (ANNs) [1,2,3] and deep learnings (DLs) [4,5,6]. Waveform-based deep neural networks have become a necessary part of many pattern recognition systems [7,8,9,10,11]. These deep neural networks directly take raw signals as input such as in infrastructure condition assessment [12], stress level identification [13], structure damage identification [14,15], structure health monitoring [16,17,18,19], structure damage diagnosis [20,21,22] and structure damage detection [23,24,25].

For feature extraction in ultrasonic signal processing, Pittner and Kamarthi [26] developed a method to automatically sort the wavelet coefficients matrix into the important frequency range and less important frequency range and the Euclidean norms have been used to calculate the features of a process wavelet signal [26]. This method was successfully applied to the diagnosis of pulmonary diseases [26]. Shi et al. concluded that the multi-stable stochastic resonance (SR) method had much good performance and capability in signal processing than the classical bistable SR method [27]. It could improve the output signal-to-noise ratio, improve the detection effect, and could also detect lower signal-to-noise ratio weak signals [27]. Shi et al. presented a method of empirical mode decomposition with cascaded multi-stable stochastic resonance system (CMSRS) denoising. He found that this method could effectively help denoise the high-frequency signals, improve the energy of low-frequency signals and identify fault characteristic signals [27]. Zhao et al. [28] proposed a piecewise tri-stable stochastic resonance (PTSR) method to extract signal fault features and compared the fault characteristics of extracted signals with the standard tri-stable SR method. The result showed that PTSR method had better signal processing performance than STSR method [28]. Despite that, the applicability of the CNN-LSTM hybrid model has not been investigated in the fault ultrasonic signal classification area. In addition, the feature parameters used to express the features of time-series data have not been used in the ultrasonic signals of damaged pipelines.

Therefore, this study aims to fill the knowledge gaps in how to achieve efficient and accurate classification of different kinds of damaged pipelines with corrosion by utilizing the multi-feature extraction capability of the hybrid deep learning model and constructing reasonable datasets to improve the accuracy of different models. In this study, the dataset used for model training was collected from field tests, and the classification results of the proposed CNN-LSTM hybrid model were compared with some benchmark models, like CNN and LSTM models, to verify its advantages. Furthermore, the influence of signal noise on classification accuracy was specifically calibrated.

The article is organized as follows: firstly, the method of wavelet threshold denoising was used to denoise the raw ultrasonic signal series. Secondly, twenty-nine feature parameters were extracted as input data for training different machine learning networks. Next, the data reduction was used to reduce the dimensionality of the twenty-nine feature parameters series and the reduced data was input to the CNN-LSTM hybrid models to verify the classification accuracy. Finally, the impacts of noise interference on the effectiveness of the CNN-LSTM model were further evaluated.

2. Framework of machine learning-enriched CNN-LSTM method for damage detection

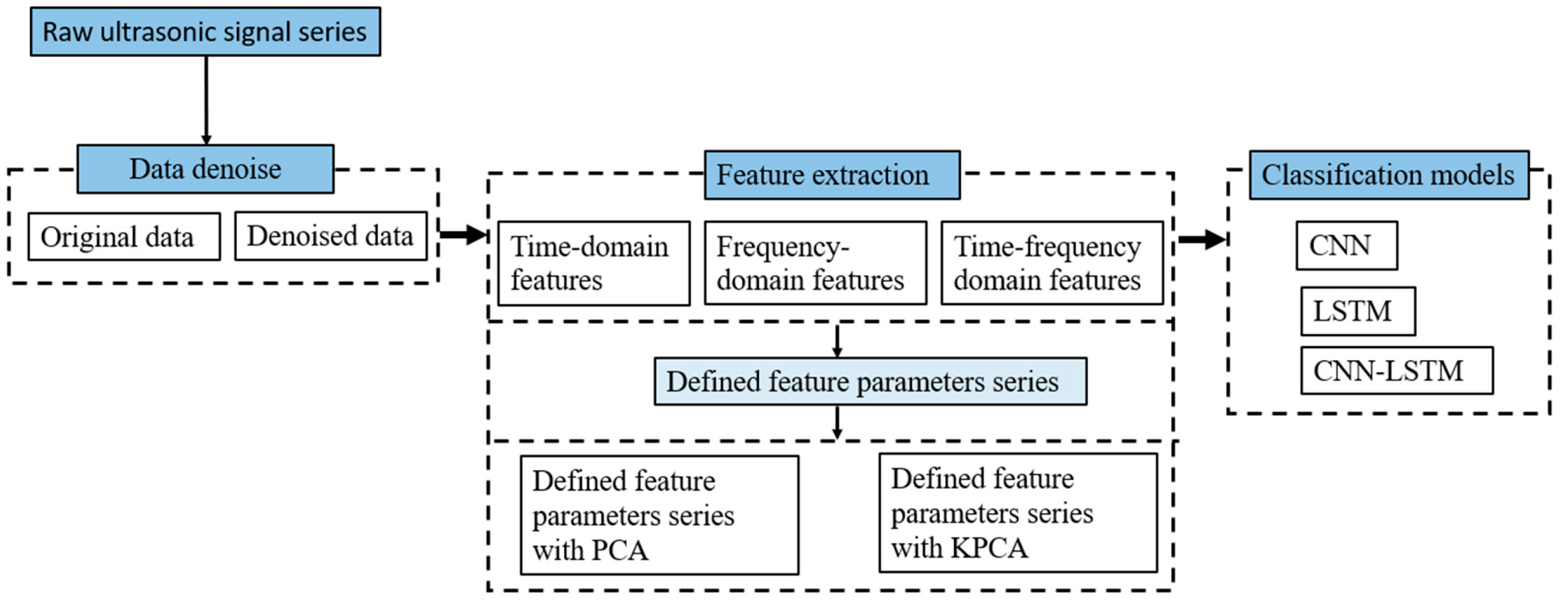
Figure 1 shows the flowchart of the methodology. The sequences of monitoring data were collected to build the dataset. The dataset included different kinds of pipeline defects status. Second, the CNN-LSTM model was established and verified as compared to CNN, and LSTM individually, and further studies were conducted to reveal the influence of the different features, and data reduction process on prediction accuracy.

2.1. CNN-LSTM hybrid model

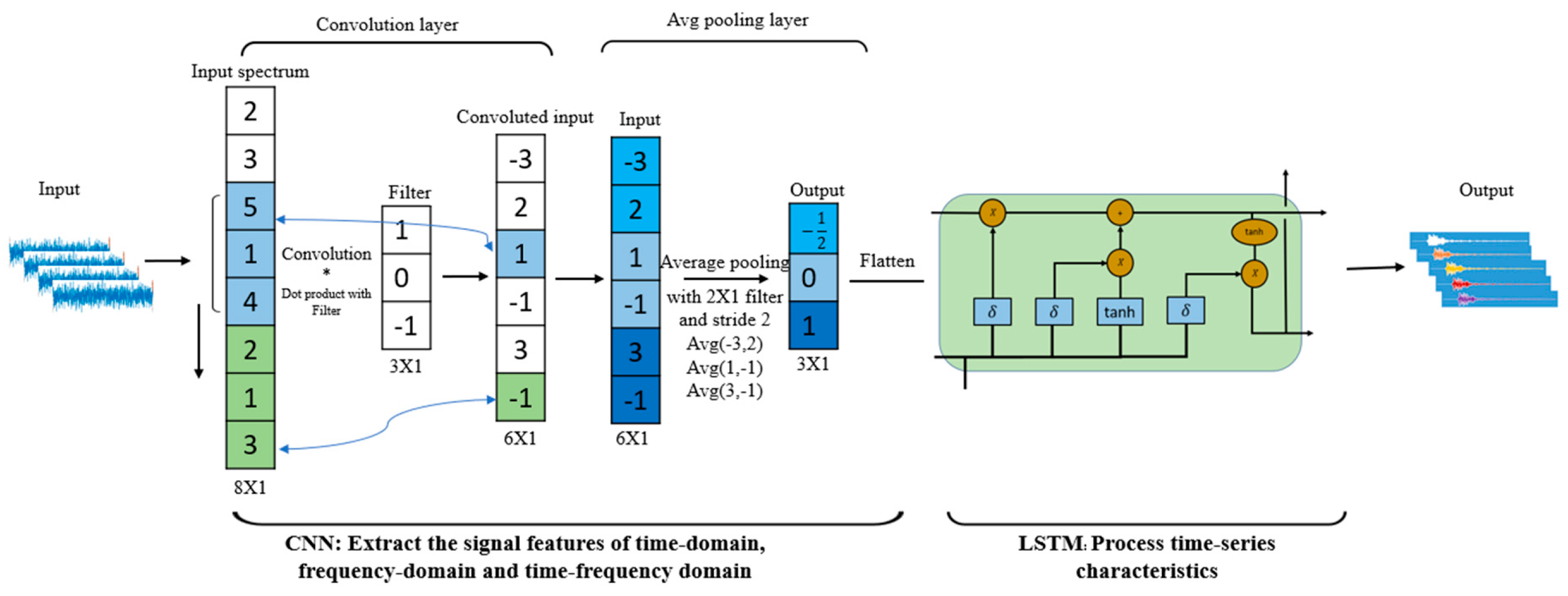
A CNN-LSTM hybrid model was proposed, and the structure and the data processing flow of the model are shown in Figure 2, which is based on Zhang’s research [29]. The purpose of the CNN layer is to extract the signal features of the time-domain, frequency-domain, and time-frequency domain from the monitoring data. The obtained features are then put into a two-dimensional array and used as the input for the LSTM layer to analyze the time-series features. The mechanism of feature extraction of CNN and feature processing of LSTM is shown in the following sections.

Convolutional neural network (CNN) is a popular deep learning algorithm, and its purpose is to process data in the form of multi arrays [30]. The convolutional layer and the max-pooling layer are the two main layers in CNN structure, as shown in Figure 1.

The convolutional layer is designed to perform convolution and activation operations on the input data and produce feature maps [29]. The mathematic procedure of convolution in layer l is exhibited as [31]

C_{j} = f (\sum_{m i E M} m i \times k j + b j)

(1)

where

m i

is the data input to the convolutional layer,

k j

is the convolutional kernel, and

b j

is the bias. f (

\cdot

) represents the activation function.

The average pooling layer follows the convolutional layer and helps to reduce the feature map resolution and decrease the network computation time. The arithmetical formula of the pooling operation in layer l is exhibited as [31]

S j = β j d o w n (c j) + b k

(2)

where down (

\cdot

) represents the average pooling method.

The input dataset for the CNN-LSTM hybrid model is collected from time series data. For CNN structure, the input layer works with the input data, the convolutional layer extracts data features with kernel functions, and the average pooling layer is to reduce the amount of data from the convolutional layer, reducing overfitting [32]. Finally, the data is flattened into the LSTM layer.

LSTM is a long-short term memory network and it is an effective tool to deal with sequence and time series data for classification and regression problems [33]. The LSTM network defines three layers. The sequence input layer and the LSTM layer are the two most important structures for an LSTM network. The purpose of the sequence input layer is to input the time series data for the LSTM network. The purpose of the LSTM layer is to memorize long-term dependencies between time steps of sequence data [34]. The last layer is used to output the information of pattern recognition.

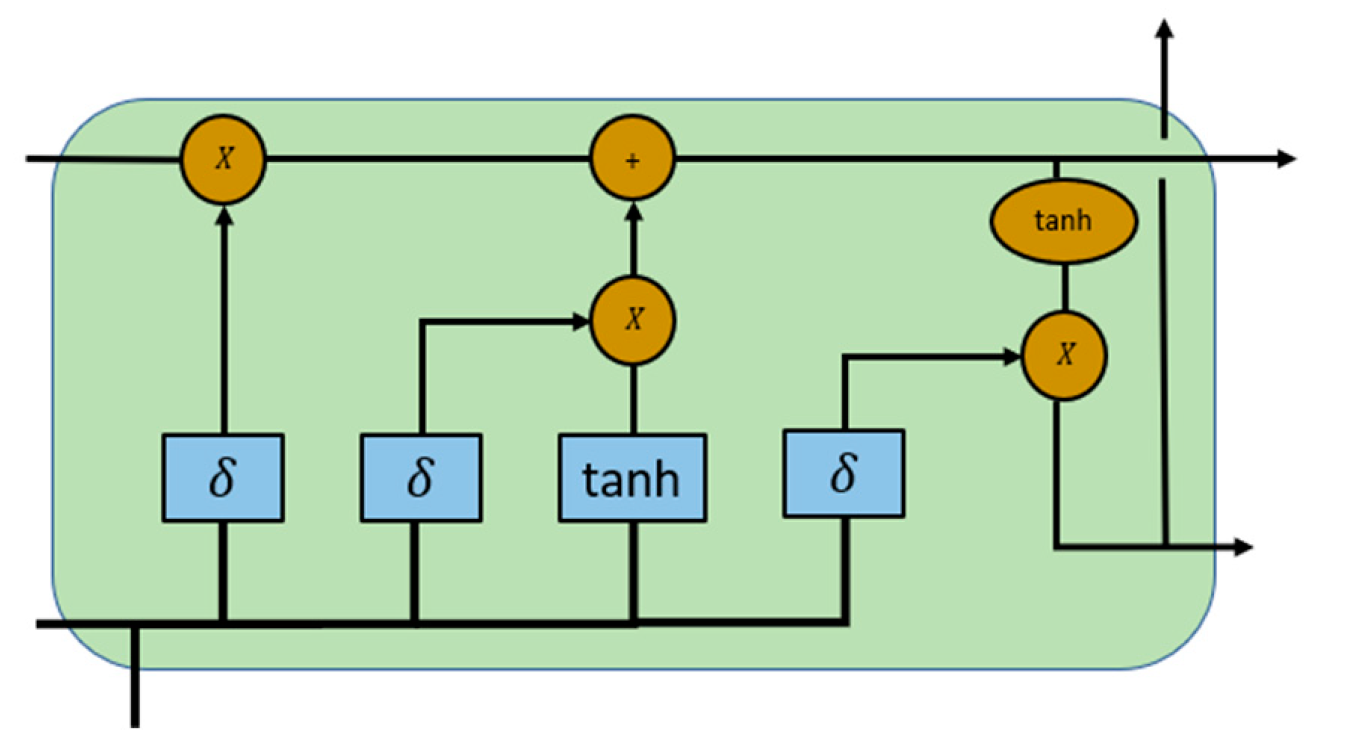
There are four components, including input gate (i), forget gate (f), cell candidate (g), and output gate (o), used to control the cell state and hidden state of the layer [35], Figure 3 is the LSTM structure, which is drawn based on Chevalier’s research [34], illustrating the flow of data at time step t.

The input gate (

i_{t}

) and the forget gate (

f_{t})

are defined to control the cell state update, and reset (forget), respectively, while the cell candidate (

g_{t}

) and the output gate (o) denote the add information to cell state, and control the cell state added to hidden state, respectively, in the form [35]

i_{t} = σ_{g} (W_{i} x_{t} + R_{i} h_{t - 1} + b_{i})

(3)

f_{t} = σ_{g} (W_{f} x_{t} + R_{f} h_{t - 1} + b_{f})

(4)

g_{t} = σ_{c} (W_{g} x_{t} + R_{g} h_{t - 1} + b_{g})

(5)

o_{t} = σ_{g} (W_{o} x_{t} + R_{o} h_{t - 1} + b_{o})

(6)

where t is the time step,

σ_{g}

is the gate activation function, The matrices W, R, and b are concatenations of the input weights, the recurrent weights, and the bias of each component, respectively.

c_{t}

is cell state at time step t and can be defined as [35]

c_{t} = f_{t} ⨀ c_{t - 1} + i_{t} ⨀ g_{t}

(7)

where

⨀

is the Hadamard product.

h_{t}

is hidden state at time step t and can be defined as [35]

h_{t - 1} = o_{t} ⨀ σ_{c} (c_{t})

(8)

where

σ_{c}

is the state activation function.

Figure 3 shows that LSTM can deal with continuous and highly correlated time series data [29]. During the corrosion process of damaged pipeline system, the current corrosion monitoring data has a closely connection with the previous days, and the series of corrosion monitoring data is highly time dependent [29]. As a result, LSTM can be used to deal with the time series information from the CNN networks and process the processed data to the layers to classify the different kinds of damaged pipelines.

2.2. Features extraction

2.2.1. Definition of features

In this study, ten dimensional time-domain characteristic indicators, six dimensionless time-domain characteristic indicators and the thirteen frequency-domain characteristic indicators are selected to characterize the fault characteristics in different kinds of damaged pipelines, as shown in Table 1 and Table 2. Here, sixteen time-domain features and thirteen frequency-domain features are chosen respectively. These indicators are chosen based on Chen’s research [36].

Dimensional indicators will become much bigger with the development of defects and they will also change with the changes in working conditions [36]. Dimensionless indicators depend on the probability density function. Both indicators can better reflect the trend of pipeline defects. Therefore, this study uses these indicators as a time domain characteristic index. These indicators are usually applied in reflecting the fault trend of space rolling bearings [36].

In Table 2,

s (k)

is the spectrum of signal x(n), k=1,2,3…, K, K is the number of spectral lines, and

f_{k}

is the frequency value of the kth spectral line. The characteristic parameter

p_{1}

reflects the vibration energy in the frequency domain,

p_{2}

p_{3}

p_{4}

p_{6}

and

p_{10}

reflect the degree of dispersion or concentration of the spectrum;

p_{5}

p_{7}

p_{8}

and

p_{9}

reflects the change of the position of the main frequency [36].

2.2.1. Data dimension reduction

The number of features in time-domain features, frequency-domain features and time-frequency domain features is too large. In order to select several main characteristics to express the fault features of damaged pipelines, two different methods of data dimension reduction have been tested, PCA method and K-PCA method.

2.2.2.1. Principal component analysis (PCA)

The PCA could be defined in the form as follows:

Step 1: standardization.

z = \frac{v a l u e - m e a n}{s t a n d a r d d e v i a t i o n}

(9)

After standardization, all the variables are transferred into the range of [0,1], it can reduce the deviation of principle components.

Step 2: Covariance matrix calculation

C = \frac{1}{l} \sum_{t = 1}^{l} {X_{t} X_{t}}^{T}

(10)

For

X_{t}, \sum_{t = 1}^{l} X_{t} = 0

X_{t} = {{(X}_{t} (1), {X_{t} (2), \dots, X}_{t} (m))}^{T}

, t=1,2,3,…,l, m is the dimension and m<l.

Step 3: Calculate the eigenvectors and eigenvalues of the covariance matrix to identify principal components

λ_{i} μ_{i} = C μ_{i}

(11)

where

λ_{i}

is one of eigenvalues of C,

μ_{i}

is the corresponding eigenvector, i=1,2,3,…,m.

Step 4: the principal components of

s_{t}

can be calculated as the orthogonal transformations of

X_{t}

based on corresponding eigenvector

μ_{i}

s_{t} (i) = {μ_{i}}^{T} X_{t}

(12)

2.2.2.1. Kernel principal component analysis (KPCA)

KPCA is to perform nonlinear transformation and achieve nonlinear analysis from linear PCA on the samples using the kernel method.

λ_{i} α_{i} = K α_{i}

(13)

where K is the kernel matrix,

K = {\{K_{i j}\}}_{n \times n}

K_{i j} = k (x_{i}, x_{j})

x_{i}

and

x_{j}

are samples in the original space.

Z^{l} (x) = \sum_{i = 1}^{n} {α_{i}}^{l} k (x_{i}, x_{j})

(14)

Y = {[Z^{1} (x), Z^{2} (x), Z^{3} (x), \dots, Z^{m} (x)]}^{T}

(15)

where

α^{l}

is the lth eigenvector. In the new space, the coordinates of the sample x on the first m nonlinear principal components constitute the sample Y. KPCA has the properties as PCA and KPCA can extract a greater number of principal components than PCA.

2.3. Evaluation of model performances

2.3.1. Confusion matrix and accuracy as performance indicators

Confusion matrix is a popular method applied to classification problems, including binary classification and multiclass classification problems [37]. Table 1 is an example of a confusion matrix for binary classification [37].

The counts of predicted and actual values are calculated from confusion matrices. The output “TN” represents for True Negative which is the number of negative examples classified accurately [37]. “TP” shows True Positive which shows the number of positive examples classified accurately [37]. “FP” stands for False Positive which means the number of actual negative examples classified as positive [37]. “FN” is False Negative which is the number of actual positive examples classified as negative [37]. The accuracy of a confusion matrix model is calculated using the given formula below [37].

A c c u r a c y = \frac{T N + T P}{T N + F P + F N + T P}

(16)

2.3.1. ROC curve as another performance indicator

The receiver operating characteristic (ROC) curves are produced by comparing the true positives rate against the false positives rate depending on various thresholds, which were used as the evaluation tool in machine learning [1,2]. The area under the ROC curve (AUC) stands for the level or measurement of separability it ranges from 0 to 1. Better model performance is associated with higher AUC. When a model has an accuracy of 100%, AUC equals one.

3. Case study

3.1. Ultrasonic guided waves collected from embedded damaged pipes

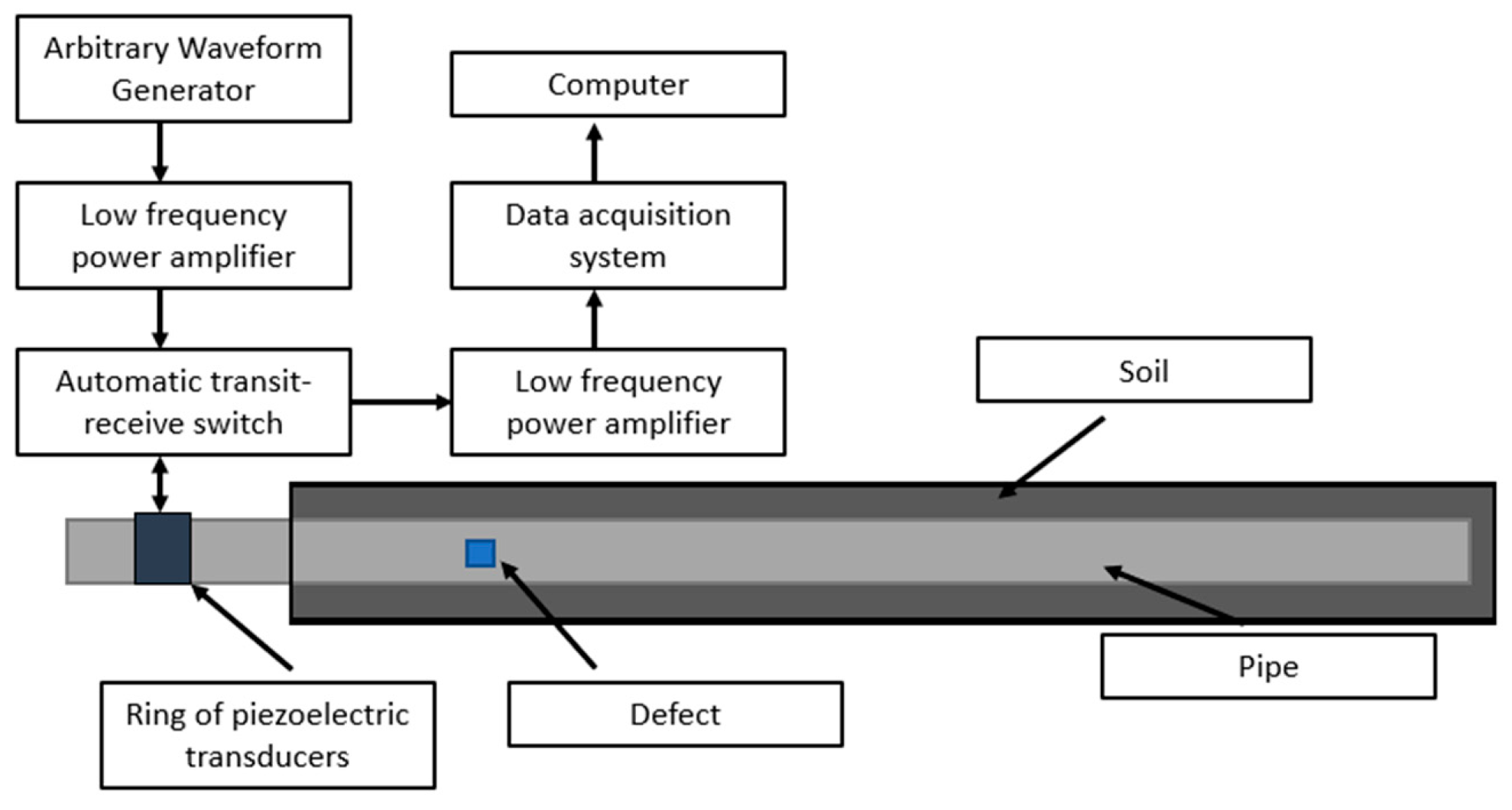
Figure 4 shows the experiment principle of the ultrasonic testing system. Torsional guided waves are excited using the piezoelectric transducers by manipulating their orientation, as used in the literature [38]. A total of nine piezoelectrical transduces were arranged axially in a ring to build the test system. Tone burst signals were used to excite the transducers and the low bandwidth nature of these signals makes the generation of torsional mode much easier. The waveform generator was the 33220A 20 MHz Function/Arbitrary Waveform Generator. The parameters of Arbitrary Waveform Generator are as follows. The waveform type was the default arbitrary waveform with the frequency of 40 Khz, the amplitude of 10 vpp, and the waveform production period of 3 seconds. In order to better read the waveform data, the Noesis 7.0 software was used to transfer the original waveform data, and will be fed into the neural networks.

A total number of 336 groups of samples are collected for each pipeline state, where 240 groups are randomly selected as training samples, and the remaining 96 groups are used as test samples. Each set of samples contains 3000 sampling points. This dataset consists of 6 classes and each class represents different kinds of damaged pipes (Table 4): a) P-1: the pipe with a small notch located at1/3L away from the left side, b) P-2: the pipe with a big notch located at 1/3L away from the left side and a weldment at 2/3L away from the left side, c) P-3: the pipe with a small notch at 1/3L and a weldment at 2/3L away from the left side, d) P-4: the pipe with a big notch located at 1/3L away from the left side, e) P-5: -the pipe with epoxy coating without damage, and f) P-6: the pipe with epoxy coating with a weldment at 2/3L away from the left side. The reason for this pairing is to detect the steps of the corrosion of different kinds of pipes. The specific description of the data set is shown in Table 4. The time-domain waveforms corresponding to the various pipeline states are shown in Figure 5.

3.2. Data denoise using wavelet threshold denoising

Wavelet threshold denoising can be realized through the following steps, which is drawn based on [39].

Step 1: Discrete wavelet decomposition of signal with noise. According to the characteristics of the signal with noise, the appropriate wavelet base and the number of decomposition layers are selected to perform discrete wavelet transform and the wavelet coefficients

d_{j, k}

of each layer are acquired.

One-dimensional non-stationary signal model is as follows [40].

x (t) = f (t) + ε (t)

(17)

where

x (t)

is original signal with noise, f(t) is original signal without noise,

ε (t)

is the white gaussian noise signal.

\int x (t) ψ_{j, k} (t) d t = \int f (t) ψ_{j, k} (t) d t + \int ε (t) ψ_{j, k} (t) d t

(18a)

d_{j, k} = u_{j, k} + e_{j, k}

(18b)

where

ψ_{j, k} (t)

is discrete wavelet basis function; and

d_{j, k}

is the wavelet coefficient of each layer after wavelet transformation of the signal with noise x(t);

u_{j, k}

is the wavelet transformation coefficient of the original signal f(t);

e_{j, k}

is the wavelet transformation coefficient of the white gaussian noise signal ε(t).

Step 2: Threshold quantization processing. the threshold λ and the threshold function are used to process the wavelet coefficients

d_{j, k}

to obtain the processed wavelet coefficients

d_{j, k}^{'}

of each layer.

Step 3: Wavelet coefficient reconstruction. The processed wavelet coefficients

d_{j, k}^{'}

and the approximate coefficients of the jth layer are reconstructed to obtain the denoised signal x′(t).

Figure 5 shows original signal and signal after wavelet threshold denoising. Signal denoising enhances the signal-to-noise ratio by eliminating interferences that don't supply relevant information and reduce the predicted accuracy of machine learning models [41].

4. Results and discussion

4.1. Classification performance of CNN, LSTM and CNN-LSTM model with twenty-nine feature parameters series

In order to demonstrate the effectiveness of the established CNN-LSTM model for data classification, this study built CNN and LSTM models as benchmark models and used the twenty-nine feature parameters series in Table 1 and Table 2 as the dataset for model training. Table 5 summarizes the preferred network structures of the two benchmark models, as determined by a number of tests. This study used padding to prevent information loss when a CNN was utilized to feature extraction [29]. The classification performance of CNN, LSTM and CNN-LSTM models were compared. The classification accuracy was evaluated by confusion matrix and the accuracy in Equation (16).

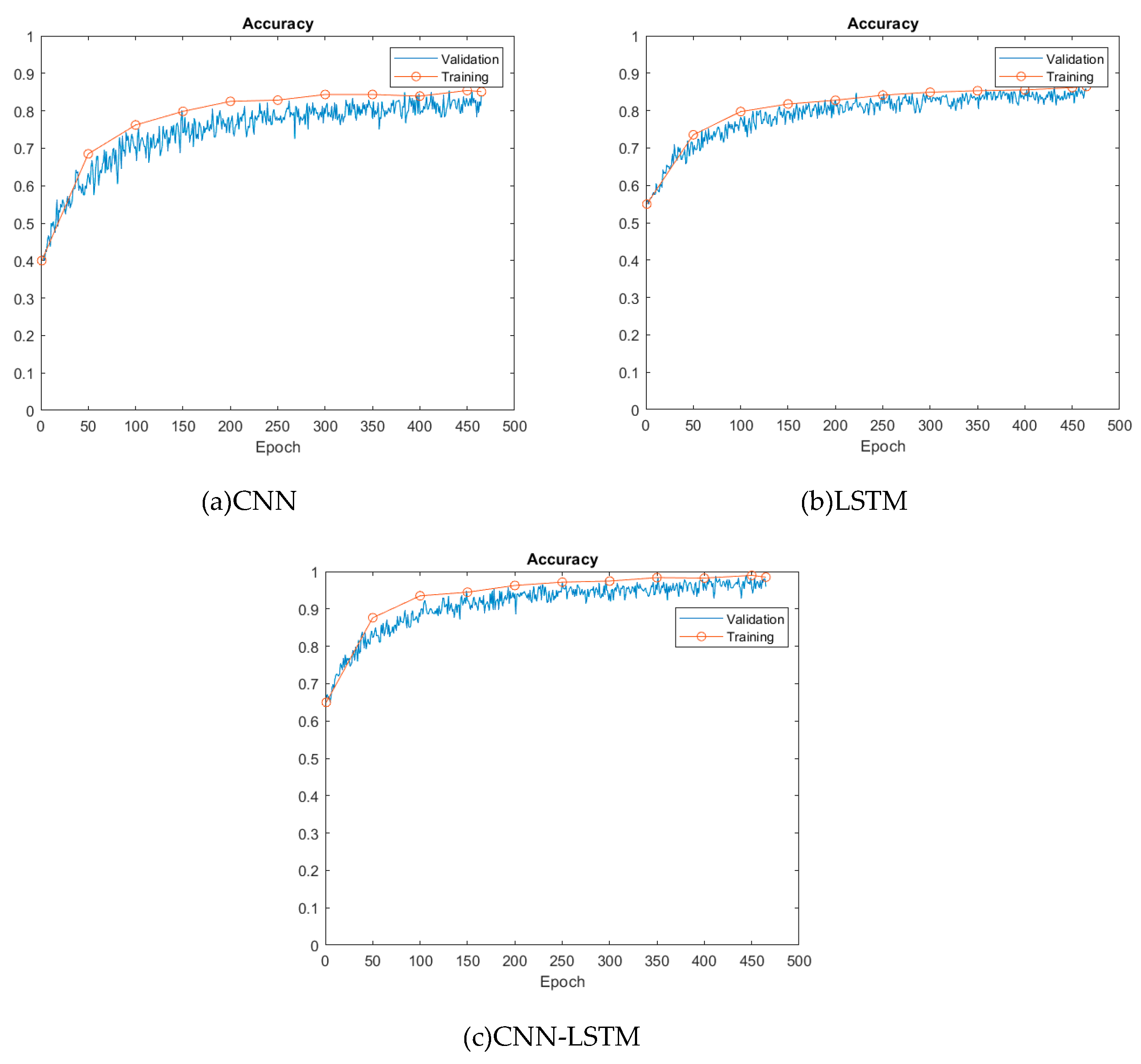
A CNN-LSTM hybrid model was established as discussed in Section 2.1 and as shown in Table 6, and the hybrid model was utilized to concurrently extract the temporal features and analyze the time series features of the dataset. Figure 6 shows the training progress for both the training and validation sets of the three models over 300 epochs. CNN-LSTM model achieve better performance than CNN and LSTM models at the very beginning. For instance, the accuracies of the CNN-LSTM model on both the training set and the test set start from 65% when epoch = 0, while the accuracies of the CNN and LSTM models on both the training set and the test set are 40% and 55% respectively.

As the number of epochs increases, the accuracies of the training set and test set of three models also show a rising trend. Furthermore, it is clear to see that the training accuracies are much higher than the validation accuracies for three models. When the number of epochs reaches 300, the model training accuracy and validation accuracy reach the highest value, 94.8% for CNN-LSTM model, 86.5% for LSTM model and 85.4% for CNN model, as shown in Table 5. The classification accuracy of both the training set and test set is stable at about the highest value at the same time, which means that the model is capable of adjusting to the training set.

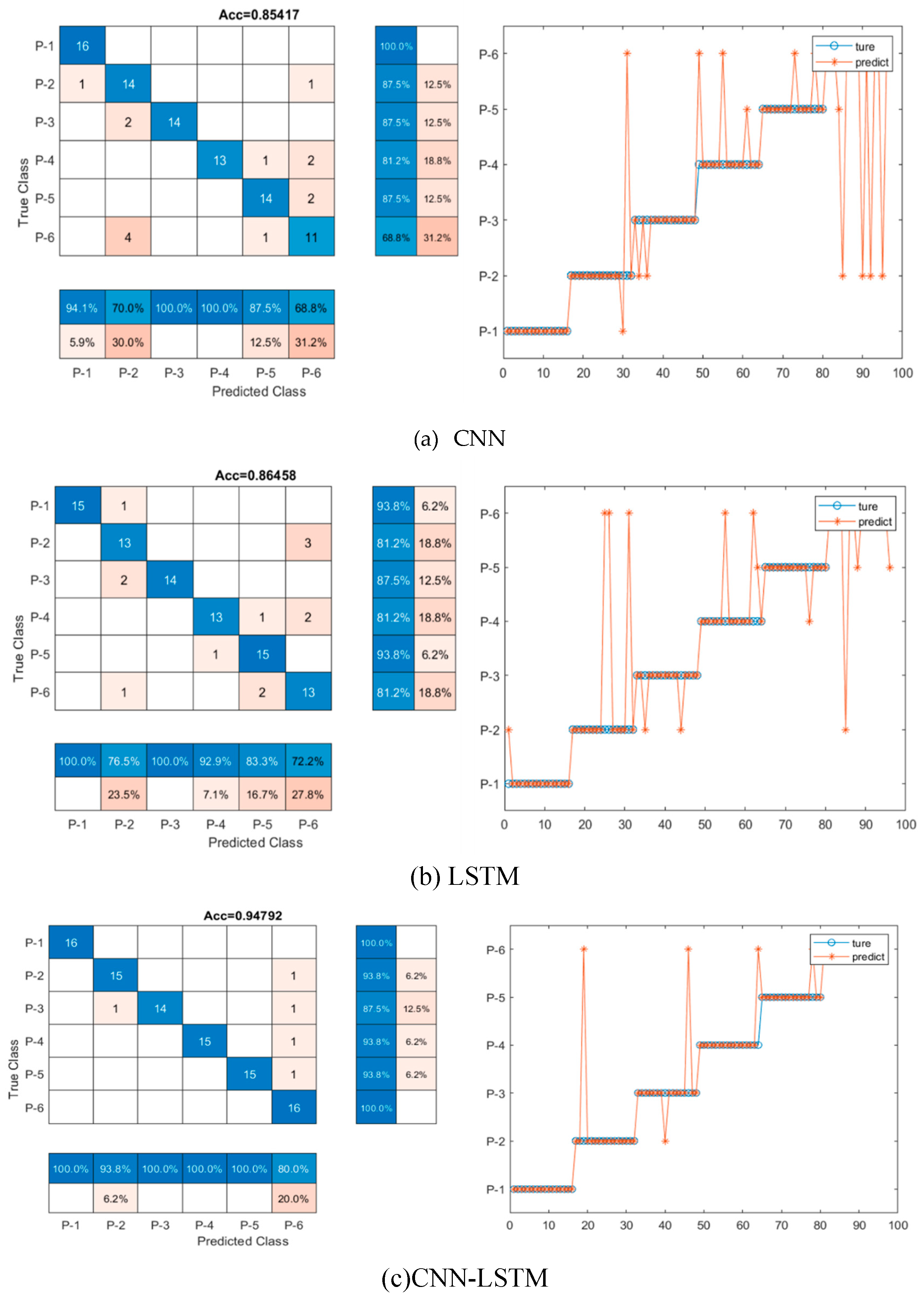
Table 5 shows the test results of three models and a total number of twenty-nine feature parameters series were used as input. Clearly, the CNN-LSTM hybrid model has a much higher accuracy by 94.8%, as compared to the CNN and the LSTM model, with accuracy of 85.4% and 86.5%, respectively. To provide a more intuitive comparison, the confusion matrix predicted for each model is shown in Figure 7. CNN-LSTM displays five signals out of ninety-six testing signal samples that are mistakenly categorized into other groups, while CNN and LSTM include fourteen and thirteen out of ninety-six incorrectly grouped into other groups, respectively, suggesting that the CNN-LSTM hybrid network could have higher capability for data classification. Even though both CNN and LSTM models come to identical accuracy, the slightly higher accuracy from the LSTM model over the CNN’s could be partially due to the fact that the LSTM structure is specifically proposed for dealing with time series data as used in this study, thus leading to slightly better results, which is also confirmed in the other sections below.

4.2. Classification performance of CNN-LSTM model with denoised data

To quantitatively study how the denoised data improves the classification accuracy of the deep learning models, the CNN-LSTM model was trained using the dataset without denoise (original signal dataset) and with denoise. And the denoised data set has a clear difference with the original data, as shown in Figure 5. The training accuracies, confusion matrix and ROC curve were used as indicators to compare, as shown in Table 6, Figure 8 and Figure 9. When considering the denoise, the accuracy of the CNN-LSTM model is 87.5%, which improves 11% than the accuracy (77.1%) of the CNN-LSTM model with original data. 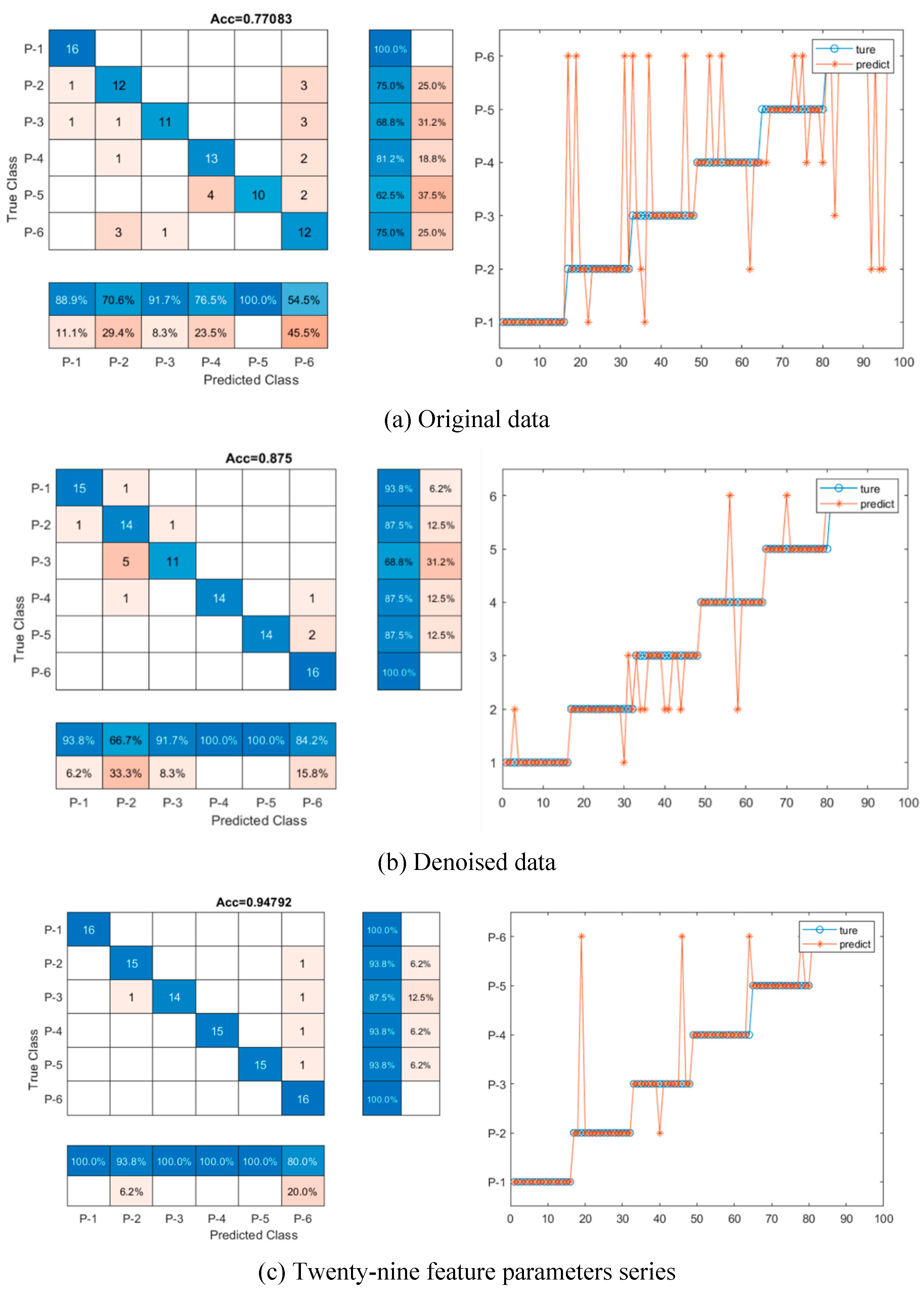As illustrated in Figure 8, seven signal samples out of ninety-six testing signal samples are incorrectly placed into other groups for denoised data model and twenty-two signal samples out of ninety-six testing signal samples are mistakenly grouped into other groups for original data model. 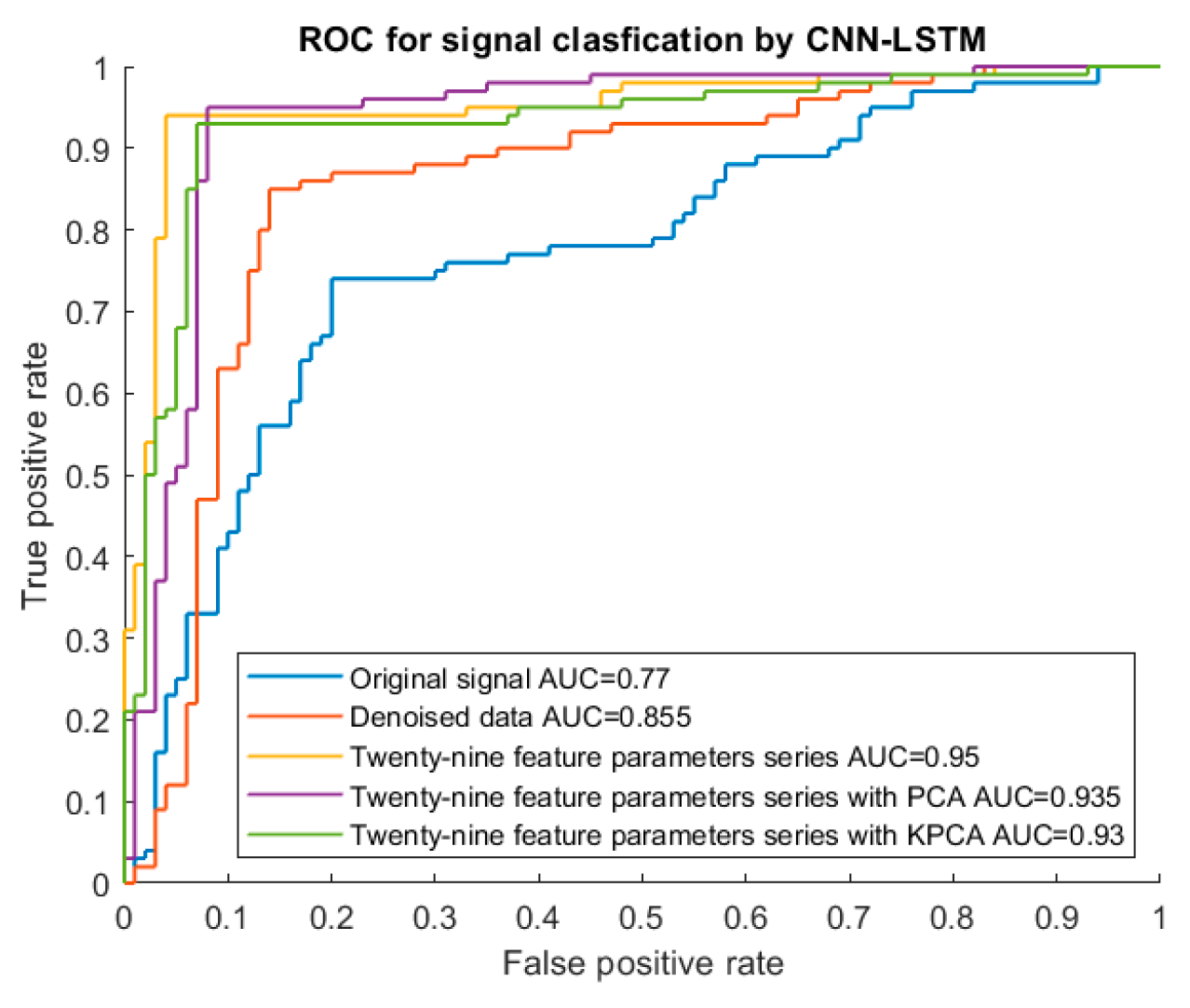Similarly, as shown in Figure 9, the AUC of CNN-LSTM model with denoised data is 0.855, which is also bigger than that of CNN-LSTM model with original data (0.770). This demonstrates that when denoise was considered in the dataset, the classification accuracy of the CNN-LSTM hybrid model can be improved.

4.3. Classification performance of CNN-LSTM model with predetermined features

To analyses the effectiveness of the twenty-nine feature parameters, CNN-LSTM model was trained using the dataset with and without twenty-nine feature parameters. As shown in Table 6 and Figure 8. The classification accuracy of CNN-LSTM model with twenty twenty-nine feature parameter series improves 22.97% and 8.33% respectively when compared with original input data (77.083%) and denoised input data (87.500%). The AUC of CNN-LSTM model with twenty-nine feature parameters series is the highest (0.950), which is close to 1, as shown in Figure 9. The result is meaningful, which means feature extraction can help improve the training accuracy and performance of the CNN-LSTM hybrid models and the twenty-nine features parameter series can be used as indicator of fault signal features to detect pipeline damage.

4.4. Classification performance of CNN-LSTM model with data dimension reduction

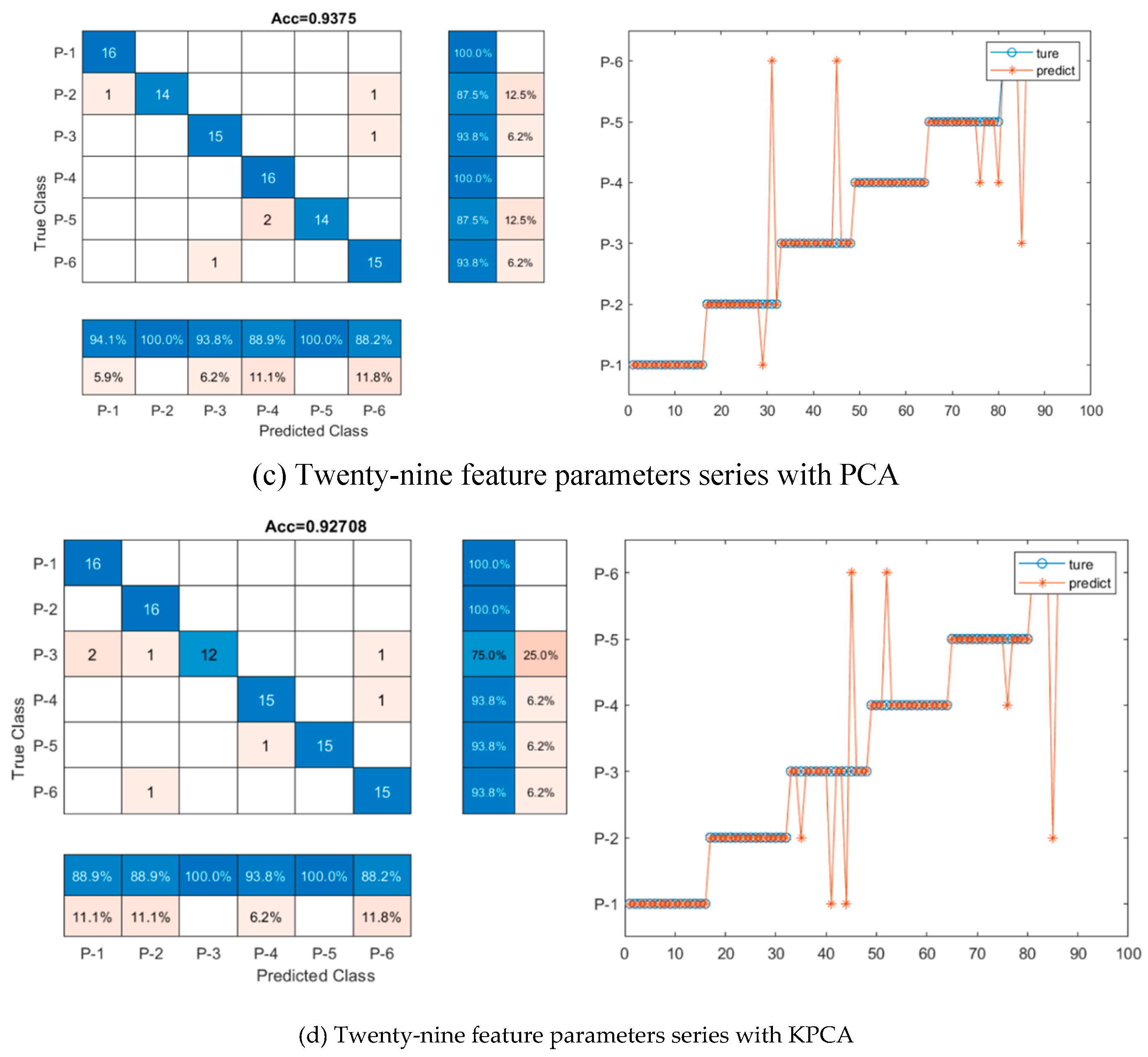
To further improve the classification accuracy of CNN-LSTM model, the feature dimension can be optimized. In this study, PCA and KPCA were applied to decrease the feature dimension of the twenty-nine feature parameters and CNN-LSTM model with and without reduction of feature dimension was trained. As shown in Table 6 and Figure 8, when twenty-nine feature parameters series with PCA are used as input data of the CNN-LSTM hybrid network, the classification accuracy is 93.8%. When twenty-nine feature parameters series with KPCA are used as input data of the CNN-LSTM hybrid network, the classification of accuracy is 92.7%. The classification accuracies reduce by 1% and 2%, for the model with twenty-nine feature parameters series with PCA and the model with twenty-nine feature parameters series with KPCA respectively, compared with network with twenty-nine feature parameters series input (94.8%). For ROC curve in Figure 9, the AUC values are 0.935 and 0.930 for the model with twenty-nine feature parameters series with PCA and the model with twenty-nine feature parameters series with KPCA respectively, which is also lower than the AUC of CNN-LSTM model with twenty-nine feature parameters series (0.950). The result indicates that the reduction of data dimension has no effective promotion to the classification accuracy but may reduce the classification accuracy to some extent.

5. Further discussion of the effectiveness of the hybrid model under noise interference

To evaluate the performance and robustness of the signal processing and model training in previous study, the noise interference on feature extraction and model training will be studied in this part. Specifically, the white Gaussian noise that will be directly applied to original signal to simulate the real situation with noise, noise levels are from 3 dB to 15 dB.

5.1. Introduction of white Gaussian noise into the signals

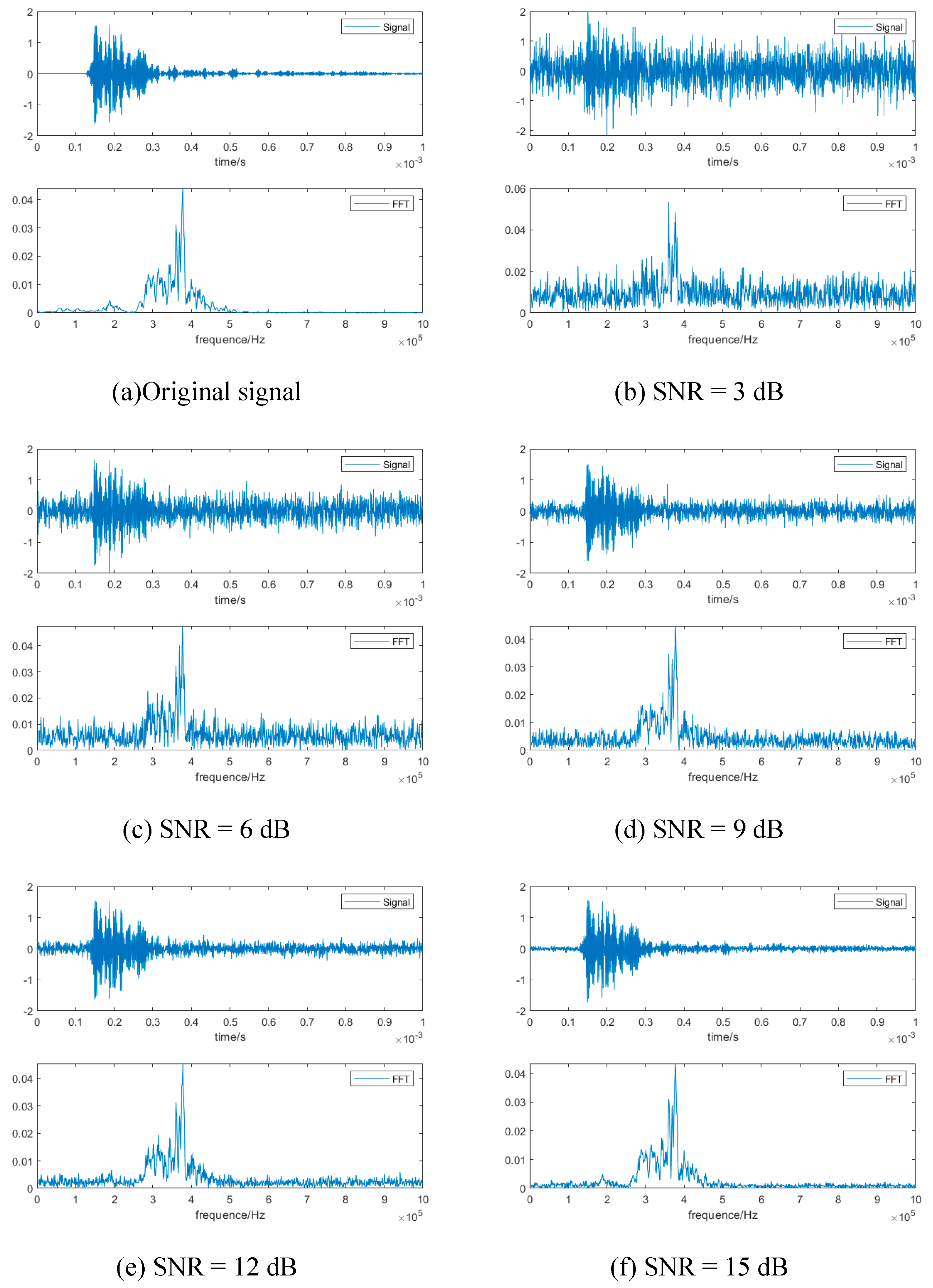
To study the robustness of signal processing and model training, the white Gaussian noise was directly added to original signal data. Taking the signal in P-1 as an example, Figure 10 shows the signals with different noise interference. It is clearly to see that with the increase of the SNR, the signal becomes more and more clear. When SNR= 15 dB, the signal is almost the same as the original signal. When SNR = 3 dB, the signal is contaminated by noise and it is hard to differentiate between noise and signal. The sensitivity of the deep learning algorithm to the uncertainty brought on by noise can also be tested by classifying signals in various noise levels.

5.2. Classification performance of CNN-LSTM model with white Gaussian noise interference

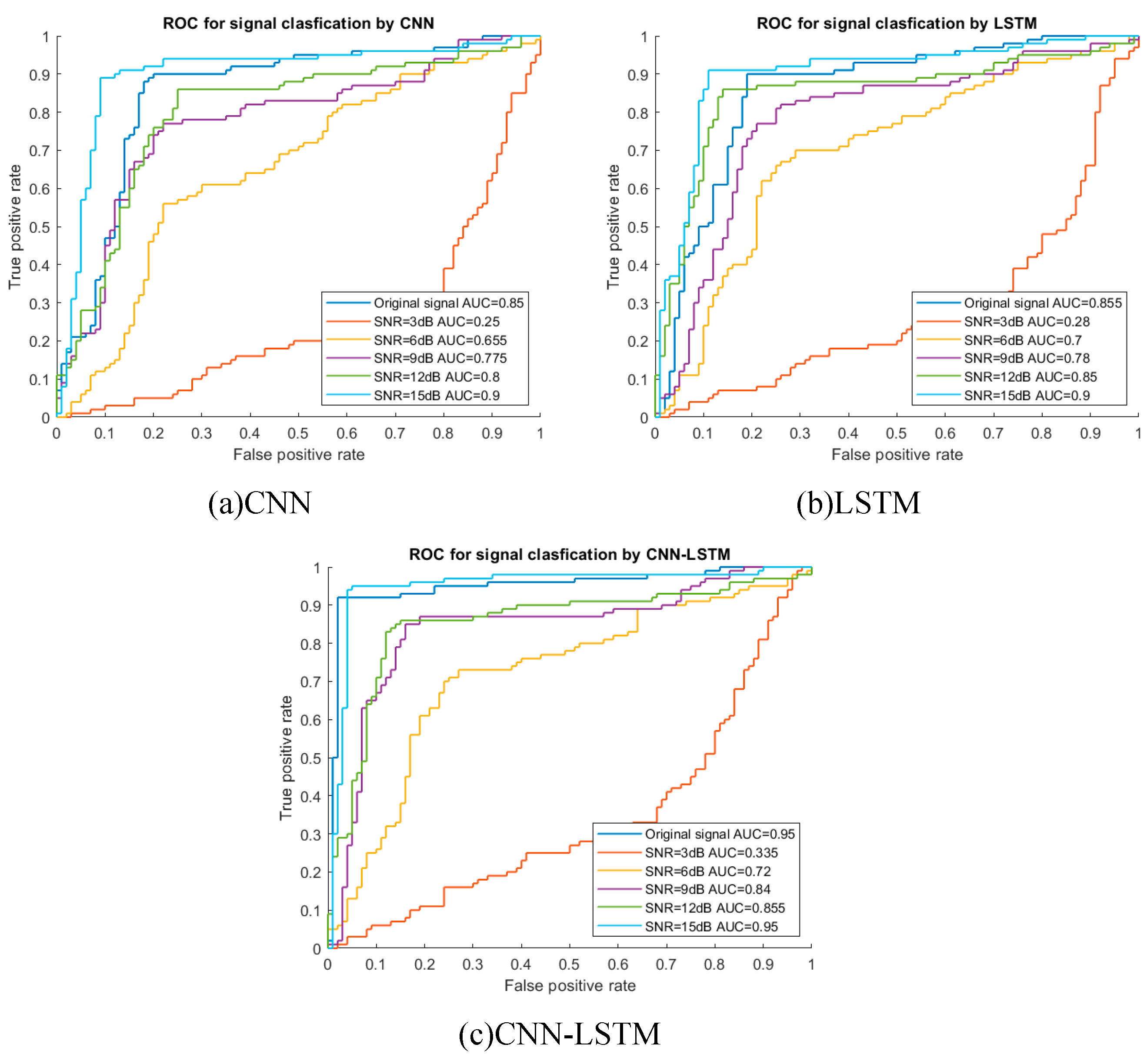
To investigate the sensitivity and effectiveness of the model training under noise interference, the CNN-LSTM model was trained with dataset with and without noise. And different noise levels are considered, as shown in Figure 11. Twenty-nine feature parameters were extracted from original signal and noised signal to be used as input of CNN-LSTM model. 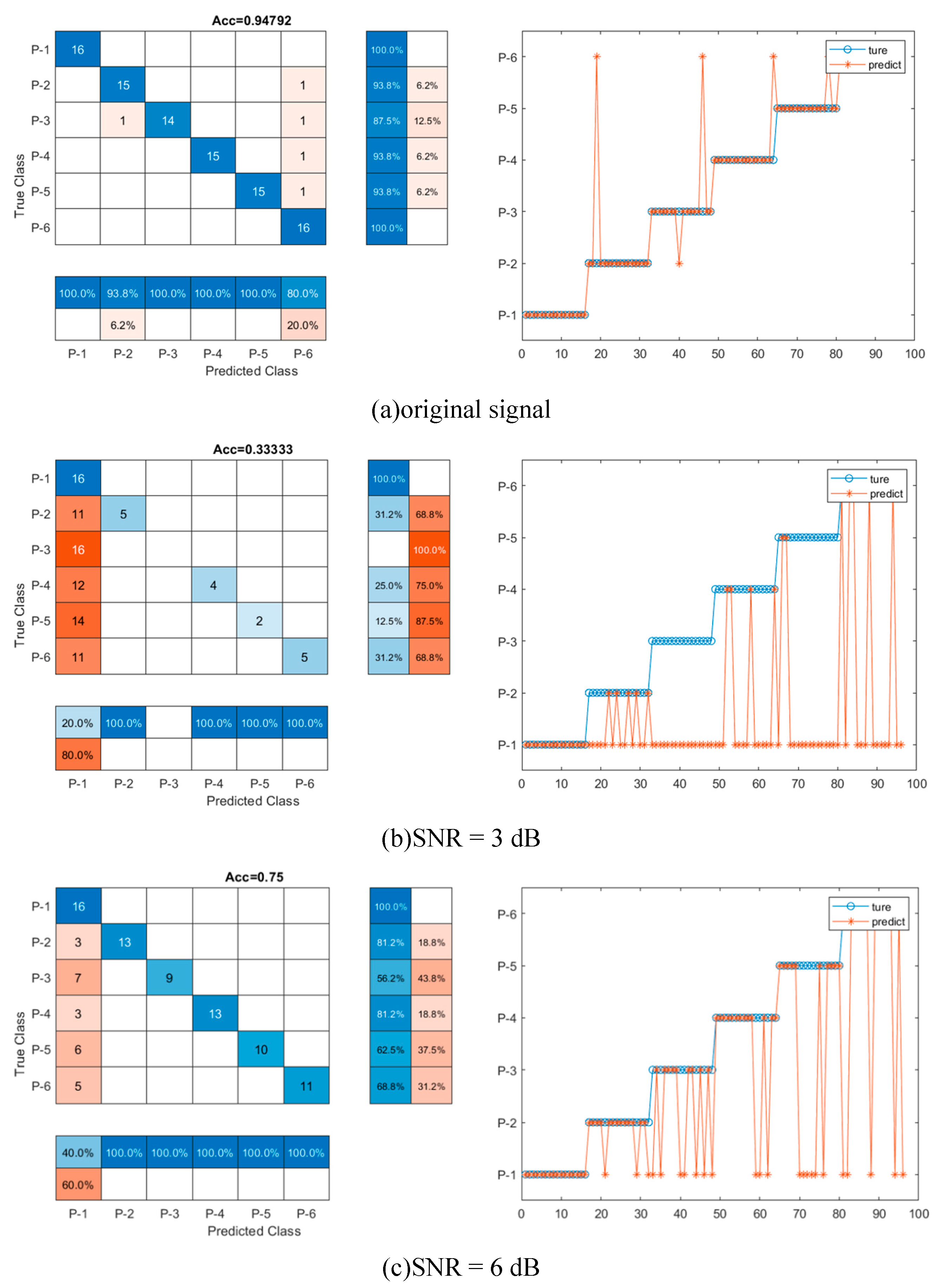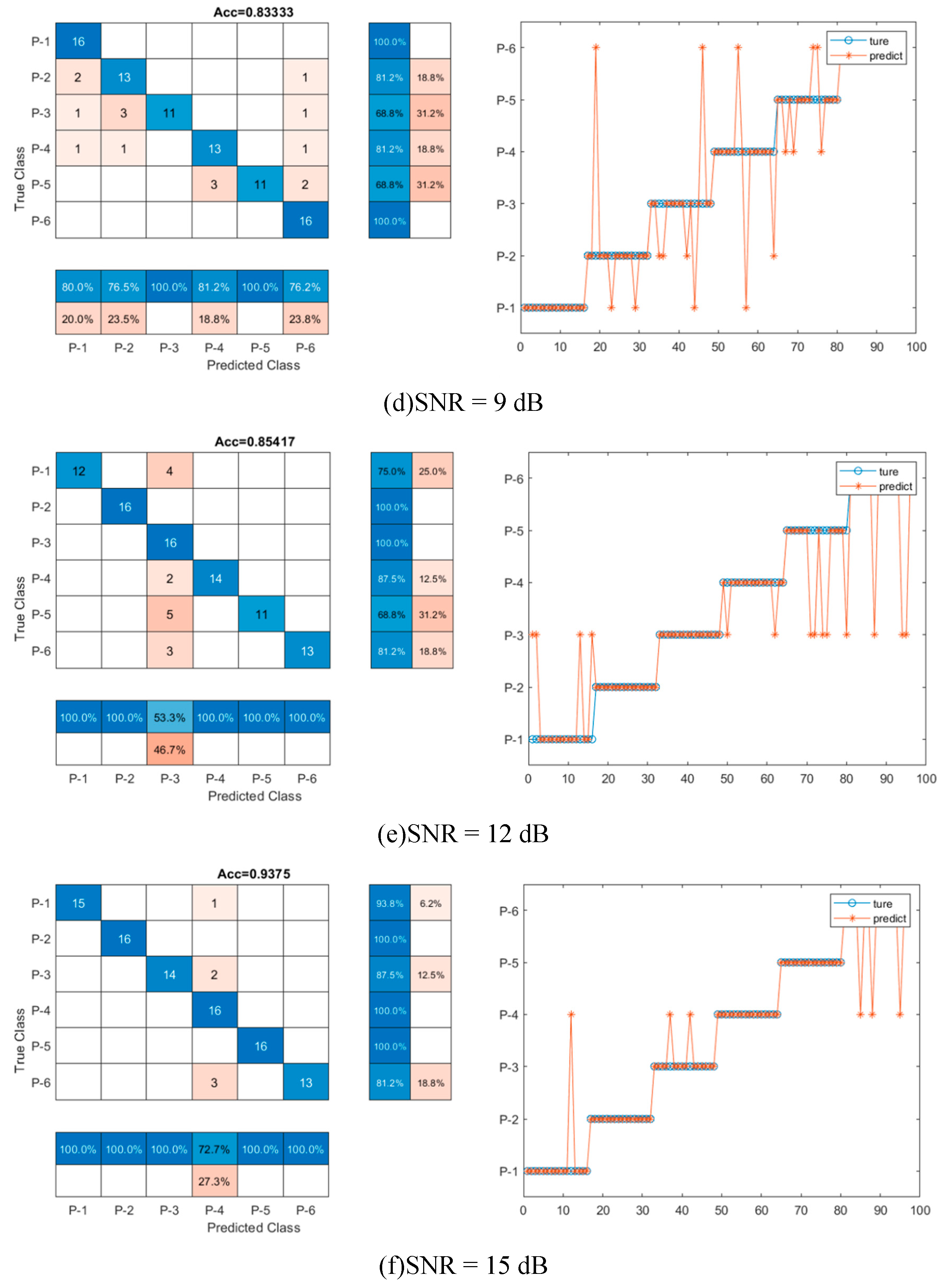The accuracies and confusion matrix of CNN-LSTM model were compared to evaluate the training performance and the results were shown in Table 7 and Figure 11. Clearly, the classification accuracy improved with the increase of SNR. A higher SNR indicates a stronger and perceptible signal in comparison to noise, which is consistent with the result. For instance, when SNR = 15 dB, the accuracy of reconstructed signals is the highest (93.8%), where P-1 and P-2 are 100% categorized into correct groups but 13% of P-3 and 6% of P-2, P-4 and P-5 are mistakenly placed into wrong groups, as shown in Figure 11. When SNR = 15 dB, there is almost no noise in signal as shown in Figure 10, which demonstrated the high accuracy. While for SNR = 3 dB, the signal is seriously contaminated by the noise and the accuracy is the lowest (33.3%), where the mislabeled data mainly occurred in P-2, P-3, P-4, P-5 and P-6. The misjudgments in these five categories were higher than 69% which means the features of the signal were hard to extract. With the decrease of noise level, data classification accuracies were improving. For example, when SNR = 6 dB, 75% data could be classified into the correct labels, in which the misclassification was mainly on P-2, P-3, P-4, P-5 and P-6, 19%, 44%, 19%, 38% and 31% misclassification rate respectively. When SNR = 9 dB and 12 dB, misclassification rate became less. When SNR = 15 dB, the accuracy of CNN-LSTM model increased by 181. 3%, 25.0%, 20.0% and 9.8% respectively when compared with the accuracy of SNR = 3 dB (33.3%), 6 dB (75.0%), 9 dB (83.3%) and 12 dB (85.4%). It means that higher SNR levels can enhance accuracy by lessening the effect of noise interference and improving the capacity to spot and categorize faults. The results also demonstrate that the signal processing (denoise and feature extraction) and CNN-LSTM model training is effective under noise interference.

AUC values were calculated to better illustrate the accuracy results, as shown in Table 2 and Figure 4. The AUC values also increased with the decrease of noise levels, which was consistency with the accuracy results. And when SNR = 15 dB, the AUC is 0.950, which is close to one. When the noise level is really high (SNR = 3 dB), the AUC value is only 0.335, suggesting that the classification accuracy is unacceptable when AUC is lower than 0.750, based on the literature [24]. When noise levels decreased to 9 dB and 12 dB, the values of AUC were 0.840 and 0.855, respectively. The results had the same regularity as the accuracy results, both the accuracies and AUC values increased with the decrease of noise levels.

5.3. The comparison of the classification performance of CNN, LSTM and CNN-LSTM model

This part compared the performance of three models (CNN, LSTM and CNN-LSTM) with different levels of white Gaussian noise and used twenty-nine feature parameters series as network input. Table 7 and Figure 12 shows the comparison results of training accuracies and AUC values of three models (CNN, LSTM and CNN-LSTM models). Clearly, CNN-LSTM hybrid model achieve better performance than CNN and LSTM on different noise levels due to its complex time series data processing structure and this result has also been demonstrated in Section 4.1.

For instance, when SNR = 3 dB, the accuracy of CNN-LSTM model increased by 33% and 16%, respectively, in comparison with CNN (25.0%) and LSTM model (28.8%). The result demonstrated that CNN-LSTM model had better feature extraction capability than CNN and LSTM model at higher noise level and LSTM model was much better than CNN model. With the decrease of noise levels, the difference of training accuracies also decreased among three models. For instance, when SNR = 15 dB, the performance of CNN-LSTM model increased by 4% for both CNN and LSTM model.

For AUC values, there is same trend as training accuracies. With the decrease of noise levels, the difference of AUC values also decreased. For instance, when SNR = 3 dB, the AUC value of CNN-LSTM model increased by 34% and 20%, respectively, in comparison with CNN and LSTM model, while when SNR = 15 dB, the performance of CNN-LSTM model increased by 6% for both CNN and LSTM model. These findings revealed that the CNN-LSTM model still performed better at classifying data than the CNN and LSTM models under the noise interference.

6. Conclusions

This study provided a comprehensive study of deep-learning-based signal process of ultrasonic guided wave and damage detection for metallic pipelines via the CNN-LSTM hybrid model. The twenty-nine features, including time-, frequency-, and time-frequency domains, were determined to evaluate the data classification. Six types of mechanical defects in pipe structures were designed for the case to demonstrate the effectiveness of the proposed methods. As a comparison, the CNN and LSTM models were selected. To further evaluate the robustness of the signal processing and model training, noise interferences on signal processing were investigated. The main findings could be summarized as follows:

The results reveal that the CNN-LSTM hybrid model exhibits a higher accuracy for decoding signals of the ultrasonic guided wave for damage detection, as compared to individual deep learning approaches (CNN and LSTM), particularly under high noise interferences.
The results also confirmed that predetermined features, including time-, frequency-, and time-frequency domains, improve the data classification. Interestingly, while it is well known that the deep learning approaches could outperform the shallow learning ones that often require hand-crafted features and thus they could provide the high capability for data classification through end-to-end manner with fewer physics restraints (“black box”), the election of features with certain physics (“physics-informed” feature extraction) could significantly improve the robustness of the deep learning approaches.
Data reduction (PCA and KPCA) used for the deep learning training/testing networks in this study display no apparent improvement to data classification. However, with the increased volume of datasets, these methods could improve efficiency in terms of shortening computation time.
The accuracy of the deep learning approaches could be dramatically affected by noise, which could be stemmed from measurement and environment. The CNN-LSTM model still exhibits a high performance when the noise level is relatively low (e.g., SNR=9 or higher) but the prediction drops gradually to the unacceptable limit, when the noise level of SNR is 6, where the amplitude of the noise level approaches to that of the signals themselves. As compared, the CNN and LSTM models fail early as expected, when the noise level is much higher.
Although this study attempts to provide a comparison study to understand the effectiveness of the hybrid deep learning model, there are still certain drawbacks that could be improved in the future. The first one is the dataset which is limited to six common defects and may not be able to account for broader applications. The simple case that tried to demonstrate the concept may not account for more complicated signal propagation, reflection, and scatters, which could challenge the effectiveness of the proposed methods.

Author Contributions

L. S. and Z. Z. designed, conducted this research and wrote the paper under the supervision of Z.L. and H.P assisted the experiments and edited the paper. F. T and Q. C assisted the study and edited the paper.

Funding

This research was funded by USDOTs (DTPH5616HCAP03, 693JK318500010CAAP, and 693JK31850009CAAP, 693JK32110003POTA, 693JK32250007CAAP).

Acknowledgments

The authors gratefully acknowledge the financial support provided by USDOTs (DTPH5616HCAP03, 693JK318500010CAAP, and 693JK31850009CAAP, 693JK32110003POTA, 693JK32250007CAAP). The results, discussion, and opinions reflected in this paper are those of the authors only and do not necessarily represent those of the sponsors.

Conflicts of Interest

The authors declare no conflict of interest.

References

Ahn, B.; Kim, J.; Mechanics, B.C.-E.F.; 2019, undefined Artificial Intelligence-Based Machine Learning Considering Flow and Temperature of the Pipeline for Leak Early Detection Using Acoustic Emission. Elsevier.
Carvalho, A.; Rebello, J.; … L.S.-N.& E.; 2006, undefined MFL Signals and Artificial Neural Networks Applied to Detection and Classification of Pipe Weld Defects. Elsevier.
Kim, J.; Sensors, S.P.-; 2018, undefined Magnetic Flux Leakage Sensing and Artificial Neural Network Pattern Recognition-Based Automated Damage Detection and Quantification for Wire Rope Non-Destructive. mdpi.com.
Lu, S.; Feng, J.; Zhang, H.; … J.L.-I.T. on; 2018, undefined An Estimation Method of Defect Size from MFL Image Using Visual Transformation Convolutional Neural Network. ieeexplore.ieee.org.
Feng, J.; Li, F.; Lu, S.; Liu, J.; on, D.M.-I.T.; 2017, undefined Injurious or Noninjurious Defect Identification from MFL Images in Pipeline Inspection Using Convolutional Neural Network. ieeexplore.ieee.org.
ZHANG, Z.; LI, B.; LV, X.; on, K.L.-Des.T.; 2018, undefined Research on Pipeline Defect Detection Based on Optimized Faster R-Cnn Algorithm. scholar.archive.org 2018.
Mohamed, A.; Dahl, G.; audio, G.H.-I. transactions on; 2011, undefined Acoustic Modeling Using Deep Belief Networks. ieeexplore.ieee.org.
Variani, E.; Lei, X.; McDermott, E.; acoustics, I.M.-… on; speech, undefined; 2014, undefined Deep Neural Networks for Small Footprint Text-Dependent Speaker Verification. ieeexplore.ieee.org.
Abdel-Hamid, O.; Mohamed, A.; Acoustics, H.J.-… on; speech, undefined; 2012, undefined Applying Convolutional Neural Networks Concepts to Hybrid NN-HMM Model for Speech Recognition. ieeexplore.ieee.org.
Zhang, C.; Interspeech, K.K.-; 2017, undefined End-to-End Text-Independent Speaker Verification with Triplet Loss on Short Utterances. isca-speech.org 2017. [CrossRef]
Nagraniy, A.; Chungy, J.S.; Zisserman, A. VoxCeleb: A Large-Scale Speaker Identification Dataset. Proceedings of the Annual Conference of the International Speech Communication Association, INTERSPEECH 2017, 2017-August, 2616–2620. [CrossRef]
Pan, H.; Zhang, Z.; Cao, Q.; … X.W.-S.S. and; 2020, undefined Conditional Assessment of Large-Scale Infrastructure Systems Using Deep Learning Approaches (Conference Presentation). spiedigitallibrary.org.
Zhang, Z.; Tang, F.; Cao, Q.; Pan, H.; Wang, X.; Buildings, Z.L.-; 2022, undefined Deep Learning-Enriched Stress Level Identification of Pretensioned Rods via Guided Wave Approaches. mdpi.com 2022. [CrossRef]
Zhang, Z.; Wang, X.; Pan, H.; Lin, Z. Corrosion-Induced Damage Identification in Metallic Structures Using Machine Learning Approaches. In Proceedings of the Proceedings of the 2019 Defense TechConnect Innovation Summit; 2019.
Zhang, Z.; Pan, H.; Lin, Z. Data-Driven Identification for Early-Age Corrosion-Induced Damage in Metallic Structures. In Proceedings of the In Proceedings of the Bridge Engineering Institute Conference; 2019.
Zhang, Z.; Pan, H.; Wang, X.; Sensors, Z.L.-; 2022, undefined Deep Learning Empowered Structural Health Monitoring and Damage Diagnostics for Structures with Weldment via Decoding Ultrasonic Guided Wave. mdpi.com 2022. [CrossRef]
Gui, G.; Pan, H.; Lin, Z.; Li, Y.; Engineering, Z.Y.-K.J. of C.; 2017, undefined Data-Driven Support Vector Machine with Optimization Techniques for Structural Health Monitoring and Damage Detection. Springer 2017, 21, 523–534. [CrossRef]
Pan, H.; Azimi, M.; Gui, G.; Yan, F.; Lin, Z. Vibration-Based Support Vector Machine for Structural Health Monitoring. Lecture Notes in Civil Engineering 2018, 5, 167–178. [CrossRef]
Lin, Z. Machine Learning, Data Analytics and Information Fusion for Structural Health Monitoring. In Proceedings of the 2019 International Conference on Artificial Intelligence, Information Processing and Cloud Computing; 2019.
Lin, Z.; Pan, H.; Wang, X.; Structures, M.L.-S. and S.; 2018, undefined Data-Driven Structural Diagnosis and Conditional Assessment: From Shallow to Deep Learning. spiedigitallibrary.org.
Pan, H.; Azimi, M.; Yan, F.; Engineering, Z.L.-J. of B.; 2018, undefined Time-Frequency-Based Data-Driven Structural Diagnosis and Damage Detection for Cable-Stayed Bridges. ascelibrary.org 2018, 23. [CrossRef]
Zhang, Z.; Pan, H.; Wang, X.; Tang, F.; Lin, Z. Ultrasonic Guided Wave Approaches for Pipeline Damage Diagnosis Based on Deep Learning. In Proceedings of the In Proceedings of the ASCE Pipelines 2022 Conference; 2022.
Pan, H.; Lin, Z.; Engineering, G.G.-J. of A.; 2019, undefined Enabling Damage Identification of Structures Using Time Series–Based Feature Extraction Algorithms. ascelibrary.org.
Zhang, Z.; Pan, H.; Wang, X.; Sensors, Z.L.-; 2020, Machine Learning-Enriched Lamb Wave Approaches for Automated Damage Detection. Sensors, mdpi.com. [CrossRef]
Zhang, Z.; Pan, H.; Wang, X.; Lin, Z. Machine Learning-Enabled Lamb Wave Approaches for Damage Detection. In Proceedings of the In Proceedings of the 2021 10th International Conference on Structural Health Monitoring of Intelligent Infrastructure; 2021.
Pittner, S.; Kamarthi, S. v. Feature Extraction from Wavelet Coefficients for Pattern Recognition Tasks. IEEE Trans Pattern Anal Mach Intell 1999, 21, 83–88. [CrossRef]
Shi, P.; An, S.; Li, P.; Han, D. Signal Feature Extraction Based on Cascaded Multi-Stable Stochastic Resonance Denoising and EMD Method. Measurement 2016, 90, 318–328. [CrossRef]
Zhao, S.; Shi, P.; Han, D. A Novel Mechanical Fault Signal Feature Extraction Method Based on Unsaturated Piecewise Tri-Stable Stochastic Resonance. Measurement 2021, 168, 108374. [CrossRef]
Zhang, W.; Zhou, H.; Bao, X.; Cui, H. Outlet Water Temperature Prediction of Energy Pile Based on Spatial-Temporal Feature Extraction through CNN–LSTM Hybrid Model. Energy 2023, 264, 126190. [CrossRef]
LeCun, Y.; Bengio, Y.; nature, G.H.-; 2015, undefined Deep Learning. nature.com.
Rani, C.J.; Devarakonda, N. An Effectual Classical Dance Pose Estimation and Classification System Employing Convolution Neural Network –Long ShortTerm Memory (CNN-LSTM) Network for Video Sequences. Microprocess Microsyst 2022, 95, 104651. [CrossRef]
Mellit, A.; Pavan, A.; Energy, V.L.-R.; 2021, undefined Deep Learning Neural Networks for Short-Term Photovoltaic Power Forecasting. Elsevier.
Greff, K.; Srivastava, R.; … J.K.-I. transactions on; 2016, undefined LSTM: A Search Space Odyssey. ieeexplore.ieee.org.
Chevalier, G. Schematic of the Long-Short Term Memory Cell, a Component of Recurrent Neural Networks.
Hochreiter, S.; J. Schmidhuber Long Short-Term Memory. Neural Comput 1997, 9, 1735–1780.
Chen, C. Reliability Assessment Method for Space Rolling Bearing Based on Condition Vibration Feature, Chongqing University, 2014.
Kulkarni, A.; Chong, D.; Batarseh, F.A. Foundations of Data Imbalance and Solutions for a Data Democracy. Data Democracy: At the Nexus of Artificial Intelligence, Software Development, and Knowledge Engineering 2020, 83–106. [CrossRef]
Akram, N.A.; Isa, D.; Rajkumar, R.; Lee, L.H. Active Incremental Support Vector Machine for Oil and Gas Pipeline Defects Prediction System Using Long Range Ultrasonic Transducers. Ultrasonics 2014, 54, 1534–1544. [CrossRef]
Davoudabadi, M.-J.; Aminghafari, M. A Fuzzy-Wavelet Denoising Technique With Applications to Noise Reduction In Audio Signals. Journal of Intelligent & Fuzzy Systems 2017, 33, 2159–2169. [CrossRef]
Wang, W.; Ruiying, D.; Wenru, Z.; B. Zhang; Y. Zheng A Wavelet De-Noising Method for Power Quality Based on an Improved Threshold and Threshold Function. Transactions of China Electrotechnical Society 2019, 34, 409–418.
Rachman, A.; Zhang, T.; Ratnayake, R.M.C. Applications of Machine Learning in Pipeline Integrity Management: A State-of-the-Art Review. International Journal of Pressure Vessels and Piping 2021, 193, 104471. [CrossRef]

Figure 1. Framework of machine learning-enriched method for damage detection.

Figure 2. Flow chart of the CNN-LSTM hybrid model.

Figure 3. The LSTM structure of a cell [34].

Figure 4. Experimental setup.

Figure 5. Original signal and signal after wavelet threshold denoising.

Figure 6. Accuracy of training and validation for three models.

Figure 7. The confusion matrix for three models.

Figure 8. The confusion matrix of the CNN-LSTM model with different kinds of input data.

Figure 9. ROC curve for the CNN-LSTM hybrid model with different input data.

Figure 10. The noised signals on different noise levels.

Figure 11. The classification accuracy of CNN-LSTM model on different SNR.

Figure 12. ROC curve for three models on different noise levels.

Table 1. Time-domain characteristic indicators.

Dimensional time-domain (with 10 indicators)
Feature index	Expressions	Features index	Expressions
Mean value	$\bar{X} = \frac{1}{N} \sum_{i = 1}^{N} x_{i}$	Kurtosis	$β = \frac{1}{N} \sum_{i = 1}^{N} x_{i}^{4}$
Root mean square value	$X_{r m s} = \sqrt{\frac{1}{N} \sum_{i = 1}^{N} x_{i}^{2}}$	variance	$σ_{x}^{2} = \frac{1}{N - 1} \sum_{i = 1}^{N} {(x_{i} - \bar{X})}^{2}$
Square root amplitude	$X_{r} = {[\frac{1}{N} \sum_{i = 1}^{N} \sqrt{\|x_{i}\|}]}^{2}$	maximum value	$X_{m a x} = m a x \{\|x_{i}\|\}$
absolute mean amplitude	$\|\bar{X}\| = \frac{1}{N} \sum_{i = 1}^{N} \|x_{i}\|$	minimum value	$X_{m i n} = m i n \{x_{i}\}$
Skewness	$\propto = \frac{1}{N} \sum_{i = 1}^{N} x_{i}^{3}$	peak-to-peak value	$X_{p - p} = \max (x_{i}) - m i n (x_{i})$
Dimensionless time-domain (with 6 indicators)
Waveform Index	$S_{f} = \frac{X_{r m s}}{\|\bar{X}\|}$	peak index	$C_{f} = \frac{X_{m a x}}{X_{r m s}}$
pulse index	$I_{f} = \frac{X_{m a x}}{\|\bar{X}\|}$	margin index	${C L}_{f} = \frac{X_{m a x}}{X_{r}}$
kurtosis index	$K_{v} = \frac{β}{x_{r m s}^{4}}$	Skewness Index	$S = \frac{\propto}{x_{r m s}^{3}}$

Table 2. Frequency-domain characteristic indicators (with 13 indicators).

Number	Expressions	Number	Expressions
1	$p_{1} = \frac{\sum_{k = 1}^{K} s (k)}{K}$	8	$p_{8} = \sqrt{\frac{\sum_{k = 1}^{K} {f_{k}}^{4} s (k)}{\sum_{k = 1}^{K} {f_{k}}^{2} s (k)}}$
2	$p_{2} = \frac{\sum_{k = 1}^{K} {(s (k) - p_{1})}^{2}}{K}$	9	$p_{9} = \frac{\sum_{k = 1}^{K} {f_{k}}^{2} s (k)}{\sqrt{\sum_{k = 1}^{K} s (k) \sum_{k = 1}^{K} {f_{k}}^{4} s (k)}}$
3	$p_{3} = \frac{\sum_{k = 1}^{K} {(s (k) - p_{1})}^{3}}{K {(\sqrt{p_{2}})}^{3}}$	10	$p_{10} = \frac{p_{6}}{p_{5}}$
4	$p_{4} = \frac{\sum_{k = 1}^{K} {(s (k) - p_{1})}^{4}}{K p_{2}^{2}}$	11	$p_{11} = \frac{\sum_{k = 1}^{K} {(f_{k} - p_{5})}^{3} s (k)}{K p_{6}^{2}}$
5	$p_{5} = \frac{\sum_{k = 1}^{K} f_{k} s (k)}{\sum_{k = 1}^{K} s (k)}$	12	$p_{12} = \frac{\sum_{k = 1}^{K} {(f_{k} - p_{5})}^{4} s (k)}{K p_{6}^{4}}$
6	$p_{6} = \sqrt{\frac{\sum_{k = 1}^{K} {(f_{k} - p_{5})}^{2} s (k)}{K}}$	13	$p_{13} = \frac{\sum_{k = 1}^{K} {(f_{k} - p_{5})}^{0.5} s (k)}{K p_{6}}$
7	$p_{7} = \sqrt{\frac{\sum_{k = 1}^{K} {f_{k}}^{2} s (k)}{\sum_{k = 1}^{K} s (k)}}$

Table 3. Confusion matrix for binary classification.

		predicted
		Negative	Positive
Actual	Negative	TN	FP
Actual	Positive	FN	TP

Table 4. Data label and damage type.

Sample ID	Damage type	Training sample	Testing sample
P-1	the pipe with a small notch located at1/3L away from the left side	240	96
P-2	the pipe with a big notch located at 1/3L away from the left side and a weldment at 2/3L away from the left side
P-3	the pipe with a small notch at 1/3L and a weldment at 2/3L away from the left side
P-4	a pipe with a big notch shaped damage
P-5	The pipe with epoxy coating without damage
P-6	The pipes with epoxy coating with a weldment at 2/3L away from the left side.

Table 5. The classification accuracy for different deep leaning models.

Deep learning models	Input	Output (Accuracy)
CNN	twenty-nine feature parameters series	85.4%
LSTM		86.5%
CNN-LSTM		94.8%

Table 6. Accuracy and AUC for the CNN-LSTM hybrid model with different input data.

Deep learning models	Input	Accuracy	AUC
CNN-LSTM	With Original data	77.1%	0.770
	With Denoised data	87.5%	0.855
	With twenty-nine feature parameters series	94.8%	0.950
	Twenty-nine feature parameters series with PCA	93.8%	0.935
	Twenty-nine feature parameters series with KPCA	92.7%	0.930

Table 7. The classification accuracy of three models on different SNR.

Input	SNR (dB)	Accuracy
Input	SNR (dB)	CNN	LSTM	CNN-LSTM
twenty-nine feature parameters series (original signal)	NAN	85.4%	86.5%	94.8%
twenty-nine feature parameters series (Noised signals)	3	25.0%	28.8%	33.3%
	6	65.5%	67.7%	75.0%
	9	76.8%	78.5%	83.3%
	12	80.0%	83.0%	85.4%
	15	83.0%	84.6%	93.8%

Table 8. The AUC values of three models on different noise levels.

Input	SNR (dB)	AUC
Input	SNR (dB)	CNN	LSTM	CNN-LSTM
twenty-nine feature parameters series (original signal)	NAN	0.850	0.855	0.950
twenty-nine feature parameters series (Noised signals)	3	0.250	0.280	0.335
	6	0.655	0.700	0.720
	9	0.775	0.780	0.840
	12	0.800	0.830	0.855
	15	0.830	0.845	0.950

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

CNN-LSTM Hybrid Model to Promote Signal Processing of Ultrasonic Guided Lamb Waves for Damage Detection of Metallic Pipelines

Abstract

1. Introduction

2. Framework of machine learning-enriched CNN-LSTM method for damage detection

2.1. CNN-LSTM hybrid model

2.2. Features extraction

2.2.1. Definition of features

2.2.1. Data dimension reduction

2.2.2.1. Principal component analysis (PCA)

2.2.2.1. Kernel principal component analysis (KPCA)

2.3. Evaluation of model performances

2.3.1. Confusion matrix and accuracy as performance indicators

2.3.1. ROC curve as another performance indicator

3. Case study

3.1. Ultrasonic guided waves collected from embedded damaged pipes

3.2. Data denoise using wavelet threshold denoising

4. Results and discussion

4.1. Classification performance of CNN, LSTM and CNN-LSTM model with twenty-nine feature parameters series

4.2. Classification performance of CNN-LSTM model with denoised data

4.3. Classification performance of CNN-LSTM model with predetermined features

4.4. Classification performance of CNN-LSTM model with data dimension reduction

5. Further discussion of the effectiveness of the hybrid model under noise interference

5.1. Introduction of white Gaussian noise into the signals

5.2. Classification performance of CNN-LSTM model with white Gaussian noise interference

5.3. The comparison of the classification performance of CNN, LSTM and CNN-LSTM model

6. Conclusions

Author Contributions

Funding

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe