1. Introduction
Artificial Intelligence (AI) refers to the simulation of human intelligence in machines, wherein they are programmed to think and learn in a manner similar to humans. The AI has been used in forest modelling for different purposes and objectives. The machine learning (ML) is a subset of AI that focuses on the development of algorithms and models that enable computer to learns from a specific dataset and make predictions or take actions without being explicitly programmed [
1,
2]. One of the most ML techniques is the artificial neural network (
ANN) and the resilient backpropagation artificial neural network (
RBPANN) perform supervised ML in multi-layer perceptron, and the main principle is to eliminate the harmful influence of the size of the partial derivative on the weight step [
3,
4,
5]. The
ANNs are computational models inspired in the natural neurons and they represent a generalization of mathematical models of human cognition or neural biology [
1,
6,
7]. In
ANNs, the training and testing datasets are used to train and evaluate the performance of the network for a specific randomly selected dataset. The training dataset is used to train the neural network. It consists of a set of input data points and their corresponding target output values, while, the testing dataset is a separate dataset that is used to evaluate the performance of the trained neural network [
1,
8,
9].
One of the most important relationships in forest modeling is the total tree height and diameter at breast height (
h-dbh) relationship, and this relationship is usually applied in forest inventory or for height estimation in forest management and planning [
10]. The knowledge of
h-dbh relationship is a fundamental both developing and applying many growth and yield models [
11,
12]. This relationship has mainly studied with nonlinear mixed effect modeling (
NLMEM) with fix and random parameters for several species and grouping level or ecological conditions [
10,
11,
13,
14,
15,
16]. Lately, this relationship has been studied with AI, and the ML thought
ANN has been used [
7,
17,
18]. Also, other variables as basal area [
19], crown width [
20], biomass [
21], volume [
22], forest fire [
23], and annual radial growth with competition indices [
24] have been studied with different ML algorithms. Occasionally, the clustering analysis based in unsupervised ML has been included in to group similar data point together based on their inherent characteristics or similarities [
1,
25,
26,
27]. The unsupervised clustering analysis could identify patterns or structures in dataset to improve the fitted models in forest modeling.
Specifically, in the Mexican Forestry the
h-dbh relationship has been extensively studied with
NLMEM for local and generalized models and occasionally the unsupervised cluster analysis was included in modelling [
12,
28,
29]. The
NLMEM are better than fitted models by ordinary least squares method and those use random parameter to explain the variability between groups, sites, or ecological regions. Lately, the ML algorithms are taken attention in forestry research and the results outperform the
NLMEM approach for the
h-dbh relationship. In
ANN analysis is convenient to separate the dataset in two parts, one for training and other one for testing or validation [
7,
17]. The main used model for
NLMEM has been th Chapman-Richards model [
30], which is base in a sigmoid relationship growth based on age [
31].
Considering the above schemes and the context of AI in forestry research, this study aim the h-dbh relationship for Durango Pine species (Pinus durangensis Martínez) by NLMEM and ANN for unsupervised clustered dataset for training and testing sets. The algorithms were compared in both training and testing phases and some conventional statistics like root mean square error, coefficient of determination, Akaike’s information criterion, Bayesian information criterion, and loglikelihood were uses to perform the approaches. The resilience backpropagation of ANN (RBPANN) was employed, and three activation functions were computed and evaluated. The activation functions were tangent hyperbolicus (RBPANN-tanh), softplus (RBPANN-softplus), and logistic (RBPANN-logistic), and those were trained by resilience backpropagation and maximum likelihood was used.
4. Discussion
Having knowledge about the total tree height and diameter at breast height is essential for both the development and application of many growth and yield models. Models focusing on the
h-dbh relationship serve as valuable tools for accurately predicting tree height based on
dbh measurements. Because of the
dbh can be conducted quickly, easily, and accurately, but the measurement of total tree height is comparatively complex, time consuming, and expensive [
11]. The
NLME had been a capable approach to generate models in
h-dbh relationship for different species and assumed fixed and random parameters for specific-groups or covariables to study the variability inter-and intra-plots, ecological regions or cluster-groups [
10,
16,
39]. Also, these models have been studied for local and generalized formulations with
NLMEM approach [
12,
13,
16,
28]. In this case of study the
NLMEM performance was accurately strong to model the
h-dbh relationship for Durango pine and the inclusion of unsupervised clustering analysis improve the estimated parameters and its statistics properties [
36,
47], which involve fixed parameter for the overall dataset in training phase and random parameter for each cluster-group, also parameter to give information about general variability and variability within cluster-group.
The
NLMEM demonstrated outstanding performance during the training phase, with the fitting process converging quickly and effortlessly. Additionally, the maximum likelihood approach yielded favorable and suitable results particularly when expressing the asymptote parameter with mixed effects (
Table 3 and
Table 4). All parameters in fitting process were significantly different to zero at 5% of significance level and the random parameters allow suitable estimations in training phase and those were used for cluster-groups in testing phase. The application of the
NLMEM approach on the testing dataset resulted in successful outcomes that aligned with the expected results (as shown in
Table 8), accompanied by the utilization of appropriate statistical measures. As an illustration, the root mean square error (RMSE) for the overall dataset during the testing phase was determined to be 3.1438 m, with an average value of 3.3773 m observed within the cluster-groups (refer to
Table 8). By employing a mixed-effect model and incorporating cluster-group inclusion, the Chapman-Richards growth equation [
30] (Equation 2) proves to be a highly effective model for predicting the height of Durango pine trees. Similar results have been conducted for several species an different conditions [
11,
16,
28]. Even though the
NLMEM method is accurate for height prediction based on diameter measurements, it is worth considering that
ANNs could be a suitable alternative for modeling the
h-dbh relationship under several dataset conditions and the incorporation of grouped strategies [
7,
14,
48]. In recent times, there has been a growing application of AI and ML techniques in the fields of biology and forestry. These advanced approaches have proven valuable in addressing challenges that require substantial computational resources and unsupervised learning methods [
1,
41], Several of these approaches have been employed in studying the height-diameter at breast height (h-dbh) relationship, leading to notable outcomes and reported successes for various species and under diverse forest management conditions, demonstrating their versatility and effectiveness [
7,
14,
15,
17,
48]. In this context the
ANNs model outperformed the
NLMEM approach.
In this study, the
ANNs were evaluated and compared with the traditional
NLMEM method. The
ANNs utilized the RBP learning algorithm along with three activation functions. In most cases, the
ANNs employing
RBPANN-tanh,
RBPANN, and
RBPANN-logistic (Equations 7, 8, an 9, respectively) exhibited superior performance compared to the results obtained by
NLMEM, both during the training and testing phases. The training statistics for three
ANNs, as presented in
Table 6, exhibited enhanced fitting performance compared to the statistics obtained by
NLMEM (see
Table 4). This improvement was observed in both the overall dataset and cluster-group analyses. These findings provide evidence that the clustering analysis using the k-means algorithm effectively grouped the dataset utilized in this study [
36,
47]. The
RBPANN-tanh model, employing a tangent hyperbolic activation function, demonstrated the highest performance in predicting height measurements during both the training and testing phases (it can see in
Table 6 and 9). Furthermore, the ranks and sum of ranks, based on the ranking system proposed by Kozak and Smith [
46], provided evidence of the advantages of the
ANNs models over the
NLMEM approach. Models such as
RBPANN-logistic were reported by Özçelik, Diamantopoulou, Crecente-Campo and Eler [
7] revealed that models such as
RBPANN-logistic exhibited advantages over
NLMEM models when predicting the growth of Crimean juniper in the southern and southwestern regions of Turkey. Conversely Shen, Hu, Sharma, Wang, Meng, Wang, Wang and Fu [
17] developed
ANNs models utilizing
RBPANN-logistic and
RBPANN-tanh transfer or activation functions for
Populus spp. L. in China, where the
RBPANN-logistic model outperformed both the NLMEN and the
RBPANN-tanh model. In our case, the best
ANN was the
RBPANN-tanh and this outperformed other tested
ANNs and
NLMEM approach. Similar results have been reported the advantages of
ANNs or deep learning algorithms over the ordinary least square and
NLMEM models in both training and testing or validation phases [
14,
15,
48,
49]. In all cases, the implementation of
ANNs exhibited significant advantages over traditional approaches when modeling the
h-dbh relationship.
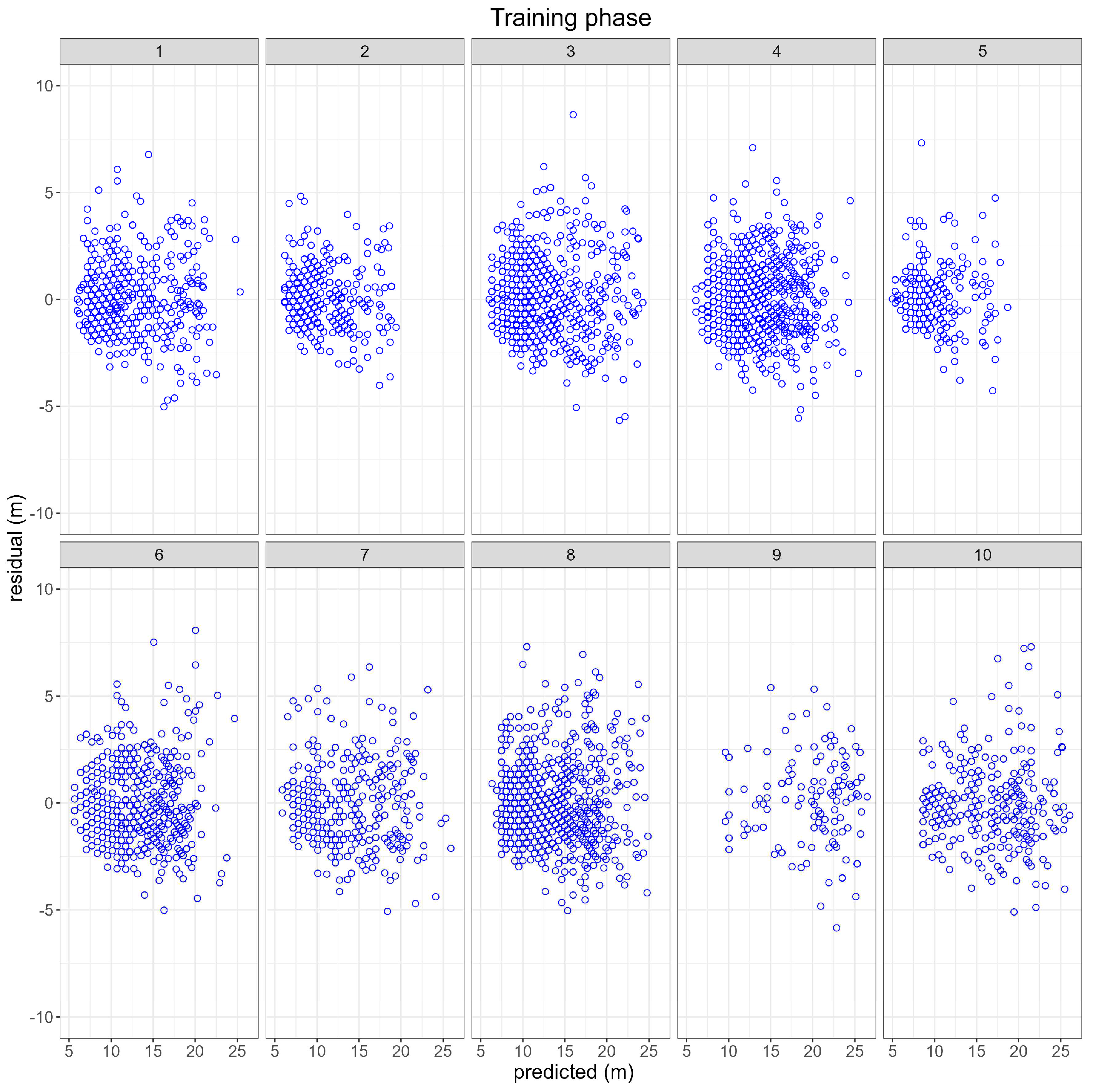
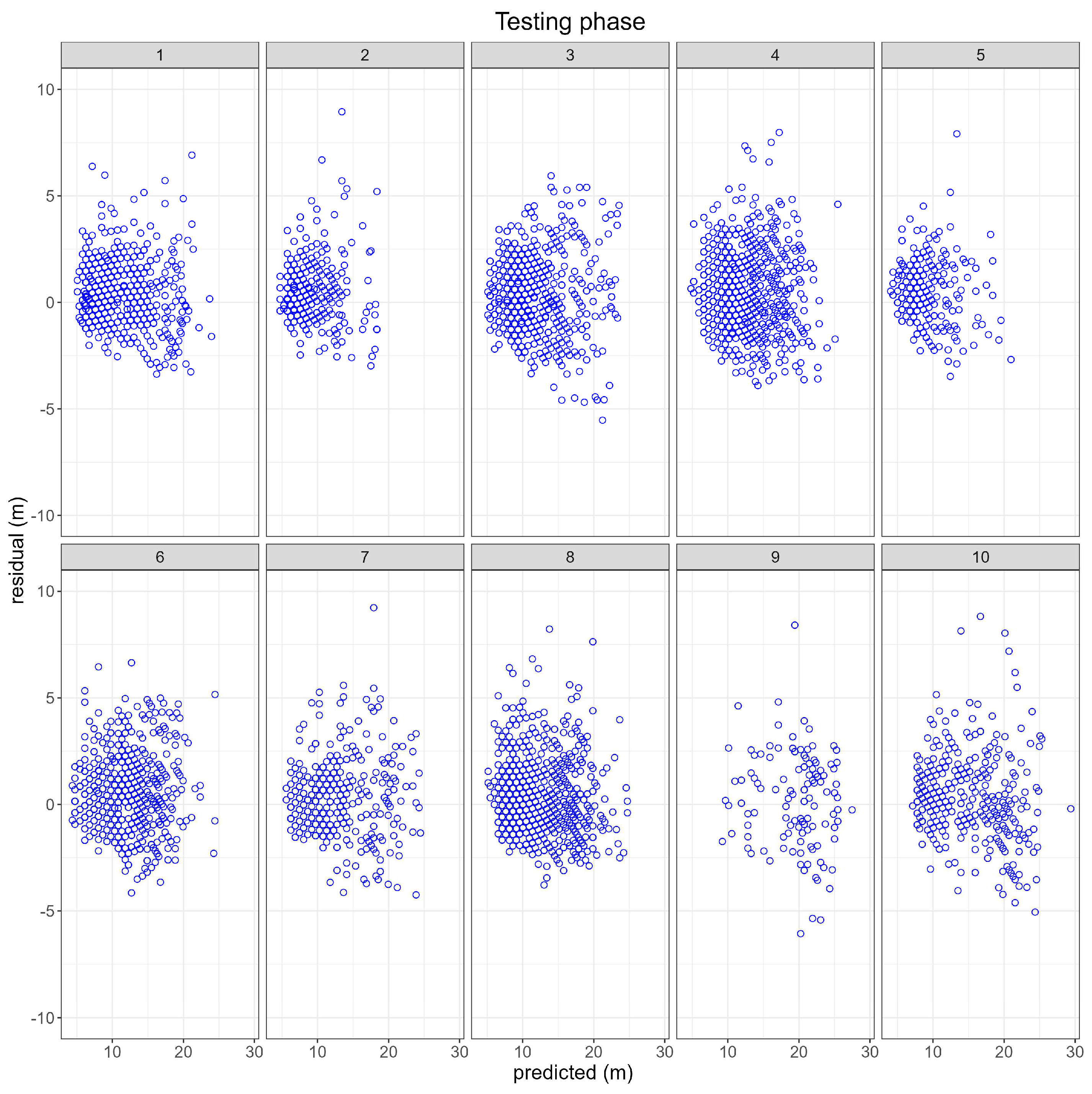
In this study, based on the implemented ranking system, the
RBPANN-tanh model emerged as the top performer (residual and predicted values are showed in
Figure 5 and
Figure 6). It achieved a sum of ranks of 176 for the training phase and 81 for the testing phase. These sums of ranks account for both the overall dataset and cluster-groups, as illustrated in
Table 7 and
Table 10, respectively. In terms of training, the
RBPANN-softplus model ranked second, whereas during the testing phase, the
RBPANN-logistic model exhibited the second-best performance. On the other hand, the
RBPANN-logistic model performed least effectively in the training phase, while the
NLMEM model demonstrated comparatively lower performance during the testing phase. The
ANNs developed in this study, as depicted in
Figure 4, were trained using the RBP algorithm. The
ANNs were then evaluated using three different activation functions:
RBPANN-tanh,
RBPANN-softplus, and
RBPANN-logistic. These models comprised a total of five layers, including three hidden layers. The training process involved ten repetitions to ensure robustness and accuracy. Even though the
RBPANN-logistic converging in 88 steps, it exhibited relatively poorer performance compared to the
RBPANN-tanh, which achieved better results within 301 steps. Interestingly, the
RBPANN-logistic required a longer convergence time of 1885 steps, indicating its comparatively poorer performance in this aspect. As a result, the developed
ANNs model showcased a high capability for predicting total tree height measurements. This highlights the potential application of AI in modeling the
h-dbh relationship, not only for Durango pine but also for general forest modeling purposes or other variables [
6,
19,
21,
50]. The
ANNs could be used to improve the estimations in forest inventory and forest management and planning in mixed-species forest in Durango, Mexico.
Figure 1.
Study area location in Northern Mexico.
Figure 1.
Study area location in Northern Mexico.
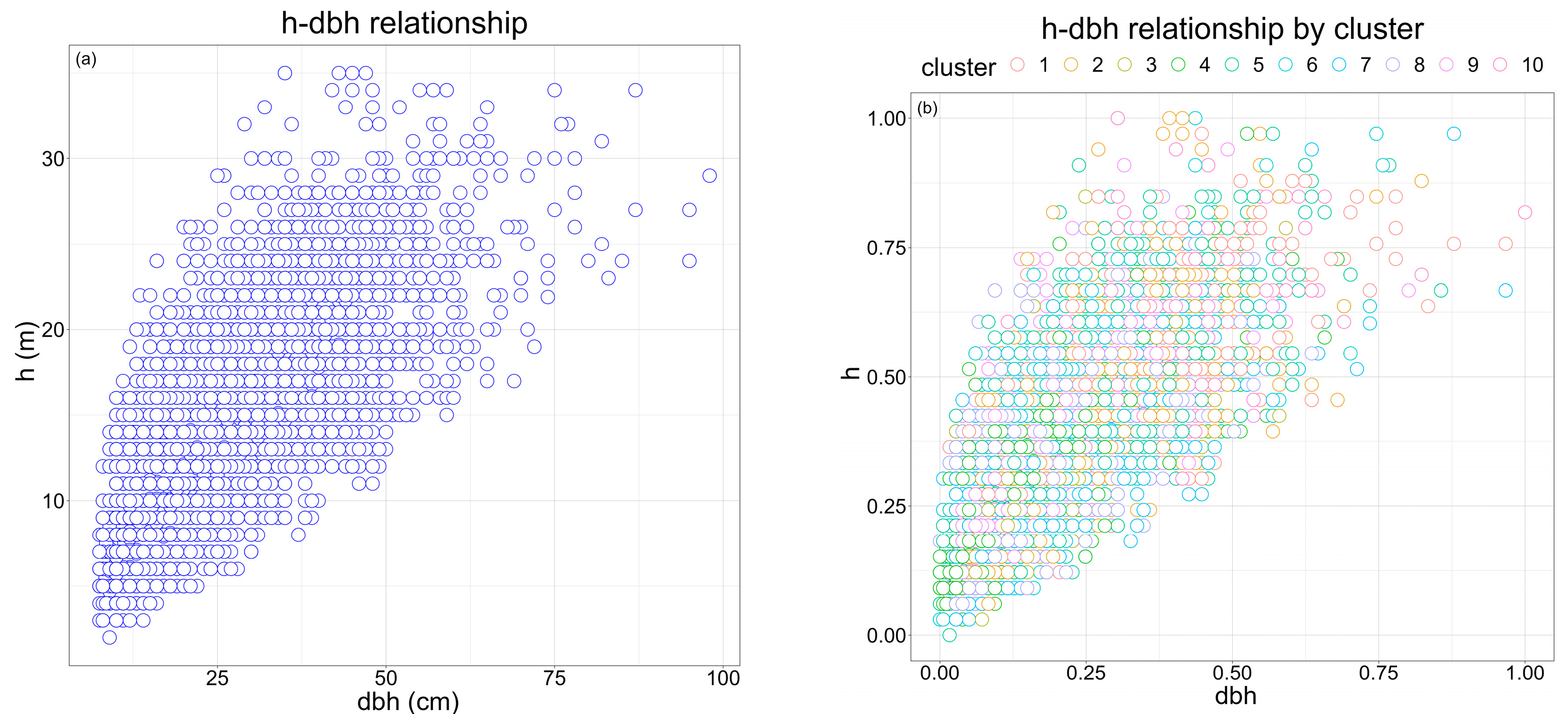
Figure 2.
Scatter plot for h-dbh relationship for full dataset (a) and grouping dataset by cluster (b).
Figure 2.
Scatter plot for h-dbh relationship for full dataset (a) and grouping dataset by cluster (b).
Figure 3.
Plots of ANNs for vectors of c(3, 3, 3) on the left, c(5, 5, 5) on the center, and c(10, 10, 10) on the right, in the hidden layer.
Figure 3.
Plots of ANNs for vectors of c(3, 3, 3) on the left, c(5, 5, 5) on the center, and c(10, 10, 10) on the right, in the hidden layer.
Figure 4.
Plots of RBPANN-tanh (left), RBPANN-softplus (center), and RBPANN-logistic (right) for h-dbh relationship with unsupervised clustering analysis. Bias is included in nodes “B”. Positive weight values in the visual representation are denoted by blue lines, while negative weight values are represented by red lines.
Figure 4.
Plots of RBPANN-tanh (left), RBPANN-softplus (center), and RBPANN-logistic (right) for h-dbh relationship with unsupervised clustering analysis. Bias is included in nodes “B”. Positive weight values in the visual representation are denoted by blue lines, while negative weight values are represented by red lines.
Figure 5.
Residual versus predicted values for RBPANN-tanh model in training phase and each cluster-group.
Figure 5.
Residual versus predicted values for RBPANN-tanh model in training phase and each cluster-group.
Figure 6.
Residual versus predicted values for RBPANN-tanh model in testing phase for each cluster-group.
Figure 6.
Residual versus predicted values for RBPANN-tanh model in testing phase for each cluster-group.
Table 1.
Descriptive statistics for plot-specific variables used in clustering analysis.
Table 1.
Descriptive statistics for plot-specific variables used in clustering analysis.
| Statistic |
|---|
| Variable |
n |
Minimum |
Mean |
Maximum |
SD |
| N |
1000 |
1.0000 |
11.4720 |
57.0000 |
8.7717 |
| BA |
1000 |
0.0007 |
0.0193 |
0.0924 |
0.0137 |
| Dm |
1000 |
8.5000 |
22.9636 |
75.0000 |
7.6788 |
| Hm |
1000 |
4.0000 |
12.8062 |
35.0000 |
3.9813 |
| QMD |
1000 |
8.5147 |
24.7478 |
75.0000 |
8.0708 |
| A |
1000 |
2032.0000 |
2588.2170 |
2978.0000 |
137.3215 |
| S |
1000 |
0.0000 |
43.0499 |
96.0000 |
20.0551 |
| As |
|
1 |
5 |
9 |
2 |
Table 2.
This is a table. Tables should be placed in the main text near to the first time they are cited.
Table 2.
This is a table. Tables should be placed in the main text near to the first time they are cited.
| Dataset |
Statistic |
| Variable |
n |
Minimum |
Mean |
Maximum |
SD |
| Training |
h |
5736 |
7.5000 |
21.5362 |
95.0000 |
11.4394 |
| dbh |
5736 |
3.0000 |
12.3900 |
35.0000 |
5.3217 |
| Testing |
h |
5736 |
7.5000 |
21.3846 |
98.0000 |
11.5267 |
| dbh |
5736 |
2.0000 |
12.1742 |
35.0000 |
5.2871 |
Table 3.
Estimated parameter for h-dbh relationship in Durango pine by NLMEM.
Table 3.
Estimated parameter for h-dbh relationship in Durango pine by NLMEM.
| Parameter |
Estimate |
SE |
DF |
t-value |
p-value |
lower |
upper |
|
26.409060 |
1.100113 |
5724 |
24.005770 |
<0.00001 |
24.252985 |
28.565134 |
|
0.029786 |
0.002534 |
5724 |
11.754320 |
<0.00001 |
0.024820 |
0.034752 |
|
1.083133 |
0.040518 |
5724 |
26.732200 |
<0.00001 |
1.003723 |
1.162543 |
|
1.928939 |
0.583997 |
5724 |
3.302992 |
0.000962 |
1.210579 |
3.073574 |
|
3.110839 |
0.029338 |
5724 |
106.033502 |
<0.00001 |
3.054379 |
3.168342 |
|
-3.371745 |
0.106547 |
407 |
-31.645570 |
<0.00001 |
-3.580578 |
-3.162913 |
|
-2.840826 |
0.089770 |
320 |
-31.645570 |
<0.00001 |
-3.016775 |
-2.664877 |
|
-0.601879 |
0.019019 |
631 |
-31.645570 |
<0.00001 |
-0.639157 |
-0.564601 |
|
3.572580 |
0.112894 |
133 |
31.645570 |
<0.00001 |
3.351309 |
3.793851 |
|
0.773802 |
0.024452 |
925 |
31.645570 |
<0.00001 |
0.725876 |
0.821729 |
|
0.478565 |
0.015123 |
1109 |
31.645570 |
<0.00001 |
0.448925 |
0.508206 |
|
0.945549 |
0.029879 |
364 |
31.645570 |
<0.00001 |
0.886985 |
1.004113 |
|
-0.308794 |
0.009758 |
876 |
-31.645570 |
<0.00001 |
-0.327919 |
-0.289668 |
|
0.012327 |
0.000390 |
654 |
31.645570 |
<0.00001 |
0.011564 |
0.013091 |
|
1.340420 |
0.042357 |
317 |
31.645570 |
<0.00001 |
1.257400 |
1.423440 |
Table 4.
Fitting statistics for h-dbh relationship in Durango pine by NLMEM.
Table 4.
Fitting statistics for h-dbh relationship in Durango pine by NLMEM.
| Dataset |
n |
RMSE |
SEE |
RSEE |
FI |
E |
RE |
AIC |
BIC |
logLik |
| All-dataset |
5736 |
3.1085 |
3.1123 |
25.1193 |
0.6588 |
-0.0005 |
-0.0042 |
13039.75 |
13139.57 |
-13009.75 |
| C1 |
631 |
2.4735 |
2.4889 |
6.4322 |
0.6182 |
-0.0324 |
-0.3161 |
8834.14 |
772.23 |
-736.18 |
| C2 |
407 |
2.5289 |
2.5489 |
6.1485 |
0.5378 |
0.0050 |
0.0515 |
7113.33 |
627.39 |
-592.78 |
| C3 |
925 |
2.9631 |
2.9749 |
8.4267 |
0.6525 |
-0.1111 |
-0.9526 |
16437.91 |
1408.51 |
-1369.83 |
| C4 |
1109 |
3.8688 |
3.9442 |
2.9876 |
0.5610 |
0.3416 |
1.7378 |
4306.53 |
388.22 |
-358.88 |
| C5 |
320 |
3.1341 |
3.1426 |
10.6971 |
0.6312 |
-0.0072 |
-0.0610 |
25348.12 |
2153.32 |
-2112.34 |
| C6 |
654 |
2.8727 |
2.8792 |
10.3014 |
0.6134 |
0.0555 |
0.4528 |
28074.42 |
2381.60 |
-2339.53 |
| C7 |
364 |
3.4345 |
3.4584 |
6.5911 |
0.6329 |
-0.0640 |
-0.4879 |
10767.05 |
932.64 |
-897.25 |
| C8 |
876 |
3.3842 |
3.3939 |
10.2592 |
0.6015 |
0.0210 |
0.1632 |
25618.61 |
2175.54 |
-2134.88 |
| C9 |
133 |
3.2098 |
3.2221 |
8.8088 |
0.6138 |
-0.0229 |
-0.1862 |
18292.63 |
1563.28 |
-1524.39 |
| C10 |
317 |
3.6168 |
3.6458 |
5.1452 |
0.6196 |
-0.0058 |
-0.0353 |
9768.73 |
848.61 |
-814.06 |
Table 5.
Main fitting statistics for RBPANN-tanh, RBPANN-softplus, and RBPANN-logistic activation functions tested for h-dbh relationship.
Table 5.
Main fitting statistics for RBPANN-tanh, RBPANN-softplus, and RBPANN-logistic activation functions tested for h-dbh relationship.
| ANN |
Error |
Reached Threshold |
Steps |
AIC |
BIC |
|
RBPANN-tanh |
27.8455 |
0.0775 |
301 |
577.69 |
2314.52 |
|
RBPANN-softplus |
27.3939 |
0.0838 |
1885 |
576.79 |
2313.62 |
|
RBPANN-logistic |
28.4113 |
0.0994 |
88 |
578.82 |
2315.65 |
Table 6.
Fitting statistics for h-dbh relationship in Durango pine by ANNs and different backpropagations activation functions.
Table 6.
Fitting statistics for h-dbh relationship in Durango pine by ANNs and different backpropagations activation functions.
| Dataset |
RMSE |
SEE |
RSEE |
FI |
E |
RE |
AIC |
BIC |
logLik |
|
RBPANN-tanh |
| All-dataset |
2.8122 |
2.8134 |
22.7071 |
0.7208 |
0.0001 |
-0.0003 |
11872.59 |
11912.52 |
-11860.59 |
| C1 |
2.6322 |
2.6427 |
8.0184 |
0.7258 |
0.0002 |
0.0018 |
14644.89 |
1259.09 |
-1220.41 |
| C2 |
2.2127 |
2.2264 |
6.1634 |
0.6945 |
0.0073 |
0.0717 |
7745.69 |
681.53 |
-645.47 |
| C3 |
2.8170 |
2.8246 |
10.2988 |
0.7020 |
-0.0087 |
-0.0741 |
22979.70 |
1955.95 |
-1914.98 |
| C4 |
2.5795 |
2.5853 |
9.9082 |
0.6883 |
0.0636 |
0.5191 |
25209.16 |
2142.83 |
-2100.76 |
| C5 |
2.4178 |
2.4370 |
6.2966 |
0.5776 |
-0.6268 |
-6.4583 |
6768.31 |
598.64 |
-564.03 |
| C6 |
2.8907 |
2.9019 |
8.4977 |
0.6867 |
0.2559 |
2.0805 |
16649.44 |
1426.35 |
-1387.45 |
| C7 |
3.1340 |
3.1558 |
6.4423 |
0.6943 |
0.3677 |
2.8037 |
9967.09 |
865.97 |
-830.59 |
| C8 |
3.0652 |
3.0740 |
9.9535 |
0.6731 |
-0.3691 |
-2.8636 |
23537.45 |
2002.11 |
-1961.45 |
| C9 |
3.7470 |
3.8200 |
3.0995 |
0.5882 |
1.5107 |
7.6864 |
4204.43 |
379.71 |
-350.37 |
| C10 |
3.2490 |
3.2751 |
4.9509 |
0.6930 |
-0.1391 |
-0.8426 |
8952.96 |
780.63 |
-746.08 |
|
RBPANN-softplus |
| All-dataset |
2.8431 |
2.8443 |
22.9565 |
0.7143 |
0.7146 |
-0.0013 |
-0.0107 |
11997.88 |
12037.81 |
| C1 |
2.6516 |
2.6621 |
8.0772 |
0.7218 |
0.0489 |
0.4190 |
14755.60 |
1268.32 |
-1229.63 |
| C2 |
2.4591 |
2.4744 |
6.8498 |
0.6226 |
-0.9459 |
-9.2408 |
8777.19 |
767.49 |
-731.43 |
| C3 |
2.8529 |
2.8606 |
10.4301 |
0.6944 |
0.4200 |
3.5697 |
23260.85 |
1979.38 |
-1938.40 |
| C4 |
2.6003 |
2.6062 |
9.9882 |
0.6833 |
0.3109 |
2.5351 |
25423.15 |
2160.66 |
-2118.60 |
| C5 |
2.4956 |
2.5154 |
6.4993 |
0.5499 |
-0.9140 |
-9.4178 |
7011.62 |
618.91 |
-584.30 |
| C6 |
2.8841 |
2.8952 |
8.4781 |
0.6882 |
-0.1042 |
-0.8472 |
16613.23 |
1423.33 |
-1384.44 |
| C7 |
3.1030 |
3.1246 |
6.3787 |
0.7003 |
0.1339 |
1.0213 |
9880.37 |
858.75 |
-823.36 |
| C8 |
3.0748 |
3.0837 |
9.9847 |
0.6711 |
-0.3712 |
-2.8799 |
23603.31 |
2007.59 |
-1966.94 |
| C9 |
3.8187 |
3.8931 |
3.1588 |
0.5723 |
1.6461 |
8.3754 |
4264.92 |
384.75 |
-355.41 |
| C10 |
3.2550 |
3.2811 |
4.9600 |
0.6919 |
0.0992 |
0.6009 |
8966.90 |
781.80 |
-747.24 |
|
RBPANN-logistic |
| All-dataset |
2.8486 |
2.8498 |
23.0012 |
0.7135 |
-0.0052 |
-0.0420 |
12020.19 |
12060.12 |
-12008.19 |
| C1 |
2.6570 |
2.6676 |
8.0938 |
0.7206 |
0.0785 |
0.6729 |
14786.65 |
1270.90 |
-1232.22 |
| C2 |
2.4675 |
2.4828 |
6.8732 |
0.6201 |
-0.9254 |
-9.0403 |
8810.45 |
770.26 |
-734.20 |
| C3 |
2.8586 |
2.8664 |
10.4510 |
0.6932 |
0.4146 |
3.5237 |
23305.34 |
1983.09 |
-1942.11 |
| C4 |
2.6024 |
2.6083 |
9.9962 |
0.6827 |
0.2868 |
2.3386 |
25444.48 |
2162.44 |
-2120.37 |
| C5 |
2.5183 |
2.5382 |
6.5583 |
0.5417 |
-0.9468 |
-9.7561 |
7081.01 |
624.69 |
-590.08 |
| C6 |
2.9055 |
2.9167 |
8.5411 |
0.6835 |
-0.1415 |
-1.1503 |
16729.32 |
1433.01 |
-1394.11 |
| C7 |
3.0957 |
3.1172 |
6.3636 |
0.7017 |
0.1066 |
0.8129 |
9859.77 |
857.03 |
-821.65 |
| C8 |
3.0740 |
3.0828 |
9.9818 |
0.6712 |
-0.3751 |
-2.9095 |
23597.18 |
2007.08 |
-1966.43 |
| C9 |
3.8192 |
3.8936 |
3.1592 |
0.5721 |
1.6756 |
8.5253 |
4265.34 |
384.79 |
-355.45 |
| C10 |
3.2584 |
3.2845 |
4.9652 |
0.6912 |
0.1835 |
1.1115 |
8974.85 |
782.46 |
-747.90 |
Table 7.
Ranks and sum of ranks based on the fitting statistics for fitted models in training phase.
Table 7.
Ranks and sum of ranks based on the fitting statistics for fitted models in training phase.
| Model |
Dataset |
RMSE |
SEE |
RSEE |
FI |
E |
RE |
AIC |
BIC |
logLik |
Rank |
| NLMEM |
Overall |
4 |
4 |
4 |
4 |
3 |
2 |
4 |
4 |
4 |
33 (4) |
|
RBPANN-tanh |
Overall |
1 |
1 |
1 |
1 |
4 |
4 |
2 |
1 |
2 |
17 (2) |
|
RBPANN-softplus |
Overall |
2 |
2 |
2 |
2 |
1 |
3 |
1 |
2 |
1 |
16 (1) |
|
RBPANN-logistic |
Overall |
3 |
3 |
3 |
3 |
2 |
1 |
3 |
3 |
3 |
24 (3) |
| NLMEM |
C1 |
1 |
1 |
1 |
4 |
2 |
2 |
1 |
1 |
1 |
14 |
|
RBPANN-tanh |
C1 |
2 |
2 |
2 |
1 |
1 |
1 |
2 |
2 |
2 |
15 |
|
RBPANN-softplus |
C1 |
3 |
3 |
3 |
2 |
3 |
3 |
3 |
3 |
3 |
26 |
|
RBPANN-logistic |
C1 |
4 |
4 |
4 |
3 |
4 |
4 |
4 |
4 |
4 |
35 |
| NLMEM |
C2 |
4 |
4 |
1 |
4 |
1 |
1 |
1 |
1 |
1 |
18 |
|
RBPANN-tanh |
C2 |
1 |
1 |
2 |
1 |
2 |
2 |
2 |
2 |
2 |
15 |
|
RBPANN-softplus |
C2 |
2 |
2 |
3 |
2 |
4 |
4 |
3 |
3 |
3 |
26 |
|
RBPANN-logistic |
C2 |
3 |
3 |
4 |
3 |
3 |
3 |
4 |
4 |
4 |
31 |
| NLMEM |
C3 |
4 |
4 |
1 |
4 |
2 |
2 |
1 |
1 |
1 |
20 |
|
RBPANN-tanh |
C3 |
1 |
1 |
2 |
1 |
1 |
1 |
2 |
2 |
2 |
13 |
|
RBPANN-softplus |
C3 |
2 |
2 |
3 |
2 |
4 |
4 |
3 |
3 |
3 |
26 |
|
RBPANN-logistic |
C3 |
3 |
3 |
4 |
3 |
3 |
3 |
4 |
4 |
4 |
31 |
| NLMEM |
C4 |
4 |
4 |
1 |
4 |
4 |
2 |
1 |
1 |
1 |
22 |
|
RBPANN-tanh |
C4 |
1 |
1 |
2 |
1 |
1 |
1 |
2 |
2 |
2 |
13 |
|
RBPANN-softplus |
C4 |
2 |
2 |
3 |
2 |
3 |
4 |
3 |
3 |
3 |
25 |
|
RBPANN-logistic |
C4 |
3 |
3 |
4 |
3 |
2 |
3 |
4 |
4 |
4 |
30 |
| NLMEM |
C5 |
4 |
4 |
4 |
1 |
1 |
1 |
4 |
4 |
4 |
27 |
|
RBPANN-tanh |
C5 |
1 |
1 |
1 |
2 |
2 |
2 |
1 |
1 |
1 |
12 |
|
RBPANN-softplus |
C5 |
2 |
2 |
2 |
3 |
3 |
3 |
2 |
2 |
2 |
21 |
|
RBPANN-logistic |
C5 |
3 |
3 |
3 |
4 |
4 |
4 |
3 |
3 |
3 |
30 |
| NLMEM |
C6 |
1 |
1 |
4 |
4 |
1 |
1 |
4 |
4 |
4 |
24 |
|
RBPANN-tanh |
C6 |
3 |
3 |
2 |
2 |
4 |
4 |
2 |
2 |
2 |
24 |
|
RBPANN-softplus |
C6 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
1 |
1 |
13 |
|
RBPANN-logistic |
C6 |
4 |
4 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
29 |
| NLMEM |
C7 |
4 |
4 |
4 |
4 |
1 |
1 |
4 |
4 |
4 |
30 |
|
RBPANN-tanh |
C7 |
3 |
3 |
3 |
3 |
4 |
4 |
3 |
3 |
3 |
29 |
|
RBPANN-softplus |
C7 |
2 |
2 |
2 |
2 |
3 |
3 |
2 |
2 |
2 |
20 |
|
RBPANN-logistic |
C7 |
1 |
1 |
1 |
1 |
2 |
2 |
1 |
1 |
1 |
11 |
| NLMEM |
C8 |
4 |
4 |
4 |
4 |
1 |
1 |
4 |
4 |
4 |
30 |
|
RBPANN-tanh |
C8 |
1 |
1 |
1 |
1 |
2 |
2 |
1 |
1 |
1 |
11 |
|
RBPANN-softplus |
C8 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
27 |
|
RBPANN-logistic |
C8 |
2 |
2 |
2 |
2 |
4 |
4 |
2 |
2 |
2 |
22 |
| NLMEM |
C9 |
1 |
1 |
4 |
1 |
1 |
1 |
4 |
4 |
4 |
21 |
|
RBPANN-tanh |
C9 |
2 |
2 |
1 |
2 |
2 |
2 |
1 |
1 |
1 |
14 |
|
RBPANN-softplus |
C9 |
3 |
3 |
2 |
3 |
3 |
3 |
2 |
2 |
2 |
23 |
|
RBPANN-logistic |
C9 |
4 |
4 |
3 |
4 |
4 |
4 |
3 |
3 |
3 |
32 |
| NLMEM |
C10 |
4 |
4 |
4 |
4 |
1 |
1 |
4 |
4 |
4 |
30 |
|
RBPANN-tanh |
C10 |
1 |
1 |
1 |
1 |
3 |
3 |
1 |
1 |
1 |
13 |
|
RBPANN-softplus |
C10 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
18 |
| RBPANN-logistic |
C10 |
3 |
3 |
3 |
3 |
4 |
4 |
3 |
3 |
3 |
29 |
Table 8.
Testing statistics for h-dbh relationship in Durango pine by NLMEM in testing phase.
Table 8.
Testing statistics for h-dbh relationship in Durango pine by NLMEM in testing phase.
| Dataset |
n |
RMSE |
SEE |
RSEE |
FI |
E |
RE |
AIC |
BIC |
logLik |
| All-dataset |
5736 |
3.1438 |
3.1476 |
25.8549 |
0.6464 |
-0.1611 |
-1.3229 |
13169.29 |
13269.10 |
-13139.29 |
| C1 |
631 |
2.7037 |
2.7141 |
24.1931 |
0.6893 |
-0.0987 |
-0.8795 |
15671.32 |
1344.87 |
-1305.94 |
| C2 |
407 |
2.9045 |
2.9228 |
29.6973 |
0.4680 |
1.2223 |
12.4194 |
10249.76 |
890.11 |
-854.15 |
| C3 |
925 |
3.0941 |
3.1029 |
27.5443 |
0.6136 |
-0.7206 |
-6.3964 |
23870.14 |
2029.86 |
-1989.18 |
| C4 |
1109 |
3.0509 |
3.0578 |
25.0690 |
0.6102 |
-0.0942 |
-0.7725 |
29971.18 |
2539.72 |
-2497.60 |
| C5 |
320 |
2.7563 |
2.7797 |
28.6992 |
0.5175 |
0.9194 |
9.4926 |
7263.59 |
639.50 |
-605.30 |
| C6 |
654 |
3.1718 |
3.1834 |
25.4080 |
0.6085 |
0.1428 |
1.1398 |
19047.71 |
1626.51 |
-1587.31 |
| C7 |
364 |
3.4512 |
3.4752 |
26.2781 |
0.6545 |
-0.7996 |
-6.0462 |
10839.28 |
938.67 |
-903.27 |
| C8 |
876 |
3.0615 |
3.0704 |
24.6303 |
0.6290 |
-0.1456 |
-1.1680 |
23216.40 |
1975.28 |
-1934.70 |
| C9 |
133 |
5.0061 |
5.1138 |
25.4219 |
0.2128 |
-2.4332 |
-12.0959 |
4665.31 |
417.55 |
-388.78 |
| C10 |
317 |
3.8668 |
3.8957 |
24.6024 |
0.5555 |
-0.7956 |
-5.0245 |
10991.37 |
950.90 |
-915.95 |
Table 9.
Testing statistics for both overall dataset and each cluster-group in testing phase with ANNs approaches.
Table 9.
Testing statistics for both overall dataset and each cluster-group in testing phase with ANNs approaches.
| Dataset |
RMSE |
SEE |
RSEE |
FI |
E |
RE |
AIC |
BIC |
logLik |
|
RBPANN-tanh |
| All-dataset |
2.8693 |
2.8706 |
23.5793 |
0.7055 |
0.6603 |
5.4241 |
12103.39 |
12143.32 |
-12091.39 |
| C1 |
2.5090 |
2.5186 |
8.1057 |
0.7324 |
0.6015 |
5.3617 |
14492.43 |
1246.63 |
-1207.70 |
| C2 |
2.4793 |
2.4949 |
7.1292 |
0.6124 |
0.8309 |
8.4421 |
8726.27 |
763.15 |
-727.19 |
| C3 |
2.7294 |
2.7372 |
10.1704 |
0.6994 |
0.4046 |
3.5917 |
21218.12 |
1808.86 |
-1768.18 |
| C4 |
2.8842 |
2.8907 |
11.1931 |
0.6516 |
0.8969 |
7.3531 |
28460.68 |
2413.85 |
-2371.72 |
| C5 |
2.3880 |
2.4083 |
6.0227 |
0.6378 |
0.0825 |
0.8517 |
6234.38 |
553.73 |
-519.53 |
| C6 |
3.0888 |
3.1001 |
9.1436 |
0.6287 |
1.2080 |
9.6415 |
18609.70 |
1590.01 |
-1550.81 |
| C7 |
3.1665 |
3.1885 |
6.4643 |
0.7091 |
0.8613 |
6.5128 |
10085.03 |
875.82 |
-840.42 |
| C8 |
2.7710 |
2.7790 |
9.2458 |
0.6961 |
0.1519 |
1.2183 |
21146.63 |
1802.80 |
-1762.22 |
| C9 |
4.2322 |
4.3232 |
3.2613 |
0.4374 |
1.8156 |
9.0259 |
4177.60 |
376.91 |
-348.13 |
| C10 |
3.4732 |
3.4992 |
5.7063 |
0.6414 |
0.5225 |
3.2997 |
10118.01 |
878.12 |
-843.17 |
|
RBPANN-softplus |
| All-dataset |
2.8764 |
2.8776 |
23.6371 |
0.7040 |
0.6578 |
5.4029 |
12131.48 |
12171.41 |
-12119.48 |
| C1 |
2.5181 |
2.5278 |
8.1353 |
0.7305 |
0.6756 |
6.0219 |
14550.00 |
1251.43 |
-1212.50 |
| C2 |
2.3388 |
2.3536 |
6.7253 |
0.6551 |
-0.0814 |
-0.8266 |
8164.99 |
716.38 |
-680.42 |
| C3 |
2.8312 |
2.8393 |
10.5500 |
0.6765 |
0.8131 |
7.2176 |
21992.85 |
1873.42 |
-1832.74 |
| C4 |
2.9657 |
2.9724 |
11.5095 |
0.6317 |
1.1148 |
9.1400 |
29209.97 |
2476.29 |
-2434.16 |
| C5 |
2.4000 |
2.4204 |
6.0529 |
0.6342 |
-0.2679 |
-2.7660 |
6270.23 |
556.72 |
-522.52 |
| C6 |
2.9772 |
2.9881 |
8.8135 |
0.6550 |
0.7866 |
6.2785 |
18002.41 |
1539.40 |
-1500.20 |
| C7 |
3.1029 |
3.1244 |
6.3344 |
0.7207 |
0.6147 |
4.6485 |
9907.23 |
861.00 |
-825.60 |
| C8 |
2.7748 |
2.7828 |
9.2584 |
0.6952 |
0.1450 |
1.1632 |
21174.89 |
1805.15 |
-1764.57 |
| C9 |
4.3045 |
4.3971 |
3.3171 |
0.4180 |
2.0025 |
9.9547 |
4226.81 |
381.01 |
-352.23 |
| C10 |
3.5266 |
3.5530 |
5.7940 |
0.6303 |
0.8555 |
5.4026 |
10242.05 |
888.46 |
-853.50 |
|
RBPANN-logistic |
| All-dataset |
2.8820 |
2.8832 |
23.6832 |
0.7029 |
0.6484 |
5.3263 |
12153.85 |
12193.77 |
-12141.85 |
| C1 |
2.5071 |
2.5168 |
8.0998 |
0.7328 |
0.6480 |
5.7760 |
14481.07 |
1245.68 |
-1206.76 |
| C2 |
2.3476 |
2.3624 |
6.7505 |
0.6525 |
-0.0800 |
-0.8123 |
8200.94 |
719.38 |
-683.41 |
| C3 |
2.8287 |
2.8368 |
10.5405 |
0.6771 |
0.8418 |
7.4726 |
21973.90 |
1871.84 |
-1831.16 |
| C4 |
2.9718 |
2.9785 |
11.5331 |
0.6302 |
1.1385 |
9.3342 |
29264.97 |
2480.87 |
-2438.75 |
| C5 |
2.3833 |
2.4035 |
6.0108 |
0.6392 |
-0.2199 |
-2.2702 |
6220.20 |
552.55 |
-518.35 |
| C6 |
2.9674 |
2.9783 |
8.7844 |
0.6573 |
0.8301 |
6.6255 |
17947.97 |
1534.87 |
-1495.66 |
| C7 |
3.1024 |
3.1240 |
6.3335 |
0.7208 |
0.6342 |
4.7956 |
9905.96 |
860.90 |
-825.50 |
| C8 |
2.7763 |
2.7843 |
9.2634 |
0.6949 |
0.1438 |
1.1539 |
21186.18 |
1806.09 |
-1765.51 |
| C9 |
4.2538 |
4.3453 |
3.2780 |
0.4316 |
1.9452 |
9.6698 |
4192.42 |
378.14 |
-349.37 |
| C10 |
3.4913 |
3.5174 |
5.7360 |
0.6377 |
0.7841 |
4.9519 |
10160.28 |
881.65 |
-846.69 |
Table 10.
Ranks and sum of ranks based on the fitting statistics for fitted models in testing phase.
Table 10.
Ranks and sum of ranks based on the fitting statistics for fitted models in testing phase.
| Model |
Dataset |
RMSE |
SEE |
RSEE |
FI |
E |
RE |
AIC |
BIC |
logLik |
Rank |
| NLMEM |
Overall |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
36 (4) |
|
RBPANN-tanh |
Overall |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
9 (1) |
|
RBPANN-softplus |
Overall |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
18 (2) |
|
RBPANN-logistic |
Overall |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
27 (3) |
| NLMEM |
C1 |
4 |
4 |
4 |
4 |
1 |
1 |
4 |
4 |
4 |
30 |
|
RBPANN-tanh |
C1 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
18 |
|
RBPANN-softplus |
C1 |
3 |
3 |
3 |
3 |
4 |
4 |
3 |
3 |
3 |
29 |
|
RBPANN-logistic |
C1 |
1 |
1 |
1 |
1 |
3 |
3 |
1 |
1 |
1 |
13 |
| NLMEM |
C2 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
36 |
|
RBPANN-tanh |
C2 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
27 |
|
RBPANN-softplus |
C2 |
1 |
1 |
1 |
1 |
2 |
2 |
1 |
1 |
1 |
11 |
|
RBPANN-logistic |
C2 |
2 |
2 |
2 |
2 |
1 |
1 |
2 |
2 |
2 |
16 |
| NLMEM |
C3 |
4 |
4 |
4 |
4 |
2 |
2 |
4 |
4 |
4 |
32 |
|
RBPANN-tanh |
C3 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
9 |
|
RBPANN-softplus |
C3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
27 |
|
RBPANN-logistic |
C3 |
2 |
2 |
2 |
2 |
4 |
4 |
2 |
2 |
2 |
22 |
| NLMEM |
C4 |
4 |
4 |
4 |
4 |
1 |
1 |
4 |
4 |
4 |
30 |
|
RBPANN-tanh |
C4 |
1 |
1 |
1 |
1 |
2 |
2 |
1 |
1 |
1 |
11 |
|
RBPANN-softplus |
C4 |
2 |
2 |
2 |
2 |
3 |
3 |
2 |
2 |
2 |
20 |
|
RBPANN-logistic |
C4 |
3 |
3 |
3 |
3 |
4 |
4 |
3 |
3 |
3 |
29 |
| NLMEM |
C5 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
36 |
|
RBPANN-tanh |
C5 |
2 |
2 |
2 |
2 |
1 |
1 |
2 |
2 |
2 |
16 |
|
RBPANN-softplus |
C5 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
27 |
|
RBPANN-logistic |
C5 |
1 |
1 |
1 |
1 |
2 |
2 |
1 |
1 |
1 |
11 |
| NLMEM |
C6 |
4 |
4 |
4 |
4 |
1 |
1 |
4 |
4 |
4 |
30 |
|
RBPANN-tanh |
C6 |
3 |
3 |
3 |
3 |
4 |
4 |
3 |
3 |
3 |
29 |
|
RBPANN-softplus |
C6 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
18 |
|
RBPANN-logistic |
C6 |
1 |
1 |
1 |
1 |
3 |
3 |
1 |
1 |
1 |
13 |
| NLMEM |
C7 |
4 |
4 |
4 |
4 |
3 |
3 |
4 |
4 |
4 |
34 |
|
RBPANN-tanh |
C7 |
3 |
3 |
3 |
3 |
4 |
4 |
3 |
3 |
3 |
29 |
|
RBPANN-softplus |
C7 |
2 |
2 |
2 |
2 |
1 |
1 |
2 |
2 |
2 |
16 |
|
RBPANN-logistic |
C7 |
1 |
1 |
1 |
1 |
2 |
2 |
1 |
1 |
1 |
11 |
| NLMEM |
C8 |
4 |
4 |
4 |
4 |
3 |
3 |
4 |
4 |
4 |
34 |
|
RBPANN-tanh |
C8 |
1 |
1 |
1 |
1 |
4 |
4 |
1 |
1 |
1 |
15 |
|
RBPANN-softplus |
C8 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
18 |
|
RBPANN-logistic |
C8 |
3 |
3 |
3 |
3 |
1 |
1 |
3 |
3 |
3 |
23 |
| NLMEM |
C9 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
4 |
36 |
|
RBPANN-tanh |
C9 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
9 |
|
RBPANN-softplus |
C9 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
27 |
|
RBPANN-logistic |
C9 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
18 |
| NLMEM |
C10 |
4 |
4 |
4 |
4 |
3 |
3 |
4 |
4 |
4 |
34 |
|
RBPANN-tanh |
C10 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
9 |
|
RBPANN-softplus |
C10 |
3 |
3 |
3 |
3 |
4 |
4 |
3 |
3 |
3 |
29 |
| RBPANN-logistic |
C10 |
3 |
3 |
3 |
3 |
4 |
4 |
3 |
3 |
3 |
29 |