The Optical Properties and Spectroscopic Limited Maximum Efficiency of SnO2 Polymorphs for Solar Cell Applications: A First-Principles Analysis

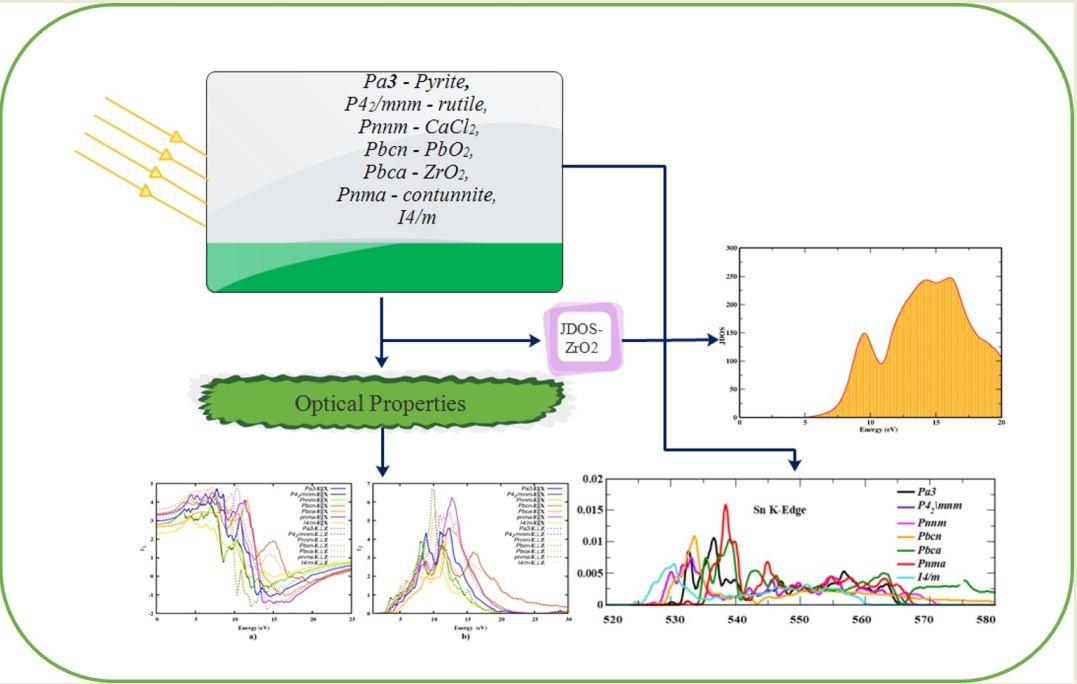
1. Introduction

New materials with enhanced optical properties have been developed to address the energy crisis for future technology. The first transparent conducting oxide (TCO) is SnO₂, which is used as the front surface electrode in all types of solar cell materials ^1–3. This is particularly true when making solar cells using thin film technology such as amorphous silicon, cadmium telluride or copper indium gallium diselenide (CIGS). These TCO materials are used as one coating, two coatings sometimes as three coatings as well ^4–6. The peculiar electronic structure and dynamical properties of SnO₂ polymorphs increase the intention to study their other optical properties. In recent years, wide bandgap semiconductors have attracted the attention of researchers due to their applications in the fields of optoelectronic device fabrication, photonics, the electron transport layer (ETL) in perovskite solar cells (PSCs) and photo-chemistry ^7–10. More recently, SnO₂ has found its most significant use in supercapacitors, where it has been shown to enhance both capacitance and energy density ¹¹. The optical properties of the material are of fundamental interest for the abovementioned application. SnO₂ needs better optoelectronic characteristics to work well in all the above devices. Hence, this study mainly concerns the optical properties of the stable SnO₂ polymorphs.

Several methods are reported in the literature to address the issue of SnO₂ optical properties; hence, an overview of related works is provided here. It has been previously reported in the literature by Rabilah Gilani et al. that the structural and optical properties of rutile-type SnO₂ for various pseudopotentials. And also shows that the band gap and optical characteristics calculated from HSE06 are quite close to the experimental values ¹². Similar research has been carried out by shao ting ting et al. which coincides with Rabilah Gilani et al. ¹³. The optical characteristics of prospective semiconducting materials such as TiO₂, SnO₂, ZrO₂ and HfO₂ have been investigated using the meta-GGA functional and it has been demonstrated that SnO₂ and TiO₂ are effective photovoltaic (PV) materials ¹⁴. Generally, a material's adjustable electronic characteristics make it efficient through doping. Sc-doped SnO₂ has been reported by Julaiba Tahsina Mazumder et al. Sc-doped SnO₂ exhibits a blue-shifted optical transmittance, low absorption and reflectivity due to a wider band gap, these properties suggest the material may find utility in transparent conducting applications ¹⁵. The optical properties of Ti-doped SnO₂ have been studied and the absorption edge varies according to the doping concentration ¹⁶. Several authors have recognized rutile SnO₂ as a potential candidate for many applications ^17–22, however, there are many polymorphs other than rutile available. Thus, we study the optical properties of seven structurally, dynamically and mechanically stable polymorphs ²³.

The effective mass, transition dipole moment (TDM), SLME and XANES of SnO₂ polymorphs have not been theoretically addressed in the literature. To determine the material's feasibility for use in PV applications, we planned to investigate the abovementioned polymorphic features in detail. There are some kinds of literature available on XANES of rutile-SnO₂ and doped rutile SnO_2. Jae-Yoon Bae et al. reported Sn k-edge spectra of tetragonal and orthogonal phases of SnO₂ thin film. The transition between the core level and the unoccupied electronic state above the fermi level is addressed. Also, the deviations between the XANES spectra of the tetragonal and orthorhombic phases were examined ²⁴. The lithiation and delithiation processes in metal-doped SnO₂ are being investigated using XANES to provide structural insight ²⁵. The photovoltaic device efficiency can be calculated from the SLME. Aleksandar Zivkovi et al. computed the photovoltaic efficiency of ZnP₂ polymorphs from SLME ²⁶. As predicted by SLME, lead-free double perovskite materials like Cs₂AgBiCl₆ have proven useful as solar cell absorber layers ²⁷. No theoretical studies exist on the solar cell efficiency and TMD of the SnO₂ polymorphs; therefore, we tried to figure out which polymorph of SnO₂ is the most essential member of perovskite solar cell material.

By applying the high-end computational code using VASP, we can calculate the optical parameters using the first-principles method. Only a few studies were available on the theoretical approach to the optical properties of SnO₂ polymorphs on HSE06 function with rutile and CaCl₂ polymorphs. This is the first time we employed the HSE06 functional to elucidate the optical properties as well as the effective mass of the seven structurally, mechanically and dynamically stable polymorphs (Pa$\stackrel{-}{3}$ - Pyrite, P4₂/mnm - rutile, Pnnm-CaCl₂, Pbcn-PbO₂, Pbca-ZrO₂, Pnma-contunnite, I4/m). It is well known that the PBE functional underestimates the electronic and optical properties of semiconductors. The hybrid functionals such as HSE06 and B3LYP may yields results comparable to the experimental results.

2. Computational methodology

The optical properties of seven stable SnO₂ polymorphs were computed through the Vienna Ab-initio Simulation Package (VASP) ^{28, 29}. The part of valence states of stannic (Sn) and oxygen (O) are 5s², 5p² and 2s², 2p⁴. The HSE06 functional has been used to calculate the optical properties of the polymorphs. As the electronic bandgap of the semiconductors can have obtained better accuracy in this functional, hence we used HSE06 for calculating the dynamic dielectric functions. This gives better accuracy compared to other functional ³⁰. The k-point sampling used for optical properties is three times greater than a k mesh for static calculations. The optimized crystal structure of the SnO₂ polymorphs was used to calculate the optical and other related properties. The computed dynamic dielectric functions were used to assess the optical properties of these compounds, including the optical spectra and absorption. Density functional perturbation theory along with local field effect approaches was used to determine static dielectric constants in HSE06 ³¹. The VASPKIT tool is used to calculate the effective mass, optical properties, TDM, SLME and XANES of the SnO₂ polymorphs ³². The optical properties were obtained from the imaginary part of the complex dielectric function.

3. Results and discussion

3.1. The effective mass of hole and electron (m*)

The effective mass provides precise information on the transfer rate of charge carriers (electrons or holes) assessed by the effective mass of electrons and holes. In addition, this is an important physical parameter that predicts the efficiency of solar cells. The photo-generated charge carrier is typically inversely proportional to their effective masses ^33–35. Consequently, the transfer rate of carriers decreases as effective mass increases and vice versa. To illustrate the various recombination rates of charge carriers among the polymorphs, the effective mass of charge carriers along specified directions was computed by fitting parabolic functions around the CBM or the VBM using the following formula:

$$m^{*}={\mathrm{ћ}}^2{\left(\frac{d^{2}E}{{dk}^2}\right)}^{-1}$$

(1)

The effective masses of the SnO₂ polymorphs were given in Table 1. The effective mass of carriers can be calculated using the band structure of the material. The band structure of the SnO₂ polymorphs was reported in the previous literature ²³. The effective mass of carriers is related to the curvature of the energy bands in the polymorphs. The curvature is defined as the second derivative of the energy with respect to the wave vector and can be calculated using finite differences between neighboring points on the band structure. The negative sign of the effective mass indicates that the band curves away from the maximum, also the electrons are responsible for conductivity. When we computed the effective masses, m_e* and m_h* of polymorphs of SnO₂ we observed the positive m* for most of the polymorphs, which shows its semiconducting nature. Though P4₂/mnm and Pnnm have similar structures, there is a variation observed in their mobility. The average effective mass of the charge carriers was given and it is infrared that the charge transfer rate in the Pbca polymorph is highest among them. The effective mass of P4₂/mnm is compared with the experimental results and has deviated 10 % from the experimental results ³⁶. In addition, the effective mass of the Pnma is lower compared to seven stable polymorphs; hence, its mobility is higher. For Pa$\stackrel{-}{3},$P4₂/mnm, Pnnm and I4/m polymorphs the effective mass of electrons lower than the effective mass of holes. Which has higher mobility and is suitable for photovoltaic devices.

3.2. Optical properties

Optical properties of solids can be used to investigate the electronic band structure, lattice vibrations, lattice defects, impurity levels and magnetic excitations in detail. In general, the two most important optical constants of a material are its refractive index n(𝜔) and extinction coefficient k(𝜔), both of which are wavelength dependent and are referred to as dispersion. These two depend on the complex dielectric function 𝜖(𝜔), once we calculated the imaginary part of the dielectric function (i.e. absorption) it can be used to find the real part (i.e., dispersion) or vice versa. The index of refraction and the other optical parameters are the same along the two transverse directions for an isotropic system, while in the other case, they are different along the two directions ³⁷. The dielectric function 𝜖(𝜔), refractive index n(ω), extinction coefficient k(ω), absorption coefficient α(ω), reflectivity R(ω), energy loss function L(ω) and optical conductivity σ(ω) were calculated using the HSE06 functional ^{31, 38}.

3.2.1. Dielectric function

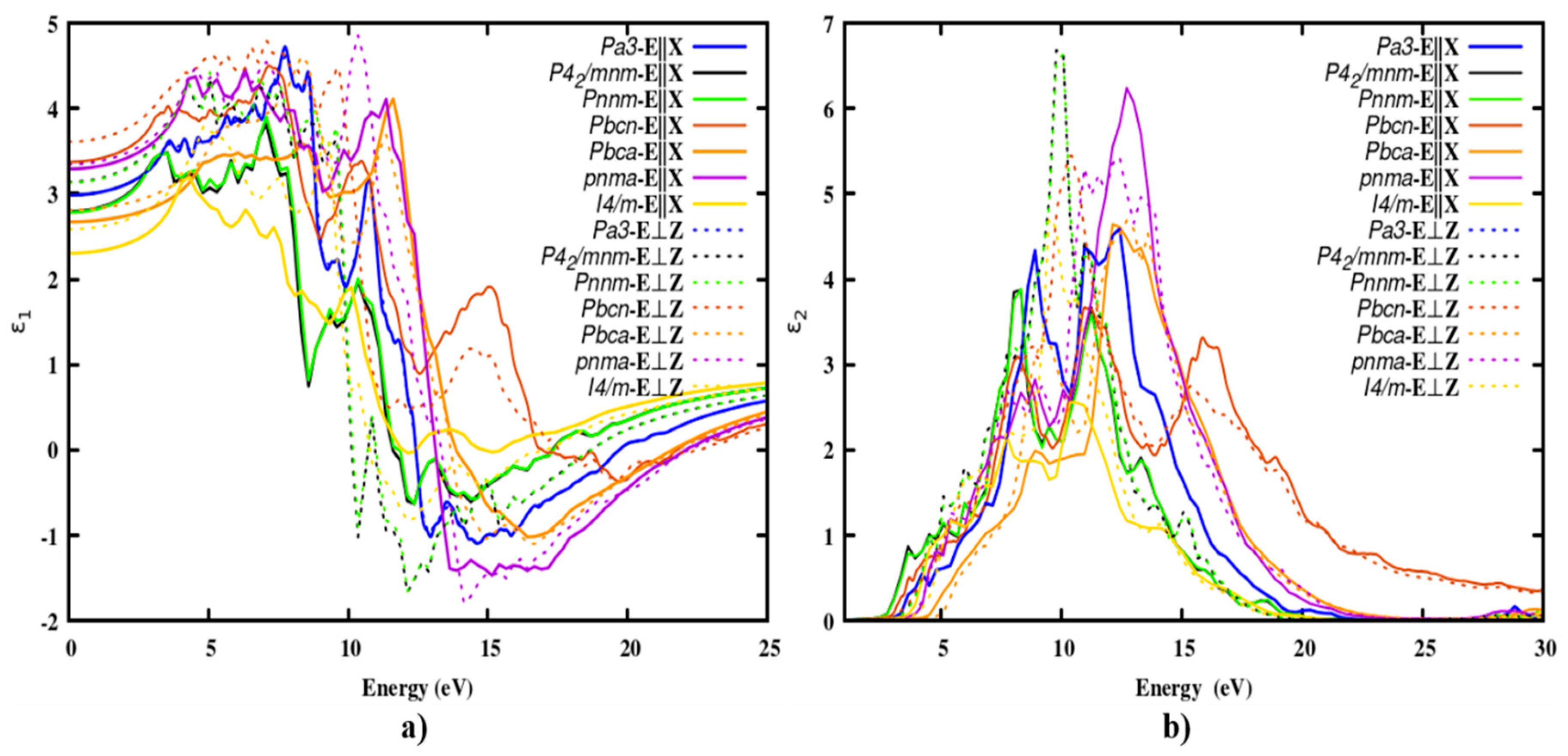
The optical parameters along all three components of polarization were studied. When light interacts with a material, the complex dielectric function offers information about the type of interaction that occurs. The real component of the complex dielectric function 𝜖₁(𝜔) was used to identify the electronic polarizability of polymorphs along different directions. The static dielectric constant at zero frequency (ω = 0) along the crystallographic axis was calculated and given in Table 2. The cubic polymorph is isotropic, as can be seen from the similar dielectric constant along in-plane and out-of-plane polarization. However, it is anisotropic for the tetragonal and orthorhombic phases, which arise due to the tetragonal distortion. The intermediate band solar cells and their anisotropic optical properties were examined by Murugesan Rasukkannu et al.^{39, 40} Figure 1 (a) and (b), show the complex dielectric functions of polymorphs of SnO₂ along in-plane (E||X) and out-of-plane (E⊥Z) of polarization. The static dielectric constant of P4₂/mnm polymorph is 2.79 which is consistent with other reported values ^{12, 30, 41}. Which is a 4 % variation from the calculated HSE06 functional value and a 9 % difference from the experimental value. The dielectric functions of P4₂/mnm and Pnnm lie one over the other due to their structure similarity and they are coming under the same space group. While the Pbcn polymorph is the biggest among the seven and the newly identified polymorph I4/m has the smallest static dielectric constant. Hence the polymorphs P4₂/mnm and I4/m were suitable for ETL in solar cells. Moreover, the real part of the dielectric function has peaks at lower energy levels revealing that the higher polarizability at the lower energy levels were shown in Figure 1(a). Two prominent peaks were appearing nearly at 7 and 10 eV along the E||X direction but for the E⊥Z direction we observed a broad peak scattered from 4 to 9.5 eV for all the polymorphs. For all SnO₂ polymorphs, the peaks arise due to the transition that occurs between the Sn-5p and O-2p states. In addition, the corresponding resonance peak appearing in the range of 9.5 to 13.6 eV.

In particular, negative values of the real component were observed in the energy range from 12.5 eV to 21.5 eV. This is because electromagnetic radiation is reflected by the materials due to the phenomenon of anomalous dispersion, this specific range of energy indicates that the material has behaved like a metal.

Also, the imaginary part of the dielectric function is directly related to the absorption of light. An inter-band transition between the valence band maximum (VBM) and conduction band minimum (CBM) led to the resonance peaks of the polymorphs. The spectral distribution of the imaginary part of the function is given in Figure 1 (b). For all polymorphs, the main peak of the imaginary part was scattered over a wide range of energies from 6 to 17 eV for both parallel and perpendicular polarization. All the reported polymorphs were effective in the UV region. In addition, the optical absorption edge was observed from 1.3 to 2.3 eV. This is due to the fundamental band gap, as already reported. The findings are consistent with the reported values. While the rutile polymorph had previously been studied with HSE06 by Sagadevan et al. the remaining polymorphs were reported for the first time with HSE06 ³⁰.

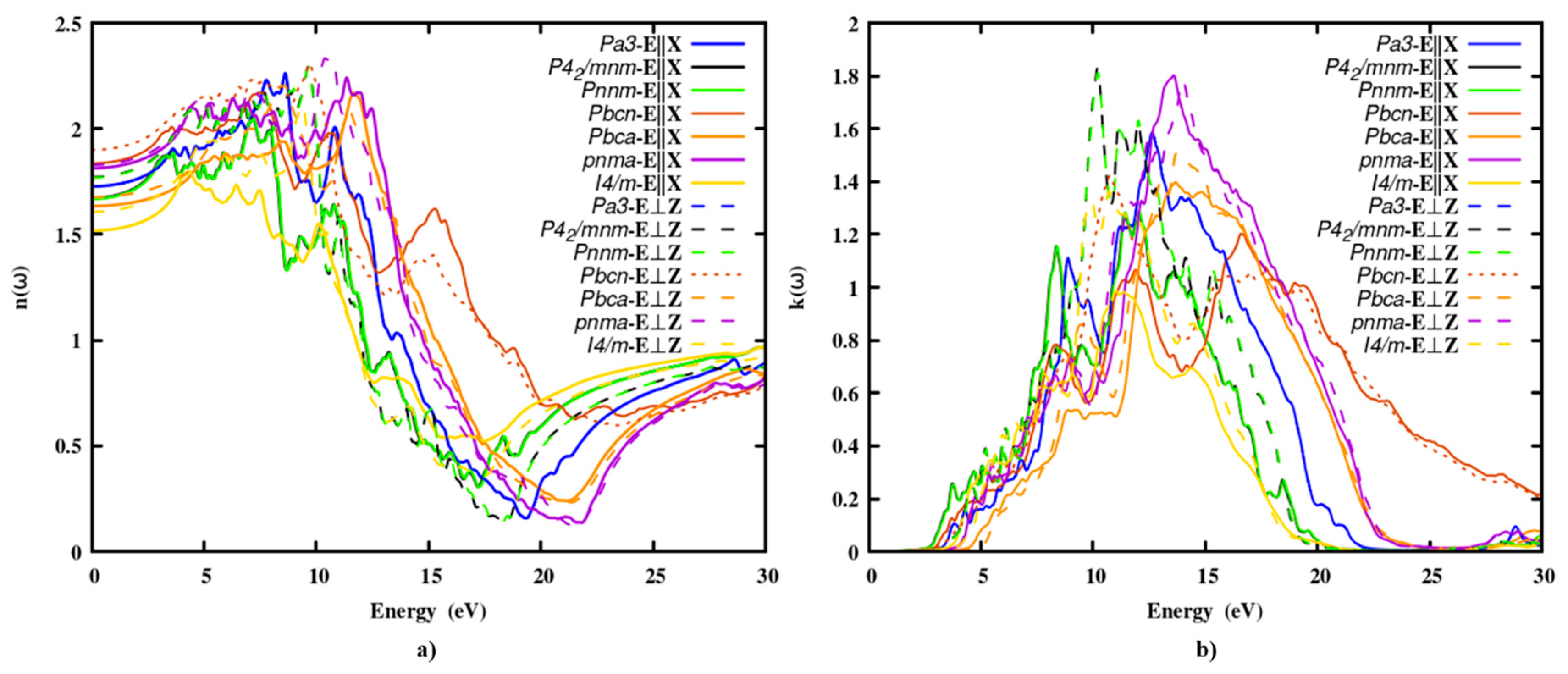
3.2.2. The refractive index and extinction coefficient

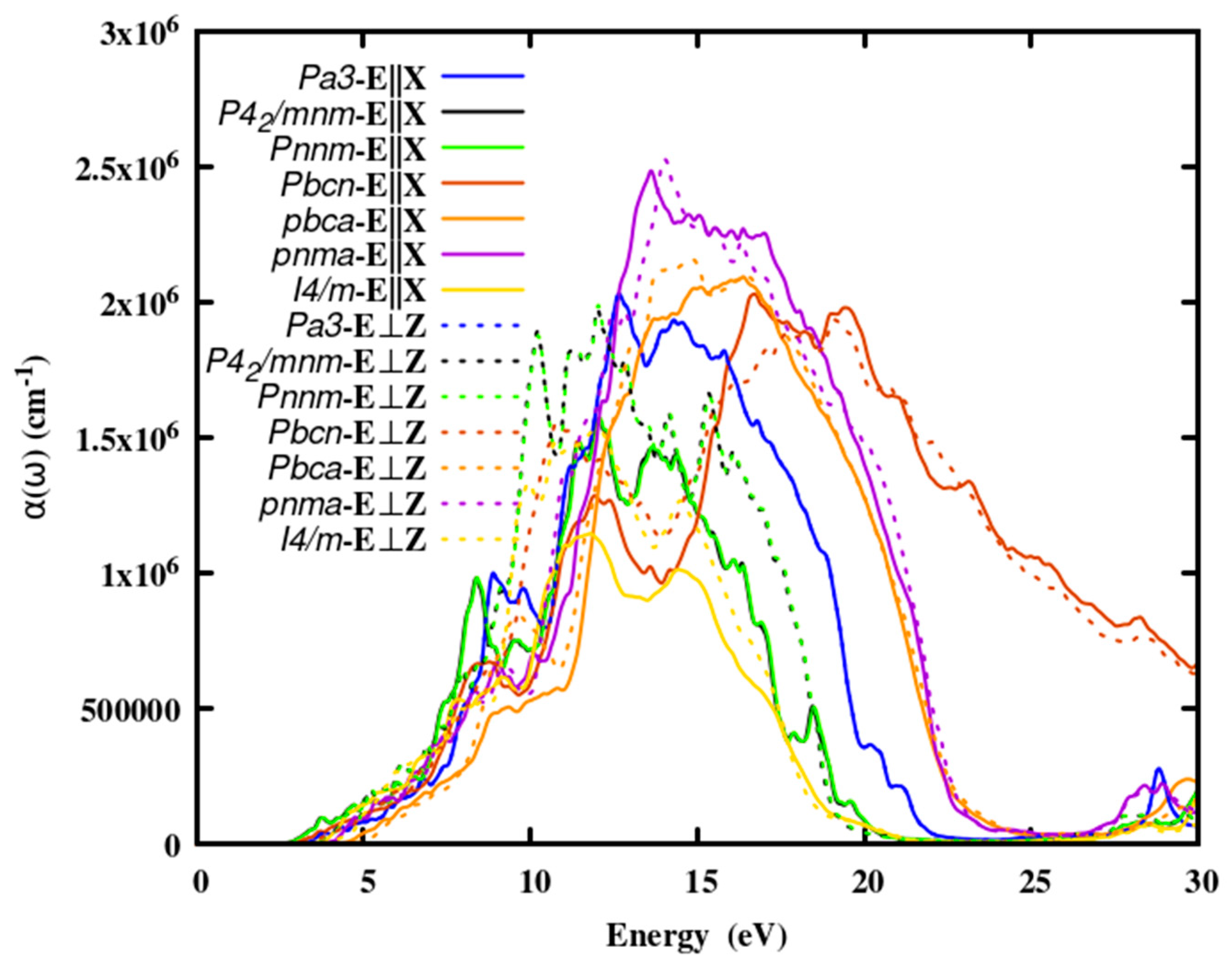
3.2.3. The absorption coefficient

Optical absorption spectra are significant in any optical material because they are a measure of the intensity of electromagnetic energy that passes through it. Figure 3, depicts the spectrum distribution of the absorption coefficient of SnO₂ polymorphs. The absorption edge energies of the polymorphs were given in Table 3. The absorption spectra increased sharply at about 10 eV after producing a broad absorption peak, it tailed off. Since the absorption spectra are insignificant below the absorption edge, photon energy is transmitted in this energy range. Energy absorption is low in the visible region but strong in the UV zone. Furthermore, as compared to other binary oxides such as TiO₂, ZrO₂, SiO₂ and HfO₂, the absorption of SnO₂ is lower, making it a good candidate for ELT.

Table 1. The absorption and the conductive intense peak of the SnO₂ polymorphs along in-plane (E||X) and out-of-plane (E⊥Z) of polarization.

Polymorphs	α(ω) (E||X)	α(ω) (E⊥Z)	σ(ω) (E||X)	σ(ω) (E⊥Z)
Pa$\stackrel{-}{3}$-697	8.8 eV(3.4) 12.1 to 15.8	--	8.8, 10.7 to 12.8	--
P42/mnm-rutile	8.1 11.3 to 14.8	10.8, 11.9 to 16.8	7.9, 11.01	9.3, 11.1
Pnnm (58) -CaCl2	9.2 13.1 to 17.5	9.2 13.1 to 17.5	8.2, 11.1, 13.4	10.7, 10.8, 15.0
Pbcn (60) -PbO2	9.9 to 13.3, 14.4	11.77, 14.5	11.4, 16.1	10.3, 15.5 to 17.8
Pbca (61)-ZrO2	9.9, 14.2 to 19.3	10.3, 14.2 to 19.3	9.1, 11.8 to 13.8	9.1, 11.8 to 13.8
Pnma	7.7, 13.2 to 19.1	7.7, 13.1 to 19.1	7.8, 10.8 to 13.4	7.8, 10.8 to 13.4
I4/m (87)	11.4, 14.4	10.07 to 12.5, 14.4	10.5	9.4

Table 1. The absorption and the conductive intense peak of the SnO₂ polymorphs along in-plane (E||X) and out-of-plane (E⊥Z) of polarization.

Polymorphs	α(ω) (E||X)	α(ω) (E⊥Z)	σ(ω) (E||X)	σ(ω) (E⊥Z)
Pa$\stackrel{-}{3}$-697	8.8 eV(3.4) 12.1 to 15.8	--	8.8, 10.7 to 12.8	--
P42/mnm-rutile	8.1 11.3 to 14.8	10.8, 11.9 to 16.8	7.9, 11.01	9.3, 11.1
Pnnm (58) -CaCl2	9.2 13.1 to 17.5	9.2 13.1 to 17.5	8.2, 11.1, 13.4	10.7, 10.8, 15.0
Pbcn (60) -PbO2	9.9 to 13.3, 14.4	11.77, 14.5	11.4, 16.1	10.3, 15.5 to 17.8
Pbca (61)-ZrO2	9.9, 14.2 to 19.3	10.3, 14.2 to 19.3	9.1, 11.8 to 13.8	9.1, 11.8 to 13.8
Pnma	7.7, 13.2 to 19.1	7.7, 13.1 to 19.1	7.8, 10.8 to 13.4	7.8, 10.8 to 13.4
I4/m (87)	11.4, 14.4	10.07 to 12.5, 14.4	10.5	9.4

3.2.4. Reflectivity spectra

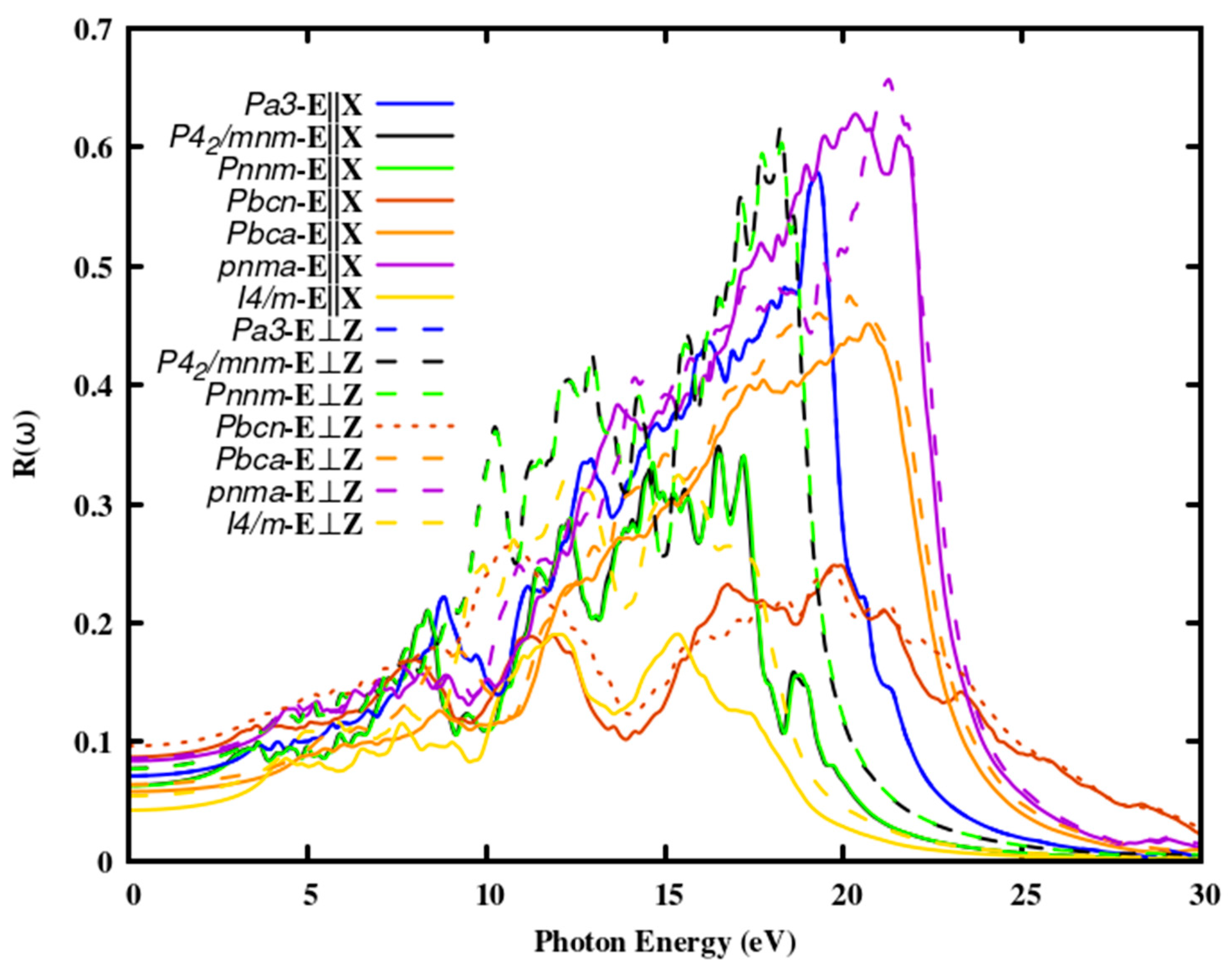
The selection of effective photovoltaic materials highly depends on their optical reflectance. The limit for the percentage of reflectivity in photovoltaic (PV) cells depends on the specific application and the technology used to manufacture the PV cells. Generally, a lower reflectivity is desirable to maximize the absorption of sunlight and improve the efficiency of the PV cell. For silicon-based PV cells, the industry standard is to aim for a reflectivity of less than 10 % in the visible spectrum (400-700 nm). This is achieved through the use of anti-reflective coatings or textures on the surface of the cell. In Figure 4, the reflectivity of the SnO₂ polymorphs is illustrated. In the visible and UV regions, the reflectance of SnO₂ polymorphs was detected to be high and lower in the near IR region.

The fact that the reflectivity of polymorph I4/m is the lowest among the six polymorphs suggests that the polymorph's transmittance or absorption is high and that it may be more transparent than the experimental polymorph P4₂/mnm. The reflectivity of the rutile polymorph is 11.12 % and the newly identified I4/m polymorph is 4.13 % at ω = 0. Which reveals that I4/m SnO₂ has the least reflectivity among all the oxides at zero photon energy. The reflectivity reaches about 20 % to 60 % towards the higher energy region of about 20 eV thus these polymorphs are a potential candidate as coating materials. Consequently, all polymorphs have a similar reflectivity pattern, although the intensity might vary between 3 and 25 eV. In this range, oscillations in reflectance up to 25 eV were detected. In the infrared and visible spectral ranges, SnO₂ polymorphs exhibit less than 15 % reflectivity; hence, they could be employed as an effective anti-reflective coating.

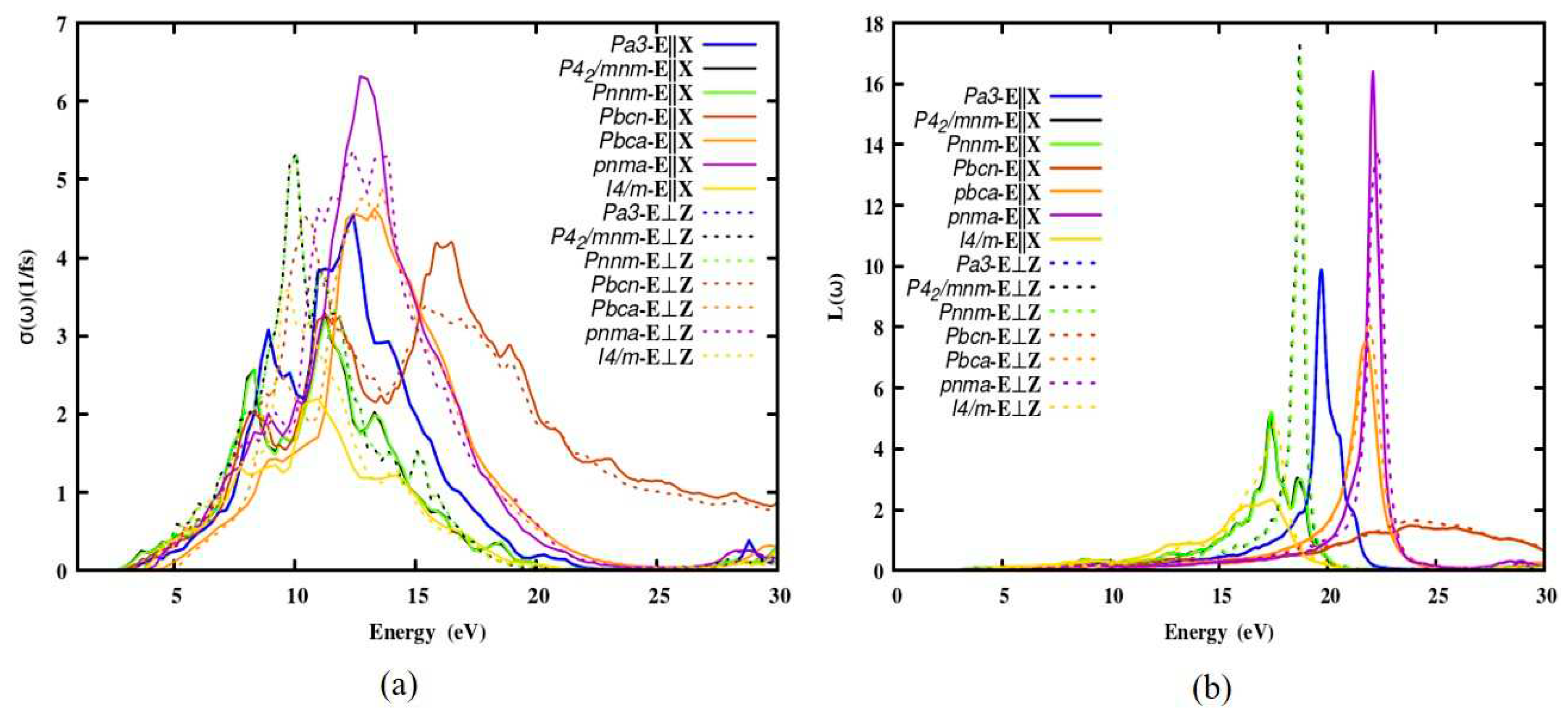
3.2.5. The optical conductivity and energy loss function

The optical conductivity and the energy loss spectra of the polymorphs were computed which are given in Figure 5. The first peak was observed near 8.6 eV, and the second peak was observed at 12.4 eV. For all the polymorphs no deviation in the optical conductivity along parallel and perpendicular polarization. Interband, intraband and plasma interactions are all defined by the electron energy-loss function (ELF). The energy is lost by a fast-moving electron through the medium. Also, the electron’s inelastic scattering is related to the energy-loss function. No loss has been observed below the optical bandgap of the polymorphs. The loss appears where there is a transition between the valence and conduction band, keeps on increasing, reaches its maximum and then comes down. The loss L (ω) of the polymorphs approaches maximum at 17.3(17 eV), 16.5(22 eV) for Pnnm and Pnma polymorphs. The polymorph Pbcn has the lowest loss function among the seven polymorphs. The change in the reflectivity arrives due to a sharp peak in the loss spectra.

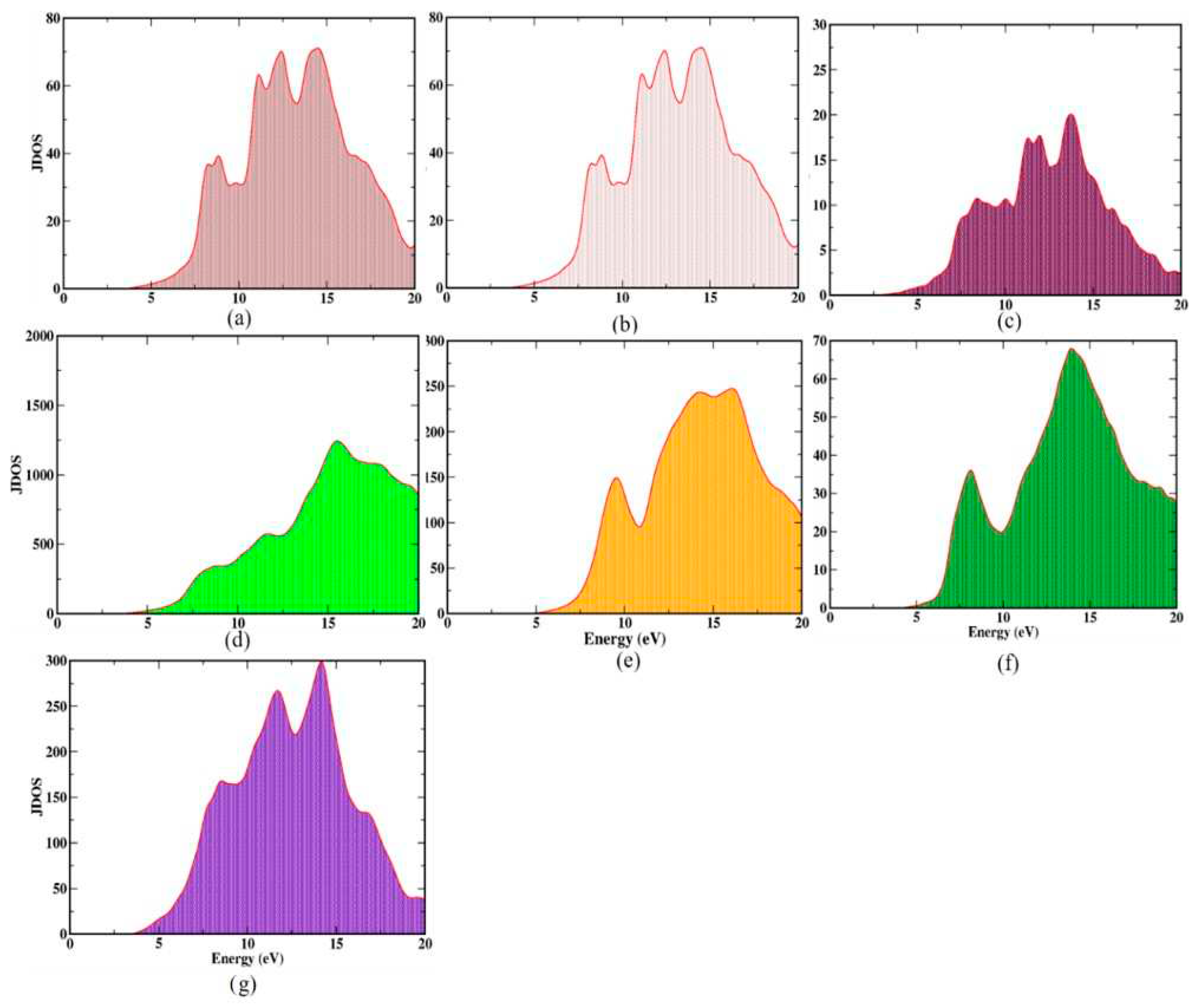
3.3. Optical joint density of states

The optical joint density of states (OJDOS) represents the number of states with which photons can interact; it simultaneously accounts for states in the VBM and CBM that are separated by energy hυ. Hence, the JDOS of SnO₂ polymorphs provides information on the number of absorption and emission states of the crystals Figure 6, shows shows the OJDOS of SnO₂ polymorphs which gives the information on both interband and intraband contribution. It possesses one broad peak from approximately 3.6 to 20 eV for all the polymorphs.

A closer examination of the broad peak reveals multiple overlapping 7-15 eV, indicating more closely spaced optical states in this region for Pa$\stackrel{-}{3}$ , P4₂/mnm and Pnnm polymorphs. Pnnm polymorph has more available optical states. Pbcn, Pbca, Pnma and I4/m polymorphs possess comparably lower optical states. In addition, among the seven polymorphs, due to its indirect bandgap, Pbcn has a stronger intraband transition contribution. In general, the electronic energy levels include both vibrational and rotational states, which results in the fine structural splitting of spectra. Consequently, these overlapping states may consist of a combination of several vibrational and rotational modes. In addition, these states are all present in the ultraviolet spectral region.

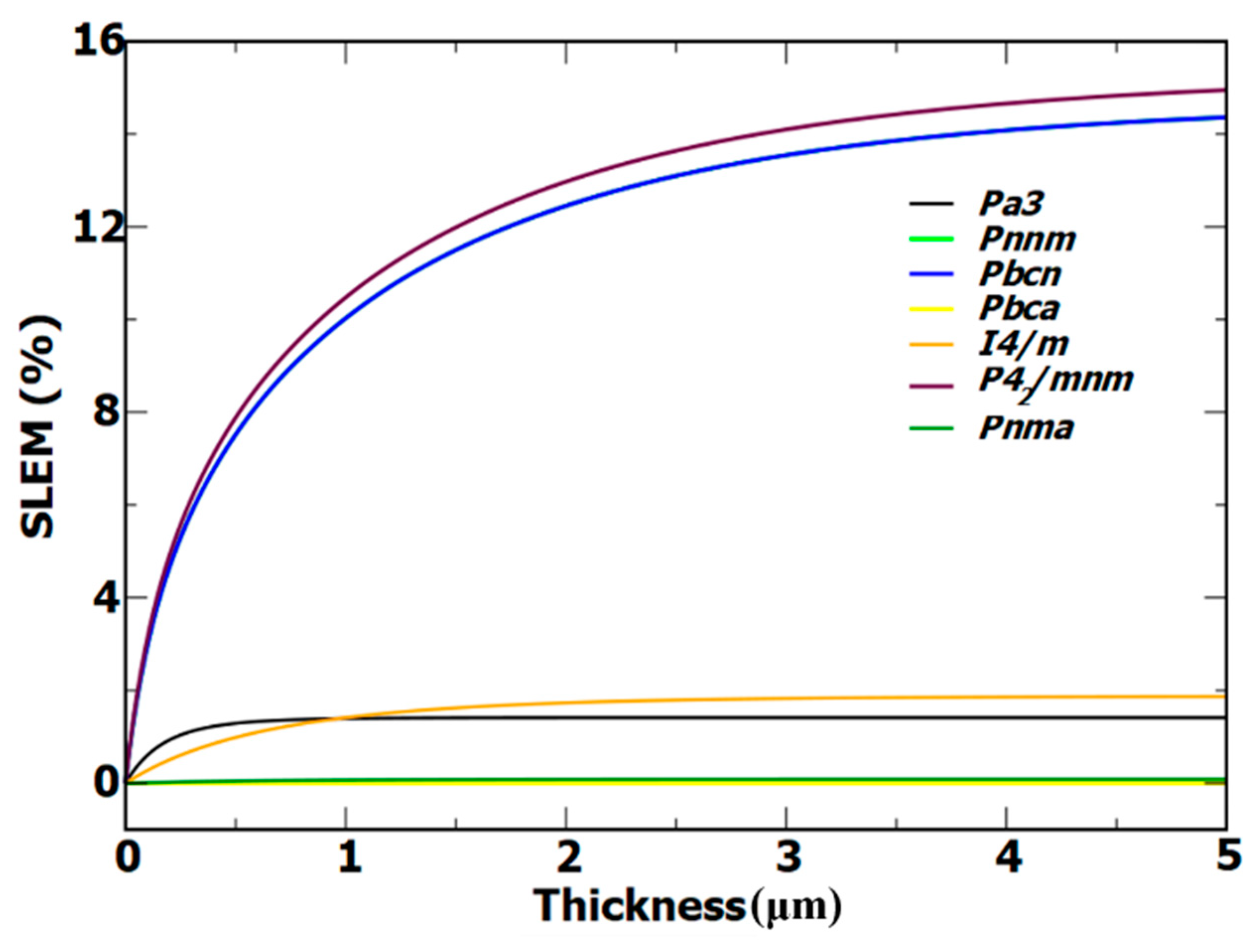
3.4. SLEM

We computed the SLME of the SnO₂ polymorphs as a function of film thickness, as shown in Figure 7. Which gives the ratio between the maximum output power density and the total incident solar energy density. In the area of photovoltaics, the Shockley-Queisser (SQ) limit can be used to calculate absorber energy efficiency; this is essential. SQ limit offered for p-n junction PV absorbers efficiency limit by numerical calculation ⁴². SLME is also an important measure for evaluating the photovoltaic absorber capabilities of materials. The SLME incorporates the leading mechanics of absorption, emission and recombination characteristics, resolving a range of efficiencies for materials with the same gap. SLME of SnO₂ polymorphs can depend on the film thickness. However, there is no specific thickness at which the SLME is optimized, as it can vary depending on the specific polymorph and other factors such as the dopants used and the deposition method. Chen et al. synthesized the SnO₂ thin films using a low-temperature solution processing method and evaluated their performance in terms of the SLME and overall photovoltaic performance. The authors found that the SnO₂ thin films had an SLME of 4.6 %, which was comparable to the SLME of TiO₂ and higher than that of ZnO. However, at a reference film thickness of 2 μm, P4₂/mnm approaches 13 % efficiency and Pnnm, Pbcn approach 12.4 % efficiency. The efficiencies of the two polymorphs, Pnnm and Pbcn are comparable, to the efficiency of the experimental polymorph P4₂/mnm. The polymorphs I4/m, Pa$\stackrel{-}{3}$ has 2 % and 1.4 % efficiency respectively hence these polymorphs were not suitable for the absorber layer. SLME efficiency of the polymorphs was listed in Table 5. The efficiency of SnO₂ polymorphs is comparable to that of organic solar cells. P4₂/mnm, Pnnm and Pbcn are excellent absorber layer materials for solar cells. These polymorphs efficiencies were comparable with chalcopyrite structures ⁴³. Also, the perovskite solar cells Cs₈Ag₂Cu₂Bi₄Cl₂₄ efficiency differs from our calculated efficiency by 20 % ²⁷.

Table 2. Comparison of SLEM of SnO₂ polymorphs at 2 μm thickness.

Polymorphs	SLME (%)
Pa$\stackrel{-}{3}$	1.3
P42/mnm	13.3
Pnnm (58)	12.2
Pbcn (60)	0.1
Pbca (61)	12.2
Pnma (62)	0.1
I4/m (87)	1.8

Table 2. Comparison of SLEM of SnO₂ polymorphs at 2 μm thickness.

Polymorphs	SLME (%)
Pa$\stackrel{-}{3}$	1.3
P42/mnm	13.3
Pnnm (58)	12.2
Pbcn (60)	0.1
Pbca (61)	12.2
Pnma (62)	0.1
I4/m (87)	1.8

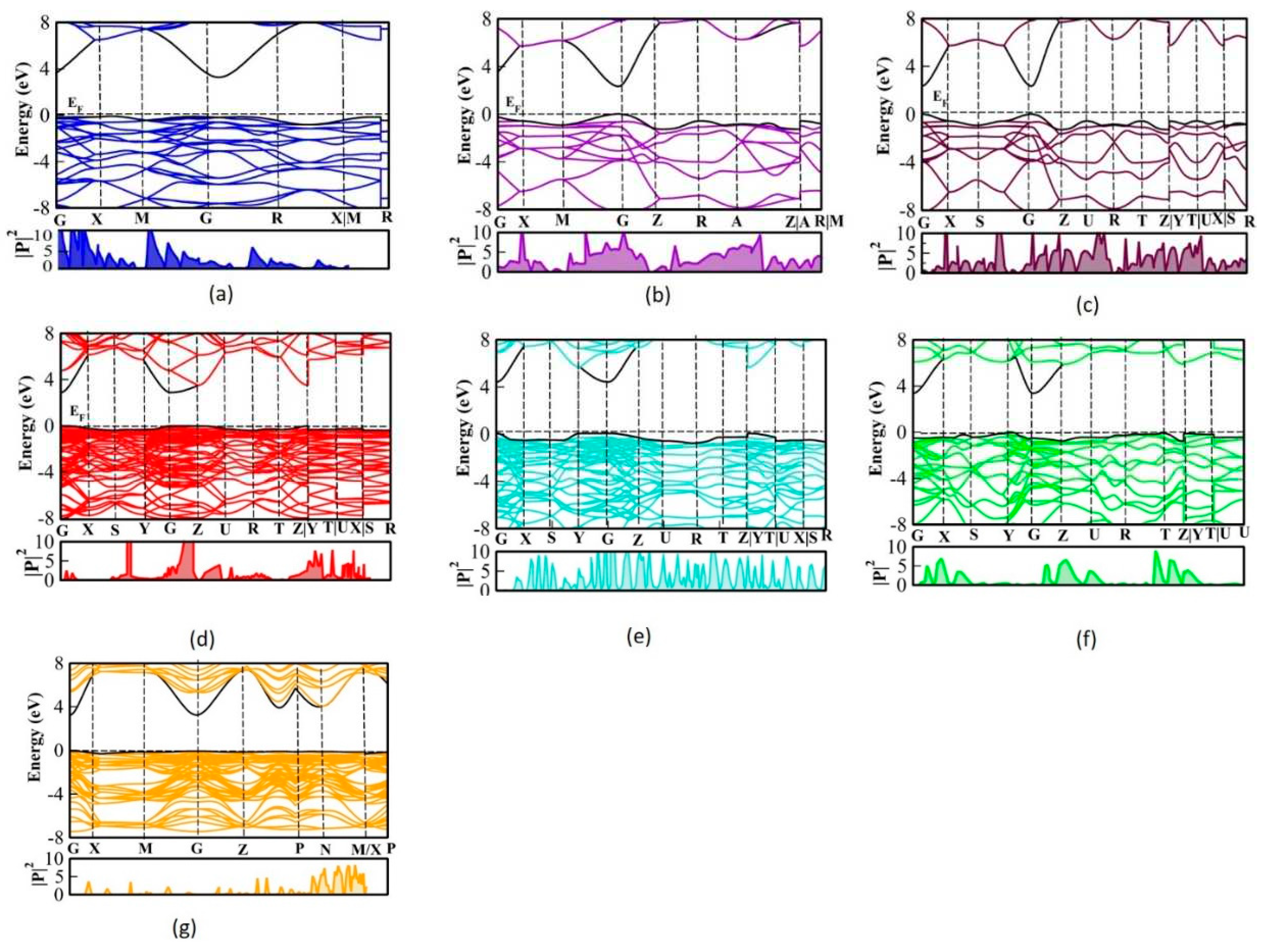
3.5. Transition dipole moment of SnO₂ polymorphs

TDM anticipates the probability of transition from valence band states to conduction band states. Figure 8, demonstrates the TDM of the SnO₂ polymorphs. The TDM of the polymorph Pa$\stackrel{-}{3}$ shows the indirect transition from G-X and G-M hence the probability is dominant in this region. The polymorph P4₂/mnm and Pnnm have occurred direct transition at G so the probability at this point is predominant compared to other high symmetric points. Pbcn and Pbca have more number of atom in a unit cell hence the bands are dense, but TDM is different for these two polymorphs Pbcn is indirect and Pbca has a direct transition. In addition, at G-Z the TDM of Pbcn has a strong transition probability. The plot reveals that the polymorph Pnma is extremely directional dependent; hence, if this polymorph is formed as a crystal on a particular stable plane, it will become a photovoltaic material with high efficiency. But for Pbca in all the planes the crystal will grow well it is directional independent. Also, the band is very narrow in these polymorphs so there are many peaks arises. From the k-points Z-T, the conduction band is flat and the valance band is parabolic hence the peaks are sharp.

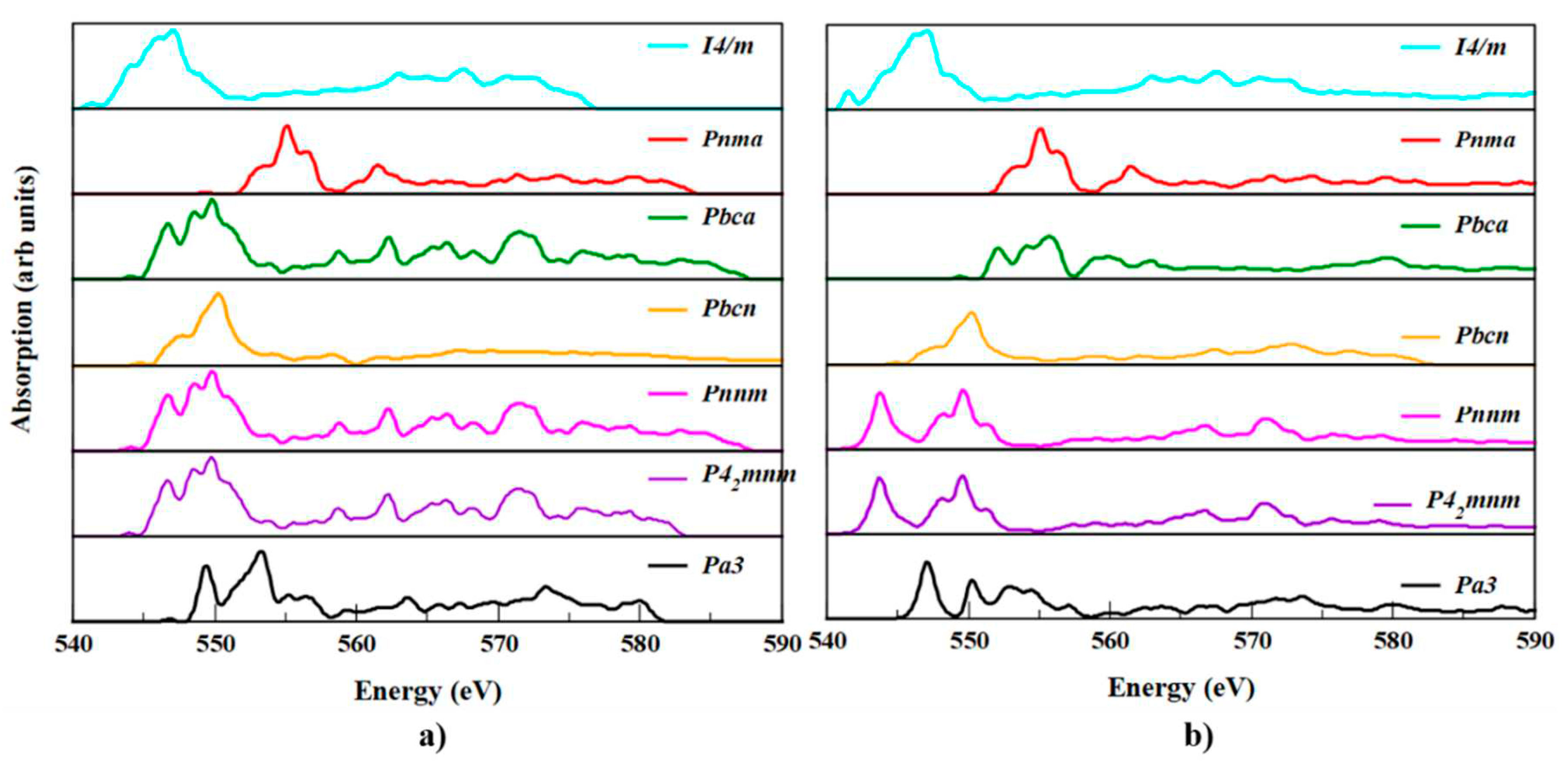
3.6. XANES spectra of SnO₂ polymorphs

XANES is a powerful experimental technique used to study the local electronic and atomic structure of materials. However, the interpretation of XANES spectra can be complex and challenging due to the complex nature of the physical processes that occur during X-ray absorption. Therefore, computational methods such as DFT are often used to help interpret and analyze XANES spectra. XANES can be used to guide the design of new materials with specific electronic and atomic structures. Computational methods can help predict XANES spectra for hypothetical materials, which can then be used to guide the synthesis and characterization of new materials with desired properties. In the present work, we reported XANES for SnO₂ polymorphs for the first time. Figure 9, shows a comparison between the calculated Sn-K edge and O-K edge spectra for SnO₂ polymorphs. From the XANES spectra, a comprehensive analysis of the electronic structure and geometry of the polymorphs was accomplished. The peaks at the k-edge of the metal in Figure 9 (a), shows show an electronic transition from the Sn 3d-core level to the 2p state and the f state in the conduction band. Each polymorph has a unique bonding type, which may be deduced from the subtle but observable shift in the peaks.

Different types of local environments for Sn can be seen in the pre-edge XANES of SnO₂ polymorphs due to the separation of the peaks. Though P4₂/mnm and Pnnm polymorphs have similar spectra, the energy difference in the prominent peak was 0.01 eV. Except for Pa$\stackrel{-}{3}$ and Pnma polymorphs remaining, the polymorphs has three peak in the lower energy pre-edge region near 546, 548 and 548 eV due to increasing distortion of the octahedral environment of Sn with O. But for the Pnma case it appears at 553, 554, 557 eV. The absorption edge of the I4/m polymorph is 545 eV and we noticed from the spectra that the absorption edges of the seven SnO₂ polymorphs were not much deviated. The absorption edge of Pmna is deviated from P4₂/mnm by 0.9 %, which is the maximum deviated polymorph. Because of this, the Sn⁴⁺ oxidation state predominates in all of the different polymorphs. Furthermore, distinct occupancy of tetrahedral and octahedral sites is possible in such phases during doping in the core polymorphs. Likewise, Figure 9 (b), depicts the oxygen geometry of polymorphs.

4. Conclusion

This study is the first to investigate the optical characteristics of seven SnO₂ polymorphs for their potential use as an energy material. The results obtained for the optical properties were summarized as follows.

• The effective mass of electrons and holes in SnO₂ polymorphs is affected by the crystal structure and orientation of the material. As a result, the effective mass can differ when measured along different axes. For instance, the P4₂/mnm and Pnnm polymorphs have lower effective mass compared to other polymorphs, making them more electronically conductive.
• HSE06 is the best functional to describe the optical properties of these materials based on the findings.
• The dielectric functions of the SnO₂ polymorphs were analyzed and different polarization due to the anisotropy of the polymorphs was discovered, varying from 3 % to 11 % in the lower energy range, but it will not affect device fabrication.
• The dielectric constants of the polymorphs I4/m and P4₂/mnm were found to be lower than TiO₂, HfO₂ and ZrO₂, making them the best ETL material compared to other oxides.
• The refractive index of the polymorphs was scattered from 1.5 to 1.8, making it a TCO in solar cells.
• SnO₂ polymorphs can be used as antireflective coatings due to their reflectance of less than 15 % in the infrared and visible spectral regions, especially the newly identified I4/m polymorph with more transparency than rutile.
• The SLME efficiency of P4₂/mnm, Pnnm and Pbca polymorphs is comparable to AgGaSe₂ and CuGaS₂.
• The XANES spectrum revealed structural differences between polymorphs, which can aid in their synthesis. The research on XANES is anticipated to help in the synthesis of many SnO₂ polymorphs.