A Data Fusion Approach to Assessing the Contribution of Wildland Fire Smoke to Fine Particulate Matter in California

1. Introduction

Airborne particles are a serious environmental health risk globally, contributing in excess of 7 million premature deaths each year [1]. Fine particulate matter (PM${}_{2.5}$, particles with a diameter of less than 2.5 micrometers) has been causally linked to cardiovascular morbidity and mortality [2] and are therefore regulated under the provisions of the Clean Air Act [3] to protect human health and wellbeing. As a result, the emissions of PM${}_{2.5}$ from many antropogenic sources, such as transpiration and industry, have been on a steady decline [4] and wildfires have become the single largest source [5], potentially off setting reduction in emissions from other sources.

High concentrations of fine particles and gasses found in smoke have also produced alarming impacts on health [6,7]. During peak wildfire seasons, smoke exposure can exacerbate health problems, causing a spike in emergency department visits [8]. In an epidemiological study of health impacts, [9] estimated that 2.2 % of annual respiratory health burden, or 92 ED visits per 100,000 people, is attributed to ambient PM and that wildfire days account for over 15% of that burden. However, providing a definite answer as to how much of particle pollution can be attributed to wildfires remains a challenging problem because instruments measure a total ambient concentration which is composed of natural, anthropogenic, and wildfire sources.

Previous research has studied the contribution of wildfires on PM${}_{2.5}$ concentrations by integrating remote sensing data on the location and extend of smoke plumes and PM${}_{2.5}$ readings from Air Quality System (AQS) monitors deployed by the Environmental Protection Agency (EPA). These studies revealed that wildfires contribute to 40% of unhealthy days and substantially increase PM${}_{2.5}$ concentrations [10,11]. Wildfire smoke impacts are dynamic and often affect areas without a monitoring station, as AQS monitors have limited spatial coverage due to the high cost and difficulty in installation. It is important to make air quality information available to the public quickly during wildfires, therefore AQS alone provides insufficient data source for monitoring wildfire emissions.

The increased incidence of days with poor air quality due to wildfires has created a demand and public interest for monitoring particulate pollution. Perhaps the most prevalent sensors are PurpleAir (PA), which are installed by members of the public, providing a near real-time monitoring of PM${}_{2.5}$ with extensive spatial coverage [12]. However, it is known that PA sensors are less reliable compared to the AQS, and thus correction to the sensor readings is needed [13,14]. [15] developed a correction equation using meteorological conditions including relative humidity and temperature, as both measurements affect the accuracy of the instrument; however, this calibration is developed for a US-wide correction and without smoke impacts. Another simple linear correction model under smoke impacted conditions was proposed in [16]. As the sensor performance can be affected by geographic and environmental conditions, it is more reasonable to relax the assumption of a constant spatially varying bias, but rather capture the spatiotemporally varying bias.

Smoke impacts are dynamic and often affect areas without a monitoring station, as AQS monitors have limited spatial coverage. Previous studies have either separated anthropogenic PM from smoke emissions using chemical transport models or by subtracting out historically observed averages [17]. However, neither approach provides a definite answer as to how much of particle pollution can be attributed to wildfires. Data fusion is a widely used method that integrates information from different types of sensors to provide a robust and complete description of a process of interest [18,19]. It has been used extensively to estimate spatially and temporally resolved air quality surfaces. For example, [20,21,22,23] use data fusion method to study the complex relationship between monitoring data and outputs from Community Multi-Scale Air Quality (CMAQ), a deterministic chemical transport model. [24] combines observations from two noisy datasets to predict the true aerosol process. More recently, several researchers have exploited the usefulness of low-cost sensors such as Purple Air to map air quality and quantify the uncertainty of estimation [25,26,27]. Most similar to our approach is Stein et al (2005), who also use a spectral transformation in time and spatial processes to capture dependence between stations for a single fixed monitoring network [28]. We extend this approach to handle multiple data networks.

This study aims to provide an estimate of wildfire contribution on air quality by supplementing the remotely sensed smoke plume indicators with PurpleAir data. We propose a multi-resolution Bayesian approach fusing information from both AQS monitors and PA sensors to estimate the contribution to PM${}_{2.5}$ caused by wildfires. We apply a Discrete Fourier Transform (DFT) to account for temporal correlation, transforming the data from the time domain to the frequency domain, and model the spatial correlation in the frequency domain. To quantify the relative increase in PM${}_{2.5}$ concentrations due to wildfires, we propose regression and matching estimators, as discussed in Section 2.3. Our findings will not only enhance understanding of the relationship between wildfires and air pollution but also inform policy and decision-making related to wildfire management, public health, and climate change impacts.

The remainder of this paper is structured as follows: In Section 2, we present an overview of the Hazard Mapping System (HMS) and its smoke plume data. We also delve into the specifics of the AQS and PurpleAir sensors, contrasting their features and functionality. The latter part of Section 2 elucidates our use of the Discrete Fourier Transform (DFT) and the data fusion model, with detailed insights into our Markov Chain Monte Carlo (MCMC) approach. Section 3 presents our findings, including the estimated smoke plume parameters and the calculated contribution of wildfires to PM${}_{2.5}$ concentrations, as determined by both regression and matching estimators. We also offer a comparison of various models, illustrating the effectiveness of the PurpleAir sensors and the benefits of our proposed data fusion method. Finally, in Section 4, we discuss the implications of our findings, the limitations of our study, and potential directions for future research.

2. Materials and Methods

2.1. Data sources and exploratory analysis

Our analysis incorporates data from three distinct sources: satellite-derived smoke plume indicators obtained through the National Oceanic and Atmospheric Administration’s Hazard Mapping System (HMS), PM${}_{2.5}$ measurements from Air Quality System (AQS) monitoring stations, and PM${}_{2.5}$ readings from PurpleAir (PA) monitoring stations. We collect hourly data and average them to daily level from each source for 2020 and 2021 fire seasons, spanning July 1 to October 31. The original PM${}_{2.5}$ readings from both AQS and PA stations are right-skewed so we apply log-transformation to all PM${}_{2.5}$ readings.

2.1.1. Satellite-derived smoke plume indicators

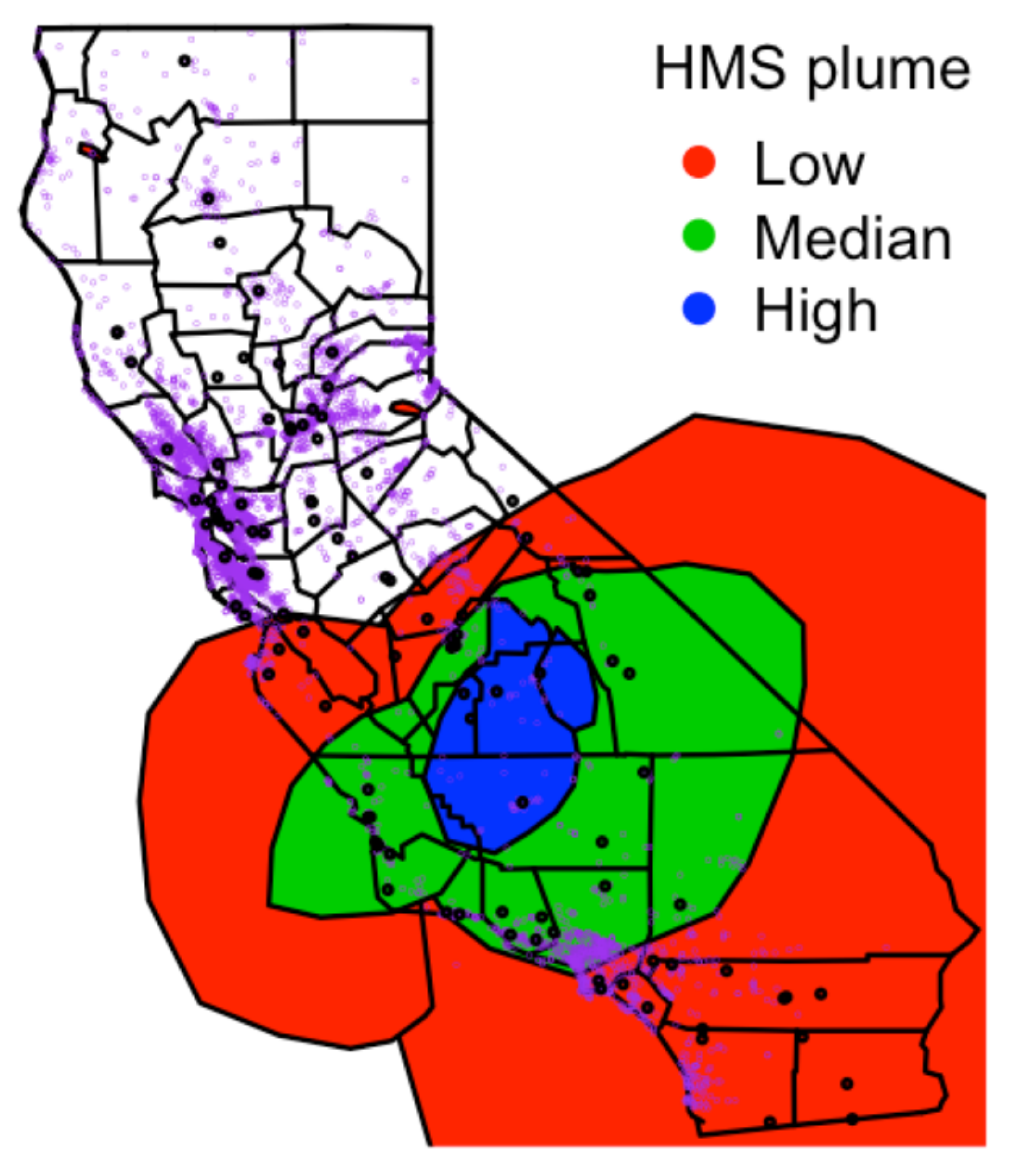
Exposure to wildland fire smoke is assessed using smoke plume indicators supplied by the Hazard Mapping System (HMS) [29]. This automated data product integrates observations from multiple polar and geostationary satellites to generate daily polygons representing smoke plume extents in near-real time. Distinct polygons are provided for low-, medium-, and high-density plumes. Figure 1 shows the HMS smoke plumes for September 20, 2021. These smoke plume indicators tend to underestimate the actual intensity of smoke, as they primarily rely on satellite imagery with an approximate spatial resolution spanning several miles [30]. Additionally, smoke visibility is limited to daytime hours, resulting in a significant underestimation of smoke levels during the night.

2.1.2. AQS monitoring stations

The Air Quality System (AQS) monitoring stations, deployed by the US Environmental Protection Agency (EPA) and state, local, and tribal air pollution control agencies, provide precise PM${}_{2.5}$ measurements. However, their distribution is spatially sparse due to the high cost and complexity associated with their installation and maintenance. The black dots in Figure 1 depict the distribution of AQS monitoring sites across California in 2021. 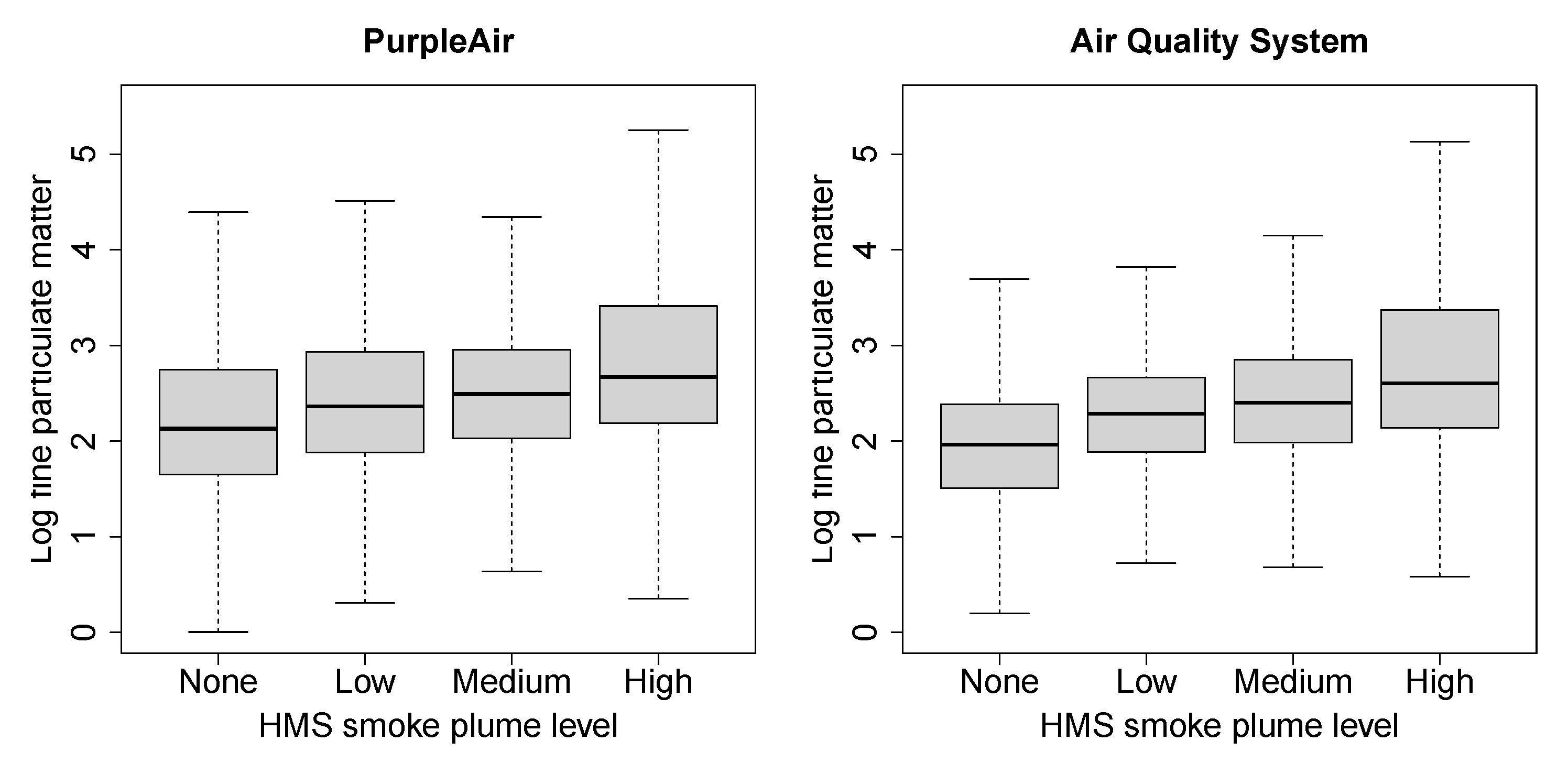Figure 2 illustrates the distribution of PM${}_{2.5}$ levels, aggregated across stations, by smoke plume intensity.

2.1.3. PurpleAir sensors

PurpleAir (PA) sensors are low-cost monitoring devices deployed by individuals and organizations for continuous ambient air pollutant tracking. Despite their affordability and ease of installation, PA sensors offer less accurate PM${}_{2.5}$ readings and are significantly influenced by environmental factors, such as temperature and humidity [15]. We use bias corrected data for all analyses. However, this initial bias correction based on [15] may be insufficient because it only depends on a linear trend in temperature and humidity and is constant across space and time. Therefore, our Bayesian data fusion model adds a more flexible spatiotemporal bias correction term.

In 2021, more than 7,800 outdoor PA sensors were operational in California. The purple dots in Figure 1 represent the distribution of PA monitoring sites throughout the state. We have included only those PA stations that reported fewer than 18 missing days during the fire seasons, resulting in a total of 1,080 for 2020 and 712 PA stations for 2021. Figure 2 displays the distribution of PM${}_{2.5}$, aggregated across stations for 2021, by smoke plume intensity. A similar pattern is observed in both PA stations and AQS stations where PM${}_{2.5}$ measurements escalate in the presence of a smoke plume.

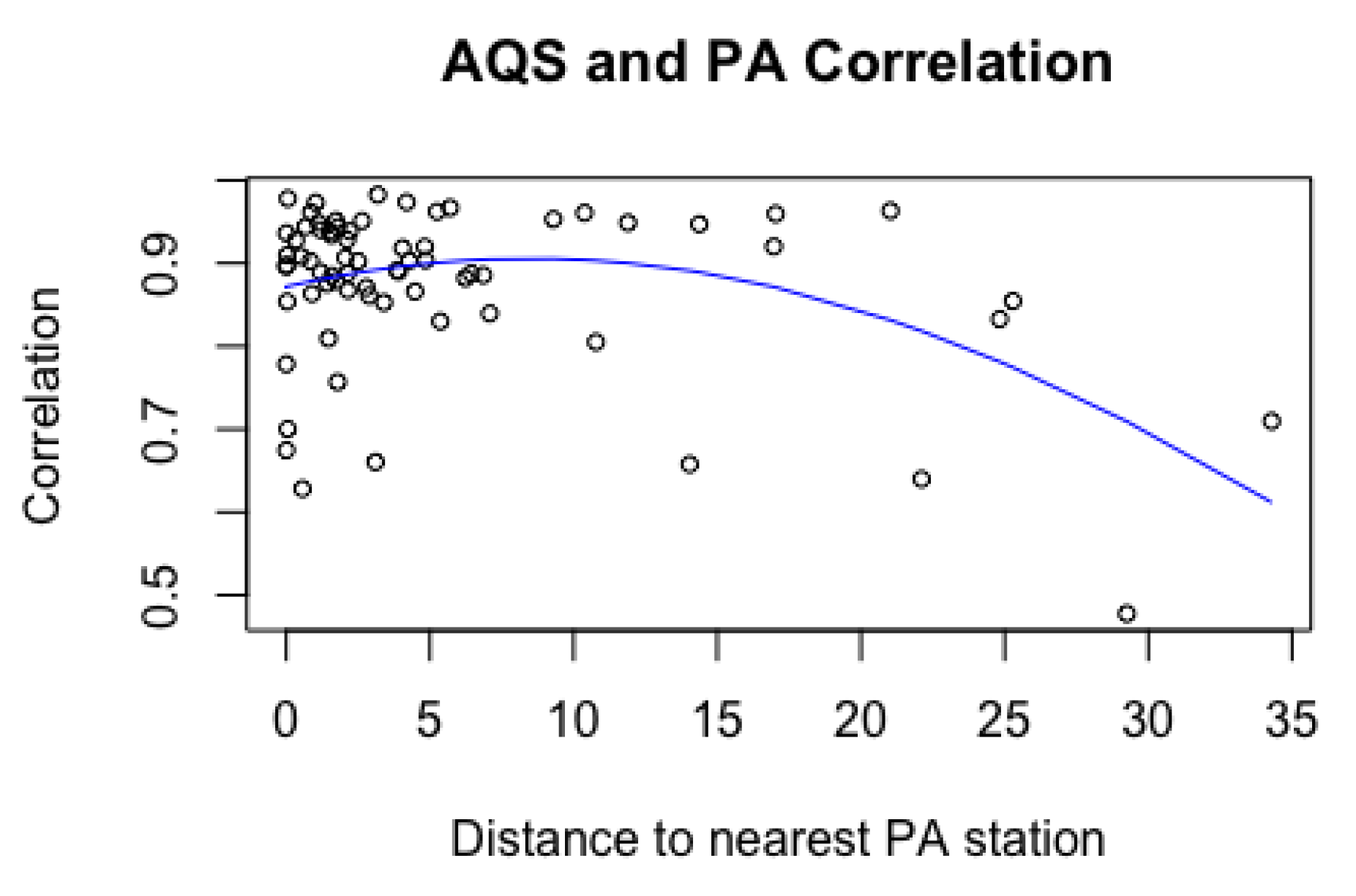
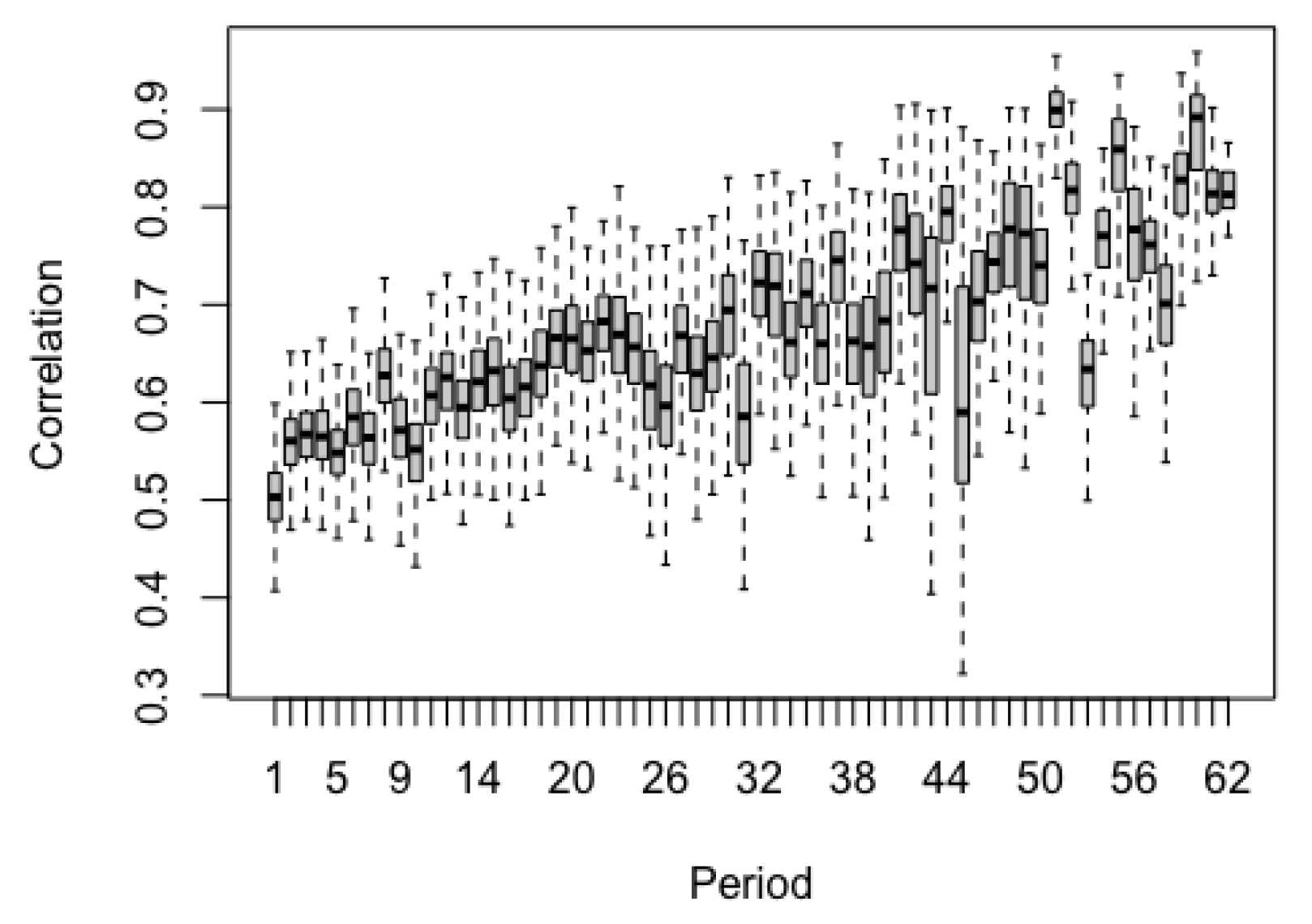
Figure 3 investigates the relationship between AQS stations and their corresponding nearby PA sites. Each point in Figure 3 symbolizes one AQS station. For every AQS station, we pinpoint the closest PA station and calculate the sample correlation between the daily PM${}_{2.5}$ measurement series for these two locations. We can see that the correlation is generally high for nearby stations and decreases with distance, suggesting that PA data will be a useful supplement to the spatial model.

2.2. Statistical model

We propose a multi-resolution Bayesian model for modeling AQS and PA measurements jointly in the spectral domain. Let $Y_{1t}\left(\mathsf{s}\right)$ and $Y_{2t}\left(\mathsf{s}\right)$ be AQS and PA measurements, respectively, for spatial location at time (day) $t\in \{1,...,n_t\}$, and ${\mathsf{X}}_t\left(\mathsf{s}\right)=\{X_{0t}\left(\mathsf{s}\right),...,X_{pt}\left(\mathsf{s}\right)\}$ be a corresponding vector of covariates with $X_{0t}\left(\mathsf{s}\right)=1$ for the intercept. The $p=5$ covariates are temperature, relative humidity and indicators of low, medium and high density smoke plumes at site S and day t. We note that temperature and relative humidity are standardized to have mean zero and variance one and that the AQS and PA measurements are not taken at the same spatial locations.

The observations are decomposed as $Y_{jt}\left(\mathsf{s}\right)=Z_{jt}\left(\mathsf{s}\right)+{\epsilon }_{jt}\left(\mathsf{s}\right)$ for $j\in \{1,2\}$, where $Z_{1t}\left(\mathsf{s}\right)$ and $Z_{2t}\left(\mathsf{s}\right)$ are spatiotemporal processes, and ${\epsilon }_{jt}\left(\mathsf{s}\right)\stackrel{\mathit{indep}}{~}Normal(0,{\tau }_j^2)$ is error. The time span of our data is relatively short, therefore, its reasonable to assume the spatiotemporal processes are stationary within the modeling period. We will apply Fourier transformation to the spatiotemporal processes $Z_{jt}\left(\mathsf{s}\right)$ with respect to time to remove the temporal dependence. The resulting spectral processes $Z_{jl}^{*}\left(\mathsf{s}\right)$ capture periodicity, are independent over frequency $\{{\omega }_l,l=1,...,n_t\}$ and spatially correlated. For time series observed at equal time intervals, we can apply the discrete Fourier transformation (DFT). The spectral processes at frequency ${\omega }_l$ is

$$Z_{jl}^{*}\left(\mathsf{s}\right)=\sum _{t=1}^{n_t}exp(-it{\omega }_l)Z_{jt}\left(\mathsf{s}\right)$$

(1)

and measures the variation in $Z_{jt}\left(\mathsf{s}\right)$ at frequency ${\omega }_l$. Terms with small ${\omega }_l$ (low frequency) represent long-term trends such as month-to-month averages and terms with large ${\omega }_l$ (high frequency) represent short-term trends such as day-to-day variation. Let $\{Z_{j1}^{*}\left(\mathsf{s}\right),...,Z_{j{n}_t}^{*}\left(\mathsf{s}\right)\}$ be the unique real components of the DFT of $\{Z_{j1}\left(\mathsf{s}\right),...,Z_{j{n}_t}\left(\mathsf{s}\right)\}$ at frequencies $\{{\omega }_1,...,{\omega }_{n_t}\}$ with ${\omega }_1\le ...\le {\omega }_{n_t}$.

The spectral processes $Z_{jl}^{*}\left(\mathsf{s}\right)$ are dependent across $j=1,2$, as they represent the two networks measuring the same underlying PM${}_{2.5}$ process. They are also spatially dependent processes as locations nearby may exhibit similar periodicity. We model the cross network dependence and spatial dependence for each ${\omega }_l$ as

$$Z_{1l}^{*}\left(\mathsf{s}\right)=U_l\left(\mathsf{s}\right)\mathrm{and}{Z}_{2l}^{*}\left(\mathsf{s}\right)=A_l{U}_l\left(\mathsf{s}\right)+V_l\left(\mathsf{s}\right),$$

(2)

where spatial process $U_l\left(\mathsf{s}\right)$ is the true PM${}_{2.5}$ concentration. The PA stations are assumed to be measuring a biased and noisy version of the true PM${}_{2.5}$ with discrepancy $V_l\left(\mathsf{s}\right)$. The coefficient $A_l$ controls the dependence across networks. Both the bias $V_l\left(\mathsf{s}\right)$ and cross-dependence $A_l$ vary by ${\omega }_l$ to allow for a multi-resolution calibration of the two networks. We model $A_l$ linearly as $A_l={\beta }_{A0}+{\beta }_{A1}·{\omega }_l$, where ${\beta }_{A0}$ and ${\beta }_{A1}$ are unknown coefficients. This allows the correlation between the processes to vary stochastically with frequency. For example, if PA is more reliable for long-term trends than day-to-day variation, then we expect larger (smaller) correlation between networks for small (large) ${\omega }_l$.

The true process $U_l\left(\mathsf{s}\right)$ and discrepancy term $V_l\left(\mathsf{s}\right)$ are both regressed onto the covariates. Since we are developing a model in the spectral domain, we will also apply DFT to each covariate in ${\mathsf{X}}_t\left(\mathsf{s}\right)$ with respect to time and denote this as ${\mathsf{X}}_j^{*}\left(\mathsf{s}\right)=\{X_{0l}^{*}\left(\mathsf{s}\right),...,X_{pl}^{*}\left(\mathsf{s}\right)\}$ Define the covariates for the true process $U_l$ as ${\mathsf{X}}_{ul}^{*}\left(\mathsf{s}\right)={\mathsf{X}}_j^{*}\left(\mathsf{s}\right)$, containing all five covariates, and define ${\mathsf{X}}_{vl}\left(\mathsf{s}\right)=\{X_{0l}^{*}\left(\mathsf{s}\right),X_{1l}^{*}\left(\mathsf{s}\right),X_{2l}^{*}\left(\mathsf{s}\right)\}$ to include only temperature and relative humidity for bias correction [15]. We model $U_l\left(\mathsf{s}\right)$ and $V_l\left(\mathsf{s}\right)$ as independent (with each other and over l) Gaussian processes with means $\mathrm{E}\left\{U_l\left(\mathsf{s}\right)\right\}={\mathsf{X}}_{ul}^{*}\left(\mathsf{s}\right){\mathit{\beta }}_u$ and $\mathrm{E}\left\{V_l\left(\mathsf{s}\right)\right\}={\mathsf{X}}_{vl}^{*}\left(\mathsf{s}\right){\mathit{\beta }}_v$, variances $Var\left\{U_l\left(\mathsf{s}\right)\right\}={\sigma }_{ul}^2$ and $Var\left\{V_l\left(\mathsf{s}\right)\right\}={\sigma }_{vl}^2$, and spatial correlations $Cor\{U_l\left(\mathsf{s}\right),U_l\left({\mathsf{s}}^{\prime }\right)\}=exp(-||\mathsf{s}-{\mathsf{s}}^{\prime }\left|\right|/{\rho }_u)$ and $Cor\{V_l\left(\mathsf{s}\right),V_l\left({\mathsf{s}}^{\prime }\right)\}=exp(-||\mathsf{s}-{\mathsf{s}}^{\prime }\left|\right|/{\rho }_v)$.

The regression coefficients ${\mathit{\beta }}_v={({\beta }_{u0},...,{\beta }_{up})}^T$ control the effects of the covariates on the true PM${}_{2.5}$ process U. Although we specify the model in the spectral domain, the DFT is a linear operator and thus the covariates can be interpreted as usual in the spatial domain since the mean AQS response is

$$E\left\{Y_{1t}\left(\mathsf{s}\right)\right\}={\mathsf{X}}_t\left(\mathsf{s}\right){\mathit{\beta }}_u.$$

Therefore, ${\mathit{\beta }}_u$ is of primary interest. In particular, the components of ${\mathit{\beta }}_u$ that correspond to the smoke plume indicators are used to summarize the wildland fire contribution to PM${}_{2.5}$.

The regression coefficients ${\mathit{\beta }}_v={({\beta }_{v0},{\beta }_{v1},{\beta }_{v2})}^T$ control the effect of the covariates on the discrepancy term V, and thus the contribution of the covariates to the PA bias. By allowing the covariance parameters ${\sigma }_{ul}^2$ and ${\sigma }_{vl}^2$ to vary by frequency (l), we allow for a different degree of dependence between the networks at different temporal scales, with

$$Cor\{Z_{1l}^{*}\left(\mathsf{s}\right),Z_{2l}^{*}\left(\mathsf{s}\right)\}=\frac{A_l}{\sqrt{A_l^2+{\sigma }_{vl}^2/{\sigma }_{ul}^2}}.$$

(3)

The prior for the variance components is

$${\sigma }_{ul}^2\sim \mathrm{InvGamma}(a_{ul},b_{ul})\mathrm{and}{\sigma }_{vl}^2\sim \mathrm{InvGamma}(a_{vl},b_{vl}),$$

where the hyperparameters are modelled as log-linear in frequency, e.g., $log\left(a_{ul}\right)={\gamma }_{au1}+{\gamma }_{au2}·{\omega }_l$ the prior captures the intuition that the variance is higher in month-to-month variation than day-to-day variation, and the correlation between two sources vary over frequencies.

2.3. Quantifying the wildland fire contribution

To estimate the PM${}_{2.5}$ contribution from wildfire, given the estimated parameters above, we consider two metrics based on either regression or matching. For the regression metric, let ${\mathsf{X}}_t^0\left(\mathsf{s}\right)$ be the covariate vector with three plume indicators fixed at zero. For the matching estimator, define $\mathcal{P}\left(\mathsf{s}\right)$ as the set of days for which site s is in a smoke plume (any density) and $\overline{\mathcal{P}}\left(\mathsf{s}\right)$ as the set of non-plume days. We match each plume day with a non-plume day with similar meteorology and time period. Let ${\mathcal{A}}_t\left(\mathsf{s}\right)=\overline{\mathcal{P}}\left(\mathsf{s}\right)\cap \{t-30,...,t+30\}$ be the set of non-plume days within 30 days of plume day t. For each plume day, we selected the matching day $m_t\left(\mathsf{s}\right)$ as

$$m_t\left(\mathsf{s}\right){=}_{{\arg \min }_{d\in {\mathcal{A}}_t\left(\mathsf{s}\right)}}|{\mathrm{temp}}_t\left(\mathsf{s}\right)-{\mathrm{temp}}_d\left(\mathsf{s}\right)|+w|{\mathrm{humidity}}_t\left(\mathsf{s}\right)-{\mathrm{humidity}}_d\left(\mathsf{s}\right)|,$$

where w above is a scaling factor adjusting the magnitude of humidity and temperature, we set $w=1$ so that the best matching station has equal weights on temperature and humidity. Then at site s the estimated contribution from wildland fires per day are

• Regression estimator: ${\delta }_1\left(\mathsf{s}\right)=\frac{1}{n_t}{\sum }_{t=1}^{n_t}{\{{\mathsf{X}}_t\left(\mathsf{s}\right)-{\mathsf{X}}_t^0\left(\mathsf{s}\right)\}}_u$
• Matching estimator: ${\delta }_2\left(\mathsf{s}\right)=\frac{1}{n_t}{\sum }_{t\in \mathcal{P}\left(\mathsf{s}\right)}\{Z_{1t}\left(\mathsf{s}\right)-Z_{1t^{\prime }}\left(\mathsf{s}\right)\}$ for $t^{\prime }=m_t\left(\mathsf{s}\right).$

In the matching estimator, $Z_{1t}\left(\mathsf{s}\right)$ is the true PM${}_{2.5}$, the transformed pairs of $Z_{1l}^{*}\left(\mathsf{s}\right)$ in (2) obtained by inverse DFT, and thus this estimator accounts for spatiotemporal bias and correlation. Since the analysis is on the log-scale, we plot $exp\left\{{\delta }_1\left(\mathsf{s}\right)\right\}$ and $exp\left\{{\delta }_2\left(\mathsf{s}\right)\right\}$ which estimate the multiplicative effect, i.e., $exp\left\{{\delta }_1\left(\mathsf{s}\right)\right\}=1.05$ corresponds to a 5% increase in PM${}_{2.5}$ in the presence of a smoke plume.

2.4. Computational Algorithm

To complete the Bayesian model, we specify uninformative prior distributions for the model parameters. The regression coefficients have Gaussian priors ${\mathit{\beta }}_u{\mathit{\beta }}_v\sim \mathrm{Normal}(0,c^2{\mathbf{I}}_{p+1})$. The variance parameters have conjugate priors ${\tau }_j^2\sim \mathrm{InvGamma}(a,b)$. The hyperpameters have Gaussian priors ${\gamma }_{au1},{\gamma }_{au2},{\gamma }_{av1},{\gamma }_{av2}\sim \mathrm{Normal}(0,c^2)$. To give uninformative priors we set $a=b=0.01$ and $c=10$. Due to poor convergence, the dependence parameters ${\beta }_{A0}$ and ${\beta }_{A1}$ were fixed based on cross-validation to minimize mean squared prediction error for AQS stations.

The main computational bottleneck of spatial modeling is manipulating spatial covariance matrices to estimate the range parameters ${\rho }_u$ and ${\rho }_v$. Given the large size of the air pollution dataset, a reasonable simplification is to estimate the range parameters using variogram and then assume they are fixed for the purpose of fitting the final model. The estimated spatial range from variograms are ${\rho }_u=177$ and ${\rho }_v=111$ kilometers.

Given the range parameters are fixed, the remaining parameters are estimated using Markov Chain Monte Carlo (MCMC) methods. In particular, we perform Gibbs sampling steps for most parameters and Metropolis sampling for some hyperparameters. Missing values are addressed using Bayesian multiple imputation (refer to Appendix A for more information). We generate 8,000 posterior samples and discard the first 5,000 as burn-in. Convergence is monitored using trace plots. A simulation study is included in the Appendix to verify the algorithm produces reliable parameter estimates. Convergence plots for several representative parameters are shown in Figure A1 in the Appendix for the real data analysis.

3. Results

3.1. Summary of the fitted model

Table 1 gives the estimates of the regression coefficients for both the true process ${\beta }_u$ and bias correction term ${\beta }_v$. All three smoke plume levels positively affect PM${}_{2.5}$ concentrations, with high smoke plumes having the greatest impact, followed by medium and low smoke plumes. These results are consistent between 2020 and 2021. The bias correction terms, however, are not significant. Given that PurpleAir readings have already been corrected as per [15] using temperature and relative humidity, it is reasonable that these variable do not explain trends in bias. We note that our model does include more general spatiotemporal bias correction in $V_l\left(\mathsf{s}\right)$ and including this bias term leads to improved results, as discussed below.

Figure 4 plots the estimated wildland fire contribution both years and both metrics. The estimated wildland fire contribution ranges from a 1-3% increase in PM${}_{2.5}$, depending on the location. Both metrics yield similar estimates of contribution and spatial patterns. The impact of wildfires varies across the state and years. In 2020, both Northern and Central California experienced significant wildfire impacts, while only Northern California faced major effects in 2021. This is in line with the fact that 2020 had the highest frequency of wildfires across all states, whereas 2021 witnessed a single, massive wildfire in Northern California [31].

In addition to covariate effects, the data-fusion model provides an evaluation of the concordance between AQS and PA stations. Equation 3 defines the correlation between the two networks as a function of the spectral frequency, ${\omega }_l$. Figure 5 plots the correlation between AQS and PA by period, i.e., $1/{\omega }_l$. For example, period 7 (30) corresponds to variation that occurs on a weekly (monthly) scale. Figure 5 shows that the correlation between AQS and PA stations increases from short-term, such as day-to-day variation, to long-term, such as month-to-month variation. In the short-term, the correlation is lower since the readings are taken at different spatial locations and are subject to small scale variability. Over the long run, the correlation is higher as both sources estimate ambient unbiased PM${}_{2.5}$ readings.

3.2. Model Comparisons

To assess the effectiveness of integrating additional PurpleAir readings, we compared the proposed data-fusion model (“Data fusion”) with two simpler alternatives. The first uses only AQS data (“AQS only”) and discards the PA data (i.e., sets $A_l=0$ for all l). The second naively (“Naive”) combines AQS and PA data and treats them as a single source without spatiotemporal bias adjustment (i.e., sets $A_l=1$ and $V_l\left(\mathsf{s}\right)=0$ for all s, and includes an indicator variable in the regression term, ${}_u$, to distinguish two types of data).

The estimated parameters for each model, along with the corresponding posterior standard deviations, are presented in Table 2. Clearly, incorporating PurpleAir monitors significantly reduces the posterior standard deviation. For many of the parameters the reduction in uncertainty is striking, with the standard deviation being 2-4 times smaller for the data-fusion model. Also, with the AQS-only model, only high smoke plumes exhibit a significant contribution due to a higher standard deviation. In contrast, when merging AQS and PurpleAir data, both medium and high smoke plume levels show significant contributions.

Furthermore, to verify that our proposed methodologies not only improve parameter estimation but also lead to accurate PM${}_{2.5}$ predictions, we performed a 5-fold cross-validation for the three models. Their performance was compared based on three key metrics: Root mean squared error, 95% prediction coverage, and prediction variance. Detailed descriptions of the models and their results can be found in the Appendix. We find that the AQS-only and data fusion model produce fairly similar out-of-sample prediction accuracy, therefore the main benefit of including the PurpleAir data is reducing uncertainty in parameter estimates. Also, the Naive model gives a 50% largers RMSE and low coverage, emphasizing the need for a careful data fusion approach.

4. Discussion

In this study, we examine the impact of wildland fires on PM${}_{2.5}$ concentrations in California during the fire seasons of 2020 and 2021. To do this efficiently, we combine remotely-sensed smoke-plume indicators with AQS and PA measurement networks. To model the spatiotemporal correlation of PM${}_{2.5}$ concentration and relationship between AQS and PA monitors, we first transform the data from spatial domain to frequency domain, and then use a data-fusion approach to model spatial correlations while accounting for biases in the PA data. Furthermore, we use a Bayesian approach to compute posterior distributions of the quantities of interest to fully characterize uncertainty.

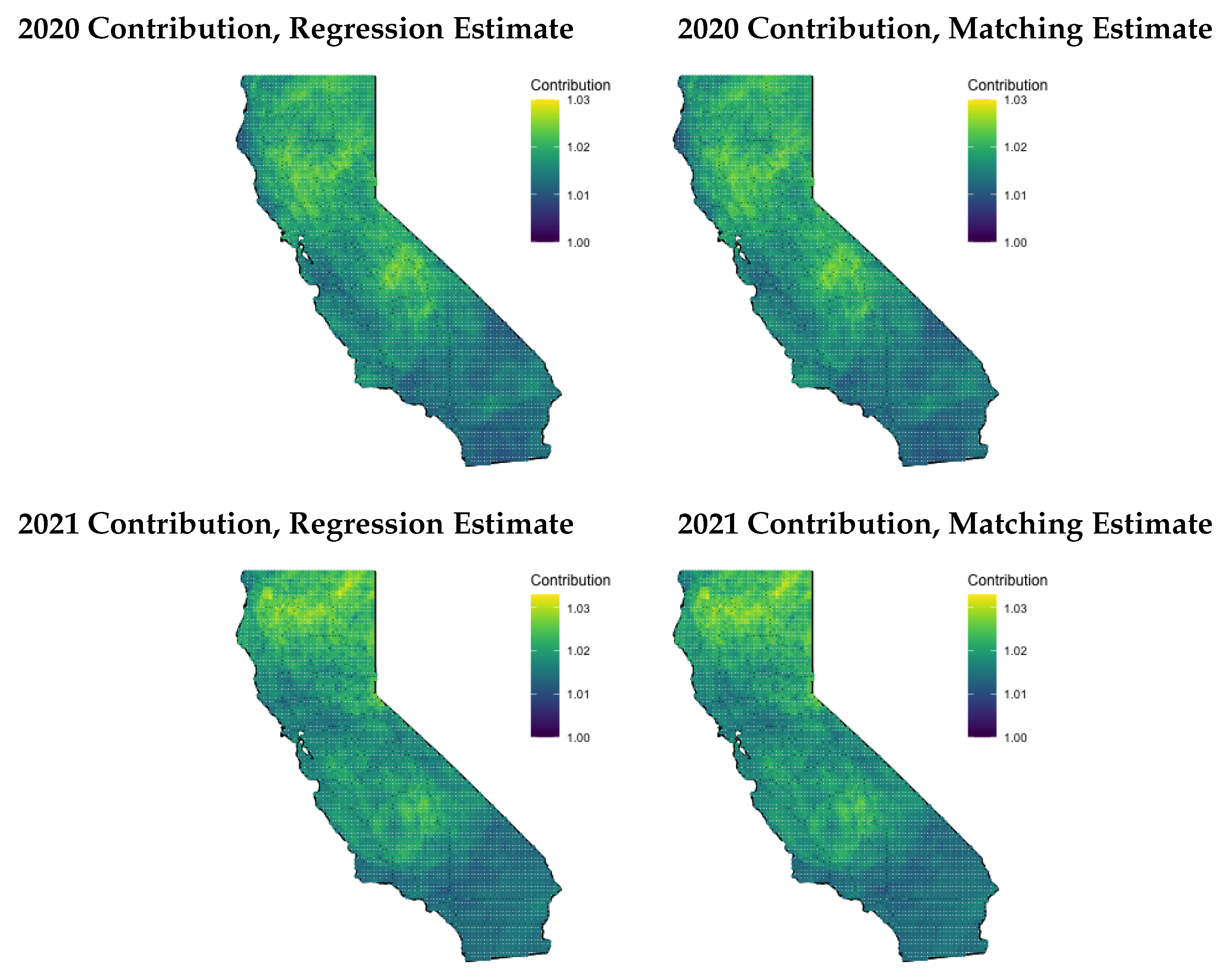
We find that including PurpleAir monitors significantly increases the precision of the estimated contribution of wildland fire smoke to total PM${}_{2.5}$. Using only AQS data we find that medium and high smoke plume levels significantly contribute to PM${}_{2.5}$ concentration with standard deviations as large as 0.017, and the data fusion approach that supplements AQS with PA data gives similar parameter estimation, with standard deviation as small as 0.004. Moreover, the data fusion model also estimates a significant low smoke plume level contribution. However, since PM${}_{2.5}$ concentration is relatively smooth across space and AQS stations are evenly distributed across the state, incorporating PurpleAir readings does not improve prediction performance even for the data-fusion approach. Comparing prediction performance does reveal that simple data fusion model such as the model that ignores bias in the PA data gives inferior prediction results. With our model, all three smoke plume levels demonstrate a significant contribution to PM${}_{2.5}$ concentration, and the impact varies across different regions depending on the year. This study highlights the value of utilizing both AQS and PurpleAir data in understanding the impact of wildfires on air quality and informs future monitoring and management efforts.

There are some limitations of our current work. First, as mentioned above, the satellite-derived smoke plume levels might underestimate the actual smoke level, which may lead to underestimation of wildfires’ contribution to PM${}_{2.5}$ [30]. Second, due to computational limitations and poor MCMC convergence, we fixed the spatial correlation range parameters for both AQS and PA monitors and parameters that control the relationships between AQS and PA data. The analysis would more fully quantify uncertainty if we are able to implement a fully Bayesian analysis.

We have taken a purely statistical approach to estimating the contribution of wildland fires on ambient air pollution. An area of future work is to incorporate numerical models to simulate the process. Dispersion models, e.g., HySPLIT [32], combine the location and size of fires and meteorological conditions in a mathematical model to track particulate matter emanating from a fire. Of course, numerical models also have bias and other limitations [33], but combining their output within our statistical framework would likely further refine our estimates. Further, instead of using one range parameter for all frequencies, it is possible to get variogram estimates of ranges over frequencies. Also, to extend the current work, we can estimate the contribution over the entire U.S. continent, and investigate how different areas suffer from wildfires, although more computational efficient models are required to analyze all US data.