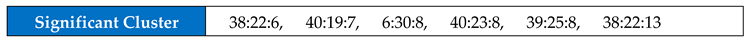1. Introduction
This paper considers the problem of predicting earthquakes. This difficult problem is a relatively new science that has been approached from different directions, but primarily by studying seismic and electromagnetic activity these days. What exactly causes earthquakes is still not clear, including the underlying mechanisms, and modelling this to allow a system to predict future events has to date yielded only modest results. After an earthquake has happened for example, do the same conditions still exist, so that a future event could be predicted. This is in fact a recognised problem where the answer is that some earthquakes repeat and some do not, so only some future earthquakes would be predictable. Most research has attempted to understand how the earthquake works and tried to build a model of that. Until recently, the available data has been a bit patchy, but now it is possible to map the whole planet, with regard to its electromagnetic footprint. This should make it easier to build machine learning models in the future. This paper suggests a machine-learning approach that uses a relatively small amount of data. It proposes that earthquakes do in fact have a footprint that can be traced and recognised. Rather than trying to understand the underlying mechanisms that cause the earthquake, the clustering method is evidence-based and builds up a picture based only on the evidence that is provided. This has some advantages over knowledge or model-based methods, including neural networks, because it can more easily learn stochastic data where random events may occur and which may be more appropriate for environmental data. If the clustering method can produce slightly different cluster sets to other algorithms, then it may be possible to realise different conclusions and in fact create a prediction algorithm.
The rest of the paper is organised as follows:
Section 2 gives some related work.
Section 3 describes the methodology of the new prediction algorithm.
Section 4 gives the results of running tests using the new method. Finally,
Section 5 gives some conclusions on the work.
2. Related Work
An earlier machine learning system called VAN [
14,
15] was shown at the time to produce better results for the Greece earthquakes and was a temporal clustering method. The VAN method tries to recognise changes in the rock’s electromagnetic emissions, with the underlying theory that rocks under stress emit different types of signal. It has since been updated [
14] with the concept of natural time, which is a time series analysis technique that puts weight on a process based on the ordering of events. However, the prediction results of the method were questioned and it has both supporters and critics. As stated in [
9]: ‘Why is temporal clustering such an important issue? Primarily because some variation in natural phenomena, such as electric field variation, which might follow earthquakes, would typically precede late events in a cluster. The electrical variations might thus appear to have some predictive capability, but this would actually come purely from the clustering of earthquakes.’ This indicates that earthquake clusters are important. The paper [
13] introduces a new model which considers that the fundamental aspects of the strain accumulation and release processes are critical to causing earthquakes. They also state that a problem with current models is that they assume that large earthquakes release all accumulated strain, despite evidence for partial strain release in earthquake histories showing clusters and gaps. The following sections will show an agreement with both these papers. While their design may be model-based however, this paper uses an evidence-based design.
In [
12] they suggest that an acceptable test for earthquake accuracy might be the ability to predict an earthquake in a region of 50km from the epicentre and up to 21 days before the event. However, only a 5% success rate with these criteria is deemed a good result. A more recent summary about machine learning methods can be found in [
2], for example. It notes that much of the progress has been in developing the data catalogs to train the AI models on, such as their own STEAD dataset. In fact, there have been recent claims of success using AI models [
1,
8,
10,
11], where some accuracy quotes are over 90%. The paper [
1] measures the upper atmosphere’s Ionospheric total electron content, which originates in the rock, while the paper [
8] considers water vapour in volcanic regions. Not only different methods, but also different aspects of the earthquake are now predicted and in practice there is still no generally accepted reliable method.
The design of this paper makes use of a new clustering algorithm called a Frequency Grid [
7]. This was also used in [
6] to predict energy usage in households, where Dr. Yaxin Bi is also an expert in modelling electromagnetic data [
3]. The frequency grid is an event-based clustering method. It reads a dataset where each row lists events that occurred at the same time. These associations produce sets of count values that represent which events more often occurred together. The grid is entropy-based however, rather than local associations only, where the aggregation into a single table can produce a holistic view of the associations. Because the clustering process is event-based, it does not have to produce a consistent underlying model or theory. A neural network, for example, may need to map from input to output using a consistent or continuous function, but the frequency grid does not have to do this. As a result, it can maybe model stochastic data more easily and so environmental data, which may include random elements, can be modelled more easily. Another idea taken from the energy paper [
6] is to discretise the seismic data into bands, thus allowing the grid a finer level of granularity. This is described further in the following sections.
3. Methodology
The proposed method is to try to recognise the events that led up to a major earthquake and represent them in some unique way. If clusters of earthquakes that occur together can be realised, then it should be easier to produce a unique description. If these clusters produced one major event, then they were not involved in a different major event, for example. The method uses the frequency grid to cluster the seismic events, which are represented by their location, magnitude, and time that they occurred. From these clusters, the larger seismic events can be found and it can be determined what occurred with them. The frequency grid is category-based and so the events need to be translated from numerical values to text-based values. Each event can therefore be represented by a key that stores its longitude – latitude location, and then a magnitude representation. The magnitude part is discretised into bands as follows: 1 band represents 0.5 of a magnitude size, so an earthquake of size 5 would have a band value of 10. Therefore, a seismic event would be represented by something like 30:20:8, where the longitude of the event would be 30, the latitude would be 20 and the actual magnitude would be 4. Then for each time unit, which is currently set to days, all events that occurred during that time unit are added to the dataset as a row of data. When the frequency grid reads the dataset, it will try to associate the events in the same row.
3.1. Discretise the Frequency Grid
To make it slightly more accurate, it has been decided to discretise the earthquake magnitude, rather than use a real value. Then, each row or column in the frequency grid is represented by a location plus a discretised band. In this way for example, location A can be associated with location B when the seismic magnitude is small, but with location C when the magnitude value is large. Consider the following example: locations A (1,1), B (1,2) and C (2,1) all have earthquake events that occur on the same days, as shown in
Table 1. On day 1, only 2 events occur, both with a magnitude of 1 and so the frequency grid would cluster A and B together with keys something like A:1 and B:1. On day 2 there are 4 events, but with different magnitudes. For the smaller magnitude, A and B still occur together, but for the larger magnitude A occurs with C. The frequency grid would therefore produce a second cluster for the larger magnitude that would be A:2 and C:2. Putting these counts into the frequency grid leads to
Table 2, where tracing through this manually can even show the clusters.
3.3. Prediction Algorithm
The test of accuracy would then be for the program to be able to predict the significant events by summarising the days before it and creating the footprint value from them. If a recognised footprint was realised, then that would indicate that the related significant event was likely to happen. The prediction algorithm was therefore quite similar to the one that created the footprints, with a few changes. It started at day 1 of the dataset and would cumulate the data rows in turn until a maximum number for a time window w was used. Then for each of the significant event clusters, a new subset would be created that contained only the data rows relevant to that cluster. From that subset the footprint key could be created. If the key was within a certain error margin of the known footprint for the cluster, then the significant event would be flagged for the last day in the time window. This would be repeated, a row at a time, through the whole dataset, where earlier days would be removed when the window moved past them. At the end of this process, the program would print out what days it considered each significant event to potentially occur on.
4. Testing and Results
A program has been written in the Java programming language to test the theory. The original Greece [
4] and USA [
5] datasets have been re-formatted slightly to be read by the program. The band size was set to 0.5, which meant that an increase of this amount in the seismic magnitude would place the event in a different category. The threshold was set to 12, meaning that only seismic events of size 6 or above would be considered as significant. The time window was set to 200, meaning that the program would look at 200 days before the significant event day, but clearly these values can be changed for a new set of tests. The Greece data was used from the start of 2005 only, so the earlier rows were removed first. It was decided that a time unit of days would be best and so the USGS dataset, which has a smaller timeframe, was aggregated to be in days rather than hours. The only columns that are required are the date, longitude, latitude, and the event magnitude. The example in the following sections is for the Greece dataset.
4.1. Data Rows and Clusters
The program firstly reads the formatted dataset and creates lists of events for each day in the record. It then feeds these lists into the frequency grid that generates clusters of events that most often occur together. The program is then given a lower threshold for what a significant event might be. A threshold value of 12 would look for major events of size 6 and above, for example, where a data row could be represented by something like the following.

The data row describes 3 events that occurred on the 1 of January 2005. The program can process in hours, but the preferred time unit is days and so the time part is set to 0. The first event ‘38:24:3’ indicates a latitude of 38, a longitude of 24 and a discrete band size of 3. The frequency grid would therefore have associated these events together and clusters with events that pass the threshold are retrieved and stored as significant or target events. For example, the following was a significant cluster for the Greece dataset, because one event had a discrete value of 13.
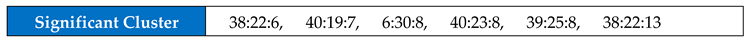
4.2. Footprint Key
The footprint is created from all events in a cluster, even if they are smaller in size. This is translated over into a list of gaps between days when events occurred and also the number of related events that occurred on each day. To determine if a related event occurred, the longitude, latitude and magnitude were all considered. The footprint key can then be created from this list and may look something like the following.

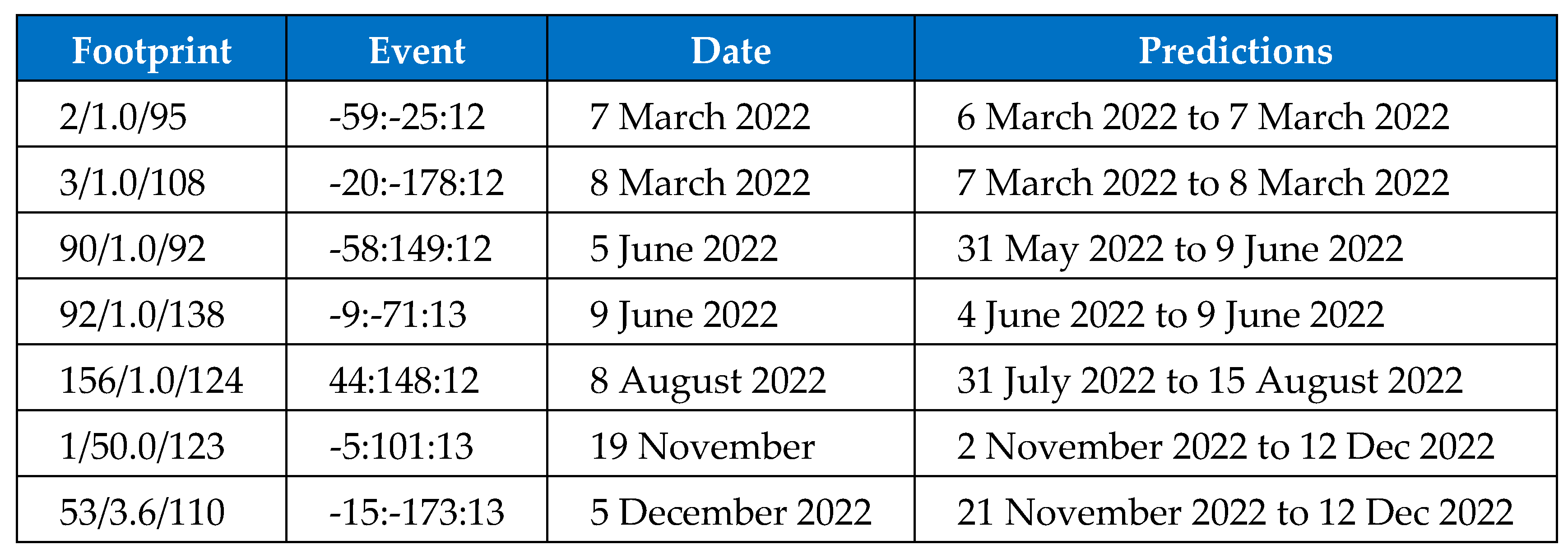
This represents the days leading up to the event as follows: there were 50 days in the time window before the event that contained any of the events in the cluster. In these 50 days, the average gap between these days was 2.5 and there was an average of 3 relevant events each day. It turns out that this description is quite unique and can describe the significant event of the cluster while excluding descriptions for the other significant clusters.
4.3. Analysis and Predictions
The program can then run an analysis phase, where it selects a time window related to a significant event and analyses the data rows that occurred in that time window. It notes the events that are part of the significant event cluster and notes when they occurred. From this it is able to generate the footprint key and store it with the event description, as has just been described. This can then be used as the marker that the prediction should try to find. The analysis data is written to a file and then read by a simulation program that makes predictions on when the significant events are likely to happen, as described in section 3.3. The footprint does not have to be exact. For this set of tests the error margin was set to 5% difference in any of the 3 parts to the footprint key. So the footprint would be considered to be the same, only if all 3 parts were within an error margin of 5% of the related actual footprint part. One thing to note however is that a significant event does not necessarily have a history that can be traced. Some events appear to happen without warning, while other events have a long history trace that can be used to calculate the footprint.
4.3.1. Greece Dataset
For the Greek dataset, most of the significant events did in fact have a footprint.
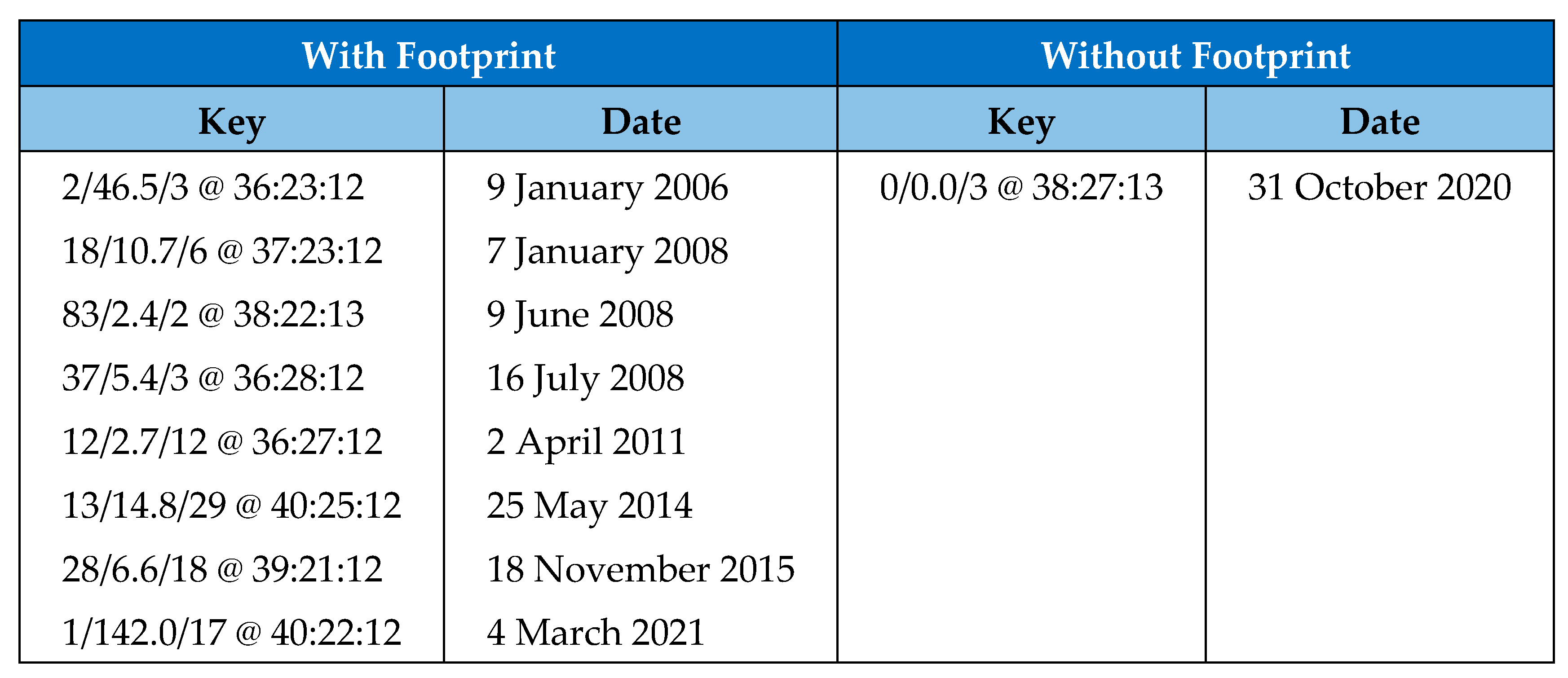
Figure 1 shows the significant events with a threshold of value 12 or above (magnitude value of 6 or above) and only 1 event occurred without an earlier trace. It is therefore not possible to make a prediction for that event. For the other events however, the predictions are listed in
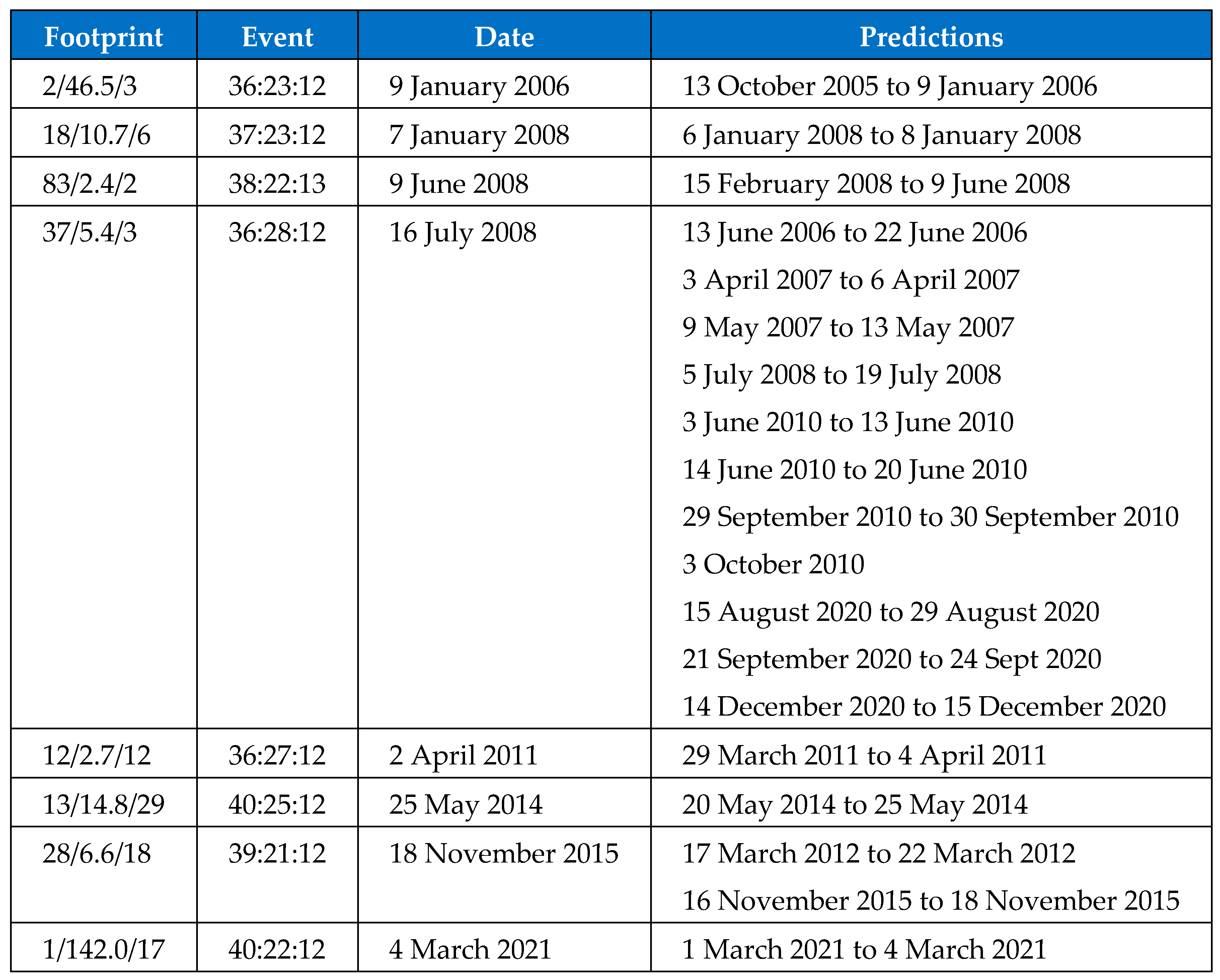
Figure 2. Most of the significant events have been predicted and within reasonable time of the real event. Some of the time spans are very short, but if the data was tested first, then it would be known to expect a short time span there. One event is a lot more messy however. It occurred on 16 July 2008, but its footprint has been repeated several times over the dataset. It happens to be the case that the other flagged events were clustered mostly in the same region and so that may have produced a similar footprint. Even if that event is not included, the author would suggest that the accuracy is 6 good predictions from 9 plus one half-prediction, which still gives 70% accuracy.
4.3.2. USA Dataset
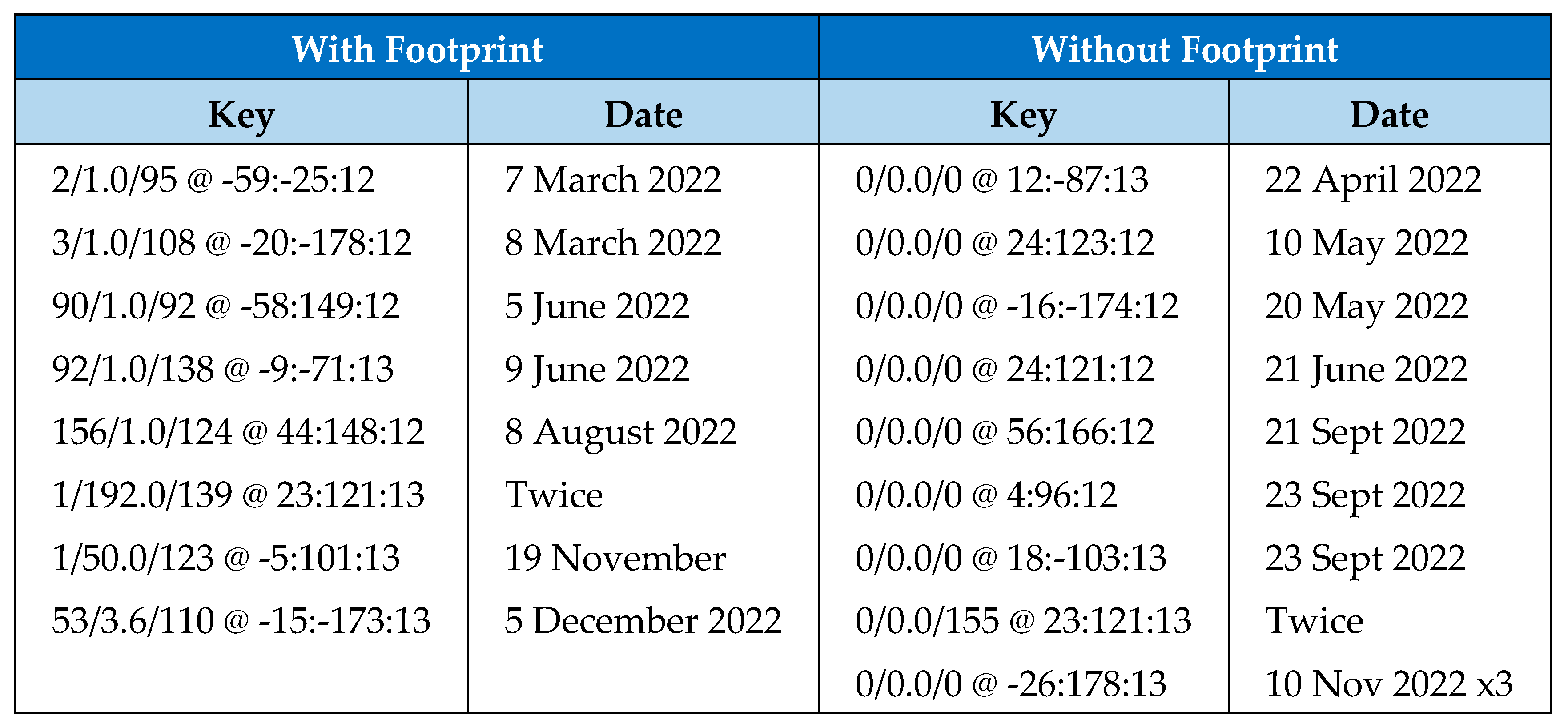
For the USA dataset however, over 50% of the significant events do not have a footprint.
Figure 3 shows the significant events with a threshold of value 12 or above and only 8 have a traceable footprint, while 9 do not. Of the 8 that have a footprint, predictions could be made for 7 of them, as listed in
Figure 4. These predictions are quite close however and so in real terms that is still a 40% accuracy.
The test was also run on both datasets with a threshold of 10 or more (magnitude of 5 or more), and 11 or more, where
Table 3 gives a summary of all the results. For the lower threshold, the clusters were not predicted as accurately and some of them could be very wrong. The story, for example, is a bit different for the USA data with a 10 threshold, but most of the misses are because no footprint was available. Of the 18 predictions that were made, 15 of them would be acceptable. The table therefore gives an accuracy score for significant events, only when predictions were made and then also for all significant events.
5. Conclusions
This paper has suggested a method of producing footprints with which to recognise seismic events. The process requires training an algorithm on previous events and so if the conditions change, the process may not work very well. It is also evidence-based, which means that it can map more easily to the data, but that it has very little knowledge or understanding of that data. It might therefore not be possible to transfer results from one region to another region. One idea when measuring gaps between days was that there were more gaps leading up to an event, so this could be a type of general indicator, but further tests did not show this as being definitive. The gaps may indicate when forces are acting against each other, for example, when if one set of forces gives way to another, it could lead to catastrophic failure.
The footprint is generated from only a small amount of information and sometimes it cannot be created. It would be possible to add other information, but the author does not know what that might be. With the clusters however, even the current key is mostly unique, for the Greece and USA datasets. Because the significant event itself occurs only once, it is really the more minor events clustered with it that are being traced, to create the footprint. The current program is only a first attempt, but it has been able to show a proof of concept and the accuracy of the predictions are probably at an acceptable level. Therefore, the author would suggest that this is an interesting method that deserves further investigation.
References
- Asaly, S., Gottlieb, L.-A., Inbar, N. and Reuveni, Y. (2022). Using Support Vector Machine (SVM) with GPS Ionospheric TEC Estimations to Potentially Predict Earthquake Events. Remote Sens., Vol. 14, p. 2822. [CrossRef]
- Beroza, G.C., Segou, M. and Mostafa Mousavi, S. (2021). Machine learning and earthquake forecasting - next steps. Nat Commun, Vol. 12, No. 4761. [CrossRef]
- Christodoulou, V., Bi, Y. and Wilkie G. (2019). A tool for Swarm satellite data analysis and anomaly detection. PLoS ONE Vol. 14, No. 4: e0212098. [CrossRef]
- Dataset, Greece. (2023). Kaggle. Available online: https://www.kaggle.com/datasets/nickdoulos/greeces-earthquakes.
- Dataset, USA. (2023). Kaggle. Available online: https://www.kaggle.com/datasets/thedevastator/ uncovering-geophysical-insights-analyzing-usgs-e.
- Greer, K. and Bi, Y. (2022). Event-Based Clustering with Energy Data, WSEAS Transactions on Design, Construction, Maintenance, Vol. 2, Art. #26, pp. 197-207. [CrossRef]
- Greer, K. (2019). New Ideas for Brain Modelling 3, Cognitive Systems Research, Vol. 55, pp. 1-13, Elsevier. [CrossRef]
- Hiraishi, H. (2022). Earthquake Prediction Software on Global Scale. Journal of Geoscience and Environment Protection, Vol. 10, pp. 34 - 45. [CrossRef]
- Kagan, Y.Y. and Jackson, D.D. (1996). Statistical tests of VAN earthquake predictions: Comments and reflections, Geophysical Research Letters, Vol. 23, No. 11, pp. 1433 - 1436. [CrossRef]
- Kavianpour, P., Kavianpour, M., Jahani, E. and Ramezani, A. (2023). A cnn-bilstm model with attention mechanism for earthquake prediction. The Journal of Supercomputing, pp. 1 - 33. [CrossRef]
- Laurenti, L., Tinti, E., Galasso, F., Franco, L. and Marone, C. (2022). Deep learning for laboratory earthquake prediction and autoregressive forecasting of fault zone stress, Earth and Planetary Science Letters, Vol. 598, p.117825. [CrossRef]
- Luen, B. and Stark, P.B. (2008). Testing earthquake predictions. In Probability and statistics: Essays in honor of David A. Freedman (Vol. 2, pp. 302-316). Institute of Mathematical Statistics.
- Neely, J.S., Salditch, L., Spencer, B.D. and Stein, S. (2023). A More Realistic Earthquake Probability Model Using Long-Term Fault Memory. Bulletin of the Seismological Society of America, Vol. 113, No. 2, pp. 843 - 855. [CrossRef]
- Varotsos, P., Sarlis, N. and Skordas, E. (2002), Long-range correlations in the electric signals that precede rupture, Physical Review E, Vol. 66, No. 1: 011902, Bibcode:2002PhRvE..66a1902V. 1902. [CrossRef] [PubMed]
- Varotsos, P., Alexopoulos, K. and Nomicos, K. (1981). Seven-hour precursors to earthquakes determined from telluric currents, Praktika of the Academy of Athens, Vol. 56, pp. 417–433.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).