Submitted:
03 July 2023
Posted:
04 July 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
1.1. Problem Overview
1.1.1. Constraints
2. Materials and Methods
2.1. Numerical study and Simulation of different case studies
2.1.1. Non-dispatchable Energy Sources
2.1.1.1. Solar Photovoltaic (PV)
2.1.1.2. Model for Economic Power Delivery Coordination Using Solar PV Energy
2.1.1.3. Constraints
2.1.2. Dispatchable Energy Sources
2.1.2.1 Batteries
2.1.2.1. Model of battery charge storage
2.1.2.3. Proposed optimised-based energy management system
2.1.2.3. Economic Power Dispatch Problem
2.1.2.4. Particle Search Optimisation Model formulation
3. Proposed Co-Optimization of EPD and EMS PSO Algorithm
3.1. EMS Classical Algorithm
- Step 1 - Input Decision Variables Lower &Upper bound; for battery MinMax(PgridV, PbattV, EbattV)
- Step 2 - Minimize cost of electricity from the grid Objective dt*cost*PgridV – FinalWeiht*EbattV(N)
- Step 3 - Power input/output to battery Constraints.energyBalance = Optimconstr(N)
- Step 4 - Power load with power from PV, grid and battery Constraints.loadBalance = Ppv+PgridV+PbattV-Pload
- Step 5 - Linear Program Options = Optimoptions(prob.optimoptions,)
- Step 6 - Parse optimization results
3.2. Solar PV – Battery – Grid Algorithm Steps
- Step 1- PSO Settings
- Step 2 -Initiate Particles
- Step 3 - Initiate condition
- Step 4 - Main PSO
- Step 5 - Results
3.3. EPD PSO Algorithm Steps [49]
-
Step 1 - Problem definition
- Z=F(X) = P=PminActual+(PmaxActual-PminActual). *x
- Create a parse.m function P=ParseSolution(x,model)
- InputPmin=model.Plants.Pmin; Pmax=model.Plants.Pmax; P=Pmin+(Pmax-Pmin).*x; PZ=model.Plants.PZ; nPlant=model.nPlant; for i=1:nPlant; forj=1:numel(PZ{i})if P(i)>PZ{i}{j}(1) && P(i)<PZ{i}{j}(2)% Correction
- CreateModel for 3, 6, 15 Units committed generators variables; with power demand of committed generators (particles) with uniformly random distribution Pmin, Pmax, alpha, beta, gamma, P0, UR, DR, transmission loss and over X (position).
- Develop CostFunction -@(x) MyCost (x, Model);
- Develop a model calculation C=alpha+beta.*P+gamma.*P.*P; PL=P*B*P'+B0*P'+B00;
- Decision Variables nVar = Model. nPlant (lower and upper bound for 3,6,15 Units committed generators variables
-
Step 2 - PSO Parameters
- MaxIt – no of iteration; nPop – Swarm Size; Constriction Coefficient – C1 = chi*phi 1 as personal Coeff., C2 = chi*Phi 2 as Global Coeff.; Velocity Limit
-
Step 3 - Initialisation
- BestSol.Cost = inf; for i=1; nPop, initialise position; initialise Velocity;
- Evaluation of each committed generators cost model considering the objective function value.
- Z=F(X) = P=PminActual+(PmaxActual-PminActual). *x; with or without prohibited zones
- Evaluation; Update Personal Best; Update Global Best; BestSol = Particle(1)’Best
-
Step 4 - PSO Main Loop
- It-1, MaxIt; for i=1: nPop, Update Velocity; Apply Velocity Limits; Update Position, Velocity mirror effect; Apply Position Limits; Evaluation; Update Personal best
- Run PSO Matlab codes by calling functions (problem definition; PSO parameters; constriction coefficients; velocity limits; initialization of particles, position, evaluation; update personal best; update global 'Best Cost')
- Results - Plot (Best Cost, x label, Y label)
- Update generators’ velocities.
- Move particles to their new positions CostFunction(particle(i).Position);
- If all committed generators present position is better than the previous best position, update the value particle(i).Cost<particle(i).Best.Cost
- Find the best committed generator update BestCost(it)=BestSol
4. Simulation Results and Discussion
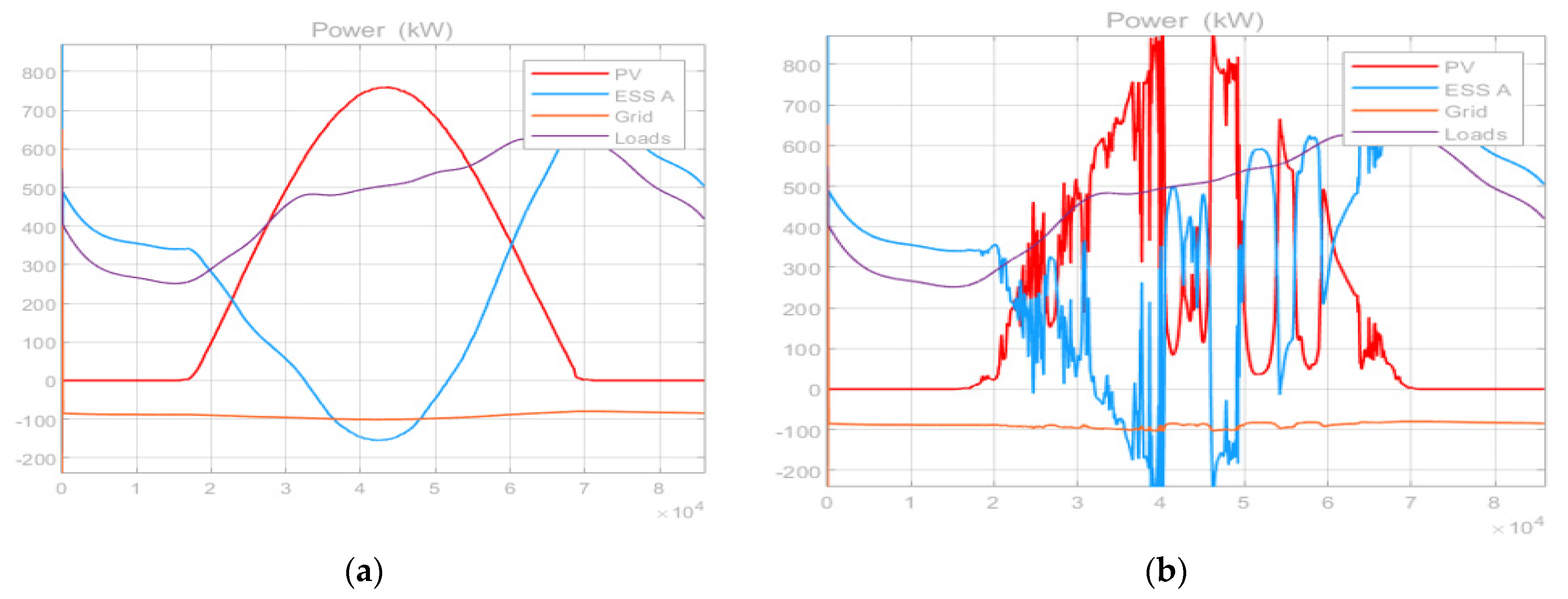
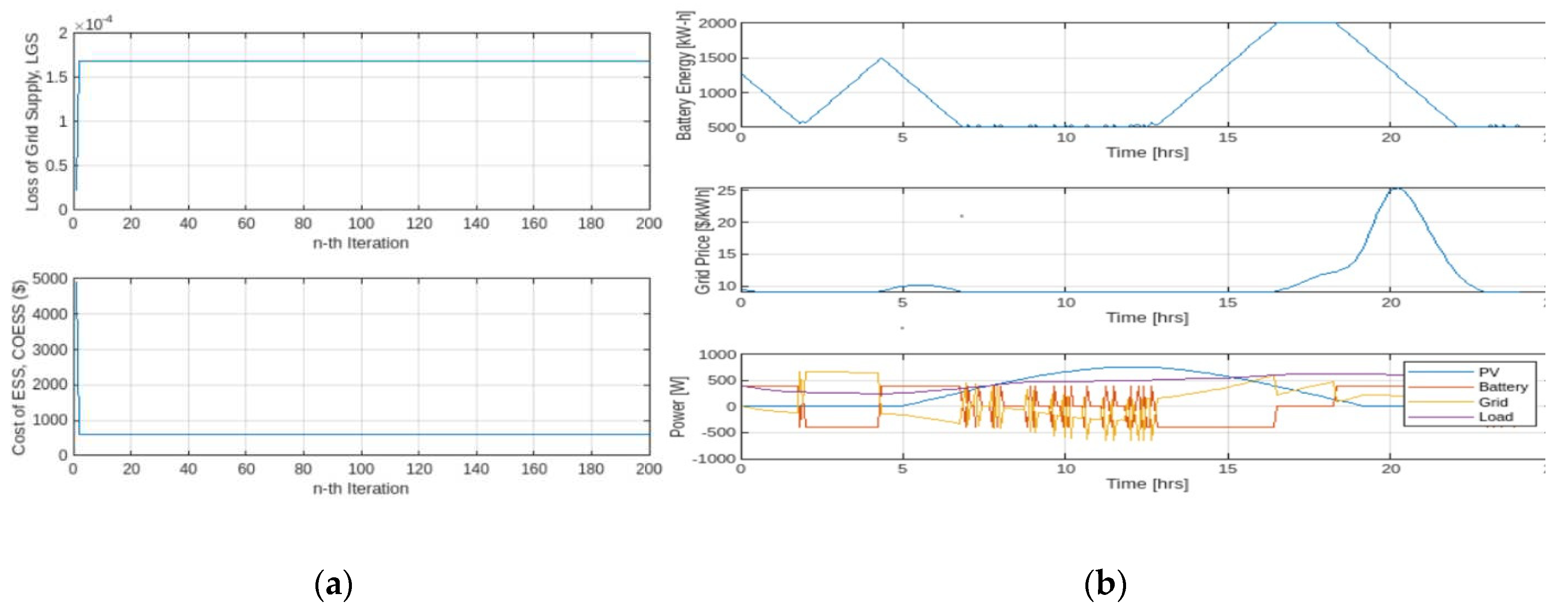
4.1. EMS Simulation Results
4.1. EPD Simulation Results
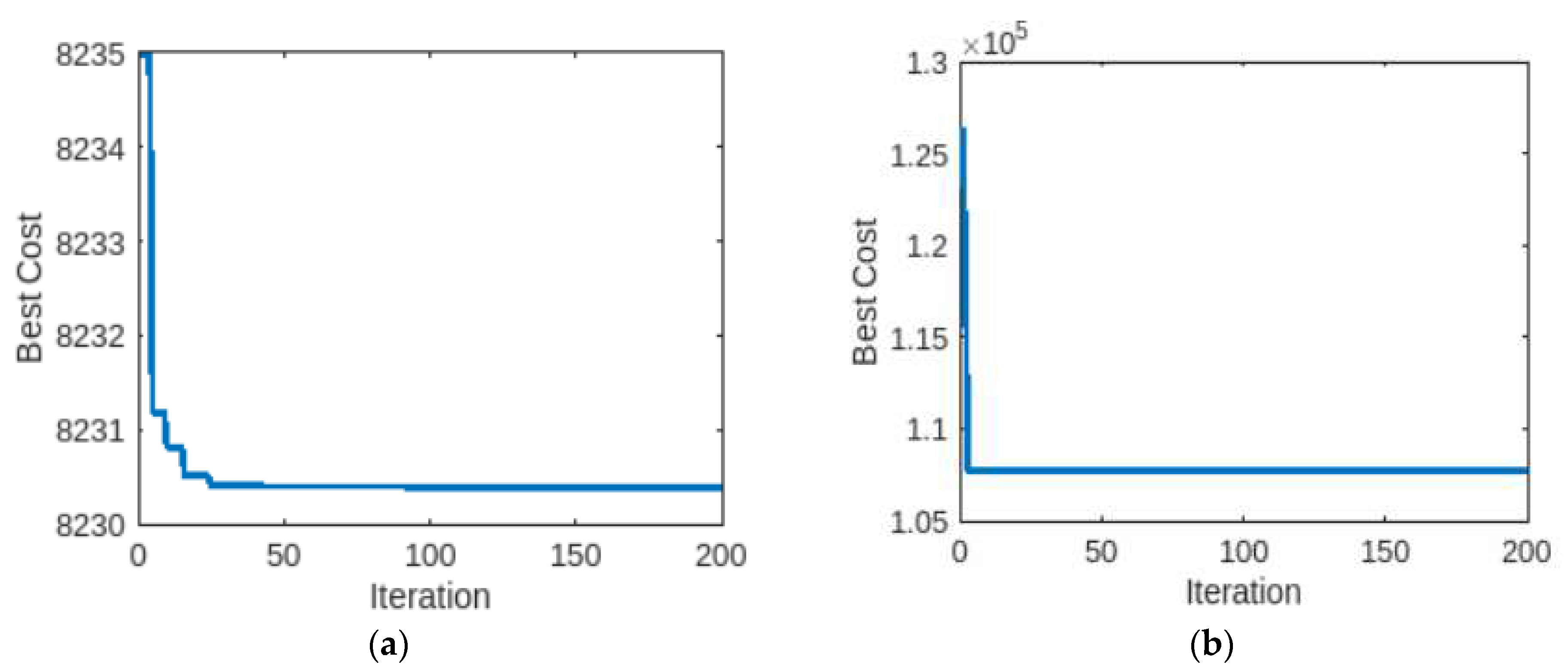
4.1.1. Case 1: 3-unit generator system with demand of 850 MW
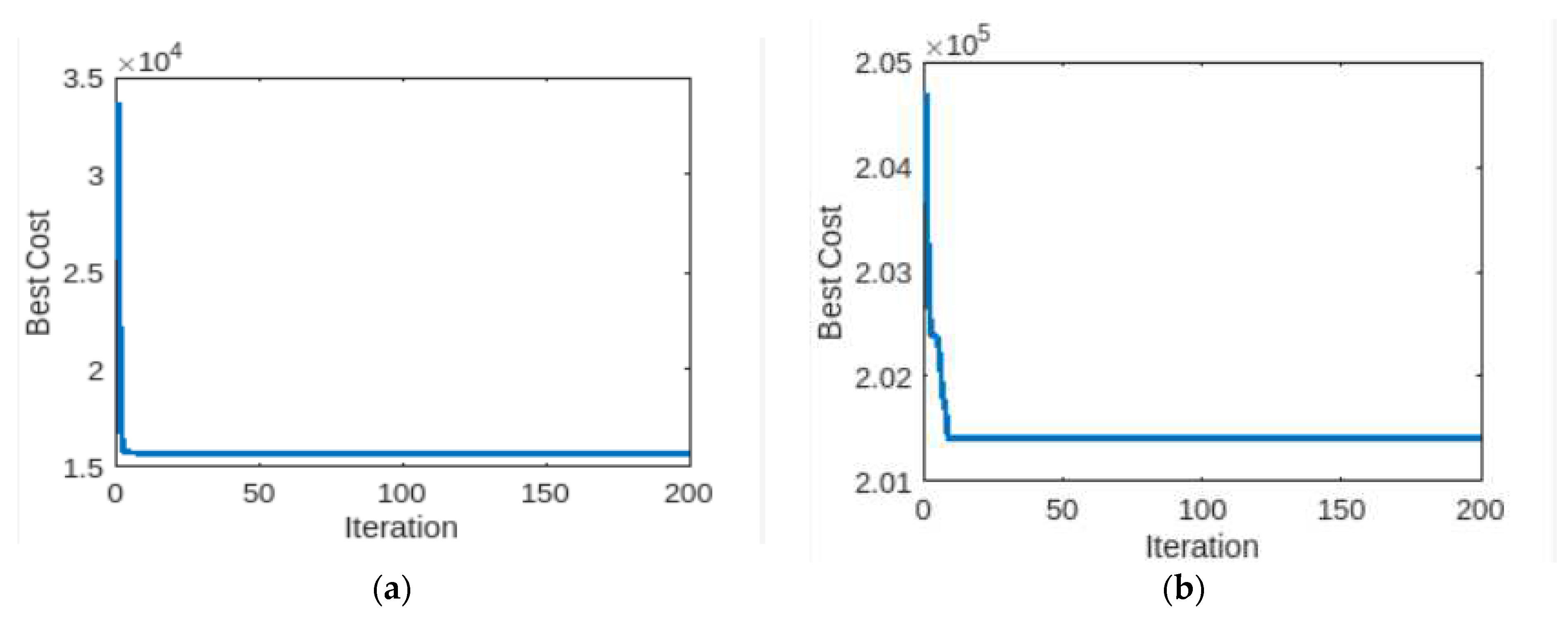
4.1.2. Case 1: 6-unit generator system with demand of 1263 MW
4.1.3. Case 1: 15-unit generator system with demand of 2630 MW
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gribkovskaia, V. Peak Price Hours in the Nordic Power Market Winter 2009/2010: Effects of Pricing, Demand Elasticity and Transmission Capacities. SSRN Electronic Journal. 2015.
- Zeng, B.; Feng, J.; Zhang, J.; Liu, Z. An optimal integrated planning method for supporting growing penetration of electric vehicles in distribution systems. Energy 2017, 126, 273–284. [Google Scholar] [CrossRef]
- Ai, X; Wu, J.; Hu, J.; Yang, Z.; Yang, G. Distributed congestion management of distribution networks to integrate prosumers energy operation. IET Generation, Transmission & Distribution, 2020; 14, 2988–2996. [Google Scholar]
- Tigas, K.; Giannakidis, G.; Mantzaris, J.; Lalas, D.; Sakellaridis, N.; Nakos, C.; Vougiouklakis, Y.; Theofilidi, M.; Pyrgioti, E.; Alexandridis, A.T. Wide scale penetration of renewable electricity in the Greek energy system in view of the European decarbonization targets for 2050, Renewable and Sustainable Energy Reviews. 2015, 42, pp. 158-169.
- Al-Hamidi, H.; Al Asfar, J. Hybrid renewable energy system with minimum noise wind turbine. Renewable Energy. 2017, 114, pp. 581–587 doiorg/101016/jrenene201707015. [Google Scholar] [CrossRef]
- Olusola, M.; Akinbami, S. R.; Oke, M.; Bodunrin, O. The state of renewable energy development in South Africa: An overview, Alexandria Engineering Journal, 2021, 60, Issue 6, pp. 5077-5093. [CrossRef]
- Gambhir, A.; Sandwell, P.; Nelson, J. The future costs of OPV – A bottom-up model of material and manufacturing costs with uncertainty analysis. Solar Energy Materials and Solar Cells 2016, 156, 49–58. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, Z. Optimal wind energy bidding strategies in real-time electricity market with multi-energy sources. IET Renewable Power Generation. 2019, 13, 2383–2390. [Google Scholar] [CrossRef]
- Jeter, S.M.; Phan, C.N. Site-specific clear-day solar irradiance model from long-term irradiance data. Journal of Energy. 1982. 6(2), pp.115–118.
- Bou-Rabee, M.; Shaharin, S. On Seasonal Variation of Solar Irradiation in Kuwait. International Journal of Renewable Energy Research (IJRER). 2015, 5.2, pp. 367-372.
- Srivastava, A.; Das, D.K. An adaptive chaotic class topper optimization technique to solve economic load dispatch and emission economic dispatch problem in power system. Soft Computing. 2022, 26, 2913–2914. [Google Scholar] [CrossRef]
- Jiawen, B.; Tao, D.; Zhe, W.; Ianhua, C. Day-Ahead Robust Economic Dispatch Considering Renewable Energy and Concentrated Solar Power Plants, Energies 2019, 12(20), pp. 3832. [CrossRef]
- Bishwajit, D.; Shyamal K., R.; Biplab, B. Solving multi-objective economic emission dispatch of a renewable integrated microgrid using latest bio-inspired algorithms, Engineering Science and Technology, an International Journal, 2019, Volume 22, Issue 1, pp. 55-66. [CrossRef]
- Lotfi Akbarabadi, M.; Sirjani, R. Achieving Sustainability and Cost-Effectiveness in Power Generation: Multi-Objective Dispatch of Solar, Wind, and Hydro Units. Sustainability 2023, 15, 2407. [Google Scholar] [CrossRef]
- Hasibuan, A.; Kurniawan, R.; Isa, M.; Mursalin, M. Economic Dispatch Analysis Using Equal Incremental Cost Method with Linear Regression Approach. Journal of Renewable Energy, Electrical, and Computer Engineering, 2021; 1, 16. [Google Scholar]
- Roy, C.; Das, D.K. A hybrid genetic algorithm (GA)–particle swarm optimization (PSO) algorithm for demand side management in smart grid considering wind power for cost optimization. Sādhanā. 2021, 46. [Google Scholar] [CrossRef]
- Stochastically coordinated transmission and distribution system operation with large-scale wind farms. CSEE Journal of Power and Energy Systems. 2020. [CrossRef]
- Silva, H.G.; Coelho, A.L.M.; Faria, I.P.; Araujo, B.G. ANN based impedance trajectory detection approach for loss of excitation protection of synchronous generators connected to transmission lines with SVCs. Electric Power Systems Research. 2022. 213:108766.
- Kusakana, K. Optimal scheduled power flow for distributed photovoltaic/wind/diesel generators with battery storage system. IET Renewable Power Generation. 2015, 9, 916–924. [Google Scholar] [CrossRef]
- Optimized Generation Scheduling of Thermal Generators Integrated to Wind Energy System with Storage. International Journal of Renewable Energy Research. 2018. (v8i2).
- Pandey, A.C.; Das, V.; Kumar, P.; Singh, R.; Maurya, S.K. AEFA Based Optimal Dynamic Economic Load Dispatch Problem Considering Penetration of Renewable Energy Systems. Distributed Generation & Alternative Energy Journal 2022.
- Xu, J.; Liu, A.; Qin, Y.; Xu, G.; Tang, Y. A Cost-Effective Solution to Dynamic Economic Load Dispatch Problem Using Improved Chimp Optimizer. Frontiers in Energy Research 2022. 10.
- Iweh, C.D.; Gyamfi, S.; Tanyi, E.; Effah-Donyina, E. Distributed Generation and Renewable Energy Integration into the Grid: Prerequisites, Push Factors, Practical Options, Issues and Merits. Energies 2021, 14, 5375 https:// doiorg/103390/en14175375. [Google Scholar] [CrossRef]
- Kempener, R.; Komor, P.; Hoke, A. Smart Grids and Renewables—A Guide for Effective Deployment; International Renewable Energy Agency (IRENA): 2013.Abu Dhabi, UAE.
- Bhattacharyya, B.; Kumar, S. Approach for the solution of transmission congestion with multi-type FACTS devices. IET Generation, Transmission & Distribution 2016. 10(11), pp. 2802–2809.
- Tuladhar, S.R.; Singh, J.G.; Ongsakul, W. Multi-objective approach for distribution network reconfiguration with optimal DG power factor using NSPSO. IET Gener. Transm. Distrib. 2016, 10, 2842–2851. [Google Scholar] [CrossRef]
- Peres, F.; Castelli, M. Combinatorial Optimization Problems and Metaheuristics: Review, Challenges, Design, and Development. Appl. Sci. 2021, 11, 6449. [Google Scholar] [CrossRef]
- Asl, S.A.F.; Gandomkar, M.; Nikoukar, J. Optimal Protection Coordination in the Micro-Grid Including Inverter-Based Distributed Generations and Energy Storage System with Considering Grid-Connected and Islanded Modes. Electric Power Systems Research 2020, 184, 106317. [Google Scholar] [CrossRef]
- Vlachogiannis, J.G. Marine-Current Power Generation Model for Smart Grids. Journal of Power Sources 2014, 249, 172–174. [Google Scholar] [CrossRef]
- Vyas, M.; Chowdhury, S.; Verma, A.; Jain, V.K. Solar Photovoltaic Tree: Urban PV Power Plants to Increase Power to Land Occupancy Ratio. Renewable Energy 2022, 190, 283–293. [Google Scholar] [CrossRef]
- Thabo, G.; Hlalele, J. Z.; Raj M., N.; Ramesh, C. Bansal. Multi-objective economic dispatch with residential demand response programme under renewable obligation. Energy 2021, 218, pp 119473. [Google Scholar]
- Lin, X. Theoretical analysis of battery soc estimation errors under sensor bias and variance, IEEE Trans. Ind. Electron 2018, 65 (9), pp. 7138–7148.
- Hu, X. , Li, S.E.; Yang, Y. Advanced machine learning approach for lithium-ion battery state estimation in electric vehicles, IEEE Trans. Transp. Electrific 2015, 2 (2), pp. 140–149.
- Naz, K.; Zainab, F.; Mehmood, K.K.; Bukhari, S.B.A.; Khalid, H.A.; Kim, C.H. An Optimized Framework for Energy Management of Multi-Microgrid Systems. Energies 2021, 14, 6012. [Google Scholar] [CrossRef]
- Babaei, M.; Azizi, E.; Beheshti, M.T.H.; Hadian, M. Data-Driven load management of stand-alone residential buildings including renewable resources, energy storage system, and electric vehicle, Journal of Energy Storage 2020, 28, pp. 10 1221.
- Leyffer, S.; Linderoth, J. Convex Mixed-Integer Nonlinear Optimization I. Summer School on Optimization of Dynamical Systems, 2018. Argonne National Laboratory, Department of Industrial and Systems, Engineering. University of Wisconsin-Madison.
- Majzoobi, A.; Khodaei, A. Application of Microgrids in Providing Ancillary Services to the Utility Grid. Energy 2017, 123, 555–563. [Google Scholar] [CrossRef]
- Fan, M.; Zhang, Z.; Wang, C. Mathematical Models and Algorithms for Power System Optimization, Modeling Technology for Practical Engineering Problems, An imprint of Elsevier. China Electric Power Press. Published by Elsevier Inc. 2019.
- Leyffer, S.; Linderoth, J. Introduction to Integer Nonlinear Optimization, Nonlinear Branch-and-Cut, Theoretical and Computational Challenges. Argonne National Laboratory. 2007. http://science.energy.gov/~/media/ascr/pdf/workshops-conferences/mathtalks/Leyffer.
- Kennedy, J. , Eberhart, R. In C. Particle swarm optimization. In Proceedings of the 1995 IEEE international conference on neural networks (Perth, Australia) 1995; 1942–1948. [Google Scholar]
- Rengasamy, S.; Murugesan, P. PSO Based Data Clustering with a Different Perception. Swarm and Evolutionary Computation 2021, 64, 100895. [Google Scholar] [CrossRef]
- Ananthan, D. Unit Commitment Solution Using Particle Swarm Optimisation (PSO). IOSR Journal of Engineering 2014, 4, 01–09. [Google Scholar] [CrossRef]
- Wang, P.; Ma, Y.; Wang, M. A Dynamic Multi-Objective Optimization Evolutionary Algorithm Based on Particle Swarm Prediction Strategy and Prediction Adjustment Strategy. Swarm and Evolutionary Computation 2022, 75, 101164. [Google Scholar] [CrossRef]
- LeSage, J. Microgrid Energy Management System (EMS) using Optimization (https://github.com/jonlesage/Microgrid-EMS-Optimization/releases/tag/v19.1.0), GitHub. Retrieved , 3 May 2023.
- Banerjee, S.; Deblina, M.; Chandan, K. C. Teaching learning-based optimization for economic load dispatch problem considering valve point loading effect. " International Journal of Electrical Power & Energy Systems 2015; 73:456-464.
- Velamuri, S.; Sreejith, S. Economic Dispatch and Cost Analysis on a Power System Network Interconnected with Solar Farm. International Journal of Renewable Energy Research 2015; 5: 4.
- Meryeme, A.; Mohammed, O.; Mohamed, M. Optimum Energy Flow Management of a Grid-Tied Photovaolatic-Wind-Battery System considering Cost, Reliabilty, and CO2 Emission. Hidawi, International Journal of Photoenergy vol 2021, Article ID 5591456.
- Xinyang, Z.; Chin-Yao, C.; Andrey, B.; Changhong, Z.; Lijun, C. Economic Dispatch with Distributed Energy Resources: Co-Optimization of Transmission and Distribution Systems, IEEE Control Systems Letters 2021; 5: 6.
- Heris, M. K. Particle Swarm Optimization (PSO) in MATLAB — Video Tutorial (URL: https://yarpiz.com/440/ytea101-particle-swarm-optimization-pso-in-matlab-video-tutorial), Yarpiz, 2016.
- Ali, R. Al-Roomi. Economic Load Dispatch Test Systems Repository [https://www.al-roomi.org/economic-dispatch]. Halifax, Nova Scotia, Canada: Dalhousie University, Electrical and Computer Engineering. 2016.
- Gaing, Z.L. Particle swarm optimization to solving the economic dispatch considering the generator constraints. IEEE Trans Power Syst 2003; 18:1187-95.
- Yoshida, H.; Kawata, K.; Fukuyama, Y.; Takayama, S.; Nakanishi, Y. A particle swarm optimization for reactive power and voltage control considering voltage security assessment," in IEEE Transactions on Power Systems 2000;15, 4 :1232-1239. [CrossRef]
- Kuo, C. C. A novel coding scheme for practical economic dispatch by modified particle swarm approach, Power Systems.
- IEEE Transactions on, 2008;23: 1825-1835,.
- Rahmani, R.; Othman, M. F.; Yusof, R.; Khalid, M. Solving Economic Dispatch Problem Using Particle Swarm Optimization by An Evolutionary Technique for Initializing Particle; Journal of Theoretical and Applied Information Technology 2012; 46: 2.
- Al-Betar, M.A.; Awadallah, M.A.; Zitar, R.A. Economic load dispatch using memetic sine cosine algorithm. J Ambient Intell Human Comput 2022. [CrossRef] [PubMed]
- Rajashree, B.; Upadhyay, P. PSO approach for ELD problem: A review, 2016 IEEE International WIE Conference on Electrical and Computer Engineering (WIECON-ECE), Pune, India, 2016: 225-228. [CrossRef]
- Senthil Krishnamurthy and Raynitchka Tzoneva, “Application of the Particle Swarm Optimization Algorithm to a Combined Economic Emission Dispatch Problem using a new penalty factor”, IEEE PES Power Africa 2012 – Conference and Exhibition, Johannesburg, South Africa, 9-13 July 2012.

| Coeff. without PV | Coeff. with PV | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Unit | Pmin (MW) |
Pmax (MW) |
ai ($/MW2h) |
bi ($/MWh) | ci ($/MW) | Unit | Pmin (MW) |
Pmax (MW) |
ai ($/MW2h) |
bi ($/MWh) | ci ($/MW) | ||
| Unit 1 | 100 | 600 | 561 | 7.92 | 0.0016 | Unit 1 | 100 | 600 | 561 | 7.92 | 0.0016 | ||
| Unit 2 | 100 | 400 | 310 | 7.85 | 0.0019 | PV 1 | 20 | 100 | 0 | 0 | 0 | ||
| Unit 3 | 50 | 200 | 78 | 7.97 | 0.0048 | PV 3 | 50 | 200 | 78 | 7.97 | 0.0048 | ||
| Coeff. without solar PV | Coeff. with solar PV | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Unit | Pmin (MW) |
Pmax (MW) |
ai ($/MW2h) |
bi ($/MWh) | ci ($/MW) | Unit | Pmin (MW) |
Pmax (MW) |
ai ($/MW2h) |
bi ($/MWh) | ci ($/MW) | |||
| Unit 1 | 100 | 500 | 240 | 7.00 | 0.0070 | Unit 1 | 100 | 500 | 240 | 7.00 | 0.0070 | |||
| Unit 2 | 50 | 200 | 200 | 10.0 | 0.0095 | PV 1 | 20 | 200 | 0 | 0 | 0 | |||
| Unit 3 | 80 | 300 | 220 | 8.5 | 0.0090 | PV 3 | 80 | 300 | 0 | 0 | 0 | |||
| Unit 3 | 50 | 150 | 200 | 11.0 | 0.0090 | PV 3 | 50 | 150 | 0 | 0 | 0 | |||
| Unit 3 | 50 | 200 | 220 | 10.5 | 0.0080 | PV 3 | 50 | 200 | 0 | 0 | 0 | |||
| Unit 3 | 50 | 120 | 190 | 12.0 | 0.0075 | PV 3 | 50 | 120 | 190 | 12.0 | 0.0075 | |||
| Coeff. without PV | Coeff. with PV | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Unit | Pmin (MW) |
Pmax (MW) |
ai ($/MW2h) |
bi ($/MWh) | ci ($/MW) | Unit | Pmin (MW) |
Pmax (MW) |
ai ($/MW2h) |
bi ($/MWh) | ci ($/MW) | |
| Unit 1 | 150 | 455 | 671 | 10.10 | 0.0003 | Unit 1 | 150 | 455 | 671 | 10.10 | 0.0003 | |
| Unit 2 | 150 | 455 | 574 | 10.20 | 0.0001 | Unit 2 | 150 | 455 | 574 | 10.20 | 0.0001 | |
| Unit 3 | 20 | 130 | 374 | 8.80 | 0.0011 | PV 1 | 20 | 130 | 0 | 0 | 0 | |
| Unit 4 | 20 | 130 | 374 | 8.80 | 0.0011 | PV 2 | 20 | 130 | 0 | 0 | 0 | |
| Unit 5 | 150 | 470 | 461 | 10.40 | 0.0002 | Unit 3 | 150 | 470 | 461 | 10.40 | 0.0002 | |
| Unit 6 | 135 | 460 | 630 | 10.10 | 0.0003 | Unit 4 | 135 | 460 | 630 | 10.10 | 0.0003 | |
| Unit 7 | 135 | 465 | 548 | 9.80 | 0.0003 | Unit 5 | 135 | 465 | 548 | 9.80 | 0.0003 | |
| Unit 8 | 60 | 300 | 227 | 11.20 | 0.0003 | Unit 6 | 60 | 300 | 227 | 11.20 | 0.0003 | |
| Unit 9 | 25 | 162 | 173 | 11.20 | 0.0008 | PV 3 | 25 | 162 | 0 | 0 | 0 | |
| Unit 10 | 25 | 160 | 175 | 10.70 | 0.0012 | PV 4 | 25 | 160 | 0 | 0 | 0 | |
| Unit 11 | 20 | 80 | 186 | 10.20 | 0.0035 | PV 5 | 20 | 80 | 0 | 0 | 0 | |
| Unit 12 | 20 | 80 | 230 | 9.90 | 0.0055 | PV 6 | 20 | 80 | 0 | 0 | 0 | |
| Unit 13 | 25 | 85 | 225 | 13.10 | 0.0003 | PV 7 | 25 | 85 | 0 | 0 | 0 | |
| Unit 14 | 15 | 55 | 309 | 12.10 | 0.0019 | PV 8 | 15 | 55 | 0 | 0 | 0 | |
| Unit 15 | 15 | 55 | 323 | 12.40 | 0.0044 | Unit 7 | 15 | 55 | 323 | 12.40 | 0.0044 | |
| Best cost (million $) (Iterations) | |||||||
| Unit | PSO plants Model | 1st | 200th | Difference | % Best cost/day | Compared Best cost | |
| 3- Units | 3 Thermal | 8234.97 | 8230.38 | 4.5932 | 0.055 | 8234.07 [55] 8194.35 [56] |
|
| 2 Thermal and 1 PV | 117238.1 | 95283.67 | 107709.5 | 91.87 | |||
| 6- Units | 6 Thermal | 33727.3 | 15709.8 | 29396.0 | 46.55 | 15447 [51; 53] 15450.00 [55] |
|
| 2 Thermal and 4 PV | 209331.5 | 201411.1 | 7920.48 | 3.784 | |||
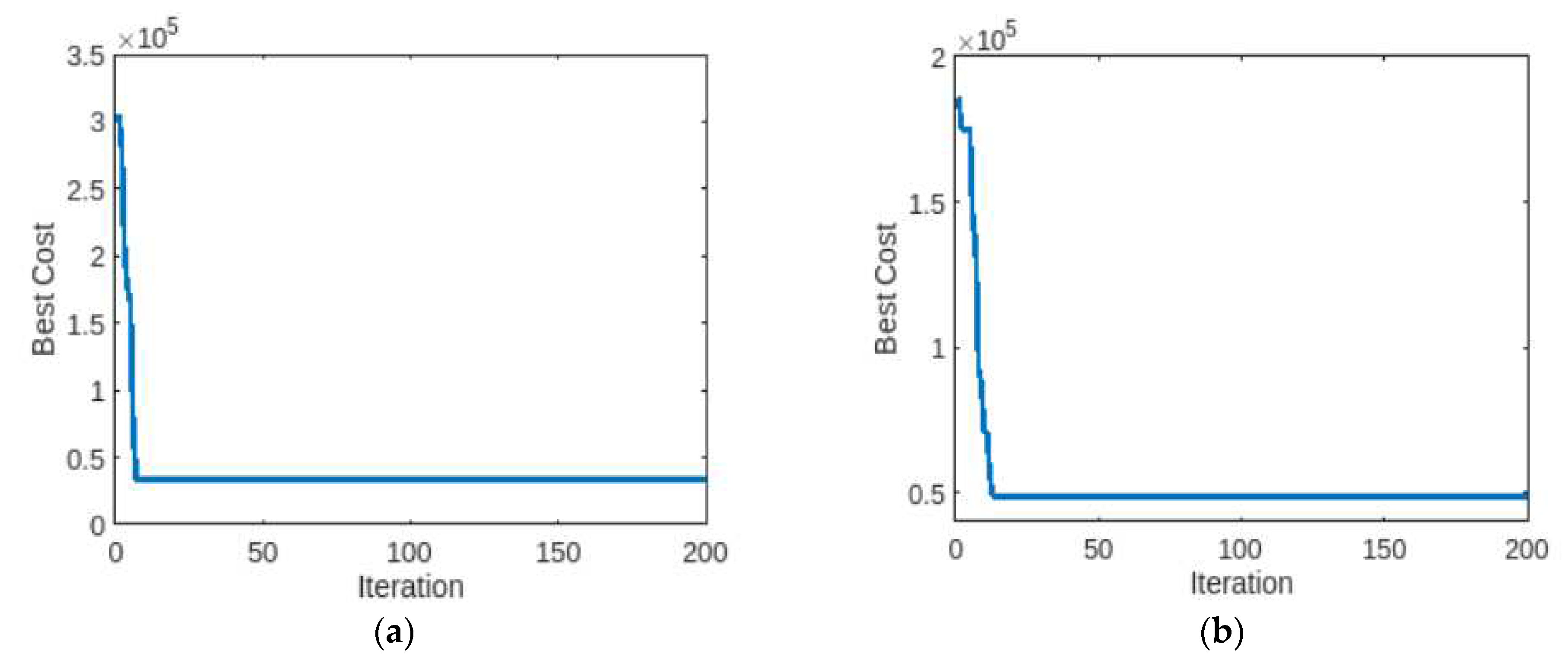
| 15- Units | 15 Thermal | 306054.0 | 33330.2 | 137487.9 | 89.10 | 33049 [51; 53] 32708 [54] 32858.00 [55] |
|
| 7 Thermal and 8 PV | 186141.8 | 48653.8 | 272723.7 | 73.86 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





