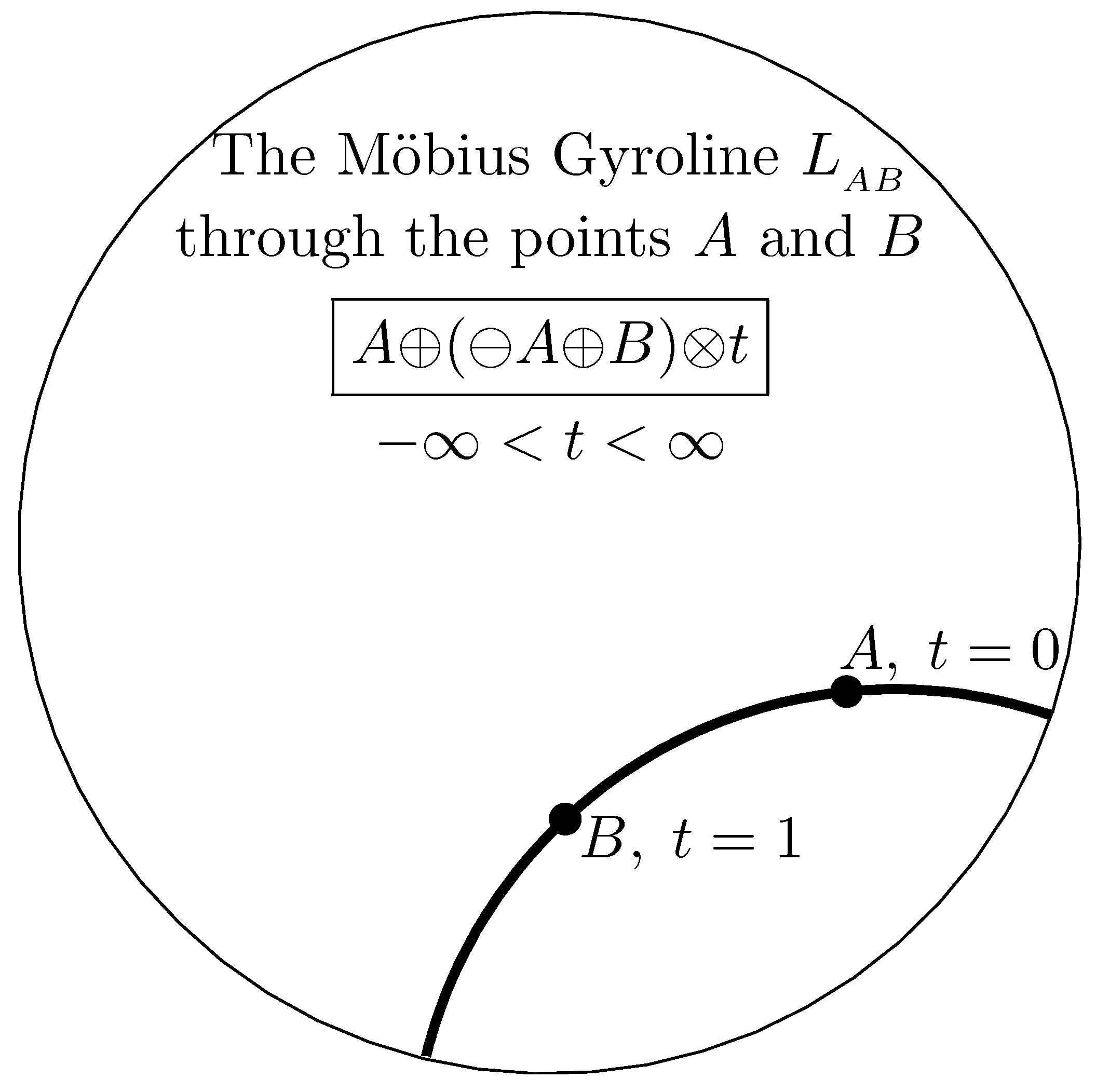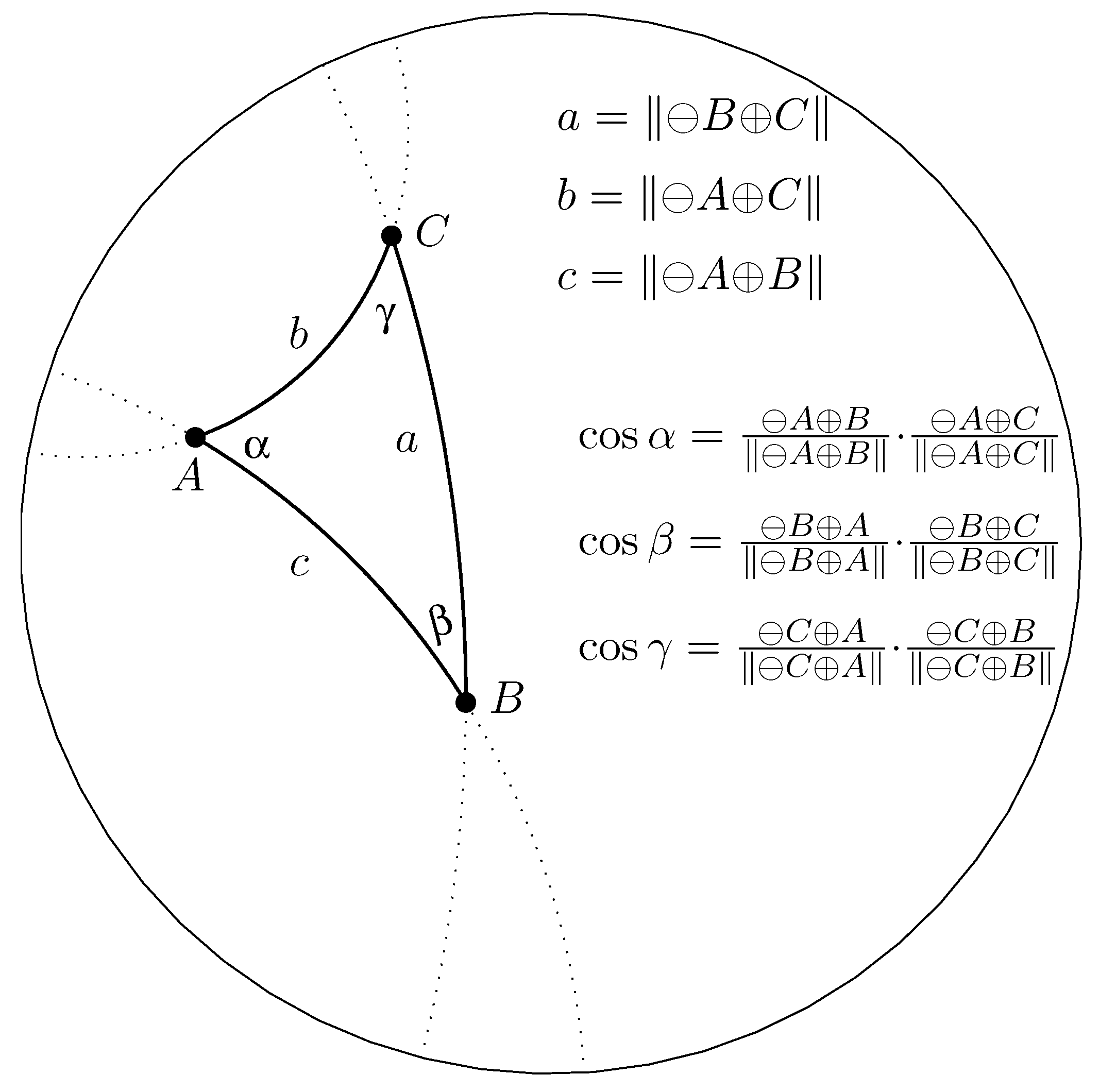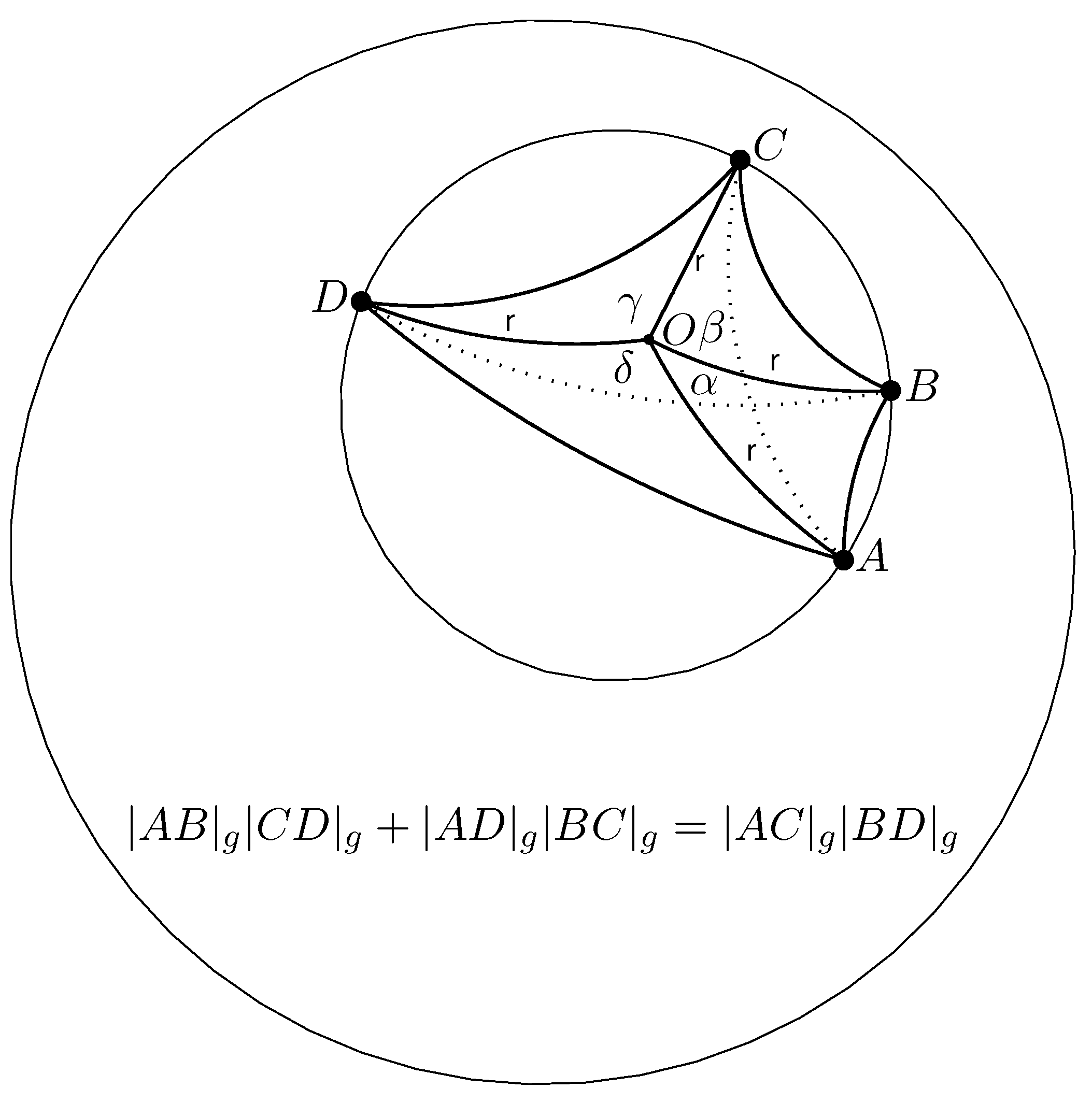The Hyperbolic Ptolemy’s Theorem in the Poincare Ball Model of Analytic Hyperbolic Geometry

1. Introduction

Analytic hyperbolic geometry is the hyperbolic geometry of Lobachevsky and Bolyai, studied analytically since 1988 [1] in full analogy with the study of Euclidean geometry analytically [2,3,4,5]. In the analytic study of hyperbolic geometry, Einstein addition and Möbius addition capture analogies with vector addition as follows:

(1)

Vector addition admits scalar multiplication, giving rise to vector spaces which, in turn, form the algebraic setting for analytic Euclidean geometry. In full analogy,

(2)

Einstein addition (of relativistically admissible velocities) admits scalar multiplication, giving rise to Einstein gyrovector spaces which, in turn, form the algebraic setting for the Klein ball model of analytic hyperbolic geometry [2,3,4,5,6,7]. Accordingly, the Klein model of hyperbolic geometry is also known as the relativistic model of hyperbolic geometry [8,9]. Furthermore, in full analogy,

(3)

Möbius addition [10] admits scalar multiplication, giving rise to Möbius gyrovector spaces which, in turn, form the algebraic setting for the Poincaré ball model of analytic hyperbolic geometry [2,3,4,5,6].

In the same way that the Euclidean vector plane admits trigonometry, each of Einstein gyrovector plane and Möbius gyrovector plane admits hyperbolic trigonometry, called gyrotrigonometry.

Ptolemy’s Theorem in Euclidean plane geometry, named after the Greek astronomer and mathematician Claudius Ptolemy, is well known.

(1)

In [8] we presented the well-known proof of Ptolemy’s Theorem in terms of the standard trigonometry of analytic Euclidean plane geometry. In particular, the associated law of cosines was employed.

(2)

In full analogy, in [8] we discovered the hyperbolic Ptolemy’s Theorem in the Klein (relativistic) model of analytic hyperbolic plane geometry. The proof of the resulting hyperbolic Ptolemy’s Theorem is obtained by means of the gyrotrigonometry that the Klein model of analytic hyperbolic geometry admits. In particular, the associated law of gyrocosines was employed.

(3)

In full analogy, in this article we discover the hyperbolic Ptolemy’s Theorem in the Poincaré ball model of analytic hyperbolic plane geometry. The proof of the resulting hyperbolic Ptolemy’s Theorem is obtained by means of the gyrotrigonometry that the Poincaré model of analytic hyperbolic geometry admits. In particular, the associated law of gyrocosines is employed.

As a prerequisite for a fruitful reading of this article it is recommended familiarity with Ref. [8], where important background about gyrogroups, gyrovector spaces and gyrotrigonometry is reviewed. In particular, the duality of trigonometry and gyrotrigonometry is reviewed and illustrated.

2. Möbius Addition and Scalar Multiplication

Let $s>0$ be any positive constant and let ${\mathbb{R}}^n=({\mathbb{R}}^n,+,·)$ be the Euclidean n-space, $n\in \mathbb{N}$, endowed with the common vector addition, +, and inner product, ·, and let ${\mathbb{R}}_s^n$ be the s-ball given by

$${\mathbb{R}}_s^n=\{\mathbf{v}\in {\mathbb{R}}^n:\parallel \mathbf{v}\parallel <s\}.$$

(1)

Möbius addition is a binary operation, ⊕, in the s-ball ${\mathbb{R}}_s^n$ given by

$$\mathbf{u}\oplus \mathbf{v}=\frac{(1+\frac{2}{s^2}\mathbf{u}·\mathbf{v}+\frac{1}{s^2}{\parallel \mathbf{v}\parallel }^2)\mathbf{u}+(1-\frac{1}{s^2}{\parallel \mathbf{u}\parallel }^2)\mathbf{v}}{1+\frac{2}{s^2}\mathbf{u}·\mathbf{v}+\frac{1}{s^4}{\parallel \mathbf{u}\parallel }^2{\parallel \mathbf{v}\parallel }^2}$$

(2)

where · and $\parallel ·\parallel$ are the inner product and the norm that the ball ${\mathbb{R}}_s^n$ inherits from its ambient space ${\mathbb{R}}^n$ [10].

Note that in the Euclidean limit, $s\to \infty$, the s-ball ${\mathbb{R}}_s^n$ expands to the whole of its ambient space ${\mathbb{R}}^n$, and Möbius addition tends to the common vector addition, $\mathbf{u}+\mathbf{v}$, in ${\mathbb{R}}^n$.

Möbius addition in ${\mathbb{R}}_s^n$, $n\ge 2$, is neither commutative nor associative. Hence, the pair $({\mathbb{R}}_s^n,\oplus )$ does not form a group. However, it forms a gyrocommutative gyrogroup as shown, for instance, in [3,4]. A gyrogroup is a group-like structure, a prominent concrete example of which is given by Einstein addition of relativistically admissible velocities studied, for instance, in [3,4,8]. The elegant road from Möbius to gyrogroups is revealed in [10].

The definition of gyrogroups, some of which are gyrocommutative, is presented, for instance, in [3,4,7,8].

Möbius addition, ⊕, admits scalar multiplication, ⊗, turning Möbius gyrogroups into Möbius gyrovector spaces $({\mathbb{R}}_s^n,\oplus ,\otimes )$. Möbius scalar multiplication is given by ([3] Sect. 8.12), ([4], Sect. 6.14)

$$\begin{array}{cc}\hfill r\otimes \mathbf{v}& =s\frac{{\left({\displaystyle 1+\frac{\parallel \mathbf{v}\parallel }{s}}\right)}^r-{\left({\displaystyle 1-\frac{\parallel \mathbf{v}\parallel }{s}}\right)}^r}{{\left({\displaystyle 1+\frac{\parallel \mathbf{v}\parallel }{s}}\right)}^r+{\left({\displaystyle 1-\frac{\parallel \mathbf{v}\parallel }{s}}\right)}^r}\frac{\mathbf{v}}{\parallel \mathbf{v}\parallel }\hfill \\ \hfill & =s\tanh \left(r{\tanh }^{-1}\frac{\parallel \mathbf{v}\parallel }{s}\right)\frac{\mathbf{v}}{\parallel \mathbf{v}\parallel }\hfill \end{array}$$

(3)

where $r\in \mathbb{R}$, $\mathbf{v}\in {\mathbb{R}}_s^n$, $\mathbf{v}\ne \mathbf{0}$; and $r\otimes \mathbf{0}=\mathbf{0}$.

Gyrovector spaces are generalized vector spaces, the definition of which is presented, for instance, in [4,8]. The resulting (i) Möbius gyrovector spaces form the algebraic setting for the Cartesian Poincaré ball model of analytic hyperbolic geometry, just as (ii) Einstein gyrovector spaces form the algebraic setting for the Cartesian Klein ball model of analytic hyperbolic geometry; and, just as (iii) vector spaces form the algebraic setting for the standard Cartesian model of analytic Euclidean geometry [2].

Gyrovector planes admit hyperbolic trigonometry, called gyrotrigonometry, just as vector planes admit the common trigonometry. The law of gyrocosines in the gyrotrigonometry of the Klein model of hyperbolic geometry is employed in [8] for the proof of Ptolemy’s Theorem in the Klein model. Similarly, the law of gyrocosines in the gyrotrigonometry of the Poincaré ball model of hyperbolic geometry is employed in this article for the proof of Ptolemy’s Theorem in the Poincaré model.

3. Gyrotrigonometry in Möbius Gyrovector Planes and its Law of Gyrocosines

Möbius addition and scalar multiplication enable Möbius gyrolines to be expressed analytically in a way fully analogous to lines in analytic Euclidean geometry. The unique Euclidean line that passes through two distinct points $A,B\in {\mathbb{R}}^n$ is given analytically by

$$A+(-A+B)t,$$

(4)

$t\in \mathbb{R}$. In full analogy, the unique Möbius gyroline that passes through two distinct points $A,B\in {\mathbb{R}}_s^n$ in a Möbius gyrovector space $({\mathbb{R}}_s^n,\oplus ,\otimes )$ is given analytically by

$$A\oplus (\ominus A\oplus B)\otimes t,$$

(5)

$t\in \mathbb{R}$, where $\ominus A=-A$, depicted in Figure 1 for $n=2$.

A Möbius gyroline (5) is a circular arc that approaches the boundary of the s-ball ${\mathbb{R}}_s^n$ orthogonally. It passes at the point A when $t=0$, and at the point B when $t=1$, and it forms a geodesic in the Poincaré ball model of hyperbolic geometry [6].

The gyrosegment $AB$ that links the two distinct points $A,B\in {\mathbb{R}}_s^n$ is given by (5) with $0\le t\le 1$. The gyrolength of a gyrosegment $AB$ is

$${\left|AB\right|}_h:=\parallel \ominus A\oplus B\parallel ,$$

(6)

$A,B\in {\mathbb{R}}_s^n$, just as the length of a segment $AB$ is

$${\left|AB\right|}_e:=\parallel -A+B\parallel ,$$

(7)

$A,B\in {\mathbb{R}}^n$.

A gyrotriangle $ABC$ whose gyrosides are the gyrosegments $AB$, $BC$ and $AC$ in ${\mathbb{R}}_s^n$, along with its gyroangles, is depicted in Figure 2. The gyrolengths of the gyrosides of gyrotriangle $ABC$ are

$$\begin{array}{cc}\hfill a& :={\left|BC\right|}_h=\parallel \ominus B\oplus C\parallel \hfill \\ \hfill b& :={\left|AC\right|}_h=\parallel \ominus A\oplus C\parallel \hfill \\ \hfill c& :={\left|AB\right|}_h=\parallel \ominus A\oplus B\parallel ,\hfill \end{array}$$

(8)

as shown in Figure 2.

Gyrotrigonometry in Möbius gyrovector spaces is studied, for instance, in ([4] Sect. 8.5). In gyrotrigonometry the gyrocosine of a gyroangle $\alpha =\angle BAC$, shown in Figure 2, is given by

$$\cos \alpha =\frac{\ominus A\oplus B}{\parallel \ominus A\oplus B\parallel }·\frac{\ominus A\oplus C}{\parallel \ominus A\oplus C\parallel },$$

(9)

just as in trigonometry the cosine of an angle $\alpha$, in the Euclidean counterpart of Figure 2, is given by

$$\cos \alpha =\frac{-A+B}{\parallel -A+B\parallel }·\frac{-A+C}{\parallel -A+C\parallel }.$$

(10)

Accordingly, viewing $\cos \alpha$ trigonometrically yields (10), while viewing $\cos \alpha$ gyrotrigonometrically yields (9). The resulting trigonometry and gyrotrigonometry duality is illustrated in ([8] Sect. 11). The usefulness of the analogies that (5) and (4) share suggests that the analogies that (9) and (10) share will prove useful as well. We will see in this article that this is, indeed, the case.

An important trigonometric identity that we will view gyrotrigonometrically as well is

$$\sin \frac{\alpha }{2}\sin \frac{\gamma }{2}+\sin \frac{\beta }{2}\sin \frac{\delta }{2}=\sin \frac{\alpha +\beta }{2}\sin \frac{\beta +\gamma }{2}$$

(11)

for any $\alpha ,\beta ,\gamma \in \mathbb{R}$, where $\delta =2\pi -(\alpha +\beta +\gamma )$. Identity (11) can be realized not only trigonometrically (i) in the Euclidean plane, but also gyrotrigonometrically (ii) in the Einstein gyrovector plane, and (iii) in the Möbius gyrovector plane. These three distinct realizations of (11) are consistent owing to the duality of trigonometry and gyrotrigonometry, as explained in [8].

Indeed, (i) realizing (11) in trigonometry gives rise to Ptolemy’s Theorem in Euclidean geometry, as shown in [8]; (ii) realizing (11) in Einstein gyrotrigonometry gives rise to Ptolemy’s Theorem in the Klein ball (relativistic) model of hyperbolic geometry, as shown in [8]; and (iii) realizing (11) in Möbius gyrotrigonometry gives rise to Ptolemy’s Theorem in the Poincaré ball model of hyperbolic geometry, as we will see in Section 4.

Having the gyrotriangle notation in Figure 2, we are now in the position to state the law of gyrocosines in a Nöbius gyrovector plane, verified in ([3] Sect. 8.4) and ([4] Sect. 8.5).

Theorem 1.

(Law of gyrocosines in Möbius gyrovector spaces).Let $ABC$ be a gyrotriangle in a Möbius gyrovector plane $({\mathbb{R}}_s^n,\oplus ,\otimes )$ with vertices $A,B,C\in {\mathbb{R}}_s^2$, side gyrolengths $0<a,b,c<s$, and gyroangles $\alpha ,\beta ,\gamma$, as shown in Figure 2. Then, the gyrosides and gyroangles of the gyrotriangle satisfy the law of gyrocosines

$$c^2=\frac{a^2+b^2-2ab\cos \gamma }{1+a_s^2{b}_s^2-2a_s{b}_s\cos \gamma }$$

(12)

and, equivalently,

$$\cos \gamma =\frac{a^2+b^2-c^2-a_s^2{b}_s^2{c}^2}{2ab(1-c_s^2)}$$

(13)

where $a_s=a/s$, $b_s=b/s$, $c_s=c/s$, with similar relations involving the other gyrosides and gyroangles of the gyrotriangle.

Note that in the Euclidean limit, $s\to \infty$, the law of gyrocosines (12) descends to the law of cosines,

$$c^2=a^2+b^2-2ab\cos \gamma$$

(14)

as expected. Also, note that in the context of Euclidean geometry, $\cos \gamma$ in (14) is viewed trigonometrically, as in (10), while in the context of hyperbolic geometry, $\cos \gamma$ in (12)-(13) is viewed gyrotrigonometrically, as in (9) and as shown in Figure 2.

4. Ptolemy’s Theorem in the Poincaré Ball Model of Hyperbolic Geometry

Applying the law of gyrocosines (13) to the O-gyrovertex gyroangle $\alpha =\angle AOB$ of gyrotriangle $ABO$, shown in Figure 3, yields

$$\cos \alpha =\frac{2r^2-{\left|AB\right|}_h^2-\frac{r^4}{s^4}{\left|AB\right|}_h^2}{2r^2(1-\frac{{\left|AB\right|}_h^2}{s^2})},$$

(15)

noting that $a,b,c$ and $\gamma$ in (13) are, respectively, realized in (15) by ${r,r,\left|AB\right|}_h$ and $\alpha$.

We now employ the trigonometric and, hence, gyrotrigonometric identity ${\sin }^2(\alpha /2)=(1-\cos \alpha )/2$, obtaining from (15) the equation

$${\sin }^2\frac{\alpha }{2}=\frac{1-\cos \alpha }{2}=\frac{{(s^2-r^2)}^2}{4s^2{r}^2(s^2-{\left|AB\right|}_h^2)}{\left|AB\right|}_h^2$$

(16)

so that, finally,

$$\sin \frac{\alpha }{2}=\frac{s^2-r^2}{2sr\sqrt{s^2-{\left|AB\right|}_h^2}}{\left|AB\right|}_h=\frac{1-r_s^2}{2r}{\gamma }_{{\left|AB\right|}_h}{\left|AB\right|}_h$$

(17)

where $r_s=r/s$, and where ${\gamma }_{{\left|AB\right|}_h}$ is the Lorentz gamma factor of ${\left|AB\right|}_h$, given by

$${\gamma }_{{\left|AB\right|}_h}=\frac{1}{\sqrt{1-\frac{{\left|AB\right|}_h^2}{s^2}}}.$$

(18)

Repeating the result in (17) for the six O-gyrovertex gyrotriangle gyroangles $\alpha$, $\beta$, $\gamma$, $\delta$, $\alpha +\beta$, and $\beta +\gamma$ in Figure 3 yields the following six equations

$$\begin{array}{cc}\hfill \sin \frac{\alpha }{2}& =\frac{1-r_s^2}{2r}{\gamma }_{{\left|AB\right|}_h}{\left|AB\right|}_h=:\frac{1-r_s^2}{2r}{\left|AB\right|}_g\hfill \\ \hfill \sin \frac{\beta }{2}& =\frac{1-r_s^2}{2r}{\gamma }_{{\left|BC\right|}_h}{\left|BC\right|}_h=:\frac{1-r_s^2}{2r}{\left|BC\right|}_g\hfill \\ \hfill \sin \frac{\gamma }{2}& =\frac{1-r_s^2}{2r}{\gamma }_{{\left|CD\right|}_h}{\left|CD\right|}_h=:\frac{1-r_s^2}{2r}{\left|CD\right|}_g\hfill \\ \hfill \sin \frac{\delta }{2}& =\frac{1-r_s^2}{2r}{\gamma }_{{\left|AD\right|}_h}{\left|AD\right|}_h=:\frac{1-r_s^2}{2r}{\left|AD\right|}_g\hfill \\ \hfill \sin \frac{\alpha +\beta }{2}& =\frac{1-r_s^2}{2r}{\gamma }_{{\left|AC\right|}_h}{\left|AC\right|}_h=:\frac{1-r_s^2}{2r}{\left|AC\right|}_g\hfill \\ \hfill \sin \frac{\beta +\gamma }{2}& =\frac{1-r_s^2}{2r}{\gamma }_{{\left|BD\right|}_h}{\left|BD\right|}_h=:\frac{1-r_s^2}{2r}{\left|BD\right|}_g\hfill \end{array}$$

(19)

where

$${\left|AB\right|}_g={\gamma }_{{\left|AB\right|}_h}{\left|AB\right|}_h$$

(20)

and so forth. We call ${\left|AB\right|}_g$ the g-modified gyrolength of gyroside $AB$, and so forth.

Substituting (19) into the gyrotrigonometric identity (11) yields the result (21) of Ptolemy’s Theorem in the Poincaré ball model of hyperbolic geometry.

Theorem 2.

(Ptolemy’s Theorem in the Poincaré Ball Model of Hyperbolic Geometry).Let $ABC$ be a gyrocyclic gyroquadrilateral, shown in Figure 3. Then, the product of the g-modified gyrodiagonals equals the sum of the products of the g-modified opposite gyrosides, that is

$${\left|AB\right|}_g{\left|CD\right|}_g+{\left|AD\right|}_g{\left|BC\right|}_g={\left|AC\right|}_g{\left|BD\right|}_g.$$

(21)

Clearly, in the Euclidean limit, $s\to \infty$, the hyperbolic Ptolemy’s Theorem (21) descends to its Euclidean counterpart, studied in [8].

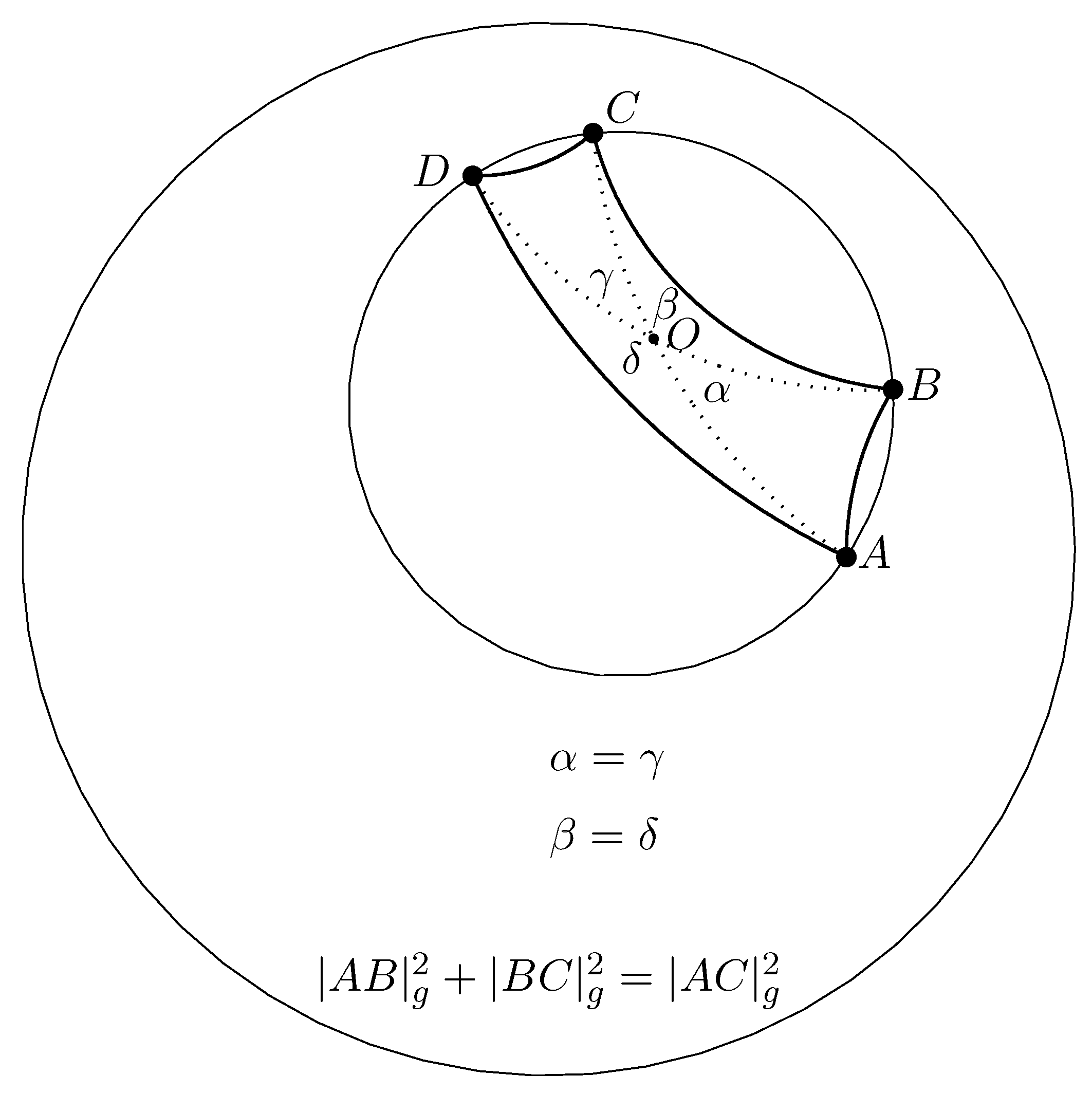
5. Gyrodiametric Gyrotriangles

Definition 1.

A gyrotriangle is gyrodiametric if one of its gyrosides coincides with a gyrodiameter of its circumgyrocircle.

In Euclidean geometry, a diametric triangle is right angled, the angle opposite to the diametric side being $\pi /2$. In contrast, non-Euclidean gyrodiametric gyrotriangles are not right gyroangled. But, they obey a Pythagorean-like identity, as theorem 3 asserts.

Definition 2.

A gyrocyclic gyroquadrilateral is gyrodiametric if its gyrodiagonals intersect at its circumgyrocenter, as shown in Figure 4.

A gyrodiametric gyroquadrilateral $ABCD$, shown in Figure 4, gives rise to the two gyrodiametric gyrotriangles $ABC$ and $ADC$. In the notation shown in Figure 4 we clearly have

$$\begin{array}{cc}\hfill \alpha & =\gamma \hfill \\ \hfill \beta & =\delta \hfill \\ \hfill \alpha +\beta & =\beta +\gamma .\hfill \end{array}$$

(22)

Hence, by (19), the equations in (22) yield, respectively, the equations

$$\begin{array}{cc}\hfill {\left|AB\right|}_g& ={\left|CD\right|}_g\hfill \\ \hfill {\left|BC\right|}_g& ={\left|AD\right|}_g\hfill \\ \hfill {\left|AC\right|}_g& ={\left|BD\right|}_g.\hfill \end{array}$$

(23)

Hence, it follows from (21) that

$${\left|AB\right|}_g^2+{\left|BC\right|}_g^2={\left|AC\right|}_g^2$$

(24)

where ${\left|AB\right|}_g$, ${\left|BC\right|}_g$ and ${\left|AC\right|}_g$ are the g-modified gyrolengths of the gyrosides of the gyrodiametric gyrotriangle $ABC$, as shown in Figure 4.

Formalizing the result in (24), we have proved the following theorem, where we use the notation in Figure 4.

Theorem 3.

(Gyrodiametric Gyrotriangle Pythagorean-like Equation).Let $ABC$ be a gyrodiametric gyrotriangle in a Möbius gyrovector space $({\mathbb{R}}_s^n,\oplus ,\otimes )$, where $AC$ is the gyrodiametric gyroside. Then, the gyrotriangle gyrosides obey the Pythagorean-like equation

$${\left|AB\right|}_g^2+{\left|BC\right|}_g^2={\left|AC\right|}_g^2$$

(25)

where

$$\begin{array}{cc}\hfill {\left|AB\right|}_g& ={\gamma }_{{\left|AB\right|}_h}{\left|AB\right|}_h\hfill \\ \hfill {\left|AB\right|}_h& =\parallel \ominus A\oplus B\parallel .\hfill \end{array}$$

(26)