Submitted:
21 June 2023
Posted:
25 June 2023
You are already at the latest version
Abstract
Keywords:
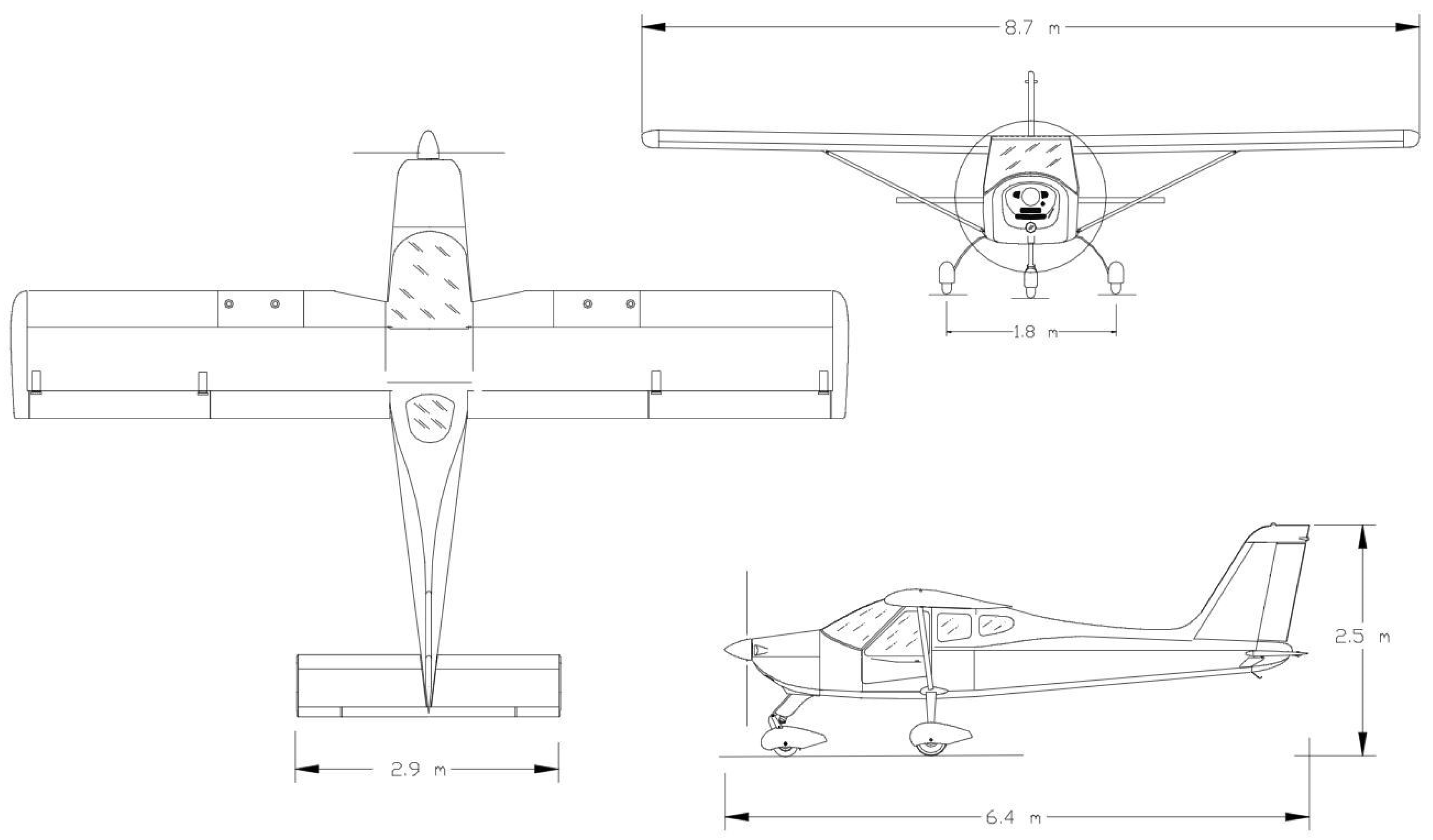
1. Introduction
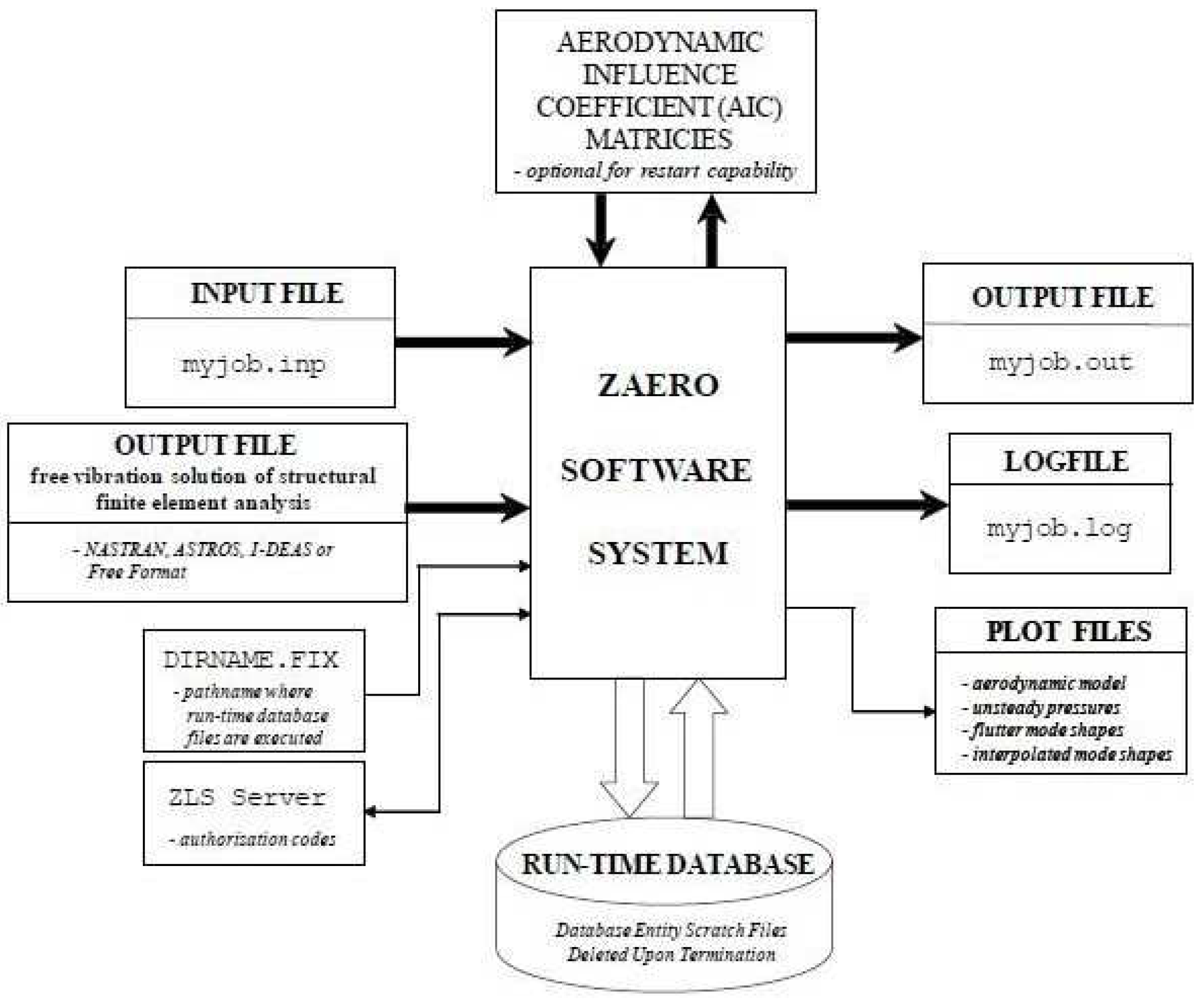
2. A brief overview of NASTRAN and ZAERO
- ZONA6 - Subsonic Unsteady Aerodynamics;
- ZSAP - Sonic Acceleration Potential Method;
- ZTAIC - Transonic Unsteady Aerodynamics using a Transonic Equivalent Strip Method;
- ZTRAN - Transonic Unsteady Aerodynamics using an Overset Field-Panel Method;
- ZONA7 - Supersonic Unsteady Aerodynamics;
- ZONA7U - Hypersonic Unsteady Aerodynamics.
- the input file which contains the executive control, case control, and bulk data sections that describe the aerodynamic model, flight conditions, etc.;
- the structural FEM output file containing the structure natural frequencies and mode shapes;
- DIRNAME.FIX which contains the pathname where the ZAERO run-time database files are to be located.
- About the outputs, a minimum of two files is generated for every ZAERO run. These are:
- the output file of the job;
- the log file which contains the elapsed and step CPU times for each module call during the execution of ZAERO. Additional output plot files can be generated through bulk data input requests.
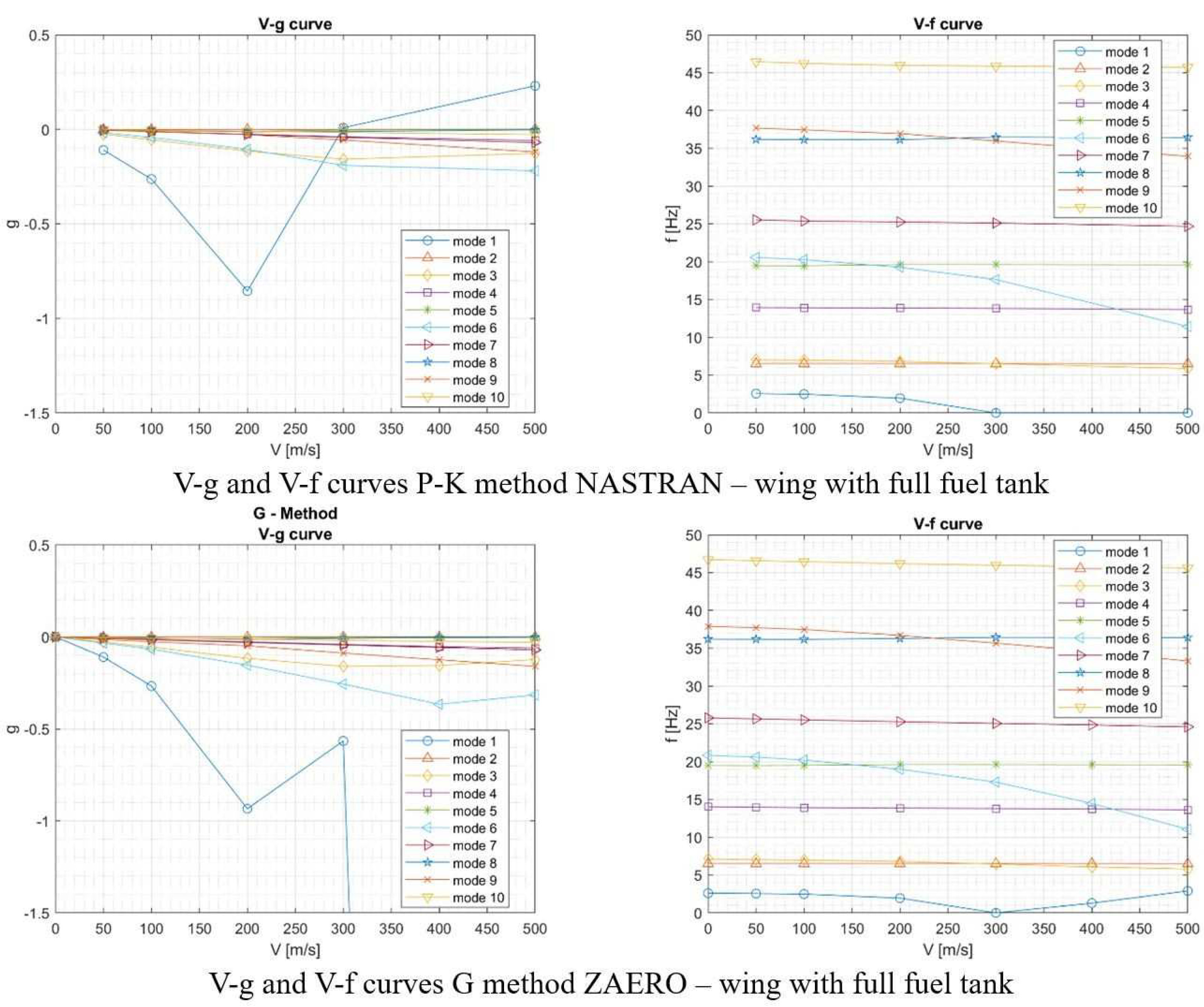
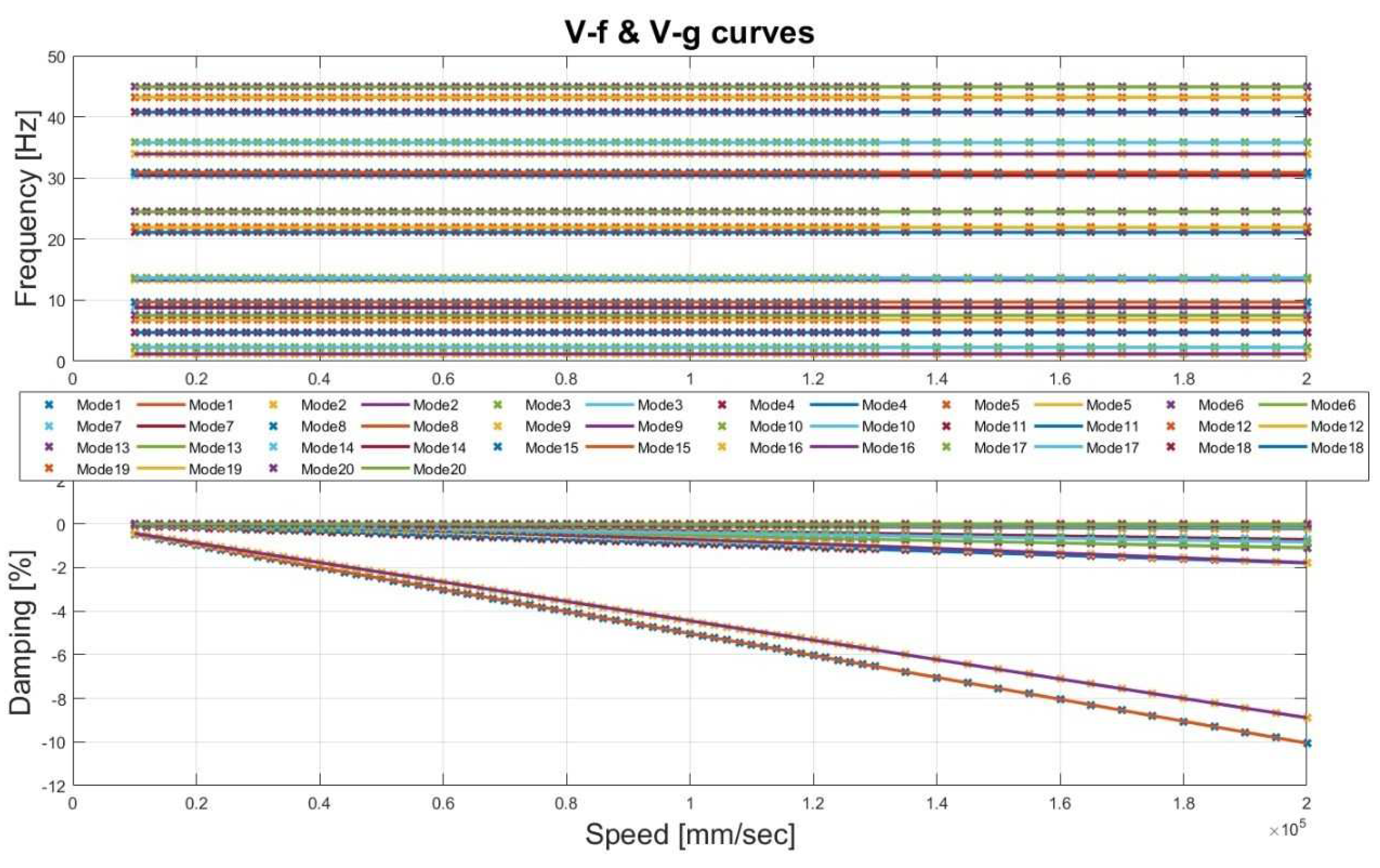
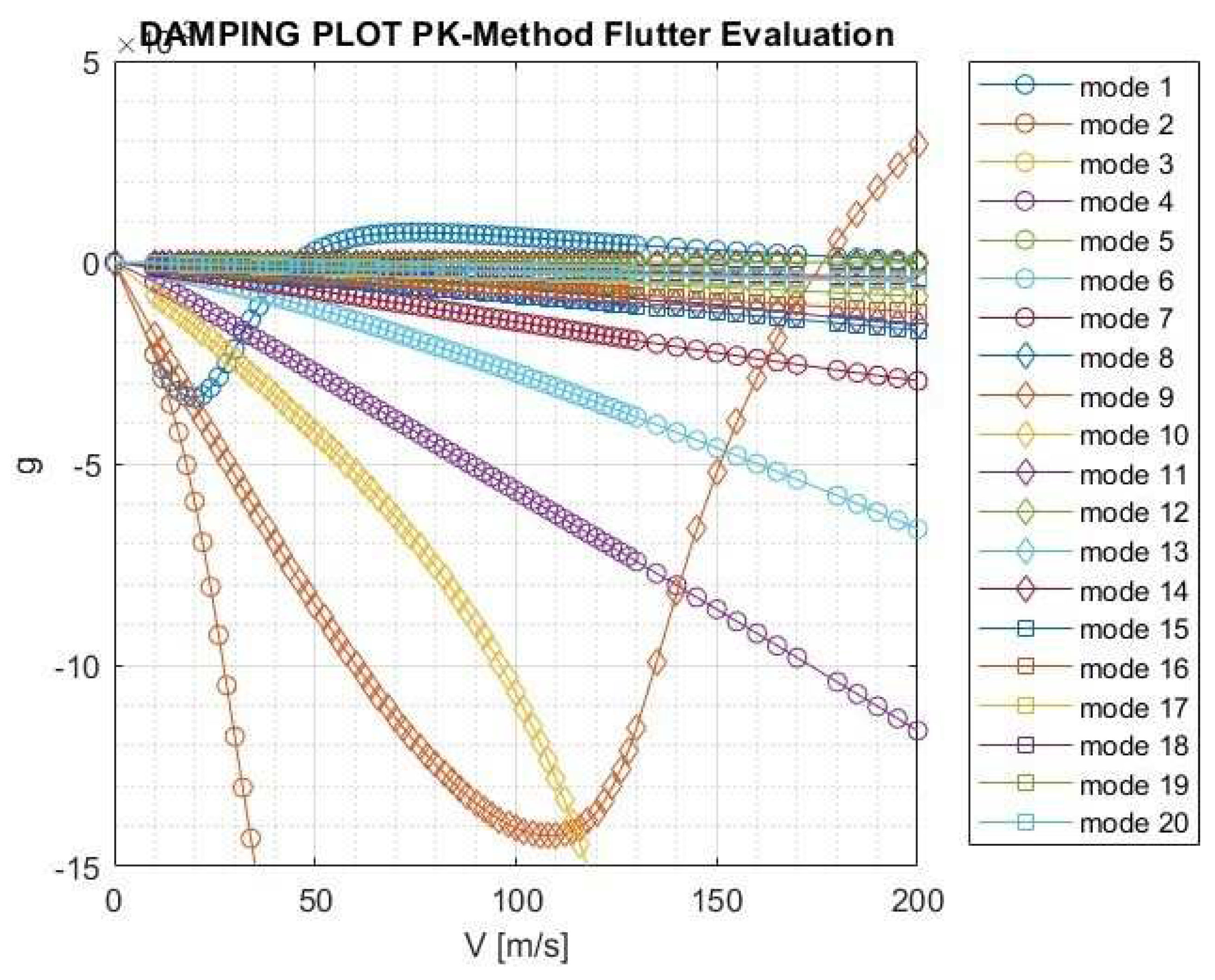
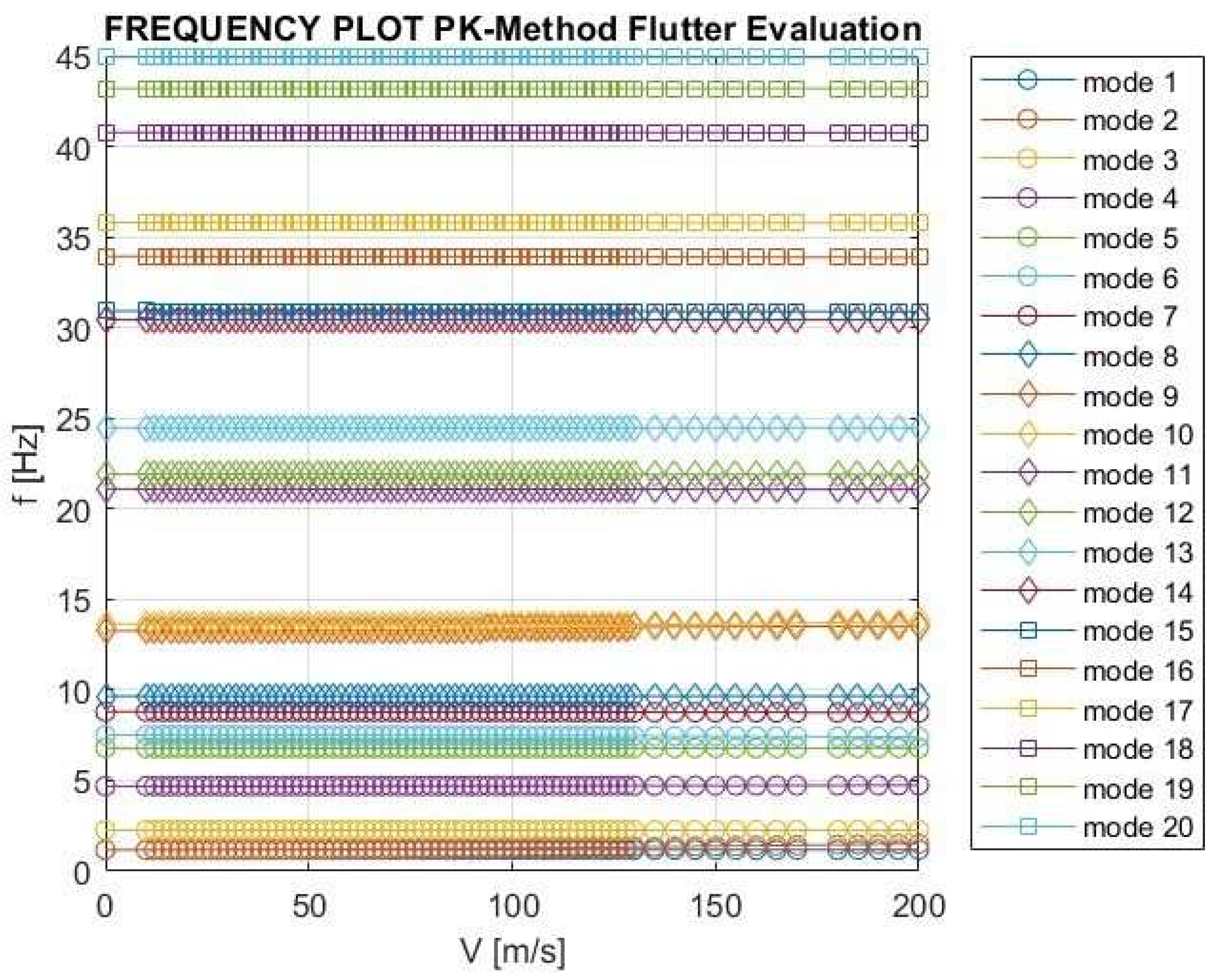
3. Comparison Between the g-Method and the P-K Method
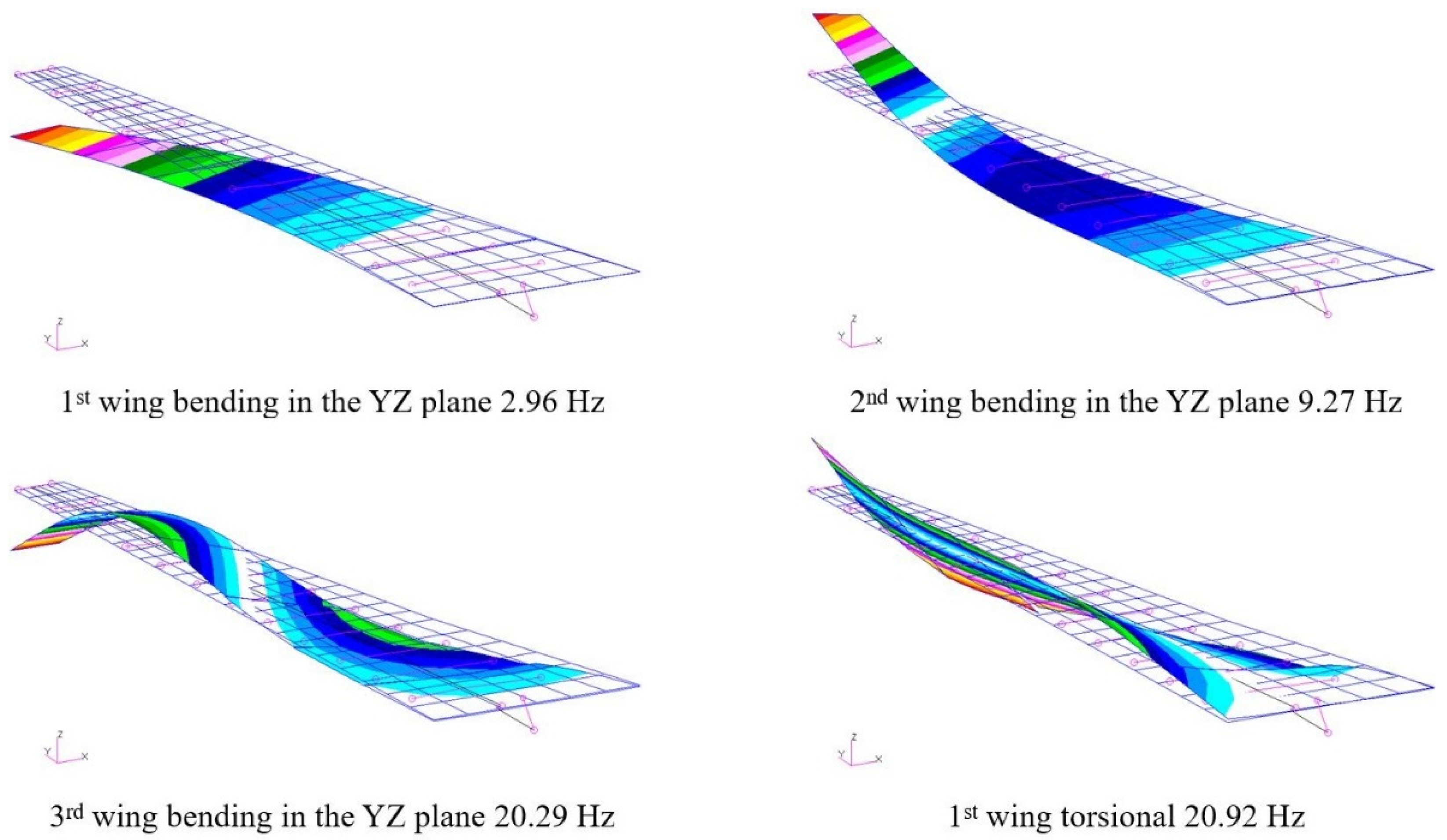
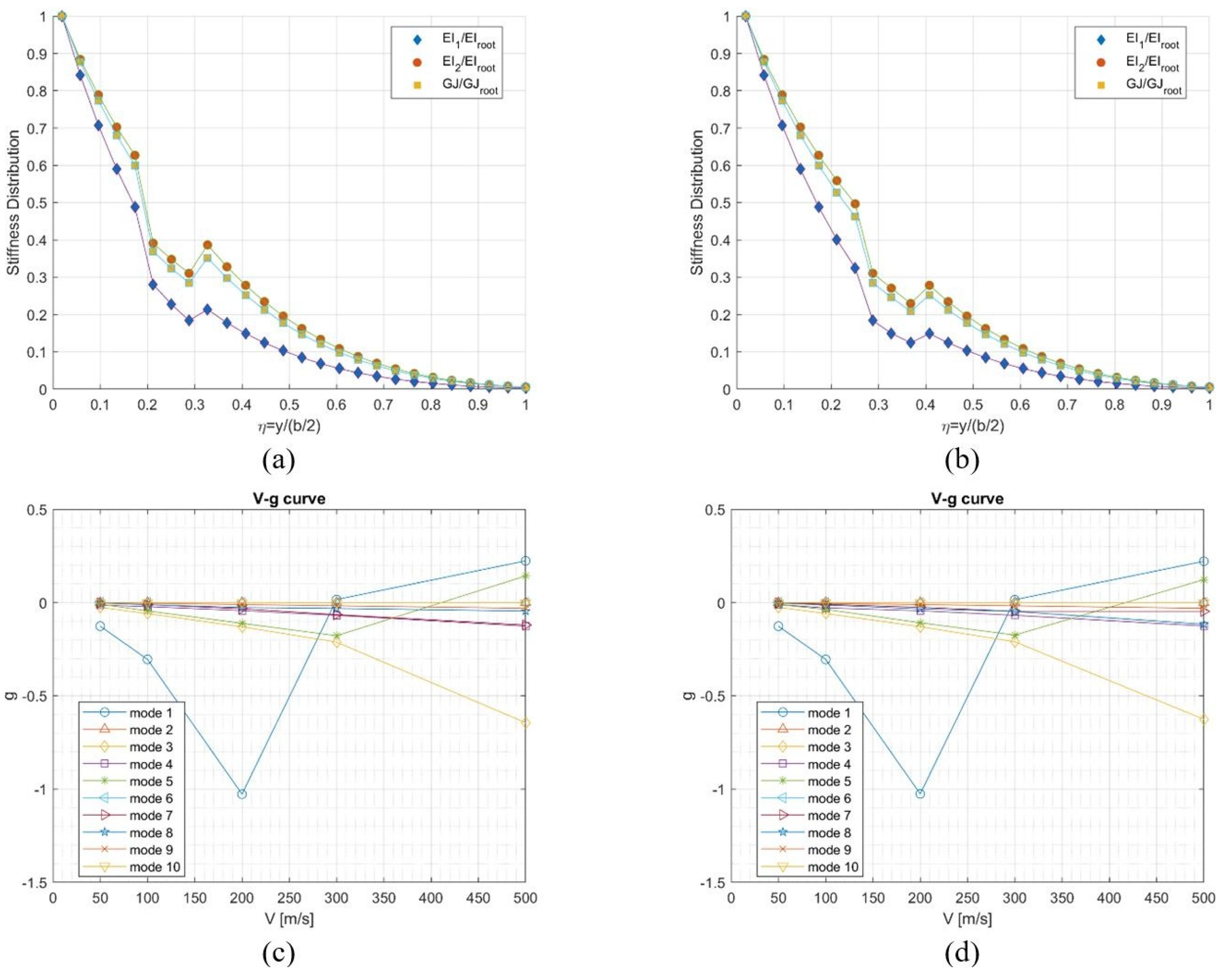
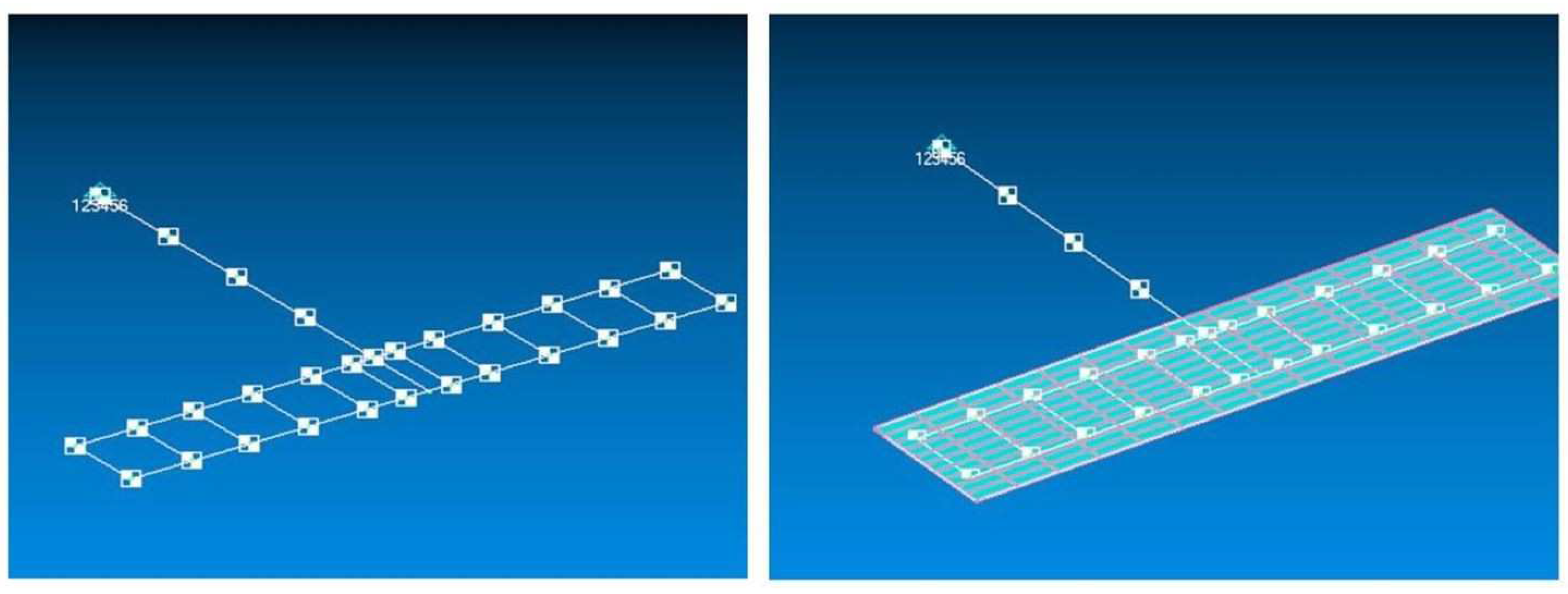
3.1. 1st Test Case - Forward swept wing
- in all the calculations the divergence condition for the wing is present, the latter being independent of the mass contributions from the model;
- in both cases, with and without fuel, the divergence rate does not change;
- the most critical condition for flutter occurs when the wing is unloaded (the addition of the masses of the fuel involves the removal of the bending frequencies from the torsional ones);
- when the wing tanks are full there is the annulment of the aerodynamic damping of the first torsional frequency at a speed of about 44% higher than in the case of empty tanks. From the V-f diagram, we can ob-serve a coalescence of the aforesaid frequency with the second flexural frequency.
| K method | G method | ||||
| mode | vf(m/s) | Freq. (Hz) | mode | vf(m/s) | Freq. (Hz) |
| 2 | 326.1 | 6.53 | 2 | 324.5 | 6.53 |
| 3 | 671.0 | 5.60 | 4 | 665.8 | 5.77 |
| 5 | 591.9 | 19.59 | 5 | 581.8 | 19.59 |
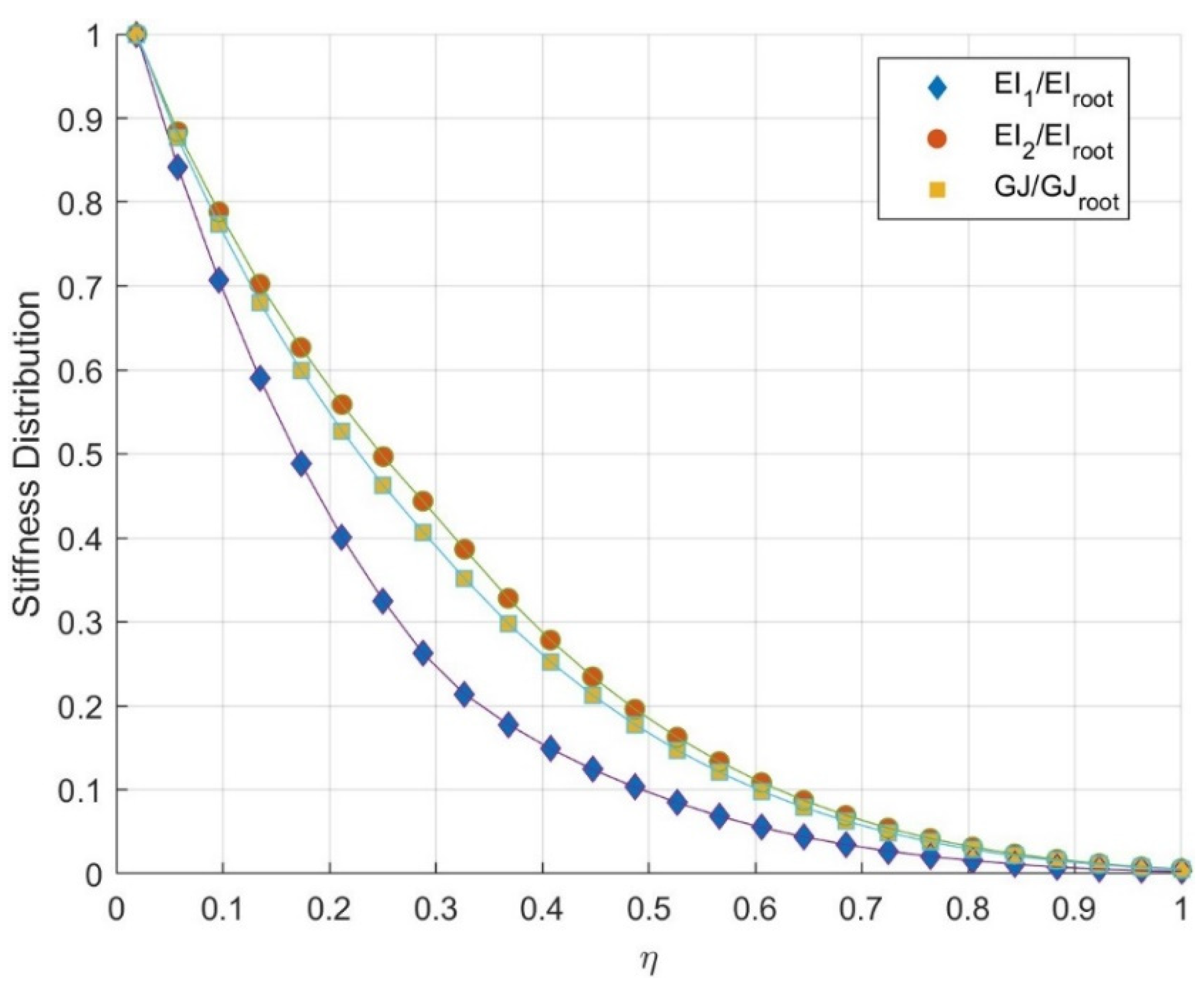
3.2. 2nd Test Case - Forward swept wing
| Reference | Stiffness var. | Stiffness var. |
| stiffness distribution | @ 20-30% | @ 30-40% |
| vf(m/s) | vf(∆%) | vf(∆%) |
| 430 | −4.7 | −2.8 |
4. Conclusions
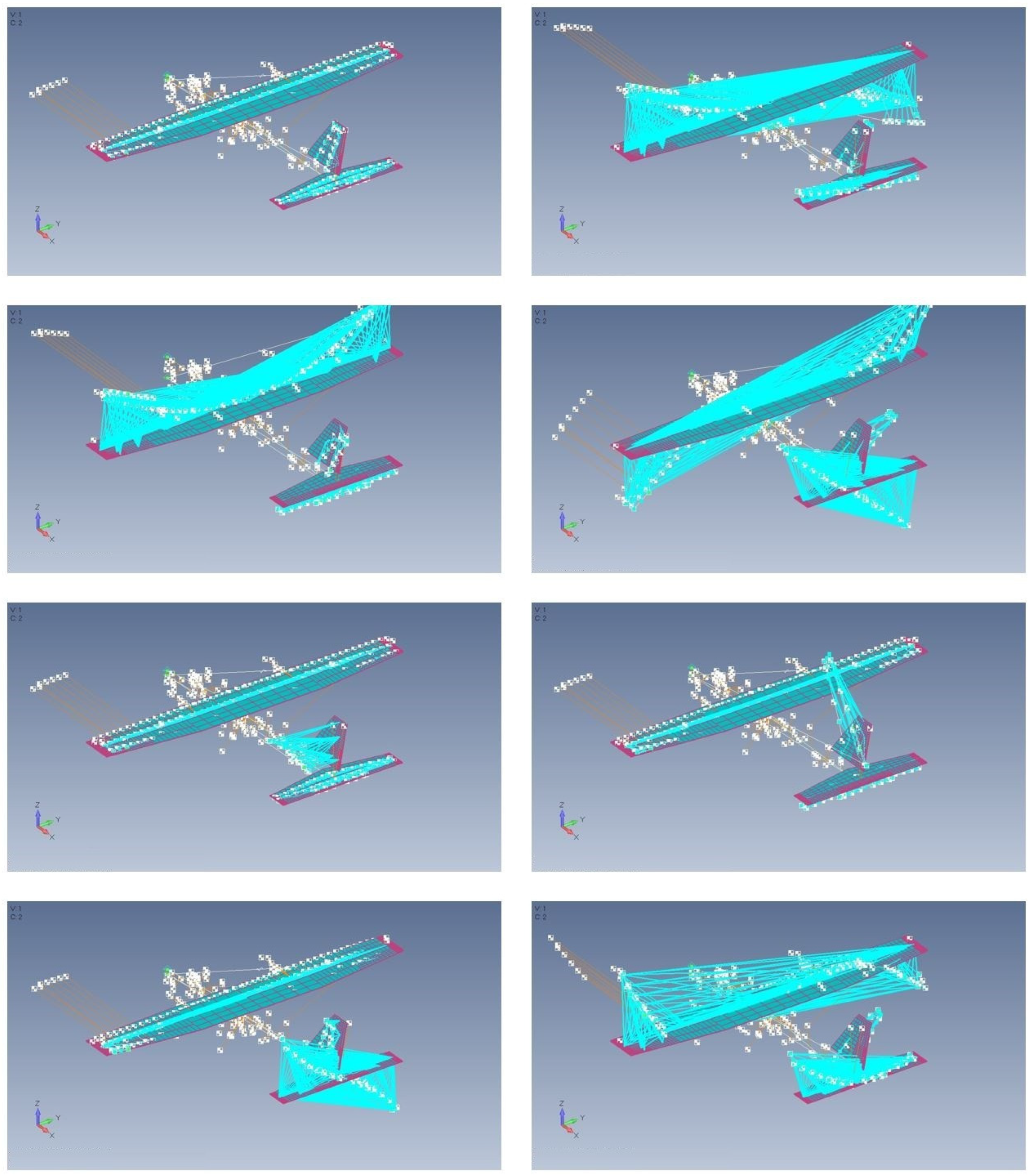
| No. mode | Freq. (Hz) | Mode shape |
|---|---|---|
| 1 | 1.99 | Rigid body mode |
| 2 | 4.0 | Rigid body mode |
| 3 | 9.76 | Fuselage tail torsion |
| 4 | 12.59 | Fuselage tail bending |
| 5 | 14.09 | Fuselage tail bending |
| 6 | 18.23 | Fuselage tail bending |
| 7 | 19.42 | Horizontal tail bending |
| 8 | 29.12 | Horizontal tail bending |
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| EMA | Experimental Modal Analysis |
| FEM | Finite Element Method |
| GVT | Ground Vibration Test |
| UAV | Unmanned Aerial Vehicle |
References
- Pines, S. An Elementary Explanation of the Flutter Mechanism, Proceedings Nat. Specialists Meeting on Dynamics and Aeroelasticity, Institute of the Aeronautical Sciences, Ft. Worth, TX, USA, pp. 52-58.
- C. Niu, M. C.-Y. Niu, Composite Airframe Structures, 1992.
- P. Lubrina, S. Giclais, C. Stephan, M. Boeswald, Y. Govers, N. Botargues, AIRBUS a350 XWB GVT: State-of-the-art tech-niques to perform a faster and better GVT campaign, in: Topics in Modal Analysis II, Volume 8, Springer International Publishing, 2014, pp. 243–256.
- G. Dessena, D. I. Ignatyev, J. F. Whidborne, A. Pontillo, L. Z. Fragonara, Ground vibration testing of a flexible wing: A benchmark and case study, Aerospace 9 (2022) 438. [CrossRef]
- J. P. N oel, L. Renson, G. Kerschen, B. Peeters, S. Manzato, J. Debille, Nonlinear dynamic analysis of an f-16 aircraft using gvt data, in: International Forum on Aeroelasticity Structural Dynamics 2013 Conference Programme Proceedings 24-26 June Bristol UK, 2013, pp. 1–13.
- K. J. Lemler, W. H. Semke, Application of modal testing and analysis techniques on a sUAV, in: Special Topics in Structural Dynamics, Volume 6, Springer New York, 2013, pp. 47–57.
- G. Coppotelli, C. Grappasonni, M. Arras, D. Valyou, J. Miller, P. Marzocca, System identification from GVT and taxiing of an unmanned aerial vehicle, in: SAE Technical Paper Series, SAE International, 2013. [CrossRef]
- Marano, A.D.; Belardo, M.; Beretta, J.; Starace, F.; Orlando, S.; Punzi, C.; Frajese, R.; Paletta, N.; Di Palma, L. Aeroelastic Tailoring of the Next Generation Civil Tiltrotor Technological Demonstrator Composite Wing. Aerospace 2022, 9, 335. [Google Scholar] [CrossRef]
- Goge, D. Automatic updating of large aircraft models using experimental data from ground vibration testing. Aerospace Science and Technology 2003, 7, 33–45. [Google Scholar] [CrossRef]
- S. Giclais, P. Lubrina, C. Stephan, Aircraft ground vibration testing at onera, AerospaceLab Journal Issue 12 (2016) December 2016; ISSN: 2107–6596.
- Dewey, H. Hodges; G. Alvin Pierce: Introduction to Structural Dynamic and Aeroelasticity. Cambridge Aerospace Series.
- B. Peeters, H. Climent, R. De Diego, J. De Alba, J. R. Ahlquist, J. M. Carreño, W. Hendricx, A. Rega, G. García, J. Deweer, J. Debille, Modern solutions for ground vibration testing of large aircraft. 26th Conference and Exposition on Structural Dynamics 2008, IMACXXVI.
- R.L. Bisplinghoff, H. Ashley Principle of Aeroelasticity, Dover Publications,1962.
- Raymond, L. Bisplinghoff; Holt Ashley; Robert L. Halfman: Aeroelasticity. Dover publications, Inc.
- Albano, E.; Rodden, W.P. A doublet-lattice method for calculating lift distributions on oscillating surfaces in subsonic flows. AIAA Journal 1969, 7, 279–285. [Google Scholar] [CrossRef]
- Rodden, W.P.; Johnson, E.H. MSC/NASTRAN Aeroelastic Analysis User’s Guide Ver.68; MSC Software Corporation: Los Angeles, CA, USA, 1994. [Google Scholar]
- MSC Software. MSC Nastran Aeroelastic Analysis User’s Guide; MSC Software Corporation: Los Angeles, CA, USA, 2004. [Google Scholar]
- Rodden, W.P. The development of the doublet-lattice method”, International Forum on Aeroelasticity and Structural Dynamics, Rome, June 1997.
- ZAERO User’s Manual ver.9.3.
- Weisshaar, T.A. Forward Swept Wing Static Aeroelasticity, AFFDL TR-79-3087, June 1979.
- Weisshaar, T.A. Aeroelastic Stability and Performance Characteristics of Aircraft with Advanced Composite Sweptforward Wing Structures, AFFDL TR-78-116, Sept. 1978.
- Wright, J.R.; Cooper, J.E. Introduction to Aircraft Aeroelasticity and Loads, 2nd Edition ed; John Wiley Sons Inc.; p. 2015.
- Wright, J.R.; Cooper, J.E. Aircraft Aeroelasticity and Loads; Jon Wiley Sons Ltd: Manchester, UK, 2007. [Google Scholar]
- W.R. Rodden; E.H. Johnson. MSC/Nastran Aeroelastic Analysis.
- Thomson, W.T. Theory of Vibration with Applications, Third Edition, Prentice-Hall, 1988.
- Reed, W.H., III. Flight Flutter Testing: Equipment and Techniques, Presented at the FAS Southwest Region Annual Designer Conference, Ft. Worth, Texas, and November 5 and 6, 1991.




| K method | G method | ||
| Mode vf(m/s) |
Freq. (Hz) | mode vf(m/s) | Freq. (Hz) |
| 2 428.7 |
7.74 | 2 452.2 |
7.74 |
| 5 486.3 |
11.57 | 5 484.2 |
11.69 |
| No. mode | Nastran | EMA | Mode shape description |
| Freq. (Hz) | Freq. (Hz) | ||
| 7 | 9.67 | 9.76 | Fuselage tail torsion |
| 8 | 12.27 | 12.59 | Fuselage bending along z, wing sym. bending |
| 9 | 14.09 | 14.61 | Fuselage torsion, wing anti-sym. bending |
| 10 | 19.32 | 18.23 | Fuselage bending along y |
| 11 | 21.10 | 20.42 | Horizontal tail bending along z |
| 12 | 25.81 | 24.48 | Fuselage torsion |
| 13 | 30.19 | 30.42 | Horizontal tail bending |
| K method | G method | |||
| Mode vf(m/s) |
Freq. (Hz) | mode | vf(m/s) | Freq. (Hz) |
| 9 176.47 |
13.57 | (No Damping, G = 0) | 211.8 | 13.54 |
| —- —- |
—- | (Damping, G = 0.5) | 259.7 | 13.54 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





