Submitted:
20 June 2023
Posted:
21 June 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Mathematical Formulation
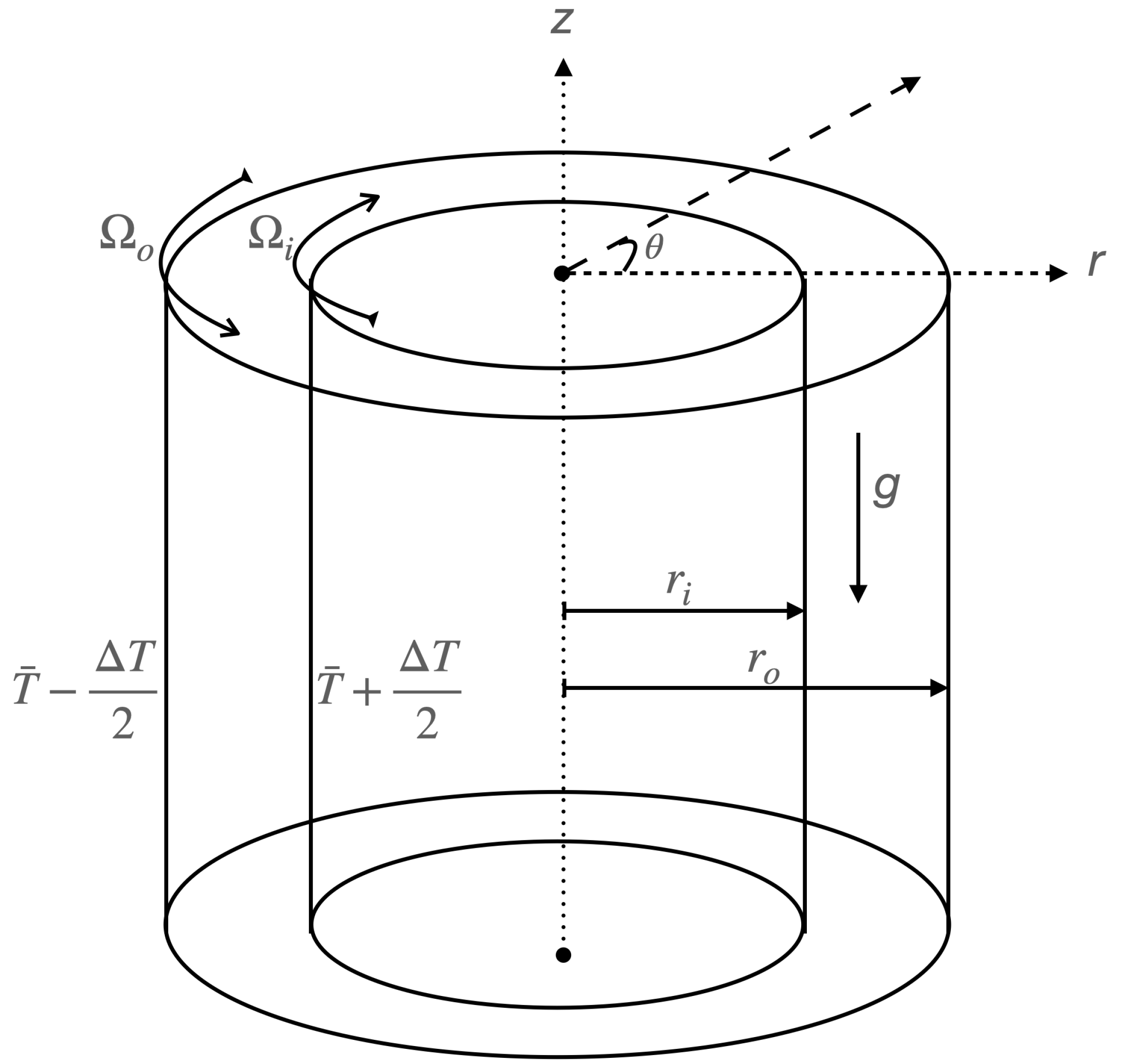
2.1. Model
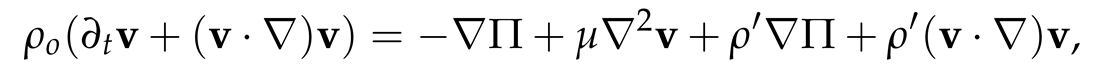

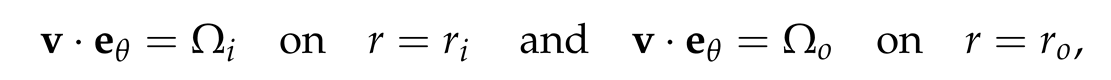
2.2. Boussinesq Approximation
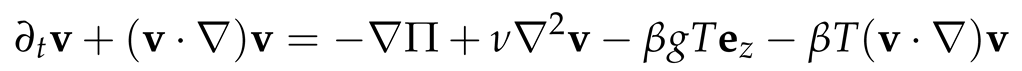
2.3. Nondimensionalization
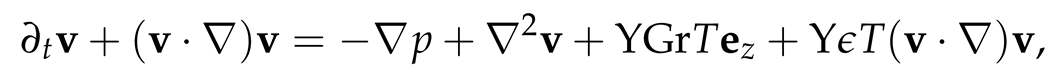
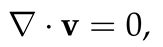
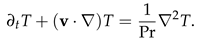
2.4. Basic Equations
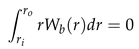
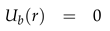
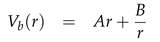
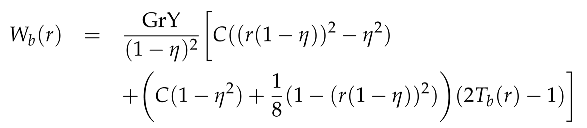
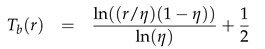
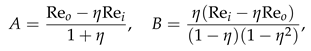
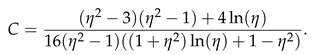
3. Linearization
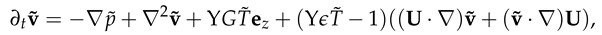
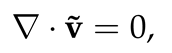
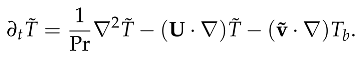
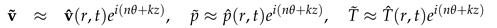 where the pressure , temperature and velocities , , and are functions of the radial, azimuthal, and axial coordinate directions. Also, n ∈ and k ∈ are the azimuthal and axial wavenumbers respectively. The frequencies of the disturbance are characterised by the wavenumbers. The wavelengths in the homogeneous directions, θ and z are Lθ = 2π/n and Lz = 2π/k respectively. Thus we proceed by substituting the above functional forms into the linearized Equations (22)–(24), and which after further simplification they become:
where the pressure , temperature and velocities , , and are functions of the radial, azimuthal, and axial coordinate directions. Also, n ∈ and k ∈ are the azimuthal and axial wavenumbers respectively. The frequencies of the disturbance are characterised by the wavenumbers. The wavelengths in the homogeneous directions, θ and z are Lθ = 2π/n and Lz = 2π/k respectively. Thus we proceed by substituting the above functional forms into the linearized Equations (22)–(24), and which after further simplification they become: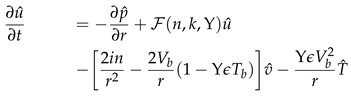
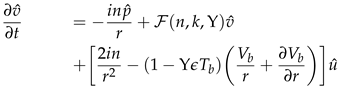
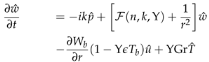
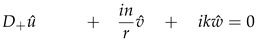
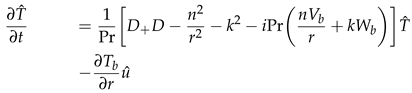
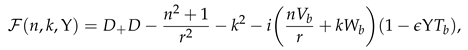
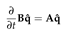
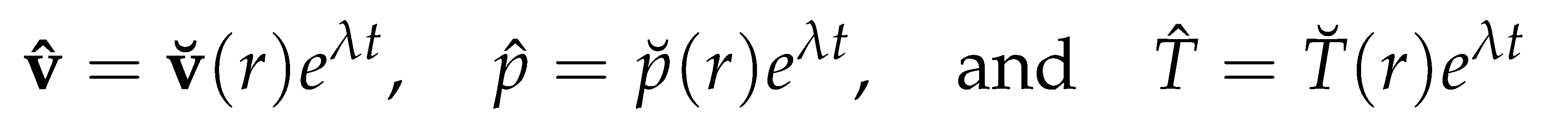
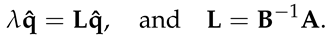
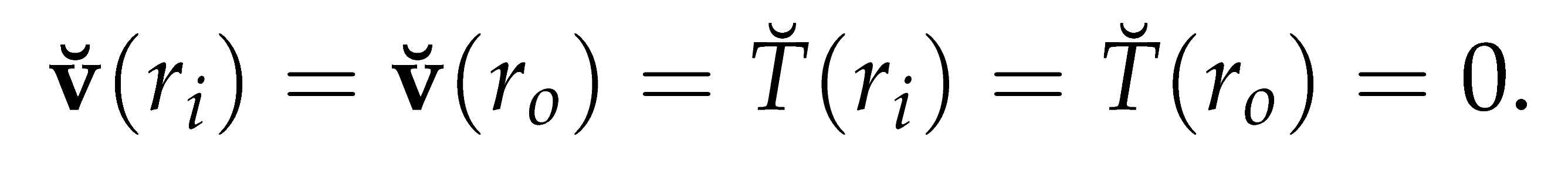
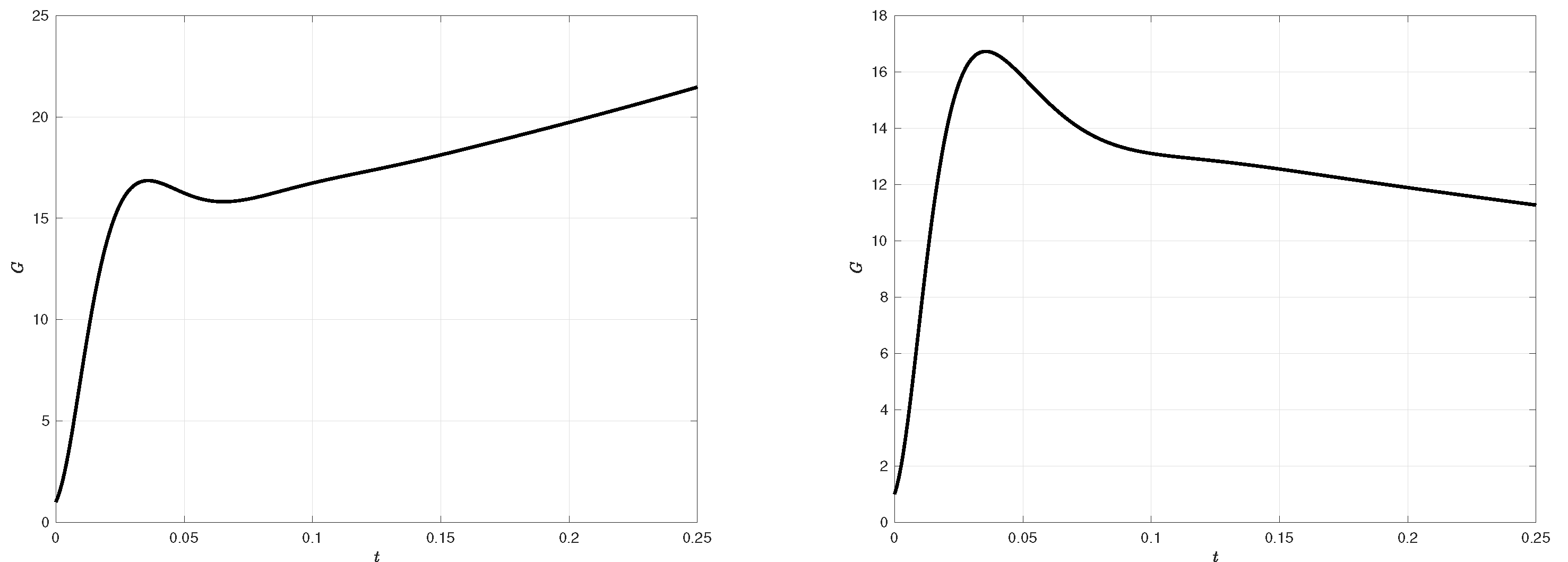
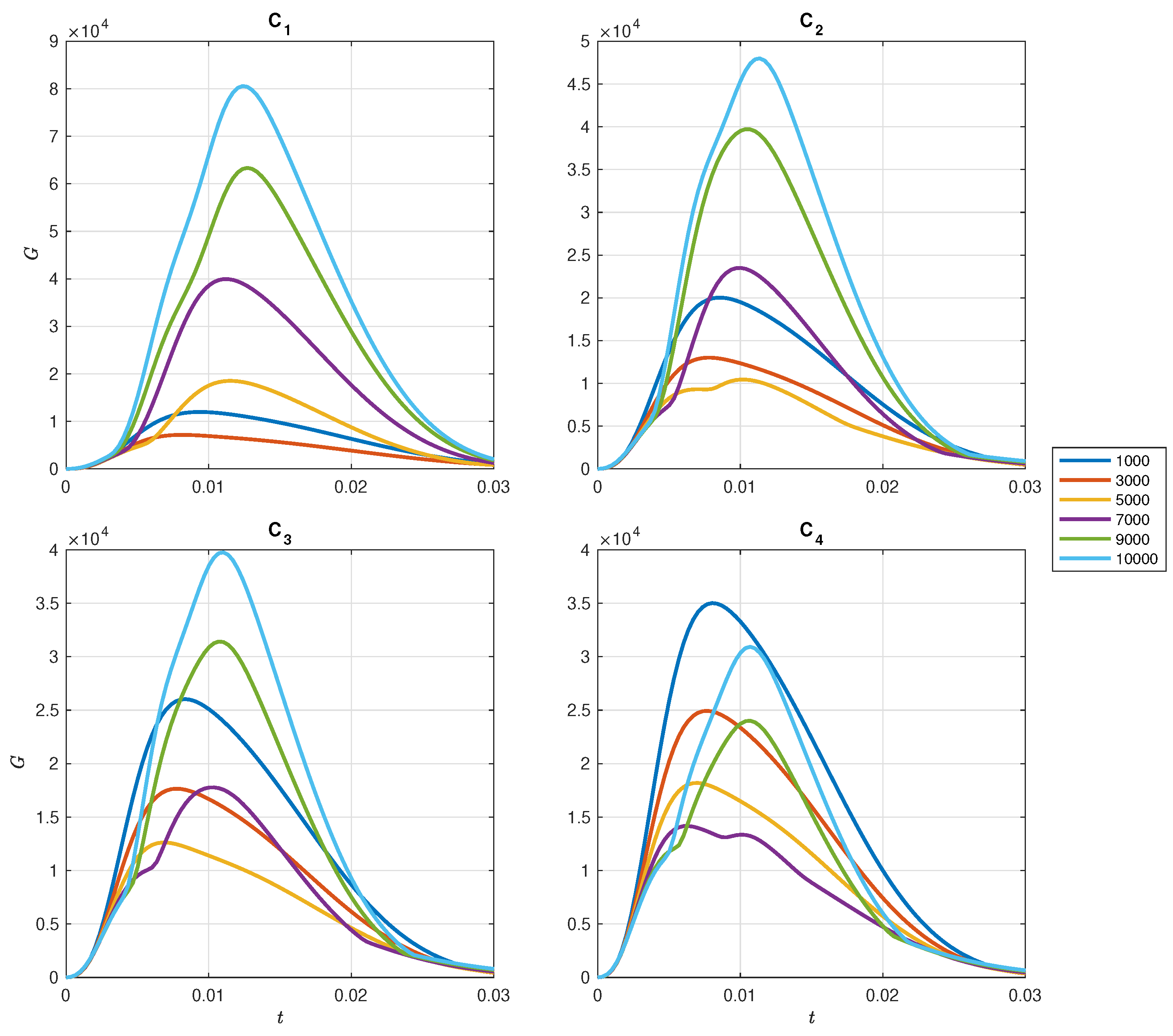
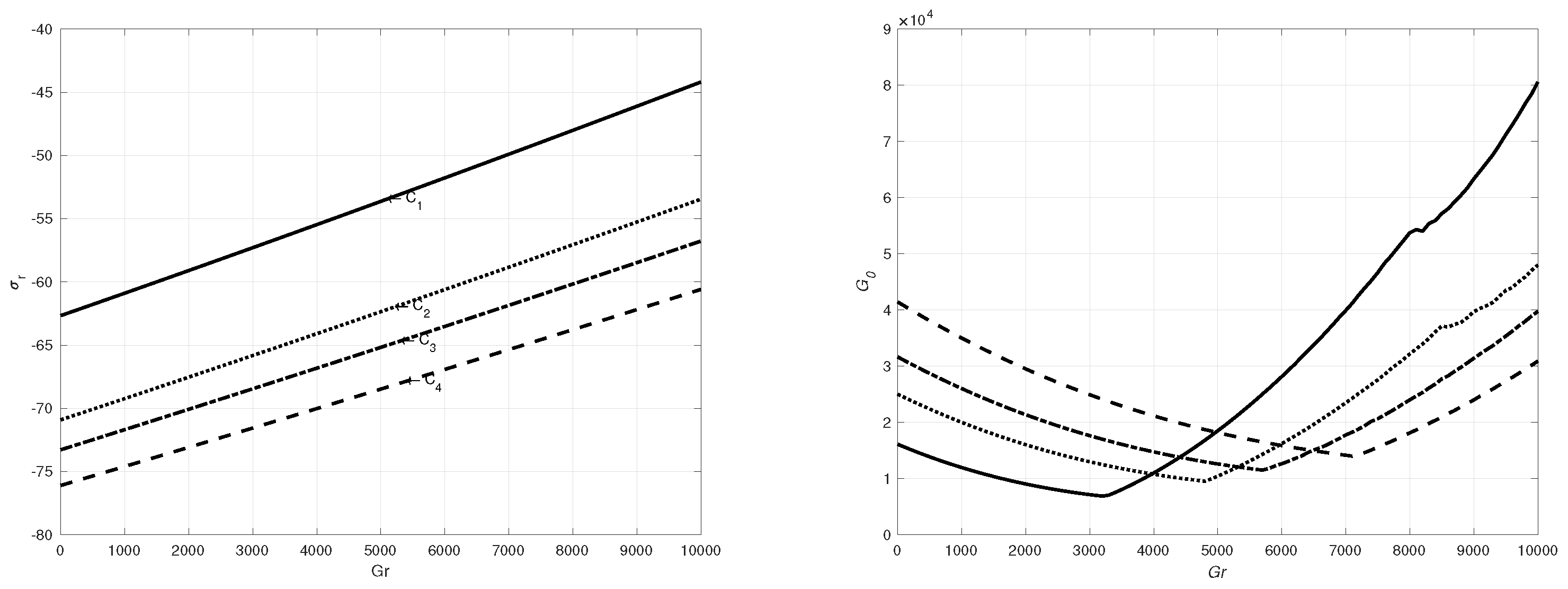
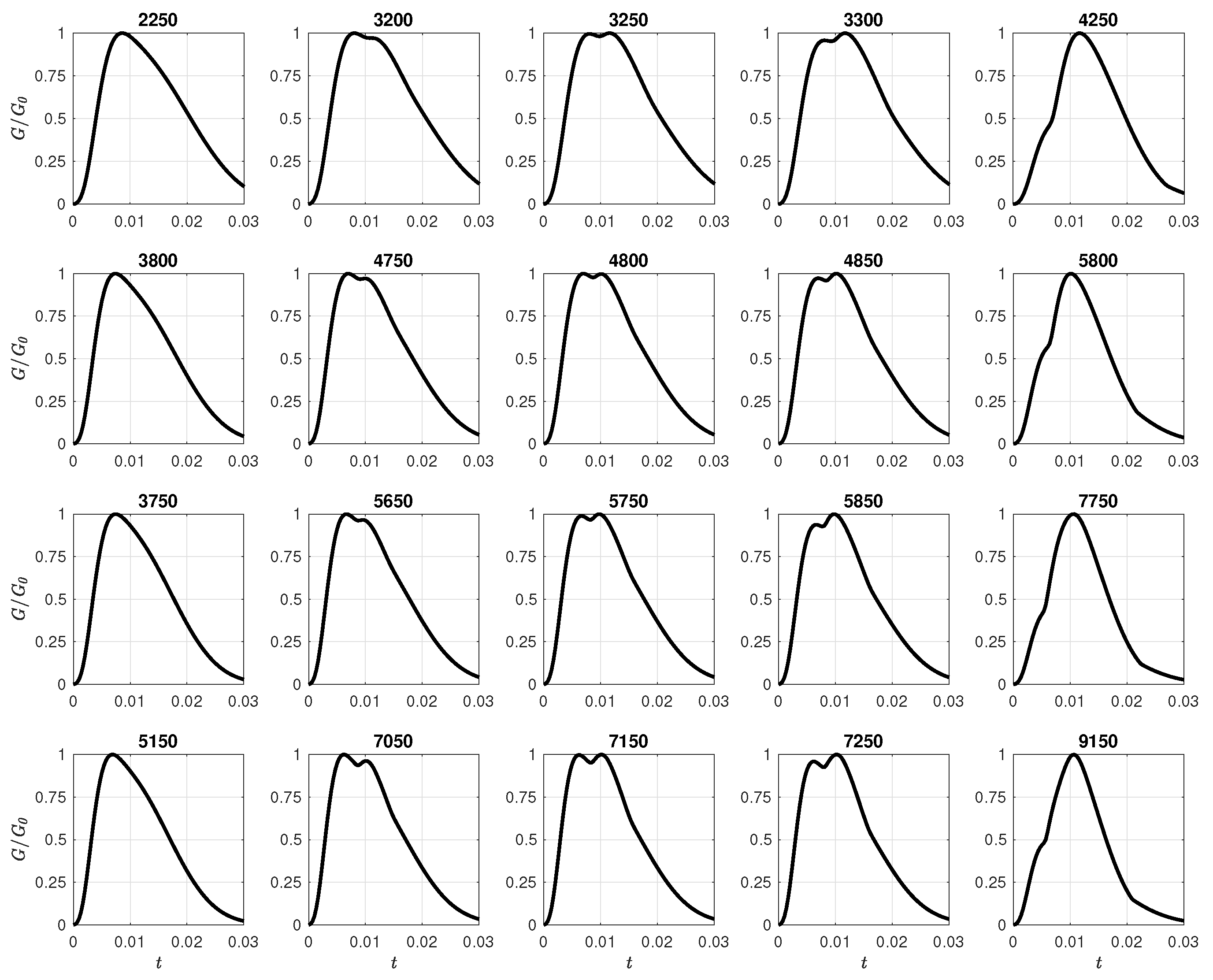
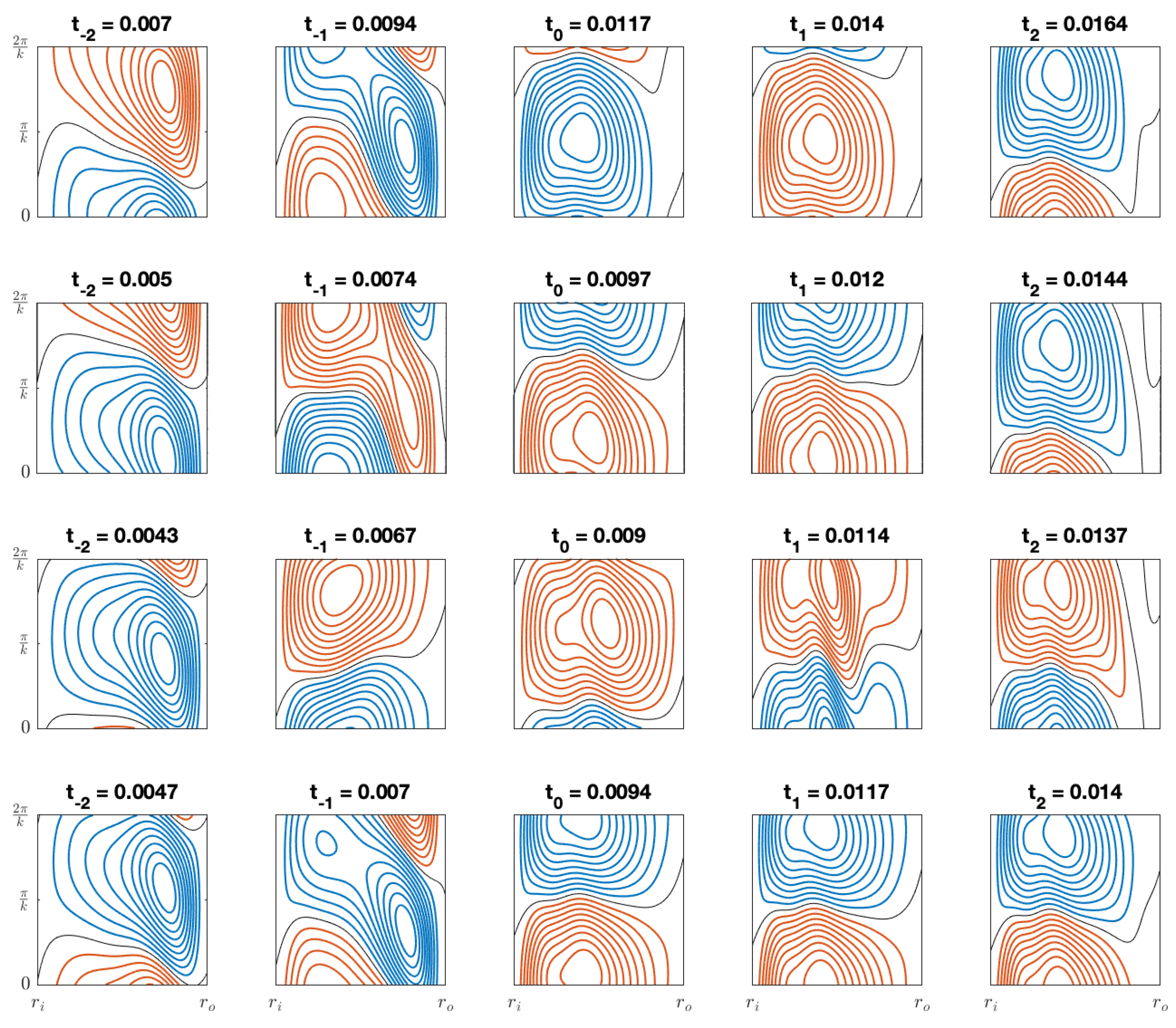
4. Numerical Results
5. Conclusion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Energy Norm
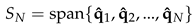
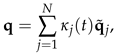
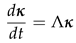
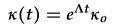
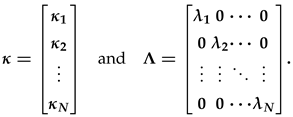
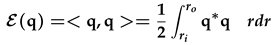
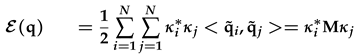
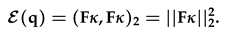
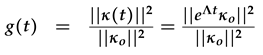
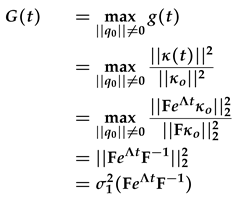
Appendix B. Definitions of matrices A and B

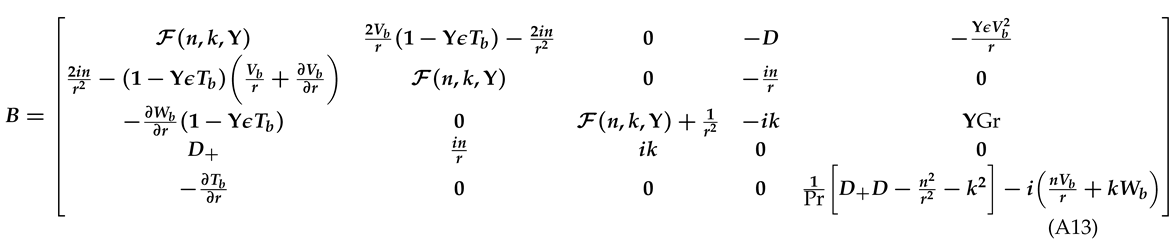
References
- Strogatz, S. In Nonlinear Dynamics and Chaos: with Applications to Physics, Biology, Chemistry, and Engineering; CRC Press: Boca Raton, USA, 2018.
- Richtmyer, R.D., Nonlinear Problems: Fluid Dynamics. In Principles of Advanced Mathematical Physics; Springer Berlin Heidelberg: Berlin, Heidelberg, 1978; pp. 364–408. [CrossRef]
- Drazin, P.G. Introduction to hydrodynamic stability; Vol. 32, Cambridge university press, 2002.
- Solomon, T.H., Non-linear Fluid Flow, Pattern Formation, Mixing and Turbulence. In Encyclopedia of Complexity and Systems Science; Meyers, R.A., Ed.; Springer New York: New York, NY, 2009; pp. 6195–6206. [CrossRef]
- Trefethen, L.N.; Trefethen, A.E.; Reddy, S.C.; Driscoll, T.A. Hydrodynamic stability without eigenvalues. Science 1993, 261, 578–584.
- Schmid, P.J.; Brandt, L. Analysis of Fluid Systems: Stability, Receptivity, Sensitivity: Lecture notes from the FLOW-NORDITA Sum- mer School on Advanced Instability Methods for Complex Flows, Stockholm, Sweden, 2013. Applied Mechanics Reviews 2014, 66, [https://asmedigitalcollection.asme.org/appliedmechanicsreviews/article-pdf/66/2/024803/6073896/amr_066_02_024803.pdf]. 024803. [CrossRef]
- Schmid, P.J.; Springer, D.S.H. Stability and Transition in Shear Flows, 2001. 556 pp. ISBN 0-387-98985-4. Journal of Fluid Mechanics 2003, 487, 377–379. [CrossRef]
- Karp, M.; Cohen, J. Tracking stages of transition in Couette flow analytically. Journal of Fluid Mechanics 2014, 748, 896–931. [CrossRef]
- Nayak, A.; Das, D. Transient growth of optimal perturbation in a decaying channel flow. Physics of Fluids 2017, 29, [https://pubs.aip.org/aip/pof/article-pdf/doi/10.1063/1.4985000/14808152/064104_1_online.pdf]. 064104. [CrossRef]
- Romanov, V.A. Stability of plane-parallel Couette flow. Functional analysis and its applications 1973, 7, 137–146.
- Davey, A. On the Stability of Plane Couette flow to Infinitesimal Disturbances. Journal of Fluid Mechanics 1973, 57, 369–380. [CrossRef]
- Drazin, P.G.; Reid, W.H. Hydrodynamic Stability. Journal of Fluid Mechanics 1981, 124. [CrossRef]
- Sano, M.; Tamai, K. A universal transition to turbulence in channel flow. Nature Physics 2016, 12, 249–253.
- Eckhardt, B. Transition to Turbulence in Shear Flows. Physica A: Statistical Mechanics and its Applications 2018, 504, 121–129. Lecture Notes of the 14th International Summer School on Fundamental Problems in Statistical Physics. [CrossRef]
- Orszag, S.A. Accurate solution of the Orr–Sommerfeld stability equation. Journal of Fluid Mechanics 1971, 50, 689–703.
- Baines, P.G.; Majumdar, S.J.; Mitsudera, H. The mechanics of the Tollmien-Schlichting wave. Journal of Fluid Mechanics 1996, 312, 107–124. [CrossRef]
- Andersson, P.; Berggren, M.; Henningson, D.S. Optimal disturbances and bypass transition in boundary layers. Physics of Fluids 1999, 11, 134–150.
- Kreilos, T.; Khapko, T.; Schlatter, P.; Duguet, Y.; Henningson, D.S.; Eckhardt, B. Bypass transition and spot nucleation in boundary layers. Physical Review Fluids 2016, 1, 043602.
- Meseguer, A.; Mellibovsky, F.; Avila, M.; Marques, F. Instability mechanisms and transition scenarios of spiral turbulence in Taylor-Couette flow. Physical Review E 2009, 80, 046315.
- Eckert, M. The troublesome birth of hydrodynamic stability theory: Sommerfeld and the turbulence problem. European Physical Journal H 2010, 35, 29–51. [CrossRef]
- Reddy, S.C.; Henningson, D.S. Energy growth in viscous channel flows. Journal of Fluid Mechanics 1993, 252, 209–238. [CrossRef]
- Heaton, C.J.; Peake, N. Transient growth in vortices with axial flow. Journal of Fluid Mechanics 2007, 587, 271–301. [CrossRef]
- Ha, K.; Chomaz, J.M.; Ortiz, S. Transient growth, edge states, and repeller in rotating solid and fluid. Phys. Rev. E 2021, 103, 033102. [CrossRef]
- Quintanilha, H.; Paredes, P.; Hanifi, A.; Theofilis, V. Transient growth analysis of hypersonic flow over an elliptic cone. Journal of Fluid Mechanics 2022, 935, A40. [CrossRef]
- Andereck, C.D.; Liu, S.; Swinney, H.L. Flow regimes in a circular Couette system with independently rotating cylinders. Journal of fluid mechanics 1986, 164, 155–183.
- Gebhardt, T.; Grossmann, S. The Taylor–Couette eigenvalue problem with independently rotating cylinders. Zeitschrift für Physik B Condensed Matter 1993, 90, 475–490.
- Bai, Y.; Latrache, N.; Kelai, F.; Crumeyrolle, O.; Mutabazi, I. Viscoelastic instabilities of Taylor-Couette flows with different rotation regimes. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 2023, 381, 20220133, [https://royalsocietypublishing.org/doi/pdf/10.1098/rsta.2022.0133]. [CrossRef]
- Lopez, J.M.; Lopez, J.M.; Marques, F. Stably stratified Taylor-Couette flows. Philosophical Transactions of the Royal Society A: Mathe- matical, Physical and Engineering Sciences 2023, 381, 20220115, [https://royalsocietypublishing.org/doi/pdf/10.1098/rsta.2022.0115]. [CrossRef]
- Merbold, S.; Hamede, M.H.; Froitzheim, A.; Egbers, C. Flow regimes in a very wide-gap Taylor-Couette flow with counter-rotating cylinders. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 2023, 381, 20220113, [https://royalsocietypublishing.org/doi/pdf/10.1098/rsta.2022.0113]. [CrossRef]
- Taylor, G.I. VIII. Stability of a viscous liquid contained between two rotating cylinders. Philosophical Transactions of the Royal Society of London. Series A, Containing Papers of a Mathematical or Physical Character 1923, 223, 289–343, [https://royalsocietypublishing.org/doi/pdf/10.1098/rsta.1923.0008]. [CrossRef]
- Coles, D. Transition in circular Couette flow. Journal of Fluid Mechanics 1965, 21, 385–425.
- Van Atta, C. Exploratory measurements in spiral turbulence. Journal of Fluid Mechanics 1966, 25, 495–512.
- Hegseth, J.J.; Andereck, C.D.; Hayot, F.; Pomeau, Y. Spiral Turbulence and Phase Dynamics. Phys. Rev. Lett. 1989, 62, 257–260. [CrossRef]
- Prigent, A.; goire, G.G.; Chaté, H.; Dauchot, O.; van Saarloos, W. Large-Scale Finite-Wavelength Modulation within Turbulent Shear Flows. Physical Review Letters 2002, 89. [CrossRef]
- Hristova, H.; Roch, S.; Schmid, P.J.; Tuckerman, L.S. Transient growth in Taylor-Couette flow. Physics of Fluids 2002, 14, 3475–3484, [https://pubs.aip.org/aip/pof/article-pdf/14/10/3475/12764697/3475_1_online.pdf]. [CrossRef]
- Meseguer, A. Energy transient growth in the Taylor-Couette problem. Physics of Fluids 2002, 14, 1655–1660, [https://pubs.aip.org/ai pdf/14/5/1655/12586152/1655_1_online.pdf]. [CrossRef]
- Maretzke, S.; Hof, B.; Avila, M. Transient growth in linearly stable Taylor–Couette flows. Journal of Fluid Mechanics 2014, 742, 254–290.
- Lopez, J.M.; Marques, F.; Avila, M. The Boussinesq approximation in rapidly rotating flows. Journal of fluid mechanics 2013, 737, 56–77.
- Lopez, J.M.; Lopez, J.M.; Marques, F. Stably stratified Taylor–Couette flows. Philosophical Transactions of the Royal Society A 2023, 381, 20220115.
- Henningson, D.S.; Reddy, S.C. On the role of linear mechanisms in transition to turbulence. Physics of Fluids 1994, 6, 1396–1398.
- Schmid, P.J. Nonmodal stability theory. Annu. Rev. Fluid Mech. 2007, 39, 129–162.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).