Submitted:
19 June 2023
Posted:
20 June 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Intuitionistic Fuzzy Sets and Their Extensions: Literature Review
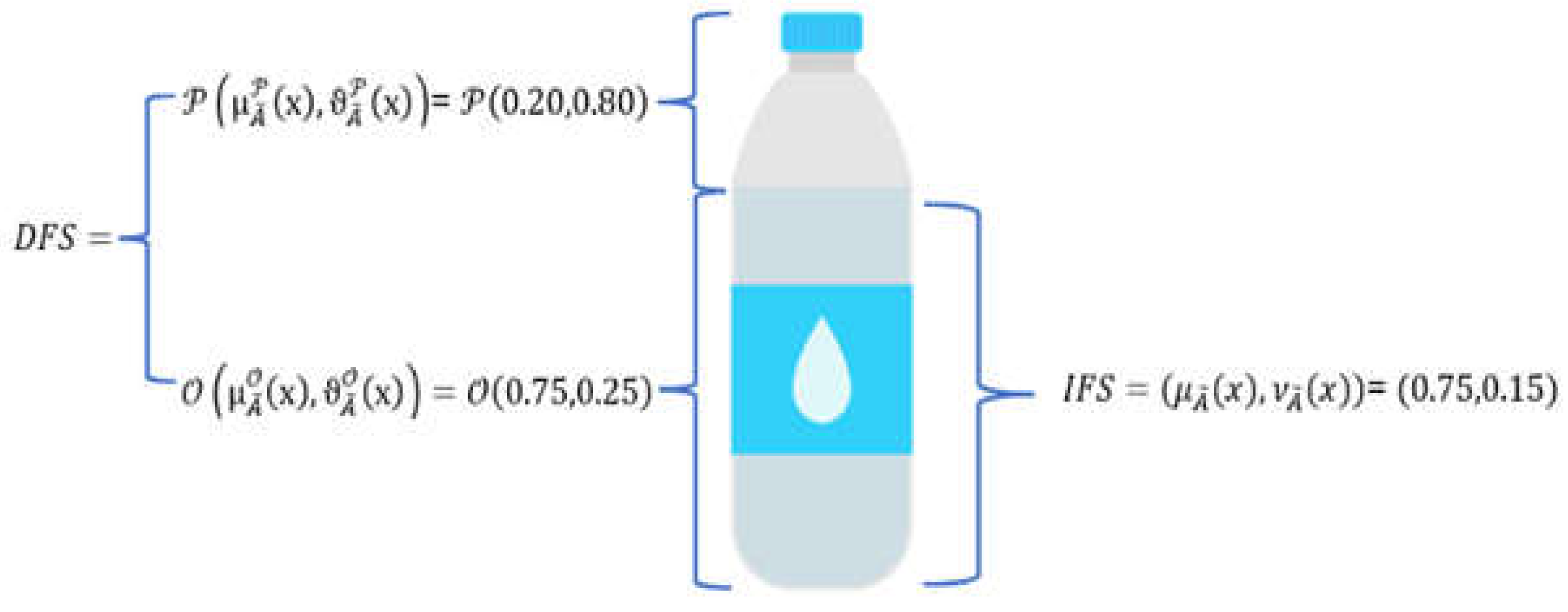
3. Decomposed Fuzzy Sets
4. Multi-Attribute Decision Making: A Novel Decomposed Fuzzy TOPSIS Method
| z | µ | v |
|---|---|---|
| Absolutely Low (AL) | 0.05 | 0.95 |
| Very Low (VL) | 0.2 | 0.8 |
| Low (L) | 0.35 | 0.65 |
| Medium (M) | 0.5 | 0.5 |
| High (H) | 0.65 | 0.35 |
| Very High (VH) | 0.8 | 0.2 |
| Absolutely High (AH) | 0.95 | 0.05 |
5. Case Study
5.1 Problem Definition
5.2 Application of DF TOPSIS
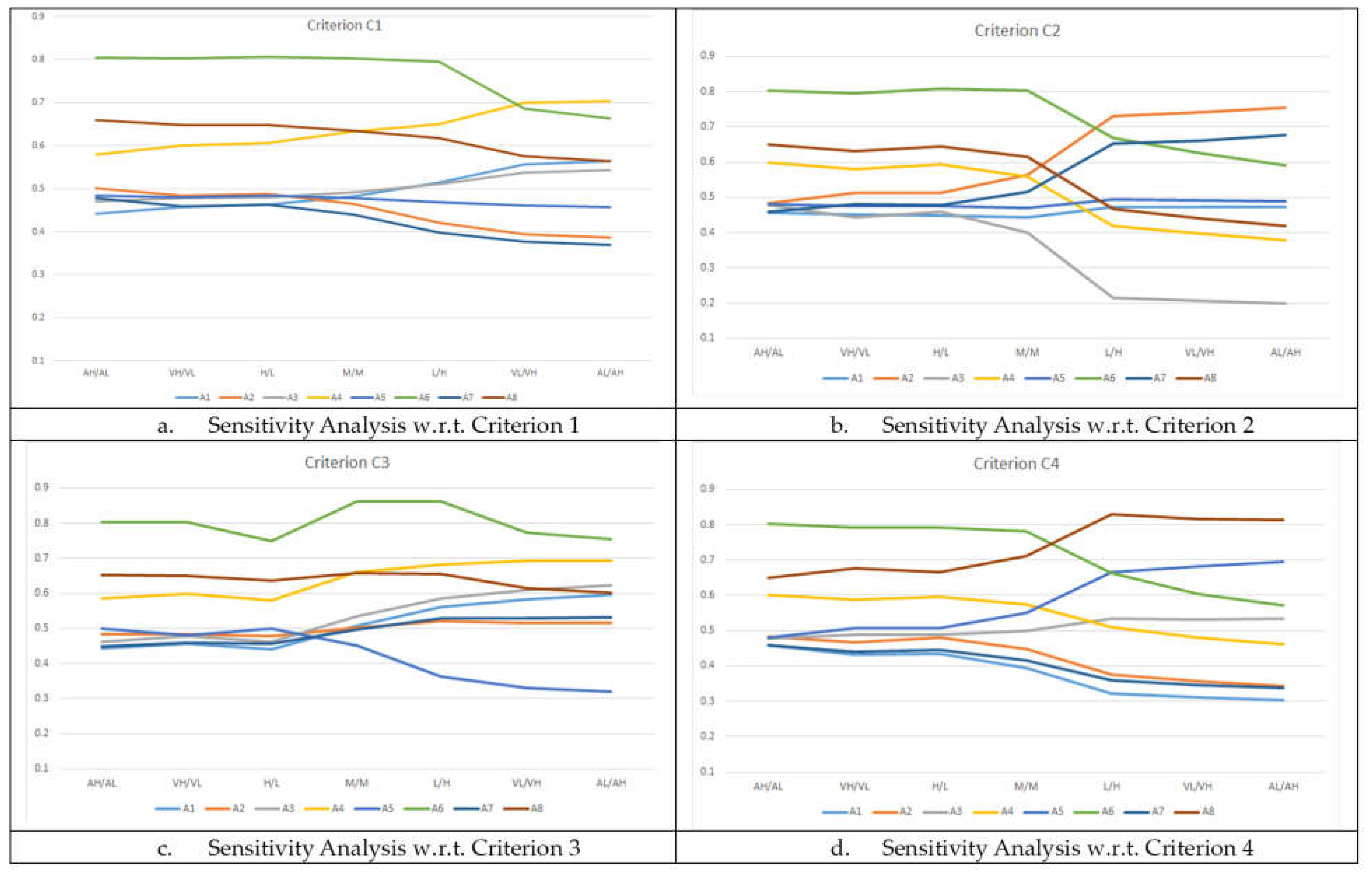
5.3. Sensitivity Analysis
6. Conclusion
References
- Atanassov, K. Intuitionistic fuzzy sets. Fuzzy Sets and Systems 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Cebi, S. , Gündoğdu, F. K., & Kahraman, C. (2022). Operational risk analysis in business processes using decomposed fuzzy sets. Journal of Intelligent & Fuzzy Systems, (Preprint), 1-18. [CrossRef]
- Cebi, S. , Gündoğdu, F. K., & Kahraman, C. (2023). Consideration of reciprocal judgments through Decomposed Fuzzy Analytical Hierarchy Process: A case study in the pharmaceutical industry. Applied Soft Computing, 110000. [CrossRef]
- Atanassov, K.T. Research on intuitionistic fuzzy sets in Bulgaria, Fuzzy Sets and Systems 1987, 22, 93. [CrossRef]
- Atanassov, K. Interval-valued intuitionistic fuzzy sets. Fuzzy Sets and Systems 1989, 31, 343–349. [Google Scholar] [CrossRef]
- Atanassov, K.T. Remarks on the intuitionistic fuzzy sets. Fuzzy Sets and Systems 1992, 51, 117–118. [Google Scholar] [CrossRef]
- Atanassov, K.T. Research on intuitionistic fuzzy sets, 1990-1992. Fuzzy Sets and Systems 1993, 54, 363–364. [Google Scholar] [CrossRef]
- Atanassov, K.T. New operations defined over the intuitionistic fuzzy sets, Fuzzy Sets and Systems, 1994, 61, 137–142. [CrossRef]
- Chen, S.M.; Chen, J.M. Intuitionistic fuzzy sets in decision making and decision support: an overview. Journal of Intelligent & Fuzzy Systems 2014, 26, 635–647. [Google Scholar]
- Verma, A.; Singh, U. Intuitionistic fuzzy sets and their applications: A review. Journal of Intelligent & Fuzzy Systems 2018, 34, 3863–3878. [Google Scholar]
- Atanassov, K.; Gargov, G. Interval valued intuitionistic fuzzy sets. Fuzzy Sets and Systems 1989, 31, 343–349. [Google Scholar] [CrossRef]
- Torra, V. Hesitant fuzzy sets. Int. J. Intell. Syst. 2010, 25, 529–539. [Google Scholar] [CrossRef]
- Atanassov, K. (1999). Intuitionistic fuzzy sets. Springer.
- Yager, R.R. (2013). Pythagorean Fuzzy Subsets, 2013 Joint IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS), Canada, 57-61, June 24th-28th, 2013.
- Atanassov, K.T. More on intuitionistic fuzzy sets. Fuzzy Sets and Systems 1989, 33, 37–45. [Google Scholar] [CrossRef]
- Zhao, T.; Xiao, J. Type-2 intuitionistic fuzzy sets. Kongzhi Lilun Yu Yingyong/Control Theory Applications 2012, 29, 1215–1222. [Google Scholar]
- Cuong, N.V.; Kreinovich, V. (2014) Picture fuzzy sets - A new concept for computational intelligence problems, 2013 3rd World Congress on Information and Communication Technologies, WICT 2013, 7113099, pp. 1–6.
- Yager, R.R. Generalized orthopair fuzzy sets. IEEE Transactions on Fuzzy Systems 2017, 25, 1222–1230. [Google Scholar] [CrossRef]
- Kahraman, C.; Gündoǧdu, F.K. (2018) From 1D to 3D membership: spherical fuzzy sets, BOS / SOR 2018, Polish Operational and Systems Research Society, September 24th - 26th 2018, Palais Staszic, Warsaw, Poland. 24 September.
- Gündoǧdu, F.K.; Kahraman, C. Spherical fuzzy sets and spherical fuzzy TOPSIS method. J. Intell. Fuzzy Syst. 2019, 36, 337–352. [Google Scholar] [CrossRef]
- Atanassov, K.T. Circular intuitionistic fuzzy sets. J. Intell. Fuzzy Syst. 2020, 39, 5981–5986. [Google Scholar] [CrossRef]
| Expert-1 | C1. Delivery time | C2. Financial instability | C3. Reputation | C4. Quality | ||||
|---|---|---|---|---|---|---|---|---|
| F* | D** | F* | D** | F* | D** | F* | D** | |
| A1 | VL | VH | M | M | L | H | H | M |
| A2 | AH | AL | AL | AH | M | M | VH | VL |
| A3 | L | H | AH | AL | VL | VH | L | H |
| A4 | L | H | AH | AL | L | H | VH | VL |
| A5 | H | L | M | M | AH | AL | AL | AH |
| A6 | AH | AL | VH | VL | H | M | AH | VL |
| A7 | AH | AL | AL | AH | L | H | H | L |
| A8 | AH | AL | AH | AL | VH | VL | AL | AH |
| Expert-2 | C1. Delivery time | C2. Financial instability | C3. Reputation | C4. Quality | ||||
| F* | D** | F* | D** | F* | D** | F* | D** | |
| A1 | VL | VH | L | H | VL | VH | VH | L |
| A2 | VH | L | AL | AH | M | M | H | VL |
| A3 | M | H | VH | VL | VL | VH | L | H |
| A4 | VL | VH | AH | AL | L | H | VH | VL |
| A5 | H | L | H | L | AH | AL | VL | VH |
| A6 | H | L | VH | VL | H | M | VH | VL |
| A7 | VH | L | AL | AH | L | H | H | L |
| A8 | AH | AL | VH | VL | H | M | L | VH |
| Expert-3 | C1. Delivery time | C2. Financial instability | C3. Reputation | C4. Quality | ||||
| F* | D** | F* | D** | F* | D** | F* | D** | |
| A1 | L | M | H | M | VL | VH | VH | VL |
| A2 | AH | AL | AL | AH | M | M | VH | VL |
| A3 | L | H | VH | VL | VL | VH | L | H |
| A4 | L | H | VH | AL | L | H | VH | VL |
| A5 | H | L | L | H | AH | AL | AL | AH |
| A6 | H | VL | H | L | VH | L | VH | L |
| A7 | H | VL | L | H | L | L | VH | L |
| A8 | H | M | VH | AL | H | L | H | VL |
| Expert-1 | C1. Delivery time | C2. Financial instability | C3. Reputation | C4. Quality |
|---|---|---|---|---|
| A1 | ((0.2,0.8),(0.8,0.2)) | ((0.5,0.5),(0.5,0.5)) | ((0.35,0.65),(0.65,0.35)) | ((0.65,0.35),(0.5,0.5)) |
| A2 | ((0.95,0.05),(0.05,0.95)) | ((0.05,0.95),(0.95,0.05)) | ((0.5,0.5),(0.5,0.5)) | ((0.8,0.2),(0.2,0.8)) |
| A3 | ((0.35,0.65),(0.65,0.35)) | ((0.95,0.05),(0.05,0.95)) | ((0.2,0.8),(0.8,0.2)) | ((0.35,0.65),(0.65,0.35)) |
| A4 | ((0.35,0.65),(0.65,0.35)) | ((0.95,0.05),(0.05,0.95)) | ((0.35,0.65),(0.65,0.35)) | ((0.8,0.2),(0.2,0.8)) |
| A5 | ((0.65,0.35),(0.35,0.65)) | ((0.5,0.5),(0.5,0.5)) | ((0.95,0.05),(0.05,0.95)) | ((0.05,0.95),(0.95,0.05)) |
| A6 | ((0.95,0.05),(0.05,0.95)) | ((0.8,0.2),(0.2,0.8)) | ((0.65,0.35),(0.5,0.5)) | ((0.95,0.05),(0.2,0.8)) |
| A7 | ((0.95,0.05),(0.05,0.95)) | ((0.05,0.95),(0.95,0.05)) | ((0.35,0.65),(0.65,0.35)) | ((0.65,0.35),(0.35,0.65)) |
| A8 | ((0.95,0.05),(0.05,0.95)) | ((0.95,0.05),(0.05,0.95)) | ((0.8,0.2),(0.2,0.8)) | ((0.05,0.95),(0.95,0.05)) |
| Expert-2 | C1. Delivery time | C2. Financial instability | C3. Reputation | C4. Quality |
| A1 | ((0.2,0.8),(0.8,0.2)) | ((0.35,0.65),(0.65,0.35)) | ((0.2,0.8),(0.8,0.2)) | ((0.8,0.2),(0.35,0.65)) |
| A2 | ((0.8,0.2),(0.35,0.65)) | ((0.05,0.95),(0.95,0.05)) | ((0.5,0.5),(0.5,0.5)) | ((0.65,0.35),(0.2,0.8)) |
| A3 | ((0.5,0.5),(0.65,0.35)) | ((0.8,0.2),(0.2,0.8)) | ((0.2,0.8),(0.8,0.2)) | ((0.35,0.65),(0.65,0.35)) |
| A4 | ((0.2,0.8),(0.8,0.2)) | ((0.95,0.05),(0.05,0.95)) | ((0.35,0.65),(0.65,0.35)) | ((0.8,0.2),(0.2,0.8)) |
| A5 | ((0.65,0.35),(0.35,0.65)) | ((0.65,0.35),(0.35,0.65)) | ((0.95,0.05),(0.05,0.95)) | ((0.2,0.8),(0.8,0.2)) |
| A6 | ((0.65,0.35),(0.35,0.65)) | ((0.8,0.2),(0.2,0.8)) | ((0.65,0.35),(0.5,0.5)) | ((0.8,0.2),(0.2,0.8)) |
| A7 | ((0.8,0.2),(0.35,0.65)) | ((0.05,0.95),(0.95,0.05)) | ((0.35,0.65),(0.65,0.35)) | ((0.65,0.35),(0.35,0.65)) |
| A8 | ((0.95,0.05),(0.05,0.95)) | ((0.8,0.2),(0.2,0.8)) | ((0.65,0.35),(0.5,0.5)) | ((0.35,0.65),(0.8,0.2)) |
| Expert-3 | C1. Delivery time | C2. Financial instability | C3. Reputation | C4. Quality |
| A1 | ((0.35,0.65),(0.5,0.5)) | ((0.65,0.35),(0.5,0.5)) | ((0.2,0.8),(0.8,0.2)) | ((0.8,0.2),(0.2,0.8)) |
| A2 | ((0.95,0.05),(0.05,0.95)) | ((0.05,0.95),(0.95,0.05)) | ((0.5,0.5),(0.5,0.5)) | ((0.8,0.2),(0.2,0.8)) |
| A3 | ((0.35,0.65),(0.65,0.35)) | ((0.8,0.2),(0.2,0.8)) | ((0.2,0.8),(0.8,0.2)) | ((0.35,0.65),(0.65,0.35)) |
| A4 | ((0.35,0.65),(0.65,0.35)) | ((0.8,0.2),(0.05,0.95)) | ((0.35,0.65),(0.65,0.35)) | ((0.8,0.2),(0.2,0.8)) |
| A5 | ((0.65,0.35),(0.35,0.65)) | ((0.35,0.65),(0.65,0.35)) | ((0.95,0.05),(0.05,0.95)) | ((0.05,0.95),(0.95,0.05)) |
| A6 | ((0.65,0.35),(0.2,0.8)) | ((0.65,0.35),(0.35,0.65)) | ((0.8,0.2),(0.35,0.65)) | ((0.8,0.2),(0.35,0.65)) |
| A7 | ((0.65,0.35),(0.2,0.8)) | ((0.35,0.65),(0.65,0.35)) | ((0.35,0.65),(0.35,0.65)) | ((0.8,0.2),(0.35,0.65)) |
| A8 | ((0.65,0.35),(0.5,0.5)) | ((0.8,0.2),(0.05,0.95)) | ((0.65,0.35),(0.35,0.65)) | ((0.65,0.35),(0.2,0.8)) |
| Aggregated | C1. Delivery time | C2. Financial instability | C3. Reputation | C4. Quality |
|---|---|---|---|---|
| A1 | ((0.26,0.75),(0.71,0.29)) | ((0.51,0.5),(0.55,0.45)) | ((0.25,0.76),(0.76,0.24)) | ((0.75,0.23),(0.35,0.65)) |
| A2 | ((0.9,0.04),(0.15,0.85)) | ((0.05,0.95),(0.95,0.05)) | ((0.5,0.5),(0.5,0.5)) | ((0.75,0.23),(0.2,0.8)) |
| A3 | ((0.4,0.6),(0.65,0.35)) | ((0.85,0.08),(0.16,0.84)) | ((0.2,0.8),(0.8,0.2)) | ((0.35,0.65),(0.65,0.35)) |
| A4 | ((0.3,0.7),(0.7,0.3)) | ((0.9,0.03),(0.05,0.95)) | ((0.35,0.65),(0.65,0.35)) | ((0.8,0.2),(0.2,0.8)) |
| A5 | ((0.65,0.35),(0.35,0.65)) | ((0.49,0.49),(0.53,0.47)) | ((0.95,0.05),(0.05,0.95)) | ((0.1,0.91),(0.92,0.08)) |
| A6 | ((0.75,0.1),(0.21,0.79)) | ((0.75,0.22),(0.26,0.74)) | ((0.7,0.29),(0.44,0.56)) | ((0.85,0.08),(0.26,0.74)) |
| A7 | ((0.8,0.08),(0.21,0.79)) | ((0.17,0.87),(0.89,0.11)) | ((0.35,0.65),(0.55,0.45)) | ((0.7,0.29),(0.35,0.65)) |
| A8 | ((0.85,0.03),(0.27,0.73)) | ((0.85,0.08),(0.1,0.9)) | ((0.7,0.27),(0.36,0.64)) | ((0.37,0.71),(0.77,0.23)) |
| C1. Delivery time | C2. Financial instability | C3. Reputation | C4. Quality | |
|---|---|---|---|---|
| A1 | ((0.21,0.8),(0.18,0.82)) | ((0.48,0.53),(0.05,0.95)) | ((0.2,0.81),(0.19,0.81)) | ((0.71,0.27),(0.05,0.95)) |
| A2 | ((0.72,0.23),(0.09,0.91)) | ((0.05,0.95),(0.05,0.95)) | ((0.4,0.6),(0.17,0.83)) | ((0.71,0.27),(0.04,0.96)) |
| A3 | ((0.32,0.68),(0.18,0.82)) | ((0.81,0.13),(0.04,0.96)) | ((0.16,0.84),(0.19,0.81)) | ((0.33,0.67),(0.05,0.95)) |
| A4 | ((0.24,0.76),(0.18,0.82)) | ((0.85,0.08),(0.03,0.97)) | ((0.28,0.72),(0.18,0.82)) | ((0.76,0.24),(0.04,0.96)) |
| A5 | ((0.52,0.48),(0.15,0.85)) | ((0.47,0.51),(0.05,0.95)) | ((0.76,0.24),(0.04,0.96)) | ((0.09,0.92),(0.05,0.95)) |
| A6 | ((0.6,0.28),(0.11,0.89)) | ((0.71,0.25),(0.04,0.96)) | ((0.56,0.43),(0.16,0.84)) | ((0.81,0.13),(0.04,0.96)) |
| A7 | ((0.64,0.26),(0.11,0.89)) | ((0.16,0.88),(0.05,0.95)) | ((0.28,0.72),(0.17,0.83)) | ((0.67,0.32),(0.05,0.95)) |
| A8 | ((0.68,0.22),(0.13,0.87)) | ((0.81,0.13),(0.03,0.97)) | ((0.56,0.42),(0.15,0.85)) | ((0.35,0.72),(0.05,0.95)) |
| C1. Delivery time | C2. Financial instability | C3. Reputation | C4. Quality | |
|---|---|---|---|---|
| A1 | 0.288 | 0.526 | 0.282 | 0.767 |
| A2 | 0.909 | 0.097 | 0.523 | 0.763 |
| A3 | 0.427 | 0.867 | 0.239 | 0.381 |
| A4 | 0.334 | 0.896 | 0.381 | 0.802 |
| A5 | 0.663 | 0.526 | 0.928 | 0.137 |
| A6 | 0.784 | 0.77 | 0.719 | 0.87 |
| A7 | 0.825 | 0.189 | 0.381 | 0.718 |
| A8 | 0.861 | 0.862 | 0.722 | 0.361 |
| C1. Delivery time | C2. Financial instability | C3. Reputation | C4. Quality | |
|---|---|---|---|---|
| A1 | 0.187 | 0.404 | 0.181 | 0.678 |
| A2 | 0.87 | 0.054 | 0.399 | 0.676 |
| A3 | 0.306 | 0.808 | 0.149 | 0.264 |
| A4 | 0.224 | 0.863 | 0.264 | 0.729 |
| A5 | 0.555 | 0.4 | 0.918 | 0.078 |
| A6 | 0.691 | 0.679 | 0.619 | 0.81 |
| A7 | 0.747 | 0.115 | 0.264 | 0.618 |
| A8 | 0.8 | 0.806 | 0.62 | 0.254 |
| C1. Delivery time | C2. Financial instability | C3. Reputation | C4. Quality | |
|---|---|---|---|---|
| PIS | ((0.86,0.09),(0.04,0.96)) | ((0.85,0.08),(0.03,0.97)) | ((0.9,0.1),(0.03,0.97)) | ((0.81,0.13),(0.04,0.96)) |
| NIS | ((0.24,0.77),(0.05,0.95)) | ((0.05,0.95),(0.05,0.95)) | ((0.19,0.81),(0.05,0.95)) | ((0.09,0.92),(0.05,0.95)) |
| D to PIS | D to NIS | CC index | Rank | |
|---|---|---|---|---|
| A1 | 0.723 | 0.543 | 0.429 | 8 |
| A2 | 0.672 | 0.67 | 0.499 | 5 |
| A3 | 0.716 | 0.596 | 0.454 | 7 |
| A4 | 0.588 | 0.768 | 0.566 | 3 |
| A5 | 0.635 | 0.647 | 0.505 | 4 |
| A6 | 0.213 | 0.885 | 0.806 | 1 |
| A7 | 0.678 | 0.596 | 0.468 | 6 |
| A8 | 0.41 | 0.811 | 0.664 | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





