Submitted:
16 June 2023
Posted:
19 June 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
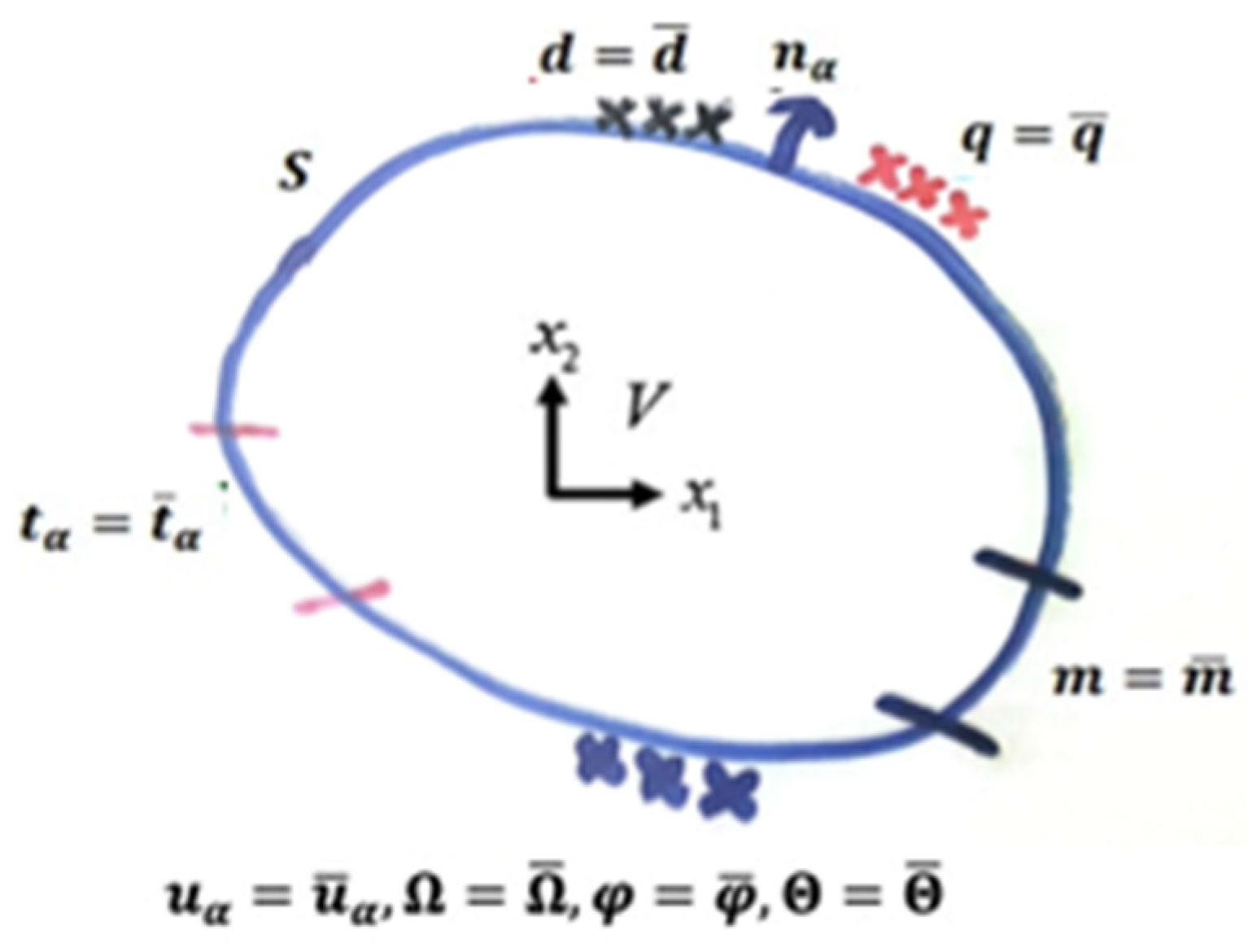
2. Formulation of the Problem
3. Boundary Conditions
4. Boundary Element Implementation
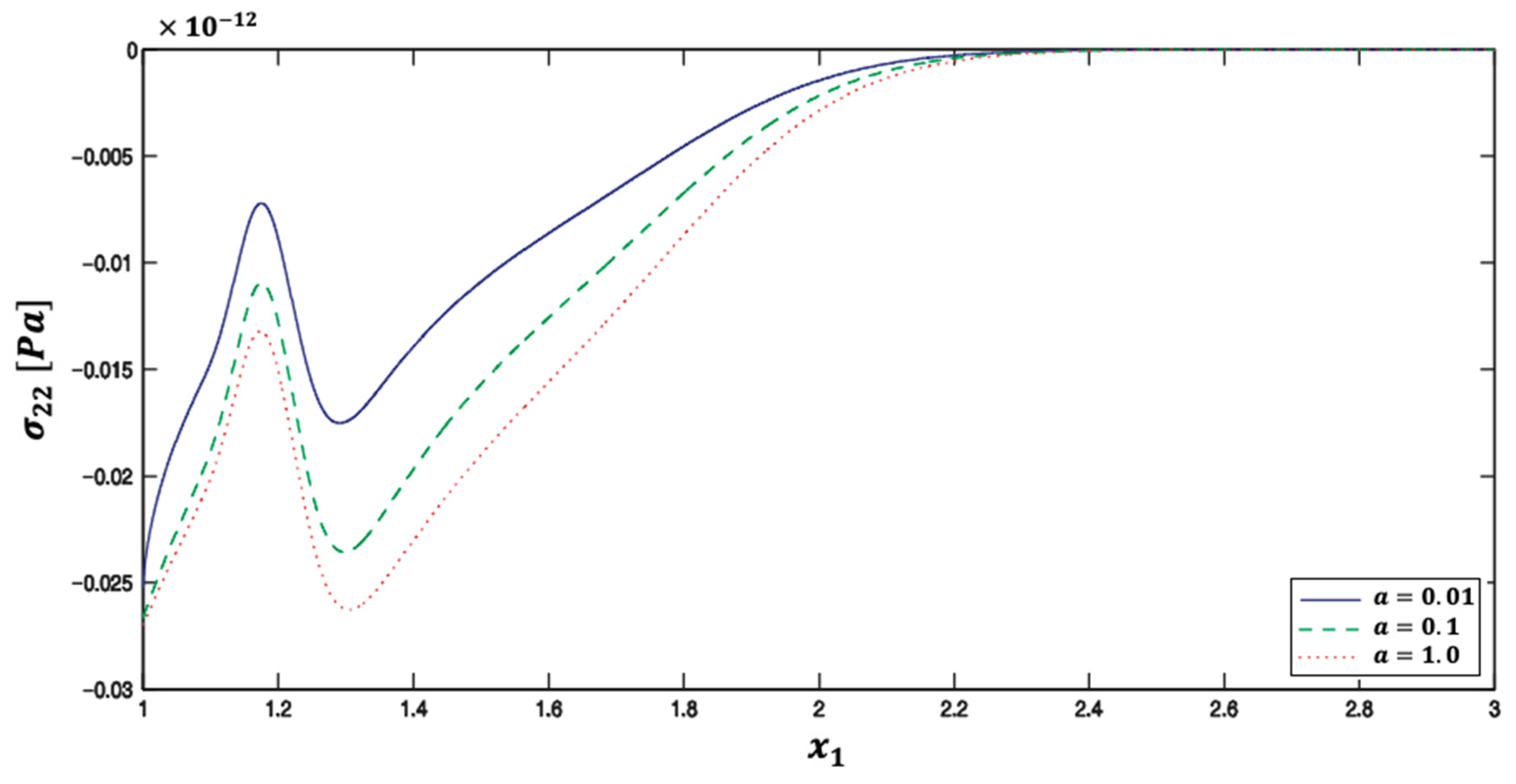
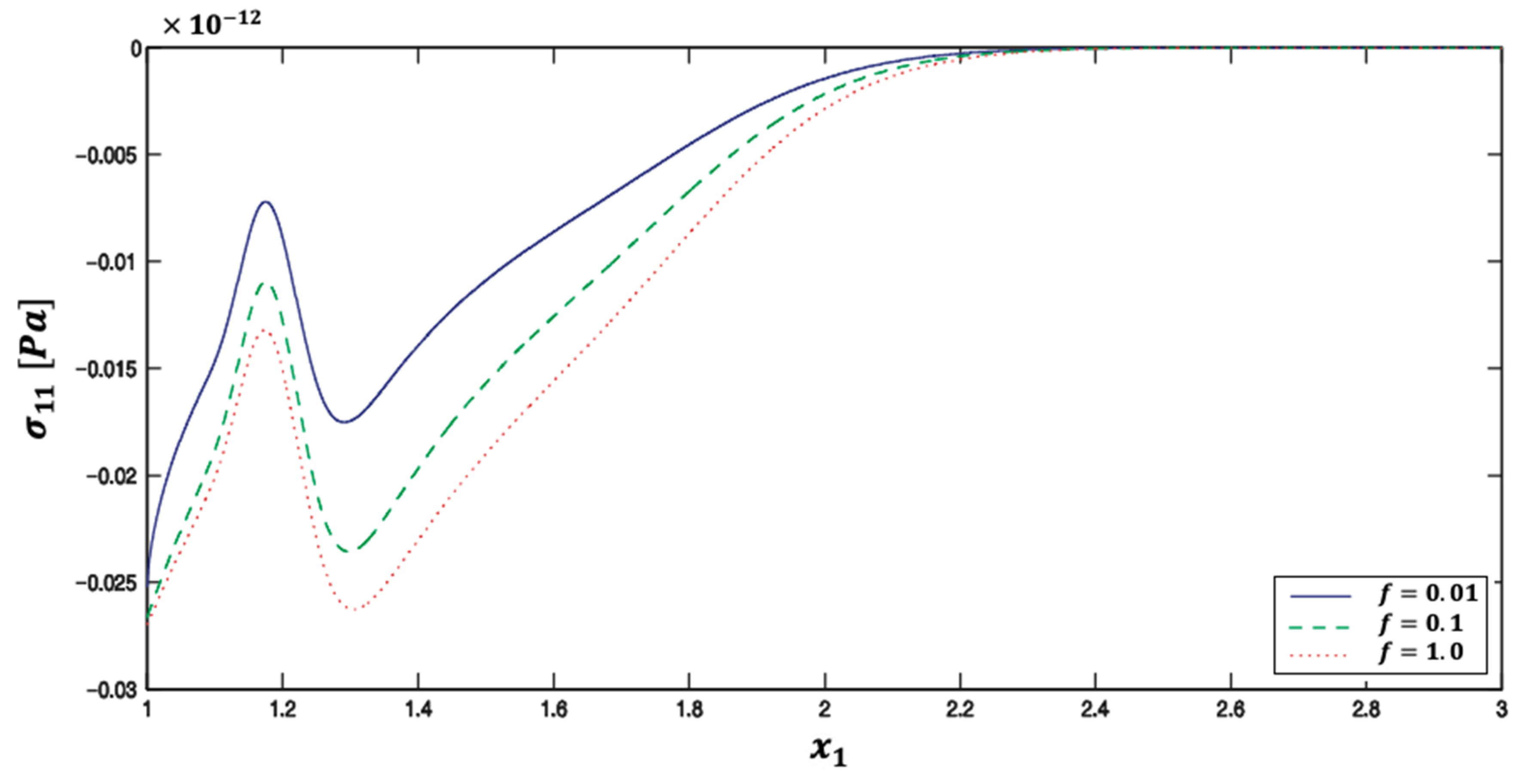
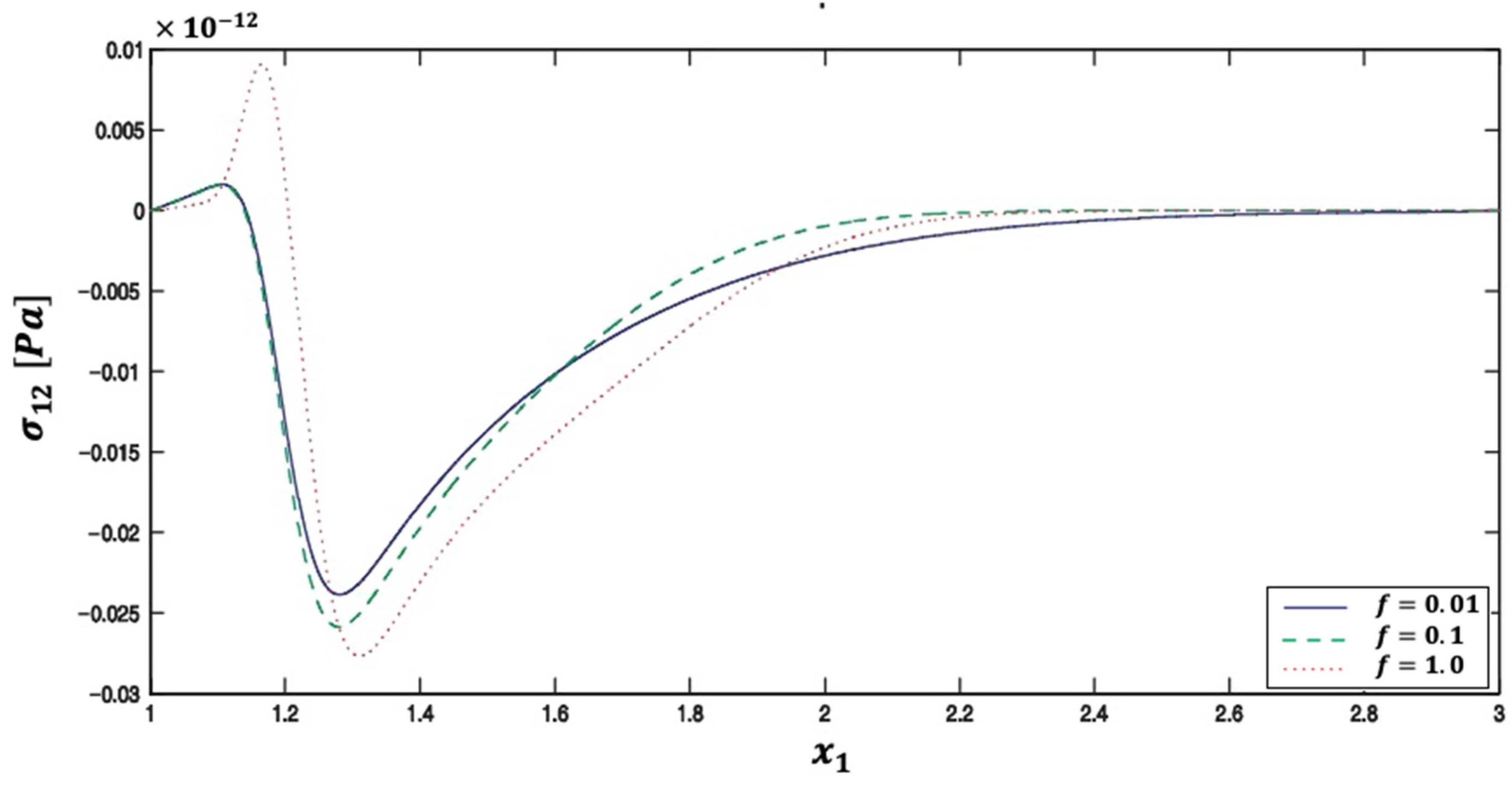
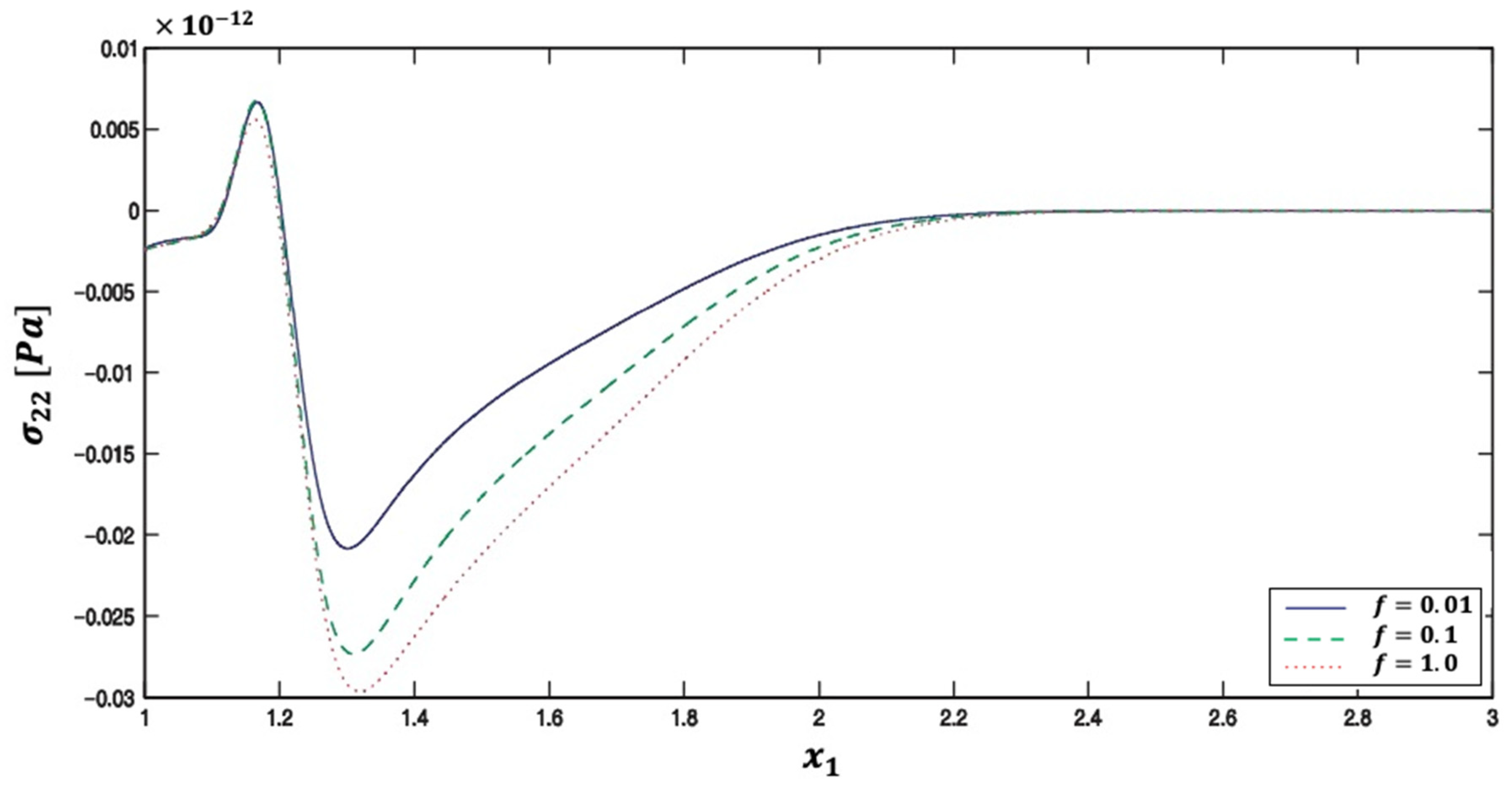
5. Numerical Results and Discussion
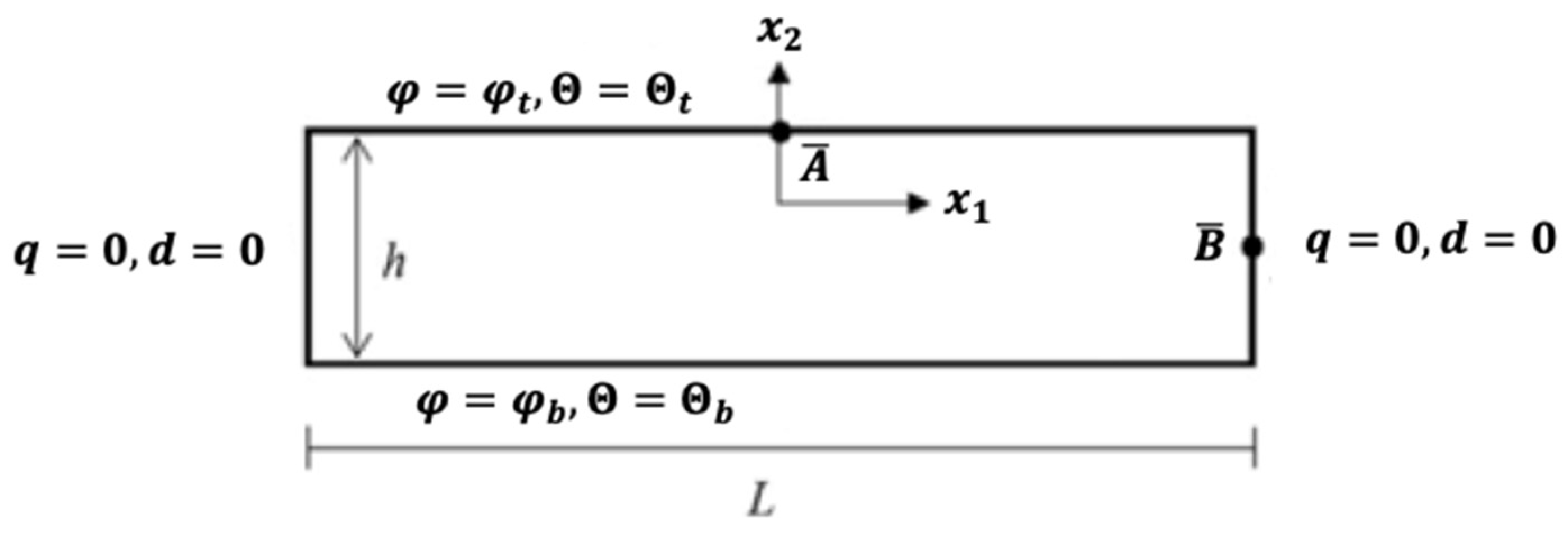
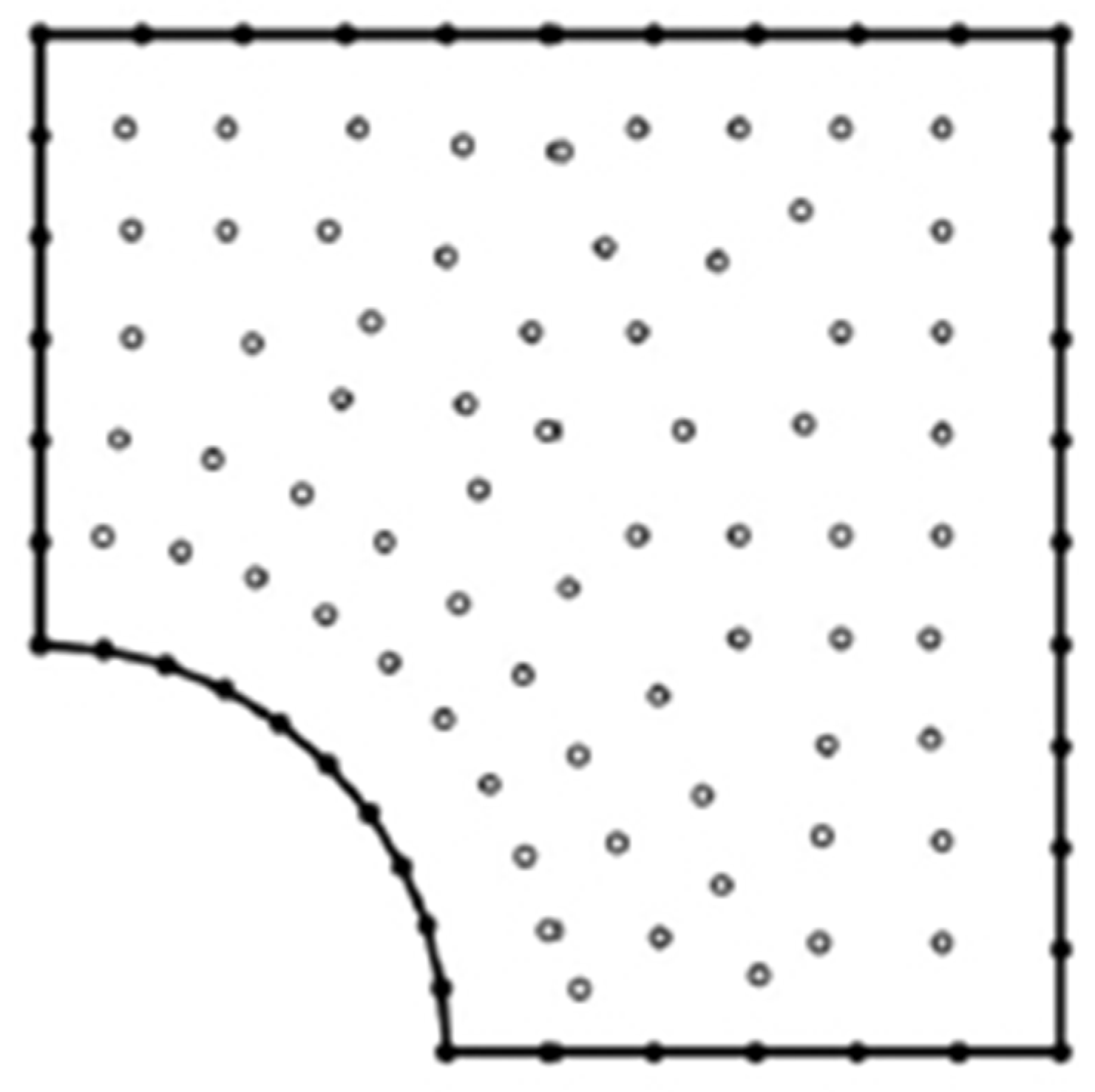
| T(oC) | 0 | 500 | 900 |
| C(J/kg) oK | 385 | 433 | 480 |
| 8930 | 8686 | 8458 |
6. Conclusion
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| coefficient of thermal expansion | Body force vector | ||
| Kronecker delta functi | Piezoelectric coefficient | ||
| & | Lamé elastic constants | Non-Gaussian temporal profile | |
| Volume electric charge density | Total energy intensity | ||
| Couple-stress parameter | Thermal conductivity | ||
| Total force-stress tensor | Mean curvature vector | ||
| Symmetric force-stress tensor | Pseudo mean curvature tensor | ||
| Skew-symmetric force-stress tensor | The material length scale parameter | ||
| Time | True couple-stress vector | ||
| Laser pulse time characteristic | Pseudo couple-stress tensor | ||
| Electric potential | Couple-traction | ||
| Rotation | Outward unit normal vector | ||
| Non-symmetric dense matrix | Polarization of piezoelectric material | ||
| Known boundary values vector | External heat source | ||
| Point couple kernel function | Point heat source kernel function | ||
| Electric displacement | Normal flux | ||
| Normal electric displacement | Heat flux vector | ||
| Young's modulus | Irradiated surface absorptivity | ||
| Electric field | Point electrical source kernel function | ||
| 2D permutation symbol | Temperature | ||
| 3D Levi-Civita permutation symbol | Generalized tractions | ||
| e | Electric permittivity | Force-traction vector | |
| Relative permittivity | Displacement vector | ||
| Vacuum permittivity | Poisson ratio | ||
| Point force kernel function | Unknown boundary values vector |
References
- H. M. Youssef and E. A. N. Al-Lehaibi. 2-D mathematical model of hyperbolic two-temperature generalized thermoelastic solid cylinder under mechanical damage effect. Archive of Applied Mechanics 92 (3), 945-960. [CrossRef]
- H. M. Youssef and E. A. N. Al-Lehaibi.. General generalized thermoelasticity theory (GGTT). Journal of Thermal Analysis and Calorimetry (2023). [CrossRef]
- H. M. Youssef and E. A. N. Al-Lehaibi. The photothermal interaction of a semiconducting solid sphere based on three Green-Naghdi theories due to the fractional-order strain and ramp-type heating. Mech Time-Depend Mater (2022). [CrossRef]
- M. I. A. Othman and M. Fekry. Effect of Magnetic field on generalized thermo-viscoelastic diffusion medium with voids, Int. J. Structural Stability & Dynamics 16 (2016) 1550033. [CrossRef]
- M. I. A. Othman, M. M. I. A. Othman, M. Fekry and M. Marin. Plane Waves in Generalized Magneto-thermo-viscoelastic Medium with Voids under the Effect of Initial Stress and Laser Pulse Heating, Struct. Eng. and Mech., An Int'l J., 73 (2020) 621-629. [CrossRef]
- M. I. A. Othman and M. Fekry. Effect of Rotation and Gravity on Generalized Thermo-viscoelastic Medium with Voids, Multi. Model. Mater. and Struct., 14 (2018) 322-338. [CrossRef]
- J. Ghanbari and R. Naghdabadi. Multiscale nonlinear constitutive modeling of carbon nanostructures based on interatomic potentials, CMC-Computers, Materials & Continua, 10 (2009) 41-64.
- Chakrabarty and, T. Çağin. Computational studies on mechanical and thermal properties of carbon nanotube based nanostructures, CMC-Computers, Materials & Continua.7 (2008) 167-190.
- S. N. Cha, J. S. Seo, S. M. Kim, H. J. Kim, Y. J. Park et al., Sound-driven piezoelectric nanowire-based nanogenerators, Advanced Materials. 22 (2010) 4726-4730. [CrossRef]
- Voiculescu and A., N. Nordin, Acoustic wave based MEMS devices for biosensing applications, Biosensors and Bioelectronics. 33 (2012) 1-9. [CrossRef]
- D. Shin, Y. D. Shin, Y. Urzhumov, Y. Jung, G. Kang, S. Baek et al., Broadband electromagnetic cloaking with smart metamaterials, Nature Communications, vol. 3, no. 11, pp. 1213, 2012. [CrossRef]
- S. Zhang, B. S. Zhang, B. Gu, H. Zhang, X. Q. Feng, R. Pan et al., Propagation of Love waves with surface effects in an electrically-shorted piezoelectric nano film on a half-space elastic substrate, Ultrasonics, vol. 66 (2016) 65-71. [CrossRef]
- F. Akyildiz and J. M. Jornet, Electromagnetic wireless nanosensor networks, Nano Communication Networks, vol. 1, no. 1, pp. 3-19, 2010. [CrossRef]
- He, X. Qi, Y. Miao, H. L. Wu, N. He et al., Application of smart nanostructures in medicine, Nanomedicine, vol. 5, no. 7, pp. 1129-1138, 2010. [CrossRef]
- Y. Al-Hossain, F. A. Y. Al-Hossain, F. A. Farhoud and M. Ibrahim, “The mathematical model of reflection and refraction of plane quasi-vertical transverse waves at interface nanocomposite smart material,” Journal of Computational and Theoretical Nanoscience, vol. 8, no. 7, pp. 1193-1202, 2011. [CrossRef]
- L. Zhu and X. J. Zheng, Stress field effects on phonon properties in spatially confined semiconductor nanostructures, CMC-Computers, Materials & Continua.18 (2010) 301-320.
- Y. Danl, I. Huynen and C. Bailly, Thin smart multilayer microwave absorber based on hybrid structure of polymer and carbon nanotubes, Applied Physics Letters. 100 (2012) 213105. [CrossRef]
- A. Ezzat, “State space approach to unsteady two-dimensional free convection flow through a porous medium,” Canadian Journal of Physics. 72 (1994) 311–317. [CrossRef]
- Ezzat, M. Zakaria, O. Shaker and F. Barakat, State space formulation to viscoelastic fluid flow of magnetohydrodynamic free convection through a porous medium, Acta Mechanica. 119 (1996) 147–164. [CrossRef]
- A. Ezzat, Free convection effects on perfectly conducting fluid, International Journal of Engineering Science. 39 (2001) 799–819. [CrossRef]
- R. Hadjesfandiari, Size-dependent piezoelectricity, International Journal of Solids and Structures. 50 (2013) 2781-2791. [CrossRef]
- M. A. Fahmy. A new BEM modeling algorithm for size-dependent thermopiezoelectric problems in smart nanostructures. CMC-Computer, Materials & Continua, 69 (2021) 931-944. [CrossRef]
- M. A. Fahmy, M. M. M. A. Fahmy, M. M. Almehmadi, F. M. Al Subhi and A. Sohail. Fractional boundary element solution of three-temperature thermoelectric problems, Scientific Reports, 12 (2022) 6760. [CrossRef]
- M. A. Fahmy. 3D boundary element model for ultrasonic wave propagation fractional order boundary value problems of functionally graded anisotropic fiber-reinforced plates, Fractal and Fractional, 6 (2022) 247. [CrossRef]
- M. A. Fahmy. Boundary element modeling of fractional nonlinear generalized photothermal stress wave propagation problems in FG anisotropic smart semiconductors, Engineering Analysis with Boundary Elements. 2022 (2022) 134:665–679. [CrossRef]
- M. A. Fahmy and M. O. Alsulami. boundary element and sensitivity analysis of anisotropic thermoelastic metal and alloy discs with holes, Materials, 15 (2022) 1828. [CrossRef]
- B. T. Darrall, A. R. B. T. Darrall, A. R. Hadjesfandiari and G. F. Dargush, Size-dependent piezoelectricity: A 2D finite element formulation for electric field-mean curvature coupling in dielectrics, European Journal of Mechanics-A/Solids, 49 (2015) 308–320. [CrossRef]
- M. A. Fahmy, 3D Boundary Element Model for Ultrasonic Wave Propagation Fractional Order Boundary Value Problems of Functionally Graded Anisotropic Fiber Reinforced Plates. Fractal Fract. 6 (2022) 247. [CrossRef]
- C. Cattaneo, Sur une forme de I’equation de la Chaleur Elinant le Paradox d’une Propagation Instantanc. Comptes Rendus de l’Académiedes Sciences; Gauthier-Villars: Paris, France, 247 (1958) 431–433.
- H. S. Carslaw, J. C. Jaeger, Conduction of Heat in Solids; Clarendon Press: Oxford, UK, 1959.
- M. A. Fahmy. A Nonlinear Fractional BEM Model for Magneto-Thermo-Visco-Elastic Ultrasound Waves in Temperature-Dependent FGA Rotating Granular Plates. Fractal Fract. 2023, 7, 214. [CrossRef]
- Wrobel, L.C. The Boundary Element Method: Applications in Thermo-Fluids and Acoustics; John Wiley & Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Hematiyan, M.R. Exact transformation of a wide variety of domain integrals into boundary integrals in boundary element method. Commun. Numer. Methods Eng. 24 (2008) 1497–1521. [CrossRef]
- Hematiyan, M.R. A general method for evaluation of 2D and 3D domain integrals without domain discretization and its application in BEM. Comput. Mech., 39 (2007) 509–520. [CrossRef]
- Khosravifard, A.; Hematiyan, M.R. A new method for meshless integration in 2D and 3D Galerkin meshfree methods. Eng. Anal. Bound. Elem. 34 (2010) 30–40. [CrossRef]
- Liu, G.R.; Gu, Y.T. An Introduction to Meshfree Methods and Their Programming; Springer: New York, NY, USA, 2005. [Google Scholar]
- R. Hadjesfandiari and G. F. Dargush, Fundamental solutions for isotropic size-dependent couple stress elasticity, International Journal of Solids and Structures, 50 (2013) 1253–1265. [CrossRef]
- Hajesfandiari, A. R. Hadjesfandiari and G. F. Dargush, Boundary element formulation for plane problems in size-dependent piezoelectricity, International Journal for Numerical Methods in Engineering, 108 (2016) 667-694. [CrossRef]
- Hajesfandiari, A. R. Hadjesfandiari and G. F. Dargush, Boundary element formulation for steady state plane problems in size-dependent thermoelasticity, Engineering Analysis with Boundary Elements, 82 (2017) 210–226. [CrossRef]
- M. A. Fahmy. A new boundary element algorithm for modeling and simulation of nonlinear thermal stresses in micropolar FGA composites with temperature-dependent properties. Advanced Modeling and Simulation in Engineering Sciences, 8 (2021) 1-23. [CrossRef]
- E. Abouelregal and M. A. Fahmy (2022). Generalized Moore-Gibson-Thompson thermoelastic fractional derivative model without singular kernels for an infinite orthotropic thermoelastic body with temperature-dependent properties, ZAMM Journal of Applied Mathematics and Mechanics. [CrossRef]
- Nikhil, V. Suramwar, Sanjay R. Thakare, Niraj T. Khaty. One pot synthesis of copper nanoparticles at room temperature and its catalytic activity. Arabian Journal of Chemistry, November, 9 (2016) S1807-S1812. [CrossRef]
- Zan Xu, Juan J. Alonso, and Eric Darve. A numerically stable communication avoiding S-stepGMRES algorithm. arXiv:2303.08953 [math.NA]. 2023 [v2]. [CrossRef]
- Xin-Hui Shao and Chong-Bo Kang. Modified DTS iteration methods for spatial fractional diffusion equations, Mathematics, 11 (2023) 931. [CrossRef]
- Zi-Hang She, Li-Min Qiu and Wei Qu. An unconditionally convergent RSCSCS iteration method for Riesz space fractional diffusion equations with variable coefficients, Mathematics and Computers in Simulation, 203,(2023) 633–646. [CrossRef]
- Sladek, V. Sladek, M. Repka and C. L. Tan. Size dependent thermo-piezoelectricity for in-plane cracks, Key Engineering Materials, 827 (2019) 147–152. [CrossRef]
- Y. J. Yu, X. G. Y. J. Yu, X. G. Tian and X. R. Liu. Size-dependent generalized thermoelasticity using Eringen's nonlocal model, European Journal of Mechanics A/Solids, 51 (2015) 96-106. [CrossRef]
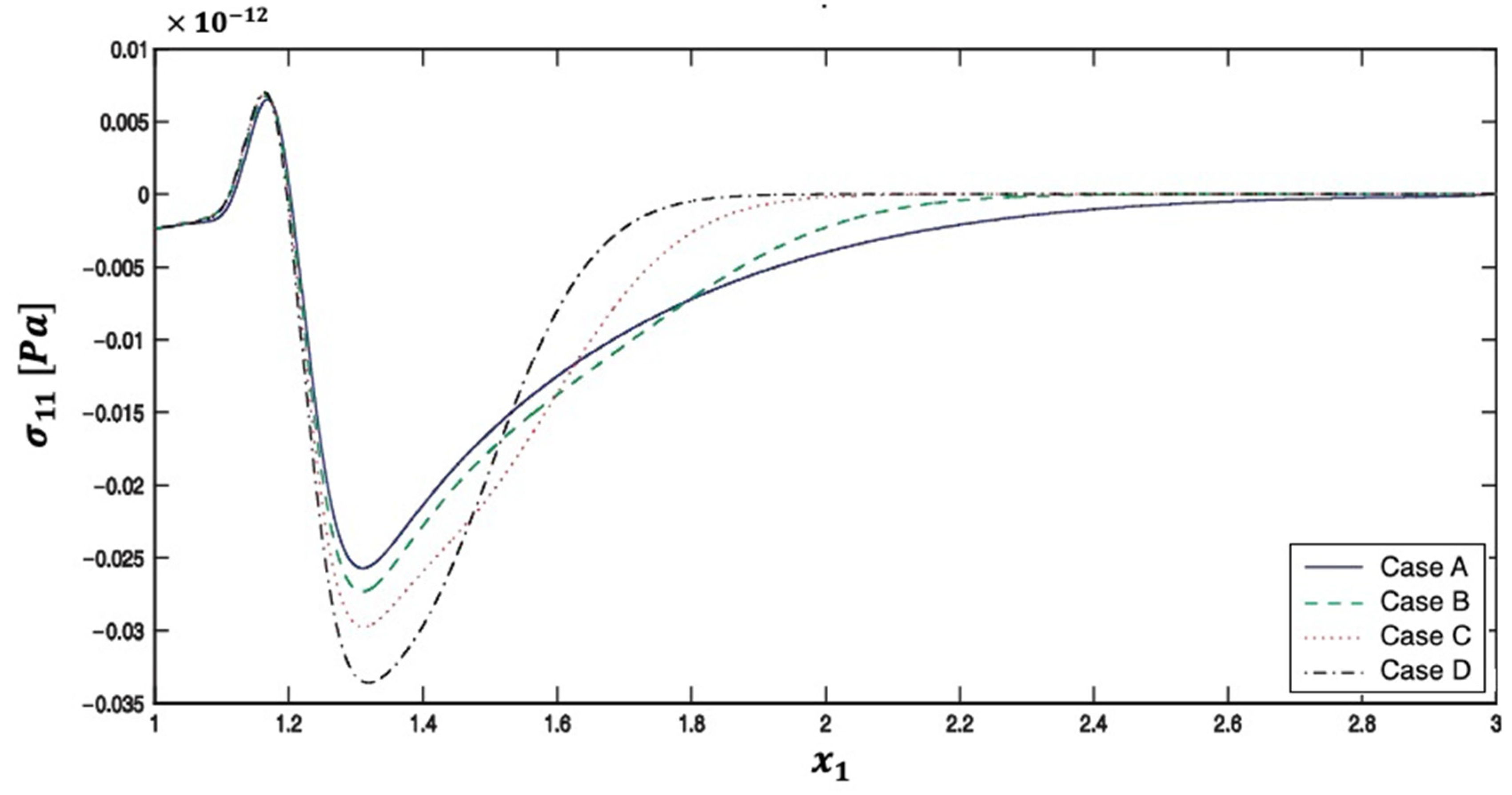
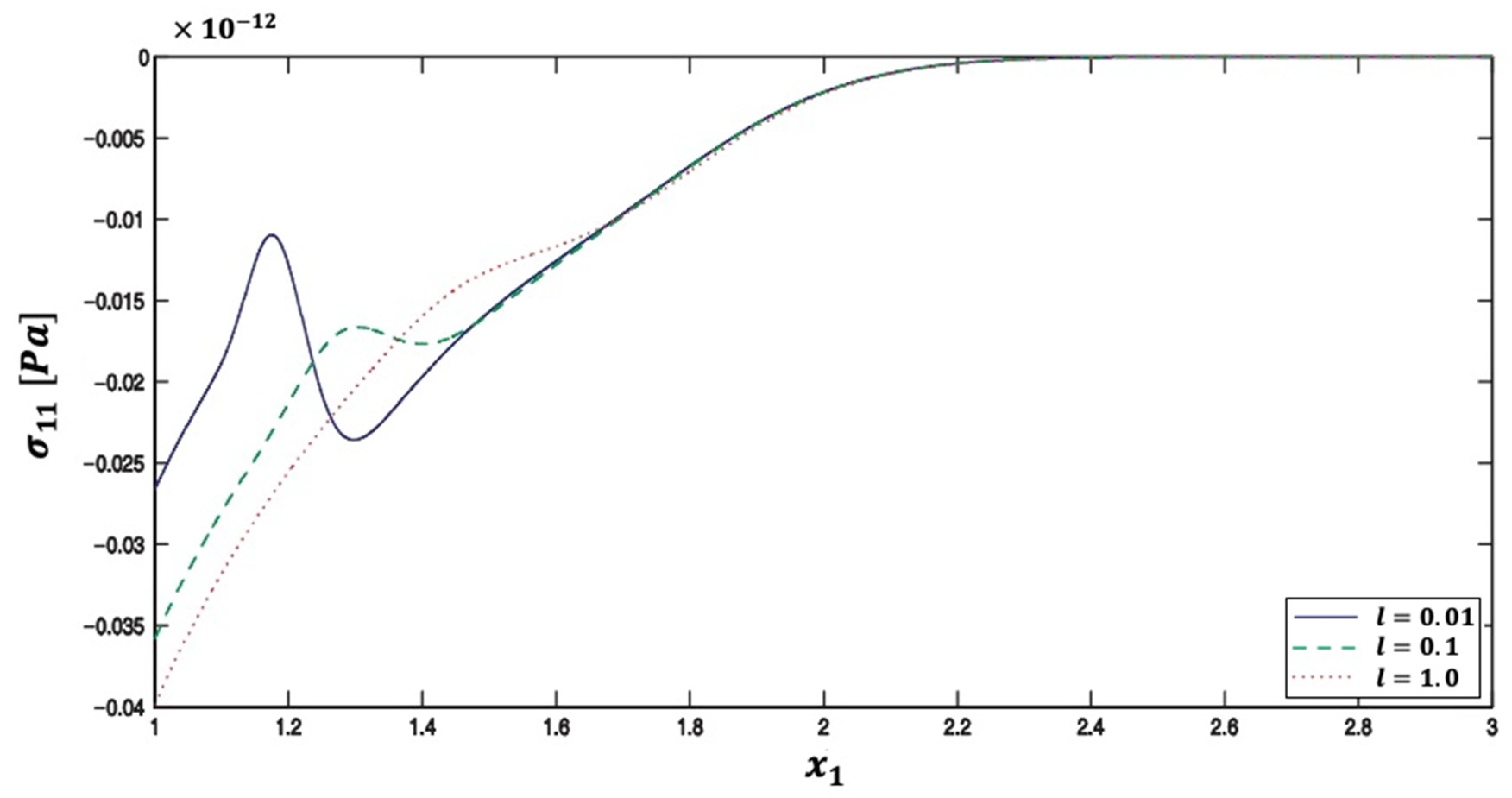
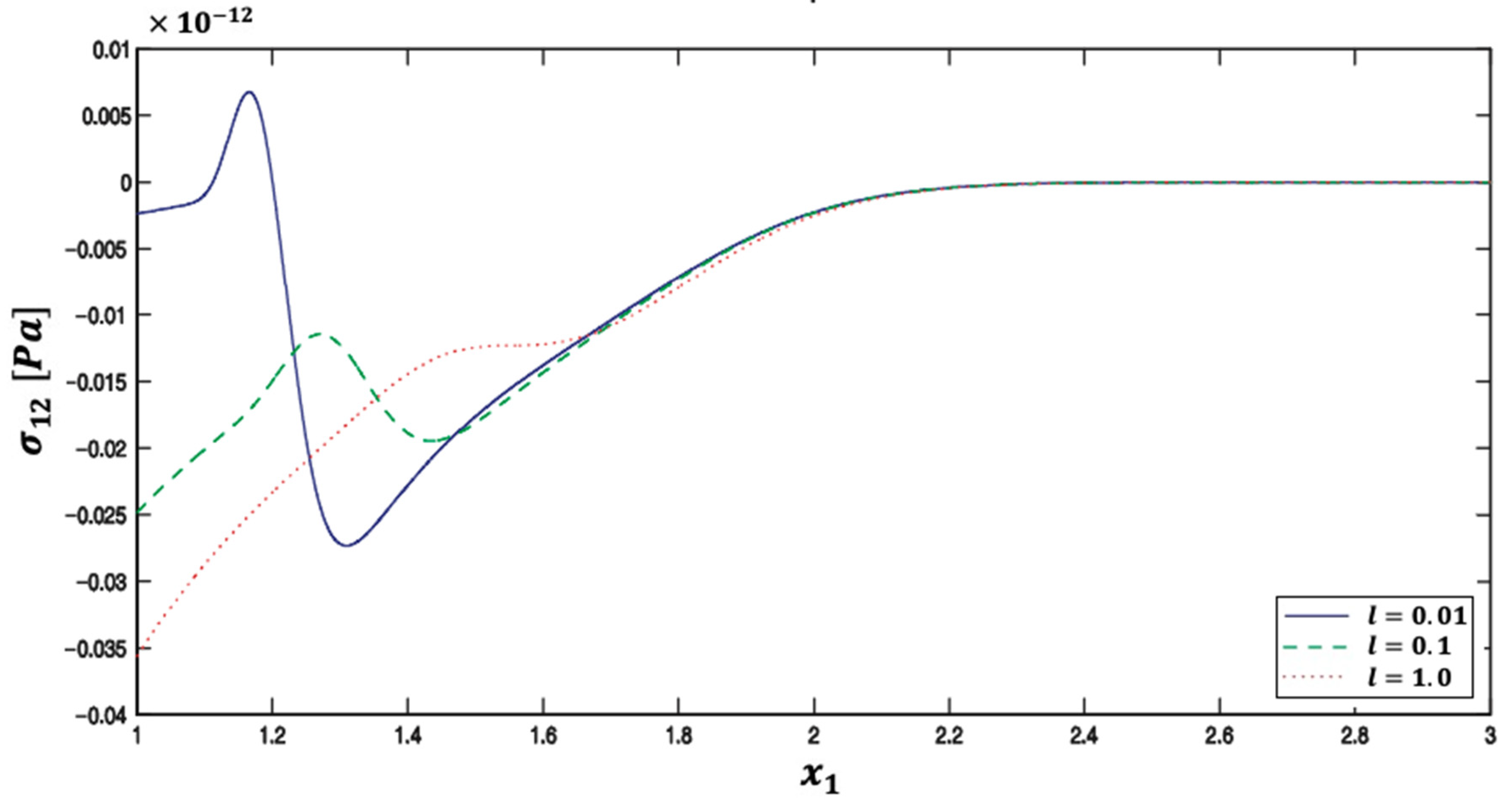
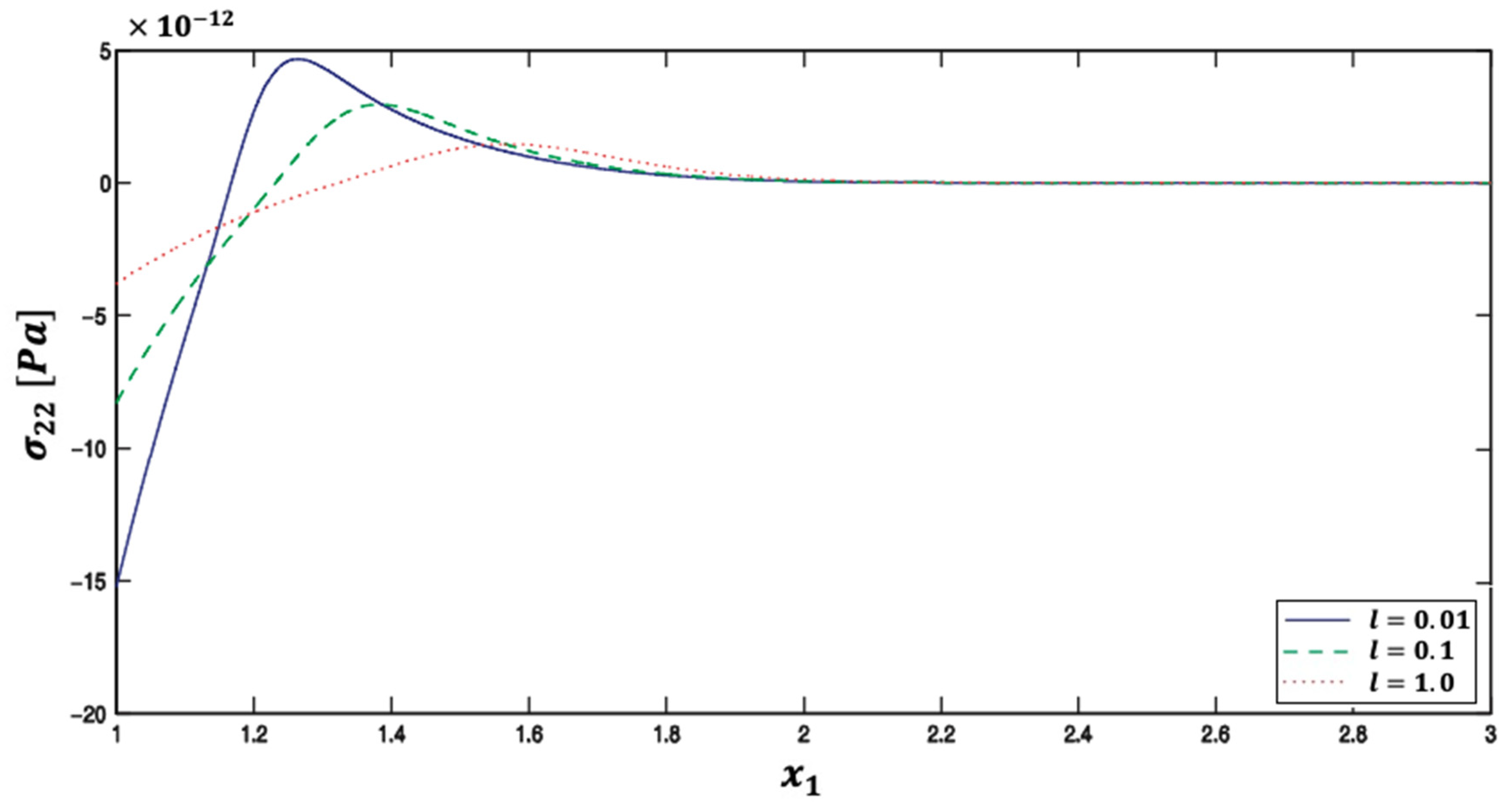
| Method | Iter. | CPU time | Rr | Err. | |
| SCAS-GMRES | 30 | 0.0119 | 1.96e-07 | 1.48e-09 | |
| FMDTS | 60 | 0.0564 | 5.50e-07 | 1.72e-07 | |
| UC-RSCSCS | 70 | 0.0730 | 7.02e-07 | 2.50e-06 | |
| SCAS-GMRES | 40 | 0.0538 | 0.19e-06 | 2.06e-08 | |
| FMDTS | 90 | 0.2239 | 1.72e-05 | 4.52e-06 | |
| UC-RSCSCS | 120 | 0.3764 | 1.16e-04 | 0.58e-05 | |
| SCAS-GMRES | 60 | 0.1758 | 2.22e-05 | 1.80e-07 | |
| FMDTS | 270 | 0.7940 | 1.80e-04 | 3.62e-05 | |
| UC-RSCSCS | 280 | 0.8950 | 1.22e-03 | 4.60e-04 |
| BEM | FEM | Analytical | ||||
|---|---|---|---|---|---|---|
| 0.01 | -0.04766 | -0.01847 | -0.04769 | -0.01850 | -0.04767 | -0.01848 |
| 0.1 | -0.02452 | -0.02113 | -0.02455 | -0.02116 | -0.02453 | -0.02114 |
| 1.0 | -0.01984 | -0.02582 | -0.01987 | -0.02586 | -0.01985 | -0.02583 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




