1. Introduction
The relationship between the fractal dimension of geomagnetic variations and magnetic storms has been studied by many researchers [
7,
8,
10,
12,
14,
16]. Moreover, fractal dimension of geomagnetic indices fluctuations, such as AE [
13] Sym-H [
1], Dst [
4], which are the result of the processing of measurements at several magnetic observatories, were studied. The majority of studies noted the effect of reducing the fractal dimension of geomagnetic variations or geomagnetic indices fluctuations during geomagnetic disturbances at high [
13] and low latitudes [
8,
12]. Wanliss and co-authors [
14] shown that fractal dimension of geomagnetical variation is increased with geomagnetical latitude. It was noted [
16] that temporal variation of geomagnetic field fractal dimension at medium and high latitudes is different.
Usually, in the studies mentioned above, the fractal dimension data were compared under quiet and disturbed geomagnetic conditions. The object of this paper is to use correlation analysis to study a relationship between Higuchi fractal dimension (HFD) of geomagnetic variations at Russian Altay (at middle latitude) and space weather characteristics, in particular, with the auroral electrojet (AE) index and solar wind characteristics.
The structure of the article consists of an introduction, which describes the methods for studying geomagnetic field variations and provides links to articles on the subject of the study.
Section 2 describes the materials and methodology of the study: information is given on the point of registration of the D,H,Z-component of the geomagnetic field, the method for constructing the fractal dimension according to Higuchi is described, and preliminary data processing is given.
Section 3 presents the results of applying the Higuchi fractal dimension to study variations in the D,H,Z components of the geomagnetic field in 2011 at the Baigazan station in Altai, and gives an interpretation of the study results.
2. Materials and Methods
Since 2009, geomagnetic field variations have been recorded at the magnetic station of Gorno-Altaisk State University "Baigazan" [
6]. The station is located at the cordon of the same name of the Altaiskiy Reserve on the northern shore of Lake Teletskoye (N51
45.596’, E87
25.916’). The territory of the reserve is protected by the law of the Russian Federation, therefore there is no magnetic pollution and technogenic noises. Measurements at the station are carried out using a quartz variometer based on the sensor of CMVS “Quartz-3EM” with the rate equaled to 5 Hz. The accuracy of sec mean values of D,H,Z-components is 10 pT. The station is powered from alternative energy sources, installed 120 meters from the station near the inspector’s house. Power consumption is 27 W.
There were a data losses at a follow periods: 28.01.2012 –07.03.2012, 27.07.2012 –11.10.2012, 24.05.2013 – 03.07.2013, 15.08.2013 – 20.10.2013. The summer losses were caused by lightning activity, which destroyed power system elements of the station and stopped the measurements. From December 11 to 23, 2012, as well as February 16-19, 2013, and May 9-24, 2013, the H-component sensor was in the second steady state, which is characterized by an increased noise level, so the calculations gave anomalously high values of the HFD. On September 7-9, 2011 and September 20-26, 2011, a similar problem was observed with the D-sensor. Data for these periods were excluded from the analysis.
For each 45-minute interval of the quartz variometer data for the years 2011-2013, the fractal dimensions of D,H,Z-geomagnetic variations were calculated using the Higuchi method [
9] by means of MATLAB. The experience of using various methods for estimating the fractal dimension time series has shown that Higuchi method is one of the most robust methods [
5,
16]. In this method, the mean distance between the elements of the time series
spaced by
k elements, for different values of the number of the initial element
m was calculated
where
N is the length of a series, and
denotes integer part of
z.
This distance is averaged over all numbers of the initial element
m
The dependence of the average distance between spaced elements on time space k has a power-law form with a coefficient equal to the fractal dimension : .
This corresponds to a linear relationship on a log scale
The fractal dimension was calculated as a linear regression coefficient between the logarithms
L and
. A accuracy of HFD estimation (a median of regression coefficient errors at 0.95-confidence level for year) equals to 0.08. The example of the variation, its FFT-spectrum and
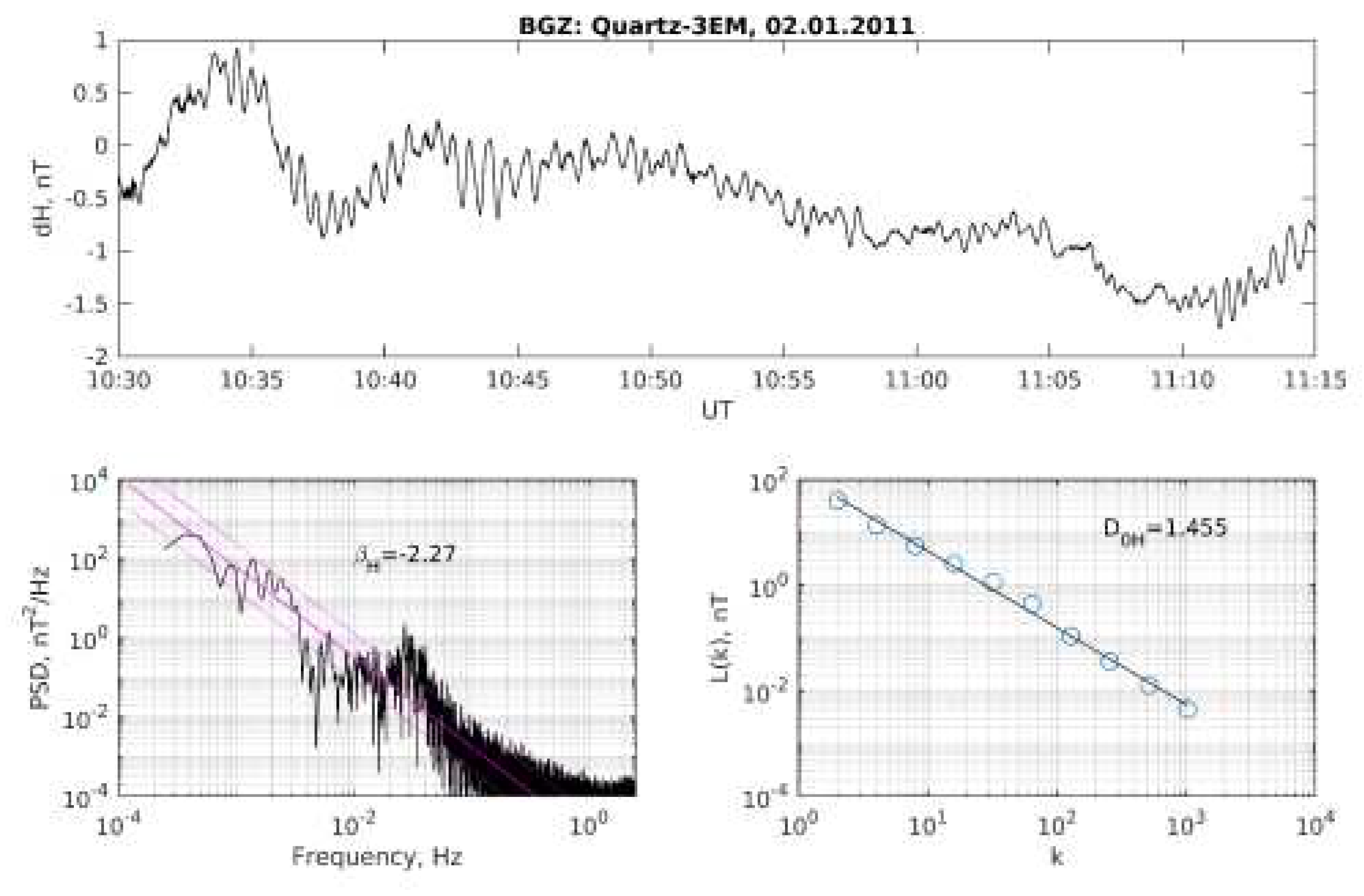
– dependence are shown in
Figure 1. As a result of calculations, series of geomagnetic variations HFD were obtained (32 values for each day).
Note that HFD allows to describe a continual part of the geomagnetic variation spectrum therefore a spectrum slope coefficient can be calculated by a formula:
[
5].
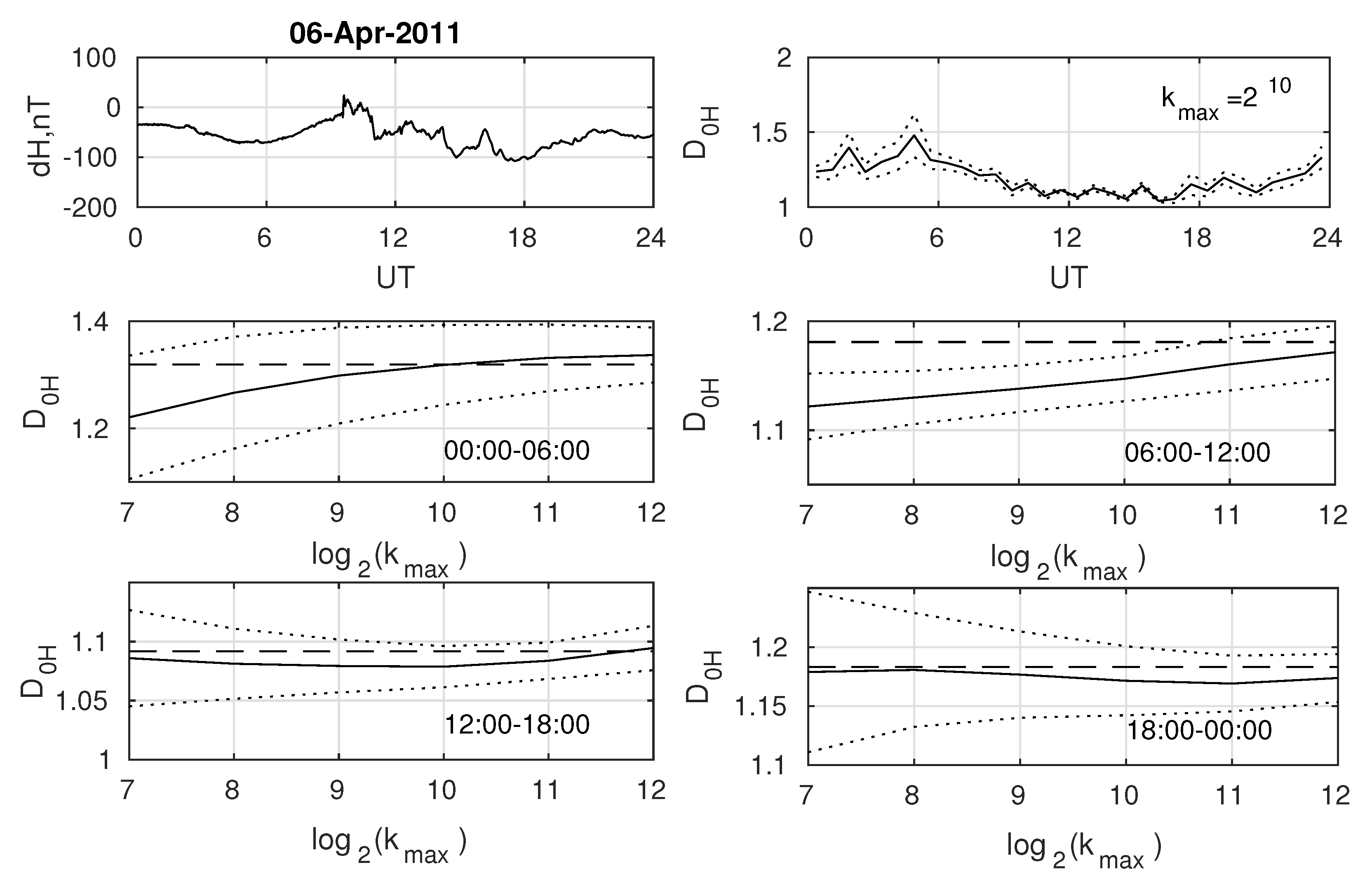
It is shown, that HFD estimation value depends on maximal time space
and data type [
15]. HFD was calculated at various values of its parameter (
) for 6 h time interval to study HFD estimation dependencies on
(see
Figure 2).
This estimations were compared to mean value of 8 values of HFD, calculated at
for 45 min intervals within this 6 h interval. A example of these calculations is shown at
Figure 2.
Similar calculations were carried out for 20 days, both in quiet and desturbed geomagnetic conditions. The analysis showed that the mean value is in the error band of the
– curve with the quiet geomagnetic field (the example is shown at
Figure 2 for time period 00-06 UT). However a difference between mean value and
– curve can reaches 0.1 at time when HFD changes rapidly. The example can be seen at time period 06-12 UT at
Figure 2, that containes a the beginning of the storm, the HFD changes from 1.3 to 1.1 at this time. Meanwhile, when the storm developed and the fractal dimension was consistently low (12-24 UT at
Figure 2), the average HFD value again began to be within the error interval of
curve. Thus, under stable geomagnetic conditions, the calculation method does not significantly affect the HFD value.
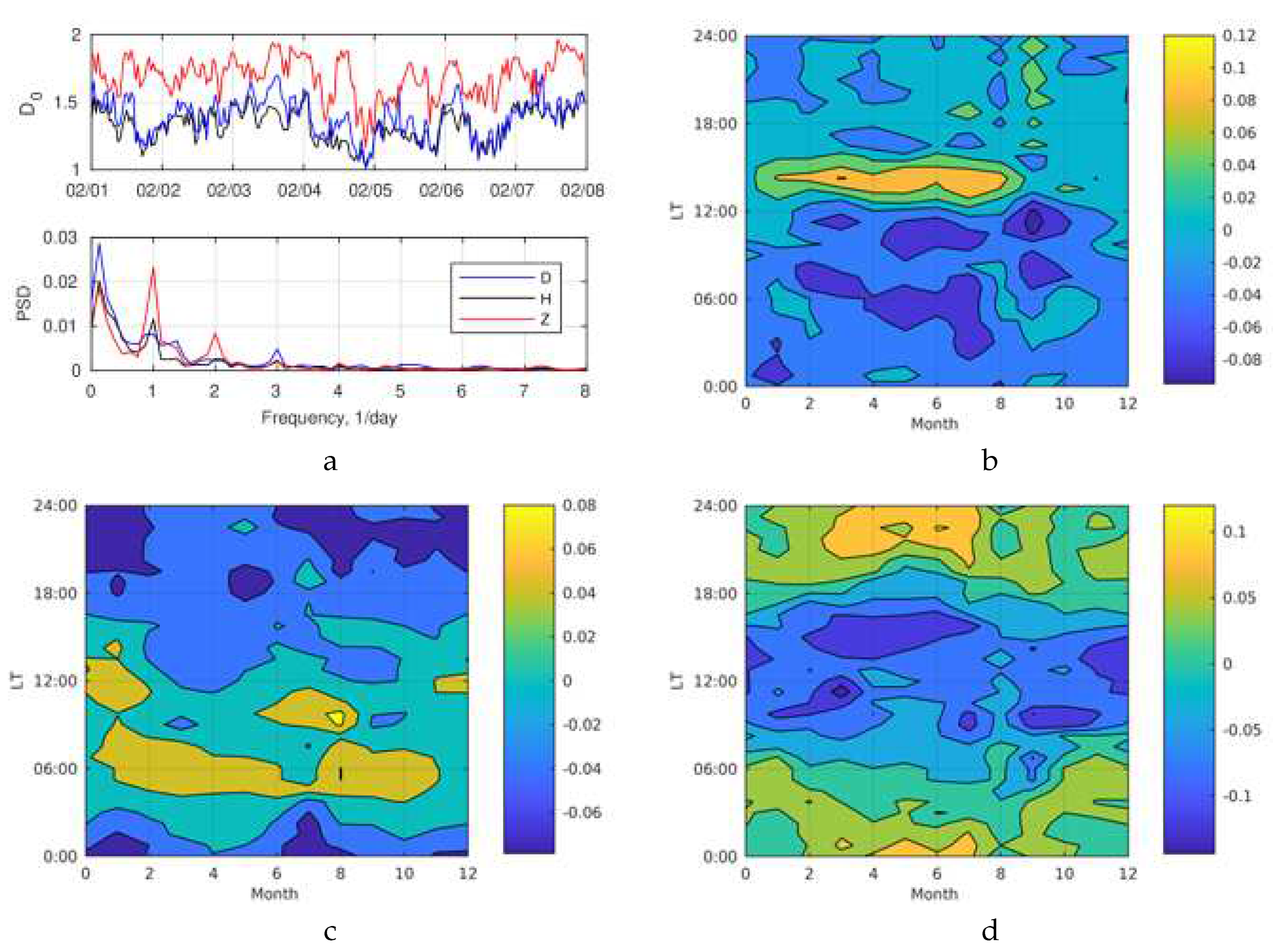
The analysis showed that the fractal dimension is subject to periodic variations, including daily variations. A spectrum of HFD variations for February 2011 data and diurnal variation of H,D,Z - component fractal dimension are shown in
Figure 2a. Daily variation of HFD for each month was calculated by the formula
where
is the day number in a month,
is the month number,
are geomagnetic components,
is the daily average of fractal dimension,
– Universal Time. A seasonal variation of HFD diurnal variation at Altay is shown in
Figure 2b-d. It is shown that the diurnal variations for the fractal dimensions of D- and H-components are roughly opposite. The maximum value of
(for the H-component) is distinguished near the sunset terminator and minimum – in night time. The maximum
(for D-components) is observed at 14 LT and minimum – in 6 LT and 11 LT (LT – Local Time). The fractal dimension of the Z-component is decreased during a day and is increased at night.
The diurnal variation amplitude is close to 0.1, and its variance ratio to the total variance of the fractal dimension for the H,D,Z-components are equaled to 0.30, 0.31 and 0.41, respectively.
Then, the diurnal variation of fractal dimension was removed from the data (
4)
and the pair and partial correlation coefficients with mean values of the space weather characteristics over 45 minutes were calculated. The data of solar wind parameters was obtained at OMNIWEB, data of AE-index – at World Data Center for Geomagnetism, Kyoto. This data was averaged for each 45-min interval.
3. Results and discussion
It is known that HFD of geomagnetical variations can be described as normally distributed random value [
14]. Annual averaged values and standard deviations of HFD for H,D,Z-component at 2011 as parameters of normal distribution were calculated. These values are presented in
Table 1.
It can be seen that HFD of Z-component is higher significantly then other components and Z-components can be described as antipersistent noise. The averaged values for H,D-components coincide to results of [
14]. The standard deviations are less than in [
14] this is due to the fact that data on 40 magnetic stations at various geomagnetical latitudes for the solar cycle are considered there. Apparently, the missing part of the variance controls the latitude dependence of the fractal dimension.
For the fractal dimension with the AE index, as well as the characteristics of the solar wind Pearson pair correlation coefficients were calculated. The correlation coefficients for H,D,Z-components for the data of 2011 are presented in
Table 2.
In order to ensure data agreement with a normal distribution, the AE index, plasma density, solar wind velocity and IMF strength were taken logarithmically. The negative correlations of geomagnetic variation fractal dimension with averaged logarithm of solar wind velocity, logarithm IMF and logarithm of AE-index are detected. In general, this result coincides with the results of the papers mentioned in the introduction. It should be noted that in our calculations, a statistically reliable relationship of HFD with the space weather characteristics was revealed for all components of the geomagnetic field (H,D,Z), and in previous studies [
10,
12,
14,
16], a significant decrease in HFD with geomagnetic disturbances was noted only for the horizontal component.
Since AE-index, solar wind speed and IMF are correlated (except
v and IMF), partial correlation coefficients were calculated for them. Partial correlation coefficients for four variables:
– are shown in
Table 3.
Here
X means one of the components of the geomagnetic field. The partial correlation coefficients are smaller than the pair coefficients for all characteristics. A determination coefficient shows at least a quarter of the fractal dimension variance is controlled by the variability of the AE index, IMF and
v. Thus, the part of variance controlled by these parameters has approximately the same value as the daily variation. Probably the variation of these parameters causes a harmonic with a period approximately equaled to a week in
Figure 3a.
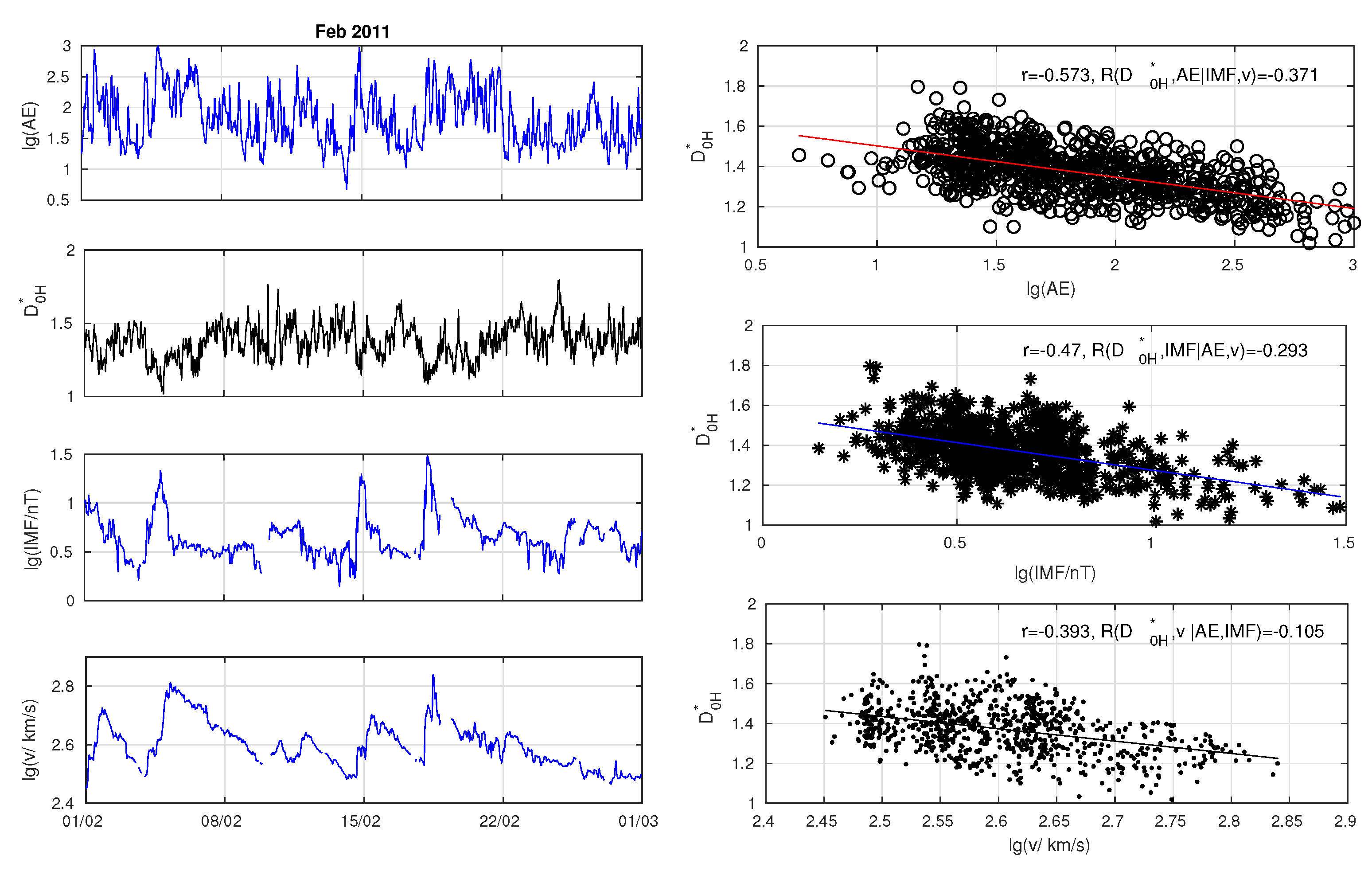
Partial correlation coefficients of HFD with logarithms of AE-index, IMF and solar wind velocity were calculated for each month of 2011-2013. The example of temporal dependences of HFD,
,
and
for a month and its scatter plots are shown in
Figure 4.
It illustrates that high values of AE-index and maximums of interpalnetary magnetic field correspond to low values of HFD in February, 2011.
The calculation results of monthly partial correlation coefficient of HFD with
,
and
for 2011-2013 years are shown in
Figure 5.
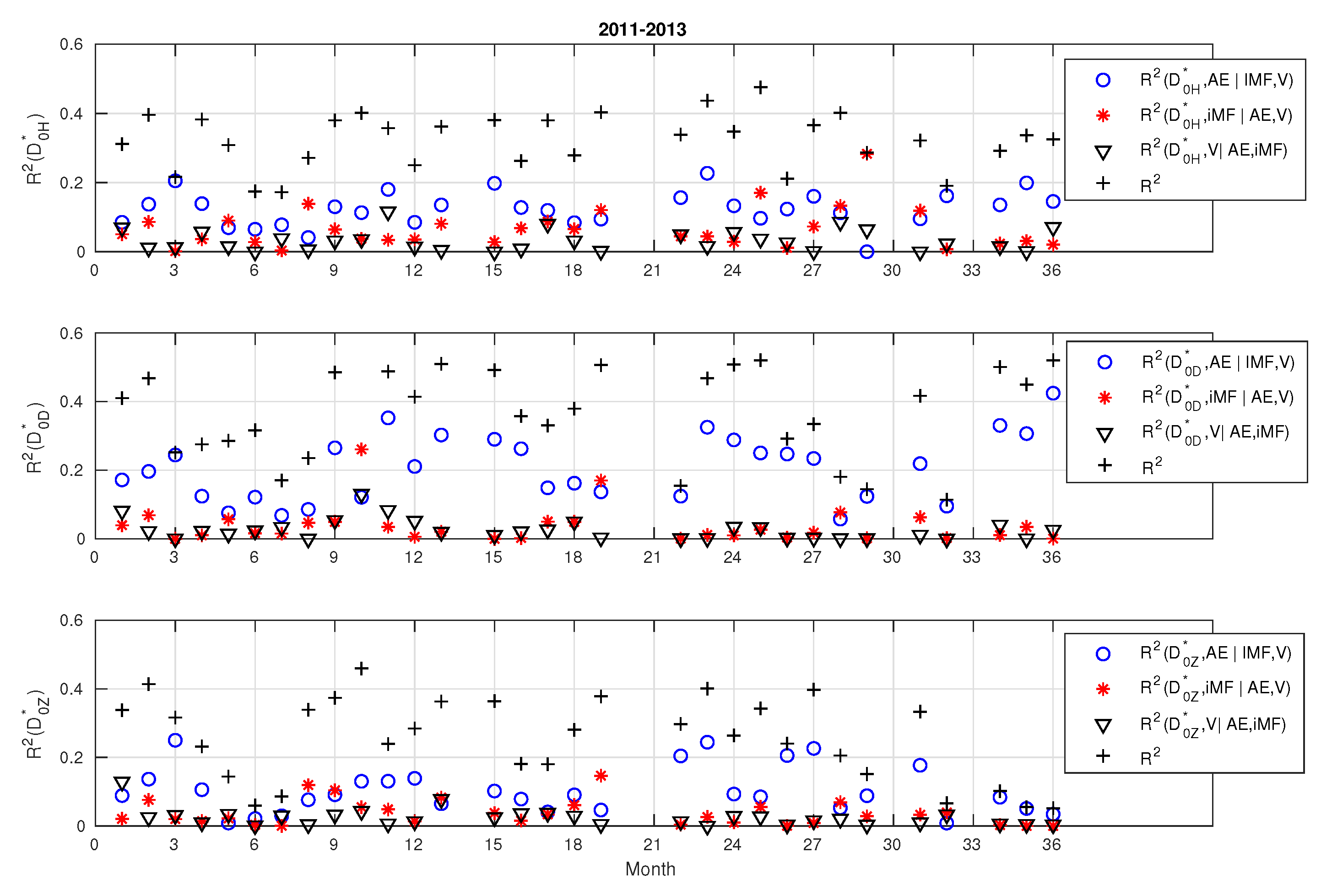
It can be seen that partial correlation coefficients for IMF and solar wind velocity smaller then for AE-index usually. The crosses show the part of HFD variance controlled by the variability of these parameters (determination coefficient). It varies widely from 0.06 (Z-component, June 2011) to 0.52 (D-component, January 2013). On average, it is 0.32, 0.38, 0.26 for the H, D, Z-components, respectively. The reasons for these changes and changes in the partial correlation coefficients require additional research.
4. Conclusions
The fractal dimension of geomagnetic variations at the Baigazan magnetic station at Russian Altay for 2011-2013 was calculated using the Higuchi method. The daily variation of HFD for the DHZ-components has been investigated, its contribution to the variability of HFD is from 30 to 40 percent of the total variance. A correlation analysis of the fractal dimension of the variations of the D,H,Z-components with AE-index and solar wind characteristics was carried out. A negative correlations with logarithms of AE-index, IMF, strength and solar wind velocity were found. About one quarter of the HFD variance is controlled by the variability of these space weather characteristics. Pair and partial correlation coefficients for these parameters were calculated for every month of 2011-2013.
Further development of the research may involve the application of the Katz method to calculate the fractal dimension of the variation in the D,H,Z components of the geomagnetic field [
3]. It should be noted here that the Hurst exponent method can also be used [
11].
Another direction of development of this work is the use of a multifractal approach in the study, by analogy with [
2], the dynamics of changes in the H,D,Z-components of the geomagnetic field.
In the future, it is also planned to make calculations for the Kamchatka Territory, where the complex geophysical observatory "Paratunka" is located.
Author Contributions
Conceptualization, A.G.; methodology, A.G.; software, A.G.; validation, A.G. and R.P.; formal analysis, A.G. and R.P; investigation, A.G.; resources, A.G.; data curation, A.G.; writing—original draft preparation, A.G. and R.P.; writing—review and editing, R.P.; visualization, A.G.; supervision, R.P.; funding acquisition, R.P. All authors have read and agreed to the published version of the manuscript
Funding
This work is founded by the Russian Foundation for Basic Research and Altay Republic government, grant No 20-45-040013 r_a and the framework of the State task on the topic (2021—2023) "Physical processes in the system of near space and geospheres under solar and lithospheric impact", registration number AAAA-A21-121011290003-0.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Acknowledgments
The authors are grateful to Evgeniy Uchaikin and Dmitry Kudin for station equipment design, and Vyacheslav and Miroslava Sakhnevich for support of measurements at the station. The au-thors expresse gratitude to two anonymous reviewers, whose comments made it possible to significantly improve the article.
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| HFD |
Higuchi Fractal Dimension |
| AE |
Auroral Electrojet |
| IMF |
Interplanetary Magnetic Field |
| FFT |
Fast Fourier Transform |
| UT |
Universal Time |
| LT |
Local Time |
References
- Alberti, T.; Lekscha, J.; Consolini, G.; De Michelis, P.; Donner, R.V. Disentangling non-linear geomagnetic variability during magnetic storms and quiescence by timescale dependent recurrence properties. J. SpaceWeather Space Clim. 2020, 10. [Google Scholar] [CrossRef]
- Babu, S. S.; Unnikrishnan, K. Analysis of Fractal Properties of Horizontal Component of Earth’s Magnetic Field of Different Geomagnetic Conditions Using MFDFA. Advances in Space Research 2023. [Google Scholar] [CrossRef]
- Bahramizadeh-Sajadi, S.; Katoozian, H.R.; Mehrabbeik, M.; Baradaran-Rafii, A.; Jadidi, K.; Jafari, S. A Fractal Approach to Nonlinear Topographical Features of Healthy and Keratoconus Corneas Pre- and Post-Operation of Intracorneal Implants. Fractal Fract. 2022, 6, 688. [Google Scholar] [CrossRef]
- Donner, R.V.; Stolbova, V.; Balasis, G; Donges, J. F.; Georgiou, M.; Potirakis, S.M.; Kurths, J. Temporal organization of magnetospheric fluctuations unveiled by recurrent patterns in the Dst index. Chaos 2018, 28, 085716. [Google Scholar] [CrossRef]
- Gotoh, K.; Hayakawa, M.; Smirnova, N. Fractal analysis of the ULF geomagnetic data obtained at Izu Peninsula, Japan in relation to the nearby earthquake swarm of June-August 2000. Natural Hazards and Earth System Science 2003, 3-4, pp–229. [Google Scholar] [CrossRef]
- Gvozdarev, A. Geomagnetic measurements on new magnetic station “Baygazan” (Teletskoe lake, Russian Altay). In Proceedings of the IAGA Workshop on Geomagnetical Measurement, Data Asquacition and Processing, Dourbes, Belgium, 5-10 September 2016; p. 14. [Google Scholar]
- Hall, C.M. Complexity signatures in the geomagnetic H component recorded by the Tromso magnetometer (70∘ N, 19∘ E) over the last quarter of a century. Nonlin. Process. Geophys. 2014, 21, 1051–1058. [Google Scholar] [CrossRef]
- Hamid, N.S.A.; Gopir, G.; Ismail, M.; Misran, N.; Hasbi, A.M.; Usang, M.D. ; Yumoto. In The Hurst exponents of the geomagnetic horizontal component during quiet and active periods. In Proceedings of the of the 2009 International Conference on Space Science and Communication, Negeri Sembilan, Malaysia, October 26–27 2009; pp. 186–190. [Google Scholar]
- Higuchi, T. Approach to an irregular time series on the basis of the fractal theory. Phys. D Nonlinear Phenom. 1988, 31, 277–283. [Google Scholar] [CrossRef]
- Nasuddin, K.A.; Abdullah, M.; Abdul Hamid, N.S. Characterization of the South Atlantic Anomaly. Nonlin. Process. Geophys. 2019, 26, 25–35. [Google Scholar] [CrossRef]
- Lu, K.-C.; Chen, K.-S. Uncovering Information Linkages between Bitcoin, Sustainable Finance and the Impact of COVID-19: Fractal and Entropy Analysis. Fractal Fract. 2023, 7, 424. [Google Scholar] [CrossRef]
- Rifqi, F.N.; Hamid, N.S.A.; Rabiu, A.B.; Yoshikawa, A. Identification of Fractal Properties in Geomagnetic Data of Southeast Asian Region during Various Solar Activity Levels. Universe 2021, 7, 248. [Google Scholar] [CrossRef]
- Uritsky, V. M.; Pudovkin, M. I. Low frequency 1/f-like fluctuations of the AE-index as a possible manifestation of self-organized criticality in the magnetosphere. Ann. Geophys. 1998, 16, 1580–1588. [Google Scholar] [CrossRef]
- Wanliss, J. A.; Shiokawa, K.; Yumoto, K. Latitudinal variation of stochastic properties of the geomagnetic field. Nonlin. Processes Geophys. 2014, 21, 1580–1588. [Google Scholar] [CrossRef]
- Wanliss, J.A.; Wanliss, G.E. Efficient calculation of fractal properties via the Higuchi method. Nonlinear Dyn. 2022, 109, 2893–2904. [Google Scholar] [CrossRef] [PubMed]
- Wawrzaszek, A.; Modzelewska, R.; Krasinska, A.; Gil, A.; Glavan, V. Fractal dimension analysis of Earth magnetic field during 26 August 2018 geomagnetic storm. Entropy 2022, 24, 699. [Google Scholar] [CrossRef] [PubMed]
- Zaourar, N. , Hamoudi, M., Holschneider, M. et al. Fractal dynamics of geomagnetic storms. Arab. J. Geosci. 2013, 6, 1693–1702. [Google Scholar] [CrossRef]
Figure 1.
Variations of geomagnetic field horizontal component on January 2, 2011 at Altay (upper panel), its FFT-spectrum (low left panel) and dependence of distance between spaced elements on the time space k (low right panel). HFD and – spectrum slope coefficient are shown on the graphs.
Figure 1.
Variations of geomagnetic field horizontal component on January 2, 2011 at Altay (upper panel), its FFT-spectrum (low left panel) and dependence of distance between spaced elements on the time space k (low right panel). HFD and – spectrum slope coefficient are shown on the graphs.
Figure 2.
The dependence of HFD estimation on maximal time space . Upper row of panels – H-component variation 06.04.2011 and dependence of HFD estimation values on time at . Medium and low panel rows show dependencies of HFD estimation on maximal time space at various 6h time interval. Horisontal line correspond to mean value of 8 estimations at .
Figure 2.
The dependence of HFD estimation on maximal time space . Upper row of panels – H-component variation 06.04.2011 and dependence of HFD estimation values on time at . Medium and low panel rows show dependencies of HFD estimation on maximal time space at various 6h time interval. Horisontal line correspond to mean value of 8 estimations at .
Figure 3.
The time series of geomagnetical variations HFD 01-07.02.2011 and its spectrums for February 2011 (a) and daily-seasonal dependence of deviation from the daily average of geomagnetic variation fractal dimension at Altay : b – D-component, c – H-component, d – Z-component. .
Figure 3.
The time series of geomagnetical variations HFD 01-07.02.2011 and its spectrums for February 2011 (a) and daily-seasonal dependence of deviation from the daily average of geomagnetic variation fractal dimension at Altay : b – D-component, c – H-component, d – Z-component. .
Figure 4.
The correlation of geomagnetic variation HFD and space weather characteristics at February 2011 It is shown: left – temporal dependencies of logarithms of AE-index, HFD of H-component geomagnetic variation, logarithms of IMF and solar wind velocity (v), right – scatter plots for HFD and (upper), (medium) and (lower). Pair and partial correlation coefficients are shown at the plots.
Figure 4.
The correlation of geomagnetic variation HFD and space weather characteristics at February 2011 It is shown: left – temporal dependencies of logarithms of AE-index, HFD of H-component geomagnetic variation, logarithms of IMF and solar wind velocity (v), right – scatter plots for HFD and (upper), (medium) and (lower). Pair and partial correlation coefficients are shown at the plots.
Figure 5.
The results of calculation of square of partial correlation coefficients of geomagnetic variation fractal dimension at Altay with logarithms of AE-index, interplanetary magnetic field strength and solar wind velocity (2011-2013). The crosses show the determination coefficient values.
Figure 5.
The results of calculation of square of partial correlation coefficients of geomagnetic variation fractal dimension at Altay with logarithms of AE-index, interplanetary magnetic field strength and solar wind velocity (2011-2013). The crosses show the determination coefficient values.
Table 1.
Annual averaged values and standard deviations of geomagnetic variation HFD for H,D,Z-component in 2011.
Table 1.
Annual averaged values and standard deviations of geomagnetic variation HFD for H,D,Z-component in 2011.
| Parameters of normal distribution |
H |
D |
Z |
| Mean value |
1.365 |
1.420 |
1.662 |
| Standard deviation |
0.124 |
0.144 |
0.142 |
Table 2.
Pair correlation coefficients of geomagnetic variation fractal dimension for H,D,Z-component and space weather parameters in 2011.
Table 2.
Pair correlation coefficients of geomagnetic variation fractal dimension for H,D,Z-component and space weather parameters in 2011.
| Parameters |
H |
D |
Z |
| Logarithm of solar wind speed
|
-0.286 |
-0.360 |
-0.366 |
| Logarithm of plasma density
|
-0.184 |
-0.091 |
-0.138 |
| Logarithm of interplanetary magnetical field strength
|
-0.355 |
-0.314 |
-0.314 |
| North component of IMF Bz |
0.087 |
0.143 |
0.116 |
| Logarithm of AE-index
|
-0.439 |
-0.541 |
-0.509 |
Table 3.
Partial correlation coefficients of geomagnetic variation fractal dimension of geomagnetic variations for H,D,Z-component and logarithms of avroral electrojet index (AE), interplanetary magnetic field (IMF) and solar wind velocity (v) in 2011.
Table 3.
Partial correlation coefficients of geomagnetic variation fractal dimension of geomagnetic variations for H,D,Z-component and logarithms of avroral electrojet index (AE), interplanetary magnetic field (IMF) and solar wind velocity (v) in 2011.
| Partial correlation coefficients |
|
|
|
|
-0.274 |
-0.389 |
-0.344 |
|
-0.242 |
-0.164 |
-0.175 |
|
-0.113 |
-0.143 |
-0.166 |
| Determination coefficient
|
0.252 |
0.329 |
0.312 |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).