Submitted:
30 May 2023
Posted:
30 May 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Conductivity
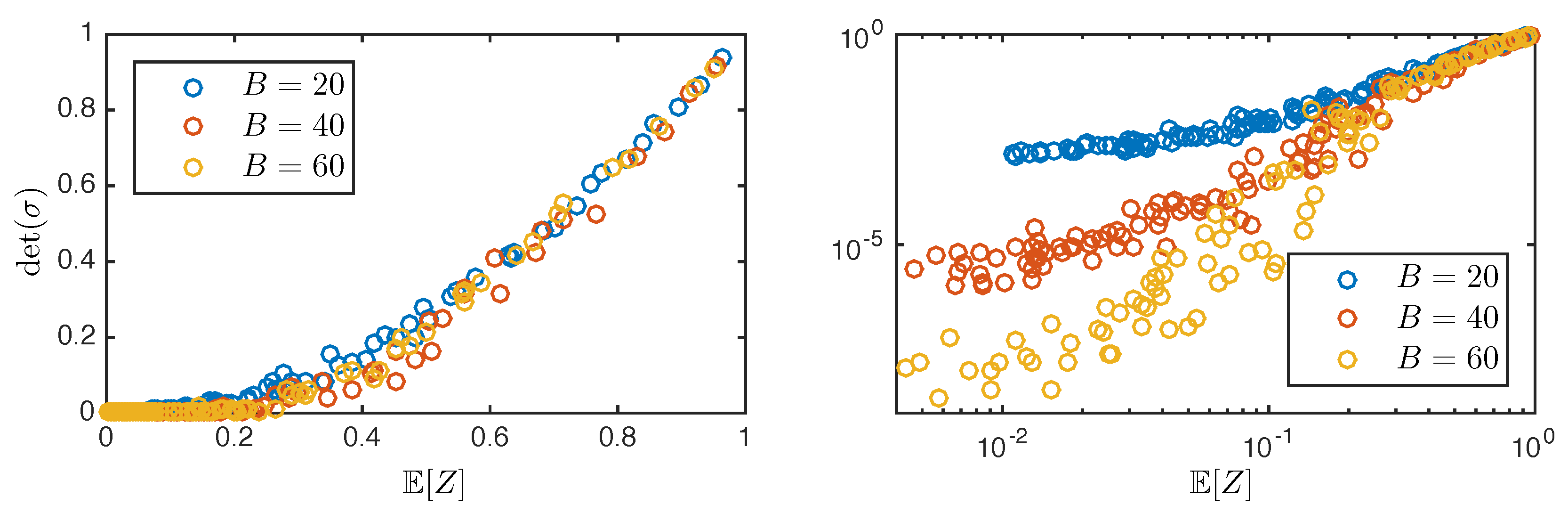
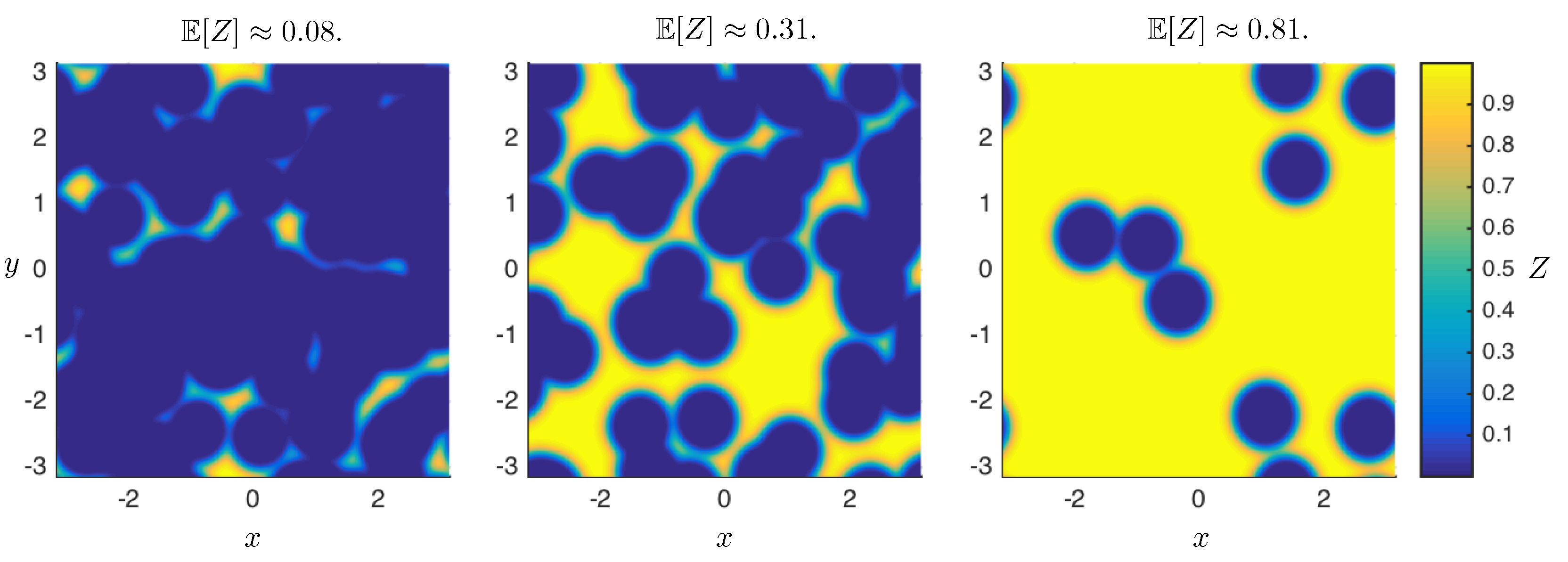
3. Conductor-Insulator Transition
3.1. Holographic Realizations
4. Outlook
Acknowledgments
References
- K. S. Thorne, R. H. Price, and D. A. MacDonald (eds.). Black Holes: The Membrane Paradigm (Yale University Press, 1986).
- N. Iqbal and H. Liu. “Universality of the hydrodynamic limit in AdS/CFT and the membrane paradigm", Physical Review D79 025023 (2009). arXiv:0809.3808.
- S. Ryu, T. Takayanagi, and T. Ugajin. “Holographic conductivity in disordered systems", Journal of High Energy Physics 04 115 (2011). arXiv:1103.6068.
- A. Donos and J. P. Gauntlett. “The thermoelectric properties of inhomogeneous holographic lattices", Journal of High Energy Physics 01 035 (2015). arXiv:1409.6875.
- M. Rangamani, M. Rozali, and D. Smyth. “Spatial modulation and conductivities in effective holographic theories". arXiv:1505.05171.
- D. Anninos, T. Anous, F. Denef, and L. Peeters. “Holographic vitrification". arXiv:1309.0146.
- G. T. Horowitz, N. Iqbal, J. E. Santos, and B. Way. “Hovering black holes from charged defects", Classical & Quantum Gravity 32 105001 (2015). arXiv:1412.1830.
- A. Lucas. “Hydrostatic transport in strongly coupled disordered quantum field theories", to appear.
- P. Chesler, A. Lucas, and S. Sachdev. “Conformal field theories in a periodic potential: results from holography and field theory", Physical Review D89 026005 (2014). arXiv:1308.0329.
- M. Blake and D. Tong. “Universal resistivity from holographic massive gravity", Physical Review D88 106004 (2013). arXiv:1308.4970.
- B. Goutéraux. “Charge transport in holography with momentum dissipation", Journal of High Energy Physics 04 181 (2014). arXiv:1401.5436.
- S. A. Hartnoll, P. K. Kovtun, M. Müller, and S. Sachdev. “Theory of the Nernst effect near quantum phase transitions in condensed matter, and in dyonic black holes", Physical Review B76 144502 (2007). arXiv:0706.3215.
- D. A. Levin, Y. Peres, and E. L. Wilmer. Markov Chains and Mixing Times (AMS, 2009).
- P. W. Anderson. “Absence of diffusion in certain random lattices", Physical Review 109 1492 (1958).
- E. Abrahams, P. W. Anderson, D. C. Licciardello, and T. V. Ramakrishnan. “Scaling theory of localization: absence of quantum diffusion in two dimensions", Physical Review Letters 42 673 (1979).
- T. Giamarchi and H. J. Schulz. “Localization and interaction in one-dimensional quantum fluids", Europhysics Letters 3 1287 (1987).
- D. M. Basko, I. L. Aleiner, and B. L. Altshuler. “Metal-insulator transition in a weakly interacting many-electron system with localized single-particle states", Annals of Physics 321 1126 (2006). arXiv:cond-mat/0506617.
- A. Donos and S. A. Hartnoll. “Interaction-driven localization in holography", Nature Physics 9 649 (2013). arXiv:1212.2998.
- A. Donos, B. Goutéraux, and E. Kiritsis. “Holographic metals and insulators with helical symmetry", Journal of High Energy Physics 09 038 (2014). arXiv:1406.6351.
- B. Derrida and J. Vannimenus. “A transfer-matrix approach to random resistor networks", Journal of Physics A15 L557 (1982).
- A. Lucas, S. Sachdev, and K. Schalm. “Scale-invariant hyperscaling-violating holographic theories and the resistivity of strange metals with random-field disorder", Physical Review D89 066018 (2014). arXiv:1401.7993.
- E. Mefford and G. T. Horowitz. “Simple holographic insulator", Physical Review D90 084042 (2014). arXiv:1406.4188.
- S. A. Hartnoll. “Theory of universal incoherent metallic transport", Nature Physics 11 54 (2015). arXiv:1405.3651.
- P. Kovtun. “Fluctuation bounds on charge and heat diffusion". arXiv:1407.0690.
- S. A. Hartnoll and A. Karch. “Scaling theory of the cuprate strange metals", Physical Review B91 155126 (2015). arXiv:1501.03165.
- D. V. Khveshchenko. “Constructing (un)successful phenomenologies of the normal state of cuprates". arXiv:1502.03375.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).




