Durability Evaluation of Hydraulic Tunnel Lining Structure Based on Set-Pair Analysis and Extension Coupling Model

1. Introduction

In order to solve the problem of water shortage and promote the development of local economy, China has invested in a series of water diversion projects, such as South to North Water Diversion, Diversion of Yellow River to Qingdao, Diversion of Yangtze River to Huaihe River, etc. These projects basically involve the construction of a large number of hydraulic tunnels. During the long-term use of these tunnels, due to the coupling effect of load, geology, environment and various erosive substances, cracks, material deterioration, water leakage and other diseases will appear in the lining structure, which seriously affects the safety condition and normal operation of hydraulic tunnels. Therefore, a reasonable evaluation of the durability of hydraulic tunnel lining structure and timely adoption of scientific and effective measures to maintain it are of great significance to prolong the service life of hydraulic tunnels.

In the area of tunnel evaluation, more research results have been achieved. Guo et al. 1 proposed an AHP-Extenics model based on the evaluation of tunnel lining structure damage, using hierarchical analysis to construct an index system for forming disease factors, determining the evaluation index weights through expert scoring, and carrying out topologizable operations on the evaluation indexes and weights to finally determine the tunnel lining structure damage levels. Zhu et al. 2 evaluated the durability of tunnel lining structure by variable fuzzy comprehensive assessment method, firstly establishing the affiliation matrix of evaluation index characteristic values to different levels, applying variable fuzzy preference model to determine the comprehensive affiliation degree, and conducting comprehensive assessment on the evaluation object, and finally determining the durability level of tunnel lining structure. Jin Chunling 3 used the PSR model to establish 31 evaluation indexes for the safety evaluation of the diversion tunnel, and determined the index weight by the AHP method. Rao et al. 4 classified the structural safety of karst road tunnels into five levels, determined quantitative evaluation indexes through the normal affiliation function, and determined their weights based on the expert scoring method, and finally evaluated the tunnel safety through a three-level fuzzy comprehensive evaluation model. Arends B J 5 proposed a method for evaluating tunnel safety based on probabilistic risk assessment based on three major aspects: economic risk, personal and social, and applied it in a practical case of a Dutch tunnel project. Ye et al. 6 used transient electromagnetic radar to detect the lack of voids and lining thickness behind the tunnel composite lining, to determine the contact state between the surrounding rock and the composite lining based on the change in apparent resistivity, and to evaluate the durability of the tunnel composite lining. Manchao et al. 7 concluded that large deformations can occur in tunnels during or after excavation due to adverse geology and design defects, and then proposed a method based on finite element software to simulate material deformations and a Bayesian neural network-based evaluation method for the condition of large tunnel deformations. Wang Y 8 combined triangular fuzzy numbers and exponential scaling, and then proposed an improved scale based on the fuzzy analysis network process, and applied it to the risk analysis of the Huma Ling tunnel to verify that the method could accurately reflect the actual engineering situation. Zhang et al. 9 identified carbon infiltration and chloride as common problems in tunnel durability, developed a procedure for assessing the strength of tunnel lining concrete under corrosive conditions and thus indirectly evaluating the durability of the lining structure, and used relevant experimental data to verify the accuracy of the method. Hussain et al. 10 calculated the rock mass of an excavated diversion tunnel based on a combination of empirical and numerical methods, and analysed the stability of the tunnel before and after excavation. Qiu W 11 constructed an evaluation index system for the sustainability of railway tunnels based on three main aspects: regional ecological environment, supporting structures and auxiliary facilities, and policy management. Li K 12 used experimental simulations of concrete immersed tube tunnels exposed to seawater and non-destructive testing to evaluate the durability of immersed tube tunnels through a fully probabilistic approach. Akula P 13 evaluated the durability of the lime treated broken concrete lining of the Friant-Kern canal from mineralogical and engineering aspects and preliminarily explored the effect of lime on the repair of hydraulic buildings.

The durability of hydraulic tunnel lining structures is not only related to the normal operation of the tunnel, but also plays a vital role in its safety and service life, but its durability is affected by a variety of complex factors, and the influencing factors themselves have certain characteristics such as randomness and ambiguity; At the same time, in the process of evaluating the durability status of hydraulic tunnel lining structures, it is necessary not only to resolve the contradictory issue of quantitative and qualitative changes, but also to reasonably characterise the degree of influence of different evaluation indexes on its durability. Set-pair analysis can reasonably describe the nature of definite and uncertain connections, while extension theory can quantitatively describe the process of quantitative and qualitative changes through the correlation function, and use the matter element model to solve the objective contradiction problem 14. The integration of set-pair analysis and extension theory can effectively solve the above problems. In addition, there are two main types of calculation methods for weights, objective and subjective. Only using one of them will make the weight calculation more objective or subjective, which will lead to the failure of the final evaluation 15.

In summary, this paper applies the set-pair analysis and extension coupling model to the evaluation of the durability of hydraulic tunnel lining structure. The G1 method and the simple correlation function method are used to calculate the subjective and objective weights of the evaluation indexes, and the minimum entropy (MIE) principle is used to calculate the comprehensive weight of the evaluation index, and then establishs a comprehensive evaluation model based on the combination weighting of the set-pair analysis and extension coupling model. The relevant calculations are also carried out using a section of water diversion project hydraulic tunnel as the research background to verify the reasonableness and scientific validity of the model in the evaluation of the durability of hydraulic tunnel lining structures.

2. The Establishment of Comprehensive Evaluation Model

2.1. Determination of Index Weight

2.1.1. G1 Method to Determine the Subjective Weight

The hierarchical analysis method (AHP) requires a high degree of awareness among evaluators in the process of calculating the weight of evaluation index, and has disadvantages such as cumbersome calculations, the need to construct judgment matrices and consistency tests. Therefore, Guo Yajun proposed the G1 method, which first ranks the importance of evaluation indexes and then determines the weights by comparing the importance between adjacent indexes, with the following calculation steps 16:

(1) Ranking the relative importance of the evaluation indexes. Based on the subjective opinions of experts, one most important index is selected from the set of evaluation indexes $\left\{C_{1,}{C}_{2\dots }{C}_n\right\}$ and recorded as $C_1^{\text{'}}$ with the weight of ${\alpha }_1$, and the most important index from the remaining n-1 indexes is selected as $C_2^{\text{'}}$ with the weight of ${\alpha }_2$, and so on, the relative importance ranking of each evaluation index can be derived: $C_1^{\text{'}}>C_2^{\text{'}}>···C_{i-1}^{\text{'}}>C_i^{\text{'}}>C_{i+1}^{\text{'}}>···C_n^{\text{'}}$.

(2) Calculate the relative importance between the neighboring indexes $C_{i-1}^{\text{'}}$ and $C_i^{\text{'}}$. The importance ratio $C_{i-1}^{\text{'}}$ and $C_i^{\text{'}}$ of the ranked neighboring indexes $r_i$ is reasonably assigned to:

$$r_i=\frac{{\alpha }_{i-1}}{{\alpha }_i} i=n,n-1,···,3,2$$

(1)

(3) The weight of the n-th evaluation index is calculated. The calculation formula is as follows:

$${\alpha }_n={(1+{\displaystyle \sum }_{i=2}^n\left({\displaystyle \prod }_{k=i}^n{r}_i\right))}^{-1}$$

(2)

(4) Calculate the weights of other evaluation indexes. The calculation formula is as follows:

$${\mathsf{\alpha }}_{\mathrm{i}-1}={\mathrm{r}}_{\mathrm{i}}{\mathsf{\alpha }}_{\mathrm{i}}\mathrm{i}=\mathrm{n},\mathrm{n}-1,···,3,2$$

(3)

2.1.2. Simple Correlation Function Method to Determine Objective Weight

The simple correlation function method is an objective assignment method calculated based on the theory of matter-element extension, and the specific calculation procedure is shown below [17,18]:

$$\mathrm{Assume}{h}_{ij}\left(v_i,V_{ij}\right)=\left\{\begin{array}{c}\frac{2\left(v_i-c_{ij}^{-}\right)}{c_{ij}^{+}-c_{ij}^{-}} v_i\le \frac{c_{ij}^{-}+c_{ij}^{+}}{2}\\ \frac{2\left(c_{ij}^{+}-v_i\right)}{c_{ij}^{+}-c_{ij}^{-}} v_i>\frac{c_{ij}^{-}+c_{ij}^{+}}{2}\end{array}\right.$$

(4)

$$(\mathrm{i}=1,2···\mathrm{n}; \mathrm{j}=1,2···\mathrm{m})$$

Where, $h_{ij}$ is the correlation between the i-th evaluation index and the j-th evaluation level; $v_i$ is the sample value of the i-th evaluation index; $V_{ij}$ is the range of values of the i-th evaluation index corresponding to the j-th evaluation level, and its value is $V_{ij}=\left(c_{ij}^{-},c_{ij}^{+}\right)$.

$$\mathrm{If}{v}_i\in V_{ip},\mathrm{then}{h}_{ijmax}\left(v_i,V_{ij}\right)=\underset{j\in \left(1，2，···，m\right)}{\max }\left\{h_{ij}\left(v_i,V_{ij}\right)\right\}.$$

If the evaluation index $C_i$ of the object $\mathrm{P}$ to be evaluated belongs to a larger evaluation level $\mathrm{j}$, the greater the weight assigned to this index, then $h_i$ is shown as follows:

$$h_i=\left\{\begin{array}{c}{j}_{max}\left[1+h_{ijmax}\left(v_i,V_{ij}\right)\right] h_{ijmax}\left(v_i,V_{ij}\right)\ge -0.5\\ 0.5j_{max} h_{ijmax}\left(v_i,V_{ij}\right)<-0.5\end{array}\right.$$

(5)

Where, $j_{max}$ is the evaluation level at which the measured sample value of evaluation index $\mathrm{i}$ in the object to be evaluated is placed, and the larger the value, the stronger the restriction on the object to be evaluated, when $h_{ijmax}={\mathrm{h}}_{im}$, $j_{max}=\max \left\{m\right\}$.

If the evaluation index $C_i$ of the object $\mathrm{P}$ to be evaluated belongs to a larger evaluation level $\mathrm{j}$, the smaller the weight assigned to this index, then $h_i$ is shown below:

$$h_i=\left\{\begin{array}{c}\left(m-j_{max}+1\right)\left[1+h_{ijmax}\left(v_i,V_{ij}\right)\right] h_{ijmax}\left(v_i,V_{ij}\right)\ge -0.5\\ 0.5\left(m-j_{max}+1\right) h_{ijmax}\left(v_i,V_{ij}\right)<-0.5\end{array}\right.$$

(6)

Where, $\mathrm{m}$ is the number of categories into which each evaluation index is classified. When $h_{ijmax}={\mathrm{h}}_{im}$, $j_{max}=\min \left\{m\right\}$.

Then, the objective weight of evaluation index $\mathrm{i}$ of the object $\mathrm{P}$ to be evaluated is:

$${\beta }_i=\frac{h_i}{{{\displaystyle \sum }}_{i=1}^n{h}_i}$$

(7)

Where, ${\beta }_i$ is the i-th index weight normalized value.

2.1.3. Calculating Combination Weight

The evaluation index weights calculated based on the G1 method and the simple correlation function method are ${\alpha }_i$ and ${\beta }_i$, respectively, and in order to make the combination weight ${\omega }_i$ as close as possible to ${\alpha }_i$ and ${\beta }_i$, the combination weight ${\omega }_i$ are obtained based on the MIE principle, and the computational model is as follows 19:

$$\left\{\begin{array}{c}min J\left(\omega \right)={\displaystyle \sum }_{i=1}^n\left({\omega }_i\ln \frac{{\omega }_i}{{\alpha }_i}+{\omega }_i\ln \frac{{\omega }_i}{{\beta }_i}\right)\\ s.t.{\displaystyle \sum }_{i=1}^n{\omega }_i=1,{\omega }_i\ge 0,i=1,2,···,n\end{array} \right.$$

(8)

Solving this optimization model based on the Lagrangian algorithm, the combination weight can be obtained as:

$${\omega }_i=\frac{\sqrt{{\alpha }_i{\beta }_i}}{{{\displaystyle \sum }}_{i=1}^n\sqrt{{\alpha }_i{\beta }_i}}$$

(9)

2.2. Set-Pair Analysis and Extension Coupling Model

2.2.1. Matter Element Model

The theory of matter-element extension usually represents the overall characteristics of the thing to be evaluated by the ordered triad $\mathrm{R}=\left(N,C,V\right)$, where $N$ is the thing to be evaluated, $C$ is the feature of the thing to be evaluated, and $V$ is the the quantitative value of the characteristics of the thing to be evaluated [20,21,22].

$$R_j=\left[N_j,C,V_j\right]=\left[\begin{array}{ccc}{N}_j& c_1& V_{1j}\\ & c_2& V_{2j}\\ & ⋮& ⋮\\ & c_n& V_{nj}\end{array}\right]=\left[\begin{array}{ccc}{N}_j& c_1& \left(c_{1j}^{-},c_{1j}^{+}\right)\\ & c_2& \left(c_{2j}^{-},c_{2j}^{+}\right)\\ & ⋮& ⋮\\ & c_n& \left(c_{nj}^{-},c_{nj}^{+}\right)\end{array}\right]$$

(10)

Where: $R_j$ is the classical domain; $N_j$ is the j-th evaluation level divided; ${\mathrm{c}}_i$ is the i-th evaluation index; $V_{ij}=\left(c_{ij}^{-},c_{ij}^{+}\right)$ is the range of quantities classified by $N_j$ with respect to the index $c_i$.

$$R_p=\left[N_p,C,V_p\right]=\left[\begin{array}{ccc}{N}_p& c_1& V_{1p}\\ & c_2& V_{2p}\\ & ⋮& ⋮\\ & c_n& V_{np}\end{array}\right]=\left[\begin{array}{ccc}{N}_p& c_1& \left(c_{1p}^{-},c_{1p}^{+}\right)\\ & c_2& \left(c_{2p}^{-},c_{2p}^{+}\right)\\ & ⋮& ⋮\\ & c_n& \left(c_{np}^{-},c_{np}^{+}\right)\end{array}\right]$$

(11)

Where: $R_p$ is the section domain; $V_{ij}\subset V_{iP}$; $c_{ip}^{-},c_{ip}^{+}$ are the minimum and maximum values taken for the evaluation indexes under each level, respectively.

The information of each evaluation index of the object to be evaluated is represented by the matter element, i.e., the matter element to be evaluated:

$$R_0=\left[\begin{array}{ccc}{N}_0& c_1& v_1\\ & c_2& v_2\\ & ⋮& ⋮\\ & c_n& v_n\end{array}\right]$$

(12)

Where: $N_0$ is the object to be evaluated; $v_i$ is the measured sample value corresponding to the evaluation index.

2.2.2. Principle of Coupling Model

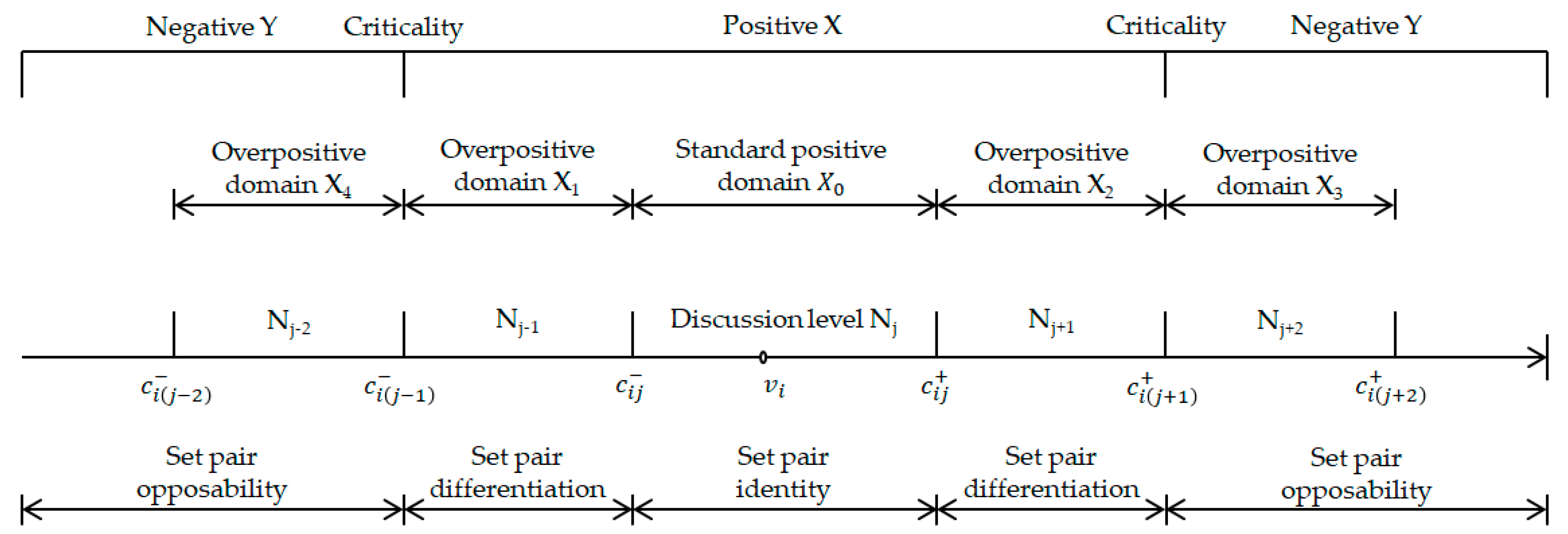
The constructed set-pair analysis and extension coupling model, based on the set pair identical-discrepancy-contrary principle and the connection between extension sets, constructs the set-pair and extension set theoretical domain between the measured sample values of the hydraulic tunnel lining structure durability index and the evaluation level, and the correspondence of the coupling model is shown in Figure 1, and the calculation process is as follows [14,23].

(1) When the measured sample value of the index $v_i$ belongs to the discussion level $\mathrm{j}$, it means that the value is within the standard positive domain $X_0$ of the discussion level $\mathrm{j}$ and exhibits the identity relation, and the linkage affiliation can be calculated according to equations (13) and (14):

$${\mu }_{N_j}\left(v_i\right)=\frac{-\rho \left(v_i,X_0\right)}{\left|c_{ij}^{+}-c_{ij}^{-}\right|}$$

(13)

$$\rho \left(v_i,X_0\right)=\left|v_i-\frac{c_{ij}^{+}+c_{ij}^{-}}{2}\right|-\frac{c_{ij}^{+}-c_{ij}^{-}}{2}$$

(14)

(2) When the measured sample value of the index $v_i$ belongs to the discussion level $\mathrm{j}-1$ or $\mathrm{j}+1$, it means that the value is within the overpositive domain $X_1$ or $X_2$ of the discussion level and exhibits a differential relation, which can be calculated according to equation (15)~(19) to calculate the linkage affiliation:

$${\mu }_{N_{j-1}}\left(v_i\right)=\frac{\rho \left(v_i,X_1\right)}{\rho \left(v_i,X\right)-\rho \left(v_i,X_1\right)}$$

(15)

$${\mu }_{N_{j+1}}\left(v_i\right)=\frac{\rho \left(v_i,X_2\right)}{\rho \left(v_i,X\right)-\rho \left(v_i,X_2\right)}$$

(16)

$$\rho \left(v_i,X\right)=\left|v_i-\frac{c_{i\left(j+1\right)}^{+}+c_{i\left(j-1\right)}^{-}}{2}\right|-\frac{c_{i\left(j+1\right)}^{+}-c_{i\left(j-1\right)}^{-}}{2}$$

(17)

$$\rho \left(v_i,X_1\right)=\left|v_i-\frac{c_{ij}^{-}+c_{i\left(j-1\right)}^{-}}{2}\right|-\frac{c_{ij}^{-}-c_{i\left(j-1\right)}^{-}}{2}$$

(18)

$$\rho \left(v_i,X_2\right)=\left|v_i-\frac{c_{i\left(j+1\right)}^{+}+c_{ij}^{+}}{2}\right|-\frac{c_{i\left(j+1\right)}^{+}-c_{ij}^{+}}{2}$$

(19)

(3) When the measured sample value of the index $v_i$ belongs to the discussion level $\mathrm{j}-2$ or $\mathrm{j}+2$, it means that the value is antagonistic to the discussion level $\mathrm{j}$, and the linkage affiliation can be calculated according to equation (20):

$${\mu }_{N_{j-2，j+2}}\left(v_i\right)=-1$$

(20)

2.2.3. Calculating the comprehensive linkage affiliation and set pair potential

Based on the linkage affiliation ${\mu }_{N_j}\left(v_i\right)$ and the combination weight ${\omega }_i$ of the evaluation index to be evaluated, the comprehensive linkage affiliation is calculated according to equation (21), and determine the durability class of hydraulic tunnel lining structure based on the principle of maximum affiliation.

$${\mu }_{N_j}={\displaystyle \sum }_{i=1}^n{\omega }_i{\mu }_{N_j}\left(v_i\right)$$

(21)

The durability state of hydraulic tunnel lining structure will change with the operational working state of the tunnel, and the expression of the connection degree of the hydraulic tunnel lining structure $N_0$ can be established according to the weight ${\omega }_i$ of each evaluation index, as shown in equation (22), and then the trend and possibility of transformation of the hydraulic tunnel lining structure $N_0$ to other durability $N_j$ is analysed according to the set-pair potential constructed by equation (23).

$$\mathsf{\epsilon }={\displaystyle \sum }_{v_i\in N_j}{\omega }_i+{\displaystyle \sum }_{v_i\in N_{j-1，j+1}}{\omega }_{i}p+{\displaystyle \sum }_{v_i\in N_{j-2，j+2}}{\omega }_{i}q$$

(22)

$$\mathrm{SHI}\left(\mathrm{H}\right)=\frac{{{\displaystyle \sum }}_{v_i\in N_j}{\omega }_i}{{{\displaystyle \sum }}_{v_i\in N_{j-2，j+2}}{\omega }_i}$$

(23)

Where: $\mathsf{\epsilon }$ is the connection degree; $p$ is the coefficient of difference; $q$ is the coefficient of opposition; $\mathrm{SHI}\left(\mathrm{H}\right)$ is the set-pair potential.

3. Durability Evaluation Process of Hydraulic Tunnel Lining Structure Based on Set-Pair Analysis and Extension Coupling Model

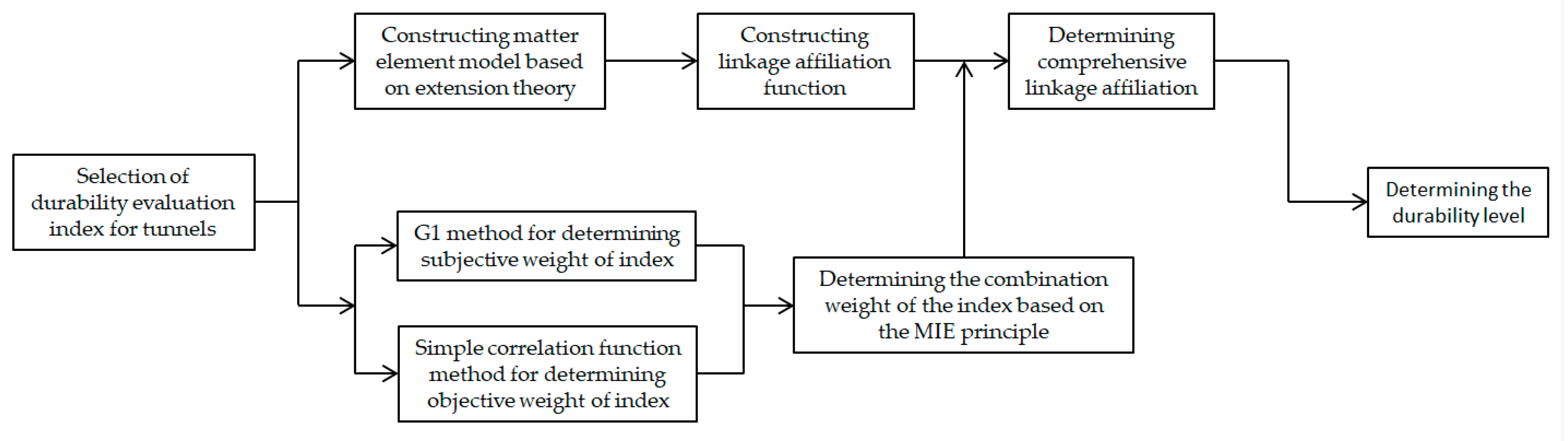
Durability evaluation of hydraulic tunnel lining structure is the process of analysing the factors affecting its durability, adopting appropriate methods to organise and evaluate these influencing factors and determine the durability status of the tunnel. In this paper, we first define the object to be evaluated which is hydraulic tunnel lining structure, and construct the durability evaluation index system from four aspects: material deterioration, lining cracks, water leakage, lining thickness and cavity behind; determine the classical and nodal domains of the index to be evaluated, construct the set-pair and extension set theoretical domain between the measured sample values of the hydraulic tunnel lining structure durability index and the evaluation level, establish the corresponding linkage affiliation function, and using the combination weight of the evaluation index obtained from the MIE principle, a comprehensive linkage affiliation of the object to be evaluated is calculated. Finally, the durability class of the hydraulic tunnel lining structure is determined based on the principle of maximum affiliation. The specific evaluation flow chart is shown in Figure 2.

4. Example Application

4.1. Project Example

In order to verify the rationality and scientific validity of this method, an application study is carried out on a section of hydraulic tunnel, located at the junction of Gansu and Qinghai, which is a pressureless hydraulic tunnel, completed and opened to water in 1994, with a length of 2099.25 m. It has been in operation for 29 years, and although several repairs and reinforcements have been carried out, there are still cracks, water leakage and other diseases due to long operation, and the lining structure has been subjected to groundwater scour and corrosion for a long time, resulting in a decrease in the strength of the secondary lining structure, which affects the normal operation and safety of the tunnel. Therefore, it is necessary to evaluate the durability of the tunnel to understand its current condition and to provide a theoretical basis for maintenance and repair work.

4.2. Constructing a Comprehensive Evaluation Index System of Durability

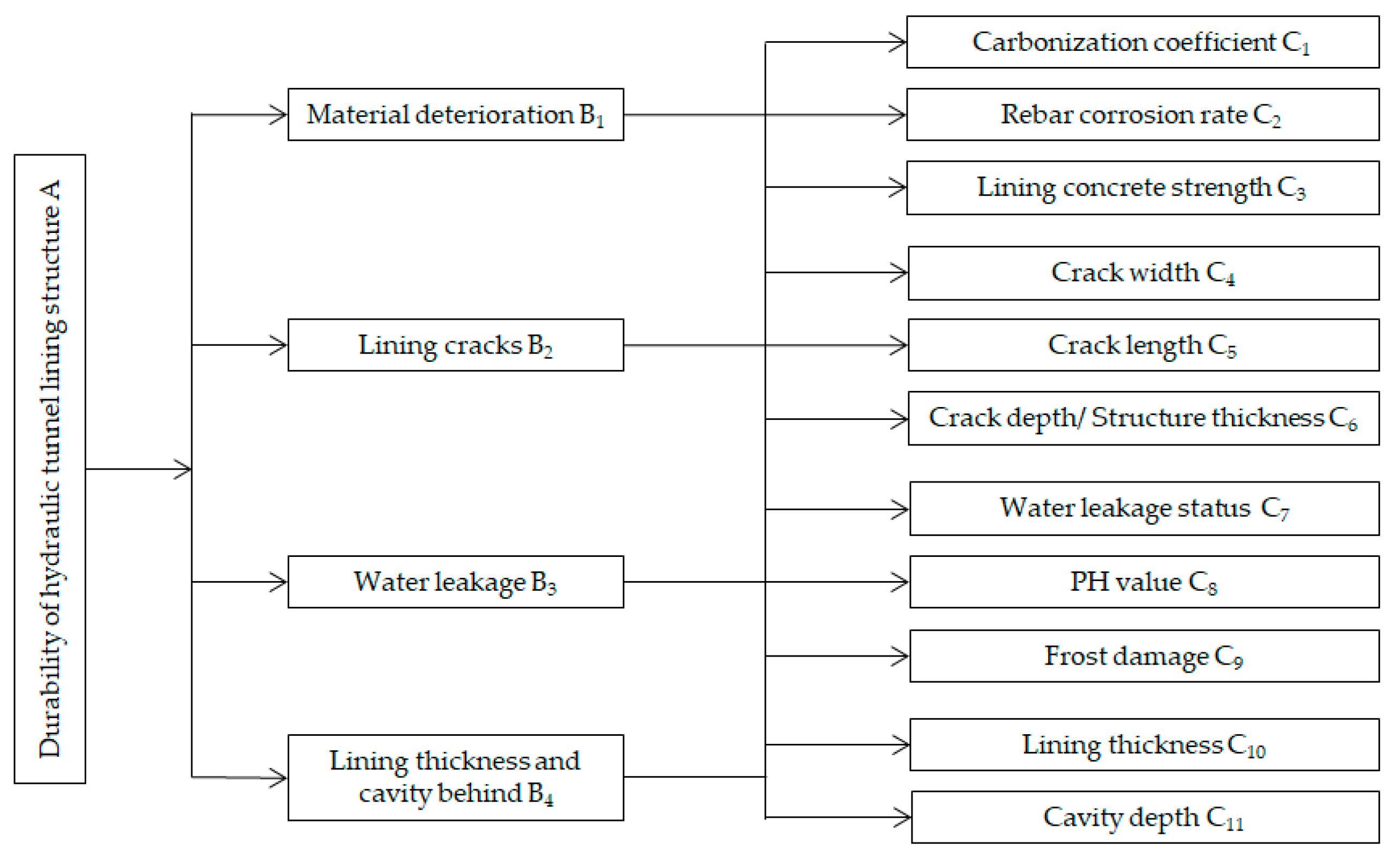
Combined with the actual engineering situation and existing literature, the factors affecting the durability of hydraulic tunnel lining structure are divided into four categories: material deterioration, lining cracks, water leakage, lining thickness and cavity behind, each of which is composed of several evaluation indexes, and the established three-layer evaluation index system of hydraulic tunnel lining structure durability is shown in Figure 3.

4.3. Determining the durability evaluation level and classification criteria

To reasonably evaluate the durability status of hydraulic tunnel lining structure, the evaluation results need to be appropriately graded. At present, there is no relevant specification for hydraulic tunnel lining in China. In this paper, the durability of tunnel lining structure is divided into four grades by referring to the Code for Durability Design of Concrete Structures in Highway Engineering (JTGT3310-2019) 24 and related literatures[25,26,27], as shown in Table 1.

There is no established division standard for the evaluation level of index, and the evaluation criteria is carried out for a tunnel section from 6+240 to 6+346.26 with reference to the Technical Code for Detection and Evaluation of Hydraulic Concrete Structure (DL/T5251-2010) 28, the Specification for Design of Hydraulic Tunnel (SL279-2016) 29 and the research results of related scholars [25,26,27] delineation, as shown in Table 2.

4.4. Analysis of Identical-Discrepancy-Contrary Linkage Affiliation and Durability Evaluation Index Weight

In order to eliminate the influence of different evaluation indexes of different magnitudes and make them comparable, the extreme value processing method is used to do dimensionless processing of the original evaluation index data. If the effect of the index on durability is positively correlated, that is, the larger the value, the worse the durability grade, it is processed according to equation (24); on the contrary, it is processed according to equation (25).

$${\mathrm{X}}_i^{\text{'}}=\frac{X_i-X_{imin}}{X_{imax}-X_{imin}}$$

(24)

$${\mathrm{X}}_i^{\text{'}}=\frac{X_{imax}-X_i}{X_{imax}-X_{imin}}$$

(25)

The rank intervals of evaluation indexes after the processing of equations (24) and (25) are shown in Table 3:

The test information and data of each evaluation index of a hydraulic tunnel are normalized and dimensionless using equations (24) and (25), and the processing results are shown in Table 4.

From equations (10) to (12), the classical domain $R_j$, the section domain $R_p$ and the element to be evaluated $R_0$ of the durability evaluation index of the hydraulic tunnel lining structure can be obtained as follows:

$$R_p=\left|\begin{array}{cc}{N}_p& \\ & c_1～c_2\\ & \left(0,1\right)\end{array}\right|$$

$$R_0=\left|\begin{array}{cccccccccccc}{N}_0& & & & & & & & & & & \\ & c_1& c_2& c_3& c_4& c_5& c_6& c_7& c_8& c_9& c_{10}& c_{11}\\ & 0.563& 0.45& 0.19& 0.15& 0.583& 5/12& 0.4& 0.213& 0.388& 5/12& 0.438\end{array}\right|$$

4.4.1. Identical-Discrepancy-Contrary Linkage Affiliation Analysis

The identical-discrepancy-contrary linkage affiliation ${\mu }_{N_j}\left(v_i\right)$ of each evaluation index of hydraulic tunnel lining structure relative to durability class is calculated according to equations (13) to (20). For example, the dimensionless value of carbonization coefficient C1 is 0.563$\in \left(0.44,0.63\right)$, that is, the dimensionless value $v_1$ of index C1 lies within the standard positive domain $X_0=\left(0.44,0.63\right)$, then index C1 belongs to the same degree ${\mu }_{N_3}\left(v_1\right)$ of durability class ${\mathrm{N}}_3$ is calculated as follows:

$${\mu }_{N_3}\left(v_1\right)=\frac{-\rho \left(v_1,X_0\right)}{\left|c_{ij}^{+}-c_{ij}^{-}\right|}=\frac{-\left|0.563-\frac{0.63+0.44}{2}\right|+\frac{0.63-0.44}{2}}{\left|0.63-0.44\right|}=0.353$$

The degree of difference ${\mu }_{N_2}\left(v_1\right)$ and ${\mu }_{N_4}\left(v_1\right)$ of index C1 belonging to durability classes ${\mathrm{N}}_2$ and ${\mathrm{N}}_4$ are calculated as follows:

$${\mu }_{N_2}\left(v_1\right)=\frac{\rho \left(v_1,X_1\right)}{\rho \left(v_1,X\right)-\rho \left(v_1,X_1\right)}=\frac{0.123}{-0.313-0.123}=-0.282$$

$${\mu }_{N_4}\left(v_1\right)=\frac{\rho \left(v_1,X_2\right)}{\rho \left(v_1,X\right)-\rho \left(v_1,X_2\right)}=\frac{0.067}{-0.313-0.067}=-0.176$$

$$\rho \left(v_1,X\right)=\left|0.563-\frac{1+0.25}{2}\right|-\frac{1-0.25}{2}=-0.313$$

$$\rho \left(v_1,X_1\right)=\left|0.563-\frac{0.44+0.25}{2}\right|-\frac{0.44-0.25}{2}=0.123$$

$$\rho \left(v_1,X_2\right)=\left|0.563-\frac{1+0.63}{2}\right|-\frac{1-0.63}{2}=0.067$$

Opposite degree of index C1 belonging to durability class ${\mathrm{N}}_1$ is ${\mu }_{N_4}\left(v_1\right)=-1$.

Similarly, the single-index identical-discrepancy-contrary linkage affiliation of each evaluation index of hydraulic tunnel lining structure for the four durability classes can be calculated, and the results are shown in Table 5.

4.4.2. Determining the Weight of Durability Evaluation Index

The subjective weight of evaluation index is calculated according to G1 method. Combined with expert opinions, the sequence relation of criteria layer indexs and the importance ratio of adjacent indexes are determined: B2>B3>B1>B4; $r_2=1.2$，$r_3=1.1$，$r_4=1.4$. According to the formula (2) can get ${\alpha }_4=0.1728$, then according to the formula (3): ${\alpha }_3=r_4{\alpha }_4=0.2419$，${\alpha }_2=r_3{\alpha }_3=0.266$，${\alpha }_1=r_2{\alpha }_2=0.3193$. Therefore, the subjective weights of criteria layer indexes B1, B2, B3 and B4 are 0.2419, 0.3193, 0.2660 and 0.1728, respectively. Similarly, the subjective weight of C1, C2 and C3 in the index layer under the criterion layer B1 can be calculated as 0.3216, 0.3860 and 0.2924, respectively.

According to the above results, the subjective weights of indexes C1, C2 and C3 relative to criterion layer B1 are multiplied by the subjective weight of B1 relative to the target layer, and then the subjective weights of C1, C2 and C3 relative to the target layer are 0.0778, 0.0934 and 0.0707 respectively. Similarly, the subjective weights of other evaluation indexes for the target layer can be obtained, and the specific calculation results are shown in Table 6.

The objective weights of evaluation indexes are calculated by using the simple correlation function method, and in this engineering example, the data in Table 3 and Table 4 are brought into equations (4) to (7) to obtain the objective weights of each evaluation index ${\beta }_i$. Finally, the MIE principle is used to eliminate the deviation of the subjective and objective weights, and the final calculation results of combination weight are obtained by substituting ${\alpha }_i$ and ${\beta }_i$ into equation (9), as shown in Table 6.

4.5. Durability evaluation grade and variation trend analysis of hydraulic tunnel lining structure

According to the single-index affiliation ${\mu }_{N_j}\left(v_i\right)$ of the hydraulic tunnel lining structure in Table 5 and the combination weight ${\mathsf{\omega }}_i$ of each evaluation index in Table 6, ccording to equation (21), the comprehensive linkage affiliation of hydraulic tunnel lining structure for the four durability classes ${\mu }_{N_j}=\left({\mu }_{N_1},{\mu }_{N_2},{\mu }_{N_3},{\mu }_{N_4}\right)=\left(-0.7090,-0.0620,0.0906,-0.5620\right)$, the durability class of the hydraulic tunnel lining structure of this section can be determined as III according to the maximum affiliation determination criterion.

According to the combination weight ${\mathsf{\omega }}_i$ of each evaluation index of the hydraulic tunnel lining structure in Table 6, the expression $\mathsf{\epsilon }=0.6425+0.2728p+0.0847q$ for the connection degree of this tunnel can be calculated using Equation (22). By ${\displaystyle \sum }_{v_i\in N_3}{\mathsf{\omega }}_i=0.6425$，${\displaystyle \sum }_{v_i\in N_{2,4}}{\mathsf{\omega }}_i=0.2728$，${\displaystyle \sum }_{v_i\in N_1}{\mathsf{\omega }}_i=0.0847$, which can be obtained as ${\displaystyle \sum }_{v_i\in N_3}{\mathsf{\omega }}_i=0.6425>{\displaystyle \sum }_{v_i\in N_{2,4}}{\mathsf{\omega }}_i=0.2728>{\displaystyle \sum }_{v_i\in N_1}{\mathsf{\omega }}_i=0.0847$, and further calculate the set pair potential $\mathrm{SHI}\left(\mathrm{H}\right)=7.5856$ for this section of the tunnel according to formula (23), indicating that the development trend of durability status of hydraulic tunnel lining structure in this section is weak homoeopathy.

From the above results, it can be seen that the durability class of hydraulic tunnel lining structure is III in this section, which means that the section of the tunnel as a whole is medium damaged, affecting operational safety and requiring major repairs. Through the analysis of tunnel damage and field survey results, it can be found that the lining structure is indeed medium damaged, with a certain degree of cracks, water leakage and rebar corrosion, the evaluation result is consistent with the actual engineering situation of the tunnel, which illustrates the scientific and reasonable nature of the established hydraulic tunnel lining structure durability evaluation index system and evaluation model. According to the results of the set pair potential of the tunnel, it is known that the development trend of its durability condition is weak homoeopathy, which indicates that the tunnel belongs to level III is not strong, and the possibility of changing to level IV condition is very large, so the relevant departments of the tunnel jurisdiction section should pay attention to it and take effective and reasonable solutions to prevent the deterioration of the durability condition of the tunnel.

4.6. Comparative Study

In order to illustrate the scientificity and rationality of this method, this paper uses the AHP-Extenics method to do a comparative study with the above content.

4.6.1. Analytic Hierarchy Process (AHP)

Analytic Hierarchy Process (AHP) is a subjective weighting method, which is a method for ranking the pros and cons of various factors and analyzing the hierarchical weight decision 30. The process of calculating the evaluation index weight is as follows:

(1)

Constructing a judgment matrix

After stratifying the studied problem based on objectives, criteria and solutions, different indexes at the same layer can be assigned relative importance by the method of two-by-two comparison, so as to judge the relative importance of the indexes at the lower layer to the indexes at the upper layer, and then calculate the weights of each evaluation index. If there are $\mathrm{n}$ evaluation indexes in a certain layer, the judgment matrix of equation (25) can be constructed.

$$A={\left(a_{ij}\right)}_{n\times n}=\left[\begin{array}{ccc}{a}_{11}& L& a_{1n}\\ L& L& L\\ a_{n1}& L& a_{nn}\end{array}\right]$$

(25)

Where: $i=1,2,···,n;j=1,2,···,n$; $a_{ij}$ is the important result of comparing the two evaluation indexes $i$ and $j$ in the criteria $A$.

In this paper, based on the expert scoring method, the relative importance between two factors is quantified by comparing the factor indexes two by two according to the 1-9 scale method 31 to determine the underlying data, and the 1-9 scale is shown in Table 7.

(2)

Calculating the weight of evaluation index

Based on the judgment matrix $A$ obtained from pairwise comparison of evaluation indexex, the eigenvector $\mathsf{\delta }$ corresponding to the maximum eigenvalue ${\lambda }_{max}$ is calculated. Then the problem of calculating the weight of the evaluation indexess is transformed into the problem of solving for the eigenvector $\mathsf{\delta }$, with the following equation:

$$A\delta ={\lambda }_{max}\delta$$

(26)

In this paper, the calculation of the weights is based on the square root method, and the calculation process is as follows 1:

Step 1: The elements in the judgment matrix $A$ are multiplied by rows to obtain $u_i$, see equation (27).

$$u_i={\displaystyle \prod }_{j=1}^n{a}_{ij},i=1,2,···n \left(27\right)$$

(27)

Step 2: $u_i$ is squared n times respectively to obtain $u_i^{\text{'}}$, see equation (28).

$$u_i^{\text{'}}=\sqrt[n]{u_i}$$

(28)

Step 3: Regularize $u_i^{\text{'}}$ to solve for the eigenvector $\mathsf{\delta }$, see equation (29).

$${\delta }_i=\frac{u_i^{\text{'}}}{{{\displaystyle \sum }}_{i=1}^n{u}_i^{\text{'}}}$$

(29)

Step 4: Calculate the maximum eigenvalue ${\lambda }_{max}$ of the judgment matrix $A$, see equation (30).

$${\lambda }_{max}={\displaystyle \sum }_{i=1}^n\frac{{\left(A\delta \right)}_i}{n{\delta }_i}$$

(30)

(3)

Consistency test

In order to judge the reasonableness of the above weight calculation, the consistency of the judgment matrix $A$ needs to be tested, and the specific process is as follows:

Step 1: Calculate the consistency index $CI$,see equation (31).

$$CI=\frac{{\lambda }_{max}-n}{n-1}$$

(31)

Step 2: Calculate the consistency ratio $CR$,see equation (32).

$$CR=\frac{CI}{RI}$$

(32)

Where: $RI$ is the average random consistency index, which can be found by checking Table 8 32.

According to the consistency test criteria, when $CR<0.10$, the judgment matrix $A$ satisfies the consistency test. On the contrary, experts are required to re-score and construct a new judgment matrix until the consistency test is satisfied.

4.6.2. Matter-element extension

The theory of matter element has already been described in the previous section and the focus here is on the calculation of the correlation function values for the element class of the hydraulic tunnel lining structures to be evaluated.

(1)

Calculation of the correlation of evaluation index

The correlation of the durability class j of the hydraulic tunnel lining structure to be evaluated is as follows:

$$\rho \left(v_i,V_{ij}\right)=\left|v_i-\frac{c_{ij}^{+}+c_{ij}^{-}}{2}\right|-\frac{c_{ij}^{+}-c_{ij}^{-}}{2}$$

(33)

$$\rho \left(v_i,V_{ip}\right)=\left|v_i-\frac{c_{ip}^{+}+c_{ip}^{-}}{2}\right|-\frac{c_{ip}^{+}-c_{ip}^{-}}{2}$$

(34)

$$K_j\left(v_i\right)=\frac{\rho \left(v_i,V_{ij}\right)}{\rho \left(v_i,V_{ip}\right)-\rho \left(v_i,V_{ij}\right)}$$

(35)

Where: $K_j\left(v_i\right)$ is the correlation degree of the object to be evaluated when the evaluation level is j.

(2)

Determine the durability level of hydraulic tunnel lining structure

By combining the weights of each index and the correlation function values, the rank correlation of the evaluation object can be obtained, see equation (36), if $K_{j_0}\left(N_0\right)=max{K}_j\left(N_0\right)$, then the evaluation object $N_0$ belongs to $j_0$ level.

$$K_j\left(N_0\right)={\displaystyle \sum }_{i=1}^n{\omega }_i{K}_j\left(v_i\right)$$

(36)

Where: ${\omega }_i$ is the weight value of the evaluation index $u_i$, the larger its value, the greater the degree of influence of the index on the evaluation object.

4.6.3. Calculation of Durability Evaluation Index

According to the durability evaluation index system of hydraulic tunnel lining structure in Figure 3, experts with rich experience in tunnel construction are invited to score, and judgment matrices for different layers of indexes are constructed according to the 1-9 scale method, and weights are calculated for the durability evaluation indexes of hydraulic tunnel lining structure. The judgment matrix of each layer of index and its weight distribution are included in Table 9, Table 10, Table 11, Table 12 and Table 13 respectively.

From the above calculation results, it can be seen that in the durability evaluation analysis of hydraulic tunnel lining structure, the index weight of target layer A-B is W_A-B=(0.2330, 0.3647, 0.2771, 0.1252)^T, and the index weight of criterion layer B-C is W_B-C=(0.3108, 0.4934, 0.1958, 0.3275, 0.2599, 0.4126, 0.4286,0.1429, 0.4286, 0.3333,0.6667)^T, and the judgment matrix of each layer meets the consistency requirements. On this basis, the comprehensive weight of each durability index can be calculated, as shown in Table 14.

4.6.4. Comprehensive evaluation of AHP-Extenics

The durability grade range value of each evaluation index and the sample measured value are normalized, and the results are shown in Table 15.

The correlation degree of durability evaluation indexes for the hydraulic tunnel lining structure to be evaluated can be calculated from Equations (33)–(35), and the calculation results are as follows:

$$K_j\left(v_i\right)=\left[\begin{array}{cccc}-0.4170& -0.2200& 0.1811& -0.1329\\ -0.4160& -0.1350& 0.1842& -0.2857\\ 0.0556& -0.0500& -0.5250& -0.6833\\ -0.3480& -0.1180& 0.1538& -0.2500\\ -0.4980& -0.2810& 0.6417& -0.3720\\ -0.3420& -0.1670& 0.2500& -0.1677\\ -0.2730& 0.3333& -0.2000& -0.4667\\ 0.2102& -0.1480& -0.4390& -0.5740\\ -0.2620& 0.4058& -0.2240& -0.4827\\ -0.1670& 0.2500& -0.1670& -0.3750\\ -0.4700& -0.4130& 0.7805& -0.3048\end{array}\right]$$

The weight values of each secondary index calculated by the AHP are: W_B1-C=(0.3108,0.4934,0.1958)^T, W_B2-C=(0.3275,0.2599,0.4126)^T, W_B3-C=(0.4286,0.1429,0.4286)^T, W_B4-C=(0.3333,0.6667)^T. According to equation (36), the comprehensive correlation degree of the criterion layer for the durability of this hydraulic tunnel lining structure regarding the evaluation level j can be calculated as:

$$K_j\left(B_1\right)=\left(-0.3239,-0.1445,0.0444,-0.3161\right)$$

$$K_j\left(B_2\right)=\left(-0.3844,-0.1803,0.3203,-0.2473\right)$$

$$K_j\left(B_3\right)=\left(-0.1993,0.2956,-0.2450,-0.4889\right)$$

$$K_j\left(B_4\right)=\left(-0.3687,-0.1919,0.4648,-0.3282\right)$$

The weight value of the first-level index calculated by the AHP is W_A-B=(0.2330,0.3647,0.2771,0.1252)^T. Similarly, according to equation (36), the comprehensive correlation degree of the target layer for the durability of this hydraulic tunnel lining structure regarding the evaluation level j can be calculated as:

$$K_j\left(A\right)=\left(-0.3170,-0.0415,0.1176,-0.3404\right)$$

According to the principle of maximum affiliation, the durability class of the hydraulic tunnel lining structure can be determined as Class III, which is medium damaged.

Throughout the text, two different methods are used to evaluate the durability of the hydraulic tunnel lining structure and the results are consistent, with a durability class of III, which is also consistent with the actual damaged state of this hydraulic tunnel lining structure. In the comparative study, the calculation of index weight through the traditional AHP method is difficult to ensure the accuracy and scientificity of the weight due to the uneven level of experts. In contrast, this paper uses the G1 method and the simple correlation function method to calculate the subjective and objective weight of evaluation index respectively, which avoids the one-sidedness of weight calculation and takes into account the subjective intention of decision makers and the objective attributes of the data itself. Meanwhile, this paper uses the set-pair analysis and extension coupling model to calculate the affiliation of each index, and then determines the durability level, and the obtained evaluation results are consistent with the results determined by the AHP-Extenics method, which highlights the scientific and rational nature of the method proposed in this paper.

5. Conclusions

(1) According to the characteristics of durability evaluation indexes of hydraulic tunnel lining structure, the subjective weights calculated by G1 method and the objective weights calculated by simple correlation function method are optimized and synthesized to obtain the combination weight of each evaluation index, eliminating the one-sidedness of single weight calculation method, improving the rationality and reliability of the weights of tunnel durability evaluation indexes, and making the evaluation results more consistent with reality.

(2) The set pair analysis can describe the definite and indefinite connection of things, and the extenics theory can quantitatively describe the process of quantitative and qualitative changes of things, and solve the objective contradiction problem. Combining the two models, a comprehensive evaluation model based on the set-pair analysis and extension coupling and the set-pair potential analysis are proposed. This method not only provides an objective and comprehensive description of the nature of tunnel durability evaluation through the extenics set, but also organically integrates the theoretical domain division of extenics set and “the identical-discrepancy-contrary idea” of set pair analysis in the description of durability evaluation grade, and then constructs the identical-discrepancy-contrary affiliation function, which realizes the comprehensive evaluation of durability level for the hydraulic tunnel lining structure. At the same time, the set-pair potential analysis can reasonably describe the trend and possibility of transformation for the tunnel durability condition, and improve the accuracy of tunnel durability evaluation.

(3) Taking a section of hydraulic tunnel as an example, the model constructed in this paper is used to calculate its durability class as III, and the set-pair potential SHI(H)=7.5856. The evaluation results are consistent with the engineering practice, and a comparative study is done in combination with the AHP-Extenics method to verify the applicability and rationality of the model, which can provide a basis for the maintenance and reinforcement of hydraulic tunnel lining structure.

(4) A comprehensive evaluation index system for the durability of hydraulic tunnel lining structure is constructed by selecting 11 factors from 4 aspects: material deterioration, lining cracks, water leakage, lining thickness and cavity behind. However, the factors that affect its durability have certain characteristics of randomness and fuzziness. In the future research process, the evaluation index system needs to be more perfect and the grading standard needs to be further refined, which can further improve the accuracy of the durability evaluation results.