Prerpints.org logo
Preprint
Article

Theoretical evidence for principles of special relativity based on isotropic and uniform four-dimensional space

Altmetrics

Downloads

274

Views

527

Comments

0

This version is not peer-reviewed

Submitted:

24 May 2023

Posted:

25 May 2023

You are already at the latest version

Alerts
Abstract
The theory of special relativity has reexamined and reconstructed the concepts of space and time, which are indispensable for describing physical laws, consequently instigating a major revolution in physics in general. Although the correctness of the special theory of relativity has been con-firmed by many observations and experiments, it is unclear why the "principle of relativity" and the "principle of the constant speed of light," which form the basis of the idea, are valid. Moreo-ver, although special relativity has advanced our understanding of time, our understanding of the fundamental question, "What is time?" is still limited. The theory of special relativity regards space as a four-dimensional construct consisting of one-dimensional time and three-dimensional space. This paper proposes an alternative framework, wherein real space is uniform and isotropic four-dimensional space, and elementary particles are waves that propagate through this four-dimensional space at a constant speed. This new perspective provides evidence to support two of Einstein’s key principles—the "principle of relativity" and the "principle of the constant speed of light." Furthermore, this model clarifies what time is and why time flows at a constant rate from the past to the future.
Keywords: 
Subject: Physical Sciences  -   Theoretical Physics

1. Introduction

The theory of relativity revolutionized physics by challenging and reconstructing the fundamental concepts of time and space, which are essential for describing the laws of physics. This theory is divided into two main branches: special relativity and general relativity. Special relativity was developed for inertial systems moving at a constant speed, and general relativity was extended to systems involving acceleration. The theory of special relativity fundamentally transformed our understanding of time and space by showing that they are intertwined and objects moving at speeds close to that of light experience length contraction and time dilation [1]. Moreover, the theory clarified that there is an upper limit to the speed of all objects and that their mass and energy are equivalent [2]. The theory of relativity, along with quantum mechanics, forms the cornerstone of modern physics. Quantum field theory [3] is a relativistic approach to quantum mechanics that incorporates special relativity. The elementary particles that comprise matter and the forces acting between them can be explained without contradiction using the quantum field theory.
In 1905, Einstein developed the special theory of relativity based on two fundamental principles, the "principle of relativity" and the "principle of the constant speed of light [4]". Prior to this theory, Galilean principle of relativity was widely accepted, stating that the laws of dynamics are the same regardless of whether the point of origin of a coordinate system is stationary or moving at a constant velocity. However, the discovery by Maxwell that light is an electromagnetic wave [5] revealed that electromagnetic waves did not conform to the Galilean principle. This was further confirmed by the Michelson-Morley experiment using interferometry, which showed that the speed of light [6] is independent of the motion of inertial systems. Based on these observations, Einstein formulated the special theory of relativity by assuming the "principle of relativity" and the "principle of the constant speed of light". These principles have been verified through numerous elementary particle collision experiments using accelerators [7,8], studies of cosmic rays traveling at nearly the speed of light [9], and experiments validating quantum field theory [10].
The principles of relativity and the constant speed of light, upon which special relativity theory is based, have been widely accepted due to numerous experimental confirmations. However, the underlying reasons for their validity have not been adequately explained [11,12]. Time is another crucial concept in physics, and it remains less well-understood than space. Although special relativity has advanced our understanding of time, it has not provided a satisfactory answer to the fundamental question "What is time? [13,14]".
This paper proposes an alternative approach by assuming that space consists of four dimensions and is isotropic and uniform, with elementary particles propagating as waves at the inherent speed of this four-dimensional medium. It is thus aimed to shed light on the nature of time and the validity of the principles of relativity and constant speed of light. While quantum field theory has proven to be a powerful tool for understanding the behavior of elementary particles and the forces that act upon them, a complete understanding of the structure of quantum fields is lacking. The present approach seeks to uncover the underlying structure of these fields, which will help address many unresolved questions in physics, such as the origin of baryons, dark matter, and dark energy. Quantum field theory provides accurate predictions of physical phenomena; however, its reliance on experimentally determined physical constants limits its ability to provide a more fundamental explanation. Revealing the underlying structure of quantum fields can help gain a more complete understanding of the physical world.

2. Overview of special relativity

Before delving into the question of "What is time?" an overview of special relativity is necessary for the discussion that follows.

2.1. Lorentz transformation [15,16] and invariants

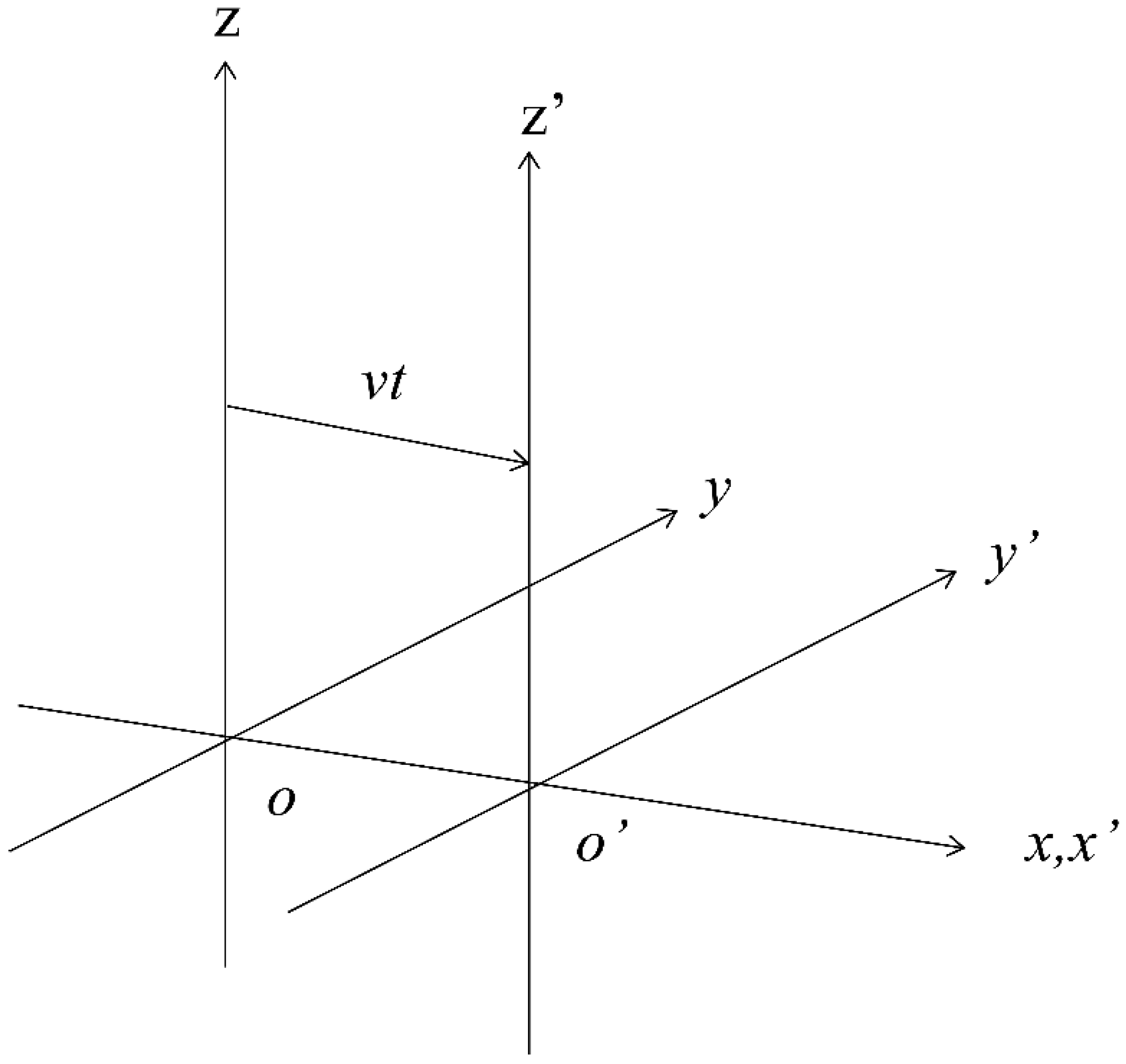
Consider two inertial systems, S and S', in a constant-speed linear motion with relative speed v in x direction, as shown in Figure 1. The coordinates of an inertial system can be expressed using four vectors (x0,x1,x2,x3 ) [17] or Minkowski coordinates (ct,x,y,z) [18] representing one dimension of time and three dimensions of space, where c is the speed of light. Using these coordinates, the S system coordinates can be expressed as follows:
x μ = ( x 0 ,   x 1 ,   x 2 ,   x 3 ) = ( c t , x , y , z )   .
The coordinate of the S' system is expressed in the following way:
x ′ μ = ( x ′ 0 ,   x ′ 1 ,   x ′ 2 ,   x ′ 3 ) = ( c t ′ , x ′ , y ′ , z ′ )
The coordinates of the S and S' systems are related by the following Lorentz transformation:
c t = c t ′ + v c x ′ 1 − v 2 c 2 .
x = x ′ + v t ′ 1 − v 2 c 2 .
y = y ′ .
z = z ′ .
Furthermore, the inverse transformation can be expressed as
c t ′ = c t − v c x 1 − v 2 c 2   .
x ′ = x − v t 1 − v 2 c 2   .
y ′ = y   .
z ′ = z   .
From (3)–(10), the following relationship can be obtained:
s 2 = c 2 t 2 − ( x 2 + y 2 + z 2 ) = c 2 t ′ 2 − ( x ′ 2 + y ′ 2 + z ′ 2 )
where s represents an invariant quantity (distance invariant to the Lorentz transformation) that holds for all inertial systems. The rest mass, m0, is also an invariant quantity and can be obtained from the energy-momentum relationship expressed below:
m 0 2 c 4 = E 2 − ( p x 2 + p y 2 + p z 2 ) c 2 = E ′ 2 − ( p x ′ 2 + p y ′ 2 + p z ′ 2 ) c 2
where E denotes the relativistic energy, and p(px, py, pz) denotes the momentum. The rest mass m0 has the same value for all inertial systems. By setting momentum zero, (12) yields the well-known eq. E0=m0c2 for the rest mass and energy.

2.2. Time delay and Lorentz contraction

Consider the time delay of the S' system from the point of view of the S system. The time in the S' system can be obtained from the point of view of the S system by substituting the position of the coordinate origin of the S' system, x’=0, into (3).
c t = c t ′ 1 − v 2 c 2   .
This implies that time t' in system S' flows more slowly than time t in system S and the relationship can be expressed as
t ′ = 1 − v 2 c 2 t   .
In the next step, the contraction of the space of the S' system is considered from the point of view of the S system. By substituting time t' = 0 into (4), the distance x' of the S' system from the perspective of the S system can be obtained.
x = x ′ 1 − v 2 c 2   .
In other words, the space of the S' system appears to be contracted compared with that of the S system, and their relation is given by
x ′ = 1 − v 2 c 2   x   .

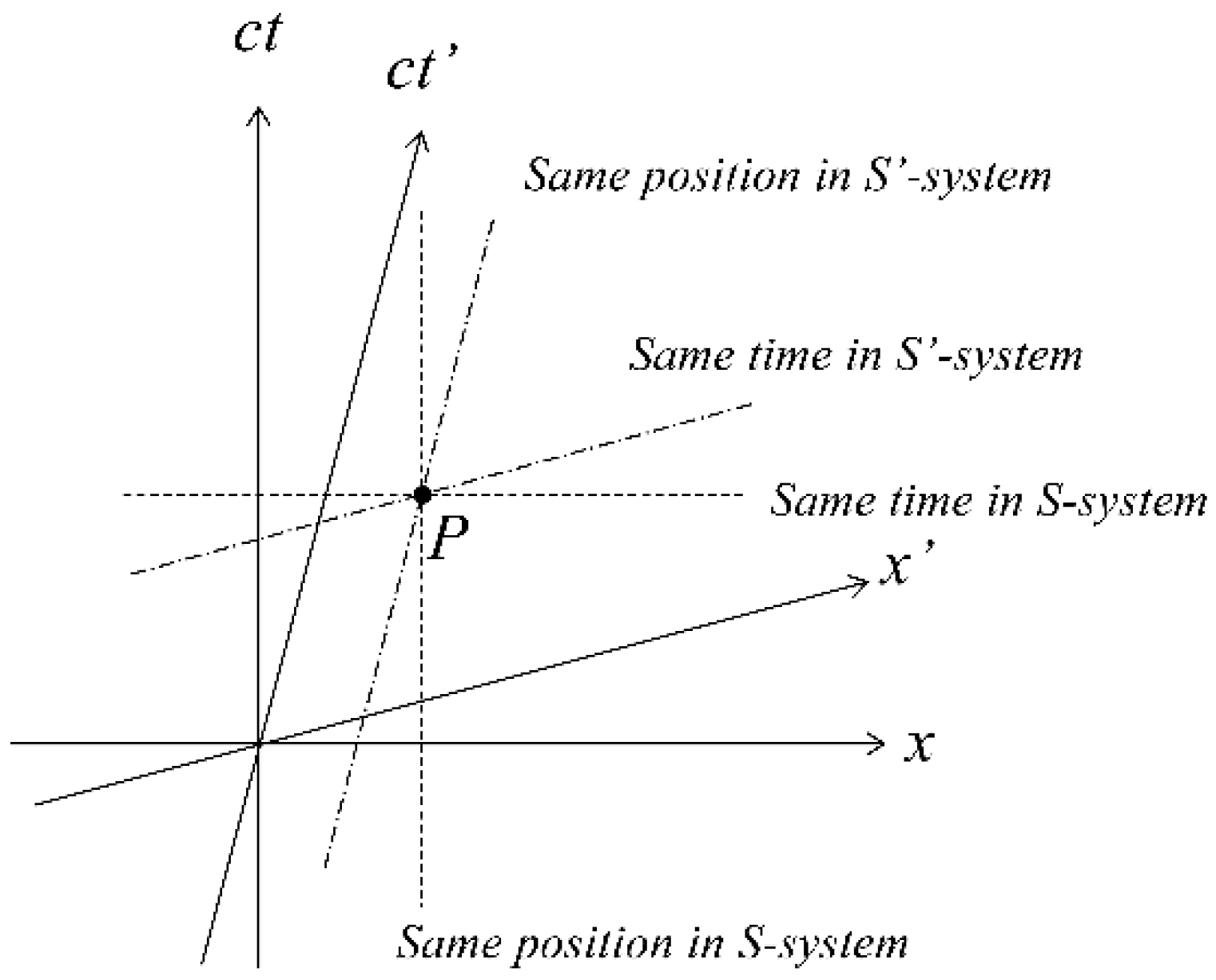
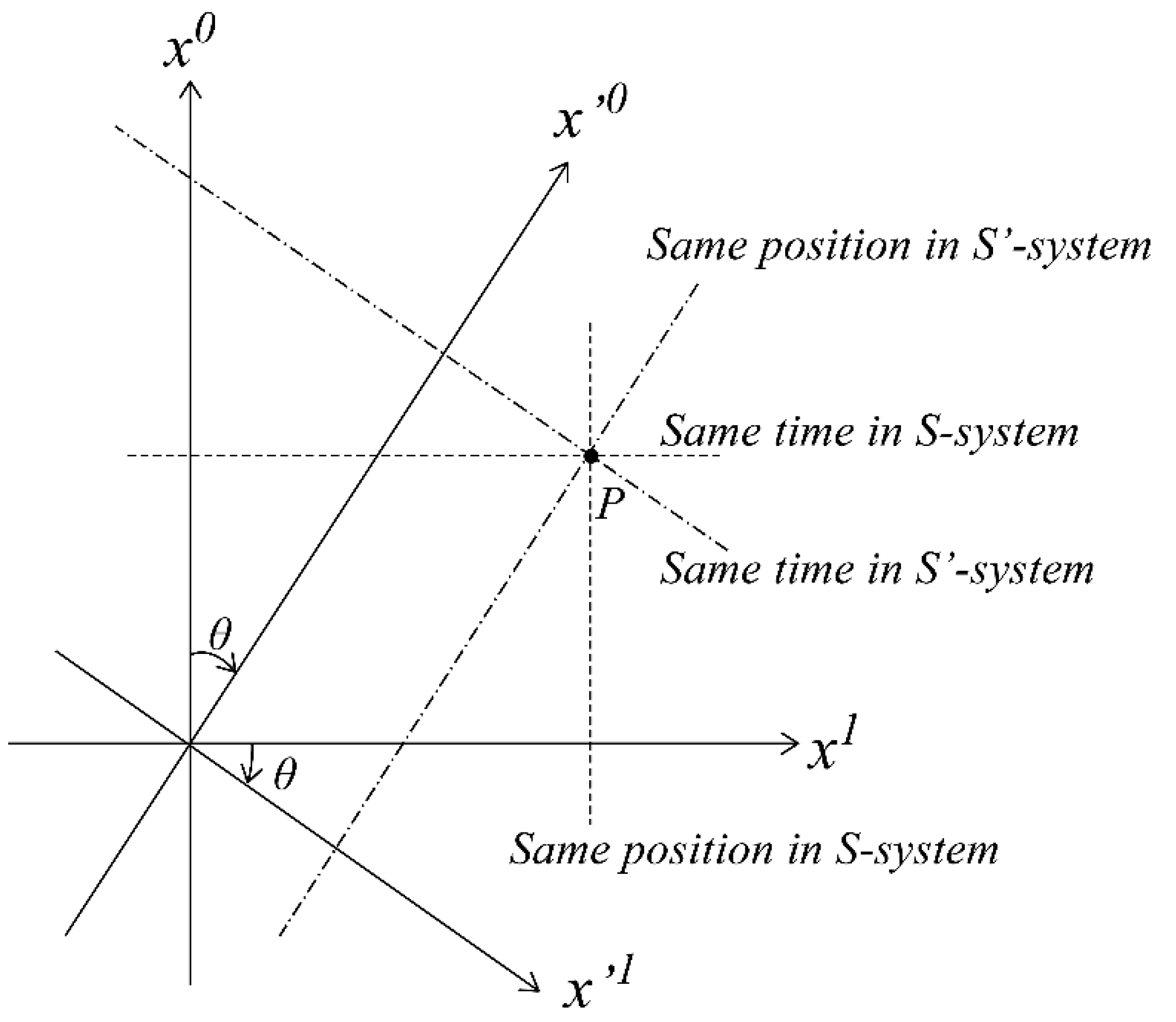
2.3. "Same time" and "same position" in the Minkowski spacetime

According to special relativity, two inertial coordinate systems moving relative to each other cannot share the same time at all points. To illustrate this, let us consider how the same time and point in the S' system appear in the S system. The same time in the S' system is defined as the coordinate at which t' is constant. By using (7), the same time in the S' system can be expressed using the following linear equation in the S system:
c t = c t ′ 1 − v 2 c 2 + v c x   .
On the other hand, the same position in the S' system is the coordinate where x' is constant. Using (8), the same position in the S' system is given by the following linear equation:
x = x ′ 1 − v 2 c 2 + v t   .
Eqs. (17) and (18) are expressed in Minkowski coordinates, as shown in Figure 2 (y and z coordinates are omitted). In the S system, the same time is represented by a line parallel to the x axis, while the same position is represented by a line parallel to the ct axis. Similarly, in the S' system, the same time is represented by a line parallel to the x' axis, and the same position is represented by a line parallel to the ct' axis. As shown in Figure 2, there is only one point (P) that has the same time and position in both the S and S' systems. In real 4-dimensional spacetime, the y-z plane with common (ct, x) coordinates represents the same time and place in both systems.

3. Assumptions on time

Although we can visually perceive space and have a general understanding of it, time remains beyond our perceptual reach, leaving us without a clear answer to the question of what time is. The theory of special relativity has undoubtedly advanced our understanding of time, but it has not provided a definite answer to the age-old question, “What is time?” Nevertheless, it is widely believed that no theory has come closer to unravelling the mystery of time than the theory of special relativity. To explore the nature of time further, the Minkowski spacetime is examined from different perspectives.
Eq. (11) of the Lorenz invariant, which describes distance in the Minkowski spacetime, does not treat time and space equally. This equation reveals that the Pythagorean theorem, which holds in Euclidean space, does not hold in the Minkowski spacetime. To address this, (11) can be transformed so that the Pythagorean theorem holds in this non-Euclidean spacetime.
c 2 t 2 = s 2 + ( x 2 + y 2 + z 2 )   .
As shown in (1), in Minkowski spacetime, x0 corresponds to the time distance ct; however, x0 is rewritten such that it corresponds to the Lorentz-invariant s as follows:
c 2 t 2 = ( x 0 ) 2 + ( x 1 ) 2 + ( x 2 ) 2 + ( x 3 ) 2   .
In other words, x0 is considered not as time but as another spatial axis orthogonal to the other three axes. The 4D spaces (x0,x1,x2,x3 ) differ from the Minkowski spacetime in that all axes are equal to each other. Eq. (20) can be expressed in difference form as follows:
c 2 d t 2 = ( d x 0 ) 2 + ( d x 1 ) 2 + ( d x 2 ) 2 + ( d x 3 ) 2   .
In addition, solving (21) for time yields the following form.
d t = ( d x 0 ) 2 + ( d x 1 ) 2 + ( d x 2 ) 2 + ( d x 3 ) 2 c   .
This equation implies that time is the distance traveled in the four dimensions of space divided by the speed of light.
In quantum field theory, elementary particles are understood as excited states of a field, and their motion is interpreted as the propagation of this excited state as a wave [19]. A medium that carries waves has a specific propagation speed, and waves always propagate at their inherent speed when nothing is around them to constrain them. While waves propagating in air or water are not stationary, elementary particles, although waves, can remain stationary in free space without being constrained. This behavior is apparently strange.
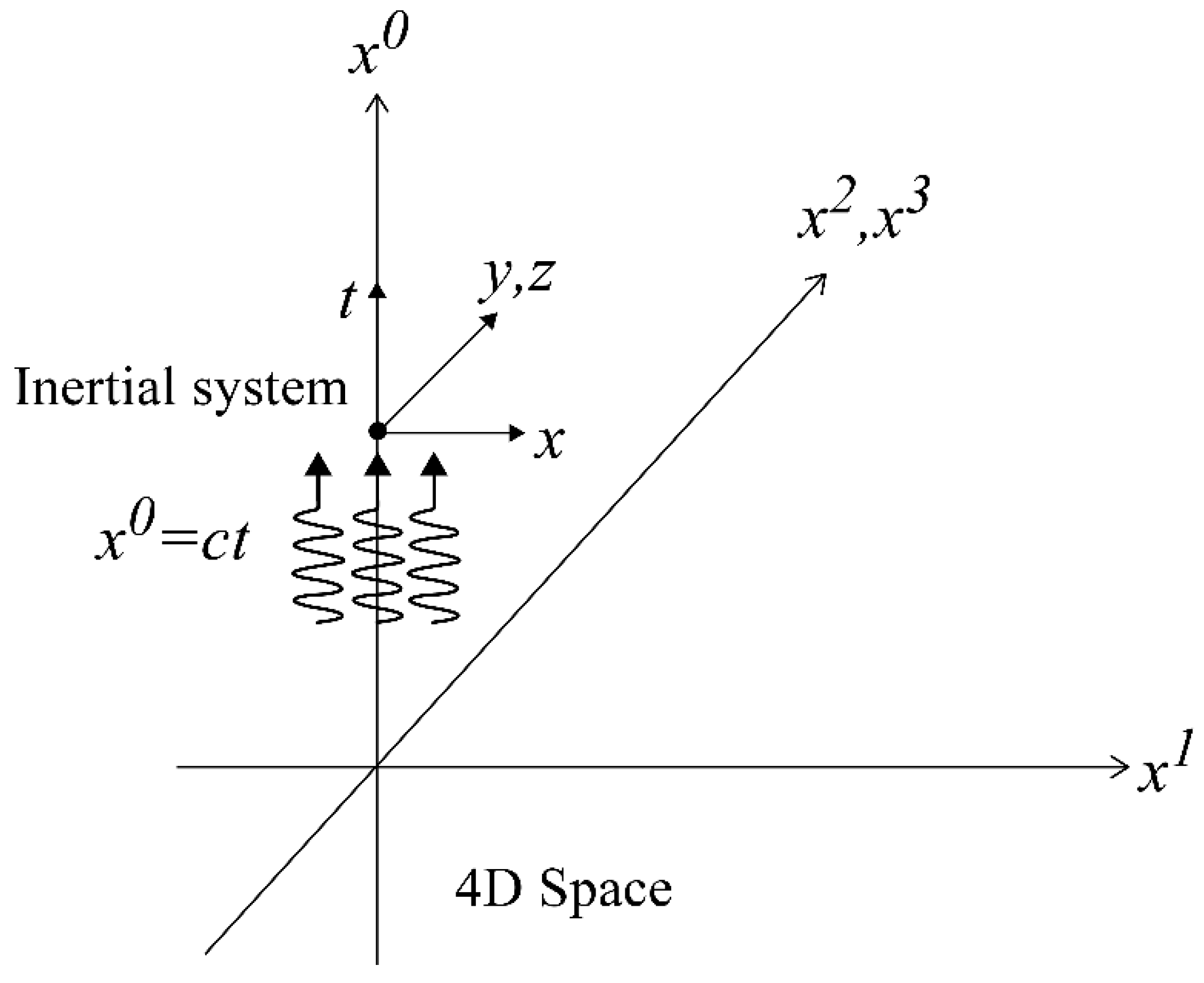
To explain this phenomenon, let us assume that all elementary particles are waves that propagate through 4D space at the speed of light c. This assumption provides a possible explanation for the stationary behavior of elementary particles. For example, the relative speed of two surfers on the same wave can be zero. If the 4D spacetime is considered as an inertial system consisting of a group of elementary particles propagating at the speed of light in the same direction in 4D space, as shown in Figure 3, the elementary particles in this inertial system appear to be at rest with respect to each other. Moreover, the propagation of the speed of light in 4D space can be considered as the underlying cause of the flow of time, which ticks at a constant speed from the past to the future. This perspective suggests a close relationship between the behavior of waves in 4D space and the flow of time.

4. Mathematical model: 4D space

In this study, using the following two assumptions, valid coordinate transformations in 4D space were obtained, and their relationship was discussed based on the Lorentz transformation:
Assumption 1: Space consists of four isotropic and uniform dimensions.
Assumption 2: Time is determined as the distance covered by an elementary particle propagating through a 4D space divided by the speed of light.

4.1. Coordinate transformation in the 4D space

The simplest system with relative motion consists of two elementary particles. Let us consider a system consisting of two elementary particles, P1 and P2, propagating in different directions in 4D space with speed c.
The motion of these particles can be analyzed by first examining P1 alone. As shown in Figure 3, if the direction of motion of elementary particle P1 is considered as the x0 axis, the direction of the x0 axis becomes the time axis of the coordinate system fixed to elementary particle P1. In other words, the distance x0 traveled by elementary particle P1 from its origin divided by its speed c is the time t of particle P1.
t = x 0 c   .
The remaining three axes, ( x 1 ,   x 2 ,   x 3 ) , orthogonal to the x0 axis, form the spatial coordinates (x,y,z) of the coordinate system fixed to particle P1. The coordinate system (ct,x,y,z) fixed to particle P1 is an inertial coordinate system that moves at a constant speed of light c in 4D space.
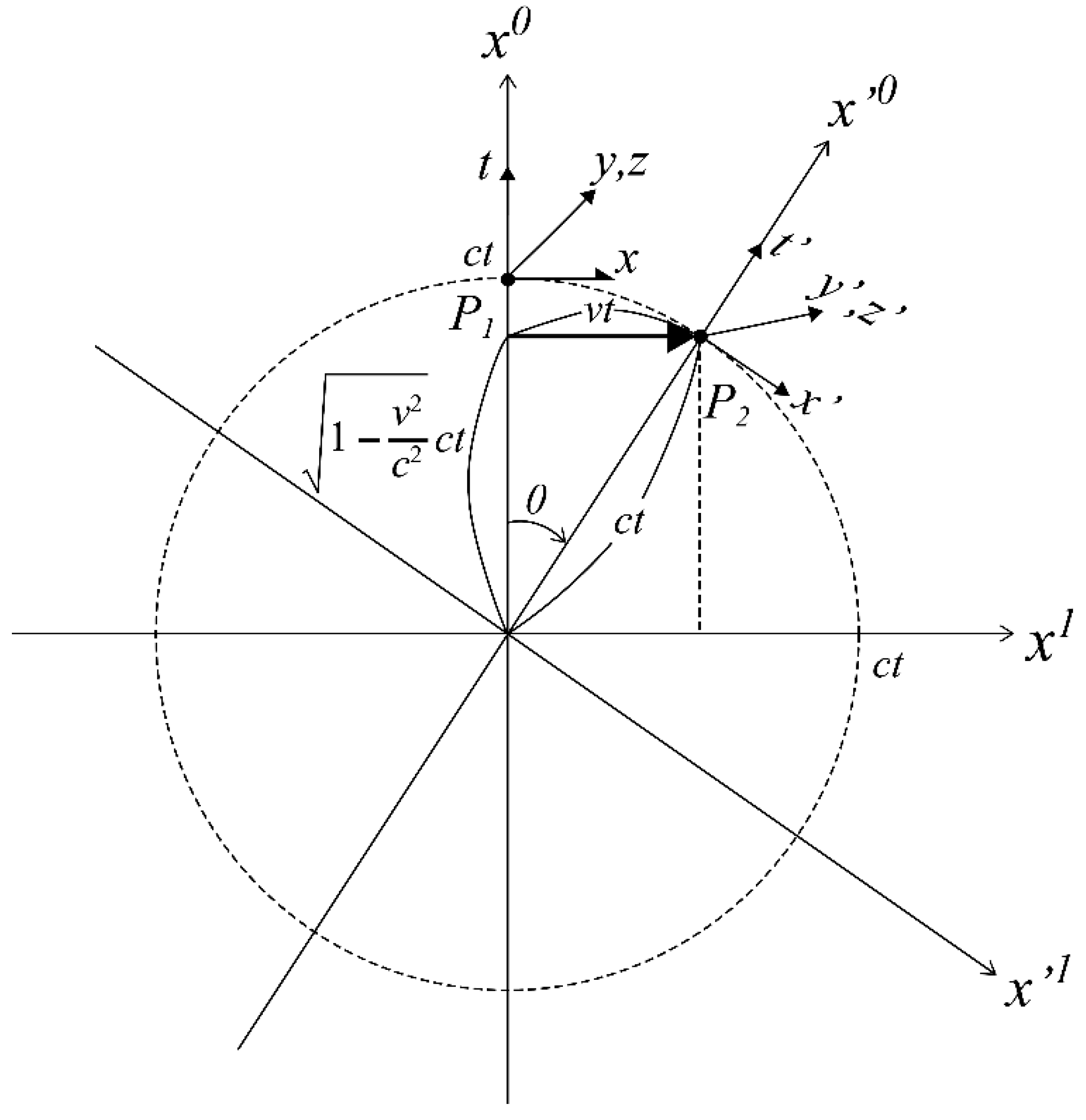
Next, the motion of elementary particle P2, which propagates in a direction different from that of elementary particle P1, is considered. As shown in Figure 4, the particle P2 starts to propagate at the same time as the particle P1 from a certain point (let this be the origin), and the direction of propagation of the particle P2 is assumed to form an angle θ with the direction of propagation of the elementary particle P1. This direction is the x'0 axis of particle P2, while x1 and x'1 axes are assumed to be in the same plane as the x0 and x'0 axes. The speed component of particle P2 in the x1 axis direction can be expressed as follows:
v = s i n θ ・ c .  
Furthermore, from (24), the following equations are obtained.
s i n θ = v c   ,  
c o s θ = 1 − s i n 2 θ = 1 − v 2 c 2   .  
The transformation from coordinates (x'0,x'1) to coordinates (x0,x1) is given by the well-known rotation of the coordinate axes.
x 0 = c o s θ ・ x ′ 0 − s i n θ ・ x ′ 1   ,  
x 1 = s i n θ ・ x ′ 0 + c o s θ ・ x ′ 1
Using (25) and (26), (27) and (28) can be rewritten as follows:
x 0 = 1 − v 2 c 2 x ' 0 − v c x ′ 1   ,
x 1 = v c x ' 0 + 1 − v 2 c 2 x ' 1   .
This is the coordinate transformation of 4D space. The inverse transformation is as follows:
x ′ 0 = 1 − v 2 c 2 x 0 + v c x 1   ,
x ′ 1 = − v c x 0 + 1 − v 2 c 2 x 1   .
The relationship of the other coordinate axes is as follows:
x ′ 2 = x 2   ,
x ′ 3 = x 3   .

4.2. "Same time" and "same position" of the inertial system moving in the 4D space

The two inertial coordinate systems moving in 4D space cannot share the same time at all points, as in Minkowski spacetime. Figure 5 shows the coordinates of the S and S' systems moving relative to each other in 4D space (x2 and x3 axes are omitted). As in the Minkowski spacetime, the same time in the S system can be represented by a line parallel to the x1 axis, and the same time in the S' system can be represented by a line parallel to the x′1 axis. Only one point (P) exists where the lines of the same time and position in the S and S' systems overlap each other (in real 4D space, x2- x3 plane with common (x0, x1) coordinates corresponds to the same time and position).
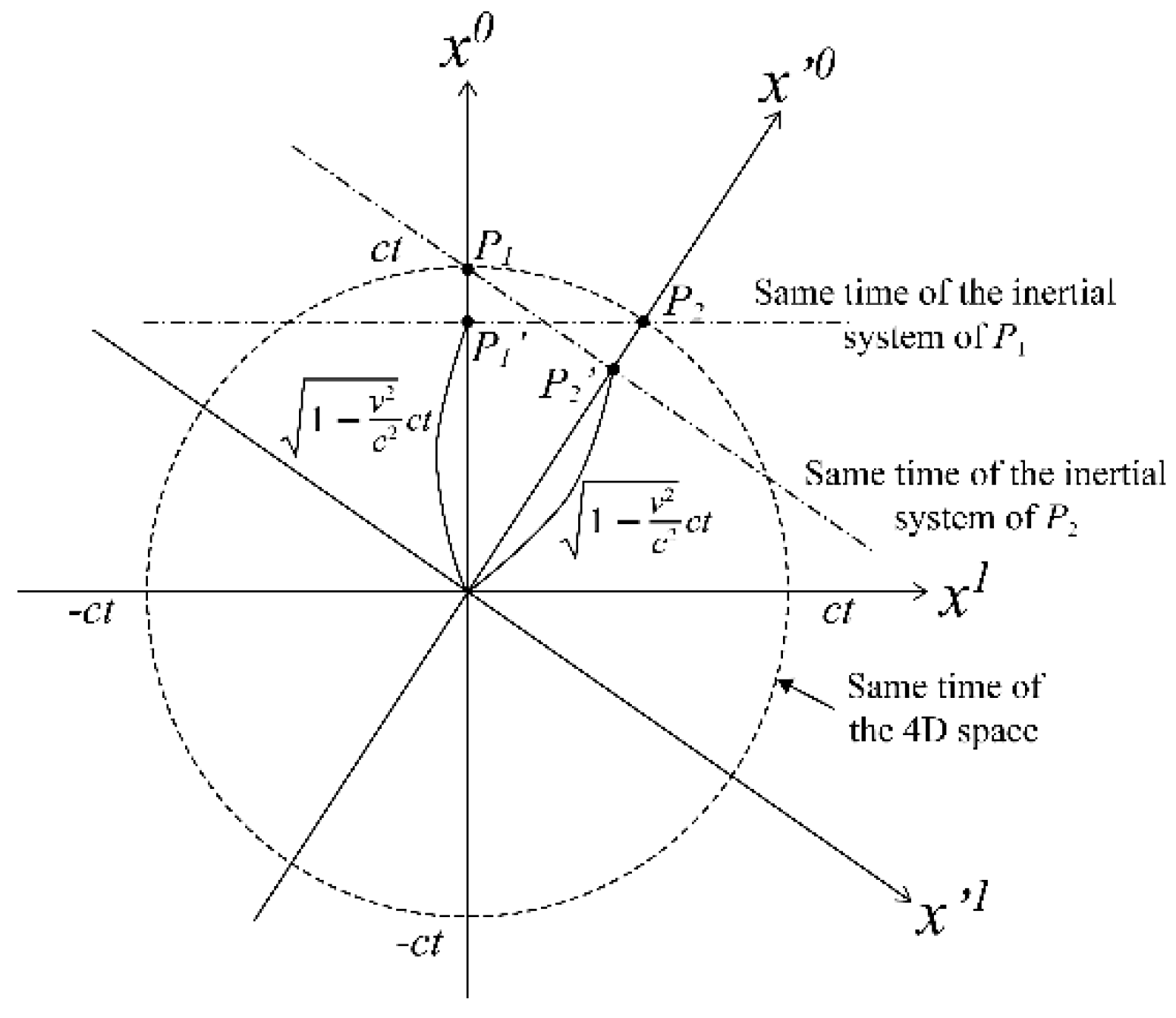
In addition to the inertial systems described earlier, there is another notion of time that must be considered. This is the same time in 4D space. To illustrate this, let us again consider two elementary particles that simultaneously start propagating in different directions from the origin. Figure 6 shows the positional relationship of the two elementary particles after time t has elapsed during their propagation. The elementary particles P1 and P2 are both located on the circumference of radius ct in the 4D space at time t. Although the same time in the inertial system of the two elementary particles is shown in Figure 6, note that there are two types of times at play here: the same time in the inertial system of the two particles and the same time in the 4D space.
As discussed in Section 2.2, when two objects move relative to each other at a speed v, they perceive each other's time as flowing slower than their own time. The relationship is expressed by
t ′ = 1 − v 2 c 2 t   .
In other words, the other person’s time, as observed by each elementary particle, is the past time of the other person’s elementary particles. As shown in Figure 6, the time at which elementary particle P2 is observed by elementary particle P1 is the time at P2’ ( t ′ = 1 − v 2 / c 2 t ). Similarly, the time at which elementary particle P1 is observed by elementary particle P2 is the time at P1’ ( t ′ = 1 − v 2 / c 2 t )
The time 1 − v 2 / c 2 t is known as the eigentime in the theory of special relativity and is denoted by τ = 1 − v 2 / c 2 t . The following relationship between the eigentime τ and the Lorentz-invariant distance s also exists:
s = cτ .

4.3. Equivalence of the Minkowski spacetime and the 4D Space

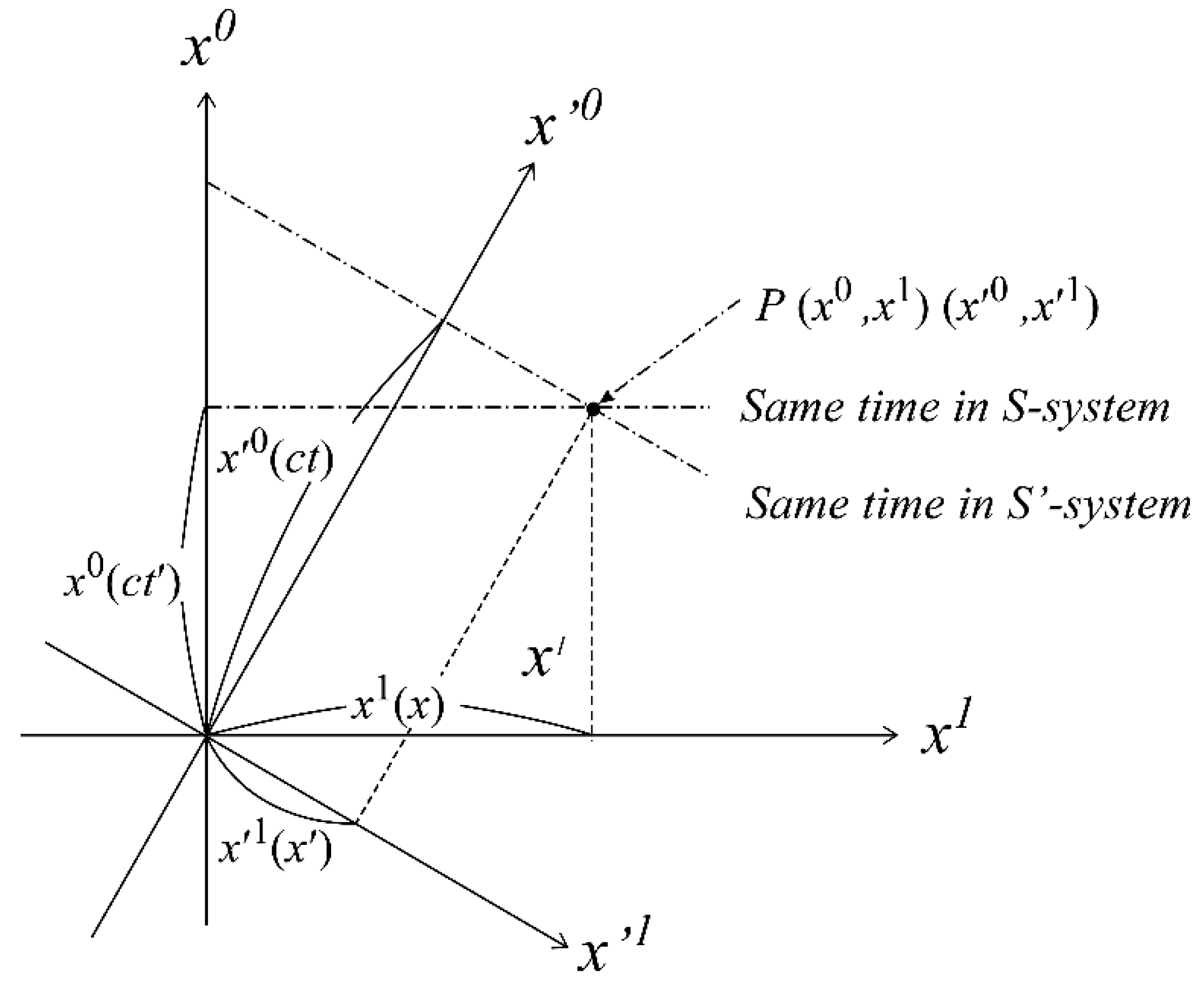
This section presents an examination as to why motion in an isotropic and uniform 4D space is transformed by the Lorentz transformation.
The Lorentz and rotational transformations in the 4D space, and their respective inverse transformations can be expressed as follows:
c t = c t ′ + v c x ′ 1 − v 2 c 2   ,
x = v c c t ′ + x ′ 1 − v 2 c 2   ,
c t ′ = c t − v c x 1 − v 2 c 2   ,
x ′ = − v c c t + x 1 − v 2 c 2   ,
x 0 = 1 − v 2 c 2 x ′ 0 − v c x ′ 1   ,
x 1 = v c x ′ 0 + 1 − v 2 c 2 x ′ 1   ,
x ′ 0 = 1 − v 2 c 2 x 0 + v c x 1   ,
x ′ 1 = − v c x 0 + 1 − v 2 c 2 x 1   .
Eqs. (37)–(40) corresponding to the Lorentz transformation and (41)–(44) corresponding to the rotational transformation in 4D space do not initially appear to be the same. To compare them directly, the rotational transformation equation is rewritten in the same form as the Lorentz transformation.
x 0 = x ′ 0 − v c x 1 1 − v 2 c 2   ,
x 1 = v c x 0 + x ′ 1 1 − v 2 c 2   ,
x ′ 0 = x 0 + v c x ′ 1 1 − v 2 c 2   ,
x ′ 1 = − v c x ′ 0 + x 1 1 − v 2 c 2   .
Compared to (37)–(40), the following correspondence between the coordinate axes of the 4D space and the coordinates of the Minkowski spacetime is observed:
x 0 　     ⇔ 　 c t ′   ,  
x 1 　   ⇔ 　 x   ,
x ′ 0 　 ⇔ 　 c t   ,
x ' 1 　 ⇔ 　 x ′   .  
This correspondence between the 4D space coordinates and the Minkowski spacetime coordinates is illustrated in Figure 7, where x0(ct') indicates that the x0 axis in the 4D space is the ct' axis in the Minkowski spacetime. The meanings of the other coordinates are the same.
Here, a few aspects are noteworthy. As shown in (49)–(52) and Figure 7, the relation between the two time axes in the Minkowski spacetime is in contrast to the relation of the time axes in the 4D space (such that ct′ corresponds to x0 and ct corresponds to x′0).
The distance between the coordinate origin and event P is given by the following equation using the coordinates in the 4D space:
( x 0 ) 2 + ( x ) 2 = ( x ′ 0 ) 2 + ( x ′ 1 ) 2   .
Substituting (49)–(52) into (53) gives the following equation:
c 2 t ′ 2 + x 2 = c 2 t 2 + x ′ 2   .
Further transposition of x to the right-hand side and x' to the left-hand side gives the following equation:
c 2 t ′ 2 − x ′ 2 = c 2 t 2 − x 2   .
This equation is simply the invariant distance formula of the Lorentz transformation, as indicated by (11).
This discussion yields the conclusion that there is a one-to-one correspondence between the Minkowski spacetime and 4D space. Each transformation equation can be obtained by substituting the coordinate variables shown in (49)–(52). Hence, it can be stated that "the Minkowski spacetime and the 4D space are completely equivalent." Notably, the reason why the invariant distance in the Minkowski spacetime is not the Pythagorean theorem but the difference between the square of the time distance and the space distance. This is because of the different approach to taking the time axis in the Minkowski spacetime and the 4D space, as aforementioned (so that ct′ corresponds to x0 and ct corresponds to x′0).

4.4. Time delay and Lorentz contraction derived from rotational transformation in the 4D space

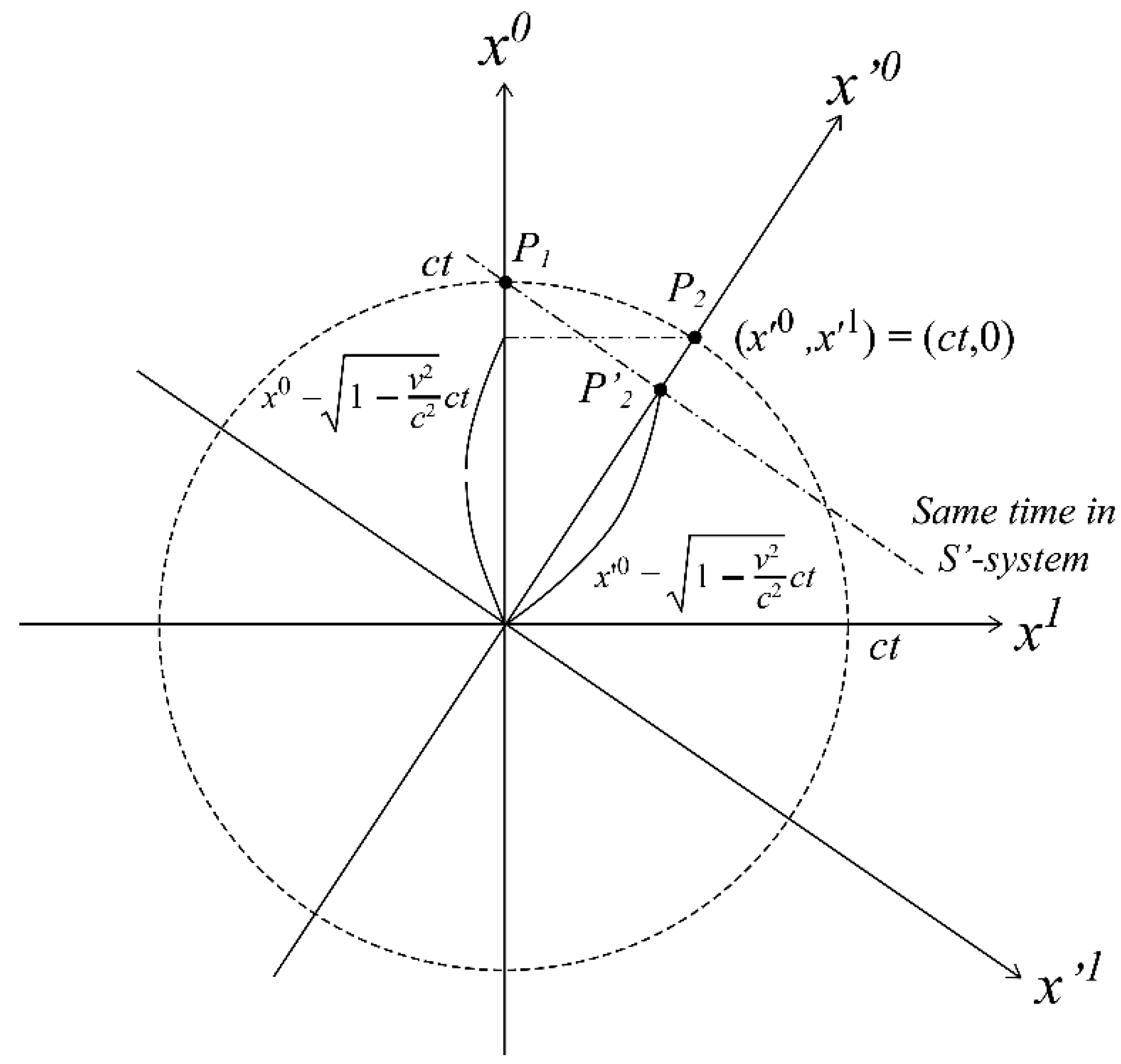
This section shows that the time delay and Lorentz contraction can be obtained from the rotational transformation in 4D space as well as from the Lorentz transformation.
Two elementary particles, P1 and P2, start linear motion at a constant speed in different directions from the same position, and their positions at time t are shown in Figure 8. The position coordinates of the elementary particle P2 at this time are represented by (x'0, x'1) = (ct,0). Substituting this into (29) and transforming it into the coordinate system of elementary particle P1, the following results:
x 0 = 1 − v 2 c 2 ・ x ′ 0 − v c ・ x ′ 1 = 1 − v 2 c 2 ・ c t   .  
If the time at this position is t',
t ′ = x 0 c = 1 − v 2 c 2 t .
Thus, from the viewpoint of particle P1, the time of particle P2 is delayed as described by equation (57), which corresponds to the "time delay" in (14). This demonstrates that the same results as the Lorentz transformation can be obtained from the rotational transformation in 4D space. From another perspective, the x0-axis component of the position coordinate of elementary particle P2 is 1 − v 2 / c 2 t . This implies that the time of elementary particle P2 as observed by elementary particle P1 is the distance that particle P2 has traveled in the direction of the time axis of particle P1. Conversely, the time of elementary particle P1 from the perspective of elementary particle P2 is the distance that particle P1 has traveled in the direction of the time axis of particle P2. These time relationships are relative to each other.
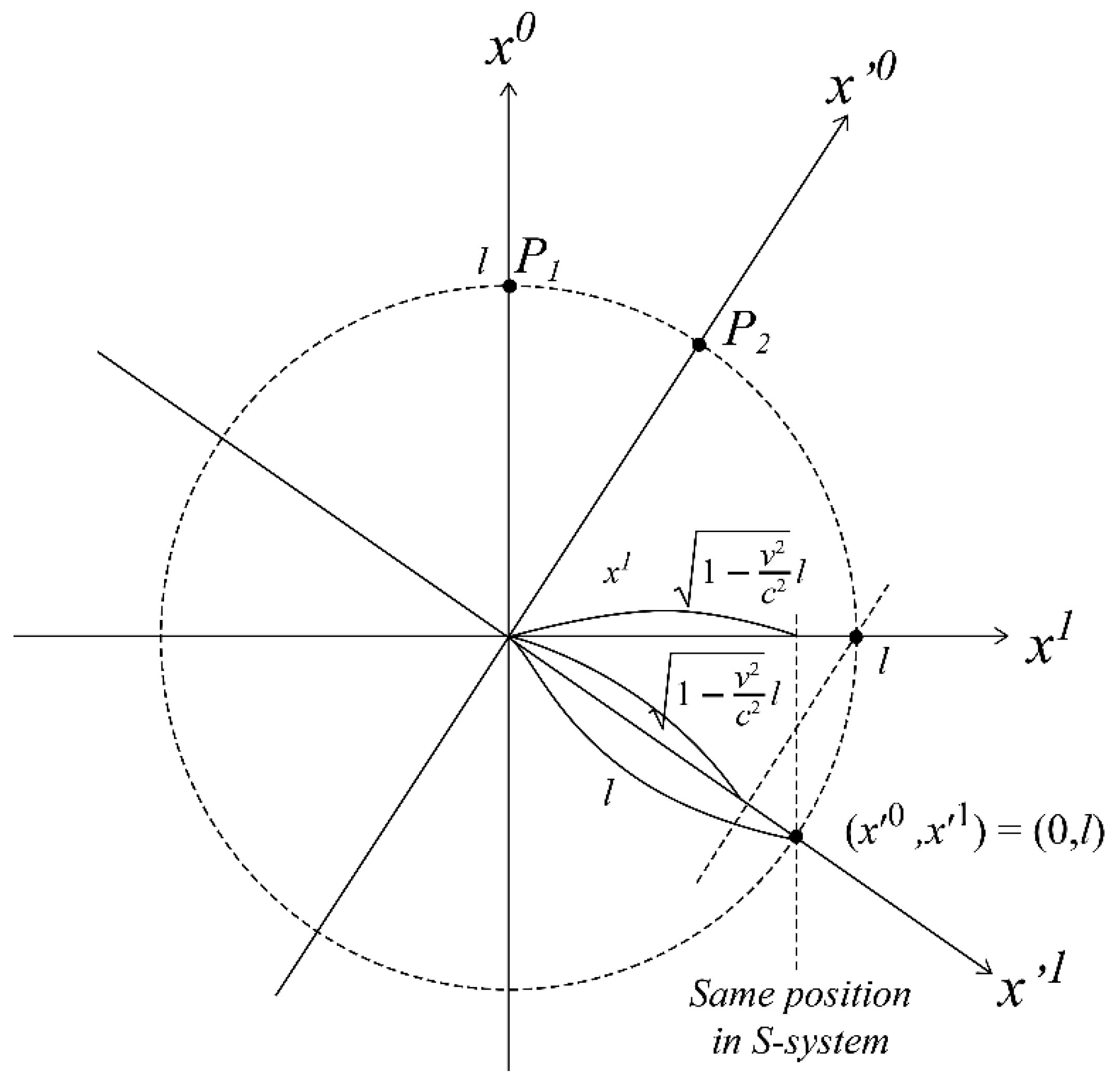
Figure 9 shows the coordinate of a position ℓ from the origin on the x'1 axis as (x'0, x'1) = (0, ℓ). By substituting this into (30) and transforming it into the coordinate system of elementary particle P1, the following results:
x 1 = v c ・ x ′ 0 + 1 − v 2 c 2 ・ x ′ 1 = 1 − v 2 c 2 ・ ℓ   .
It appears that the distance in the x'1 direction of elementary particle P2 contracts in the coordinate system of elementary particle P1, according to the ratio given in (58). This is the equivalent to the "Lorentz contraction" in (16). It can be observed that the spatial distance of the elementary particle P2 corresponds to the distance projected onto the x1 axis of the coordinate system of the elementary particle P1. Similarly, the spatial distance of the elementary particle P1 is the distance projected onto the x'1 axis of the coordinate system of the elementary particle P2. It is important to note that spatial distance relationships, such as time relationships, are relative to each other.

4.5. Upper limit of speed and the principle of constant speed of light

As mentioned in Section 4.1, the relative speed occurs due to the difference in the direction of propagation of each elementary particle and is given by the following equation:
v = s i n θ ・ c   .  
This implies that the relative speed is maximum when the direction of propagation of each elementary particle differs by 90°, that is, when their directions of motion are orthogonal to each other. Therefore, an upper limit to the relative speed of elementary particles is set, which is equal to the speed of light c.
As mentioned in Section 2.1, the four vectors of special relativity are defined by the following equation:
x μ = ( x 0   , x 1   , x 2 , x 3 ) = ( c t   , x ) .
The four-momentum p μ is defined by the following equation:
p μ = m 0 u μ = ( m 0 d ( c t ) d τ   , p )   .
The following equation gives the relationship between energy and momentum:
E 2 = m 0 2 c 4 + p 2 c 2   ,
where m0 is the rest mass of the elementary particle. Further,
m 0 2 c 4 = E 2 − p 2 c 2 = E ′ 2 − p ′ 2 c 2   ,
is Lorentz-invariant, and the rest mass m0 is the same for all inertial systems.
In contrast, the four vectors in the 4D space are defined as follows (considering x0 as cτ instead of ct):
x μ = ( x 0   , x 1   , x 2 , x 3 ) = ( c τ   , x ) .
Thus, the four-momentum p μ in the 4D space is defined as follows:
p μ = m 0 u μ = ( m 0 c   , p )   .
The relationship between energy and momentum is given by the following equation (as in special relativity):
E 2 = m 0 2 c 4 + p 2 c 2   .
The relationship between energy and momentum for elementary particles with zero mass is given by the following equation for both special relativity and 4D space:
E = | p | c .
The four-momentum equation for elementary particles with zero mass is given by
p μ = ( 0   , p )   .
Because the rest mass is Lorentz-invariant, elementary particles with zero mass have zero mass in all inertial systems. Elementary particles with zero mass have zero momentum in the direction of the time axis, as expressed in (68). As mentioned earlier, the speed of elementary particles with a direction of motion that differs by 90° from the time axis, is the speed of light. In other words, the speed of elementary particles with zero mass is the speed of light in all inertial systems. This is the reason for the validity of the principle of the constant speed of light.

4.6. Klein–Gordon and Dirac equations

The Klein–Gordon and Dirac equations are important as they support the quantum field theory [3,19]. Therefore, it is necessary to show that the assumption of a 4D space is consistent with these equations.
The Klein–Gordon equation is obtained by making the following quantum mechanical replacement to (62), which is established between the energy and momentum:
E → i ℏ ∂ ∂ t 　 , 　 p → − i ℏ ∇   .
As discussed in Section 4.5, the relationship between the energy and momentum in a 4D space is given by (66), similar to the theory of special relativity. Therefore, the Klein–Gordon equation has the same form in special relativity and 4D space. By replacing (69) and rewriting (66) in the form of a wave equation, the well-known Klein–Gordon equation is obtained.
( 1 c 2 ∂ 2 ∂ t 2 − ∇ 2 + m 0 2 c 2 ℏ 2 ) φ ( x ) = 0   .  
However, the four-momentum in 4D space is given by (65). If it is considered as a vector in a 4D space, it takes the following form:
p 4 = m 0 c e 0 + p 1 e 1 + p 2 e 2 + p 3 e 3   .
where e μ represents the unit vector of the x μ (μ = 0 ∼ 3) axis. In addition, p4 is a vector in the 4D space, and this notation is used to distinguish it from the usual vector p in 3D space. Using replacement (69) in (71) yields:
i ℏ 1 c ∂ ∂ t p 4 | p 4 | = m 0 c e 0 − i ℏ ∂ ∂ x 1 e 1 − i ℏ ∂ ∂ x 2 e 2 − i ℏ ∂ ∂ x 3 e 3   .  
Using the correspondence between (65) and (66), the following replacement is used:
| p 4 | 　 → 　 1 c E 　 → 　 i ℏ 1 c ∂ ∂ t   .  
Furthermore, by transposing the right-hand side of (72) to the left-hand side, the following equation is obtained:
i ℏ 1 c ∂ ∂ t p 4 | p 4 | + i ℏ ∂ ∂ x 1 e 1 + i ℏ ∂ ∂ x 2 e 2 + i ℏ ∂ ∂ x 3 e 3 − m 0 c e 0 = 0   .
On the other hand, the Dirac equation is as follows:
( i ℏ ∂ ∂ x 0 γ 0 + i ℏ ∂ ∂ x 1 γ 1 + i ℏ ∂ ∂ x 2 γ 2 + i ℏ ∂ ∂ x 3 γ 3 − m 0 c I 4 ) ψ ( x ) = 0
where γ μ (μ = 0 ∼ 3) denotes a 4 × 4 matrix (gamma matrix) satisfying the following relation:
γ μ γ ν + γ ν γ μ = 2 η μ ν I 4   .
I 4 is the unit matrix and η μ ν is the metric tensor.
η μ ν = { + 1     f o r     μ = ν = 0               − 1     f o r     μ = ν = 1 , 2 , 3 0     f o r     μ ≠ ν                           .
Eqs. (74) and (75) can now be compared. The Dirac equation (75) differs from the vector equation in (74) because it is an equation for four-component spinors; however, it has the same formal form. The following correspondence is observed between the unit vector e μ , the gamma matrix γ μ and the four-vector xμ:
e 0 ⇔ I 4   ⇔ x 0   ,
p 4 | p 4 | ⇔ γ 0 ⇔ c t   ,
e 1 ⇔ γ 1 ⇔ x 1   ,
e 2 ⇔ γ 2 ⇔ x 2   ,
e 3 ⇔ γ 3 ⇔ x 3   .
The correspondences mentioned above suggest that the gamma matrix γ μ plays the role of both a unit vector and a matrix that acts on the spinor. On this basis, the Klein–Gordon equation can be interpreted as an energy conservation law in 4D space, and the Dirac equation can be interpreted as a four-momentum conservation law in the 4D space. From the above discussion, the following relationship between 4D space and Minkowski spacetime may be recalled:
-4D space    : Space   : Quantum field
-Minkowski spacetime: Spacetime: Inertial system
This implies that the 4D space is an isotropic and uniform space with four dimensions that lacks time and constitutes a field of elementary particles. In contrast, the Minkowski spacetime is an inertial system in which time is obtained by a group of elementary particles that propagate through 4D space at the speed of light. Our universe may consist of only one 4D space, forming a field and countless inertial systems propagating through 4D space at the speed of light

5. Discussion

This paper presents the derivation of the principle of relativity from the motion of elementary particles in 4D space. The invisibility of the time axis, equivalence of mass and energy, and dilation of time are also discussed.

5.1. The principle of relativity

The principle of relativity implies that the laws of physics are the same for all inertial systems. Because it is a fundamental assumption, its validity does not need to be questioned further as long as experimental or observational evidence supports the conclusions drawn from it. However, it is still worthwhile to explore its underlying meaning.
An inertial system consists of a group of elementary particles that propagate at the speed of light in the same direction through an isotropic and uniform 4D space. Because inertial systems moving in different directions differ only in the direction of propagation, there is no reason for the laws of physics to differ owing to differences in the direction of propagation if the space is isotropic and uniform. Therefore, the principle of relativity can be explained by assuming an isotropic and uniform 4D space.
Although the principle of relativity can be explained by assuming an isotropic and uniform 4D space, it is important to note that this assumption has been experimentally verified accurately. Nevertheless, understanding the underlying meaning of the principle can help deepen our understanding of the nature of the universe.

5.2. Why time is invisible

Our ability to observe and measure the depth of space and position of objects depends on the transfer of information between objects through light and sound waves. For instance, we rely on light to see, while animals such as bats use ultrasound to locate their prey. However, elementary particles with zero mass, such as photons, cannot convey information about the direction of the time axis since they have no momentum in that direction. Moreover, elementary particles with mass can travel at the speed of light along the direction of the time axis, but they cannot transfer information back and forth along it. As a result, we have no means of determining the depth the time axis and, therefore, we cannot precisely measure determine the time.

5.3. Equivalence of mass and energy

Einstein’s famous equation E= m0c2 was derived from special relativity [2], and its validity has been proven through numerous experiments and observations. This equation expresses the equivalence between the rest mass of an object and its energy. For instance, evidence of this equation can be observed in nuclear power and the energy of the sun, both of which result from a small amount of mass being converted to energy through fission and fusion reactions.
In an inertial coordinate system moving with elementary particles, m0 represents the rest mass of the particles. However, in 4D space, elementary particles propagate through space at the speed of light and have momentum p= m0c and kinetic energy E= m0c2. It can be challenging to understand how the rest mass is equivalent to energy; however, this becomes simpler if E= m0c2 is interpreted as the kinetic energy of an object moving at the speed of light.

5.4. Time dilation [20]

Section 4.4 explains that a moving object experiences time dilation according to (57). This leads to an interesting hypothetical scenario known as the twin paradox [21], where one twin who travels into space in a spaceship and returns to Earth years later, finds that their time has slowed down compared to their younger twin, who has aged significantly.
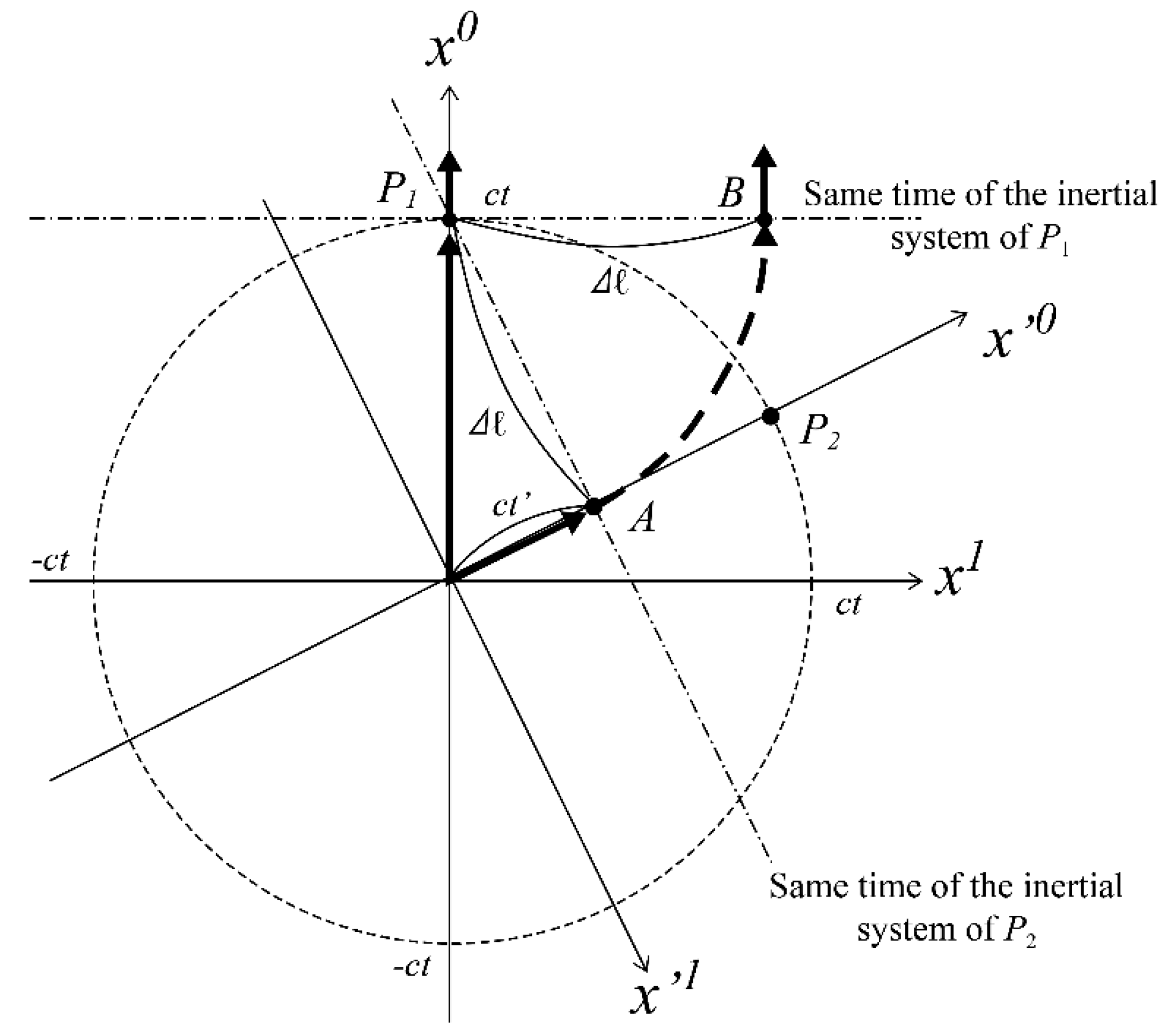
This phenomenon can be explained using the concept of 4D space as follows: Consider two elementary particles P1 and P2, which move in different directions starting from the same point at time zero, as shown in Figure 10. As long as their motions remain unchanged, their relative motions will remain unchanged as they move in different directions but marking the same time with each other.
However, when the direction of motion changes, things get interesting. At time t, the positions of P1 and P2 in 4D space are shown in Figure 10. If P2 changes its direction of motion in the same direction as P1 at point A, it implies that P2 moves into the same inertial system as P1.
As a result, when P2 arrives at point A, which is represented by a straight line parallel to the x′1 axis and corresponds to the same time as P1, it moves to point B, which is simultaneously located in the inertial system of particle P1. The time when P2 arrives at point A is t′, which is obtained from (57). However, as soon as P2 enters the same inertial system as P1, it moves to time t at the same time as P1.
Thus, the time of P2 is delayed relative to P1 due to its motion in a different direction, and it experiences time dilation. This mechanism explains the twin paradox and the reason why the moving brother in our hypothetical scenario would experience slower time than the stationary brother.

5.5. Field that creates 4D space and the ticks of time

This section presents an exploration of the structure of the field that gives rise to 4D space and examine how time operates within this space.
According to quantum field theory, a vacuum is not empty but composed of harmonic oscillators. Elementary particles are considered to be excited states of these oscillators that propagate as waves. For these waves to propagate, they require a medium and a foundation to hold the harmonic oscillators. In order for quantum field theory to be valid, there must be an absolute foundation to hold these oscillators, such as 4D space. As previously described, if the inertial coordinate system is considered to be a group of elementary particles that propagate at the speed of light in a 4D space, this 4D space can be considered a medium that transmits waves of elementary particles and as an absolute space.
The universe is composed of four isotropic and uniform dimensions, and 4D space is the medium through which elementary particles propagate at the speed of light. Time is a secondary phenomenon that arises from the excited state of a field propagating at a constant speed. The excited state of the field creates time by moving through 4D space, much like falling dominoes. Time does not exist in the space before or after the dominoes fall; only the quantum field fluctuations are present. Time moves at a constant speed from the past to the future because these dominoes fall at a constant speed in a constant direction. Our universe can be considered as the tip of a domino that keeps time ticking as it falls.

6. Conclusion

This paper proposes that space is composed of isotropic and uniform 4D space and that elementary particles are waves that propagate at an inherent speed in this medium. Based on these assumptions, the following conclusions were drawn:
  • A one-to-one correspondence exists between Minkowski spacetime and 4D space, indicating their complete equivalence. The Lorentz transformation in Minkowski spacetime is equivalent to a rotational transformation in a 4D space.
  • It is demonstrated that time delay and Lorentz contraction can be derived not only from Lorentz transformations, but also from rotational transformations in a 4D space.
  • The principle of relativity and the principle of the constant speed of light, which Einstein assumed when deriving the special theory of relativity, can be derived by assuming the 4D space. The present study also clarified why time flows at a constant speed from the past to the future.
There remain several unsolved problems in physics, such as the origin of baryons and the nature of dark matter and dark energy. To solve these problems, the structure of quantum fields comprising the universe must be unraveled. It is believed that the 4D space proposed in this study is an important step towards unraveling the structure of quantum fields.

Author Contributions

Not applicable.

Funding

This research received no external funding.

Data Availability Statement

Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.

Acknowledgments

I would like to thank Editage (www.editage.com) for English language editing.

Conflicts of Interest

The author declares no conflict of interest.

References

  1. Einstein, A. The Meaning of Relativity: Including the Relativistic Theory of the Nonsymmetric Field; Princeton University Press: Princeton, 1955.
  2. Einstein, A. Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig? Ann. Phys. 1905, 323, 639–641. [Google Scholar] [CrossRef]
  3. Weinberg, S. The quantum theory of field. Foundations: 01; Cambridge University Press: Cambridge. 1955, 1.
  4. Einstein, A. Zur Elektrodynamik bewegter Körper. Ann. Phys. 1905, 322, 891–921. [Google Scholar] [CrossRef]
  5. Maxwell, J.C., VIII. A dynamical theory of the electromagnetic field. Philos. Trans. R. Soc. Lond. 1865, 155, 459–512. [Google Scholar] [CrossRef]
  6. Shankland, R.S. Michelson-Morley experiment. Am. J. Phys. 1964, 32, 16–35. [Google Scholar] [CrossRef]
  7. Rizzo, R.G. Phenomenology and the LHC. Available online: https://arxiv.org/abs/hep-ph/0610104, 2006.
  8. Anthony, K. ATLAS celebrates results of 1000 collision papers. Available online: https://atlas.cern/updates/news/1000-collision-papers. (accessed 18 Jun 2021), 2021.9. Resnick, B. Extremely powerful cosmic rays are raining down on us. No one knows where they come from. Available online: https://www.vox.com/the-highlight/2019/7/16/17690740/cosmic-rays-universe-theory-science. (accessed 25 Jul 2019), 2019.
  9. Resnick, B. Extremely powerful cosmic rays are raining down on us. No one knows where they come from. Available online: https://www.vox.com/the-highlight/2019/7/16/17690740/cosmic-rays-universe-theory-science, 2019. (Accessed 25 July 2019).
  10. Gabrielse, G.; Hanneke, D.; Kinoshita, T.; Nio, M.; Odom, B. New determination of the fine structure constant from the electron g value and QED. Phys. Rev. Lett. 2006, 97, 030802. [Google Scholar] [CrossRef] [PubMed]
  11. Schutz, B. A Student’s Manual for A First Course in General Relativity, third ed.; Cambridge University Press: Cambridge, 2022.
  12. Wald, R.M. ; General Relativity, the University of Chicago Press: Chicago, 1984.
  13. Hawking, S.W. A Brief History of Time; Bantam Books: New York, 1989.
  14. Roberts, B.W. Roberts, B.W. Reversing the Arrow of Time; Cambridge University Press: Cambridge, 2022.
  15. Landau, L.D.; Lifshitz, E.M. Course of Theoretical Physics; Vol. 2; The Classical Theory of Fields: Butterworth-Heinemann; Oxford, 1980.
  16. LibreTexts PHYSICS, The Lorentz transformation. Available online: https://phys.libretexts.org/Bookshelves/University_Physics/Book%3A_University_Physics_(OpenStax)/University_Physics_III_-_Optics_and_Modern_Physics_(OpenStax)/05%3A__Relativity/5.06%3A_The_Lorentz_Transformation (accessed 13 Sep 2022), 2022.
  17. Rindler, W. Introduction to Special Relativity, second ed.; Clarendon Press: Oxford, 1991. 1991.
  18. LibreTexts PHYSICS. Minkowski coordinates. Available online: https://phys.libretexts.org/Bookshelves/Relativity/Book%3A_Special_Relativity_(Crowell)/01%3A_Spacetime/1.02%3A_Minkowski_Coordinates (accessed 6 Mar 2022), 2022.
  19. Sakamoto, M. Quantum field theory, Focus on invariance and free fields, Shokabo Tokyo. Available online: https://www.shokabo.co.jp/mybooks/ISBN978-4-7853-2511-4.htm.
  20. Ives, H.E.; Stilwell, G.R. An experimental study of the rate of a moving atomic clock. J. Opt. Soc. Am. 1938, 28, 215–226. [Google Scholar] [CrossRef]
  21. Zimmerman Jones, A. What is the twin paradox? Real time travel. Available online: https://www.thoughtco.com/twin-paradox-real-time-travel-2699432#:~:text=The%20twin%20paradox%20is%20a%20thought%20experiment%20that,relativity.%20Consider%20two%20twins%2C%20named%20Biff%20and%20Cliff (accessed 6 Mar 2018), 2018.
Preprints 74547 g001
Figure 1. Two inertial systems S and S' in constant linear motion with relative speed v in x direction.
Figure 1. Two inertial systems S and S' in constant linear motion with relative speed v in x direction.
Preprints 74547 g001
Preprints 74547 g002
Figure 2. Same time and same position in the Minkowski spacetime.
Figure 2. Same time and same position in the Minkowski spacetime.
Preprints 74547 g002
Preprints 74547 g003
Figure 3. Inertial coordinate system created by elementary particles propagating through the 4D space at the speed of light.
Figure 3. Inertial coordinate system created by elementary particles propagating through the 4D space at the speed of light.
Preprints 74547 g003
Preprints 74547 g004
Figure 4. Elementary particles P1 and P2 moving in the 4D space with relative speed v in x direction.
Figure 4. Elementary particles P1 and P2 moving in the 4D space with relative speed v in x direction.
Preprints 74547 g004
Preprints 74547 g005
Figure 5. Same time and same position of two inertial systems in motion in the 4D space.
Figure 5. Same time and same position of two inertial systems in motion in the 4D space.
Preprints 74547 g005
Preprints 74547 g006
Figure 6. Same time in the inertial system and same time in the 4D space.
Figure 6. Same time in the inertial system and same time in the 4D space.
Preprints 74547 g006
Preprints 74547 g007
Figure 7. Correspondence between the 4D space coordinate and the Minkowski spacetime coordinate.
Figure 7. Correspondence between the 4D space coordinate and the Minkowski spacetime coordinate.
Preprints 74547 g007
Preprints 74547 g008
Figure 8. Positions of elementary particles P1 and P2 at time t.
Figure 8. Positions of elementary particles P1 and P2 at time t.
Preprints 74547 g008
Preprints 74547 g009
Figure 9. Lorentz contraction of the coordinate axes of the elementary particle P2.
Figure 9. Lorentz contraction of the coordinate axes of the elementary particle P2.
Preprints 74547 g009
Preprints 74547 g010
Figure 10. Time travel occurring at the moment when the inertial coordinate system changes.
Figure 10. Time travel occurring at the moment when the inertial coordinate system changes.
Preprints 74547 g010
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated