Bayesian Estimations of Shannon Entropy and Rényi Entropy of Inverse Weibull Distribution

1. Introduction

Information is an abstract concept. In the face of a large amount of data, it is easy to know how much data there is, but it is not clear how much information this data contain. Entropy is one of the important terms in physics. Shannon [1] introduced the concept of entropy into statistics, which represents the uncertainty of events. This entropy is generally called “Shannon entropy”. Generally speaking, when we hear a message within expectation, we think it contains less information. When we hear an unexpected message, we think that the amount of information it conveys to us is huge. In statistics, the probability is usually used to describe the uncertainty of an event. Therefore, Shannon believes that probability can be used to describe the amount of information contained in an event. After that, Alred Rényi [2] generalized Shannon entropy and put forward the concept of Rényi entropy. Since then, the study of entropy has attracted a lot of attention [3,4]. For example, Chacko and Asha [5] considered the maximum likelihood (ML) estimation and Bayesian estimation of Shannon entropy for generalized exponential distribution by the importance sampling method based on record values. Liu and Gui [6] considered the ML estimation and Bayesian estimation of Shannon entropy for two-parameter Lomax distribution by the Lindley method and the Tierney-Kadane method under a generalized progressively hybrid censoring test. Shrahili et al. [7] considered the estimation of entropy of Log-Logistic distribution. The estimations of different entropy functions are obtained by the ML method, and the approximate confidence intervals are obtained by using various censoring methods and sample sizes. Mahmoud et al. [8] considered the estimation of entropy and residual entropy of two-parameter Lomax distribution based on the generalized type-II hybrid censoring scheme. The ML estimators and Bayesian estimators of entropy and residual entropy are obtained. The simulation study of estimating performance under different sample sizes is described. Finally, the conclusion is discussed. Hassan and Mazen [9] estimated three entropy measures for the inverse Weibull distribution using progressively Type-II censored data, which are Shannon entropy, Rényi entropy, and q-entropy. The method of maximum likelihood and maximum product of spacing are used to estimate them. Mavis et al. [10] proposed and studied gamma-inverse Weibull distribution, and some mathematical properties were given including moments, mean deviations, Bonferroni and Lorenz curves, and entropies. Basheer [11] introduced a new generalized alpha power inverse Weibull distribution, and the Shannon entropy and Rényi entropy were obtained. Valeriia and Broderick [12] proposed the weighted inverse Weibull class of distributions and derived the expressions of Shannon entropy and Rényi entropy.

In 1982, Keller and Kamath [13] introduced the Inverse Weibull Distribution (IWD) to model the degradation of mechanical components of diesel engines. It is a useful lifetime probability distribution, and it can be used to represent various failure characteristics. Depending on the value of the shape parameter of the IWD, the risk function can be changed flexibly. The use of IWD for data fitting is therefore more appropriate in many cases. For example, Abhijit and Anindya [14] found that the use of IWD was superior to previous normal models when measuring concrete structures using ultrasonic pulse velocities. Chiodo et al. [15] proposed a new model generated from an appropriate mixture of IWD for modeling extreme wind speed scenarios. Langlands et al. [16] observed that breast cancer mortality data could be analyzed using IWD for modeling analysis. That is why two-parameter IWD has attracted more and more researchers to pay attention to and discuss in recent years [17,18]. For example, Asuman and Mahmut [19] considered the classical and Bayesian estimation of parameters and the reliability function of the IWD. In classical estimation, they derived the ML estimators and modified ML estimators. In Bayesian estimation, they utilized the Lindley method to calculate the Bayesian estimators of parameters under symmetric and asymmetric loss functions. Sultan et al. [20] discussed the estimation of parameters of IWD based on the progressive type-II censored sample. They put forward an approximate maximum likelihood method to obtain the ML estimator and used Lindley's approximation to obtain the Bayesian estimators. Amirzadi et al. [21] considered the Bayesian estimation of scale parameter and reliability in the inverse generalized Weibull distribution. In addition to general entropy, squared log error, and weight squared error function. They introduced a new loss function to carry out Bayesian estimation. Peng and Yan [22] studied the Bayesian estimation and prediction for shape and scale parameters of the IWD under a general progressive censoring test. Sindhu et al. [23] assumed different priors and loss functions, and discussed the Bayesian estimation of inverse Weibull mixture distributions based on doubly censored data. Mohammad and Sana [24] obtained the Bayes estimators and ML estimators for the unknown parameters of IWD under lower record values. Faud [25] developed a linear exponential loss function, and estimated parameter and reliability of IWD based on lower record values under this loss function. Li and Hao [26] considered the estimation of a stress-strength model when stress and strength are two independent IWDs with different parameters. Ismail and Tamimi [27] proposed a constant stress partially accelerated life test model and analyzed it using type-I censored data from IWD. Kang and Han [28] derived the approximate maximum likelihood estimators of parameters of IWD under multiply type-II censoring and also proposed a simple graphical method for a goodness-on-fit test. Saboori et al. [29] introduced generalized modified inverse Weibull distribution, and some statistical and probabilistic properties were derived.

This paper will consider the Bayesian estimation of Shannon entropy and Rényi entropy of two-parameter IWD based on complete samples. In Section 2, some related knowledge is introduced first, and then the specific expressions of Shannon entropy and Rényi entropy of two-parameter IWD are derived. In Section 3, the maximum likelihood estimators of the scale parameter and shape parameter of IWD are derived by the dichotomy method, and then the ML estimators of Shannon entropy and Rényi entropy are obtained. In Section 4, the gamma distribution is adopted as the prior distribution (PD) of the scale parameter. A non-informative PD is adopted as the PD of the shape parameter. And then the Bayesian estimators of Shannon entropy and Rényi entropy are obtained based on the symmetric entropy loss function and scale squared error loss function. Lindley approximation is used to achieve the numerical calculation of the Bayesian estimators of entropy, on account of the complexity of these Bayesian estimators. In Section 5, Monte Carlo simulations are utilized to simulate and compare the estimators that are mentioned above. In Section 6, a real data set has been analyzed for illustrative purposes. Finally, the conclusions of the article are given in Section 7.

2. Preliminary Knowledge

The probability density function (pdf) of two-parameter IWD is defined as Eq. (1).

$$f(t;\omega ,\upsilon )=\omega \upsilon t^{-\upsilon -1}\exp (-\omega t^{-\upsilon }),\omega >0,\upsilon >0,t>0$$

(1)

and the cumulative distribution function (cdf) of two-parameter IWD is defined as Eq. (2)

$$F(t;\omega ,\upsilon )=\exp (-\omega t^{-\upsilon }),\omega >0,\upsilon >0,t>0$$

(2)

where the scale parameter is $\omega$, and the shape parameter is $\upsilon$.

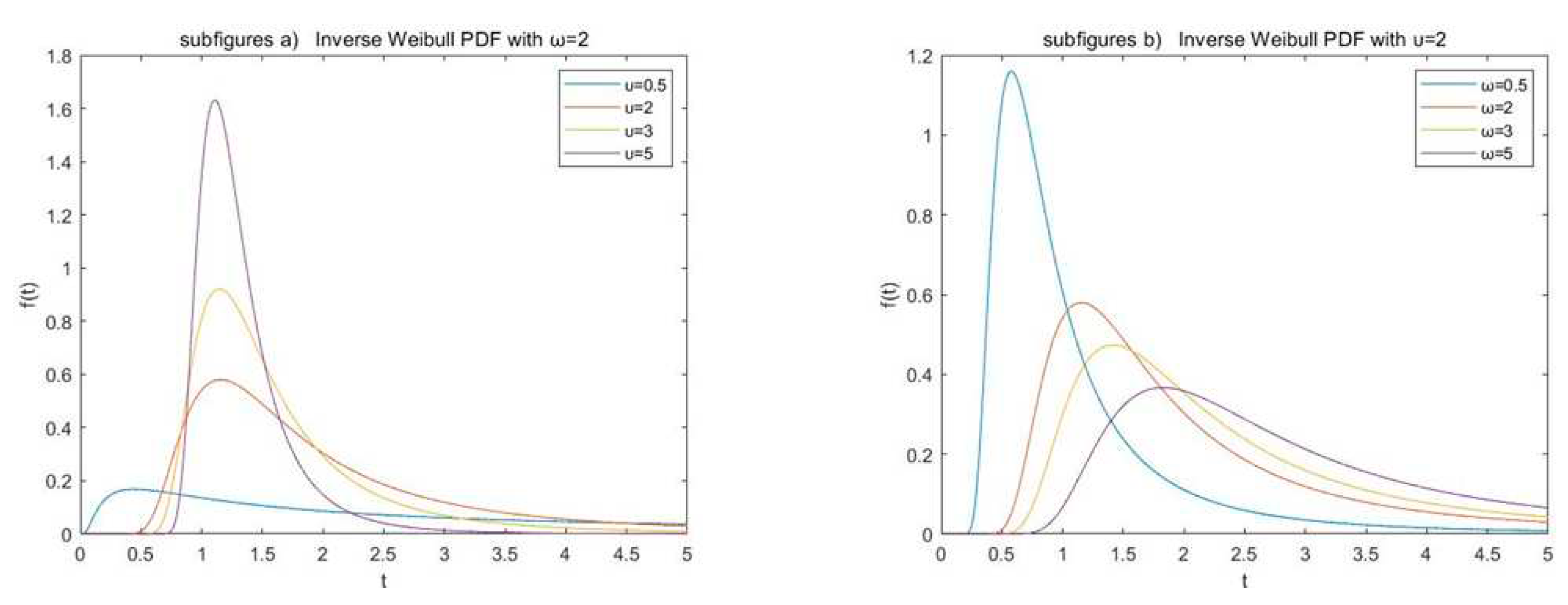
Figure 1 shows the pdf of IWD under different values of shape and scale parameters, respectively.

The Shannon entropy is defined in Equation (Eq. 3) [1]

$$H_s(t)=-{\displaystyle {\int }_{-\infty }^{+\infty }f(t)\ln [f(t)]}dt$$

(3)

and the Rényi entropy is defined in Equation (Eq. 4) [2]

$$H_r(t)=\frac{1}{1-r}\ln {\displaystyle {\int }_{-\infty }^{+\infty }{f}^r(t)}dt,r>0,r\ne 1,$$

(4)

where $f(t)$ is the pdf of a continuous random variable $T$.

Theorem 1.

Let$T_1,T_2,\mathrm{...},T_n$is a random sample that follows IWD with the pdf (1),$t_1,t_2,\mathrm{...},t_n$are the sample observations of$T_1,T_2,\mathrm{...},T_n$.

(i) Shannon entropy of IWD is showed in Eq. (5)

$$H_s=\frac{\upsilon +1}{\upsilon }(\ln \omega +\gamma )-\ln \omega \upsilon +1$$

(5)

(ii) Rényi entropy of IWD is showed in Eq. (6)

$$H_r=\frac{1}{1-r}[-\frac{r\upsilon +r}{\upsilon }\ln r+\frac{r}{\upsilon }\ln \omega +r\ln \upsilon +\ln \mathsf{\Gamma }(r+\frac{r}{\upsilon }+1)]$$

(6)

where $\mathsf{\Gamma }(\cdot )$the gamma function and $\gamma$ is Euler constant.

Proof. The log density of pdf (1) of IWD is showed in Eq. (7)

$$\ln [f(t)]=\ln \omega \upsilon -(\upsilon +1)\ln t-\omega t^{-\upsilon }$$

(7)

According to the log-density function (7), and Eq. (3), the Shannon entropy of IWD can be derived as follows:

$$\begin{array}{c}{H}_s=-{\displaystyle {\int }_0^{+\infty }f(t)[\ln \omega \upsilon -(\upsilon +1)\ln t-\omega t^{-\upsilon }]}dt\\ =-(\ln \omega \upsilon ){\displaystyle {\int }_0^{+\infty }f(t)}dt+(\upsilon +1){\displaystyle {\int }_0^{+\infty }f(t)\ln t}dt+\omega {\displaystyle {\int }_0^{+\infty }{t}^{-\upsilon }f(t)}dt\\ =-\ln \omega \upsilon +(\upsilon +1)E(\ln T)+\omega E(T^{-\upsilon })\end{array}$$

(8)

Obviously,

$$\begin{array}{c}E(T^c)={\displaystyle {\int }_0^{+\infty }\omega \upsilon t^c{t}^{-\upsilon -1}{e}^{-\omega t^{-\upsilon }}}dt\\ ={\omega }^{\frac{t}{\upsilon }}{\displaystyle {\int }_0^{+\infty }{(\omega t^{-\upsilon })}^{-\frac{c}{\upsilon }}{e}^{-\omega t^{-\upsilon }}}d(\omega t^{-\upsilon })\\ ={\omega }^{\frac{c}{\upsilon }}\mathsf{\Gamma }(1-\frac{c}{\upsilon })\end{array}$$

(9)

Let $c=-\upsilon$,

$$E(T^{-\upsilon })={\omega }^{-1}\mathsf{\Gamma }(2)=\frac{1}{\omega }$$

Because

$$\begin{array}{c}E(T^c\ln T)=\frac{dE(T^c)}{dc}\\ =\frac{1}{\upsilon }{\omega }^{\frac{c}{\upsilon }}\mathsf{\Gamma }(1-\frac{c}{\upsilon })\ln \omega -\frac{1}{\upsilon }{\omega }^{\frac{c}{\upsilon }}{\mathsf{\Gamma }}^{\prime }(1-\frac{c}{\upsilon })\\ =\frac{1}{\upsilon }{\omega }^{\frac{c}{\upsilon }}[\mathsf{\Gamma }(1-\frac{c}{\upsilon })\ln \omega -{\mathsf{\Gamma }}^{\prime }(1-\frac{c}{\upsilon })].\end{array}$$

Let $c=0$,

$$E(\ln T)=\frac{1}{\upsilon }(\ln \omega +\gamma )$$

Therefore, Shannon entropy of two-parameter IWD can be expressed as

$$\begin{array}{c}{H}_s=-\ln \omega \upsilon +(\upsilon +1)E(\ln T)+\omega E(T^{-\upsilon })\\ =\frac{\upsilon +1}{\upsilon }(\ln \omega +\gamma )-\ln \omega \upsilon +1\end{array}$$

Obviously,

$$\begin{array}{c}{\displaystyle {\int }_{-\infty }^{+\infty }{f}^r(t)}dt={\displaystyle {\int }_0^{+\infty }{(\omega \upsilon t^{-\upsilon -1}{e}^{-\omega t^{-\upsilon }})}^r}dt\\ ={(\omega \upsilon )}^r{\displaystyle {\int }_0^{+\infty }{t}^{-r\upsilon -r}{e}^{-r\omega t^{-\upsilon }}}dt\\ =r^{\frac{-r\upsilon -r}{\upsilon }}{\omega }^{\frac{r}{\upsilon }}{\upsilon }^r\mathsf{\Gamma }(1+\frac{r+r\upsilon }{\upsilon })\end{array}$$

Then, according to Eq. (4), the Rényi entropy of two-parameter IWD can be expressed as

$$H_r=\frac{1}{1-r}[\frac{-r\upsilon -r}{\upsilon }\ln r+\frac{r}{\upsilon }\ln \omega +r\ln \upsilon +\ln \mathsf{\Gamma }(1+\frac{r\upsilon +r}{\upsilon })]$$

3. Maximum Likelihood Estimation

Suppose that $T_1,T_2,\mathrm{...},T_n$ is a random sample that follows IWD with the pdf (1), $t_1,t_2,\mathrm{...},t_n$ are the sample observations of $T_1,T_2,\mathrm{...},T_n$. Thus, the likelihood function (LF) can be derived as Eq. (8)

$$s(t;\omega ,\upsilon )={\omega }^n{\upsilon }^n({\displaystyle \prod _{i=1}^n{t}_i^{-\upsilon -1}})\exp (-\omega {\displaystyle \sum _{i=1}^n{t}_i^{-\upsilon }})$$

(8)

Then, the corresponding log LF of Eq. (8) is showed in Eq. (9)

$$S(t;\omega ,\upsilon )=\ln s(t;\omega ,\upsilon )=n\ln \omega \upsilon -(\upsilon +1){\displaystyle \sum _{i=1}^n\ln t_i}-\omega {\displaystyle \sum _{i=1}^n{t}_i^{-\upsilon }}$$

(9)

For convenience, we denote $S(t;\omega ,\upsilon )$ as $S$. Thus, the likelihood equations can be expressed respectively as Eq. (10) and Eq. (11)

$$\frac{\partial S}{\partial \omega }=\frac{n}{\omega }-{\displaystyle \sum _{i=1}^n{t}_i^{-\upsilon }}=0$$

(10)

$$\frac{\partial S}{\partial \upsilon }=\frac{n}{\upsilon }-{\displaystyle \sum _{i=1}^n\ln t_i}+\omega {\displaystyle \sum _{i=1}^n{t}_i^{-\upsilon }\ln t_i}=0$$

(11)

The ML estimators $\widehat{\omega }$ and $\widehat{\upsilon }$ can be obtained by solving Eq. (10) and Eq. (11) with dichotomy, whose calculation steps are listed as follows:

(i) According to Eq. (10) and Eq. (11), there are

$$\widehat{\omega }=n{({\displaystyle \sum _{i=1}^n{t}_i^{-\widehat{\upsilon }}})}^{-1}$$

$$\frac{n}{\upsilon }-{\displaystyle \sum _{i=1}^n\ln t_i}+n{({\displaystyle \sum _{i=1}^n{t}_i^{-\upsilon }})}^{-1}{\displaystyle \sum _{i=1}^n{t}_i^{-\upsilon }\ln t_i}=0$$

(13)

(ii) Denote $y(\upsilon )=\frac{n}{\upsilon }-{\displaystyle \sum _{i=1}^n\ln t_i}+n{({\displaystyle \sum _{i=1}^n{t}_i^{-\upsilon }})}^{-1}{\displaystyle \sum _{i=1}^n{t}_i^{-\upsilon }\ln t_i}$, given the accuracy $\epsilon$, determine the interval $[{\upsilon }_u,{\upsilon }_l]$ and verify $y({\upsilon }_u)\cdot y({\upsilon }_l)<0$.

(iii) Find the midpoint ${\upsilon }_m$ of the interval $[{\upsilon }_u,{\upsilon }_l]$ and calculate $y({\upsilon }_m)$.

(iv) If $y({\upsilon }_m)=0$, $\widehat{\upsilon }={\upsilon }_m$.

(v) If $y({\upsilon }_u)\cdot y({\upsilon }_m)<0$, ${\upsilon }_l={\upsilon }_m$; If $y({\upsilon }_l)\cdot y({\upsilon }_m)<0$, ${\upsilon }_u={\upsilon }_m$.

(vi) If $|{\upsilon }_u-{\upsilon }_l|<\epsilon$, $\widehat{\upsilon }$ is equal to ${\upsilon }_u$ or ${\upsilon }_l$. If not, return to step (iii) to step (vi).

Due to the invariance of ML estimation, the ML estimators of Shannon entropy and Rényi entropy can be obtained by putting $\widehat{\omega }$ and $\widehat{\upsilon }$ into Eq. (3) and Eq. (4), and their mathematical expressions are showed in Eq. (14) and Eq. (15)

$${\widehat{H}}_{s1}=\frac{\widehat{\upsilon }+1}{\widehat{\upsilon }}(\ln \widehat{\omega }+\gamma )-\ln \widehat{\omega }\widehat{\upsilon }+1$$

(14)

$${\widehat{H}}_{r1}=\frac{1}{1-r}[\frac{-r\widehat{\upsilon }-r}{\widehat{\upsilon }}\ln r+\frac{r}{\widehat{\upsilon }}\ln \widehat{\omega }+r\ln \widehat{\upsilon }+\ln \mathsf{\Gamma }(1+\frac{r\widehat{\upsilon }+r}{\widehat{\upsilon }})]$$

(15)

Next, the Delta method is used to derive the approximate confidence intervals (briefly, ACIs) of Shannon entropy and Rényi entropy.

Denote vector$D_s$and$D_r$as

$$D_s=(\frac{\partial H_s}{\partial \omega },\frac{\partial H_s}{\partial \upsilon })|{ }_{\omega =\widehat{\omega },\upsilon =\widehat{\upsilon }}$$

(16)

$$D_r=(\frac{\partial H_r}{\partial \omega },\frac{\partial H_r}{\partial \upsilon })|{ }_{\omega =\widehat{\omega },\upsilon =\widehat{\upsilon }}$$

(17)

in which$D_s$and$D_r$are calculated through Eq. (18) and Eq. (19).

$$\frac{\partial H_s}{\partial \omega }=\frac{1}{\omega \upsilon },\frac{\partial H_s}{\partial \upsilon }=\frac{-\gamma -\ln \omega }{{\upsilon }^2}-\frac{1}{\upsilon }$$

(18)

$$\frac{\partial H_r}{\partial \omega }=\frac{r}{(1-r)\omega \upsilon },\frac{\partial H_r}{\partial \upsilon }=\frac{r}{(1-r)\upsilon }[1+\frac{\ln r-\ln \omega }{\upsilon }-\frac{{\mathsf{\Gamma }}^{\prime }(1+r+r{\upsilon }^{-1})}{\upsilon \mathsf{\Gamma }(1+r+r{\upsilon }^{-1})}]$$

(19)

According to the Delta method, calculate the estimated variance of${\widehat{H}}_{s1}$and${\widehat{H}}_{r1}$as Eq. (20) and Eq. (21).$I$is the Fisher information matrix of$\omega$and$\upsilon$, and Eq. (22) gives the elements of$I$. $I^{-1}$is the inverse matrix of$I$.

$$V_s=D_s{I}^{-1}{D}_s^{\mathrm{T}}|{ }_{\omega =\widehat{\omega },\upsilon =\widehat{\upsilon }}$$

(20)

$$V_r=D_r{I}^{-1}{D}_r^{\mathrm{T}}|{ }_{\omega =\widehat{\omega },\upsilon =\widehat{\upsilon }}$$

(21)

$$\begin{array}{l}\frac{{\partial }^{2}S}{\partial {\omega }^2}=-\frac{n}{{\omega }^2},\frac{{\partial }^{2}S}{\partial \omega \partial \upsilon }=\frac{{\partial }^{2}S}{\partial \upsilon \partial \omega }={\displaystyle \sum _{i=1}^n{t}_i^{-\upsilon }\ln t_i}\\ \frac{{\partial }^{2}S}{\partial {\upsilon }^2}=-\frac{n}{{\upsilon }^2}-\omega {\displaystyle \sum _{i=1}^n{t}_i^{-\upsilon }{(\ln t_i)}^2}\end{array}$$

(22)

Then, the$100(1-\alpha )\%$ACI of Shannon entropy is Eq. (23), and the$100(1-\alpha )\%$ACI of Rényi entropy is Eq. (24), where$z_{\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$is the upper ($\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$2$}\right.$)th quantile of the standardized normal distribution.

$$({\widehat{H}}_{s1}-z_{\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\sqrt{V_s},{\widehat{H}}_{s1}+z_{\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\sqrt{V_s})$$

(23)

$$({\widehat{H}}_{r1}-z_{\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\sqrt{V_r},{\widehat{H}}_{r1}+z_{\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\sqrt{V_r})$$

(24)

4. Bayesian Estimation

Bayesian estimation is a method of introducing prior information to deal with decision problems. The advantage is that it can include the prior information in statistical inference and improve the accuracy of the taken decision. From the time when Bayesian estimation was proposed to now, many researchers have adopted this method in estimating parameters and related functions. For example, Kundu and Howlader [30] considered the Bayesian inference and prediction of inverse Weibull distribution, based on type-II censored data. A Gibbs sampling procedure was used for MCMC samples, and Bayes estimation was computed by this sample. Sultan et al. [31] considered the Bayesian estimation of inverse Weibull parameters based on progressive type-II censored data. Because the Bayes estimators can’t be obtained explicitly, the Lindley approximation was used to calculate them. Mohammad and Mina [32] presented the Bayesian inferences of parameters of inverse Weibull distribution based on type-I hybrid censored data and computed the Bayes estimates using Lindley approximation. Algarni et al. [33] considered the Bayes estimation of parameters for the inverse Weibull distribution employing a progressive type-I censored sample. Metropolis-Hasting (MH) algorithm was used to compute the Bayesian estimates.

In addition to the areas mentioned above, there are some recent applications of the Bayesian method. Zhou and Luo [34] developed a supplier's recursive multiperiod discounted profit model based on Bayesian information updating. Yulin et al. [35] put forward a Bayesian approach to tackle the misalignments for over-the-air computation. Taborsky et al. [36] presented a novel generic Bayesian probabilistic model to solve the problem of parameters marginalization under the constraint of forced community structure. Oliver [37] introduced the Bayesian toolkit and showed how geomorphic models might benefit from probabilistic concepts. Ran et al. [38] proposed a Bayesian approach to measure the loss of privacy in a mechanism. Luo et al. [39] used the Bayesian information criterion for model selection when revisiting the lifetime data of brake pads. Peng et al. [40] extended a general Bayesian framework to deal with the degradation analysis of sparse degradation observations and evolving observations. František et al. [41] illustrated Bayesian estimation of how to benefit parametric survival analysis. Liu et al. [42] proposed fuzzy Bayesian knowledge tracing models to address continuous score scenarios.

In this paper, the Bayesian estimations of Shannon entropy and Rényi entropy of IWD are investigated under symmetric entropy (SE) and scale squared error (SSE) loss functions, which are widely used in Bayesian statistical inference [43,44,45].

(i) SE loss function is defined in Equation (Eq. 25) [43]

$$L_1(H,\widehat{H})=\frac{H}{\widehat{H}}+\frac{\widehat{H}}{H}-2$$

(25)

where $\widehat{H}$ is the estimator of $H$.

Lemma 1. Suppose that $T$ is the historical data information about the entropy function $H$. Then, under the SE loss function (25), the Bayesian estimator ${\widehat{H}}_1$ for any prior distribution is showed in Eq. (26)

$${\widehat{H}}_1={[\frac{E(H|T)}{E(H^{-1}|T)}]}^{\frac{1}{2}}$$

(26)

where $E(H|T)$ is the posterior expectation of $H$and $E(H^{-1}|T)$ is the posterior expectation of $H^{-1}$.

Proof. Under the SE loss function (25), the Bayesian risk of $\widehat{H}$ is

$$R(\widehat{H})=E_H(E(L_1(H,\widehat{H})|T))$$

To minimize $R(\widehat{H})$, only need to minimize $E(L_1(H,\widehat{H})|T)$. For convenience, let$g(\widehat{H})=E(L_1(H,\widehat{H})|T)$.

Because

$$g(\widehat{H})={\widehat{H}}^{-1}E(H|T)+\widehat{H}E(H^{-1}|T)-2$$

and the derivative is

$$g^{\prime }(\widehat{H})=-{\widehat{H}}^{-2}E(H|T)+E(H^{-1}|T)$$

The Bayesian estimator ${\widehat{H}}_1$ can be obtained by $g^{\prime }(\widehat{H})=0$.

(ii) SSE loss function is defined in Equation (Eq. 27) [45]

$$L_2(H,\widehat{H})=\frac{{(H-\widehat{H})}^2}{H^k}$$

(27)

where $k$ is a nonnegative integer.

Lemma 2. Suppose that  $T$ is the historical data information about the entropy function $H$. Then, under the SSE loss function (27), the Bayesian estimator ${\widehat{H}}_2$ for any prior distribution is

$${\widehat{H}}_2=\frac{E(H^{1-k}|T)}{E(H^{-k}|T)}$$

(28)

where $E(H^{1-k}|T)$ is the posterior expectation of $H^{1-k}$and $E(H^{-k}|T)$ is the posterior expectation of $H^{-k}$.

Proof. Under the SSE loss function (27), the Bayesian risk of $\widehat{H}$ is

$$R(\widehat{H})=E_H(E(L_2(H,\widehat{H})|T))$$

To minimize $R(\widehat{H})$, only need to minimize $E(L_2(H,\widehat{H})|T)$. Similarly, let $h(\widehat{H})=E(L_2(H,\widehat{H})|T)$.

Because

$$\begin{array}{c}h(\widehat{H})=E(\frac{H^2-2H\widehat{H}+{\widehat{H}}^2}{H^k}|T)\\ =E(H^{2-k}|T)-2\widehat{H}E(H^{1-k}|T)+{\widehat{H}}^{2}E(H^{-k}|T)\end{array}$$

and the derivative of $h(\widehat{H})$ is

$$h^{\prime }(\widehat{H})=-2E(H^{1-k}|T)+2\widehat{H}E(H^{-k}|T)$$

The Bayes estimator ${\widehat{H}}_2$ can be obtained by $h^{\prime }(\widehat{H})=0$.

Assume that the scale parameter $\omega$ and shape parameter $\upsilon$ of two-parameter IWD are independent random variables, which $\omega$ obey $\mathsf{\Gamma }(a,b)$ and $\upsilon$ obey non-informative PD as follows:

$$P_1(\omega )=\frac{a^b}{\mathsf{\Gamma }(b)}{\omega }^{b-1}{e}^{-a\omega },a>0,b>0$$

(29)

$$P_2(\upsilon )\propto \frac{1}{\upsilon }$$

(30)

Thus, the joint PD of $\omega$ and $\upsilon$ is

$$P(\omega ,\upsilon )\propto \frac{a^b}{\upsilon \mathsf{\Gamma }(b)}{\omega }^{b-1}{e}^{-a\omega }$$

(31)

Referring to Bayesian formulation, the posterior distribution of $\omega$ and $\upsilon$ is

$$P(\omega ,\upsilon |T)=\frac{P(\omega ,\upsilon )s(t;\omega ,\upsilon )}{{\displaystyle {\int }_0^{+\infty }{\displaystyle {\int }_0^{+\infty }P(\omega ,\upsilon )s(t;\omega ,\upsilon )}}d\omega d\upsilon }$$

(32)

Thus, the Bayesian estimators of Shannon entropy and Rényi entropy under SE can be expressed as

$${\widehat{H}}_{s2}={[\frac{E(H_s|T)}{E(H_s^{-1}|T)}]}^{\frac{1}{2}}={[\frac{{\displaystyle {\int }_0^{+\infty }{\displaystyle {\int }_0^{+\infty }{H}_{s}P(\omega ,\upsilon |T)}}d\omega d\upsilon }{{\displaystyle {\int }_0^{+\infty }{\displaystyle {\int }_0^{+\infty }{H}_s{ }^{-1}P(\omega ,\upsilon |T)}}d\omega d\upsilon }]}^{\frac{1}{2}}$$

(33)

$${\widehat{H}}_{r2}={[\frac{E(H_r|T)}{E(H_r^{-1}|T)}]}^{\frac{1}{2}}={[\frac{{\displaystyle {\int }_0^{+\infty }{\displaystyle {\int }_0^{+\infty }{H}_{r}P(\omega ,\upsilon |T)}}d\omega d\upsilon }{{\displaystyle {\int }_0^{+\infty }{\displaystyle {\int }_0^{+\infty }{H}_r^{-1}P(\omega ,\upsilon |T)}}d\omega d\upsilon }]}^{\frac{1}{2}}$$

(34)

The Bayesian estimators of Shannon entropy and Rényi entropy under SSE can be expressed as

$${\widehat{H}}_{s3}=\frac{E(H_s^{1-k}|T)}{E(H_s^{-k}|T)}=\frac{{\displaystyle {\int }_0^{+\infty }{\displaystyle {\int }_0^{+\infty }{H}_s^{1-k}P(\omega ,\upsilon |T)}}d\omega d\upsilon }{{\displaystyle {\int }_0^{+\infty }{\displaystyle {\int }_0^{+\infty }{H}_s^{-k}P(\omega ,\upsilon |T)}}d\omega d\upsilon }$$

(35)

$${\widehat{H}}_{r3}=\frac{E(H_r^{1-k}|T)}{E(H_r^{-k}|T)}=\frac{{\displaystyle {\int }_0^{+\infty }{\displaystyle {\int }_0^{+\infty }{H}_r^{1-k}P(\omega ,\upsilon |T)}}d\omega d\upsilon }{{\displaystyle {\int }_0^{+\infty }{\displaystyle {\int }_0^{+\infty }{H}_r^{-k}P(\omega ,\upsilon |T)}}d\omega d\upsilon }$$

(36)

From Eq. (33) to Eq. (36), it can be seen that the calculation of Bayesian estimators of Shannon and Rényi entropy are complex and difficult to calculate. Thus, Lindley approximation will be employed to achieve the approximate calculation results of ${\widehat{H}}_{s3}$ and ${\widehat{H}}_{r3}$.

4.1. Bayesian Estimation by using Lindley approximation under SE loss function

Referring to Lindley approximation, $I(t)$ can be defined as

$$I(t)=E[U(\omega ,\upsilon )|T]=\frac{{\displaystyle \int U(\omega ,\upsilon )e^{S(t;\omega ,\upsilon )+G(\omega ,\upsilon )}}d(\omega ,\upsilon )}{{\displaystyle \int e^{S(t;\omega ,\upsilon )+G(\omega ,\upsilon )}}d(\omega ,\upsilon )}$$

(37)

where $U(\omega ,\upsilon )$ is a function of independent variables $\omega$ and $\upsilon$, $S(t;\omega ,\upsilon )$ is log LF defined in Eq. (9), $G(\omega ,\upsilon )$ is the log of joint PD defined in Eq. (31).

If the sample size is large, Eq. (37) can be expressed as

$$I(t)=U(\widehat{\omega },\widehat{\upsilon })+\frac{1}{2}(A+B+C+D)$$

(38)

where $\widehat{\omega }$ and $\widehat{\upsilon }$ are the ML estimators of $\omega$ and $\upsilon$, and

$$\begin{array}{l}A=({\widehat{U}}_{\omega \omega }+2{\widehat{U}}_{\omega }{\widehat{G}}_{\omega }){\widehat{\sigma }}_{\omega \omega }+({\widehat{U}}_{\upsilon \omega }+2{\widehat{U}}_{\upsilon }{\widehat{G}}_{\omega }){\widehat{\sigma }}_{\upsilon \omega }\\ B=({\widehat{U}}_{\omega \upsilon }+2{\widehat{U}}_{\omega }{\widehat{G}}_{\upsilon }){\widehat{\sigma }}_{\omega \upsilon }+({\widehat{U}}_{\upsilon \upsilon }+2{\widehat{U}}_{\upsilon }{\widehat{G}}_{\upsilon }){\widehat{\sigma }}_{\upsilon \upsilon }\\ C=({\widehat{U}}_{\omega }{\widehat{\sigma }}_{\omega \omega }+{\widehat{U}}_{\upsilon }{\widehat{\sigma }}_{\omega \upsilon })({\widehat{S}}_{\omega \omega \omega }{\widehat{\sigma }}_{\omega \omega }+{\widehat{S}}_{\omega \upsilon \omega }{\widehat{\sigma }}_{\omega \upsilon }+{\widehat{S}}_{\upsilon \omega \omega }{\widehat{\sigma }}_{\upsilon \omega }+{\widehat{S}}_{\upsilon \upsilon \omega }{\widehat{\sigma }}_{\upsilon \upsilon })\\ D=({\widehat{U}}_{\omega }{\widehat{\sigma }}_{\upsilon \omega }+{\widehat{U}}_{\upsilon }{\widehat{\sigma }}_{\upsilon \upsilon })({\widehat{S}}_{\omega \omega \upsilon }{\widehat{\sigma }}_{\omega \omega }+{\widehat{S}}_{\omega \upsilon \upsilon }{\widehat{\sigma }}_{\omega \upsilon }+{\widehat{S}}_{\upsilon \omega \upsilon }{\widehat{\sigma }}_{\upsilon \omega }+{\widehat{S}}_{\upsilon \upsilon \upsilon }{\widehat{\sigma }}_{\upsilon \upsilon })\end{array}$$

(39)

${\sigma }_{ij}$($i,j=\omega ,\upsilon$) is the element of inverse matrix of $-S_{ij}$.

The ${\widehat{U}}_{\omega \omega }$ is denoted that taking the second derivative of $U(\omega ,\upsilon )$ with respect to $\omega$ and putting $\widehat{\omega }$ into it. Similarly, others can be expressed as

$$\begin{array}{l}{S}_{\omega \omega \upsilon }=S_{\omega \upsilon \omega }=S_{\upsilon \omega \omega }=0,S_{\omega \omega \omega }=\frac{3n}{{\omega }^3}\\ S_{\omega \upsilon \upsilon }=S_{\upsilon \omega \upsilon }=S_{\upsilon \upsilon \omega }=-{\displaystyle \sum _{i=1}^n{t}_i^{-\upsilon }\ln t_i},S_{\upsilon \upsilon \upsilon }=\frac{2n}{{\upsilon }^3}+\omega {\displaystyle \sum _{i=1}^n{t}_i^{-\upsilon }{(\ln t_i)}^3}\\ G_{\omega }=\frac{b-1}{\omega }-a,G_{\upsilon }=\frac{1}{\upsilon }\end{array}$$

(40)

Under the SE loss function, the step of numerical calculation of Shannon entropy ${\widehat{H}}_{s2}$ by Lindley approximation is shown as follows:

When $U(\omega ,\upsilon )=H_s$,

$$\begin{array}{l}{U}_{\omega }=\frac{1}{\omega \upsilon },U_{\upsilon }=\frac{-\gamma -\ln \omega }{{\upsilon }^2}-\frac{1}{\upsilon }\\ U_{\omega \omega }=-\frac{1}{{\omega }^2\upsilon },U_{\upsilon \upsilon }=\frac{2\ln \omega +2\gamma }{{\upsilon }^3}+\frac{1}{{\upsilon }^2},U_{\omega \upsilon }=U_{\upsilon \omega }=-\frac{1}{\omega {\upsilon }^2}\end{array}$$

(41)

Put Eq. (40) and Eq. (41) into Eq. (38), $E(H_s|T)$ is obtained.

$$\begin{array}{l}{U}_{\omega }=-H_s^{-2}\frac{1}{\omega \upsilon },U_{\upsilon }=H_s^{-2}(\frac{\gamma +\ln \omega }{{\upsilon }^2}+\frac{1}{\upsilon })\\ U_{\omega \omega }=2H_s^{-3}\frac{1}{{\omega }^2{\upsilon }^2}+H_s^{-2}\frac{1}{{\omega }^2\upsilon }\\ U_{\upsilon \upsilon }=2H_s^{-3}{(\frac{-\gamma -\ln \omega }{{\upsilon }^2}-\frac{1}{\upsilon })}^2-H_s^{-2}(\frac{2\ln \omega +2\gamma }{{\upsilon }^3}+\frac{1}{{\upsilon }^2})\\ U_{\omega \upsilon }=U_{\upsilon \omega }=2H_s^{-3}(\frac{-\gamma -\ln \omega }{\omega {\upsilon }^3}-\frac{1}{\omega {\upsilon }^2})+H_s^{-2}\frac{1}{\omega {\upsilon }^2}\end{array}$$

(42)

Similarly, when $U(\omega ,\upsilon )=H_s{ }^{-1}$,

Then, put Eq. (40) and Eq. (42) into Eq. (38), $E(H_s^{-1}|T)$ is obtained. Thus, the numerical calculation of Shannon entropy ${\widehat{H}}_{s2}$ is calculated by Eq. (33).

Under the SE loss function, the numerical calculation of Rényi entropy ${\widehat{H}}_{r2}$ by Lindley approximation is shown as follows:

When $U(\omega ,\upsilon )=H_r$,

$$\begin{array}{l}{U}_{\omega }=\frac{r}{(1-r)\omega \upsilon },U_{\omega \omega }=\frac{-r}{(1-r){\omega }^2\upsilon },U_{\omega \upsilon }=U_{\upsilon \omega }=\frac{-r}{(1-r)\omega {\upsilon }^2}\\ U_{\upsilon }=\frac{r}{(1-r)\upsilon }[1+\frac{\ln r-\ln \omega }{\upsilon }-\frac{{\mathsf{\Gamma }}^{\prime }(1+r+r{\upsilon }^{-1})}{\upsilon \mathsf{\Gamma }(1+r+r{\upsilon }^{-1})}]\\ U_{\upsilon \upsilon }=\frac{2r(\ln \omega -\ln r)}{(1-r){\upsilon }^3}-\frac{{[{\mathsf{\Gamma }}^{\prime }(1+r+r{\upsilon }^{-1})]}^2-{\mathsf{\Gamma }}^{″}(1+r+r{\upsilon }^{-1})\mathsf{\Gamma }(1+r+r{\upsilon }^{-1})}{(1-r)r^{-2}{\upsilon }^4{[\mathsf{\Gamma }(1+r+r{\upsilon }^{-1})]}^2}-\frac{r}{(1-r){\upsilon }^2}\end{array}$$

(43)

Put Eq. (40) and Eq. (43) into Eq. (38), $E(H_r|T)$ is obtained.

When $U(\omega ,\upsilon )=H_r{ }^{-1}$,

$$\begin{array}{c}{U}_{\omega }=\frac{-r{H}_r^{-2}}{(1-r)\omega \upsilon },U_{\upsilon }=\frac{-r{H}_r^{-2}}{(1-r)\upsilon }[1+\frac{\ln r-\ln \omega }{\upsilon }-\frac{{\mathsf{\Gamma }}^{\prime }(1+r+r{\upsilon }^{-1})}{\upsilon \mathsf{\Gamma }(1+r+r{\upsilon }^{-1})}]\\ U_{\omega \omega }=\frac{2r^2{H}_r^{-3}}{{(1-r)}^2{\omega }^2{\upsilon }^2}+\frac{r{H}_r^{-2}}{(1-r){\omega }^2\upsilon },\\ U_{\omega \upsilon }=U_{\upsilon \omega }=\frac{r^{2}2H_r^{-3}}{{(1-r)}^2\omega {\upsilon }^2}[1+\frac{\ln r-\ln \omega }{\upsilon }-\frac{1}{\upsilon }\frac{{\mathsf{\Gamma }}^{\prime }(1+r+r{\upsilon }^{-1})}{\mathsf{\Gamma }(1+r+r{\upsilon }^{-1})}]\\ U_{\upsilon \upsilon }=\frac{{[{\mathsf{\Gamma }}^{\prime }(1+r+r{\upsilon }^{-1})]}^2-{\mathsf{\Gamma }}^{″}(1+r+r{\upsilon }^{-1})\mathsf{\Gamma }(1+r+r{\upsilon }^{-1})}{(1-r)r^{-2}{\upsilon }^4{[\mathsf{\Gamma }(1+r+r{\upsilon }^{-1})]}^2{H}_r^2}+\frac{r{H}_r^{-2}}{(1-r){\upsilon }^2}-\frac{2r(\ln \omega -\ln r)}{(1-r){\upsilon }^3{H}_r^2}\\ +\frac{2r^2{H}_r^{-3}}{{(1-r)}^2{\upsilon }^2}[1+\frac{\ln r-\ln \omega }{\upsilon }-\frac{{\mathsf{\Gamma }}^{\prime }(1+r+r{\upsilon }^{-1})}{\upsilon \mathsf{\Gamma }(1+r+r{\upsilon }^{-1})}]\end{array}$$

(44)

Put Eq. (40) and Eq. (44) into Eq. (38), $E(H_r^{-1}|T)$ is obtained. Thus, the numerical calculation of Shannon entropy ${\widehat{H}}_{r2}$ is calculated by Eq. (34).

4.2. Bayesian Estimation by using Lindley approximation under SSE loss function

Under the SSE loss function, the step of numerical calculation of Shannon entropy ${\widehat{H}}_{s3}$ by Lindley approximation is shown as follows:

When $U(\omega ,\upsilon )=H_s^{1-k}$,

$$\begin{array}{l}{U}_{\omega }=(1-k)H_s^{-k}\frac{1}{\omega \upsilon },U_{\upsilon }=(1-k)H_s^{-k}(\frac{-\gamma -\ln \omega }{{\upsilon }^2}-\frac{1}{\upsilon })\\ U_{\omega \omega }=-k(1-k)H_s^{-k-1}{(\frac{1}{\omega \upsilon })}^2-(1-k)H_s^{-k}\frac{1}{{\omega }^2\upsilon }\\ U_{\upsilon \upsilon }=k(1-k)H_s^{-k-1}{(\frac{\gamma +\ln \omega }{{\upsilon }^2}+\frac{1}{\upsilon })}^2+(1-k)H_s^{-k}(\frac{2\ln \omega +2\gamma }{{\upsilon }^3}+\frac{1}{{\upsilon }^2})\\ U_{\omega \upsilon }=U_{\upsilon \omega }=k(1-k)H_s^{-k-1}\frac{1}{\omega \upsilon }(\frac{\gamma +\ln \omega }{{\upsilon }^2}+\frac{1}{\upsilon })-(1-k)H_s^{-k}\frac{1}{\omega {\upsilon }^2}\end{array}$$

(45)

Then, putting Eq. (40) and Eq. (45) into Eq. (38), $E(H_s^{1-k}|T)$ is obtained.

When $U(\omega ,\upsilon )=H_s^{-k}$,

$$\begin{array}{l}{U}_{\omega }=-k{H}_s^{-k-1}\frac{1}{\omega \upsilon },U_{\upsilon }=k{H}_s^{-k-1}(\frac{\gamma +\ln \omega }{{\upsilon }^2}+\frac{1}{\upsilon })\\ U_{\omega \omega }=k(k+1)H_s^{-k-2}{(\frac{1}{\omega \upsilon })}^2+k{H}_s^{-k-1}\frac{1}{{\omega }^2\upsilon }\\ U_{\upsilon \upsilon }=k(k+1)H_s^{-k-2}{(\frac{-\gamma -\ln \omega }{{\upsilon }^2}-\frac{1}{\upsilon })}^2-k{H}_s^{-k-1}(\frac{2\ln \omega +2\gamma }{{\upsilon }^3}+\frac{1}{{\upsilon }^2})\\ U_{\omega \upsilon }=U_{\upsilon \omega }=k(k+1)H_s^{-k-2}\frac{1}{\omega \upsilon }(\frac{-\gamma -\ln \omega }{{\upsilon }^2}-\frac{1}{\upsilon })+k{H}_s^{-k-1}\frac{1}{\omega {\upsilon }^2}\end{array}$$

(46)

Then, putting Eq. (40) and Eq. (46) into Eq. (38), $E(H_s^{-k}|T)$ is obtained. Thus, the numerical calculation of Shannon entropy ${\widehat{H}}_{s3}$ is calculated by Eq. (35).

Under the SSE loss function, the step of numerical calculation of Rényi entropy ${\widehat{H}}_{r3}$ by Lindley approximation is shown as follows:

When $U(\omega ,\upsilon )=H_r^{1-k}$,

$$\begin{array}{c}{U}_{\omega }=\frac{(1-k)r{H}_r^{-k}}{(1-r)\omega \upsilon },U_{\upsilon }=\frac{(1-k)r{H}_r^{-k}}{(1-r)\upsilon }[1+\frac{\ln r-\ln \omega }{\upsilon }-\frac{{\mathsf{\Gamma }}^{\prime }(1+r+r{\upsilon }^{-1})}{\upsilon \mathsf{\Gamma }(1+r+r{\upsilon }^{-1})}]\\ U_{\omega \omega }=(k-1)[\frac{k{r}^2{H}_r^{-k-1}}{{(1-r)}^2{\omega }^2{\upsilon }^2}+\frac{r{H}_r^{-k}}{(1-r){\omega }^2\upsilon }]\\ U_{\omega \upsilon }=U_{\upsilon \omega }=\frac{k{r}^2{H}_r^{-k-1}(k-1)}{{(1-r)}^2\omega {\upsilon }^2}[1+\frac{\ln r-\ln \omega }{\upsilon }-\frac{{\mathsf{\Gamma }}^{\prime }(1+r+r{\upsilon }^{-1})}{\upsilon \mathsf{\Gamma }(1+r+r{\upsilon }^{-1})}]+\frac{r{H}_r^{-k}(k-1)}{(1-r)\omega {\upsilon }^2}\\ U_{\upsilon \upsilon }=\frac{r^{2}k{H}_r^{-k-1}(k-1)}{{(1-r)}^2{\upsilon }^2}{[1+\frac{\ln r-\ln \omega }{\upsilon }-\frac{{\mathsf{\Gamma }}^{\prime }(1+r+r{\upsilon }^{-1})}{\upsilon \mathsf{\Gamma }(1+r+r{\upsilon }^{-1})}]}^2+\frac{2r(\ln \omega -\ln r)(1-k)}{(1-r){\upsilon }^3{H}_r^k}\\ -\frac{{[{\mathsf{\Gamma }}^{\prime }(1+r+r{\upsilon }^{-1})]}^2-{\mathsf{\Gamma }}^{″}(1+r+r{\upsilon }^{-1})\mathsf{\Gamma }(1+r+r{\upsilon }^{-1})}{(1-r){(1-k)}^{-1}{r}^{-2}{\upsilon }^4{[\mathsf{\Gamma }(1+r+r{\upsilon }^{-1})]}^2{H}_r^k}-\frac{(1-k)H_r^{-k}r}{(1-r){\upsilon }^2}\end{array}$$

(47)

Put Eq. (40) and Eq. (47) into Eq. (38),$E(H_r^{1-k}|T)$is obtained.

When$U(\omega ,\upsilon )=H_r^{-k}$,

$$\begin{array}{c}{U}_{\omega }=-\frac{rk{H}_r^{-k-1}}{(1-r)\omega \upsilon },U_{\upsilon }=\frac{rk{H}_r^{-k-1}}{(1-r)\upsilon }[\frac{{\mathsf{\Gamma }}^{\prime }(1+r+r{\upsilon }^{-1})}{\upsilon \mathsf{\Gamma }(1+r+r{\upsilon }^{-1})}-1-\frac{\ln r-\ln \omega }{\upsilon }]\\ U_{\omega \omega }=\frac{kr}{(1-r){\omega }^2\upsilon }[\frac{r{H}_r^{-k-2}(k-1)}{\upsilon }+H_r^{-k-1}]\\ U_{\omega \upsilon }=U_{\upsilon \omega }=\frac{r^{2}k(k-1)H_r^{-k-2}}{{(1-r)}^2\omega {\upsilon }^2}[1+\frac{\ln r-\ln \omega }{\upsilon }-\frac{{\mathsf{\Gamma }}^{\prime }(1+r+r{\upsilon }^{-1})}{\upsilon \mathsf{\Gamma }(1+r+r{\upsilon }^{-1})}]+\frac{rk{H}_r^{-k-1}}{(1-r)\omega {\upsilon }^2}\\ U_{\upsilon \upsilon }=\frac{r^{2}k(k-1)H_r^{-k-2}}{{(1-r)}^2{\upsilon }^2}{[1+\frac{\ln r-\ln \omega }{\upsilon }-\frac{{\mathsf{\Gamma }}^{\prime }(1+r+r{\upsilon }^{-1})}{\upsilon \mathsf{\Gamma }(1+r+r{\upsilon }^{-1})}]}^2-\frac{2rk(\ln \omega -\ln r)}{(1-r){\upsilon }^3{H}_r^{k+1}}\\ +\frac{{[{\mathsf{\Gamma }}^{\prime }(1+r+r{\upsilon }^{-1})]}^2-{\mathsf{\Gamma }}^{″}(1+r+r{\upsilon }^{-1})\mathsf{\Gamma }(1+r+r{\upsilon }^{-1})}{(1-r)r^{-2}{\upsilon }^4{k}^{-1}{H}_r^{k+1}{[\mathsf{\Gamma }(1+r+r{\upsilon }^{-1})]}^2}+\frac{rk{H}_r^{-k-1}}{(1-r){\upsilon }^2}\end{array}$$

(48)

Put Eq. (40) and Eq. (48) into Eq. (38), $E(H_r^{-k}|T)$ is obtained. Thus, the numerical calculation of Rényi entropy ${\widehat{H}}_{r3}$ is calculated by Eq. (36).

5. Monte Carlo simulation

In this chapter, Monte Carlo simulation is used to generate random samples that obey two-parameter IWD, and repeat 1000 experiments respectively with different sample sizes ($n=10,20,30,40,50,60,70,80,90,100$). The true values of the parameters in the two-parameter IWD are taken as $\omega =1$ and $\upsilon =2$, the parameters of the gamma distribution are taken as $a=5$ and $b=1$, the parameters in SSE are taken as $k=10$, and the parameters of the Rényi entropy are taken as $r=0.5$. Then, the mean squared error (briefly, MSE) is used to compare the performance of each estimator. The results of Shannon entropy are shown in Table 1, and the results of Rényi entropy are shown in Table 2. For showing the performance of $100(1-\alpha )\%$ ACIs, the coverage probability is calculated and the results are shown in Table 3.

For convenience, $H_{s0}$ and $H_{r0}$ represent the true values of Shannon entropy and Rényi entropy, ${\widehat{M}}_{s1}$ and ${\widehat{M}}_{r1}$ represent mean values of 1000 ML estimates of entropy respectively, ${\widehat{M}}_{s2}$ and ${\widehat{M}}_{r2}$ represent mean values of 1000 Bayesian estimates of entropy respectively under SE loss function, ${\widehat{M}}_{s3}$ and ${\widehat{M}}_{r3}$ represent mean values of 1000 Bayesian estimates of entropy respectively under SSE loss function, $MS{E}_{s1}$ and $MS{E}_{r1}$ represent MSEs of ML estimates of entropy respectively, $MS{E}_{s2}$ and $MS{E}_{r2}$ represent MSEs of Bayesian estimates of entropy respectively under SE loss function, $MS{E}_{s3}$ and $MS{E}_{r3}$ represent MSEs of Bayesian estimates of entropy respectively under SSE loss function. The ${\widehat{M}}_{sj}$ and $MS{E}_{sj}$($j=1,2,3$) are calculated by Eq. (49) and Eq. (50), where $m=1000$ and ${\widehat{H}}_{sj,i}$ represents the i-th ML estimate or Bayesian estimate of Shannon entropy. The ${\widehat{M}}_{rj}$ and $MS{E}_{rj}$($j=1,2,3$) are calculated by Eq. (51) and Eq. (52), where $m=1000$ and ${\widehat{H}}_{rj,i}$ represents the i-th ML estimate or Bayesian estimate of Rényi entropy.

$${\widehat{M}}_{sj}=\frac{1}{m}{\displaystyle \sum _{i=1}^m{\widehat{H}}_{sj,i}}$$

(49)

$$MS{E}_{sj}=\frac{1}{m}{\displaystyle \sum _{i=1}^m{({\widehat{H}}_{sj,i}-H_{s0})}^2}$$

(50)

$${\widehat{M}}_{rj}=\frac{1}{m}{\displaystyle \sum _{i=1}^m{\widehat{H}}_{rj,i}}$$

(51)

$$MS{E}_{rj}=\frac{1}{m}{\displaystyle \sum _{i=1}^m{({\widehat{H}}_{rj,i}-H_{r0})}^2}$$

(52)

Based on the above tables, the following conclusions can be drawn:

(1) For Shannon entropy, the ML estimation performs better than the Bayesian estimation. While for Rényi entropy, the performance of ML estimation is similar to Bayesian estimation.

(2) In Bayesian estimation, it is better to select the SE to estimate Shannon entropy. On the contrary, it is better to select the SSE to estimate Rényi entropy.

(3) The sample size has a great influence on Shannon entropy than Rényi entropy. When the sample size increases gradually, the Bayesian estimation of Shannon entropy under SE is close to the ML estimation, but it has no obvious effect on Rényi entropy.

(4) In Table 3, it can be noted that the coverage probability of ACIs is quite close to confidence levels.

6. Real data analysis

There is a real data set given by Bjerkdal [46], which represents the survival time (in days) of guinea pigs after the injection of different doses of tubercle bacilli. Kundu and Howlader [47] proved that this set of data sets using the IWD fitting effect is very good, therefore, this data set can be seen as a sample of IWD. In Reference [46], the regimen number refers to the common logarithm of bacillary units contained in 0.5 ml of challenge solution. In other words, regimen 6.6 represents 4.0*10⁶ bacillary units per 0.5 ml. Corresponding to regimen 6.6, the 72 observed observations are listed as follows:

12, 15, 22, 24, 24, 32, 32, 33, 34, 38, 38, 43, 44, 48, 52, 53, 54, 54, 55, 56, 57, 58, 58, 59, 60, 60, 60, 60, 61, 62, 63, 65, 65, 67,68, 70, 70, 72, 73, 75, 76, 76, 81, 83, 84, 85, 87, 91, 95, 96, 98, 99, 109, 110, 121, 127, 129, 131, 143, 146, 146, 175, 175, 211,233, 258, 258, 263, 297, 341, 341, 376.

Using the proposed estimates described in the above sections, the ML estimates and Bayesian estimates of Shannon entropy and Rényi entropy are displayed in Table 4. It’s obvious that the ML estimates of entropies are all smaller than Bayesian estimates under SE respectively, and the Bayesian estimates under SSE of entropies are all smaller than ML estimates respectively.

7. Conclusions

This paper considers the Bayesian estimations of Shannon entropy and Rényi entropy based on two-parameter IWD. First, the expressions of these entropies of two-parameter IWD are derived in Theorem 1. For ML estimation, due to the invariance of ML estimation, the ML estimators of parameters are obtained by the dichotomy method at first. And then, the ML estimators of entropies can be obtained. Additionally, the approximate confidence intervals are given by the Delta method. For Bayesian estimation, the symmetric entropy loss function and scale squared error loss function are chosen. However, the forms of Bayesian estimators are complex and difficult to calculate. Lindley approximation is used to solve this problem. Finally, the mean square errors of the above estimators are used to compare their performances. For Shannon entropy, it’s better to use ML estimator. And for Rényi entropy, the performances of the ML estimator and Bayesian estimator are analogous.