How Accurate Should a Medical Test be to Meet Cost-Effectiveness

Preprint

Article

How Accurate Should a Medical Test be to Meet Cost-Effectiveness

This version is not peer-reviewed.

Ermo Chen^*

This version is not peer-reviewed.

Altmetrics

Downloads

123

Views

Comments

Submitted:

03 May 2023

Posted:

05 May 2023

You are already at the latest version

Abstract

Medical tests' cost-effectiveness analysis reveals a strong correlation between their accuracy and analysis results. Theoretically, we provide two lower bounds that medical tests' accuracy must exceed to be considered cost-effective. Theoretically, we provide two lower bounds that the accuracy of medical tests meeting cost-effectiveness must exceed. First, medical tests' accuracy should surpass the lower bound of matching requirements for each patient to receive the most appropriate intervention based on their test results. Second, the overall lower limit should be exceeded for the medical testing to be cost-effective for the patients as a whole. Furthermore, the conclusions from this model also provide an economic explanation for the under-diagnosis of rare diseases and the challenges faced in implementing precision medicine for minority patients. A numerical simulation example validates the conclusions of this paper.

Keywords:

Subject:

Public Health and Healthcare - Public Health and Health Services

This preprints belongs to the Topic

Economics of Public Health: Assessment of Health Interventions

Highlights

For each patient to receive a corresponding intervention based on their test results, the accuracy of medical test needs to exceed a lower bound of matching requirements.
For medical test to be cost-effective for patients in general, the accuracy of medical test needs to exceed a lower bound for overall cost-effectiveness.
Enhancing the accuracy of medical tests can increase their cost-effectiveness and improve fairness in medical decision-making.

1. Introduction

Cost-effectiveness analysis (CEA) is a commonly used tool for evaluating interventions and medications in health economics, providing valuable insights through health technology assessments (HTAs). Gradually, researchers have discovered its potential application in diagnosis and medical test. In recent years, CEA has been deployed in numerous HTAs for diagnosis and medical test, including studies such as Thomas et al. [1], Jacobsen et al. [2], and Choi et al. [3]. However, some studies (Fang et al. [4], Yang et al. [5], and Snowsill [6]) indicate that applying CEA to diagnosis and testing HTAs is becoming more popular, but various crucial factors such as optional interventions, additional information, and test accuracy have not been adequately considered.

Designs for CEA analysis of diagnosis and testing require specific considerations given their distinct characteristics. As noted by Augustovski et al. [7], particular aspects necessitating unique consideration in this context include their classification and importance, which require inclusion in the analysis. Additionally, Van Dorst et al. [8] emphasizes the contextual relevance and dynamics of diagnosis and tests and recommends that CEA be conducted in tandem with corresponding interventions and medications. To ensure reliability in results, Van der Pol et al. [9] suggests that Consolidated Health Economic Evaluation Reporting Standards (CHEERS) should include disclosure of inherent features of diagnosis and tests. Particularly, Seo and Strong [10] offers modeling guidelines that highlight the importance of considering and prioritizing accuracy in CEA of diagnosis and tests.

The significance of accuracy in medical diagnosis and tests is crucial. Over two decades ago, Hernandez [11] emphasized the importance of accuracy in CEA for medical tests. Additionally, Van den Bruel et al. [12] stressed the necessity of analyzing the accuracy of tests and diagnosis when reporting CEA. Numerous CEA studies on particular matters have reported the sensitivity of results regarding accuracy, including Novielli et al. [13], Novielli et al. [14], Garg et al. [15], Biltaji et al. [16], and others. Consequently, further research on the accuracy for the CEAs of medical tests is imperative.

However, research on the relationship between the CEA of medical tests and accuracy remains largely qualitative and case-specific, with few quantitative analyses of accuracy’s role under general assumptions. This paper aims to fill this gap by establishing a model using general assumptions to quantitatively analyze the relationship between test accuracy and the standards required to meet cost-effectiveness. In summary, our study addresses the following question: What level of accuracy is necessary for a medical test to meet cost-effectiveness?

2. Model Settings

To illustrate the relationship between test accuracy and CEA results, we utilize a simplified model. We assume that patients can be divided into finite classes, each of which is suited to a particular medical intervention, and there are only two possible health outcomes: receiving the appropriate intervention or not. Furthermore, this paper employs Net Monetary Benefit (NMB) as the measure to assess which health intervention is more cost-effective, from the viewpoint of classical CEA.

2.1. General Settings

Consider a patient population, in which each patient has unique unobservable intrinsic characteristics that can be categorized into N classes. Each patient class has a unique medical intervention that is the most appropriate. It is assumed that the most suitable medical intervention can lead to the gain of

Q^{+}

quality-adjusted life years (QALYs) for a patient belonging to the respective class, whereas an unsuitable one can only allow the acquisition of

Q^{-}

QALYs. Specifically, the QALY returns obtained from intervention j for patients in class i,

q (i, j)

, can be expressed as

\forall i, j \in {1, 2, . . ., N}, q (i, j) = \{\begin{matrix} Q^{+}, & j = i, \\ Q^{-}, & j \neq i . \end{matrix}

(1)

That is, patients belonging to class i gain

Q^{+}

QALYs when they undergo their designated intervention i, while the use of interventions not designed for their class can only result in

Q^{-}

QALYs, with

Q^{+} > Q^{-}

The cost of an intervention is denoted as

c (j)

, where j refers to the intervention. The NMB approach combines the QALY and the cost of an intervention through a monetary constant

λ

. That is, the NMB of using intervention j for patients in class i,

S^{i} (j)

, can be expressed as

S^{i} (j) = λ q (i, j) - c (j), \forall i, j \in {1, 2, . . ., N} .

(2)

The structure of patients’ intrinsic characteristics can be observed through retrospective statistics over time. Let

p (\cdot)

be a discrete distribution that represents the probability of patients being assigned to a specific class i, where i is one of the classes. The primary objective of medical intervention decisions is to maximize the expected NMB of patients.

2.2. The Medical Test and the Accuracy

Suppose a medical test is available to identify patients’ intrinsic characteristics that incurs a cost of

c_{0}

, as previously mentioned. The medical test, however, is not always accurate, with a level of accuracy denoted as

α

. In other words, the probability that the medical test correctly identifies class i patients is

α

. Errors are equally likely to be assigned to each of the other classes. Denote the random outcome of the medical test as

T (\cdot)

. Then, there exists

\forall i, j \in {1, 2, . . ., N}, P (T (i) = j) = \{\begin{matrix} α, & j = i, \\ \frac{1 - α}{N - 1}, & j \neq i . \end{matrix}

(3)

Notably, a patient’s own intrinsic type i cannot be directly observed. The only observable result is the patient’s medical test, which produces a result of

T (i)

. Following the medical test, any intervention decision can only be made based on the outcome

T (i)

. However, the outcome

T (i)

is a random variable. This is the primary factor that contributes to the effect of medical test accuracy on the evaluation results of CEA.

Let

J = {j_{1}, j_{2}, . . ., j_{N}}

be an intervention strategy based on the medical test, where

j_{i}

denotes the intervention assigned to patients with a test result of i. It is important to note that the class of patients with a test result of i may not necessarily correspond to the patients with intrinsic type i. If the medical test is performed and the intervention strategy

J

is chosen, the expected NMB per unit for all patients is denoted as

S_{T} (J)

. If no medical test is performed, the same intervention is assigned to all the patients. The expected NMB per unit in this case is denoted as

S_{N T} (J)

2.3. Expected NMB with the Medical Test

This subsection focuses on the expressions of

S_{N T} (J)

and

S_{T} (J)

. The expected NMB per unit,

S_{T} (J)

, is defined as

S_{T} (J) = E [λ E [q (i, j_{T (i)}) | i] - E [c (j_{T (i)}) | i]] - c_{0},

(4)

where

E [\cdot | i]

denotes the conditional expectation with respect to class i. Although complex, we can decompose the expression using

T (\cdot)

in Lemma 1.

Lamma 1.

S_{T} (J)

has a decomposition with the result of

T (\cdot)

, which is

S_{T} (J) = \sum_{i = 1}^{N} S_{T}^{i} (j_{i}),

(5)

where

S_{T}^{i} (j_{i})

is the part of NMB that the class of patients with result

T (\cdot) = i

contributes and could be expressed as

\{\begin{matrix} λ (α p (i) Q^{+} + (1 - p (i)) \frac{1 - α}{N - 1} Q^{-}) - (c (i) + c_{0}) (α p (i) + (1 - p (i)) \frac{1 - α}{N - 1}), & j_{i} = i, \\ λ (p (i_{0}) \frac{1 - α}{N - 1} Q^{+} + α p (i) Q^{-} + (1 - p (i_{0}) - p (i)) \frac{1 - α}{N - 1} Q^{-}) - (c (i_{0}) + c_{0}) (α p (i) + (1 - p (i)) \frac{1 - α}{N - 1}), & j_{i} = i_{0} \neq i . \end{matrix}

(6)

Proof of Lamma 1.

nitially, we can craft the expression for

S_{T} (J)

by implementing the total probability formula, subsequently sorting it based on the outcome of

T (\cdot)

. This approach enables us to derive:

\begin{matrix} S_{T} (J) = & \sum_{i = 1}^{N} p (i) (λ E [q (i, j_{T (i)}) | i] - E [c (j_{T (i)}) | i]) - c_{0} \\ = & \sum_{i = 1}^{N} p (i) (λ E [q (i, j_{T (i)}) | i] - E [c (j_{T (i)}) | i]) - c_{0} \\ = & \sum_{i = 1}^{N} p (i) (\sum_{k = 1}^{N} P (T (i) = k) (λ q (i, j_{k}) - c (j_{k})) - c_{0}) \\ = & \sum_{k = 1}^{N} \sum_{i = 1}^{N} p (i) P (T (i) = k) (λ q (i, j_{k}) - c (j_{k}) - c_{0}) = \sum_{k = 1}^{N} S_{T}^{k} (j_{k}), \end{matrix}

(7)

where

S_{T}^{i} (j_{i}) = \sum_{k = 1}^{N} p (k) P (T (k) = i) (λ q (k, j_{i}) - c (j_{i}) - c_{0}) .

(8)

Moreover,

\begin{matrix} S_{T}^{i} (j_{i}) = & \sum_{k = 1}^{N} p (k) P (T (k) = i) (λ q (k, j_{i}) - c (j_{i}) - c_{0}) \\ = & p (i) P (T (i) = i) (λ q (i, j_{i}) - c (j_{i}) - c_{0}) + \sum_{k \neq i} p (k) P (T (k) = i) (λ q (k, j_{i}) - c (j_{i}) - c_{0}) \\ = & α p (i) (λ q (i, j_{i}) - c (j_{i}) - c_{0}) + \sum_{k \neq i} p (k) \frac{1 - α}{N - 1} (λ q (k, j_{i}) - c (j_{i}) - c_{0}) . \end{matrix}

(9)

Next, if

j_{i} = i

\begin{matrix} S_{T}^{i} (j_{i}) = & α p (i) (λ Q^{+} - c (i) - c_{0}) + \sum_{k \neq i} p (k) \frac{1 - α}{N - 1} (λ Q^{-} - c (i) - c_{0}) \\ = & λ (α p (i) Q^{+} + (1 - p (i)) \frac{1 - α}{N - 1} Q^{-}) - (c (i) + c_{0}) (α p (i) + (1 - p (i)) \frac{1 - α}{N - 1}), \end{matrix}

(10)

and else if

j_{i} = i_{0} \neq i

\begin{matrix} S_{T}^{i} (j_{i}) = & α p (i) (λ Q^{-} - c (i) - c_{0}) + \sum_{k \neq i, i_{0}} p (k) \frac{1 - α}{N - 1} (λ Q^{-} - c (i) - c_{0}) + p (i_{0}) \frac{1 - α}{N - 1} (λ Q^{+} - c (i) - c_{0}) \\ = & λ (p (i_{0}) \frac{1 - α}{N - 1} Q^{+} + α p (i) Q^{-} + (1 - p (i_{0}) - p (i)) \frac{1 - α}{N - 1} Q^{-}) - (c (i_{0}) + c_{0}) (α p (i) + (1 - p (i)) \frac{1 - α}{N - 1}) . \end{matrix}

(11)

□

Lamma 1 presents a technique for evaluating a patient’s expected NMB using the medical test, dependent on the decision strategy

J

. In cases where the test is not available, we can compute

S_{N T} (J)

S_{N T} (J) = S_{T} (J) + c_{0}, \forall J \in J_{N T} .

(12)

In this instance,

J_{N T}

refers to the set of unique strategies where

j_{i} = k

for all i.

3. Decision Making

Medical decision makers must select the most cost-effective intervention from available treatments whether or not medical testing is present. Hence, analyzing the output level of the system under the most cost-effective intervention for each situation is crucial before comparing changes in system output with and without medical testing. To align with the classical CEA decision framework, we utilize maximizing the expected NMB as the selection criterion in each case and investigate the most suitable intervention decisions.

3.1. Decision Making without the Test

When medical testing is absent, medical decision makers cannot differentiate between various patient types and have to select a single intervention as the most cost-effective choice for all patients. Thus, comparing the expected NMB results of the N interventions would suffice for determining the best-intervention alternative in this case. Without considering patient characteristics to dictate treatment decisions, the optimal strategy is "the one" intervention that offers the highest expected NMB for the overall patient population among the N options. The expression for this strategy is:

j_{N T}^{*} = {argmax}_{j \in {1, 2 . . ., N}} {S_{N T} (J) | j_{i} = j, \forall i} .

(13)

The forthcoming Theorem 1 presents the most cost-effective intervention selection for the situation without medical testing.

Theorem 1.

Without a medical testing, the optimal intervention

j_{N T}^{*}

should be chosen as

j_{N T}^{*} = {argmax}_{j \in {1, 2 . . ., N}} λ (Q^{+} - Q^{-}) p (j) - c (j) .

(14)

Proof of Theorem 1.

Mark

J_{N T} = {j_{N T}, j_{N T}, . . ., j_{N T}}

, then

\begin{matrix} S_{N T} (J_{N T}) = & λ \sum_{i = 1}^{N} p (i) q (i, j_{N T}) - c (j_{N T}) \\ = & λ p (j_{N T}) Q^{+} + λ (1 - p (j_{N T})) Q^{-} - c (j) \\ = & λ Q^{-} + λ (Q^{+} - Q^{-}) p (j_{N T}) - c (j_{N T}), \end{matrix}

(15)

where

λ Q^{-}

is free from

j_{N T}

and the proof is done.

□

From Theorem 1, two simple corollaries can be deduced. First, when the interventions have the same costs, the optimal strategy is the one suitable for the largest number of patients, i.e., the intervention with the highest proportion of suitable patients. Second, when the proportions of varying patient types are uniform, the most cost-effective intervention is the least expensive. Both align with traditional CEA decision-making and are consistent with economic intuition.

Besides, the optimal expected NMB in the absence of medical testing is stated as

S_{N T} (J_{N T}^{*}) = λ Q^{-} + λ (Q^{+} - Q^{-}) p (j_{N T}^{*}) - c (j_{N T}^{*}),

(16)

which serves as the decision benchmark to determine whether to use a medical test.

3.2. Decision Making with the Test

In the case of medical testing, the situation becomes more complicated. On one hand, it is unethical to subject patients to inappropriate treatments due to the accuracy of medical testing since each patient category has the ideal intervention. On the other hand, even if patients receive the "ideal" interventions based on the test results, there may still be incorrect matches if the testing accuracy is inadequate. As a result, determining the accuracy level required to assure that patients receive the most fitting treatments based on the test results is a matter that needs prior investigation.

We refer to assigning patients to respective interventions based on the test results as the "Matching Interventions Strategy", denoted as

J_{M}

. In this scenario,

J_{M} = {1, 2, . . ., N}

, that is,

j_{i} = i, \forall i

. The following Theorem 2 provides the minimum accuracy level required for the "Matching Interventions Strategy" to be most cost-effective subject to some regular conditions.

Theorem 2

(Lower Bound Theory for Matching Interventions). Under the condition that

\forall i, i_{0} \in {1, 2, . . ., N}, (N p (i) - 1) Δ_{i, i_{0}} < (N - 1) p (i) + p (i_{0}),

(17)

for the "Matching Interventions Strategy",

J_{M}

, to be the most efficiency strategy, the accuracy for the medical test should satisfy

α \geq sup_{i \in {1, 2, . . ., N}} sup_{i_{0} \neq i} \frac{p (i_{0}) + (1 - p (i)) Δ_{i, i_{0}}}{(N - 1) p (i) + p (i_{0}) - (N p (i) - 1) Δ_{i, i_{0}}},

(18)

where

Δ_{i, i_{0}} = (c (i) - c (i_{0})) / (λ (Q^{+} - Q^{-}))

Proof of Theorem 2.

Clearly, the necessary condition for the "Matching Interventions Strategy",

J_{M}

, to be the most efficiency stargegy is

\forall i, S_{t}^{i} (i) \geq sup_{i_{0} \neq i} S_{t}^{i} (i_{0}),

(19)

which means that for the observation class i, intervention i is more efficiency than any other intervention

i_{0}

. Moreover, there is

\begin{matrix} S_{t}^{i} (i) - S_{t}^{i} (i_{0}) = & λ (α p (i) (Q^{+} - Q^{-}) - p (i_{0}) \frac{1 - α}{N - 1} (Q^{+} - Q^{-})) - (c (i) - c (i_{0})) (α p (i) + (1 - p (i)) \frac{1 - α}{N - 1}) \\ = & α (λ (Q^{+} - Q^{-}) [p (i) + \frac{p (i_{0})}{N - 1}] - (c (i) - c (i_{0})) [p (i) - \frac{1 - p (i)}{N - 1}]) \\ - & \frac{1}{N - 1} (λ (Q^{+} - Q^{-}) p (i_{0}) + (c (i) - c (i_{0})) (1 - p (i))) . \end{matrix}

(20)

So under the regular condition, we have

\begin{matrix} S_{t}^{i} (i) \geq S_{t}^{i} (i_{0}) \\ \Leftrightarrow & α (λ (Q^{+} - Q^{-}) [p (i) + \frac{p (i_{0})}{N - 1}] - (c (i) - c (i_{0})) [p (i) - \frac{1 - p (i)}{N - 1}]) \geq \frac{1}{N - 1} (λ (Q^{+} - Q^{-}) p (i_{0}) + (c (i) - c (i_{0})) (1 - p (i))) \\ \Leftrightarrow & α ((N - 1) p (i) + p (i_{0}) - Δ_{i, i_{0}} (N p (i) - 1)) \geq p (i_{0}) + Δ_{i, i_{0}} (1 - p (i)) \\ \Leftrightarrow & α \geq \frac{p (i_{0}) + Δ_{i, i_{0}} (1 - p (i))}{(N - 1) p (i) + p (i_{0}) - Δ_{i, i_{0}} (N p (i) - 1)} . \end{matrix}

(21)

\forall i_{0} \neq i, S_{t}^{i} (i) \geq S_{t}^{i} (i_{0})

is equivalent to

α \geq sup_{i_{0} \neq i} \frac{p (i_{0}) + Δ_{i, i_{0}} (1 - p (i))}{(N - 1) p (i) + p (i_{0}) - Δ_{i, i_{0}} (N p (i) - 1)},

(22)

and for all i to hold this, we have

α \geq sup_{i \in {1, 2, . . ., N}} sup_{i_{0} \neq i} \frac{p (i_{0}) + Δ_{i, i_{0}} (1 - p (i))}{(N - 1) p (i) + p (i_{0}) - Δ_{i, i_{0}} (N p (i) - 1)} .

(23)

□

According to Theorem 2, achieving the target of maximizing expected NMB would require exceeding the minimum level of accuracy while assigning the theoretically optimal interventions to every observation class. That is to say, that only accurate enough testing can ensure cost-effective intervention decisions based on test results. Notably, the regularity conditions in Theorem 2 entail that the ideal interventions cannot be too costly for patient subclasses with a relatively high proportion.

To enhance comprehension, we provide an illustration of Theorem 2 under equivalent probabilities, outlined in the subsequent Corollary 1.

Corollary 1.

\forall i, p (i) = 1 / N

, the lower bound in Theorem 2 equals

\frac{1}{N} + (1 - \frac{1}{N}) \frac{C_{m a x} - C_{m i n}}{λ (Q^{+} - Q^{-})},

(24)

where

C_{m a x} = {max}_{i} {c (i)}

and

C_{m i n} = {max}_{i} {c (i)}

Proof of Corollary 1.

Substitute the designated probabilities in Theorem 2. □

Corollary 1 shows that for intervention decisions based on test results to be the most cost-effective under equal probabilities, accuracy needs to surpass the accuracy of random selection,

1 / N

, by a specific level. This specific level is determined by the ICER for patients suitable for the most expensive intervention switching from the least expensive one to the most expensive one. However, considering

α \leq 1

, if the most expensive intervention is too costly, choosing that intervention would still not be cost-effective, even if the test is perfectly accurate.

Finally, once the lower bound is satisfied, we can calculate the expected NMB for the medical test case.

S_{T} (J_{M}) = \sum_{i = 1}^{N} \{λ (α p (i) Q^{+} + (1 - p (i)) \frac{1 - α}{N - 1} Q^{-}) - (c (i) + c_{0}) (α p (i) + (1 - p (i)) \frac{1 - α}{N - 1})\} .

(25)

4. Cost-Effectiveness Analysis for the Medical Test

We have obtained both the optimal expected NMB with and without the test. Therefore, we can conduct a cost-effectiveness analysis of the medical test by examining the increase in optimal expected NMB gained through testing. Using this analytical framework, the following Theorem 3 will determine if the medical test is cost-effective.

Theorem 3.

The sufficient and necessary condition for the test,

T (\cdot)

, to be cost-effective, i.e.,

S_{T} (J_{M}) \geq S_{N T} (J_{N T}^{*})

α \geq \frac{E_{q^{α}} [c (i)] + c_{0} - c (j_{N T}^{*})}{λ (Q^{+} - Q^{-})} + p (j_{N T}^{*}),

(26)

where

j_{N T}^{*}

is the optimal intervention without the test, see Theorem 1, and

E_{q^{α}}

is the expectation operator under the probability measure

q^{α}

, a measure induces by α, where

\forall i \in {1, 2, . . ., N}, q^{α} (i) = α p (i) + \frac{1 - α}{N - 1} (1 - p (i)) .

(27)

Proof of Theorem 3.

First, we show that

q^{α}

is a probability measure. As

α, p (i) \in [0, 1]

, we have

α p (i) \geq 0

and

\frac{1 - α}{N - 1} (1 - p (i)) \geq 0

, so

\forall i, q^{α} \geq 0

. Moreover, there is

\sum_{i = 1}^{n} q^{α} (i) = α \sum_{i = 1}^{n} p (i) + \frac{1 - α}{N - 1} (N - \sum_{i = 1}^{n} p (i)) = α + 1 - α = 1 .

(28)

So that

q^{α}

is a probability measure. And with Equation (16) and Equation (25), we could get

\begin{matrix} S_{T} (J_{M}) - S_{N T} (J_{N T}^{*}) & = λ (Q^{+} - Q^{-}) [α (1 - p (j_{N T}^{*})) - p (j_{N T}^{*}) + α p (j_{N T}^{*})] \\ - \sum_{i \neq j_{N T}^{*}} [(c (i) - c (j_{N T}^{*})) (α p (i) + \frac{1 - α}{N - 1} (1 - p (i)))] - c_{0} \\ = λ (Q^{+} - Q^{-}) (α - p (j_{N T}^{*})) - [E_{q^{α}} [c (i)] + c_{0} - c (j_{N T}^{*})], \end{matrix}

(29)

then the proof is finished. □

Theorem 3 provides the conditions necessary and sufficient for a medical test to be cost-effective in the form of a lower bound requirement for accuracy,

α

. This means that the optimal expected NMB with testing will exceed that without testing if and only if the medical test’s accuracy meets the criteria stated in Theorem 3.

In particular, we interpret the probability measure

q^{α}

induced by

α

. It can be seen that when

α = 1

q^{α} (i) = p (i)

, and when

α = 1 / N

q^{α} (i) = 1 / N

. This measure acts as a weighted average between

p (\cdot)

and the uniform distribution

1 / N

. Furthermore, from a practical standpoint,

q^{α} (i)

represents the probability of all patients receiving a test result of i. Consequently,

E_{q^{α}} [c (i)]

is the expected cost of intervention when all interventions are made perfectly according to the test results.

Theorem 3 can be used to show that the accuracy requirement,

α

, increases with the test cost,

c_{0}

. Therefore, to support a higher price, the medical test must have higher accuracy. In addition, it can be seen from Theorem 3 that if a significant proportion of patients receive adequately inexpensive, high-suitable intervention, where

p (j_{N T}^{*})

is large, and

c (j_{N T}^{*})

is small, then the required lower bound may exceed 1, indicating that no test will be cost-effective. Thus, the left minority groups with complex medical needs may lack sufficient medical intervention. This also provides an explanation for the lack of diagnosis and targeted therapies for rare diseases.

5. A Numerical Example with Simulation

In this section, we employ numerical simulation to illustrate and confirm the previously mentioned findings. Concretely, we define a set of patient groups with corresponding medical interventions, assign costs and QALY outcomes, and calculate the expected NMBs for both scenarios - with and without the medical test - as previously mentioned. This enables us to derive a precise correlation between the accuracy of a medical test and its CEA outcomes. Additionally, we shall validate and expound on Theorem 2 introduced in this paper, and substantiate it by analyzing the percentage of patients receiving the most suitable treatment within each class.

To balance the variety of patient classes alongside comprehensible simulation results, we presume that patients can be categorized into six innate classes,

N = 6

, and each class relates to a distinct most suitable medical intervention. Each patient who gets the most fitting intervention achieves a QALY output of

Q^{+} = 20

, and

Q^{-} = 10

for the rest. Additionally, we assume a monetization constant of

λ = 30000

. Furthermore, we present Table 1 to demonstrate the probability of patients being allocated in distinct classes and the respective cost level of the most fitting intervention for each class.

During the simulation, we initially analyze the correlation between precise medical testing and its cost-effectiveness. Specifically, we examine various

c_{0}

and calculate the expected NMB,

S_{T} (J_{M})

at the optimum level corresponding to different

α

under each

c_{0}

and compare it to the expected NMB without medical testing,

S_{N T} (J_{N T}^{*})

. This enables us to conclude whether the testing is cost-effective.

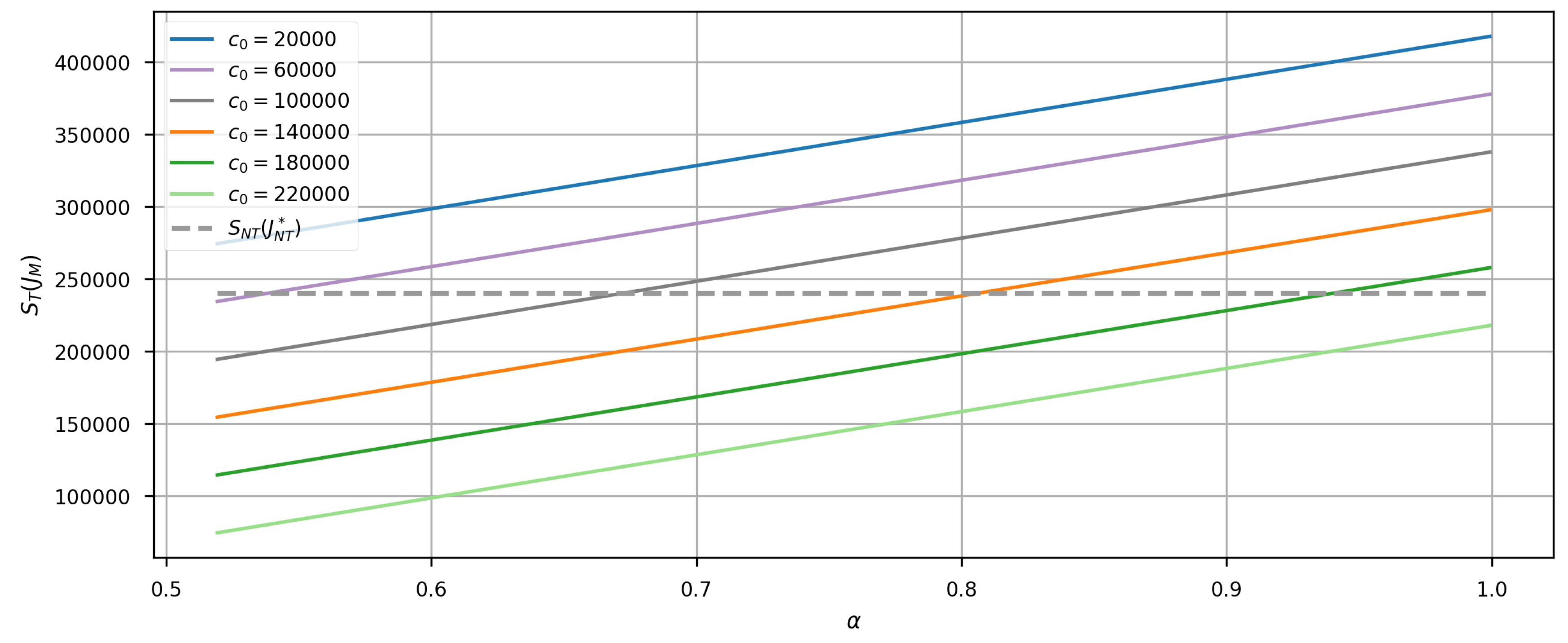
Figure 1 illustrates the results of this calculation. The graph shows that the expected NMB obtained from using medical tests increases linearly with the accuracy of the test. This indicates that a more accurate medical test yields a better outcome in total. Additionally, the intersection of the curve and the dashed line determines the minimum accuracy level at which the testing cost is worth efficiency. As

c_{0}

rises, so does the intersection’s position, signifying that a more expensive test necessitates greater accuracy to meet cost-effectiveness.

Figure 1 features two critical cases significant in practice. Firstly, for the curve of

c_{0} = 220000

, the medical test does not meet cost-effectiveness regardless of how accurate it is. This implies an upper limit on the pricing of medical tests for meeting cost-effectiveness for the patient population. Any test priced above this limit would be unlikely accepted, regardless of its accuracy. Therefore, this can serve as a futuristic pricing reference for companies developing differential diagnostic tests for specific diseases. Secondly, for the curve of

c_{0} = 20000

, the test is always cost-effective as long as the lower bound of matching interventions is met. Thus, when the test is priced low enough, it can be evaluated for cost-effectiveness by merely determining whether Theorem 2 is satisfied. This serves as a reference for health insurance procurement.

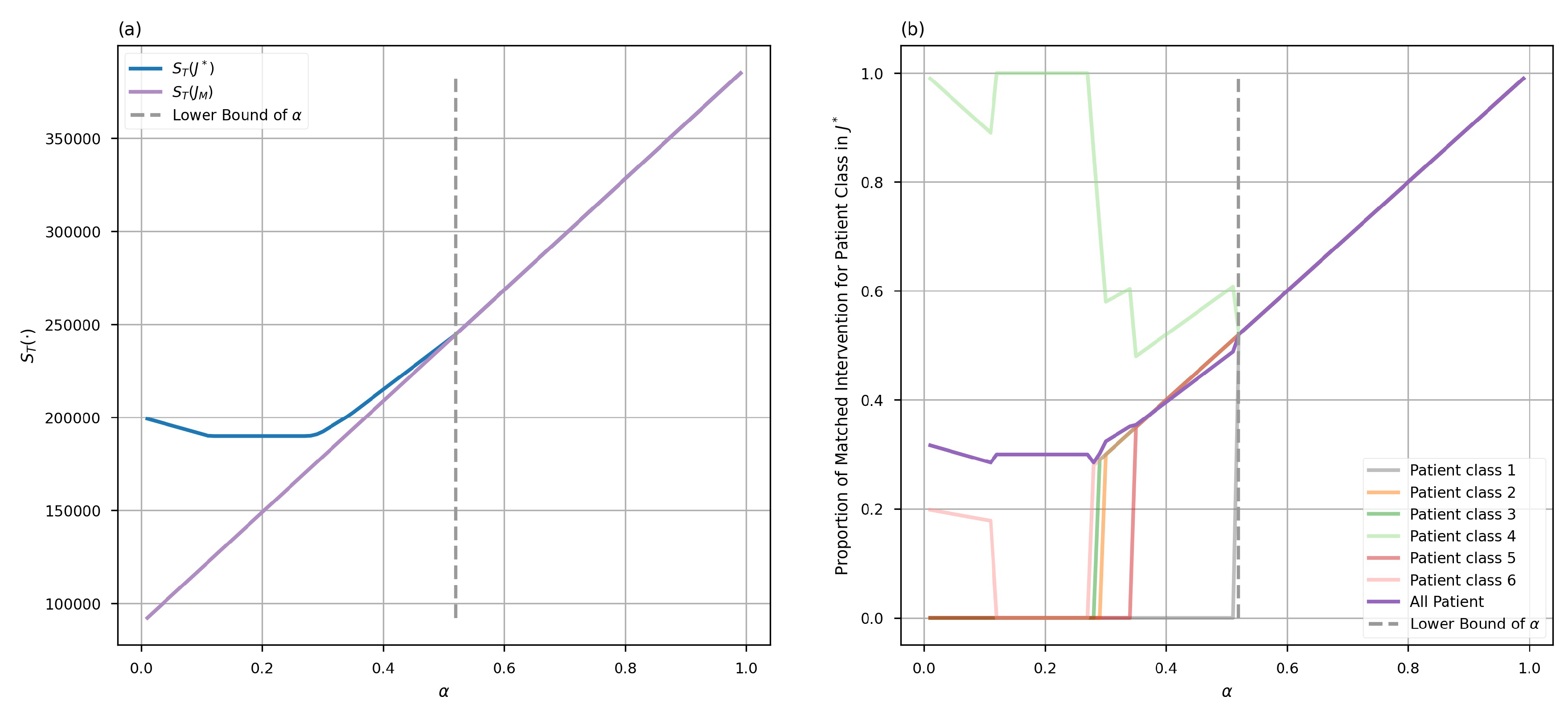
In the second simulation phase, we verify Theorem 2. We calculate the expected NMB output,

S_{T} (J)

, for each feasible intervention decision

J

(totaling

6^{6} = 46656

) at specific

α

levels. Afterward, we compare the maximum result to the expected NMB output of the matched intervention decision,

S_{T} (J_{M})

, to determine the

α

level at which the matched intervention decision satisfies the optimal requirement. Meanwhile, we determine the percentage of patients receiving the most appropriate medical intervention in each class under the strategy (

J^{*}

) corresponding to the highest expected NMB result. This shows the significant loss of welfare for some patient groups when the lower bound in Theorem 2 is not met.

The calculation results are presented in Figure 2. Figure 2(a) indicates that using the matched intervention decision

J^{*}

may not correspond to the decision with the maximum expected NMB when the accuracy falls below the lower bound, but it does remain optimal among all intervention decisions when the accuracy goes beyond the lower bound. This finding confirms Theorem 2. Moreover, Figure 2(b) shows that, for the left side of the dashed line where the accuracy is below the lower bound, the proportion of patients in different classes receiving corresponding interventions fluctuates drastically and is significantly lower on average than the level observed on the right side of the dashed line. On the right side of the dashed line, the intervention proportion for each class remains consistent and steadily increases as the accuracy increases, eventually reaching 1. These results suggest that when the lower bound of accuracy is not met, many patients may receive inappropriate interventions that do not align with the test results. This situation leads to a significant decrease in the proportion of patients that eventually receive appropriate interventions. Additionally, the proportion of patients receiving appropriate interventions may vary considerably across different patient classes, leading to further unfairness.

It should be highlighted that in the scenario of very low accuracy, the optimal expected NMB might decrease with increasing levels of accuracy. Such a situation occurs since an accuracy lower than complete randomness holds more information. To illustrate this point, suppose that only two types of patients are involved. If the accuracy is 0, which means that the test results are diametrically opposite for each type of patient, then the decision could be made opposite to the result of test. On the other hand, even if the optimal decision

J^{*}

is chosen after surpassing the lower bound of accuracy, the proportion of patients receiving appropriate matched interventions might not reach 100% since the accuracy is not 1.

Overall, this numerical example offers empirical evidence of the importance of the lower bound of accuracy and its impact on the assessment of medical testing effectiveness. Additionally, it suggests a methodology for pricing or procuring medical testing services. The results reveal a common correlation between the accuracy of medical testing and the acceptable price range within a specified interval. In summary, for a given problem, the accuracy of medical test needs to meet the requirements of the lower bound of matching in Theorem 2 and the overall lower bound of cost-effectiveness in Theorem 3.

6. Conclusion and Discussion

This paper proposes a quantitative model for estimating the association between the cost-efficiency level of a imperfect medical test with its accuracy. To meet cost-effectiveness, we identified two lower bounds for accuracy through quantitative analysis. Firstly, for matched interventions to meet each observation class’s cost-effectiveness, the accuracy needs to meet the lower bound on matching in Theorem 2. Secondly, to meet the cost efficiency requirements for the overall patient population, the accuracy must fall above the lower bounds for overall cost-effectiveness in Theorem 3.

These findings reveal an important relationship between the accuracy of a medical test and its cost-effectiveness. A quantitative analysis of this relationship highlights that the accuracy of medical testing must reach a certain level to claim cost-effectiveness. This conclusion aligns with economic intuition and previous CEA studies on medical tests. Providing quantitative accuracy requirements is essential for guiding research, pricing, and market decisions for medical tests. Medical test providers can estimate the maximum market price of their tests, determine the economic viability of developing a test or identifying existing profitable tests, based on the accuracy of their tests. Similarly, consumers of medical tests can efficiently evaluate its cost-effectiveness based on its accuracy and pricing.

The findings of this paper also offer an explanation for two common pharmacoeconomic phenomena. Firstly, it explains the under-diagnosis of rare diseases. In this paper’s context, for rare diseases and their more common counterparts, the patient population with rare diseases is classified under the "low probability, high complexity" class. Corollary 1 suggests that under these circumstances, no matter the detection accuracy or price, applying the test is not cost-effective. This insight offers an explanation for the lack of market incentive to create differential diagnostic tests for rare diseases. Secondly, the study offers insights into the mismatching of interventions that arise due to insufficient testing accuracy. Theorem 2 provides a novel perspective that explains the factors that limit some observation classes from receiving interventions that match their respective test results when the accuracy of test falls below the lower bound.

To better comprehend these associations, this paper excludes heterogeneity in QALY outcomes and medical costs within the classes, and it refrains from exploring complex stochastic CEA results like the cost-effective analysis curve (CEAC). Further studies will investigate the impact that including randomness in CEA evaluations has on the conclusions presented in this paper. Moreover, it is essential to note that inexact test results may provide inexact but still valuable information instead of no information at all. That is, partially accurate test results can lead to suboptimal treatment recommendations rather than entirely meaningless ones, and analyzing non-binary test accuracy holds great research value. Future studies will delve into these issues in greater detail.

7. Declarations

I.: Funding - No funding has been received for the conduct of this study..
II.: Conflicts of Interest - Author Ermo Chen declares that he has no conflict of interest.
III.: Availability of data and material - Not applicable.
IV.: Ethics approval - Not applicable.
V.: Consent to participate - Not applicable.
VI.: Consent for publication - Not applicable.
VII.: Code availability - The code in this study is available on request from the corresponding author.
VIII.: Author contributions - Not applicable.

References

R. Thomas, W. J. M. Probert, R. Sauter, L. Mwenge, S. Singh, S. Kanema, N. Vanqa, A. Harper, R. Burger, A. Cori, M. Pickles, N. Bell-Mandla, B. Yang, J. Bwalya, M. Phiri, K. Shanaube, S. Floyd, D. Donnell, P. Bock, H. Ayles, S. Fidler, R. J. Hayes, C. Fraser, K. Hauck, Cost and cost-effectiveness of a universal hiv testing and treatment intervention in zambia and south africa: evidence and projections from the hptn 071 (popart) trial, The Lancet Global Health 9 (2021) e668–e680. [CrossRef]
E. Jacobsen, S. Sawhney, M. Brazzelli, L. Aucott, G. Scotland, M. Aceves-Martins, C. Robertson, M. Imamura, A. Poobalan, P. Manson, C. Kaye, D. Boyers, Cost-effectiveness and value of information analysis of nephrocheck and ngal tests compared to standard care for the diagnosis of acute kidney injury, BMC nephrology 22 (2021) 399–399. [CrossRef]
N. Choi, S. Jang, K. H. Yoo, C. K. Rhee, Y. Kim, The effectiveness and harms of screening for chronic obstructive pulmonary disease: An updated systematic review and meta-analysis, Journal of Korean medical science 37 (2022) e117–e117. [CrossRef]
C. Fang, H. J. Otero, D. Greenberg, P. J. Neumann, Cost-utility analyses of diagnostic laboratory tests: A systematic review, Value in health 14 (2011) 1010–1018. [CrossRef]
Y. Yang, L. Abel, J. Buchanan, T. Fanshawe, B. Shinkins, Use of decision modelling in economic evaluations of diagnostic tests: An appraisal and review of health technology assessments in the uk, PharmacoEconomics - open 3 (2019) 281–291. [CrossRef]
T. Snowsill, Modelling the cost-effectiveness of diagnostic tests, PharmacoEconomics 41 (2023) 339–351. [CrossRef]
F. Augustovski, V. Alfie, A. Alcaraz, S. García Martí, M. F. Drummond, A. Pichon-Riviere, A value framework for the assessment of diagnostic technologies: A proposal based on a targeted systematic review and a multistakeholder deliberative process in latin america, Value in health 24 (2021) 486–496. [CrossRef]
P. Van Dorst, M. Sultanov, S. Pokharel, M. Postma, C. Boersma, S. Van der Pol, A. van Asselt, Mt34 the dynamic and context-specific value of a medical test - a health economic perspective, Value in health 25 (2022) S384–S384. [CrossRef]
S. Van der Pol, P. Rojas Garcia, F. Antonanzas, M. J. Postma, A. D. I. van Asselt, Health-economic analyses of diagnostics: Guidance on design and reporting, PharmacoEconomics 39 (2021) 1355–1363. [CrossRef]
M. K. Seo, M. Strong, A practical guide to modeling and conducting a cost-effectiveness analysis of companion biomarker tests for targeted therapies using r: Tutorial paper, PharmacoEconomics 39 (2021) 1373–1381. [CrossRef]
J. S. Hernandez, Cost-effectiveness of laboratory testing, Archives of pathology and laboratory medicine (1976) 127 (2003) 440–445.
A. Van den Bruel, I. Cleemput, B. Aertgeerts, D. Ramaekers, F. Buntinx, The evaluation of diagnostic tests: evidence on technical and diagnostic accuracy, impact on patient outcome and cost-effectiveness is needed, Journal of clinical epidemiology 60 (2007) 1116–1122. [CrossRef]
N. Novielli, N. J. Cooper, K. R. Abrams, A. J. Sutton, How is evidence on test performance synthesized for economic decision models of diagnostic tests? a systematic appraisal of health technology assessments in the uk since 1997, Value in Health 13 (2010) 952–957. [CrossRef]
N. Novielli, N. J. Cooper, A. J. Sutton, Evaluating the cost-effectiveness of diagnostic tests in combination: Is it important to allow for performance dependency?, Value in health 16 (2013) 536–541. [CrossRef]
V. Garg, N. Y. Gu, M. E. Borrego, D. W. Raisch, A literature review of cost-effectiveness analyses of prostate-specific antigen test in prostate cancer screening, Expert review of pharmacoeconomics and outcomes research 13 (2013) 327–342. [CrossRef]
E. Biltaji, B. Bellows, D. Stenehjem, D. Brixner, Validation of a cost-effectiveness model comparing accuracy of genetic tests for brca mutations, Value in health 19 (2016) A79–A79. [CrossRef]

Figure 1. Curves of Accuracy vs. Expected NMB under Different

c_{0}

with Corresponding Cost-Effectiveness Decisions

Figure 1. Curves of Accuracy vs. Expected NMB under Different

c_{0}

with Corresponding Cost-Effectiveness Decisions

Figure 2. (a)The Expected NMB for the Theoretical Optimal and the Matched Intervention Decision, (b) The Proportion of Patients Receiving the Matched Intervention in Each Class with the Theoretical Optimal Decision

Table 1. The Cost of Interventions and the Probability of Patients in Corresponding Classes

Patient Class i	1	2	3	4	5	6
$c (i)$	200,000	180,000	175,000	150,000	140,000	120,000
$p (i)$	0.1	0.2	0.2	0.3	0.1	0.1

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Alerts

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

How Accurate Should a Medical Test be to Meet Cost-Effectiveness

Abstract

Keywords:

Subject:

Highlights

1. Introduction

2. Model Settings

2.1. General Settings

2.2. The Medical Test and the Accuracy

2.3. Expected NMB with the Medical Test

3. Decision Making

3.1. Decision Making without the Test

3.2. Decision Making with the Test

4. Cost-Effectiveness Analysis for the Medical Test

5. A Numerical Example with Simulation

6. Conclusion and Discussion

7. Declarations

References

MDPI Initiatives

Important Links

Subscribe