Submitted:
03 May 2023
Posted:
04 May 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Experimental data of PME
2.1. Comparison of the PME in HTSc and metallic superconductors
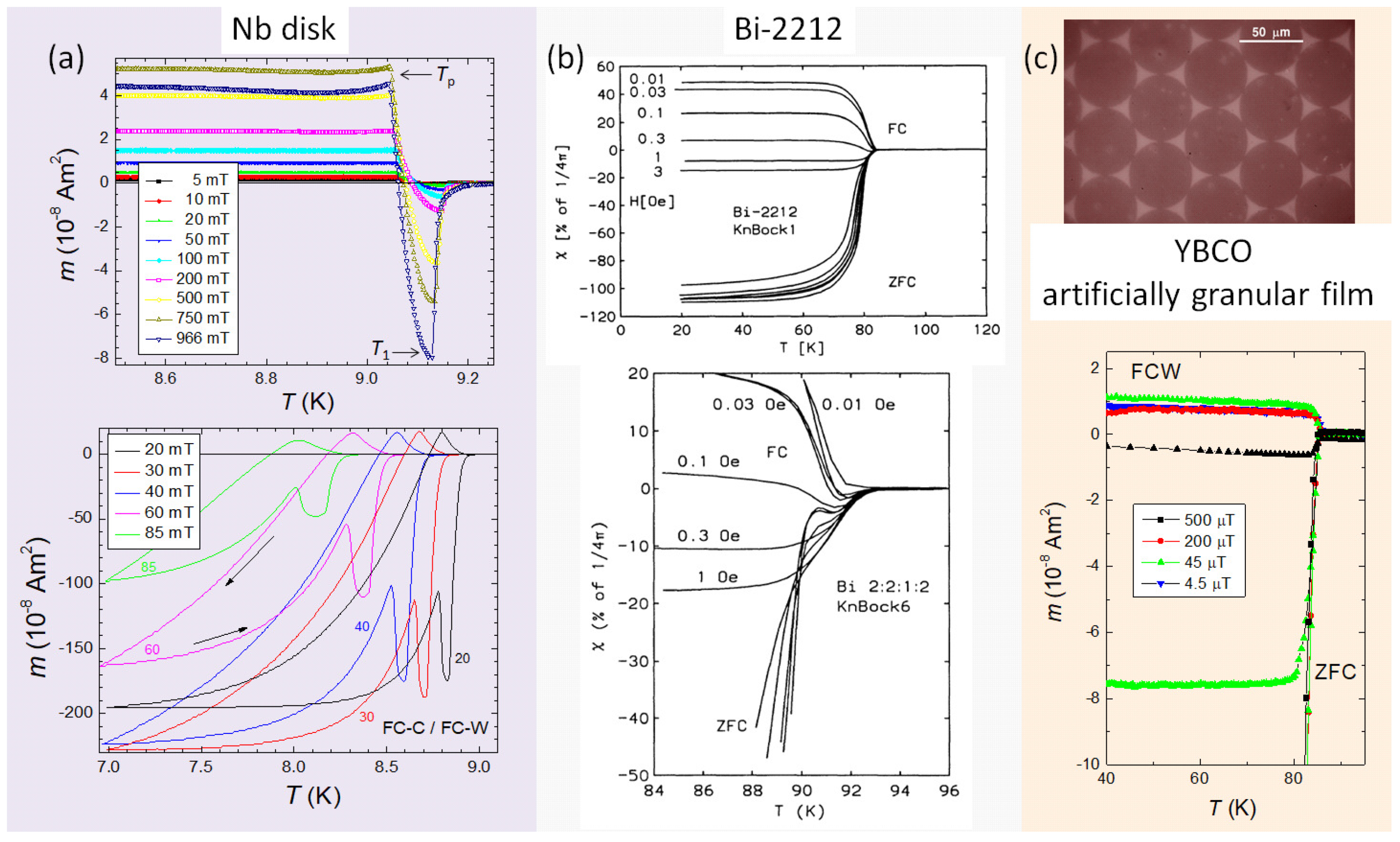
2.2. Metallic superconducting samples with PME
 , FC (⊥) ∘). The inset shows details of the superconducting transition. Reprinted with permission from Ref. [49]. (b) Pb-films on PEEK, rolled up into cylinders. Data shown are FC curves in various applied fields (0.01 T – 0.3 T). Graph redrawn from the data presented in Ref. [50]. (c) Pb porous. FC and ZFC data are shown for various applied fields. The inset gives the standard measurement at low applied field. Reprinted with permission from Ref. [33]. (d) Ta foil. Shown are the superconducting transitions at 30 mT (300 Oe) and for 3 different angles (0, 45 and 90 of the field to the sample surface). Reprinted with permission from Ref. [35]. (e) ZrB crystals, measured at 0.1 mT (1 Oe), 0.5 mT (5 Oe), and 1.5 mT (15 Oe) applied field. The insets give details of the transition at 5 T (0.05 Oe) (FFC-W), 0.5 mT (5 Oe) (FFC-W and ZFC) and 5 mT (50 Oe) (SFC-C), where the F stands for ‘fast’ and S for ‘slow’. Reprinted with permission from Ref. [37]. (f) Susceptibility of an Al mesoscopic disk (2.5 m dia., thickness 0.1 m) at applied fields of 0.9, 3.5, 4.0, 6.5 and 12 mT (9, 35, 40, 65 and 120 G). The last 4 curves were multiplied by a factor of 10. The authors point out that there is no hysteresis when cooling/warming. Reprinted with permission from Ref. [63].
, FC (⊥) ∘). The inset shows details of the superconducting transition. Reprinted with permission from Ref. [49]. (b) Pb-films on PEEK, rolled up into cylinders. Data shown are FC curves in various applied fields (0.01 T – 0.3 T). Graph redrawn from the data presented in Ref. [50]. (c) Pb porous. FC and ZFC data are shown for various applied fields. The inset gives the standard measurement at low applied field. Reprinted with permission from Ref. [33]. (d) Ta foil. Shown are the superconducting transitions at 30 mT (300 Oe) and for 3 different angles (0, 45 and 90 of the field to the sample surface). Reprinted with permission from Ref. [35]. (e) ZrB crystals, measured at 0.1 mT (1 Oe), 0.5 mT (5 Oe), and 1.5 mT (15 Oe) applied field. The insets give details of the transition at 5 T (0.05 Oe) (FFC-W), 0.5 mT (5 Oe) (FFC-W and ZFC) and 5 mT (50 Oe) (SFC-C), where the F stands for ‘fast’ and S for ‘slow’. Reprinted with permission from Ref. [37]. (f) Susceptibility of an Al mesoscopic disk (2.5 m dia., thickness 0.1 m) at applied fields of 0.9, 3.5, 4.0, 6.5 and 12 mT (9, 35, 40, 65 and 120 G). The last 4 curves were multiplied by a factor of 10. The authors point out that there is no hysteresis when cooling/warming. Reprinted with permission from Ref. [63].
 , FC (⊥) ∘). The inset shows details of the superconducting transition. Reprinted with permission from Ref. [49]. (b) Pb-films on PEEK, rolled up into cylinders. Data shown are FC curves in various applied fields (0.01 T – 0.3 T). Graph redrawn from the data presented in Ref. [50]. (c) Pb porous. FC and ZFC data are shown for various applied fields. The inset gives the standard measurement at low applied field. Reprinted with permission from Ref. [33]. (d) Ta foil. Shown are the superconducting transitions at 30 mT (300 Oe) and for 3 different angles (0, 45 and 90 of the field to the sample surface). Reprinted with permission from Ref. [35]. (e) ZrB crystals, measured at 0.1 mT (1 Oe), 0.5 mT (5 Oe), and 1.5 mT (15 Oe) applied field. The insets give details of the transition at 5 T (0.05 Oe) (FFC-W), 0.5 mT (5 Oe) (FFC-W and ZFC) and 5 mT (50 Oe) (SFC-C), where the F stands for ‘fast’ and S for ‘slow’. Reprinted with permission from Ref. [37]. (f) Susceptibility of an Al mesoscopic disk (2.5 m dia., thickness 0.1 m) at applied fields of 0.9, 3.5, 4.0, 6.5 and 12 mT (9, 35, 40, 65 and 120 G). The last 4 curves were multiplied by a factor of 10. The authors point out that there is no hysteresis when cooling/warming. Reprinted with permission from Ref. [63].
, FC (⊥) ∘). The inset shows details of the superconducting transition. Reprinted with permission from Ref. [49]. (b) Pb-films on PEEK, rolled up into cylinders. Data shown are FC curves in various applied fields (0.01 T – 0.3 T). Graph redrawn from the data presented in Ref. [50]. (c) Pb porous. FC and ZFC data are shown for various applied fields. The inset gives the standard measurement at low applied field. Reprinted with permission from Ref. [33]. (d) Ta foil. Shown are the superconducting transitions at 30 mT (300 Oe) and for 3 different angles (0, 45 and 90 of the field to the sample surface). Reprinted with permission from Ref. [35]. (e) ZrB crystals, measured at 0.1 mT (1 Oe), 0.5 mT (5 Oe), and 1.5 mT (15 Oe) applied field. The insets give details of the transition at 5 T (0.05 Oe) (FFC-W), 0.5 mT (5 Oe) (FFC-W and ZFC) and 5 mT (50 Oe) (SFC-C), where the F stands for ‘fast’ and S for ‘slow’. Reprinted with permission from Ref. [37]. (f) Susceptibility of an Al mesoscopic disk (2.5 m dia., thickness 0.1 m) at applied fields of 0.9, 3.5, 4.0, 6.5 and 12 mT (9, 35, 40, 65 and 120 G). The last 4 curves were multiplied by a factor of 10. The authors point out that there is no hysteresis when cooling/warming. Reprinted with permission from Ref. [63].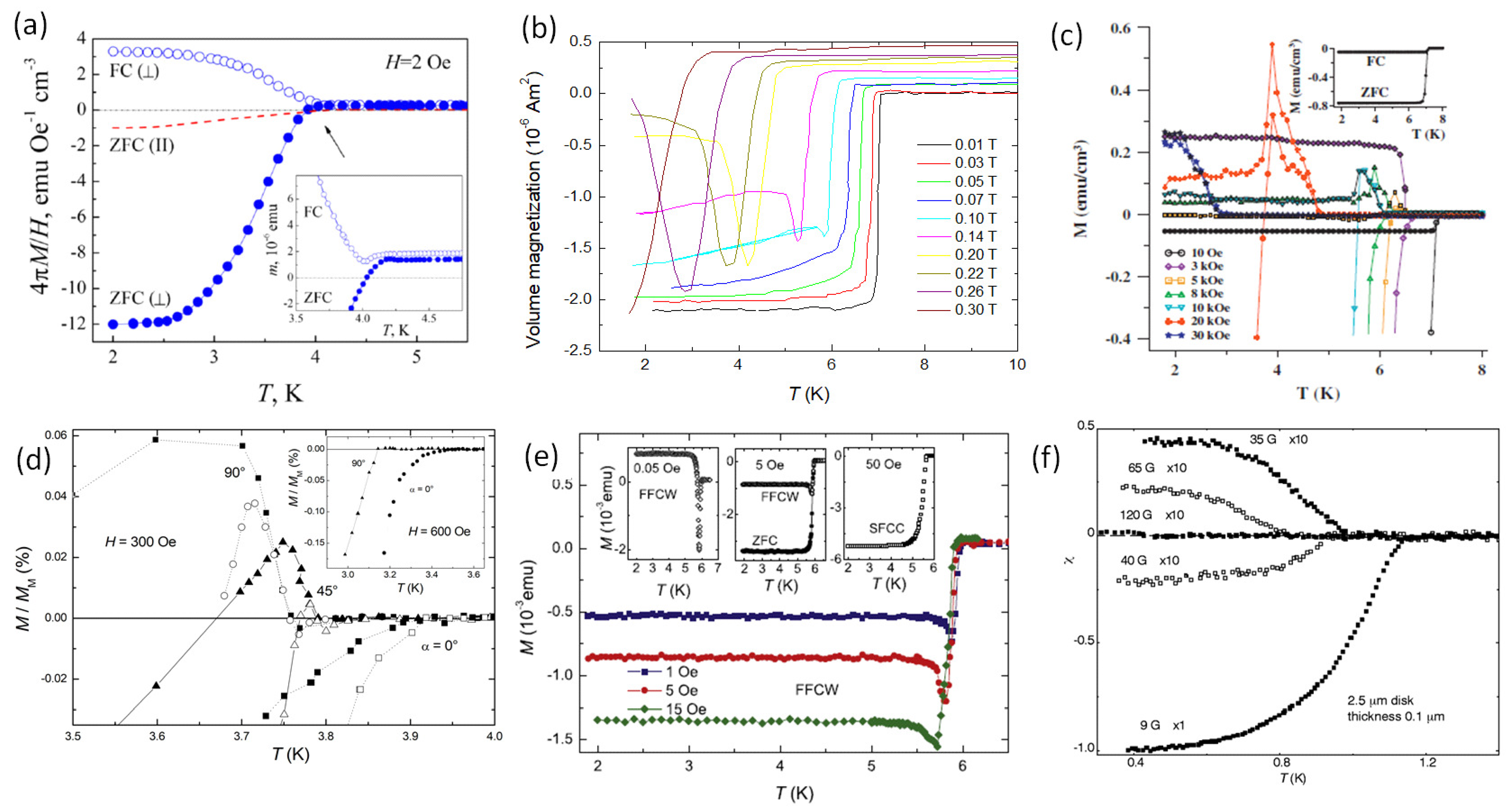
| name | type | citation | remarks | |||
|---|---|---|---|---|---|---|
| Nb bulk | commercial | 9.26 | ∼0.1 | – | [25,30,31,32,114,115,116,117] | stationary sample, SQUID |
| Nb bulk | from ingot | 9.25 | 0.05–0.1 | ∼1 | [27] | several types of samples, |
| disk-shaped, 3–6 mm ⌀ | ||||||
| Nb | calculated | – | – | – | [39,40] | disks, cylinders |
| Nb | crystal, poly | 9.38 | – | – | [35] | Nb crystal bar, polycryst. disks |
| Ag-Nb | wires | 9.2 | – | – | [64] | Nb-wires with Al sheath |
| Nb | films | 9.2 | 0.03 | – | [91] | strain-free thin films |
| Nb | films | 8.8/8.3 | – | – | [52] | thin films, relaxation |
| Nb-Gd | films | 8.85/4 | – | – | [54] | Gd-doped Nb films, various doping |
| nano-Nb | Nb powder+corund | – | – | – | [44] | granular Nb with various pore sizes |
| Nb/Cu | multilayers | 9.25 | 0.3 | – | [51] | PME, AC frequency dep. |
| Nb/Co | multilayers | 9.2 | – | – | [55] | Co-layer top/bottom of Nb (240 nm) |
| Au-Ho-Nb | trilayer | 8.52 | 0.3 | – | [56] | SR-study |
| Nb-AlOx-Nb | multiply connected | – | – | – | [58,59] | Josephson junction arrays |
| Pb | films on PEEK | 7.2 | 0.1 | – | [50] | rolled up as cylinders |
| Pb-glass | porous glass | 7.2 | ∼0.5 | – | [33] | 85 % filling of pores with Pb |
| Pb-nw | NWs 40nm dia | 7.2/4 | – | – | [53] | filled alumina template |
| Pb-Co | nanocomposite | 6.2 | – | – | [62] | Pb thin film with 1 vol-% Co |
| Al | thin film/disks | 1.1 | 0.7 | 0.3 | [63] | Al and Nb mesoscopic structures |
| Al | disk 1.5 m ⌀ | – | – | – | [65] | Al mesoscopic disk, 0.03 K |
| Ta | foil | 4.38 | – | 1.39 | [35] | Ta foil |
| Bi/Ni | Ni layer on top | 3.9 | 0.1 | – | [60] | PME in positive/negative fields |
| NbSe | single crystals | 7.15 | broad | – | [41] | very clean crystals |
| CaRhSn | single crystals | 8.4 | ∼ 2.5 | – | [46] | SQUID-VSM with various amplitudes |
| DyYRhB | crystals | ∼ 6 | 0.5 | – | [36] | various contents x tested |
| LiRhB | polycrystalline | 2,4-2,6 | – | 1 | [47] | different composition, partly 2 ’s |
| BiTe-FeTe | bilayer | ∼ 6 | – | – | [61] | BiTe (9 nm)/FeTe (140 nm) |
| In-Sn | cylinders, 3 phases | 6.2/4.7/3.7 | 0.2 | – | [34] | -InSn, -InSn, -Sn → extrinsic PME |
| In-Sn-O | films, Mg-dop. | 4.81 | 0.09 | – | [49] | doped ITO with Mg, 90/10 |
| MoRe | bulk | 4.47 | – | – | [45] | high-field PME |
| TiV | bulk | 4.15 | 0.2 | – | [38] | high-field PME |
| V/Fe | bilayers | 3.3–3.5 | – | 11–20 | [57] | 40.1 nm V / 1.1 nm Fe |
| ZrB | crystals | 5.95 | 0.08 | 0.8 | [37] | type II-1 sc., vortex interaction |
| B-doped diamond | thin film | 5.8–2.1 | – | – | [76] | various doping |
| MgB | granular | 38.2 | ∼ 2 | – | [70] | bulk/powder |
| MgB | granular/sintered | 38 | ∼ 2 | – | [71] | bulk, -irradiation |
| MgB | TiO np | – | – | 29.1 | [72,73] | 2 % TiO |
| MgB | tapes | 35–29.9 | ∼5 | – | [74] | Fe-sheated tapes with CoO nps |
| MgB | MgO | 37.1/38.8 | 15/0.5 | – | [75] | MgO ∼ 40%/ ∼ 7.3 % |
2.3. Apparatus
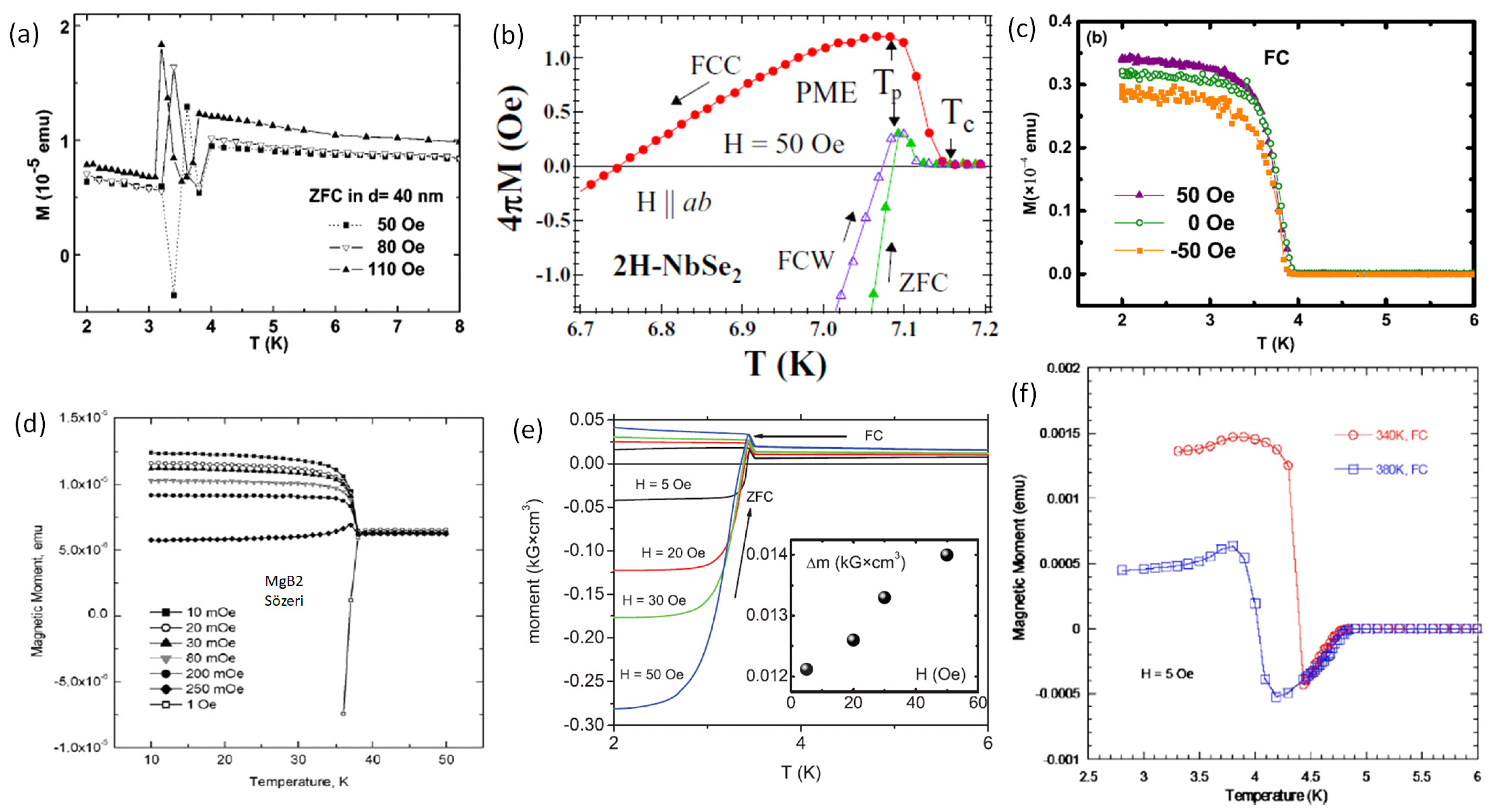
 ) Conventional QD SQUID measurement with moving sample and field generated by the superconducting magnet. (
) Conventional QD SQUID measurement with moving sample and field generated by the superconducting magnet. ( ) The magnetic moment is evaluated directly from the SQUID voltage, whereas the field was generated by a copper coil. More details on such magnetization loops will be discussed in Section 3.3 below. (a) Comparison of hysteresis loops measured by the two methods, sample Nb1. (b) Comparison of the virgin curves and their merging to the main hysteresis loops, sample Nb1.
) The magnetic moment is evaluated directly from the SQUID voltage, whereas the field was generated by a copper coil. More details on such magnetization loops will be discussed in Section 3.3 below. (a) Comparison of hysteresis loops measured by the two methods, sample Nb1. (b) Comparison of the virgin curves and their merging to the main hysteresis loops, sample Nb1.
 ) Conventional QD SQUID measurement with moving sample and field generated by the superconducting magnet. (
) Conventional QD SQUID measurement with moving sample and field generated by the superconducting magnet. ( ) The magnetic moment is evaluated directly from the SQUID voltage, whereas the field was generated by a copper coil. More details on such magnetization loops will be discussed in Section 3.3 below. (a) Comparison of hysteresis loops measured by the two methods, sample Nb1. (b) Comparison of the virgin curves and their merging to the main hysteresis loops, sample Nb1.
) The magnetic moment is evaluated directly from the SQUID voltage, whereas the field was generated by a copper coil. More details on such magnetization loops will be discussed in Section 3.3 below. (a) Comparison of hysteresis loops measured by the two methods, sample Nb1. (b) Comparison of the virgin curves and their merging to the main hysteresis loops, sample Nb1.
 ) and stationary sample (
) and stationary sample ( ) during an MHL run is depicted in Figure 4. The results of this comparison enabled then the further measurements of the PME on more standard magnetometers as the specific features of the PME curves were known. Of course, the reduced scan length was kept for all further measurements of the PME on different SQUID systems (Tokyo, Nancy).
) during an MHL run is depicted in Figure 4. The results of this comparison enabled then the further measurements of the PME on more standard magnetometers as the specific features of the PME curves were known. Of course, the reduced scan length was kept for all further measurements of the PME on different SQUID systems (Tokyo, Nancy).3. Specific measurements, details of the superconducting transitions of Nb disks and discussion
3.1. Investigated Nb samples
| sample | Nb1 | Nb2 | Nb3 | Nb4 |
|---|---|---|---|---|
| sample origin | D4S2 | D2S2 | D10S2-1 | DI08-1 |
| Comment | “basic” | abraded | edge sand | implanted |
| PME | yes | no | yes | yes |
| radiusr (mm) | 3.2 | 3.2 | 3.2 | 3.2 |
| thicknesst (m) | 127 | ∼110 | 127 | 250 |
| (K) | 9.20 | 9.26 | 9.24 | 9.28 |
| (K) | 9.15 | n/a | 9.24 | 9.17(5) |
| (K) | 9.05(5) | n/a | 9.06(5) | 9.08 |
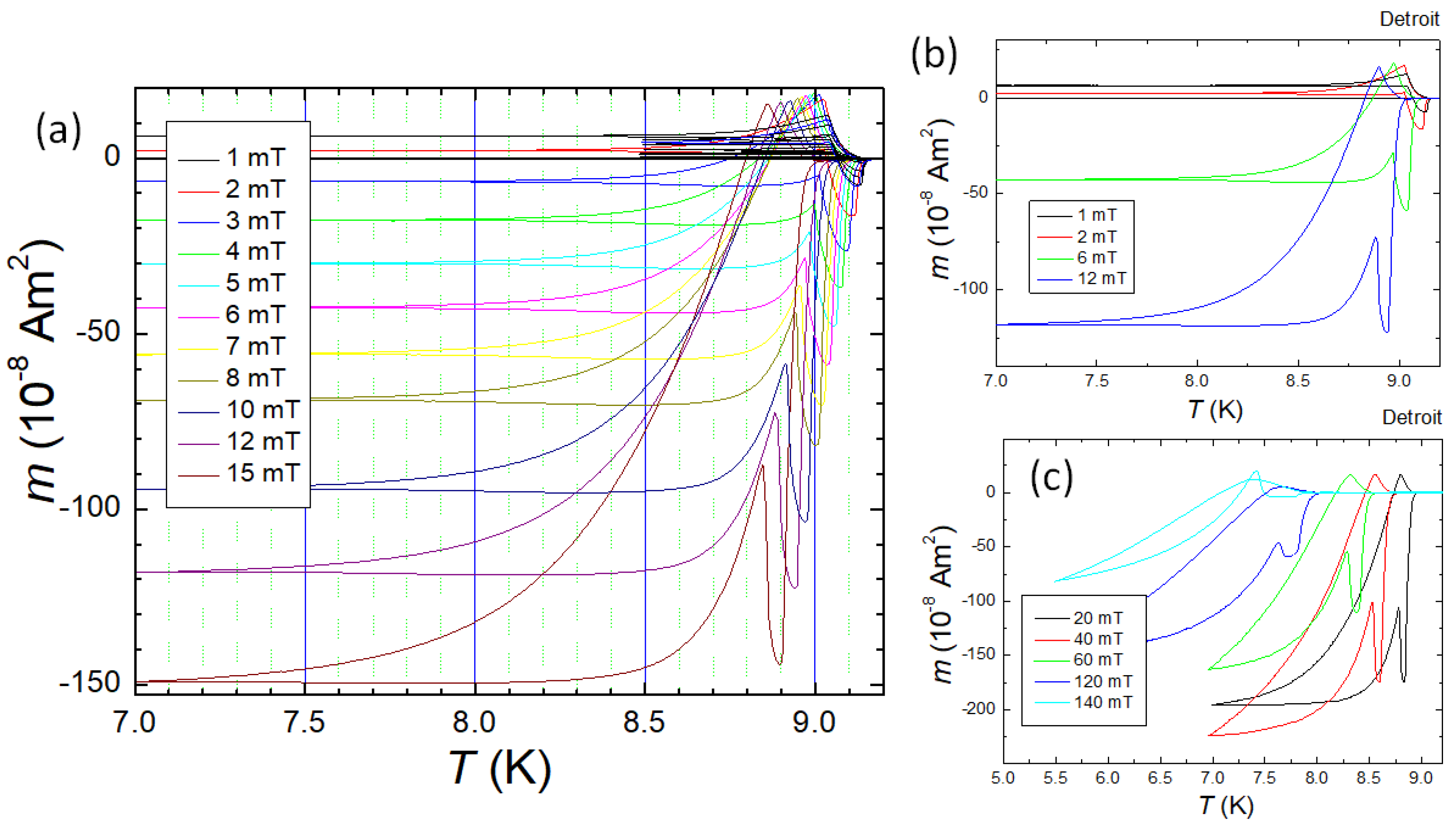
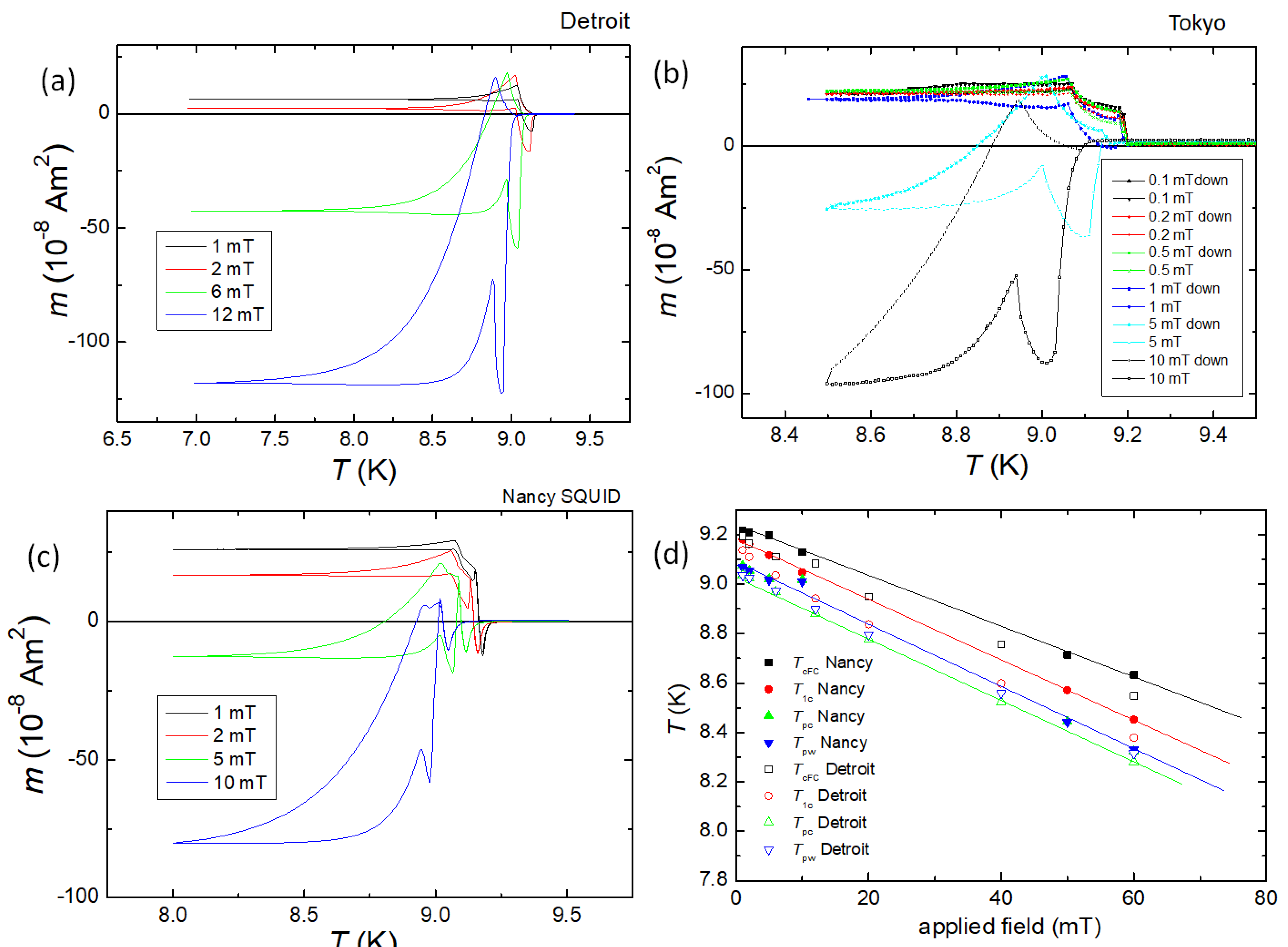
3.2. Observation of PME – superconducting transitions
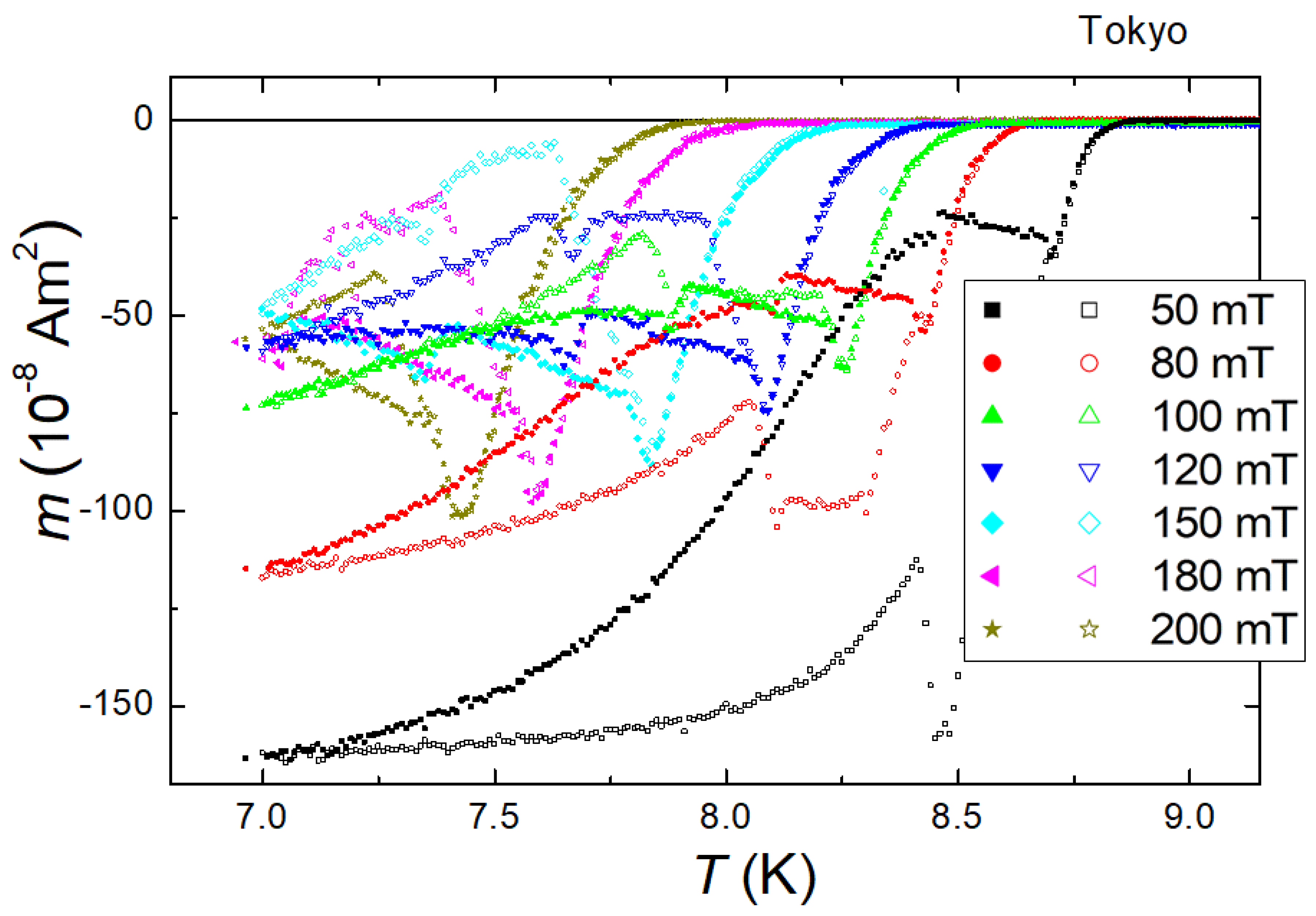
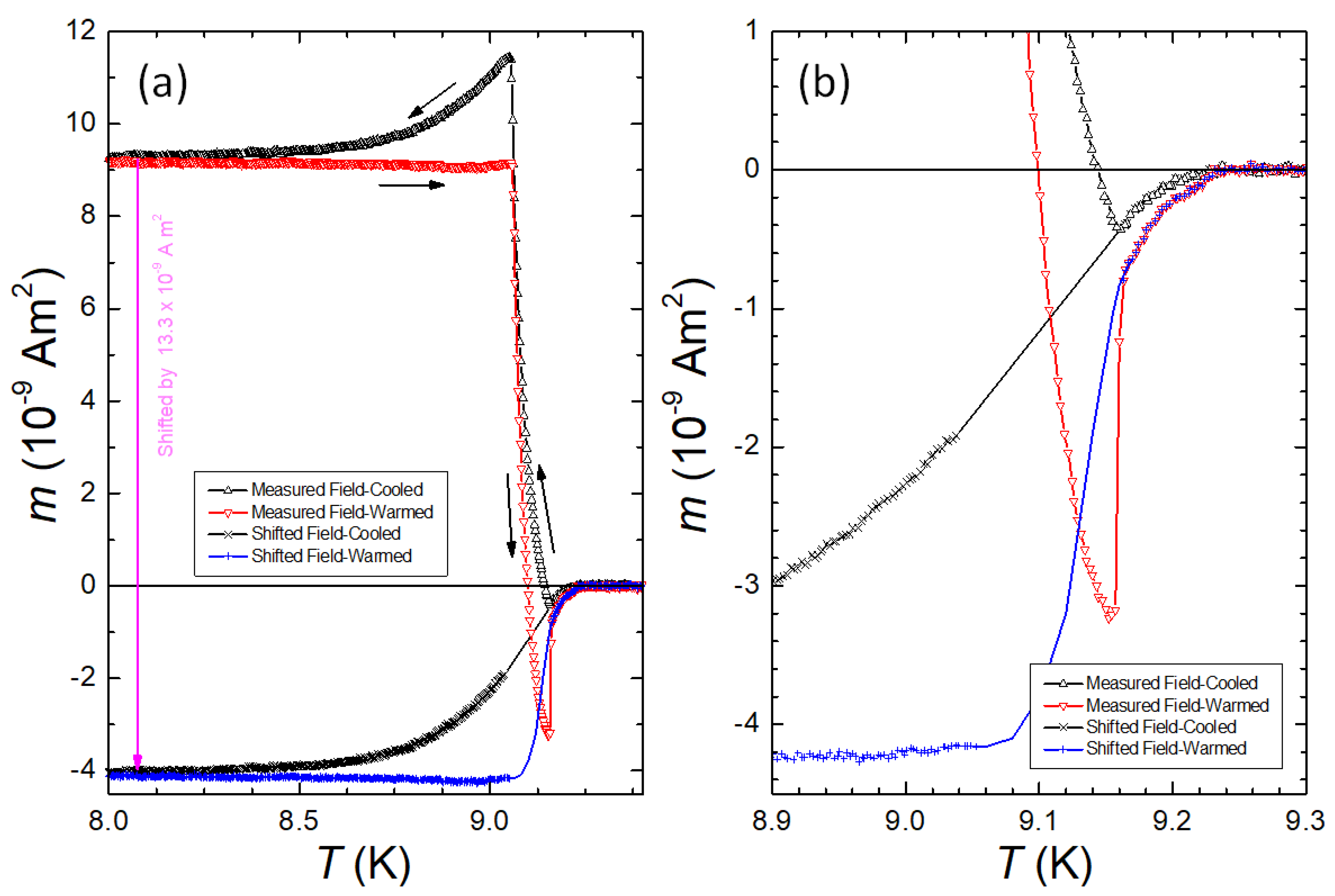
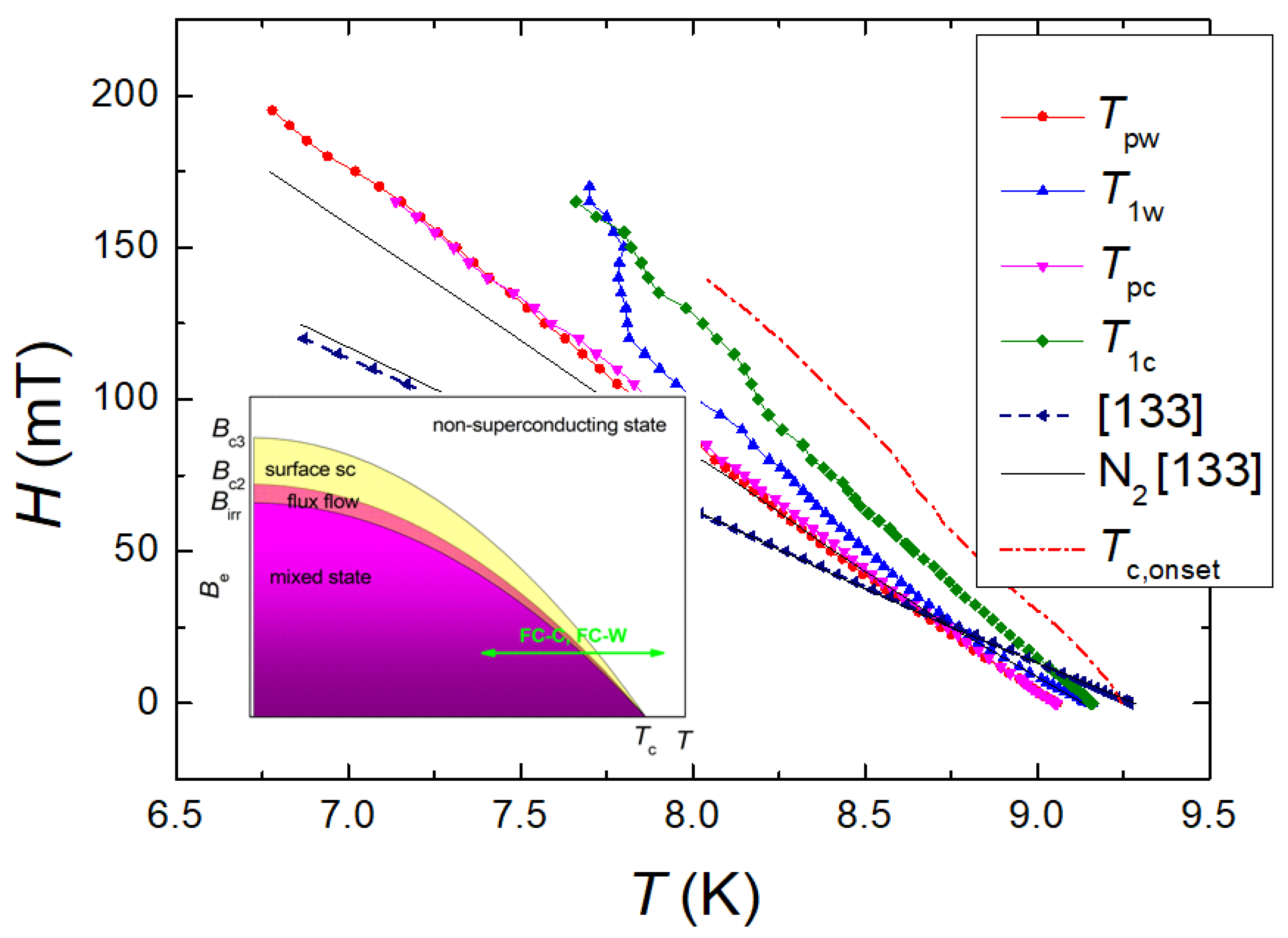
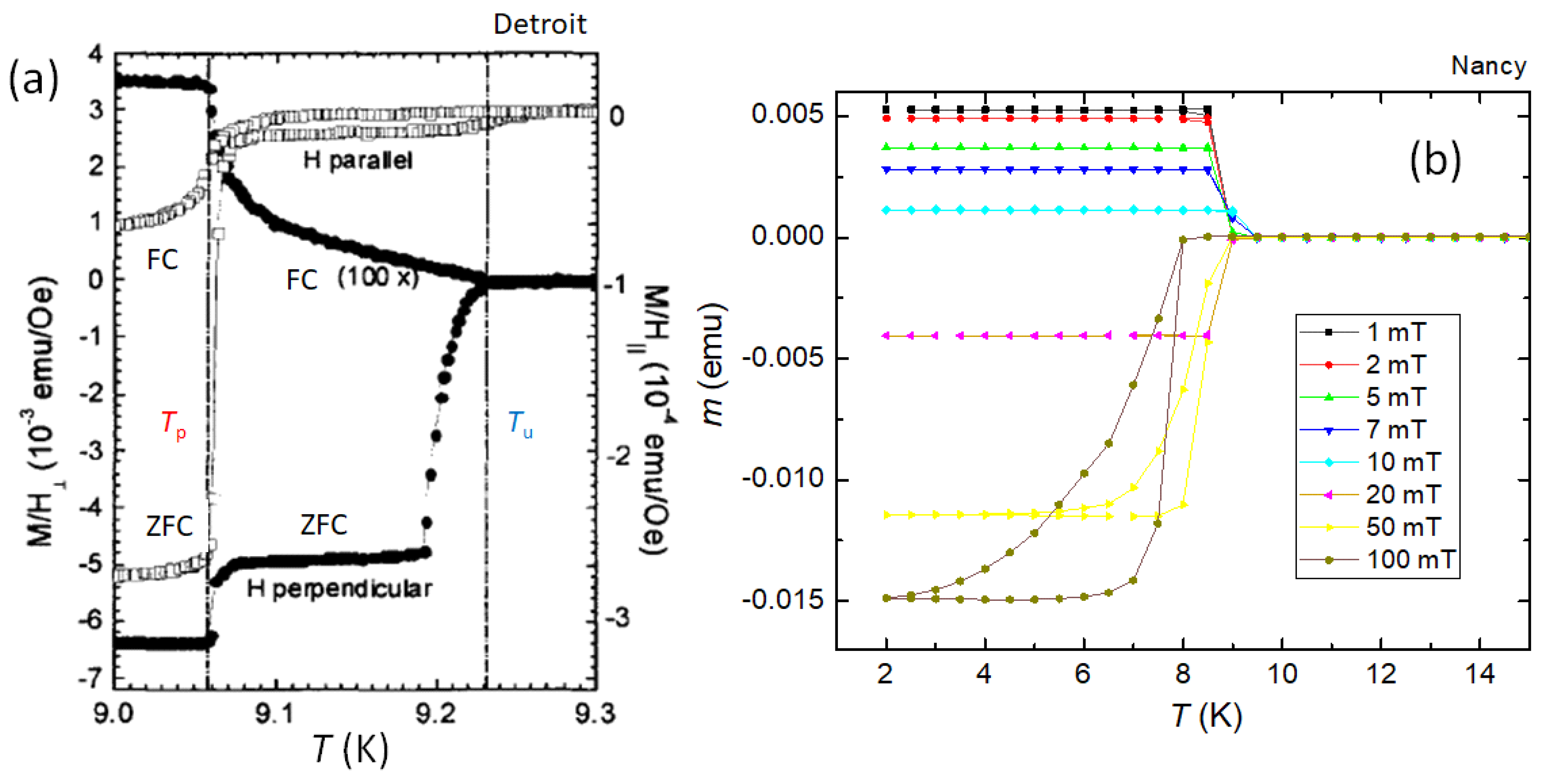
3.3. Magnetization loops close to the superconducting transition
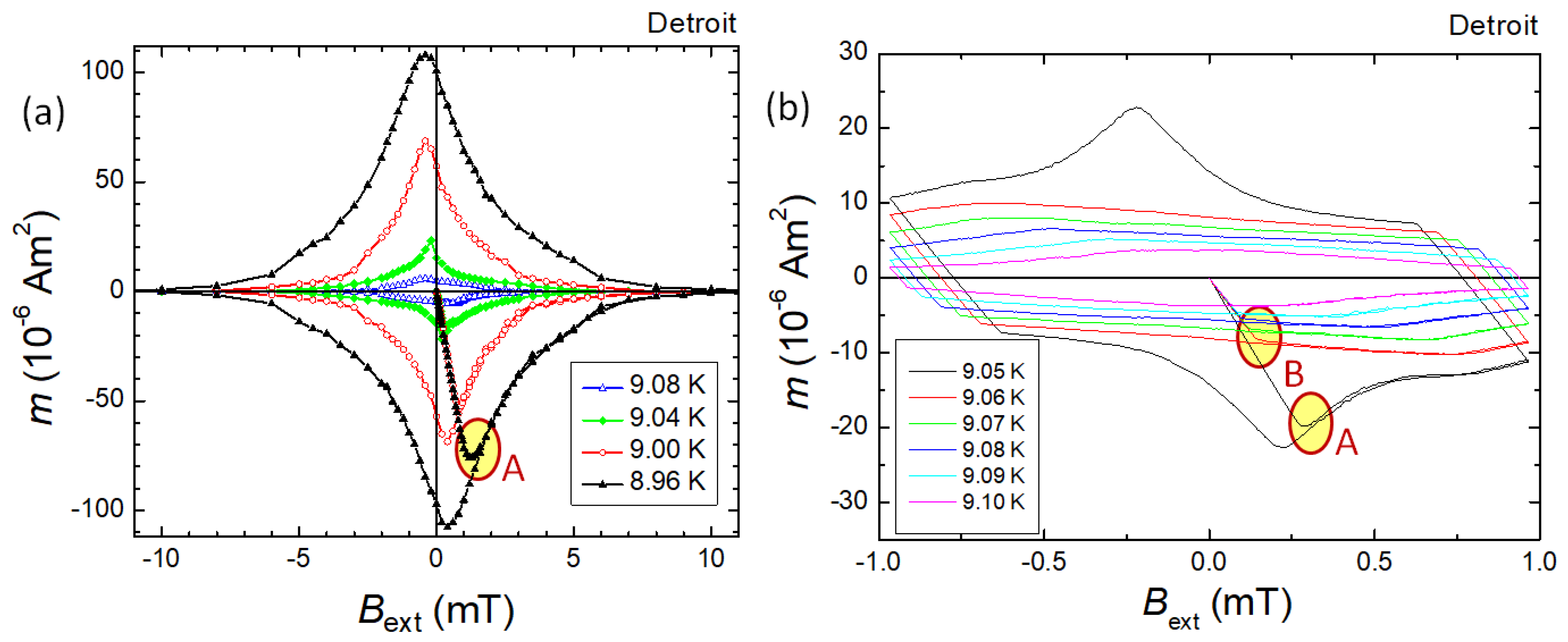
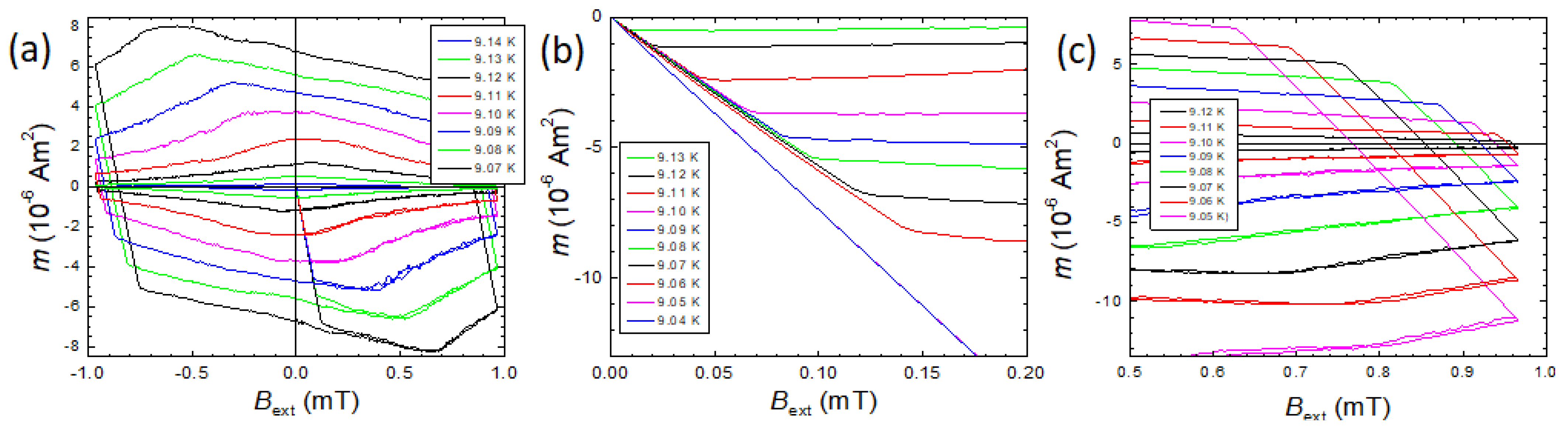
 ) and the slope of the component C in the main panel (
) and the slope of the component C in the main panel ( ) are the same. It is obvious from this graph that at an abrupt change in the MHL shape takes place, and the normal flux pinning vanishes. At 9.06 K, the component P is measured follwing a completely different slope (
) are the same. It is obvious from this graph that at an abrupt change in the MHL shape takes place, and the normal flux pinning vanishes. At 9.06 K, the component P is measured follwing a completely different slope ( ).
).
 ) and the slope of the component C in the main panel (
) and the slope of the component C in the main panel ( ) are the same. It is obvious from this graph that at an abrupt change in the MHL shape takes place, and the normal flux pinning vanishes. At 9.06 K, the component P is measured follwing a completely different slope (
) are the same. It is obvious from this graph that at an abrupt change in the MHL shape takes place, and the normal flux pinning vanishes. At 9.06 K, the component P is measured follwing a completely different slope ( ).
).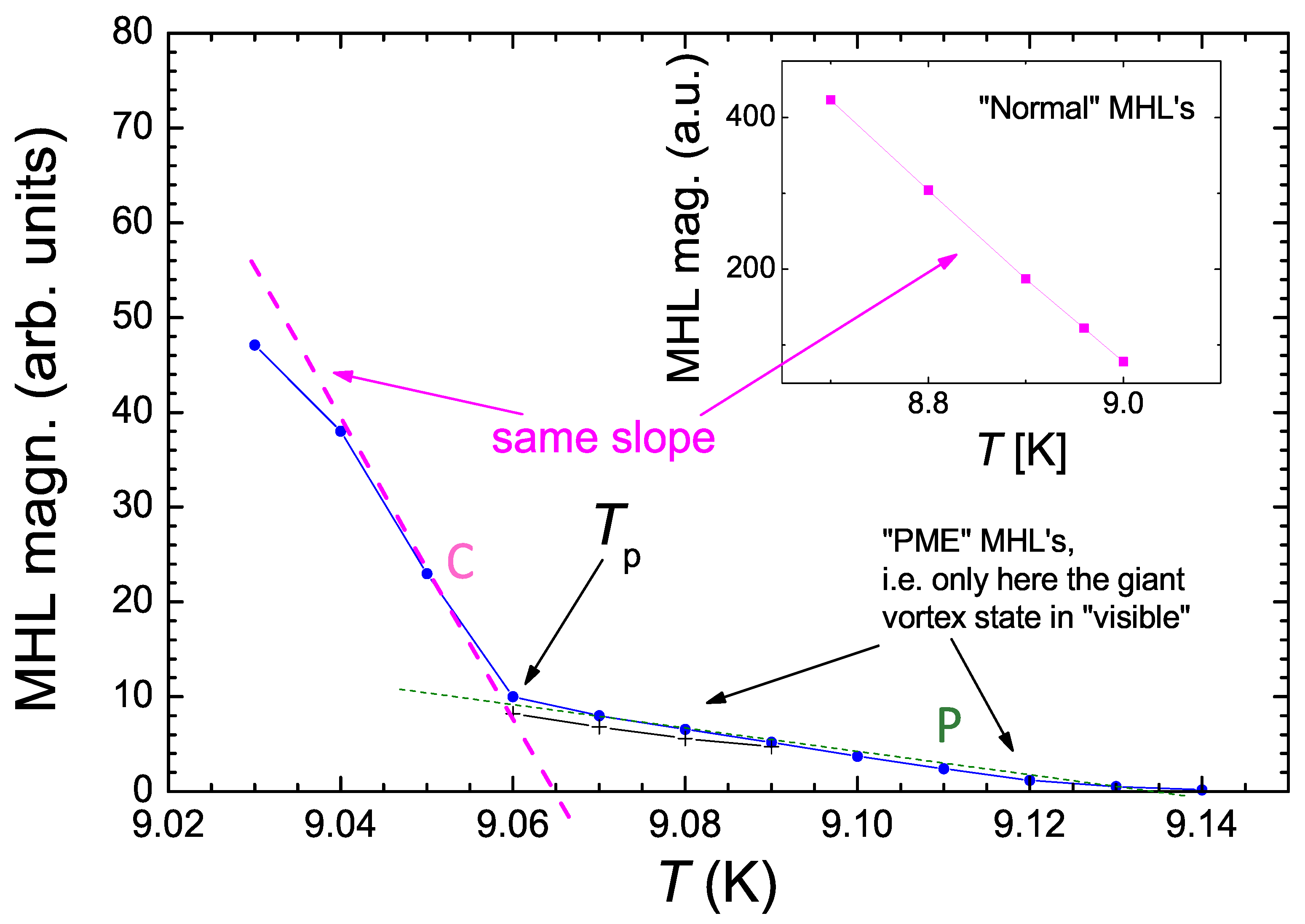
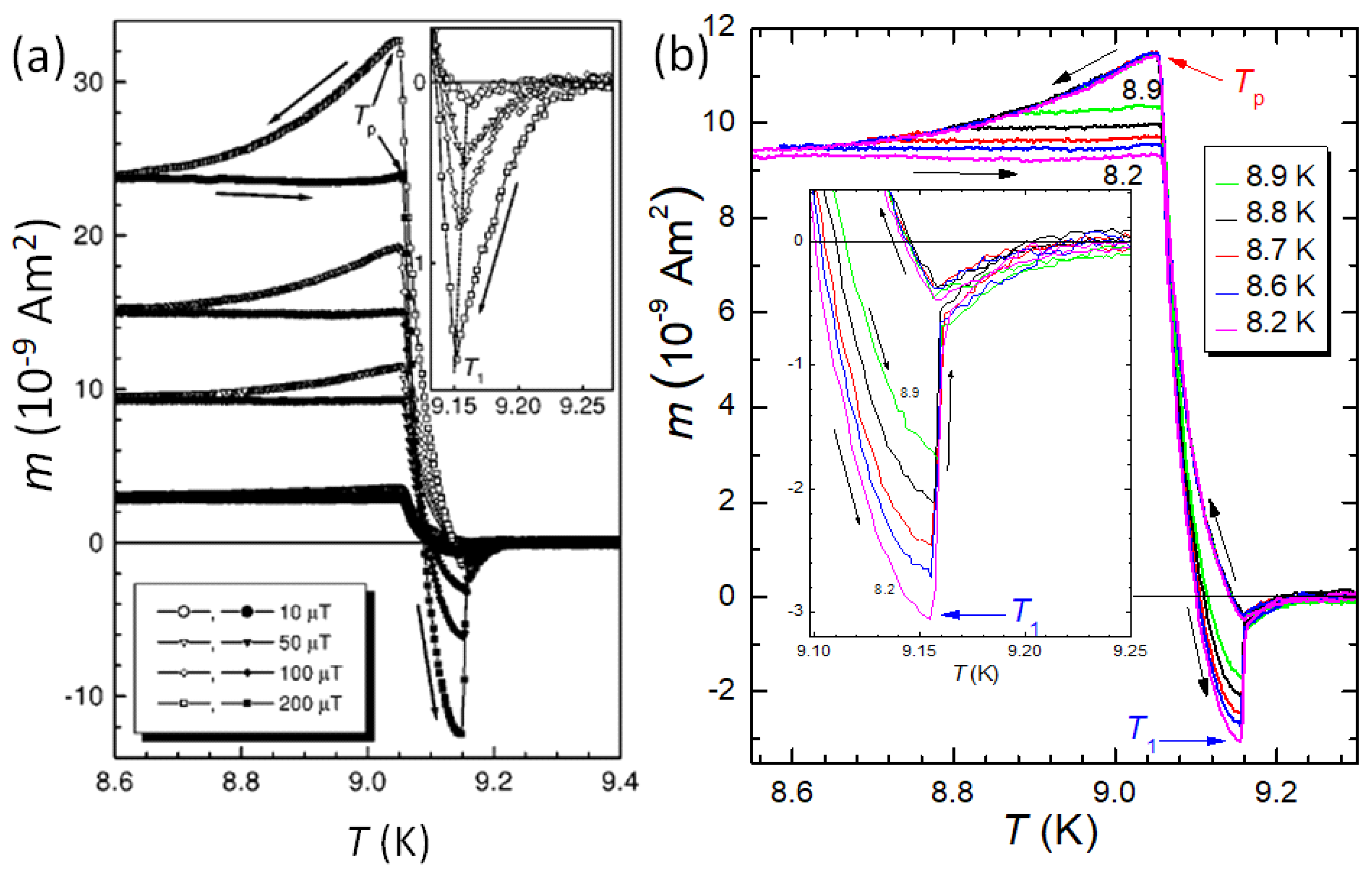
 ). The inset to Figure 13 presents the same analysis for the temperature range 8.7 9.0 K, i.e., the range where the "normal" MHL shape is found. The slope obtained here and the slope of the magenta dashed line in the main panel are the same. However, above 9.06 K, abruptly changes the slope and decreases, again nearly linearly, but with a slope being about one order of magnitude smaller, as indicated by the dashed green line (
). The inset to Figure 13 presents the same analysis for the temperature range 8.7 9.0 K, i.e., the range where the "normal" MHL shape is found. The slope obtained here and the slope of the magenta dashed line in the main panel are the same. However, above 9.06 K, abruptly changes the slope and decreases, again nearly linearly, but with a slope being about one order of magnitude smaller, as indicated by the dashed green line ( ). Thus, in the temperature range , the PME-MHLs are visible, giving an indication of the giant vortex state.
). Thus, in the temperature range , the PME-MHLs are visible, giving an indication of the giant vortex state. ), and sample Nb2 (abraded,
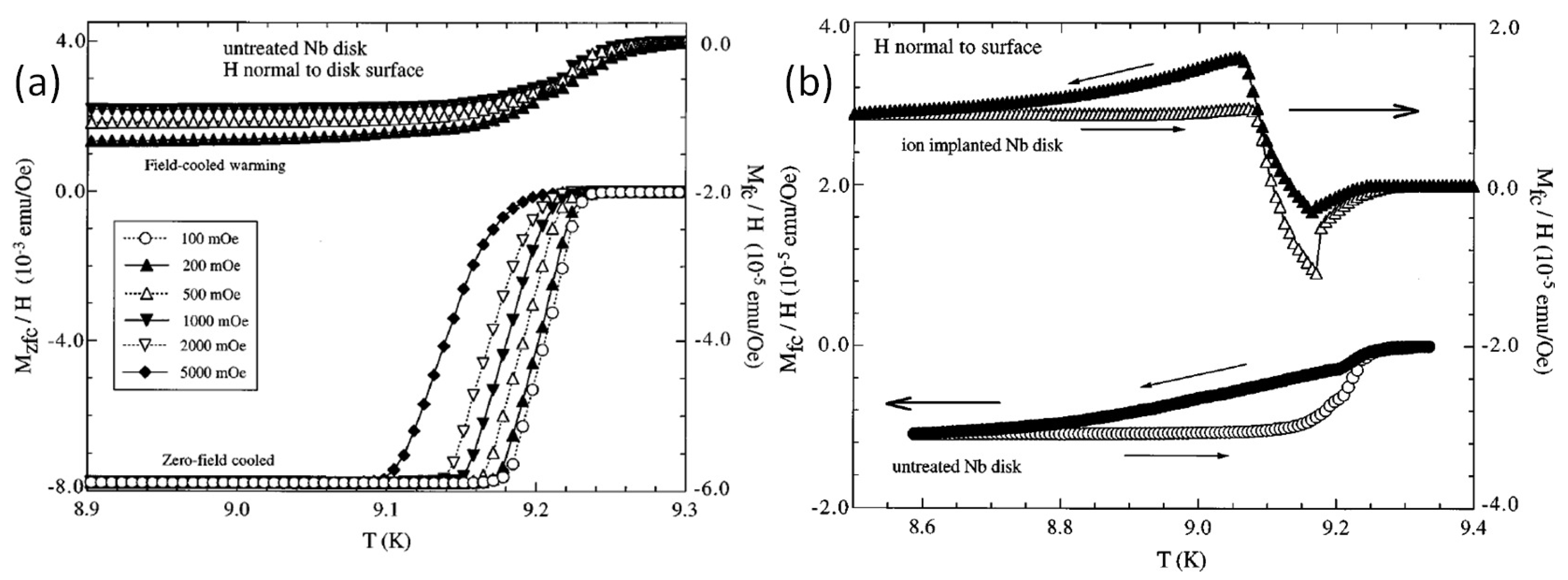
), and sample Nb2 (abraded,  ). (b). Details around of the data shown in (a). (c). FCC and FCW curves in an applied field of 20 mT. (d). FCC and FCW curves in an applied field of 60 mT. The abraded sample does not show any feature of the PME at any temperature/field as compared to the as-prepared sample Nb1.
). (b). Details around of the data shown in (a). (c). FCC and FCW curves in an applied field of 20 mT. (d). FCC and FCW curves in an applied field of 60 mT. The abraded sample does not show any feature of the PME at any temperature/field as compared to the as-prepared sample Nb1.
 ), and sample Nb2 (abraded,
), and sample Nb2 (abraded,  ). (b). Details around of the data shown in (a). (c). FCC and FCW curves in an applied field of 20 mT. (d). FCC and FCW curves in an applied field of 60 mT. The abraded sample does not show any feature of the PME at any temperature/field as compared to the as-prepared sample Nb1.
). (b). Details around of the data shown in (a). (c). FCC and FCW curves in an applied field of 20 mT. (d). FCC and FCW curves in an applied field of 60 mT. The abraded sample does not show any feature of the PME at any temperature/field as compared to the as-prepared sample Nb1.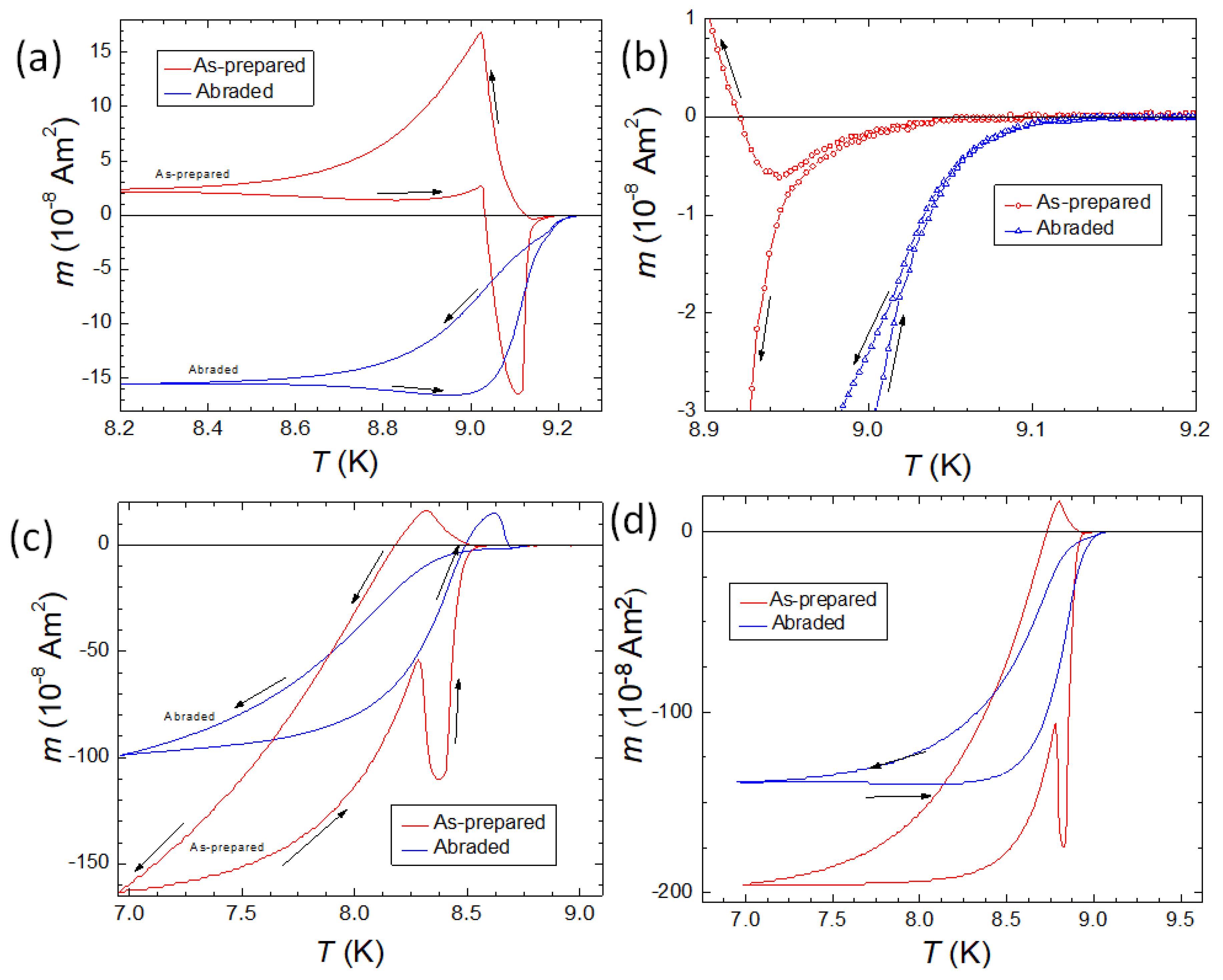
3.4. Manipulating the PME
3.5. Time evolution of PME in Nb
3.6. AC susceptibility measurements on Nb disks
 ) and the imaginary part (,
) and the imaginary part (,  ). Both cooling and warming curves are represented. A tiny positive signal is obtained for , similar to the case of ZrB. Figure 17b shows the same experiments but with an applied DC field of 2 mT, Figure 17c for an applied DC field of 5 mT and Figure 17d for an applied DC field of 10 mT. Thus, traces of PME in Nb can only be observed at low frequencies (1 Hz) and small applied DC fields (1 mT) and AC amplitudes (1 mT). As the warming (72 mK/min) /cooling (30 mK/min) experiments were done with different temperature sweep rates, this may be a reason for the shift of the loss peak towards higher temperatures, but the different shape of peak and the kinks do correspond well to the DC measurements. These observations demonstrate the presence of PME signatures also in the AC susceptibility measurements, and the signatures are present in both the real and imaginary part of the susceptibility.
). Both cooling and warming curves are represented. A tiny positive signal is obtained for , similar to the case of ZrB. Figure 17b shows the same experiments but with an applied DC field of 2 mT, Figure 17c for an applied DC field of 5 mT and Figure 17d for an applied DC field of 10 mT. Thus, traces of PME in Nb can only be observed at low frequencies (1 Hz) and small applied DC fields (1 mT) and AC amplitudes (1 mT). As the warming (72 mK/min) /cooling (30 mK/min) experiments were done with different temperature sweep rates, this may be a reason for the shift of the loss peak towards higher temperatures, but the different shape of peak and the kinks do correspond well to the DC measurements. These observations demonstrate the presence of PME signatures also in the AC susceptibility measurements, and the signatures are present in both the real and imaginary part of the susceptibility.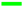 ) and 1 mT (
) and 1 mT ( ) were applied. (a). Measurement with an applied DC field of 1 mT. The blue arrow points to a secondary loss peak when warming up. The inset presents the superconducting transition for 1 Hz, DC field 1 mT, AC amplitude 1 mT. The imaginary part, , is given by
) were applied. (a). Measurement with an applied DC field of 1 mT. The blue arrow points to a secondary loss peak when warming up. The inset presents the superconducting transition for 1 Hz, DC field 1 mT, AC amplitude 1 mT. The imaginary part, , is given by  , and the real part by
, and the real part by  . The magenta arrow indicates a tiny positive signal in . (b). Measurement with an applied DC field of 2 mT. (c). Measurement with an applied DC field of 5 mT. (d). Measurement with an applied DC field of 10 mT.
. The magenta arrow indicates a tiny positive signal in . (b). Measurement with an applied DC field of 2 mT. (c). Measurement with an applied DC field of 5 mT. (d). Measurement with an applied DC field of 10 mT.
 ) and 1 mT (
) and 1 mT ( ) were applied. (a). Measurement with an applied DC field of 1 mT. The blue arrow points to a secondary loss peak when warming up. The inset presents the superconducting transition for 1 Hz, DC field 1 mT, AC amplitude 1 mT. The imaginary part, , is given by
) were applied. (a). Measurement with an applied DC field of 1 mT. The blue arrow points to a secondary loss peak when warming up. The inset presents the superconducting transition for 1 Hz, DC field 1 mT, AC amplitude 1 mT. The imaginary part, , is given by  , and the real part by
, and the real part by  . The magenta arrow indicates a tiny positive signal in . (b). Measurement with an applied DC field of 2 mT. (c). Measurement with an applied DC field of 5 mT. (d). Measurement with an applied DC field of 10 mT.
. The magenta arrow indicates a tiny positive signal in . (b). Measurement with an applied DC field of 2 mT. (c). Measurement with an applied DC field of 5 mT. (d). Measurement with an applied DC field of 10 mT.
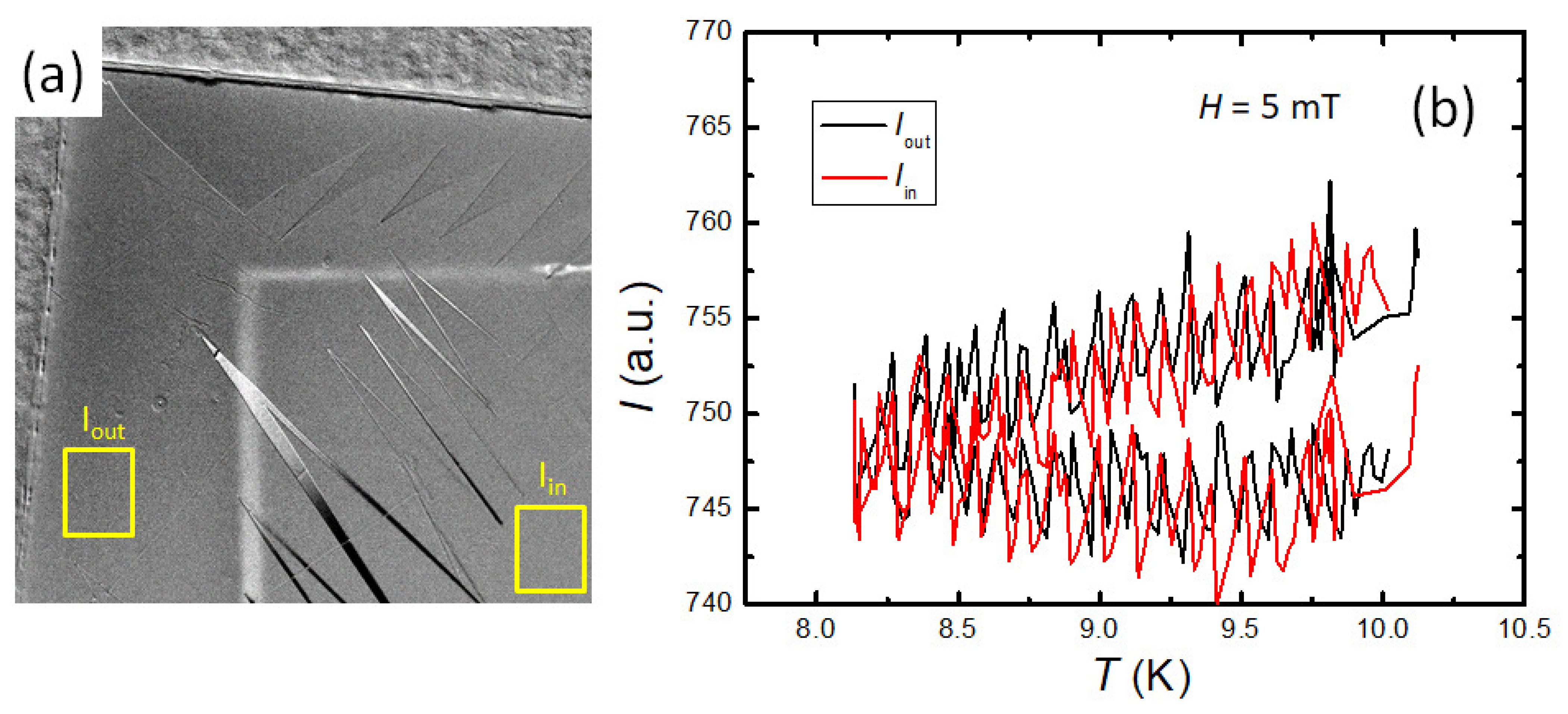
4. Magnetic Imaging

 , left y-axis) and theoretical model (
, left y-axis) and theoretical model ( , left y-axis); calculated dimensionless screening current density, flowing parallel to the x-axis in (a) inside the plane of the thin film heterostructure (gray curve, right side y-axis). Dashed lines show that the position of the maximum in coincides with that of the null in . Image reproduced with permission from Ref. [56].
, left y-axis); calculated dimensionless screening current density, flowing parallel to the x-axis in (a) inside the plane of the thin film heterostructure (gray curve, right side y-axis). Dashed lines show that the position of the maximum in coincides with that of the null in . Image reproduced with permission from Ref. [56].
 , left y-axis) and theoretical model (
, left y-axis) and theoretical model ( , left y-axis); calculated dimensionless screening current density, flowing parallel to the x-axis in (a) inside the plane of the thin film heterostructure (gray curve, right side y-axis). Dashed lines show that the position of the maximum in coincides with that of the null in . Image reproduced with permission from Ref. [56].
, left y-axis); calculated dimensionless screening current density, flowing parallel to the x-axis in (a) inside the plane of the thin film heterostructure (gray curve, right side y-axis). Dashed lines show that the position of the maximum in coincides with that of the null in . Image reproduced with permission from Ref. [56].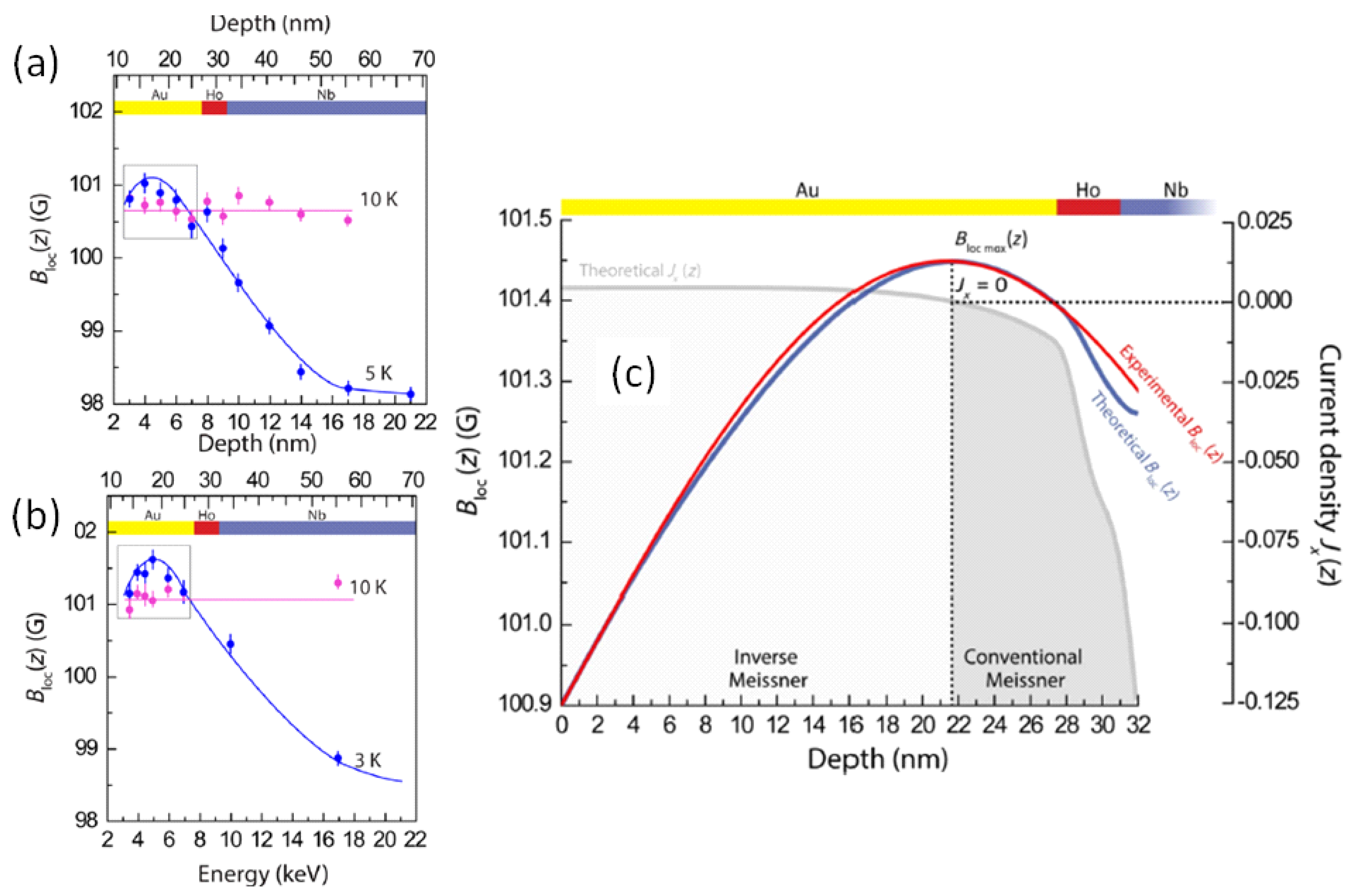
5. Discussion
6. Conclusions and outlook
Author Contributions
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Meissner, W.; Ochsenfeld, R. Ein neuer Effekt bei Eintritt der Supraleitfähigkeit. Naturwissenschaften 1933, 21, 787–788. [Google Scholar] [CrossRef]
- Tinkham, M. Introduction to Superconductivity, 2nd ed.; Dover Publications Inc.: New York, USA, 1996. [Google Scholar]
- Savitskii, E. M.; Baron, V. V.; Efimov, Yu. V.; Bychkova, M. I.; Myzenkova, L. F. Superconducting Materials, 1st ed.; Plenum Press: New York, London, 1973. [Google Scholar]
- Rose-Innes, A.C.; Rhoderick, E.H. Introduction to Superconductivity, 2nd ed.; Pergamon Press plc.: Oxford, U.K, 1978. [Google Scholar]
- Huebener, R. P. Magnetic Flux Structures in Superconductors, 2nd ed.; Springer: Heidelberg, Germany, 2001. [Google Scholar]
- Poole, C. P. (ed.) Handbook of Superconductivity, 1st ed.; Elsever: Amsterdam, The Netherlands, 1995. [Google Scholar]
- Buckel, W.; Kleiner, R. Supraleitung. Grundlagen und Anwendungen, 7th ed.; Wiley-VCH: Weinheim, Germany, 2013. [Google Scholar] [CrossRef]
- Koblischka, M. R. Magnetic properties of high-temperature superconductors; Alpha Science International Ltd.: Oxford, UK, 2009. [Google Scholar]
- Pitaevskii, L. Phenomenology and Microscopic Theory: Theoretical Foundations. In Superconductivity. Conventional and Unconventional Superconductors, Vol. 1; Bennemann, K.H., Ketterson, J.B., Eds.; Springer: Berlin, Heidelberg, 2008. [Google Scholar]
- Mangin, P.; Kahn, R. Superconductivity. An Introduction; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Svedlindh, P.; Niskanen, K.; Norling, P.; Nordblad, P.; Lundgren, L.; Lönnberg, B.; Lundström, T. Anti-Meissner Effect in the BiSrCaCuO System. Physica C 1989, 162–164, 1365–1366. [Google Scholar] [CrossRef]
- Blunt, F. J.; Perry, A. R.; Campbell, A. M.; Liu, R. S. An investigation of the appearance of positive magnetic moments on field cooling some superconductors. Physica C 1991, 175, 539–544. [Google Scholar] [CrossRef]
- Braunisch, W.; Knauf, N.; Kataev, V.; Neuhausen, S.; Grütz, A.; Kock, A.; Roden, B.; Khomskii, D.; Wohlleben, D. Paramagnetic Meissner Effect in Bi High-Temperature Superconductors. Phys. Rev. Lett. 1992, 68, 1908–1911. [Google Scholar] [CrossRef]
- Braunisch, W.; Knauf, N.; Bauer, G.; Kock, A.; Becker, A.; Freitag, B.; Grütz, A.; Kataev, V.; Neuhausen, S.; Roden, B.; Khomskii, D.; Wohlleben, D. Paramagnetic Meissner effect in high-Tc superconductors. Phys. Rev. B 1993, 48, 4030–4042. [Google Scholar] [CrossRef]
- Kusmartsev, F. V. Destruction of the Meissner effect in granular high-temperature superconductors. Phys. Rev. Lett. 1992, 69, 2268–2271. [Google Scholar] [CrossRef]
- Heinzel, C.; Theilig, T.; Ziemann, P. Paramagnetic Meissner effect analyzed by second harmonics of the magnetic susceptibility: consistency with a ground state carrying spontaneous currents. Phys. Rev. B 1993, 48, 3445–3454. [Google Scholar] [CrossRef]
- Riedling, S., Bräuchle, G., Lucht, R., Röhberg, K., v. Löhneysen, H., Claus, H., Erb, A., Müller-Vogt, G. Observation of the Wohlleben effect in YBa2Cu3O7-δ single crystals. Phys. Rev. B 1994 49, 13283-13286. [CrossRef]
- Khomskii, D. Wohlleben effect (Paramagnetic Meissner effect) in high-temperature superconductors. J. Low Temp. Phys. 1994, 95, 205–223. [Google Scholar] [CrossRef]
- Niskanen, K.; Magnusson, J.; Svedlindh, P.; Ullström, A.-S.; Lundström, T. Anti-Meissner effect and low magnetic relaxation in sintered Bi-2212. Physica B 1994 194-196, 1549-1550. [CrossRef]
- Chen, D.-X.; Hernando, A. Paramagnetic Meissner effect and 0-π Josephson junctions. Europhys. Lett. 1994, 26, 365–370. [Google Scholar] [CrossRef]
- Dominguez, D.; Jagla, E. A.; Balseiro, C. A. Phenomenological theory of the paramagnetic Meissner effect. Phys. Rev. Lett. 1994, 72, 2773–2776. [Google Scholar] [CrossRef]
- Kötzler, J.; Baumann, M.; Knauf, N. , Complete inversion of the Meissner effect in Bi2Sr2CaCu2O8+δ ceramics. Phys. Rev. B 1995, 52, 1215–1218. [Google Scholar] [CrossRef]
- Chen, F.H.; Horng, W.C.; Hsu, H.T.; Tseng, T.Y. Paramagnetic Meissner effect of high-temperature granular superconductors - Interpretation by anisotropic and isotropic models. J. Supercond. 1995, 8, 43–56. [Google Scholar] [CrossRef]
- Magnusson, J.; Papadopoulou, E.; Svedlindh, P.; Nordblad, P. AC susceptibility of a paramagnetic Meissner effect sample. Physica C 1998, 297, 317–325. [Google Scholar] [CrossRef]
- Thompson, D. J.; Minhaj, M. S. M.; Wenger, L. E.; Chen, J. T. Observation of Paramagnetic Meissner Effect in Niobium Disks, Phys. Rev. Lett. 1995, 75, 529–532. [Google Scholar] [CrossRef]
- Minhaj, M. S. M.; Thompson, D. J.; Wenger, L. E.; Chen, J. T. Paramagnetic Meissner Effect in a Niobium Disk. Physica C 1995 235-240, 2519-2520.
- Kostić, P.; Veal, B.; Paulikas, P.; Welp, U.; Todt, V. K.; Gu, C.; Geiser, U.; Williams, J. M.; Carlson, K. D.; Klemm, R. A. Paramagnetic Meissner effect in Nb. Phys. Rev. B 1996, 53, 791–801. [Google Scholar] [CrossRef]
- Rice, T. M.; Sigrist, M. Comment on `Paramagnetic Meissner effect in Nb’. Phys. Rev. B 1997, 55, 14647–14648. [Google Scholar] [CrossRef]
- Kostić, P.; Veal, B.; Paulikas, P.; Welp, U.; Todt, V. K.; Gu, C.; Geiser, U.; Williams, J. M.; Carlson, K. D.; Klemm, R. A. Reply to Comment on `Paramagnetic Meissner effect in Nb’. Phys. Rev. B 1997, 55, 14649–14652. [Google Scholar] [CrossRef]
- Thompson, D. J.; Wenger, L. E.; Chen, J. T. Inducing and enhancing the paramagnetic Meissner effect in Nb disks. Czech J. Phys. 1996, 46, 1195–1196. [Google Scholar] [CrossRef]
- Thompson, D. J.; Wenger, L. E.; Chen, J. T. Paramagnetic Meissner effect in conventional Nb superconductors. J. Low Temp. Phys. 1996, 105, 509–514. [Google Scholar] [CrossRef]
- Thompson, D. J.; Wenger, L. E.; Chen, J. T. Inducing the paramagnetic Meissner effect in Nb disks by surface ion implantation. Phys. Rev. B 1996, 54, 16096–16100. [Google Scholar] [CrossRef]
- Charnaya, E. V.; Lee, M. K.; Ciou, Y. S.; Tien, C.; Chang, L. J.; Kumzerov, Yu. A. Paramagnetic response in a Pb-porous glass nanocomposite superconductor. Physica C 2013, 495, 221–224. [Google Scholar] [CrossRef]
- Chu, S.; Schwartz, A. J.; Massalski, T. B.; Laughlin, D. E. Extrinsic paramagnetic Meissner effect in multiphase indium-tin alloys. Appl. Phys. Lett. 2006, 89, 111903. [Google Scholar] [CrossRef]
- de Lima, O.F.; Avila, M.A.; Cardoso, C.A. Study of paramagnetic frozen states in superconducting Nb and Ta samples. Physica C 1997, 282-287, 2201–2202. [Google Scholar] [CrossRef]
- Dmitriev, V.M.; Terekhov, A.V.; Zaleski, A.; Khatsko, E.N.; Kalinin, P.S.; Rykova, A.I.; Gurevich, A.M.; Glagolev, S.A.; Khlybov, E.P.; Kostyleva, I.E.; Lachenkov, S.A. The Volleben effect in magnetic superconductors Dy1–xYxRh4B4 (x= 0.2, 0.3, 0.4, and 0.6). Low Temp. Phys. 2012, 38, 154–156. [Google Scholar] [CrossRef]
- Ge, J.Y.; Gladilin, V.N.; Sluchanko, N.E.; Lyashenko, A.; Filipov, V.B.; Indekeu, J.O.; Moshchalkov, V.V. Paramagnetic Meissner effect in ZrB12 single crystal with non-monotonic vortex-vortex interactions. New. J. Phys. 2017, 19, 093020; [Google Scholar] [CrossRef]
- Matin, M.; Sharath Chandra, L. S.; Chattopadhyay, M. K.; Singh, M. N.; Sinha, A. K.; Roy, S. B. High field paramagnetic effect in the superconducting state of Ti0.8V0.2 alloy. Supercond. Sci. Technol. 2013, 26, 115005. [Google Scholar] [CrossRef]
- Nakagawa, M.; Utsumi, S.; Hirayama, T.; Sumiyama, A.; Oda, Y. Measurement of paramagnetic Meissner effect in s-wave superconductor. J. Magn. Magn. Mat. 1998 177-181, 533-534. [CrossRef]
- Nakagawa, M.; Utsumi, S.; Oda, Y. Maximum magnetic moment in a field-cooled superconducting disk. Phys. Rev. B 1999, 60, 1372–1376. [Google Scholar] [CrossRef]
- Kumar, S.; Tomy, C. V.; Balakrishnan, G.; McK Paul, D.; Grover, A. K. Paramagnetic magnetization signals and curious metastable behaviour in field-cooled magnetization of a single crystal of superconductor 2H-NbSe. J. Phys. Condensed Matteer 2015, 27, 295701. [Google Scholar] [CrossRef]
- Proslier, T.; Kharitonov, M.; Pellin, M.; Zasadzinski, J.; Ciovati, G. Evidence of Surface Paramagnetism in Niobium and Consequences for the Superconducting Cavity Surface Impedance. IEEE Trans. Appl. Supercond. 2011, 21, 2619–2622; [Google Scholar] [CrossRef]
- Sharma, M. M.; Kumar, K.; Sang, L.N.; Wang, X. L.; Awana, V. P. S. Type-II superconductivity below 4 K in Sn0.4Sb0.6. J. Alloys Compounds 2020, 844, 156140; [Google Scholar] [CrossRef]
- Smolyak, B.M.; Ermakov, G.V. The paramagnetic effect of clusters in granular superconductors under the Meissner magnetization. J. Magn. Magn. Mat. 1996, 153, 311–314. [Google Scholar] [CrossRef]
- Sundar, S.; Chattopadhyay, X.; Sharath Chandra, L. S.; Roy, S. B. High field paramagnetic Meissner effect in Mo100-xRex alloy superconductors. Supercond. Sci. Technol. 2015, 28, 075011. [Google Scholar] [CrossRef]
- Suresh Babu, M.; Thamizhavel, A.; Ramakrishnan, S.; Grover, A.K.; Pal, D. Switching effect in the magnetization response in a superconducting specimen of Ca3Rh4Sn13. J. Phys. D: Appl. Phys. 2016, 49, 185502. [Google Scholar] [CrossRef]
- Takeya, H. , Massalami, M. E., Amorim, H. S., Fujii, H., Mochiku, T., and Takano, Y. On the superconductivity of the LixRhBy compositions. Mater. Res. Expr. 2014, 1, 046001. [Google Scholar] [CrossRef]
- Zhang, L.Z.; Zhang, A.L.; Lu, W.L.; Xiao, Q.L.; Chen, F.; Feng, Z.; Cao, S.X.; Zhang, J.C.; Ge, J.-Y. Paramagnetic Meissner Effect Observed in SrBi3 with kappa Close to the Critical Regime. J. Supercond. Novel. Magn. 2020, 33, 1691–1695. [Google Scholar] [CrossRef]
- Aliev, A. E.; de Andrade, M. J.; Salamon, M. B. Paramagnetic Meissner effect in electrochemically doped indium-tin oxide films. J. Supercond. Nov. Magn. 2016, 29, 1793–1803. [Google Scholar] [CrossRef]
- Brandt, D.; Binns, C.; Gurman, S. J.; Torricelli, G.; Gray, D. S. W. Paramagnetic Meissner transitions in Pb films and the vortex compression model. J. Low Temp. Phys. 2011, 163, 170–175. [Google Scholar] [CrossRef]
- Sandim, M. J. R., Stamopoulos, D., Ghivelder, L., Lim, S. C. V., and Rollett, A. D. Paramagnetic Meissner effect and AC magnetization in roll-bonded Cu-Nb layered composites. J. Supercond. Nov. Magn. 2010 23, 1533-1541. [CrossRef]
- Terentiev, A., Watkins, D. B., De Long, L. E., Morgan, D. J., and Ketterson, J. B. Paramagnetic relaxation and Wohlleben effect in field-cooled Nb thin films. Phys. Rev. B 1999 60, R761-R764. [CrossRef]
- Yuan, S., Ren, L., and Li, F. Paramagnetic Meissner effect in Pb nanowire arrays. Phys. Rev. B 2004 69, 092509. [CrossRef]
- Bawa, A.; Gupta, A.; Singh, S.; Awana, V. P. S.; Sahoo, S. Ultrasensitive interplay between ferromagnetism and superconductivity in NdGd composite thin films. Sci. Rep. 2016, 6, 18689. [Google Scholar] [CrossRef]
- Chuang, T.M.; Lee, S.F.; Huang, S.Y.; Yao, Y.D.; Cheng, W.C.; Huang, G.R. Anomalous magnetic moments in Co/Nb multilayers. J. Magn. Magn. Mat. 2002, 239, 301–303. [Google Scholar] [CrossRef]
- Di Bernardo, A.; Salman, Z.; Wang, X.L.; Amado, M.; Egilmez, M.; Flokstra, M.G.; Suter, A.; Lee, S.L.; Zhao, J.H.; Prokscha, T.; Morenzoni, E.; Blamire, M.G.; Linder, J.; Robinson, J.W.A. Intrinsic Paramagnetic Meissner Effect Due to s-Wave Odd-Frequency Superconductivity. Phys. Rev. X 2015, 5, 041021. [Google Scholar] [CrossRef]
- Nagy, B.; Khaydukov, Y.; Efremov, D.; Vasenko, A. S.; Mustafa, L.; Kim, J. -H.; Keller, T.; Zhernenkov, K.; Devishvili, A.; Steitz, R.; Keimer, B.; Bottyan, L. On the explanation of the paramagnetic Meissner effect in superconductor/ferromagnet heterostructure. Europhys. Lett. 2016, 116, 17005. [CrossRef]
- Nielsen, A. P.; Cawthorne, A. B.; Barbara, P.; Wellstood, F. C.; Lobb, C. J.; Newrock, R. S.; Forrester, M. G. Paramagnetic Meissner effect in multiply-connected superconductors. Phys. Rev. B 2000, 62, 14380–14383. [Google Scholar] [CrossRef]
- Nielsen, A.P.; Holzer, J.; Cawthorne, A.B.; Lobb, C.J.; Newrock, R.S.; Markus, J. The paramagnetic Meissner effect in Nb/AlOx/Nb Josephson junction arrays. Physica B 2000, 280, 444–445; [Google Scholar] [CrossRef]
- Zhou, H.; Gong, X.; Jin, X. Magnetic properties of superconducting Bi/Ni bilayers. J. Magn. Magn. Mat. 2017, 422, 73–76. [Google Scholar] [CrossRef]
- He, Q.; He, M.; Shen, J.; Lai, Y.; Liu, Y.; Liu, H.; He, H.; Wang, G.; Wang, J.; Lortz, R.; Sou, I. Anisotropic magnetic responses of a 2D-superconducting Bi2Te3/FeTe heterostructure. J. Phys.: Condens. Matter 2015, 27, 345701. [Google Scholar] [CrossRef]
- Xing, Y. T., Miklitz, H., and Baggio-Saitovich, E. Controlled switching between paramagnetic and diamagnetic Meissner effects in superconductor-ferromagnet Pb-Co nanocomposites. Phys. Rev. B 2009 80, 224505. [CrossRef]
- Geim, A. K.; Dubonos, S. V.; Lok, J. G. S.; Henini, M.; Maan, J. C. Paramagnetic Meissner effect in small superconductors. Nature 1998, 396, 144–146. [Google Scholar] [CrossRef]
- Müller-Allinger, F.B.; Mota, A.C. Paramagnetic Reentrant Effect in High Purity Mesoscopic AgNb Proximity Structures. Phys. Rev. Lett. 2000, 84, 3161–3164. [Google Scholar] [CrossRef]
- Kanda, A.; Ootuka, Y. Response of a mesoscopic superconducting disk to magnetic fields. Microelectronic Eng. 2002, 63, 313–317. [Google Scholar] [CrossRef]
- Kanda, A.; Ootuka, Y. Paramagnetic supercurrent and transition points between different vortex states in mesoscopic superconducting disks. Physica C 2004, 404, 205–208. [Google Scholar] [CrossRef]
- A. Kanda,1,* B. J. Baelus,2,3,† F. M. Peeters,3 K. Kadowaki,2 and Y. Ootuka1 Experimental Evidence for Giant Vortex States in a Mesoscopic Superconducting Disk. Phys. Rev. Lett. 2004 93, 257002. [CrossRef]
- Nagamatsu, J.; Nakagawa, N.; Muranaka, T.; Zenitani, Y.; Akimitsu, J. Superconductivity at 39 K in magnesium diboride. Nature 2001, 410, 63–64. [Google Scholar] [CrossRef]
- Buzea, C.; Yamashita, T. Review of the superconducting properties of MgB2. Supercond. Sci. Technol. 2001, 14, R115–R146. [Google Scholar] [CrossRef]
- Passos, W. A. C.; Lisboa-Filho, P. N.; Fraga, G. L.; Fabris, F. W.; Purreur, P.; Ortiz, W. A. Paramagnetic Meissner effect and magnetic remanence in granular MgB2. Brazil. J. Phys. 2002, 32, 777–779. [Google Scholar] [CrossRef]
- Sözeri, H.; Dorosinskii, L.; Topal, U.; Ercan, I. Paramagnetic Meisser effect in MgB2. Physica C 2004 408-410, 109-11. [CrossRef]
- Prokhorov, V. G.; Kaminsky, G. G.; Svetchnikov, V. L.; Park, J. S.; Eom, T. W.; Lee, Y. P.; Kang, J.-H.; Khokhlov, V. A.; Mikheenko, P. Flux pinning and vortex dynamics in MgB2 doped with TiO2 and SiC inclusions. Low Temp. Phys. 2009, 35, 439–448. [Google Scholar] [CrossRef]
- Prokhorov, V. G.; Svetchnikov, V. L.; Park, J. S.; Kim, G. H.; Lee, Y. P.; Kang, J.-H.; Khokhlov, V. A.; Mikheenko, P. Flux pinning and the paramagnetic Meissner effect in MgB2 with TiO2 inclusions. Supercond. Sci. Technol. 2009, 22, 045027. [Google Scholar] [CrossRef]
- Kuroda, T.; Nakane, T.; Kumakura, H. Effects of doping with nanoscale Co3O4 particles on the superconducting properties of powder-in-tube processed MgB2 tapes. Physica C 2009, 469, 9–14. [Google Scholar] [CrossRef]
- Singh, D. S., Tiwari, B., Jha, R., Kishan, H., and Awana, V. P. S. Role of MgO impurity on the superconducting properties of MgB2. Physica C 2014, 505, 104–108. [CrossRef]
- Govindaraj, L.; Arumugam, S.; Thiyagarajan, R.; Kumar, D.; Kannan, M.; Das, D.; Suraj, T.S.; Sankaranarayanan, V.; Sethupathi, K.; Baskaran, G.; Sankar, R.; Rao, M.M.C.D. Wohlleben Effect and Emergent 7C junctions in superconducting Boron doped Diamond thin films. Physica C 2022, 598, 1354065; [Google Scholar] [CrossRef]
- Asano, Y.; Sasaki, A. Odd-frequency Cooper pairs in two-band superconductors and their magnetic response. Phys. Rev. B 2015, 92, 224508. [Google Scholar] [CrossRef]
- Barbara, P.; Araujo-Moreira, F.M.; Cawthorne, A. B.; Lobb, C. J. Reentrant ac magnetic susceptibility in Josephson-junction arrays: An alternative explanation for the paramagnetic Meissner effect. Phys. Rev. B 1999, 60, 7489–7495. [Google Scholar] [CrossRef]
- Chaban, I. A. Paramagnetic Meissner effect. J. Supercond. Nov. Magn. 2000, 13, 1011–1017. [Google Scholar] [CrossRef]
- He, Y.; Muirhead, C. M.; Vinen, W. F. Paramagnetic Meissner effect in high-temperature superconductors: experiments and interpretation. Phys. Rev. B 1996, 53, 12441–12453. [Google Scholar] [CrossRef]
- He, Y.; Muirhead, C. M.; Vinen, W. F. Paramagnetic Meissner effect of high Tc superconductors (I). Science in China 1998, 41, 647–655. [Google Scholar] [CrossRef]
- He, Y.; Muirhead, C. M.; Vinen, W. F. Paramagnetic Meissner effect of high Tc superconductors (II). Science in China 1998, 41, 762–772. [Google Scholar] [CrossRef]
- Higashitani, S. Mechanism of paramagnetic Meissner effect in high-temperature superconductors. J. Phys. Soc. Jpn. 1997, 66, 2556–2559. [Google Scholar] [CrossRef]
- Kallio, A.; Sverdlov, V.; Rytivaara, M. Paramagnetic Meissner effect and time-reversal non-invariance from spin polarization. Superlatt. Microstruct. 1997, 21, 481–486. [Google Scholar] [CrossRef]
- Koshelev, A. E.; Larkin, A. I. Paramagnetic moment in field-cooled superconducting plates: Paramagnetic Meissner effect. Phys. Rev. B 1995, 52, 13559–13562. [Google Scholar] [CrossRef]
- Lebed, A. G. , Paramagnetic intrinsic Meissner effect in a bulk. JETP Lett. 2008, 88, 201–204. [Google Scholar] [CrossRef]
- Lebed, A. G. , Paramagnetic intrinsic Meissner effect in layered superconductors. Phys. Rev. B 2008, 78, 012506. [Google Scholar] [CrossRef]
- Moshchalkov, V. V.; Qiu, X. G.; Bruyndoncx, V. Paramagnetic Meissner effect from the self-consistent solution of the Ginzburg-Landau equations. Phys. Rev. B 1997 55, 11793-11801.
- Moshchalkov, V. V.; Qiu, X. G.; Bruyndoncx, V. The paramagnetic Meissner effect resulting from the persistence of the giant vortex state. J. Low Temp. Phys. 1996, 105, 515–520. [Google Scholar] [CrossRef]
- Obukhov, Yu. V. The ”Paramagnetic” Meissner effect in superconductors. J. Supercond. 1998, 11, 733–736. [Google Scholar] [CrossRef]
- Ortiz, W. A.; Lisboa-Filho, P. N.; Passos, W. A. C.; Araujo-Moreira, F. M. Field-induced networks of weak-links: an experimental demonstration that the paramagnetic Meissner effect is inherent to granularity. Physica C 2001, 361, 267–273. [Google Scholar] [CrossRef]
- Schweigert, V. A.; Peeters, F. M. Field-cooled vortex states in mesoscopic superconducting samples. Physica C 2000, 332, 426–431. [Google Scholar] [CrossRef]
- Schweigert, V. A.; Peeters, F. M. Phase transitions in thin mesoscopic superconducting disks. Phys. Rev. B 1998, 57, 13817–13832. [Google Scholar] [CrossRef]
- Sergeenkov, S. Polarization effects induced by a magnetic field in intrinsically granular superconductors. J. Exp. Theo. Phys. 2005, 101, 919–925. [Google Scholar] [CrossRef]
- Sigrist, M., Rice, T. M. Unusual paramagnetic phenomena in granular high-temperature superconductors – A consequence of d-wave pairing? Rev. Mod. Phys. 1995, 67, 503–513. [CrossRef]
- Tempere, J., Gladilin, V. N., Silvera, I. F., Devreese, J. T., Moshchalkov, V. V. Coexistence of the Meissner and vortex states on a nanoscale superconducting spherical shell. Phys. Rev. B 2009, 79, 134516. [CrossRef]
- Zha, G.-Q., Zhou, S.-P., Zhu, B.-H., Shi, Y.-M. Charge distribution in thin mesoscopic superconducting rings with enhanced surface superconductivity. Phys. Rev. B 2006, 73, 104508. [CrossRef]
- Zharkov, G. F. Paramagnetic Meissner effect in superconductors from self-consistent solution of Ginzburg-Landau equations. Phys. Rev. B 2001, 63, 214502. [Google Scholar] [CrossRef]
- Zhu, B.-H., Zhou, S.-P., Shi, Y.-M., Zha, G.-Q., Yang, K. Influence of de Gennes boundary conditions on the charge distribution of the Meissner state and the single-vortex state in thin mesoscopic rings. Phys. Rev. B 2006 74, 014501. [CrossRef]
- Li, M.S. Paramagnetic Meissner effect and related dynamical phenomena. Phys. Rep. 2003, 376, 133–223. [Google Scholar] [CrossRef]
- Koblischka, M.R.; Pust, L.; Chikumoto, N.; Murakami, M.; Nilsson, B.; Claeson, T. Paramagnetic Meissner response of an artificially granular YBCO thin film. Physica B 2000, 284-288, 599–600. [Google Scholar] [CrossRef]
- Koblischka, M.R.; Pust, L.; Galkin, A.; Nalevka, P.; Jirsa, M.; Johansen, T.H.; Bratsberg, H.; Nilsson, B.; Claeson, T. Flux penetration into an artificially granular high-Tc superconductor. Phys. Rev. B 1999, 59, 12114–12120. [Google Scholar] [CrossRef]
- Koblischka, M. R.; Pust, L.; Chikumoto, N.; Murakami, M.; Nilsson, B.; Claeson, T. Paramagnetic Meissner response of an artificially granular YBCO thin film. Physica B 2000, 284-288, 599–600. [Google Scholar] [CrossRef]
- Kirtley, J. R.; Mota, A. C.; Sigrist, L.; Rice, T. M. Magnetic imaging of the paramagnetic Meissner effect in the granular high-Tc superconductor Bi2Sr2CaCu2Ox. J. Phys.: Condens. Matter. 1998 10, L97-L103. [CrossRef]
- Gross, R. private communication with Kirtley, J.R.
- Magnusson, J.; Nordblad, P.; Svedlindh, P. Zero-field flux noise in granular Bi2Sr2CaCu2O8. Physica C 1997, 282-287, 2369-2370. [CrossRef]
- Pessoa, A.L.; Koblischka-Veneva, A.; Carvalho, C.L.; Zadorosny, R.; Koblischka, M.R. Paramagnetic Meissner Effect and Current Flow in YBCO Nanofiber Mats. IEEE Trans. Appl. Supercond. 2021, 31, 7200105. [Google Scholar] [CrossRef]
- Pessoa, A.L.; Koblischka-Veneva, A.; Carvalho, C. L.; Zadorosny, R.; Koblischka, M. R. Microstructure and paramagnetic Meissner effect of YBa2Cu30y nanowire networks. J. Nanoparticle Res. 2020, 22, 360. [Google Scholar] [CrossRef]
- Dias, F.T.; Pureur, P.; Rodrigues, P.; Obradors, X. High-field paramagnetic Meissner effect in melt-textured YBCO. Physica C 2004, 408, 653–654. [Google Scholar] [CrossRef]
- Gouvea, C.; Dias, F.T.; Vieira, V.D.; da Silva, D.L.; Schaf, J.; Wolff-Fabris, F.; Rovira, J.J.R. Paramagnetic Meissner effect and strong time dependence at high fields in melt-textured high-T(C) superconductors. J. Korean Phys. Soc. 2013, 62, 1414–1417. [Google Scholar] [CrossRef]
- Rykov, A.I.; Tajima, S.; Kusmartsev, F.V. High-field paramagnetic effect in large crystals of YBa2Cu307-δ. Phys. Rev. B 1997, 55, 8557–8563. [Google Scholar] [CrossRef]
- Koblischka, M.R.; Muralidhar, M.; Higuchi, T.; Waki, K.; Chikumoto, N.; Murakami, M. Superconducting transitions of Nd-based 123 superconductors in fields up to 7 T. Supercond. Sci. Technol. 1999, 12, 288–292. [Google Scholar] [CrossRef]
- Koblischka, M.R.; Murakami, M. Magnetic Properties of Superconducting and Nonsuperconducting (Nd0.33Eu0.33Gd0.33)Ba2Cu3Oy. J. Supercond. Novel Magn. 2001, 14, 415–419. [Google Scholar] [CrossRef]
- Pust, L.; Wenger, L. E.; Koblischka, M. R. Detailed investigation of the superconducting transition of niobium disks exhibiting the paramagnetic Meissner effect. Phys. Rev. B 1998, 58, 14191–14194. [Google Scholar] [CrossRef]
- Pust, L.; Wenger, L. E.; Koblischka, M. R. Details of the Superconducting Phase Transition in Nb showing the Paramagnetic Meissner Effect. Phys. stat. solidi (b) 1999, 212, R13–R14. [Google Scholar] [CrossRef]
- Fodor, P. S.; Wenger, L. E. Paramagnetic Meissner effect in Nb disks. Physica C 2000, 341-348, 2043–2044. [Google Scholar] [CrossRef]
- Wenger, L. E.; Pust, L.; Koblischka, M. R. Investigation of the paramgnetic Meissner effect on Nb disks. Physica B 2000, 284-288, 797–798. [Google Scholar] [CrossRef]
- Papadopoulou, E.L.; Nordblad, P.; Svedlindh, P.; Schoneberger, R.; Gross, R. The ageing effect in a superconducting sample displaying the paramagnetic Meissner effect. Physica C 1999, 317, 637–639. [Google Scholar] [CrossRef]
- Papadopoulou, E.L.; Svedlindh, P.; Nordblad, P. Flux dynamics of a superconductor showing a glassy paramagnetic Meissner state. Phys.Rev. B 2002, 65, 144524. [Google Scholar] [CrossRef]
- Bhat, S. V.; Rastogi, A.; Kumar, N.; Nagarajan, R.; Rao, C. N. R. Paramagnetic Meissner effect in YBa2Cu307-δ. Physica C 1994, 219, 87–92. [Google Scholar] [CrossRef]
- Luzhbin, D. A.; Pan, A. V.; Komashenko, V. A.; Flis, V. S.; Pan, V. M.; Dou, S. X.; Esquinazi, P. Origin of paramagnetic magnetization in field-cooled YBa2Cu3O7-δ films. Phys. Rev. B 2004, 69, 024506. [Google Scholar] [CrossRef]
- Prusseit, W.; Walter, H.; Semerad, R.; Kinder, H.; Assmann, W.; Huber, H.; Kabius, B.; Burkhardt, H.; Rainer, D.; Sauls, J. A. Observation of paramagnetic Meissner currents – evidence for Andreev bound surface states. Physica C 1999 317-318, 396-402. [CrossRef]
- Tsoy, G. M.; Janu, Z.; Novak, M. Paramagnetic Meissner effect in YBa2Cu3O7: influence of AC magnetic field and magnetic relaxation. Physica B 2000 284-288, 811-812. [CrossRef]
- Felner, I.; Tsindlekht, M.I.; Drachuck, G.; Keren, A. Anisotropy of the upper critical fields and the paramagnetic Meissner effect in La1.85Sr0.15CuO4 single crystals. J. Phys.: Condens. Matter 2013, 25, 065702. [Google Scholar] [CrossRef]
- Okram, G.S.; Adroja, D.T.; Padalia, B.D. The paramagnetic Meissner effect in Nd2-xCexCuOy superconductors at 40 G and flux trapping. J. Phys. Cond. Matt. 1997, 9, L525–L531. [Google Scholar] [CrossRef]
- Kim, H.T.; Minami, H.; Schmidbauer, W.; Hodby, J.W.; Iyo, A.; Iga, F.; Uwe, H. Paramagnetic Meissner effect in superconducting single crystals of Ba1-xKxBiO3. J. Low. Temp. Phys. 1996, 105, 557–562. [Google Scholar] [CrossRef]
- Awana, V. P. S.; Menon, L.; Malik, S. K. Synthesis, superconductivity and magnetism of RSr2Cu2Nb07-δ compounds (R= Y, Pr, and Gd). Physica C 1996, 262, 266–271. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, L.; Sun, K.W.; Straszheim, W.E.; Tanatar, M.A.; Prozorov, R.; Lograsso, T.A. Doping evolution of the second magnetization peak and magnetic relaxation in (Ba1-xKx)Fe2As2 single crystals. Phys. Rev. B 2018, 97, 054511; [Google Scholar] [CrossRef]
- Eisterer, M. Magnetic properties and critical currents of MgB2. Supercond. Sci. Technol. 2007, 20, R47–R74. [Google Scholar] [CrossRef]
- Koblischka, M.R.; Wiederhold, A.; Koblischka-Veneva, A.; Chang, C.; Berger, K.; Nouailhetas, Q.; Douine, B.; Murakami, M. On the origin of the sharp, low-field pinning force peaks in MgB2 superconductors. AIP Adv. 2020, 10, 015035. [Google Scholar] [CrossRef]
- Narlikar, A. V. Superconductors, Oxford University Press: Oxford, U.K., 2014.
- Atzmony, U., Bennett, L. H., Swartzendruber, L. J. Is there is a paramagnetic Meissner effect? IEEE Trans. Magn. 1995, 31, 4118–4120. [CrossRef]
- McElfresh, SQUID magnetometry, brochure, Quantum Design, CA.
- Quantum Design, San Diego, CA. SQUID models MPMS-5, MPMS-XL, MPMS3 with various options (ultra-low field option, VSM option, AC susceptibility).
- Thompson, D. J. PhD work, University of Michigan, Detroit, USA, 1996.
- Weber, H.W.; Schachinger, E. Hc2-anisotropy effects in superconducting niobium polycrystals. Helvetica Physica Acta 1988, 61, 478–487. [Google Scholar]
- Koblischka, M.R.; Koblischka-Veneva, A. Magnetic properties of superconductors. In: Superconducting Materials. Fundamentals, Synthesis and Applications; Slimani, Y.; Hannachi, E.; Springer-Nature, Singapore, 2022, Chap. 3, pp. 61-88.
- Koblischka, M.R.; Pust, L.; Jirsa, M.; Johansen, T.H. Formation of the low-field peak in magnetization loops of high-Tc superconductors. Physica C 1999, 320, 101–114. [Google Scholar] [CrossRef]
- Shantsev, D.V.; Koblischka, M.R.; Galperin, Y.M.; Johansen, T.H.; Pust, L.; Jirsa, M. Central Peak Position in Magnetization Loops of High-Tc Superconductors. Phys. Rev. Lett. 1999, 82, 2947–2950. [Google Scholar] [CrossRef]
- Halbritter, J. Low temperature oxidation of Nb and of Nb-compounds in relation to superconducting application. J. Less-Common Met. 1988, 139, 133–148. [Google Scholar] [CrossRef]
- Koblischka, M. R.; Chang, C.S.; Pust, L. The PME in Nb: 20 years after. submitted to Europhys. Lett.
- Koblischka, M. R.; Wijngaarden, R. J. Magneto-optical investigations of superconductors. Supercond. Sci. Technol. 1995, 8, 199–213. [Google Scholar] [CrossRef]
- Jooss, C.; Albrecht, J.; Kuhn, H.; Leonhardt, S.; Kronmüller, H. Magneto-optical studies of current distributions in high-Tc superconductors. Rep. Prog. Phys. 2002, 65, 651–788. [Google Scholar] [CrossRef]
- Kirtley, J. R.; Tsuei, C. C.; Rupp, M.; Sun, J. Z.; Yu-Jahnes, L.S.; Gupta, A.; Ketchen, M. B.; Moler, K. A.; Bhushan, M. Direct Imaging of Integer and Half-Integer Josephson Vortices in High-Tc Grain Boundaries. Phys. Rev. Lett. 1996, 76, 1336–1339. [Google Scholar] [CrossRef] [PubMed]
- Kirtley, J.R. Fundamental studies of superconductors using scanning magnetic imaging. Rep. Prog. Phys. 2010, 73, 126501. [Google Scholar] [CrossRef]
- Rondin, L.; Tetienne, J.-P.; Hingant, T.; Roch, J.-F.; Maletinsky, P.; Jacques, V. Magnetometry with nitrogen-vacancy defects in diamond. Rep. Prog. Phys. 2014, 77, 056503. [Google Scholar] [CrossRef] [PubMed]
- Doherty, M.W.; Manson, N.B.; Delaney, P.; Jelezko, F.; Wrachtrup, J.; Hollenberg, L.C. The nitrogen-vacancy colour centre in diamond. Phys. Rep. 2013, 528, 1–45. [Google Scholar] [CrossRef]
- Shaw, G.; Blanco Alvarez, S.; Brisbois, J.; Burger, L.; Pinheiro, L. B. L. G.; Kramer, R. B. G.; Motta, M.; Fleury-Frenette, K.; Ortiz, W. A.; Vanderheyden, B.; Silhanek, A. V. Magnetic Recording of Superconducting States. Metals 2019, 9, 1022. [Google Scholar] [CrossRef]
- Brisbois, J.; Gladilin, V. N.; Tempere, J.; Devreese, J.T.; Moshchalkov, V.V.; Colauto, F.; Motta, M.; Johansen, T.H.; Fritzsche, J.; Adami, O.-A.; Nguyen, N. D.; Ortiz, W. A.; Kramer, R. B. G.; Silhanek, A.V. Flux penetration in a superconducting film partially capped with a conducting layer. Phys. Rev. B 2017, 95, 094506. [Google Scholar] [CrossRef]
- Nusran, N. M.; Joshi, K.R.; Cho, K.; Tanatar, M.A.; Meier, W. R.; Bud’ko, S. I.; Canfield, P. C.; Liu, Y.; Lograsso, T. A.; Prozorov, R. Spatially-resolved study of the Meissner effect in superconductors using NV-centers-in-diamond optical magnetometry. New J. Phys. 2018, 20, 043010. [Google Scholar] [CrossRef]
- Suter, A.; Morenzoni, E.; Garifianov, N.; Khasanov, R.; Kirk, E.; Luetkens, H.; Prokscha, T.; Horisberger, M. Observation of Nonexponential Magnetic Penetration Profiles in the Meissner State: A Manifestation of Nonlocal Effects in Superconductors. Phys. Rev. B 2005, 72, 024506. [Google Scholar] [CrossRef]
- Morenzoni, E.; Wojek, B.M.; Suter, A.; Prokscha, T.; Logvenov, G.; Božović, I. The Meissner Effect in a Strongly Underdoped Cuprate Above Its Critical Temperature, Nat. Commun. 2011, 2, 272. [Google Scholar] [CrossRef]
- Geim, A.K.; Dubonos, S.V.; Lok, J.G.S.; Grigorieva, I.V.; Maan, J.C.; Theil Hansen, L.; Lindelof, P.E. Ballistic Hall micromagnetometry. Appl. Phys. Lett. 1997, 71, 2379–2381. [Google Scholar] [CrossRef]
- Schweigert, V.A.; Peeters, F.M. Phase transitions in thin superconducting disks. Phys. Rev. B 1998, 57, 13817–13832. [Google Scholar] [CrossRef]
- Schweigert, V. A.; Peeters, F. M.; Deo, P. S. Vortex phase diagram for mesoscopic superconducting disks. Phys. Rev. Lett. 1998, 81, 2783–2786. [Google Scholar] [CrossRef]
- Mishra, P. K.; Ravikumar, G.; Sahni, V. C.; Koblischka, M. R. Grover, A. K. Surface pinning in niobium and a high-Tc superconductor. Physica C 1996, 269, 71–75. [Google Scholar] [CrossRef]
- Benoist, R.; Zwerger, W. Critical fields of mesoscopic superconductors. Z. Phys. B 1997, 103, 377–381. [Google Scholar] [CrossRef]
- E. Babaev, E.; Carlström, J.; Silaev, M.; Speight, J.M. Type-1.5 superconductivity in multicomponent system. Physica C 2017, 533, 20–35. [CrossRef]
- Babaev, E.; Speight, M. Semi-Meissner state and neither type-I nor type-II superconductivity in multicomponent superconductors. Phys. Rev. B 2005, 72, 180502. [Google Scholar] [CrossRef]
- Moshchalkov, V.; Menghini, M.; Nisho, T.; Chen, Q.H.; Dao, V.H.; Chibotaru, L.F.; Zhigadlo, N.D.; Karpinski, J. Type-1.5 Superconductivity. Phys. Rev. Lett. 2009, 102, 117001. [Google Scholar] [CrossRef]
- da Silva, R.M.; Milosevic, M.V.; Shanenko, A.A.; Peeters, F.M.; Aguiar, J.A. Giant paramagnetic Meissner effect in multiband superconductors. Sci. Rep. 2015, 5, 12695. [Google Scholar] [CrossRef] [PubMed]
- da Silva, R. M.; Milošević, M. V.; Shanenko, A. A.; Peeters, F. M.; Albino Aguiar, J. Giant paramagnetic Meissner effect in multiband superconductors. Sci. Rep. 2015, 5, 12695. [Google Scholar] [CrossRef]
- Zhuravel, A. P.; Bae, S.; Shevchenko, S. N.; Omelyanchouk, A. N.; Lukashenko, A. V.; Ustinov, A. V.; Anlage, S. M. Imaging the paramagnetic nonlinear Meissner effect in nodal gap superconductors. Phys. Rev. B 2018, 97, 054504. [Google Scholar] [CrossRef]
- Zhang, T.; Cheng, P.; Li, W.-J.; Sun, Y.-J.; Wang, G.; Zhu, X.-G.; Ke, H.; Wang, L.; Ma, X.; Chen, X.; Wang, Y.; Liu, Y.; Lin, H.-Q.; Jia, J.-F.; Xue, Q.-K. Superconductivity in one-atomic-layer metal films grown on Si(111). Nature Phys. 2010, 6, 104–108. [Google Scholar] [CrossRef]
- Lin, Y.-H.; Nelson, J.; Goldman, A.M. Superconductivity of Very Thin Films: The Superconductor-Insulator Transition. Physica C 2015, 514, 130–141. [Google Scholar] [CrossRef]
- Nam, H.; Chen, H.; Liu, T.; Kim, J.; Zhang, C.; Yong, J.; Lemberger, T.R.; Kratz, P.A.; Kirtley, J.R.; Moler, K.A.; Adams, P.W.; MacDonald, A.H.; Shih, C.-K. Ultrathin two-dimensional superconductivity with strong spin–orbit coupling. PNAS 2016, 113, 10513–10517. [Google Scholar] [CrossRef]
- Lei, C.; Chen, H.; MacDonald, A.H. Ultrathin Films of Superconducting Metals as a Platform for Topological Superconductivity. Phys. Rev. Lett. 2018, 121, 227701. [Google Scholar] [CrossRef]
- Sibanda, D.; Oyinbo, S.T.; Jen, T.-C.; Ibitoye, A.I. A Mini Review on Thin Film Superconductors. Processes 2022, 10, 1184. [Google Scholar] [CrossRef]
- Koblischka, M.R.; Koblischka-Veneva, A. Superconductivity 2022. Metals 2022, 12, 568. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




