Preprint

Article

Inclusion of Significant Markers Identified With GWAS Into Prediction Models

Altmetrics

Downloads

161

Views

Comments

Olufunke Ayegbidun^*

This version is not peer-reviewed

This preprints belongs to the Topic

Vegetable Breeding, Genetics and Genomics

Submitted:

01 May 2023

Posted:

02 May 2023

You are already at the latest version

Alerts

Abstract

Advancement in biotechnology and genomics research have promoted access to DNA markers and their use in breeding programs. Genome-wide association study (GWAS), Genomic selection (GS) and Marker-Assisted Selection (MAS) are some of the applications of DNA markers in plant breeding. Researchers have suggested combining these individual applications for better selection accuracies. This study examines the potential advantages of incorporating GWAS-results into MAS and GS as well as the validity of the different methods for combining these approaches. From this study, it was concluded that number of QTNs have greater effects on prediction accuracies compared to heritability estimates. Also, the increase in prediction accuracy from the invalid method of incorporating GWAS results into GS and MAS model is similar to results recorded with using the valid approach. However, greater difference may be observed in another scenario which can lead to spurious results when used to make breeding decisions.

Keywords:

Subject: Biology and Life Sciences - Agricultural Science and Agronomy

Introduction

Breakthroughs in genomic research increased accessibility and cost of genotyping. This advancements promote the use of molecular markers to detect relationships that may be lacking due to incomplete or lack of pedigree data (Zhang et al., 2007). In addition to detecting unclear relationships, molecular markers have been extensively used in Genome-Wide Association Studies (GWAS) to unravel the complex genetic architecture controlling numerous traits (Korte & Farlow). GWAS uses statistical models to test each SNP for an association with the phenotype of interest (Hayes & Goddard, 2010) and identify significant markers associated with the traits by setting a stringent threshold (Zhang et al., 2014). Thousands of significant markers associated with traits of agronomic or economic values have been identified in animals (Crispim et al., 2015; Freebern et al., 2020) and crop species such as wheat (Tsai et al., 2020), maize (M. Wang et al., 2012) and rice (Yuan et al., 2020) using GWAS.

Another direct application of molecular markers in breeding programs is predicting the phenotypes of individuals with only genotype data but no phenotype data. This application is crucial in breeding because breeders can make several possible crosses and will like to conduct field trials to evaluate the phenotypes. Due to limited resources, only a few of those possible crosses can make it to the field. Thus, breeders use genomic selection to predict the phenotypic performance of lines that have genotypic data but lack phenotype information. Genomic selection uses statistical models to predict phenotypes from genotypes (Zhou et al., 2016). Marker-Assisted Selection predicts phenotypes using a few markers with large effects that have strong association with the desired trait (McGowan et al., 2021). Genomic selection uses genome-wide markers to compute the relatedness matrix among individuals to estimate their phenotype (breeding value) by ranking all the markers equally or by the intensity of their association (McGowan et al., 2021). Marker-Assisted selection is similar to GS in its approach and application, the major difference between these two is MAS is effective for traits that are controlled with few genes of large effects (Mendelian traits) while GS is suitable for quantitative traits that are controlled with many genes each with very little effects (which is the case for many agronomic traits). Prediction accuracy is the Pearson correlation coefficient between the observed and predicted phenotypes (Genomic Estimated Breeding Values -GEBV) (Zhou et al., 2016).

One of the major problems with GS is low predictive abilities. Since GWAS and GS require the same data and genetic structure of complex traits impact prediction accuracies (Zhang et al., 2014), several studies have combined these two methods and reported higher prediction accuracies following inclusion of SNPs detected in GWAS model in GS models (Lozada et al., 2020; Odilbekov et al., 2019; Yan et al., 2023). An approach commonly referred to as GWAS-Assisted GS.

In a GS model, the whole population is divided into two uneven parts. The larger set makes up the training population while the smaller set is tagged testing population (Zhou et al., 2016). The training population is used to develop a prediction model which is then used to predict the phenotype of the testing population. Incorporating GWAS into GS model follows the same approach. Association study is conducted on the training population only, and significant markers detected in the GWAS for training population are then included as fixed effect covariates in a GS model. However, some studies have shown increased prediction accuracies using questionable approaches. These studies used significant markers identified from GWAS from the whole population as fixed effects in a GS model. This latter approach is invalid because data from the testing group were included in the association analysis and serve as contamination to the prediction model developed from GS. It is also logical that this latter approach is invalid since the purpose of the model is to predict phenotypes of individuals with only genotype information. Thus, it is only appropriate that the model should not contain any information about the individuals to be tested since they are not available in the real sense.

This study uses simulated data to examine if incorporating GWAS result improves GS and MAS prediction accuracies compared to the stand-alone methods. Therefore, the objectives of the study include: 1) Determine if including GWAS results in GS and MAS improves prediction accuracies compared to the stand-alone MAS and GS 2) Determine if a pattern exists for change in prediction accuracies using the stand-alone GS methods, GWAS-Assisted GS valid method and GWAS-Assisted Invalid method.

Materials and Methods

Simulation of Phenotypic Data

Phenotypes were simulated using publicly available single nucleotide polymorphism (SNP) data set generated from a study of heavy metals in rice in 323 rice lines (Frouin et al., 2019). Rice genotypes were collected using the genotype by sequencing (GBS) resulting in 22,370 SNPs. The markers were used to simulate phenotypes using the GAPIT.Phenotype.Simulation function as implemented in GAPIT (version 3) (Wang & Zhang, 2021). The phenotypes in this simulation have a narrow sense heritability of 85% and 5 markers were randomly designated as underlying QTNs. The simulated phenotypes are a sum of additive genetic effect and residual effects. The additive effect is the total of all QTNs randomly sampled from all SNPs. The QTN effects were drawn from a normal distribution.

GWAS, MAS and GS.

The BLINK model (Huang et al., 2019), as implemented in GAPIT (version 3) (Wang & Zhang, 2021), was used for all GWAS reported in this study. The BLINK model uses two fixed effect models. Fixed effect model (FEM) 1 is shown as:

y_{i} = S_{i 1}^{*} b_{1} + S_{i 2}^{*} b_{2} + \dots + S_{i k}^{*} b_{k} + S_{i j} d_{j} + e_{i}

(1)

FEM 2 is given as:

y_{i} = S_{i 1}^{*} b_{1} + S_{i 2}^{*} b_{2} + \dots + S_{i k}^{*} b_{k} + e_{i}

(2)

For genomic prediction, phenotypes were predicted from the genotypic information using gBLUP model (Zhang et al., 2007) as implemented in GAPIT (Wang & Zhang, 2021). The mixed linear model for gBLUP is shown as:

y = X b + Z u + e

(3)

Where y is the observed phenotype, b is the fixed effect, X is the incidence matrix, u is the random additive genetic effects of all individuals in the population, Z is the incidence matrix for marker effects and e is a random residual effect with a variance of residuals.

GWAS-Methods

Method 1: GWAS on whole population

A genotype-phenotype association was conducted using phenotype as the dependent variable. The threshold for significance was set to 0.01 after Bonferroni multiple test correction

(α = 0.01 / n u m b e r o f m a r k e r s)

. Significant SNPs were identified and stored in an R object to be used for further analysis.

Method 2: GWAS on a subset of the population

This approach splits the whole population into two sets. Eighty percent of the population were designated as training data set and twenty percent as testing data set. GWAS was conducted on the training datasets only, and significant SNPs were identified using the same method in method 1 above.

Marker-Assisted Selection and Genomic Selection

Method 3: Standalone MAS and Genomic Selection

The dataset was divided into 5 parts. Four of these parts were used as training population and the fifth part used as testing population to validate the prediction accuracies of the model. GLM option (Price et al., 2006) in GAPIT was used to run Marker Assisted Selection. The Pearson correlation coefficient between the predicted phenotypes and observed phenotype for the testing population was calculated. As an extra step, correlation coefficient for the training population was also computed. The same process was repeated for GS using gBLUP model in GAPIT.

Method 4: Incorporate GWAS result from method 1 into MAS and GS

To develop a prediction model that incorporates significant markers identified in GWAS result into MAS and GS, 80% of the population were used as training population and 20% as testing population. Only the phenotypes of the training population were included in the model and SNPs that passed the threshold of significance using Method 1 were included as covariates in the MAS and GS model. The prediction model was used to determine the phenotype of the testing population. The correlation between the predicted phenotype and the observed phenotype was calculated. This step was also repeated for the training set to further validate the prediction accuracies of the model.

Method 5: Incorporate GWAS result from method 2 into MAS and GS

Similar to method 3 and 4, a subset of the population was used as training set and others as testing set. However, only the significant SNPs identified using method 2 were included in the MAS and GS models. The models were used to predict the phenotype of the testing and training population. Correlation coefficients between observed and predicted phenotype in both testing and training sets were calculated.

The whole process was iterated 10 times. The mean and standard deviations for the correlation in each iteration was calculated in R.

Results and Discussion

A total of 10 replications of phenotypic data were simulated using 323 rice genotypes., using two levels of heritability

(h^{2} = 0.25 a n d 0.85)

and two NQTNs

(10 a n d 20)

. Using these simulated phenotypes, the predictive accuracies of standalone GS (Method 2), GS + GWAS with entire population (Method 3) and GS + GWAS result with subset of the population (Method 5) were compared. For each iteration, the Pearson correlation coefficient between predicted and simulated phenotype was calculated and the mean across all iterations is reported as the prediction accuracy.

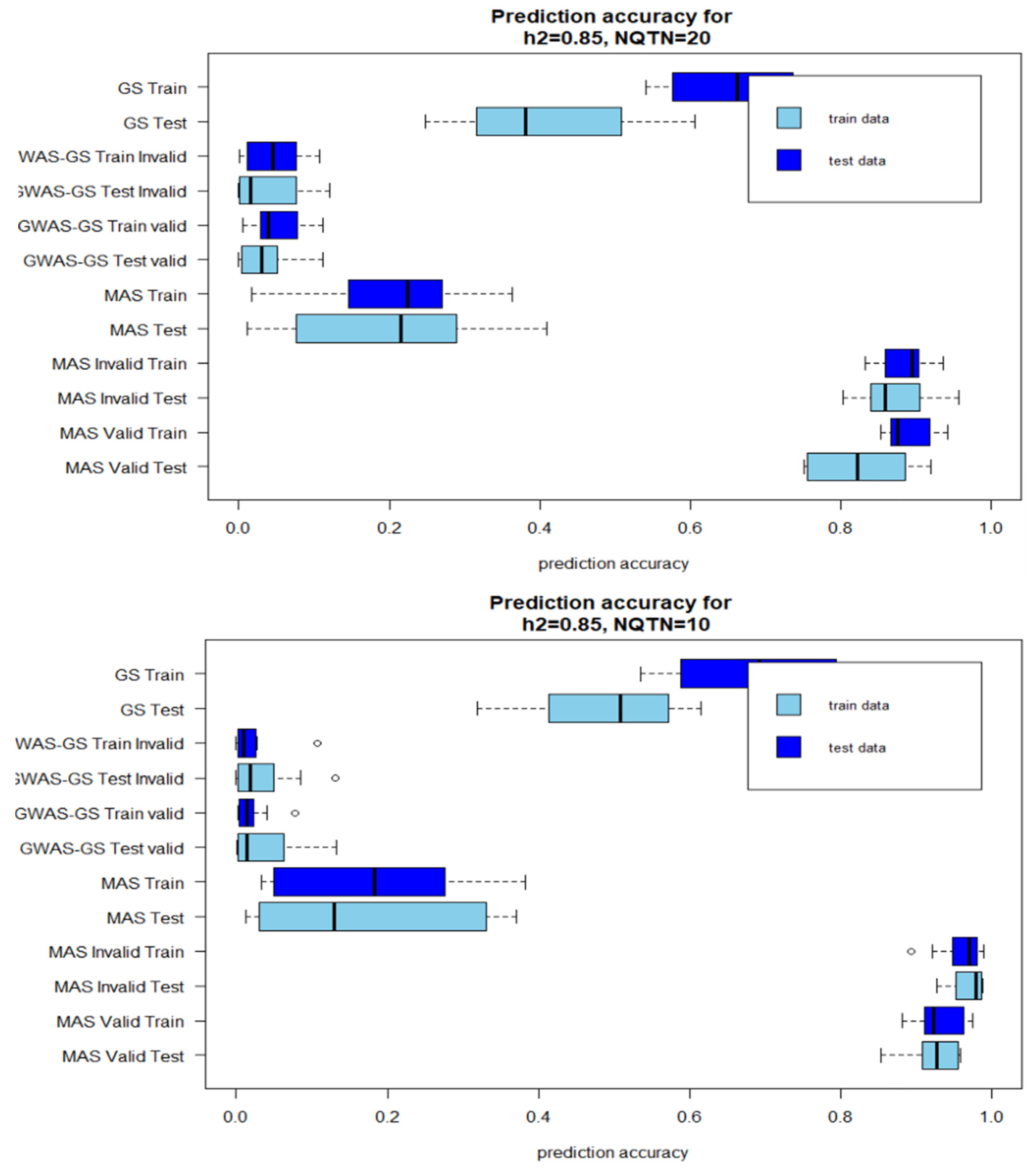
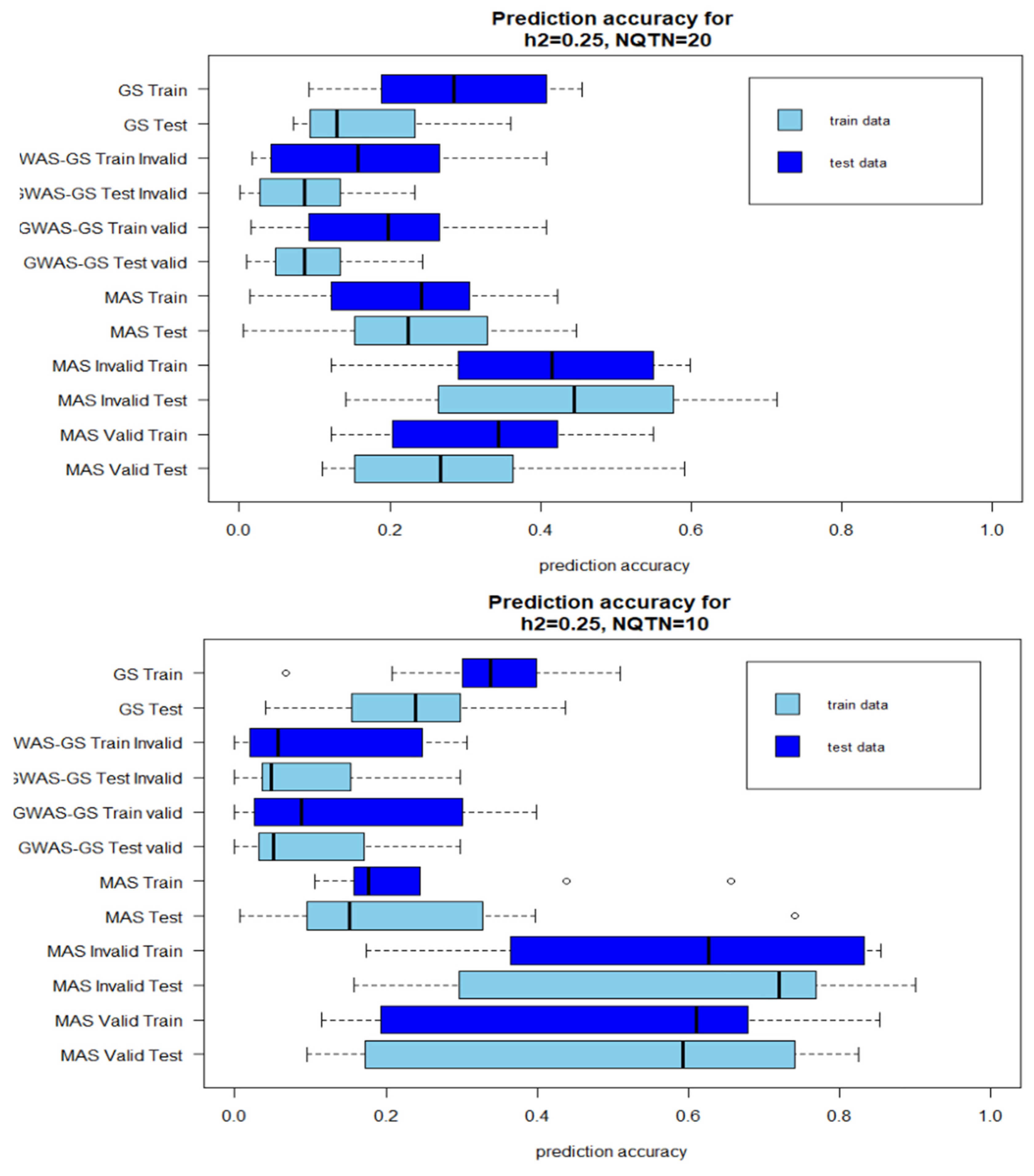
The prediction accuracies of GWAS-Assisted MAS with high heritability were higher than prediction accuracies of stand-alone MAS. However, the reverse was observed with GWAS-Assisted GS. The prediction accuracies of the stand-alone GS were higher than the GWAS-Assisted method at

h^{2} = 0.85

. With

h^{2} = 0.25

, a similar pattern with observed with high heritability was observed for MAS. GWAS-Assisted MAS performed better than MAS alone. The average number significant SNPs identified in GWAS with the whole population (Method 1) and used in method 4 as fixed-effect covariates varied with levels of heritability and number of QTNs. The highest number of significant markers (9) were identified in the simulation with 85% heritability and 20 QTNs, while the lowest (1) was found in heritability of 22=5% and 10 QTNs.

A higher prediction accuracy was observed in the testing population when results from GWAS were included in the GS model. In the stand-alone GS method, the prediction accuracy for the testing population was 0.91, while the training population accuracy was 0.69. However, including the significant SNPs as fixed effect increased the prediction accuracy for the testing model to 0.91 using method 4 and 0.86 using method 5. For the training population, a different pattern was observed. An increase in prediction accuracy was observed by including the GWAS result from the invalid approach into the MAS models. These prediction accuracies were not significantly different from the estimates derived with the valid method. The mean of number of significant SNPs accuracies identified in the GWAS with whole population and training population, and prediction are shown in Table 1 and Table 2.

Although, four factors were compared in this study (Low heritability-Less QTN, High heritability-Less QTN, Low-heritability-More QTN, High heritability-high QTN), the number of QTNs influenced the prediction accuracies more than heritability levels. With higher genetic effects controlling the phenotype (

h^{2} = 85 %)

, prediction accuracies with 10 QTNs were higher than the prediction accuracies recorded in method with 20 QTNs. No main differences were observed between the accuracies for the training model and test model. Where the training model had high correlations between the observed and predicted values the testing models also did.

Table 1. Average prediction accuracy and Standard error after 10 iterations (

h^{2} = 85)

Table 1. Average prediction accuracy and Standard error after 10 iterations (

h^{2} = 85)

Average and Standard error for $h^{2} = 85 %, Q T N = 20$			Average and Standard error for $h^{2} = 85 %, N Q T N = 10$
	Average	Standard Error		Average	Standard Error
MAS Valid Test	0.8226663	0.019889	MAS Valid Test	0.9242896	0.01139
MAS Valid Train	0.8885877	0.009525	MAS Valid Train	0.9286134	0.0098
MAS Invalid Test	0.868941	0.016272	MAS Invalid Test	0.9678176	0.00724
MAS Invalid Train	0.886489	0.009863	MAS Invalid Train	0.9601768	0.00974
MAS Test	0.1981047	0.042797	MAS Test	0.1631252	0.04648
MAS Train	0.2046981	0.035423	MAS Train	0.190746	0.0408
GWAS-GS Test valid	0.0391132	0.013331	GWAS-GS Test valid	0.0339402	0.01399
GWAS-GS Train valid	0.0502768	0.010603	GWAS-GS Train valid	0.0205814	0.00734
GWAS-GS Test Invalid	0.0336816	0.013474	GWAS-GS Test Invalid	0.0352133	0.01354
GWAS-GS Train Invalid	0.0455791	0.011636	GWAS-GS Train Invalid	0.0201073	0.0102
GS Test	0.4161396	0.039848	GS Test	0.4981874	0.03029
GS Train	0.6710488	0.035889	GS Train	0.6922155	0.03662
Whole SNP	9.3	0.61554	Whole SNP	8.6	2.31517
Sub SNP	9.8	0.866667	Sub SNP	6.7	1.21152

Figure 1. Box plot of prediction accuracies after 10 iterations for high heritability

(h^{2} = 0.85)

. A: QTNs=20 B: QTN=10 (Invalid: GWAS results from the whole population is included in the prediction models; Valid: GWAS results from only training population is used in the prediction model).

Figure 1. Box plot of prediction accuracies after 10 iterations for high heritability

(h^{2} = 0.85)

. A: QTNs=20 B: QTN=10 (Invalid: GWAS results from the whole population is included in the prediction models; Valid: GWAS results from only training population is used in the prediction model).

Table 2. Average prediction accuracy and Standard error after 10 iterations (

h^{2} = 25)

Table 2. Average prediction accuracy and Standard error after 10 iterations (

h^{2} = 25)

Average and Standard error for $h^{2} = 25 % N Q T N = 10$			Average and Standard error for $h^{2} = 25 % N Q T N = 20$
	Average	Standard Error		Average	Standard Error
MAS Valid Test	0.4940677	0.093271	MAS Valid Test	0.294763	0.047516
MAS Valid Train	0.5222947	0.084046	MAS Valid Train	0.3378347	0.042063
MAS Invalid Test	0.5635225	0.089345	MAS Invalid Test	0.4175132	0.059998
MAS Invalid Train	0.5747814	0.080735	MAS Invalid Train	0.40157	0.052611
MAS Test	0.2240256	0.068155	MAS Test	0.2332255	0.040257
MAS Train	0.2441448	0.054612	MAS Train	0.2180399	0.042167
GWAS-GS Test valid	0.1007296	0.034091	GWAS-GS Test valid	0.1031593	0.025685
GWAS-GS Train valid	0.1397514	0.045274	GWAS-GS Train valid	0.1848436	0.03703
GWAS-GS Test Invalid	0.0878147	0.02914	GWAS-GS Test Invalid	0.0859258	0.022457
GWAS-GS Train Invalid	0.1150422	0.039219	GWAS-GS Train Invalid	0.1687294	0.041146
GS Test	0.2298843	0.037039	GS Test	0.1587481	0.029446
GS Train	0.3226581	0.037679	GS Train	0.2871672	0.041178
Whole SNP	1	0.258199	Whole SNP	1.1	0.314466
Sub SNP	0.7	0.213438	Sub SNP	0.8	0.326599

Figure 2. Boxplot of prediction accuracies after 10 iterations with low heritability

(h^{2} = 0.25)

. A: QTN=20; B: QTN=10 (Invalid: GWAS results from the whole population is included in the prediction models; Valid: GWAS results from only training population is used in the prediction model).

Figure 2. Boxplot of prediction accuracies after 10 iterations with low heritability

(h^{2} = 0.25)

. A: QTN=20; B: QTN=10 (Invalid: GWAS results from the whole population is included in the prediction models; Valid: GWAS results from only training population is used in the prediction model).

In conclusion, genomic selection is an effective method for predicting phenotypic performance in different species. Several studies have advocated for the use of significant markers with strong effects on the phenotype as fixed-effect covariate in genomic selection model to increase prediction accuracy. However, the prediction accuracies of MAS benefitted more from inclusion of significant markers identified in GWAS than GS. Finally, in the instances where the invalid GWAS-Assisted MAS and GS improved prediction accuracies, there were not significantly different from the valid approach.

References

Crispim, A. C., Kelly, M. J., Guimarães, S. E. F., e Silva, F. F., Fortes, M. R. S., Wenceslau, R. R., & Moore, S. (2015). Multi-Trait GWAS and New Candidate Genes Annotation for Growth Curve Parameters in Brahman Cattle. PLOS ONE, 10(10), e0139906. [CrossRef]
Freebern, E., Santos, D. J. A., Fang, L., Jiang, J., Parker Gaddis, K. L., Liu, G. E., VanRaden, P. M., Maltecca, C., Cole, J. B., & Ma, L. (2020). GWAS and fine-mapping of livability and six disease traits in Holstein cattle. BMC Genomics, 21(1), 41. [CrossRef]
Frouin, J., Labeyrie, A., Boisnard, A., Sacchi, G. A., & Ahmadi, N. (2019). Genomic prediction offers the most effective marker assisted breeding approach for ability to prevent arsenic accumulation in rice grains. PLOS ONE, 14(6), e0217516. [CrossRef]
Hayes, B., & Goddard, M. (2010). Genome-wide association and genomic selection in animal breedingThis article is one of a selection of papers from the conference “Exploiting Genome-wide Association in Oilseed Brassicas: A model for genetic improvement of major OECD crops for sustainable farming”. Genome, 53(11), 876–883. [CrossRef]
Huang, M., Liu, X., Zhou, Y., Summers, R. M., & Zhang, Z. (2019). BLINK: A package for the next level of genome-wide association studies with both individuals and markers in the millions. GigaScience, 8(2). [CrossRef]
Korte, A., & Farlow, A. (2013). The advantages and limitations of trait analysis with GWAS: A review. Plant Methods, 9(1), 29. [CrossRef]
Lozada, D. N., Ward, B. P., & Carter, A. H. (2020). Gains through selection for grain yield in a winter wheat breeding program. PLOS ONE, 15(4), e0221603. [CrossRef]
McGowan, M., Wang, J., Dong, H., Liu, X., Jia, Y., Wang, X., Iwata, H., Li, Y., Lipka, A. E., & Zhang, Z. (2021). Ideas in Genomic Selection with the Potential to Transform Plant Molecular Breeding: A Review. In I. Goldman (Ed.), Plant Breeding Reviews (1st ed., pp. 273–319). Wiley. [CrossRef]
Odilbekov, F., Armoniené, R., Koc, A., Svensson, J., & Chawade, A. (2019). GWAS-Assisted Genomic Prediction to Predict Resistance to Septoria Tritici Blotch in Nordic Winter Wheat at Seedling Stage. Frontiers in Genetics, 10, 1224. [CrossRef]
Price, A. L., Patterson, N. J., Plenge, R. M., Weinblatt, M. E., Shadick, N. A., & Reich, D. (2006). Principal components analysis corrects for stratification in genome-wide association studies. Nature Genetics, 38(8), 904–909. [CrossRef]
Tsai, H.-Y., Janss, L. L., Andersen, J. R., Orabi, J., Jensen, J. D., Jahoor, A., & Jensen, J. (2020). Genomic prediction and GWAS of yield, quality and disease-related traits in spring barley and winter wheat. Scientific Reports, 10(1), 3347. [CrossRef]
Wang, J., & Zhang, Z. (2021). GAPIT Version 3: Boosting Power and Accuracy for Genomic Association and Prediction. Genomics, Proteomics & Bioinformatics, 19(4), 629–640. [CrossRef]
Wang, M., Yan, J., Zhao, J., Song, W., Zhang, X., Xiao, Y., & Zheng, Y. (2012). Genome-wide association study (GWAS) of resistance to head smut in maize. Plant Science, 196, 125–131. [CrossRef]
Yan, H., Guo, H., Xu, W., Dai, C., Kimani, W., Xie, J., Zhang, H., Li, T., Wang, F., Yu, Y., Ma, M., Hao, Z., & He, Z. (2023). GWAS-assisted genomic prediction of cadmium accumulation in maize kernel with machine learning and linear statistical methods. Journal of Hazardous Materials, 441, 129929. [CrossRef]
Yuan, J., Wang, X., Zhao, Y., Khan, N. U., Zhao, Z., Zhang, Y., Wen, X., Tang, F., Wang, F., & Li, Z. (2020). Genetic basis and identification of candidate genes for salt tolerance in rice by GWAS. Scientific Reports, 10(1), 9958. [CrossRef]
Zhang, Z., Ober, U., Erbe, M., Zhang, H., Gao, N., He, J., Li, J., & Simianer, H. (2014). Improving the Accuracy of Whole Genome Prediction for Complex Traits Using the Results of Genome Wide Association Studies. PLoS ONE, 9(3), e93017. [CrossRef]
Zhang, Z., Todhunter, R. J., Buckler, E. S., & Van Vleck, L. D. (2007). Technical note: Use of marker-based relationships with multiple-trait derivative-free restricted maximal likelihood. Journal of Animal Science, 85(4), 881–885. [CrossRef]
Zhou, Y., Isabel Vales, M., Wang, A., & Zhang, Z. (2016). Systematic bias of correlation coefficient may explain negative accuracy of genomic prediction. Briefings in Bioinformatics, bbw064. [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.