Prerpints.org logo
Preprint
Article

This version is not peer-reviewed.

The Quadratic Equation for the Quaternions: The Closed Form Solution

Submitted:

30 April 2023

Posted:

06 May 2023

Read the latest preprint version here

Abstract
This article derives the closed form solution to finding the roots of a quadratic equation in SU3.
Keywords: 
Quaternion
;  
Quadratic Equation
;  
Roots
Subject: 
Computer Science and Mathematics  -   Algebra and Number Theory

Table of Contents

Abstract 1
Statements and Declarations 1
Classifications 1
 1 Theorem 1 The Quadratic Equation , The General Depressed Case 3
 65 Definition 1 Orthogonal Imaginary Bases 5
 70 Definition 2 A Two-Dimensional Plane in Hypercomplex Space, Absolute Shape. 5
 82 Definition 3 Affine Two Dimensional Planes Hypercomplex Space. 6
 82 Corollary 4 Parallel Two Dimensional Planes Hypercomplex Space. 6
 87 Lemma 5 Cayley Multiplication over the General Quaternions, The Square of a Quaternion, Polar and Cartesian Forms. 6 6
 100 Definition 6 Hypercomplex Chiral Orthogonal Basis Conversion, For the Quaternions 7
 117 Theorem 7 The Lambda Choice Quaternion Eraser 8
 144 Theorem 8 The Right Triangle Theorem 9
 Theorem 9 The Orthogonal Basis Rotation Theorem; The Relative Frame Theorem 10
 Theorem 10 The Fully Depressed Case of the Quadratic Equation 11
 Lemma 11 The Mu Part and Nu Part Equivalence. 11
 Lemma 13 The Lambda Part Identity 12
 Lemma 14 The Real Part Identity 13
 Definition 15 Cardano’s Theorem: The Real Cubic Identity of the Nu Part 14
 Definition 16 Vieta’s Theorem: The Resolution of the Nu Part. 14
 Theorem 17 The Offset Circle Theorem 15
 Theorem 18 The Six Root Equivalence Theorem 16
 Theorem 19 The Closed Form Solution for a General Quadratic Equation for the Quaternions. 17
 Appendix A: Overview of Cayley Geodesicity, Orientability, Chirality, Algebraicity 20
  Algebraic Icosidgions 20
  Algebraic Hexonions 21
  Algebraic Octonions 21
  Algebraic Sedenions 21
 Appendix B: The M-th Root of N-Unity for Class of Algebraic Hypercomplex Numbers of Even Dimensions, The Great Circle Theorem 23
 405 Appendix B2: Corollary: The Square Root of a Quaternion, The Well Defined Positive and Negative Square Roots 23
 Appendix C: The Quadratic Equation , The Trivial Case of Symmetric Roots, For All Hypercomplex Dimensions 24
References 25
Theorem 1 
The Quadratic Equation , The General Depressed Case
Quadratic Quaternionic Calculator, Closed Form Solution
https://docs.google.com/spreadsheets/d/1X8sKNNuxFq5HLq5qk-93SDVdk6yeh14Xp_OV3bVl2ZI/edit?usp=sharing
Let f → = x → 2 + x →   b → + a →   x →
− c → = x → + a → x → + b → = x → 2 + x → b → + a → x → + a → b → ; − c → = f → + a → b →
We know that there exists a two dimensional basis in the four dimensional space of quaternions that describes vectors a → and b → . Namely the bisector of the roots (mistakenly known as the Axis of Symmetry) and the straight line that is between the two roots and the bisector.
We shall define the bisector as u → = 1 2 a → + b →   as the first vector of the basis.
We now define the locator   as v → = 1 2 a → − b →  
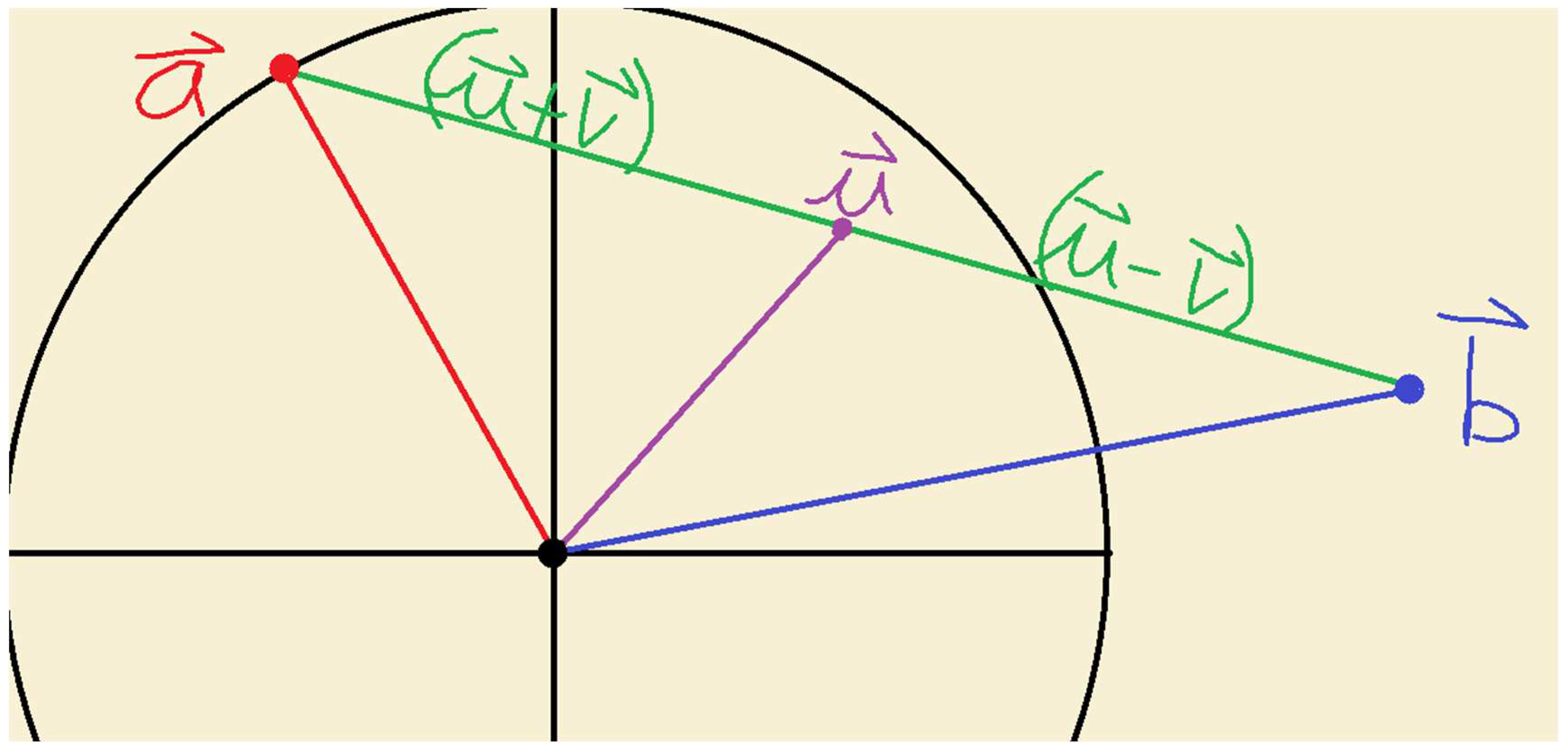
Preprints 72345 i001
EQ.1     u → = 1 2 a → + b →
EQ.2     v → = 1 2 a → − b →   , compelling a → = u → + v → and b → = u → − v →
EQ.3  Let t → = x → + u → , therefore x → = t → − u →
EQ.4a     − c → = x → 2 + x →   b → + a →   x → + a → b →
EQ.5      − c → = x → 2 + x → u → − v → + u → + v → x → + u → + v → u → − v →
EQ.6     − c → = t → − u → 2 + t → − u → u → − v → + u → + v → t → − u → + u → + v → u → − v →
EQ.7     − c → = t → 2 − t → u → − u → t → + u → 2 + t → u → − t → v → − u → 2 + u → v → + u → t → − u → 2 + v → t → − v → u → + u → 2 − u → v → + v → u → − v → 2
EQ.8a     − c → = t → 2 − t → v → + v → t → − v → 2 = t → + v → t → − v →
EQ.9a        − c → = t → 2 − t → v → + v → t → − v → 2
EQ.9b         d → = t → 2 − t → v → + v → t →                           ;           d → = − c → + v → 2 .
This is the fundamental middle handed form, from which we derive the solution.
EQ.10a       Let w → = t → + v → , such that t → = w → − v →
EQ.11a        − c → =                       w → − v → 2                     − w → − v → v → + v → w → − v → − v → 2
EQ.12a        − c → = w → 2 − w → v → − v → w → + v → 2 − w → v → − v → 2 + v → w → − v → 2 − v → 2
EQ.13a        − c → = w → 2 − w → v → − v → w → + v → 2 − w → v → + v → 2 + v → w → − v → 2 − v → 2
EQ.14a        − c → = w → 2 − 2 w → v →
EQ.15a        − c → = w → 2 − 2 w → v → = w → w → − 2 v →
EQ.16a     Let y → = − 2 v →
EQ.17a         − c → = w → 2 + w → y →     = w →   w → + y →   . This is the second fundamental form, the left-handed form.
EQ.9b        − c → = t → 2 − t → v → + v → t → − v → 2 (a restatement of EQ 9a)
EQ.10b     Let z → = t → − v → , such that t → = z → + v → , thence:
           w → = z → + 2 v → = z → − y →  
           z → = w → − 2 → v → = w → + y →
EQ.11b         − c → =                   z → + v → 2                       −     z → + v → v →     +   v → z → + v →   − v → 2
EQ.12b         − c → = z → 2 + z → v → + v → z → + v → 2 + − z → v → − v → 2 + + v → z → + v → 2 − v → 2
EQ.13b         − c → = z → 2 + 2 v → z → = z → 2 − y → z → =   z → − y →   z → . This is the third fundamental form, the right-handed form.
However, before we can proceed to resolve the roots of d → = t → 2 − t → v → + v → t →     , some general definitions and lemmas are in order.
Definition 1 
Orthogonal Imaginary Unit Vector Bases
EQ.1 i →   j → = − k → and λ → μ → = − ν → ; furthermore that, j →   i → = + k → and μ → λ → = + ν → .
EQ.2 i →   k → = + j → and λ → ν → = + μ → ; furthermore that, k →   i → = − j → and ν → λ → = − μ → .
EQ.3 j →   k → = − i → and μ → ν → = − λ → ; furthermore that, k →   j → = + i → and ν → μ → = + λ → .
If, and only if:
  • Let z → = z 0 q → + z 1 i → + z 2 j → + z 3 k → ; let α = A T A N 2 z 2 z 1 ; let β = A T A N 2 z 3 z 1 2 + z 2 2 ; let M = z 1 2 + z 2 2 + z 3 2
  • λ → = + i → c o s α c o s β + j → s i n α c o s β + k → s i n β . This is Lambda in respect to z → .
  • μ → = − i → s i n α + j → c o s α + 0 k → . This is Mu in respect to z → .
  • ν → = − i → c o s α s i n β + j → s i n α s i n β + k → c o s β . This is Nu in respect to z → .
  • This rigid body rotation of …
    • i → = 1 i → + 0 j → + 0 k → to λ →
    • j → = 0 i → + 1 j → + 0 k → to μ →
    • k → = 0 i → + 0 j → + 1 k → to ν →
    which maintains the relative spatial property that ν →   μ → = λ → = − μ →   ν →     ;     − μ   → 4 L ν → = + μ   → 4 R ν → , such that:
  • z → = z 0 q → + M λ → + 0 μ → + 0 ν → = z 0 q → + z 1 i → + z 2 j → + z 3 k →
Definition 6 
Hypercomplex Chiral Orthogonal Basis Conversion, For the Quaternions
EQ.1f x → = c 0 q → + c 1 i → + c 2 j → + c 3 k → = d 0 q → + d 1 λ → + d 2 μ → + d 3 ν → ; c 0 = d 0
Since     c 0 = d 0 , we are only concerned with the imaginary bases, thus:
EQ.2f y → = x → − c 0 q →   = c 1 i → + c 2 j → + c 3 k → = d 1 λ → + d 2 μ → + d 3 ν →
We already know that:
  • α = A T A N 2 c 2 c 1 ; β = A T A N 2 3 c 1 2 + c 2 2
  • λ → = + i → c o s α c o s β + j → s i n α c o s β + k → s i n β
  • μ → = − i → s i n α + j → c o s β + 0 k →
  • ν → = − i → c o s α s i n β + j → s i n α s i n β + k → c o s β
Let us rename the above as:
EQ.3f  λ → = γ 1,1 i → + γ 1,2 j → + γ 1,3 k →
EQ.4f  μ → = γ 2,1 i → + γ 2,2 j → + γ 2,3 k →
EQ.5f  ν → = γ 3,1 i → + γ 3,2 j → + γ 3,3 k →
Which yields the system of three linear equations:
EQ.5f  d 1 γ 1,1 i → + d 2 γ 2,1 i → + d 3 γ 3,1 i → = c 1 i →
EQ.6f  d 1 γ 1,2 j → + d 2 γ 2,2 j → + d 3 γ 3,2 j → = c 2 j →
EQ.7f  d 1 γ 1,3 k → + d 2 γ 2,3 k → + d 3 γ 3,2 k → = c 3 k →
EQ8f  Let 𝚪 be a 3x3 real matrix whose pairwise entries are equal to γ m , n .
EQ9f  Let C be a 1x3 real column matrix whose entries are c 1 ,   c 2 and c 3 respectively.
EQ10f Let D =𝚪-1 C , which is also a 1x3 real column matrix
Then d 1 , d 2 , d 3 are the respective entries of D from top to bottom.
Theorem 7 
The Lambda Choice Quaternion Eraser
Statement One       0 → = − t → v → + v → t → when both t → and v → are on the same Great Circle of λ → .
Statement Two   α 1 μ → + α 2 v → = − t → v → + v → t → when both t → and v → are not on the same Great Circle and α 1 μ → + α 2 v → is orthogonal to both t → and v → .
Proof:
EQ.1     Let    v → = v 0 q → + v 1 λ → , establishing v → as the reference frame, compelling the orthogonal basis λ → ,   μ → ,   ν → , then:
EQ.2     Let   t → = t 0 q → + t 1 λ → + t 2 μ → + t 3 ν →
EQ.3    − t → v → + v → t → = − t 0 q → + t 1 λ → + t 2 μ → + t 3 ν → v 0 q → + v 1 λ → + v 0 q → + v 1 λ → t 0 q → + t 1 λ → + t 2 μ → + t 3 ν →
EQ.4        0 → = − t 0 q → − t 1 λ → v 0 q → + v 1 λ → + v 0 q → + v 1 λ → + t 0 q → + t 1 λ → , since they commute upon the same Great Circle.
EQ.5      − t → v → + v → t → = − t 2 μ → − t 3 ν → v 0 q → + v 1 λ → + v 0 q → + v 1 λ → + t 2 μ → + t 3 ν →
EQ.6      − t → v → + v → t → = − t 2 v 0 μ → − t 2 v 1 ν → − t 3 v 0 ν → + t 3 v 1 μ → + t 2 v 0 μ → + t 3 v 0 ν → − t 2 v 1 ν → + t 3 v 1 μ →
EQ.7      − t → v → + v → t → = 2 t 3 v 1 μ → − t 2 v 1 ν → , such that − t → v → + v → t → is orthogonal to v → , vanishing t 0 and t 1 and v 0 .    
Q.E.D.
Likewise we could establish t → as the reference frame via: t → = t 2,0 q → + t 2,1 λ → 2 , compelling the orthogonal basis λ → 2 , μ → 2 , ν → 2 , and the expression
− t → v → + v → t → will result in vector that is also orthogonal to t → , vanishing the real part and λ → 2 part of y → , leaving only μ → 2 and ν → 2 as the remaining dimensions.
Regardless of which reference frame we choose, we know that − t → v → + v → t →   is orthogonal to both t → and v → , and, by definition, anything in the form of
M ( μ v → c o s θ + ν → v s i n θ ) is strictly orthogonal to v → ; however, not everything in form of M ( μ v → c o s θ + ν → v s i n θ ) is strictly orthogonal to t → .
However, the most important takeaway is that − t → v → + v → t → = 2 t 3 v 1 μ → − t 2 v 1 ν → , meaning the real part of v → , which is v 0 , has no effect; thus, the equation d → = t → 2 − t → v → + v → t → remains equal to d → , no matter the real parts of either t → or v → , nor the lambda part of t → , thus t 0 , t 1 and v 0 are erased from existence, allowing us to reduce the equation to (let M and N be positive reals):
d → = t → 2 − t → v → + t → v → = t → 2 + 2 N ( t 3 μ → − t 2 ν → )   ;       N = v 1
Theorem 8 
The Right Triangle Theorem
Thence, the expression: d → = t → 2 − t → v → + v → t → geometrically compels d → to be the hypotenuse of a right triangle, since − t → v → + v → t → is orthogonal to both t → and its square, as both t → and t → 2 lay upon the same Great Circle.
Although there exists an entire family of right triangles that share d → as the hypotenuse, there are only two congruent right triangles within this family that satisfy t → .
EQ.1         d → = t → 2 − t → v → + v → t →   ;             v → = v 0 q → + v 1 λ → v       ⇒   λ → v , μ → v , ν → v , which is the orthogonal basis in respect to v → .
EQ.2     − t → v → + v → t → = α μ → v + β ν → v
EQ.3     μ → v c o s θ + ν → v s i n θ is orthogonal to − μ → v s i n θ + ν → v c o s θ by definition. We shall choose this orthogonality to generate the family of solutions.
EQ.4     μ → v c o s θ + ν → v s i n θ is orthogonal to + μ → v s i n θ − ν → v c o s θ by definition. We discard this orthogonality in favor of the former.
EQ.5         d → = d 0 q → + d 1 λ → v + d 2 μ → v + d 3 ν → v
EQ.6         t → = t 0 q → + t 1 λ → v + t 2 μ → v + t 3 ν → v
EQ.7         t → 2 =       t 0 2 − t 1 2 − t 2 2 − t 3 2 q → + 2 t 0 t 1 λ → v + 2 t 0 t 2 μ → v + 2 t 0 t 3 ν → v     ;                 d 0 =   t 0 2 − t 1 2 − t 2 2 − t 3 2 ;       d 1 = 2 t 0 t 1
EQ.8     Let     f → = d 2 μ → v + d 3 ν → v  
EQ.9  Let   g → = G   + μ → v c o s β + ν → v s i n β = − t → v → + t → v →   = + 2 t 3 v 1 μ → v   − 2 t 2 v 1 ν → v = x μ → v + y ν → v
EQ.10     Let   t → 2 = h → = H − μ → v s i n β + ν → v c o s β = + 2 t 0 t 2 μ → v + 2 t 0 t 3 ν → v = w μ → v + z ν → v
EQ.11             f → = G g → + H h →  
EQ.12     d 2 μ → v = + G μ → v c o s θ − H μ → v s i n θ = + 2 t 3 v 1 μ → v + 2 t 0 t 2 μ → v = x μ → v + w μ → v
EQ.13       d 3 ν → v = + G ν → v s i n θ + H ν → v c o s θ = − 2 t 2 v 1 ν → v + 2 t 0 t 3 ν → v = y ν → v + z ν → v
EQ.14             t → 2 = d → − g →         ⇒         t → = ± d → − g →
The above relationship provides us with enough information to brute the roots of the quadratic equation by simply comparing every value of the angular argument of β against the real number magnitude of error from the return on d → in a preliminary search, and then converge rapidly upon the roots via bisection.
In fact, it was by empirical observation of the roots (using the above rapidly convergent algorithm) that I was able to resolve the closed form solution. We shall first simplify the quadratic equation further in lieu of those empirical results.
Theorem 9 
The Orthogonal Basis Rotation Theorem; The Relative Frame Theorem
EQ.1         Let    d → = d 0 q → + d 1 λ → v + d 2 μ → v + d 3 ν → v = A q → c o s α + λ → v s i n α + Ω μ → v c o s ϕ + ν → v s i n ϕ ;     Ω = d 2 2 + d 3 2
EQ.2a             μ 2 → = + μ → v c o s ϕ + ν → v s i n ϕ  
EQ.2b             ν 2 → = − μ → v s i n ϕ + ν → v c o s ϕ  
EQ.3             d → = d 0 q → + d 1 λ → v + d 2 μ → v + d 3 ν → v = A q → c o s α + λ → v s i n α + Ω μ → 2 + 0 ν → 2
We are able to perform this basis conversion because all we did was rotate μ → v , ν → v about λ → v ; hence, λ → v , μ → 2 , ν → 2 preserves the multiplicative relationships 171 expected in the original basis. In fact, there is no preferred frame of reference for the μ → and ν → axes for an Observer on the Great Circle of λ → , only λ → is absolute from the Observer’s perspective. The Observer is free to rotate the μ → v , ν → v axes in any manner that simplifies the existing problem.
Thus, in the equation d → = t → 2 − t → v → + v → t → , the v → variable establishes λ → , and the d → variables establishes μ → 2 and ν → 2 .
Theorem 10 
The Fully Depressed Case of the Quadratic Equation
We now combine Theorems 14 and 15 to yield the fully depressed case of the quadratic equation.
EQ.1a             d → = t → 2 − t → v → + v → t → = t → 2 − t → v 0 q → + N λ → + v 0 q → + N λ → t → , where λ → v is in respect to v → .
EQ.1b             d → = t → 2 − t → N λ → + N λ → t →
EQ.1c             d → = d 0 q → + d 1 λ → + ω 1 μ → v + ω 2 ν → v , where μ → v , ν → v is the initial orthogonal basis in respect to v → .
EQ.2a         Let    Ω = ω 1 2 + ω 2 2
EQ.2b         Let    ϕ = A T A N 2 ω 2 ω 1
EQ.2c         Let    μ → 2 = + μ → v c o s ϕ + ν → v s i n ϕ
EQ.2d         Let    ν → 2 = − μ → v s i n ϕ + ν → v c o s ϕ
EQ.2e         Let    d → = d 0 q → + d 1 λ → + Ω μ → 2 + 0 ν → 2
EQ.3a             t → = t 0 q → + t 1 λ → + t 2 μ → 2 + t 3 ν → 2
EQ.3b         t → 2 = t 0 2 − t 1 2 − t 2 2 − t 3 2 q → + 2 t 0 t 1 λ → + 2 t 0 t 2 μ → 2 + 2 t 0 t 3 ν → 2
EQ.3c     − t → N λ → + N λ → t → = 2 N t 3 μ → 2 − 2 N t 2 ν → 2 (Lambda Choice Quaternion Eraser)
EQ.4a         d 0 = t 0 2 − t 1 2 − t 2 2 − t 3 2
EQ.4b         d 1 = 2 t 0 t 1
EQ.4c         Ω = 2 t 0 t 2 + 2 N t 3
EQ.4d         0 = 2 t 0 t 3 − 2 N t 2
Lemma 11 
The Mu Part and Nu Part Equivalence.
EQ.5a         0 = 2 t 0 t 3 − 2 N t 2
EQ.5b         0 = t 0 t 3 − N t 2
EQ.5c         t 0 = N t 2 t 3
EQ.6a         Ω = 2 t 0 t 2 + 2 N t 3
EQ.6b     Ω − 2 N t 3 = 2 t 0 t 2
EQ.6c         t 0 = Ω − 2 N t 3 2 t 2
EQ.7a         N t 2 t 3 = Ω − 2 N t 3 2 t 2
EQ.7b         2 N t 2 2 = Ω t 3 − 2 N t 3 2
EQ.7c             t 2 2 = Ω t 3 − 2 N t 3 2 2 N .        
Lemma 12 
The Real Part and Nu Part Equivalence.
EQ.1a         0 = 2 t 0 t 3 − 2 N t 2
EQ.1b         0 = t 0 t 3 − N t 2
EQ.2a         t 2 = t 0 t 3 N
EQ.2b         Ω = 2 t 0 t 2 + 2 N t 3
EQ.2c     Ω − 2 N t 3 = 2 t 0 t 2
EQ.2d         t 2 = Ω − 2 N t 3 2 t 0
EQ.3a         t 0 t 3 N = Ω − 2 N t 3 2 t 0
EQ.3b         2 t 0 2 t 3 = Ω N − 2 N 2 t 3
EQ.3c         t 0 2 = Ω N − 2 N 2 t 3 2 t 3
EQ.3d         1 t 0 2 = 2 t 3 Ω N − 2 N 2 t 3             
Lemma 13 
The Lambda Part Identity
EQ.1         d 1 = 2 t 0 t 1
EQ.2         t 1 = d 1 2 t 0
EQ.3         t 1 2 = d 1 2 4 t 0 2 = d 1 2 4 2 t 3 Ω N − 2 N 2 t 3 = 2 d 1 2 t 3 4 Ω N − 8 N 2 t 3
Lemma 14 
The Real Part Identity
EQ.1         d 0 = t 0 2 − t 1 2 − t 2 2 − t 3 2
EQ.2         d 0 = t 0 2 − d 1 2 4 t 0 2 − t 2 2 − t 3 2
EQ.3         d 0 = Ω N − 2 N 2 t 3 2 t 3 − 2 d 1 2 t 3 4 Ω N − 8 N 2 t 3 − Ω t 3 − 2 N t 3 2 2 N − t 3 2     
EQ.4         d 0 = Ω N − 2 N 2 t 3 2 t 3 − 2 d 1 2 t 3 4 Ω N − 8 N 2 t 3 − Ω t 3 − 2 N t 3 2 2 N + t 3 2
EQ.5         d 0 = Ω N − 2 N 2 t 3 2 t 3 − 2 d 1 2 t 3 4 Ω N − 8 N 2 t 3 − Ω t 3 2 N
EQ.6         d 0 = Ω N 2 − 2 N 3 t 3 − Ω t 3 2 2 N t 3 − 2 d 1 2 t 3 4 Ω N − 8 N 2 t 3
EQ.7         d 0 = Ω N 2 − 2 N 3 t 3 − Ω t 3 2 2 N t 3 − 2 N t 3 2 N t 3 2 d 1 2 t 3 4 Ω N − 8 N 2 t 3
EQ.8         d 0 = Ω N 2 − 2 N 3 t 3 − Ω t 3 2 2 N t 3 − 4 N d 1 2 t 3 2 8 Ω N 2 t 3 − 16 N 3 t 3 2
EQ.9         d 0 = 4 Ω N − 8 N 2 t 3 4 Ω N − 8 N 2 t 3 Ω N 2 − 2 N 3 t 3 − Ω t 3 2 2 N t 3 − 4 N d 1 2 t 3 2 8 Ω N 2 t 3 − 16 N 3 t 3 2
EQ.10         d 0 = 4 Ω 2 N 3 − 8 Ω N 4 t 3 − 4 Ω 2 N t 3 2 − 8 Ω N 4 t 3 + 16 N 5 t 3 2 + 8 Ω N 2 t 3 3 − 4 N d 1 2 t 3 2 8 Ω N 2 t 3 − 16 N 3 t 3 2
EQ.11         d 0 = + 8 Ω N 2 t 3 3 + 16 N 5 − 4 N d 1 2 − 4 Ω 2 N t 3 2 − 16 Ω N 4 t 3 + 4 Ω 2 N 3 8 Ω N 2 t 3 − 16 N 3 t 3 2
EQ.12     8 Ω N 2 d 0 t 3 − 16 N 3 d 0 t 3 2 = + 8 Ω N 2 t 3 3 + 16 N 5 − 4 N d 1 2 − 4 Ω 2 N t 3 2 − 16 Ω N 4 t 3 + 4 Ω 2 N 3
EQ.13     0 = 8 Ω N 2 t 3 3 + 16 N 5 − 4 N d 1 2 − 4 Ω 2 N t 3 2 − 16 Ω N 4 t 3 + 4 Ω 2 N 3 − 8 Ω N 2 d 0 t 3 + 16 N 3 d 0 t 3 2
EQ.14      0 = 8 Ω N 2 t 3 3 + 16 N 5 + 16 N 3 d 0 − 4 N d 1 2 − 4 Ω 2 N t 3 2 − 16 Ω N 4 + 8 Ω N 2 d 0 t 3 + 4 Ω 2 N 3
EQ.15     0 = 2 Ω N 2 t 3 3 + 4 N 5 + 4 N 3 d 0 − N d 1 2 − Ω 2 N t 3 2 − 4 Ω N 4 + 2 Ω N 2 d 0 t 3 + Ω 2 N 3
EQ.16     0 = 2 Ω N t 3 3 + 4 N 4 + 4 N 2 d 0 − d 1 2 − Ω 2 t 3 2 − 4 Ω N 3 + 2 Ω N d 0 t 3 + Ω 2 N 2
EQ.17     0 = A t 3 3 + B t 3 2 + C t 3 + D EQ.17a     A = + 2 Ω N
EQ.17b     B = + 4 N 4 + 4 N 2 d 0 − d 1 2 − Ω 2
EQ.17c     C = − 4 Ω N 3 − 2 Ω N d 0
EQ.17d     D = + Ω 2 N 2
Definition 15 
Cardano’s Theorem: The Real Cubic Identity of the Nu Part
We now use the Cardano Method to depress the Cubic of the Nu Part.
EQ.1     0 = A t 3 3 + B t 3 2 + C t 3 + D
EQ.2     0 = ζ 3 + p ζ + q
EQ.3     ζ = t 3 + B 3 A
EQ.4     p = 3 A C − B 2 3 A 2
EQ.5     q = 2 B 3 − 9 A B C + 27 A 2 D 27 A 3     Completing Cardano’s depression of the Cubic. We now implement Vieta’s Substitution:
Definition 16 
Vieta’s Theorem: The Resolution of the Nu Part.
EQ.1     ζ = w − p 3 w
EQ.2     0 = w 3 + q − p 3 27 w 3
EQ.3     0 = w 6 + q w 3 − p 3 27
EQ.4     y = w 3
EQ.5     0 = y 2 + q y − p 3 27
EQ.6     y = − q 2 ± q 2 4 + p 3 27
EQ.7     w = − q 2 ± q 2 4 + p 3 27 3 , either sign of the square root shall suffice.
EQ.8     t 3 + B 3 A = w − p 3 w
EQ.9         t 3 = − B 3 A + w − p 3 w
We now use the identities from t 3 to yield t 0 ,   t 1 and t 2 .
EQ.10     t 0 = ± Ω N − 2 N 2 t 3 2 t 3
EQ.11      t 1 = d 1 2 t 0
EQ.12     t 2 = ± Ω t 3 − 2 N t 3 2 2 N
Of course, we have a serious dilemma. Which of the three real roots do we accept for t 3 ? Which sign of the above squares do we choose in unison? Only the polar form of solution will elucidate which root of t 3 to accept, and then how to produce t 0 , t 1 and t 2 .
Theorem 17 
The Offset Circle Theorem
For the moment, let us suppose we know which cubic root to select as t 3 , then we now examine the following relationship: N t 2 t 3 = Ω − 2 N t 3 2 t 2 . This equation informs us that the coordinate t 2 μ → 2 + t 3 ν → 2 lays upon a circle, with a radius of Ω 4 N , offset from the origin by + Ω 4 N .
Let t 2 μ → 2 + t 3 ν → 2 = M μ → 2 c o s θ + ν → 2 s i n θ , then the Law of Cosines reveals that:
EQ.1     M 2 = Ω 4 N 2 + Ω 4 N 2 − 2 Ω 4 N 2 c o s 2 θ
EQ.2     M 2 = 2 Ω 4 N 2 1 − c o s 2 θ
EQ.3      M = Ω 2 N s i n θ , upholding the Law of Sines.
We now examine the relationship t 0 = N t 2 t 3 .
EQ.4             t 0 = N M c o s θ M s i n θ
EQ.5             t 0 = N c o t θ
EQ.6             t 1 = d 1 2 t 0 = d 1 2 N t a n θ
EQ.7     d 0 = t 0 2 − t 1 2 − t 2 2 − t 3 2
EQ.8     d 0 = N 2 c o t 2 θ − d 1 2 4 N 2 t a n 2 θ − M 2 c o s 2 θ − M 2 s i n 2 θ
EQ.9     d 0 = N 2 c o t 2 θ − d 1 2 4 N 2 t a n 2 θ − M 2 c o s 2 θ + s i n 2 θ ; M 2 = Ω 2 4 N 2 s i n 2 θ ; c o s 2 θ + s i n 2 θ = 1
EQ.10     d 0 = N 2 c o t 2 θ − 1 4 N 2 d 1 2 t a n 2 θ + Ω 2 s i n 2 θ , which leads to a nasty degree six equation with 6 pairs of conjugate solutions for θ .
Before we proceed, the below image is the geometric appearance of the question at hand in μ → 2 , ν → 2 space.
In the following url link, q is Omega, N is N, and t is theta: https://www.desmos.com/calculator/q2bfcbs7wq
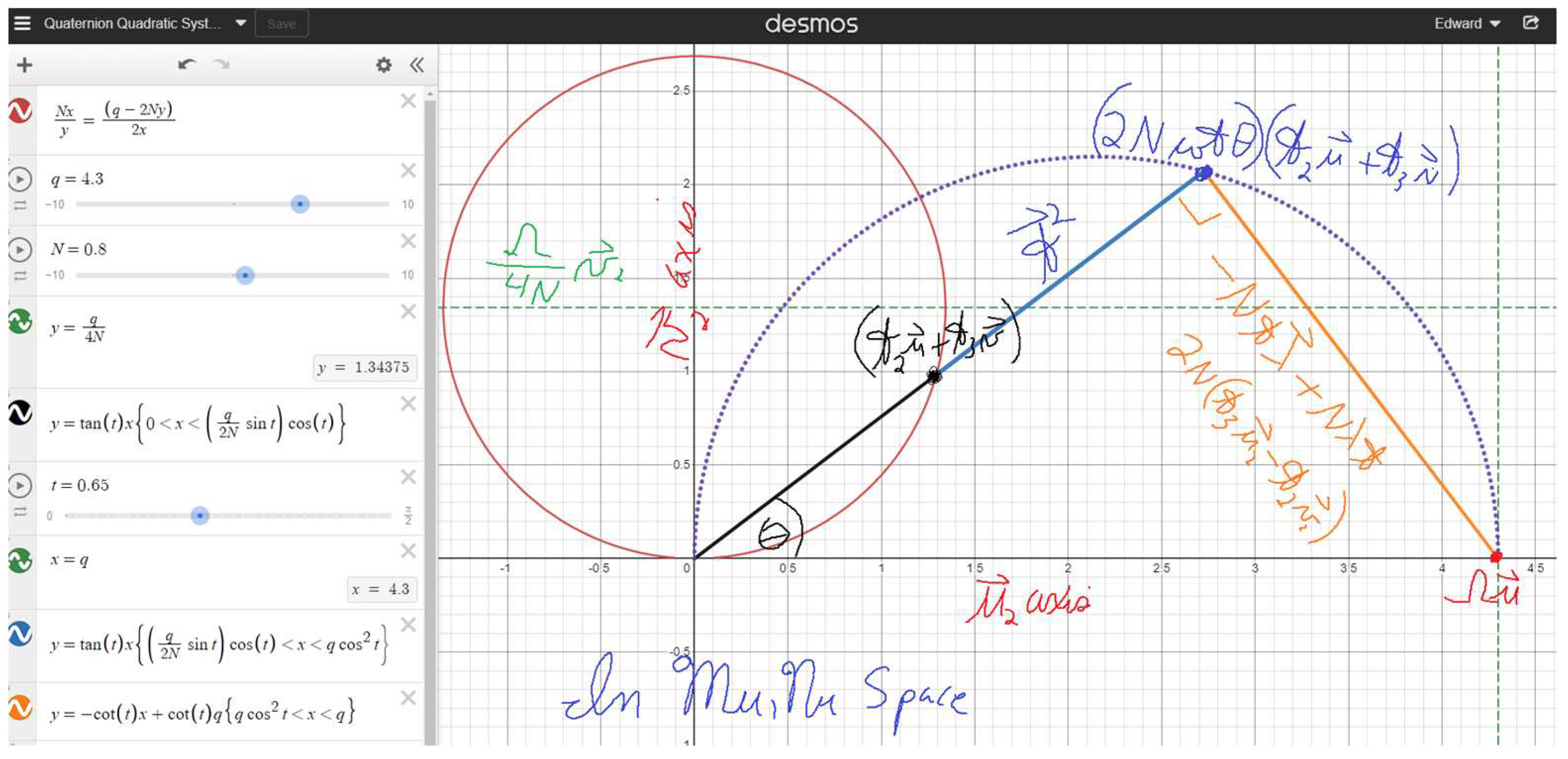
Preprints 72345 i002
However, when we yield the roots of the cubic to produce t 3 we can solve for theta without any of the hassle that the polar form introduces.
EQ.11     t 2 μ → 2 + t 3 ν → 2 = M μ → 2 c o s θ + ν → 2 s i n θ
EQ.12         t 3 = M s i n θ
EQ.13         t 3 = Ω 2 N s i n 2 θ
EQ.14     2 N t 3 Ω = s i n 2 θ ; 2 N t 3 Ω = s i n θ
EQ.15     θ = A r c s i n e + 2 N t 3 Ω . We know to take the positive root, since the t 2 , t 3 coordinate resides in the first quadrant, since both magnitude variables, N and Ω , are positive by definition, forcing the red circle (in the above image) in the upper two quadrants. We also both angles for the Arcsine function. This is not because we cannot resolve the ambiguity; rather, both θ solutions fulfill d → = t → 2 − t → v → + v → t → simultaneously. Hence:
EQ.16     θ 1 = A r c s i n e + 2 N t 3 Ω ;     θ 2 = π − θ 1 ; yielding the empirically observed form: t → = t 3 ν → 2 ± Ψ 2 , where Ψ has no ν → 2 part.
With both values of theta known, we simply use the identities above to yield t 0 ,   t 1 , t 2
EQ.17a  t 0,1 = N c o t θ 1 ; t 1,1 = d 1 2 t 0,1 ; t 2,1 = Ω 2 N s i n θ 1 c o s θ 1
EQ.17b  t 0,2 = N c o t θ 1 ; t 1,2 = d 1 2 t 0,1 ; t 2,2 = Ω 2 N s i n θ 2 c o s θ 2 ; t 0,1 = − t 0,2 ; t 1,1 = − t 1,2 ; t 2,1 = − t 2,2 ; t 3,1 = t 3,2 .    Q.E.D.
Theorem 18 
Which Root Theorem
We shall use the randomly generated components of f → = x → 2 + x → b → + a → x → seen below to demonstrate that all three roots of t 3 are valid by symmetry.
a → = − 6.198 q → − 0.877 i → + 7.020 j → + 8.469 k → b → = + 6.472 q → − 7.628 i → + 5.019 j → + 1.531 k → f → = − 8.299 q → + 5.952 i → + 6.088 j → + 2.996 k → x → 1 = + 1.1457138 q → + 1.5397790 i → + 1.6404340 j → − 0.1822954 k → x → 2 = − 1.4197138 q → − 4.1986025 i → − 3.0201749 j → − 2.0290342 k →
The resultant equation d → = t → 2 − t → v → + v → t → ; Ω = 91.20815237 ; N = 4.942566287
d → = − 87.5983675 q → + 36.5451060 i → + 70.9961880 j → − 44.7808970 k → = − 87.5983675 q → + 7.89969368971 λ → + Ω μ 2 → + 0 ν → 2
v → = − 6.33500000 q → + 3.3755000 i → + 1.0005000 j → + 3.4690000 k → = − 6.33500000 q → + N λ → + 0 μ 2 → + 0 ν → 2 λ → = 0 q → + 0.6829448113 i → + 0.2024252062 j → + 0.7018621094 k → μ → 2 = 0 q → + 0.3415270497 i → + 0.7608650002 j → − 0.551764194 k → ν → 2 = 0 q → − 0.6457132948 i → + 0.6165293888 j → + 0.4504951205 k →
Has the roots, accepting the angular argument of θ 1 = 1.316874331 r a d i a n s ; θ 2 = π − θ 1 = 1.824718323 r a d i a n s
t → 1 = + 1.282713777 q → + 3.079289328 λ → + 2.243471181 μ → 2 + 8.644566873 ν → 2 t → 2 = − 1.282713777 q → − 3.079289328 λ → − 2.243471181 μ → 2 + 8.644566873 ν → 2
Preprints 72345 i003
The three roots for t 3 are as follows: t 3 = + 10.08356777 , + 8.644566873 , − 2.585822472 θ 1 = A r c s i n e + 2 N t 3 Ω = π 2 − 0.300194 i , 1.316874331 + 0 i , 0 + 0.5073412535 i
t 0,1 = N c o t θ 1 ; t 1,1 = d 1 2 N t a n θ ; t 2,1 = Ω 2 N s i n θ 1 c o s θ 1 ; t 2,1 = Ω 2 N s i n θ 1 2 .
t 0,1 = 0 + 1.4407 i ; t 1,1 = 0 − 2.7416 i ; t 2,1 = 0 + 2.93926 i ; t 3,1 = 10.08356 + 0 i for θ 1 = π 2 − 0.300194 i
t 0,1 = 1.28277 + 0 i ; t 1,1 = 3.07928 + 0 i ; t 2,1 = 2.24347 + 0 i ; t 3,1 = 8.64456 + 0 i  for θ 1 = 1.31687 + 0 i
t 0,1 = 0 − 10.5639 i ; t 1,1 = 0 + 0.37389 i ; t 2,1 = 0 + 5.52678 i ; t 3,1 = − 2.58582 + 0 i  for θ 1 = 0 + 0.50734 i
d 0 = − 87.5983675 = 1.4407 i 2 − − 2.7416 i 2 − 2.93926 i 2 − 10.08356 2 = − 2.0756 + 7.5163 + 8.6392 − 101.6781 d 0 = − 87.5983675 = 1.28277 2 − 3.07928 2 − 2.24347 2 − 8.64456 2 = + 1.6454 − 9.4819 − 5.0332 − 74.7284 d 0 = − 87.5983675 = − 10.5639 i 2 − 0.37389 i 2 − 5.52678 i 2 − − 2.58582 2 = − 111.59 + 0.1397 + 30.545 − 6.68646 d 1 = 7.89969 = 2 t 0 t 1 = 2 0 + 1.4407 i 0 − 2.7416 i = 2 1.28277 3.07928 = 2 0 − 10.5639 i 0 + 0.37389 i d 2 = 91.2081 = Ω = 2 t 0 t 2 + 2 N t 3 = 2 1.4407 i 2.93926 i + 2 4.9425 10.0835 = − 8.4691 + 99.6753 d 2 = 91.2081 = Ω = 2 t 0 t 2 + 2 N t 3 = 2 1.28277 2.24347 + 2 4.9425 8.64456 = + 5.7557 + 85.4514 d 2 = 91.2081 = Ω = 2 t 0 t 2 + 2 N t 3 = 2 − 10.5639 i 5.52678 i + 2 4.9425 − 2.58582 = + 116.7687 − 25.5608 0 = 2 t 0 t 3 + 2 N t 2 = 2 1.4407 i 10.0835 − 2 4.9425 2.93926 i = 29.054 i − 29.054 i 0 = 2 t 0 t 3 + 2 N t 2 = 2 1.28277 8.64456 − 2 4.9425 2.24347 = 22.177 i − 22.177 i 0 = 2 t 0 t 3 + 2 N t 2 = 2 − 10.5639 i − 2.58582 − 2 4.9425 5.52678 i = 54.632 i − 54.632 i
That is, all three Arcsine arguments of t 3 produce the same d → vector after recombination. In other words, a Quadratic Equation over the Quaternions has one pair of roots with four real coefficients, and two pairs of roots with three purely imaginary coefficients for q → ,   λ → ,   μ → 2 and one pure real coefficient for ν → 2 .
However, the geometric meaning of complex coefficients remains unclear. For now, we accept the guaranteed real argument for θ 1     Q.E.D.
Theorem 19 
The Closed Form Solution for a General Quadratic Equation for the Quaternions.
We now combine all of the steps to solve original query:
EQ.1     f → = x → 2 + x →   b → + a →   x →
EQ.2    Let − c → = f → + a →   b →
EQ.3     − c → = x → 2 + x →   b → + a →   x → + a →   b →
EQ.4     u → = 1 2 a → + b →
EQ.5     v → = 1 2 a → − b →  
EQ.6     Let t → = x → + u → , therefore x → = t → − u →
EQ.7     − c → = t → 2 − t →   v → + v →   t → − v →   2
EQ.8     Let       d → = − c → + v → 2 = d 0,0 q → + d 1,0 i → + d 2,0 j → + d 3,0 k →
EQ.9         d → = t → 2 − t →   v → + v →   t →
EQ.10     v → = v 0,0 q → + v 1,0 i → + v 2,0 j → + v 3,0 k →
EQ.11     α = A T A N 2 v 2 v 1
EQ.12     β = A T A N 2 v 3 v 1 1 + v 2 2
EQ.13     λ → = + i → c o s α c o s β + j → s i n α c o s β + k → s i n β = γ 1,1 i → + γ 1,2 j → + γ 1,3 k →
EQ.14     μ → 1 = − i → s i n α + j → c o s α + 0 k → = γ 2,1 i → + γ 2,2 j → + γ 2,3 k →
EQ.15     ν → 1 = − i → c o s α s i n β + j → s i n α s i n β + k → c o s β = γ 3,1 i → + γ 3,2 j → + γ 3,3 k →
EQ.16  Let 𝚪 be a 3x3 real matrix whose pairwise entries are equal to γ m , n .
EQ.17  Let A be a 1x3 real column matrix whose entries are v 1,0 ,   v 2,0 and v 3,0 respectively.
EQ.18  Let B be a 1x3 real column matrix whose entries are d 1,0 ,   d 2,0 and d 3,0 respectively.
EQ.19 Let 𝐕 =𝚪 A , which is also a 1x3 real column matrix, let it the results be named N , 0,0 . N is our first primary variable.
EQ.20 Let D =𝚪 B , which is also a 1x3 real column matrix, let it the results be named d 1,1 , d 2,1 , d 3,1 We do not require the inverse Gamma Matrix for this process.
𝚪 Gamma Matrix         A Matrix     B Matrix    𝚪 A = V Matrix 𝚪 B = D Matrix
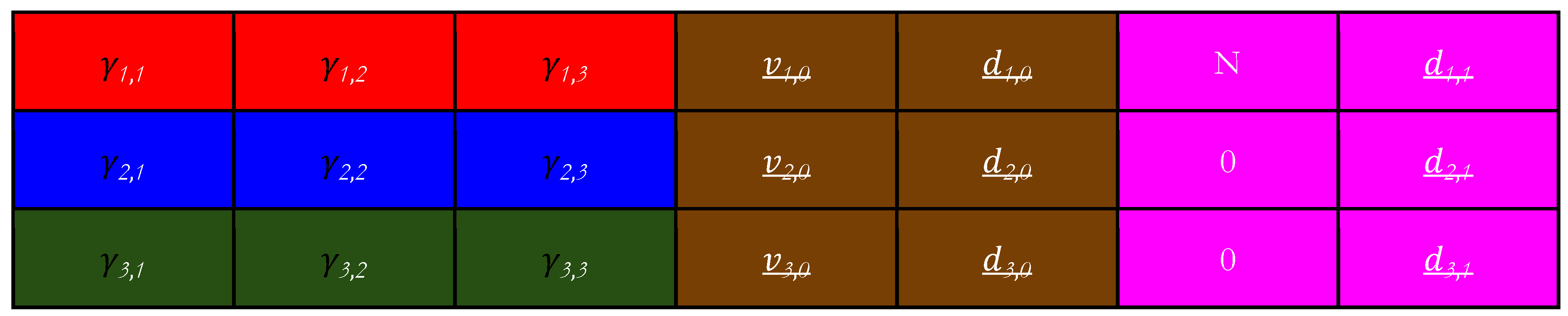
Preprints 72345 i004
EQ.21     ϕ = A T A N 2 d 3,1 d 2,1 ;     Ω = d 2,1 2 + d 3,1 2
EQ.22 μ → 2 = + μ → 1 c o s ϕ + ν → 1 s i n ϕ = + i → − s i n α c o s ϕ − c o s α s i n β s i n ϕ + j → + c o s α c o s ϕ + s i n α s i n β s i n ϕ + k → c o s β s i n ϕ
EQ.23 μ → 2 = μ 1 i → + μ 2 j → + μ 3 k →
EQ.24 ν → 2 = − μ → 1 s i n ϕ + ν → 1 c o s ϕ = + i → + s i n α s i n ϕ − c o s α s i n β c o s ϕ + j → − c o s α s i n ϕ + s i n α s i n β c o s ϕ + k → c o s β c o s ϕ
EQ.25 ν → 2 = ν 1 i → + ν 2 j → + ν 3 k →
EQ.26 v → = 1 2 a → − b → = v 0,0 q → + N λ → + 0 μ → 1 + 0 ν → 1 = v 0,0 q → + N λ → + 0 μ → 2 + 0 ν → 2
EQ.27         d → = d 0,0 q → + d 1,1 λ → + d 2,1 μ → 1 + d 3,1 ν → 1 = d 0,0 q → + d 1,1 λ → + Ω μ → 2 + 0 ν → 2
EQ.28     A = + 2 Ω N
EQ.29     B = + 4 N 4 + 4 N 2 d 0,0 − d 1,1 2 − Ω 2
EQ.30     C = − 4 Ω N 3 − 2 Ω N d 0,0
EQ.31     D = + Ω 2 N 2
EQ.32     0 = A t 3 3 + B t 3 2 + C t 3 + D
EQ.33     0 = ζ 3 + p ζ + q
EQ.34     ζ = t 3 + B 3 A
EQ.35    p = 3 A C − B 2 3 A 2
EQ.36    q = 2 B 3 − 9 A B C + 27 A 2 D 27 A 3
EQ.37    ζ = w − p 3 w
EQ.38    0 = w 3 + q − p 3 27 w 3
EQ.39    0 = w 6 + q w 3 − p 3 27
EQ.40    y = w 3
EQ.41    0 = y 2 + q y − p 3 27
EQ.42    y = − q 2 ± q 2 4 + p 3 27
EQ.43    w = − q 2 ± q 2 4 + p 3 27 3 , either sign of the square root shall suffice, and any cube root will suffice.
EQ.44     t 3 + B 3 A = w − p 3 w
EQ.45       t 3 = − B 3 A + w − p 3 w . All roots will be real.
EQ.46     θ = A r c s i n + 2 N t 3 Ω . If θ is a complex number, then λ → is the imaginary unit.
We evaluate θ for all three roots of t 3 and select the real-valued argument. Hopefully someone will elucidate the meaning of the complex arguments in due time, for I dare not feign knowledge of their geometric interpretation.
EQ.47 t → 1 = + q → N c o t θ + λ → d 1 , , 1 2 N t a n θ + μ → 2 Ω 2 N s i n θ c o s θ + ν → 2 Ω 2 N s i n 2 θ = t 0,1 q → + t 1,1 λ → + t 2,1 μ → 2 + t 3,1 ν → 2
EQ.48 t → 2 = − q → N c o t θ − λ → d 1 , , 1 2 N t a n θ − μ → 2 Ω 2 N s i n θ c o s θ + ν → 2 Ω 2 N s i n 2 θ = t 0,2 q → + t 1,2 λ → + t 2,2 μ → 2 + t 3,2 ν → 2
The above two equations are the roots in the proper orthogonal basis of λ → ,   μ → 2 , ν → 2 , however we must now convert back to i → ,   j → ,   k → .
EQ.49 t 0,1 q → + t 1,1 λ → + t 2,1 μ → 2 + t 3,1 ν → 2 = t 0,3 q → + t 1,3 i → + t 2,3 j → + t 3,3 k →
EQ.50     t 0,3 = t 0,1
EQ.51     t 1,3 = t 1,1 γ 1,1 + t 2,1 μ 1 + t 3,1 ν 1
EQ.52     t 2,3 = t 1,1 γ 1,2 + t 2,1 μ 2 + t 3,1 ν 2
EQ.53     t 2,3 = t 1,1 γ 1,3 + t 2,1 μ 3 + t 3,1 ν 3
EQ.54 t 0,2 q → + t 1,2 λ → + t 2,2 μ → 2 + t 3,2 ν → 2 = t 0,4 q → + t 1,4 i → + t 2,4 j → + t 3,4 k →
EQ.55     t 0,4 = t 0,2
EQ.56     t 1,4 = t 1,2 γ 1,1 + t 2,2 μ 1 + t 3,2 ν 1
EQ.57     t 2,4 = t 1,2 γ 1,2 + t 2,2 μ 2 + t 3,2 ν 2
EQ.58     t 2,4 = t 1,2 γ 1,3 + t 2,2 μ 3 + t 3,2 ν 3
Recall that t → = x → + u → and therefore x → = t → − u → and that u → = 1 2 a → + b → .
EQ.59 t → 1 = x → 1 + u → = t 0,3 q → + t 1,3 i → + t 2,3 j → + t 3,3 k →
EQ.60 t → 2 = x → 2 + u → = t 0,4 q → + t 1,4 i → + t 2,4 j → + t 3,4 k →
EQ.61       u → = u 0 q → + u 1 i → + u 2 j → + u 3 k →
EQ.62       x → 1 = t 0,3 − u 0 q → + t 1,3 − u 1 i → + t 2,3 − u 2 j → + t 3,3 − u 3 k →
EQ.63       x → 2 = t 0,4 − u 0 q → + t 1,4 − u 1 i → + t 2,4 − u 2 j → + t 3,4 − u 3 k →
The above two equations satisfy the original query f → = x → 2 + x →   b → + a →   x → , proving that all Quadratic Equations over the Quaternions adhere to the same closed form solution.
Q.E.D.

Appendix B: The M-th Root of N-Unity for Class of Algebraic Hypercomplex Numbers of Even Dimensions, The Great Circle Theorem

Assuming that we are in a Hypercomplex Space that is Cayley Algebraic, then let x → n ,   m be the function that returns the m t h principal root unity for x → .
EQ.11d Let q → be the observation vector.
EQ.12d Let D be the set of pairwise orthogonal imaginary unit vectors, D = n and n must be odd, such that D   ∪     q →   is even.
EQ.13d Let x → = α 0 q → + ∑ z = 1 z = n α z d → z such that ∀ z ,   α z ∈ R
EQ.14d Let β = + ∑ z = 1 z = n α z 2 , which is the real number magnitude of the imaginary part of x → .
EQ.15d Let γ = + α 0 2 + ∑ z = 1 z = n α z 2 , which is the real number magnitude of x → .
EQ.16d Let λ → = 1 β x → − α 0 q →   , compelling λ → to be a unit vector.
EQ.17d Let τ = 1 β α 0 , giving us the ratio between the magnitudes of the real part and the imaginary part.
EQ.18d Let θ = A T A N 2 1 τ = A C O T A N 2 τ , that is, the four-quadrant arccotagent of τ .
EQ.19d    x → = γ q → c o s θ + λ → s i n θ
EQ.20d  x → n , m = γ n q → c o s θ + 2 π m n + λ → s i n θ + 2 π m n , ∀ m , n ∈ Z , m ≤ n

Appendix B.2: Corollary: The Square Root of a Quaternion, The Well Defined Positive and Negative Square Roots

For a quaternion x → = α 0 q → + α 1 i → + α 2 j → + α 3 k →   , the square root is given by:
EQ.21d
+ x → = + α 0 2 + α 1 2 + α 2 2 + α 3 2 ( q → c o s 0 + 1 2 A T A N 2 + α 1 2 + α 2 2 + α 3 2 α 0           + 1 + α 1 2 + α 2 2 + α 3 2 x → − α 0 q → s i n 0 + 1 2 A T A N 2 + α 1 2 + α 2 2 + α 3 2 α 0 )
− x → = ( + α 0 2 + α 1 2 + α 2 2 + α 3 2 ) ( q → c o s π + 1 2 A T A N 2 + α 1 2 + α 2 2 + α 3 2 α 0           + 1 + α 1 2 + α 2 2 + α 3 2 x → − α 0 q → s i n π + 1 2 A T A N 2 + α 1 2 + α 2 2 + α 3 2 α 0 )

Appendix C: The Quadratic Equation , The Trivial Case of Symmetric Roots, For All Hypercomplex Dimensions

EQ.1e   − C → = x → 2 + x → y → + y → x → can be readily solved for x → even if C → and y → are not on the same Great Circle.
EQ.2e Let t → = x → + y → , such that x → = t → − y →
EQ.3e   − C → = t → − y → 2 + t → − y → y → + y → t → − y →
EQ.4e   − C → = t → 2 − t → y → − y → t → + y → 2 + t → y → − y →   2 + y → t → − y → 2  
EQ.5e   − C → = t → 2 − y → 2
EQ.6e    t → 2 = y → 2 − C →
EQ.7e    t → = ± y → 2 − C →           ⇔ x → + y → = ± y → 2 − C →    
EQ.8e    x → = − y → ± y → 2 − C →  
EQ.9e    0 → = − y → ± y → 2 − C → 2 + − y → ± y → 2 − C → y → + y → − y → ± y → 2 − C → + C →
Q.E.D
It is our goal to transform the earlier equation, − c → = w → 2 + w → y → , into the Symmetric Case via a series of additional substitutions.
The Symmetric Case occurs when     − C → = x → 2 +   y →   4 L +   y →   4 R x → .
Statements and Declarations: I have nothing to declare.
Quadratic Quaternionic Calculator, Closed Form Solution
https://docs.google.com/spreadsheets/d/1X8sKNNuxFq5HLq5qk-93SDVdk6yeh14Xp_OV3bVl2ZI/edit?usp=sharing
Preprints 72345 i005

References

  1. Available online: https://mathworld.wolfram.com/VietasSubstitution.
  2. Available online: https://www.math.ucdavis.edu/~kkreith/tutorials/sample.lesson/cardano.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
bsky
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

Privacy Settings

© 2025 MDPI (Basel, Switzerland) unless otherwise stated