Submitted:
28 April 2023
Posted:
28 April 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
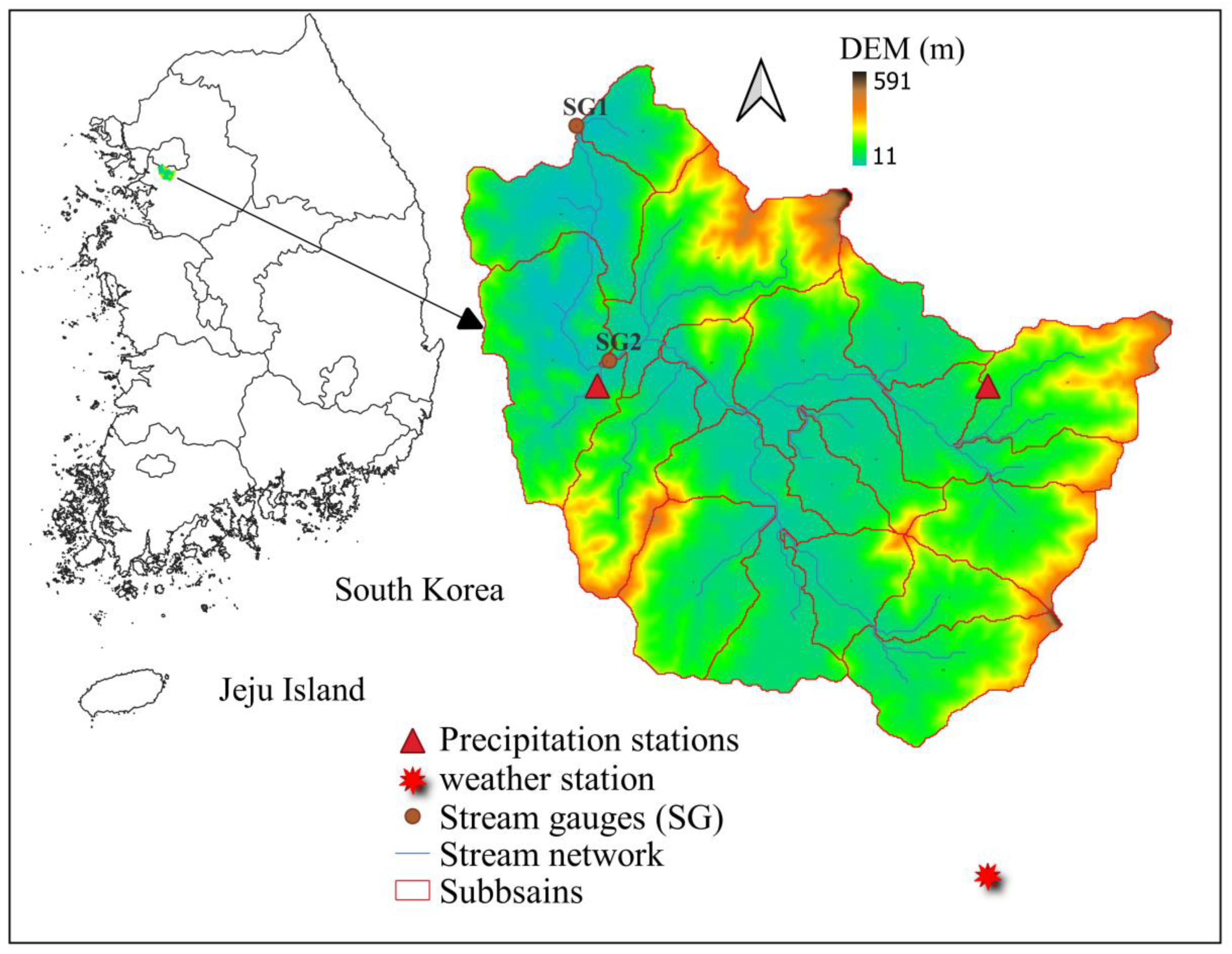
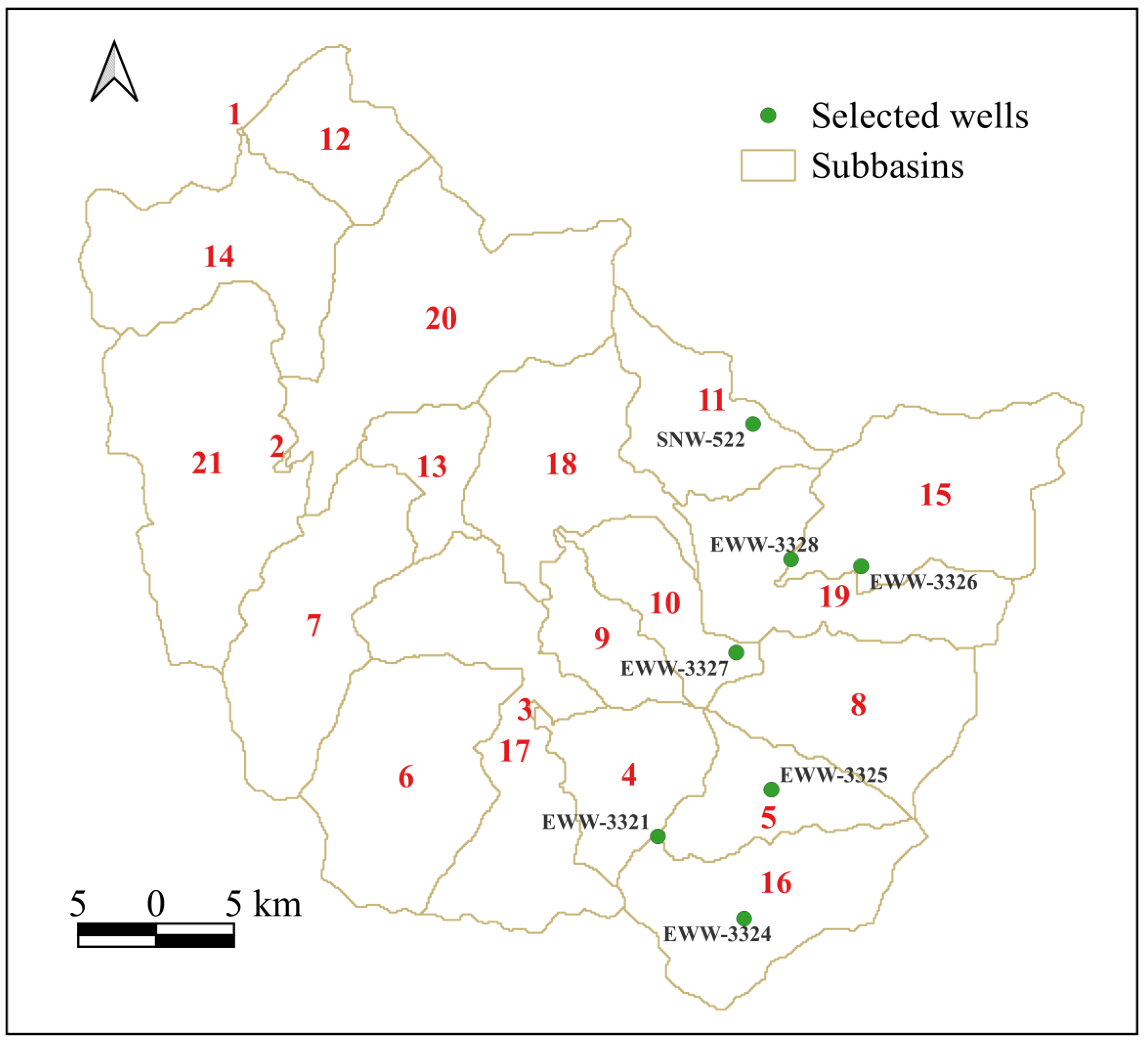
2.1. Description of Study Region
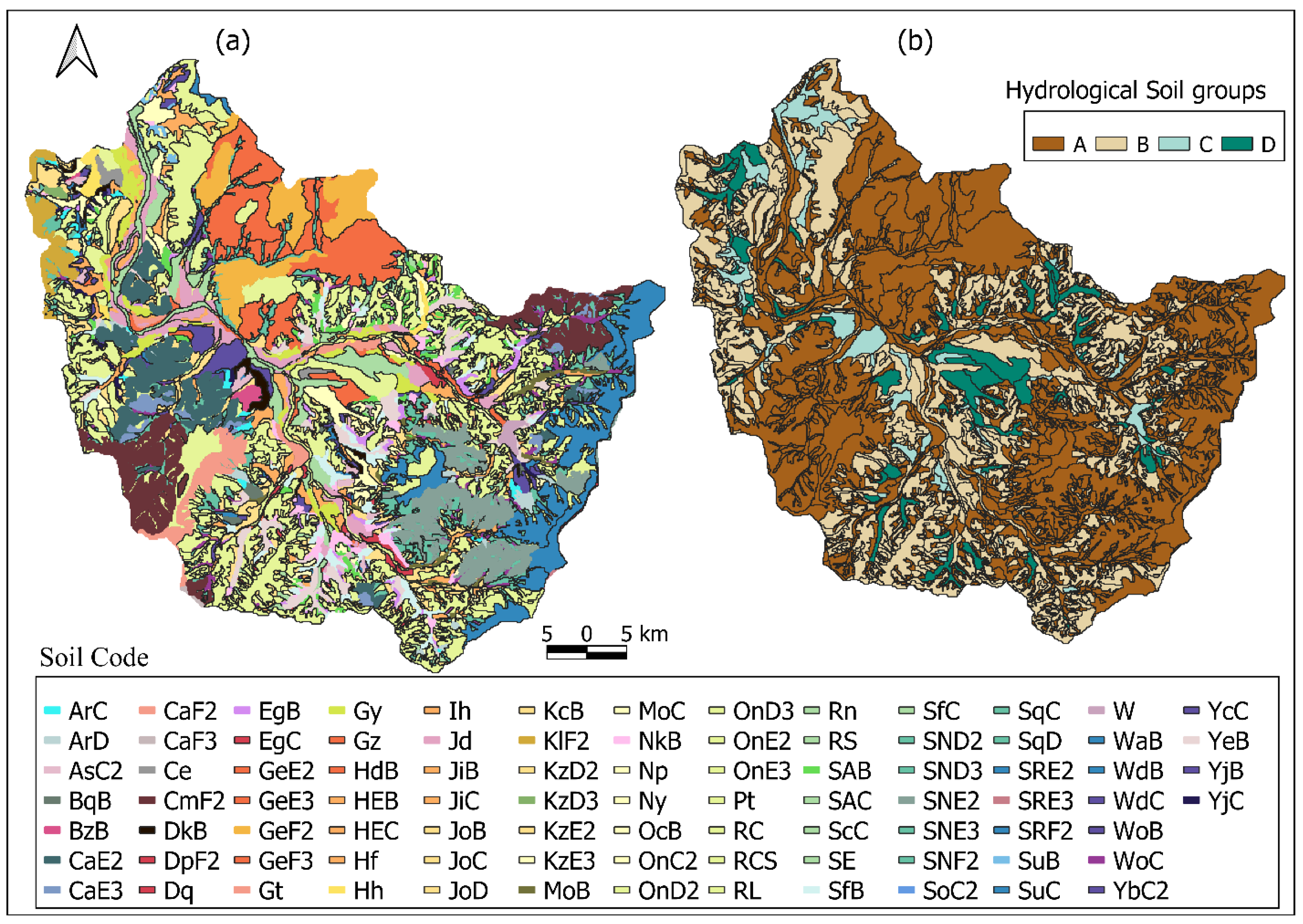
2.2. Evaluation of Recharge Using Integrated Model and Transient Water Table Fluctuation Method
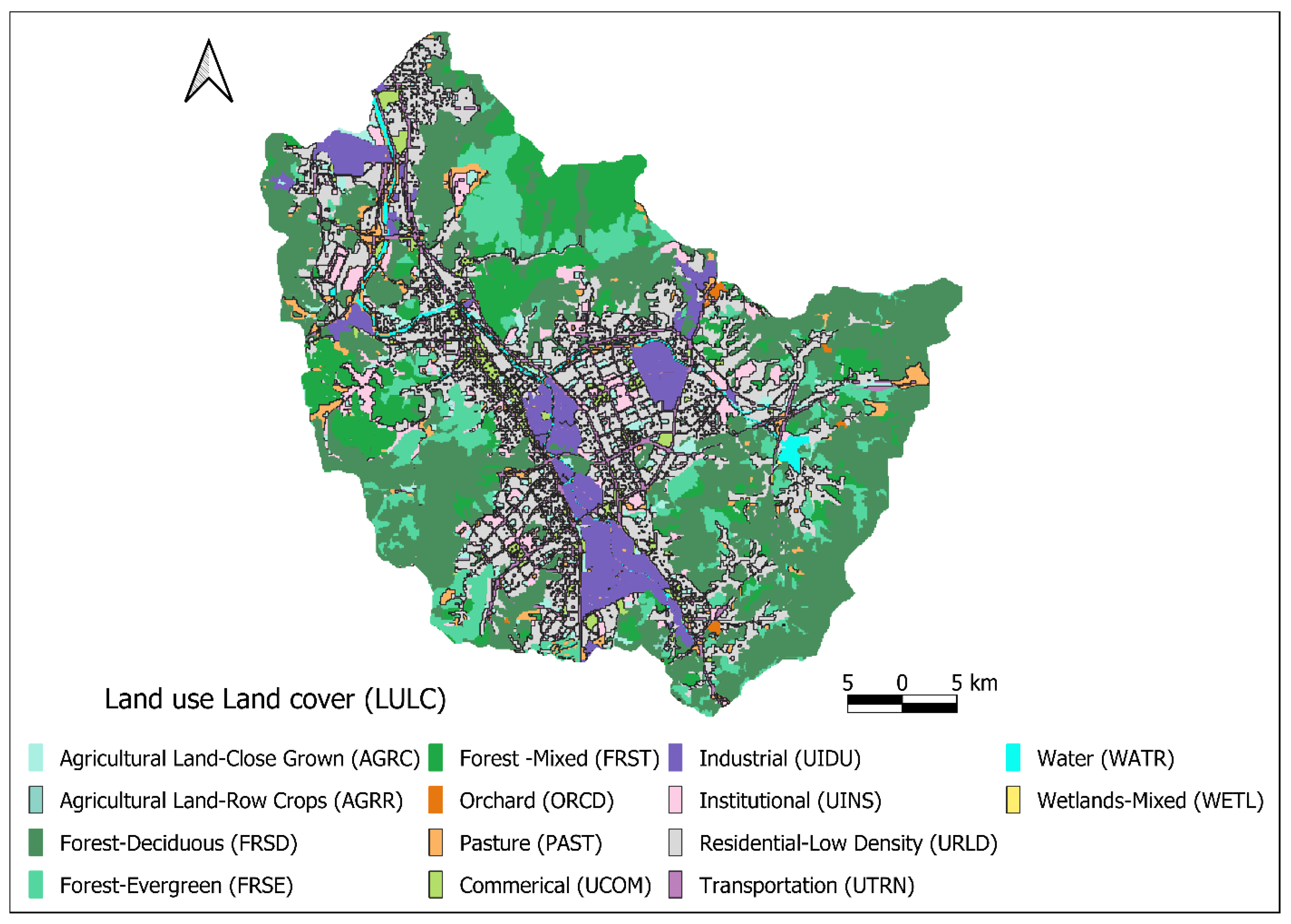
2.2.1. SWAT-MODFLOW Model
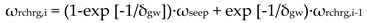
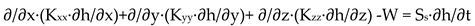
2.2.2. Transient Water Table Fluctuation Method (TWTFM)
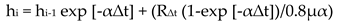
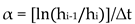
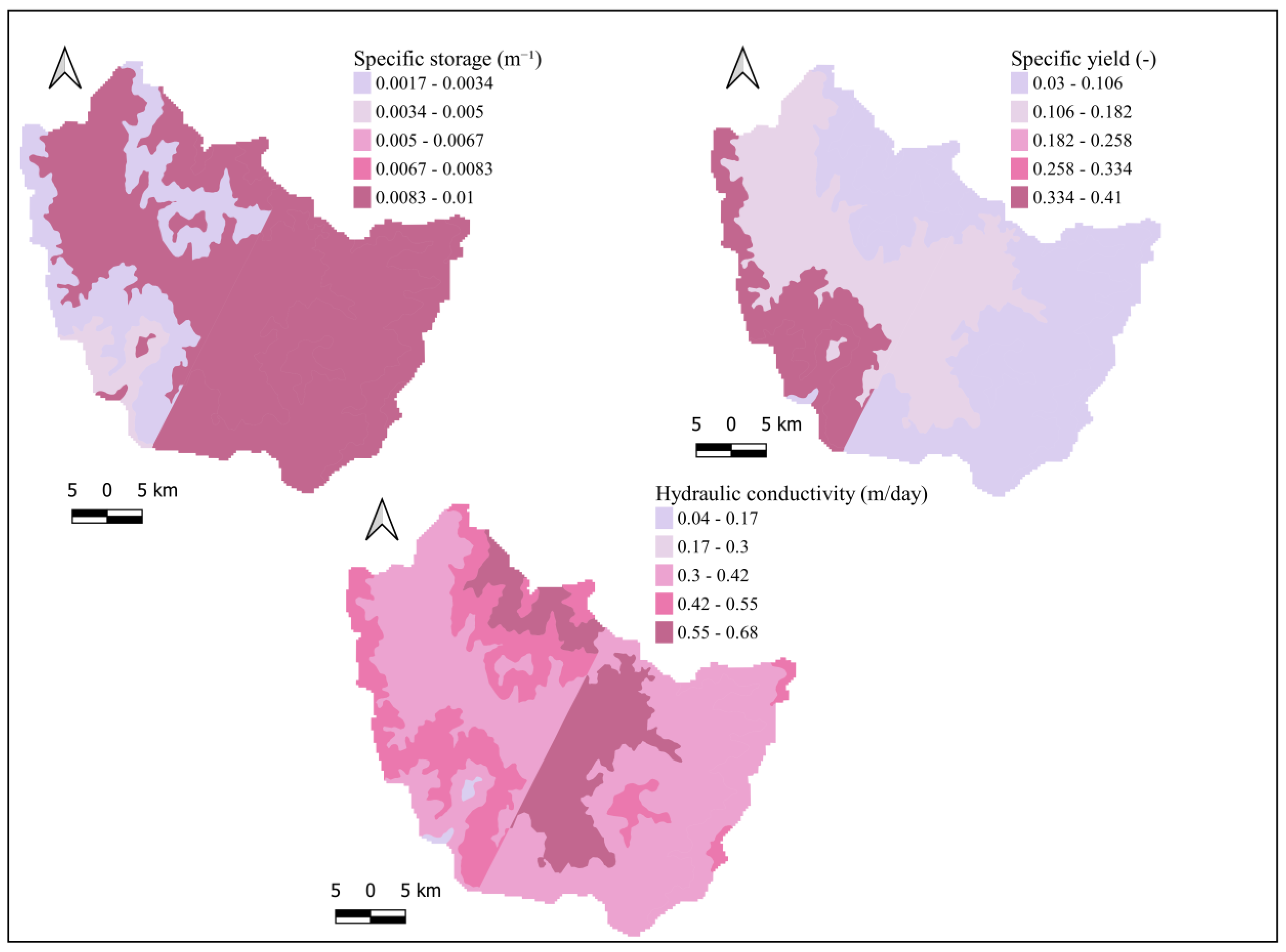
2.3. Model Setup and Coupling
2.3.1. SWAT Model
2.3.2. MODFLOW Model
2.3.3. SWAT-MODFLOW Model Integration
2.4. Model Calibration and Performance Evaluation
2.4.1. SWAT Calibration
2.4.2. SWAT-MODFLOW Model Calibration
3. Results and Discussions
3.1. Calibrated Parameters
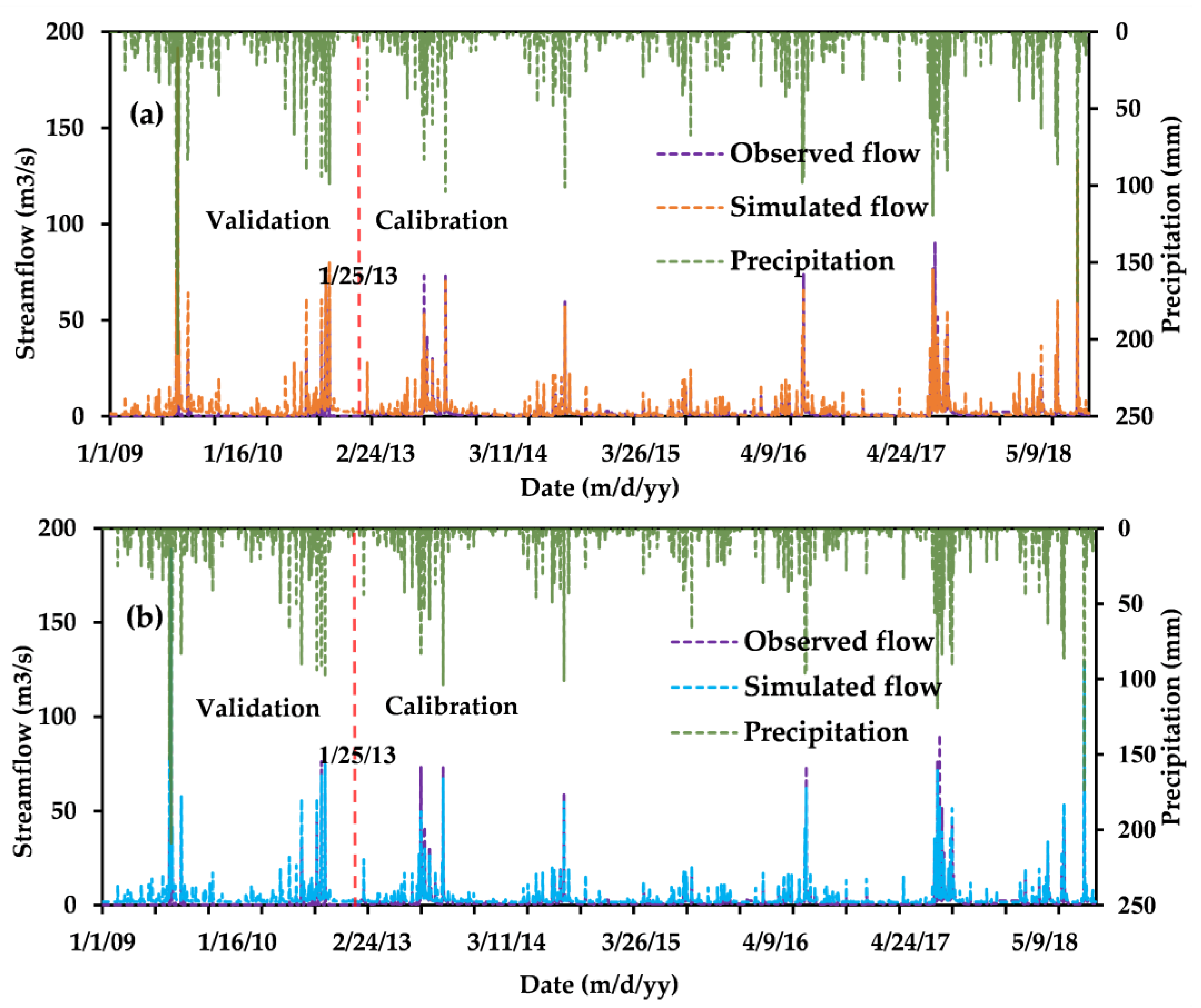
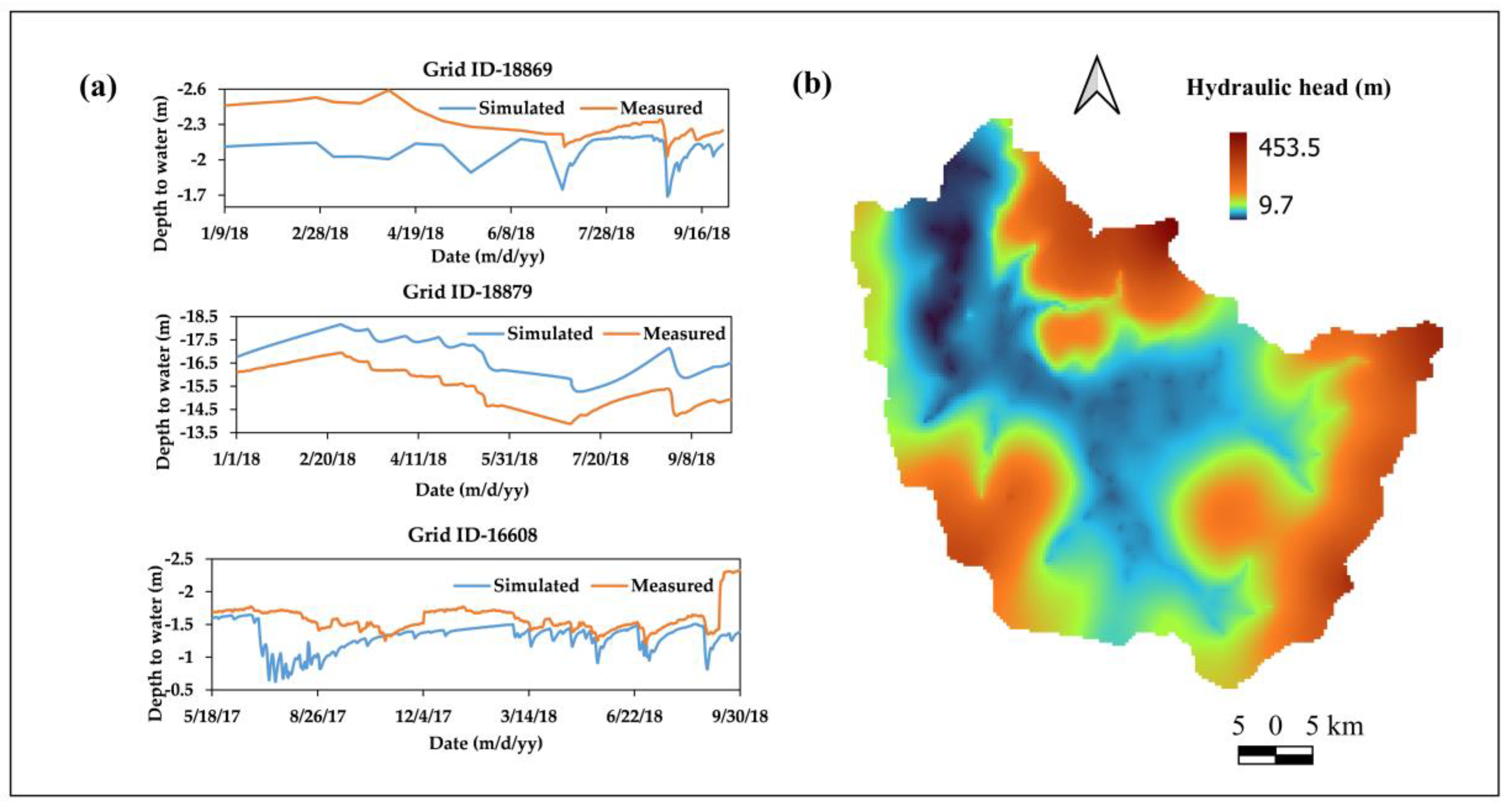
3.2. Model Performance during Calibration and Validation
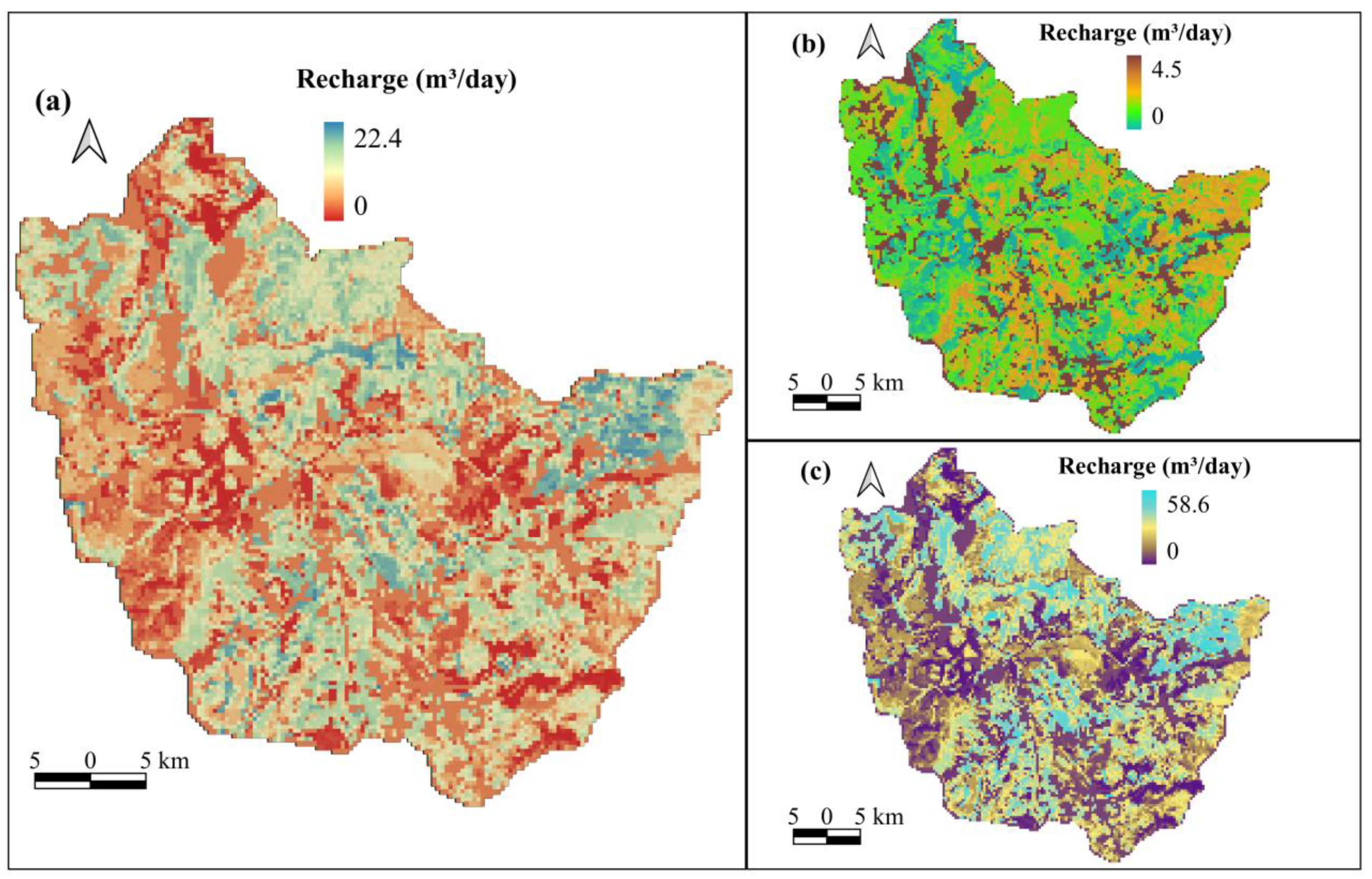
3.3. Groundwater Recharge
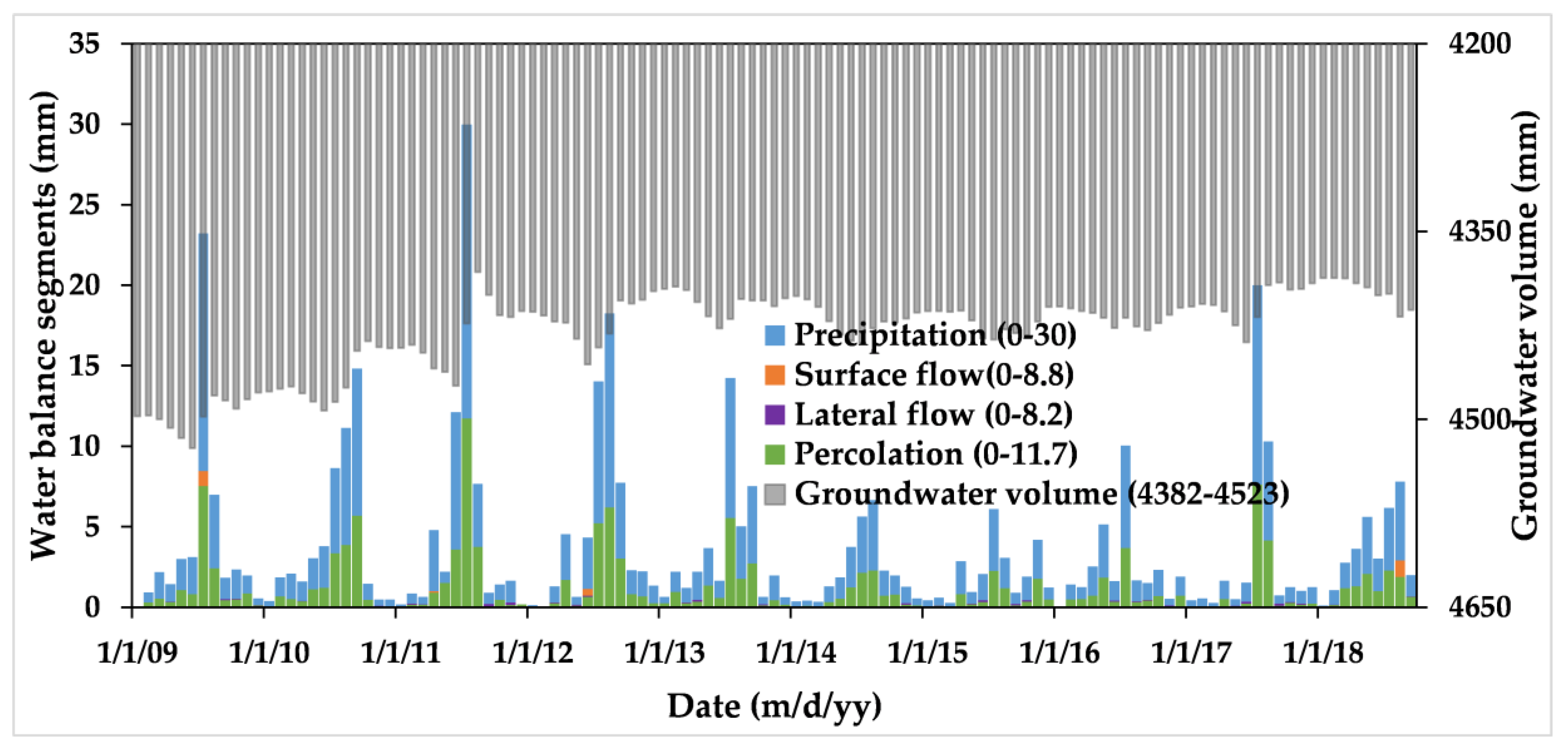
3.4. Water Balance Components of Study Watershed
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Aslam, R.A.; Shrestha, S.; Usman, M.N.; Khan, S.N.; Ali, S.; Sharif, M.S.; Sarwar, M.W.; Saddique, N.; Sarwar, A.; Ali, M.U.; et al. Integrated SWAT-MODFLOW Modeling-Based Groundwater Adaptation Policy Guidelines for Lahore, Pakistan under Projected Climate Change, and Human Development Scenarios. Atmosphere (Basel). 2022, 13, 2001. [Google Scholar] [CrossRef]
- Arshad, A.; Mirchi, A.; Samimi, M.; Ahmad, B. Combining Downscaled-GRACE Data with SWAT to Improve the Estimation of Groundwater Storage and Depletion Variations in the Irrigated Indus Basin (IIB). Sci. Total Environ. 2022, 838. [Google Scholar] [CrossRef] [PubMed]
- Locatelli, L.; Mark, O.; Mikkelsen, P.S.; Arnbjerg-Nielsen, K.; Deletic, A.; Roldin, M.; Binning, P.J. Hydrologic Impact of Urbanization with Extensive Stormwater Infiltration. J. Hydrol. 2017, 544, 524–537. [Google Scholar] [CrossRef]
- Barron, O.V.; Donn, M.J.; Barr, A.D. Urbanisation and Shallow Groundwater: Predicting Changes in Catchment Hydrological Responses. Water Resour. Manag. 2013, 27, 95–115. [Google Scholar] [CrossRef]
- Fleckenstein, J.H.; Krause, S.; Hannah, D.M.; Boano, F. Groundwater-Surface Water Interactions: New Methods and Models to Improve Understanding of Processes and Dynamics. Adv. Water Resour. 2010, 33, 1291–1295. [Google Scholar] [CrossRef]
- Sophocleous, M. Interactions between Groundwater and Surface Water: The State of the Science. Hydrogeol. J. 2002 101 2002, 10, 52–67. [Google Scholar] [CrossRef]
- Sharp, J.M. The Impacts of Urbanization on Groundwater Systems and Recharge. Aquamundi 2010, 1, 51–56. [Google Scholar]
- Wang, Y.; Zheng, C.; Ma, R. Review: Safe and Sustainable Groundwater Supply in China. Hydrogeol. J. 2018, 26, 1301–1324. [Google Scholar] [CrossRef]
- Yifru, B.A.; Chung, I.M.; Kim, M.G.; Chang, S.W. Assessment of Groundwater Recharge in Agro-Urban Watersheds Using Integrated SWAT-MODFLOW Model. Sustain. 2020, 12, 6593. [Google Scholar] [CrossRef]
- Lee, C.H.; Yeh, H.F.; Chen, J.F. Estimation of Groundwater Recharge Using the Soil Moisture Budget Method and the Base-Flow Model. Environ. Geol. 2008, 54, 1787–1797. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Healy, R.W.; Cook, P.G. Choosing Appropriate Techniques for Quantifying Groundwater Recharge. Hydrogeol. J. 2002, 10, 18–39. [Google Scholar] [CrossRef]
- Healy, R.; journal, P.C.-H. ; 2002, undefined Using Groundwater Levels to Estimate Recharge. Springer 2002, 10, 91–109. [Google Scholar] [CrossRef]
- Chand, R.; Chandra, S.; Rao, V.A.; Singh, V.S.; Jain, S.C. Estimation of Natural Recharge and Its Dependency on Sub-Surface Geoelectric Parameters. J. Hydrol. 2004, 299, 67–83. [Google Scholar] [CrossRef]
- Rangarajan, R.; Muralidharan, D.; Deshmukh, S.D.; Hodlur, G.K.; Gangadhara Rao, T. Redemarcation of Recharge Area of Stressed Confined Aquifers of Neyveli Groundwater Basin, India, through Tritium Tracer Studies. Environ. Geol. 2005, 48, 37–48. [Google Scholar] [CrossRef]
- Shahul Hameed, A.; Resmi, T.R.; Suraj, S.; Warrier, C.U.; Sudheesh, M.; Deshpande, R.D. Isotopic Characterization and Mass Balance Reveals Groundwater Recharge Pattern in Chaliyar River Basin, Kerala, India. J. Hydrol. Reg. Stud. 2015, 4, 48–58. [Google Scholar] [CrossRef]
- Cheema, M.J.M.; Immerzeel, W.W.; Bastiaanssen, W.G.M. Spatial Quantification of Groundwater Abstraction in the Irrigated Indus Basin. Groundwater 2014, 52, 25–36. [Google Scholar] [CrossRef] [PubMed]
- Yifru, B.A.; Chung, I.M.; Kim, M.G.; Chang, S.W. Assessing the Effect of Land/Use Land Cover and Climate Change on Water Yield and Groundwater Recharge in East African Rift Valley Using Integrated Model. J. Hydrol. Reg. Stud. 2021, 37, 100926. [Google Scholar] [CrossRef]
- Taie Semiromi, M.; Koch, M. Analysis of Spatio-Temporal Variability of Surface–Groundwater Interactions in the Gharehsoo River Basin, Iran, Using a Coupled SWAT-MODFLOW Model. Environ. Earth Sci. 2019, 78, 1–21. [Google Scholar] [CrossRef]
- Dowlatabadi, S.; Ali Zomorodian, S.M. Conjunctive Simulation of Surface Water and Groundwater Using SWAT and MODFLOW in Firoozabad Watershed. KSCE J. Civ. Eng. 2015, 20, 485–496. [Google Scholar] [CrossRef]
- Arnold, J., Kiniry, R., Williams, E., Haney, S., Neitsch, S. Soil & Water Assessment Tool, Texas Water Resources Institute-TR-439. 2012.
- Arnold, J.-F.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; Van Griensven, A.; Liew, M.W. Van; et al. SWAT: MODEL USE, CALIBRATION, AND VALIDATION. Trans. ASABE 55, 1491–1508.
- Molina-Navarro, E.; Bailey, R.T.; Estrup Andersen, H.; Thodsen, H.; Nielsen, A.; Park, S.; Skødt Jensen, J.; Birk Jensen, J.; Trolle, D.; Piniewski, M.; et al. Comparison of Abstraction Scenarios Simulated by SWAT and SWAT-MODFLOW. 2019, 64, 434–454. [CrossRef]
- Gassman, P.W.; Sadeghi, A.M.; Srinivasan, R. Applications of the SWAT Model Special Section: Overview and Insights. J. Environ. Qual. 2014, 43, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Al Khoury, I.; Boithias, L.; Labat, D. A Review of the Application of the Soil and Water Assessment Tool (SWAT) in Karst Watersheds. Water 2023, 15, 954. [Google Scholar] [CrossRef]
- Ashu, A.B.; Lee, S. Il Assessing Climate Change Effects on Water Balance in a Monsoon Watershed. Water 2020, 12, 2564. [Google Scholar] [CrossRef]
- Lee, J.; Lee, Y.; Woo, S.; Kim, W.; Kim, S. Evaluation of Water Quality Interaction by Dam and Weir Operation Using SWAT in the Nakdong River Basin of South Korea. Sustain. 2020, 12, 6845. [Google Scholar] [CrossRef]
- Ahn, S.R.; Kim, S.J. Analysis of Water Balance by Surface–Groundwater Interaction Using the SWAT Model for the Han River Basin, South Korea. Paddy Water Environ. 2018, 16, 543–560. [Google Scholar] [CrossRef]
- Lee, J.; Jung, C.; Kim, S.; Kim, S. Assessment of Climate Change Impact on Future Groundwater-Level Behavior Using SWAT Groundwater-Consumption Function in Geum River Basin of South Korea. Water 2019, 11, 949. [Google Scholar] [CrossRef]
- Kim, S.; Noh, H.; Jung, J.; Jun, H.; Kim, H.S. Assessment of the Impacts of Global Climate Change and Regional Water Projects on Streamflow Characteristics in the Geum River Basin in Korea. Water 2016, 8, 91. [Google Scholar] [CrossRef]
- Liu, W.; Park, S.; Bailey, R.T.; Molina-Navarro, E.; Andersen, H.E.; Thodsen, H.; Nielsen, A.; Jeppesen, E.; Jensen, J.S.; Jensen, J.B.; et al. Quantifying the Streamflow Response to Groundwater Abstractions for Irrigation or Drinking Water at Catchment Scale Using SWAT and SWAT–MODFLOW. Environ. Sci. Eur. 2020, 32, 1–25. [Google Scholar] [CrossRef]
- Zhang, X.; Ren, L.; Kong, X. Estimating Spatiotemporal Variability and Sustainability of Shallow Groundwater in a Well-Irrigated Plain of the Haihe River Basin Using SWAT Model. J. Hydrol. 2016, 541, 1221–1240. [Google Scholar] [CrossRef]
- Pfannerstill, M.; Guse, B.; Fohrer, N. A Multi-Storage Groundwater Concept for the SWAT Model to Emphasize Nonlinear Groundwater Dynamics in Lowland Catchments. Hydrol. Process. 2014, 28, 5599–5612. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Dietrich, J. Modification of the SWAT Model to Simulate Regional Groundwater Flow Using a Multicell Aquifer. Hydrol. Process. 2018, 32, 939–953. [Google Scholar] [CrossRef]
- Ntona, M.M.; Busico, G.; Mastrocicco, M.; Kazakis, N. Modeling Groundwater and Surface Water Interaction: An Overview of Current Status and Future Challenges. Sci. Total Environ. 2022, 846, 157355. [Google Scholar] [CrossRef]
- Sanz, D.; Castaño, S.; Cassiraga, E.; Sahuquillo, A.; Gómez-Alday, J.J.; Peña, S.; Calera, A. Modeling Aquifer-River Interactions under the Influence of Groundwater Abstraction in the Mancha Oriental System (SE Spain). Hydrogeol. J. 2011, 19, 475–487. [Google Scholar] [CrossRef]
- May, R.; Mazlan, N.S.B. Numerical Simulation of the Effect of Heavy Groundwater Abstraction on Groundwater-Surface Water Interaction in Langat Basin, Selangor, Malaysia. Environ. Earth Sci. 2014, 71, 1239–1248. [Google Scholar] [CrossRef]
- Rumph Frederiksen, R.; Molina-Navarro, E. The Importance of Subsurface Drainage on Model Performance and Water Balance in an Agricultural Catchment Using SWAT and SWAT-MODFLOW. Agric. Water Manag. 2021, 255, 107058. [Google Scholar] [CrossRef]
- Sophocleous, M.A.; Koelliker, J.K.; Govindaraju, R.S.; Birdie, T.; Ramireddygari, S.R.; Perkins, S.P. Integrated Numerical Modeling for Basin-Wide Water Management: The Case of the Rattlesnake Creek Basin in South-Central Kansas. J. Hydrol. 1999, 214, 179–196. [Google Scholar] [CrossRef]
- Gao, F.; Feng, G.; Han, M.; Dash, P.; Jenkins, J.; Liu, C. Assessment of Surface Water Resources in the Big Sunflower River Watershed Using Coupled SWAT–MODFLOW Model. Water 2019, 11, 528. [Google Scholar] [CrossRef]
- Wei Liu; Seonggyu Park; Bailey, R.; Eugenio Molina-Navarro; Hans Estrup Andersen; Hans Thodsen; Anders Nielsen; Jeppesen; Erik Jensen; Jacob Skødt; et al. Comparing SWAT with SWAT-MODFLOW Hydrological Simulations When Assessing the Impacts of Groundwater Abstractions for Irrigation and Drinking Water. Hydrol. Earth Syst. Sci. Discuss. 2019, 1–51.
- Bailey, R.T.; Wible, T.C.; Arabi, M.; Records, R.M.; Ditty, J. Assessing Regional-Scale Spatio-Temporal Patterns of Groundwater–Surface Water Interactions Using a Coupled SWAT-MODFLOW Model. Hydrol. Process. 2016, 30, 4420–4433. [Google Scholar] [CrossRef]
- Techniques, M. MODFLOW-NWT , A Newton Formulation for MODFLOW-2005. Groundw. B. 6, Sect. A, Model. Tech. 2005, Book 6-A37, 44.
- Wang, Y.; Chen, N. Recent Progress in Coupled Surface–Ground Water Models and Their Potential in Watershed Hydro-Biogeochemical Studies: A Review. Watershed Ecol. Environ. 2021, 3, 17–29. [Google Scholar] [CrossRef]
- Guevara-Ochoa, C.; Medina-Sierra, A.; Vives, L. Spatio-Temporal Effect of Climate Change on Water Balance and Interactions between Groundwater and Surface Water in Plains. Sci Total Env. 2020, 722. [Google Scholar] [CrossRef]
- Taie Semiromi, M.; Koch, M. Analysis of Spatio-Temporal Variability of Surface-Groundwater Interactions in the Gharehsoo River Basin, Iran, Using a Coupled SWAT-MODFLOW Model. Env. Earth Sci 2019, 78, 201. [Google Scholar] [CrossRef]
- Guzman, J.A.; Moriasi, D.N.; Gowda, P.H.; Steiner, J.L.; Starks, P.J.; Arnold, J.G.; Srinivasan, R. A Model Integration Framework for Linking SWAT and MODFLOW. Environ. Model. Softw. 2015, 73, 103–116. [Google Scholar] [CrossRef]
- Chung, I.M.; Kim, N.W.; Lee, J.; Sophocleous, M. Assessing Distributed Groundwater Recharge Rate Using Integrated Surface Water-Groundwater Modelling: Application to Mihocheon Watershed, South Korea. Hydrogeol. J. 2010, 18, 1253–1264. [Google Scholar] [CrossRef]
- Liu, W.; Bailey, R.T.; Andersen, H.E.; Jeppesen, E.; Park, S.; Thodsen, H.; Nielsen, A.; Molina-Navarro, E.; Trolle, D. Assessing the Impacts of Groundwater Abstractions on Flow Regime and Stream Biota: Combining SWAT-MODFLOW with Flow-Biota Empirical Models. Sci. Total Environ. 2020, 706, 135702. [Google Scholar] [CrossRef]
- Surinaidu, L.; Muthuwatta, L.; Amarasinghe, U.A.; Jain, S.K.; Ghosh, N.C.; Kumar, S.; Singh, S. Reviving the Ganges Water Machine: Accelerating Surface Water and Groundwater Interactions in the Ramganga Sub-Basin. J. Hydrol. 2016, 540, 207–219. [Google Scholar] [CrossRef]
- Mosase, E.; Ahiablame, L.; Park, S.; Bailey, R. Modelling Potential Groundwater Recharge in the Limpopo River Basin with SWAT-MODFLOW. Groundw. Sustain. Dev. 2019, 9, 100260. [Google Scholar] [CrossRef]
- Sophocleous, M.; Perkins, S.P. Methodology and Application of Combined Watershed and Ground-Water Models in Kansas. J. Hydrol. 2000, 236, 185–201. [Google Scholar] [CrossRef]
- Chunn, D.; Faramarzi, M.; Smerdon, B.; Alessi, D. Application of an Integrated SWAT–MODFLOW Model to Evaluate Potential Impacts of Climate Change and Water Withdrawals on Groundwater–Surface Water Interactions in West-Central Alberta. Water 2019, 11, 110. [Google Scholar] [CrossRef]
- Pisinaras V Assessment of Future Climate Change Impacts in a Mediterranean Aquifer. Glob. NEST J. 2016, 18, 119–130. [CrossRef]
- Zambrano-Bigiarini, M.; Rojas, R. A Model-Independent Particle Swarm Optimisation Software for Model Calibration. Environ. Model. Softw. 2013, 43, 5–25. [Google Scholar] [CrossRef]
- Yuan, L.; Sinshaw, T.; Forshay, K.J. Review of Watershed-Scale Water Quality and Nonpoint Source Pollution Models. Geosci. 2020, Vol. 10, Page 25 2020, 10, 25. [Google Scholar] [CrossRef]
- Hung Vu, V.; Merkel, B.J. Estimating Groundwater Recharge for Hanoi, Vietnam. Sci. Total Environ. 2019, 651, 1047–1057. [Google Scholar] [CrossRef]
- Şimşek, C.; Demirkesen, A.C.; Baba, A.; Kumanlıoğlu, A.; Durukan, S.; Aksoy, N.; Demirkıran, Z.; Hasözbek, A.; Murathan, A.; Tayfur, G. Estimation Groundwater Total Recharge and Discharge Using GIS-Integrated Water Level Fluctuation Method: A Case Study from the Alaşehir Alluvial Aquifer Western Anatolia, Turkey. Arab. J. Geosci. 2020, 13, 1–14. [Google Scholar] [CrossRef]
- Delottier, H.; Pryet, A.; Lemieux, J.M.; Dupuy, A. Estimating Groundwater Recharge Uncertainty from Joint Application of an Aquifer Test and the Water-Table Fluctuation Method. Hydrogeol. J. 2018, 26, 2495–2505. [Google Scholar] [CrossRef]
- Chung, I.M.; Kim, Y.J.; Kim, N.W. Estimating the Temporal Distribution of Groundwater Recharge by Using the Transient Water Table Fluctuation Method and Watershed Hydrologic Model. Appl. Eng. Agric. 2021, 37, 95–104. [Google Scholar] [CrossRef]
- Park, E. Delineation of Recharge Rate from a Hybrid Water Table Fluctuation Method. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Gumuła-Kawęcka, A.; Jaworska-Szulc, B.; Szymkiewicz, A.; Gorczewska-Langner, W.; Pruszkowska-Caceres, M.; Angulo-Jaramillo, R.; Šimůnek, J. Estimation of Groundwater Recharge in a Shallow Sandy Aquifer Using Unsaturated Zone Modeling and Water Table Fluctuation Method. J. Hydrol. 2022, 605, 127283. [Google Scholar] [CrossRef]
- Jie, Z.; van Heyden, J.; Bendel, D.; Barthel, R. Combination of Soil-Water Balance Models and Water-Table Fluctuation Methods for Evaluation and Improvement of Groundwater Recharge Calculations. Hydrogeol. J. 2011, 19, 1487–1502. [Google Scholar] [CrossRef]
- 국가수자원관리종합정보시스템. Available online: http://www.wamis.go.kr/ (accessed on 11 November 2022).
- 기상자료개방포털. Available online: https://data.kma.go.kr/cmmn/main.do (accessed on 11 November 2022).
- Welcome to the National Academy of Agricultural Sciences. Available online: http://www.naas.go.kr/ (accessed on 11 November 2022).
- Guevara Ochoa, C.; Medina Sierra, A.; Vives, L.; Zimmermann, E.; Bailey, R. Spatio-Temporal Patterns of the Interaction between Groundwater and Surface Water in Plains. Hydrol. Process. 2020, 34, 1371–1392. [Google Scholar] [CrossRef]
- hydrology, M.S.-J. of; 1991, undefined Combining the Soilwater Balance and Water-Level Fluctuation Methods to Estimate Natural Groundwater Recharge: Practical Aspects. Elsevier.
- Moon, S.K.; Woo, N.C.; Lee, K.S. Statistical Analysis of Hydrographs and Water-Table Fluctuation to Estimate Groundwater Recharge. J. Hydrol. 2004, 292, 198–209. [Google Scholar] [CrossRef]
- Rasmussen, W.C.; Andreasen, G.E. Hydrologic Budget of the Beaverdam Creek Basin, Maryland: USGS Water Supply Paper 1472. 1959, 106.
- Turnadge, C.; Crosbie, R.S.; Barron, O.; Rau, G.C. Comparing Methods of Barometric Efficiency Characterization for Specific Storage Estimation. Groundwater 2019, 57, 844–859. [Google Scholar] [CrossRef]
- Park, E.; Parker, J.C. A Simple Model for Water Table Fluctuations in Response to Precipitation. J. Hydrol. 2008, 356, 344–349. [Google Scholar] [CrossRef]
- Cobb, A.R.; Harvey, C.F. Scalar Simulation and Parameterization of Water Table Dynamics in Tropical Peatlands. Water Resour. Res. 2019, 55, 9351–9377. [Google Scholar] [CrossRef]
- Hussain, F.; Wu, R.S.; Shih, D.S. Water Table Response to Rainfall and Groundwater Simulation Using Physics-Based Numerical Model: WASH123D. J. Hydrol. Reg. Stud. 2022, 39, 100988. [Google Scholar] [CrossRef]
- Smedema, L.K.; Rycroft, D.W. Land Drainage: Planning and Design of Agricultural Drainage Systems. 1983. [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large Area Hydrologic Modeling and Assessment Part I: Model Development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Her, Y.; Frankenberger, J.; Chaubey, I.; Srinivasan, R.; Srinivasan, R.; Member, A. Threshold Effects in HRU Definition Ofthe Soil and Water Assessment Tool. elibrary.asabe.org 2015, 58, 47907–2093. [Google Scholar] [CrossRef]
- Mathias, S.; research, A.B.-W. resources; 2007, undefined Flow to a Finite Diameter Well in a Horizontally Anisotropic Aquifer with Wellbore Storage. Wiley Online Libr. 2007, 43. [Google Scholar] [CrossRef]
- Park, S.; Nielsen, A.; Bailey, R.T.; Trolle, D.; Bieger, K. A QGIS-Based Graphical User Interface for Application and Evaluation of SWAT-MODFLOW Models. Environ. Model. Softw. 2019, 111, 493–497. [Google Scholar] [CrossRef]
- Faramarzi, M.; Srinivasan, R.; Iravani, M.; Bladon, K.D.; Abbaspour, K.C.; Zehnder, A.J.B.; Goss, G.G. Setting up a Hydrological Model of Alberta: Data Discrimination Analyses Prior to Calibration. Environ. Model. Softw. 2015, 74, 48–65. [Google Scholar] [CrossRef]
- Abbaspour, K.C. SWAT-CUP SWATCalibration and Uncertainty Programs. Arch. Orthop. Trauma Surg. 2010, 130, 965–970. [Google Scholar]
- D. N. Moriasi; J. G. Arnold; M. W. Van Liew; R. L. Bingner; R. D. Harmel; T. L. Veith Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Blöschl, G.; Sivapalan, M. Scale Issues in Hydrological Modelling: A Review. Hydrol. Process. 1995, 9, 251–290. [Google Scholar] [CrossRef]
- Jafari, T.; Kiem, A.S.; Javadi, S.; Nakamura, T.; Nishida, K. Fully Integrated Numerical Simulation of Surface Water-Groundwater Interactions Using SWAT-MODFLOW with an Improved Calibration Tool. J. Hydrol. Reg. Stud. 2021, 35, 100822. [Google Scholar] [CrossRef]
- Park, S. Enhancement of Coupled Surface / Subsurface Flow Models in Watersheds: Analysis, Model Development, Optimization, and User Accessibility by Using SWAT-MODFLOW Simulation, 2018.
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Kløve, B. A Continental-Scale Hydrology and Water Quality Model for Europe: Calibration and Uncertainty of a High-Resolution Large-Scale SWAT Model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
| Parameters | Description | Calibrated Value | Range Value |
| r_CN2.mgt | Initial SCS runoff curve no. for moisture condition II | 0.3 | 0.2-1.0 |
| v_ALPHA.BF.gw | Baseflow alpha factor (days) | 0.03 | 0.01-0.05 |
| v_GW_DELAY.gw | Groundwater delay (days) | 1 | 1-4 |
| v_GWQMN.gw | Threshold depth of water in the shallow aquifer for "revap" to occur (mm) | 530 | 460-1400 |
| v_GW_REVAP.gw | Groundwater "revap" coefficient | 0.05 | 0.01-0.09 |
| v_ESCO.hru | Soil evaporation compensation factor(-) | 0.3 | 0.15-0.5 |
| r_SOL_AWC.sol | Available water capacity of the soil layer (mm mm-1 ) | 0.03 | 0.01-0.05 |
| v_REVAPMN.gw | Threshold depth of water in the shallow aquifer for "revap" to occur (mm) | 430 | 187-450 |
| v_EPCO.hru | Plant uptake compensation factor(-) | 0.3 | 0.1-0.5 |
| v_RCHRG.gw | Deep aquifer percolation fraction | 0.3 | 0.05-0.4 |
| Parameter | Value Range | Description |
| ALPHA_BF | 0.01-0.2 | Baseflow alpha factor (days),SWAT |
| CH_k2 | 1-50 | Main channel effective hydraulic conductivity (mm/h), SWAT |
| CN2 | 0.01-1 | Initial SCS runoff curve no. for moisture condition II, SWAT |
| EPCO | 0.1-1 | Plant uptake compensation factor(-), SWAT |
| ESCO | 0.1-1 | Soil evaporation compensation factor(-), SWAT |
| Hk | 0.01-100 | Hydraulic conductivity of aquifer (m/day), MODFLOW |
| Ss | 0.00001-0.01 | Specific storage (m-1), MODFLOW |
| Sy | 0.0001-0.4 | Specific yield (-), MODFLOW |
| Parameter | Calibrated Value | Description |
| ALPHA_BF | 0.01 | Baseflow alpha factor (days), SWAT |
| CH_k2 | 26 | Main channel effective hydraulic conductivity (mm/h), SWAT |
| CN2 | 0.08 | Initial SCS runoff curve no. for moisture condition II, SWAT |
| EPCO | 0.01 | Plant uptake compensation factor(-), SWAT |
| ESCO | 0.01 | Soil evaporation compensation factor(-), SWAT |
| Model | Calibration | Validation | ||
| R2 | NSE | R2 | NSE | |
| SWAT | 0.79 | 0.76 | 0.75 | 0.69 |
| SWAT-MODFLOW | 0.82 | 0.75 | 0.83 | 0.73 |
| Subbasins | Observed wells Name | Recharge (mm) (SWAT) | Recharge (mm) (TWTFM) | Specific yield (–) | Reaction factor (d-1) |
| 19 | EWW-3328 | 1001.2 | 994.4 | 0.017 | 0.2 |
| 16 | EWW-3324 | 1021.3 | 1020 | 0.022 | 0.04 |
| 15 | EWW-3326 | 806.2 | 806 | 0.01 | 0.12 |
| 11 | SNW-522 | 982.7 | 976.3 | 0.0078 | 0.2 |
| 10 | EWW-3327 | 702.5 | 702 | 0.0109 | 0.2 |
| 5 | EWW-3325 | 962.4 | 957.2 | 0.011 | 0.2 |
| 4 | EWW-3321 | 553.6 | 553.6 | 0.008 | 0.068 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





