Prerpints.org logo
Preprint
Article

Analyzing the Time Spectrum of Supernova Neutrinos to Constrain Their Effective Mass or Lorentz Invariance Violation

Altmetrics

Downloads

67

Views

22

Comments

0

A peer-reviewed article of this preprint also exists.

C. Moura  *,‡
,
L. Quintino  ‡,
F. Rossi-Torres  ‡

  ‡ These authors contributed equally to this work.

This version is not peer-reviewed

Submitted:

27 April 2023

Posted:

28 April 2023

You are already at the latest version

Alerts
Abstract
We analyze the expected arrival time spectrum of supernova neutrinos using simulated luminosity and computing the expected number of events in future detectors such as the DUNE Far Detector and Hyper-Kamiokande. We develop a general method using minimum square statistics that can compute the sensitivity to any variable affecting neutrino time of flight. We apply this method in two different situations: First, we compare the time spectrum changes due to different neutrino mass values to put limits in electron (anti)neutrino effective mass. Second, we constrain Lorentz Invariance Violation through the mass scale, MQG, at which it would occur. We consider two main neutrino detection techniques: 1. DUNE-like liquid argon TPC, for which the main detection channel is νe+40Ar→e−+40K*, related to the supernova neutronization burst, and 2. HyperK-like water Cherenkov detector, for which ν¯e+p→e++n is the main detection channel. We consider a fixed supernova distance of 10 kpc and two different masses of the progenitor star: (i) 15 M⊙ with neutrino emission time up to 0.3 s and (ii) 11.2 M⊙ with neutrino emission time up to 10 s. The best mass limits at 3σ are of O(1) eV. For νe, the best limit comes from a DUNE-like detector if the mass ordering happens to be inverted. For ν¯e, the best limit comes from a HyperK-like detector. The best limit for the Lorentz Invariance Violation mass scale at 3σ level, considering superluminal or subluminal effect, is MQG≳1013 GeV (MQG≳5×105 GeV) for linear (quadratic) energy dependence.
Keywords: 
Subject: Physical Sciences  -   Nuclear and High Energy Physics

1. Introduction

One of the most important and still open questions in neutrino physics is the absolute value of neutrino masses. In addition to this question, we do not have a completely proven model of a mass generation mechanism that could explain the existence of this non-zero mass. Despite the lack of a complete picture of the neutrino mass generation mechanism, in recent years, we have seen a great progress in neutrino physics especially coming from oscillation experiments [1]. These experiments point to the fact that neutrino mass eigenstates mix during propagation, giving rise to neutrino flavor oscillation. The present oscillation experimental data cannot point out which mass eigenstate is the lightest one, two options being possible: normal ordering (NO), m 1 < m 2 < m 3 ; or inverted ordering (IO), m 3 < m 1 < m 2 . Oscillation experiments usually measure | Δ m i j 2 | , the mass squared differences in module, and θ j i , the mixing angles of the mass eigenstates, where i , j = 1 , 2 , 3 and i > j . From matter effect in oscillation, we do know that Δ m 21 2 is positive. Recent values of the oscillation parameters, with 1 σ uncertainty, can be found in, e.g., Ref. [1].
One of the possible sources of neutrinos is the collapse of stars. This process emits around 99% of the star internal energy in the form of neutrinos and antineutrinos with average energy of the order of 10 MeV. The detection of the supernova (SN) neutrino burst is crucial in order to understand the stellar explosion mechanism and it can provide an early warning for electromagnetic observation experiments [2].
During the stellar collapse that leads to the explosion of a SN, neutrino emission occurs in different stages. The first stage is neutronization, in which a fusion reaction between electrons and protons produces neutrons and electron neutrinos ( ν e ). This process produces a peak in the ν e luminosity curve as a function of time that lasts for about 25 ms. During neutronization, ν e s are trapped behind the shock wave formed by the collapse and are only released when the matter density becomes sufficiently low. The second stage is accretion, in which the matter from the collapsing star is attracted to the newly formed neutron star, producing neutrinos of all flavors. In this stage, all types of neutrinos are emitted. The third stage is the cooling, which occurs after the SN explosion. During the cooling, the neutron star releases all types of neutrinos and decreases its binding energy. For reviews of SN neutrinos and neutrino emission properties, see Ref. [3]. The impact of neutrino mass ordering - NO or IO - is relevant for the measurement of the neutronization burst [4].
There are several ways for measuring the neutrino mass and important constraints already exist. Before we discuss our estimate using SN neutrinos, we list a few constraints from different techniques.
From the high energy spectrum range of tritium beta decay, the Katrin experiment found a limit of 0.8 eV at 90% C.L. [5]. Other nuclei, such as   187 Re and   163 Ho may also β decay and provide limits [6]. From the electron capture decays of   163 Ho (   163 H o + + e − → 163 D y + ν e ), m ν e < 225 eV at 95% C.L. [7] and m ν e < 460 eV at 68% C.L. [8]. In the MANU experiment, with   187 Re β decay, it was found an upper limit of 26 eV at 95% C.L. [9]. The MiBeta Collaboration obtained an upper limit of 15 eV at 90% C.L. [10]. Recently, the Project 8 Collaboration, using the Cyclotron Radiation Emission Spectroscopy (CRES) technique and a cm   3 scale physical detection volume, obtained m ν < 152 eV from the continuous tritium beta spectrum [11].
Despite the uncertainties in the nuclear matrix elements from neutrinoless double β decay ( ( Z , A ) → ( Z + 2 , A ) + e − + e − ) [12], experiments that study 0 ν β β from   136 Xe nuclei, such as the KamLAND-ZEN [13] and EXO-200 [14], constrained, respectively, m e e < 0.061 − 0.165 eV and m e e < 0.093 − 0.286 eV. In this lepton-number violating process, the decay rate of the nuclei scales with the effective neutrino mass, where the neutrino is a Majorana fermion. The Heidelberg-Moscow collaboration claimed evidence of this phenomenon with m e e ≈ 0.3 eV, m e e representing the coherent sum of masses ( m i ) of the mass eigenstates [15].
Cosmology also imposes limits on neutrino masses. Neutrinos have large free streaming length, which depends on their masses. They smear out fluctuations that are imprinted in the cosmic microwave background and in galaxies. From cosmic microwave background, using the Planck satellite, m ν < 0.09 eV at 95% C.L. [16], even though there are several degeneracies related to the cosmological model parameters [17].
All bounds described above are summarized in Table 1.
Neutrino mass bounds can be obtained from type II SN bursts, which have short duration and happen at astronomical distances. The idea is that neutrinos travel long distances in a time that depends on their mass as well as on their energy. So there is a delay compared to the time of flight of a supposedly massless particle that impacts the time spectrum of the neutrino events at the Earth [18,19].
Using SN1987A inverse β decay data ( ν ¯ e + p → n + e + ) from Kamiokande [20], IMB [21] and Baksan [22], an upper limit of m ν < 5.8 eV at 95% C.L. [23] was obtained using a proper likelihood of event-by-event analysis [24]. Lamb & Loredo, in a similar analysis, constrained the neutrino mass to be less than 5.7 eV [25]. The future Jiangmen Underground Neutrino Observatory (JUNO) [26], a 20 kton liquid-scintilator detector using the inverse beta decay channel, may limit the neutrino mass with a SN at 10 kpc distance and NO as m ν < ( 0.83 ± 0.24 ) eV at 95% C.L. A sub-eV mass limit, for a future SN, may be reached in several detectors using a time structured signal, as demonstrated in Ref. [27].
Liquid Argon TPC (LArTCP), such as the far detector of the future Deep Underground Neutrino Experiment (DUNE) [28,29], is sensitive to the detection of electron neutrinos ( ν e ) from SN [30]. Depending on the type of neutrino mass ordering, such detector can be important to prove the existence of the neutronization process in explosions of massive stars. A detector with 40 kton of liquid argon can detect thousands of events. Furthermore, the short temporal duration of the neutronization peak may place more restrictive constraints on physical parameters associated with arrival time spectrum changes. It is expected a sensitivity of around 0.90-2.00 eV for the neutrino mass [30,31].
Cherenkov light detectors, sensitive to ν ¯ e , can probe the entire neutrino emission period of a SN event, making it possible to establish limits on neutrino mass [23,25]. Hyper-Kamiokande (HyperK) - the next generation and improved Super-Kamiokande (SK) - will work with a water Cherenkov detector (WtCh) and is very sensitive to the detection of ν ¯ e via ν ¯ e + p → n + e + . For HyperK, it is expected an absolute mass sensitivity from 0.5 to 1.3 eV [32].
In this work, we revisit the obtention of an effective mass limit and, inspired by [33], we also include an analysis of Lorentz Invariance Violation (LIV). We explore the time spectrum changes caused, independently, by neutrino mass or LIV along the neutrino propagation from the SN to the Earth. We consider two different masses of progenitor star at a distance of 10 kpc and two types of detectors: a DUNE-like 40 kton LArTPC and a HyperK-like 100 kton WtCh detector. The two mass orderings are considered in order to explore the different sensitivities to neutrino mass and LIV energy scale.
This article is organized as follows: In Section 2, we show how to evaluate the neutrino fluxes in SN and their respective fluxes at Earth after oscillations. In Section 3, we discuss the method developed to evaluate the number of events and the calculation of the squared function, χ 2 , minimized in order to put bounds on the neutrino mass or LIV. Section 4 presents some details of the experiments we simulate in our study and their related number of events per channel of detection. In Section 5, we present our main results for the limits of neutrino mass or LIV and discuss them. Finally, in Section 6, we present our main conclusions and future perspectives.

2. Neutrino fluxes

Inside the star, each neutrino flavor ν β ( β = e , μ , τ ) has a differential flux, at time t after the bounce of the SN core, described as [3],
d 2 Φ ν β 0 d t d E = L ν β ( t ) 4 π d 2 f ν β ( t , E ) 〈 E ν β ( t ) 〉 ,
where L ν β ( t ) is the neutrino flavor luminosity, d is the SN distance to the Earth detector, f ν β ( t , E ) is the neutrino energy spectra and 〈 E ν β ( t ) 〉 is the mean neutrino energy. L ν β ( t ) , 〈 E ν β ( t ) 〉 and f ν β ( t , E ) depend on the SN model.
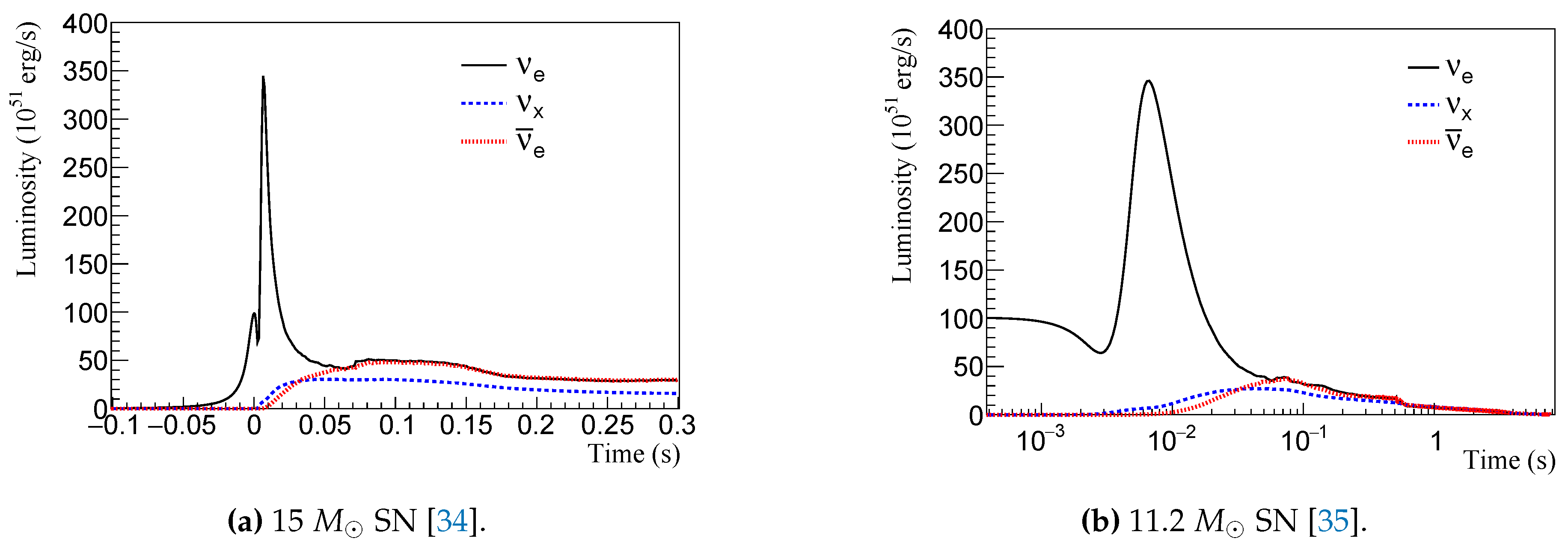
We consider two models with different progenitor masses: One with 15 solar masses (15 M ⊙ ) [34] and one with 11.2 M ⊙ [35]. Figure 1a and Figure 1b show the ν e (black solid line), ν ¯ e (red dotted line), and ν x (blue dashed line) luminosity time evolution the two models.
The neutrino energy spectra can be parameterized as [36],
f ν β ( t , E ) = λ β ( t ) E 〈 E ν β ( t ) 〉 α β ( t ) exp − [ α β ( t ) + 1 ] E 〈 E ν β ( t ) 〉   ,
where α β ( t ) is the so-called pinching parameter that is model dependent and accounts for the variations in the quasi-thermal spectrum. λ β ( t ) is the time dependent normalization factor, so that ∫ E f ν β ( t , E )   d E = 1 .
Inside the star environment, neutrinos interact with electrons, protons, and neutrons, suffering flavor conversion in the resonances (low and high) according to the MSW effect [37]. After crossing the stellar matter, neutrinos travel incoherently through vacuum until when they are detected at Earth. The expressions for the oscillated differential fluxes, which are shown below, are obtained from Ref. [38].
The differential ν e flux at Earth for NO is,
d 2 Φ ν e d t d E = d 2 Φ ν x 0 d t d E   ,
while for the flavors ν μ , ν τ , ν ¯ μ , and ν ¯ τ , represented by ν x , can be written as,
4 d 2 Φ ν x d t d E = d 2 Φ ν e 0 d t d E + sin 2 θ 12 d 2 Φ ν ¯ e 0 d t d E + ( 2 + cos 2 θ 12 ) d 2 Φ ν x 0 d t d E   ,
where θ 12 is the mixing angle between ν 1 and ν 2 mass eigenstates.
The differential ν ¯ e flux is,
d 2 Φ ν ¯ e d t d E = cos 2 θ 12 d 2 Φ ν ¯ e 0 d t d E + sin 2 θ 12 d 2 Φ ν ¯ x 0 d t d E   .
The mixing angle θ 13 is considered small compared to θ 12 and the expressions above are evaluated accordingly. The θ 12 value is: 33 . 45 − 0 . 75 ∘ ∘ + 0 . 77 ∘ for NO and 33 . 45 − 0 . 75 ∘ ∘ + 0 . 78 ∘ for IO [1].
Now, for IO, we can write the following differential fluxes for ν e , ν x , and ν ¯ e , respectively:
d 2 Φ ν e d t d E = sin 2 θ 12 d 2 Φ ν e 0 d t d E + cos 2 θ 12 d 2 Φ ν x 0 d t d E   ,
4 d 2 Φ ν x d t d E = cos 2 θ 12 d 2 Φ ν e 0 d t d E + d 2 Φ ν ¯ e 0 d t d E + ( 2 + sin 2 θ 12 ) d 2 Φ ν x 0 d t d E   ,
and
d 2 Φ ν ¯ e d t d E = d 2 Φ ν ¯ x 0 d t d E   .
We do not consider nonlinear collective effects in this work. They are not relevant particularly in the neutronization burst [3] and would bring unnecessary complication to the oscillation treatment. In Ref. [39], the authors considered Earth matter effects on neutrino oscillation and their possible effects on the neutrino masses, however, such effects do not considerably affect their results - see their Table I. For the current status of the neutrino flavor conversion in high density environments and its relevance in astrophysical systems as SN, see Ref. [40].

3. Methodology

In this section we describe our basic methodology in order to compute the number of events using the neutrino fluxes produced in SN introduced in the previous Section 2. We explain how to compute the number of events when one includes the modification in time propagation caused by mass or LIV. After the calculation of the number of events we present the minimum square statistical analysis used to constrain the neutrino mass or LIV.

3.1. Number of events

The event rate, R ( t , E ) , the number of neutrino events in a given detector per energy and time units, is evaluated as,
R ( t , E ) = n t σ ( E ) ϵ ( E ) d 2 Φ ν β d t d E   ,
where n t is the number of targets in the detector, σ ( E ) and ϵ ( E ) are, respectively, the cross section and the detector efficiency, both dependent on the neutrino energy. The actual computation, which includes the detector material, efficiency, and each process interaction cross section is conducted by the fast event-rate calculation tool SNOwGLoBES [41].
The standard time of detection for a massless particle is given by,
t d e t = t e m + d / c   ,
where t e m is the time of emission and d / c is the travel time from the source to the detector. The time change due to mass or a nonstandard effect like LIV is approximately,
t d e t ′ = t e m + d / c + Δ t   ,
where Δ t is calculated by the mass effect or by a nonstandard effect like LIV. So the arrival time difference in the neutrino flux is,
t d e t ′ − t d e t = Δ t   .
We integrate Eq. (9) in energy bins of 0.2 MeV in the energy interval from 0 to 100 MeV, obtaining the number of events per time unit in each energy bin,
d N d t E i , t = ∫ E i − δ E E i + δ E R ( t , E ) d E   ,
where E i is the average energy of the i-th energy bin, E 1 = 0.1 MeV, and δ E = 0.1 MeV is half of the energy interval of the bin. This gives the energy spectrum for standard physics and massless neutrinos. In order to obtain the time spectrum, i.e., the number of events per time interval, we compute,
N j = ∫ t j t j + δ t ∑ i d N d t E i , t d t   ,
where N j and t j are the event number and the initial time of the j-th time bin, and δ t is the bin width. Considering the effect of propagation time delay,
d N d t ′ E i , t ′ = d N d t E i , t + Δ t i = ∫ E i − δ E E i + δ E R ( t ′ , E ) d E   ,
The time delay, Δ t i , for each energy bin, considering its average, E i , is given by Eq. (12). The effect of the different delay for each bin of the energy spectrum is to spread neutrinos that are emitted in a given time through different time bins. The number of events in a given time bin is,
N j ′ = ∫ t j t j + δ t ∑ i d N d t E i , t + Δ t i d t   ,
where we sum over all the events per time unit for which the delay brings them to the j-th time bin.

3.2. Time delay

We consider the time delay during the neutrino propagation in two different situations:
First, neutrinos from galactic and extra-galactic sources experience a modification in their time of flight because of their masses [18,19]. The delay caused by the neutrino mass, m ν , can be written as
Δ t = d 2 m ν E 2   ,
where E is the neutrino energy and d is the distance from the neutrino source to the detector. Figure 2a shows the delay, in seconds, as a function of energy, considering different values of neutrino masses and d = 10 kpc. The black solid line is for m ν = 1.0 eV and the blue dash-dotted line is for m ν = 2.0 eV. This plot clearly demonstrates the effect of the neutrino mass and neutrino energy on the time of flight for a given distance: the combination of large mass and low energy generates longer delays.
Second, Lorentz Invariance Violation (LIV) may cause time modification along neutrino propagation. For a review on the effects of LIV in astrophysical neutrinos, such as SN neutrinos, see Ref. [42]. Here, we consider LIV without violation of C P T symmetry. In this kind of model the dispersion relation of particles is affected during their propagation by the interaction with the medium [43,44]. When we translate this in a temporal effect there is a time change that can be written as [33],
Δ t = ± d E M Q G n   ,
where M Q G is the energy (mass) scale that corresponds to the Lorentz symmetry breaking of a high energy theory, n is the order of the effect, which we consider linear or quadratic in energy, and the + or − signs correspond to subluminal (delay) or superluminal (advance) differences in the expected detection time, respectively.
Figure 2b shows Δ t for different LIV energy dependence and scales: Linear dependence ( n = 1 ) – M Q G = 10 12 GeV (solid black line) and M Q G = 10 13 GeV (green dash-dotted line); quadratic dependence ( n = 2 ) – M Q G = 10 5 GeV (dashed red line) and M Q G = 10 6 GeV (dotted magenta line). The effect of LIV is opposite to the effect of mass: Δ t is larger when E increases. As expected, higher energy scale, M Q G , decreases Δ t , making the sensitivity to LIV lower.
Limits for the parameters considered in this work - mass ( m ν ) and LIV scale ( M Q G ) - are obtained through a minimum square statistical analysis of the function,
χ 2 = ∑ i N i ′ − N i 2 σ i 2   ,
where N i and N i ′ are, respectively, the number of events given by Eqs. (14) and (16) and σ i accounts for the uncertainties. In our analysis we include the statistical uncertainty σ i = N i . The confidence levels are given by Δ χ 2 = χ 2 − χ m i n 2 = 1 ( 1 σ = 68.27 % C.L.), Δ χ 2 = 4 ( 2 σ = 95.45 % C.L.) and Δ χ 2 = 9 ( 3 σ = 99.73 % C.L.) .

4. Detection Techniques

Before showing our results, we present some general features of the two detector types that we use in the analysis and point out a few suppositions about their role in the precision of our results.

4.1. Liquid Argon TPC

The main detection channel in a Liquid Argon Time Projection Chamber (LArTPC) is the weak charged current (CC) interaction between ν e and Ar: ν e +   40 A r → e − +   40 K * . The e − produced in this reaction is observable together with deexcitation products from the excited state of   40 K * . This reaction has a detection threshold energy of approximately 5 MeV. Other detection channels include ν ¯ e CC and elastic scattering (ES) on e − . Neutral current (NC) scattering, ν + A r → ν + A r * , is a considerable channel and it can be detected in the deexcitation gammas (9.8 MeV decay line) from the excited state of A r * [30]. In our analysis we consider the possibility of detection of all channels. We do not include any background events, uncertainties on neutrino production or propagation, or any systematics. This approach do not significantly change the sensitivity of the parameters [39].

4.2. Water Cherenkov Detector

The main detection channel of a water Cherenkov (WtCh) detector is the inverse β decay: ν ¯ e + p → e + + n . Events related to this channel have a nearly isotropic distribution. The future main example of this kind of detector is HyperK, that can detect SN neutrinos with energies as low as 3 MeV and has directional sensitivity [32]. In this work we consider a 100 kton of WtCh detector. Despite the inverse β decay is the main channel, HyperK can detect neutrinos through other channels as well: ν -e scattering ( ν + e − → ν + e − ) and ν e or ν ¯ e CC interaction with oxygen ( ν e +   16 O → e − +   16 F ( * ) or ν ¯ e +   16 O → e + +   16 N ( * ) ). The ν -e scattering events are strongly peaked in the direction coming from the SN. In our work we consider that the SN events will point directly to the detector. The same suppositions taken into account for the LArTPC are also considered in the WtCh case, so we can conduct an analysis under equal conditions and following the same hypotheses.

5. Results and Discussion

In this section, we show the limits on the neutrino masses and LIV scale, M Q G , subluminal and superluminal cases, for NO and IO and both detector types described in Section 4. The SN distance is fixed at 10 kpc and we consider two distinct models with progenitor masses: 15 M   ⊙ and 11.2 M   ⊙ .
In the analysis of the neutrino mass limit, we assume all ν e interaction channels for the DUNE-like detector and all ν ¯ e interaction channels for the HyperK-like detector. For M Q G , we sum all neutrino flavor events from all interaction channels, since LIV may affect equally the neutrino eigenstates during their propagation.
We discuss the results for the 15 M ⊙ SN model [34] first.
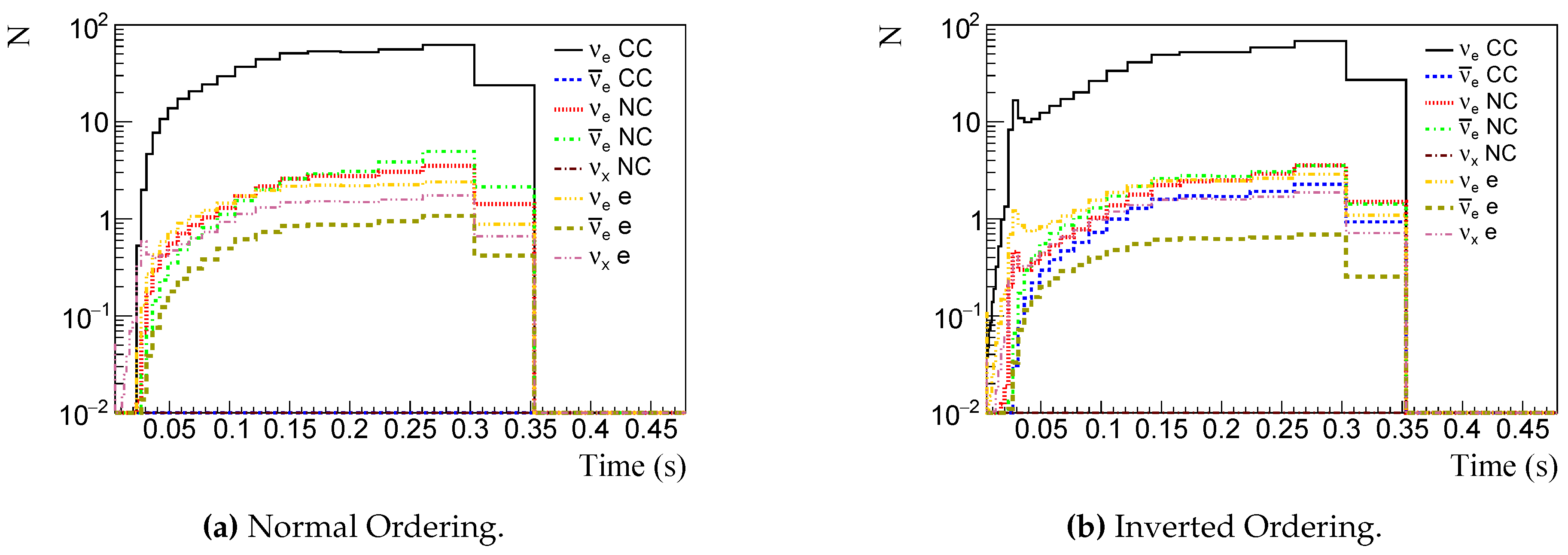
In Figure 3a and Figure 3b one sees the number of events, N, in a 40 kton LArTPC, as a function of bins of time. Each curve shows a different detection channel. On the left (right) side of Figure 3, Figure 3a (Figure 3b) considers NO (IO). The ν e interactions are represented by: (i) black solid curves - CC interaction with Argon; (ii) red dotted - NC interaction with Ar; (iii) yellow dash-dotted - ES on e − . The ν ¯ e interactions are represented by: (i) blue dashed curves - CC interaction with Argon; (ii) green dash-dotted - NC interaction with Ar; (iii) brown dashed - ES on e − . Other flavors interact with Argon by NC (violet dashed-dot curves) and ES (magenta dash-double dotted curves).
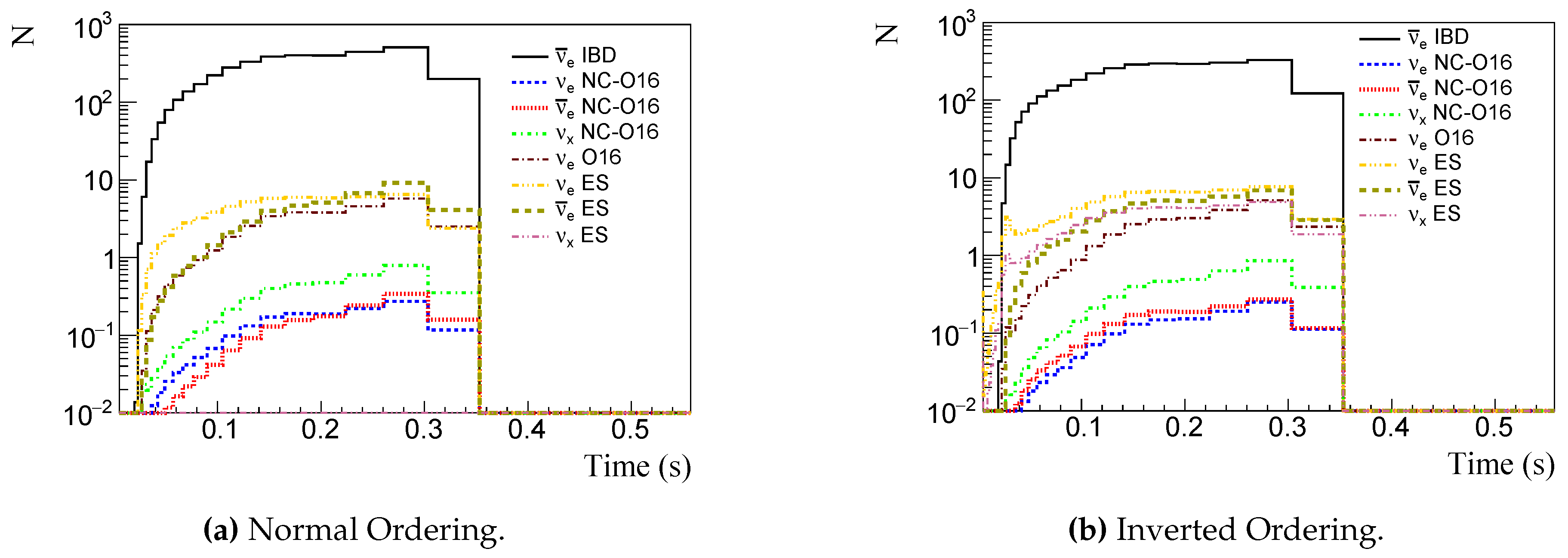
We show equivalent curves in Figure 4a and Figure 4b for a 100 kton WtCh detector. The main channel in this case is the inverse beta decay (IBD) used to probe ν ¯ e . Colored lines show ν ¯ e NC interaction with   16 O (red dotted) and ES on e − (brown dashed); ν e interactions with   16 O via CC (violet dash-dotted) and NC (blue dashed), and ν e ES on e − (yellow dash-two dotted). Other flavors interact via ES on e − (magenta dash-two dotted) and NC interaction with   16 O (green dash-dotted).
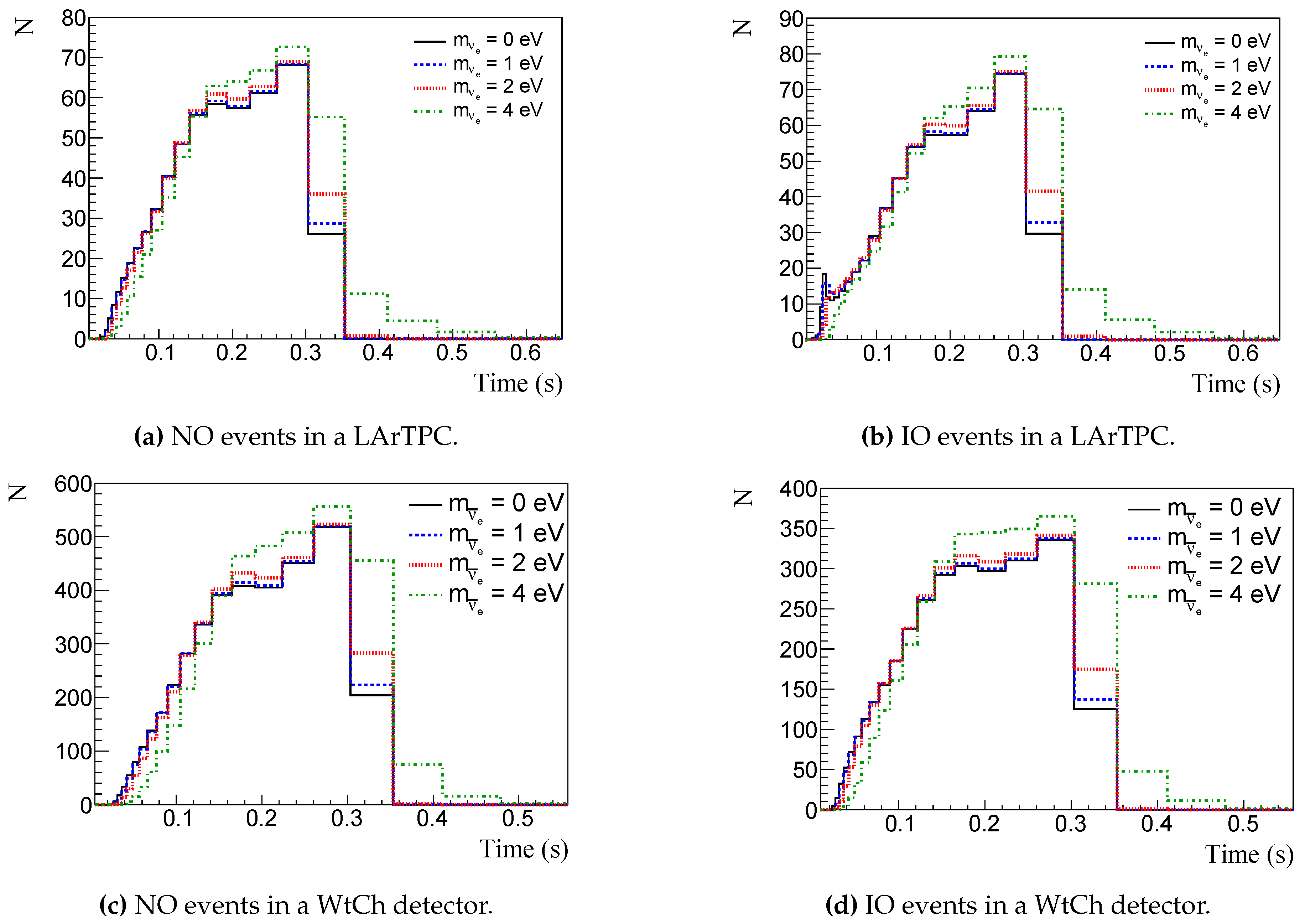
Figure 5 shows the time distribution of the ν e (Figure 5a and Figure 5b) and ν ¯ e (Figure 5c and Figure 5d) event number for a 40 kton LArTPC detector and 100 kton WtCh detector, respectively. Left (Right) plots consider NO (IO). The solid black line refers to a massless neutrino. To illustrate the time delay caused by different mass values, blue dashed refers to 1 eV neutrino mass, red dotted to 2 eV, and green dash-dotted to 4 eV.
The mass values were chosen in order to illustrate the effect of the mass in the signal time delay as described by Eq. (17). Figure 5a and Figure 5b show the relevance of mass ordering to probe the neutronization burst, which is suppressed in NO. On the other hand, for ν ¯ e , Figure 5c and Figure 5d, the neutronization burst is not present. We notice a larger number of events in the HyperK-like detector since it is larger in size and the inverse β decay cross section, which is the main channel of interaction, is larger than the CC ν e -Ar cross section.
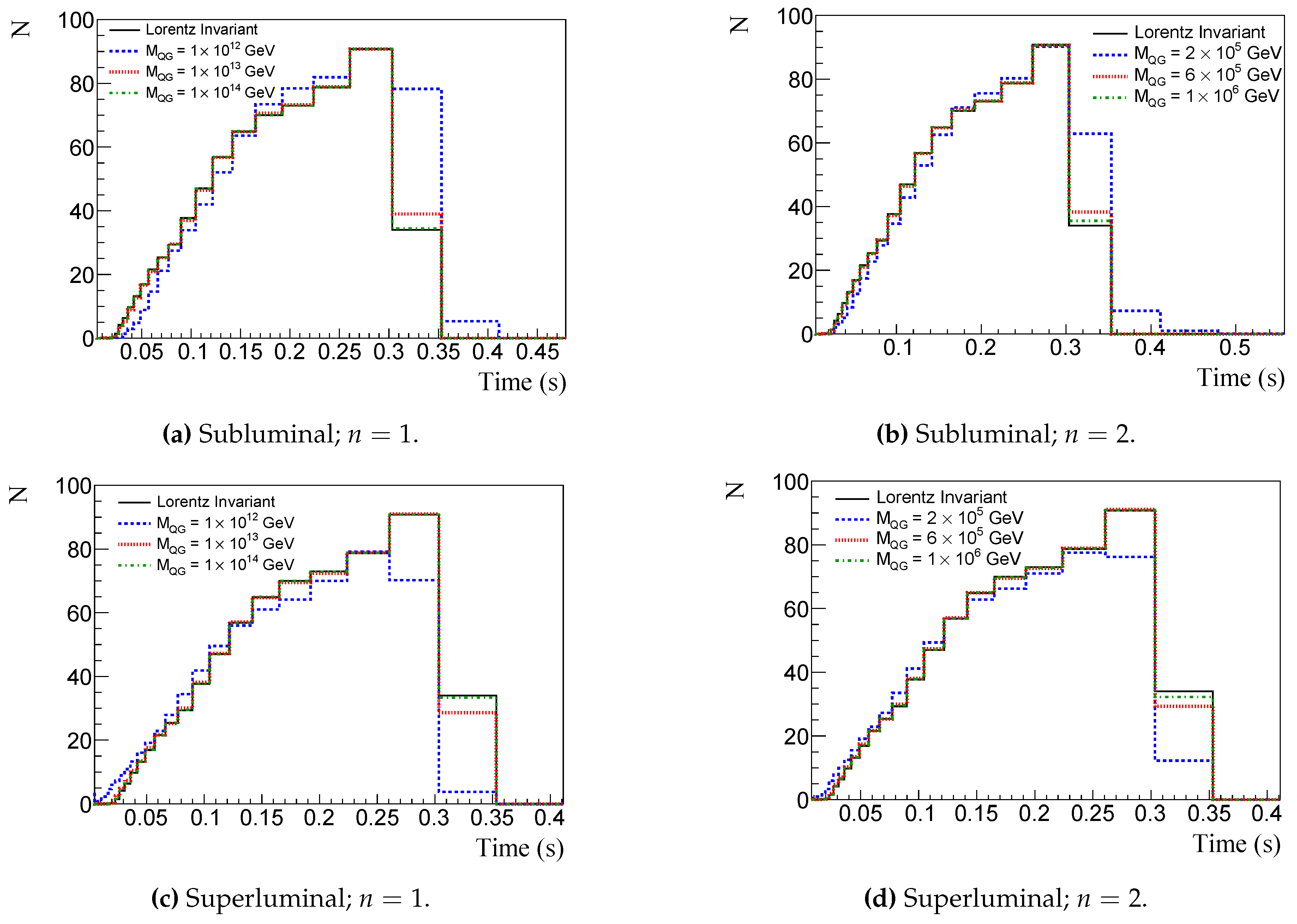
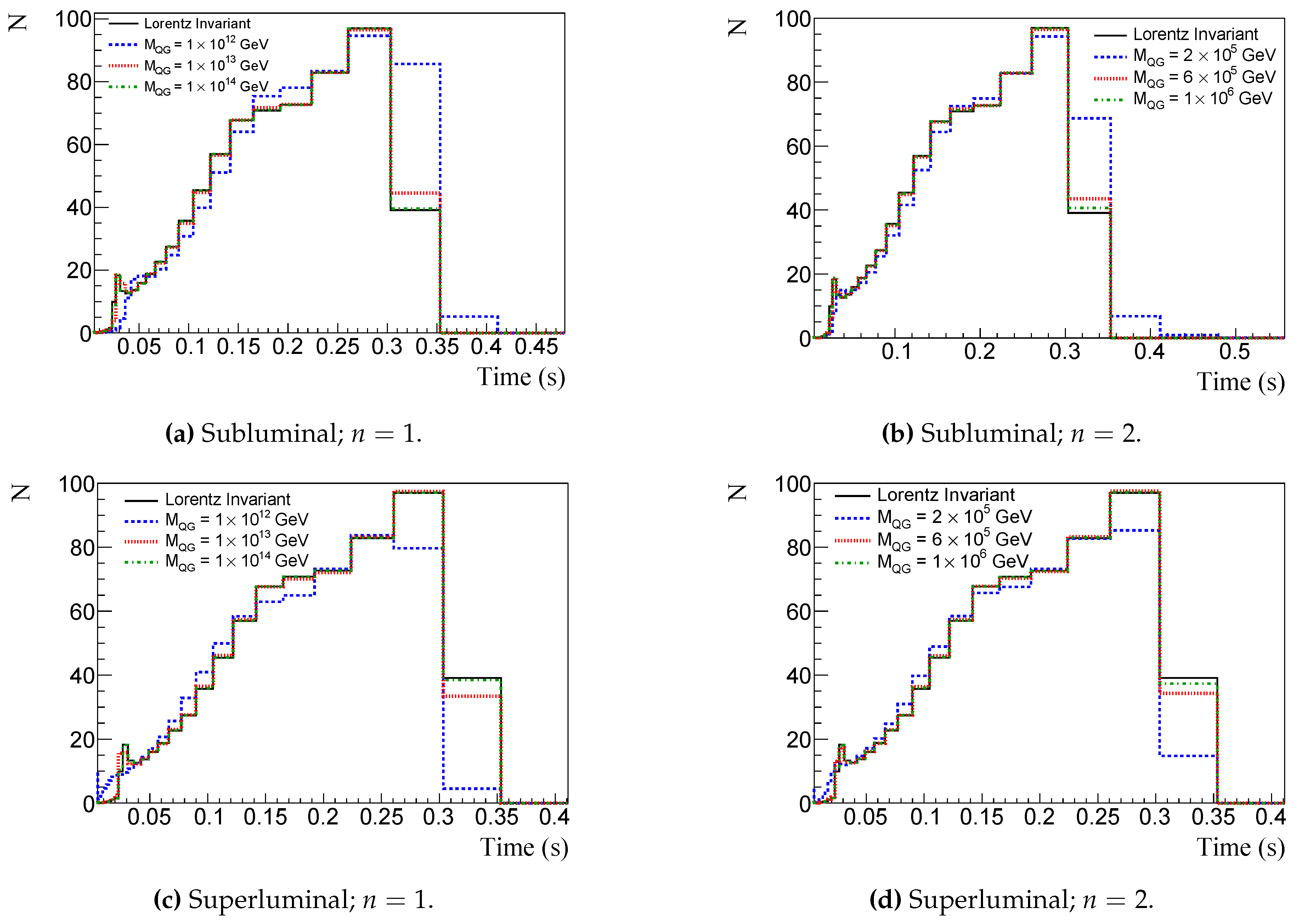
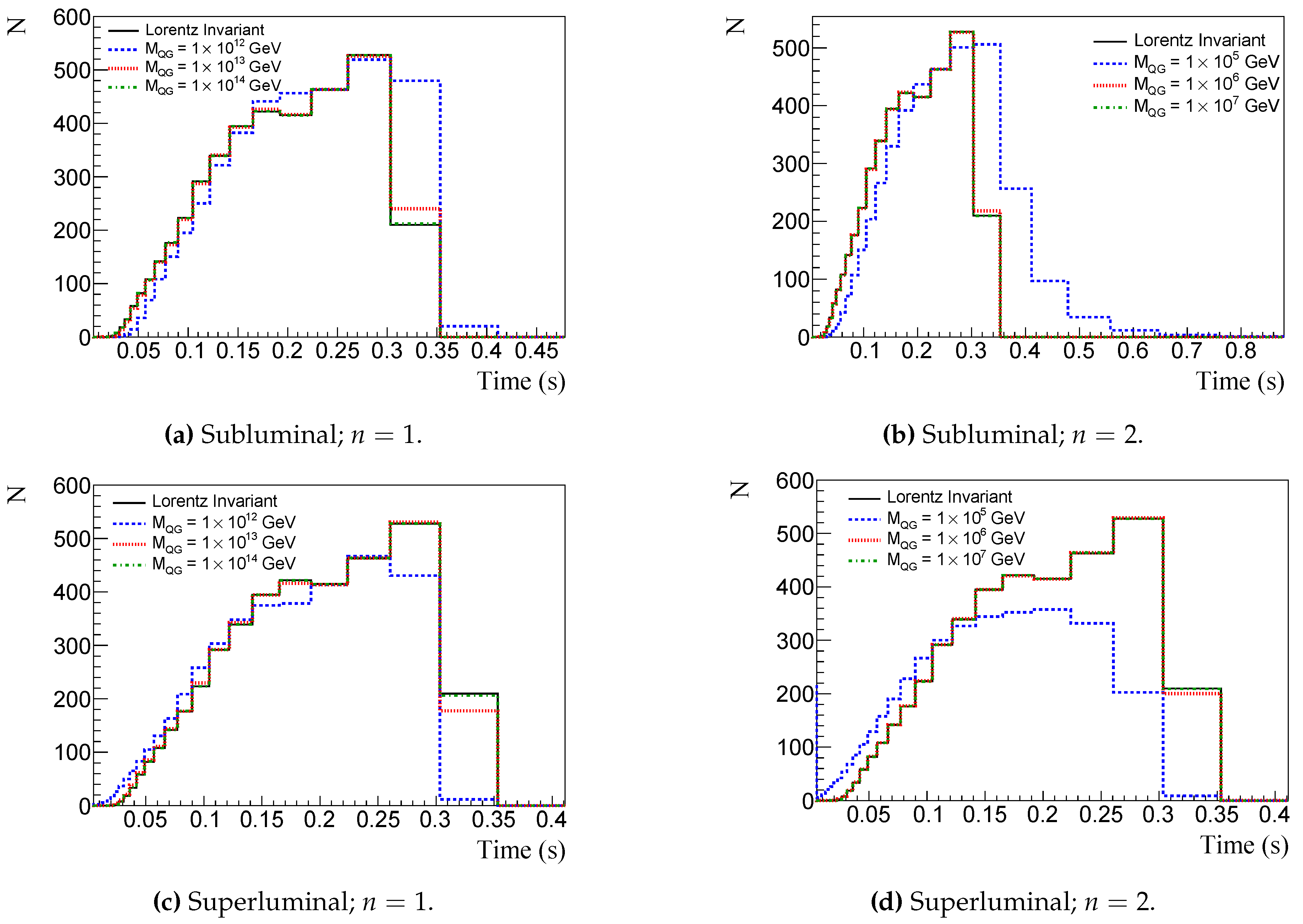
Figure 6 and Figure 8 (Figure 7 and Figure 9) show the time spectrum considering NO (IO) for a 40 kton LArTPC detector and a 100 kton WtCh detector, respectively. In all figures top (bottom) panels show the time spectrum change due to subluminal (superluminal) LIV, left (right) panels consider energy dependence n = 1 ( n = 2 ), black solid lines refer to conserved Lorentz invariance, blue dashed line to M Q G = 10 12 GeV ( M Q G = 2 × 10 5 GeV), red dotted line to M Q G = 10 13 GeV ( M Q G = 6 × 10 5 GeV), and green dash-dotted to M Q G = 10 14 GeV ( M Q G = 10 6 GeV). We notice that the less the value of M Q G the greater the effect of LIV in Δ t - see Eq. (18). As we mentioned before, LIV models predict the possibility of superluminal propagation, causing an advance in the detection time. 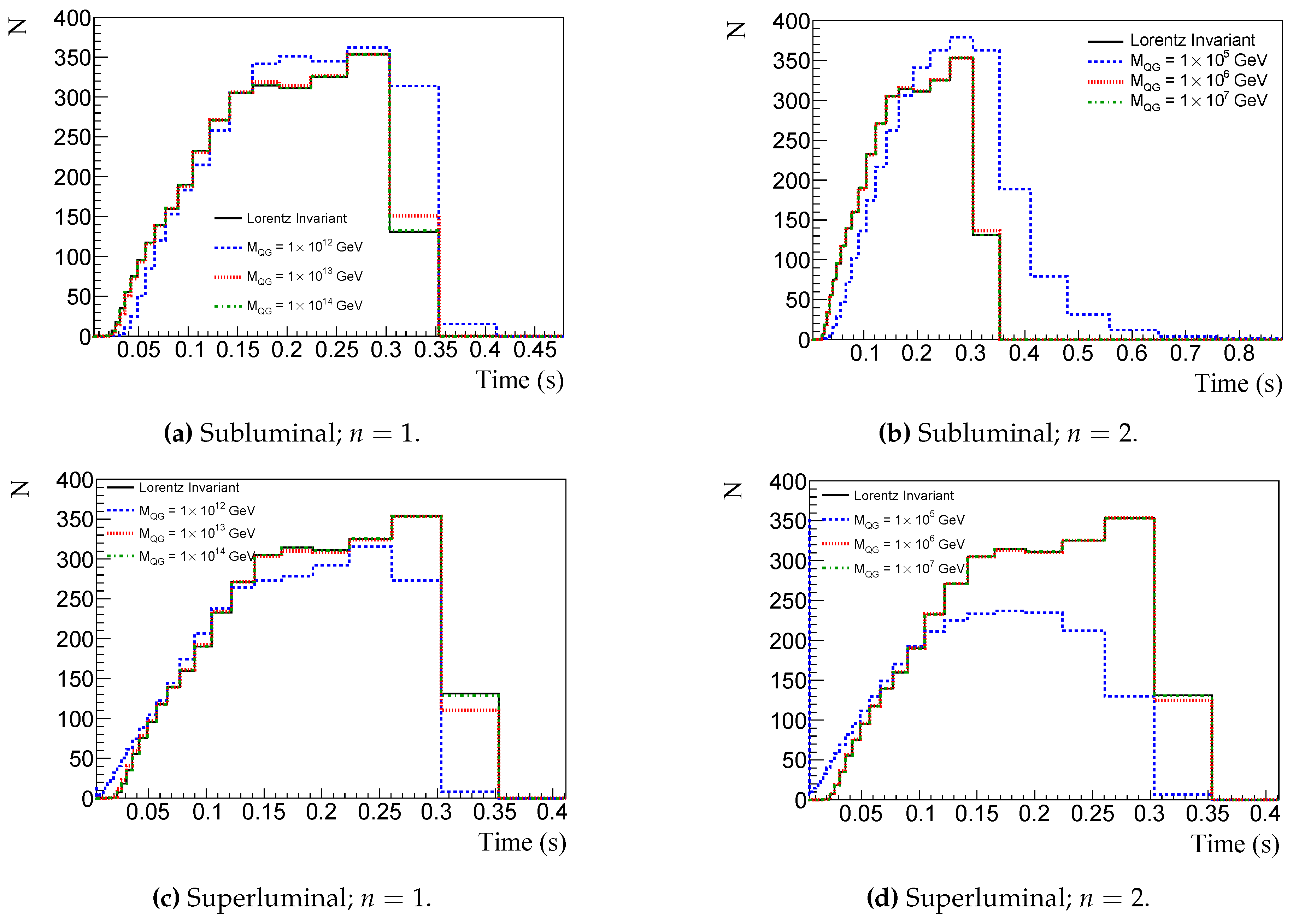This can be seen in the bottom of Figure 6, Figure 7, Figure 8 and Figure 9. A time delay like the effect of neutrino mass, but with different energy dependence, can be seen by the subluminal LIV effect in the top of Figure 6, Figure 7, Figure 8 and Figure 9.
Using Eq. (19), we obtain the Δ χ 2 in terms of neutrino mass and M Q G .
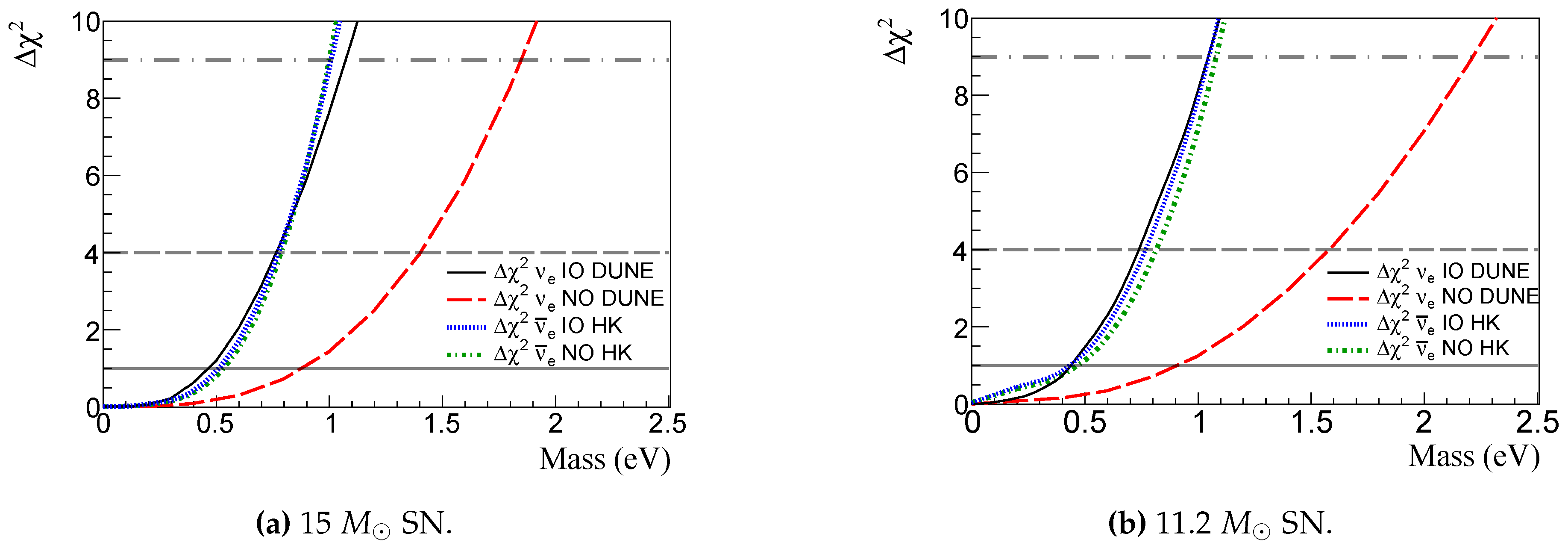
The mass limits are shown in Figure 10a for the LArTPC and WtCh detectors. The mass bounds for ν e ( ν ¯ e ) in a 40 kton LArTPC (100 kton WtCh) are represented by solid black (dotted blue) line and dashed red (dash-dotted green) line, respectively, for IO and NO.
As expected, we see better limits for IO and ν e in the DUNE-like detector because of the peak of neutronization. In the NO, the suppression of the neutronization peak worsen the sensitivity. For the HyperK-like detector, the limits on ν ¯ e , for both mass orderings, are very similar, as the time spectrum does not change significantly.
Our results for ν e and ν ¯ e are summarized in Table 2. The numbers inside parentheses and without parentheses represent the mass limits for the LArTPC and WtCh detector, respectively.
Some comments on the mass are important. Supposedly, the mass eigenstates of neutrinos travel freely through space and arrive incoherently at the detector, i.e., ν 1 , ν 2 , and ν 3 arrive separately and these mass eigenstates have in fact the mass information. Consider for instance NO, where ν 1 is the lightest mass eigenstate and reaches the detector first. If there is an interaction, the wave function collapses,2 thus selecting the flavor state of the neutrino, such as e.g. ν e , with a detection probability given by the PMNS matrix element | U e 1 | 2 .3 If ν 1 does not interact, the eigenstate ν 2 , which arrives at the detector with its respective delay associated with its mass m 2 , may interact. The time interval between ν 1 and ν 2 can be estimated as [46],
δ t = L 2 E 2 ( m 2 2 − m 1 2 )   .
Using m 2 2 − m 1 2 ≈ 7 × 10 − 5 eV   2 , L = 10 kpc, and E = 10 MeV in Eq. (20), we obtain δ t ≈ 10 − 7 s. For m 3 2 − m 1 2 ≈ 10 − 3 eV   2 , δ t ≈ 10 − 5 s. One needs a detector with time resolution better than δ t to allow the determination of the mass bound of each mass eigenstate. In our analysis, according to the expected experimental time resolution, we group the events in certain time intervals longer than the δ t . So we put limits for an effective mass of the detected flavor.
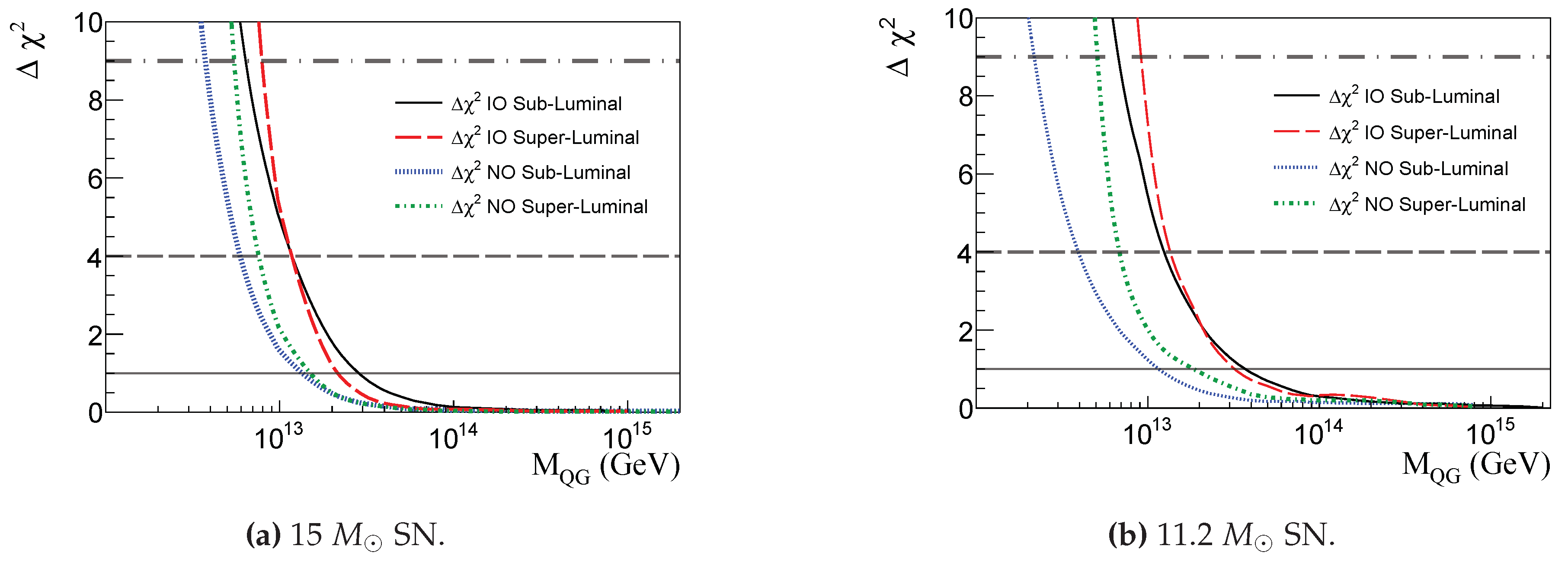
The limits on LIV are shown in Figure 11a with the Δ χ 2 in terms of M Q G for the 40 kton LArTPC. We show the superluminal and subluminal cases, for NO and IO, and n = 1 in Eq. (18). Solid black curve represents the subluminal and IO case, red dashed line represents the superluminal and IO case, dotted blue curve is for the subluminal and NO, and green dash-dotted curve is for the superluminal and NO.
The Δ χ 2 has a similar behavior compared to Figure 11a for n = 2 and for the WtCh detector for both n. So we do not show those curves.
The inferior limits on the M Q G for the subluminal and superluminal LIV effects are summarized in Table 3 and Table 4 for n = 1 and n = 2 , respectively. Numbers without (inside) parentheses are for WtCh (LArTPC) detectors.
We can use the same methodology for other SN models and we choose one model with 11.2 M ⊙ [35]. This model includes a longer period of neutrino emission, of about 10 seconds, which includes the cooling time in the SN explosion. The main purpose here is to verify the impact of the later neutrino emission times on the bounds of the mass and LIV scale. The time spectrum and Δ χ 2 are very similar to the ones presented in the 15 M ⊙ SN case. In Figure 10b (Figure 11b), we present, for the 11.2 M ⊙ SN, the Δ χ 2 in terms of neutrino mass (LIV energy scale). Like for the neutrino mass, the LIV Δ χ 2 for n = 2 and for the WtCh detector for both n have similar behaviors compared to the one in Figure 11b. So we do not show the Δ χ 2 plots for those cases, but only tables with the results.
Our results using the 11.2 M ⊙ SN model, for the ν e and ν ¯ e mass limits are shown in Table 5. The numbers inside and without parentheses show limits for LArTPC and WtCh, respectively.
Table 5. Limits on neutrino masses for a 100 kton WtCh (40 kton LArTPC) detector, for NO and IO, and 11.2 M ⊙ SN at 10 kpc.
Table 5. Limits on neutrino masses for a 100 kton WtCh (40 kton LArTPC) detector, for NO and IO, and 11.2 M ⊙ SN at 10 kpc.
ν mass(eV)
Mass Ordering ν flavor 1 σ 2 σ 3 σ
NO ν ¯ e 0.45 (1.71) 0.82 (3.13) 1.08 (4.64)
IO ν ¯ e 0.43 (1.66) 0.77 (3.27) 1.05 (5.05)
NO ν e 1.31 (0.92) 2.43 (1.58) 3.71 (2.22)
IO ν e 0.65 (0.44) 1.23 (0.74) 2.43 (1.04)
Following the same steps previously mentioned, the inferior limits on the M Q G , considering the subluminal and superluminal LIV effects, using the 11.2 M ⊙ SN model, are summarized in Table 6 and Table 7 for n = 1 and n = 2 , respectively.
Table 6. Inferior limits on LIV parameter M Q G , n = 1 in Eq. (18), for WtCh (LArTPC) detector, considering NO and IO, and the cases of subluminal and superluminal effects for 11.2 M ⊙ SN, 10 kpc from Earth.
Table 6. Inferior limits on LIV parameter M Q G , n = 1 in Eq. (18), for WtCh (LArTPC) detector, considering NO and IO, and the cases of subluminal and superluminal effects for 11.2 M ⊙ SN, 10 kpc from Earth.
M Q G ( × 10 13 GeV)
Mass Ordering 1 σ 2 σ 3 σ
subluminal NO 4.1 (1.3) 1.4 (0.4) 0.6 (0.2)
subluminal IO 8.7 (3.8) 2.0 (1.4) 1.2 (0.7)
superluminal NO 11.0 (1.9) 1.7 (0.7) 0.9 (0.5)
superluminal IO 5.1 (3.2) 1.8 (1.7) 0.9 (0.9)
The above results show that for obtaining the neutrino mass limit there is no significant impact when we compare both SN progenitor star masses, with different neutrino emission time periods.4 For ν e , the best limit comes from the DUNE-like detector and IO, due to the neutronization burst. In fact, different progenitor masses do not modify significantly the neutronization phase [45]. This, somehow, demonstrates the relevance to study well the neutronization phase for determining neutrino properties, such as its mass. For the ν ¯ e , the best limit comes from the HyperK-like detector and either mass orderings do not present significant differences for their limits.
For the LIV scale sensitivity, we obtain, with both detectors and both mass orderings, either for n = 1 or n = 2 , very similar limits. This is related to the fact that LIV affects equally the different neutrino mass eigenstates and the analysis is conducted assuming all detection channels. There is no significant difference in the results for the SN models that we consider. The inferior limits obtained by Chakraborty et al. [33], for a Mton water Cherenkov detector and using the neutronization burst signal are M Q G ∼ 10 12 GeV ( M Q G ∼ 2 × 10 5 GeV) for n = 1 ( n = 2 ). They are very similar to ours - see Table 3, Table 4, Table 5, Table 6 and Table 7 - however, they did not conduct a statistical analysis.
Before the conclusions, we would like to point out some important details to be explored in future analyses: First, the necessity of extending our analysis for other simulations of core-collapse SN, so we can explore the effective impacts of astrophysical parameters of the explosion and their relation to the bounds on neutrino masses and LIV. In addition, other and more massive progenitor stars can produce more events from accretion and cooling [49]. So, a deeper relation among astrophysical and neutrino parameters can be explored. Second, even though in Ref. [39] they pointed out that several uncertainties do not seem to impact significantly their parameter limits, it seems reasonable to explore deeply the uncertainties when more details are learned from the detectors developed for experiments like DUNE and HyperK.

6. Conclusions

Summarizing our results, we conduct an analysis comparing the time spectrum of supernova neutrino events taking as a baseline the expected event rate for massless neutrinos and invariance under Lorentz transformation. We compute the event rate for two kinds of detectors and two supernova progenitor star masses considering their location at 10 kpc from the detectors. We also analyze the two neutrino mass ordering possibilities.
Comparing the two supernova models, we did not see big influence in the results coming from different masses or considering later neutrino emission times, with events from the cooling phase of the supernova.
The two kinds of detectors, one a 40 kton liquid argon TPC like DUNE and the other a 100 kton water Cherenkov light detector like Hyper-Kamiokande, are sensitive to different neutrino interaction channels. The former is especially sensitive to electron neutrinos, which are produced in great amounts during the neutronization phase of the supernova, while the later is sensitive to electron antineutrinos through inverse beta decay.
We observe a balance between the event rate during the neutronization phase, for which a DUNE-like detector is more sensitive if the inverted mass ordering happens to be the case, and the detector mass, which is more than two times bigger for a Hyper-Kamiokande-like detector. We verify this fact obtaining the best limits on the neutrino effective masses of approximately 1 eV at 3 σ . The best antineutrino mass limit comes from a Hyper-Kamiokande-like detector and is essentially the same independent of the mass ordering, while the best neutrino mass limit comes from a DUNE-like detector for inverted mass ordering.
We also put limits on Lorentz Invariance Violation considering the energy scale at which Lorentz invariance could be broken. We sum the event rate over all neutrino flavors given that the same violating effect would influence their propagation. It is possible to distinguish between a superluminal and a subluminal violation effect, even though the constraints on the energy scale are similar. For a linear energy dependence, the sensitivity is higher and we find an energy scale limit of M Q G ∼ O ( 10 13 ) GeV. For a quadratic energy dependence, we find a limit of M Q G ∼ O ( 10 5 ) GeV. This limits are compatible with results elsewhere, but here we conduct a more accurate statistical analysis.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

L. Quintino thanks the partial financial support provided by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior - Brasil (CAPES) - Finance Code 001. F. Rossi-Torres thanks UFABC for the hospitality.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
SN Supernova
NO Normal ordering
IO Inverted ordering
LIV Lorentz Invariant Violation
CC Charged Current
NC Neutral Current
ES Elastic Scattering
IBD Inverse Beta Decay
DUNE Deep Underground Neutrino Experiment
HyperK Hyper-Kamiokande
SK Super-Kamiokande
MSW Mikheyev-Smirnov-Wolfenstein
LArTPC Liquid Argon Time Projection Chamber
PMNS Pontecorvo–Maki–Nakagawa–Sakata
WtCh Water Cherenkov

References

  1. Gonzalez-Garcia, M.C.; Maltoni, M.; Schwetz, T. NuFIT: Three-Flavour Global Analyses of Neutrino Oscillation Experiments. Universe 2021, 7, 459. [Google Scholar] [CrossRef]
  2. Kharusi, S.A.; et al. [SNEWS] SNEWS 2. 0: a next-generation supernova early warning system for multi-messenger astronomy. New J. Phys. 2021, 23, 031201. [Google Scholar] [CrossRef]
  3. Mirizzi, A.; Tamborra, I.; Janka, H.T.; Saviano, N.; Scholberg, K.; Bollig, R.; Hudepohl, L.; Chakraborty, S. Supernova Neutrinos: Production, Oscillations and Detection. Riv. Nuovo Cim. 2016, 39, 1–112, H. T. Janka Neutrino-driven Explosions. 10.1007/978-3-319-21846-5_109. [Google Scholar] [CrossRef]
  4. Scholberg, K. Supernova Signatures of Neutrino Mass Ordering. J. Phys. G 2018, 45, 014002. [Google Scholar] [CrossRef]
  5. Aker, M.; et al. [KATRIN] Direct neutrino-mass measurement with sub-electronvolt sensitivity. Nature Phys. 2022, 18, 160–166. [Google Scholar] [CrossRef]
  6. Drexlin, G.; Hannen, V.; Mertens, S.; Weinheimer, C. Current direct neutrino mass experiments. Adv. High Energy Phys. 2013, 2013, 293986. [Google Scholar] [CrossRef]
  7. Springer, P.T.; Bennett, C.L.; Baisden, P.A. Measurement of the Neutrino Mass Using the Inner Bremsstrahlung Emitted in the Electron-Capture Decay og 163Ho. Phys. Rev. A 1987, 35, 679–689. [Google Scholar] [CrossRef]
  8. Yasumi, S.; Maezawa, H.; Shima, K.; Inagaki, Y.; Mukoyama, T.; Mizogawa, T.; Sera, K.; Kishimoto, S.; Fujioka, M.; Ishii, K.; et al. “The Mass of the electron-neutrino from electron capture in Ho-163. Phys. Lett. B 1994, 334, 229–233. [Google Scholar] [CrossRef]
  9. Gatti, F. Microcalorimeter measurements. Nucl. Phys. B Proc. Suppl. 2001, 91, 293–296. [Google Scholar] [CrossRef]
  10. Sisti, M.; Arnaboldi, C.; Brofferio, C.; Ceruti, G.; Cremonesi, O.; Fiorini, E.; Giuliani, A.; Margesin, B.; Martensson, L.; Nucciotti, A.; et al. “New limits from the Milano neutrino mass experiment with thermal microcalorimeters. Nucl. Instrum. Meth. A 2004, 520, 125–131. [Google Scholar] [CrossRef]
  11. Esfahani, A.A.; et al. [Project 8] Tritium Beta Spectrum and Neutrino Mass Limit from Cyclotron Radiation Emission Spectroscopy. arXiv:2212.05048 [nucl-ex]].
  12. Giuliani, A.; Poves, A. Neutrinoless Double-Beta Decay. Adv. High Energy Phys. 2012, 2012, 857016. [Google Scholar] [CrossRef]
  13. Gando, A.; et al. [KamLAND-Zen] Search for Majorana Neutrinos near the Inverted Mass Hierarchy Region with KamLAND-Zen. Phys. Rev. Lett. 2016, 117, 082503. [Google Scholar] [CrossRef] [PubMed]
  14. Anton, G.; et al. [EXO-200] Search for Neutrinoless Double-β Decay with the Complete EXO-200 Dataset. Phys. Rev. Lett. 2019, 123, 161802. [Google Scholar] [CrossRef]
  15. Klapdor-Kleingrothaus, H.V.; Krivosheina, I.V. The evidence for the observation of 0nu beta beta decay: The identification of 0nu beta beta events from the full spectra. Mod. Phys. Lett. A 2006, 21, 1547–1566. [Google Scholar] [CrossRef]
  16. Valentino, E.D.; Gariazzo, S.; Mena, O. Most constraining cosmological neutrino mass bounds. Phys. Rev. D 2021, 104, 083504. [Google Scholar] [CrossRef]
  17. Lesgourgues, J.; Pastor, S. Neutrino mass from Cosmology. Adv. High Energy Phys. 2012, 2012, 608515. [Google Scholar] [CrossRef]
  18. Zatsepin, G.T. On the possibility of determining the upper limit of the neutrino mass by means of the flight time. Pisma Zh. Eksp. Teor. Fiz. 1968, 8, 333–334. [Google Scholar]
  19. Pakvasa, S.; Tennakone, K. Neutrinos of Non-zero Rest Mass. Phys. Rev. Lett. 1972, 28, 1415. [Google Scholar] [CrossRef]
  20. Hirata, K.S.; Kajita, T.; Koshiba, M.; Nakahata, M.; Oyama, Y.; Sato, N.; Suzuki, A.; Takita, M.; Totsuka, Y.; Kifune, T.; et al. “Observation in the Kamiokande-II Detector of the Neutrino Burst from Supernova SN 1987a. Phys. Rev. D 1988, 38, 448–458. [Google Scholar] [CrossRef]
  21. Bratton, C.B.; et al. [IMB] Angular Distribution of Events From Sn1987a. Phys. Rev. D 1988, 37, 3361. [Google Scholar] [CrossRef]
  22. Alekseev, E.N.; Alekseeva, L.N.; Volchenko, V.I.; Krivosheina, I.V. Possible Detection of a Neutrino Signal on 23 February 1987 at the Baksan Underground Scintillation Telescope of the Institute of Nuclear Research. JETP Lett. 1987, 45, 589–592. [Google Scholar]
  23. Pagliaroli, G.; Rossi-Torres, F.; Vissani, F. Neutrino mass bound in the standard scenario for supernova electronic antineutrino emission. Astropart. Phys. 2010, 33, 287–291. [Google Scholar] [CrossRef]
  24. Ianni, A.; Pagliaroli, G.; Strumia, A.; Torres, F.R.; Villante, F.L.; Vissani, F. The Likelihood for supernova neutrino analyses. Phys. Rev. D 2009, 80, 043007. [Google Scholar] [CrossRef]
  25. Loredo, T.J.; Lamb, D.Q. Bayesian analysis of neutrinos observed from supernova SN-1987A. Phys. Rev. D 2002, 65, 063002. [Google Scholar] [CrossRef]
  26. Lu, J.S.; Cao, J.; Li, Y.F.; Zhou, S. Constraining Absolute Neutrino Masses via Detection of Galactic Supernova Neutrinos at JUNO. JCAP 2015, 05, 044. [Google Scholar] [CrossRef]
  27. Hansen, R.S.L.; Lindner, M.; Scholer, O. Timing the neutrino signal of a Galactic supernova. Phys. Rev. D 2020, 101, 123018. [Google Scholar] [CrossRef]
  28. Abi, B.; et al. arXiv:2002.03005 [hep-ex]].
  29. B. Abi et al. [DUNE], JINST 2020, 15, T08008. [CrossRef]
  30. Abi, B.; et al. [DUNE] Supernova neutrino burst detection with the Deep Underground Neutrino Experiment. Eur. Phys. J. C 2021, 81, 423. [Google Scholar] [CrossRef]
  31. Rossi-Torres, F.; Guzzo, M.M.; Kemp, E. Boundaries on Neutrino Mass from Supernovae Neutronization Burst by Liquid Argon Experiments. arXiv:1501.00456 [hep-ph]].
  32. Abe, K.; et al. [Hyper-Kamiokande] Hyper-Kamiokande Design Report. arXiv:1805.04163 [physics.ins-det]].
  33. Chakraborty, S.; Mirizzi, A.; Sigl, G. Testing Lorentz invariance with neutrino bursts from supernova neutronization. Phys. Rev. D 2013, 87, 017302. [Google Scholar] [CrossRef]
  34. Serpico, P.D.; Chakraborty, S.; Fischer, T.; Hudepohl, L.; Janka, H.T.; Mirizzi, A. Probing the neutrino mass hierarchy with the rise time of a supernova burst. Phys. Rev. D 2012, 85, 085031. [Google Scholar] [CrossRef]
  35. Hudepohl, L. Neutrinos from the Formation, Cooling and Black Hole Collapse of Neutron. Stars. Thesis, : PhD Munich, Tech. U. (defense: Feb 3 2014).
  36. Keil, M.T.; Raffelt, G.G.; Janka, H.T. Monte Carlo study of supernova neutrino spectra formation. Astrophys. J. 2003, 590, 971–991. [Google Scholar] [CrossRef]
  37. Wolfenstein, L. Neutrino Oscillations in Matter. Phys. Rev. D Mikheyev, S.P.; Smirnov, A.Y. Resonance Amplification of Oscillations in Matter and Spectroscopy of Solar Neutrinos. Sov. J. Nucl. Phys. 1985, 42, 913-917 Mikheev, S.P.; Smirnov, A.Y. Resonant amplification of neutrino oscillations in matter and solar neutrino spectroscopy. Nuovo Cim. C 1986, 9, 17-26 10.1007/BF02508049. 1978, 17, 2369–2374. [Google Scholar] [CrossRef]
  38. Dighe, A.S.; Smirnov, A.Y. Identifying the neutrino mass spectrum from the neutrino burst from a supernova. Phys. Rev. D 2000, 62, 033007. [Google Scholar] [CrossRef]
  39. Pompa, F.; Capozzi, F.; Mena, O.; Sorel, M. Absolute ν Mass Measurement with the DUNE Experiment. Phys. Rev. Lett. 2022, 129, 121802. [Google Scholar] [CrossRef]
  40. FCapozzi; Saviano, N. Neutrino Flavor Conversions in High-Density Astrophysical and Cosmological Environments. Universe 2022, 8, 94. [CrossRef]
  41. Available online: https://webhome.phy.duke.edu/ schol/snowglobes/.
  42. Moura, C.A.; Rossi-Torres, F. Searches for Violation of CPT Symmetry and Lorentz Invariance with Astrophysical Neutrinos. Universe 2022, 8, 42. [Google Scholar] [CrossRef]
  43. Amelino-Camelia, G.; Ellis, J.R.; Mavromatos, N.E.; Nanopoulos, D.V.; Sarkar, S. Tests of quantum gravity from observations of gamma-ray bursts. Nature 1998, 393, 763–765. [Google Scholar] [CrossRef]
  44. Garay, L.J. Thermal properties of space-time foam. Phys. Rev. D 1998, 58, 124015. [Google Scholar] [CrossRef]
  45. Kachelriess, M.; Tomas, R.; Buras, R.; Janka, H.T.; Marek, A.; Rampp, M. Exploiting the neutronization burst of a galactic supernova. Phys. Rev. D 2005, 71, 063003. [Google Scholar] [CrossRef]
  46. Kayser, B. On the Quantum Mechanics of Neutrino Oscillation. Phys. Rev. D 1981, 24, 110. [Google Scholar] [CrossRef]
  47. Porto-Silva, Y.P.; de Oliveira, M.C. Theory of Neutrino Detection – Flavor Oscillations and Weak Values. Eur. Phys. J. C 2021, 81, 330. [Google Scholar] [CrossRef]
  48. Olsen, J.; Qian, Y.Z. Prospects for distinguishing supernova models using a future neutrino signal. Phys. Rev. D 2022, 105, 083017. [Google Scholar] [CrossRef]
  49. Janka, H.T. Neutrino Emission from Supernovae. [CrossRef]
1
The experiment performed in this work has no specific name, so we refer in this table to the first name author.
2
See Ref. [47] for a more precise discussion about the theory of neutrino detection.
3
See Ref. [1] for a recent value of | U e 1 | 2 and other neutrino oscillation parameters.
4
Other analysis using WtCh detectors like HyperK showed that it is possible to distinguish between SN simulation models with different neutrino emission mechanisms, considering times of neutrino emission up to ≈ 9 s [48]. They did not consider MSW on the neutrino propagation.
Preprints 72081 g001
Figure 1. Luminosity time evolution for the two SN progenitor star models analyzed in this work. Black solid line - ν e , red dotted line - ν ¯ e , and blue dashed line - ν x .
Figure 1. Luminosity time evolution for the two SN progenitor star models analyzed in this work. Black solid line - ν e , red dotted line - ν ¯ e , and blue dashed line - ν x .
Preprints 72081 g001
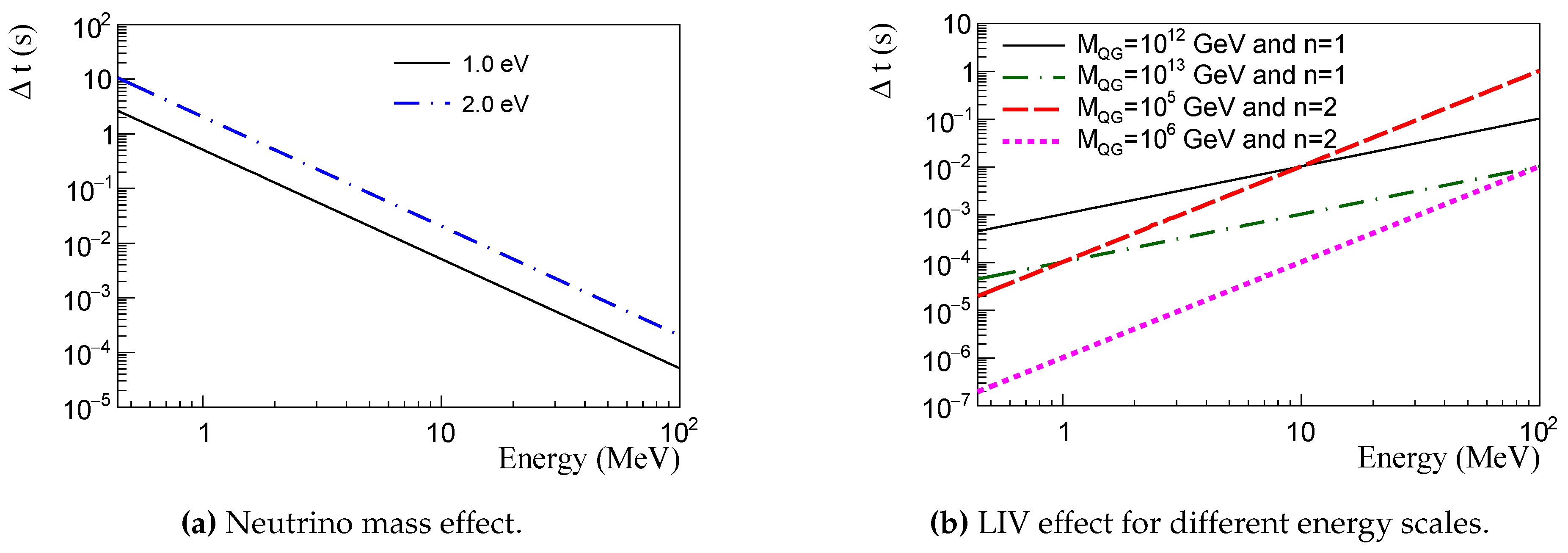
Preprints 72081 g002
Figure 2. Delay, Δ t , in seconds, considering a source at distance d = 10 kpc, for different neutrino masses (left plot) and different LIV energy scale (right plot) as a function of neutrino energy. Neutrino mass values presented in the left plot. LIV energy scale and energy dependence, n, presentend in the right plot. See also text for details.
Figure 2. Delay, Δ t , in seconds, considering a source at distance d = 10 kpc, for different neutrino masses (left plot) and different LIV energy scale (right plot) as a function of neutrino energy. Neutrino mass values presented in the left plot. LIV energy scale and energy dependence, n, presentend in the right plot. See also text for details.
Preprints 72081 g002
Preprints 72081 g003
Figure 3. Number of events per time bin in a 40 kton LArTPC. The ν e interactions are representend by (i) Black solid - CC interaction with Argon; (ii) red dotted - NC interaction with Ar; (iii) yellow dash-dotted - ES on e − . The ν ¯ e interactions are: (i) blue dashed curves - CC interaction with Argon; (ii) green dash-dotted - NC interaction with Ar; (iii) brown dashed - ES on e − . Other flavors interact with Argon by NC (violet dashed-dot curves) and ES (magenta dash-double dotted curves).
Figure 3. Number of events per time bin in a 40 kton LArTPC. The ν e interactions are representend by (i) Black solid - CC interaction with Argon; (ii) red dotted - NC interaction with Ar; (iii) yellow dash-dotted - ES on e − . The ν ¯ e interactions are: (i) blue dashed curves - CC interaction with Argon; (ii) green dash-dotted - NC interaction with Ar; (iii) brown dashed - ES on e − . Other flavors interact with Argon by NC (violet dashed-dot curves) and ES (magenta dash-double dotted curves).
Preprints 72081 g003
Preprints 72081 g004
Figure 4. Number of events per bins of time for a 100 kton WtCh detector. Several detection channels can be distinguished: (i) for ν ¯ e - IBD (black solid lines), NC interaction with   16 O (red dotted), and ES on e − (brown dashed); (ii) ν e - CC (violet dash-dotted) and NC (blue dashed) interaction with   16 O, and ES on e − (yellow dash-two dotted); (iii) ν x - ES on e − (magenta dash-two dotted) and NC interaction with   16 O (green dash-dotted).
Figure 4. Number of events per bins of time for a 100 kton WtCh detector. Several detection channels can be distinguished: (i) for ν ¯ e - IBD (black solid lines), NC interaction with   16 O (red dotted), and ES on e − (brown dashed); (ii) ν e - CC (violet dash-dotted) and NC (blue dashed) interaction with   16 O, and ES on e − (yellow dash-two dotted); (iii) ν x - ES on e − (magenta dash-two dotted) and NC interaction with   16 O (green dash-dotted).
Preprints 72081 g004
Preprints 72081 g005
Figure 5. The top (bottom) panels show the number of ν e ( ν ¯ e ) events per time bin in a 40 kton LArTPC (100 kton WtCh detector). Left (right) panels consider NO (IO). Black solid line refers to a massless neutrino events, blue dashed to 1 eV neutrino mass, red dotted to 2 eV, and green dash-dotted to 4 eV.
Figure 5. The top (bottom) panels show the number of ν e ( ν ¯ e ) events per time bin in a 40 kton LArTPC (100 kton WtCh detector). Left (right) panels consider NO (IO). Black solid line refers to a massless neutrino events, blue dashed to 1 eV neutrino mass, red dotted to 2 eV, and green dash-dotted to 4 eV.
Preprints 72081 g005
Preprints 72081 g006
Figure 6. Event number per time bin in a 40 kton LArTPC, considering NO, different LIV energy dependence, n, and different energy scale, M Q G . Top (bottom) panels show subluminal (superluminal) effect. Left (Right) panels show n = 1 ( n = 2 ). Blue dashed lines represent event numbers for M Q G = 10 12 GeV ( 2 × 10 5 GeV), red dotted for M Q G = 10 13 GeV ( 6 × 10 5 GeV), and green dash-dotted for M Q G = 10 14 GeV ( 10 6 GeV). Black solid line refers to conserved Lorentz invariance.
Figure 6. Event number per time bin in a 40 kton LArTPC, considering NO, different LIV energy dependence, n, and different energy scale, M Q G . Top (bottom) panels show subluminal (superluminal) effect. Left (Right) panels show n = 1 ( n = 2 ). Blue dashed lines represent event numbers for M Q G = 10 12 GeV ( 2 × 10 5 GeV), red dotted for M Q G = 10 13 GeV ( 6 × 10 5 GeV), and green dash-dotted for M Q G = 10 14 GeV ( 10 6 GeV). Black solid line refers to conserved Lorentz invariance.
Preprints 72081 g006
Preprints 72081 g007
Figure 7. The same as in Figure 6, but for IO.
Figure 7. The same as in Figure 6, but for IO.
Preprints 72081 g007
Preprints 72081 g008
Figure 8. Event number per time bin in a 100 kton WtCh detector, considering NO, different LIV energy dependence, n, and different energy scale, M Q G . Top (bottom) panels show subluminal (superluminal) effect. Left (Right) panels show n = 1 ( n = 2 ). Blue dashed lines represent event numbers for M Q G = 10 12 GeV ( 2 × 10 5 GeV), red dotted for M Q G = 10 13 GeV ( 6 × 10 5 GeV), and green dash-dotted for M Q G = 10 14 GeV ( 10 6 GeV). Black solid line refers to conserved Lorentz invariance.
Figure 8. Event number per time bin in a 100 kton WtCh detector, considering NO, different LIV energy dependence, n, and different energy scale, M Q G . Top (bottom) panels show subluminal (superluminal) effect. Left (Right) panels show n = 1 ( n = 2 ). Blue dashed lines represent event numbers for M Q G = 10 12 GeV ( 2 × 10 5 GeV), red dotted for M Q G = 10 13 GeV ( 6 × 10 5 GeV), and green dash-dotted for M Q G = 10 14 GeV ( 10 6 GeV). Black solid line refers to conserved Lorentz invariance.
Preprints 72081 g008
Preprints 72081 g009
Figure 9. The same as in Figure 8, but for IO.
Figure 9. The same as in Figure 8, but for IO.
Preprints 72081 g009
Preprints 72081 g010
Figure 10. Δ χ 2 depending on ν mass considering ν e ( ν ¯ e ) event number in a 40 kton LArTPC (100 kton WtCh). Solid black (dotted blue) line and dashed red (dash-dotted green) line, respectively, for IO and NO. SN at 10 kpc. See Table 2 (Table 5) for 15 M ⊙ (11.2 M ⊙ ) SN.
Figure 10. Δ χ 2 depending on ν mass considering ν e ( ν ¯ e ) event number in a 40 kton LArTPC (100 kton WtCh). Solid black (dotted blue) line and dashed red (dash-dotted green) line, respectively, for IO and NO. SN at 10 kpc. See Table 2 (Table 5) for 15 M ⊙ (11.2 M ⊙ ) SN.
Preprints 72081 g010
Preprints 72081 g011
Figure 11. Δ χ 2 in terms of M Q G for the superluminal and subluminal cases and NO and IO for n = 1 , considering the 40 kton LArTPC. Black solid curve represents the subluminal and IO case, red dashed represents the superluminal and IO case, blue dotted curve is for the subluminal and NO, and green dash-dotted curve is for the superluminal and NO. SN at 10 kpc. See Table 3 (Table 6) for 15 M ⊙ (11.2 M ⊙ ) SN.
Figure 11. Δ χ 2 in terms of M Q G for the superluminal and subluminal cases and NO and IO for n = 1 , considering the 40 kton LArTPC. Black solid curve represents the subluminal and IO case, red dashed represents the superluminal and IO case, blue dotted curve is for the subluminal and NO, and green dash-dotted curve is for the superluminal and NO. SN at 10 kpc. See Table 3 (Table 6) for 15 M ⊙ (11.2 M ⊙ ) SN.
Preprints 72081 g011
Table 1. Neutrino mass limits for different experiments and different experimental methods. Except where it is written otherwise, the confidence intervals are given at 90% C.L.
Table 1. Neutrino mass limits for different experiments and different experimental methods. Except where it is written otherwise, the confidence intervals are given at 90% C.L.
Experiment Method Mass Limit
Katrin [5] Tritium beta decay 0.8 eV
Springer et al. [7]1 e − capture decays of 163Ho 225 eV at 95% C.L
MANU [9] 187Re β decay 26 eV at 95% C.L.
MiBeta [10] 187Re β decay 15 eV
Project 8 [11] CRES 152 eV
KamLAND-ZEN [13] 0 ν β β 0.061 - 0.165 eV
EXO-200 [14] 0 ν β β 0.093 - 0.286 eV
Planck [16] Cosmic microwave 0.09 eV at 95% C.L.
Table 2. Limits on neutrino masses for a 100 kton WtCh (40 kton LArTPC) detector, for NO and IO, and 15 M ⊙ SN at 10 kpc.
Table 2. Limits on neutrino masses for a 100 kton WtCh (40 kton LArTPC) detector, for NO and IO, and 15 M ⊙ SN at 10 kpc.
ν mass(eV)
Mass Ordering ν flavor 1 σ 2 σ 3 σ
NO ν ¯ e 0.52 (1.23) 0.79 (1.93) 1.00 (2.83)
IO ν ¯ e 0.49 (1.29) 0.77 (2.11) 1.01 (3.08)
NO ν e 1.71 (0.88) 1.90 (1.40) 2.64 (1.85)
IO ν e 0.68 (0.47) 1.25 (0.77) 2.01 (1.07)
Table 3. Inferior limits on LIV scale M Q G , n = 1 in Eq. (18), for a 100 kton WtCh (40 kton LArTPC) detector, NO and IO, and the cases of subluminal and superluminal effects. A SN with 15 M ⊙ and 10 kpc from Earth is considered.
Table 3. Inferior limits on LIV scale M Q G , n = 1 in Eq. (18), for a 100 kton WtCh (40 kton LArTPC) detector, NO and IO, and the cases of subluminal and superluminal effects. A SN with 15 M ⊙ and 10 kpc from Earth is considered.
M Q G ( × 10 13 GeV)
Mass Ordering 1 σ 2 σ 3 σ
subluminal NO 2.9 (1.5) 1.7 (0.6) 0.9 (0.4)
subluminal IO 3.1 (2.9) 1.7 (1.3) 0.9 (0.7)
superluminal NO 3.1 (1.7) 1.8 (0.8) 1.1 (0.6)
superluminal IO 3.2 (2.3) 1.8 (1.3) 1.2 (0.8)
Table 4. Inferior limits on LIV scale M Q G , n = 2 in Eq. (18), for a 100 kton WtCh (40 kton LArTPC) detector, NO and IO, and the cases of subluminal and superluminal effects. A SN with 15 M ⊙ and 10 kpc from Earth is considered.
Table 4. Inferior limits on LIV scale M Q G , n = 2 in Eq. (18), for a 100 kton WtCh (40 kton LArTPC) detector, NO and IO, and the cases of subluminal and superluminal effects. A SN with 15 M ⊙ and 10 kpc from Earth is considered.
M Q G ( × 10 5 GeV)
Mass Ordering 1 σ 2 σ 3 σ
subluminal NO 8.5 (5.9) 5.9 (4.0) 4.9 (3.3)
subluminal IO 8.6 (7.5) 5.9 (4.8) 4.8 (3.7)
superluminal NO 8.8 (6.2) 6.3 (4.6) 5.2 (3.9)
superluminal IO 8.8 (6.9) 6.3 (5.0) 5.2 (4.2)
Table 7. Inferior limits on LIV scale M Q G , n = 2 in Eq. (18), for WtCh (LArTPC) detector, considering NO and IO, and the cases of subluminal and superluminal effects for 11.2 M ⊙ SN, 10 kpc from Earth.
Table 7. Inferior limits on LIV scale M Q G , n = 2 in Eq. (18), for WtCh (LArTPC) detector, considering NO and IO, and the cases of subluminal and superluminal effects for 11.2 M ⊙ SN, 10 kpc from Earth.
M Q G ( × 10 5 GeV)
Mass Ordering 1 σ 2 σ 3 σ
subluminal NO 8.6 (4.7) 4.6 (2.9) 3.4 (2.1)
subluminal IO 14.6 (7.7) 6.1 (4.7) 4.4 (3.2)
superluminal NO 9.9 (5.6) 5.4 (4.0) 4.5 (3.7)
superluminal IO 9.4 (7.9) 5.5 (5.3) 4.7 (4.4)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated