Prerpints.org logo
Preprint
Article

Control of Wind Farm Power Output for Green Hydrogen Production without a Grid Connection

Altmetrics

Downloads

151

Views

85

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

26 April 2023

Posted:

27 April 2023

You are already at the latest version

Alerts
Abstract
Green hydrogen is likely to play an important role in meeting the net zero targets of countries around the globe. Hence, producing green hydrogen cheaply and effectively is an important area of research. One potential option for green hydrogen production is to run electrolysers directly from offshore wind turbines, with no grid connection and hence no expensive cabling to shore. The removal of the grid presents an unusual integration challenge. The variable nature of wind turbines and farms results in a power output that can fluctuate more quickly than the electrolyser’s ability to respond without significantly stressing the electrolyser. Thus, the use of a battery, with the wind farm, becomes essential to even out some of the power variations that the electrolyser cannot deal with. In this work, a proof of concept of a wind farm control methodology designed to reduce variability in wind farm active power output is presented. Smoothing the power supplied by the wind farm to the battery reduces the size and number of battery charge cycles and helps to increase battery lifetime. Considering off-grid wind farms which exclusively power an electrolyser, this work quantifies the impact of the wind farm control method on battery lifetime for wind farms of 1, 4, 9 and 16 wind turbines. This is achieved using suitable wind farm, battery and electrolyser models. As an example, for the largest wind farm studied, consisting of 16 x 5 MW wind turbines, batteries with a lifetime of 15 years have approximately a 30 % reduction in required capacity (reduced from 14 MWh to 10 MWh) compared to operating without wind farm control. It is found that reducing the variability of the active power output of wind farms through the wind farm control methodology presented can have a significant impact on battery degradation and hence on battery lifetime. Hence, wind farm control can reduce the required battery capacity for a given lifetime or it can increase the lifetime of a given battery capacity. The work presented shows that wind farm control could play a critical role in reducing the levelised cost of green hydrogen produced from wind farms with no grid connection and paves the way for the design and testing of a full implementation of the wind farm control.
Keywords: 
Subject: Engineering  -   Energy and Fuel Technology

1. Introduction

Green hydrogen, produced through renewable energy-powered electrolysis, is expected to play an important role in achieving full decarbonisation of today’s energy system. Producing green hydrogen provides a means for energy storage and adds to flexibility, especially in energy systems with high renewable power penetration [1]. In electricity networks, green hydrogen can support the grid integration of renewable energy sources (RES), which are intermittent and varying in nature [2]. Green hydrogen can also assist in the decarbonisation and electrification of heating, by meeting future seasonal energy storage requirements [3]. Furthermore, sectors that are difficult to electrify, such as long distance heavy-duty transport, the chemical industry, iron & steel manufacturing and the heat sector could benefit from using green hydrogen to decarbonise [1,4,5]. Today, green hydrogen production is virtually zero worldwide, but various countries are starting to make it a strategic priority. In the UK, for example, the recent Energy Security Strategy portrays a clear support for green hydrogen. The strategy aims to have up to 10 GW of hydrogen by 2030, with at least half of this being from electrolysis [6].
Recent years have seen a significant expansion in offshore wind capacity world wide, with a large increase in capacity expected in the coming decades [7,8]. In the UK, for example, the government’s ambition is to have 50 GW of offshore wind by 2030 [6] and between 75 GW and 140 GW by 2050 [9,10], building from a 2022 base of about 23 GW of operational and consented capacity [11]. Considering both the push for green hydrogen and the expansion of offshore wind capacity, green hydrogen produced from offshore wind power is likely to be an important part of the world’s energy future. Producing green hydrogen would be a viable option especially in areas with a high offshore wind resource and a significant hydrogen demand, but where the electricity networks have severe constraints.
One of the main challenges facing green hydrogen is the high costs currently associated with electrolysis. Currently, more than 98 % of the world’s hydrogen production is sourced from fossil fuels, mostly from natural gas (76 %) but also from coal (22 %) [12]. This is down to cost - before the invasion of Ukraine, hydrogen manufactured through low carbon electrolysis (i.e. nuclear and wind) cost more than double any other alternative [12]. If a viable green hydrogen industry is to emerge from the current global production of 88 Mt per year of fossil-fuel based hydrogen and grow to enable a net zero world, which may require as much as 2.3 Gt per year [3], the production of green hydrogen must be cost competitive.
In order to accelerate the cost reduction of green hydrogen, recent literature is increasingly proposing to connect offshore wind farms directly to offshore electrolysers. For example, [13] undertakes a techno-economic feasibility study of an offshore wind-powered electrolyser for ship refuelling purposes, with a payback time of up to 11 years. The cost modelling includes the wind farm, electrolyser, water treatment and liquefaction plant. An overview on the integration of electrolysers offshore is provided in [14], which highlights the benefits of hydrogen for grid balancing services such as frequency control; and also [2], which undertakes a techno-economic study of onshore and offshore electrolysers. More specifically, [2] compares three different electrolyser and offshore wind farm configurations: a single centralised onshore electrolyser, a single centralised offshore electrolyser on its own platform, and multiple distributed electrolysers where each electrolyser is integrated with one wind turbine. The offshore electrolysers were found to be the most cost-effective option.
The above mentioned papers on offshore electrolysis [2,13,14] have favoured proton exchange membrane (PEM) electrolysers over alternatives such as alkaline electrolysers. This is because PEM electrolysers are capable of faster responses to load changes and are relatively compact machines with high current densities. They also do not require a concentrated corrosive alkaline electrolyte [15], and have slightly lower operational temperatures relative to other technologies. This makes them appropriate for offshore applications were space is limited, electrical generation can fluctuate greatly, and safety is paramount. However, there are aspects of the technology that can be improved.
One potential improvement for PEM electrolysers is their relatively poor durability [16]. To better understand the degradation of electrolysers connected to RES, [17] subjects a PEM electrolyser to fluctuating power supplies by alternating high and low current densities. This resulted in accelerated degradation of the electrolyser compared to the control electrolyser (which was subjected to steady conditions). The main cause of performance loss is the result of increased high frequency resistance caused by parasitic contact resistance between cell components. If the conductivity is compromised, the electrolyser performance is reduced. The degradation of PEM electrolysers when subjected to fluctuating renewable energy sources is also outlined in [18].
Battery systems can help to reduce the rate of electrolyser degradation by reducing the rate of change in power experienced by the electrolyser and balancing power mismatch. Additionally, they can help with controlling the DC link voltage between the wind farm and the electrolyser and with black start of the wind turbine or wind farm. However, battery systems are also prone to degradation, especially when subjected to high levels of cycling at very high or very low charge levels [19]. Furthermore, introducing batteries will add to the wind farm costs, especially if they degrade quickly and require regular replacement. Hence, if the required capacity of the batteries or the number of charge and discharge cycles can be reduced, the cost of hydrogen could potentially be reduced.
A typical modern wind turbine controller has the primary aim of maximising power capture below a set rated wind speed via changes to the generator torque and maintaining the rated power above the set rated wind speed via the blade pitch actuators. Often this goal has constraints on the maximum (rated) rotor speed, with the rated rotor speed maintained via a Proportional Integral (PI) controller. The secondary goal is to keep any structural and component mechanical loads within an acceptable range to achieve a set design life. There is typically minimal consideration of the rate of change of power during operation. Hence, in below rated operation, particularly at rated rotor speed, the power output of a wind turbine can change rapidly. As an example, the NREL 5 MW wind turbine [20], operating using the controller described in [21], can output changes in power as rapid as 1 MW/s during power production in the below rated power, constant speed region. It is clear that there is a disconnect between the smooth power requirements of an electrolyser and the typical power output of a variable speed pitch regulated wind turbine. If the wind turbine and electrolyser were attached to the electrical grid then the difference between the power output by the turbine and input to the electrolyser could simply be exported to the grid. In the case of a green hydrogen system without a grid connection then some other solution must be found.
As turbine size has increased, the amount of inertial energy stored in the rotor has likewise risen. Using estimates that account for technological innovation as well as increasing size of turbines [22], a power law exponent of 3.14 for the energy stored in the blades is calculated. The rotor could potentially be used as an energy store, increasing rotor speeds when reduced electrical power output is required and decreasing rotor speeds when increased electrical power output is required. Whilst care must be taken when altering the operational strategy of a turbine, the idea of increasing or decreasing the rotor speed to store or release energy is not new [23,24], though it has typically been suggested as a means of providing synthetic inertia. Assuming an acceptable change in the rotor/generator speed of 10 % , the NREL 5 MW wind turbine can store/release approximately 6.4 MJ (1.78 kWh) of energy. If used appropriately, a controller could be designed at either a wind turbine or a wind farm level to use the energy stored in the rotor to smooth the power output of a wind turbine and hence reduce the cost of the required battery storage when producing green hydrogen without a grid connection. Such a controller is the focus of the work presented here.
To summarise, this paper presents a proof of concept for novel control methods to smooth the active power of wind turbines and wind farms, connected in an off-grid fashion to a battery and an electrolyser. The active power smoothing has the overall aim of reducing battery costs by either increasing battery lifetime for a given battery size or reducing battery size for a given lifetime. This is a means of reducing the Levelised Cost of Energy (LCOE) of green hydrogen production by wind turbines with no grid connection. To be clear, the LCOE impacts are not quantified in this work. Also not under consideration is the modelling of electrolyser degradation. Both could form the basis of future work. The results presented here focus on changes in battery lifetime and/or battery sizing. The detailed implementation of the necessary wind turbine and wind farm control methodologies is beyond the scope of this work and is suggested as future work. The methodology for simulating the idealised control action and analysing the results and the models for the wind turbines, electrolyser, and battery used in the work are detailed in Section 2. The specific case studies to be assessed are presented in Section 3. The results and discussions are presented in Section 4, and conclusions presented in Section 6.

2. Model description

An overview of the data flow for the work presented is given in Section 2.1. The required models of the wind farm, the electrolyser, and the battery, and the required links between these models are identified. Each model is then described in detail in its own subsection.

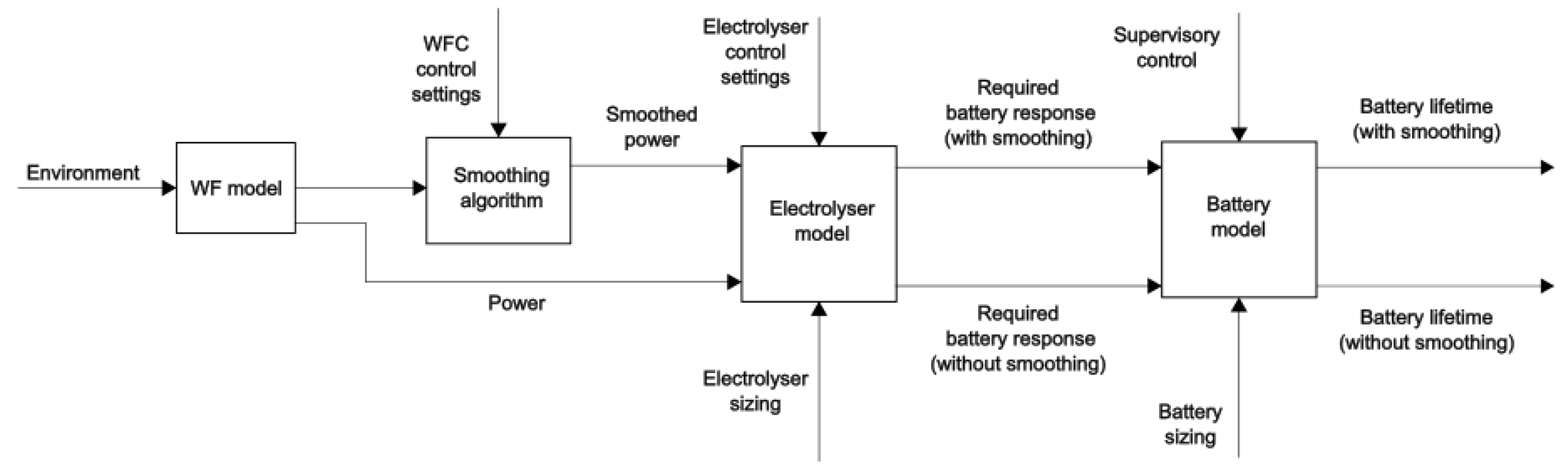
2.1. High level data flow

The flow of data in the analysis is presented in Figure 1. The wind farm model runs based on environmental inputs, comprised of the definition of the mean wind speed and the turbulence intensity. The output of the wind farm model is the power logged from the simulation at 100 Hz. The power output is provided as the input to the novel wind farm control (WFC) smoothing algorithm, along with the WFC settings. The smoothing algorithm adjusts the power to be representative of the smoothing achieved through the novel WFC. The subsequent models have two parallel paths, one using the novel WFC smoothed power and the other using the unsmoothed power as the input. First, the electrolyser model is used to calculate the required response from the battery to appropriately, further, smooth the power to avoid damage to the electrolyser. The required battery responses, with and without smoothing, are then fed into the battery model, in which the battery lifetime is calculated.

2.2. Wind turbine and wind farm models

The wind farm is modelled using StrathFarm [25,26,27], a wind farm simulation tool consisting of enhanced actuator disc models of wind turbines. The wind turbine models are based on the original modelling of [28,29,30]. The basic wind turbine model consists of: an effective wind model; a non-linear rotor model, whose dynamics are modelled through the concept of a single blade; a linear actuator model and a non-linear drive train model. A basic schematic of the StrathTurb turbine model used by StrathFarm is shown in Figure 2. Note that a fuller explanation of the basic model dynamics can be found in [30].

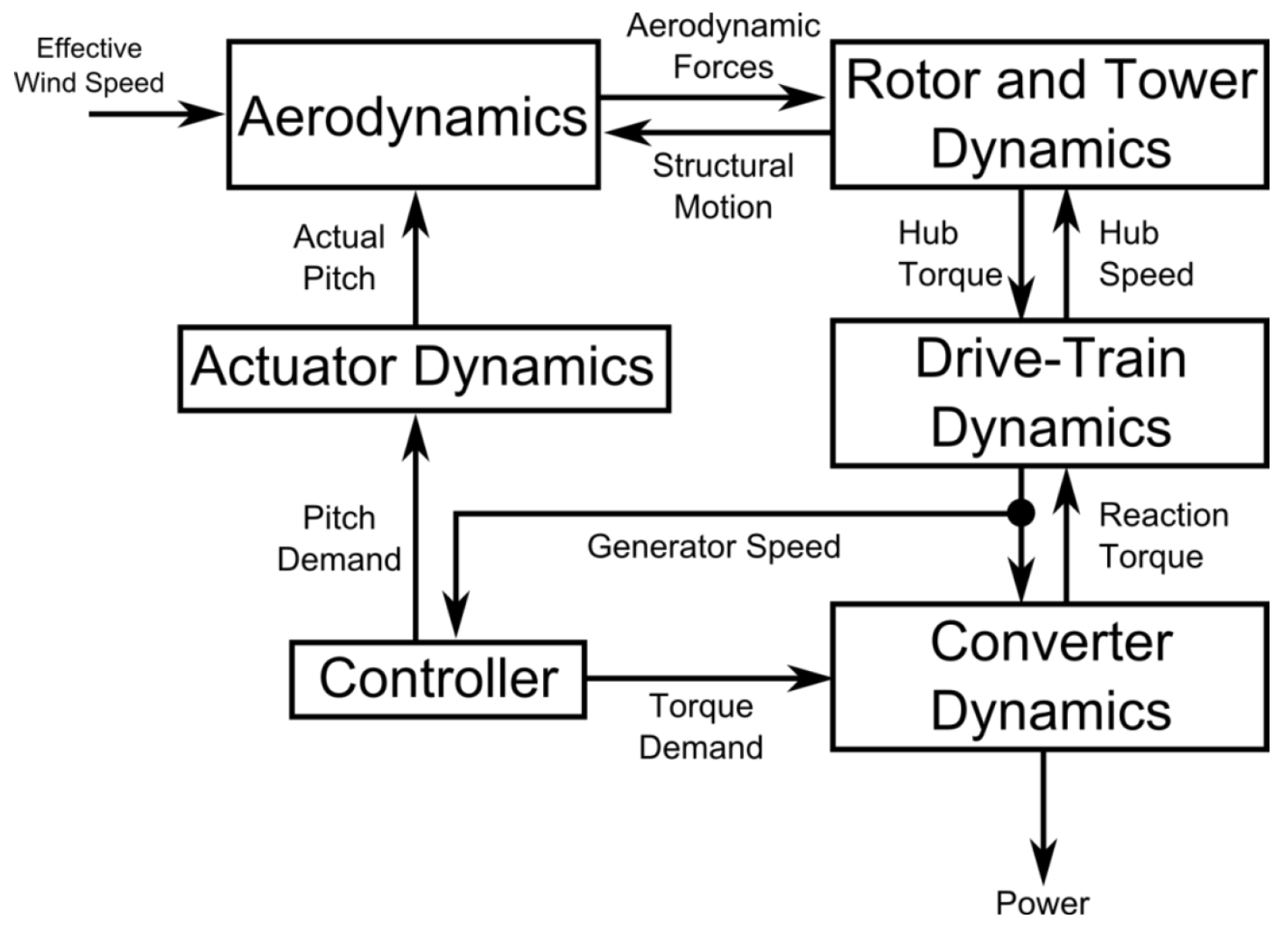
2.2.1. Wind Turbine Model

The aerodynamics of the turbine rotor are modelled using actuator disc theory, with the wind speed input as a rotor effective wind speed. The pitch of the rotor is the demanded pitch passed through the actuator dynamics; which consist of a rate limiter and a linear second order model. The effective wind speed is adjusted based on the structural motion of the rotor and tower, with wind corrections applied to account for the relative motion of the rotor with respect to the wind field. The aerodynamic model outputs the aerodynamic forces that serve as one of the inputs to the rotor and tower dynamics. As discussed in [28], the rotor modes (both in-plane and out-of-plane) originate from each blade, that, in turn, have dominant structural modes in the flap-wise and edge-wise directions. These are skewed from the in-plane and out-of-plane directions by the pitch angle, β . The rotor’s oscillating motions are a combination of blade modes, that are only transmitted to the rest of the turbine, via the drive train, when all three blades oscillate in phase. Thus, the rotor dynamics of the basic model were modelled based on the dynamics of a single blade.
The rotor and tower cross-coupling dynamics are included by modelling the rotor as a single blade `smeared’ through the rotor using a Lagrangian mechanics / lumped parameter approach. The drive train is modelled using the simple non-linear model discussed in [28], whilst the power converter dynamics are assumed to be fast in comparison to the structural dynamics and so are modelled simply as a fractional loss in the output power compared to the mechanical power.

2.2.2. Wind Farm Model

The correlated components of a wind farm wind field have low frequencies, including low frequency turbulence and wake propagation. On the other hand, the loads on the wind turbine structure tend to be at higher frequencies, resulting from higher frequency turbulence and rotational sampling of the wind field. Hence, there is a natural frequency separation that can be exploited to ensure that the wind farm model is computationally efficient. The low frequency turbulence and wakes in the wind-field model are modelled with a significantly lower frequency (1 Hz) than the higher frequency components (100 Hz). Further, the low frequency components of the correlated turbulence can be pre-calculated offline, leaving only the wake interactions to be calculated at the wind farm level, with the high frequency turbulence incorporated into the wind turbine model. The wind model includes correlation of the low frequency turbulence using Veers’ method [31], and wake meandering via a random walk as described in [32].
The wake is modelled as a Gaussian distributed velocity deficit, using an adapted form of the model in [33]. The model in [33] is applicable to point wind speeds, however, for the longitudinal wind speed, StrathFarm uses a rotor effective wind speed that is generated from the Veers correlated longitudinal point wind speeds discussed previously. To calculate the effective wind speed from the correlated point wind speed, the method described in [30] is used.
The model as described thus far models only the lower frequency components of the wind flow. The higher frequency components arise due to rotational sampling of the wind. These higher frequency components are modelled within each turbine model in StrathFarm as additional oscillations in the effective wind speed such that an appropriate spectrum of the torque is produced.
As a blade sweeps the rotor area it encounters differing wind speeds due to stochastic variation in the wind, tower shadow and wind shear effects (the latter two being deterministic). These variations are modelled using Fourier series corrections to the effective wind speed as described in [34].

2.3. Idealised control methodology

Typical wind turbine controllers follow a set strategy of a given generator torque or power output for a given generator speed. Though some wind turbines can adjust this strategy, turbines tend to do this solely for curtailment purposes, whereby the strategy is updated at a frequency of the order of 0.01 Hz or lower. In order to affect a change in a wind turbine’s power output at a frequency of the order of 1 Hz or higher (required such that the frequency is of the same order as the changes in power output due to turbulence), an augmentation to the wind turbine’s controller is required. To allow a wind farm to respond at similar time scales, an appropriate wind farm control methodology is also required. A wind turbine controller augmentation suitable for the task is the Power Adjusting Controller described in [35], which is further described alongside an appropriate wind farm control methodology in [36]. In the work presented here it is assumed that the wind turbines have such a capability, and an appropriate wind farm control methodology is also implemented.
Assuming that the turbines are able to adjust their power output by some increment Δ P , the control task becomes one of designing a suitable wind farm controller to achieve "smoothing" of the wind farm power though appropriate Δ P increments. The input to the wind farm controller is the total power of the wind farm and the output is a set of Δ P N increments delivered to each wind turbine in the farm.

2.3.1. Available kinetic energy

When extracting additional energy from the wind turbine rotor to increase wind turbine electrical power output, the rotor will necessarily slow down. If the rotor speed slows down too much then the turbine is at risk of entering aerodynamic stall. Conversely, when injecting additional energy into the wind turbine rotor to decrease the wind turbine electrical power output there is a risk of over-speeding the wind turbine. However, unlike the previous case of extracting power, when injecting power to the rotor the wind turbine can pitch its blades to reduce the aerodynamic torque input and hence over-speed can be avoided [35,36]. Of course, in the case of power smoothing, where increases in electrical power can follow reductions in electrical power, it can be useful to allow the rotor to accelerate to some limited increase in rotor speed when reducing electrical power to provide additional energy reserves for future increases in electrical power.
The kinetic energy available in the rotor of a turbine can be estimated by,
E T u r b = 1 2 J Ω a 2 − 1 2 J Ω b 2
where Ω a is the rotor speed during normal operation, Ω b is the lowest limit in rotor speed that is acceptable and J is the inertia of the rotor and drive train of the wind turbine. Hence, the total kinetic energy available to the wind farm is E F a r m = N E T u r b , where N is the number of turbines.

2.3.2. Wind farm control structure

The structure of the wind farm controller from requested change in power Δ P to actuated change in power is shown in Figure 3a, with A and B representing controller transfer functions, P representing the plant transfer function (in this case the wind farm), and the disturbance d representing changes in power due to the wind speed. It is assumed that the augmentation to the controller, to allow changes in power, is fast and accurate, and so the plant transfer function is set to unity. Hence the diagram is redrawn with the disturbance, caused by variation in the wind speed, set to be the input in Figure 3b.
In order to smooth the power, it is desirable to eliminate the power variations to as low a frequency as possible. Such an outcome is analogous to providing a first order filter to the output power. A controller realisation that achieves this goal is where A and B are first order transfer functions of the form 1 τ s + 1 , where τ A > τ B . The value of τ B is set to remove any high frequency noise in the signal. A value of 1 s is chosen as this is a good estimate of the power smoothing imparted by the wind turbines’ power electronics [37]. The higher the value of τ A the more the power is "smoothed". The value of τ A is limited by the available kinetic energy in the rotor.

2.3.3. Example of WFC outputs

An example is presented for an 8 m/s simulation of 16 wind turbines with turbulence intensity of 14 %. The value of τ A is set to 6.5 s. Figure 4 shows the power output of the farm for both cases (applying smoothing via WFC and no smoothing) in the upper plot. In the lower plot the average kinetic energy extracted from each turbine rotor is shown. To check if the value of τ A is suitable, the difference between the maximum and minimum energy (values shown on lower plot of Figure 4) can be compared to an estimate of the available energy (found from Equation 1). Note that by finding the difference between the maximum energy extracted and the minimum (which may be negative), the estimate is made conservative as, even if the largest change was the first action of the controller, it would still be able to deliver the required response.

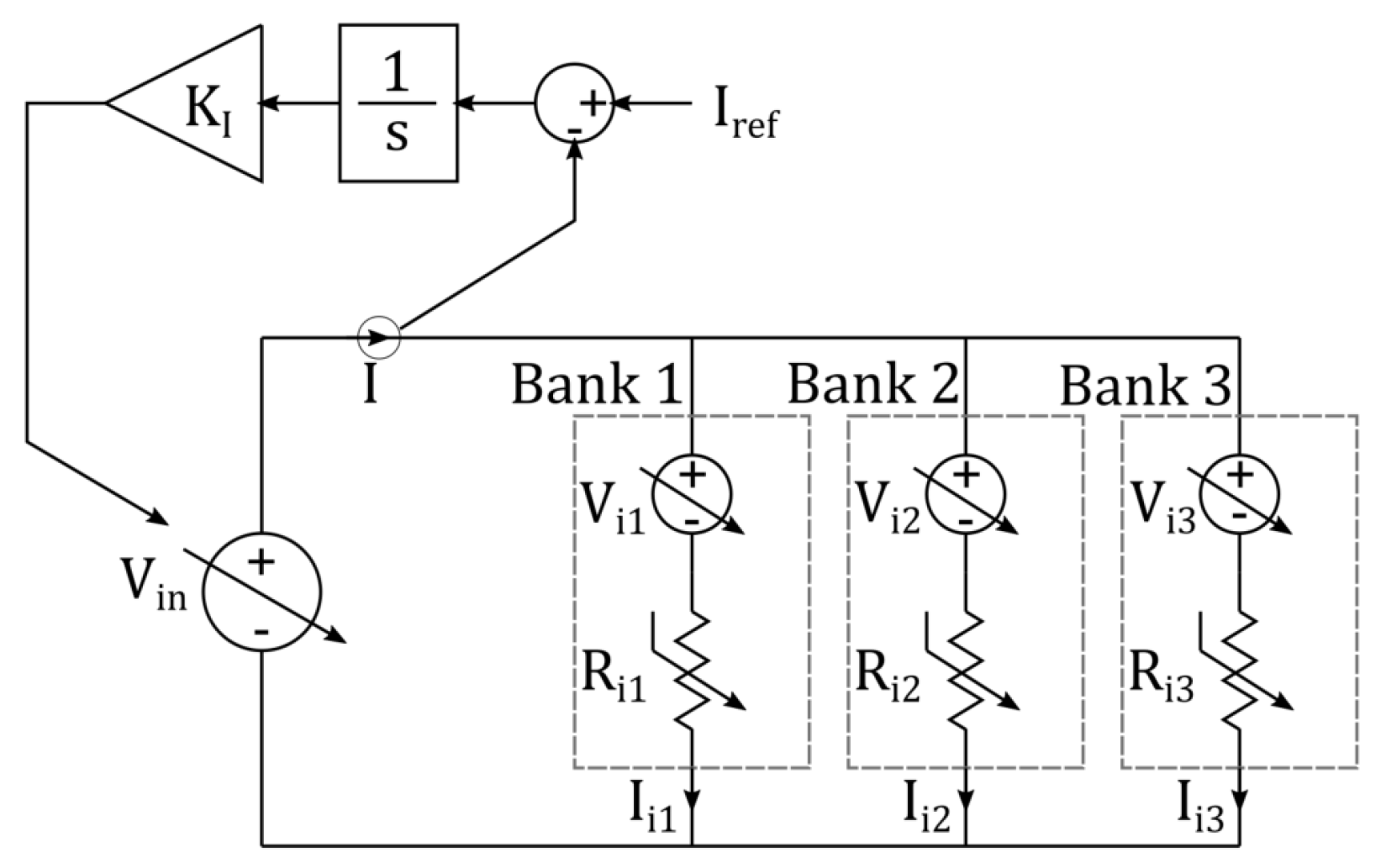
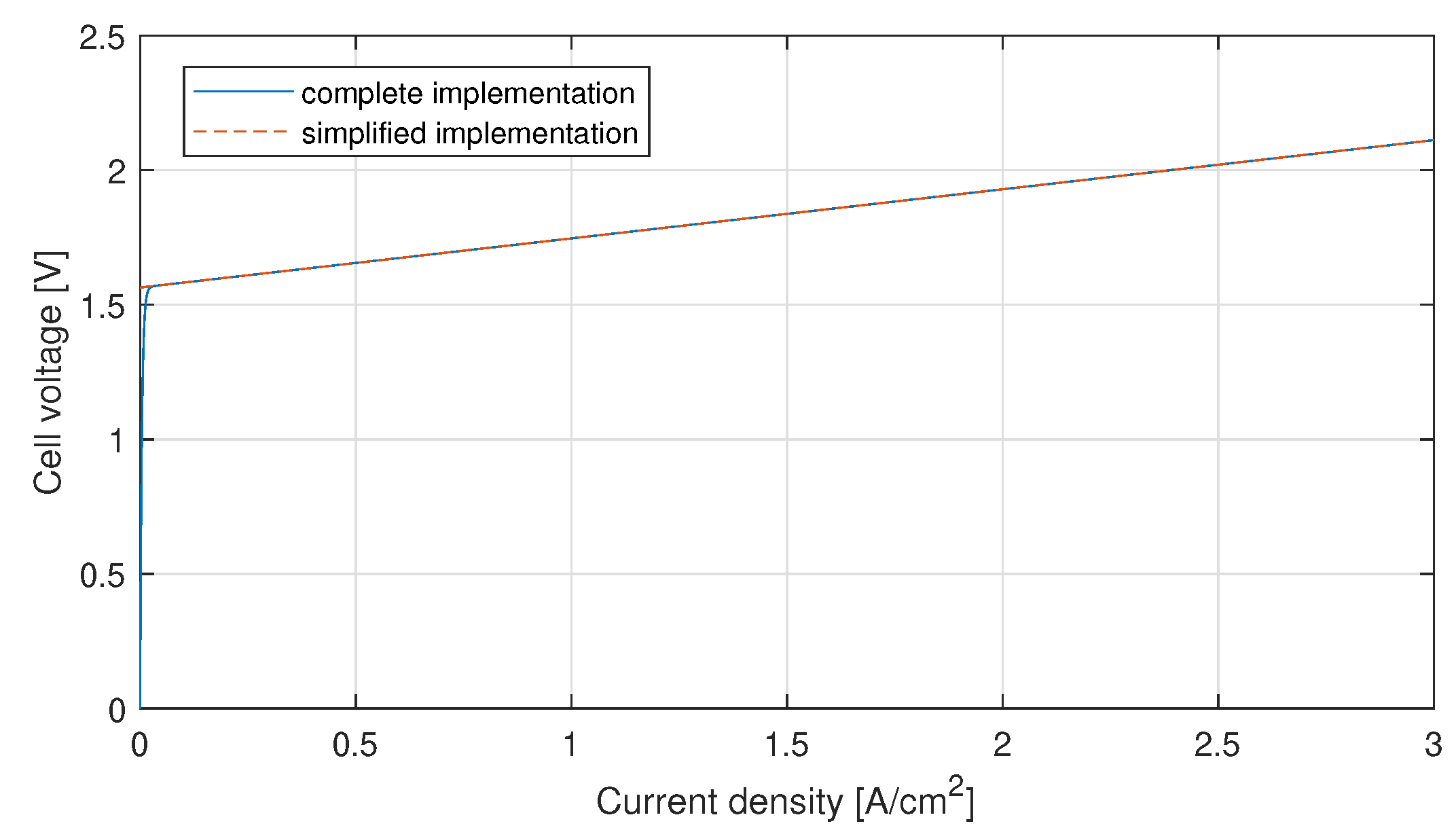
2.4. Electrolyser model

There are two electrolyser requirements: it must be representative of existing PEM electrolysers, and it must be rated at slightly more than a wind turbine to avoid curtailment in a single wind turbine and electrolyser system. Thus, the current density to voltage (i-V) curve is based on exisiting PEM electrolyser curves presented in [38]. Furthermore, each unit of the electrolyser is composed of three parallel banks, with each bank housing three stacks of 100 cells. With 900 cells at a nominal voltage of 2.1 V and a nominal current of 3000 A, the rated power of each unit is about 5.7 MW, i.e. approximately 15 % more than the wind turbine. This is deemed appropriate for this study, which is focused on wind farm control and battery degradation modelling. Electrolyser parameters are presented in Table 1. The following assumptions are made:
  • Power consumption of supporting system is neglected.
  • Isothermal operation, i.e. the system is at rated temperature throughout.
  • Isobaric operation, i.e. the system is at rated pressure throughout.
  • Minimal degradation of the electrolyser.
The electrical system and control schematic is presented in Figure 5, where I r e f is the current reference of the electrolyser, I is the current of the electrolyser unit, K I is the controller integral gain and is chosen to represent an electrolyser response of 1 s, and V i n is the voltage input of the electrolyser. Each electrolyser bank is represented by an equivalent electrical subsystem, comprised of an internal voltage source, V i and an internal resistance, R i . V i and R i are determined by Equations (2) - (6) [39].
e m i n = e m i n 0 + R ( 270 + T ) 2 F
V c e l l = e m i n − e m i n e − 250 i + R c e l l i
R c e l l = ( T − T 0 ) d r t + r 0
V i = V c e l l n c e l l s n s t a c k s
R i = R c e l l n c e l l s n s t a c k s
where e m i n is the minimum potential required for the reaction to start in a real cell, e m i n 0 is the reference value for e m i n , T is the temperature in degrees Celsius, and V c e l l and R c e l l are the cell voltage and resistance, i is the current density (current divided by cell area), and n c e l l s and n s t a c k s are the numbers of cells and stacks.
The resultant i-V curve for each cell is presented in Figure 6. The simplified implementation removes the initial ramp from zero, and is achieved by removing the exponential component from Equation (3) – this simplification is also included in Figure 6 to demonstrate the similarity between both implementations for the majority of current density values. The use of the simplified version can be justified on the grounds that electrolyser systems may have a minimum turn down ratio (e.g. they can only operate at 0.3 A / c m 3 or above) and thus the more complex equation merely captures behaviour that would not be seen in an operational system.

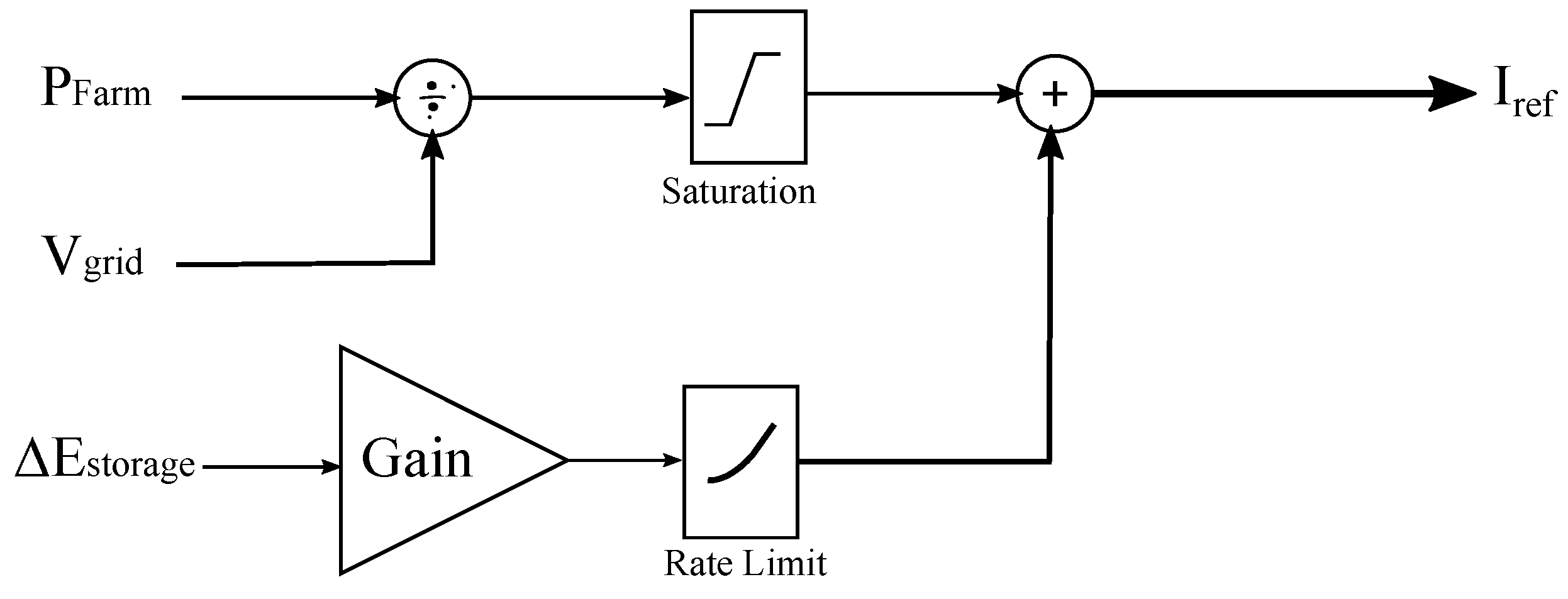
2.5. Supervisory control

To minimise the necessary battery size, a supervisory controller can be added at the input of the electrolyser control. By altering the current reference of the electrolyser, the power mismatch between the wind turbine and the electrolyser can be compensated for, thus reducing the magnitude of the energy excursions required by the battery. The supervisory control schematic is presented in Figure 7.
The supervisory control for the battery system uses the deviation of the stored energy in the battery from the baseline level as an input into the calculation for I r e f . This inclusion has a very small impact on the magnitude of I r e f but is large enough that it restores the state of charge of the battery to the baseline level over time.

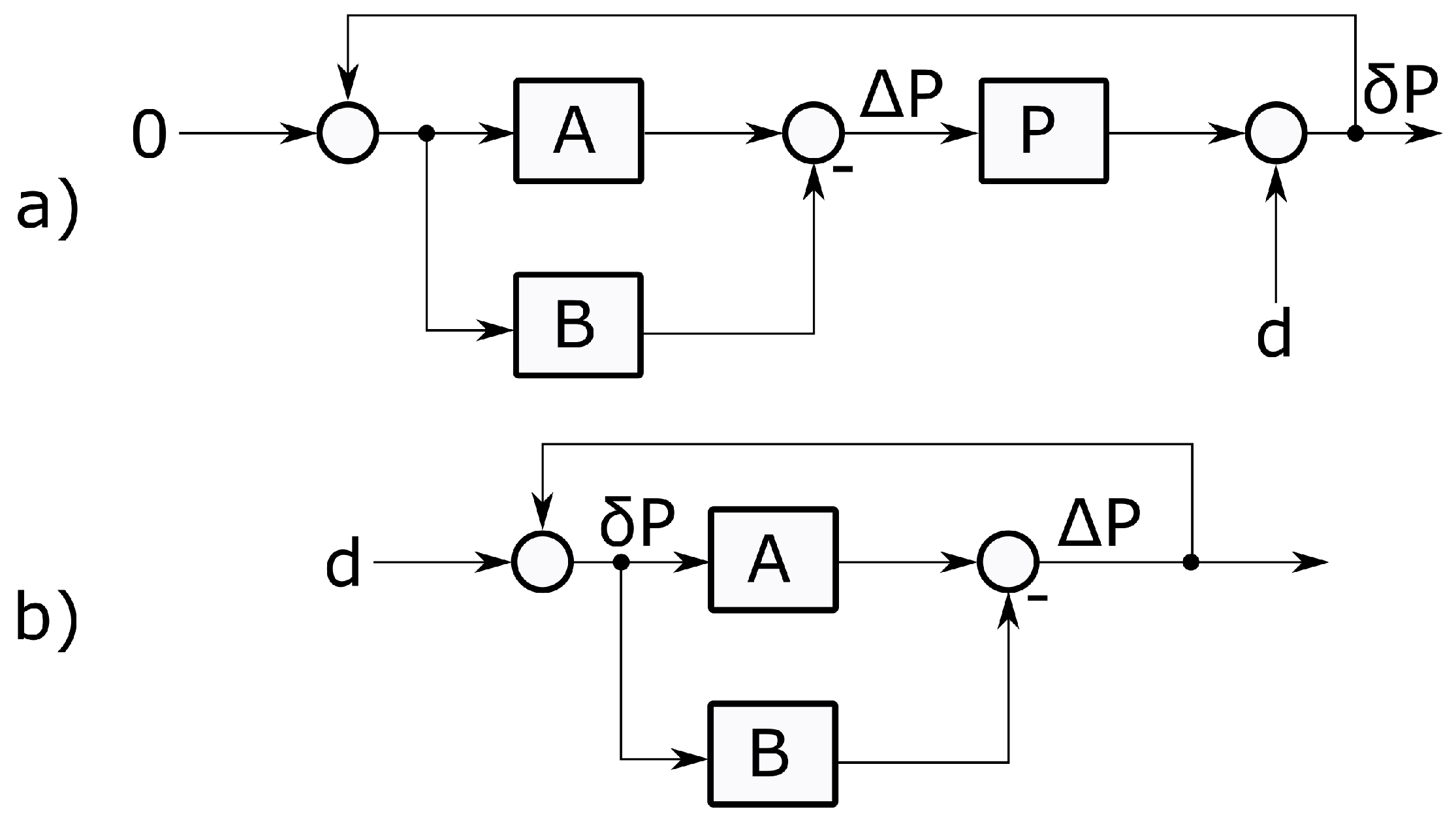
2.6. Battery lifetime model

The power outputs of the battery driven by the differences between wind export and electrolyser import will not only vary the state of charge (SoC) of the battery but also induce energy capacity degradation over time. The degradation of a lithium-ion battery is affected by various factors including elapsed time, cell temperature, SoC, depth of discharge (DoD), etc., and can be considered to be a combination of calendar ageing and cycle ageing [19]. Given that the calendar ageing function f t ( · ) and the cycle ageing function f c ( · ) are linearly related to the number of cycles performed, the battery degradation f d ( · ) over a particular elapsed time period t d is formulated by Equation (7) [19].
f d ( t d , d o d i , s o c i , T c , i ) = f t ( t d , s o c ¯ , T c ¯ ) + Σ i = 1 N c f c ( d o d i , s o c i , T c , i )
where terms d o d i , s o c i , and T c , i denote the DoD, average SoC, and average cell temperature of the i t h cycle ( i = 1 , ⋯ , N c ) within t d respectively; terms s o c ¯ and T ¯ c are averages of s o c i and T c , i across t d respectively. Considering the irregularity of SoC profiles, the rainflow counting algorithm is employed here to identify (half or full) battery cycles and estimate their associated d o d i and s o c i [40]. While f t ( · ) and f c ( · ) both reflect the stress of SoC and cell temperature, they are additionally attributed to the stress of elapsed time and DoD respectively, as formulated by Equations (8) and (9).
f t ( t d , s o c ¯ , T ¯ c ) = S t ( t d ) · S s ( s o c ¯ ) · S T ( T ¯ c )
f c ( d o d i , s o c i , T c , i ) = c i · S d ( d o d i ) · S s ( s o c i ) · S T ( T c , i )
where c i equalling 0.5 or 1 indicates a half or full battery cycle. Terms S t ( · ) , S s ( · ) , S T ( · ) , and S d ( · ) denote the stress of elapsed time, SoC, cell temperature, and DoD, which are formulated by Equations (10), (11), (12), and (13) respectively.
S t ( t d ) = k t · t d
S s ( s o c ) = e k s · ( s o c − s o c r e f )
S T ( T c ) = e k T · ( T c − T c r e f ) · ( T c r e f / T c )
S d ( d o d ) = ( k d 1 · d o d k d 2 + k d 3 ) − 1
where terms k t , k s , and k T are the coefficients of the stress models for elapsed time, SoC, and cell temperature respectively, and k d 1 , k d 2 , and k d 3 are a set of coefficients associated with the DoD stress model. Their specific values adjusted based on the lithium manganese oxide (LMO) battery degradation test data are tabulated in Table 2[19]. Terms s o c r e f and T c r e f denote the reference SoC of 50 % and the reference cell temperature of 25 ∘ C in their respective stress models.
Given the battery degradation being daily updated (i.e., t d = 24 h ) across D days, denoted by f d , j ( j = 1 , ⋯ , D ), the remaining capacity r c D of the LMO battery in percentage of its rated energy capacity at the end of D days is calculated as a two-exponential function: [19].
r c D = α S E I · e − β S E I Σ j = 1 D f d , j + ( 1 − α S E I ) · e − Σ j = 1 D f d , j
where α S E I is the portion of the normalised energy capacity related to the solid electrolyte interphase (SEI) film which is assumed to fade at a linearised rate equalling the product of f d , j and a coefficient β S E I . The rest portion ( 1 − α S E I ) will degrade at the rate f d , j . The values of α S E I and β S E I tuned based on the LMO battery degradation test data are listed in Table 2.

3. Case study

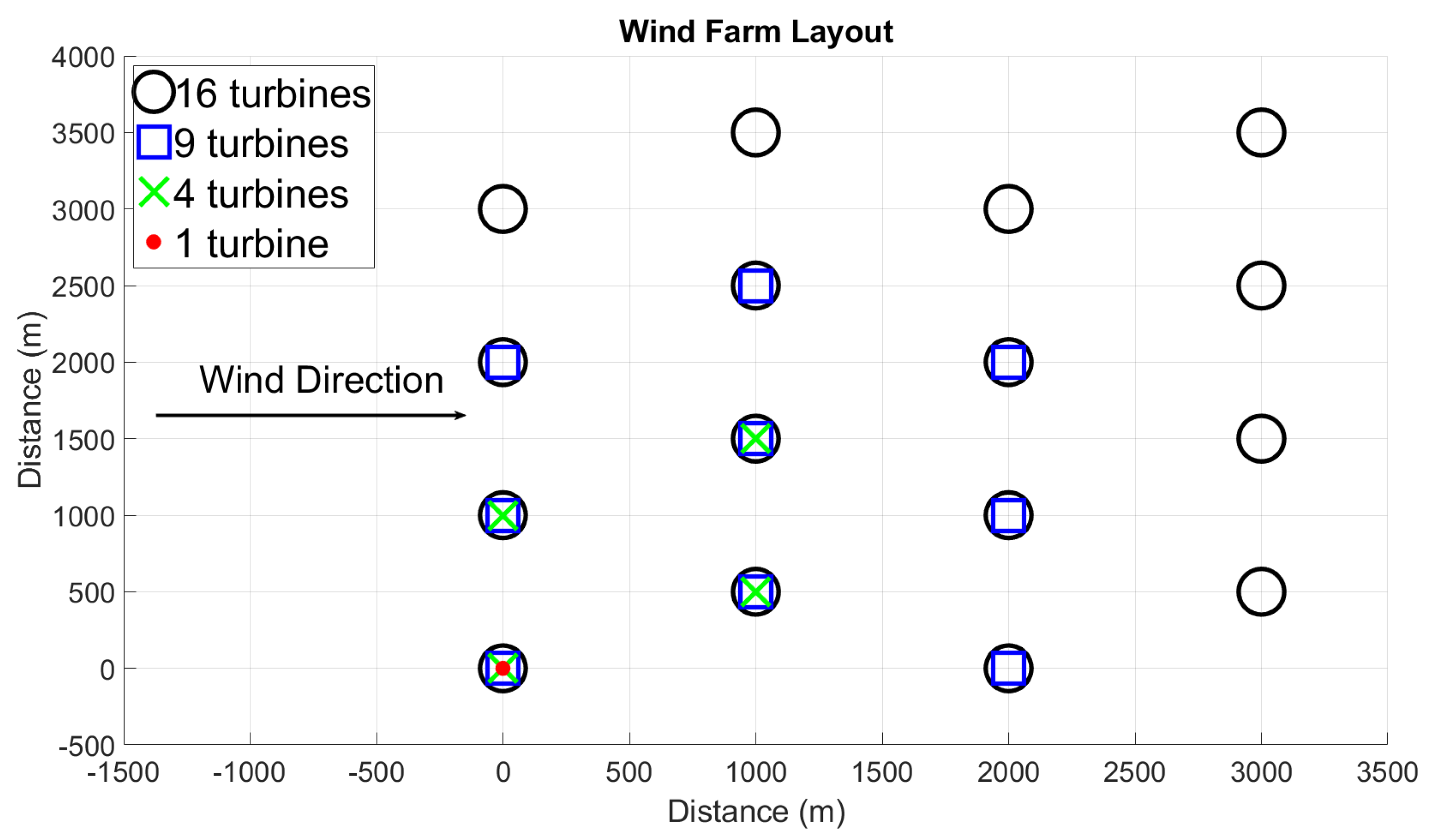
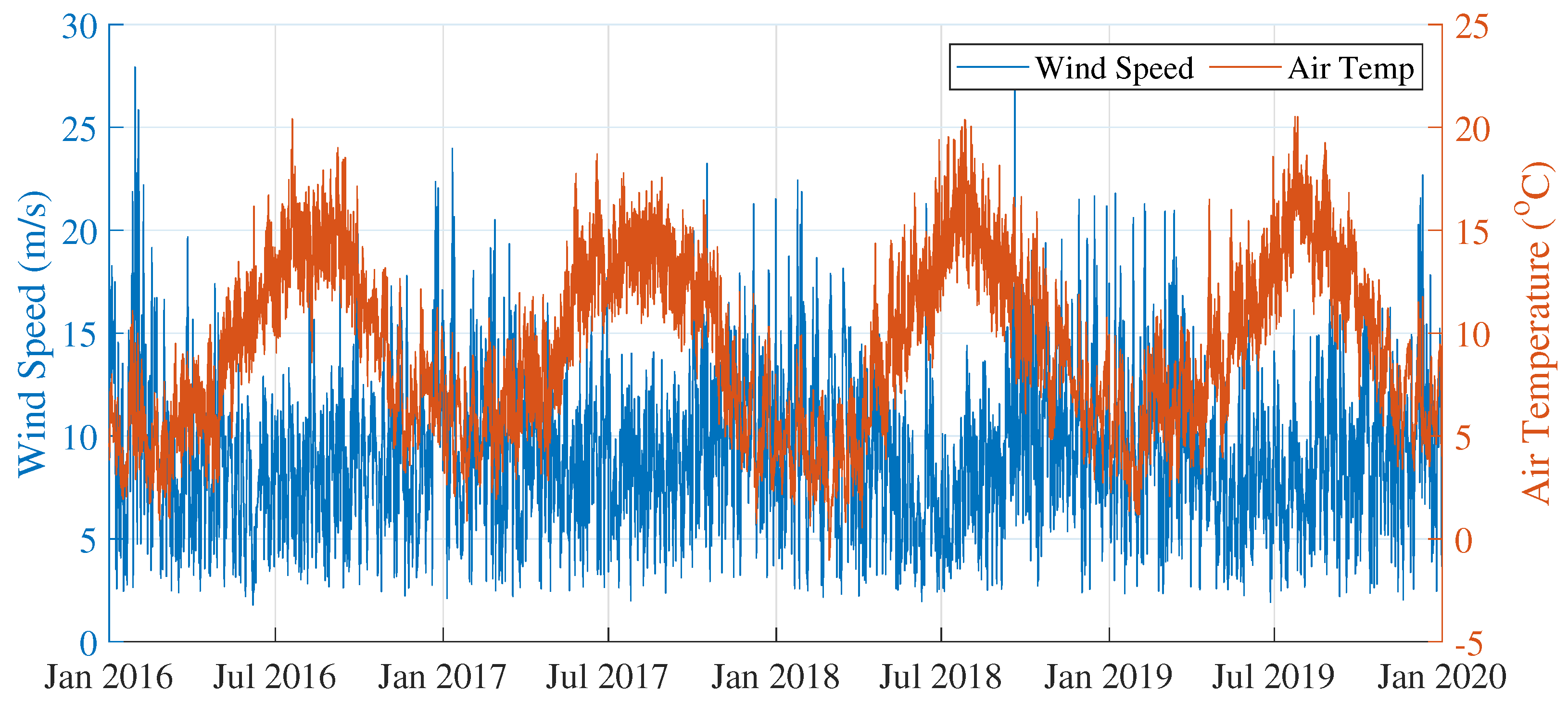
3.1. Wind farm layout and wind properties

The work described here considers four baseline wind farms - a single wind turbine, a two by two wind farm layout, a three by three wind farm layout and a four by four wind turbine layout. These layouts are shown in Figure 8. The wind farm sizes have been chosen so that wind farm simulations are practical to accomplish, and the simple layout is implemented for ease. Six ten minute simulations are conducted for every mean wind speed from 4 m/s to 16 m/s in steps of 1 m/s and from 16 m/s to 24 m/s in steps of 2 m/s. The mean wind direction is assumed to be identical for all simulations to limit the number of simulations required. The turbulence is assumed to follow the IEC standards class B [41].

3.2. Wind turbine model

The wind turbine model used for this work is the NREL 5 MW wind turbine. This turbine is sufficiently large to be representative of offshore wind turbines, though at the smaller end of the range. Importantly, it is well studied and validated. The turbine is modelled in StrathFarm, as described in Section 2.2.

3.3. Applying outputs from the electrolyser to the battery model

The MERRA-2 wind speed reanalysis data recorded at a particular offshore wind farm over 2016-2019 are employed here to simulate the hourly variations of wind speeds, as shown in Figure 9 [42]. For each hourly wind speed reanalysis data, the outputs of the six ten-minute wind farm simulations for the closest mean wind speed are used to synthesise the time series of battery energy outputs in the corresponding hour. Furthermore, the battery cell temperature is assumed to equal the ambient temperature reanalysis data recorded at the same location in the same period, as shown in Figure 9. Presuming that the LMO batteries of a given energy capacity starts with a SoC of 50 %, their degradation is daily updated based on Equations (7)-(14) until they cannot deliver the required energy outputs or their remaining energy capacity r c D falls below a retention limit of 80 % [43]. Then the number of years that the energy interchange requirement could be always met by the batteries is estimated.

3.4. Wind Farm Control Design

Combining the controller design from Section 2.3 and kinetic energy availability of Section 2.3.1 allows the value of τ A to be scheduled with wind farm wind speed. A set of wind farm simulations are conducted using the models described in Section 2.2 and the total electrical power output is calculated. It is assumed that the controller delivers the requested change in power accurately and effectively and hence the maximum difference in kinetic energy (i.e. the maximum minus the minimum energy) is found as described in Section 2.2. For the full set of simulations at each mean wind speed the appropriate value of τ A (the time constant of the transfer function A in Figure 3) is set such that the required change in available energy does not exceed the maximum available energy for any simulation. The value of τ A was also limited such that the value increased monotonically with wind speed. The values of τ A for each mean wind speed are presented in Table 3.
The appropriate values of τ A are then used to post process the wind farm simulations to generate smoothed power outputs to be input to the electrolyser model. It is notable that for the 16 turbine case the value of τ A is often lower than in the 9 turbine case, which is against the trend of increasing τ A values with wind farm size. The cause of this relative drop in the value of τ A is attributed to increased wake interactions in some simulations coupled with the stochastic turbulence reducing the maximum value of τ A for a given set wind speed. The method of setting τ A , particularly the requirements for monotonically increasing values and using the minimum value of all simulations at each wind speed, results in conservative estimates. A more exact method for setting (and varying) the value of τ A for the WFC will be a key part of any future work regarding a full implementation of the controller.
This paper is presented as a proof of concept and so it is assumed that all the turbines in the wind farm have similar energy available and that the change in power is distributed evenly between the turbines. For an actual implementation it would be sensible to consider the distribution of the changes in power across the turbines in the farm, using a variable and likely unequal distribution to minimise the mechanical loads on the turbines.

3.4.1. Note on implementation for one turbine

The wind farm control method of [36] that is implemented here is typically applied to wind farms of around 10 or more wind turbines. The larger the number of wind turbines in the farm, the weaker the induced feedback loop. For a single wind turbine, or for wind farms of fewer than around 4 wind turbines, the induced feedback from the wind farm control implementation would be strong and have a deleterious impact on the turbine control. However, for a single wind turbine it is possible to use an estimate of the wind speed based on aerodynamic coefficients and the turbine operational state to produce an estimated power output that is sufficiently decoupled from the turbine’s controller that it can be used in a similar manner to the wind farm power used in [36]. The description of the wind speed estimator and power estimate is outside the scope of the work presented here, where it is assumed that the estimated power output is a good estimate suitable for implementing the wind farm control strategy.

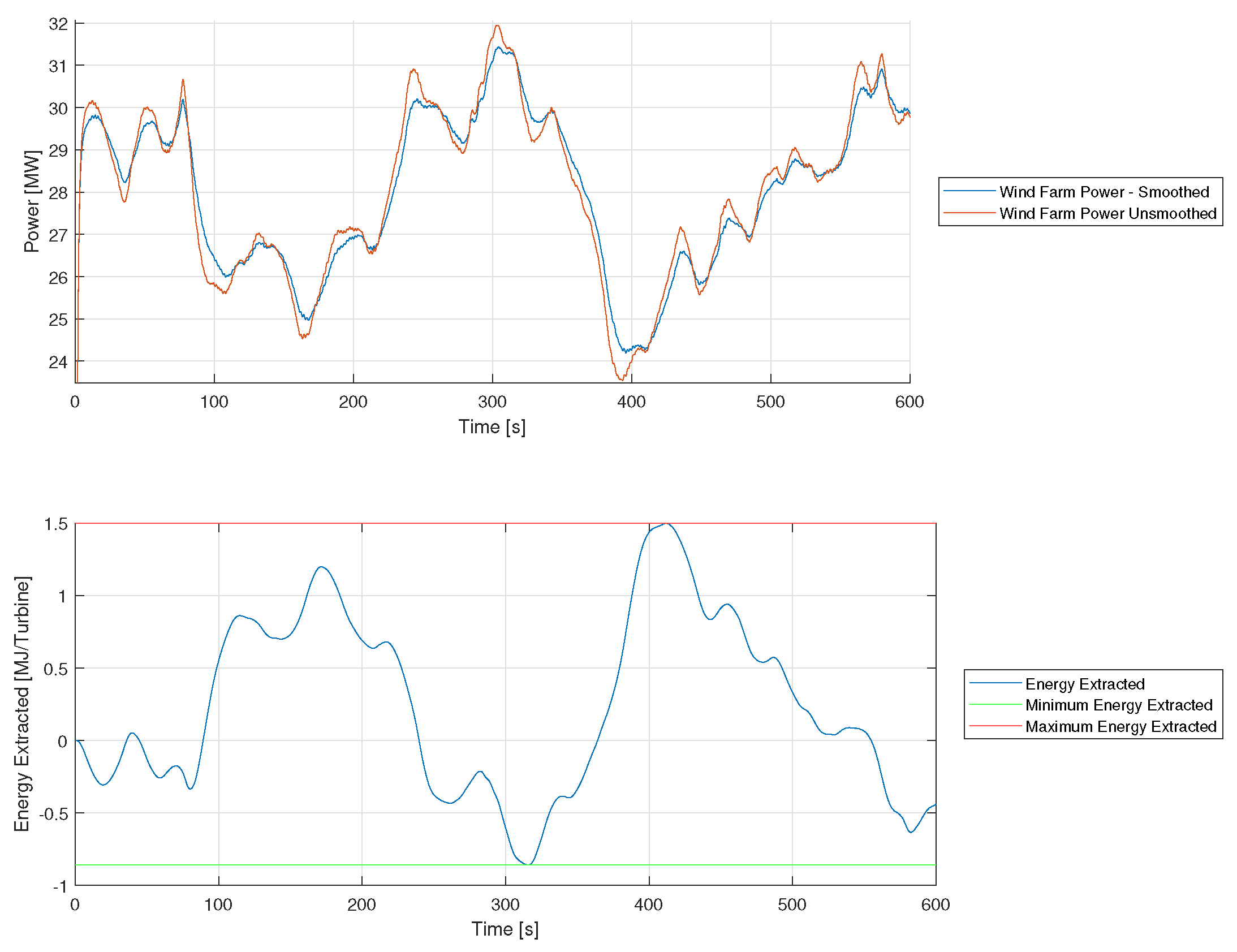
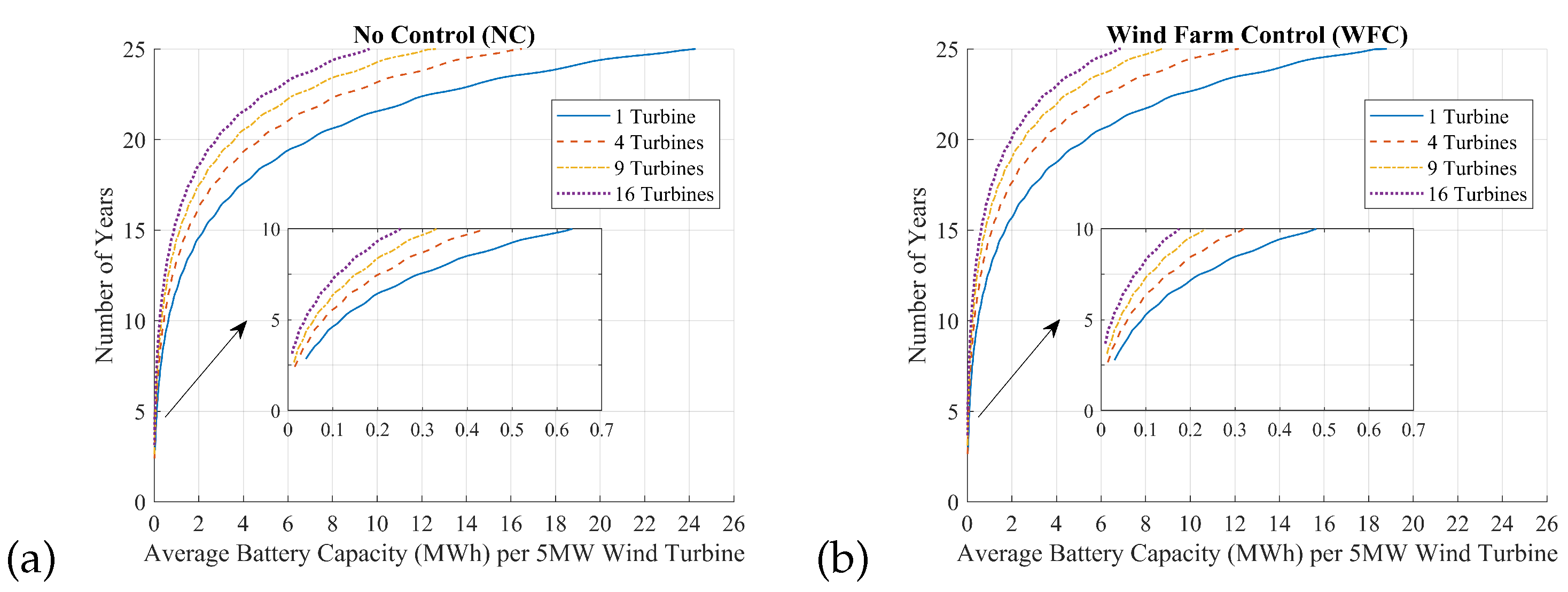
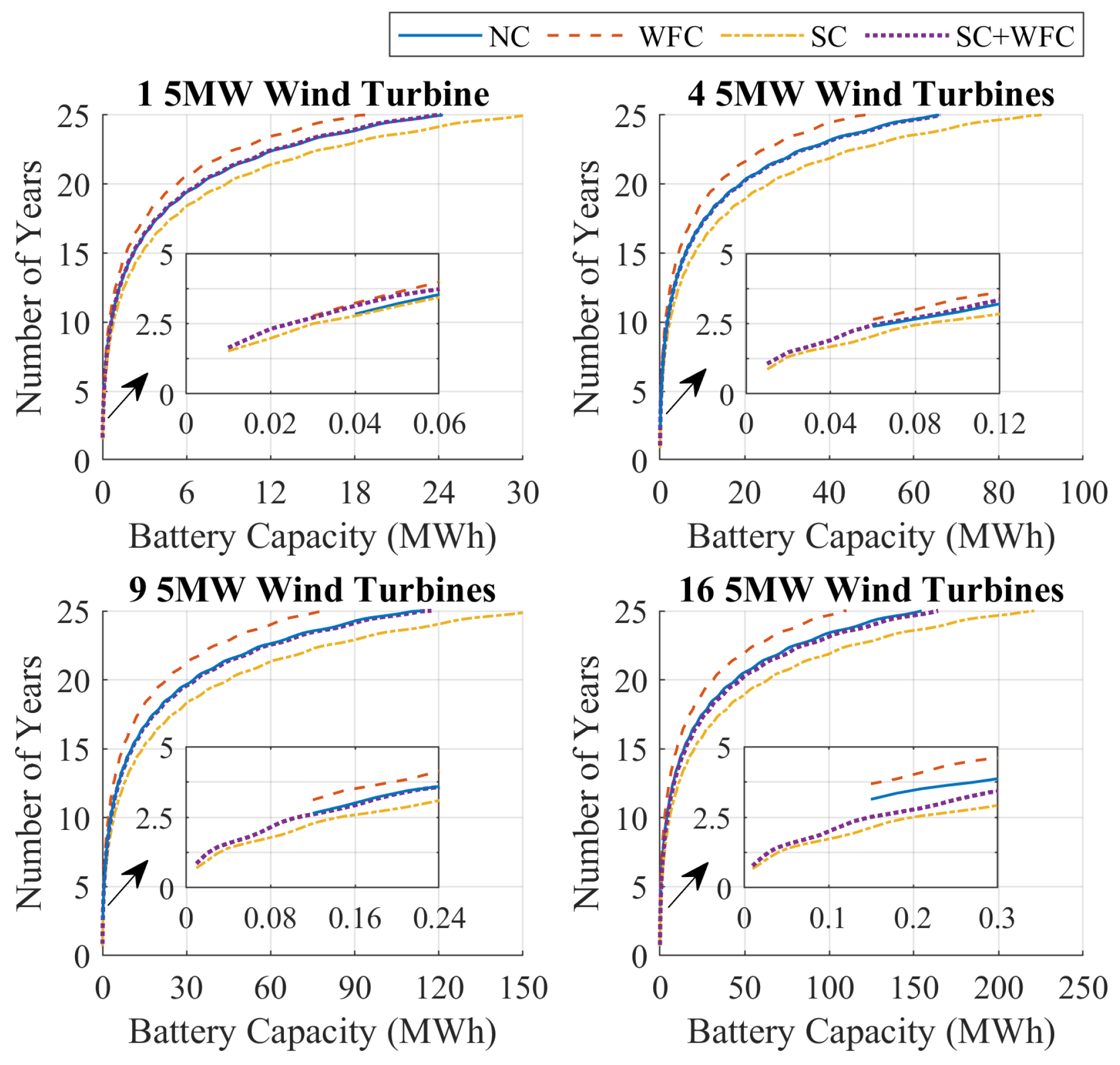
4. Results

The first result considered is the smoothing effect of increasing the size of the wind farm itself on battery capacity. Figure 10 compares the number of operating years that could be achieved by the average battery capacity per 5 MW of wind power between different wind farm sizes with and without WFC. For both the WFC and no control (NC) cases, the increase of the wind farm size is shown to not only extend the battery lifetime given the same average battery capacity, but also reduce the minimum average battery capacity that would meet all the energy required until the retention limit. This result is as expected, as increasing the number of turbines naturally smooths the power of the wind farm. The stochastic variations in wind resource from turbulence experienced by different turbines cancel one another out to a greater extent as the number of turbines increases.
For batteries with an expected lifetime of 15 years, the WFC-based average battery capacity per 5 MW wind turbine is decreased by around 65 % from 1.7 MWh to 0.6 MWh when the wind farm scale increases from 1 x 5 MW wind turbine to 16 x 5 MW wind turbines.
Next, the impact of WFC on battery lifetime can be considered. Figure 11 compares the number of years that batteries of different energy capacities could operate, for a wind farm of 1, 4, 9 or 16 x 5 MW wind turbines when no control (NC), wind farm control (WFC), supervisory control (SC) or both (SC+WFC) are applied. WFC to smooth the required energy output of the batteries leads to longer battery lifetimes given the same battery capacity than the NC case, showing that the use of the WFC greatly alleviates the battery degradation. For a wind farm of 16 x 5 MW wind turbines, batteries with a lifetime of 15 years (which require one replacement over a typical 25-year wind farm lifetime with some safety margin) have approximately a 30 % reduction in required capacity (reduced from from 14 MWh to 10 MWh).
Finally, the minimum battery capacity that allows the batteries to meet all the energy requirements and last until the retention limit (i.e. the minimum size of the battery regardless of lifetime) can also be considered. For the NC and WFC cases, the minimum battery size is 0.04 MWh, 0.06 MWh, 0.12 MWh, or 0.15 MWh for each wind farm size respectively. This is reduced to 0.01 MWh in all cases by the SC due to the significant reduction in the energy required from batteries. However, the increased number of discharge/charge cycles due to the use of the SC accelerates the battery capacity fading, which reduces the lifetime of the batteries, as shown in Figure 11. It is worth noting that the supervisory controller used here is tuned in a heuristic manner and so the tuning is unlikely to be optimal. However, it is logical that the supervisory control would reduce the lifetime whilst also reducing the minimum battery size, as SC must by necessity introduce additional charge cycles, reducing lifetime, but will keep the battery SoC more optimal during use. It is likely that, with improved tuning, the SC+WFC) lifetime could be positioned between the WFC and NC lifetimes in Figure 11 whilst facilitating smaller minimum battery sizes. Note that the near equality of the NC and SC+WFC) results in the results shown is coincidental.

5. Discussion

The results presented in Section 4 show that WFC can be used to increase battery life for a wind farm used for hydrogen electrolysis without a grid connection. The results considering wind farm size imply that, as wind farms get larger, the natural smoothing that results will have a positive effect on battery lifetime. However, there is likely still an advantage to smoothing power through WFC for large wind farms, and, given that implementation of a control algorithm is very cheap compared to the cost of the wind farm, even small benefits are useful. Further, it is likely that the first wind farms to power electrolysis without a grid connection will be small, within the sizes of wind farms considered here, as developers would be unlikely to want to risk the large cost of a very large wind farm prior to wider acceptance of the concept. Hence, WFC for smoothing power could be a valuable tool in reducing LCOE.
This paper presented a proof of concept, and demonstrated that the smoothing of wind farm power output by a wind farm controller can have a significant impact on battery lifetime and/or sizing for wind farms without grid connections used for hydrogen electrolysis. This proof of concept opens up a range of potential future work.
The work presented here does not attempt to quantify the impact of the control approach on the LCOE of a wind farm. Cost analyses are complex, and the impact of increased battery lifetime and/or reduced required battery size is not a simple calculation. For example, optimal battery sizing is directly linked to the O&M strategy, which is in turn highly dependent upon the detailed turbine design, the distance to shore, and a range of other factors. By including hydrogen production as an income, the financial viability of hydrogen electrolysis powered by wind farms without grid connections could be ascertained. An analysis of this type would be an interesting area for future work.
The control algorithm presented is shown to work here as a proof of concept. Whilst the control method is possible to implement, a full implementation is not presented here. In order for the controller to be tested in the field it needs to be fully implemented in wind farm simulations to show that it is robust across all operating conditions including edge cases. Such an implementation is considered another interesting area for future work.
The battery and electrolyser models used here are representative of current technology and are of sufficient fidelity to produce reliable results of this proof of concept. However, both models could be built upon further to include additional variables pertinent to powering electrolysers from wind farms without grid connections. The electrolyser model could be expanded to include degradation, hence expanding the work presented here to include electrolyser lifetime that could feed into a future cost study. It may be possible to "trade-off" electrolyser and battery life by varying the smoothing of the power by the battery (after the wind farm smoothing). The battery model (and a future electrolyser model with degradation included) could have a thermal model added to account for temperature changes.
Finally, the production of hydrogen could be increased by optimising the number of operational stacks at any given time. This would require further development of electrolyser supervisory control.

6. Conclusions

Producing green hydrogen from electrolysers directly connected to offshore wind turbines, with no grid connection, may play an important role in the future. Without any remedial control, wind turbine power is highly variable and is not ideal for electrolysers. A battery can be used to smooth the power. The battery’s lifetime is dependent upon its charge cycles and so the smoother the input power to the battery the greater its lifetime. Larger wind farms naturally smooth the power output more than smaller wind farms through averaging of the stochastic variation. For batteries with an expected lifetime of 15 years, the WFC-based average battery capacity per 5 MW wind turbine is decreased by around 65 % from 1.7 MWh to 0.6 MWh when the wind farm scale increases from 1 x 5 MW wind turbine to 16 x 5 MW wind turbines.
WFC can further smooth the power of wind farms to facilitate direct electrolysis of hydrogen, increasing battery lifetime for a given battery size and hence facilitating the use of smaller, less costly batteries. For example, for a wind farm of 16 x 5 MW wind turbines, batteries with a lifetime of 15 years (which require one replacement over a typical 25-year wind farm lifetime with some safety margin) have approximately a 30 % reduction in required capacity (reduced from from 14 MWh to 10 MWh).
Whilst supervisory control can reduce the minimum size of battery (disregarding lifetime), it necessarily introduces additional charge cycles, impacting lifetime. Supervisory control must therefore be carefully tuned.
Future work could include:
  • A full implementation of the WFC and supervisory controller
  • Further study in the tuning of the supervisory controller gain
  • Further development of the electrolyser model to include degradation
  • Further development of the battery model to include thermal considerations
  • A LCOE analysis of wind to hydrogen with no grid connection

Author Contributions

“Conceptualization, A.S, M.C, and M.K.; methodology, A.S., M.C, M.K, A.N., and F.F.; software, A.S, M.C, M.K., and F.F.; validation, A.S., M.C, and F.F.; formal analysis, A.S., M.C, and F.F.; investigation, A.S., M.C, and F.F.; resources, A.S; data curation, M.C and F.F.; writing—original draft preparation, A.S., M.K, A.N., and F.F.; writing—review and editing, A.S, M. K, J.F, and A.N. ; visualization, M.C, F.F. and B.P.; supervision, A.S, and D.C.; project administration, A.S. and M.S.; funding acquisition, A.S, and D.C. All authors have read and agreed to the published version of the manuscript.”, please turn to the CRediT taxonomy for the term explanation. Authorship must be limited to those who have contributed substantially to the work reported.

Funding

This work was conducted as part of the research programme of the Electrical Infrastructure Research Hub in collaboration with the Offshore Renewable Energy Catapult

Data Availability Statement

All data from the study is available from the authors on request.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
NC No Control
WFC Wind Farm Control
SC Supervisory Control
DoD Depth of Discharge
SoC State of Charge
LMO Lithium Manganese Oxide
SEI Solid Electrolyte Interphase
MERRA-2 Modern-Era Retrospective Analysis for Research and Applications, Version 2
LCOE Levelised Cost of Energy

References

  1. Spyroudi, A.; Stefaniak, K.; Wallace, D.; Mann, S.; Smart, G.; Kurban, Z. Offshore wind and hydrogen: Solving the integration challenge. Technical report, ORE Catapult, UK, 2020.
  2. Jang, D.; Kim, K.; Kim, K.H.; Kang, S. Techno-economic analysis and Monte Carlo simulation for green hydrogen production using offshore wind power plant. Energy Conversion and Management 2022. [Google Scholar] [CrossRef]
  3. Oliveira, A.M.; Beswick, R.R.; Yan, Y. A green hydrogen economy for a renewable energy society. Science Direct 2021. [Google Scholar] [CrossRef]
  4. Song, S.; Lin, H.; Sherman, P.; Yang, X.; Nielsen, C.P.; Chen, X.; McElroy, M.B. Production of hydrogen from offshore wind in China and cost-competitive supply to Japan. Nature 2021. [Google Scholar] [CrossRef] [PubMed]
  5. Office of Energy Efficiency & Renewable Energy, US DOE. Hydrogen’s Role in Transportation. Available online: https://www.energy.gov/eere/vehicles/articles/hydrogens-role-transportation (accessed on 14 September 2022).
  6. Department of Business, Energy & Industrial Strategy. British Energy Security Strategy. Available online: https://www.energy.gov/eere/vehicles/articles/hydrogens-role-transportation (accessed on 28 April 2022).
  7. McKinsey & Company. How to succeed in the expanding global offshore wind market. Available online: https://www.mckinsey.com/industries/electric-power-and-natural-gas/our-insights/how-to-succeed-in-the-expanding-global-offshore-wind-market (accessed on 14 September 2022).
  8. International Energy Agency. Wind Power. Available online: https://www.iea.org/reports/wind-power (accessed on 14 September 2022).
  9. Climate Change Committee. Net Zero: The UK’s contribution to stopping global warming. Available online: https://www.theccc.org.uk/publication/net-zero-the-uks-contribution-to-stopping-global-warming/ (accessed on 28 April 2022).
  10. Climate Change Committee. The Sixth Carbon Budget. Available online: https://www.theccc.org.uk/publication/sixth-carbon-budget/ (accessed on 28 April 2022).
  11. Renewable, UK. Wind Energy Statistics. Available online: https://www.renewableuk.com/page/UKWEDhome/Wind-Energy-Statistics.htm (accessed on 14 September 2022).
  12. USDOE. Hydrogen Strategy: Enabling a Low-Carbon Economy. Technical report, US Department of Energy, 2020.
  13. Bonacina, C.N.; Gaskare, N.B.; Valenti, G. Assessment of offshore liquid hydrogen production from wind power for ship refueling. International Journal of Hydrogen Energy 2021. [Google Scholar] [CrossRef]
  14. Calado, C.; Castro, R. Hydrogen Production from Offshore Wind Parks: Current Situation and Future Perspectives. Applied Sciences 2021. [Google Scholar] [CrossRef]
  15. Schug, C. Operational characteristics of high-pressure, high-efficiency water-hydrogen-electrolysis. International journal of hydrogen energy 1998, 23, 1113–1120. [Google Scholar] [CrossRef]
  16. Zeng, Z.; Ouimet, R.; Bonville, L.; Niedzwiecki, A.; Capuano, C.; Ayers, K.; Soleymani, A.P.; Jankovic, J.; Yu, H.; Mirshekari, G.; et al. Degradation Mechanisms in Advanced MEAs for PEM Water Electrolyzers Fabricated by Reactive Spray Deposition Technology. Journal of the Electrochemical Society 2022. [Google Scholar] [CrossRef]
  17. Weiss, A.; Siebel, A.; Bernt, M.; Shen, T.H.; Tileli, V. Impact of Intermittent Operation on Lifetime and Performance of a PEM Water Electrolyzer. Journal of The Electrochemical Society 2018. [Google Scholar]
  18. Papakonstantinou, G.; Algara-Siller, G.; Teschner, D.; Vidaković-Koch, T.; Schlögl, R.; Sundmacher, K. Degradation study of a proton exchange membrane water electrolyzer under dynamic operation conditions. Applied Energy 2020, 280, 115911. [Google Scholar] [CrossRef]
  19. Xu, B.; Oudalov, A.; Ulbig, A.; Andersson, G.; Kirschen, D.S. Modeling of Lithium-Ion Battery Degradation for Cell Life Assessment. IEEE Transactions on Smart Grid 2018, 9, 1131–1140. [Google Scholar] [CrossRef]
  20. Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW reference wind turbine for offshore system development. Technical report, National Renewable Energy Lab.(NREL), Golden, CO (United States), 2009.
  21. Chatzopoulos, A.P. Full envelope wind turbine controller design for power regulation and tower load reduction. PhD thesis, University of Strathclyde, 2011.
  22. Jamieson, P. Innovation in wind turbine design; John Wiley & Sons, 2018.
  23. Stock, A.; Leithead, W. Providing grid frequency support using variable speed wind turbines with augmented control. In Proceedings of the European Wind Energy Conference and Exhibition 2012. WindEurope; 2012; pp. 153–160. [Google Scholar]
  24. Lalor, G.; Mullane, A.; O’Malley, M. Frequency control and wind turbine technologies. IEEE Transactions on Power Systems 2005, 20, 1905–1913. [Google Scholar] [CrossRef]
  25. Giles, A.; van der Hoek, D.; Bedon, G.; Merz, K.; Kühn, M.; Vali, M.; Anaya-Lara, O.; Kanev, S.; Petrović, V.; Trabucchi, D.; et al. Integrated Research Programme on Wind Energy: Offshore array control Work Package 6.3-Deliverable number 63.4. Technical report, University of Strathclyde, 2018.
  26. Hur, S.H.; Poushpas, S.; Amos, L.; Leithead, B. Supergen Wind Hub: D3. 1 Report of Wind Farm Modelling. Technical report, University of Strathclyde, 2019.
  27. Stock, A.; Leithead, W.; Anaya-Lara, O.; Amos, L.; Cole, M.; Taylor, P.; Pirrie, P.; Campos-Gaona, D. Wind farm control work at the University of Strathclyde, past, present and future. In Proceedings of the 5th Wind Energy Systems Engineering Workshop; 2019. [Google Scholar]
  28. Leithead, W.; Rogers, M. Drive-train characteristics of constant speed HAWT’s: Part I–Representation by simple dynamic models. Wind Engineering.
  29. Leithead, W.; Rogers, M. Drive-train characteristics of constant speed HAWT’s: Part II–Simple characterisation of dynamics. Wind Engineering.
  30. Neilson, V.W. Individual Blade Control for Fatigue Load Reduction of Large-scaled Wind Turbines : Theory and Modelling. Mphil, University of Strathclyde, 2010.
  31. Veers, P.S. Three-dimensional wind simulation. Technical report, Sandia National Labs., Albuquerque, NM (USA), 1988.
  32. Poushpas, S. Wind farm simulation modelling and control. PhD thesis, University of Strathclyde, 2016.
  33. Bastankhah, M.; Porté-Agel, F. A new analytical model for wind-turbine wakes. Renewable Energy 2014, 70, 116–123. [Google Scholar] [CrossRef]
  34. Gala-Santos, M.L. Aerodynamics and Wind-Field Models for Wind Turbine Control. Phd, University of Strathclyde, 2018.
  35. Stock, A. Augmented control for flexible operation of wind turbines. PhD thesis, University of Strathclyde, 2015.
  36. Stock, A.; Leithead, W. A generic approach to wind farm control and the power adjusting controller. Wind Energy 2022. [Google Scholar] [CrossRef]
  37. Anaya-Lara, O.; Campos-Gaona, D.; Moreno-Goytia, E.; Adam, G. Offshore wind energy generation: control, protection, and integration to electrical systems; John Wiley & Sons, 2014.
  38. Buttler, A.; Spliethoff, H. Current status of water electrolysis for energy storage, grid balancing and sector coupling via power-to-gas and power-to-liquids: A review. Renewable and Sustainable Energy Reviews 2018, 82, 2440–2454. [Google Scholar] [CrossRef]
  39. Ferguson, J.L. Technoeconomic Modelling of Renewable Hydrogen Supply Chains on Islands with Constrained Grids. PhD thesis, University of Edinburgh, 2021.
  40. Lee, Y.L.; Tjhung, T. Chapter 3 - Rainflow Cycle Counting Techniques. In Metal Fatigue Analysis Handbook; Lee, Y.L., Barkey, M.E., Kang, H.T., Eds.; Butterworth-Heinemann: Boston, 2012; pp. 89–114. [Google Scholar]
  41. IEC. IEC 61400-1: 2019: Wind energy generation systems - Part 1: Design requirements. Standard, International Electrotechnical Commission, Geneva, CH, 2019.
  42. Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). Journal of Climate 2017, 30, 5419–5454. [Google Scholar] [CrossRef] [PubMed]
  43. Fan, F.; Zorzi, G.; Campos-Gaona, D.; Nwobu, J. Wind-plus-battery system optimisation for frequency response service: the UK perspective. Electric Power Systems Research 2022, 211, 108400. [Google Scholar] [CrossRef]
Preprints 71962 g001
Figure 1. High level overview of the data flow between the different component models
Figure 1. High level overview of the data flow between the different component models
Preprints 71962 g001
Preprints 71962 g002
Figure 2. Schematic of the StrathTurb wind turbine model (adapted from [30])
Figure 2. Schematic of the StrathTurb wind turbine model (adapted from [30])
Preprints 71962 g002
Preprints 71962 g003
Figure 3. Wind farm control structure
Figure 3. Wind farm control structure
Preprints 71962 g003
Preprints 71962 g004
Figure 4. Wind farm control structure
Figure 4. Wind farm control structure
Preprints 71962 g004
Preprints 71962 g005
Figure 5. Schematic of electrolyser’s electrical system and control
Figure 5. Schematic of electrolyser’s electrical system and control
Preprints 71962 g005
Preprints 71962 g006
Figure 6. i-V curve of electrolyser.
Figure 6. i-V curve of electrolyser.
Preprints 71962 g006
Preprints 71962 g007
Figure 7. Supervisory controller
Figure 7. Supervisory controller
Preprints 71962 g007
Preprints 71962 g008
Figure 8. The wind farm layout used for the simulations
Figure 8. The wind farm layout used for the simulations
Preprints 71962 g008
Preprints 71962 g009
Figure 9. Hourly times series of MERRA-2 reanalysis data of wind speed (m/s) and air temperature ( ∘ C ) for a particular offshore wind farm over 2016-2019.
Figure 9. Hourly times series of MERRA-2 reanalysis data of wind speed (m/s) and air temperature ( ∘ C ) for a particular offshore wind farm over 2016-2019.
Preprints 71962 g009
Preprints 71962 g010
Figure 10. Battery lifetime (year) against average capacity (MWh) for each 5 MW wind turbine within a wind farm consisting of 1, 4, 9 or 16 wind turbines under (a) no control or (b) wind farm control.
Figure 10. Battery lifetime (year) against average capacity (MWh) for each 5 MW wind turbine within a wind farm consisting of 1, 4, 9 or 16 wind turbines under (a) no control or (b) wind farm control.
Preprints 71962 g010
Preprints 71962 g011
Figure 11. Battery lifetime (year) against capacity (MWh) for a wind farm of 1, 4, 9 or 16 5 MW wind turbines under different control strategies.
Figure 11. Battery lifetime (year) against capacity (MWh) for a wind farm of 1, 4, 9 or 16 5 MW wind turbines under different control strategies.
Preprints 71962 g011
Table 1. Electrolyser parameters.
Table 1. Electrolyser parameters.
Component Symbol Value Unit
Cell area A c e l l 1000 cm 2
Rated current density i r a t e d 3 A/cm 2
Rated temperature T 0 55 ∘ C
Rated pressure p 0 20 bar
Cell voltage at nominal current and temperature V c e l l n o m i n a l 2.1 V
Voltage rating per bank V b a n k 633.5 V
Current rating per bank I b a n k 3000 A
Power rating of one electrolyser unit P e l e c 5.7 MW
Reference voltage e m i n 0 1.55 V
Ideal gas constant R 8.314 J/mol/K
Faraday constant F 96,485 As/mol
Reference resistance r 0 0.34 Ω
Gradient constant d r t -0.0045 Ω cm 2 / ∘ C
Table 2. Stress model coefficients for LMO battery degradation.
Table 2. Stress model coefficients for LMO battery degradation.
Coefficient Value Coefficient Value
k t 4.14E-10 ( s − 1 ) k d 1 1.40E5
k s 1.04 k d 2 -5.01E-1
k T 6.93E-2 k d 3 -1.23E5
α S E I 5.75E-2 β S E I 121
Table 3. Values of τ A used in the WFC
Table 3. Values of τ A used in the WFC
Wind Speed 5 6 7 8 9 10 11 12 13 14 15 16 18 20 22 24
1 Turbine 1 1 2 2 2 3.5 3.5 3.5 3.5 3.5 3.5 3.5 6 6 6 6
4 Turbines 1 1 2.4 3.3 3.3 3.9 3.9 3.9 9.4 10 10 10 10 18 18 20
9 Turbines 1 1 3.2 6 6 6 6 6 15 15 20 20 20 20 20 20
16 Turbines 1 1 3.2 3.2 3.8 4.7 4.9 4.9 5 5 5 5 20 20 20 20
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated