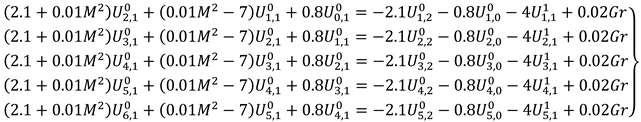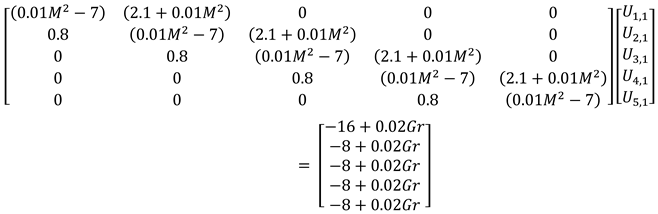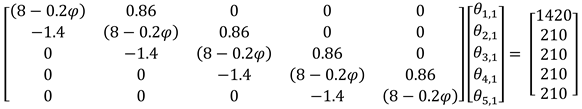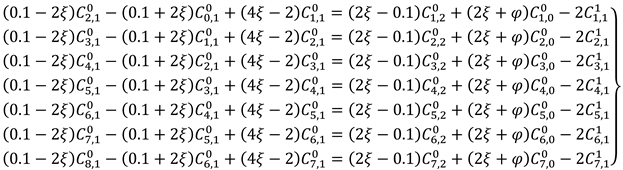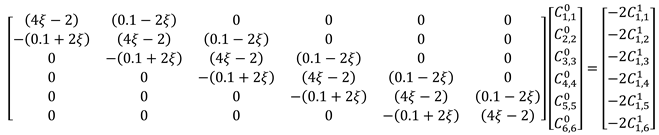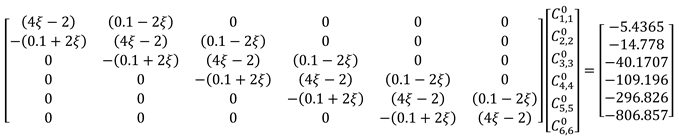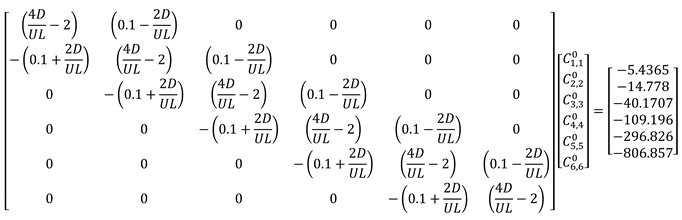Numerical Analysis of the Effect of Magnetic Field and Heat Transfer on Plasma Through an Asymmetric Non-Uniform Channel

1.0. Introduction

Blood Plasma is a fluid which constitutes the liquid part of mammalian blood. Blood plasma is considered as MHD consisting of an aqueous and magnetic fluid of organic substances such as proteins and electrolytes. Similar to water, plasma behaves as a Newtonian Fluid whose viscosity depends on temperature. Its main function in blood is to transport nutrients to the cells of various body organs as well as for transporting waste products resulting from cell metabolic activities to excretory organs such as the liver, kidney and lungs. It also serves as a transport medium for blood cells. Plasma plays an important role in maintaining normal blood pressure in the body. Moreover, Plasma helps to spread heat throughout the body and to maintain biological stability, such as acid-base balance in the blood (Sinha A., Misra J.C., Shit G.C., 2016).

Blood Plasma Flow (BPF) through the body is regulated by three main factors: the size of blood vessels, the action of smooth muscle and by the fluid pressure of the plasma itself. BPF is vital for maintaining life and the factors that govern plasma flow are pressure, the resistance to flow, blood viscosity cardiac output, compliance, blood volume, blood viscosity, the length and diameter of the blood vessels. These characteristics of blood plasma together with the motion of the arterial wall, play an important role in the physiology of the cardiovascular system. The BPF in human arterial system can be considered as a fluid dynamics problem. Therefore, there is need to look at ways to improve and avoid risks of heart diseases in the circulatory system (Abubakar J.U. and Adeoye A.D., 2020).

Simulation of BPF in the arterial network system provides a better understanding of the physiology of human body. Simulation studies of plasma flow in the diseased condition can diagnose the health problem easily and also have many applications in areas such as surgical planning and design of medical devices (Jiangye Li, Hulin Huang2010).

Magnetic fields can reduce blood viscosity, a leading cause of heart attack and strokes. Strong magnetic fields can dramatically reduce the thickness or viscosity of BPF. The magnetic effect all comes down to hemoglobin, the iron-based protein inside red blood cells. In the same way that iron filings align themselves along the field lines around a bar magnet, so the red blood cells align themselves along the straight field lines of electromagnet. This reduces viscosity in several ways. For one, the cells become streamlined with the direction of flow. The alignment also encourages the cells to stick together, forming clumps of various sizes (Akar1, S. et al., 2019).

Heat transfer concerns the generation, use, conversion and exchange of thermal energy between physical systems. Circulation of blood transfers heat between tissues and the dimensions of the blood vessels are various, whenever more blood plasma is needed in some vessels of the body due to more activity, these blood vessels expand to supply the required blood while other vessels tight to compensate it. The arterioles, capillaries and venules act as perfect heat exchangers in which the blood quickly reaches the tissue temperature (Jahangir Alam, et al., 2021).

Heat increases blood flow by expanding blood vessels. It increases blood plasma flow to a specific area and improves circulation. Increased blood flow can help relax a tight muscle, restore movement and reduce pain. Heat eases stiffness after inflammation has resolved. This is because heat on an inflamed area causes the blood vessels to dilate, promoting blood flow to the injured area. Applying heat to an affected area can provide comfort and increase muscle flexibility, as well as heal damaged tissues. Heat boosts the flow of blood plasma and nutrients to an area of the body. It often works best for morning stiffness or to warm up muscles before activity (Phyllis Mumbi Macharia, 2018).

This paper is organized as follows. First, the background to the study is described in section1. Then, the governing mathematical principles and equations are given in section 2, model formulation and applications are presented in section 3, results and discussion on results is provided in section 4, summary and conclusion in section 5, and recommendations in section 6.

2.0. Background

The blood plasma behaves as an electrically conducting fluid exhibiting magnetization. The electrical conductivity of blood is sensitive to the temperature which makes it not to be constant. The characteristics of flow and heat transfer in arteries are extremely useful to understand in relation to design of different heat exchangers and chemical processing equipment. Similar situations prevail in wire and fiber coating, transpiration cooling, food stuff processing, reactor fluidization and manufacture of plastic and rubber sheets. Primary objective of this study is to maintain steady laminar flow of the fluid in arteries and understand the possible effects of non-steady flow and how to clear these effects (Maxwell, B.H. and Ralph Baierlein, 2000).

Magnetic field and heat transfer effects help to reduce blood plasma viscosity, high blood pressure and accumulation of cholesterol in the body which are causes of cardiovascular diseases. The common method used to reduce the blood viscosity is through medication, such as aspirin. In our work we are going to find out how magnetic field and heat transfer enhance the flow of blood plasma in the body. Previous studies on the effect of magnetic field on blood plasma flow through arteries using one dimension model equations have been done with little attention to magnetic field and heat transfer effect in asymmetrical non-uniform arteries. In this study we will consider a 2-dimensional flow model in which blood plasma will be considered to be laminar, unsteady and incompressible. To adequately describe blood plasma flow in circulatory systems there is need to use the mathematical theoretical approach to study effect of magnetic field and heat transfer on blood plasma taking into consideration an asymmetric non-uniform arterial channel of flow (Shit, G. C., and Sreeparna Majee, 2020).

Simulation studies of blood plasma flow in the diseased condition can diagnose the health problem easily and also have many applications in the areas such as surgical planning and design of medical devices. Magnetic field application reduces rate of flow of blood in human arterial system, which is useful in treatment of certain cardiovascular and in the problems which increase the rate of circulation of blood like hemorrhage and hypertension.

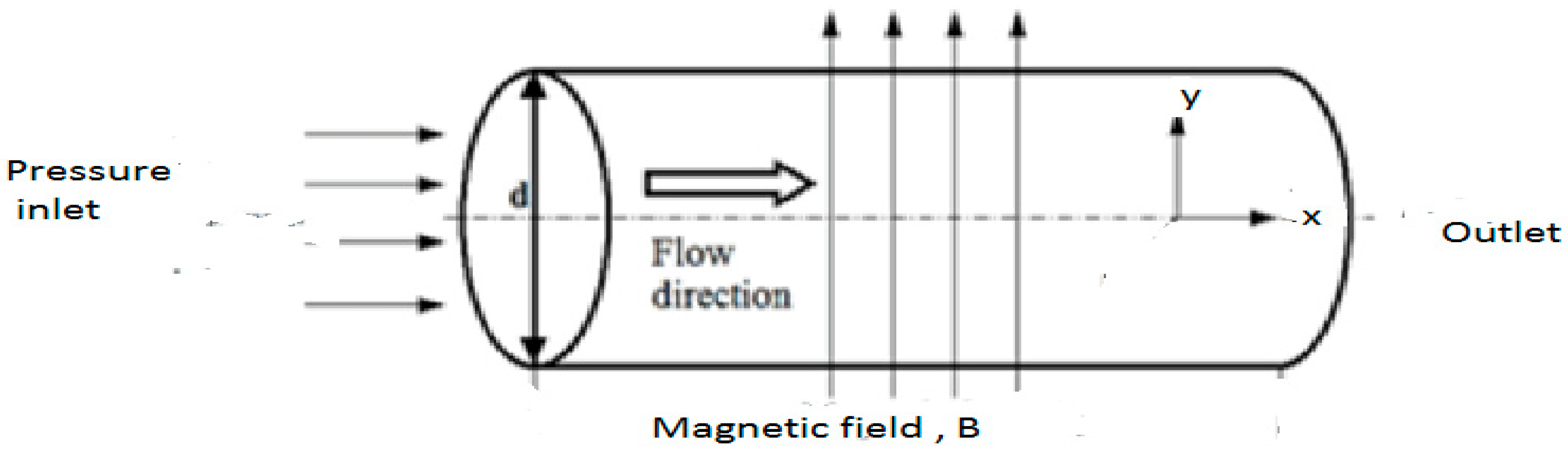
Figure 1.1. Physical configuration of the model problem.

Figure 1.1. Physical configuration of the model problem.

3.0. Governing Equations and Method of Solution

The governing equations were presented based on the following assumptions on blood plasma.

• Plasma is considered to be Newtonian,
• Blood plasma is incompressible,
• Plasma is homogeneous and a viscous fluid.

The above assumptions explain the unsteady flow of blood in the presence of magnetic field governed by two-dimensional boundary layer equations where u and v are the velocity components in the direction of x and y, respectively at time t in the flow field.

Continuity Equation

$$\frac{\mathsf{\partial }u}{\mathsf{\partial }x}+\frac{\mathsf{\partial }v}{\mathsf{\partial }y}=0$$

(3.1)

Momentum Equation

$$x-direction, \rho \left(\frac{\mathsf{\partial }u}{\mathsf{\partial }t}+u\frac{\mathsf{\partial }u}{\mathsf{\partial }x}+v\frac{\mathsf{\partial }u}{\mathsf{\partial }y}\right)=-\frac{\mathsf{\partial }P}{\mathsf{\partial }x}+\mu \left(\frac{{\mathsf{\partial }}^{2}u}{\mathsf{\partial }{x}^2}+\frac{{\mathsf{\partial }}^{2}u}{\mathsf{\partial }{y}^2}\right)+\rho g_x$$

(3.2)

$$y-direction, \rho \left(\frac{\mathsf{\partial }v}{\mathsf{\partial }t}+u\frac{\mathsf{\partial }v}{\mathsf{\partial }x}+v\frac{\mathsf{\partial }v}{\mathsf{\partial }y}\right)=-\frac{\mathsf{\partial }P}{\mathsf{\partial }x}+\mu \left(\frac{{\mathsf{\partial }}^{2}v}{\mathsf{\partial }{x}^2}+\frac{{\mathsf{\partial }}^{2}v}{\mathsf{\partial }{y}^2}\right)+\rho g_y$$

(3.3)

Energy Equations

$$\rho C_p\left(\frac{\mathsf{\partial }T}{\mathsf{\partial }t}+u\frac{\mathsf{\partial }T}{\mathsf{\partial }x}+v\frac{\mathsf{\partial }T}{\mathsf{\partial }y}\right)=\kappa \left(\frac{{\mathsf{\partial }}^{2}T}{\mathsf{\partial }{x}^2}+\frac{{\mathsf{\partial }}^{2}T}{\mathsf{\partial }{y}^2}\right)+\phi \theta ,$$

(3.4)

$$\phi =\mu \left\{2\left[{\left(\frac{\mathsf{\partial }u}{\mathsf{\partial }x}\right)}^2+{\left(\frac{\mathsf{\partial }v}{\mathsf{\partial }y}\right)}^2+{\left[\frac{\mathsf{\partial }u}{\mathsf{\partial }y}+\frac{\mathsf{\partial }v}{\mathsf{\partial }x}\right]}^2-\frac{2}{3}{\left(div. u\right)}^2\right]\right\},$$

(3.5)

where, ρ is the density of the blood while p stands for pressure. C_p is the specific heat at constant pressure, T is the temperature and $\phi$ is the viscous dissipation.

Concentration Equation

$$\frac{\mathsf{\partial }C}{\mathsf{\partial }t}+u\frac{\mathsf{\partial }C}{\mathsf{\partial }x}+v\frac{\mathsf{\partial }C}{\mathsf{\partial }y}=D\frac{{\mathsf{\partial }}^{2}C}{\mathsf{\partial }{x}^2}+D\frac{{\mathsf{\partial }}^{2}C}{\mathsf{\partial }{y}^2},$$

(3.6)

where, C is concentration and D is the diffusion term.

3.3. Discretizing the Momentum Equation

Using equations (3.2) and (3.3) above, the following momentum equation (3.7) was obtained and applied to investigate the velocity of blood plasma in arteries.

$$\frac{\mathsf{\partial }u}{\mathsf{\partial }t}+u\frac{\mathsf{\partial }u}{\mathsf{\partial }x}+v\frac{\mathsf{\partial }u}{\mathsf{\partial }y}=\left(\frac{{\mathsf{\partial }}^{2}u}{\mathsf{\partial }{x}^2}+\frac{{\mathsf{\partial }}^{2}u}{\mathsf{\partial }{y}^2}\right)+Gr\theta +M^{2}u$$

(3.7)

Applying the central space scheme (CS), the values $u_t$ were replaced by forward difference approximation while $u_{xx}$ and $u_{yy}$ were replaced by central difference approximation. When these values were substituted into the partial derivatives appearing in (3.7) to obtain a Forward Time central space scheme provided in equation (3.8) below:

$$\left[\frac{U_{i.j}^{n+1}-U_{i,j}^n}{\Delta t}\right]+\left[\frac{U_{i+1,j}^n-U_{i-1,j}^n}{2\Delta x}\right]+\left[\frac{U_{i,j+1}^n-U_{i,j-1}^n}{2\Delta y}\right]$$

$$=\left[\frac{U_{i+1,j}^n-2U_{i,j}^n+U_{i-1,j}^n}{{\left(\Delta x\right)}^2}\right]+\left[\frac{U_{i,j+1}^n-2U_{i,j}^n+U_{i,j-1}^n}{{\left(\Delta y\right)}^2}\right]$$

(3.8)

$$+M^2\left[\frac{U_{i+1,j}^n+U_{i,j}^n}{2}\right]+Gr\theta$$

The effects of M and Gr on the axial blood plasma velocity were investigated using equation (3.9) obtained by setting $\Delta t=0.01$and$\Delta x=\Delta y=0.01$ and $\theta =1$, yielding

$$\begin{gathered} \left(2.1+0.01M^2\right)U_{i+1,j}^n+\left(0.01M^2-7\right)U_{i,j}^n+0.8U_{i-1,j}^n \\ =-2.1U_{i,j}^{n+1}-0.8U_{i,j-1}^n-4U_{i,j}^n+0.02Gr \end{gathered}$$

(3.9)

Taking $i=1,2,3,\dots ,5, n=0$and $j=1$, a system of linear algebraic equations given in equation (3.10) was formed.

(3.10)

Applying initial conditions $U_{i,0}^0=U_{i,j}^0=1$, and boundary conditions $U_{1,1}^1=0$, an augmented matrix in equation (3.11) below was obtained from the set of algebraic equations (3.10).

(3.11)

3.3. Discretization of Energy Equation

Equation (3.4) can be rewritten as

$$U\frac{\mathsf{\partial }\theta }{\mathsf{\partial }X}+V\frac{\mathsf{\partial }\theta }{\mathsf{\partial }Y}=\left[\frac{{\mathsf{\partial }}^2\theta }{\mathsf{\partial }{X}^2}+\frac{{\mathsf{\partial }}^2\theta }{\mathsf{\partial }{Y}^2}\right]+\phi \theta$$

(3.12)

Equation (3.12) was used to investigate the blood plasma temperature distribution. For the central scheme (CDS), the values, ${\theta }_x$,${\theta }_y$, ${\theta }_{xx}$ and ${\theta }_{yy}$ were replaced by central difference approximation, yielding,

$$u\left(\frac{{\theta }_{i+1,j}-{\theta }_{i-1,j}}{2\Delta x}\right)+v\left(\frac{{\theta }_{i,j+1}-{\theta }_{i,j-1}}{2\Delta y}\right)=\left(\frac{{\theta }_{i+1,j}-2{\theta }_{i,j}+{\theta }_{i-1,j}}{{\left(\Delta x\right)}^2}+\frac{{\theta }_{i+1,j+1}-2{\theta }_{i,j+1}+{\theta }_{i-1,j+1}}{{\left(\Delta y\right)}^2}\right)+\phi {\theta }_{i,j}$$

(3.13)

Setting ${u=v=N}_C=\theta =1$, and multiplying both sides of equation (3.13) by 2$\left(\Delta x\right),$and letting Pr = 0.71 and taking $\Delta x=\Delta y=0.1$ on a square mesh into equation (3.13) the following scheme in equation (3.14) results,

$$-19{\theta }_{i+1,j}+\left(80-0.2\phi \right){\theta }_{i,j}-21{\theta }_{i-1,j}=19{\theta }_{i,j+1}+21{\theta }_{i,j-1}.$$

(3.14)

Taking and i = 1,2,3, … ,5 and j = 1, the following systems of linear algebraic equations (3.16) yields,

$$-19{\theta }_{2,1}+\left(80-0.2\phi \right){\theta }_{1,1}-121{\theta }_{0,1}=19{\theta }_{1,2}+21{\theta }_{1,0}$$

$$-19{\theta }_{3,1}+\left(80-0.2\phi \right){\theta }_{2,1}-21{\theta }_{1,1}^n=19{\theta }_{2,2}+21{\theta }_{2,0}$$

$$-19{\theta }_{4,1}+\left(80-0.2\phi \right){\theta }_{3,1}-21{\theta }_{2,1}=19{\theta }_{3,2}+21{\theta }_{3,0}$$

(3.15)

$$-19{\theta }_{5,1}+\left(80-0.2\phi \right){\theta }_{4,1}-21{\theta }_{3,1}=19{\theta }_{4,2}+21{\theta }_{4,0}$$

$$-19{\theta }_{6,1}+\left(80-0.2\phi \right){\theta }_{5,1}-21{\theta }_{4,1}=19{\theta }_{5,2}+21{\theta }_{5,0}$$

Setting initial and boundary conditions ${\theta }_{i,0}={\theta }_{0,j}=10$ and ${\theta }_{i,2}=0$, respectively, the above algebraic equations (3.15) can be written in augmented as

(3.16)

3.4. Discretizing the Concentration Equation

A dimensionalized form of the concentration (or advection-diffusion equation) of equation (3.6) is given as

$$\frac{\mathsf{\partial }C}{\mathsf{\partial }t}+u\frac{\mathsf{\partial }C}{\mathsf{\partial }x}+v\frac{\mathsf{\partial }C}{\mathsf{\partial }y}=\frac{1}{Pe}\left(\frac{{\mathsf{\partial }}^{2}C}{\mathsf{\partial }{x}^2}+\frac{{\mathsf{\partial }}^{2}C}{\mathsf{\partial }{y}^2}\right),$$

(3.17)

where u(x, y ,t) and v(x ,y, t) are the given divergence-free advective velocity vector fields along x and y directions, respectively, while t is time and C(x, y, t) is the blood plasma concentration levels in arteries.

But the Peclet number is given by

$$Pe=\frac{UL}{D} ,$$

(3.18)

where, U is a axial velocity, L is arterial length, and D is the diffusivity of the blood plasma.

Substituting (3.18) into (3.17) gives

$$\frac{\mathsf{\partial }C}{\mathsf{\partial }t}+u\frac{\mathsf{\partial }C}{\mathsf{\partial }x}+v\frac{\mathsf{\partial }C}{\mathsf{\partial }y}=\frac{D}{UL}\left(\frac{{\mathsf{\partial }}^{2}C}{\mathsf{\partial }{x}^2}+\frac{{\mathsf{\partial }}^{2}C}{\mathsf{\partial }{y}^2}\right)$$

(3.19)

The partial differential equation (3.19) was discretized to form a central scheme provided in equation (3.20) which eventually solved using the finite difference method to determine the effects of diffusivity (D) arterial length (L) and axial velocity (U) for blood plasma concentration levels. Using a central difference numerical scheme, $C_t$was replaced by forward difference scheme while $C_{xx}$, and $C_{yy}$ were replaced by central difference approximation. Substituting these approximations into equation (3.19), and letting $u=v=1$ the following equation (3.20) was obtained.

$$\frac{C_{i,j}^{n+1}-C^n{}_{i,j}}{\Delta t}+\frac{C_{i+1,j}^n-C^n{}_{i-1,j}}{2\Delta x}+\frac{C_{i,j+1}^n-C^n{}_{i,j-1}}{2\Delta y}=\frac{D}{UL}\left[\frac{C_{i+1,j}^n-2C_{i,j}^n+C_{i-1,j}^n}{{\left(\Delta x\right)}^2}+\frac{C_{i,j+1}^n-2C_{i,j}^n+C_{i,j-1}^n}{{\left(\Delta y\right)}^2}\right]$$

(3.20)

Taking $\phi =\frac{\Delta t}{\left(\Delta x\right)}=\frac{\Delta t}{\left(\Delta y\right)}$, $\mu =\frac{\Delta t}{{\left(\Delta x\right)}^2}=\frac{\Delta t}{{\left(\Delta y\right)}^2}$, $\xi =\frac{D}{UL}$, $\Delta x=\Delta y$and multiplying by $2\Delta t$ throughout equation (3.20) and re-arranging, the following scheme in equation (3.21) yields

$$\left(\phi -\mu \xi \right)C_{i+1,j}^n-\left(\phi +\mu \xi \right)C_{i-1,j}^n+\left(2\mu \xi -2\right)C_{i,j}^n=\left(\mu \xi -\phi \right)C_{i,j+1}^n+\left(\mu \xi +\phi \right)C_{i,j-1}^n-2C_{i,j}^{n+1}$$

(3.22)

Taking $\Delta x=\Delta y=0.1$, and $\Delta t=0.01$, $\Rightarrow \phi =0.1$and $\mu =2$ results to the following central difference scheme in equation (3.23).

$$\left(0.1-2\xi \right)C_{i+1,j}^n-\left(0.1+2\xi \right)C_{i-1,j}^n+\left(4\xi -2\right)C_{i,j}^n=\left(2\xi -0.1\right)C_{i,j+1}^n+\left(2\xi +\phi \right)C_{i,j-1}^n-2C_{i,j}^{n+1}$$

(3.23)

For i = 1,2, … ,6, j = 1 and n = 0 the following algebraic equations (3.24) arise from the above central difference scheme in equation (3.23).

(3.24)

The algebraic equations in equation (3.24) results to the following augmented matrix in equation (3.25).

(3.25)

The following initial conditions in equation (3.26) and boundary conditions in equation (3.27) were considered on the flow region,

$$C\left(\mathrm{x},\mathrm{y},0\right)=0,\mathrm{t}=0$$

(3.26)

$$\mathrm{C}\left(0,\mathrm{y},\mathrm{t}\right)=0,\mathrm{C}\left(\mathrm{x},\mathrm{y},1\right)=e^t,\mathrm{t}>0,\mathrm{x}\ne \mathrm{y}$$

(3.27)

Inserting the above initial and boundary conditions into equation (3.25) gives,

(3.28)

Substituting $\xi =\frac{D}{UL}$ into (3.28) gives

(3.29)

3.4. Method of Solution

Numerical schemes were developed using Finite Difference Scheme (FDS). The Finite Difference method was used to solve the developed coupled partial differential equations governing the flow of blood plasma. Conditions associated with the concepts of stability, convergency, accuracy and consistency were applied on the solution of the obtained finite difference equations for accurate approximation of the solution. The results were presented for different parameters under investigation and compared. MATLAB software was used to solve the governing equations and to plot graphs.

4.0. Results

The simulation results obtained in this study focus on the effects of the $D, U, L, \phi , Gr$and $M$ on blood plasma Concentration levels, temperature distribution and velocity profiles.

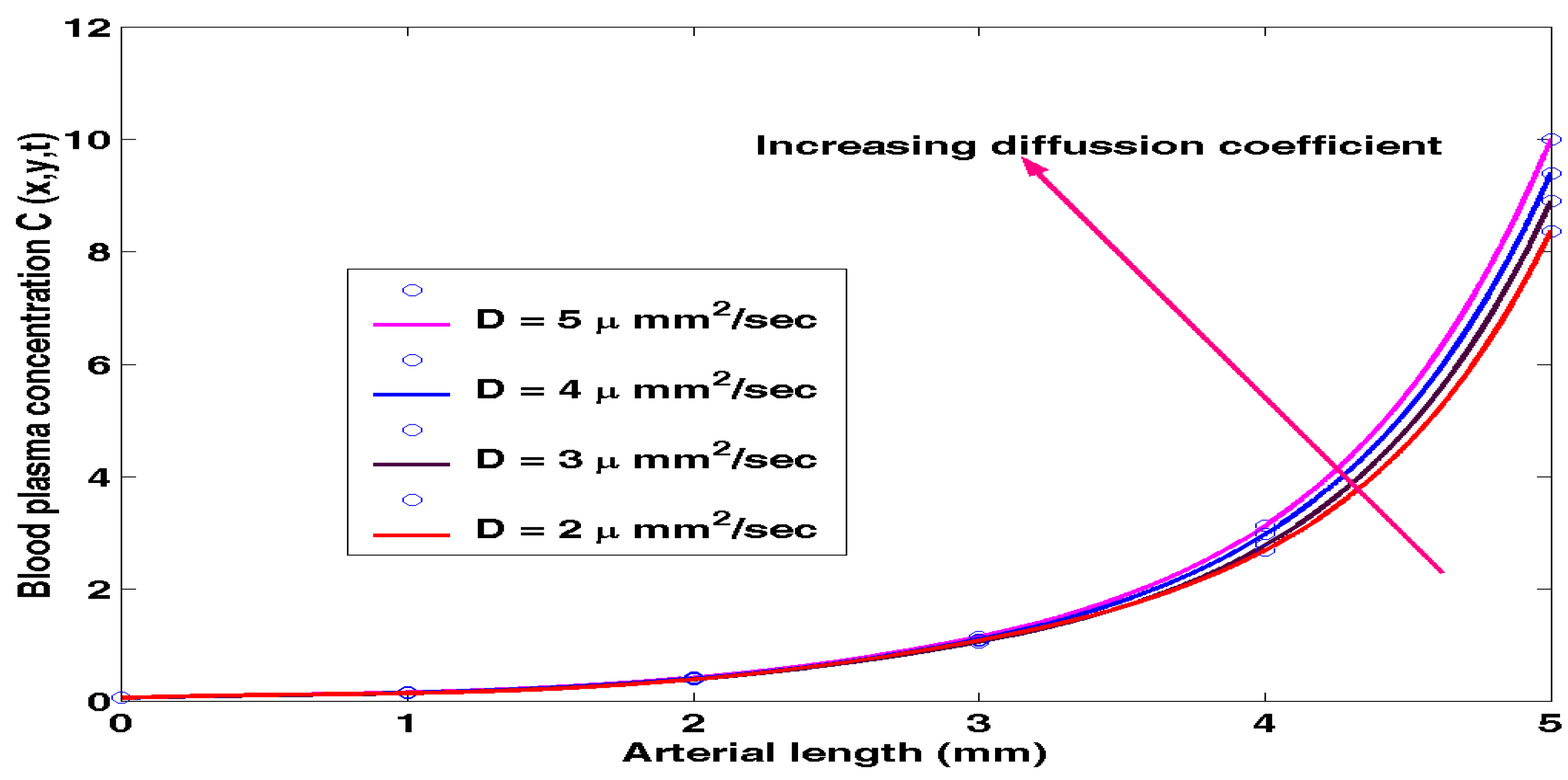
4.1. Effects of Diffusion Coefficient on blood plasma Concentration level

Equation (3.29) was solved using MATLAB and results obtained for the effects of Diffusion Coefficient (D) on blood plasma concentration levels were recorded as shown in Table 4.1 below.

The above results were presented in Figure 4.1 provided below.

The effect of diffusivity coefficient can be observed from Figure 4.1. Increase in diffusion coefficient leads to increases in the blood plasma concentration levels.

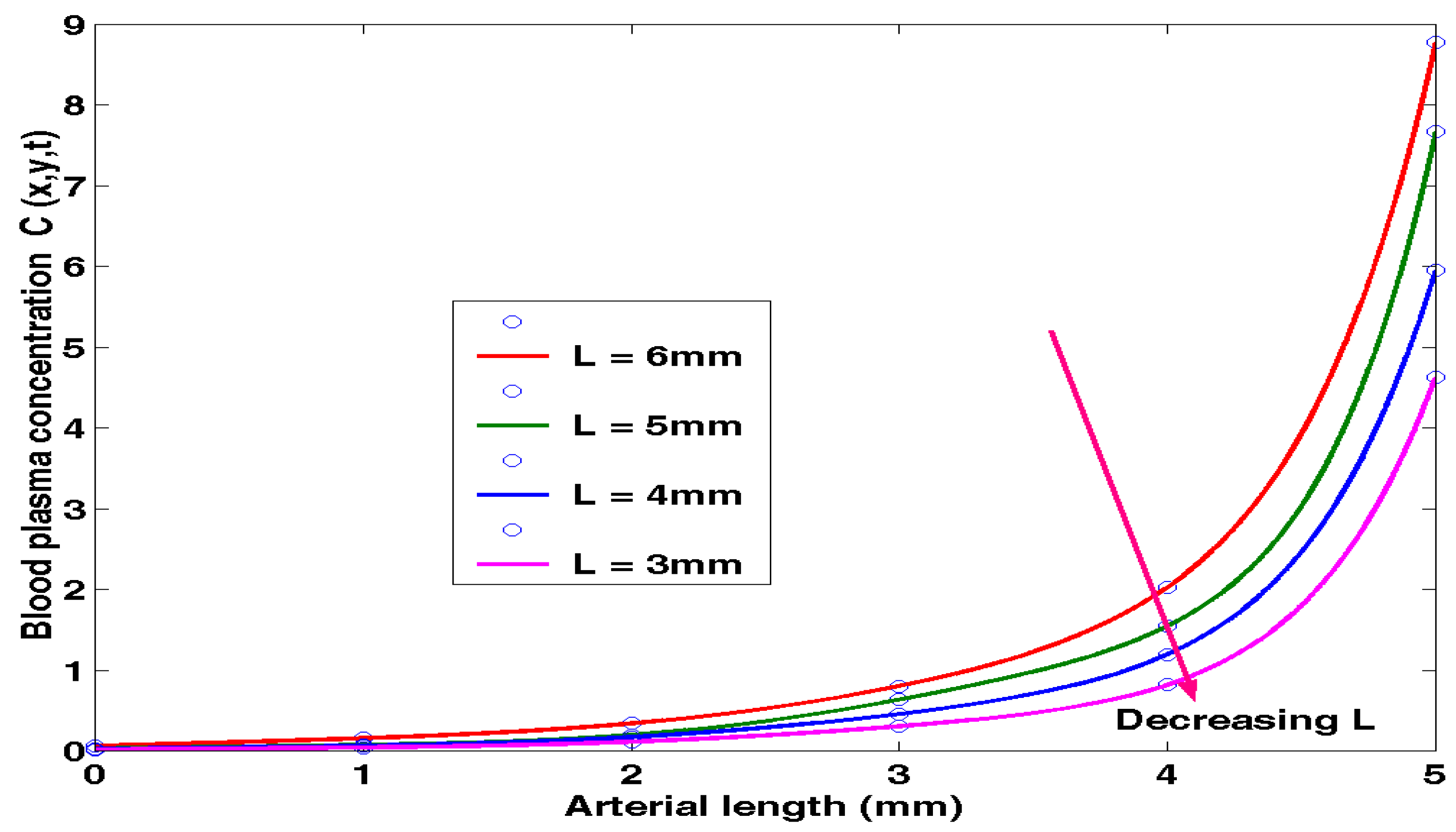
4.2. Effects of Characteristic Length on blood plasma Concentration level

Again, equation (3.29) was numerically solved using MATLAB and the results obtained were provided in Table 4.2 to show the effects of characteristic length L on blood plasma Concentration level.

The above results were presented in Figure 4.2 below

Figure 4.3 indicates that an increase in the arterial length results to a decrease in the blood plasma concentration levels.

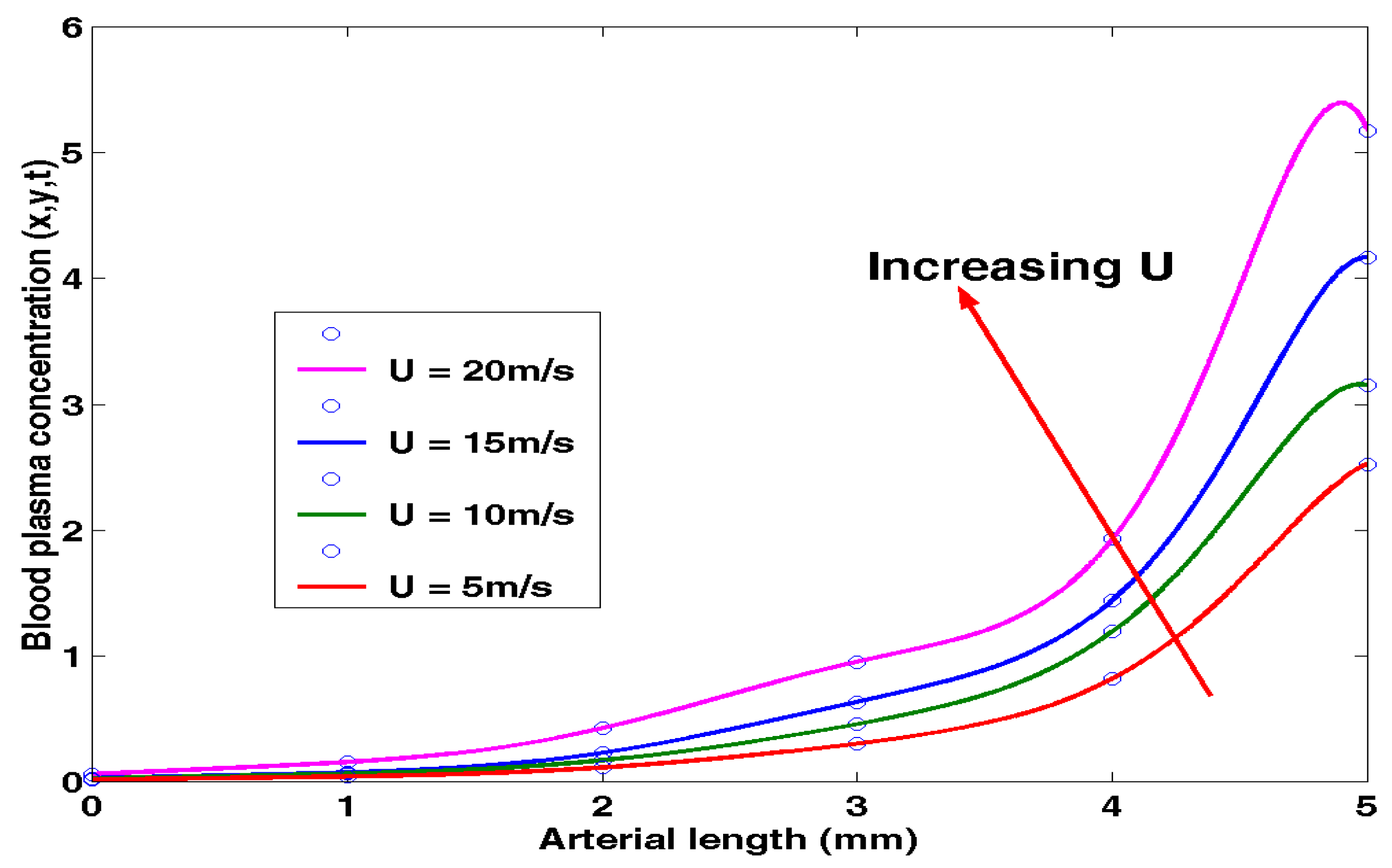
4.3. Effects of Axial Velocity on Blood Plasma Concentration Level

Equation (3.29) was solved using MATLAB and the results of the effects of Axial Velocity (U) on blood plasma Concentration levels were recorded as shown in Table 4.3 below.

The above results were presented in Figure 4.3 below.

It is observed from Figure 4.3 that an increase in characteristic length tends to increase the blood plasma concentration levels. Also, an increase in the arterial length leads to increase in the blood concentration levels. The blood plasma speed is proportional to the shear rate, and the shear rate is large, and the uniform axial speeds up. Increasing the speed will increase the temperature of the blood, resulting in a decrease in the viscosity and shear stress of the blood plasma.

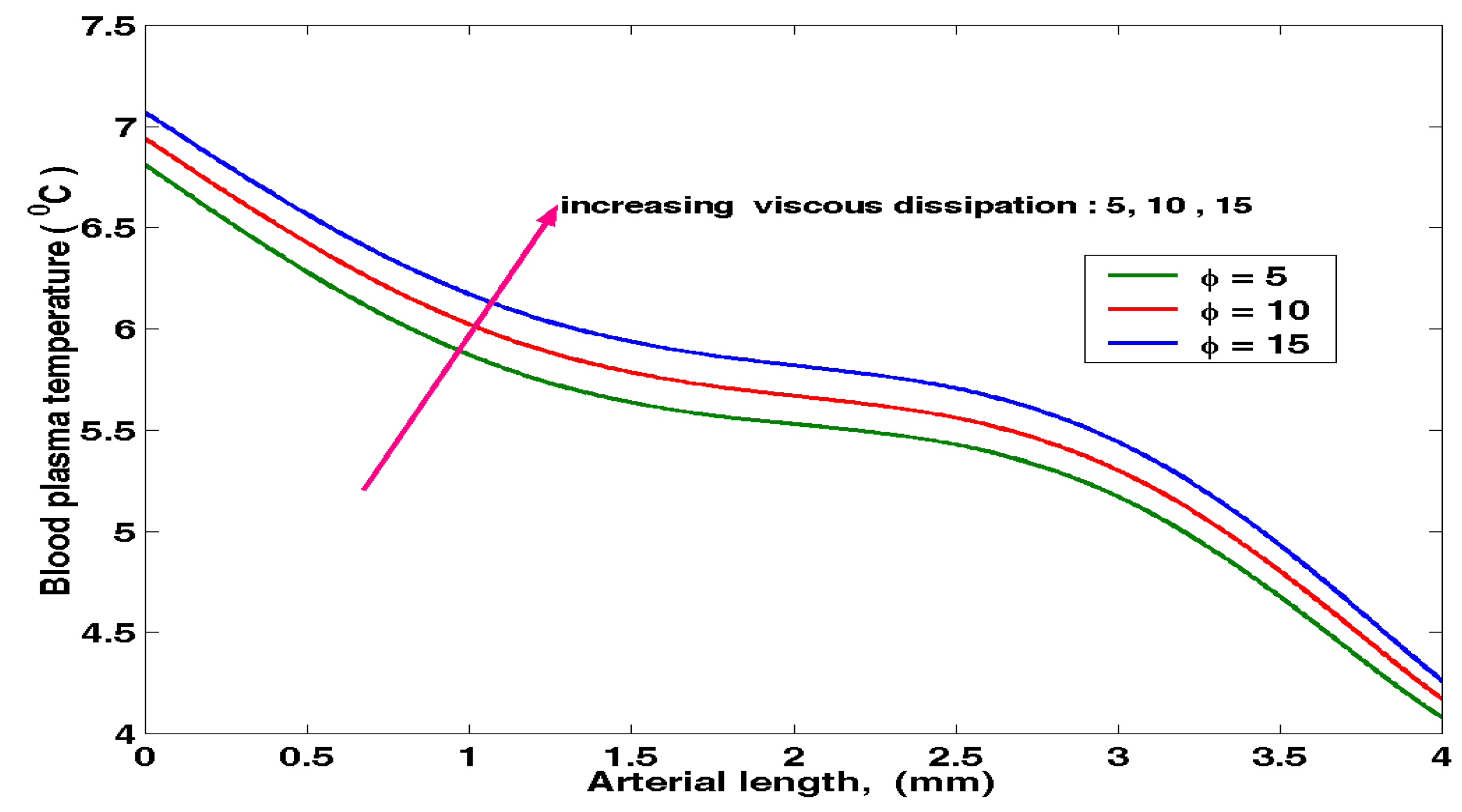
4.4. Effects of Viscous dissipation on Blood Temperature Distribution

The values of $v=u=1.0 m/s$ were held constant and $\phi$ kept varying in equation (3.16). Solving equation (3.16) for varying values of $\phi$ , the results obtained were recorded in Table 4.4 below.

The results in Table 4.4 were represented graphically as shown in Figure 4.4 below.

Figure 4.4 indicates that for several values of viscous dissipation $\left(\phi \right)$, numerical results obtained show that the blood plasma surface heat transfer tends to decrease by increasing in $\phi$.

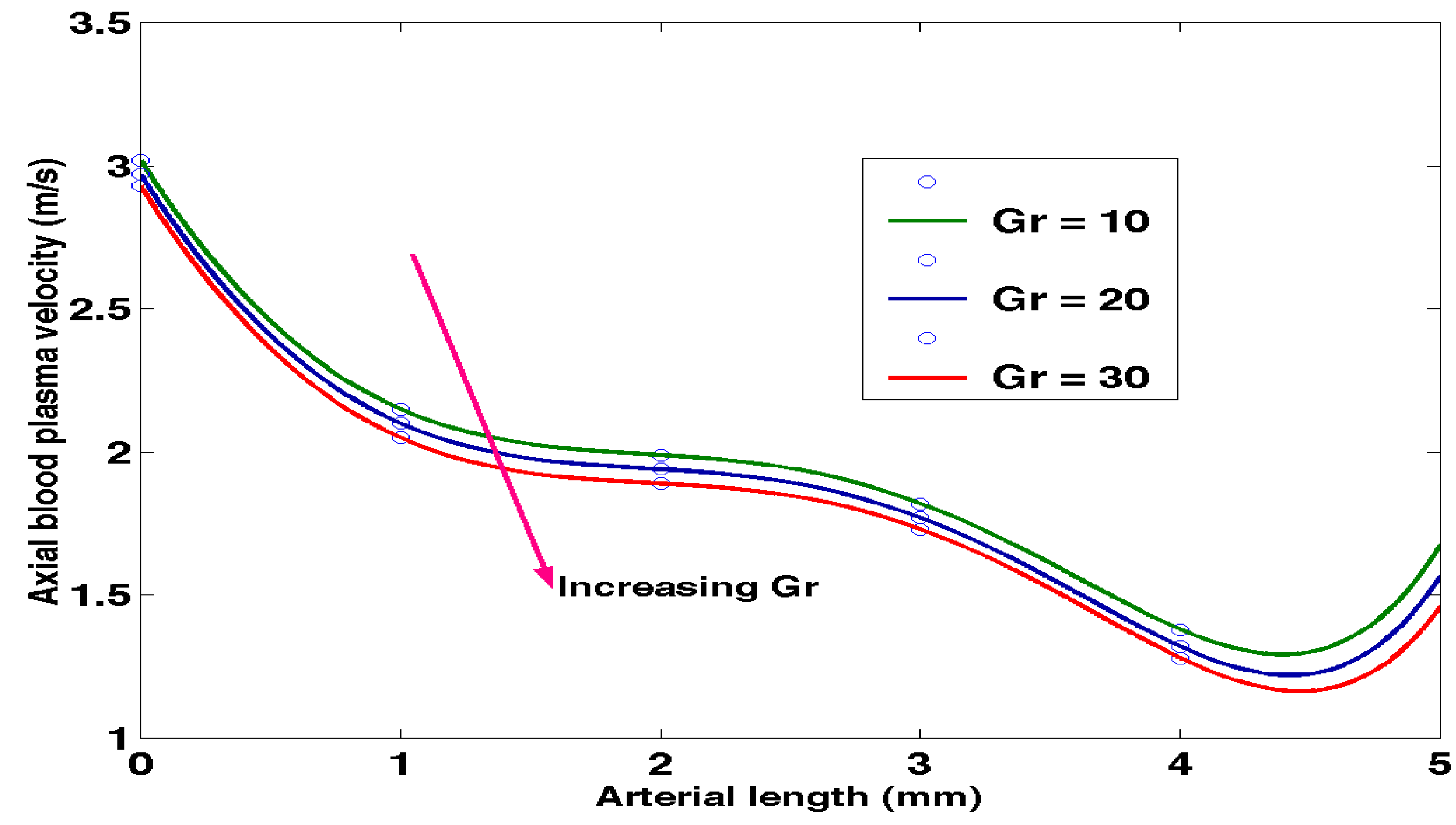
4.5. Effects of Grashof number on blood plasma velocity

Considering equation (3.11), the values of M = 5, v = u = 1.0 m/s, were held constant while Gr were varied. Solving equation (3.11) for varying values of Gr, the solutions obtained were recorded in Table 4.5 below.

The results in Table 4.5 were represented graphically as shown in Figure 4.5 below;

Figure 4.5 shows that for different values of Grashof number, numerical results for axial velocity of blood plasma tends to decrease with increase in Gr.

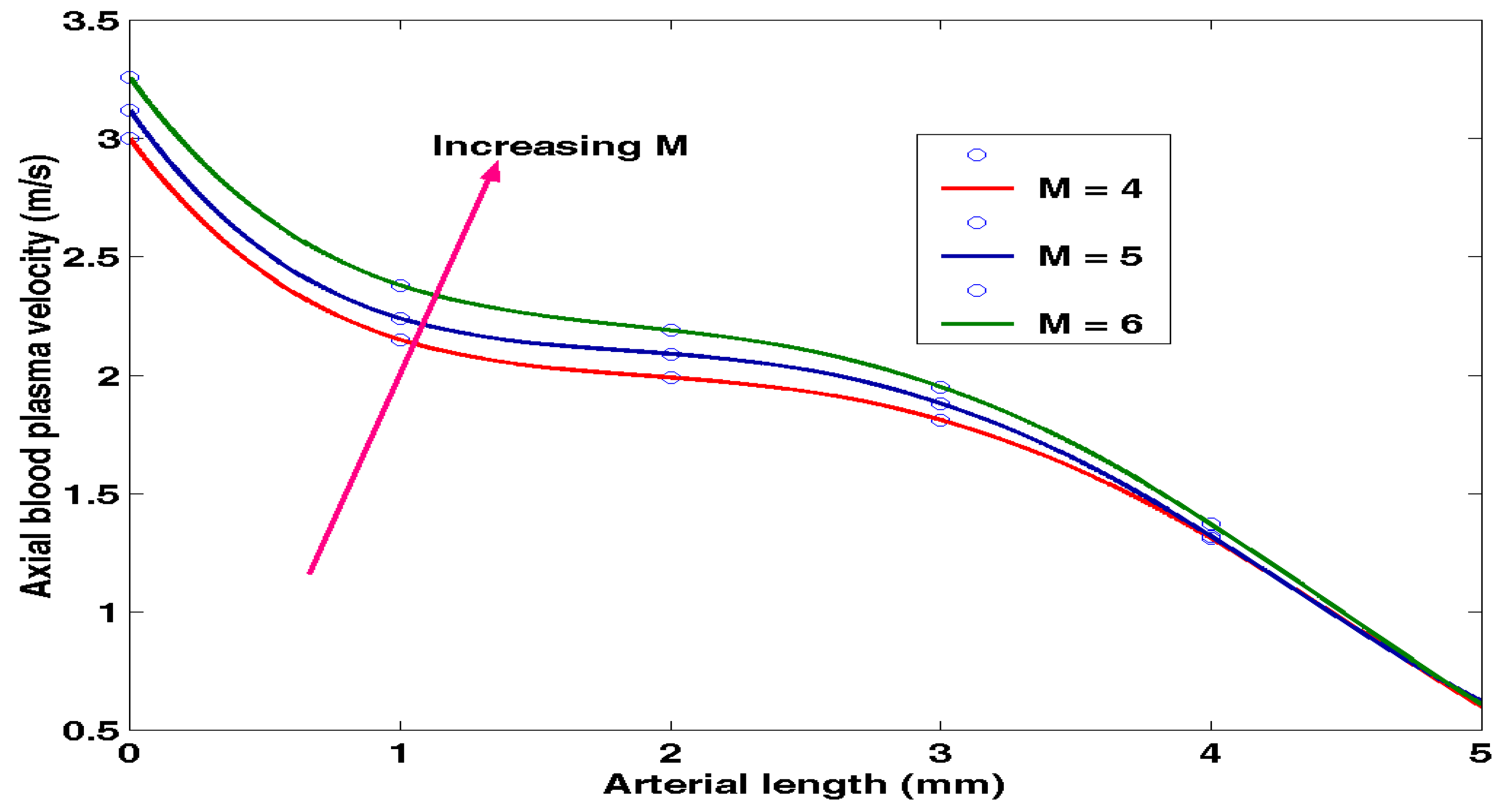
4.6. Effects of Magnetic Field on Blood Plasma Velocity

Equation (3.11) was solved by holding constant the values of Gr = 10, v = u = 1.0 m/s, while varying M. The results obtained were recorded in Table 4.6 below.

The results in Table 4.6 were presented graphically as shown in Figure 4.6 below.

Figure 4.6 indicates that for several values of Magnetic field, the blood plasma velocity tends to increase by increasing in M.

5.0. Conclusion

A numerical study was performed to analyze the effects of Diffusion Coefficient, Characteristic Length, and Axial Velocity on blood plasma Concentration levels; effects of Viscous dissipation on Blood Plasma Temperature Distribution; and Effects of Grashof number on blood plasma velocity.

The following outcomes were obtained from the study.

• Increase in the Diffusion Coefficient leads to an increase in the blood plasma Concentration levels.
• Decrease in Arterial Length tends to increase in blood plasma Concentration levels.
• Axial Velocity leads to a decrease in blood plasma Concentration levels.
• An increase in Viscous dissipation leads to a decrease in Blood Temperature Distribution.
• An increase in Grashof number causes an increase in blood plasma velocity.
• An increase in magnetic field leads to increase of velocity of blood plasma.

6.0. Recommendations

From the results of this study, a mathematical model in three-dimensions is recommended to more realistically present the physical dynamics of flow of blood plasma. This higher dimension will also provide additional confined parameters on the magnetic field and heat transfer affecting flow of blood plasma.