Numerical Modeling of the Dynamic Elastic Modulus of Concrete

1. Introduction

Dynamic modulus of elasticity (E_d) is related to a very small instantaneous strain, geometrically similar to the initial tangent modulus [1]. Mehta and Monteiro [1] reported E_d higher than the initial tangent modulus in approximately 20%, 30% and 40%, for concretes of high, medium and low resistance. Nevertheless, the relation between the static and dynamic moduli is not precise, since no physics law correlates their values to the necessary precision [1,2,3]. The use of E_d, which can be accurately determined by acoustic tests [4,5], is more appropriate for analyses of structures subjected to impact loading [1], e.g., vibration serviceability limit state.

E_d is strongly influenced by mixture parameters, such as water-cement ratio of mortar (porosity), maturity, elastic properties of coarse aggregate, volumetric fraction of interfacial transition zone (ITZ) and aggregate-cement proportion [1,3,6,7,8].

Classical models predict with success the elastic modulus of a perfect biphasic composite. Since 19^th century, homogenization models, as Voigt (or parallel) [1,9,10,11,12] and Reuss [1,10,11,12,13] (or series) have been used for determining the elastic static properties of concretes. According to Hill [14], Voigt and Reuss are upper and lower bounds for any biphasic material. Hashin-Shtrikman (H-S) [11,15] developed the most stringent bounds of behavior for a composite material [11,15,16,17]. Nilsen and Monteiro [16,17] showed limitations in the application of H-S bounds, since concrete is not a perfectly biphasic material. Consequently, a third composite component (i.e., Transition Zone, ITZ) must be considered in the model. In 2013, Nemat-Nasser and Srivastava [18] reported another limitation of H-S bounds: the approach cannot apply to dynamic situations perfectly. This is a severe limitation, especially for the estimation of dynamic elastic modulus through modal analysis.

Other classical homogenization models have predicted the elastic properties of biphasic materials. Counto [1,11] assumed a prismatic coarse aggregate in the center of the mortar prism, whereas Hansen [1,11] adopted a spherical coarse aggregate in the same region. Hirsch [1,11] proposed a semi empirical model that relates the modulus of elasticity of the concrete to the Young modulus' of the two phases (aggregate and matrix), their volume fractions, and an empirical constant, x. The “x value” is a combination factor obtained by Voigt and Reuss models and calibrated either experimentally, or via a numerical simulation. Topçu [11] obtained x = 0.3 experimentally. The present study aims to obtain x through numerical simulations.

Sophisticated models have been proposed towards predictions of effects, as size and shape of aggregate particles and influence of porosity and transition zone [19,20,21,22,23,24,25,26]. Hashin and Monteiro [27] described concrete as a three-phase material formed by a matrix with embedded spherical particles and surrounded by a concentric spherical shell that represents an ITZ. According to the authors, the Young’s modulus of ITZ is 50% of the elastic modulus of the cement mortar (i.e., E_ITZ = E_m/2). Duplan et al. [28] designed a very realistic model constituted by aggregates surrounded by a layer of ITZ and a layer of cement paste, while air bubbles are considered mono-sized inclusions with no elastic behavior, which result in 5% error. Zheng, Zhou and Jin [22,23] proposed a model in which concrete is represented as a three-phase composite material composed of mortar, spherical or elliptical aggregate and an inhomogeneous ITZ, based on semi-empirical gradient model, dependent on water/cement ratio, degree of hydration, and porosity at the ITZ. Pichler et al. [26] predict the dynamic modulus of cements pastes with w/c = 0.35 and 0.60, considering a material constituted by clinker, pores (with spherical shapes) and hydration products (with spherical and/or non-spherical shapes).

Although such models are complex for practical applications, those recent studies have opened up new possibilities for the micromechanical modeling of concrete through numerical simulations, especially simulations that allow the study of dynamic elastic modulus (E_d). The current research focuses on simulations of the concrete as a 2D theoretical material (biphasic or triphasic) with controlled elastic properties of each phase (mortar and aggregate). The purpose is to evaluate the behavior of dynamic effective elastic modulus (E_d) regarding porosity, individual elastic properties of coarse aggregate and/or mortar (i.e., E_a , ν_a, E_m and ν_m, respectively), volumetric fraction, and the presence of ITZ with known properties (i.e. ITZ thickness and elastic modulus E_ITZ). Further, this approach with controlled properties was compared with classical models, as Voigt, Reuss, Hirsch, H-S, Hansen and Counto, aiming show the most accuracy classical model could predict the E_d. An experimental validation showed the coherence and limitations of our numerical simulations. Therefore, this paper advances in the methodology to predict the dynamic elastic modulus of concrete and contributes to comprehension of its response under dynamical excitations.

2. Numerical simulations

Numerical simulations were performed with the general-purpose finite element software Abaqus release 6.14. A theoretical material was modeled by a 150 mm x 150 mm x 50 mm square with fined mesh 1 mm maximum dimension and a quadrilateral and four-node bilinear element with reduced integration (CPS4R, Figure 1.a). Plane stress was considered in this 2D shell structure. This model was chosen due the low computational cost. The boundary conditions weren’t considered in the model, representing a free model subject to vibrations..

In this study, modal analysis in Abaqus with the Lanczos solution method was utilized to investigate the dynamic behavior of a free shell structure. The Lanczos solution is an iterative method that enables the calculation of the eigenvectors and eigenvalues of a large sparse symmetric matrix, making it ideal for modal analysis. The shell structure was modeled using a linear elastic material with a Poisson ratio and elastic modulus, and a density of 2400 kg/m³ was considered. The shell was allowed to vibrate freely to demonstrate all modes of vibration. Abaqus was employed to generate the mass and rigidity matrices and to determine the eigenvalues and eigenvectors for the shell structure.

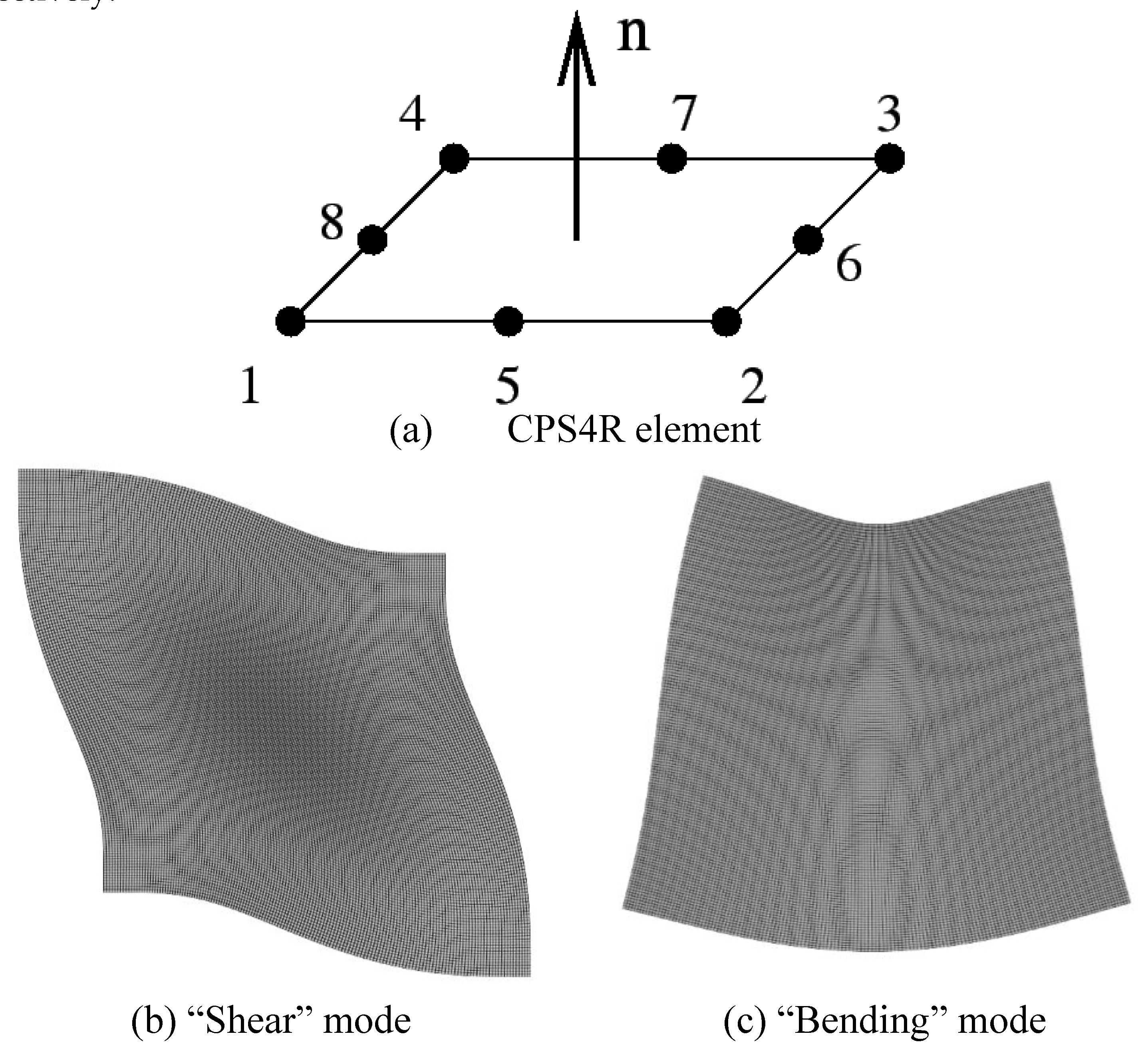
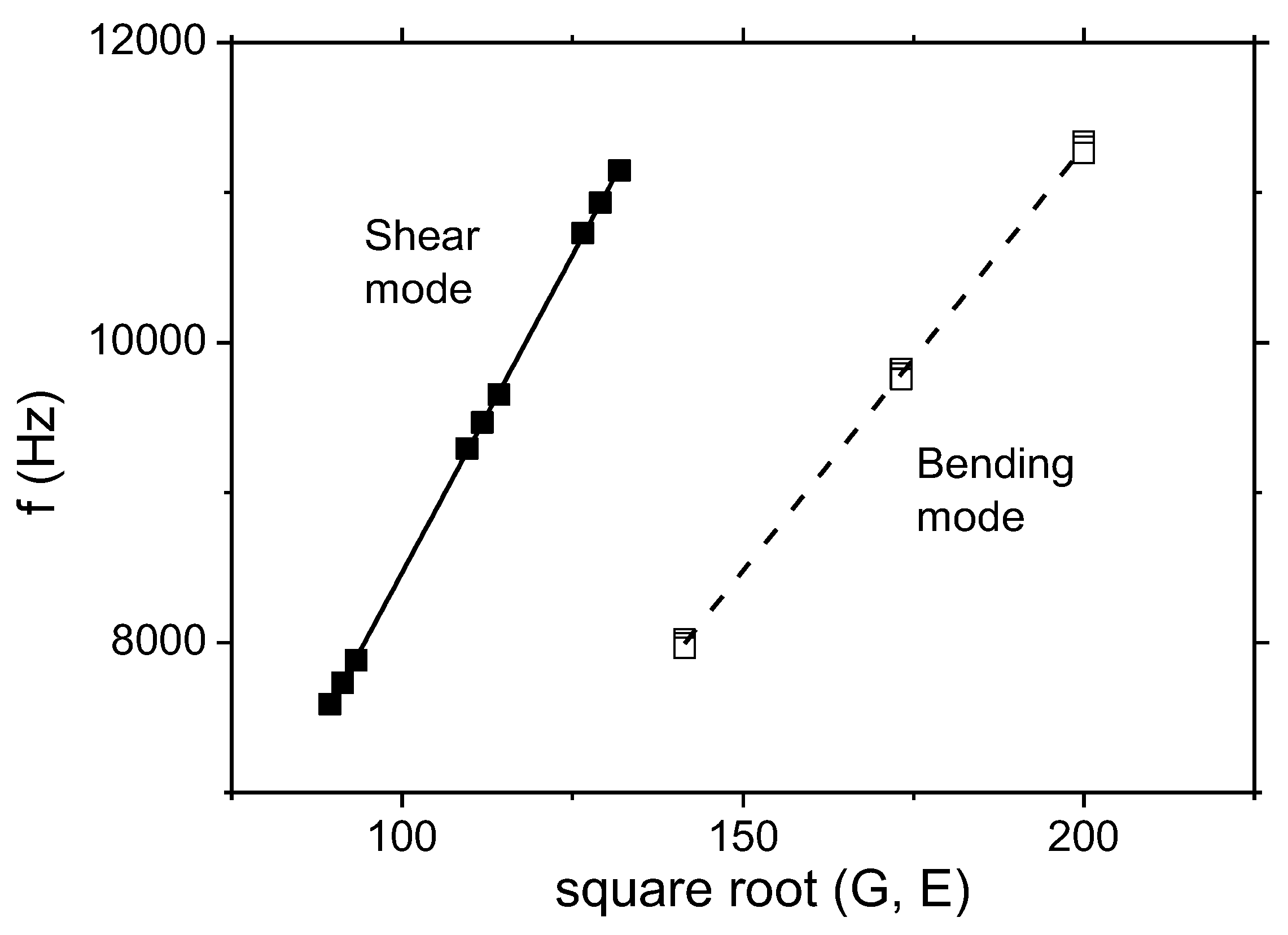
2.1. Frequency equations of an Isotropic and homogeneous material

The relation between 1^st natural frequency (bending or shear mode of vibration) and Effective elastic properties are established. The theoretical modal analysis determines the shear and flexural 1^st natural frequency for a free vibration of a homogeneous isotropic square structure (see Figure 1). “Shear” frequency can be related to Effective Dynamic Shear Modulus (G_d), whereas “flexural” frequency is associated with Effective Dynamic Elastic Modulus (E_d ) [4,5,29] through “Frequency equations”.

Table 1 shows an analysis performed with a homogeneous isotropic material of ρ = 2400 kg/m³ density and variations in elastic and shear modulus. Simulations determined the frequency equation and confirmed the expected relationships of “shear” frequency and shear modulus (Eq. 1), as well as “bending” frequency and elastic modulus (Eq. 2), see Figure 2. Constants C₁ and C₂ are dependent on the geometry of the specimens and were determined by a linear regression analysis, C₁ = 131.16 and C₂ = 87.56 (with R² → 1), respectively.

$$f_{shear}=C_1\sqrt{\frac{G_d}{\rho }}$$

(1)

$$f_{bend}=C_2\sqrt{\frac{E_d}{\rho }}$$

(2)

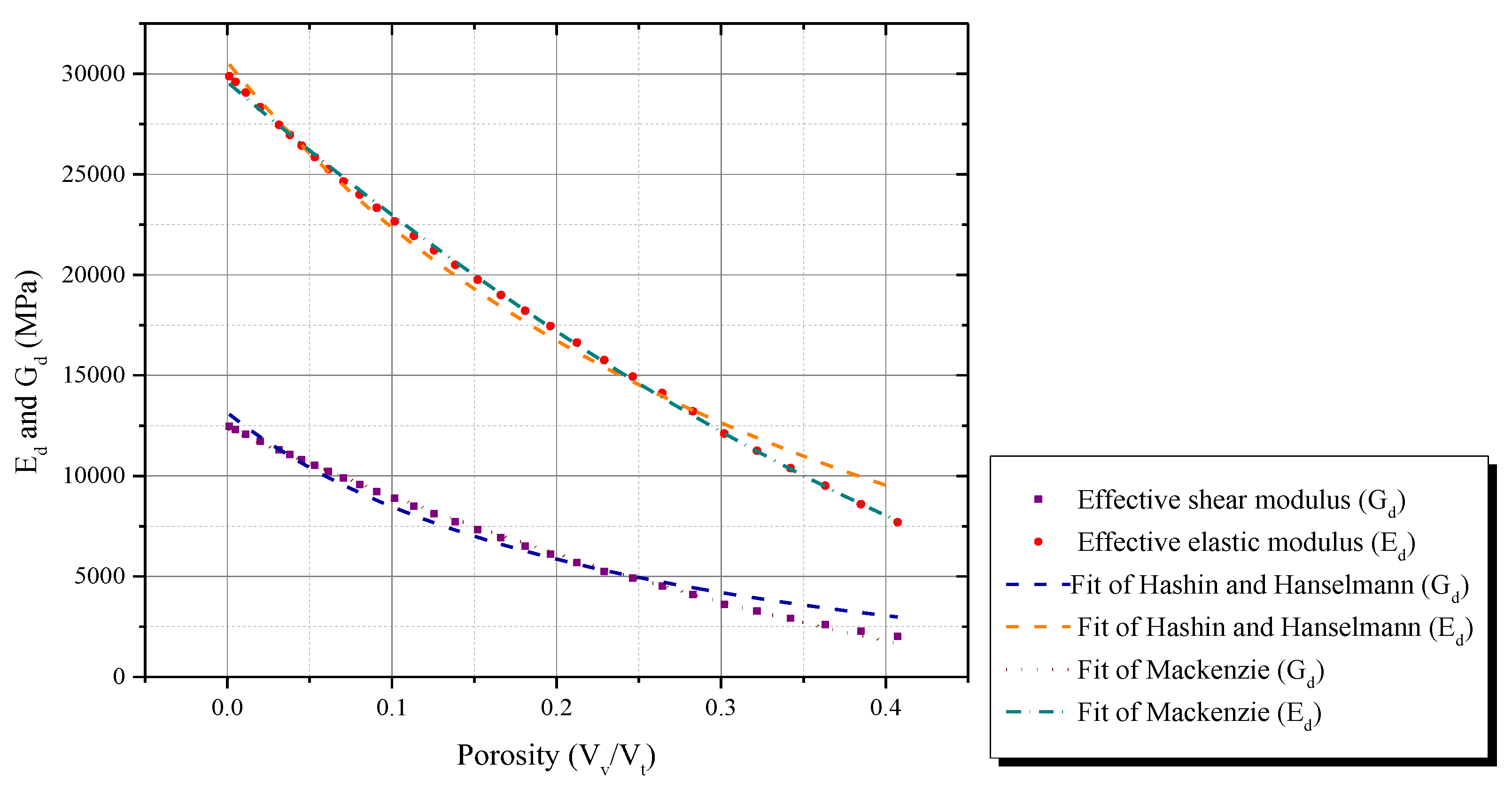
2.2. Effect of Porosity

Influence of porosity (P) was checked on effective elastic properties G_d and E_d. We suppose a theoretical material constituted by spherical voids of 3 mm diameter, distributed in a matrix (e.g. Figure 3). Voids were incrementally added to the matrix, i.e., 4 voids (2 by 2 – 0.13 % porosity) until 1296 voids (36 by 36 – 40.72 % porosity). For all cases, the cement paste had constant properties of ρ_p = 2100 kg/m³, Ε_p = 20000 MPa and ν_p = 0.2, whereas the voids had ρ_v = 1 kg/m³ and Ε_v = 0,1 MPa (i.e., ρ_v/ρ_p = 0.0004 and Ε_v/Ε_p = 0.000005). An approximately 0.13 % to 40.72% porosity increase decreased E_d (Figure 4), since porosity is inversely linked to the material rigidity [8]. Boccacini and Fan [30] reviewed several theoretical models to correlate E_d and porosity of ceramic materials. Hanselmann-Hashin [31,32] (Eq. 3) and Mackenzie [33] (Eq. 4) achieved the best fit with numerical results (see Figure 4 and Table 2). The fit with R² close to 0.97 showed coherence of simulations.

$$E=E_0\left(1+\frac{AP}{1-(A+1)P}\right)$$

(3)

$$E(P)=E_0[1-K\times P+(K-1)\times P^2]$$

(4)

where E is the effective elastic modulus, E₀ is the intact elastic modulus under porosity equal to zero (value recovered from E₀ ≅ 30000 MPa), P is porosity and A and K are empirical adjustments;

2.3. Biphasic material

A perfectly biphasic material with coarse aggregate (of elastic modulus E_a) perfectly encrusted in a mortar phase (with elastic modulus E_m) without transition zone was simulated and the influence of individual elastic properties of each phase (E_a/E_m), volumetric fraction of the aggregates, and Poisson ratio of each phase on effective E_d was checked. The accuracy of homogenization composite models was measured under the above-mentioned conditions.

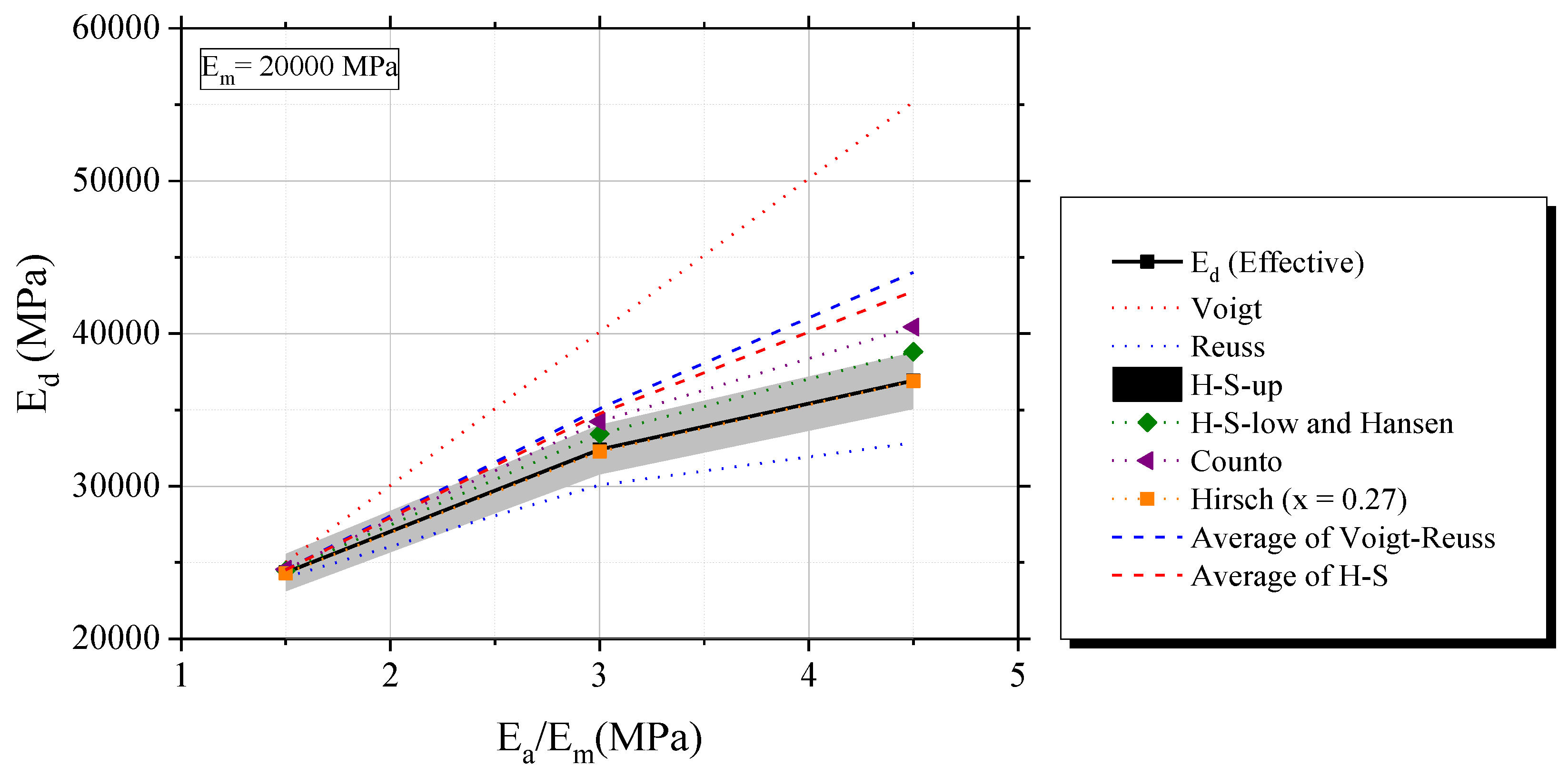
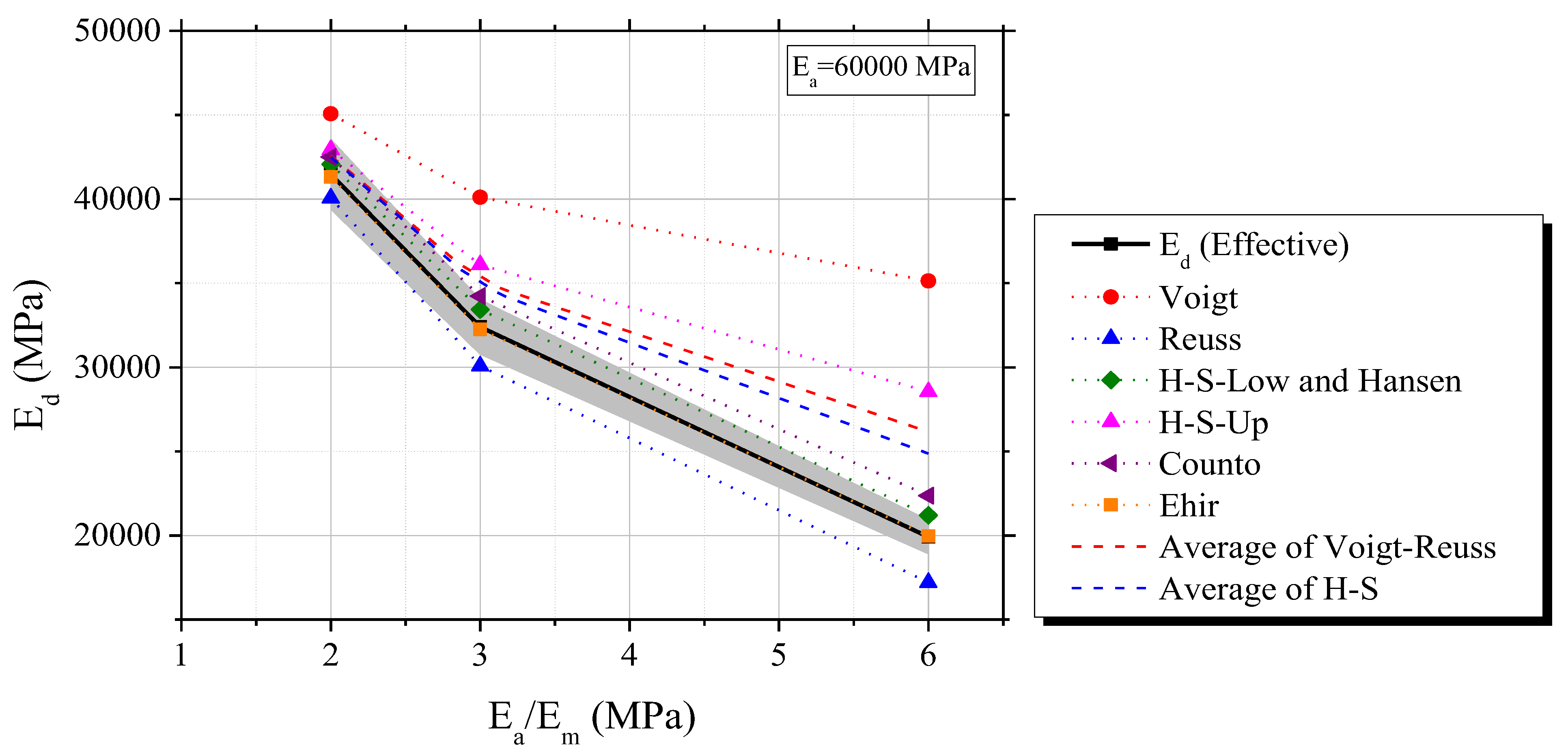
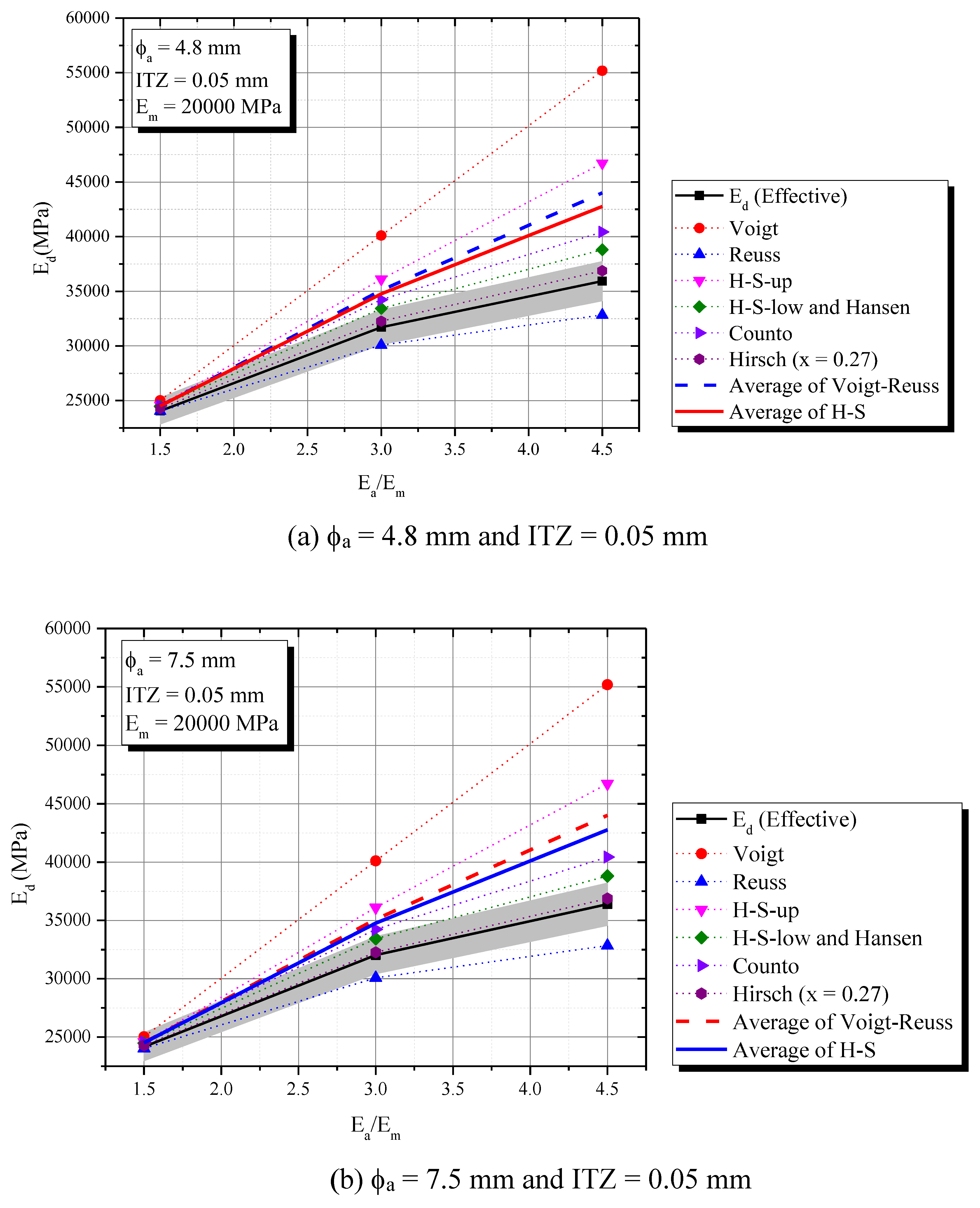
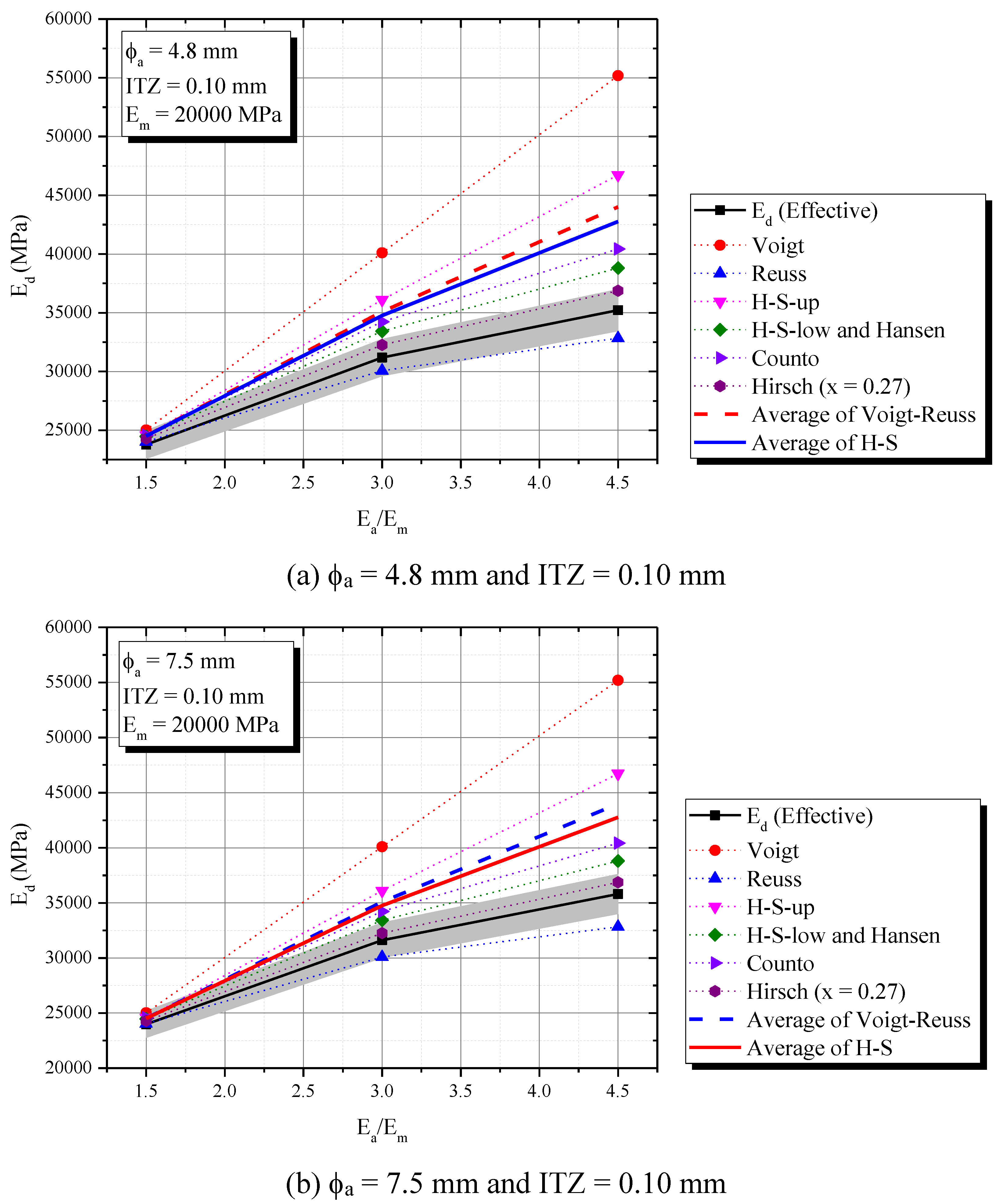
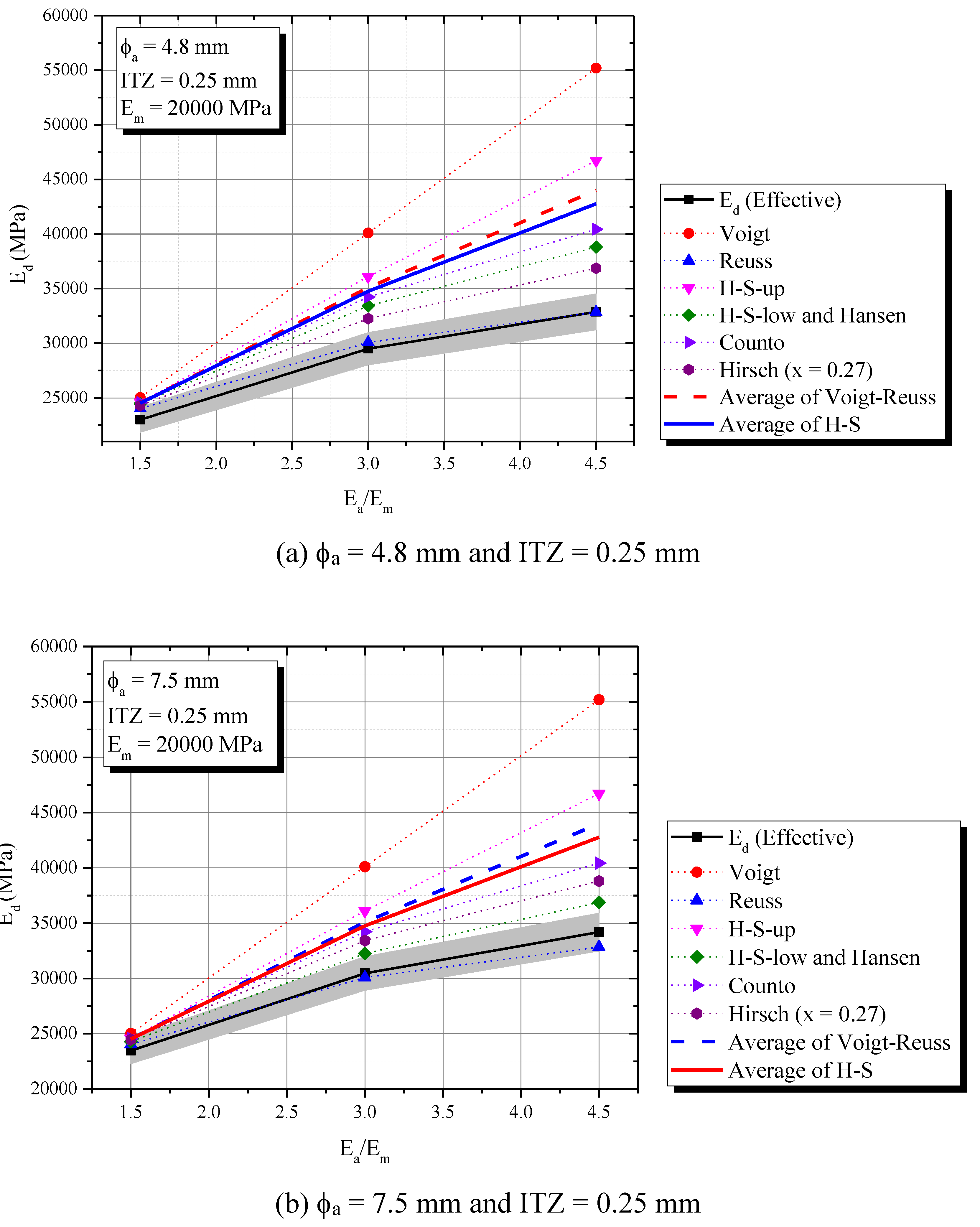
2.3.1. Influence of individual elastic properties of phases (E_a/E_m)

We supposed an effective material composed of 625 perfectly spherical aggregates of 4.8 mm diameter, arranged in a mortar, with no transition zone (ITZ) and/or porosity, as shown in Figure 5. An analysis was performed with mortar properties of ρ_m = 2100 kg/m³, Ε_m = 10000 MPa, 20000 MPa or 30000 MPa and ν_m = 0.2, and aggregates properties of ρ_a = 2700 kg/m³, Ε_a = 30000 MPa, 60000 MPa or 90000 MPa, and ν_a = 0.2.

Figure 6 shows an increase in E_a increases E_d in the same volumetric proportion and constant E_m, explained by “Mixture Rule” [9,13]. The gray area in Figure 6 represents ± 5 % error, as of the effective model. This error is used in the verification of the accuracy of classical models and is similar to the admissible error adopted by Duplan et al. [28]. When the elastic modulus of the mortar (E_m = 20000 MPa) and aggregates (E_a = 30000 MPa) were relatively close (i.e., E_a/E_m = 1.5), the prediction of E_d for all classical models was accurate; however, when E_a/E_m > 2, almost all homogenization models overestimated effective E_d (i.e., Voigt, H-S, Counto, mean of H-S and Voigt-Reuss). An exception of this was Reuss model (series), which underestimated E_d for all cases of E_a/E_m. The Hirsch model calibrated to x = 0.27 accurately represented the phenomenon. The x value is very similar to that obtained experimentally by Topçu for static elastic modulus [11] (i.e., x = 0.3). H-S-Low (and Hansen) also showed a good approximation level, with an almost 5% error. Although, H-S-Low accurately represented the phenomenon, H-S bounds contained no biphasic material. According to Nilsen and Monteiro [16], the H-S limits diverge because concrete is not considered a biphasic material, and a third phase (i.e., transition zone) should be included. This is partially true, since a portion of error due to biphasic H-S does not consider the ITZ phase, nevertheless Figure 6 shows only cases of a perfectly biphasic material with no ITZ. Actually, this divergence of H-S and the biphasic material occur because Hashin-Shtrikman bounds were formulated from a static consideration [18], which is not valid here. Therefore, H-S bounds are not perfectly applied to dynamic situations and should be used with caution for modal analysis. Voigt and Reuss bounds always contain a biphasic material, and a simple average of those limits was inferior to 10 %, when E_a/E_m < 3. The same tendency was observed for the H-S average. On the other hand, when E_a extrapolates E_a/E_m > 3, Voigt-Reuss and H-S significantly diverge, which causes a very high error.

In the same volumetric proportions and E_a, a decrease of E_m (and increase in ration E_a/E_m) decreases E_d, according to Figure 7. About classical biphasic models presented same anteriorly postulated tendencies.

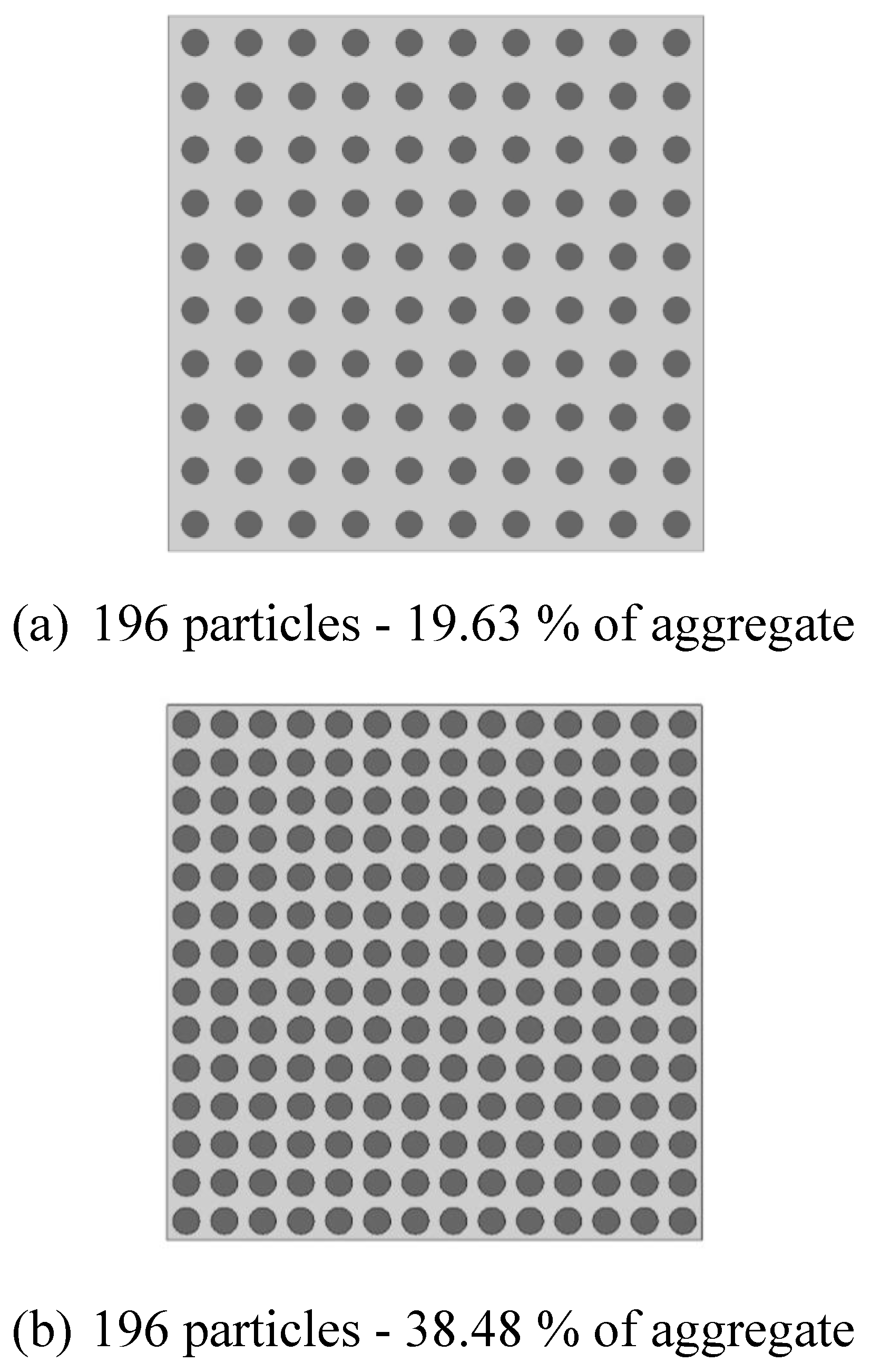
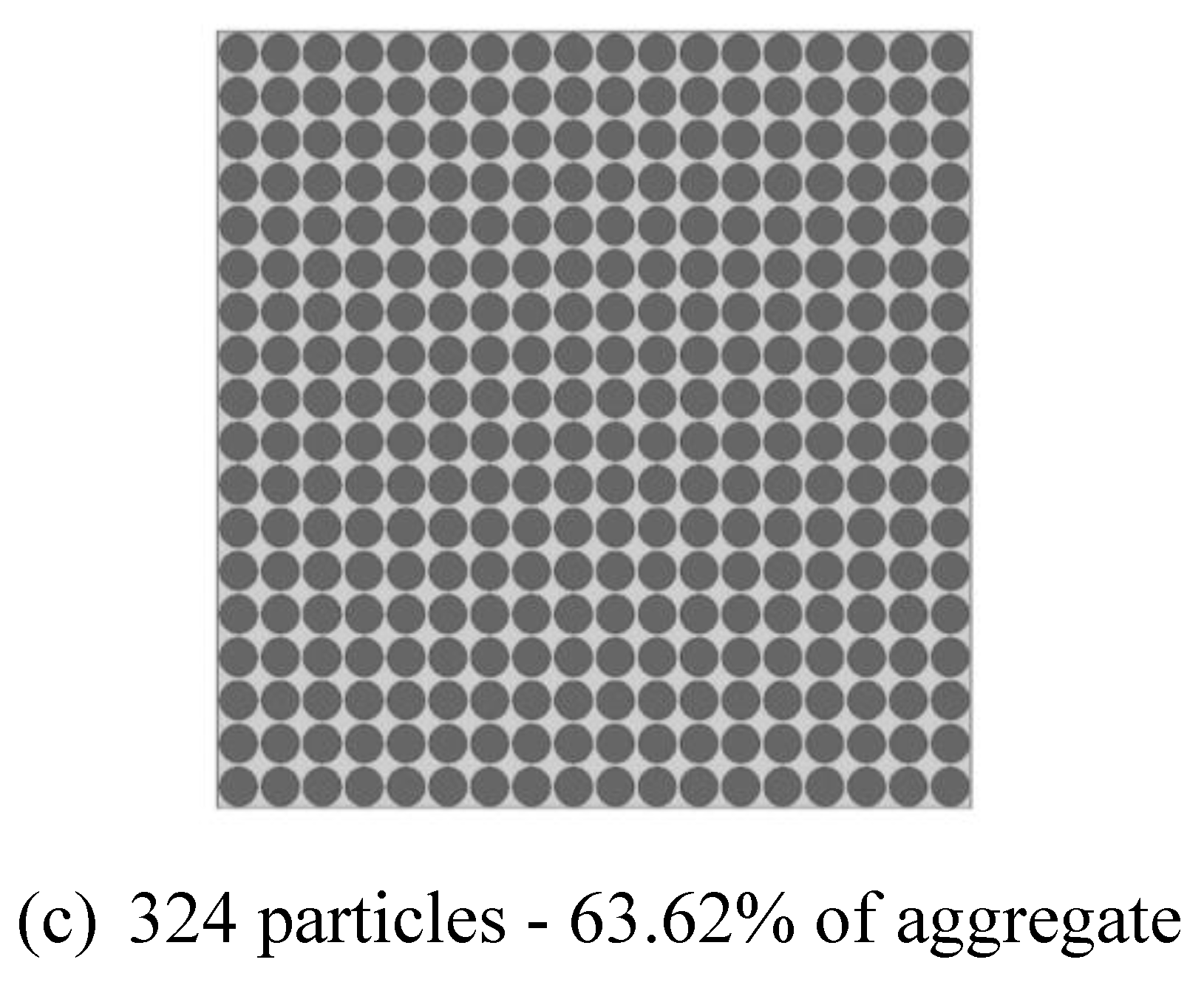
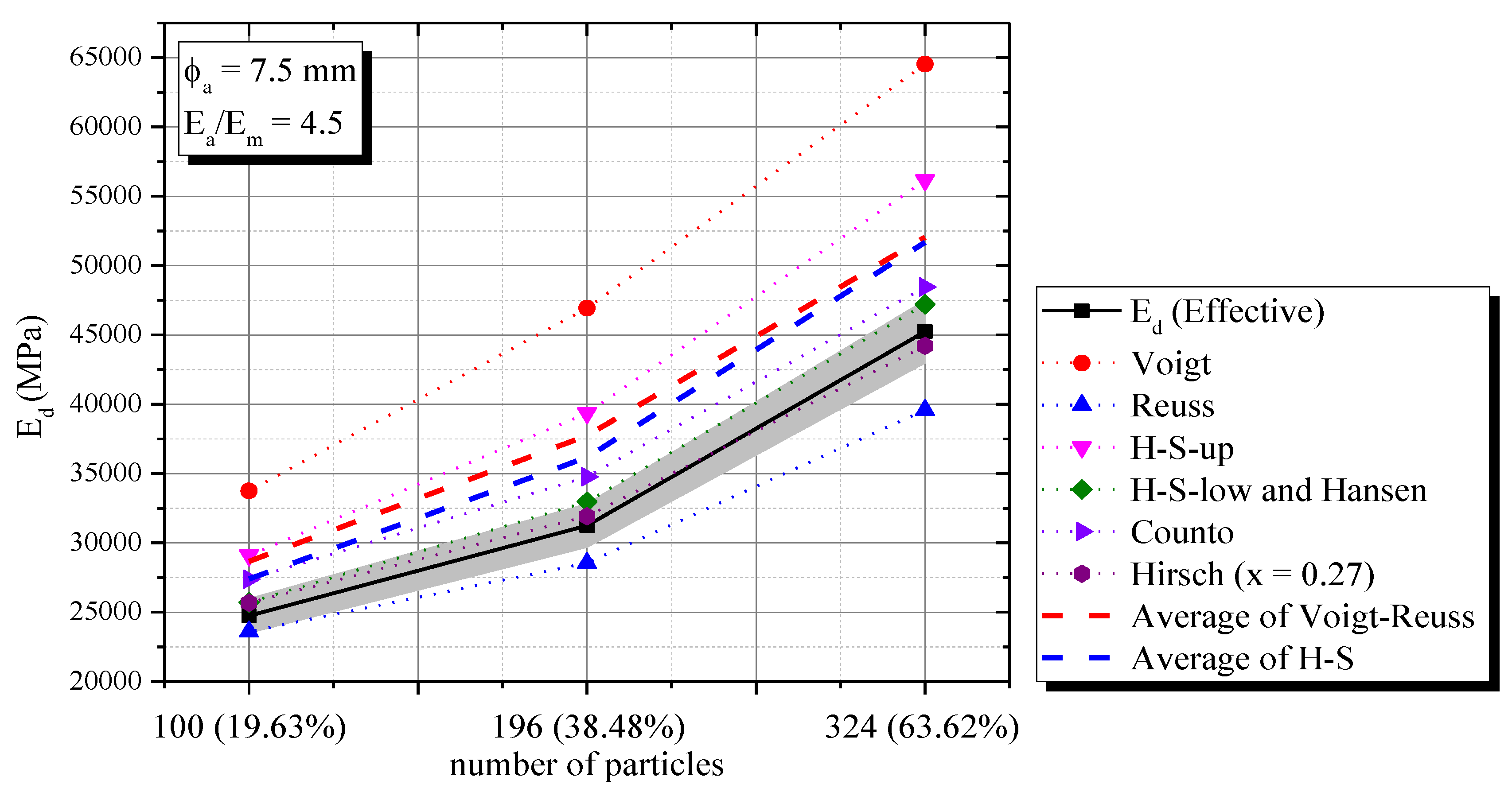
2.3.2. Effect of Volumetric fraction

Variations in the volumetric portion can also influence E_d, with fixed E_a and E_m [1,3,34]. Theoretical materials whose volumetric fraction increases progressively (i.e., 196 to 324 particles, according to Figure 8) were simulated. The aggregate diameter, elastic modulus and density of each phase were constant (φ_a = 7.5 mm, E_a = 90000 MPa, E_m = 20000 MPa, ρ_a = 2700 kg/m³ and ρ_m = 2100 kg/m³).

Figure 9 shows the correlation between volumetric fraction and E_d. In this case, an H-S and/or Voigt-Reuss average did not describe the phenomenon successfully, since E_a/E_m > 3. Hirsch x = 0,27 and H-S-Low accurately captured the phenomenon with 5% error. All tendencies already mentioned are observed.

2.4. Triphasic composite material

The models were constituted by coarse aggregate, mortar and a transition zone with known properties, i.e., 0.05 mm [35,36] - 0.25 mm thickness and E_m/2 (E_ITZ = 10 GPa) elastic modulus [1,27,35,36]. Two diameters of aggregates, namely φ_a = 4.8 mm (256 particles) and φ_a = 7.5 mm (625 particles), were used at 50.27% constant volumetric fraction (c_a). For simplicity and reductions in the computational costs, the theoretical material contains no voids.

Figure 14 (ΙΤZ of 0.05 mm), Figure 15 (ΙΤZ of 0.10 mm) and Figure 16 (ΙΤZ of 0.25 mm) show an increase in E_a/E_m increased the composite elastic modulus (E_d), fixed mortar-aggregate proportions and E_m = 20000 MPa. This tendency is very similar to that observed in simulations of a theoretical biphasic material.

According to Figure 14 and Figure 15, Hirsch model with x = 0.27 best predicted E_d for ITZ of 0.05 mm and 0.10 mm, with 5% error. However, it failed to capture the phenomenon when ITZ increased to 0.25 mm and the behavior of the triphasic model was similar to inferior biphasic model, i.e., Reuss (see Figure 16).

Hashin-Shtrikman confirmed again its limitations, i.e., influence of ITZ and application of H-S under dynamic situations. Although H-S bounds showed limitations, H-S-Low revealed good accuracy when ITZ was 0.05 mm (Figure 14) and E_a/E_m < 3. A simple average of Voigt-Reuss or H-S showed errors higher than 5 %.

Classic biphasic models can consider ITZ, if applied twice, for the obtaining of a triphasic material. The methodology consists in the obtaining of a preliminary composite constituted by mortar and ITZ and associated with a coarse aggregate for the generation of a triphasic composite. Figure 17 shows the numerical data for φ_a = 4.5 mm, E_a/E_m = 4.5 or 3, E_m = 20000 MPa and variable ITZ. Although ITZ is incorporated, the same tendencies above mentioned are observed.

3. Experimental validation

3.1. Materials and mixes

Concrete and mortar samples were produced for the validation of the numerical study. Portland cement type III of 3.10 g/cm³ density, specified according to the classification of ASTM C150 [37] and ABNT NBR 5733:1991[38], was used in the samples. Natural sand of 2.19 fineness modulus [39] and 2.65 g/cm³ density and crushed diabase of 3.30 g/cm³ density and 12.5 mm nominal maximum sizes were used as aggregates. Their grading curves are shown in Figure 18.

The proportions (in weight) of mortar and concrete mixtures are shown in Table 5.a and Table 5.b. Water cement ratios, amounts of sand, coarse aggregates and superplasticizers were varied among the mixtures. The production of mortars and/or concrete samples consisted in (i) mix the cement and aggregates with no water addition, then (ii) water was a then added and the mixing procedure was performed until the material had shown a homogeneous appearance. After hardening, the molds were removed and immediately stored in a moist chamber for curing until the age of testing.

3.2. Specimens

The following samples were produced:

(i)

Mortars (1-M, 2-M and 3-M) - five prismatic specimens of 40 mm x 40 mm x 160 mm).

(ii)

Concretes (1-C, 2-C and 3-C) - five prismatic specimens of 150 mm x 150 mm x 500 mm.

(iii)

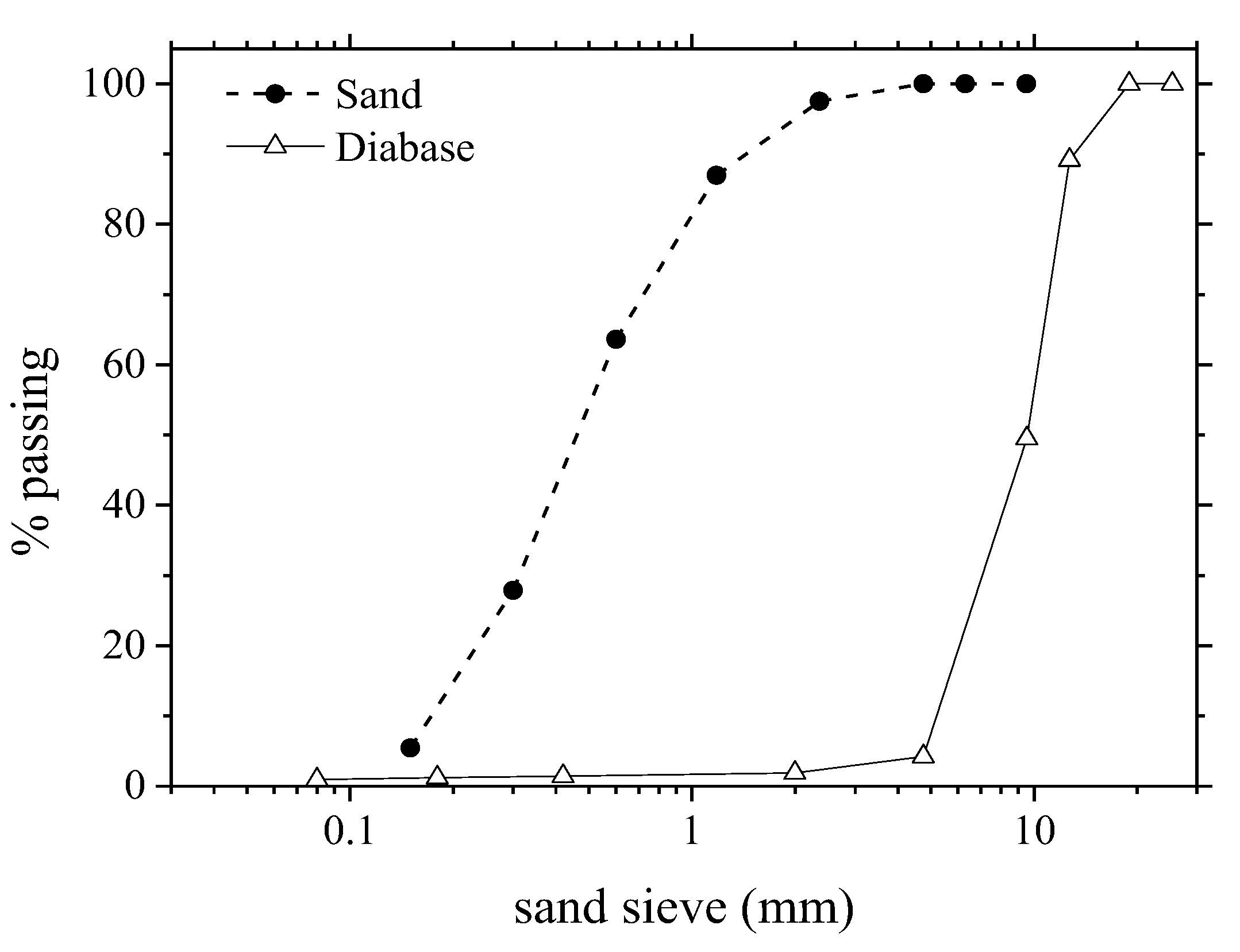
Rocks’ samples - Five cylindrical samples of 55 mm x 125 mm made by core drills extracted from an intact diabase rock.

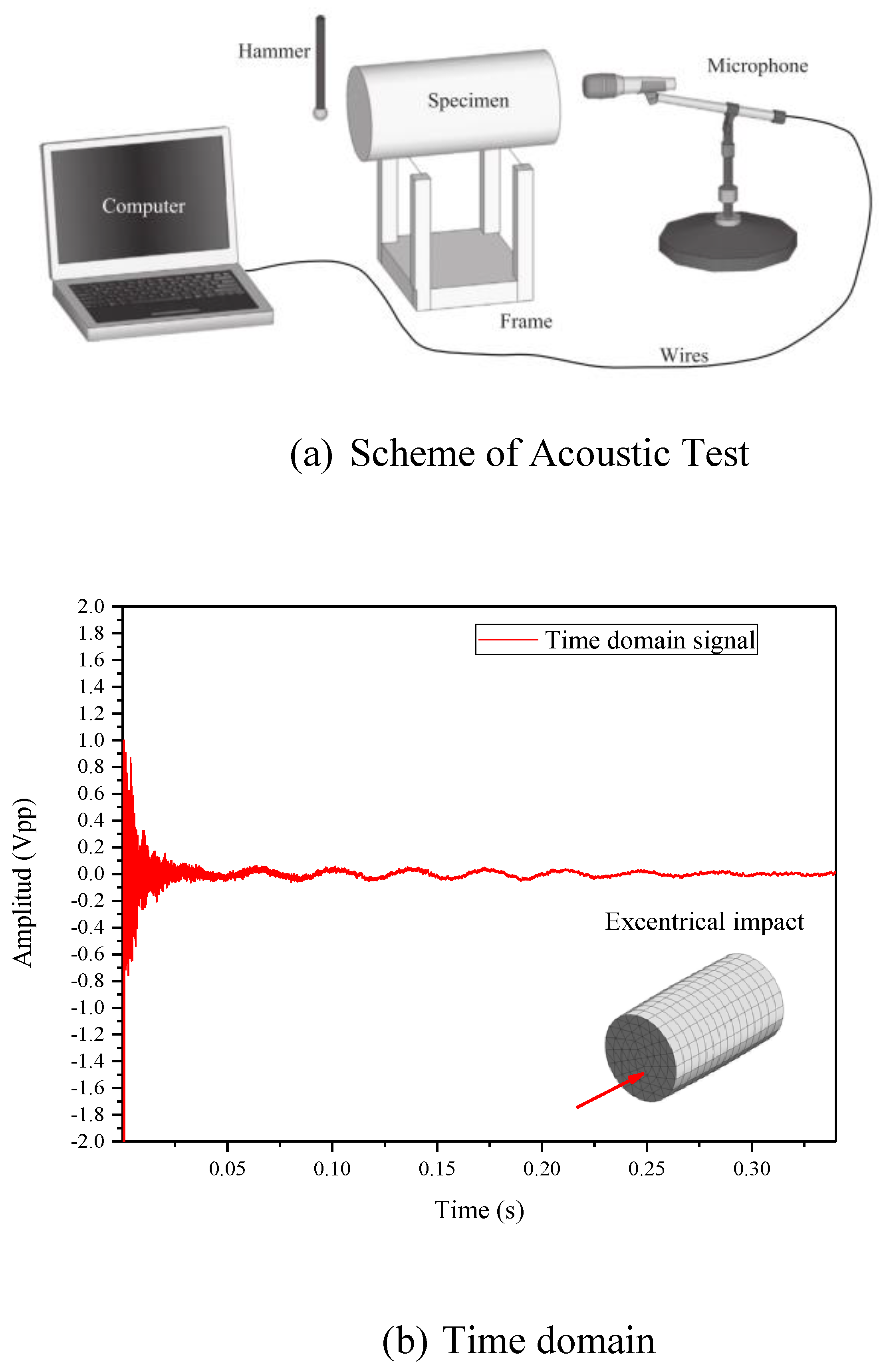
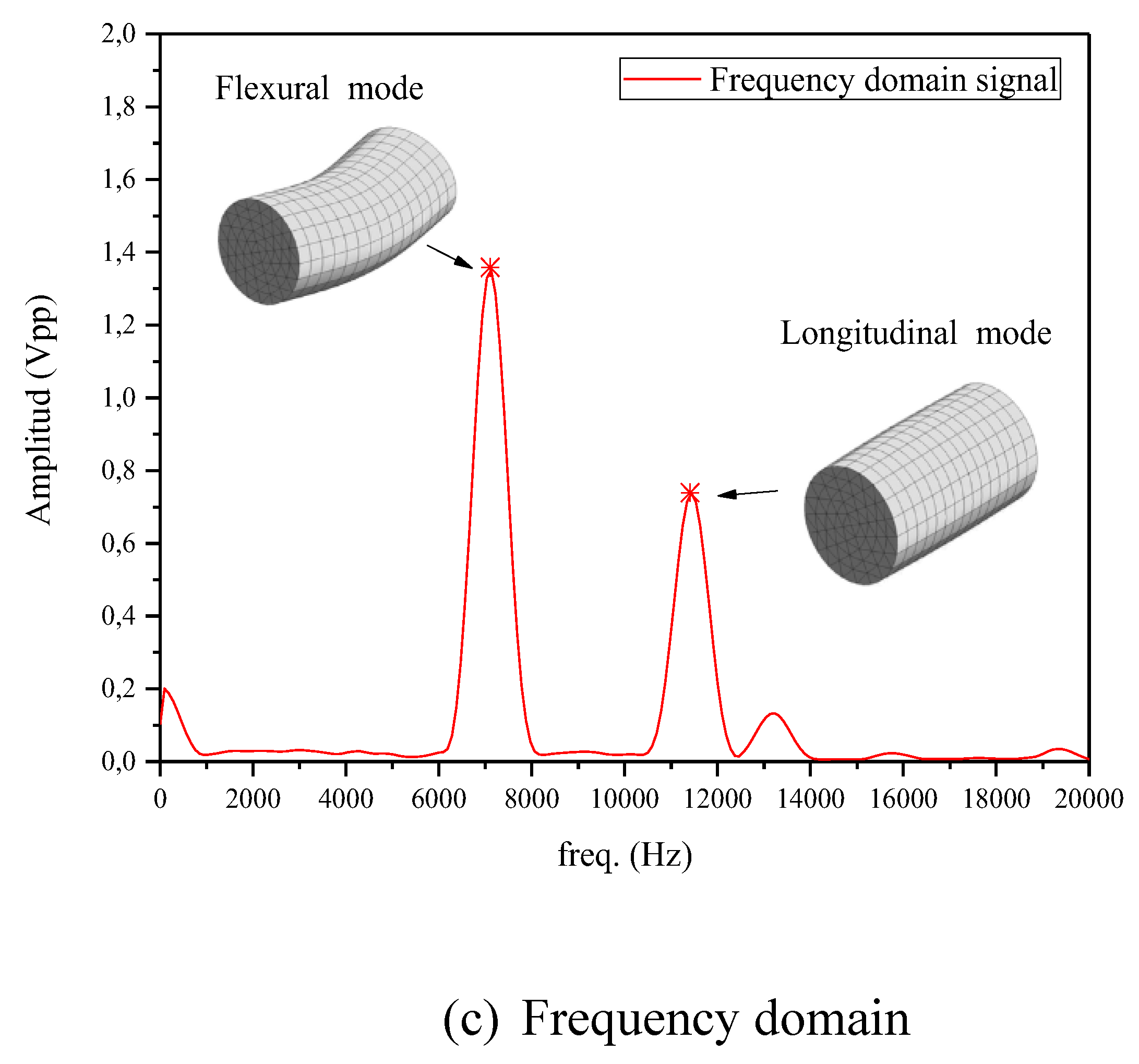
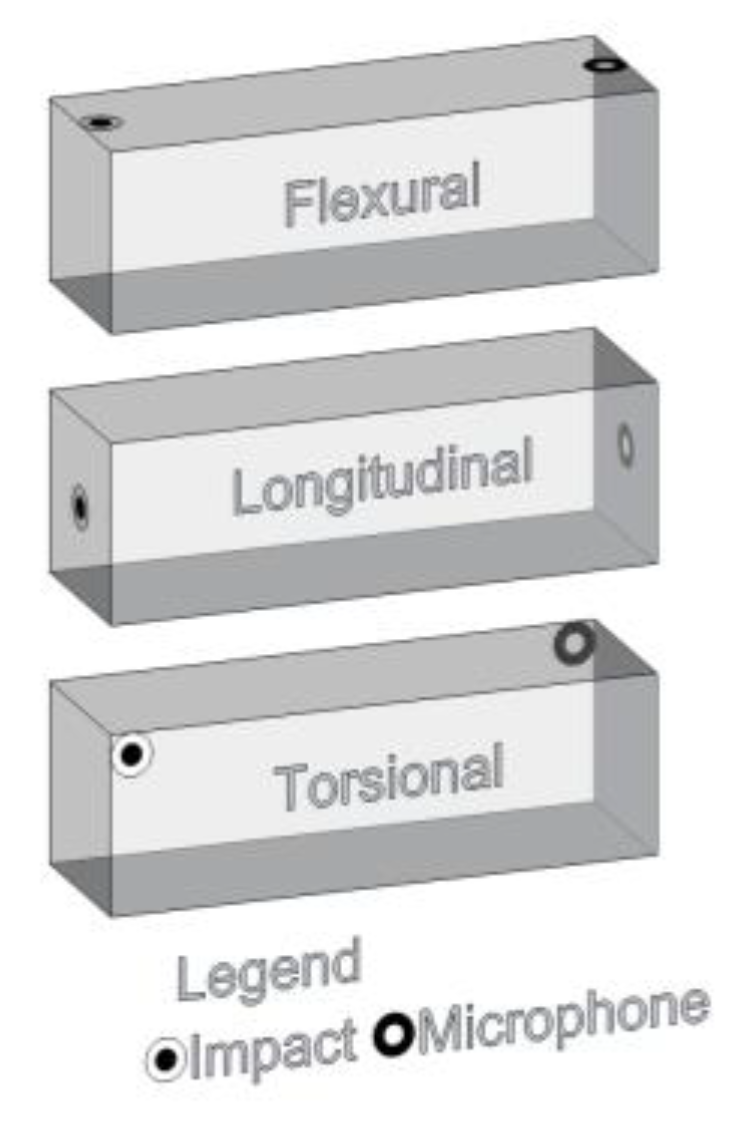
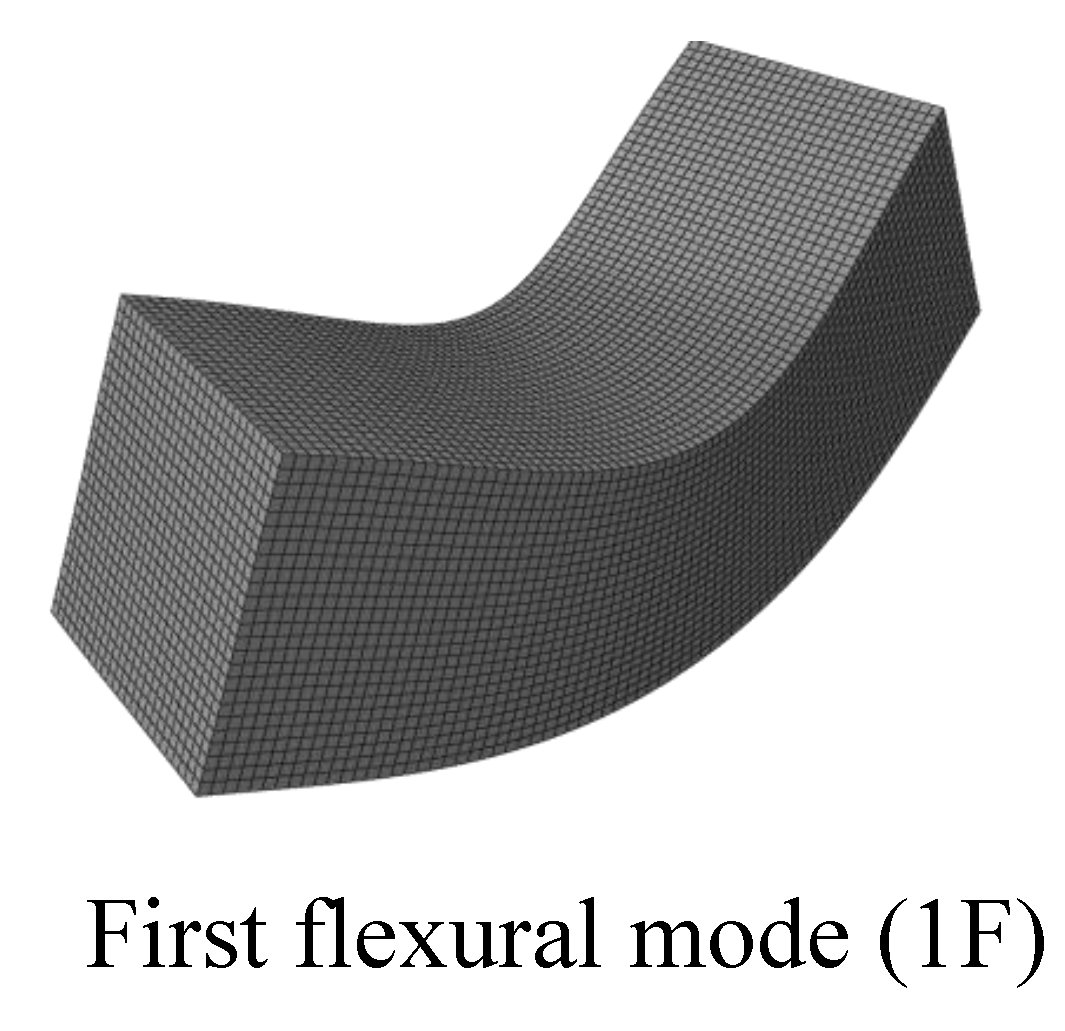
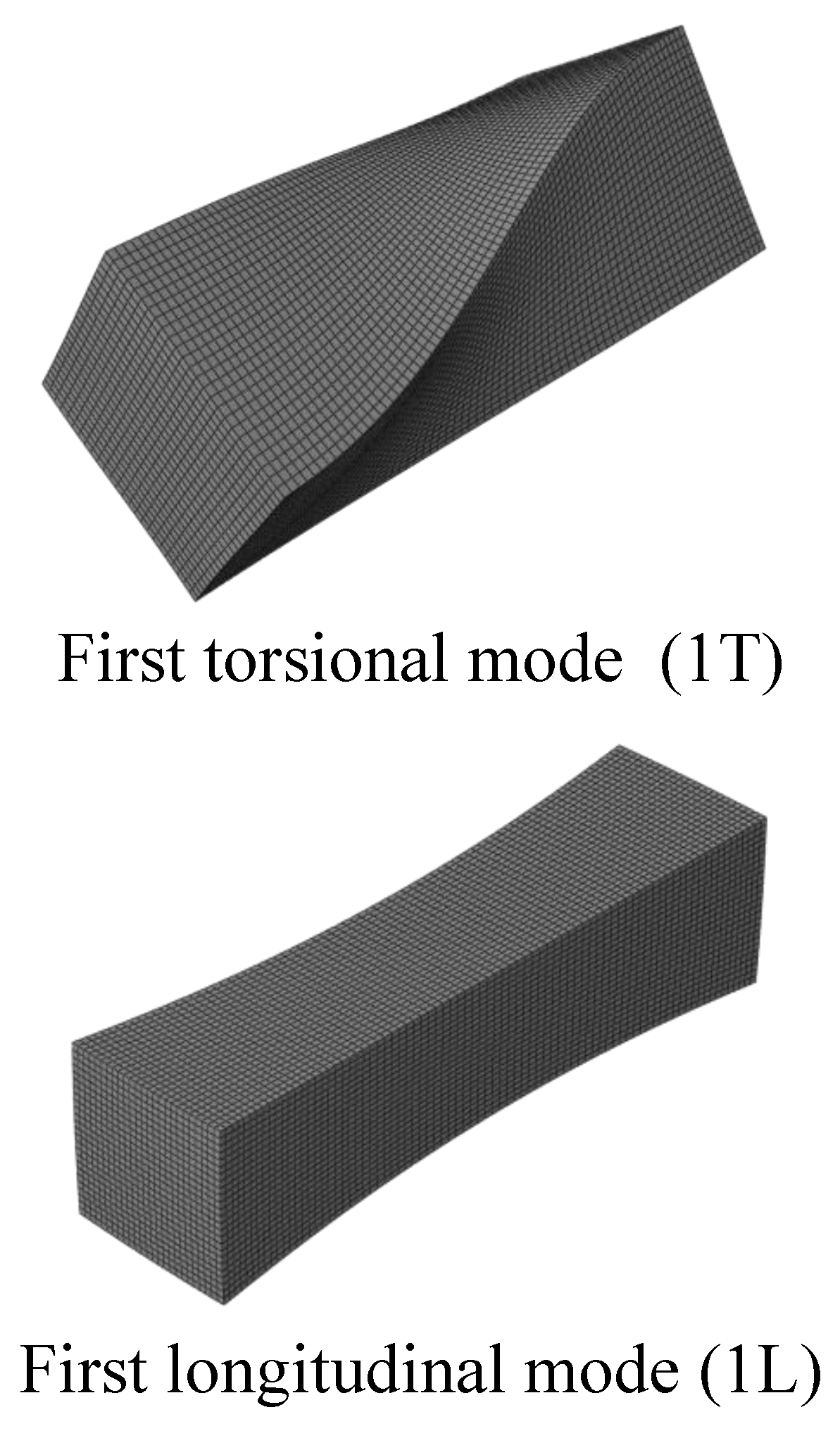
3.3. Acoustic tests and evaluation of experimental E_d

Acoustic tests (Figure 19.a) were performed in mortars and concretes specimens, according to ASTM C215 [4]. The mass of each sample was measured prior to each acoustic test. The sample was then positioned on steel wires attached to a metal frame (Figure 19.a) and an impact was manually applied with a hammer on the surface of the specimen, while a microphone captured the sound radiated by the specimen’s surface in another position. Depending on the vibration mode evaluated (flexural, torsional or longitudinal), different impact and measurement positions were selected, as suggested by ASTM E1876-01 [5] and shown schematically in Figure 20. The first two modes of each type (flexural, torsional and longitudinal) (see Figure 21) were easily identified in the prismatic specimens. However, this study focused on 1^st flexural and 1^st longitudinal modes (see Figure 19.c and Figure 21), i.e., the necessary vibration modes for the obtaining of the dynamic elastic modulus (E_d). After excitation, an onboard sound card of a regular notebook captured the acoustic signal at a 96 kHz acquisition rate. Figure 19.b shows a typical time vs. amplitude signal in a prismatic concrete sample tested at 28 days of age, obtained by an impact applied for activating the flexural and longitudinal modes (eccentric excitation). The first 1024-point block was selected, multiplied by a Hanning window and then zero-padded for the obtaining of an 8192-point vector. A Fast Fourier Transform was applied for the detection of peaks of natural frequencies.

Once experimental f_1,flex and f_1,long are obtained by acoustic test and exciting flexural and/or longitudinal vibrations modes, the elastic properties are evaluated through frequency equations, according to ASTM E1876 [5]. The sample’s dynamic modulus of elasticity (E_d) was obtained from the first flexural mode of vibration (E_d,f) by Eqs. 6 and 7, for prismatic or cylindrical specimens, respectively:

$$E_{d,f}=0.9465\frac{m{L}^3}{b{t}^3}{f}_{flex,1}{}^{2}B$$

(6)

$$E_{d,f}=1.6067\frac{m{L}^3}{D^4}{f}_f{}^{2}A$$

(7)

where b and t are dimensions of the prismatic cross section, D is the diameter of the cylindrical cross section, L is the specimen length, m is the specimen mass (in kg) and A and B are a correction factor dependent on Poisson coefficient (ν, generally 0.20, according to Mehta and Monteiro [1]) and dimensions of the specimens (b, t and D), computed by Eqs. 8 and 9:

$$A=1+4.939(1+0.0752{\upsilon }_d+0.8109{\upsilon }_d{}^2){\left(\frac{D}{L}\right)}^2-0.4883{\left(\frac{D}{L}\right)}^4-\left[\frac{4.691\left(1+0.2023{\upsilon }_d+2.173{\upsilon }_d{}^2\right){\left(\frac{D}{L}\right)}^4}{1.000+4.754\left(1+0.1408{\upsilon }_d+1.536\upsilon {}_d{}^2\right){\left(\frac{D}{L}\right)}^2}\right]$$

(8)

$$B=1+6.585(1+0.0752{\upsilon }_d+0.8109{\upsilon }_d{}^2){\left(\frac{t}{L}\right)}^2-0.868{\left(\frac{t}{L}\right)}^4-\left[\frac{8.340\left(1+0.2023{\upsilon }_d+2.173{\upsilon }_d{}^2\right){\left(\frac{t}{L}\right)}^4}{1.000+6.338\left(1+0.1408{\upsilon }_d+1.536{\upsilon }_d{}^2\right){\left(\frac{t}{L}\right)}^2}\right]$$

(9)

Similarly, the dynamic modulus of elasticity was obtained from the first longitudinal mode of vibration (E_d,l), in accordance with Eq. 10 for prismatic specimens:

$$E_{d,l}=4\frac{mL}{bt}{f}_l{}^2\frac{1}{K}$$

(10)

In this case, K is a correction factor given by Eq. 11 and D_e is the effective diameter of the bar, equal to D for a cylinder and given by Eq. 12 for a prismatic specimen.

$$K=1-\frac{{\pi }^2{\nu }_d{}^2{D}_e{}^2}{8L^2}$$

(11)

$$D_e{}^2=2\frac{b^2+t^2}{3}$$

(12)

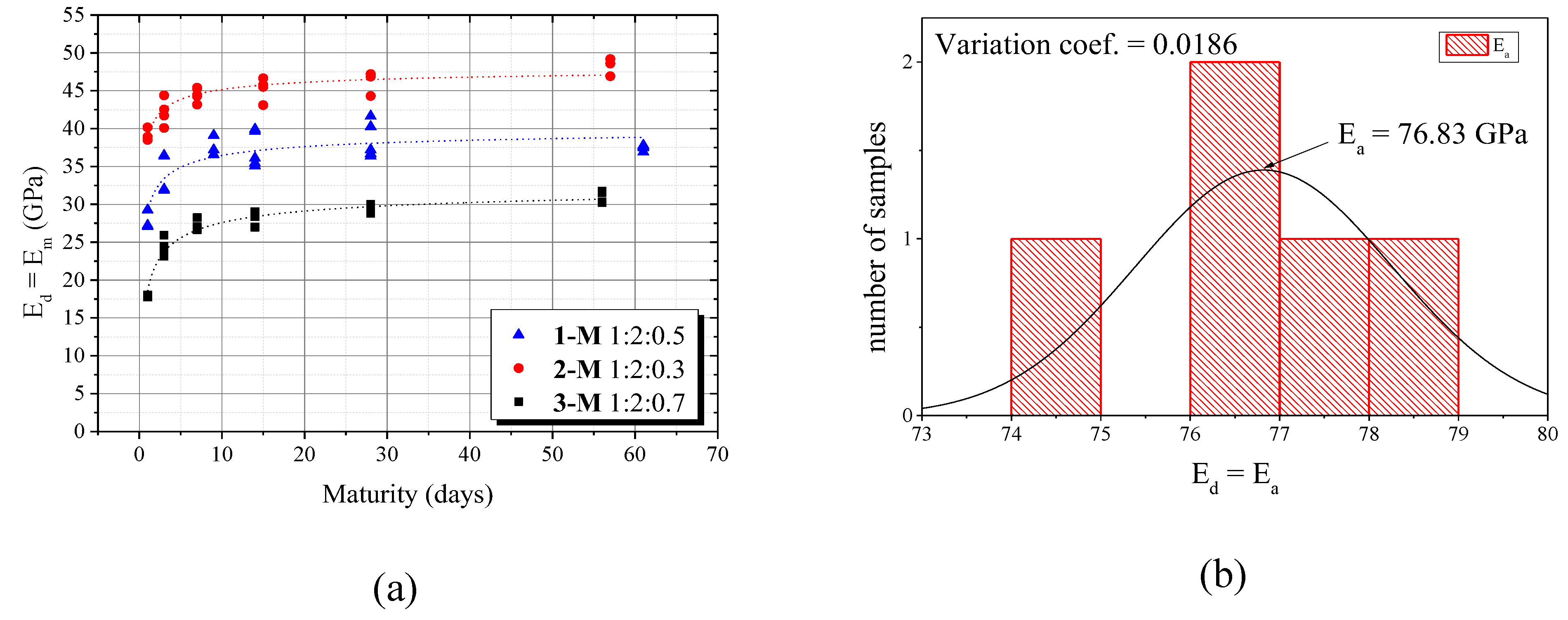
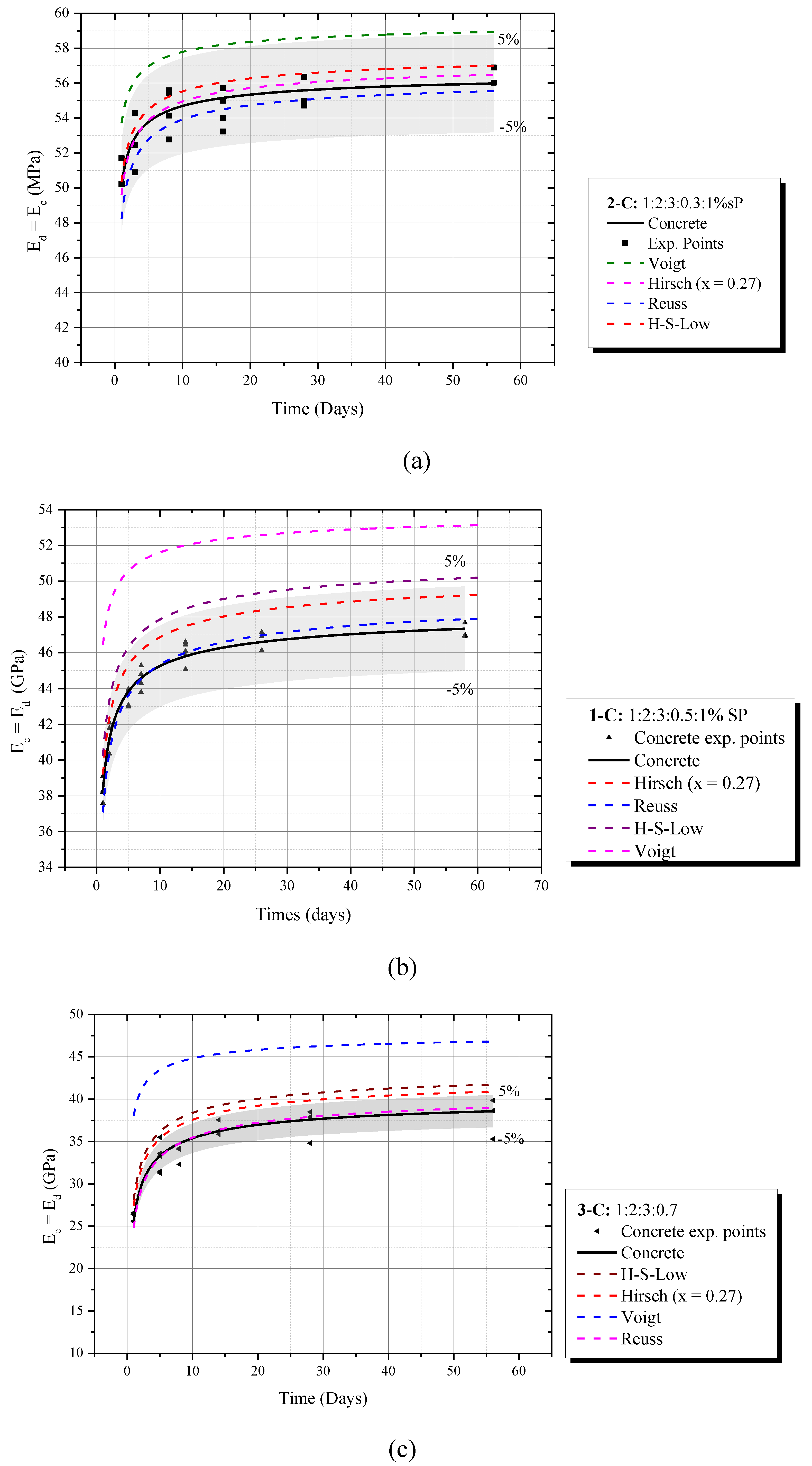
3.4. Experimental Results and discussion

The problem of evolution of elastic modulus over time was chosen to demonstrate the observed tendencies presented in above numerical results. All curves were calibrated by CEB FIB [40] (Eq. 13 and 14) for ages of 1 to 60.

$$E(t)={\beta }_E\times E_{28}$$

(13)

where E (t) is the function that represents the evolution of the elastic modulus over time, E28 is the modulus of elasticity at 28 days, and β_E is the contribution of time, according to Eq. 14:

$${\beta }_E={\left\{\exp \left\{s\left[1-{\left(\frac{28}{t}\right)}^{0,5}\right]\right\}\right\}}^{0,5}$$

(14)

The input of the biphasic model was the evolution over time of the dynamic elastic modulus of mortar E_m (see Figure 22.a) and the dynamic elastic modulus of samples of diabase rock E_a (see Figure 22.b).

Figure 23.a, b and c show the behavior of the dynamic elastic modulus of the concrete (E_d) over time and the biphasic models that predicted this evolution.

The experimental investigation showed Hirsch (x = 0.27) achieved good accuracy when w/c = 0.3 and 0.5, with errors within the 5% limit and identical to the maximum error observed in numeric simulations. However, its absolute error was slightly higher than 5 % for concretes with w/c = 0.7. This phenomenon is explained by a complex interaction of mortar, ITZ, water and coarse aggregate surface at early ages. According to Simeonov and Ahmad [17], a fresh concrete mixture undergoes a process of water migration to the surface of the coarse aggregates and this “water attraction” increase the ITZ thickness. Such a decrease is more pronounced at high water-cement ratios (e.g. w/c = 0.7), the E_d(t) curve moves to Reuss model, which also justified the same tendency of concretes with w/c = 0.5 (within 5% error). Therefore, numerical simulations revealed that, when ITZ increases, the best prediction is achieved by Reuss model, similarly to the experimental behavior. On the other hand, this phenomenon is reduced for concretes with little ITZ (e.g. w/c = 0.3) and dynamic elastic modulus is very close to Hirsch (x = 0.27).

4. Conclusions and final remarks

Numerical simulations of a porous, biphasic and triphasic material were developed. The study was focused in dynamic elastic modulus. The main finds are:

(i)

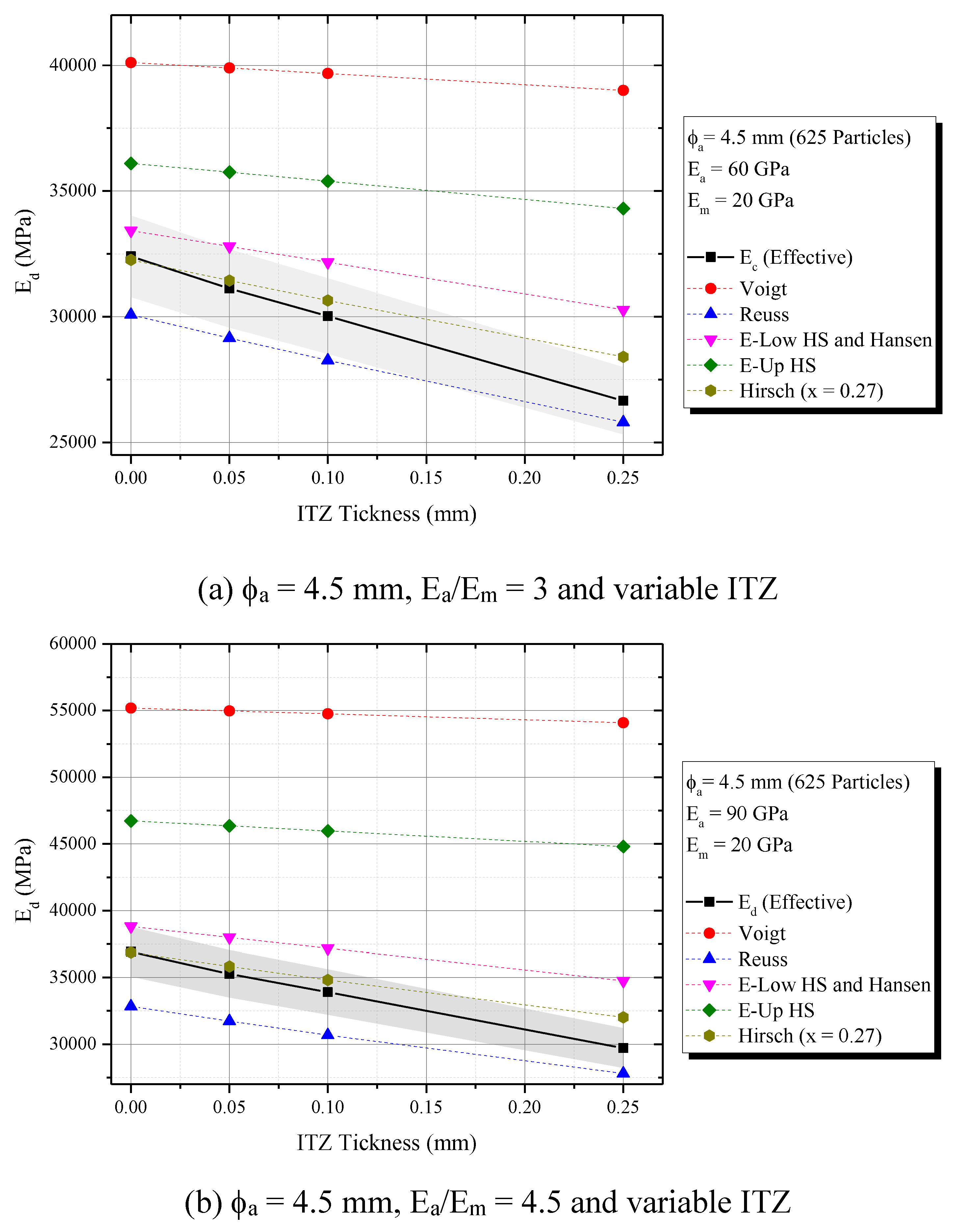
Homogenization composite models as Reuss and Hirsch (x = 0.27) are simple and accuracy ways to predict the dynamic elastic modulus with 5 % maximum error, regarding the ITZ conditions. Hirsch (x = 0.27) best predicts E_d for ITZ = 0.05 mm and 0.10 mm while Reuss model for ITZ = 0.25 mm. In the experimental field, a similar tendency was observed, once Hirsch (x = 0.27) successfully represented the E_d (t) phenomenon for concretes with low and moderate water cement ratios (w/c = 0.3 and 0.5), and Reuss was the only to predict the mixture with w/c = 0.70 with an error always lower than 5%;

(ii)

Voigt, H-S and Hansen always overestimate E_d for all numerical simulations and experimental validation;

(iii)

Hashin-Shtrikman limits does not contain biphasic theoretical models and cannot be applied to dynamic situations perfectly [18];

(iv)

Although biphasic models, as Reuss, Hirsch (x = 0.27), Voigt and H-S have incorporated ITZ, they will display the same tendencies observed for classic biphasic models. An advantage is the predict of the decrease in E_d in function of ITZ.

(v)

The effective Poisson ratio obtained by natural frequency shows a considerable error, due to some degree of anisotropy generated by the configuration of aggregates inside the mortar. The arrangement of coarse aggregates also influences this measure, since different arrangements with same elastic properties and volumetric fraction might generate a certain divergency in the Poisson ratio.

Our study has enhanced our understanding of the response of concrete under dynamical excitations. Numerical simulations of the theoretical material enabled the refining of the models, hence, a reliable and prudent control of dynamic deflections and verification of natural frequencies of the concrete’s structures.