Submitted:
17 April 2023
Posted:
18 April 2023
Read the latest preprint version here
Abstract
Keywords:
1. Introduction
2. Etalon Picture with the Exclusion of the Redundant Degrees of Freedom
3. Evolution in the Extended Space
4. Mean values of scale factor degrees
5. Discussion and Conclusion
Appendix A. Resolving constraints in path integrals
References
- Gitman, D.; Tyutin, I.V. Quantization of Fields with Constraints; Springer: Berlin, Germany, 1990. [Google Scholar]
- Henneaux, M.; Teitelboim, C. Quantization of Gauge Systems; Princeton Univ. Press: Princeton, NJ, USA, 1992. [Google Scholar]
- Dirac, P. Lectures on Quantum Mechanics; Belfer Graduate School of Science, Yeshiva University: NY, 1967. [Google Scholar]
- Giddings, S. Black hole information, unitarity, and nonlocality. Phys. Rev. D 2006, 74. [Google Scholar] [CrossRef]
- Barvinsky, A.O.; Kamenshchik, A.Y.; Vardanyan, T. Comment about the vanishing of the vacuum energy in the Wess–Zumino model. Phys. Lett. B 2018, 782, 55–60. [Google Scholar] [CrossRef]
- Cherkas, S.L.; Kalashnikov, V.L. An approach to the theory of gravity with an arbitrary reference level of energy density. Proc. Natl. Acad. Sci. Belarus, Ser. Phys.-Math. 2019, 55, 83. [Google Scholar] [CrossRef]
- Cherkas, S.L.; Kalashnikov, V.L. Eicheons instead of Black holes. Phys. Scr. 2020, 95, 085009. [Google Scholar] [CrossRef]
- Cherkas, S.L.; Kalashnikov, V.L. Vacuum Polarization Instead of “Dark Matter” in a Galaxy. Universe 2022, 8, 456. [Google Scholar] [CrossRef]
- Cherkas, S.L.; Kalashnikov, V.L. Dark Matter in the Milky Way as the F-Type of Vacuum Polarization. Phys. Sci. Forum 2023, 7, 8. [Google Scholar] [CrossRef]
- Carballo-Rubio, R.; Filippo, F.D.; Liberati, S.; Visser, M. Singularity-free gravitational collapse: From regular black holes to horizonless objects. arXiv 2023, arXiv:2302.00028. [Google Scholar]
- Haridasu, B.S.; Cherkas, S.L.; Kalashnikov, V.L. A reference level of the Universe vacuum energy density and the astrophysical data. Fortschr. Phys. 2020, 68, 2000047. [Google Scholar] [CrossRef]
- Burdík, C̆; Navrátil, O. Dirac formulation of free open string. Univ. J. Phys. Appl. 2007, 4, 487–506. [Google Scholar]
- Cherkas, S.L.; Kalashnikov, V.L. Quantum evolution of the universe in the constrained quasi-Heisenberg picture: From quanta to classics? Grav. Cosmol. 2006, 12, 126–129. [Google Scholar]
- Cherkas, S.L.; Kalashnikov, V.L. An inhomogeneous toy model of the quantum gravity with the explicitly evolvable observables. Gen. Rel. Grav. 2012, 44, 3081–3102. [Google Scholar] [CrossRef]
- Cherkas, S.; Kalashnikov, V. Quantization of the inhomogeneous BianchiI model: quasi-Heisenberg picture. Nonlin. Phenom. Complex Syst. 2013, 18, 1–15. [Google Scholar]
- Cherkas, S.; Kalashnikov, V. Quantum Mechanics Allows Setting Initial Conditions at a Cosmological Singularity: Gowdy Model Example. Theor. Phys. 2017, 2, 124–135. [Google Scholar] [CrossRef]
- Faddeev, L.; Popov, V.N. Covariant quantization of the gravitational field. Sov. Phys. Usp. 1974, 16, 777–789. [Google Scholar] [CrossRef]
- Faddeev, L.; Slavnov, A. Gauge Fields. Introduction to Quantum Theory; Addison-Wesley Publishing: Redwood, CA, USA, 1991. [Google Scholar]
- Savchenko, V.; Shestakova, T.; Vereshkov, G. Quantum geometrodynamics in extended phase space - I. Physical problems of interpretation and mathematical problems of gauge invariance. Grav. Cosmol. 2001, 7, 18–28. [Google Scholar]
- Vereshkov, G.; Marochnik, L. Quantum Gravity in Heisenberg Representation and Self-Consistent Theory of Gravitons in Macroscopic Spacetime. J. Mod. Phys. 2013, 4, 285–297. [Google Scholar] [CrossRef]
- Ruffini, G. Quantization of simple parametrized systems. arXiv 2005, arXiv:gr-qc/0511088.
- Cianfrani, F.; Montani, G. Dirac prescription from BRST symmetry in FRW space-time. Phys. Rev. D 2013, 87, 084025. [Google Scholar] [CrossRef]
- Garay, L.J.; Halliwell, J.J.; Marugán, G.A.M. Path-integral quantum cosmology: A class of exactly soluble scalar-field minisuperspace models with exponential potentials. Phys. Rev. D 1991, 43, 2572–2589. [Google Scholar] [CrossRef]
- Bojowald, M. Quantum cosmology: A review. Rep. Progr. Phys. 2015, 78, 023901. [Google Scholar] [CrossRef]
- Balcerzak, A.; Lisaj, M. Spinor wave function of the Universe in non-minimally coupled varying constants cosmologies. arXiv 2023, arXiv:2303.13302. [Google Scholar] [CrossRef]
- Lehners, J.L. Review of the No-Boundary Wave Function. arXiv 2023, arXiv:2303.08802. [Google Scholar]
- Barvinsky, A.O.; Kamenshchik, A.Y. Selection rules for the Wheeler-DeWitt equation in quantum cosmology. Phys. Rev. D 2014, 89, 043526. [Google Scholar] [CrossRef]
- Cherkas, S.L.; Kalashnikov, V.L. Evidence of time evolution in quantum gravity. Universe 2020, 6, 67. [Google Scholar] [CrossRef]
- Cherkas, S.L.; Kalashnikov, V.L. Illusiveness of the Problem of Time. Nonlin. Phen. Complex Syst. 2021, 24, 192–197. [Google Scholar] [CrossRef]
- Shestakova, T.P.; Simeone, C. The Problem of time and gauge invariance in the quantization of cosmological models. II. Recent developments in the path integral approach. Grav. Cosmol. 2004, 10, 257–268. [Google Scholar]
- Shestakova, T.P. Is the Wheeler-DeWitt equation more fundamental than the Schrödinger equation? Int. J. Mod. Phys. D 2018, 27, 1841004. [Google Scholar] [CrossRef]
- Kaku, M. Introduction to Superstrings; Springer: New York, 2012. [Google Scholar]
- DeWitt, B.S. Dynamical Theory in Curved Spaces. I. A Review of the Classical and Quantum Action Principles. Rev. Mod. Phys. 1957, 29, 377–397. [Google Scholar] [CrossRef]
- Mostafazadeh, A. Quantum mechanics of Klein-Gordon-type fields and quantum cosmology. Ann. Phys. (N.Y.) 2004, 309, 1–48. [Google Scholar] [CrossRef]
- Silenko, A.J. Zitterbewegung of Bosons. Phys. Part. Nucl. Lett. 2020, 17, 116–119. [Google Scholar] [CrossRef]
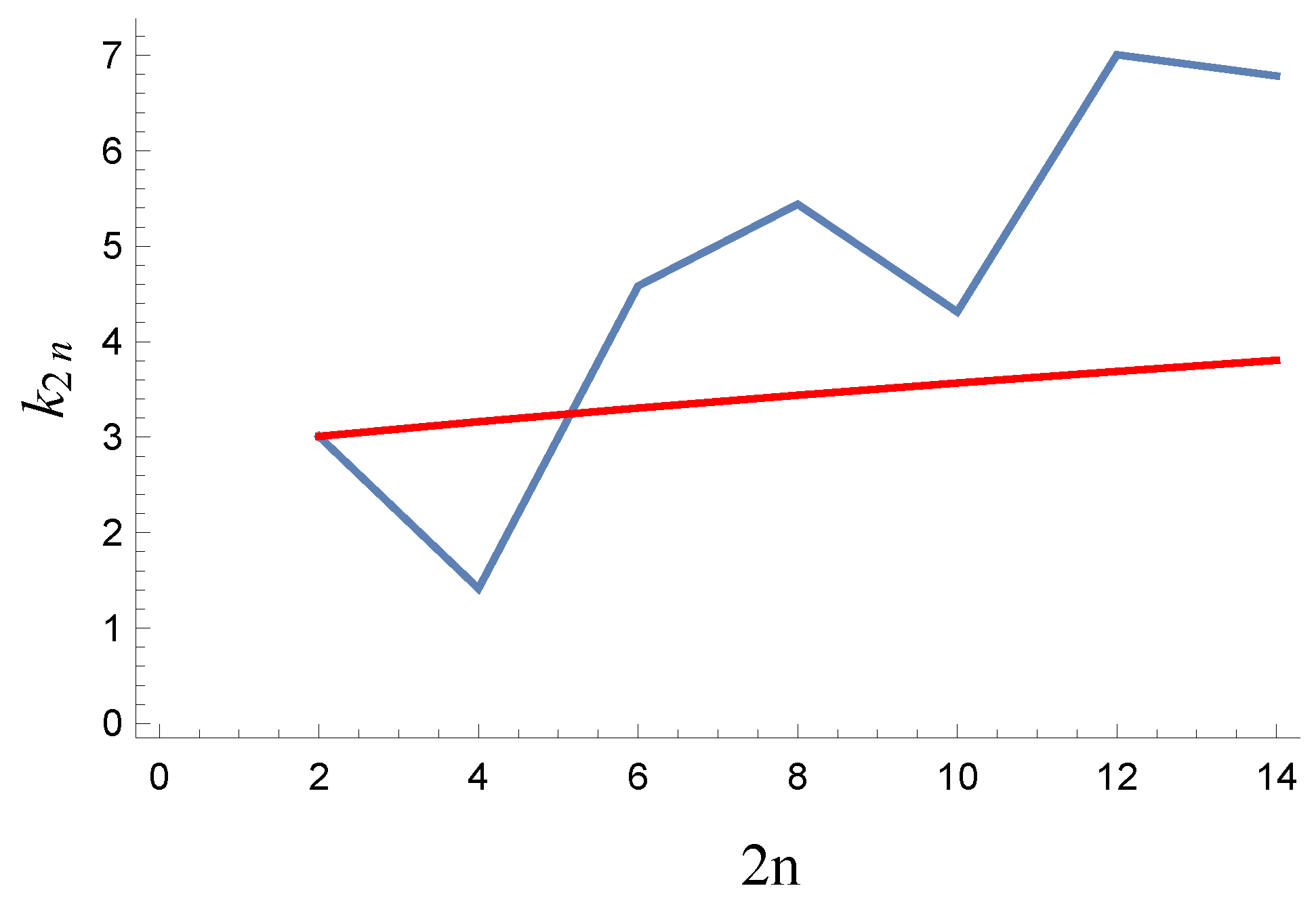
| 2 | 4 | 6 | 8 | 10 | 12 | 14 | |
|---|---|---|---|---|---|---|---|
| for the etalon model | |||||||
| for the model with the Grassmann variables |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





