The Role of Neutral Wind Velocity and Its Vertical Component on Predictability of Formation and Localization of Sporadic E(Es)

1. Introduction

Sporadic E (Es) is a high density narrow, irregular ionosphere layer [1,2], its existence was noticed in the ionograms of 1933-1935 [3]. In this layer the ion/electron density can be comparable to or greater than those of the regular ionosphere E, F1 and F2 layers. Therefore, Es may influence the quality of radio communications [4,5].

Es layers mainly occur during nighttime in the lower thermosphere, at altitudes between 90-150km. This fact indicates that in this range of altitudes is provided conditions for ion/electron convergence into narrow layer in this region [6,7,8,9,10,11,12]. This convergence and consequently the formation of the Es layer can be caused by horizontal wind with vertical shear (windshear theory) [6,7,13,14,15,16,17,18], by electric field and its variations [19,20] or/and by the combined action of all these effects [21,22,23]. In the mid-latitude lower-thermosphere the ion vertical drift velocity can be estimated by the wind velocity, the vertical distribution of dominant neutrals and the geomagnetic field. By this drift velocity and its vertical changes can be estimated the height regions where the ion/electron convergence or depletion occur [10,12,24] The loss rate of molecular ions (e.g., NO+ and O2+) increases during ion/electron convergence into thin dense layer, which in turn causes the dominance of long-lived heavy metallic ions (e.g., Fe+ and Mg+), which is a phenomenon that has been observed in nighttime Es layers [25,26].

In the recent studies [10,24] have shown that, in adition to earlier considerations [2,3,15,27,28], taking into account the “windshear” effect, the wind magnitude and direction were important for development of ion/electron convergence (or divergence/deplition) in certain height regions. It was also shown that Es layer density is also controlled by ion ambipolar diffusion.

In the present study the suggested theoretical mechanism of the Es layer formation takes into account an arbitrary wind height profile. This approach is different from earlier considerations [10,24]. In this study the recently obtained results of the case of horizontal wind are also generalized. This makes more predictable the formation of the Es layers. These processes can also be described by analytical approach. The behavior of the vertical distribution of ion density $N_i(z,t)$ in ambipolar approach and correspondingly the formation of ionosphere layers, similarly to [10,24,29] (with some extension – including gravity effect as well), can be described by the following equation:

$$\frac{\partial N_i}{\partial t}=-\frac{\partial w_{iv}}{\partial z}{N}_i-w_{iv}(z)\frac{\partial N_i}{\partial z}+\frac{\partial }{\partial z}{D}_a(z)\left(\frac{\partial N_i}{\partial z}+\frac{N_i}{H_i}\right)+Q-L$$

(1)

Here, in the expression of ion vertical drift velocity $w_i$ the $w_{iv}$part caused by neutral wind and the part $-D_a(z)\left(\frac{\partial N_i}{\partial z}+\frac{N_i}{H_i}\right)$ caused by ions ambipolar diffusion ($\propto D_a$) are separated. This separation makes further analysis more convenient. $D_a$ is the coefficient of ions ambipolar diffusion. Q and L are the ions production and loss rates, respectively. $H_i$ is the ion scale height. The effect of gravity in the lower thermosphere (h<140km) is relatively small ($\left|\frac{\partial N_i}{\partial z}\right|>>\frac{N_i}{H_i}$). Here and hereafter the vertical coordinate z represents the residual between some actual $h$ and initial heights $h_o$ ( $z=h-h_o$).

Despite of the fact that ionosphere plasma is weakly ionized and the influence of neutrals on the ion/electron drift velocity and correspondingly on their density behavior is important, the formation of the regular ionosphere E, F1 and F2 layers is still possible even in the absence of neutral wind ($V=0$ and $w_{iv}=0$). For example, in the lower thermosphere, the formation of E layer by Chapman mechanism is mainly determined by photoionization rate ($Q$) of molecules (e.g., O₂ and N₂) with vertically decreasing density [5].

For the formation of F1 layer during daytime (mostly in summer season, at height about 180-250 km), the photoionization of atomic oxygen is important, which decreases in density with height, since the electron production is dominated by extreme ultraviolet (UV, 10–100 nm) radiation ionizing atomic oxygen. During night the photoionization is absent ($Q=0$), so the F1 layer vanishes, and the dominant layer becomes the F2. This layer regularly exists (with peak electron density at about 300-400km height) and it is maintained by the increase of ions ambipolar diffusion displacement ($-D_a(z)\left(\frac{\partial N_i}{\partial z}+\frac{N_i}{H_i}\right)$) above the electron density peak height [5]) as well as by the increase of ions recombination below this height. Here these processes are slower than in the E and F1 regions, allowing the F2 layer to exist during both daytime, when photoionization increases ($Q>0$) and nighttime when ionization is absent ($Q=0$). Although the neutral wind is not necessary for formation of the E, F1 and F2 layers, it can significantly influence ion/electron vertical drift described by $w_{iv}$, Equation (1) and therefore affect behavior of these layers.

In the suggested study, unlike the regular ionosphere E, F1 and F2 layers, the formation of the sporadic E (Es) layer at mid-latitude lower thermosphere is mainly determined by the neutral wind. The ion vertical drift velocity, caused by the combined effect of vertically changing ion-neutral collision and Lorentz forcing, changes during existence of homogeneous or inhomogeneous wind ($\frac{\partial w_{iv}}{\partial z}\ne 0$). At some height regions this drift velocity is zero ($w_{iv}=0$), depending on the direction of wind. These height regions with $w_{iv}=0$ will be noted as a node of ion drift velocity. When the ions upstream and downstream flows ($(divw\approx \frac{\partial w_{iv}}{\partial z})\min <0$) towards this region occur, then their convergence into a thin Es type layer is possible at this node [24]. The processes of ions convergence into a thin layer should take place until the increase of the density due to the convergence exceeds its decrease due to diffusive displacement ($\propto D_a$), and total loss ($Q-L<0$) caused by their production ($Q$) and loss ($L$) rates.

For those wind directions when the ions downstream and upstream flows occur ($(divw\approx \frac{\partial w_{iv}}{\partial z})\max >0$), the opposite phenomenon takes place in these height regions – the ion/electron depletion. Further we will show that both horizontal and vertical components of the wind velocity are important for estimation of the ion/electron convergence/divergence regions and prediction of the development of corresponding processes.

To show the suggested theoretical mechanism of sporadic E formation, we will solve Equation (1) using analytic approach when

$$-\frac{\partial w_{iv}}{\partial z}\equiv C\text{'}=constant$$

(2)

and $D_a=const$. In this case the solution of Equation (1) has the following form:

$$N_i(z,t)=\frac{e^{C\text{'}(t-t_o)}}{2{[\pi D_a(t-t_o)]}^{1/2}}{\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}{e}^{-\frac{{[z-w_{iv}(t-t_o)-z\text{'}]}^2}{4D_a(t-t_o)}}{N}_{io}(z\text{'})dz\text{'}}$$

(3)

Here

$$G_i(z,t)=\frac{e^{C\text{'}(t-t_o)}}{2{[\pi D_a(t-t_o)]}^{1/2}}{e}^{-\frac{{[z-w_{iv}(t-t_o)\text{'}]}^2}{4D_a(t-t_o)}}$$

(4)

is the analogy of the source function [30], which corresponds to the solution of Equation (1) in case of $Q-L=0$. When $C\text{'}>0$ then $G_i(z,t)$ increases with time and when $C\text{'}<0$ it decreases. The Equation (3) also shows that for ion vertical drift velocity $w_{iv}>0$ the initial peak height $z_m(t=t_o)=0$ of $G_i(z,t)$ shifts upward and for $w_{iv}<0$ it descends. We note that upward shift of the ions initial layer by $w_{iv}$ is not noticeable ion diffusion is neglected.

In Equation (3) the value of $\propto {\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}{e}^{-\frac{{[z-w_{iv}(t-t_o)-z\text{'}]}^2}{4D_a(t-t_o)}}{N}_{io}(z\text{'})dz\text{'}}$ indicates that, in addition to the diffusive displacement of the ions initial distribution $N_{io}(z)$, their redistribution also occurs in the height region of its drift velocity node $w_{iv}=0$.

When the increase in ions density $\propto e^{C\text{'}(t-t_o)}>1$ , caused by vertical changes of ion vertical drift velocity $C\text{'}>0$, exceeds the diffusive displacement of their initial density ( $\propto {\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}{e}^{-\frac{{[z-w_{iv}(t-t_o)-z\text{'}]}^2}{4D_a(t-t_o)}}{N}_{io}(z\text{'})dz\text{'}}$), then the density in the layers, formed in the nodes increases, see Equation (3). The Equation (3) also shows that when $C\text{'}<0$ and correspondingly $e^{C\text{'}(t-t_o)}<1$, then in this region the opposite phenomena takes place - its density decreases (depletes).

Actually, $C\text{'}=-\frac{\partial w_{iv}}{\partial z}$ changes with height and its influence on ion/electron density variations will differ across various height regions. If at certain height $C\text{'}$ has maximal positive value ($C_{\max }^{\text{'}}>0$), then, considering ion/electron density behavior approximation by the Equation (3), ions/electrons will be accumulated into a thin layer in the vicinity of this height and the Es type layer formation is expectable.

Here and hereafter, the superscript prime denotes the vertical derivative of the corresponding function, and the subscript max or min denotes its minimum and maximum values, respectively.

Using the approximated value of $w_{iv}(z)$ at the region of $z=z_o$, it can be shown that

$$w_{iv}\approx w_{iv}(z=z_o)+(z-z_o){\left(\frac{\partial w_{iv}}{\partial z}\right)}_{z=z_o}+\frac{1}{2}{(z-z_o)}^2{\left(\frac{{\partial }^2{w}_{iv}}{\partial z^2}\right)}_{z=z_o}$$

(5)

where $C\text{'}=-{\left(\frac{\partial w_{iv}}{\partial z}\right)}_{z=z_o}$ is maximal ($C_{\max }^{\text{'}}>0$) or minimal ($C_{\min }^{\text{'}}<0$), than ${\left(\frac{{\partial }^2{w}_{iv}}{\partial z^2}\right)}_{z=z_o}=0$.

Equations (2)-(5) show that, when $C_{\max }^{\text{'}}>0$, then the ions flow upstream ${\left(N_i{w}_{iv}\right)}_{z<z_o}\propto (z-z_o){\left(\frac{\partial w_{iv}}{\partial z}\right)}_{z=z_o}>0$ and downstream ${\left(N_i{w}_{iv}\right)}_{z>z_o}\propto (z-z_o){\left(\frac{\partial w_{iv}}{\partial z}\right)}_{z=z_o}<0$ to the region $z=z_o$, where their density increases maximally ($\propto \exp [C\text{'}(t-t_o)]>1$), Equations (3) and (4). So, the formation of a high density Es type narrow layer occurs at the region of the ion vertical drift velocity node $z=z_o$ ($w_{iv}=0$).

We note that this process can be developing along with the vertical drift of ions, during which the formed layer moves or is localized in the region where $w_{iv}\to 0$. If the height region with $w_{iv}=0$ is shifted from the region with $C\text{'}>0$, then, according to Equations (3) and (4), the ion vertical convergence at this region is expectable during ions upward ($w_{iv}(z=z_o>z_c)>0$) or downward ($w_{iv}(z=z_o>z_c)<0$) drift. The equation (4) also shows that, when $C\text{'}<0$, then at $z=z_o$ region the opposite effect occurs: the ions downstream ${\left(N_i{w}_{iv}\right)}_{z<z_o}\propto (z-z_o){\left(\frac{\partial w_{iv}}{\partial z}\right)}_{z=z_o}<0$ and upstream ${\left(N_i{w}_{iv}\right)}_{z>z_o}\propto (z-z_o){\left(\frac{\partial w_{iv}}{\partial z}\right)}_{z=z_o}>0$ flows increase resulting in the depletion of ions density at regions with $C_{\min }^{\text{'}}<0$, Equations (4) and (5).

We note that, for certain directions of the horizontal wind, vertical changes of the ion vertical drift velocity already have minimal negative ($C_{\max }^{\text{'}}>0$) or/and maximal positive ($C_{\min }^{\text{'}}<0$) values, even if the wind is homogeneous [10]. Therefore, at the heights ranging 90-150km the processes of ions convergence into a thin layer or their depletion are possible. Formation of the Es type layer (at a region with $w_{iv}=0$) occurs until its density increase is balanced by the increased ions diffusive outflow from this layer ($e^{C\text{'}(t-t_o)}=\frac{1}{2{[\pi D_a(t-t_o)]}^{1/2}}{\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}{e}^{-\frac{{[z-w_{iv}(t-t_o)-z\text{'}]}^2}{4D_a(t-t_o)}}{N}_{io}(z\text{'})dz\text{'}}$).

It is also important to note that heavy ions are mainly distributed between about 90-150 km [31,32] and correspondingly increase in density of the Es layer continues during its upward $w_{iv}\to +0$ (towards the topside) or downward $w_{iv}\to -0$ (towards the bottom) motions where vertical changes of the vertical drift velocity vanish ($\frac{\partial w_{iv}}{\partial z}\to 0$).

The wind in the lower thermosphere can be caused by vertically propagating tidal motion, planetary waves or/and atmospheric gravity waves (AGWs). In this case the ion vertical drift velocity can have several nodes where the ions convergence (when $C_{\max }^{\text{'}}>0$) or divergence (when $C_{\min }^{\text{'}}<0$) is possible. So, during the presence of more than one node with condition $C_{\max }^{\text{'}}>0$ the formation of multilayered sporadic E is expectable [24].

So, on the bases of the the realistic height profile of the neutral wind velocity and the ions initial distribution, the prediction of the formation of the Es layer in the mid-latitude lower thermosphere is possible. Under the same conditions the estimation of ions depletion region is also possible. In these cases, both horizontal and vertical components of the wind profile are important, which will be shown in the suggested study.

Hereafter, for demonstration of the above derived analytical theory of formation of sporadic E and ions density depletion under the influence of neutral wind, we will solve Equation (1) numerically. In the equation for ions vertical drift velocity $w_i$ the neutral wind effect ($w_{iv}$) will be distinguished from its drift by ions ambipolar diffusion. The convergence/divergence rate parameter $-\frac{\partial w_{iv}}{\partial z}\equiv C\text{'}=constant$ will be generalized for a variable wind velocity profile and the equations describing the role of (1) its magnitude and direction, (2) the vertical changes of the horizontal components, and (3) the vertical changes of the vertical component will be separated. Unlike earlier consideration [10], the influence of vertical wind on both the convergence of ions and their depletion in a region of a certain height of the lower thermosphere will be shown.

In the first stage, we show only the effect of vertical wind on convergence/divergence of ions. Further, we will consider its existence in the horizontal wind, whose meridional and zonal velocity profiles are determined by HWM14 data [33].

We will choose small magnitude of vertical wind velocity, which can be caused by both tidal motions and AGWs often observed in the lower thermosphere [34,35]. We show its influence on the location of Es layer (e.g., the location with $w_{iv}=0$ or $w_{iv}\to 0$), as well as the presence of convergence (with $\left(\partial w_{iv}/\partial z\right)\min <0$) and divergence (with $\left(\partial w_{iv}/\partial z\right)\max >0$) height regions, and the development of corresponding ion/electrons density convergence/depletion processes in them. For the considered wind velocity profiles, the location of the height regions of maximum convergence and divergence rates, as well as the parameters caused by the magnitude, direction and vertical change of the wind will be demonstrated. Theoretical and corresponding numerical simulations show that in the formation of the sporadic E (Es) along with the vertical shear of the horizontal wind (sheartheory), the factor of the magnitude and direction of the realistic (three-dimensional) wind is important.

Sporadic E contains mainly metallic ions and consequently it is important to know the realistic wind velocity height profile, to study their global and regional distributions.

2. Parameters describing the formation of sporadic E under the influence of neutral wind

In this section we consider the behavior of ions/electrons and the possibility of sporadic E formation in the mid-latitude lower thermosphere under the influence of arbitrarily directed neutral wind.

In this case we use Equation (1) to study the behavior of heavy metallic ions (Fe+) and electrons under assumption of quasi-neutrality ($N_i=N_e$), where the ion vertical drift velocity $w_{iv}$ (determined by the wind) and its vertical changes $\frac{\partial w_{iv}}{\partial z}$ vary in time. Here, along with the effect of wind shear, the influence of its magnitude and direction on the process of ions/electrons convergence into a narrow Es type layer (convergence instability) and the importance of balancing this convergence by ambipolar diffusion will be taken into account. We also solve the ion/electron continuity equation with analytical approach, which, similar to solutions (2)-(4), shows the formation of the Es layer and the tendency for its localization in the region of nodes of ion drift velocity $w_{iv}$. We use the analytical profiles of ion/electron density to set initial conditions, an then solve their basic equation, which takes into account the presence of wind with arbitrary direction, using numerical methods in the following cases: 1) in the presence of vertical wind only, 2) in the presence of horizontal wind whose meridional and zonal components are determined by HWM14 data and 3) in the presence of wind determined by above mentioned vertical and zonal components. In these cases the process of formation and localization of the Es layer throughout the night (covering 12-hour interval) will be shown. Assuming the presence of a vertical wind component, we demonstrate its significant influence on the formation and localization of the Es layer, demonstrated numerical results align with its analytically predicted behavior. Additionally, we will show the impact of vertical wind on the ion/electron depletion process.

The neutral particles with velocity $V(V_x,\hspace{0.17em} V_y\hspace{0.17em}{V}_z)$ in the lower thermosphere influence the ion vertical drift via combined action of the Lorentz forcing and ion-neutral collision. We take a right-handed set of coordinates (x, y, z) with x directed to the magnetic north, y to the west and z vertically upward. In this case the dependence of the ions vertical drift velocity $w_i$ on the neutral wind velocity, taking into account their ambipolar diffusion ($\propto D_a$), can be described by the equation [20,27,28]:

$${\mathrm{w}}_i={\mathrm{w}}_{iv}-D_a(z)\frac{1}{N_i}\frac{\partial N_i}{\partial z}$$

(6)

where the influence of neutral wind velocity $V(V_x,\hspace{0.17em} V_y\hspace{0.17em}{V}_z)$ on the ion vertical drift velocity$w_i$ is considered in the value of ${\mathrm{w}}_{iv}$, which has the following form [2,21,28]:

$${\mathrm{w}}_{iv}(z,t)=-C_x(z)V_x(z,t)-C_y(z)V_y(z,t)+C_z(z)V_z(z,t)$$

(7)

Here, considerations of the recent studies [10,24] are extended and Equation (7) for ${\mathrm{w}}_{iv}$takes into account not only the horizontal $V_x$ (meridional) and $V_y$ (zonal) components of neutral wind velocity, but also the influence of its vertical $V_z$ components on ion vertical drift velocity is included.

In Equations (6) and (7):

$$C_x(z)=\frac{1}{1+{\kappa }^2(z)}\sin I\cos I$$

(8)

$$C_y(z)=\frac{\kappa (z)}{1+{\kappa }^2(z)}\cos I$$

(9)

$$C_z(z)=\frac{{\sin }^{2}I+{\kappa }^2(z)}{{\kappa }^2(z)+1}$$

(10)

$$D_a(z)=\frac{{\kappa }^2(z)+{\sin }^{2}I}{1+{\kappa }^2(z)}\frac{2kT}{m_i{\nu }_{in}(z)}$$

(11)

Here$\kappa (z)={\nu }_{in}(z)/{\omega }_i$, ${\nu }_{in}$ is the ion-neutral collision frequency, whose height profile will be used similarly to the one applied in [10,36]. ${\omega }_i=eB/m_i$ is the ion gyrofrequency; $B(B_x=B\cos I,\hspace{0.17em}0,\hspace{0.17em}{B}_z=-B\sin I)$ is the Earth’s magnetic field vector, I is the magnetic dip angle. $T=(T_e+T_i)/2$ is the mean plasma temperature; $T_i$ and $T_e$ are the ion and electron temperatures respectively; $k_B$ is the Boltzmann constant; $m_i$ is the ion mass.

To investigate the behavior of the height profile of electron/ion density $N_e(z,t)$ (described in the previous section) in more details, assuming quasi-neutrality $N_e=N_i$, neglecting production Q and loss rates L, and using ions vertical drift velocity, Equations (6) and (7), we rewrite the continuity Equation (1) as follows:

$$\frac{\partial N_i}{\partial t}=C_t^{\text{'}}{N}_i-w_{iv}\frac{\partial N_i}{\partial z}+\frac{\partial }{\partial z}\left(D_a\frac{\partial N_i}{\partial z}\right)$$

(12)

where

$$C_t^{\text{'}}(z,t)\equiv -\frac{\partial w_{iv}}{\partial z}=C_v^{\text{'}}(z,t)+C_{sh}^{\text{'}}(z,t)+C_{vz}^{\text{'}}(z,t)$$

(13)

Here, in the value of ions/electrons total convergence $C_t^{\text{'}}(z,t)>0$ ($\frac{\partial w_{iv}}{\partial z}<0$) or divergence $C_t^{\text{'}}(z,t)<0$ ($\frac{\partial w_{iv}}{\partial z}>0$) rate, Equation (13), we have separated the terms depending on: (1) the effects of wind velocity direction (with meridional $V_x(z,t)$, zonal $V_y(z,t)$ and vertical $V_z(z,t)$ components) and magnitude described by $C_v^{\text{'}}(z,t)$; (2) the effects of meridional and zonal wind velocity vertical shear ($\frac{\partial V_x(z,t)}{\partial z}$ and $\frac{\partial V_y(z,t)}{\partial z}$) described by $C_{sh}^{\text{'}}(z,t)$and (3) the effects of vertical changes of wind velocity vertical component ($\frac{\partial V_z(z,t)}{\partial z}$) described by $C_{vz}^{\text{'}}(z,t)$. In this case, see Equation (7), $C_v^{\text{'}}(z,t)$, $C_{sh}^{\text{'}}(z,t)$ and $C_{vz}^{\text{'}}(z,t)$ have the following forms:

$$C_v^{\text{'}}(z,t)=V_x(z,t)\frac{\partial C_x(z)}{\partial z}+V_y(z,t)\frac{\partial C_y(z)}{\partial z}-V_z(z,t)\frac{\partial C_z(z)}{\partial z}$$

(14)

$$C_{sh}^{\text{'}}(z,t)=C_x(z)\frac{\partial V_x(z,t)}{\partial z}+C_y(z)\frac{\partial V_y(z,t)}{\partial z}$$

(15)

$$C_{vz}^{\text{'}}(z,t)=-C_z(z)\frac{\partial V_z(z,t)}{\partial z}$$

(16)

Equations (14)-(16) show that the neutral meridional $V_x(z,t)$, zonal $V_y(z,t)$ , vertical $V_z(z,t)$ wind velocity factors $-C_x$ , $-C_y$ ,$C_z$ , of ion vertical drift velocity $w_{iv}$, Equation (6), as well as their vertical changes $\frac{\partial C_x(z)}{\partial z}$, $\frac{\partial C_y(z)}{\partial z}$ ,$\frac{\partial C_z(z)}{\partial z}$ significantly determine the condition of the ion/electrons convergence ($(\frac{\partial w_{iv}}{\partial z})\min <0$) or divergence ($(\frac{\partial w_{iv}}{\partial z})\max >0$) caused by the magnitude and direction of velocity V and its vertical changes ($\frac{\partial V_x(z,t)}{\partial z}$ , $\frac{\partial V_y(z,t)}{\partial z}$ and $\frac{\partial V_z(z,t)}{\partial z}$). The role of ambipolar diffusion of ions ($\propto D_a\frac{\partial N_i}{\partial z}$), Equations (6) and (11), is also important in the development of these processes.

In this case the tendency of ion/electron convergence into a thin layer, when minimal negative value in $\frac{\partial w_{iv}}{\partial z}$ (maximal value of $C_{tot}^{\text{'}}(z,t)$) is present, also can be seen and analyzed from analytic approach of solution of Equation (12), which has the following form:

$$\begin{array}{l}{N}_e(z,t)\approx N_{om}\exp \left\{\left[-\frac{2D_a}{H_{ic}^2}+C_t^{\text{'}}(z,t)\right](t-t_o)-{\left(\frac{z-[z_{om}+w_{iv}(t-t_o)]}{H_{ic}}\right)}^2\right\}\\ \end{array}$$

(17)

Here the slight changes in $C_t^{\text{'}}(z,t)$ over time $t-t_o<<H_{ic}^2/2D_a$ are assumed.

$H_{ic}$ is the characteristic scale height of ions which at some initial time $t=t_o$ determines the main ion/electron layer thickness ($2H_{ic}$) and the height region $z-z{}_{om}=\pm H_{ic}$, where their density decreases by factor of e. $\frac{H_{ic}^2}{2D_a}$ is the characteristic time of the ion density decrease by their ambipolar diffusion. The behavior of ion/electron density described by Equation (17) is similar to Equation (3) under assumption of Gaussian type distribution, at the initial time $t=t_o$, with the maximal density (peak density)$N_{om}$ at the height $z=z_{om}$ (initial peak height). When $C_t^{\text{'}}(z,t=t_o)>\frac{2D_a}{H_{ic}^2}$, then Equation (17) shows a tendency of formation of ions/electrons high density sporadic Es-type layer ($\frac{N_m(t>t_o)}{N_{om}}>1$). The peak height of this layer varies in time as follows:

$$z=z_{om}+w_{iv}(t-t_o)$$

(18)

i.e. moves upward ($w_{iv}>0$) or downward ($w_{iv}<0$) by ions vertical drift velocity $w_{iv}$ and it could be localized at the height region with $w_{iv}=0$ (the drift velocity node). When $C_t^{\text{'}}(z,t=t_o)<0$ occurs at the region of ion drift velocity node, ion/electron density experiences depletion ($\frac{N_m(t>t_o)}{N_{om}}<1$), as predicted by Equation (17).

Thus, the behavior of the ion/electron density profile described by Equation (17), which is similar to [10,24], shows the tendency of Es layer formation, when considering both horizontal and vertical winds. This solution takes into account the effect of ions ambipolar diffusion on the density of their layer, as well as its vertical drift, Equation (18). In this case, the velocity factor $C_z(z)$ and its vertical change profile $\frac{\partial C_z(z)}{\partial z}$, the Equation (15), significantly determine the effect of the vertical wind on the ions/electrons vertical drift, Equation (7), and on their convergence into an Es type layer. These quantities, as well as these ones: the meridional $C_x(z)$ and zonal $C_y(z)$ velocity factors, their vertical changes $\frac{\partial C_x(z)}{\partial z}$ and $\frac{\partial C_y(z)}{\partial z}$, the meridional and zonal wind vertical shears, the vertical changes of vertical wind determine the minimal negative value of vertical changes of the ion vertical drift velocity, Equation (13), necessary for formation of the Es type layer, Equation (17).

3. Numerical results and discussion

In order to assess the role of vertical wind in the process of ion convergence, as the first step, we present (numerically) the behavior of ions/electrons, described by Equation (12), in the night conditions, in the cases of constant vertical wind directed upward ($V_z>0$) or downward ($V_z<0$). Similarly, we consider the behavior of ions/electrons density and the possibility of Es layer formation under the influence of horizontal wind, with the meridional $V_x$ and zonal $V_y$ components of the velocity determined by HWM14 data. Further, in order to illustrate the influence of the vertical component of the three-dimensional (arbitrary direction) wind on the ions/electrons density and accordingly, on the formation of the Es layer, we will incorporate the vertical component in the model horizontal wind. As an example, we will choose a vertical wind velocity magnitude of $V_z=\pm 4m/s$. This value, in the lower thermosphere, is about an order of magnitude lower than the typical values of meridional and zonal wind speeds caused by tidal motions (about 30-80 m/s) [37]. Neutral wind velocity vertical component of this magnitude and higher can be caused by both tidal motions and the propagation of AGWs frequently observed in the lower thermosphere and mesopause regions [34,35].

We will perform numerical simulations for the location of the initial layer of ions at: (1)$h_{om}=115\mathrm{km}$, where their maximal density in the E region is mostly observed, and (2)$h_{om}=100\mathrm{km}$, where high density of metallic ions (e.g., Fe+) is expected [31]. These initial ion/electron distributions $N_i(z,t=t_o)=N_e(z,t=t_o)\equiv N_o(z)$ correspond to the Gaussian-type distribution defined at the initial moment $t=t_o$ by Equation (17), where the ion scale is chosen to be approximately twice as large ($H_{ic}=16\mathrm{km}$ ) as the atmospheric scale (H=8-10km). In the presented simulation, the neutral particle densities of the lower thermosphere are used from the NRLMSISE-00 model [38], for the mid-latitude regions 45° ± 2° N, 45° ± 2° E, and I = 61° ± 2°.

The height profile of the ion vertical drift velocity $w_i(z,t)$, its vertical changes $\partial w_i(z,t)/\partial z$ and correspondingly the ion/electron density $N_i(z,t)=N_e(z,t)$, Equation (11), will be solved numerically similarly to [10,39,40,41] for whole night $t-t_o\le 12h$.

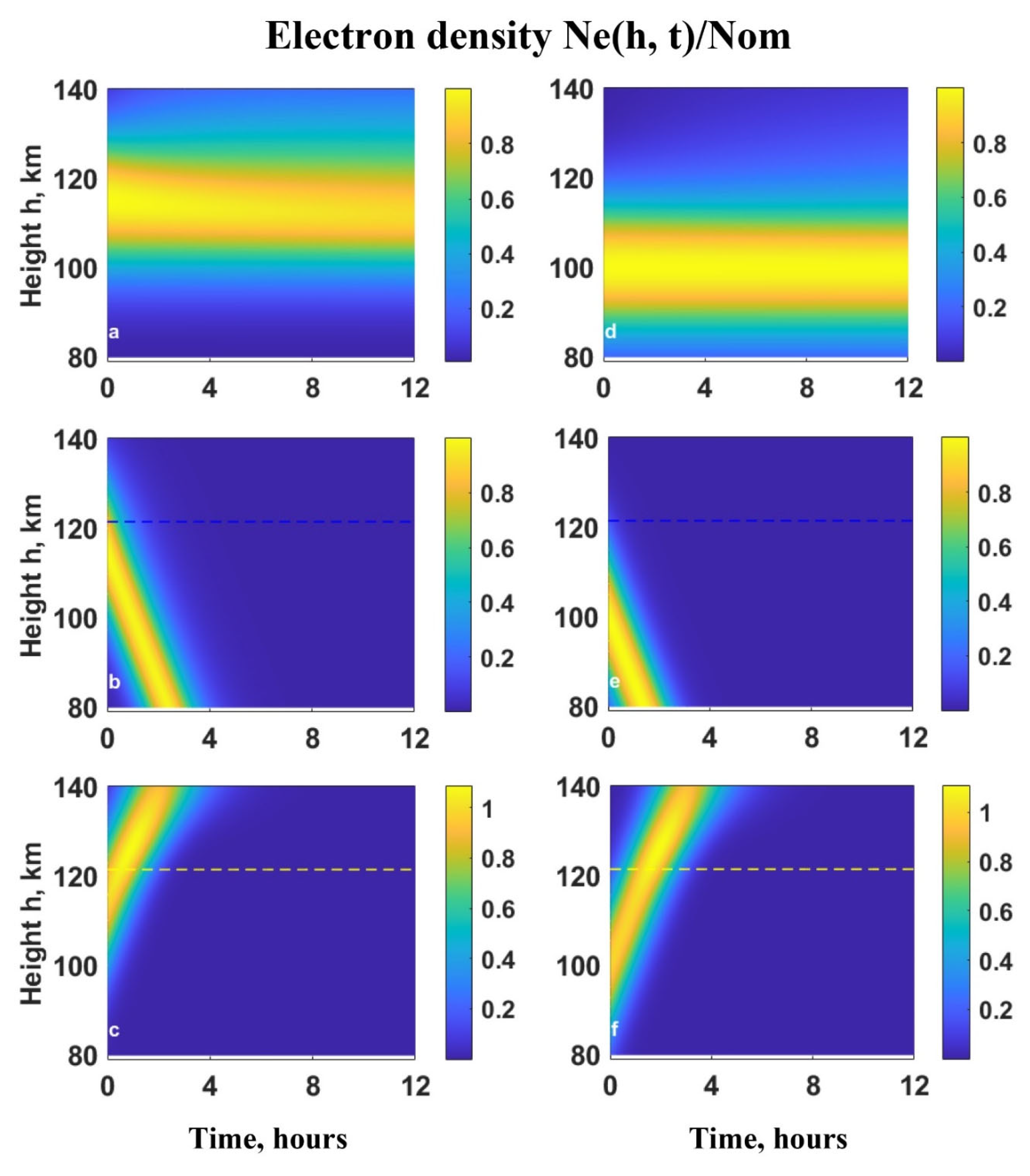
Figure 2 shows that the initial layer of ion/electron density $N_i(z,t=t_o)=N_e(z,t=t_o)\equiv N_o(z)$ (panel a) undergoes a slight decrease caused by the ions ambipolar diffusion. The downward neutral wind velocity $V_z=-4m/s$ causes ions downward flux with velocity ${\mathrm{w}}_{iv}(z,t)=C_z(z)V_z$ accompanied by maximal decrease of density at height h≈121km (panel b) by divergence rate $C_{v\min }^{\text{'}}(V_x=0,\hspace{0.17em}V=0,\hspace{0.17em}{V}_z=-4m/s)=-4.9\cdot {10}^{-5}{s}^{-1}$. The upward neutral wind with $V_z=4m/s$ (panel c) causes ions/electron upward flux, accompanied by their increased diffusive displacement for upper heights and convergence with maximal rate $C_{v\max }^{\text{'}}(V_x=0,\hspace{0.17em}V=0,\hspace{0.17em}{V}_z=4m/s)=4.9\cdot {10}^{-5}{s}^{-1}$ at h≈121 km resulting in density increase (up to about 1.09) for time $t-t_o\le 0.9h$.

The similar behavior of the ion/electron density occurs for its initial distribution with peak height at $h_{om}=100\mathrm{km}$ (Figure 2d) and undergoes negligibly small changes due to ambipolar diffusion. In this case downward neutral wind with $V_z=-4m/s$ causes most of the initial layer downward flux by ion drift velocity ${\mathrm{w}}_{iv}(z,t)=C_z(z)V_z$, which is about the same as neutrals velocity (${\mathrm{w}}_{iv}\approx V_z$) for lower heights about h<110km ($C_z\to 1$ , Figure 1a ). In this case at ions divergence rate peak height h=121km for time interval $t-t_o\le 3h$ relatively significant decrease ($N_e(h=121\mathrm{km},t-t_o=3h)/N_o(h=121\mathrm{km},\hspace{0.17em}t=t_o)\approx 0.003$) occurs compared to the upper location of initial layer ($N_e(h=121\mathrm{km},\hspace{0.17em}t-t_o=3h)/N_o(h=121\mathrm{km},\hspace{0.17em}t=t_o)\approx 0.02$). For this lower location of initial layer the upward neutral wind $V_z=4m/s$ causes upward drift of this layer, which converges ($N_e(h=121\mathrm{km},t-t_o)/N_o(h=121\mathrm{km},\hspace{0.17em}t=t_o)>1$) at about h=121km, with a slightly smaller density ($N_e(h=126\mathrm{km},t-t_o=0.9h)/N_{om}(h_{om}=100\mathrm{km},\hspace{0.17em}t-t_o=1.9h)\approx 1.07$), compared to the one at upper location of initial peak ($N_e(h\approx 126\mathrm{km},t-t_o=0.9h)/N_{om}(h_{om}=115\mathrm{km},\hspace{0.17em}t-t_o=1.9h)\approx 1.09$), and peak value at about height region h=126km occurs a little later $t-t_o=1.9h$, than in the case when the initial peak is located at upper height.

So the vertical wind can influence the dynamics of ion/electrons convergence processes in the lower thermosphere. In the considered cases of constant wind velocity $V_z$ (Figure 2) the maximal/minimal value of convergence/divergence rate determined by the peak value of $-\frac{\partial C_z}{\partial z}$, Equation (19), and located at the same height about h=121km (with ${\nu }_{in}={\omega }_i$). This location is the same (Figure 1) as the one of the maximal value of vertical changes of the meridional wind velocity factor $\frac{\partial C_x}{\partial z}$.

So, the ion/electron convergence/divergence rate due to vertical neutral wind always occurs in the lower thermosphere, and its influence on their density, in combination with horizontal wind is expected to be important. In this case the atmospheric waves, i.e., AGWs can also cause regions (spaced with distances about vertical wavelength) with maximal ($C_{vz\max }^{\text{'}}>0$)/minimal ($C_{vz\min }^{\text{'}}<0$) values in $C_{vz}^{\text{'}}$, Equation (16) and the development of additional convergence/divergence processes and formation of multilayered sporadic E is expectable similarly to the cases given in [24].

The presence of neutral wind with meridional and zonal components will have combined effect on ions/electron convergence/divergence processes. In this case the existence of the region with minimalized downstream and upstream flows (e.g., $w_{iv}=0$), Equation (7), is possible and additional convergence (or divergence) of ions at height (h=121km) with $C_{z\max }^{\text{'}}=\frac{{\cos }^{2}I}{2H}$ can be more important for ions convergence close to this height region, compared to the case of absence of meridional and zonal components i.e. compared to the case of only vertical wind (Figure 2).

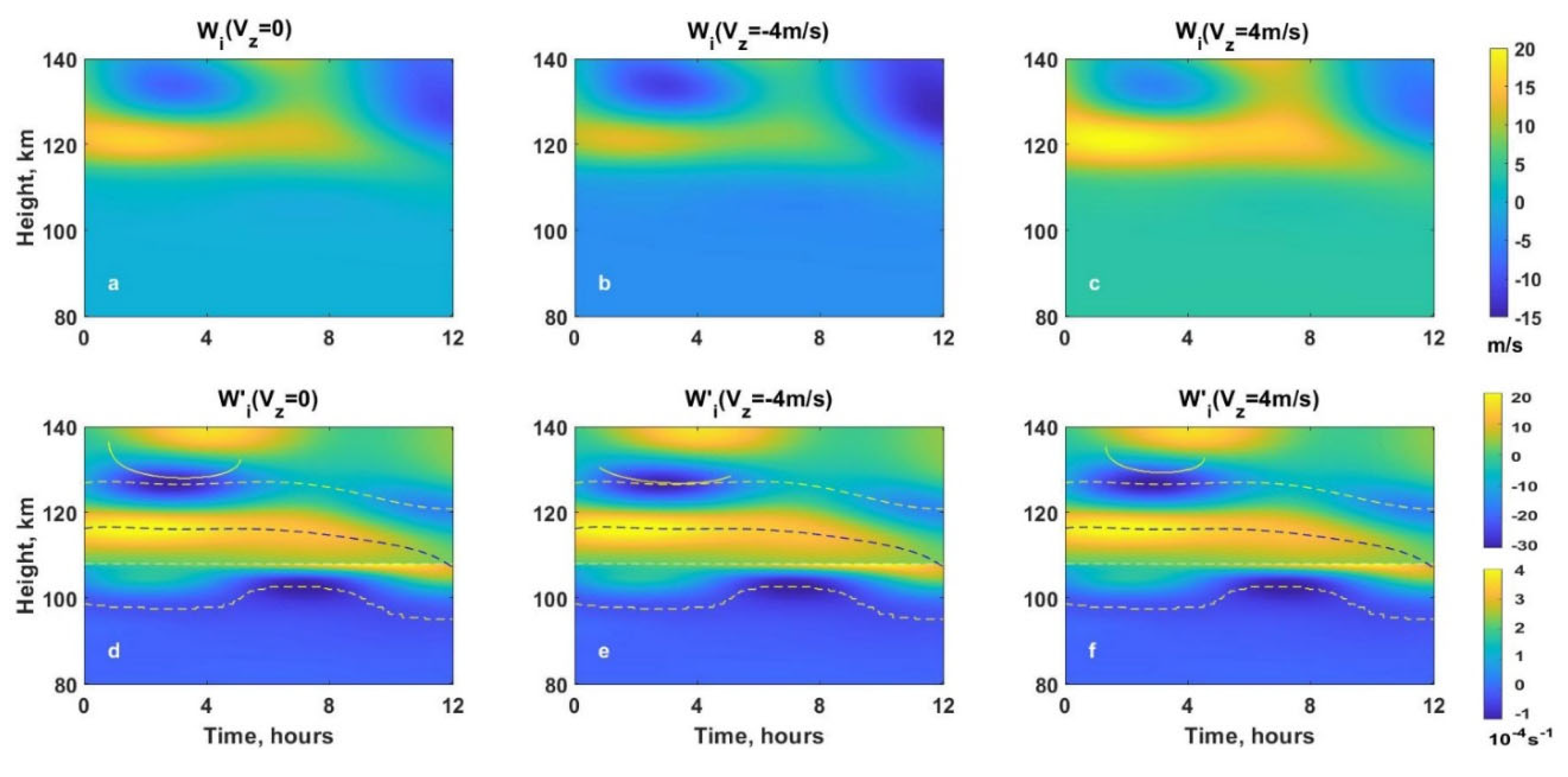
Thus, the vertical wind can have a significant effect on the vertical movement of the ion/electron layer, as well as on their convergence/depletion process. Note that for a constant vertical wind ($V_z=\pm 4m/s$), the height profile of the ion drift velocity ${\mathrm{w}}_{iv}(z,t)=C_z(z)V_z$ is proportional to $C_z$ (Figure 1a), Equation (7). Therefore, the height profile of its vertical change $\frac{\partial w_{iv}}{\partial z}=-V_z\frac{\partial C_z}{\partial z}$, determining ion convergence rate, Equation (14), is proportional to $-\frac{\partial C_z}{\partial z}$ (Figure 1b) . For sake of brevity these profiles are not demonstrated.

We consider the only horizontal wind whose meridional $V_x(z,t)$ and zonal $V_y(z,t)$ velocities are determined by the HWM14 data [33], as well as the cases when the vertical component ($V_z=\pm 4m/s$) is incorporated. In these cases, we will estimate the profiles of the ions vertical drift velocity and its vertical change. Also, we will identify the regions of maximum convergence ($C_{t\max }^{\text{'}}>0$) and divergence ($C_{t\min }^{\text{'}}<0$) rates of ions/electrons, as well as regions (with$w_{iv}=0$) where the formation of the Es type layer is possible. In the same cases, the behavior of ions/electrons during the night will be presented and processes of expected Es type layer, along with processes of ion/electron density depletion will be shown.

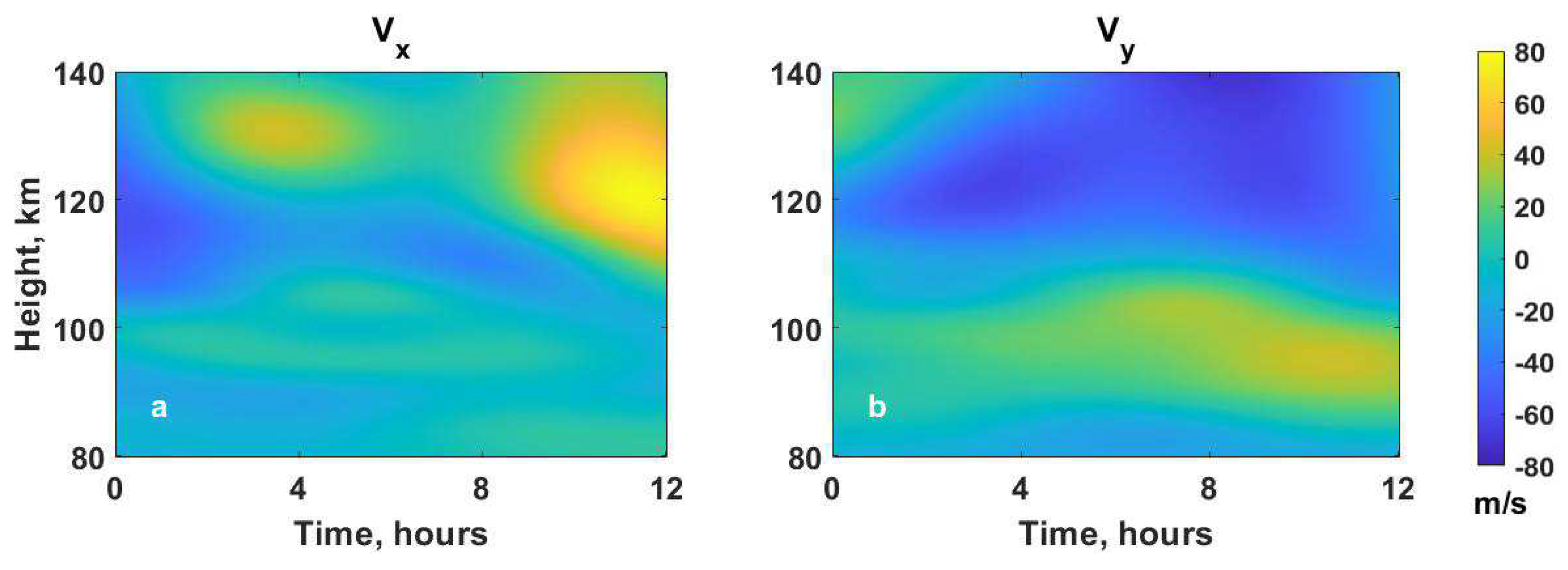
Figure 3 demonstrates nightly variations of the typical height profiles of (a) the meridional wind velocity $V_x(z,t)$ and (b) the zonal wind velocity $V_y(z,t)$, described by HWM14 data (Day102, $t_o=UT\hspace{0.17em}20:00$). To determine the height profile of the ions vertical drift velocity $w_{iv}$ , Equations (7)-(10), and its vertical changes $\frac{\partial w_{iv}}{\partial z}$, Equations (13)-(16), we will use the above mentioned meridional $V_x(z,t)$ and zonal $V_y(z,t)$ wind velocity data (Figure 2), as well as the data where the vertical wind with $V_z=-4m/s$ and $V_z=4m/s$is incorporated.

Figure 4a-c show that in the lower thermosphere, in case of existence of neutral wind, the ion vertical drift velocity $w_{iv}$, height profile is characterized by regions with $w_{iv}=0$ or $w_{iv}\to 0$. In these cases vertical changes of the ion vertical drift velocity (Figure 4d-f) also have minimal negative values $\left(\frac{\partial w_{iv}}{\partial z}\right)\min <0$ ($C_{t\max }^{\text{'}}>0$). According to Equations (17) and (18), in the regions where above mentioned conditions are satisfied the Es type layers can be formed. These layers are localizing at regions with $w_{iv}=0$ or descent to the regions where$w_{iv}\to 0$.

In case of presence of wind with downward vertical velocity component $V_z=-4m/s$ (Figure 2b,e) the regions with $w_{iv}=0$ are shifted downward compared to the case of only horizontal wind (Figure 4a,d). For example, the height regions with $w_{iv}=0$ (Figure 4a) and highest minimal negative value in $\left(\frac{\partial w_{iv}}{\partial z}\right)\min <0$ ($C_{t\max }^{\text{'}}>0$) (about -0.003s^-1), located at about 128 km-129km (Figure 4d), for time interval$1.5h\le t-t_o\le 4.5h$ (Figure 4a), are shifted downward to about 126-127 km (Figure 4b).

In case of upward component of the neutral wind velocity with $V_z=4m/s$ (Figure 4f) the regions of upper nodes are displaced upward. For example the height regions with $w_{iv}=0$ located at about 128-129 km, for time interval$1.5h\le t-t_o\le 4.5h$, are displaced upward to about 129-130km (Figure 2c).

At lower heights h<110, in case of only horizontal wind ($V_z=0$), the ion drift velocity vanishes $w_{iv}\to 0$ (Figure 4a), Equations (7)-(10). When the vertical wind component is directed upward ($V_z>0$) or downward ($V_z<0$), then for these regions of lower thermosphere (about h<110km) the ion vertical drift velocity is directed downward with $w_{iv}\to -4m/s$ or upward with$w_{iv}\to 4m/s$, respectively.

Figure 4 also shows the presence of the regions with $\left(\frac{\partial w_{iv}}{\partial z}\right)\max >0$ ($C_{t\min }^{\text{'}}<0$), where ion/elecrons depletion are expectable. Altitude of these regions vary in the height interval from about 116 km ($t=t_o$) to 112 km ($t-t_o=12h$ ). The noticeable minimal values about $C_{t\min }^{\text{'}}\approx -0.0021\hspace{0.17em}{s}^{-1}$ occur for time$t-t_o\approx 1.7h$. The presence of the constant downward $V_z=-4m/s$ (panel e) and upward $V_z=4m/s$ (Figure 4f) vertical components of neutral wind do not give significant changes in these parameters compared to those in case only horizontal wind (Figure 4d).

We will demonstrate the behavior of ion/electron density height profile $N_e(z,t)/N_{om}$ and formation of the Es type high density thin layer (with peak density $N_{em}/N_{om}>1$ and $H_{ic}(t=t_o)>H_{ic}(t>t_o)$ or/and ion/electron density depletion ($N_e/N_{om}<<1$). These phenomena can be predicted by analyses of ions drift velocity$w_i(z,t)$ (Figures 4a-4c) and its vertical changes $\frac{\partial w_{iv}}{\partial z}$ (Figures 4d-4f) which are estimated using HWM14 data of meridional $V_x(z,t)$ and zonal wind velocities $V_y(z,t)$ (Figure 3a,b).

Neutral wind leads to the existence of the regions where the condition $\left(\frac{\partial w_{iv}}{\partial z}\right)\min <0$ i.e. $C_{t\max }^{\text{'}}>0$ is satisfied (Figure 3 and Figure 4). Figure 5 shows that, close to the above mentioned regions, the formation of the Es layers and its localization at regions with $w_i=0$ ( all panels) and $w_{iv}\to 0$ (Figure 5a,d) occurs. For the used horizontal wind profile (Figure 3) the high density Es layer $N_{m1}/N_{om}=5.4$ (with $H_{ic}=1.8\mathrm{km}$) is formed for time around $t-t_o\le 3-5h$ (Figure 5a,d) at location of ion drift velocity node $h_{m1}=128\mathrm{km}$ ($w_i=0$). Also, the secondary Es layer with $N_{m2}/N_{om}=1.02$ is formed at time $t-t_o=12h$ at lower heights ($h_{m2}<100\mathrm{km}$) and it descends towards the height about$h_{m2}=93.4\mathrm{km}$ where $w_{iv}\to 0$. When the density peak height the ion/electron initial distribution is relatively higher $h_{om}=115\mathrm{km}$ (close to height region of upper maximum of convergence rate $C_{t\max }^{\text{'}}>0$ and node $w_i=0$) the density in the upper Es layer (with $H_{ic}=1.8\mathrm{km}$) is higher $N_{m1}/N_{om}=5.4$ (Figure 5a) than when initial distribution density peak height is lower $h_{om}=100\mathrm{km}$, ($N_{m1}/N_{om}=2.8$,$H_{ic}=1.8\mathrm{km}$) (Figure 5d). In these cases (Figure 5a,d) , the lower location (close to the lower maximum of convergence rate $C_{t\max }^{\text{'}}>0$ around h=99km-104km) of initial peak height (panel d, $h_{om}=100\mathrm{km}$) causes higher density $N_{m2}/N_{om}=2.7$ in the lower Es layer ($h_{m2}=93.4\mathrm{km}$) (Figure 5d) than in case of higher location $h_{om}=115\mathrm{km}$ of initial peak height (Figure 5a).

Figure 5 also shows existence of divergence region with $C_{t\min }^{\text{'}}<0$, where the ion/electron density continuously decreases/deplete ($N_e(z,t)/N_{om}<1$). The location of this region varies in the height interval from 116 km ($t=t_o$) to 112 km ($t-t_o=12h$ ) . For example, at time $t-t_o=3h$, for the higher location of the initial peak height $N_e(h=116\mathrm{km},\hspace{0.17em}{h}_{om}=115\mathrm{km},\hspace{0.17em}t-t_o=3h)/N_o(h=116\mathrm{km},\hspace{0.17em}\hspace{0.17em}t=t_o)\approx 0.02$ (Figure 5a), while for lower location$N_e(h=100\mathrm{km},\hspace{0.17em}{h}_{om}=115\mathrm{km},\hspace{0.17em}t-t_o=3h)/N_o(h=116\mathrm{km},\hspace{0.17em}\hspace{0.17em}t=t_o)\approx 0.09$ (Figure 5d).

Below the height regions of ions depletion (e.g., h<110km) where the ions drift velocity $w_{iv}\to 0$, at around h=105km the ion/electron total convergence rate is maximal $C_{t\max }^{\text{'}}\approx (2\pm 9)\cdot {10}^{-5}{\sec }^{-1}$ and there ions converge into descending ($w_i\to -0$) Es type layer ($N_e(z,t)/N_{om}>1$), with continuous increase of densities and with the peak height located at about $h_{m2}=93.4\mathrm{km}$ at $t-t_o=12h$. Here, the peak density of the formed Es $N_{m2}/N_{om}=1.02$ (Figure 5a) is smaller for higher location of ion/electron initial layer ($h_{mo}=115\mathrm{km}$) compared to those for lower location (close to the region with $C_{t\max }^{\text{'}}>0$) of initial layer ($h_{mo}=100\mathrm{km}$) when $N_{m2}/N_{om}=2.7$ (Figure 5d).

So, in case of presence of horizontal wind with only meridional and zonal components of velocities (Figure 3) two regions with condition $C_{t\max }^{\text{'}}>0$ (Figure 4) occur. This leads to formation of sporadic E with double peak at about $h_{m1}=128\mathrm{km}$ and $h_{m2}=93.4\mathrm{km}$ (Figure 5a,d). In this case the upper Es layer is located at the height region with $w_{iv}=0$ ($h_{m1}=128\mathrm{km}$) while the lower one descends to the height region where ions vertical drift velocity vanishes $w_{iv}\to 0$.

Figure 5b and Figure 5e show that the downward direction of vertical component of wind velocity $V_z<0$, which causes an increase of ion/electron downward flux, in case of $V_z=-4m/s$, leads to the lower location $h_{m1}(V_z=-4m/s)=126.4\mathrm{km}<h_{m1}(V_z=0)=128\mathrm{km}$ of the ion vertical drift velocity node ($w_i=0$) and therefore, the Es layer formation occurs at about $h_{m1}=126.8\hspace{0.17em}\mathrm{km}$. Here the higher location of the initial density peak height ($h_{mo}=115\mathrm{km}$) and increase of ion/electron flux from upper regions to the region of ion drift velocity node h≈126.4km lead to the higher density $N_{m1}/N_{om}=5.6$ ($H_{ic}=1.7\mathrm{km}$) (Figure 5b) in the formed Es layer for time around $t-t_o=3.4h$. Here, the relatively small value in the ions diffusive displacement to the heights above its convergence region also causes increase in their peak density. In the case of the lower location, below the divergence region (about height 116 km) of the initial layer ($h_{mo}=100\mathrm{km}$) the increased downward flux of ions, caused by downward vertical wind with $V_z=-4m/s$, lead to the formation of sporadic E with relatively lower density $N_{m1}/N_{om}=1.3$ ($H_{ic}=1.7\mathrm{km}$) and at the lower location 126.4km (Figure 5e), than in the case of higher location of initial density peak (Figure 5b).

Figure 5b and Figure 5e show that the downward wind with additional depletion around h≈121km region (Figure 2b,e) causes relatively higher decrease in ion electron density, compared to the case of the wind with only horizontal components of velocity.

In the case of downward vertical wind velocity, secondary high density Es layers are not formed at the lower heights h<110 km. This is because, unlike the case of wind with only horizontal velocity components, the region with $w_{iv}\to 0$ does not occur and ion/electrons layer descends with velocity close to neutral vertical wind velocity $w_{iv}\approx -4m/s$ ($w_{iv}\approx V_z$) without significant changes in its density (Figure 5b and Figure 5e). During the downward drift with velocity $w_{iv}\approx -4m/s$, the ion/electrons cross the region of their convergence rate maximum (around h=99-104 km) within short time (about 1 hour). For the values$C_{t\max }^{\text{'}}\approx 2\cdot {10}^{-5}{\sec }^{-1}$ this does not lead to the significant increase in the ion/electrons density neither in case of higher ($h_{mo}=115\mathrm{km}$) nor lower ($h_{mo}=100\mathrm{km}$) location of the initial layer. As a result, the formation of the secondary Es type layer ($N_e(z,t)/N_{om}>1$) at lower heights <110km does not occur. Figure 5c and Figure 5f show that the wind velocity component directed upward $V_z>0$ causes the additional upward drift of ions/electrons i.e. reduction in their downward drift velocity, Equation (7). In this case the value of $V_z=4m/s$ leads to the relatively higher location of ions drift velocity node $w_i(h\approx 129.4\mathrm{km})=0$ (compared to $h_{m1}=128\mathrm{km}$ in the case of $V_z=0$) and the Es layer formation occurs at about $h_{m1}=129.4\mathrm{km}$. In this case, of the higher location of the ion/electron initial layer ($h_{mo}=115\mathrm{km}$) the additional ion/electron upward drift and increase in ambipolar diffusion also lead to the lower density $N_{m1}/N_{om}=1.9$ (Figure 5c) in the formed Es layer than it was in cases of $V_z=0$ (Figure 5a) and $V_z=-4m/\sec$ (Figure 5b).

The lower location of the initial peak height ($h_{mo}=100\mathrm{km}$) and upward vertical wind ($V_z=-4m/\sec$) support the increase of ion/electron flux from lower to upper heights and their additional convergence at the height region about 121km (Figure 2f) lead to the relatively high density $N_{m1}/N_{om}=4.7$ in this Es layer formed at about 129.4km height compared to the densities in Es layers formed for cases of $V_z=0$ ($N_{m1}/N_{om}=2.7$, $h_{m1}=128\mathrm{km}$ – Figure 5d) and $V_z=-4m/\sec$ ($N_{m1}/N_{om}=1.3$, $h_{m1}=126.8km$ - Figure 5e). In this case, in spite of relatively lower value of the convergence rate, due to upward vertical wind ($\approx 4.9\cdot {10}^{-5}{\sec }^{-1}$), the combined effect of horizontal wind direction, its shear and vertical wind gives high density ($N_{m1}(Vz=4m/s)/N_{1m}(V_z=0)\approx 1.7$) in Es type layer at about 129.4km height.

The upward neutral wind and corresponding increased upward ion/electrons flux also result in their depletion in the divergence region (around 116 km). In both cases of the ion/electron initial layer being located at higher or lower altitudes their depletion in the divergence region with $C_{t\min }^{\text{'}}<0$ is bigger, compared to one during absence of vertical wind (Figure 5c and Figure 5f).

Figure 5c and Figure 5f also show that the increased ion/electrons upward flux at lower height (h<110km) due to upward vertical wind $V_z>0$ also results in their density rarefication at lower height regions with maximal values of convergence rate (99km-104km) and the formation of the secondary Es type layer at these height regions do not occur.

The upward/downward wind causes the vanishing of region with $w_{iv}\to 0$ at lower heights h<110 km ( $w_{iv}\approx V_z$) and the formation of Es type layer in this region is less expectable. So, in this case of vertical wind velocity, the necessary condition $C_{t\max }^{\text{'}}>0$ for Es layer formation at regions about 99km-104km occurs, but it is not sufficient for its formation. It is important to note, that the presence of condition $C_{t\max }^{\text{'}}>0$ for the formation of the Es type is necessary but not sufficient. In the considered cases (Figure 5) the condition $C_{t\max }^{\text{'}}>0$ occurs for whole night, but the development of the processes of ion/elecrons convergence into thin dense Es type layer also depends on initial distribution of these charged particles. For instance, if we use the same distribution for ion/electron density (Figure 2a and Figure 2d) for different moments of the night, then the convergence of ions/electrons into Es type layer and its localization will occur at the regions where conditions $C_{t\max }^{\text{'}}>0$, $w_{iv}=0$ and $w_{iv}\to 0$ are satisfied at particular moment of night mentioned above. This is not demonstrated for sake of brevity.

Note that we have demonstrated theoretically the formation of the Es layer for one typical wind profile, including the HWM14 data, for the meridional and zonal wind velocities at mid-latitudes (45^oN; 45^oS). This methodology is not limited to HWM14 and can be applied to other model data, as well as measured wind profiles, including the data close to real time.

We can also apply our model to different initial distributions of charged particles which fits both theory and measurements. In this case, by theoretically estimated height profile of ions vertical drift velocity$w_{iv}$, Equation (7), and $\frac{\partial w_{iv}}{\partial z}$ , the regions with conditions $\left(\frac{\partial w_{iv}}{\partial z}\right)\min <0$ ( $C_{t\max }^{\text{'}}>0$) necessary for development of ion/electron convergence into narrow dense Es type layer also can be identified. This layer is located at the altitudes with minimal value of ions upstream and downstream flows (e.g., $w_{iv}=0$) or it moves to the region with $w_{iv}\to 0$ and $C_{t\max }^{\text{'}}>0$. In this case the condition $C_{t\max }^{\text{'}}=(C_v^{\text{'}}+C_{sh}^{\text{'}}+C_{vz}^{\text{'}})\max >\frac{2D_a}{H_{ic}^2}$ necessary for sporadic E formation, for particular mid-latitude region (with given B and I), is determined not only by the horizontal ‘windshear’ convergence rate $C_{sh}^{\text{'}}$, Equation (15), but also by combined effect of rates caused by the realistic wind (three-dimensional) velocity magnitude, direction $C_v^{\text{'}}$ , Equation (14) and the vertical changes of vertical wind $C_{vz}^{\text{'}}$, Equation (16). Note, that in the lower thermosphere the value of ions ambipolar diffusion, Equation (10), does not exceed 0.00001 m² /s . As a result, the condition $C_{t\max }^{\text{'}}>\frac{2D_a}{H_{ic}^2}$ at initial time ($H_{ic}=10÷16km$) is satisfied for the small values (e.g., $\pm 4m/s$) of wind velocity. However, the effect of diffusion control on Es layer is important during its formation (e.g., when $H_{ic}=1÷3km$.

Below we demonstrate the values of $C_{t\max }^{\text{'}}>0$ and $C_{t\min }^{\text{'}}<0$ (Figure 4 and Figure 5) and corresponding values of parameters $C_v^{\text{'}}(z,t)$ and$C_{sh}^{\text{'}}(z,t)$. These values are determined by $\frac{\partial w_{iv}}{\partial z}$ profile, which in turn is estimated using the HWM14 data (Figure 3).

Figure 6 shows that the condition $C_{t\max }^{\text{'}}>0$ ( $\left(\frac{\partial w_{iv}}{\partial z}\right)\min <0$) necessary for ions/electron convergence into Es type thin layer (panels a and c) and the condition $C_{t\min }^{\text{'}}<0$ ($\left(\frac{\partial w_{iv}}{\partial z}\right)\max >0$) necessary for their divergence/depletion (panel b) are determined by combined effect of convergence/divergence rates $C_v^{\text{'}}(z,t)$ determined by wind velocity direction and magnitude, and $C_{sh}^{\text{'}}(z,t)$ determined by horizontal wind velocity vertical shear. For instance, in case of only horizontal wind, the convergence rate in upper Es layer, formed for time t-to=3-5hours at heights about 126-130 km (Figure 5), $C_{t\max }^{\text{'}}\approx 0.0027\hspace{0.17em}{s}^{-1}$(Figure 4 and Figure 5) is the sum of $C_v^{\text{'}}\approx 0.00099\hspace{0.17em}{s}^{-1}$ and $C_{sh}^{\text{'}}\approx 0.0017{\sec }^{-1}$. The latter shows that in the upper Es layer (Figure 5) about 60% of ion/electron convergence into this layer is attributed to the ‘shear effect’ (by the presence of horizontal wind with vertical shear).

At lower heights (h<110km), the higher value of $C_{t\max }^{\text{'}}\approx 9\cdot {10}^{-5}\hspace{0.17em}{s}^{-1}$, in Es layer (Figure 5a and Figure 5d), is primarily caused by the convergence rate $C_v^{\text{'}}$ which is determined by wind value and direction. In this region shear effect is negligible and even negative$C_{sh}^{\text{'}}<0$.

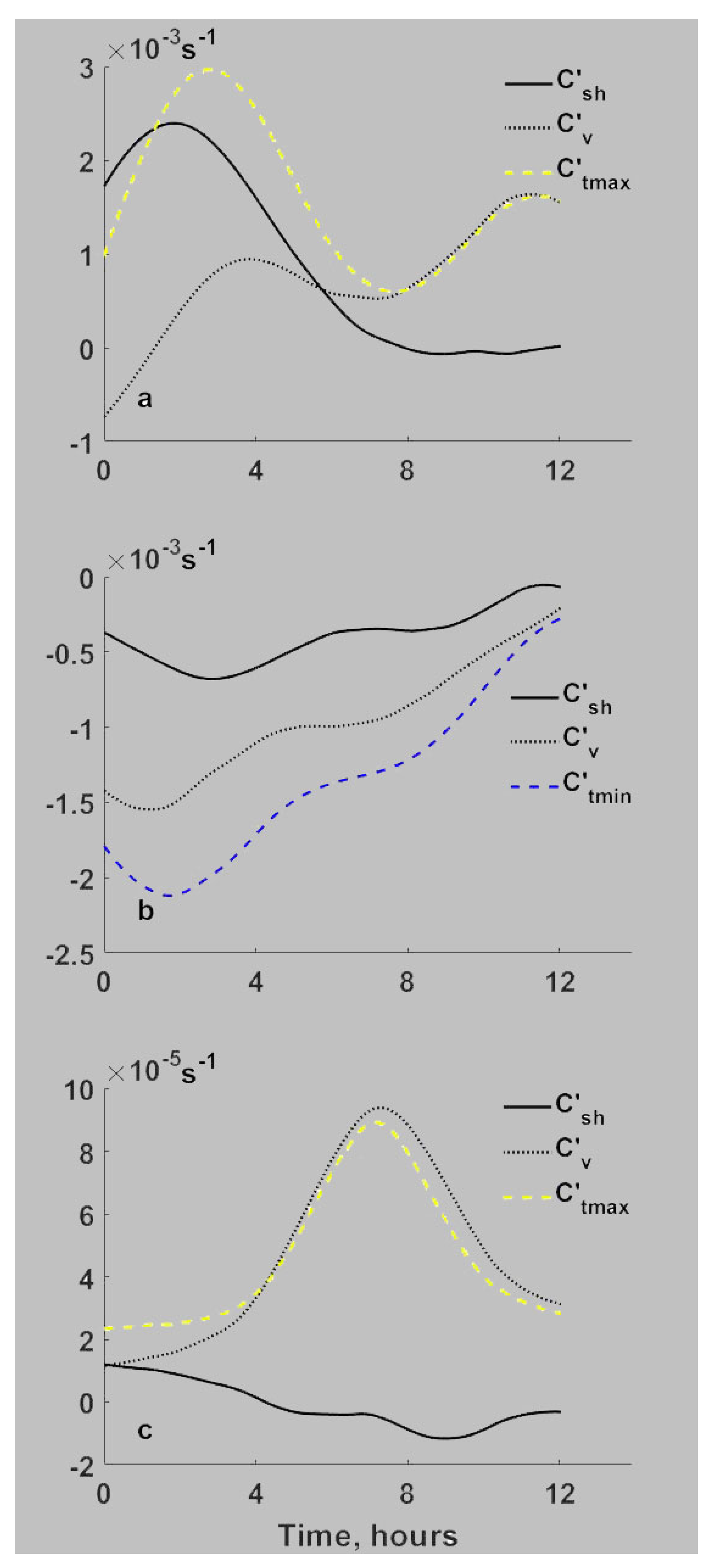
At the altitudes of approximately =116 km, in the time interval t-to<4h, the magnitude of $C_{t\min }^{\text{'}}<0$ $\left(\frac{\partial w_{iv}}{\partial z}\right)\max >0$) reaches $\approx -0.002\hspace{0.17em}1s^{-1}$, with approximately 30% ($C_{sh}^{\text{'}}\approx -0.0006s^{-1}$) of this value caused by the horizontal wind shear effect, while the remaining 70% ($C_v^{\text{'}}\approx -0.0015s^{-1}$) is determined by the wind magnitude and direction.

At the heights of the peaks of the upper Es layer (h=126km-130km), the divergence (≈116km), and lower Es layer (93-104km), the component of the wind velocity has negligible contribution in the values of $C_{t\max }^{\text{'}}>0$ and $C_{t\min }^{\text{'}}<0$. However, the ions, due to their vertical drift caused by vertical component of the wind velocity, pass through the region where only upward/downward vertical wind ($V_z=\pm 4m/s$) causes the maximum convergence/divergence effect ( height h≈121 km), therefore vertical wind component influences the densities of ions in Es layers as well as in the depletion regions.

The presented analytical and numerical study shows that the realistic (three-dimensional) profile of the neutral wind velocity in the lower thermosphere (h=90km-150km) significantly determines the behavior of ion/electrons density in this region and therefore, the regions of sporadic E (Es) formation and localization. Here, vertical profiles of the ions and vertical drift velocity and its vertical change, estimated by taking into account the vertical component of the wind velocity along with its horizontal component, influence the Es layer formation processes, since above mentioned profiles determine the condition, $\left(\frac{\partial w_i}{\partial z}\right)\min <0$ (or $C_{t\max }^{\text{'}}>0$) , necessary for ion/electron convergence into a narrow dense layer. Also, by the condition $\left(\frac{\partial w_i}{\partial z}\right)\max >0$ (or $C_{t\min }^{\text{'}}<0$) the location of ion/electrons depletion regions is identified. It is important to take into account the presence of vertical wind because it affects both the location of regions of ions/electrons convergence into a narrow dense layer, as well as the dynamics of development of these processes.

The presented theory can be extended by taking into account the production and loss rates (Q and L) of charged particles (e.g., NO⁺ and O₂⁺) in Equation (1), as well as considering effects of electric field and the ion drift caused by this field, in Equation (6). This extended study is planned for the near future.

The wind velocity profile given by the HWM14 is mainly determined by tidal motions and planetary waves [33]. The presented theoretical model allows its application for relatively short-term wind variations caused by AGWs and/or other dynamical processes. As a result it is possible to study the regional features of the origin of the discussed ionospheric irregular structures caused by above mentioned processes. To study the feature of ions global and regional distributions, it is important to consider molecular ions (e.g., NO⁺ and O₂⁺), along with metal ions (e.g., Fe+, Be+) in the three-dimensional wind. This is also the subject of future studies.

5. Conclusions

1. The behavior of the ion/electron concentration and the possibility of the formation of an Es-type layer, as well as their depletion processes under the influence of realistic wind, which takes into account its vertical $V_z$

component along with the meridional $V_x$ and zonal $V_y$ components of the velocity $V$, are shown. In this case, the presence of a minimum negative value of the vertical change of the vertical drift velocity of ions $\left(\frac{\partial w_{iv}}{\partial z}\right)\min <0$ in the lower thermosphere, as the main condition for predicting the formation of the Es layer [Didebulidze Dalakishvili Todua, 2020], was extended analytically and with appropriate numerical methods, in case of presence of the vertical component of the wind velocity $V_z$.

2. Using the analytical approach for ion/electron concentration with consideration of ambipolar diffusion (17) shows that their narrow-layer total convergence rate $C_t^{\text{'}}=C_v^{\text{'}}+C_{sh}^{\text{'}}+C_{vz}^{\text{'}}$

($\frac{\partial N_e}{\partial t}\propto -\frac{\partial w_{iv}}{\partial z}=C_t^{\text{'}}>0$) is determined by both horizontal and vertical wind velocity magnitude, direction ($C_v^{\text{'}}$) and vertical change ( $C_{sh}^{\text{'}}$ and $C_{vz}^{\text{'}}$), Equations (14 )-(16). The vertical movement of the ion/electron layer and, accordingly, the localization of the Es type layer in the regions of minimal reduction (or with ${\mathrm{w}}_{iv}=0$) of their lower and upper fluxes or regions where these fluxes vanish (${\mathrm{w}}_{iv}\to 0$), is determined by the profile of the ions vertical drift velocity ${\mathrm{w}}_{iv}$, Equation (7). In a given region (with particular B and I) it is possible to identify the regions of the development of ion convergence $C_{t\max }^{\text{'}}>\frac{2D_a}{H_{ic}^2}$ (Es type layer formation) and their depletion conditions $C_{t\min }^{\text{'}}<0$. The convergence ($C_{vz}^{\text{'}}>0$)/divergence ($C_{vz}^{\text{'}}<0$) factor caused by the vertical wind is also influenced by the neutral particles wind velocity profile.

3. Downward/upward vertical wind will shift the convergence regions (with $w_{iv}=0$

or $w_{iv}\to 0$) down/up, respectively from their locations that existed in case of just meridional and zonal winds. In case of presence of the wind velocity vertical component the rates of convergence and divergence of the ions are different from their values in case of just a horizontal wind.

Along with the profiles of the meridional ($-C_x$, $\partial C_x/\partial z$) and zonal ($-C_y$, $\partial C_y/\partial z$) factors of the wind velocity, the one of the vertical wind factor ($C_z$) and its vertical change ($-\partial C_z/\partial z$) are important in the height profile of the ion drift velocity $w_{iv}$ and its vertical change $\frac{\partial w_{iv}}{\partial z}$ (see Figure 1). In this case, it is shown for the first time that the upward constant wind ($V_z>0$), like the northward wind ($V_x>0$), causes the convergence of ions with the maximum rate in the region of the maximum of $-\partial C_z/\partial z$ (h≈121km), where the collision frequency of ions-neutrals is equal to their cyclotron frequency ${\nu }_{in}={\omega }_i$ (Figure 1). In this height region, a downward wind ($V_z<0$), like a southward one ($V_x<0$), causes ion/electron depletion (Figure 2).

4. The significant influence of horizontal wind, ions diffusion and their initial distribution, and also vertical wind on the behavior of ions/electrons and therefore the formation of Es layer (as well as ion density depletion) has been demonstrated by numerical simulations (Figure 2 and Figure 5).

Accordingly, at first the behavior of ions/electrons in the presence of only vertical wind was demonstrated (Figure 2), then case of only horizontal wind determined by typical HWM14 data was considered (Figure 3), and finally the case of three-dimensional wind with the horizontal and vertical components was considered.

The vertically upward/downward component of the three-dimensional wind velocity will shift the regions of ion convergence (e.g., ${\mathrm{w}}_{iv}=0$or $w_{iv}\to 0$) upward or downward, respectively, and change both the location of the formed Es layer and its density relatively to values of corresponding parameters estimated in the case of only horizontal wind (Figure 5). Here, the increase of diffusive displacement towards the upper regions (e.g., h>120 km) also reduces the density of the upper Es layer, and increases it at the lower location.

The location of the initial ion/electron layer relative to the expected regions of convergence, as well as the ions drift caused by the vertical wind, influences the conditions for their convergence into a narrow layer in these regions (Figure 4 and Figure 5). For example, in the lower regions (h<110 km), due to downward/upward drift of ions ($w_{iv}\approx V_z$), caused by downward/upward wind, respectively, the ions localization does not occur in the regions with $w_{iv}\to 0$ (Figure 5b, Figure 5c, Figure 5e and Figure 5f), which appeared in case of only horizontal wind (Figure 5a and Figure 5d). So, the presence of maximum rate of convergence ($C_{t\max }^{\text{'}}>0$) in the lower regions may not be sufficient for the formation of a high-density Es layer during the vertical wind.

In case of three-dimensional wind with an upward component (Figure 5f) the formation of Es layer with density higher than in case of only horizontal wind was shown (Figure 5d). In this case, the additional convergence caused by the vertically upward wind in the region increases their convergence caused by the horizontal wind, in the regions close to the ion vertical drift velocity node.

5. In the region of maximum ion/electron divergence$\left(\frac{\partial w_i}{\partial z}\right)\max >0$ (or ) (e.g., at height about 116km), during the presence of vertical upward/downward wind the depletion of ion/electron concentration is higher than in case of the horizontal wind alone (Figure 5).

6. The convergence/divergence factors caused by the values of both the horizontal wind vertical shear ($C_{sh}^{\text{'}}$) and magnitude, and the direction of the wind velocity ($C_{vz}^{\text{'}}$), which determine the maximum rates of convergence ($C_{t\max }^{\text{'}}>0$) and divergence ($C_{t\min }^{\text{'}}<0$), has been shown for the whole considered nightime interval (Figure 6).

7. The vertical wind velocity used in the numerical simulations is much smaller in the lower thermosphere than its observed [37] and model horizontal wind averages [33]. This can be caused by the tidal motions, as well as propagation of AGWs. In the presented theoretical model, the realistic (three-dimensional) profile of the wind velocity, which takes into account the vertical component along with its zonal and meridional ones, is important for prediction of the regions of the ion convergence and formation of Es layers, and also the regions of ion depletion. Therefore, consideration of the wind described above is important to study the global and regional distributions of the main metal ions that make up it in the lower thermosphere.