Submitted:
23 September 2023
Posted:
25 September 2023
You are already at the latest version
Abstract
Keywords:
MSC: 22E43; 22E70; 53B30
1. Introduction
2. The first and the second pairs and their transformation properties
3. Outer products of 4-component spinors
4. Quaternion forms and 4-vectors
5. Two more pairs of spinors
6. Complex conjugated forms
7. Four types of transformations for SL(2,C)
8. Conjugate spaces in diagonal basis
9. Rotations in spinor space
10. State space and inner product of states
11. Observables and states
12. 8-component Dirac spinor
Appendix A
Appendix A.1. Various forms of Z and L matrices
Appendix A.2. The Lorentz matrix
Appendix A.3. Geometric phase with 4-component spinors
Appendix A.4. Coherent parallel combination of transformations and interpretation of Z as a state of the transforming medium
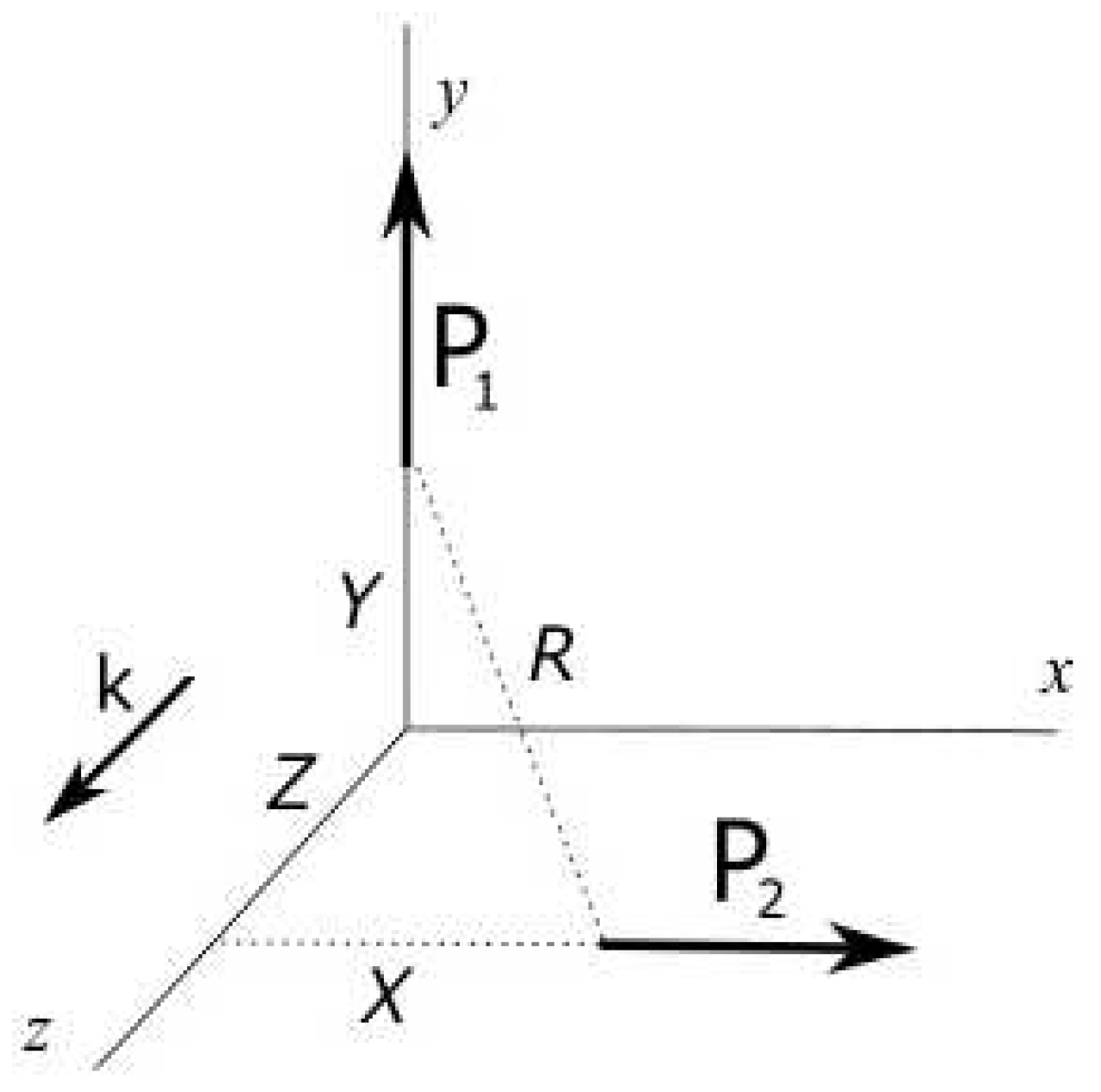
Appendix A.4.1. Unitary formulation of the rotation of the medium in space
Appendix A.5. Table for vector and matrix states of optical elements
| Optical element | N | M | |
| Free space | |||
| Half-wave plate (Ideal mirror) | |||
| Half-wave plate 45º fast axis | |||
| Circular retarder | |||
| Horizontal Linear Polarizer | |||
| Vertical Linear Polarizer | |||
| Linear Polarizer at 45º | |||
| Linear Polarizer at 135º | |||
| Circular Polarizer (right handed) | |||
| Circular Polarizer (left handed) |
| Optical element | N | M | |
| QWP horizontal fast axis | |||
| QWP vertical fast axis | |||
| QWP fast axis 135º | |||
| QWP fast axis 45º | |||
| Circular retarder | |||
| Circular retarder |
References
- J. Hladik, "Spinors in Physics," Springer-Verlac, New York (1996).
- Başkal, S. , Kim Young S., Noz, Marilyn E, "Physics of the Lorentz Group," Morgan and Claypool Publishers, CA (2015).
- Sudha and, A.V. Gopala Rao, "Polarization Elements: A Group Theoretical Study". [CrossRef]
- R. Barakat, "Exponential versions of the Jones and Mueller–Jones polarization matrices," J. Opt. Soc. Am. A/Vol. 13, No. 1 (1996). [CrossRef]
- R. M. A. Azzam, "Propagation of partially polarized light through anisotropic media with or without depolarization: A differential 4 × 4 matrix calculus," J. Opt. Soc. Am. 68, 1756 (1978). [CrossRef]
- A. A. Bogush, V. M. Red’kov, "On unique parametrization of the linear group GL(4.C) and its subgroups by using the Dirac matrix algebra basis," arXiv:hep-th/0607054V1 (2006). [CrossRef]
- E. Ovsiyuk, O. Veko, M. Neagu, V. Balan, V. Red’kov, "Some Properties of Parameters of Lorentz Matrices and Transitivity Equations," BSG Proceedings, Vol. 20, 2013, pp. 11-63.
- E. Kuntman, M. A. Kuntman, and O. Arteaga, "Vector and matrix states for Mueller matrices of nondepolarizing optical media," J. Opt. Soc. Am. 2017; 34, 82–86. [CrossRef]
- S.R. Cloude, “Group theory and polarization algebra”, Optik 75, 26-36 (1986).
- D. Han, Y.S. Kim, M. E. Noz, "Stokes parameters as a Minkowskian four-vector,". Phys. Rev E 1997, 56. [CrossRef]
- D. Han, Y. S. Kim, M. E. Noz, "Jones-matrix Formalism as a Representation of the Lorentz Group," J. Opt. Soc. Am. A, 14 (1997). [CrossRef]
- W. R. Hamilton, "On a new species of imaginary quantities connected with the theory of quaternions," Proceedings of the Royal Irish Academy, 2:424–434 (1844).
- Katsusada Morita, "Quaternions, Lorentz Group and the Dirac Theory," Progress of Theoretical Physics, Volume 117, Issue 3 (2007), pp 501-532. [CrossRef]
- Lanlan Liu, Chonging Wu, Chao Shang, Zhengyong Li, Jian Wang, IEEE Photonics Journal ( Volume: 7, Issue: 4, Aug. 2015 ).
- E. Kuntman, M. A. Kuntman, A. Canillas, and O. Arteaga, "Quaternion algebra for Stokes-Mueller formalism," J. Opt. Soc. Am. A 36, 492-497 (2019). [CrossRef]
- E. Kuntman and O. Arteaga, "Decomposition of a depolarizing Mueller matrix into its nondepolarizing components by using symmetry conditions," Appl. Opt. 55 (2016). [CrossRef]
- R. Ossikovski, E. Garcia-Caurel, M, Foldyna and J.J. Gil, "Application of the arbitrary decomposition to finite spot size Mueller matrix measurements," Appl. Opt. 53 (2014). [CrossRef]
- E. Kuntman, M. A. Kuntman, J. Sancho-Parramon and O. Arteaga, "Formalism of optical coherence and polarization based on material media states," Phys. Rev. A 95 (2017). [CrossRef]
- M. A. Kuntman, E. Kuntman, J. Sancho-Parramon and O. Arteaga, "Light scattering by coupled oriented dipoles: Decomposition of the scattering matrix," Phys. Rev B 98 (2018). [CrossRef]
- O. Arteaga, R. Ossikovski, E. Kuntman, M. A. Kuntman, A. Cannilas and E. Garcia-Caurel, "Mueller matrix polarimetry on a Young’s double-slit experiment analog," Optics Letters 45 (2017). [CrossRef]
- M. A. Kuntman, E. Kuntman, O. Arteaga, "Asymmetric scattering and Reciprocity in a Plasmonic Dimer," Symmetry 12 (2020). [CrossRef]
- K. Kim, L. Mandel and E. Wolf, J. Opt.Soc. Am. 1987.
- A. M. Steane, "An introduction to spinors,". arXiv 2013, arXiv:1312.3824v1.
- J. D. Bjorken, S. D. Drell, "Relativistic Quantum Mechanics," McGraw-Hill, NY (1964).
- Sudha and A., V. Gopala Rao, "Polarization Elements-A Group Theoretical Study," arxiv:physics/0007079v1 (2000).
- J. J. Gil, Eur. Phys. J. Appl. Phys. 40, 1 (2007).
- N. G. Parke, J. Math. Phys. 28, 131 (1949).
- R. C. Jones, J. Opt. Soc. Am. 31, 488 (1941).
- D. Goldstein, "Polarized Light, Revised and Expanded," Optical Science and Engineering, 2nd ed. (CRC Boca Raton, FL., 2003).
- J. J. Gil and I. S. Jose, J. Opt. Soc. Am. A 30 (2013).
- J. J. Gil. J. Appl. Remote Sens. 2014, 8.
- S. Pancharatnam, Proc. Indian Acad. Sci 44, 247 (1956).
- M. V. Berry, Proc. R. Soc. Lond. A 392, 84 (1984).
- M. V. Berry, J. Mod. Opt. 34, 1401 (1987).
- J. P. Gutierrez-Vega, "Pancharatnam-Berry phase of optical sysytems," Opt. Lett. 36, 1143-1145 (2011). [CrossRef]
- T. van Dijk, H.F. Schouten, W. Ubachs, T.D. Visser, Optics Express 18 (2010) 10796.
- José Lages, Remo Giust, Jean-Marie Vigoureux, "Geometric phase and Pancharatnam phase induced by light wave polarization," Physica E: Low-dimensional Systems and Nanostructures, Volume 59, 2014, Pages 6-14. [CrossRef]
| 1 | This representation will be studied in detail in Section 8
|
| 2 | The basis set is equivalent to the Dirac basis set, . |
| 3 | We can define the spinor metric for SL(4,C) as or if we like. These metrics also have the same properties as g. |
| 4 | Besides , we will subsequently define other types and that preserve both g and . Dotted versions of all four types of transformations also preserve both g and . All types of and preserve and (). |
| 5 | We may use the generalized eigenvectors of or matrices as well, but, in that case, we have to employ the other forms of the spinor metric. |
| 6 |
corresponds to a CCW rotation about the axis in SL(2,C). |
| 7 | The upper dot on a spinorial object simply means complex conjugation: . But, the upper dot on an element of SL(2,C) or SL(4,C) has a particular meaning. . Similarly, . |
| 8 | These are matrix representations of quaternions, because matrices have the same properties as the Hamilton’s quaternion basis, : , . |
| 9 | In these expressions complex conjugation is not explicit, but , i.e., is based on matrices. |
| 10 | Actually, there is one more way:
|
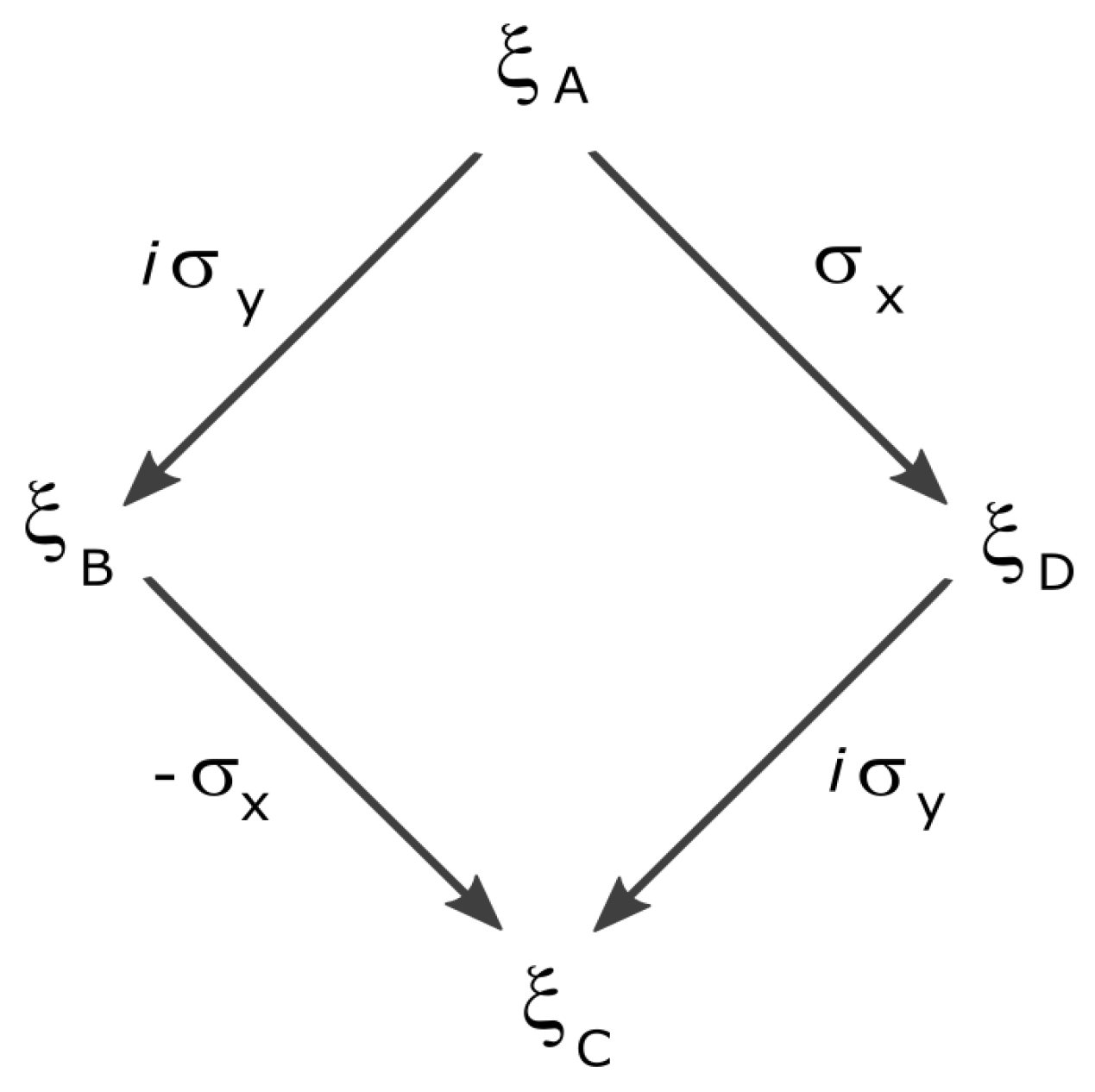
| 11 | The set is equal to the set due to the relations given in Equation (111), and due to the relations , , , the set is equal to the set . |
| 12 | |
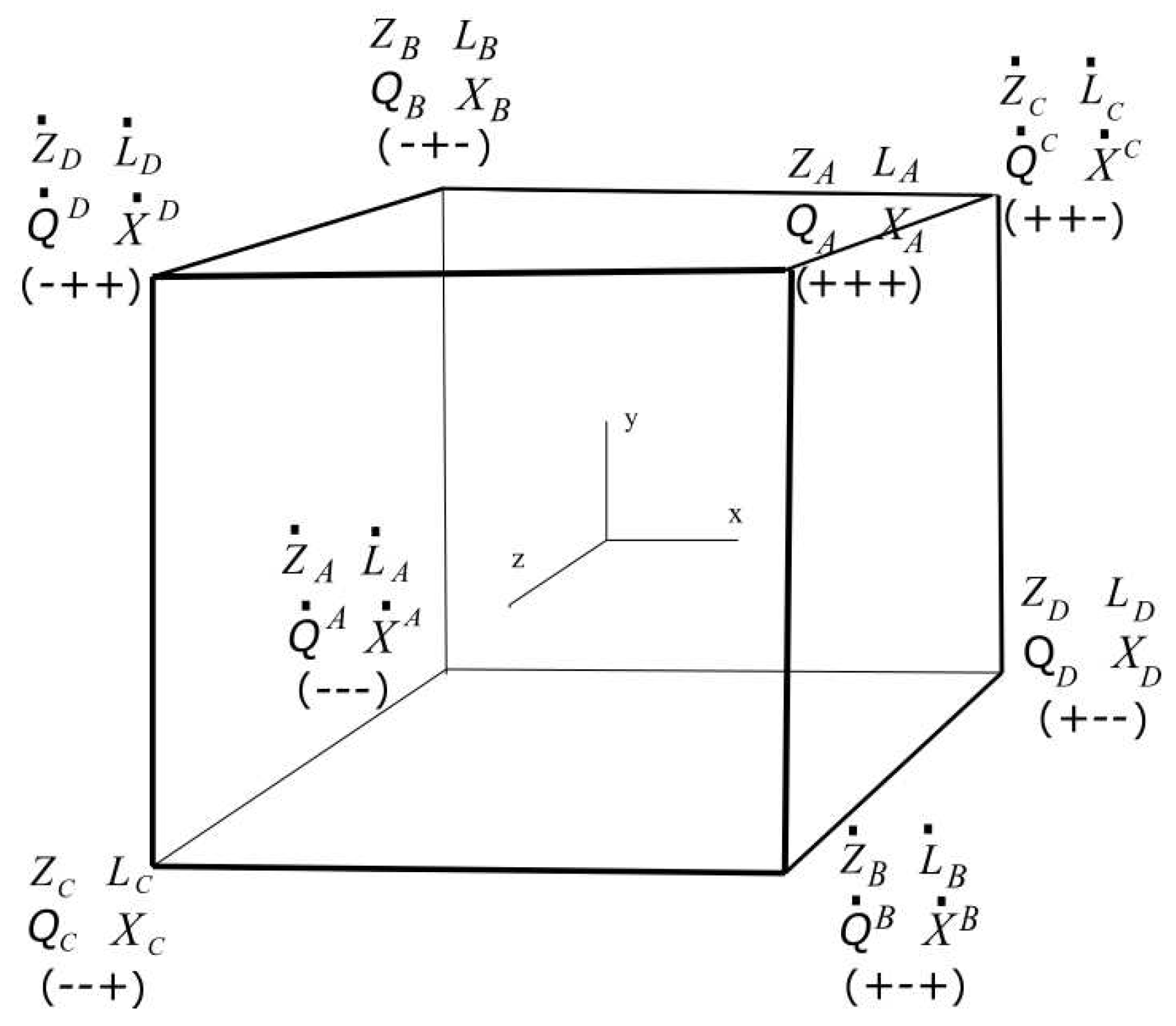
| 13 | We can also obtain 16 independent spinor pairs for the diagonal basis from the eigenvectors of and by applying the procedure described in Section 5
|
| 14 |
is an eigenvector of
|
| 15 | The pairs that obey this pattern are the generalized eigenvectors of . First column corresponds to the eigenvalue and the second column corresponds to the eigenvalue . |
| 16 | Let denote a state vector of any kind and let be its dotted contravariant version. These objects live in the state space and they all fit the pattern that given in Equation (149). All undotted covariant objects transform with and all dotted contravariant objects transform with which are based on . Under these transformations the pattern of the transformed object remains the same. Similar considerations also apply to the conjugated counterparts that live in the conjugate space. The only difference is that, in this case, the sign of the imaginary unit in Equation (149) is flipped and all matrix forms are now based on . |
| 17 | The conjugate space is also two dimensional. Basis for the conjugate space can be obtained by simply changing the sign of the imaginary unit in Equation (161). Comjugate basis cannot be expressed as linear combinations of and basis. |
| 18 | There does not exists a fourth matrix that anticommutes with matrices. |
| 19 | Sign depends on the sense of the cyclic path. |
| 20 | Geometric phase can also be defined and calculated for an open loop operations on the Poincare sphere. |
| 21 | Negative sign is due to the CCW cyclic path. |
| 22 | In polarization optics, convention is usual. |
| 23 | Birefringence parameters correspond to rotations and dichroism parameters correspond to boosts. |
| 24 | We may think of more complicated combinations involving many branches with serial, parallel or mixed operations. |
| 25 | |
| 26 | When we interpret as the state of the component system (medium), the linear combination given in Eqations (215) may look like a superposition of states, but the elements in the sum are not representing different states of the same system, they are the states corresponding to different systems. |
| 27 |
. Only the isotropic amplitude absorption survives in . |
| 28 | In this simple example, and the state space is two dimensional, hence we can truncate the third and fourth components of the vector states. |
| 29 | This is also true for crossed orthogonal nanorods. |
| 30 | Lorentzian polarizability and the interaction coefficient are functions of the wavelength of the incident light, hence the phenomenon of plasmonic hybridization occurs at wavelengths that make the denominator of g zero. |
| 31 | Optical activity can be observed even in a planar geometry in sideways scattering directions [21]. |
| 32 | The vector state is rotated as . |
| 33 |
, because any complex conjugate form commutes with any Hermitian adjoint form ( commutes with for all ), hence . |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).



