Submitted:
18 February 2023
Posted:
21 February 2023
You are already at the latest version
Abstract
Keywords:
I. INTRODUCTION
II. Symmergent Black hole
III. Particle tunnel from the symmergent black hole
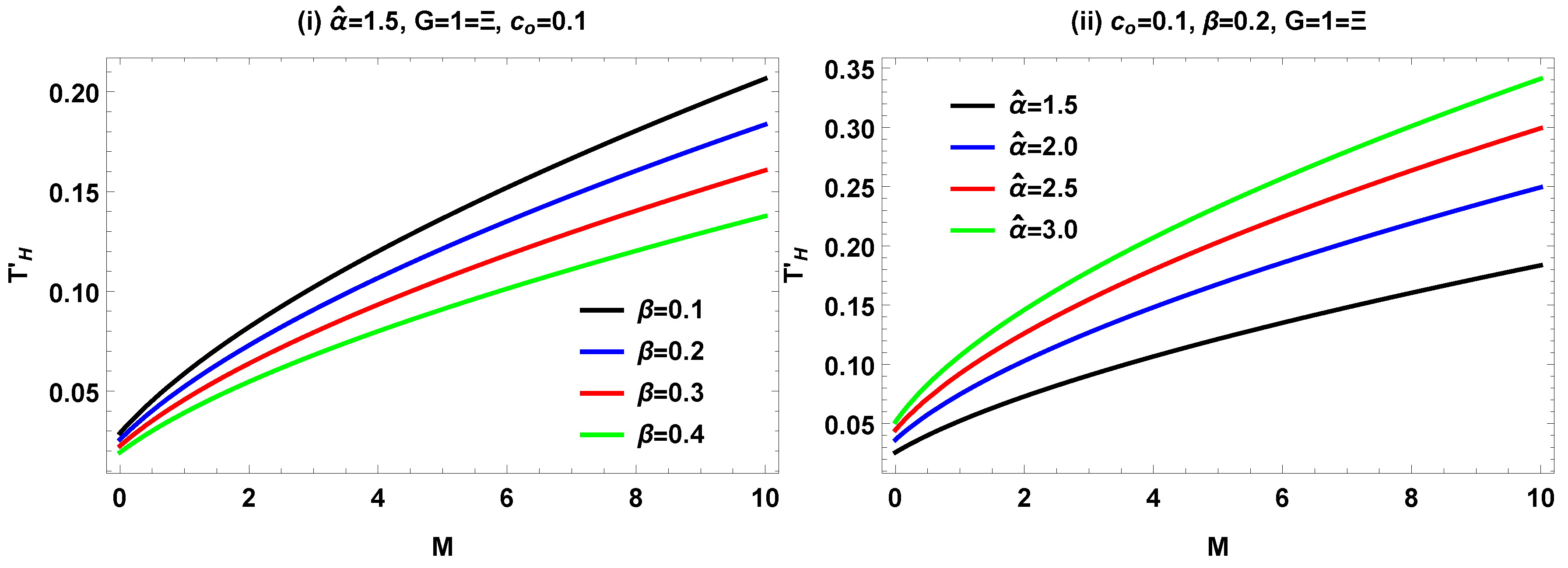
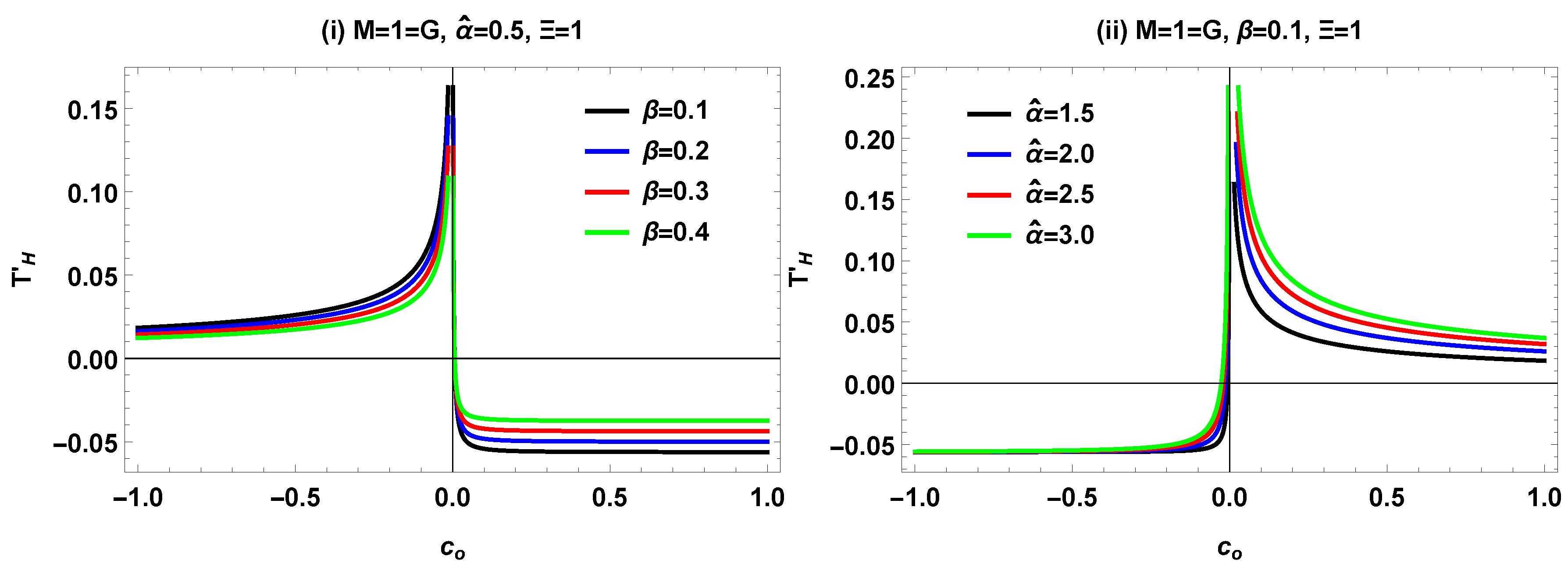
IV. Graphical Analysis of for symmergent BH
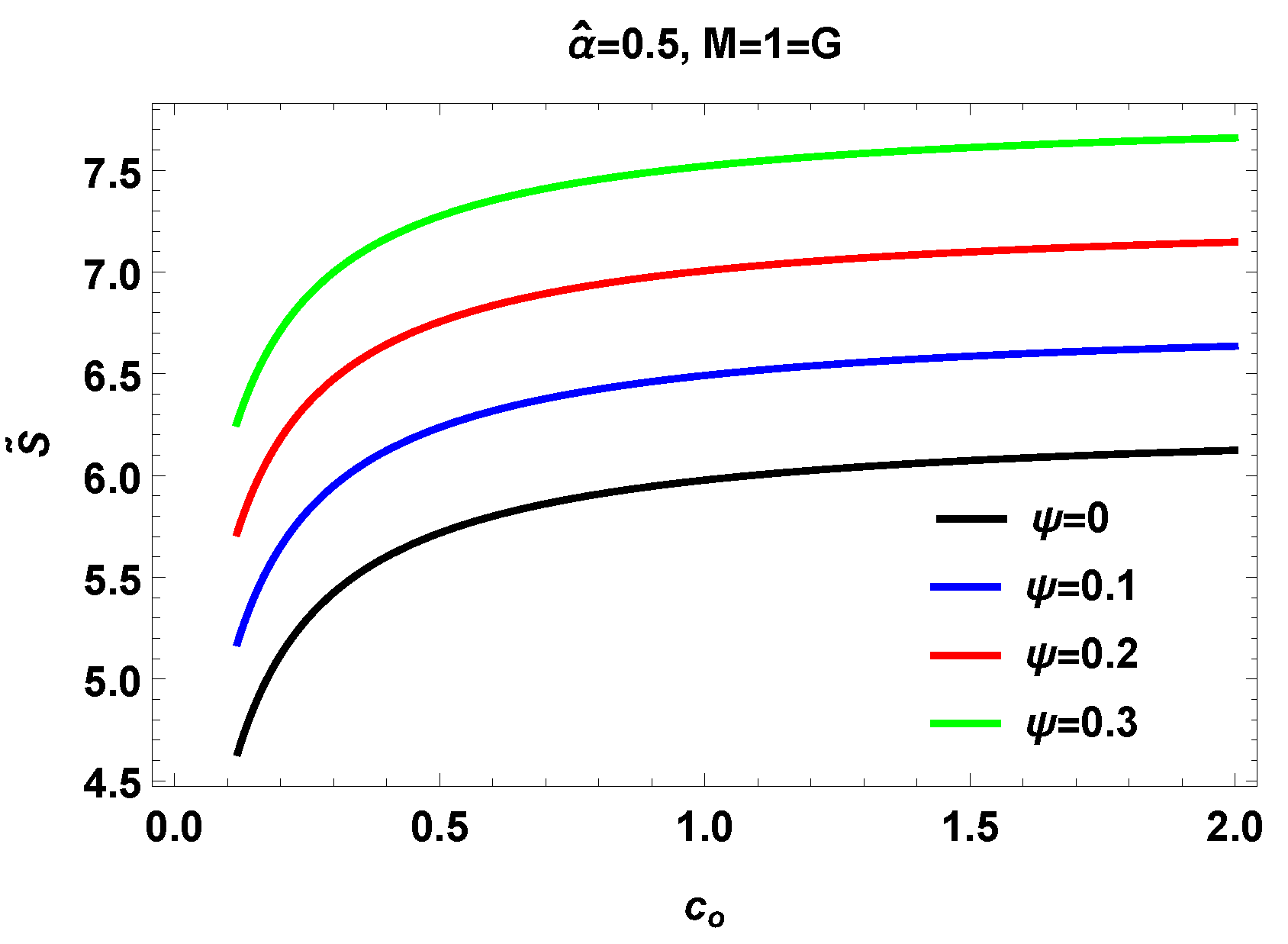
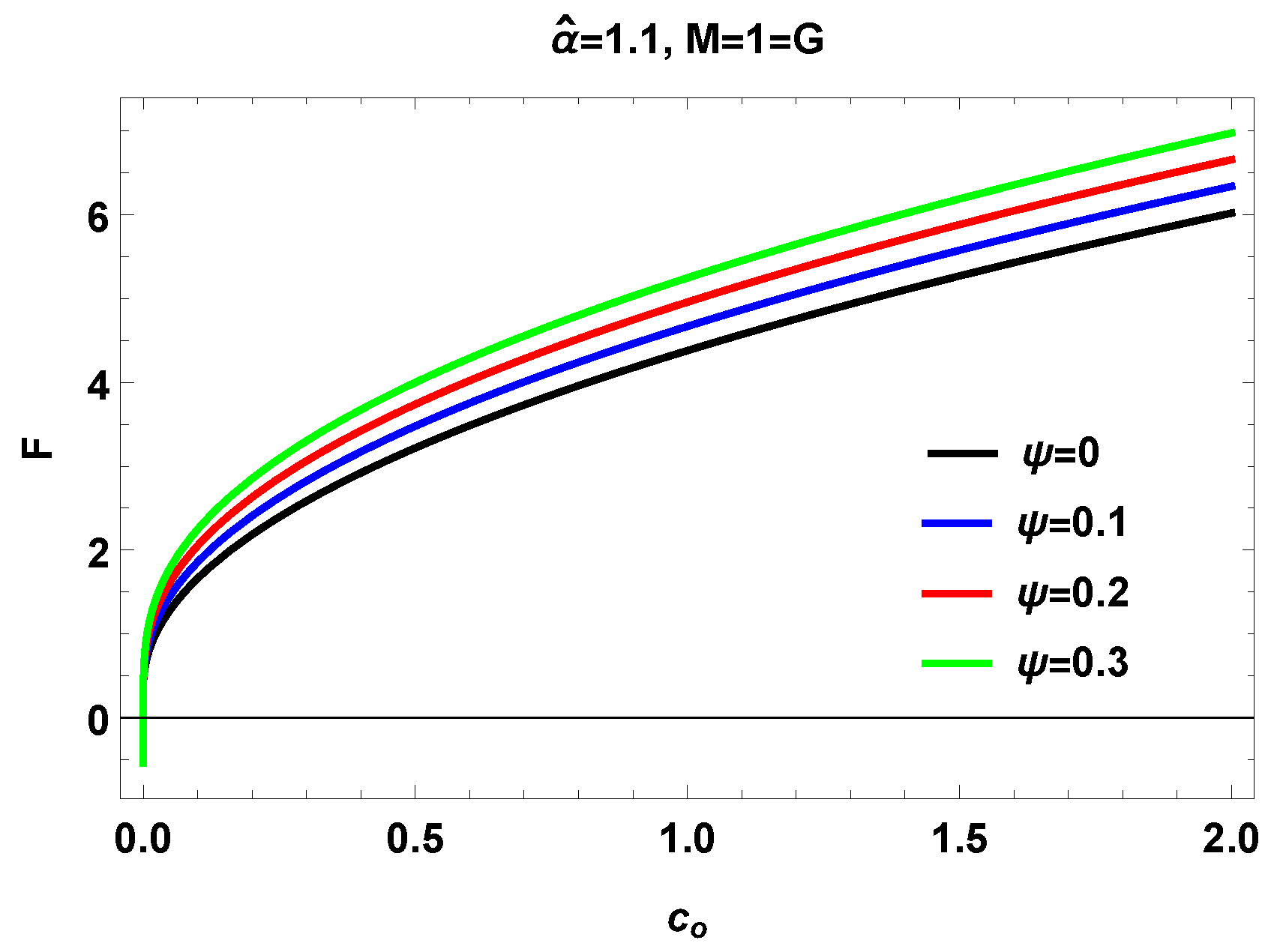
V. Thermal fluctuations
VI. Summary and Discussion
Acknowledgments
References
- S. W. Hawking, M. J. Perry and A. Strominger. Soft Hair on Black Holes. Phys. Rev. Lett. 2016, 116, 231301. [CrossRef] [PubMed]
- M. Angheben, M. Nadalini, L. Vanzo and S. Zerbini. Hawking radiation as tunneling for extremal and rotating black holes. JHEP 2005, 05, 014. [CrossRef]
- P. Kraus and F. Wilczek. Effect of self-interaction on charged black hole radiance. Nucl. Phys. B 1995, 437, 231. [Google Scholar] [CrossRef]
- W. Javed, R. Ali, R. Babar and A. Övgün. Tunneling of massive vector particles from types of BTZ-like black holes. Eur. Phys. J. Plus 2019, 134, 511. [CrossRef]
- A. Övgün, W. Javed and R. Ali. Tunneling Glashow-Weinberg-Salam Model Particles from Black Hole Solutions in Rastall Theory. Adv. High Energy Phys. 2018, 2018, 3131620. [CrossRef]
- W. Javed, G. Abbas and R. Ali. Charged vector particle tunneling from a pair of accelerating and rotating and 5D gauged super-gravity black holes. Eur. Phys. J. C 2017, 77, 296. [CrossRef]
- W. Javed, R. Ali and G. Abbas. Charged Vector Particles Tunneling From 5D Black Hole and Black Ring. Can. J. Phys. 2019, 97, 176. [CrossRef]
- W. Javed, R. Ali, R. Babar and A. Övgün. Tunneling of Massive Vector Particles under the Influence of Quantum Gravity. Chin. Phys. C 2020, 44, 015104. [Google Scholar] [CrossRef]
- W. Javed and R. Babar. Fermions Tunneling and Quantum Corrections for Quintessential Kerr-Newman-AdS Black Hole. Adv. High Energy Phys 2019, 2019, 2759641. [Google Scholar] [CrossRef]
- W. Javed, R. Babar and A. Övgün. Hawking radiation from cubic and quartic black holes via tunneling of GUP corrected scalar and fermion particles. Mod. Phys. Lett. A 2019, 34, 1950057. [Google Scholar] [CrossRef]
- R. Babar, W. Javed and A. Övgün. Effect of the GUP on the Hawking radiation of black hole in 2+1 dimensions with quintessence and charged BTZ-like magnetic black hole. Mod. Phys. Lett. A 2020, 35, 2050104. [Google Scholar] [CrossRef]
- Kerner, R.; Mann, R.B. Fermions tunnelling from black holes. Class. Quant. Grav. 2008, 25, 095014. [Google Scholar] [CrossRef]
- Kerner, R.; Mann, R.B. Tunnelling, temperature and Taub-NUT black holes. Phys. Rev. D 2006, 73, 104010. [Google Scholar] [CrossRef]
- Kerner, R.; Mann, R.B. Charged Fermions Tunnelling from Kerr-Newman Black Holes. Phys. Lett. B 2008, 665, 277–283. [Google Scholar] [CrossRef]
- Kerner, R.; Mann, R.B. Tunnelling from Godel black holes. Phys. Rev. D 2007, 75, 084022. [Google Scholar] [CrossRef]
- Kuang, X.M.; Liu, B.; Övgün, A. Nonlinear electrodynamics AdS black hole and related phenomena in the extended thermodynamics. Eur. Phys. J. C 2018, 78, 840. [Google Scholar] [CrossRef]
- Kuang, X.M.; Saavedra, J.; Övgün, A. The Effect of the Gauss-Bonnet term to Hawking Radiation from arbitrary dimensional Black Brane. Eur. Phys. J. C 2017, 77, 613. [Google Scholar] [CrossRef]
- Akhmedov, E.T.; Akhmedova, V.; Singleton, D. Hawking temperature in the tunneling picture. Phys. Lett. B 2006, 642, 124–128. [Google Scholar] [CrossRef]
- Akhmedova, V.; Pilling, T.; de Gill, A.; Singleton, D. Temporal contribution to gravitational WKB-like calculations. Phys. Lett. B 2008, 666, 269–271. [Google Scholar] [CrossRef]
- Akhmedov, E.T.; Akhmedova, V.; Pilling, T.; Singleton, D. Thermal radiation of various gravitational backgrounds. Int. J. Mod. Phys. A 2007, 22, 1705–1715. [Google Scholar] [CrossRef]
- Singleton, D.; Vagenas, E.C.; Zhu, T.; Ren, J.R. Insights and possible resolution to the information loss paradox via the tunneling picture. JHEP 2010, 08, 089, [Erratum: JHEP 01, 021 (2011)]. [Google Scholar] [CrossRef]
- Kruglov, S.i. Black hole radiation of spin-1 particles in (1+2) dimensions. Mod. Phys. Lett. A 2014, 29, 1450203. [Google Scholar] [CrossRef]
- Ali, M.H. Hawking radiation via tunneling from hot NUT-Kerr-Newman-Kasuya spacetime. Class. Quant. Grav. 2007, 24, 5849–5860. [Google Scholar] [CrossRef]
- Ali, M.H. Charged Particles’ Tunneling from Hot-NUT-Kerr-Newman-Kasuya Spacetime. Int. J. Theor. Phys. 2008, 47, 2203–2217. [Google Scholar] [CrossRef]
- Singh, A.K.; Meitei, I.A.; Singh, T.I.; Singh, K.Y. Generalized Klein–Gordon equation and quantum gravity corrections to tunneling of scalar particles from Kerr–Newman black hole. Eur. Phys. J. C 2019, 79, 692. [Google Scholar] [CrossRef]
- Ibungochouba Singh, T.; Ablu Meitei, I.; Yugindro Singh, K. Hawking radiation as tunneling of vector particles from Kerr-Newman black hole. Astrophys. Space Sci. 2016, 361, 103. [Google Scholar] [CrossRef]
- Ibungochouba Singh, T.; Ablu Meitei, I.; Yugindro Singh, K. Quantum radiation of Maxwell’s electromagnetic field in nonstationary Kerr–de Sitter black hole. Int. J. Mod. Phys. D 2016, 25, 1650061. [Google Scholar] [CrossRef]
- Singh, T.I.; Meitei, I.A.; Singh, K.Y. Quantum gravity effects on Hawking radiation of Schwarzschild-de Sitter black holes. Int. J. Theor. Phys. 2017, 56, 2640–2650. [Google Scholar] [CrossRef]
- Meitei, Y.K.; Singh, T.I.; Meitei, I.A. GUP effects on Hawking temperature in Riemann space-time. Turk. J. Phys. 2020, 44, 373–383. [Google Scholar] [CrossRef]
- S. Shahraeini, K.N.; Saghaf., S. Radiation from Hayward Black Hole via Tunneling Process in Einstein-Gauss-Bonnet Gravity. Journal of Holography Applications in Physics 2022, 2, 55. [Google Scholar] [CrossRef]
- A. Kempf. On Quantum Field Theory with Nonzero Minimal Uncertainties in Positions and Momenta. J. Math. Phys. 1997, 38, 1347. [Google Scholar] [CrossRef]
- B. Carr, J. Mureika and P. Nicolini. Sub-Planckian black holes and the Generalized Uncertainty Principle. JHEP 2015, 2015, 52. [Google Scholar] [CrossRef]
- A. Kempf, G. Mangano and R. B. Mann. Hilbert Space Representation of the Minimal Length Uncertainty Relation. Phys. Rev. D 1995, 52, 1108. [Google Scholar] [CrossRef] [PubMed]
- G. Gecim and Y. Sucu. Quantum gravity effect on the tunneling particles from Warped-AdS3 black hole. Mod. Phys. Lett. A 2018, 33, 1850164. [Google Scholar] [CrossRef]
- G. Gecim and Y. Sucu. The GUP effect on Hawking Radiation of the 2+1 dimensional Black Hole. Phys. Lett. B 2017, 773, 391. [Google Scholar] [CrossRef]
- G. Gecim and Y. Sucu. Quantum Gravity Effect on the Tunneling Particles from 2+1 dimensional New-type Black Hole. Adv. High Energy Phys. 2018, 2018, 8728564. [Google Scholar] [CrossRef]
- A. Övgün and K. Jusufi. Massive vector particles tunneling from noncommutative charged black holes and their GUP-corrected thermodynamics. Eur. Phys. J. Plus 2016, 131, 177. [Google Scholar] [CrossRef]
- A. Övgün and K. Jusufi. The effect of the GUP on massive vector and scalar particles tunneling from a warped DGP gravity black hole. Eur. Phys. J. Plus 2017, 132, 298. [Google Scholar] [CrossRef]
- K. Jusufi and A. Övgün. Hawking Radiation of Scalar and Vector Particles from 5D Myers-Perry Black Holes. Int. J. Theor. Phys. 2017, 56, 1725. [Google Scholar] [CrossRef]
- J. M. Bardeen, B. Carter and S. W. Hawking. The four laws of black hole mechanics. Commun. Math. Phys. 1973, 31, 161. [Google Scholar] [CrossRef]
- S. W. Hawking, D. N. Page. Thermodynamics of black holes in anti-de Sitter space. Commun. Math. Phys. 1983, 87, 577. [Google Scholar] [CrossRef]
- J. D. Bekenstein. Black Holes and Entropy. Phys. Rev. D 1973, 7, 2333. [Google Scholar] [CrossRef]
- B. Pourhassan and M. Faizal. Thermal fluctuations in a charged AdS black hole. Europhysics Letters 2015, 111, 40006. [Google Scholar] [CrossRef]
- B. Pourhassan, S.Upadhyay, H.Saadat and H.Farahani. Quantum gravity effects on Horava–Lifshitz black hole. Nuclear Physics B 2018, 928, 415. [Google Scholar] [CrossRef]
- B. Pourhassan and M. Faizal. Thermodynamics of a Sufficient Small Singly Spinning Kerr-AdS Black Hole. Nuclear Physics B 2016, 913, 834. [Google Scholar] [CrossRef]
- M. Faizal and M. M. Khalil. GUP-corrected thermodynamics for all black objects and the existence of remnants. Int. J. Mod. Phys. A 2015, 30, 1550144. [Google Scholar] [CrossRef]
- R. K. Kaul, P. Majumdar. Logarithmic correction to the Bekenstein-Hawking entropy. Phys. Rev. Lett. 2000, 84, 5255. [Google Scholar] [CrossRef] [PubMed]
- S. Carlip. Logarithmic corrections to black hole entropy from the Cardy formula. Class. Quant. Gravity 2000, 17, 4175. [Google Scholar] [CrossRef]
- Zhang, M. Corrected thermodynamics and geometrothermodynamics for anti-de Sitter black hole. Nuclear Physics B 2018, 935, 170. [Google Scholar] [CrossRef]
- B. Pourhassan, M. Faizal and U. Debnath. Effects of thermal fluctuations on the thermodynamics of modified Hayward black hole. Eur. Phys. J. C 2016, 76, 145. [Google Scholar] [CrossRef]
- Bargueño, P.; Contreras, E.; Rincón, A. Thermodynamics of scale-dependent Friedmann equations. Eur. Phys. J. C 2021, 81, 477. [Google Scholar] [CrossRef]
- Demir, D. Emergent Gravity as the Eraser of Anomalous Gauge Boson Masses, and QFT-GR Concord. Gen. Rel. Grav. 2021, 53, 22. [Google Scholar] [CrossRef]
- Demir, D. Symmergent Gravity, Seesawic New Physics, and their Experimental Signatures. Adv. High Energy Phys. 2019, 2019, 4652048. [Google Scholar] [CrossRef]
- Demir, D.A. Curvature-Restored Gauge Invariance and Ultraviolet Naturalness. Adv. High Energy Phys. 2016, 2016, 6727805. [Google Scholar] [CrossRef]
- Çimdiker, I.; Demir, D.; Övgün, A. Black hole shadow in symmergent gravity. Phys. Dark Univ. 2021, 34, 100900. [Google Scholar] [CrossRef]
- Rayimbaev, J.; Pantig, R.C.; Övgün, A.; Abdujabbarov, A.; Demir, D. Quasiperiodic oscillations, weak field lensing and shadow cast around black holes in Symmergent gravity 2022.
- Pantig, R.C.; Övgün, A.; Demir, D. Testing Symmergent gravity through the shadow image and weak field photon deflection by a rotating black hole using the M87* and Sgr. A* results 2022.
- Bekenstein, J.D. Black holes and entropy. Phys. Rev. D 1973, 7, 2333–2346. [Google Scholar] [CrossRef]
- Brevik, I.H.; Nojiri, S.; Odintsov, S.D.; Vanzo, L. Entropy and universality of Cardy-Verlinde formula in dark energy universe. Phys. Rev. D 2004, 70, 043520. [Google Scholar] [CrossRef]
- R. Ali and M. Asgher. Tunneling analysis under the influences of Einstein–Gauss–Bonnet black holes gravity theory. New Astronomy 2022, 93, 101759. [Google Scholar] [CrossRef]
- R. Ali, R. Babar, M. Asgher and S. A. A. Shah. Evaporation of Black Hole Under the Effect of Quantum Gravity. Int. J. Geom. Methods Mod. Phys 2022, 19, 2250017. [Google Scholar] [CrossRef]
- R. Ali, R. Babar, M. Asgher and S. A. A. Shah. Gravity Effects on Hawking Radiation from Charged Black Strings in Rastall Theory. Ann. Phys. 2021, 432, 168572. [Google Scholar] [CrossRef]
- R. Ali, K. Bamba, S. A. A. Shah and M. J. Saleem. Tunneling Analysis of Kerr-Newman Black Hole-Like Solution in Rastall Theory. Int. J. Mod. Phys. D 2022, 31, 2250069. [Google Scholar] [CrossRef]
- R. Ali, K. Bamba, M. Asgher and S. A. A. Shah. Tunneling Under the Influence of Quantum Gravity in Black Rings. Int. J. Mod. Phys. D 2021, 30, 2150002. [Google Scholar] [CrossRef]
- R. Ali, R. Babar, M. Asgher and X. T. Cheng. Tunneling Analysis of Regular Black Holes with Cosmic Strings-Like Solution in Newman-Janis Algorithm. Int. J. Mod. Phys. A 2022, 37, 2250108. [Google Scholar] [CrossRef]
- R. Ali, R. Babar and P. K. Sahoo. Quantum gravity evolution in the Hawking radiation of a rotating regular Hayward black hole. Phys. Dark Universe 2022, 35, 100948. [Google Scholar] [CrossRef]
- R. Ali, R. Babar and M. Asgher. Gravitational Analysis of Rotating Charged Black-Hole-Like Solution in Einstein–Gauss–Bonnet Gravity. Annalen der Physik 2022, 534, 2200074. [Google Scholar] [CrossRef]
- S. Upadhyay, N. islam and P. A. Ganai. A modified thermodynamics of rotating and charged BTZ black hole. Journal of Holography Applications in Physics 2022, 2, 25. [Google Scholar] [CrossRef]
- T. R. Govindarajan, R. K. Kaul and V. Suneeta. Logarithmic correction to the Bekenstein-Hawking entropy of the BTZ black hole. Class. Quantum Grav. 2001, 18, 2877. [Google Scholar] [CrossRef]
- J. Sadeghi, B. Pourhassan and F. Rahimi. Logarithmic corrections of charged hairy black holes in (2 + 1) dimensions. Can. J. Phys 2014, 92, 1638. [Google Scholar] [CrossRef]
- M. M. Akbar and S. Das. Entropy corrections for Schwarzschild and Reissner-Nordstrom black holes. Class. Quantum Grav. 2004, 21, 1383. [Google Scholar] [CrossRef]
- Z. Akhtar, R. Babar and R. Ali. Thermal fluctuations evolution of the new Schwarzschild black hole. Ann. Phys. 2023, 448, 169190. [Google Scholar] [CrossRef]
- Gibbons, G.W.; Hawking, S.W. Action Integrals and Partition Functions in Quantum Gravity. Phys. Rev. D 1977, 15, 2752–2756. [Google Scholar] [CrossRef]
- Iyer, V.; Wald, R.M. A Comparison of Noether charge and Euclidean methods for computing the entropy of stationary black holes. Phys. Rev. D 1995, 52, 4430–4439. [Google Scholar] [CrossRef] [PubMed]
- Das, S.; Majumdar, P.; Bhaduri, R.K. General logarithmic corrections to black hole entropy. Class. Quant. Grav. 2002, 19, 2355–2368. [Google Scholar] [CrossRef]
- Sadeghi, J.; Pourhassan, B.; Rahimi, F. Logarithmic corrections of charged hairy black holes in (2 + 1) dimensions. Can. J. Phys. 2014, 92, 1638–1642. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




