A Mathematical Theory of Knowledge for Intelligent Agents

Preprint

Article

A Mathematical Theory of Knowledge for Intelligent Agents

Altmetrics

Downloads

281

Views

196

Comments

Zie Eya Ekolle^*

Ryuji Kohno,Hideki Ochiai

Zie Eya Ekolle^*

Ryuji Kohno,Hideki Ochiai

This version is not peer-reviewed

Submitted:

01 November 2023

Posted:

02 November 2023

You are already at the latest version

Alerts

Abstract

Knowledge is a property that measures the degree of awareness of an agent about a target in an environment. The goal in conventional intelligent and cognitive agent development is to build agents that can be trained to gain knowledge about a target. The definition and operations of this knowledge associated to the agent is not clear, whereas these are required for developing a reliable, scalable and flexible agent. In this paper, we provide a concise theoretical framework for the description and quantification of the knowledge property needed for an efficient design of cognitive and rational intelligent agents. We relate the quantification scheme to the epistemological description of knowledge and present many illustrative examples on the usefulness of the quantification scheme.

Keywords:

Subject: Computer Science and Mathematics - Artificial Intelligence and Machine Learning

1. Introduction

Intelligent agent design has been around for many years, with a major goal to build machines that can act as we (humans) think [1]. The purposes of such a goal are diverse, giving rise to many varieties of agent design methods and techniques. One important aspect in all agent design is the acquisition of a value about a target and the optimization of this value. Many of such values are defined in the literature [2,3,4] but are not exhaustive enough to capture what we (human) think. This also makes such values less useful in the design of a reliable, scaleable and flexible agent needed in today’s fast growing intelligent agent industry.

To address this issue, we present a value quantification scheme for intelligent agent and use it to quantify knowledge, which we consider as a justified true belief [5,6,7] of an agent about a target. We start by introducing the cognitive nature of an agent, and define different cognitive properties required by an intelligent agent. We classify these cognitive properties into; intelligence, action, and cognitive value.

Many types of intelligence, actions, and cognitive values can be defined for an agent, but base on the title of this article, we focus more on the cognitive value property, specifically the knowledge property of an agent. More so, since the notion of knowledge is literally confused with that of intelligence, belief, and information, we mathematically distinguish it from and relate it to them as literally discussed in [8,9,10,11]. Apart from this, other cognitive values such as understanding, trust, and wisdom are introduced.

Logically, the knowledge quantity in most literature is considered as information [11,12]. However, the definition of information itself is diverse [13,14,15,16]. If we focus on Shannon’s definition of information [13], where information is considered as a type of uncertainty and defined using probabilistic logic, then such type of information theoretic knowledge is invariant to the environment in which it is generated, because it does not consider the environment influence on the events and observer during cognition.

Consider Shannon’s information content and the expected information content (also called entropy):

Information content:

I = log (\frac{1}{P (x)})

Entropy:

H = \sum_{i = 1}^{n} P (x_{i}) log (\frac{1}{P (x_{i})})

where x is a single state event,

x_{i}

is a state in a multi-states event, and

P (x)

is probability of a single state event.

In his logical definition of information [13], Shannon considers the information content as a value generated by an event which causes a surprisal to an observer of the event. The degree of this surprise is considered to increase when the event rarely occurs and vice versa. This implies that the initial state of the observer is not considered, because, if the observer already has prior knowledge about the event, no matter how long it takes for the event to occur, the observer may likely not be surprised about it. It is therefore clear that such definition is tied more to the event than to the observer.

In relation to this, Shannon’s entropy, which is the expected information content, is actually a type of uncertainty measure of an event and not of the observer of the event. Together with its different variants such as, joint entropy, mutual information, cross entropy, Kullback–Leibler (KL) divergence, etc., they are all used to measure different quantities of an event rather than an observer of the event. More so, there is no link between this information and the epistemological definition of knowledge [5,17]. In addition to this, the environment in which the event occurs or that in which the observer exists, is not considered in any entropy value generation.

Generally, the environment plays an important role in the justification of values such as belief, information, etc., and this type of justification is highly used in the epistemological definitions of knowledge [18,19] in any rational agent.

Imagine a scenario where there are two human agents, Ekane and Aki, living in different environments defined by different cultural, religious, political, geographical, and social features. Assume Ekane’s environment is defined culturally by language A, geographically by a hilly topography, religiously by monotheism, politically by democracy, and socially in support for free speech. On the other hand, Aki’s environment is defined culturally by language B, geographically by a coastal topography, religiously by polytheism, politically by autocracy, and socially against free speech.

If both Ekane and Aki have high knowledge, understanding, and trust (consciously or unconsciously) in their respective environments, then any event that occurs in their environments will be perceived and interpreted based on how their environments define the event. Consider an event such as "occurrence of peace", how both agents perceive and interpret this event may be completely different, and this is simply based on the influence of their environments on their cognition and rationality about the event.

Ekane, living and trusting in a democratic system will likely have the belief that peace can only occur via democracy, while Aki who lives and trusts in an autocratic system will likely belief that peace can only occur via autocracy. Clearly, placing both agents together to work for peace without any consideration of their respective environments will instead lead to disagreements and conflicts, unless their belief systems and/or environments are revised to align with the required definition (environment) of peace.

Same phenomenon will arise on different events such as "occurrence of success on a project", "occurrence of a cyber attack in a network", etc., because all these events and how the agent perceives and interprets them are influenced by the environment of the event and agent. So, the environment forms an invisible barrier to knowledge generation and harmonization among agents, and taking into account its influence on the event and agent is important in justifying the information about the event and belief of an agent about the event in any rational process. Many researches in cognition such as the work of Lewin [20,21], Audi [22,23], and many others, consider the environment as a major factor in value generation of a cognitive and rational agent.

In this paper, we focus on the influence of the environment on an agent belief system and how such influence is used to generate knowledge in the agent. We derive the logical definition of knowledge from an epistemological viewpoint. This enables a concise and precise view about knowledge, its operations and properties. Furthermore, we relate this concept of knowledge to other cognitive values of an agent such as understanding, trust, and wisdom.

1.1. Related Work

In reality, a study of knowledge in relation to intelligent agent is challenging and exhaustive. This is due to the large amount of diversity, misunderstanding, and misconception related to the topic. To some, knowledge is a type of belief, to others, it is a type of information, and to some extent, it is considered to be both belief and information. In most cases, the entity which possesses knowledge is not clearly defined and how the knowledge ecosystem operates in an environment of entities is not mentioned. What is presented in most literature is a definition of knowledge using either logic without semantics or semantics without logic.

Considering the definition of knowledge in [5], it is clearly a literal description of knowledge, rooted from philosophical literature and with main focus on the meaning (semantics) of knowledge. More so, the article consider knowledge as a type of belief and much about its operation is not mentioned. A similar concept about knowledge is given in [7], where knowledge is considered to consist of true belief and can only exist if three conditions are satisfied; truth condition, belief condition, and evidence condition. The evidence condition is considered as a justification of the true belief. In many other theories [6] related to the semantic definition of knowledge, such as the ontological description of knowledge [24,25], the operations on knowledge and the entity that generates it are not defined.

Related to the logical definition of knowledge, in [11], knowledge is defined using a probabilistic logic and it is considered at some point to be both belief and information. The article also focuses on defining the semantic content of information as the only property that can cause Shannon information [13] to yield knowledge. There have been many critics to this theory, e.g., in [26], due to its lack of coherence with the same information it tries to redefine. In [10], the logical definition of knowledge is not different to the definition of belief in Section 3.1 of this paper. In reality, such indifference between knowledge and belief is epistemologically misleading.

In [12], knowledge is defined as a mathematical function based on probability logic and information theory, but with no clear semantics and relation to epistemology.

In this paper, we take into consideration both the semantic and logical definitions of knowledge, to enable a concise understanding of the subject matter.

1.2. Contributions

The contributions of this work are summarized below.

A detailed abstraction of cognitive properties and their interrelationships in a cognitive intelligent agent.
A classification scheme for intelligent agents.
A concise mathematical definition of belief, knowledge, ignorance, stability, and exactness properties in relation to cognition and epistemology.

1.3. Organization

The rest of the paper is organized as follows: Section 2 focuses on the mathematical description of entities and the properties that can be associated to them. Section 3 concerns the quantification of cognitive properties. We made conclusion on the paper in Section 4.

2. Definition of Entities and Properties

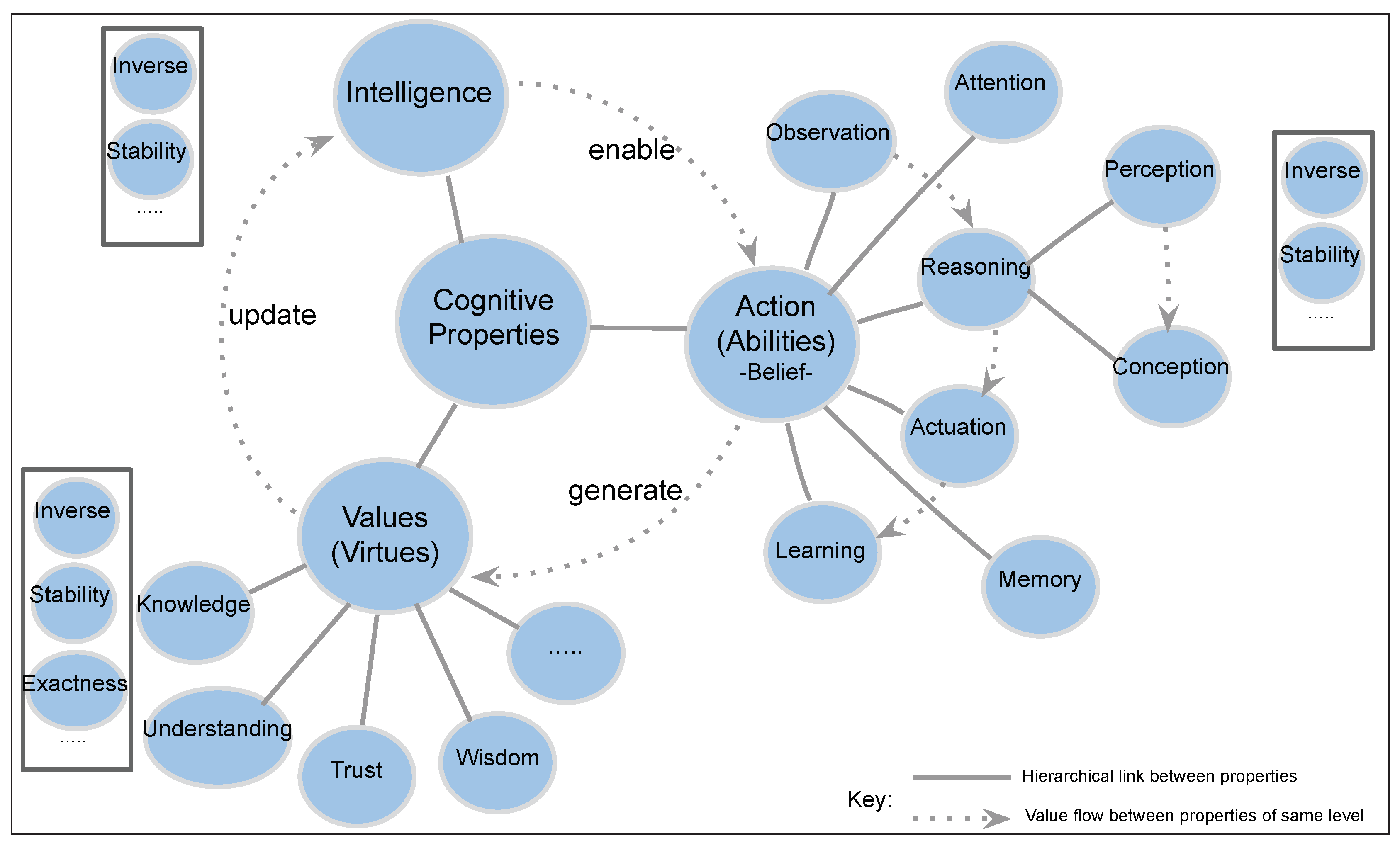
2.1. Cognitive Property

For an agent to gain awareness about targets in its environment, the agent needs to have some properties that will define its abilities, such as: what type of value it can gain, what actions it takes to acquire such value, and what strategy does it need to support such action. We call these sets of proprieties the cognitive properties of an agent.

In accordance with the definitions in [27,28,29], we define cognitive property as,

Definition 1.

Cognitive property is a set of properties that define the values, actions, and intelligence of an agent.

In this paper, we group cognitive properties of an agent into three types: intelligence properties, action properties, and cognitive value properties, as shown in Figure 1.

Figure 1 shows a proposed cognitive property model for our research. Unlike other models [8,9,10] that depict the relationships between cognitive properties as a sequential chain of properties, our model describes cognitive properties as a parallel hierarchical chain of properties and processes. Starting with the intelligence, action, and cognitive value properties, each property has other attributes such as inverse, stability, and exactness. We shall provide mathematical descriptions of these attributes for the knowledge property. This model gives a detailed abstraction of cognitive properties in any cognitive intelligent agent such as a human agent.

We focus on the value properties [30,31,32], specifically the knowledge property, and introduce its related properties and operations. With respect to this research, we define a cognitive value [31,32,33] as follows:

Definition 2.

Cognitive value is any property of an agent that depends on the action of the agent on a target.

So the action value, also called belief in Section 3.1, is not a cognitive value but a quantity on which cognitive values are defined as shown in Figure 1 and discussed in Section 3.1.

Lastly, related to cognition, this paper focuses on conscious cognition [34] based on beliefs, e.g., knowledge. Other conscious cognition such as those based on emotion, e.g., happiness, are reserved for future publications. We consider the former as hard consciousness and the latter as soft consciousness. Unconscious cognition such as intuition [35] for cognitive agents will also be discussed in future publications.

2.1.1. Knowledge, Action, and Intelligence

Knowledge has been defined and studied extensively in the literature in relation to cognitive and intelligent agent design [8,9,10,11]. Together with [36,37,38], we adopt a literal definition of knowledge link to cognition as follows:

Definition 3.

Knowledge, K, represents the level of comprehension an agent has or conclusion an agent has made about a target, with respect to the environment of the target.

An agent may seek knowledge about a target for various reasons, but the acquisition of a complete knowledge about a target is a progressive process. The absence of knowledge in such case is also important. This has been less studied in agent design, but literally exists in [39] and is given the name ignorance [40], which we adopt as follows:

Definition 4.

Ignorance, I, is a property that represents the level of absence of knowledge of an agent about a target.

An agent may seek to reduce ignorance about a target for various reasons, but the reduction of the complete ignorance about a target is a progressive process.

Axiom 2.1.

The increase in knowledge of an agent about a target leads to a decrease in ignorance of the agent about same or related target, and vice versa.

Hence, seeking knowledge implies reducing ignorance, and vice versa. The target in this case can be a task, a project, a discussion topic, an event, an agent, a property, etc.

Knowledge and ignorance are cognitive value properties whose operations are based on the action property.

Definition 5.

Action, A, is a property with the ability to receive, select, control, generate, store, optimize, and transfer cognitive values about a target.

Much about actions exist in literature [41,42,43,44]. We focus on knowledge based actions, which are actions carried on the knowledge value of an agent. We categorize actions into: receive (observation), select (attention), control (actuate), generate (reasoning), store (memorization), optimize (learning), and transfer (interoperability) operations.

These cognitive actions are supported by or based on the intelligence [45] of the agent, which we define as follows:

Definition 6.

Intelligence, $ϕ$ , is a property with the ability to enable an action on a target.

An intelligence can be a strategy, logic, algorithm, etc., of the action. We will also focus more on intelligence that enables knowledge based actions.

Much literature exists about intelligence [46,47,48] and the different action operations: observation (acquisition) [49,50,51], attention [52,53,54,55,56], actuation [57], reasoning [58,59,60], memorization [54,56,61,62,63], learning [54,56,64,65] and interoperability (transfer) [66,67,68]. Each of these operations will be discussed in detail in future publications.

Axiom 2.2.

An agent is said to be intelligent about a target if it has the ability to take an action on the target, no matter how less likely the action may be.

Axiom 2.3.

An agent is said to posses knowledge about a target if it has taken an action on the target, no matter how less likely the action may be.

From the definitions above, we can logically assume that,

Axiom 2.4.

((K \to A) \land (A \to ϕ)) ⊢ K \to ϕ

Axiom 2.5.

Given that

(K \to A \to ϕ)

\neg ϕ \to \neg A \to \neg K ⊢ \neg ϕ \to (\neg A \land \neg K)

\neg K \to \neg A \to (ϕ \lor \neg ϕ) ⊢ \neg K \to (\neg A \land (ϕ \lor \neg ϕ))

where → is logical dependency,

y \to x

indicates that y is logically dependent on x, ⊢ is logical consequence, ∧ indicate logical disjunction, and ¬ is logical negation.

In Section 3, we shall transform these literal and logical constructs to mathematical definitions and relationships of knowledge, ignorance, action, and intelligence. These mathematical definitions and relationships of cognitive properties will be quantified, making it possible for various mathematical operations to be perform on them.

Apart from the generation of knowledge value, action and intelligence also generate other cognitive values such as understanding, trust, and wisdom, which we define below.

Definition 7.

Understanding represents the degree of convergence or divergence between the actions of agents about a target.

Definition 8.

Trust represents the amount of mutual value between agents about a target.

Definition 9.

Wisdom represents the complete value an agent can achieve about a target.

The mathematical definition and features of understanding, trust and wisdom properties will be describe in future publications.

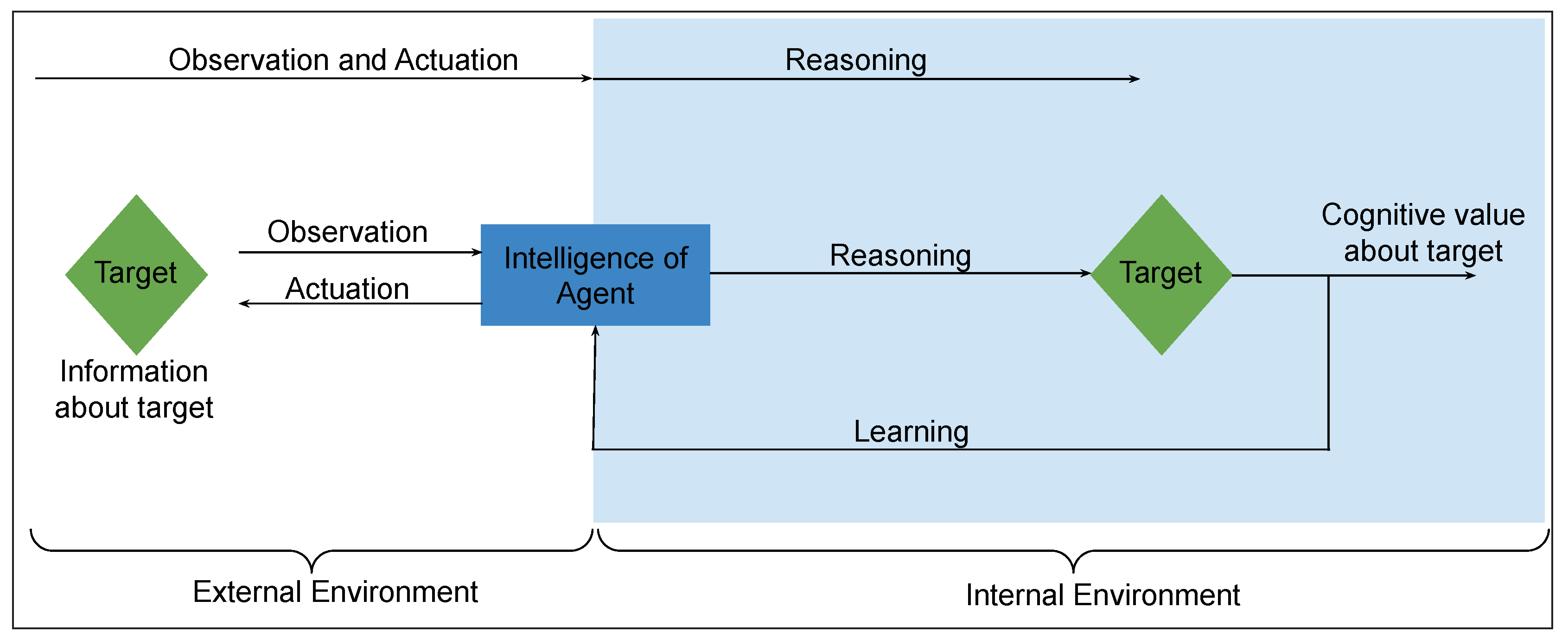
2.1.2. Observation, Reasoning, and Actuation

An intelligent agent with a perceptual and conceptual abilities observes an environment and collects information about a target to perceive and conceive the target. Many approaches have been used to quantify information [13,14,15,16,69], but not entirely with respect to an agent. We adopt a definition that is based on the cognitive property of an agent, specifically the value property.

Definition 10. Information, X, is any input value to an agent based on which the agent takes action about a target.

This imply that information can take any form, such as, beliefs, knowledge, ignorance, stability, etc., use as input during reasoning. So, all cognitive property values which are used as a source value to achieve other values about a target are considered here as information.

To achieve a target, the agent collects information from its environment about the target using its senses [49,51]. Through a reasoning process, it takes action on the target based on the collected information [57,70]. During this process, the values of the cognitive properties may change to reflect the agent’s current cognitive state about the target.

For an agent with an added ability to learn a value, these cognitive values can be optimized directly through a forward reasoning process, or indirectly through a backward reasoning process where the value is reinserted back to the intelligence that supports its generation [64,65]. In this paper, the word optimization will be used interchangeably with the word learning because we consider learning as a value optimization process.

For clarity, we present in Figure 2 an agent with four cognitive action operations: observation, reasoning, learning, and actuation.

In this paper, we consider that during these operations, both the agent and target exist in an environment. The environment can be external (real) and internal (abstract) environments with respect to the agent as shown in Figure 2. Examples of real environments include physical space, geographical regions, etc., and abstract environment include perspectives, culture, context, consciousness, etc. Same description holds for a cyber-physical system. We assume that the internal environment is fully observable to the agent.

With respect to the agent and its environments, we define these four action operations: observation, reasoning, actuation and learning.

Definition 11.

Observation, O, is the process of information identification and collection from an environment.

Based on the agent, we can distinguish two types of observation: internal (abstract) and external (real) observation. During internal observation of an agent, the internal information can come from the actions of the agent (local value acquisition) or that of a remote agent (remote value acquisition).

Definition 12.

Reasoning, R, is the process of cognitive value generation about a target.

This generates the values for all the actions of an agent and can be seen as the central process for value generation in an agent. An agent will therefore have a reasoning process for observation, attention, memory, actuation, and learning to generate their respective cognitive values. The output of a reasoning action is quantified and stored as belief.

We classify the reasoning actions related to observation into perception [71,72] and conception [73,74], and it can be executed for different purpose on the target such as for description, diagnosis, prediction, prescription, and cognition of a target [75,76,77]. Reasoning actions for actuation generate cognitive values related to the influence on both agent and target environment [57], and those for learning generate values related to cognitive value optimization about a target [58,65].

Also, based on its execution logic, reasoning can be inductive, deductive, abductive, etc., [78], and based on its input-output relationship, it can be classified as deterministic, non deterministic, stochastic, etc.

Since the reasoning action forms a large part of agent design, we use the terms reasoning and action interchangeably in this paper, unless stated otherwise.

Definition 13.

Actuation, $ζ$ , is the process through which an agent influences its environments.

The purpose of the influence may consist of controlling, changing, etc., the target or agent environments. Actuation can be external (real) or internal (abstract) to an agent.

Definition 14.

Learning, $γ$ , is an optimization process that involves cognitive value increases through revision and update.

Agents can choose to learn from their self acquired value, remotely acquired values or both. They can also unlean the values they have learned about a target. More on learning and unlearning will be discussed in a future publication.

Moreover, the agent can do any of these operations on a target by itself (unsupervised), assisted by another agent (supervised), by both itself and another agent (semi-supervised), or by another agent (remote). Most of these relationships with its target environment are well studied in the literature [64,65].

Also, related to the operations of an agent, we can classify agents based on the existence and non existence of any of the four operations, with reasoning being the compulsory operation for all intelligent agents. Any agent without a reasoning process is considered in this research as a non intelligent agent. Intelligent agents can thus be classify into different distinct types as shown in the table below.

Table 1. A classification scheme for Intelligent Agents.

	Main abilities
Types	Observation	Actuation	Learning	Reasoning	Examples
Type 0	no	no	no	no	non intelligent agent
Type 1	no	no	no	yes	clock
Type 2	no	no	yes	yes	learning clock
Type 4	no	yes	no	yes	controllers
Type 5	no	yes	yes	yes	learning controllers
Type 6	yes	no	no	yes	sensors
Type 7	yes	no	yes	yes	learning sensors
Type 8	yes	yes	no	yes	Automata, computers
Type 9	yes	yes	yes	yes	AI bot, humans

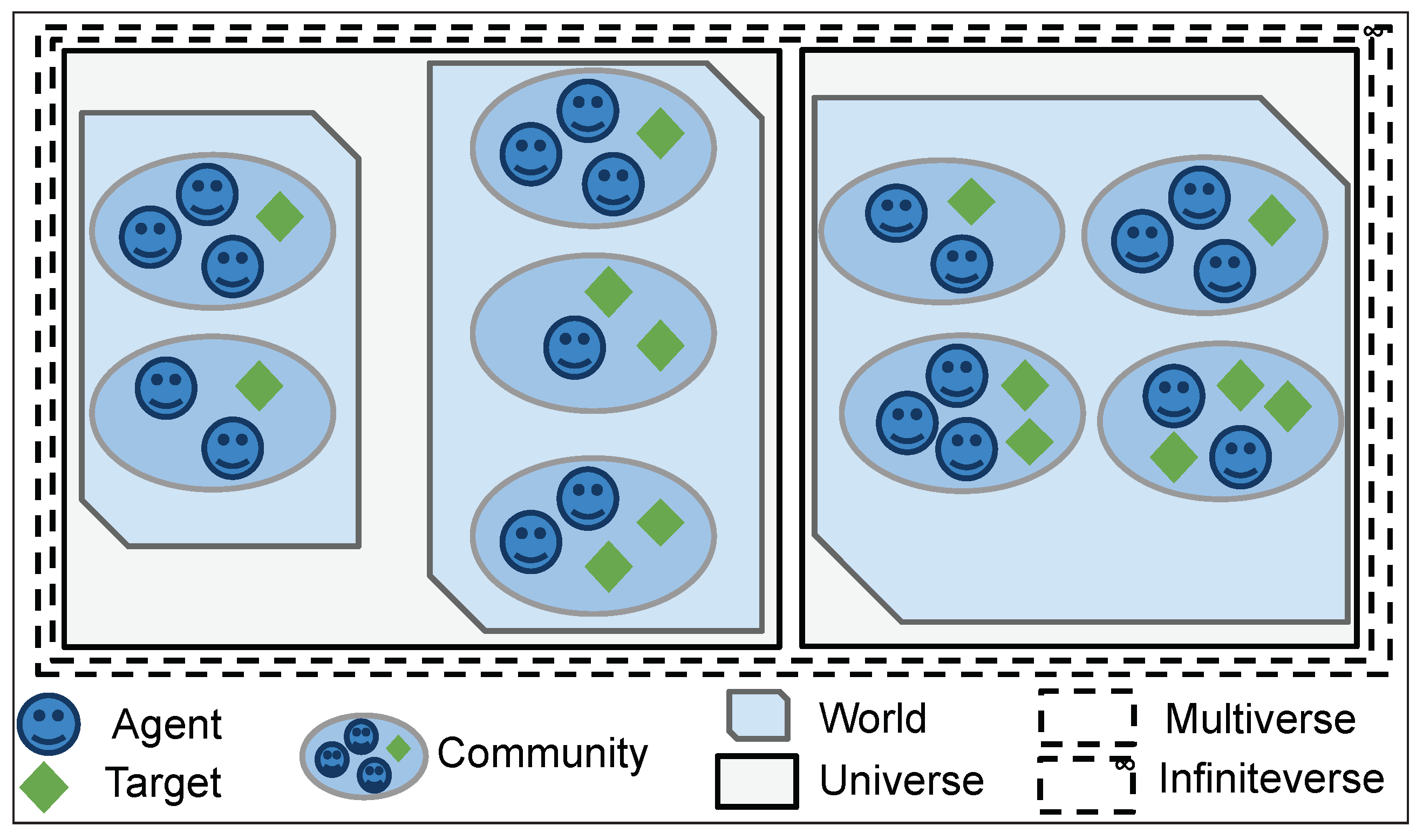
2.2. Definitions of Entities

One cannot define the quantification and operations on knowledge without defining the entities that will generate and use the knowledge. An entity is generally considered as anything that exists. The main philosophical question related to existence is, how do we know if something exists? In response to this, we think anything that exists must possess a value. So, with respect to this research, we define an entity as follows:

Definition 15.

An entity, $ρ$ , is anything that exists and possesses value.

In this section, we mathematically define different types of entities, their logical relationships and operations.

2.2.1. Description and Properties

We distinguish and define three types of entities: agent, target, and environment, together with their properties.

Definition 16.

An agent, g, is an entity that possesses cognitive property values.

The different cognitive properties an agent can posses are presented in Figure 1. An agent can also be considered as a cognitive actor in an environment.

Definition 17.

A target, t, is an entity that an agent seeks, and is define by a set of input and output property values, and the relationship value between the two properties.

The properties of the target represent the domains of the environment in which the target is found. The output domains define the existence of the target and are considered as the existential properties of the target. The input domains influence the existence of the target and are considered as the evidential properties of the target.

The process where an agent uses input properties of a target to act on the output properties of the target is called Perception [71,72], and it is the main focus in conventional agent design. Whereas, the process where the agent seeks to reproduce the output properties of a target is called Conceptualization [72,73]. In most conventional agent design, the output properties are given to the agent (with or without labels) during learning and testing, and this does not imply conceptualization.

To fully act on a target, an agent must not only identify the input and output properties of the target but also the relationship between them. Thus, the main goal of an agent during learning is to recreate the relationship between the input and output properties of a target. This is summarized in the axiom below.

Axiom 2.6.

The value an agent attributes to the input-output relationship of a target is a property of the agent and defines the relationship between the agent and the target.

We define an environment entity, which acts as a container of agents and targets.

Definition 18.

An environment, e, is an entity which contains agents and targets and defines their relationships.

Environments may contain other environments which we group into: community, world, universe, multiverse, and infiniteverse. A community is an environment with agents and targets, a world is a collection of communities, a universe is a collection of world, a multiverse is a collection of universes, and infiniteverse is an infinite hierarchy of multiverse. We consider all environments as containers as illustrated in Figure 3.

We logically define these structural properties as follows:

e = {g, t}

Q = {e, g, t}

and

\forall ρ \in Q

q = {ρ_{1}, ρ_{2}, . . . ρ_{n}}

where e is an environment entity, g is an agent entity, t is a target entity, Q is the set of entity types,

ρ

is an entity, and q is a container or set of entities.

To support our operations on agent design, we define the following functional properties of the different entities.

\begin{matrix} Agent : \forall g \in e, g = (Φ, A, C, f_{g}, P_{e}), \end{matrix}

(2.1)

where

Φ

is intelligence property, A is action property, C is cognitive value property,

f_{g}

is relationship between properties, and

P_{e}

is inherited property from the environment.

Generally, using the knowledge property, we can simply express the agent as follows:

\begin{matrix} g = (ϕ, A, K), \end{matrix}

(2.2)

\begin{matrix} A {(g)}_{t} = f_{A} (y, X, ϕ), \end{matrix}

(2.3)

\begin{matrix} K {(g)}_{t} = f_{K} (A {(g)}_{t}, A {(e)}_{t}), \end{matrix}

(2.4)

where g is an agent, t is target of the agent, y is a target output information, X is the vector of target input information,

A {(g)}_{t}

is action value (or belief) of the agent on the target,

ϕ

is the intelligence (or parameters) of the agent that enables the action, and

K {(g)}_{t}

is knowledge generated by the agent based on its action and the environment action

A {(e)}_{t}

on the target.

\begin{matrix} Target : \forall t \in e, t = (X, Y, f_{t}, P_{e}), \end{matrix}

(2.5)

where

f_{t} : X \Leftrightarrow Y

, X is input property, Y is output property.

Generally, we can simply express the target as an entity of the environment as follows:

\begin{matrix} t = (X, Y, f_{t} (X, Y)), \\ X \subset P_{e}, Y \subset P_{e}, f_{t} (X, Y) \in R, \end{matrix}

(2.6)

where t is a target in an environment, X is vector of properties of the environment that act as input (or evidential) properties of the target, Y is vector of properties of the environment that act as output (or existential) properties of the target, and

f_{t} (X, Y)

is a property of the target that defines a logical relationship between X and Y.

\begin{matrix} Environment : \forall e \in q, e = (P_{e}, f_{e}, P_{q}), \end{matrix}

(2.7)

where

P_{e}

is property of the environment,

f_{e}

defines the relationship between the properties of the environment, and

P_{q}

is inherited property from the environment container.

Also, depending on the content of the environment, its properties can be grouped into those of the agents

P_{g}

, target

P_{t}

and their relationship

f_{t g}

, i.e.,

P_{e} = {P_{t}, P_{g}, f_{t g}}

Generally, we can simply express the environment as follows:

\begin{matrix} e = (P_{e}, f_{e} (P_{e})), \\ P_{e} \in R^{n}, f_{e} (P_{e}) \in R, \end{matrix}

(2.8)

where e is an environment,

P_{e}

is a vector of all properties of the environment, and

f_{e} (P_{e})

is a logical relationship define over all the properties of the environment.

Figure 4 shows the interaction between agents and targets in different environments.

After defining the entities and properties, we then define logical relations and operations on them. The next section answers questions about the equality, equivalence, superiority, inferiority, dependency, association, dissociation, and intersection of entities. For example, when are agents equal?

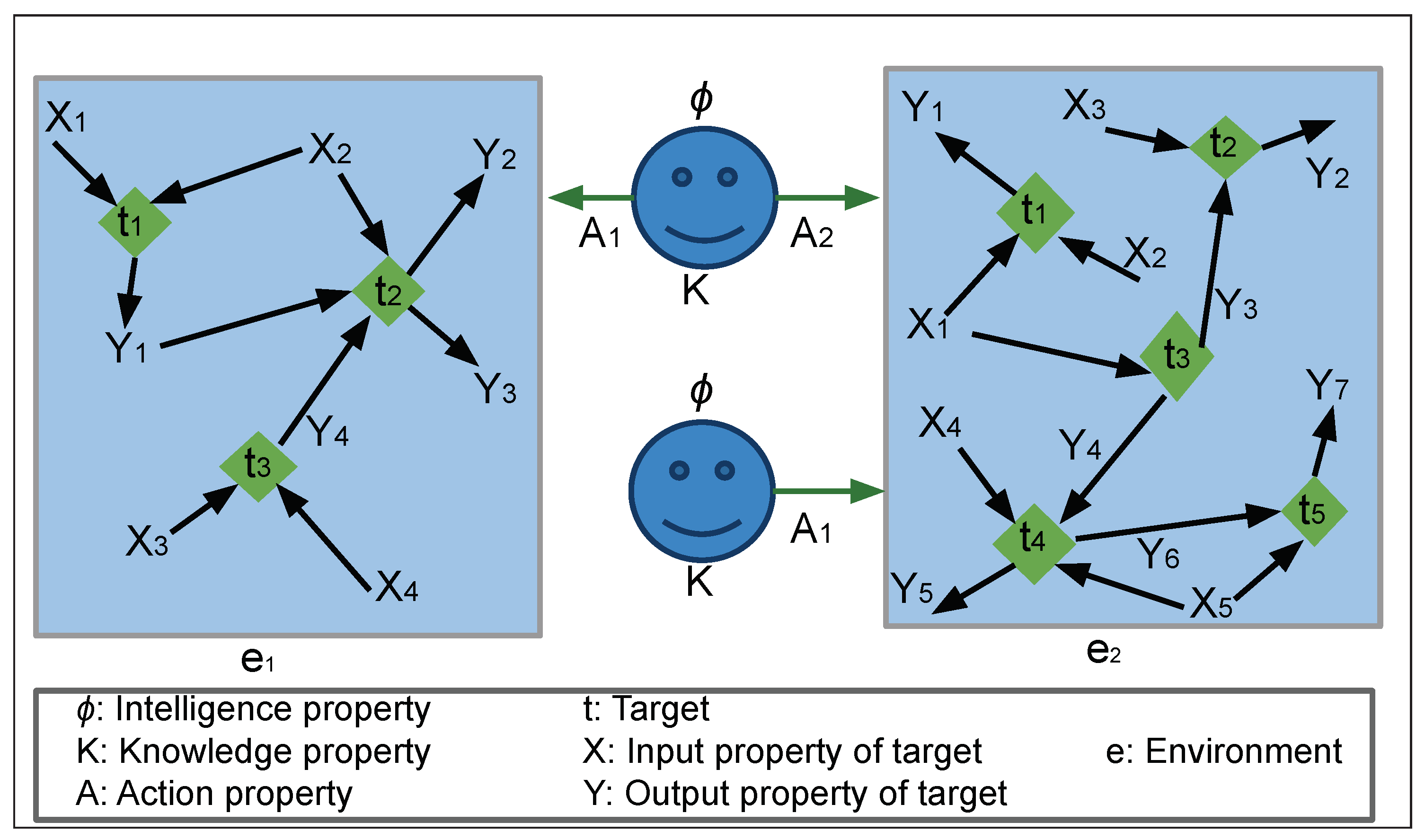
2.2.2. Logical Relationships Between Entities

We define different logical relationships between entities, where

ω

is entity property,

{(ρ_{i} * ρ_{j})}_{ω}

indicates the logical relationship (∗) between entities

ρ_{i}

and

ρ_{j}

over the property

ω

i \neq j

, and

i, j \in N

. Also, iff means `if and only if’, and ⊥ means logical independence.

i. Equivalence (≡)

Two entities are equivalent over a set of properties if at least one of the properties (weak equivalence) or all (strong equivalence) have same value and structure.

We distinguish two types of equivalence.

a) Agent equivalence:

\forall g_{i}, g_{j} \in q, {(g_{i} \equiv g_{j})}_{ω}

iff

(ω_{i} \equiv ω_{j}) \land t_{i} \equiv t_{j}

b) Target equivalence:

\forall t_{i}, t_{j} \in q, {(t_{i} \equiv t_{j})}_{ω}

iff

(X_{i} \equiv X_{j} \lor Y_{i} \equiv Y_{j} \lor f_{i} \equiv f_{j})

Equivalent relationships must also be reflexive, symmetrical and transitive over the properties. Example of equivalent relationship between entities is an equality relationship.

ii. Equality (=)

Two entities are equal over a set of properties if at least one of the properties (weak equality) or all (strong equality) have same value. We distinguish two types of equality.

a) Agent equality:

\forall g_{i}, g_{j} \in q, {(g_{i} = g_{j})}_{ω}

iff

(ω_{(1, i)} = ω_{(1, j)} \lor ω_{(2, i)} = ω_{(2, j)} \lor \dots ω_{(n, i)} = ω_{(n, j)}) \land t_{i} = t_{j}

b) Targets equality:

\forall t_{i}, t_{j} \in q, {(t_{i} = t_{j})}_{ω}

iff

(X_{(1, i)} = X_{(1, j)} \lor X_{(2, i)} = X_{(2, j)} \dots X_{(n, i)} = X_{(n, j)}) \lor (Y_{(1, i)} = Y_{(1, j)} \lor Y_{(2, i)} = Y_{(2, j)} \dots Y_{(n, i)} = Y_{(n, j)} \lor (f_{i} = f_{j})

iii. Superiority (>)

One entity is superior over another entity on a set of properties if at least in one of the properties (weak equality) or all (strong equality), it has a greater value. We distinguish two types of superiority.

a) Agents superiority:

\forall g_{i}, g_{j} \in q, {(g_{i} > g_{j})}_{ω}

iff

(ω_{(1, i)} > ω_{(1, j)} \lor ω_{(2, i)} > ω_{(2, j)} \lor \dots ω_{(n, i)} > ω_{(n, j)}) \land t_{i} = t_{j}

b) Targets superiority:

\forall t_{i}, t_{j} \in q, {(t_{i} > t_{j})}_{ω}

iff

(X_{(1, i)} > X_{(1, j)} \lor X_{(2, i)} > X_{(2, j)} \dots X_{(n, i)} > X_{(n, j)}) \lor (Y_{(1, i)} > Y_{(1, j)} \lor Y_{(2, i)} > Y_{(2, j)} \dots Y_{(n, i)} > Y_{(n, j)} \lor (f_{i} > f_{j})

iv. Inferiority (<)

One entity is inferior over another on a set of properties if at least in one the properties (weak equality) or all (strong equality), it has a lesser value. We distinguish two types.

a) Agents inferiority:

\forall g_{i}, g_{j} \in q, {(g_{i} < g_{j})}_{ω}

iff

(ω_{(1, i)} < ω_{(1, j)} \lor ω_{(2, i)} < ω_{(2, j)} \lor \dots ω_{(n, i)} < ω_{(n, j)}) \land t_{i} = t_{j}

b) Targets inferiority:

\forall t_{i}, t_{j} \in (ρ, q), {(t_{i} < t_{j})}_{ω}

iff

(X_{(1, i)} < X_{(1, j)} \lor X_{(2, i)} < X_{(2, j)} \dots X_{(n, i)} < X_{(n, j)}) \lor (Y_{(1, i)} < Y_{(1, j)} \lor Y_{(2, i)} < Y_{(2, j)} \dots Y_{(n, i)} < Y_{(n, j)} \lor (f_{i} < f_{j})

v. Dependency (→)

An entity

ρ_{i}

depends on

ρ_{j}

over a set of properties if at least one (weak dependency) or all (strong dependency) properties of

ρ_{i}

are defined by those of

ρ_{j}

. We distinguish two types of dependency.

a) Agents dependency:

\forall g_{i}, g_{j} \in q, {(g_{i} \to g_{j})}_{ω}

iff

{(ω_{k})}_{i} = f ({(ω_{1} \lor . . . ω_{n})}_{j})

b) Target dependency:

\forall t_{i}, t_{j} \in q, {(t_{i} \to t_{j})}_{ω}

iff

{(X_{k})}_{i} = f ({(X_{1} \lor \dots X_{n})}_{j}) \lor {(Y_{k})}_{i} = f ({(Y_{1} \lor \dots Y_{n})}_{j}) \lor {(f_{k})}_{i} = f ({(f_{1} \lor \dots f_{n})}_{j})

By definition, we can consider that, all entities depend on their properties.

ρ = f (ω) ⊢ ρ \to ω

Dependency between entities can be bidirectional,

\forall ρ_{i}, ρ_{j} \in q, {(ρ_{i} \leftrightarrow ρ_{j})}_{ω}

iff

{(ρ_{i} \to ρ_{j})}_{ω} \land {(ρ_{j} \to ρ_{i})}_{ω}

vi. Conditional dependency( $\to ∣$ )

It is a type of dependency where the relationship between the properties of the two entities is conditioned on one of the entities or a third entity. An entity

ρ_{i}

is conditionally dependent on another entity

ρ_{j}

over a set of properties if (the occurrence of) at least one property (weak condition) or all properties (strong condition) of

ρ_{j}

are conditioned on those of

ρ_{i}

, or those of a third entity

ρ_{z}

. We distinguish two types of conditional dependency;

a) Agents conditional dependency:

\forall ρ_{i}, ρ_{j} \in q, {(ρ_{i} \to ∣ ρ_{j})}_{ω}

iff

{(ω_{i})}_{i} \to ∣ {(ω_{1} \lor . . . ω_{n})}_{j}

b) Targets conditional dependency:

\forall ρ_{i}, ρ_{j} \in q, {(ρ_{i} \to ∣ ρ_{j})}_{ω}

iff

\forall X, Y, f \in t, ({(X_{i})}_{i} \to ∣ {(X_{1} \lor \dots X_{n})}_{j}) \lor ({(Y_{i})}_{i} \to ∣ {(Y_{1} \lor \dots Y_{n})}_{j}) \lor ({f_{i}}_{i} \to ∣ {(f_{1} \lor \dots f_{n})}_{j})

Conditional dependency can also be bidirectional,

\forall ρ_{i}, ρ_{j} \in q, {(ρ_{i} ∣ \leftrightarrow ∣ ρ_{j})}_{ω}

iff

{(ρ_{i} \to ∣ ρ_{j})}_{ω} \land {(ρ_{j} \to ∣ ρ_{i})}_{ω}

{(ρ_{i} \to ∣ ρ_{j})}_{ω} = {(ρ_{j} \to ∣ ρ_{i})}_{ω}

, we say the entities are conditionally equivalent over the property

ω

. That is,

{(ρ_{i} \to ∣ ρ_{j})}_{ω} = {(ρ_{j} \to ∣ ρ_{i})}_{ω} \Rightarrow {(ρ_{i})}_{ω} = {(ρ_{j})}_{t}

vii. Mutual dependency(⊸)

It is a type of dependency where the self relationships of the entities on their property are excluded from their conditional relationships.

An entity

ρ_{i}

is mutually dependent on another entity

ρ_{j}

over a set of properties if (the occurrence of) at least one (weak condition) or all the self properties (strong condition) of

ρ_{i}

are excluded from its conditional relationship with those of

ρ_{j}

, or those of a third entity

ρ_{z}

{(ρ_{i} ⊸ ρ_{j})}_{ω} = {(ρ_{i} \to ∣ ρ_{j})}_{ω} \ {(ρ_{i})}_{ω}

Excluding their self-relationships imply that mutual dependency captures a bidirectional relationship between entities. Hence, Two entities in a mutual dependency over a property have a birectional equality over the property.

{(ρ_{i} ⊸ ρ_{j})}_{ω} = {(ρ_{j} ⊸ ρ_{i})}_{ω}

(reciprocity).

Similar to conditional dependency, mutual dependency can be established on the properties of targets and agents.

viii. Container (⊔ , □)

An entity q is a container to another entity

ρ

over a set of properties if for these properties,

ρ

is equal or inferior to q.

{(q ⊔ ρ)}_{ω}

iff

\forall ω, (ω_{ρ} < = ω_{q})

Axiom 2.7.

Containers can be defined based on their entities and entities can be defined based on their containers.

From Axiom 2.7 and the definition of a container, we can conclude that, all entities in a container depend on the container and all containers depend on their entities.

q ⊔ ρ \Rightarrow (ω_{ρ} = f_{ρ} (ω_{q})) \land (ω_{q} = f_{q} (ω_{ρ})) ⊢ q \leftrightarrow ρ

We distinguish two categories of containers and entities dependency relation, that is, coupling and cohesion.

ix. Coupling (⋈)

It defines the dependency between containers. A container entity

q_{i}

is coupled with a container entity

q_{j}

iff

(q_{i} \to q_{j}) \lor (q_{i} \leftarrow q_{j}) \lor (q_{i} \leftrightarrow q_{j})

x. Cohesion (⨂)

It defines the dependencies between entities in a container. An entity

ρ_{i}

is considered to be cohesive with an entity

ρ_{j}

, iff

(ρ_{i} \to ρ_{j}) \lor (ρ_{i} \leftarrow ρ_{j}) \lor (ρ_{i} \leftrightarrow ρ_{j})

. Cohesive dependency can exist between entities in same container or different containers. We distinguish two types of cohesion;

a) Local cohesion:

q ⊔ ρ_{j}, ρ_{j}

and

(ρ_{i} \to ρ_{j}) \lor (ρ_{i} \leftarrow ρ_{j}) \lor (ρ_{i} \leftrightarrow ρ_{j})

b) Remote cohesion:

(q_{i} ⊔ ρ_{j}) \land (q_{j} ⊔ ρ_{j})

and

(ρ_{i} \to ρ_{j}) \lor (ρ_{i} \leftarrow ρ_{j}) \lor (ρ_{i} \leftrightarrow ρ_{j})

Also, based on the dependency and exchange of properties between containers and their host, we can distinguish three types of containers; open, close and isolated containers.

xi. Open container (⊔)

A container q is open over a host h if values for some

ω

of q depend on h, i.e.,

{(q \to h)}_{ω}

, and

ρ

ω

can be exchanged between q and h.

xii. Close container (□)

A container q is closed over a host h if values for some

ω

of q depend on h, i.e.,

{(q \to h)}_{ω}

, and

ρ

ω

cannot be exchanged between q and h.

xiii. Isolated containers (□)

A container q is isolated over a host h if values for all

ω

of q is independent on h, i.e.,

\neg {(q \to h)}_{ω}

, and

ρ

ω

cannot be exchanged between q and h. In addition, entities can be considered as a container because even if they may not contain other entities, they contain at least some properties, making them property containers.

xiv. Referencing ( $\to ∣ ∣$ )

A relationship where an entity uses another entity as its container or content in defining its property value.

Axiom 2.8.

Any referencing to a referent equal to the referral on a value is insignificant (null) to the referral.

{(ρ_{1} ⊥ ρ_{2})}_{ω} \land {(ρ_{1} = ρ_{2})}_{ω} \Rightarrow (ρ_{1} | | ρ_{2})_{ω} = {(ρ_{1})}_{ω}

Axiom 2.9.

A referral will downgrade if it references a referent less significant than it on a value, and upgrade if otherwise.

{(ρ_{1} ⊥ ρ_{2})}_{ω} \land {(ρ_{1} > ρ_{2})}_{ω} \Rightarrow {(ρ_{1} | | ρ_{2})}_{ω} < {(ρ_{1})}_{ω}

(downgrade),

{(ρ_{1} ⊥ ρ_{2})}_{ω} \land {(ρ_{1} < ρ_{2})}_{ω} \Rightarrow (ρ_{1} | | ρ_{2})_{ω} > {(ρ_{1})}_{ω}

(upgrade).

Referencing can be considered as a relative relationship or a type of dependency of an entity on another entity.

In general, an agent can relate to different entities for different purposes to achieve a value, to some (e.g., targets) it builds a conditional relation, while to others (e.g., environments) it builds a reference relation. The operation on the relationships of an entity is important, and requires a logical construct, which we define in the following axiom.

Axiom 2.10.

The operation on the relationships of an entity can be defined as a vector operation on the relationships.

For example, if entities

ρ_{1}

and

ρ_{2}

are non-referentially (e.g., conditionally, mutually, jointly, etc.) related to

ρ_{3}

independently, then any referential relationship we define between

ρ_{1}

and

ρ_{2}

ρ_{3}

will be equal to the vector sum of their individual relationships on

ρ_{3}

Let

{(ρ_{1} \to ρ_{3})}_{ω} | | ρ_{e 1} = \vec{r_{1}}

{(ρ_{2} \to ρ_{3})}_{ω} | | ρ_{e 2} = \vec{r_{2}}

, and

{(ρ_{1} ∣ ∣ ρ_{2})}_{ω} = \vec{r_{3}}

Then, using an n-dimensional Euclidean vector space of

ω

, on a relationship

\vec{r}

between entities, we propose that,

Conjecture 1.

\begin{matrix} \vec{r_{3}} = \vec{r_{1}} + \vec{r_{2}} i f {(ρ_{e 1} = ρ_{e 2})}_{ω, ρ_{3}} (collinear on ρ_{3}), \end{matrix}

(2.9)

\begin{matrix} \vec{r_{3}} \neq \vec{r_{1}} + \vec{r_{2}} i f {(ρ_{e 1} \neq ρ_{e 2})}_{ω, ρ_{3}} (noncollinear on ρ_{3}) . \end{matrix}

(2.10)

For

\vec{r_{3}} = \vec{r_{1}} + \vec{r_{2}}

to exist during non-collinearity, the environment of one entity needs to be transformed to the environment of the other, leading to a collinear situation.

Furthermore, with collinearity, other vector algebra operations such as operations on vector magnitude can be evaluated easily using vector rules such as the cosine rule.

\begin{matrix} {\vec{r_{3}}}^{2} = {\vec{r_{1}}}^{2} + {\vec{r_{2}}}^{2}, if ρ_{1} ⊥ ρ_{2}, \end{matrix}

(2.11)

\begin{matrix} {\vec{r_{3}}}^{2} = {\vec{r_{1}}}^{2} + {\vec{r_{2}}}^{2} - 2 \vec{r_{1}} \vec{r_{2}} c o s (θ_{3}), if ρ_{1} ⊥ / ρ_{2}, \end{matrix}

(2.12)

where

{(ρ_{e 1} = ρ_{e 2})}_{ω, ρ_{3}}

In such case, the angle between the non-referential (i.e., absolute) values of two entities about a third entity represent their referential (i.e., relative) relationships about the entity.

Conjecture 2.

The angle

θ_{3}

between any two entities

ρ_{1}

and

ρ_{2}

ρ_{3}

is a measure of their referential relationship.

These relationships between non-referential and referential values of entities are represented in Figure 5.

For a relationship over space and time, we shall apply hyperbolic functions to the Euclidean vector in a future publication to present important effects of time and space on cognition. The relationships can also be represented using tensors on the euclidean and non-euclidean (e.g., hyperbolic) space.

2.2.3. Logical operations between entities

We define three types of operations (association, dissociation, intersection) between containers and entities.

i. Operations Between Containers

a) Association(∪) of containers

This involves the union of the entities of many containers to form a new container.

q_{i} \cup q_{j} = \{\forall ρ \in q_{i} \lor ρ \in q_{j}\}

b) Dissociation (-) of containers

This involves the separation of a container from another container to form a new container.

q_{i} - q_{j} = \{\forall ρ_{i} \in q_{i} \lor ρ_{j} \notin q_{j}\}

c) Intersection (∩) of containers

This involves the intersection of many containers to form a new container based on their equivalent entities.

q_{i} \cap q_{j} = \{\forall ρ \in q_{i} \land ρ \notin q_{j}\}

ii. Operations between entities

a) Association (∪) of entities

This involves the union of the properties of many entities to form a new entity.

ρ_{i} \cup ρ_{j} = \{\forall ω \in ρ_{i} \lor ω \in ρ_{j}\}

b) Dissociation (-) of entities

This involves the separation of an entity from another to form a new entity.

ρ_{i} - ρ_{j} = \{\forall ω \in ρ_{i} \lor ω \notin ρ_{j}\}

c) Intersection (∩) of entities

This involves the joining of many entities to form a new entity based on their equivalence properties.

ρ_{i} \cap ρ_{j} = \{\forall ω \in ρ_{i} \land ω \in ρ_{j}\}

iii. Operations between properties

This involves operations between the values of the properties of entities, rather than the entities themselves. Due to the dependency possibility of the properties, we use probability logic operations [79] to define the operations between properties. Nevertheless, other logic, such as, functional, fuzzy, symbolic, etc., can also be used.

Concerning property and value, the main difference between them in this paper is that, a property is a variable (or container) that holds a value which can be optimized within the property, while a value is the content of a property and defines the nature of the property. Values can be static, dynamic, discrete, continuous, etc.

In this section, we presented three types of entities and defined the properties, relationship and operations they can posses. In the next section, we will introduce the quantification of the knowledge property and different cognitive properties related to it.

3. Cognitive Property Quantification

As defined in Section 2.1, cognitive properties include the action, intelligence and cognitive values of an agent. We quantify the action and intelligence properties and, for the cognitive value property, we focus on the knowledge property.

3.1. Action Property

In an environment, an agent performs actions on one or more targets to acquire values. As discussed in Section 2.1.2, the reasoning action is the main action for cognitive value generation. The value generated by an agent irrespective of the target environment is considered as the action value and stored as belief in the agent. We quantify this value using epistemological perspective [7] as described below.

3.1.1. Action Quantification

The Action value of an agent on a target is the likelihood of that action on the target given an intelligence.

\begin{matrix} A_{ϕ} {(g)}_{t} = f (t, ϕ) = L (ϕ; t) \Rightarrow A_{ϕ} {(g)}_{t} = P (t; ϕ), \end{matrix}

(3.1)

where

L (ϕ; t)

is likelihood of an intelligence

ϕ

on the target t,

P (t; ϕ)

is probability of t based on

ϕ

Each action value generation process about a target is considered as an event on which cognitive values depend. An agent can generates different types of action values (belief) about a target. Below is a summary of these action values.

3.1.2. Types of Action Values

i. Domain action and Specific action

These are action values that define an agent’s belief about the relationship between the input and output features of a target.

The Domain action is an action that leads to the comprehension of a target.

\begin{matrix} {[A_{ϕ} {(g)}_{t}]}_{d} = L (ϕ; Y \leftrightarrow X) \Rightarrow P (Y \cap X; ϕ) . \end{matrix}

(3.2)

The Specific or Causal action is an action that leads to the conclusion about a target.

\begin{matrix} {[A_{ϕ} {(g)}_{t}]}_{s} = L (ϕ; Y \to ∣ X) \Rightarrow P (Y ∣ X; ϕ) . \end{matrix}

(3.3)

The conversion from domain action to specific action and vice versa is defined using the probability logic below.

From Domain to Specific action:

\begin{matrix} {[A_{ϕ} {(g)}_{t}]}_{s} = \frac{{[A_{ϕ} {(g)}_{t}]}_{d}}{P (X; ϕ)} . \end{matrix}

(3.4)

From Specific to Domain action:

\begin{matrix} {[A_{ϕ} {(g)}_{t}]}_{d} = {[A_{ϕ} {(g)}_{t}]}_{s} (P (X; ϕ)) . \end{matrix}

(3.5)

From these expressions, we deduce the following:

Conjecture 3.

It is required to exclude information about input space existence during domain to specific action conversion but such information is needed in the reverse process.

This is intuitively true because during causality, such information will be less helpful and will lead to more noise.

ii. Abstract action and Real action

These are action values defined based on the agent’s environment in which the actions are executed. The Abstract action is an action performed on targets in the internal environment of an agent. The Real action is an action performed on targets in the external environment of an agent.

An example of an abstract and a real action are respectively the internal and external locus of control [80] of an agent, which is also just a type of actuation action.

It is important to note that both the real and abstract actions can have domain and specific types. Also, real actions represent practical actions while abstract actions represent theoretical actions. Their conversion is described below.

Theoretical and practical action conversion:

\begin{matrix} {[A_{ϕ} {(g)}_{t}]}_{T} = f_{P \to T} ({[A_{ϕ} {(g)}_{t}]}_{P}), \end{matrix}

(3.6)

\begin{matrix} {[A_{ϕ} {(g)}_{t}]}_{P} = f_{T \to P} ({[A_{ϕ} {(g)}_{t}]}_{T}), \end{matrix}

(3.7)

where

f_{P \to T} ()

is a conversion from practical action to theoretical action, and

f_{T \to P} ()

is a conversion from theoretical action to practical action.

In a cognitive agent, the deviation from theoretical to practical action and vice versa of a single action is important.

Theoretical and practical action deviations:

\begin{matrix} D_{P \to T} = \frac{{[A_{ϕ} {(g)}_{t}]}_{P}}{{[A_{ϕ} {(g)}_{t}]}_{T}}, \end{matrix}

(3.8)

\begin{matrix} D_{T \to P} = \frac{{[A_{ϕ} {(g)}_{t}]}_{T}}{{[A_{ϕ} {(g)}_{t}]}_{P}}, \end{matrix}

(3.9)

\begin{matrix} D_{T \to P} = D_{T \to T} i f f {[A_{ϕ} {(g)}_{t}]}_{P} = {[A_{ϕ} {(g)}_{t}]}_{T}, \end{matrix}

(3.10)

where

D_{P \to T}

is a deviation from practical action to theoretical action, and

D_{T \to P}

is a deviation from theoretical action to practical action.

The deviation between theoretical and practical actions will lead to incoherence of actions on a target. This may not be desirable if the agents are required to collaborate on the target. To reduce such deviation, one action is optimized relative to the other. Such type of optimization process based on relative values forms an important part of this research.

3.1.3. Logical Operations on Action Values

The operations on the action values are the logical relationships that define two or more actions of agents on targets. As mentioned in Section 2.2.3, we use a probabilistic logic [79] for definition of properties relationships. We define the operations for two agents (

g_{i}, g_{j}

) with actions (

A_{i}, A_{j}

) on a set of targets, assuming

ϕ_{i} ⊥ ϕ_{j}

. Extension to multi-actions can simply be done using probability logic.

i. Self action: It is the action value on a target irrespective of other actions.

\begin{matrix} A {(g)}_{t} = L (ϕ; t) \Rightarrow A {(g)}_{t} = P (t; ϕ) . \end{matrix}

(3.11)

ii. Joint action: It is the action value representing the joint relationship between agents on targets.

\begin{matrix} A {(g_{1}, g_{2})}_{t} = P (t; ϕ_{1}, ϕ_{2}) = P (t; ϕ_{1}) P (t; ϕ_{2}), ϕ_{i} ⊥ ϕ_{j}, \end{matrix}

(3.12)

\begin{matrix} A {(g)}_{t_{1}, t_{2}} = P (t_{1}, t_{2}; ϕ) = P (t_{1}; ϕ) P (t_{2}; ϕ) r, \neg (t_{i} ⊥ t_{j}), \end{matrix}

(3.13)

where,

r = P (t_{1}, t_{2}; ϕ) / [P (t_{1}; ϕ) P (t_{2}; ϕ)]

iii. Mutual action: It is the action value representing the mutual relationships between agents on targets.

\begin{matrix} A {(g_{1}; g_{2})}_{t} = \frac{P (t; ϕ_{1}, ϕ_{2})}{P (t; ϕ_{1}) P (t; ϕ_{2})} = 1, ϕ_{i} ⊥ ϕ_{j}, \end{matrix}

(3.14)

\begin{matrix} A {(g)}_{t_{1}; t_{2}} = \frac{P (t_{1}, t_{2}; ϕ)}{P (t_{1}; ϕ) P (t_{2}; ϕ)}, \neg (t_{i} ⊥ t_{j}) . \end{matrix}

(3.15)

iv. Conditional action: It is the action of an agent on a target conditioned on another target on action.

\begin{matrix} A {(g_{1} | g_{2})}_{t} = \frac{P (t; ϕ_{1}, ϕ_{2})}{P (t; ϕ_{2})} = P (t; ϕ_{1}), ϕ_{i} ⊥ ϕ_{j}, \end{matrix}

(3.16)

\begin{matrix} A {(g)}_{t_{1} | t_{2}} = \frac{P (t_{1}, t_{2}; ϕ)}{P (t_{2}; ϕ)}, \neg (t_{i} ⊥ t_{j}) . \end{matrix}

(3.17)

v. Relative action: It is the action of an agent on a target referenced to another target on action

\begin{matrix} A (g_{1} | | g_{2})_{t} = \frac{P (t; ϕ_{1})}{P (t; ϕ_{2})}, \end{matrix}

(3.18)

\begin{matrix} A {(g)}_{t_{1} | | t_{2}} = \frac{P (t_{1}; ϕ)}{P (t_{2}; ϕ)} . \end{matrix}

(3.19)

3.2. Intelligence Property ( $Φ$ )

As defined in Section 2.1.1, the intelligence is the enabler of an action. Based on Axiom 2.5, we express the intelligence property with respect to knowledge.

3.2.1. Intelligence Quantification

The Intelligence value,

ϕ

, is a function of the knowledge value generated by an action.

\begin{matrix} Φ = f_{k \to ϕ} (K), \end{matrix}

(3.20)

where

f_{k_{\to} ϕ} ()

is the conversion function from knowledge value to intelligence value.

Likewise, knowledge can be defined with respect to intelligence using a knowledge to intelligence conversion function.

\begin{matrix} K = f_{ϕ \to k} (ϕ) . \end{matrix}

(3.21)

Proposition 1.

The conversion of an Intelligence value to a Knowledge value is only possible through an action value and the convention of a Knowledge value to an Intelligence value is only possible through a reverse action value.

\begin{matrix} f_{k \to ϕ} : (f_{a \to k} : A \to K) \to Φ, \end{matrix}

(3.22)

\begin{matrix} f_{ϕ \to k} : (f_{ϕ \to a} : Φ \to A) \to K . \end{matrix}

(3.23)

The proof of Proposition 1 is given in Appendix A.1.

In this paper, we focus on the definition of knowledge with respect to action and not intelligence and assume an equality relationship between knowledge and intelligence.

Just like any cognitive property, intelligence can be abstract or real, based on the environment in which it operates. Most importantly, intelligence can also be intermediary, where it supports the convention of one property to another. More on intelligence will be discussed in a future publication.

3.3. Cognitive Value Property

Cognitive values as defined in Section 2.1 are values that are generated by agents based on the actions of the agents on a target. One of such values is the knowledge value of an agent, whose inverse is the ignorance value. Other cognitive values mentioned in this article include understanding, trust, and wisdom.

In this paper, we shall quantify the knowledge value, its properties and operations in an agent. We shall reserve the quantification of understanding, trust, wisdom and their respective operations for future publications.

Knowledge as defined in Section 2.1.1 is a cognitive value property that an agent seeks from a target. Here, we quantify this knowledge from an epistemological viewpoint [5,7].

3.3.1. Knowledge Quantification

Epistemologically, knowledge is consider as a justify true belief [5,6,7]. From this universally accepted axiom, we then build a mathematical quantification of knowledge.

In epistemology, the concept of justification, truth, and belief are crucial concepts for any rational agent with cognitive and intelligent abilities. As defined in this paper, belief is the output of the reasoning action. To address the issue of justification and the truthfulness of belief, the question we may ask is, why do agents hold beliefs about a target, and if such beliefs have met a standard that renders them true and rational for the agent to hold?

As discussed in Section 1 of this paper, the aim for an agent to hold a belief about a target is to guide the agent in achieving a cognitive value about the target. Thus, belief is considered as the base value on which cognitive values are generated.

The truthfulness of a belief in this research is the truth value [81] of the belief, as oppose to the false value. The truthfulness of a belief can either depend on the agent that generates it or on another agent. These are considered in the literature as absolute and relative truth [81], respectively. We mathematically represent these two types of truth as follows:

\begin{matrix} Absolute true belief & = A {(g)}_{t}, \end{matrix}

(3.24)

\begin{matrix} Relative true belief & = \frac{A {(g)}_{t}}{A {(e)}_{t}} = A {(g | | e)}_{t}, \end{matrix}

(3.25)

where

A (g)

is the absolute belief of an agent g on a target t, and

A (e)

is the absolute belief of an agent e which is referenced by g as g generates beliefs on t. In the definition of knowledge, e is considered to have more influence or accurate definition about t than g. With respect to the definition of knowledge, we consider e as the environment of t.

Justification, also called epistemic justification [18], is a controversial concept in epistemology [17] and is considered to determine the rational ability of an agent about a target. Normally, a rational agent is an agent that possesses and seeks to optimize a justified true belief (i.e., knowledge) about a target.

Conventionally, the relative truth value of belief is considered as a justified true belief [81]. This is called the fundamentalism view of justification [19]. In this view, the belief of an agent about a target is justified by referencing it to the belief of another agent considered to possess a more rational belief value about the target. Such a rational chain can be endless, unless it ends with an absolute true belief value. Another problem with this view is that, what if the referenced belief is wrong or less accurate?

Our view of justification in this paper is that of externalism [82,83], without undermining internalism [83], because we think both views are required for a complete justification. In this context, we consider justification not only as a relative truth value but also as a process of standardizing a truth value. This is because, not all beliefs that are true maybe rational and not all belief that are rational maybe true.

This external layer of justification is a logical process rather than a logical value, independent on the belief generation process of the agent, but which is a requirement for the agent in order to justify its belief value. This accords with the suggestion of the Greek philosopher (Socrates) through Theatetus, that knowledge is true judgment plus a logos - an account or argument [18,84].

Defining such an external layer of justification as a standardization process is important in the mathematical quantification of knowledge. Mathematically, standardization is a scaling operation. The likelihood function we used in Section 3.1.1 to define the belief value is considered to generate an unstandardized value, and even the transformed version using the probabilistic constraint (

\sum_{i = 1}^{i = n} P (t_{i}; θ) = 1

) will not guarantee a sound logic for knowledge quantification, because although the probabilistic logic is a good measure for the uncertainties of random quantities, it is not suitable as a scaling function for this justification.

For this purpose, we use the logarithmic scale as a standardization logic for belief value defined either using the likelihood function or the probabilistic logic. This is because of the operational simplicity, computational advantage, and application diversity of the logarithmic scale. Nevertheless, other sound deterministic scaling logics can still be used.

We express the knowledge value of an agent about a target by justifying the expressions for the relative true belief and absolute true belief of an agent.

Knowledge based on relative true belief, also called relative knowledge, is the relative likelihood of the true action of an agent to that of its environment.

\begin{matrix} K_{a} ((g \to t) | | e) = log (\frac{A {(g)}_{t}}{A {(e)}_{t}}) \equiv {J [A (g | | e)}_{t}] . \end{matrix}

(3.26)

Knowledge based on absolute true belief, also called absolute knowledge, is the log likelihood of the true action of an agent irrespective of the environment.

\begin{matrix} K_{a} (g \to t) = log (A {(g)}_{t}) \equiv J [A {(g)}_{t}], \end{matrix}

(3.27)

where g is agent, e is environment of the agent influencing the target,

A {(g)}_{t}

is true dependency action of g on t,

A {(e)}_{t}

is true influence action of e on t,

K_{a} ((g \to t) | | e) = K_{a} {(g | | e)}_{t}

is knowledge of g on t referenced to e,

K_{a} (g \to t)

K_{a} {(g)}_{t}

are identical and represent absolute knowledge of g on t, and

J [\cdot]

is justification function.

It should be noted that, false action of environment

\bar{A} {(e)}_{t}

can also be used for knowledge quantification but this quantification should be the same for ignorance.

The use of the environment as a reference point in a cognitive value generation of an agent is similar to that of the field theory of psychology [20,21] by Lewin, where he presented the behavior of an individual (i.e., agent) as a function of the ability of the individual and his environment.

One important aspect here is the case where the environment of the agent has little or no influence on the target. In such case, the agent needs to consider generating knowledge using the influences of remote environments. While doing so, it needs to take into account the divergence between its environment influence on the target to that of the remote environments. This divergence is considered as a semantic difference of agents on targets, and will lead to an environment divergence problem of the agents during knowledge acquisition, optimization, and transfer.

Furthermore, considering the fact that an agent can receive influence from and exert influence to another agent about a target, we classify the justification (or rationality) process of an agent in this research into exopistemic and endopistemic justification (or rationality).

Definition 19.

Endopistemic justification is that which is based on the dependency of an agent on other entities such that values flow from the other entities to the agent.

Definition 20.

Exopistemic justification is that which is based on the dependency of other entities to an agent such that values flow from the agent to the other entities.

This implies, the endopistemic process is a process through which value from the environment enters or is pulled into the agent, while exopistemic process is a process through which value leave or is pushed out of the agent to the environment. If values are consider as a type of energy, then these process can be seen as a type of energy input and output processes. If we consider the values as a type of influences, then the processes can be seen as push and pull processes, similar in operation to the forces defined by Sir Isaac Newton in his Principia [85], but whose evaluation will require a Lagrangian or Hamiltonian approach. The mechanics of such dynamics is given the name cognimatics in this research.

For the fact that endopistemic process entails influence from the environment, we consider this process as an environment driven cognition. During endopistemic learning, the agent seeks to reach the environment. On the other hand, in an exopistemic process, since the agent influences the environment, we considered this process as an agent-driven cognition. During exopistemic learning, the agent seeks to lead the environment.

Examples of an endopistemic and exopistemic cognition are observation and actuation, respectively. The ability to switch between endopistemic and exopistemic processes during cognition is important to an agent, but such operation is not considered in conventional agent design. We shall discuss more about this in future publications.

The endopstemic and exopistemic processes for referential and non-referential relationships are presented in Figure 6.

During a referential (i.e., relative) endopistemic process of any agent, the agent depends on other entities and the values the agent generates are based on how the agent perceives such dependencies. Whereas, during a referential exopistemic process of same agent, the agent influences other agents and the values it generates represent how the agent perceives its influence on other entities.

Also, in both endopistemic and exopistemic cognition, the referential value may either be fixed or varied. This is analogous to the initial and non-initial reference frames in relativity [86] where initial reference frame implies fixed referential value and non-initial reference frame implies variable referential value.

If we consider that an agent’s environment can be distinguished into internal and external environments, then the endopistemic and exopistemic processes of an agent can take place between these environments, where values of the agent about a target can flow from the external environment to the internal environment and vice versa.

Examples of such environments are the theoretical (internal) and practical (external) environments of an agent. The values an agent generates in a theoretical environment are transferred to the practical environment and vice versa. Such a value exchange process will enable the agent to have a more balanced rational actions, hence reliable. This process is also discussed in the literature [22,23] by Audi, where he proposed a practical and theoretical reasoning structure for a rational agent.

In general, as defined in this paper, an endopistemic process of an agent about a target can be considered as the inverse of its exopistemic process about same target and vice versa. These processes can be interactively carried out by an agent during cognition. Such an interactive combination of both endopistemic and exopistemic values of an agent leads to a resultant value that can be used to balance the cognitive processes of an agent. We consider this value as a Cognitive balancing factor (CBF) of an agent during cognition. For a knowledge based on true relative belief (i.e., relative knowledge), the CBF of knowledge for an agent during cognition between any two environments is defined as: .

Endopistemic Knowledge-Exopistemic Knowledge = CBF,

\begin{matrix} log (\frac{A {(g)}_{t}}{A {(e)}_{t}}) - log (\frac{A^{'} {(e)}_{t}}{A^{'} {(g)}_{t}}) = C B F, \end{matrix}

(3.28)

where

A^{'} (e)

is dependency of e on t as perceived by g,

A^{'} (g)

is influence of g on t as perceived by g,

A (g)

is real dependency of g on t, and

A (e)

is real dependency of e on t.

For a perfect balance of g on t in the different environments (in this case, the abstract and real environments),

\begin{matrix} C B F = 0 \Leftrightarrow A^{'} (e) = A (g) a n d A^{'} (g) = A (e) . \end{matrix}

(3.29)

Being an inverse process to one another, and using a logarithmic justification, an endopistemic process for knowledge value is the additive inverse of its exopistemic process and vice versa. The value generated by such processes will depend on the ability and CBF value of the agent.

The structure semantics of knowledge from the definition of belief and the truth property of belief, are presented in Figure 7. Using this structure semantics, we can relate the absolute properties of knowledge and action values to the relative properties.

For example, if

g \to t

and

t \to e

non-referentially, and

g \to e

referentially, as shown in Figure 6, then the knowledge value about t that flows from e to g is given using vector addition as,

\begin{matrix} K ((g \to t) | | e) = K (g \to t) + K (t \to e), \end{matrix}

(3.30)

\begin{matrix} K ((g \to t) | | e) = log A (g) + (- log A (e)) = log \frac{A (g)}{A (e)}, \end{matrix}

(3.31)

where

g \to t

generates an absolute endopistemic knowledge value

(log A (g))

of g from t,

e \to t

generates an absolute exopistemic knowledge value

(- log A (e))

of e to t,

(g \to t) | | e

generates a relative endopistemic knowledge value

(log (A (g) / A (e)))

of g from e about t.

Similarly, without a logarithmic justification, the endopistemic and exopistemic values for referential and non-referential relationships are expressed as beliefs.

\begin{matrix} A ((g \to t) | | e) = A (g \to t) A (t \to e), \end{matrix}

(3.32)

\begin{matrix} A ((g \to t) | | e) = A (g) . A^{- 1} (e), \end{matrix}

(3.33)

\begin{matrix} Considering, A^{- 1} (e) = \frac{1}{A (e)}, \end{matrix}

(3.34)

\begin{matrix} \Rightarrow A ((g \to t) | | e) = A (g) . \frac{1}{A (e)} = \frac{A (g)}{A (e)}, \end{matrix}

(3.35)

where

A (g)

is endopistemic action of g,

(A^{- 1} (e))

is exopistemic action of e, i.e., reciprocal (or multiplicative inverse) of the endopistemic action of e,

A (g) / A (e)

is dot product of endopistemic and exopistemic actions of g and e, respectively.

In reality, during a relative endopistemic cognition on a target, such as learning to observe a target with respect to a referenced observer of the target, e.g., a teacher, the learning (dependent) agent tries to acquire the complete relative endopistemic value of the target as defined by the referenced (influencing) agents. This entails maximizing its relative dependency on t as referenced from its influencers.

The maximum value about a target that an agent can acquire from its environment during cognition depends on the value of the environment about the target and the ability of the agent. The value of the environment about the target is consider as the complete (or wisdom) value of the agent about the target in that environment. This complete value can be achieved by varying the relative endopistemic value of the agent or by varying its corresponding absolute exopistemic value. These variational quantities use by an agent to achieve complete value are also consider as the cost or work value of the agent.

Considering an agent interacting with an environment, the absolute exopistemic value of the agent on a target in the environment turns to act as a counter-action on the absolute endopistemic value of same agent and the absolute exopistemic value of its influencer (i.e., environment) on the target. This implies that cognition is analogous to a battle of influences between an agent and the environment, about a target. The number of entities under the influence of another entity constitute its exopistemic sphere (i.e., sphere of influence), and the number of influencers on which an entity depends on constitute its endopistemic sphere (i.e., sphere of dependency). An entity can have both influences and dependencies to and from other entities as shown in Figure 6.

Using an absolute exopistemic value as cost value of an agent g, the knowledge value about a target t, that flow from an environment e to the agent g can also be expressed as,

\begin{matrix} K ((g \to t) | | e) = K (e \leftarrow t) - K (g \leftarrow t), \end{matrix}

(3.36)

\begin{matrix} K ((g \to t) | | e) = (- log A (e)) - (- log A (g)), \end{matrix}

(3.37)

\begin{matrix} K ((g \to t) | | e) = log \frac{A (g)}{A (e)}, \end{matrix}

(3.38)

where

K (e \leftarrow t)

is exopistemic knowledge of e about t,

K (g \leftarrow t)

is counteractive (i.e., counter-intuitive) or exopistemic knowledge of g about t, and

K ((g \to t) | | e)

is resultant knowledge from the counteractive interaction process.

Similarly, the action value of g about t relative to e can also be expressed as,

\begin{matrix} A ((g \to t) | | e) = A (e \leftarrow t) {(A (g \leftarrow t))}^{- 1}, \end{matrix}

(3.39)

\begin{matrix} A ((g \to t) | | e) = (1 / A (e)) \div (1 / A (g)) = \frac{A (g)}{A (e)}, \end{matrix}

(3.40)

where

A (e \leftarrow t)

is exopistemic action of e about t,

A (g \leftarrow t)

is counteractive (i.e., counter-intuitive) or exopistemic action of g about t, and

A ((g \to t) | | e)

is resultant action from the counteractive interaction of exopistemic processes on t.

Thus, varying the absolute expopistemic value of an agent about a target will vary its relative endopistemic value. In general, this logic of relating absolute values to relative values can be elaborated for multiple interactive targets and agents. Focusing on a logarithmic justification relationships, we present in Figure 8, multiple interactive targets and agents.

We can identify the dependencies and express the value flow between entities in Figure 8 as shown in Table 2.

Analysis of such cognitive relationships and value flows between entities is one of the basis of this mathematical theory, a process which we called cognimatics; the dynamics of cognition. In a future publication, we shall extend and use it to solve the environmental divergence problem of knowledge acquisition, which may arise in situations such as finding the relationship and valuation between

g_{1}

and

e_{2}

g_{1}

and

g_{2}

t_{1}

of Figure 8.

The following axiom defines the basic rules in analysing any cognitive entity dependency relationships.

Axiom 3.1.

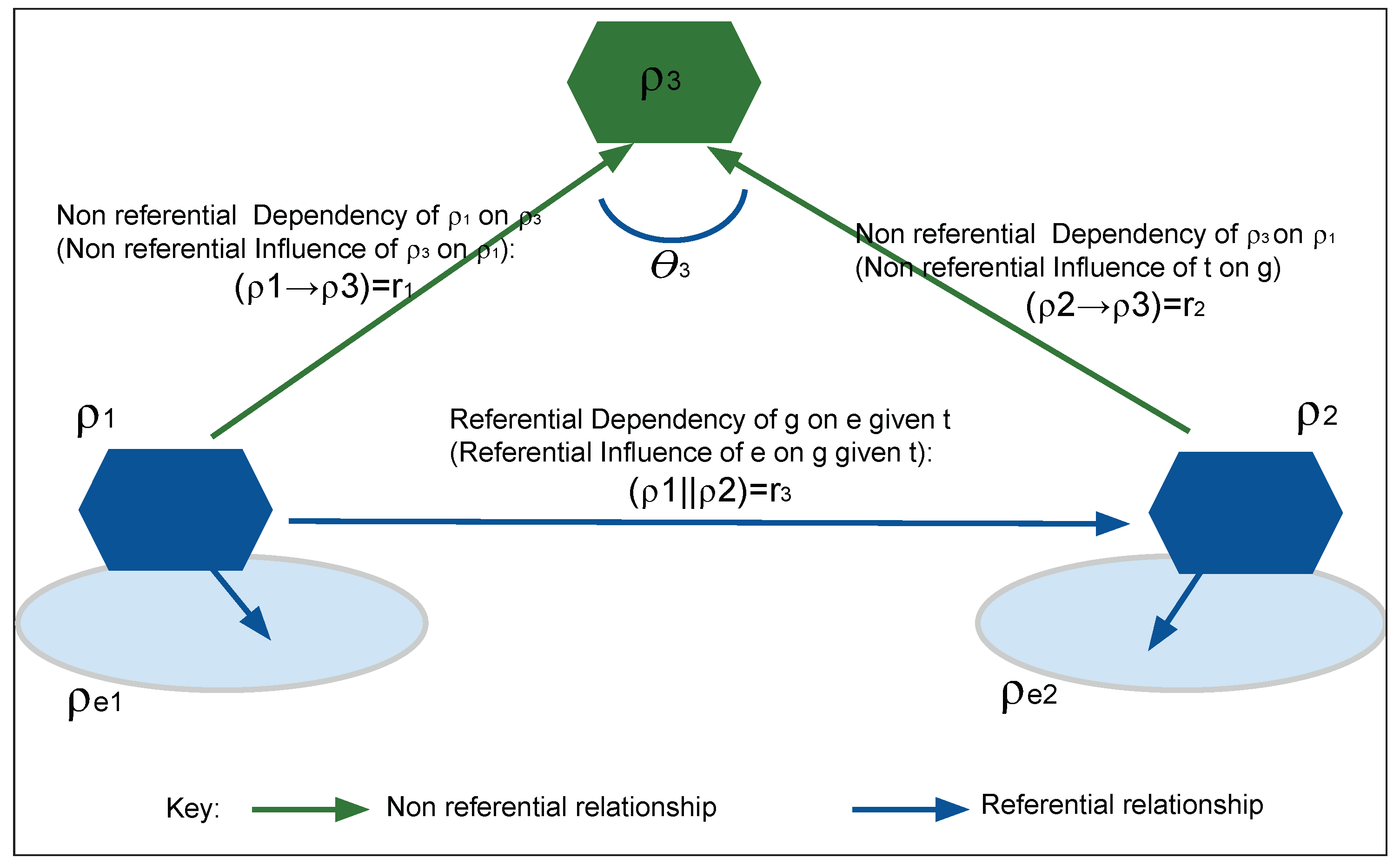
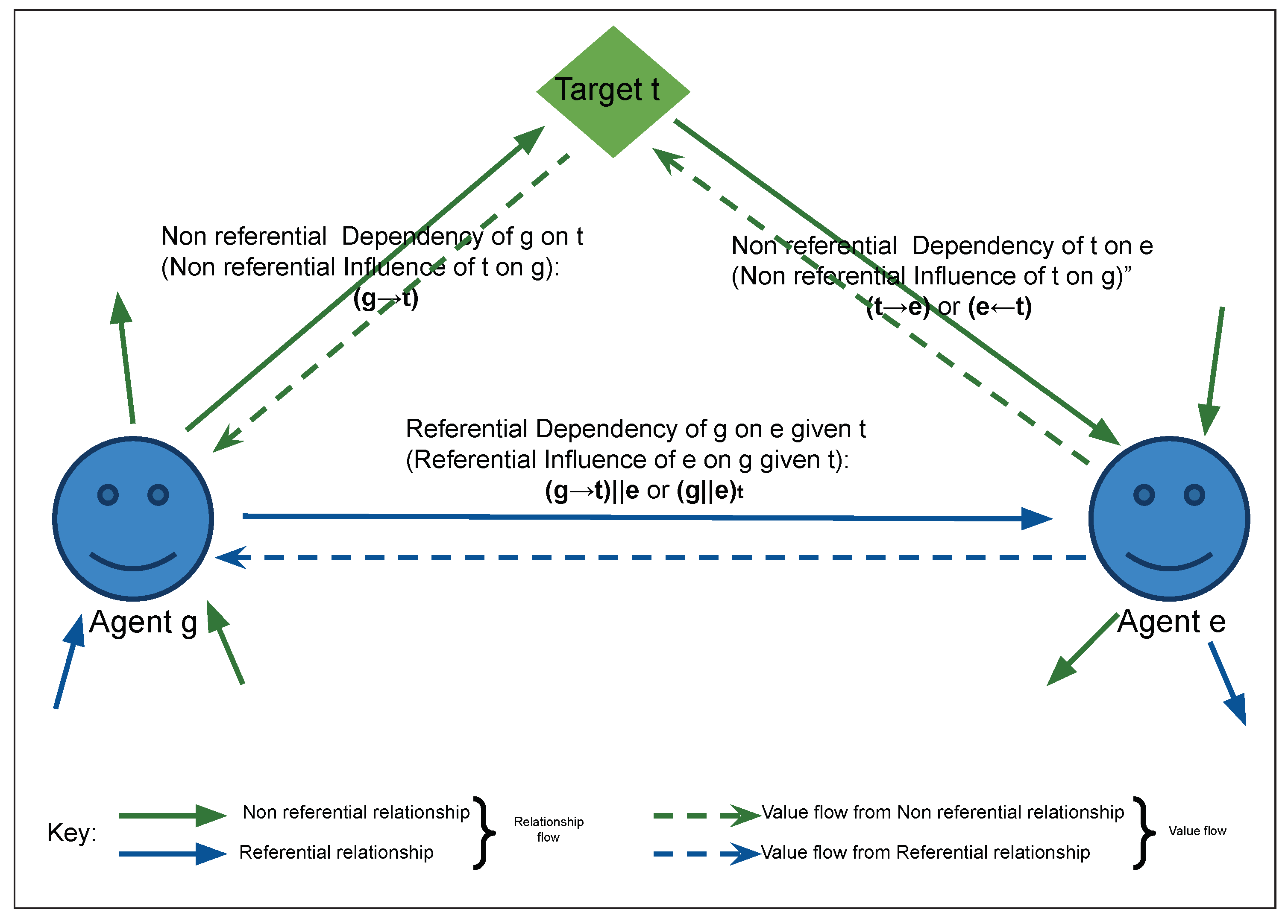
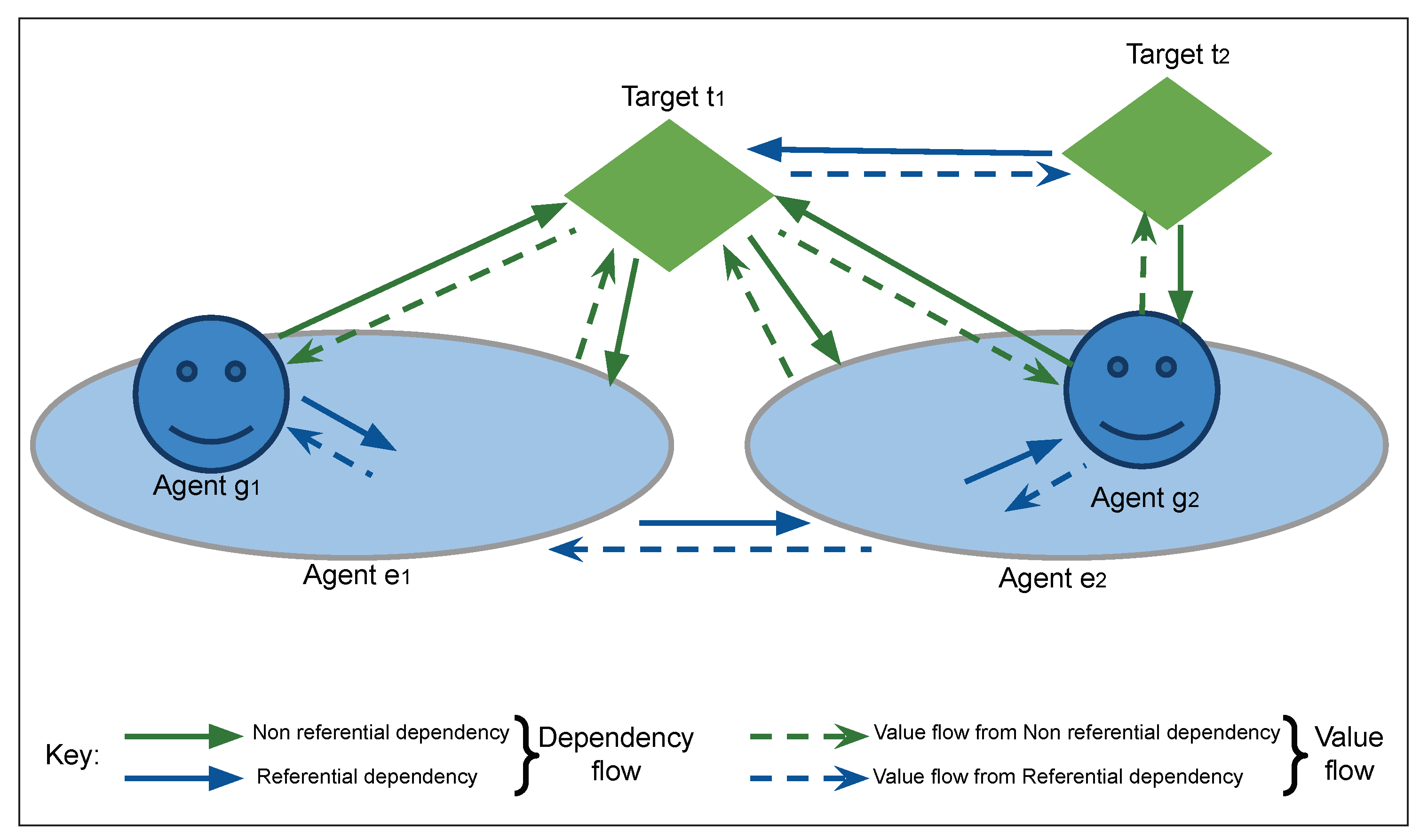
For any relationship, and at any time instance, all entities are either of two types: agent or target.
The target is the center (purpose) of all cognitive actions and value generation of an agent.
All value generated during cognition flow from the influencer entity to the dependent entity, contrary to the flow of dependency.
All relationships between same entity type are dependent relationships: self, conditional, mutual joint, referencing, etc.
The relationship between targets is defined by agent (action) and the relationship between agents is defined by target (state).
The relationship between agent and its environment is referential but between agent and its target is non-referential.

It should be noted that an entity can transition between entity types over space and time, and one entity can have different types in different relationships. Such complexities will be avoided in this paper and reserved for a future publication. Also, relationships can be non-referential (self, conditional, joint, etc.) or referential, base (self, conditional, mutual, joint, and referencing) or composite (conditional mutual, etc.).

The acquisition, optimization, and transfer of endopistemic and exopistemic values are important processes to an agent because all actions possesses endopistemic and exopistemic properties consciously or unconsciously. For example, the observation action of a human agent is consciously endopistemic in the external environment but unconsciously exopistemic in the internal environment. We focus on the endopistemic process and value in a relativistic setting.

As discussed in Section 2.1.1, cognitive values also have their respective inverse properties. The inverse of knowledge was considered as ignorance. With respect to the epistemological definition of knowledge, we can define ignorance as a justified true disbelief. Disbelief is a type of irrational action, and defined in the Cambridge dictionary as the inability or refusal to accept that something is true. Hence, ignorance can also be considered as a justify false belief of an agent.

Thus, similar to knowledge, ignorance can have a relative and absolute dimension based on the truth property. We express these in the following statements below.

Ignorance based on relative false belief, also called, relative ignorance, is relative likelihood of the false action of an agent to true action of its environment.

\begin{matrix} I_{a} ((g \to t) | | e) = log (\frac{\bar{A} {(g)}_{t}}{A {(e)}_{t}}) \equiv J [\bar{A} {(g | | e)}_{t}] . \end{matrix}

(3.41)

Ignorance base on absolute false belief, also called absolute ignorance, is the log likelihood of the false action of an agent irrespective of the environment.

\begin{matrix} I_{a} (g \to t) = log (\bar{A} {(g)}_{t}) \equiv J [\bar{A} {(g)}_{t}], \end{matrix}

(3.42)

where g is agent, e is environment of the agent influencing the target,

\bar{A} {(g)}_{t}

is false action of g on t,

A {(e)}_{t}

is true influence action of e on t,

I_{a} ((g \to t) | | e) = I_{a} {(g | | e)}_{t}

is ignorance of g on t referenced to e,

I_{a} (g \to t) = I_{a} {(g)}_{t}

is absolute ignorance of g on t, and

J [\cdot]

is justification function.

It should be noted that, false action of environment

\bar{A} {(e)}_{t}

can also be used for ignorance definition but this should be same for the corresponding knowledge.

Similar to knowledge, the ignorance value of an agent possesses an endopistemic and exopistemic property as presented in the structure semantic shown in Figure 9.

Also, the ignorance value can be considered as a measure of the amount of uncertainty (or impurity) in cognition.

Moreover, to ease understanding of the quantification analysis of the relative property of knowledge and ignorance, using the first two terms of a Taylor expansion, we can prove that the relative change between two actions is a linear approximation of the logarithm of their ratio.

The first order expansion of

log (x)

around

x = 1

is,

\begin{matrix} {log}_{b} (x) \approx {log}_{b} (1) + (\frac{d}{d x} {({log}_{b} (x))}_{x = 1}) (x - 1) = \frac{1}{ln (b)} (x - 1), \end{matrix}

(3.43)

Hence, for

x \approx 1

, if

x = \frac{A (g)}{A (e)}

, then,

\begin{matrix} {log}_{b} (\frac{A (g)}{A (e)}) \approx \frac{1}{ln (b)} (\frac{A (g)}{A (e)} - 1) = \frac{1}{ln (b)} (\frac{A (g) - A (e)}{A (e)}), \end{matrix}

(3.44)

Also, for all

x > 0

, it can be proven that,

\begin{matrix} {log}_{b} (x) \leq \frac{1}{ln (b)} (x - 1), \end{matrix}

(3.45)

This implies, since

ln (b)

is a constant that depends on logarithmic base b, for each given value of b, our relativistic quantification of knowledge and ignorance can be consider as a relative change of belief (action) values.

3.3.2. Cognitropy: Expected Cognitive Property Value

The above mathematical quantification of knowledge and ignorance focused on a single target. In case of a set of targets, related or not related to each other, we can actually estimate the average knowledge or ignorance over all the target set. We call such expected property in this research as cognitropy, defined as follows:

Definition 21.

Cognitropy is the expectation of any cognitive property value of an agent over a set of targets.

It is actually a type of summarization of a cognitive property value over targets or actions states. In relation to knowledge and ignorance, the cognitropy of knowledge or ignorance is the expected knowledge or ignorance of an agent about a target over its environment influences on the target.

\begin{matrix} Z_{a} {(g)}_{t} = \sum_{i, j} A_{j} {(e)}_{t_{i}} V_{a_{j}} {(g)}_{t_{i}} (discrete states), \end{matrix}

(3.46)

\begin{matrix} Z_{a} {(g)}_{t} = \int_{i, j} A_{j} {(e)}_{t_{i}} V_{a_{j}} {(g)}_{t_{i}} (continuous states), \end{matrix}

(3.47)

where V is K or I (values for a single independent action and target states),

A_{j} (e)

is action of environment e, i is independent target states, j is independent action states, and the expressions

Z_{a} {(g)}_{t} \equiv Z_{V} {(g)}_{t}

In a similar way, the cognitropy value for both knowledge and ignorance can be endopistemic and exopistemic.

Endopistemic cognitropy of knowledge or ignorance:

\begin{matrix} Z_{a} {(g)}_{t} = \sum_{i, j} A_{j} {(e)}_{t_{i}} V_{a_{j}} {(g)}_{t_{i}} . \end{matrix}

(3.48)

Exopistemic cognitropy of knowledge or ignorance:

\begin{matrix} - Z_{a} {(g)}_{t} = - \sum_{i, j} A_{j} {(e)}_{t_{i}} V_{a_{j}} {(g)}_{t_{i}}, \end{matrix}

(3.49)

where V can be the relative or absolute value of K or I. Thus, endopistemic and exospisemic cognitropies can also be relative or absolute.

For example, using Figure 6, the relative endopistemic cognitropy of g from e is given as,

\begin{matrix} Z {(g | | e)}_{t} = Z ({(g \to e)}_{t}) = Z (g \to t) + Z (t \to e), \end{matrix}

(3.50)

\begin{matrix} Z {(g | | e)}_{t} = \sum_{i = 1}^{n} A (e) log A (g) + (- \sum_{i = 1}^{n} A (e) log A (e)), \end{matrix}

(3.51)

\begin{matrix} Z {(g | | e)}_{t} = \sum_{i = 1}^{n} A (e) log \frac{A (g)}{A (e)}, \end{matrix}

(3.52)

where

g \to t

is an absolute endopistemic cognitropy

\sum_{i = 1}^{n} A (e) log A (g)

of g from t,

e \to t

is an absolute exopistemic cognitropy value

(- \sum_{i = 1}^{n} A (e) log A (e))

of e to t, and

{(g \to e)}_{t}

is a relative endopistemic cognitropy

\sum_{i = 1}^{n} A (e) log \frac{A (g)}{A (e)}

of g from e about t.

Concerning the action value, we consider the expected action of an agent g on a target t over an environment e as the action cognitropy and it is given as,

\begin{matrix} A_{Z} {(g)}_{t} = \sum_{i = 1}^{n} t_{i} A {(g)}_{t_{i}}, \end{matrix}

(3.53)

where

t_{i}

is possible states of the target, and

A {(g)}_{t_{i}}

is action value of the agent on the target outcomes.

Furthermore, the endopistemic and exopistemic values of the Action cognitropy are given as follows:

\begin{matrix} Endopistemic cognitropy of action = A_{Z} {(g)}_{t}, \end{matrix}

(3.54)

\begin{matrix} Exopistemic cognitropy of action = \frac{1}{A_{Z} {(g)}_{t}} . \end{matrix}

(3.55)

3.3.3. Resultant Values

Apart from the expected values of agents on targets, i.e., cognitropy, the resultant values of agents on targets are also important quantities. They capture the resultant effect of a set of values of the agents on a targets in same or different environments.

For example, the resultant action value of two referential related environments can be defined as the average of their values.

\begin{matrix} A_{r} {(g)}_{t} = \frac{A {(g)}_{t} + A {(e)}_{t}}{2} (s i n g l e a c t i o n p a i r), \end{matrix}

(3.56)

\begin{matrix} A_{r} {(g)}_{t} = \frac{\sum_{i = 1}^{n} A {(g)}_{t} + \sum_{j = 1}^{m} A {(e)}_{t}}{n + m} (m u l t i p l e a c t i o n), \end{matrix}

(3.57)

where

{(g | | e)}_{t}

and if

A_{r} {(g)}_{t} = A {(e)}_{t}

, then

A {(g)}_{t} = A {(e)}_{t}

More about the different resultant values and operations related to them will be discussed in future publications.

Same logic of cognitropy and resultant values can be used for multiple relationships to generate a complex value analysis of the cognitive processes of an agent.

Moreover, while the environment is the container of the agent and target, the target and agent can be ubiquitous over different environments which have different action values on the target. In this paper, we focus more on ubiquitous targets and non-ubiquitous agents.

Furthermore, concerning the unit for cognitive values, we introduce the binary cognitive value (bcv) or binary cognition (bic) if the logarithm is in base 2, the zie-kohno (ziko) if in base 10, and the natural cognitive value (ncv) or natural cognition (nac) if in the base is euler’s number. The action value is unit-less under this scheme.

3.3.4. Dissimilarities of Cognitropy from Other Quantities

It should be noted that the cognitropy value of knowledge or ignorance of an agent depends on the intelligence and belief of the agent, the value of its environment, its number of targets and actions together with their states. This makes cognitropy different from Shannon entropy [13] and the Kullback–Leibler (KL) divergence [87].

It is worth noting that, the environment for a single and multiple states target in this research are considered respectively as surprisal and entropy by Shannon in his theory of communication [13]. Linking his research to ours, an environment with high surprise about a target will require more value from an agent. In other words, an agent in a highly surprising situation will require more value to reach completeness about the situation. Also, the degree of surprisal and entropy of an agent about a target is a measure of the influence of the target on the agent. So, Shannon entropy and surprisal are properties of only the target and not the agent, but cognitropy is a property of both agent and target.

Unlike entropy which quantifies the uncertainty of a target, cognitropy quantifies the uncertainty in an agent about a target. So, while entropy measures information about a target, cognitropy measure the value of that information in an agent.

Another important difference is that cognitropy can be negative or positive depending on the direction of value flow, but entropy can only be positive.

Also, our expression for relative exopistemic knowledge should not be confused with Kullback–Leibler (KL) divergence because even if they are mathematically identical, their interpretation and significance are different. The main difference being that KL divergence is a measure of the divergence between two distributions, while relative exopistemic knowledge is a measure of the expectation of a justified relative true belief of an agent over the environment of its target.

Similar to knowledge and ignorance, the cognitropy of knowledge and ignorance can be relative, absolute, endopistemic, and exopistemic. As previously mentioned, we shall focus more on relative knowledge because of its double justification process, i.e., fundamentalism and logical justification.

Similar to the action property, the cognitive value property such as knowledge can be classified into different types such as domain knowledge, abstract knowledge, etc. We discuss this in the next section.

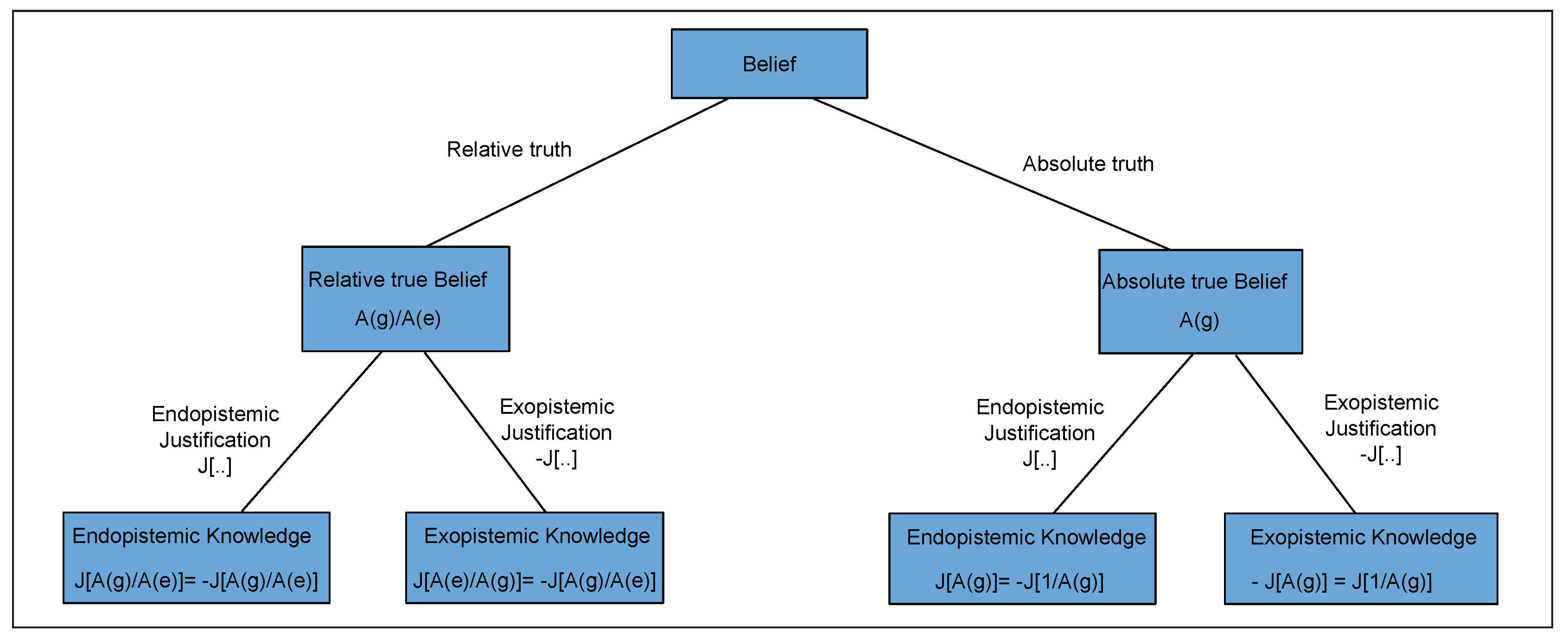
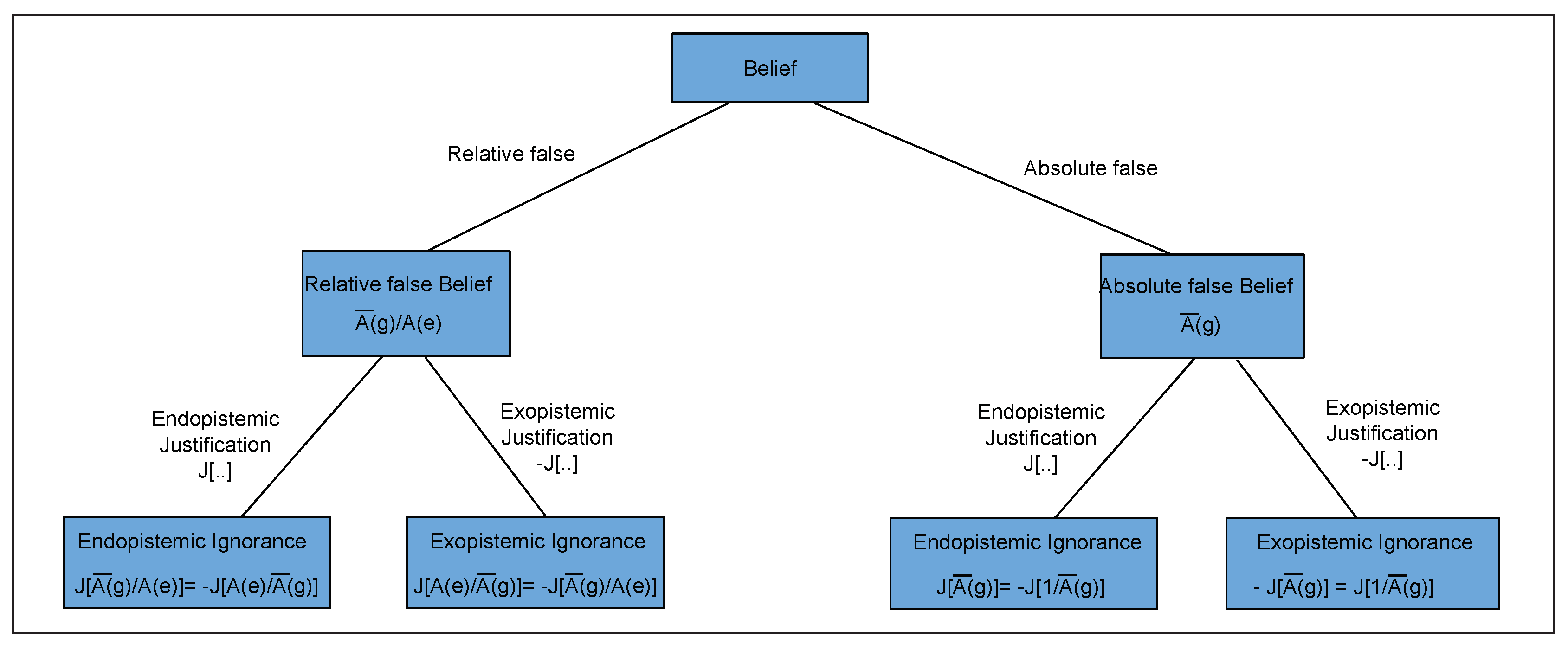
3.3.5. Types of Knowledge

i. Domain and Specific Knowledge

Domain knowledge is knowledge acquired through domain actions.

\begin{matrix} {[V_{a} {(g)}_{t}]}_{d} = J [\frac{{[A {(g)}_{t}]}_{d}}{{[A {(e)}_{t}]}_{d}}] = J [\frac{L (ϕ_{g}; Y \cap X)}{L (ϕ_{e}; Y \cap X)}], \end{matrix}

(3.58)

\begin{matrix} {[Z_{a} {(g)}_{t}]}_{d} = \sum_{i = 1}^{n} {[A {(e)}_{t}]}_{d} {[V_{a} {(g)}_{t}]}_{d} . \end{matrix}

(3.59)

Specific knowledge is knowledge acquired through specific actions.

\begin{matrix} {[V_{a} {(g)}_{t}]}_{s} = J [\frac{{[A {(g)}_{t}]}_{s}}{{[A {(e)}_{t}]}_{s}}] = J [\frac{L (ϕ_{g}; Y | X)}{((ϕ_{e}; Y | X)}], \end{matrix}

(3.60)

\begin{matrix} {[Z_{a} {(g)}_{t}]}_{s} = \sum_{i = 1}^{n} {[A {(e)}_{t}]}_{s} {[V_{a} {(g)}_{t}]}_{s} . \end{matrix}

(3.61)

The conversion from domain to specific knowledge and vice versa is possible and can be defined as describe below.

From Domain to Specific knowledge:

\begin{matrix} {[V_{a} {(g)}_{t}]}_{s} = {[V_{a} {(g)}_{t}]}_{d} - J [\frac{P (X; ϕ_{g})}{P (X; ϕ_{e})}], \end{matrix}

(3.62)

\begin{matrix} {[Z_{a} {(g)}_{t}]}_{s} = {[Z_{a} {(g)}_{t}]}_{d} - \sum_{i = 1}^{n} P (X; ϕ_{e}) J [\frac{P (X; ϕ_{g})}{P (X; ϕ_{e})}] . \end{matrix}

(3.63)

From Specific to Domain knowledge:

\begin{matrix} {[V_{a} {(g)}_{t}]}_{d} = {[V_{a} {(g)}_{t}]}_{s} + J [\frac{P (X; ϕ_{g})}{P (X; ϕ_{e})}], \end{matrix}

(3.64)

\begin{matrix} {[Z_{a} {(g)}_{t}]}_{d} = {[Z_{a} {(g)}_{t}]}_{s} + \sum_{i = 1}^{n} P (X; ϕ_{e}) J [\frac{P (X; ϕ_{g})}{P (X; ϕ_{e})}] . \end{matrix}

(3.65)

From these expressions, we can deduce the following.

Conjecture 4.

Excluding the knowledge about the input space existence during domain to specific action conversion is required, but such knowledge is needed in the reverse process.

Such knowledge will be less helpful during causality.

ii. Abstract and Real Knowledge

Abstract knowledge is knowledge acquired through abstract action.

\begin{matrix} {[V_{a} {(g)}_{t}]}_{μ} = J [(A (g_{μ} | | e_{μ})], \end{matrix}

(3.66)

\begin{matrix} {[Z_{a} {(g)}_{t}]}_{μ} = \sum_{i = 1}^{i = n} (A (e_{μ}) J [(A (g_{μ} | | e_{μ})] . \end{matrix}

(3.67)

Real knowledge is knowledge acquired through real action.

\begin{matrix} {[V_{a} {(g)}_{t}]}_{υ} = J [(A (g_{υ} | | e_{υ})], \end{matrix}

(3.68)

\begin{matrix} {[Z_{a} {(g)}_{t}]}_{υ} = \sum_{i = 1}^{n} (A (e_{υ}) J [(A (g_{υ} | | e_{υ})] . \end{matrix}

(3.69)

Both the real and abstract knowledge can have domain and specific types. Furthermore, abstract knowledge represents theoretical knowledge while real knowledge represents practical knowledge. Their conversion process is expressed below.

Theoretical and practical knowledge conversion:

\begin{matrix} {[Z_{a} {(g)}_{t}]}_{T} = f_{P \to T} ({[Z_{a} {(g)}_{t}]}_{T}), \end{matrix}

(3.70)

\begin{matrix} {[Z_{a} {(g)}_{t}]}_{P} = f_{T \to P} {([Z_{a} {(g)}_{t}]}_{P}), \end{matrix}

(3.71)

where

f_{P \to T} ()

is a conversion function from practical to theoretical knowledge, and

f_{T \to P} ()

is a conversion function from theoretical to practical knowledge.

The deviation between theory and practical is also an important quantity considered as a knowledge gap.

Theoretical and practical knowledge gap:

\begin{matrix} D_{P \to T} = {[Z_{a} {(g)}_{t}]}_{P} - {[Z_{a} {(g)}_{t}]}_{T}, \end{matrix}

(3.72)

\begin{matrix} D_{T \to P} = {[Z_{a} {(g)}_{t}]}_{T} - {[Z_{a} {(g)}_{t}]}_{P}, \end{matrix}

(3.73)

\begin{matrix} D_{P \to T} = D_{T \to P} iff {[Z_{a} {(g)}_{t}]}_{P} = {[Z_{a} {(g)}_{t}]}_{T} . \end{matrix}

(3.74)

where

D_{P \to T}

is practical to theoretical knowledge deviation, and

D_{T \to P}

is theoretical to practical knowledge deviation.

The deviation between theoretical and practical actions will lead to incoherence of knowledge about a target. This may not be desirable if the agents are required to collaborate on the target. To reduce such deviation, the deviated knowledge is optimized, through learning, relative to the other. Such type of learning of a relative knowledge will entail both agent and environment action, and is consider in this research as semantic learning. More on semantic learning will be discussed in future publications.

The aspect of theoretical and practical knowledge can be related to the works of Audi [22,23], who distinguished practical reasoning from theoretical reasoning and provided a philosophical structure of reasoning in this context.

Apart from knowledge acquired through actions (abstract, real, domain or specific), there is another classification of knowledge based on the ability of an agent to do action (i.e., actuate) with the knowledge acquired. In the literature [88], these are called, procedural and declarative knowledge.

iii. Procedural and Declarative Knowledge

Procedural knowledge is knowledge acquired to do real action.

\begin{matrix} [V_{a} {(g_{υ})}_{t}] = α_{1} {[V_{a} {(g)}_{t}]}_{μ} + α_{2} {[V_{a} {(g)}_{t}]}_{υ}, \end{matrix}

(3.75)

\begin{matrix} [Z_{a} {(g_{υ})}_{t}] = α_{1} {[Z_{a} {(g)}_{t}]}_{μ} + α_{2} {[Z_{a} {(g)}_{t}]}_{υ} . \end{matrix}

(3.76)

Declarative knowledge is knowledge acquired to do abstract action.

\begin{matrix} [V_{a} {(g_{μ})}_{t}] = α_{1} {[V_{a} {(g)}_{t}]}_{μ} + α_{2} {[V_{a} {(g)}_{t}]}_{υ}, \end{matrix}

(3.77)

\begin{matrix} [Z_{a} {(g_{μ})}_{t}] = α_{1} {[Z_{a} {(g)}_{t}]}_{μ} + α_{2} {[Z_{a} {(g)}_{t}]}_{υ}, \end{matrix}

(3.78)

where

α_{1}, α_{2} \in [0, 1]

We consider that both the abstract and real knowledge are needed by an agent to take any action. Also,

α

and

β

are the proportion of the abstract and real environment involve in generating the procedural and declarative values.

Based on Proposition 1, for knowledge to enable an action, it must be converted to intelligence through a reverse action because only intelligence can directly enable an action. Thus, the procedural and declarative knowledge represent the intelligence of an agent to take practical and theoretical actions, respective. They do not represent the knowledge property as conventionally presented [88].

3.3.6. Knowledge Structures

An agent can generate knowledge over many targets for same or different actions. We present three knowledge structures to describe this phenomenon: knowledge matrix, knowledge block, and knowledge area.

i. Knowledge Matrix (KM)

A Knowledge matrix, KM, is a set of all knowledge values for all actions and targets of an agent.

\begin{matrix} KM {(g)}_{a_{i}, t_{j}} = \{Z_{a_{i}} {(g)}_{t_{j}}, \forall a, t \in g\} . \end{matrix}

(3.79)

ii. Knowledge Block (KB)

A Knowledge block, KB, is a set of knowledge values for an action on different targets or different actions on a given target.

\begin{matrix} KB {(g)}_{a, t_{j}} = \{Z_{a} {(g)}_{t_{j}}, \forall t \in g\}, \end{matrix}

(3.80)

\begin{matrix} KB {(g)}_{a_{i}, t} = \{Z_{a_{i}} {(g)}_{t}, \forall a \in g\} . \end{matrix}

(3.81)

This represents a row or column in the knowledge matrix.

iii. Knowledge Area (KA)

A Knowledge area, KA, is a set of targets and actions on which the agent have high knowledge value beyond a certain knowledge limit.

\begin{matrix} KA {(g)}_{a_{i}, t_{j}} = \{Z_{a_{i}} {(g)}_{t_{j}}, \forall a, t \in g \land Z = c\}, \end{matrix}

(3.82)

where c is the limit value. The knowledge limit, can be the average or maximum knowledge about a target or by an action in an environment. It can also be defined otherwise.

KM, KB, and KA are important features for knowledge structurization and representation during memorization. We shall discuss this in a future publication. More so, other values such as the action value (i.e., beliefs), the ignorance value, the understanding value, the trust value, the wisdom value, the attention value, the exactness value, the stability value, etc., of an agent can be structured and represented in the same way, that is, as a matrix, a block, and an area over a set of targets.

3.3.7. Logical Operations on Knowledge

Similar to operations on the action value in Section 3.1.3, we introduce in this section different operations on knowledge, which can also be applied to ignorance. We focus on the relative endopistemic knowledge value based on relative truth, but same approach can be applied to exopistmeic value. We define the operations for action by multi-agents on multi-targets with discrete states, assuming

ϕ_{i} ⊥ ϕ_{j}

. Extension to continuous state can be done using integral calculus.

i. Self knowledge: It is the knowledge value of an agent about a target based on a self action.

\begin{matrix} Z_{a} {(g)}_{t} = \sum_{i = 1}^{n} A {(e)}_{t_{i}} V_{a} {(g)}_{t_{i}}, \end{matrix}

(3.83)

\begin{matrix} V_{a} {(g)}_{t_{i}} = J [\frac{A {(g)}_{t_{i}}}{A {(e)}_{t_{i}}}] = {J [A (g | | e)}_{t_{i}}] = J [a {(g)}_{t_{i}}], \end{matrix}

(3.84)

where i is state of the target.

ii. Joint knowledge: It is the knowledge value of agents about targets based on their joint actions. 1) Multiple agents with same target and action

\begin{matrix} Z_{a} {(g_{1}, g_{2})}_{t} = \sum_{i = 1}^{n} A {(e_{1}, e_{2})}_{t_{i}} V_{a} {(g_{1}, g_{2})}_{t_{i}}, ϕ_{1} ⊥ ϕ_{2}, \end{matrix}

(3.85)

\begin{matrix} V_{a} {(g_{1}, g_{2})}_{t_{i}} = J [a (ϕ_{1}, ϕ_{2})], ϕ_{1} ⊥ ϕ_{2}, \end{matrix}

(3.86)

\begin{matrix} J [a (ϕ_{1}, ϕ_{2})] = J [\frac{A {(g_{1}, g_{2})}_{t_{i}}}{A {(e_{1}, e_{2})}_{t_{i}}}] = V_{a} {(g_{1})}_{t_{i}} + V_{a} {(g_{2})}_{t_{i}} . \end{matrix}

(3.87)

From these expressions, we can conclude that, the knowledge of independent collaborative agents to an action on a target is the sum of their individual knowledge values.

2) Multiple targets by same agent and action

\begin{matrix} Z_{a} {(g)}_{t_{1}, t_{2}} = \sum_{t_{1}, t_{2}} A {(e)}_{t_{1}, t_{2}} V_{a} {(g)}_{t_{1}, t_{2}}, \neg (t_{1} ⊥ t_{2}), \end{matrix}

(3.88)

\begin{matrix} V_{a} {(g)}_{t_{1}, t_{2}} = J [\frac{A {(g)}_{t_{1}, t_{2}}}{A {(e)}_{t_{1}, t_{2}}}], \neg (t_{1} ⊥ t_{2}), \end{matrix}

(3.89)

\begin{matrix} J [\frac{A {(g)}_{t_{1}, t_{2}}}{A {(e)}_{t_{1}, t_{2}}}] = V_{a} {(g)}_{t_{1}} + V_{a} {(g)}_{t_{2}} + V_{a} {(g)}_{t_{1}; t_{2}} . \end{matrix}

(3.90)

3) Multiple actions of same agent and target

\begin{matrix} Z_{a_{1}, a_{2}} {(g)}_{t} = \sum_{i = 1}^{n} A_{12} {(e)}_{t_{i}} V_{a_{1}, a_{2}} {(g)}_{t_{i}}, \neg (a_{1} ⊥ a_{2}), \end{matrix}

(3.91)

\begin{matrix} V_{a_{1}, a_{2}} {(g)}_{t_{i}} = J [a_{1} (ϕ), a_{2} (ϕ)], \neg (a_{1} ⊥ a_{2}) . \end{matrix}

(3.92)

\begin{matrix} J [a_{1} (ϕ), a_{2} (ϕ)] = V_{a_{1}} {(g)}_{t_{i}} + V_{a_{2}} {(g)}_{t_{i}} + V_{a_{1}; a_{2}} {(g)}_{t_{i}} . \end{matrix}

(3.93)

4) Multiple agents with multiple actions and targets

\begin{matrix} Z_{a_{1}, a_{2}} {(g_{1}, g_{2})}_{t_{1}, t_{2}} = \sum_{t_{1}, t_{2}} A {(e_{1}, e_{2})}_{t_{1}, t_{2}} V_{a} {(g_{1}, g_{2})}_{t_{1}, t_{2}}, \\ V_{a_{1} a_{2}} {(g_{1}, g_{2})}_{t_{1}, t_{2}} = J [a_{1} {(ϕ_{1}, ϕ_{2})}_{t_{1}, t_{2}}, a_{2} {(ϕ_{1}, ϕ_{2})}_{t_{1} t_{2}}] \end{matrix}

(3.94)

\begin{matrix} = V_{a_{1}} {(g_{1}, g_{2})}_{t_{1}, t_{2}} + V_{a_{2}} {(g_{1}, g_{2})}_{t_{1}, t_{2}} + V_{a_{1}; a_{2}} {(g_{1}, g_{2})}_{t_{1}, t_{2}}, \end{matrix}

(3.95)

where

A_{12} (e)

is joint action of state 1 and 2 of agent e,

A (e_{1}, e_{2})

is action enable by intelligence of agent

e_{1}

and

e_{2}

iii. Mutual knowledge: It is the knowledge value of agents about targets based on their mutual actions. 1) Multiple agents with same target and action

\begin{matrix} Z_{a} {(g_{1}; g_{2})}_{t_{i}} = \sum_{i = 1}^{n} A {(e_{1}, e_{2})}_{t_{i}} V_{a} {(g_{1}; g_{2})}_{t_{i}}, ϕ_{1} ⊥ ϕ_{2}, \end{matrix}

(3.96)

\begin{matrix} V_{a} {(g_{1}; g_{2})}_{t_{i}} = J [a {(ϕ_{1}; ϕ_{2})}_{t_{i}}], ϕ_{1} ⊥ ϕ_{2}, \end{matrix}

(3.97)

\begin{matrix} J [a {(ϕ_{1}; ϕ_{2})}_{t_{i}}] = J [\frac{a (g_{1}, g_{2})}{a (g_{1}) a (g_{2})}] = J [\frac{a (g_{1}) a (g_{2})}{a (g_{1}) a (g_{2})}] = 0 . \end{matrix}

(3.98)

From these expressions, we can conclude that, independent collaborative agents to an action on a target have no mutual knowledge on the target.

2) Multiple targets by same agent and action

\begin{matrix} Z_{a} {(g)}_{t_{1}; t_{2}} = \sum_{t_{1}, t_{2}} A {(e)}_{t_{1}, t_{2}} V_{a} {(g)}_{t_{1}; t_{2}}, \neg (t_{1} ⊥ t_{2}), \end{matrix}

(3.99)

\begin{matrix} V_{a} {(g)}_{t_{1}; t_{2}} = J [\frac{a {(g)}_{t_{1}, t_{2}}}{a {(g)}_{t_{1}} a {(g)}_{t_{2}}}], \neg (t_{1} ⊥ t_{2}), \end{matrix}

(3.100)

\begin{matrix} J [\frac{a {(g)}_{t_{1}, t_{2}}}{a {(g)}_{t_{1}} a {(g)}_{t_{2}}}] = V_{a} {(g)}_{t_{1}, t_{2}} - V_{a} {(g)}_{t_{1}} - V_{a} {(g)}_{t_{2}} . \end{matrix}

(3.101)

3) Multiple actions of same agent and target

\begin{matrix} Z_{a_{1}; a_{2}} {(g)}_{t} = \sum_{i = 1}^{n} A_{12} {(e)}_{t_{i}} V_{a_{1}; a_{2}} {(g)}_{t_{i}}, \neg (a_{1} ⊥ a_{2}), \end{matrix}

(3.102)

\begin{matrix} V_{a_{1}; a_{2}} {(g)}_{t} = J [\frac{a_{12} {(g)}_{t_{i}}}{a_{1} {(g)}_{t} a_{2} {(g)}_{t_{i}}}], \neg (a_{1} ⊥ a_{2}), \end{matrix}

(3.103)

\begin{matrix} J [\frac{a_{12} {(g)}_{t_{i}}}{a_{1} {(g)}_{t_{i}} a_{2} {(g)}_{t_{i}}}] = V_{a_{1}, a_{2}} {(g)}_{t_{i}} - V_{a_{1}} {(g)}_{t_{i}} - V_{a_{2}} {(g)}_{t_{i}} . \end{matrix}

(3.104)

4) Multiple agents with multiple actions and targets

\begin{matrix} Z_{a_{1}; a_{1}} {(g_{1}; g_{2})}_{t_{1}; t_{2}} = \sum_{t_{1}, t_{2}} A {(e_{1}, g_{2})}_{t_{1}; t_{2}} f (a_{1}, a_{2}, t_{1}, t_{2}), \\ f (a_{1}, a_{2}, t_{1}, t_{2}) = V_{a_{1}; a_{2}} {(g_{1}; g_{2})}_{t_{1}; t_{2}} = V_{a_{1}, a_{2}} {(g_{1}; g_{2})}_{t_{1}; t_{2}}, \end{matrix}

(3.105)

\begin{matrix} - V_{a_{1}} {(g_{1}; g_{2})}_{t_{1}; t_{2}} - V_{a_{2}} {(g_{1}; g_{2})}_{t_{1}; t_{2}} . \end{matrix}

(3.106)

iv. Conditional knowledge: It is knowledge of agents about targets based on their conditional actions.

1) Multiple agents with same target and action

\begin{matrix} Z_{a} {(g_{1} | g_{2})}_{t} = \sum_{i = 1}^{n} A {(e_{1}, e_{2})}_{t_{i}} V_{a} {(g_{1} | g_{2})}_{t_{i}}, ϕ_{1} ⊥ ϕ_{2}, \end{matrix}

(3.107)

\begin{matrix} V_{a} {(g_{1} | g_{2})}_{t_{i}} = J [a {(ϕ_{1} | ϕ_{2})}_{t_{i}}] = J [a {(ϕ_{1})}_{t_{i}}] = V_{a} {(g_{1})}_{t_{i}} . \end{matrix}

(3.108)

From these expressions, we can conclude that, the conditional knowledge of independent collaborative agents on a target is the knowledge value of the conditioned agent.

2) Multiple targets by same agent and action

\begin{matrix} Z_{a} {(g)}_{t_{1} | t_{2}} = \sum_{t_{1}, t_{2}} A {(e)}_{t_{1}, t_{2}} V_{a} {(g)}_{t_{1} | t_{2}}, \neg (t_{1} ⊥ t_{2}), \end{matrix}

(3.109)

\begin{matrix} V_{a} {(g)}_{t_{1} | t_{2}} = J [\frac{a {(g)}_{t_{1}, t_{2}}}{a {(g)}_{t_{2}}}] = V_{a} {(g)}_{t_{1}, t_{2}} - V_{a} {(g)}_{t_{2}}, \end{matrix}

(3.110)

\begin{matrix} J [\frac{a {(g)}_{t_{1}, t_{2}}}{a {(g)}_{t_{2}}}] = V_{a} {(g)}_{t_{1}} + V_{a} {(g)}_{t_{1}; t_{2}}, \neg (t_{1} ⊥ t_{2}) . \end{matrix}

(3.111)

3) Multiple actions of same agent and target

\begin{matrix} Z_{a_{1} | a_{2}} {(g)}_{t} = \sum_{i = 1}^{i = n} A_{12} {(e)}_{t_{i}} V_{a_{1} | a_{2}} {(g)}_{t_{i}}, \neg (a_{1} ⊥ a_{2}), \end{matrix}

(3.112)

\begin{matrix} V_{a_{1} | a_{2}} {(g)}_{t_{i}} = J [\frac{a_{12} {(g)}_{t_{i}}}{a_{2} {(g)}_{t_{i}}}] = V_{a_{1}, a_{2}} {(g)}_{t_{i}} - V_{a_{2}} {(g)}_{t_{i}}, \end{matrix}

(3.113)

\begin{matrix} J [\frac{a_{12} {(g)}_{t_{i}}}{a_{2} {(g)}_{t_{i}}}] = V_{a_{1}} {(g)}_{t} + V_{a_{1}; a_{2}} {(g)}_{t_{i}}, \neg (a_{1} ⊥ a_{2}) . \end{matrix}

(3.114)

4) Multiple agents with multiple actions and targets

\begin{matrix} Z_{a_{1} | a_{2}} {(g_{1} | g_{2})}_{t_{1} | t_{2}} = \sum_{t_{1}, t_{2}} A {(e_{1}, e_{2})}_{t_{1} | t_{2}} f (a_{1}, a_{2}, t_{1}, t_{2}), \end{matrix}

(3.115)

\begin{matrix} f (a_{1}, a_{2}, t_{1}, t_{2}) = V_{a_{1} | a_{2}} {(g_{1}; g_{2})}_{t_{1} | t_{2}}, \end{matrix}

(3.116)

\begin{matrix} f (a_{1}, a_{2}, t_{1}, t_{2}) = V_{a_{1}, a_{2}} {(g_{1} | g_{2})}_{t_{1} | t_{2}} - V_{a_{2}} {(g_{1} | g_{2})}_{t_{1} | t_{2}} . \end{matrix}

(3.117)

3.3.8. Properties of the Knowledge Value

As we mentioned in Section 2, cognitive value also have properties that define their nature. These properties can also be considered as separate cognitive values. One of such property is the inverse property of a cognitive value, which for the knowledge property, we consider it as the ignorance of an agent. Other properties of a cognitive value introduce in this paper are the exactness and stability properties.

i. Exactness property

The exactness of a cognitive property is the precision of its value about a target.

\begin{matrix} E_{v} (g) = \frac{V_{a} (g)}{V_{a} (e)}, \end{matrix}

(3.118)

\begin{matrix} E_{Z_{v}} (g) = \frac{Z_{a} (g)}{Z_{a} (e)} . \end{matrix}

(3.119)

This is the exactness property of the agent’s knowledge over that of the environment.

Furthermore, the exactness property of the agent’s knowledge or ignorance can also be expressed over the cost value of the agent in an environment as follows.

\begin{matrix} E_{v} {(g)}_{c r} = \frac{V_{a} (g)}{V_{(c r)} a (g)}, \end{matrix}

(3.120)

\begin{matrix} E_{Z_{v}} {(g)}_{c r} = \frac{Z_{a} (g)}{Z_{(c r)} a (g)} . \end{matrix}

(3.121)

where

V_{(c r)}

and

Z_{(c r)}

are absolute exopistemic cost values, also called the cross values.

An important fact about the exactness value is that it can be expressed as a gradient of a line defining the cognitive process.

\begin{matrix} Y = m X + C, \end{matrix}

(3.122)

where Y is a knowledge value of the agent, X is value of the environment or the cost of the agent, m is the exactness value on environment or cost, and C is a constant of exactness in cognition of an agent g about a target t given intelligence

ϕ

Equation (3.122) can be expanded as follows:

\begin{matrix} V_{a} (g) = E_{v} {(g)}_{c} + C_{v}, Z_{a} (g) = E_{Z_{v}} (g) + C_{z}, \end{matrix}

(3.123)

\begin{matrix} V_{a} (g) = E_{v} {(g)}_{c r} + C_{v}, Z_{a} (g) = E_{Z_{v}} {(g)}_{c r} + C_{z} . \end{matrix}

(3.124)

Thus, Equation (3.122) gives a linear relationship between knowledge of an agent and its cost value or the knowledge of a referenced agents. This can be used as a cognitive tool for a knowledge value acquisition and optimization over a single state or multi-state target.

Furthermore, on a single state target, the exactness value can be considered as a log-log ratio, hence, the action values can be extracted at any moment in a cognitive process or projected for a future value defined by the exactness linear equation.

\begin{matrix} E_{v} (g) = \frac{V_{g}}{V_{e}} = {log}_{\frac{1}{p}} \frac{q}{p} \Rightarrow \frac{q}{p} = {(\frac{1}{p})}^{E_{v} (g)}, \end{matrix}

(3.125)

\begin{matrix} E_{v} (g) = \frac{V_{g}}{V_{c r}} = {log}_{\frac{1}{q}} \frac{q}{p} \Rightarrow \frac{q}{p} = {(\frac{1}{q})}^{E_{v} (g)}, \end{matrix}

(3.126)

where

V_{g} = log \frac{q}{p}

V_{e} = log \frac{1}{p}

, and

V_{c r} = log \frac{1}{q}

ii. Stability property

The stability of a cognitive property is the rate of change of its value with respect to space or time. Stability can be expressed with respect to time such as the learning time, or with respect to space such as the action space, intelligence space, target space, information space, and cognitive value space.

1) Stability with respect to action:

\begin{matrix} S_{V} {(g)}_{a (e)} = \frac{\partial V_{a} (g)}{\partial A (e)}, \end{matrix}

(3.127)

\begin{matrix} \Rightarrow S_{K} {(g)}_{a (e)} = \frac{\partial K_{a} (g)}{\partial A (e)} = - \frac{1}{A (e) ln (b)}, S_{I} {(g)}_{a (e)} = \frac{\partial I_{a} (g)}{\partial A (e)} = \frac{1}{A (e) ln (b)}, \end{matrix}

(3.128)

\begin{matrix} S_{Z_{v}} {(g)}_{a (g)} = \frac{\partial Z_{a} (g)}{\partial A (g)}, \end{matrix}

(3.129)

\begin{matrix} S_{Z_{K}} {(g)}_{a (g)} = \frac{\partial Z_{K} (g)}{\partial A (g)}, S_{Z_{I}} {(g)}_{a (g)} = \frac{\partial Z_{I} (g)}{\partial A (g)}, \end{matrix}

(3.130)

where V is K or I,

K_{a} (g) = {log}_{b} \frac{A (g)}{A (e)}

I_{a} (g) = {log}_{b} \frac{A (e)}{A (g)}

2) Stability with respect to intelligence:

\begin{matrix} S_{V} {(g)}_{ϕ} = \frac{\partial V_{a} (g)}{\partial ϕ} = \frac{\partial log (A (g))}{\partial ϕ} - \frac{\partial log (A (e))}{\partial ϕ}, \end{matrix}

(3.131)

\begin{matrix} S_{Z_{v}} {(g)}_{ϕ} = \frac{\partial Z_{a} (g)}{\partial ϕ}, \end{matrix}

(3.132)

\begin{matrix} \frac{\partial Z_{a} (g)}{\partial ϕ} = \frac{\partial \sum A (e) log (A (g))}{\partial ϕ} - \frac{\partial \sum A (e) log (A (e))}{\partial ϕ}, \end{matrix}

(3.133)

where

A {(.)}_{t} = f (X, ϕ)

V_{a} (g)

, and

Z_{a} (g) = f (A (g)

A (e))

The stability with respect to intelligence is mostly use in conventional learning process of an agent, specifically the gradient-based learning process.

3) Stability with respect to information:

\begin{matrix} S_{V} {(g)}_{X} = \frac{\partial V_{a} (g)}{\partial X} = \frac{\partial log (A (g))}{\partial X} - \frac{\partial log (A (e))}{\partial X}, \end{matrix}

(3.134)

\begin{matrix} S_{Z_{v}} {(g)}_{X} = \frac{\partial Z_{a} (g)}{\partial X}, \end{matrix}

(3.135)

\begin{matrix} \frac{\partial Z_{a} (g)}{\partial X} = \frac{\partial \sum A (e) log (A (g))}{\partial X} - \frac{\partial \sum A (e) log (A (e))}{\partial X}, \end{matrix}

(3.136)

where

A {(.)}_{t} = f (X, ϕ)

V_{a} (g)

, and

Z_{a} (g) = f (A (g)

A (e))

The stability with respect to information defines the variance of the agent. The information change can be; the change in input domain or input instances about the target.

For the stability with respect to the target, the change in target can be the change in the target instance or domain. This is considered as the variance over the output space of the target. We shall handle this case in a future publication. Also, the case with the stability of one cognitive value property over another type of cognitive value property is treated in a future publication.

4. Conclusion

In this paper, we focused on description and quantification of cognitive properties, more precisely, the knowledge and action properties of an agent. Other properties such as ignorance, stability, and exactness were also presented in this paper.

This research can be considered as a framework that can be used in the design and development of an intelligent and cognitive agent. More so, since the concepts presented are closely related to that of natural cognitive agents like humans, the research can be used not only to design an agent that does what we think but also what they think, thereby interacting, selecting and solving problems, as they want.

This is related to the statement of Alain Turing in his paper, Computing machinery and intelligence [1], which has shaped the AI field for decades, in which he asked the question, "Can machine think?", and responded to his own question by proposing that we can rather seek to build machines that do as we think rather those that think as we do.

In addition to this, the challenge in building such a machine is based on the logical definitions and operations of a thinking (reasoning) process. In this research, we provided a concise definitions and operations of a thinking process of any agent, which can be used in designing and developing an agent. Hence, providing a pathway in the design and development of a rational thinking machine, that can also communicate and interact rationally in a conscious, subconscious, and unconscious cognition.

Using this framework, we look forward to provide more materials on the science, development and applications of intelligent and cognitive agents that do not only do as we think, but most especially, that do as they think.

Appendix A. Proofs

Appendix A.1

Proof of Proposition 1,

f_{k \to ϕ} : (f_{a \to k} : A \to K) \to Φ

f_{ϕ \to k} : (f_{ϕ \to a} : Φ \to A) \to K

Proof:

Φ = f_{k \to ϕ} (K)

Since

K = (f_{a \to k} (A))

This imply that

Φ = f_{k \to ϕ} (f_{a \to k} (A))

Therefore

f_{k \to ϕ} : (f_{a \to k} : A \to K) \to Φ

K = f_{ϕ \to k} (Φ)

Since

Φ = f_{k \to ϕ} (K)

This imply that

K = {[f_{ϕ \to k}]}^{- 1} (Φ)

But

f_{ϕ \to k} = {[f_{k \to ϕ}]}^{- 1} = {[f_{k \to ϕ}]}^{- 1} ({[f_{a \to k} (A)]}^{- 1})

Therefore

f_{ϕ \to k} : (f_{ϕ \to a} : Φ \to a) \to K

Appendix B. List of Symbols

References

Turing, A.M. Computing machinery and intelligence. Mind 1950, LIX, 433–460. [CrossRef]
Russell, S.; Norvig, P. Artificial Intelligence: A Modern Approach, 3 ed.; Prentice Hall, 2010.
Shrestha, A.; Mahmood, A. Review of Deep Learning Algorithms and Architectures. IEEE Access 2019, 7, 53040–53065. [CrossRef]
Sun, S.; Cao, Z.; Zhu, H.; Zhao, J. A Survey of Optimization Methods From a Machine Learning Perspective. IEEE Transactions on Cybernetics 2020, 50, 3668–3681. [CrossRef]
de Grefte, J. Knowledge as Justified True Belief. Erkenntnis 2021. [CrossRef]
Ichikawa, J.J.; Steup, M. The Analysis of Knowledge. In The Stanford Encyclopedia of Philosophy, Summer 2018 ed.; Zalta, E.N., Ed.; Metaphysics Research Lab, Stanford University, 2018.
Armstrong, D.M. Belief, Truth And Knowledge, 1 ed.; Cambridge University Press, 1973. [CrossRef]
Liew, A. DIKIW: Data, Information, Knowledge, Intelligence, Wisdom and their Interrelationships. Business Management Dynamics 2013.
Rowley, J. The wisdom hierarchy: Representations of the DIKW hierarchy. J Inf Sci 2007, 33. [CrossRef]
Zhong, Y. Knowledge theory and information-knowledge-intelligence trinity. Proceedings of the 9th International Conference on Neural Information Processing, 2002. ICONIP ’02., 2002, Vol. 1, pp. 130–133 vol.1. [CrossRef]
Dretske, F.I. Knowledge and the Flow of Information; MIT Press, 1981. [CrossRef]
Topsoe, F. On truth, belief and knowledge. IEEE International Symposium on Information Theory - Proceedings, 2009, pp. 139 – 143. [CrossRef]
Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423.
Kolmogorov, A.N. Three approaches to the quantitative definition of information. International Journal of Computer Mathematics 1968, 2, 157–168.
Konorski, J.; Szpankowski, W. What is information? 2008 IEEE Information Theory Workshop, 2008, pp. 269–270. [CrossRef]
Valdma, M. A general classification of information and systems. Oil Shale 2007, 24.
Steup, M.; Neta, R. Epistemology. In The Stanford Encyclopedia of Philosophy, Fall 2020 ed.; Zalta, E.N., Ed.; Metaphysics Research Lab, Stanford University, 2020.
.
Hasan, A.; Fumerton, R. Foundationalist Theories of Epistemic Justification. In The Stanford Encyclopedia of Philosophy, Fall 2018 ed.; Zalta, E.N., Ed.; Metaphysics Research Lab, Stanford University, 2018.
Lewin, K. Field Theory and Experiment in Social Psychology: Concepts and Methods. American Journal of Sociology 1939, 44, 868 – 896.
Martin, J. What is Field Theory? American Journal of Sociology - AMER J SOCIOL 2003, 109, 1–49. [CrossRef]
Audi, R. The Architecture of Reason: The Structure and Substance of Rationality; Oxford University Press, 2001.
Audi, R. Précis of the Architecture of Reason. Philosophy and Phenomenological Research, Wiley-Blackwell 2003, 67, 177–180. [CrossRef]
Lenat, D. Ontological versus knowledge engineering. IEEE Transactions on Knowledge and Data Engineering 1989, 1, 84–88. [CrossRef]
Wang, W.; De, S.; Toenjes, R.; Reetz, E.; Moessner, K. A Comprehensive Ontology for Knowledge Representation in the Internet of Things. 2012 IEEE 11th International Conference on Trust, Security and Privacy in Computing and Communications, 2012, pp. 1793–1798. [CrossRef]
Lombardi, O. Dretske, Shannon’s Theory and the Interpretation of Information. Synthese 2005, 144, 23–39. [CrossRef]
Oxford University Press and Dictionary.com.
Kiely, K.M. Cognitive Function; Springer Netherlands: Dordrecht, 2014; pp. 974–978. [CrossRef]
Gudivada, V.N.; Pankanti, S.; Seetharaman, G.; Zhang, Y. Cognitive Computing Systems: Their Potential and the Future. Computer 2019, 52, 13–18. [CrossRef]
Douglas, H. The Value of Cognitive Values. Philosophy of Science 2013, 80, 796–806. [CrossRef]
Hirsch Hadorn, G. On Rationales for Cognitive Values in the Assessment of Scientific Representations. Journal for General Philosophy of Science 2018, 49, 1–13. [CrossRef]
Todt, O.; Luján, J.L. Values and Decisions: Cognitive and Noncognitive Values in Knowledge Generation and Decision Making. Science, Technology, & Human Values 2014, 39, 720–743. [CrossRef]
Wirtz, P., Entrepreneurial finance and the creation of value: Agency costs vs. cognitive value; 2015; pp. 552–568. [CrossRef]
Cleeremans, A. Conscious and unconscious cognition: A graded, dynamic perspective. Int. J. Psychol 2004, 39. [CrossRef]
Epstein, S. Demystifying Intuition: What It Is, What It Does, and How It Does It. Psychological Inquiry 2010, 21, 295–312. [CrossRef]
Oxford Dictionary.
Biggam, J. Defining knowledge: an epistemological foundation for knowledge management. Proceedings of the 34th Annual Hawaii International Conference on System Sciences, 2001, pp. 7 pp.–. [CrossRef]
Beránková, M.; Kvasnička, R.; Houška, M. Towards the definition of knowledge interoperability. 2010 2nd International Conference on Software Technology and Engineering, 2010, Vol. 1, pp. V1–232–V1–236. [CrossRef]
Firestein, S. Ignorance: How it drives science; Oxford University Press, 2012. [CrossRef]
Oxford Dictionary.
Foo, N.; Vo, B. Reasoning about Action: An Argumentation - Theoretic Approach. Journal of Artificial Intelligence Research 2011, 24. [CrossRef]
Giordano, L.; Martelli, A.; Schwind, C. Reasoning about actions in dynamic linear time temporal logic. Logic Journal of the IGPL 2001, 9, 273–288. [CrossRef]
Hartonas, C. Reasoning about types of action and agent capabilities. Logic Journal of the IGPL 2013, 21, 703–742. [CrossRef]
Zhong, S.; Xia, K.; Yin, X.; Chang, J. The representation and simulation for reasoning about action based on Colored Petri Net. 2010 2nd IEEE International Conference on Information Management and Engineering, 2010, pp. 480–483. [CrossRef]
Legg, S.; Hutter, M. A Collection of Definitions of Intelligence. Advances in Artificial General Intelligence: Concepts, Architectures and Algorithms 2007, 157.
Wilhelm, O.; Engle, R. Handbook of understanding and measuring intelligence; 2005; p. 542. [CrossRef]
Wang, Y.; Widrow, B.; Zadeh, L.; Howard, N.; Wood, S.; Bhavsar, V.; Budin, G.; Chan, C.; Gavrilova, M.; Shell, D. Cognitive Intelligence: Deep Learning, Thinking, and Reasoning by Brain-Inspired Systems. International Journal of Cognitive Informatics and Natural Intelligence 2016, 10, 1–20. [CrossRef]
Zhong, Y. Mechanism approach to a unified theory of artificial intelligence. 2005 IEEE International Conference on Granular Computing, 2005, Vol. 1, pp. 17–21 Vol. 1. [CrossRef]
Rens, G.; Varzinczak, I.; Meyer, T.; Ferrein, A. A Logic for Reasoning about Actions and Explicit Observations. 2010, Vol. 6464, pp. 395–404. [CrossRef]
Pereira, L.; Li, R. Reasoning about Concurrent Actions and Observations 1999.
Kakas, A.C.; Miller, R.; Toni, F. E-RES: A System for Reasoning about Actions, Events and Observations. ArXiv 2000, cs.AI/0003034.
Costa, A.; Salazar-Varas, R.; Iáñez, E.; Úbeda, A.; Hortal, E.; Azorín, J.M. Studying Cognitive Attention Mechanisms during Walking from EEG Signals. 2015 IEEE International Conference on Systems, Man, and Cybernetics, 2015, pp. 882–886. [CrossRef]
Wickens, C. Attention: Theory, Principles, Models and Applications. International Journal of Human–Computer Interaction 2021, 37, 403–417. [CrossRef]
Atkinson, R.C.; Shiffrin, R.M. Human Memory: A Proposed System and its Control Processes. Psychology of Learning and Motivation, 1968.
Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is All You Need; Curran Associates Inc.: Red Hook, NY, USA, 2017; NIPS’17.
Miller, G.A. The magical number seven plus or minus two: some limits on our capacity for processing information. Psychological review 1956, 63 2, 81–97.
Fatemi, M.; Haykin, S. Cognitive Control: Theory and Application. IEEE Access 2014, 2, 698–710. [CrossRef]
Nunes, T. Logical Reasoning and Learning. In Encyclopedia of the Sciences of Learning; 2012; pp. 2066–2069. [CrossRef]
Stenning, K.; van Lambalgen, M. Reasoning, logic, and psychology. WIREs Cognitive Science, 2, 555–567. [CrossRef]
Johnson-Laird, P.N. Mental models and human reasoning 2010. 107, 18243–18250. [CrossRef]
Atkinson, R.; Shiffrin, R. Human Memory: A proposed system and its control processes. In Human Memory; BOWER, G., Ed.; Academic Press, 1977; pp. 7–113. [CrossRef]
Baddeley, A.D.; Hitch, G. Working Memory; Academic Press, 1974; Vol. 8, Psychology of Learning and Motivation, pp. 47–89. [CrossRef]
Baddeley, A.; Conway, M.; JP, A. Episodic Memory: New Directions in Research 2002. [CrossRef]
Angluin, D. Computational Learning Theory: Survey and Selected Bibliography. Proceedings of the Twenty-Fourth Annual ACM Symposium on Theory of Computing. Association for Computing Machinery, 1992, p. 351–369. [CrossRef]
Vapnik, V. An overview of statistical learning theory. IEEE Transactions on Neural Networks 1999, 10, 988–999. [CrossRef]
Beránková, M.; Kvasnička, R.; Houška, M. Towards the definition of knowledge interoperability. 2010 2nd International Conference on Software Technology and Engineering, 2010, Vol. 1, pp. V1–232–V1–236. [CrossRef]
Chen, Z.; Duan, L.Y.; Wang, S.; Lou, Y.; Huang, T.; Wu, D.O.; Gao, W. Toward Knowledge as a Service Over Networks: A Deep Learning Model Communication Paradigm. IEEE Journal on Selected Areas in Communications 2019, 37, 1349–1363. [CrossRef]
Corbett, D. Semantic interoperability of knowledge bases: how can agents share knowledge if they don’t speak the same language? Sixth International Conference of Information Fusion, 2003. Proceedings of the, 2003, Vol. 1, pp. 94–98. [CrossRef]
Hunter, A.; Konieczny, S. Approaches to Measuring Inconsistent Information. 2005, Vol. 3300, pp. 191–236. [CrossRef]
Sayood, K. Information Theory and Cognition: A Review. Entropy 2018, 20, 706. [CrossRef]
Démuth, A. Perception Theories; Kraków: Trnavská univerzita, 2013.
Briscoe, R.; Grush, R. Action-based Theories of Perception. In The Stanford Encyclopedia of Philosophy; 2020.
Guizzardi, G. On Ontology, ontologies, Conceptualizations, Modeling Languages, and (Meta)Models. Seventh International Baltic Conference, DB&IS, 2006, pp. 18–39.
Chitsaz, M.; Hodjati, S.M.A. Conceptualization in ideational theory of meaning: Cognitive theories and semantic modeling. Procedia - Social and Behavioral Sciences 2012, 32, 450–455. [CrossRef]
El Morr, C.; Ali-Hassan, H., Descriptive, Predictive, and Prescriptive Analytics: A Practical Introduction; 2019; pp. 31–55. [CrossRef]
Megha, C.; Madhura, A.; Sneha, Y. Cognitive computing and its applications. 2017 International Conference on Energy, Communication, Data Analytics and Soft Computing (ICECDS), 2017, pp. 1168–1172. [CrossRef]
Zhang, X.N. Formal analysis of diagnostic notions. 2012 International Conference on Machine Learning and Cybernetics, 2012, Vol. 4, pp. 1303–1307. [CrossRef]
Francesco, B.; Ahti-Veikko, P. Charles Sanders Peirce: Logic. In The Internet Encyclopedia of Philosophy; 2022.
Pishro-Nik, H. Introduction to Probability, Statistics, and Random Processes; Kappa Research LLC, 2014.
Lefcourt, H.M. Locus of control: Current trends in theory and research; Psychology Press, 1982. [CrossRef]
Shramko, Y.; Wansing, H. Truth Values. In The Stanford Encyclopedia of Philosophy; 2021.
Parent, T. Externalism and Self-Knowledge. In The Stanford Encyclopedia of Philosophy; 2017.
Ted, P. Epistemic Justification. In The Internet Encyclopedia of Philosophy; 2022.
Artemov, S.; Fitting, M. Justification Logic. In The Stanford Encyclopedia of Philosophy; 2021.
Smith, G. Newton’s Philosophiae Naturalis Principia Mathematica. In The Stanford Encyclopedia of Philosophy; 2008.
Eddington, A.S.S. The mathematical theory of relativity; Cambridge University Press, 1924. [CrossRef]
Kullback, S.; Leibler, R.A. On Information and Sufficiency. The Annals of Mathematical Statistics 1951, 22, 79 –86. [CrossRef]
Berge, T.; van Hezewijk, R. Procedural and Declarative Knowledge. Theory & Psychology 1999, 9, 605 – 624. [CrossRef]

Figure 1. Cognitive property organization in a cognitive intelligent agent.

Figure 2. Cognitive action processes of an agent.

Figure 3. Entities and environment hierarchical relationships.

Figure 4. Two agents interacting with two environments.

e_{1}

has one agent,

e_{2}

has two agents.

Figure 4. Two agents interacting with two environments.

e_{1}

has one agent,

e_{2}

has two agents.

Figure 5. Interrelationship between the referential and non referential relationships of entities

ρ_{1}, ρ_{2}, ρ_{e 1}

, and

ρ_{e 2}

Figure 5. Interrelationship between the referential and non referential relationships of entities

ρ_{1}, ρ_{2}, ρ_{e 1}

, and

ρ_{e 2}

Figure 6. Dependency and value flow diagrams. (a) Endopistemic and Exopistemic processes of g and e on t. (b) Cost dynamics of g and e on t.

Figure 7. Structure semantic of Knowledge from Belief and Truth.

Figure 8. Dependency and value flow diagrams of endopistemic and exopistemic processes of

g_{1}, g_{2}, e_{1}, e_{1}, t_{1}, t_{2}, t_{3}

Figure 8. Dependency and value flow diagrams of endopistemic and exopistemic processes of

g_{1}, g_{2}, e_{1}, e_{1}, t_{1}, t_{2}, t_{3}

Figure 9. Structure semantic of Ignorance from Belief and Falsehood.

Table 2. Entity dependencies and values.

Symbols	Dependency types	Action values	Knowledge values
$g_{1} \to t_{1}$	non-referential	$A {(g_{1})}_{t_{1}}$	$K {(g_{1})}_{t_{1}} = log A {(g_{1})}_{t_{1}}$
$g_{1} \to e_{1}$	referential	$A (g_{1} \| \| e_{1})_{t_{1}}$	$K (g_{1} \| \| e_{1})_{t_{1}} = log \frac{A {(g_{1})}_{t_{1}}}{A {(e_{1})}_{t_{1}}}$
$g_{2} \to t_{1}$	non-referential	$A {(g_{2})}_{t_{1}}$	$K {(g_{2})}_{t_{1}} = log A {(g_{2})}_{t_{1}}$
$g_{2} \to t_{2}$	non-referential	$A {(g_{2})}_{t_{2}}$	$K {(g_{2})}_{t_{2}} = log A {(g_{2})}_{t_{2}}$
$g_{2} \to e_{2}$	referential	$A (g_{2} \| \| e_{2})_{t_{2}}$	$K (g_{2} \| \| e_{2})_{t_{2}} = log \frac{A {(g_{2})}_{t_{2}}}{A {(e_{2})}_{t_{2}}}$
$e_{1} \to t_{1}$	non-referential	$A {(e_{1})}_{t_{1}}$	$K {(e_{1})}_{t_{1}} = - log A {(e_{1})}_{t_{1}}$
$e_{2} \to t_{1}$	non-referential	$A {(e_{2})}_{t_{2}}$	$K {(e_{2})}_{t_{1}} = - log A {(e_{2})}_{t_{1}}$
$e_{1} \to e_{2}$	referential	$A (e_{1} \| \| e_{2})_{t_{1}}$	$K (e_{1} \| \| e_{2})_{t_{1}} = - log \frac{A {(e_{1})}_{t_{1}}}{A {(e_{2})}_{t_{1}}}$
$t_{2} \to t_{1}$	referential	$A {(g_{2})}_{t_{2} \| \| t_{1}}$	$K {(g_{2})}_{t_{2} \| \| t_{1}} = log \frac{A {(g_{2})}_{t_{2}}}{A {(g_{2})}_{t_{1}}}$
$t_{3} \to t_{1}$	non-referential	$A {(g_{1})}_{t_{3} \| t_{1}}$	$K {(g_{1})}_{t_{3} \| t_{1}} = log A {(g_{1})}_{t_{3} \| t_{1}}$
It should be noted that, other non-referential dependencies can be used such as mutual (;), joint (,), etc., apart from conditional dependency (\|).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Mathematical Theory of Knowledge for Intelligent Agents

Abstract

1. Introduction

1.1. Related Work

1.2. Contributions

1.3. Organization

2. Definition of Entities and Properties

2.1. Cognitive Property

2.1.1. Knowledge, Action, and Intelligence

2.1.2. Observation, Reasoning, and Actuation

2.2. Definitions of Entities

2.2.1. Description and Properties

2.2.2. Logical Relationships Between Entities

2.2.3. Logical operations between entities

3. Cognitive Property Quantification

3.1. Action Property

3.1.1. Action Quantification

3.1.2. Types of Action Values

3.1.3. Logical Operations on Action Values

3.2. Intelligence Property ( Φ )

3.2.1. Intelligence Quantification

3.3. Cognitive Value Property

3.3.1. Knowledge Quantification

3.3.2. Cognitropy: Expected Cognitive Property Value

3.3.3. Resultant Values

3.3.4. Dissimilarities of Cognitropy from Other Quantities

3.3.5. Types of Knowledge

3.3.6. Knowledge Structures

3.3.7. Logical Operations on Knowledge

3.3.8. Properties of the Knowledge Value

4. Conclusion

Appendix A. Proofs

Appendix A.1

Appendix B. List of Symbols

References

MDPI Initiatives

Important Links

Subscribe

3.2. Intelligence Property ( $Φ$ )