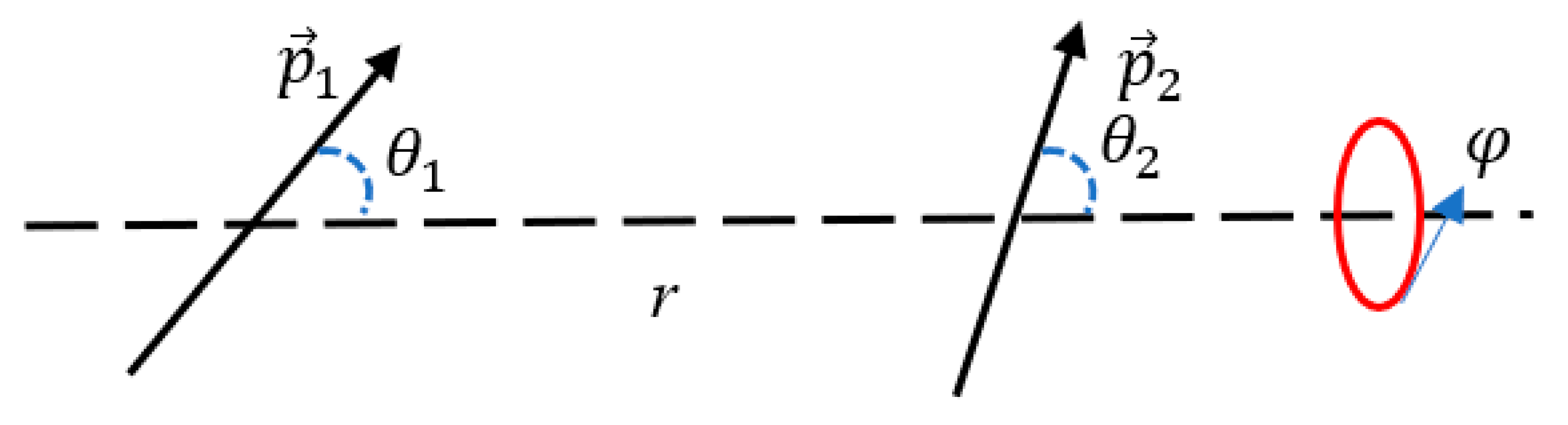Prerpints.org logo
Preprint
Article

Universe as a Graph (Ramsey Approach to Analysis of Physical Systems)

Altmetrics

Downloads

368

Views

174

Comments

0

Submitted:

19 January 2023

Posted:

20 January 2023

You are already at the latest version

Alerts
Abstract
Application of the Ramsey graph theory to the analysis of physical systems is reported. Physical interactions may be very generally classified as attractive and repulsive. This classification creates the premises for the application of the Ramsey theory to the analysis of physical systems built of electrical charges, electric and magnetic dipoles. The notions of mathematical logic, such as transitivity and intransitivity relations, become crucial for understanding of the behavior of physical systems. The Ramsey theory explains why nature prefers cubic lattices over hexagonal ones for systems built of electric or magnetic dipoles. The Ramsey approach may be applied to the analysis of mechanical systems when actual and virtual paths between the states in the configurational space are considered. Irreversible mechanical and thermodynamic processes are seen within the reported approach as directed graphs. Chains of irreversible processes appear as transitive tournaments. These tournaments are acyclic; the transitive tournaments necessarily contain the Hamiltonian path. The set of states in the phase space of the physical system, between which irreversible processes are possible, is considered. The Hamiltonian path of the tournament emerging from the graph uniting these states is a relativistic invariant. Applications of the Ramsey theory to the general relativity become possible when the discrete changes in the metric tensor are assumed. Reconsideration of the concept of “simultaneity” within the Ramsey approach is reported.
Keywords: 
Subject: Physical Sciences  -   Theoretical Physics

1. Introduction

In discrete mathematics, graph theory is a framework unifying the study of graphs, which are mathematical structures used to model pairwise relations between objects [1,2]. Pairwise interactions constitute the core of physics; thus, it is well expected, that the graphs theory will play an important role in the modern physical picture of the world. Graphs are one of the principal objects of study in discrete mathematics [1,2]. We adopt the reasonable hypothesis that both physics and the corresponding mathematics have to be described by means of discrete concepts on the Planck-scale; thus, graphs theory is well-expected to supply powerful instruments for understanding the discrete physical Universe [3,4]. A graph in this context is made up of vertices representing physical bodies which are connected by edges (also called links) representing physical interactions, which may differ in their nature. A distinction should be made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically.
In particular, we apply the Ramsey theory for the analysis of the physical behavior of a physical system built of interacting particles [5]. These interactions very generally may be classified as attractions or repulsions, thus providing the base for application of the Ramsey theory. Ramsey theory is a field of the graphs theory that investigates the emergence of interconnected/interrelated sub-structures within a structure/graph of a known size [6,7,8,9,10]. Ramsey's theorem, in one of its graph-theoretic forms, states that one will find monochromatic cliques in any edge labelling (with colors) of a sufficiently large complete graph [6,8,9]. An accessible introduction to the Ramsey theory is found in refs. ]6, 9[. A more rigorous approach is supplied in ref. ]10[. We demonstrate that the Ramsey theory is useful for the analysis of a broad variety of physical systems, including thermodynamics and relativity problems. Thus, notions and concepts of mathematical logic become crucial for understanding the behavior of physical systems.

2. Results

2.1. Ramsey theory for a set of interacting bodies

Consider a set of interacting bodies between which attractive and repulsive interactions are possible. Let us pose the following question: what is the minimal number of bodies giving rise to appearance of sub-systems, in which only attractive or repulsive interactions are acting? These interactions may be homogeneous and heterogeneous in their physical nature. In the case of heterogeneous interactions, for example, the origin of the attractive force may be gravity, and repulsion may be electrostatic forces. Until now, we have not specified the kind of these interactions (we will demonstrate below that the physical nature of these interactions is important for answering the posed question). The solution of the aforementioned problem is supplied by the Ramsey theory. Consider the system of n physical bodies, interacting one with another via attraction or repulsion. What is the minimal number of bodies giving rise to m attractions and l repulsions in the system? From the pure mathematical point of view, we have to answer the question: what is the Ramsey number R m , l ?
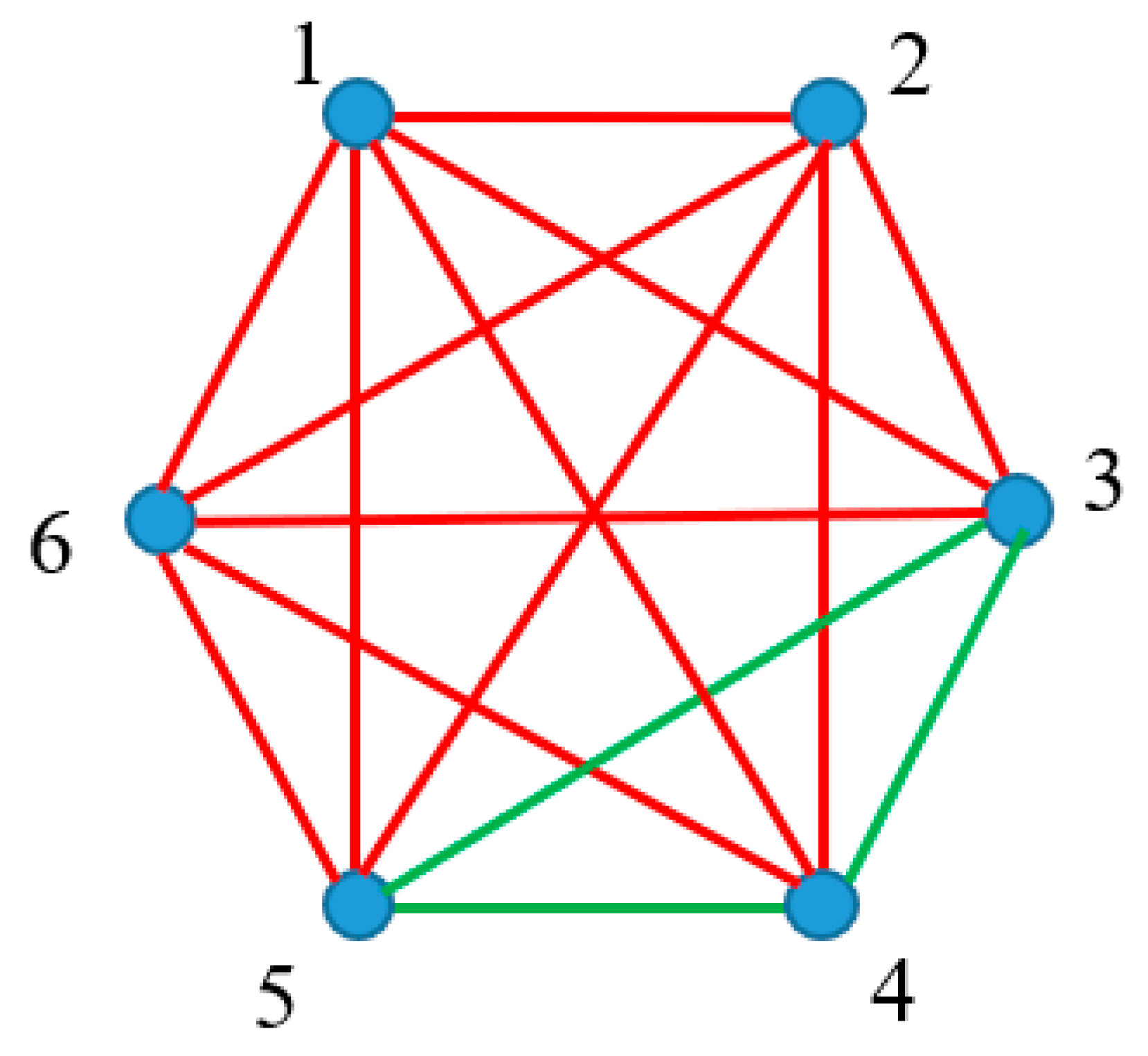
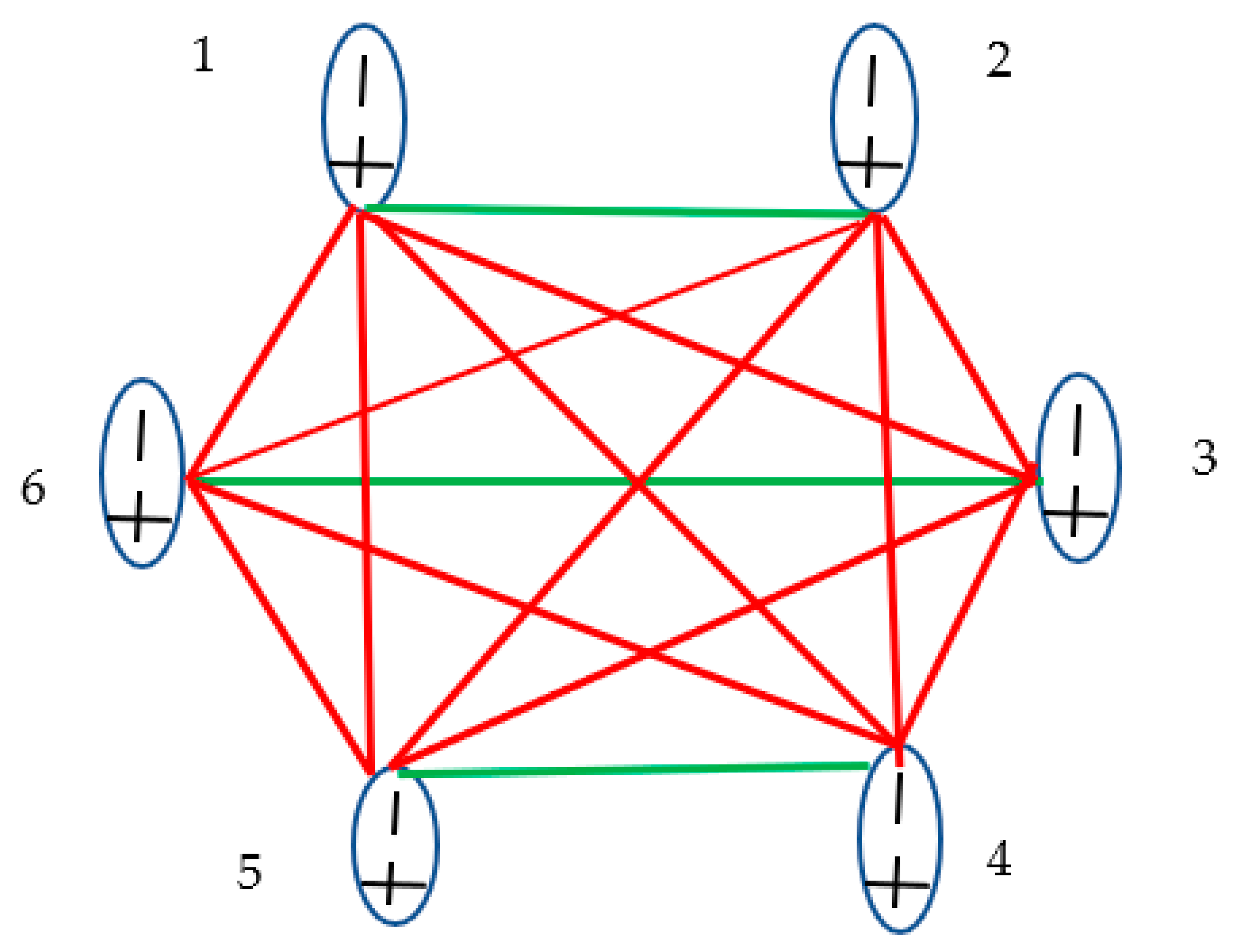
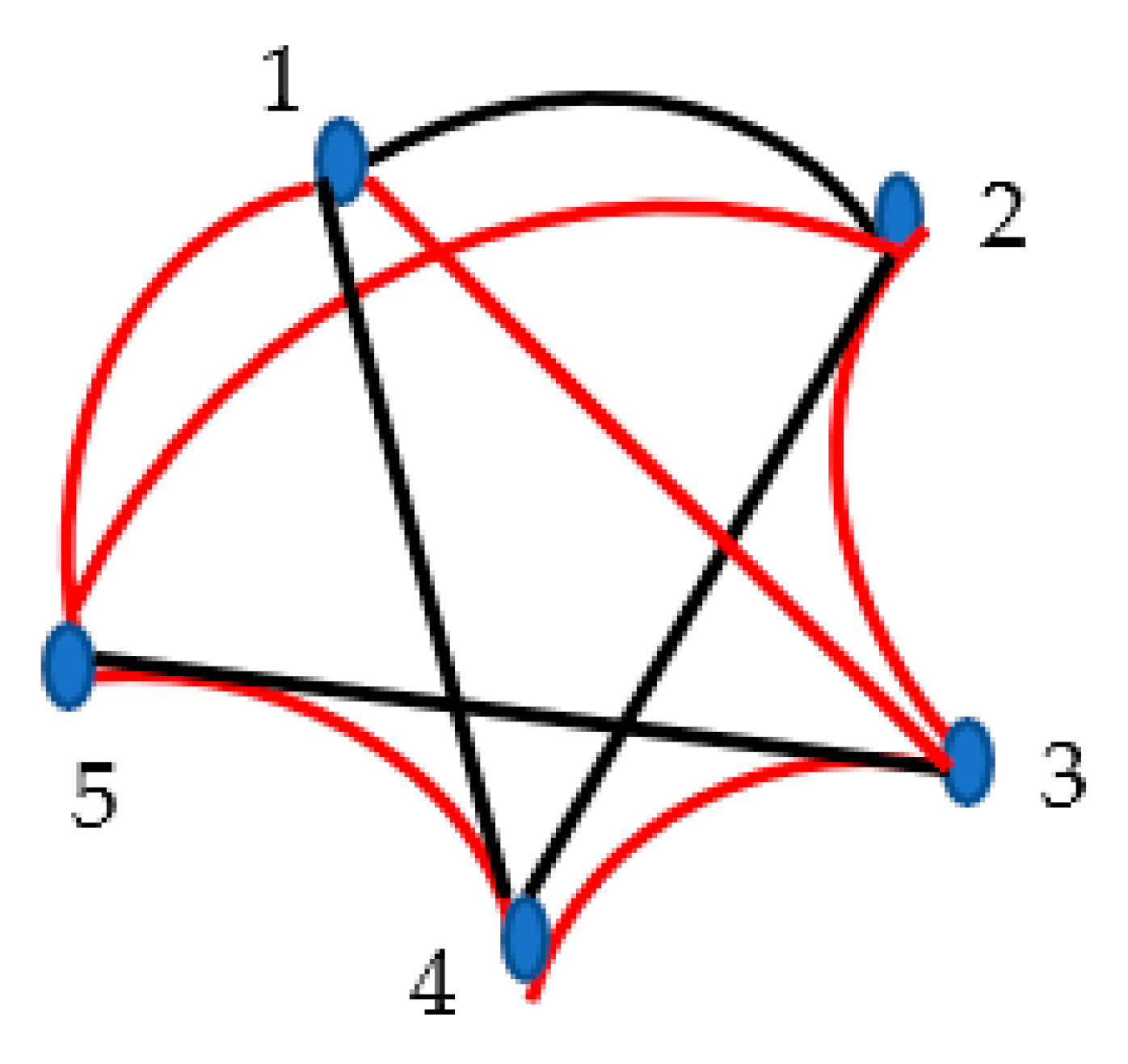
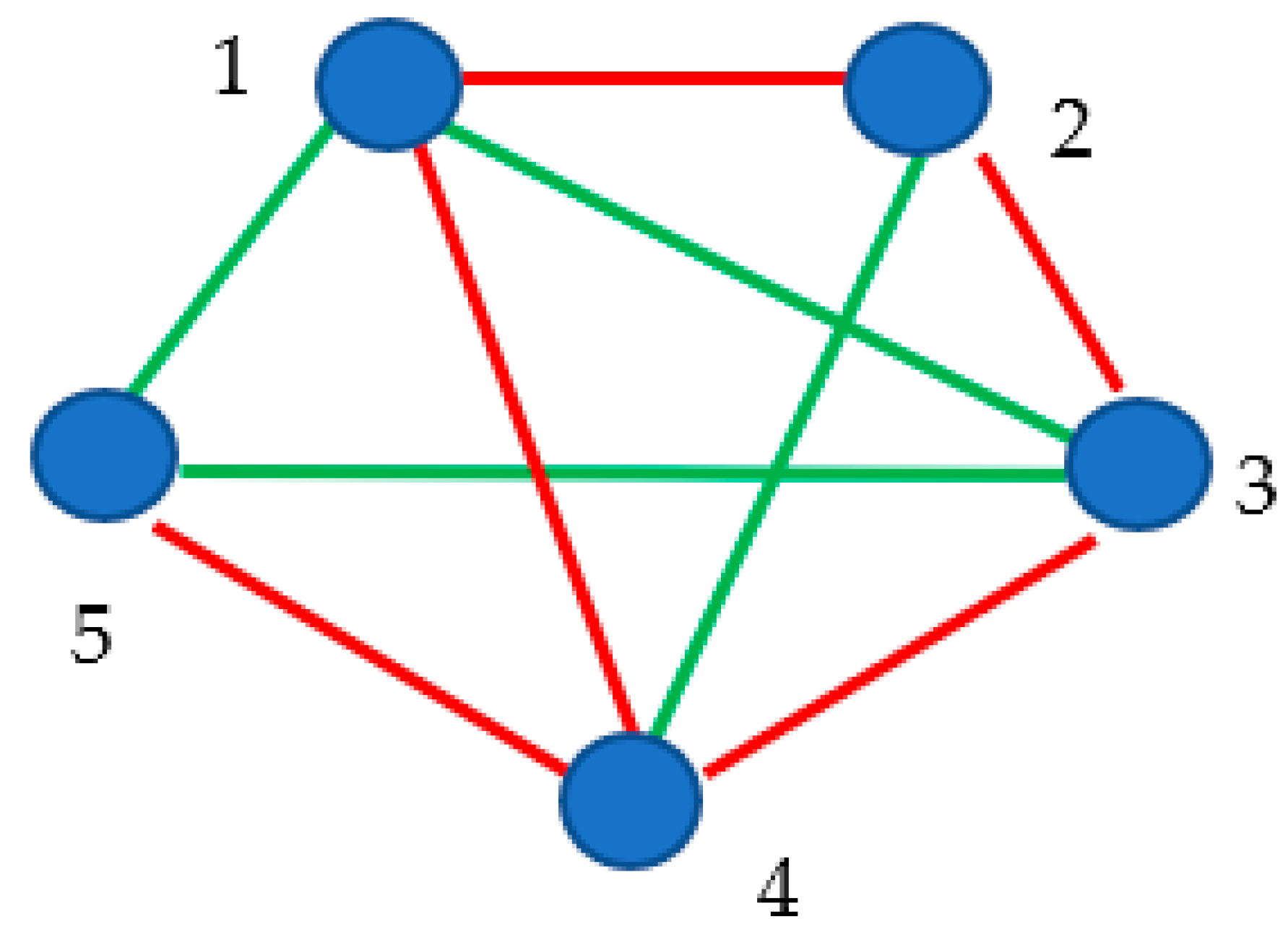
We start from the analysis of a set of n = 6 interacting physical bodies, illustrated with Figure 1. We adopt that two kind of interactions are possible within the system: namely attraction and repulsion. Attraction is depicted in Figure 1 with the red solid line/edge, whereas repulsion is shown with the green solid line/edge.
The physical interactions acting within the system form the complete graph, i.e. a graph in which each pair of graph vertices (masses) is connected by an edge/link (interaction, i.e. repulsion or attraction); the situation when zero interaction between the bodies is possible gives rise to the three-color Ramsey problem and it will be considered below. Let us pose the following question: what is the minimal number of bodies for which three mutual attractions or three mutual repulsions will necessarily appear in the graph? An answer to this question is important for the theory of crystals, indeed, the triads of particles between which only attractive or repulsive forces act, are unstable. The Ramsey theory supplies an exact answer to this question, namely R 3,3 = 6 . Indeed, we recognize that within the subsystem labeled “345” only repulsions are present; whereas, in the subsystems “123”, “124”,”125”, “126”, ”136”, “146”, ”156”, “236”, “246” and “256” only attractive interactions are present.
Now consider physical exemplifications of the aforementioned Ramsey approach. Numerous applications of the Ramsey approach to physics are foreseen; let us quote from ref: 11: “interactions are present in almost all areas of physics: soft and hard condensed matter, field theory, atomic physics, quantum chemistry, nuclear physics, astrophysics, and so on. Interactions between particles are responsible for a plethora of effects and many-body states, from the band structure of crystals to superconductivity in metals, from the quark-gluon plasma in heavy ion collisions to asymptotic freedom in quantum chromodynamics (QCD)”.
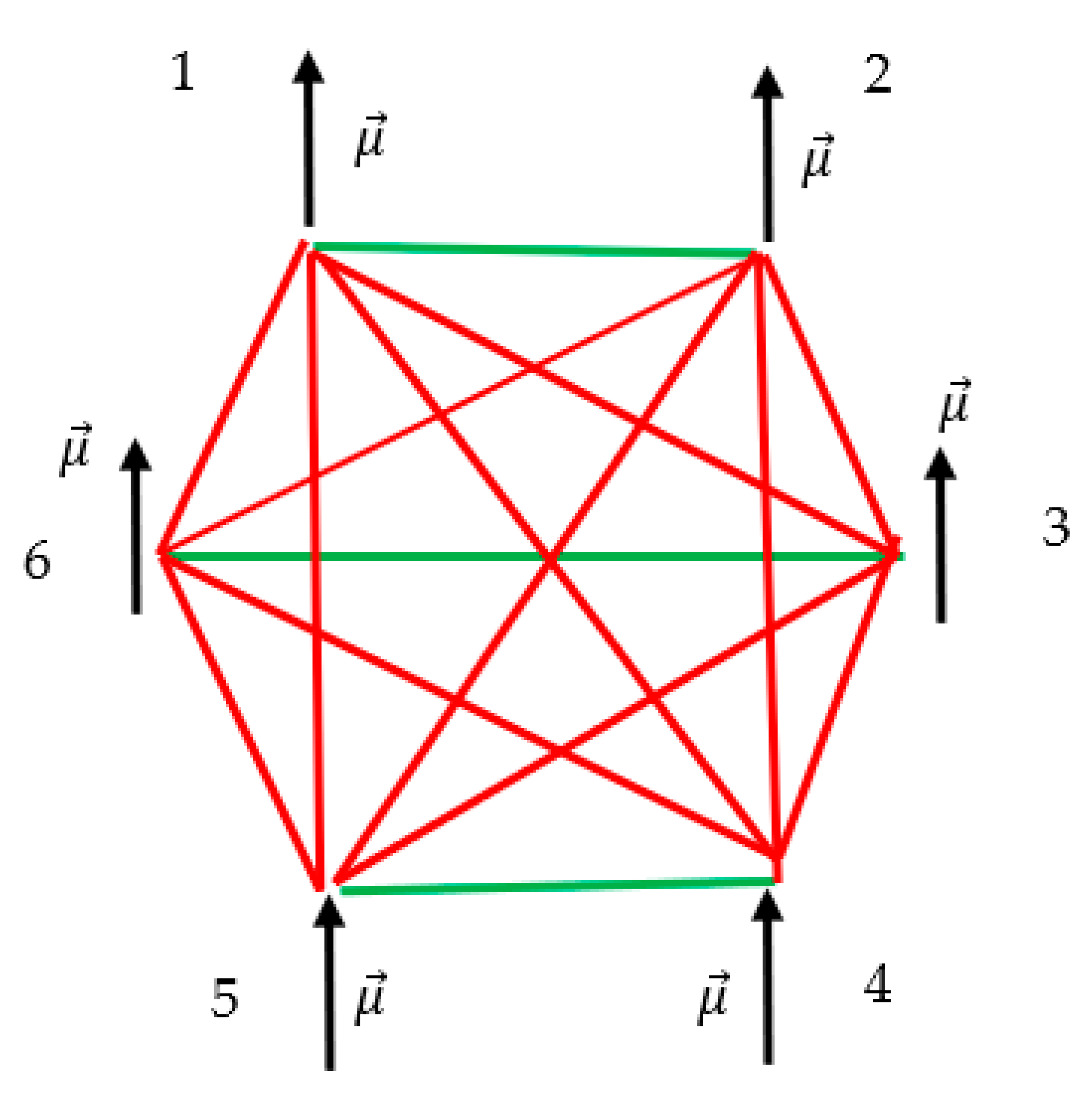
Consider the straightforward consequence of the Ramsey analysis of the six-body interaction problem, illustrated with Figure 1. It should be emphasized that the six-body physical system depicted in Figure 1 may be in mechanical equilibrium, and it may be out of equilibrium. If the system is in equilibrium (due to co-appearance of attractive and repulsing forces) Eq. 1 holds:
F → i = ∑ k = 1 , k ≠ i 6 f → i k = 0   i ≠ k ,   i = 1 … 6 , k = 1 . . . 6 ,
where F → i is the resulting force acting on the i-th body; f → i k is the force representing interaction between i-th and k-th bodies. The Ramsey theory states that within an equilibrium six-body physical system (in which attractive and repulsive force provide the equilibrium), necessarily appears at least one non-equilibrium three-body system in which only repulsive or attractive interactions are present, giving rise to the condition, summarized with Eq. 2:
F → i = ∑ k = 1 , k ≠ i 3 f → i k ≠ 0   i ≠ k ,   i = 1 … 3 , k = 1 … 3
Thus, following general theorem is proven: in any equilibrium, six-body system in which equilibrium arises from the balance of attraction and repulsion forces, at least one non-equilibrium, three-body system is necessarily present. The straightforward application of this theorem to the theory of simple liquids is noteworthy. Indeed, in the theory of liquid state, the separation of an intermolecular interaction potential into a part containing all the repulsive forces and a part containing all the attractive forces is useful, as shown in ref. 12, and “this separation is distinctly different from the separation into positive and negative parts of the potential frequently used in perturbation theories of liquids” [12]. Thus, when we consider six-liquid-molecule equilibrium cluster appearing in the liquid, the non-equilibrium triple-body sub-system will be necessarily present in the system.

2.2. Ramsey approach for a set of bodies interacting via Coulomb electrostatic interaction: transitive and intransitive physical interactions

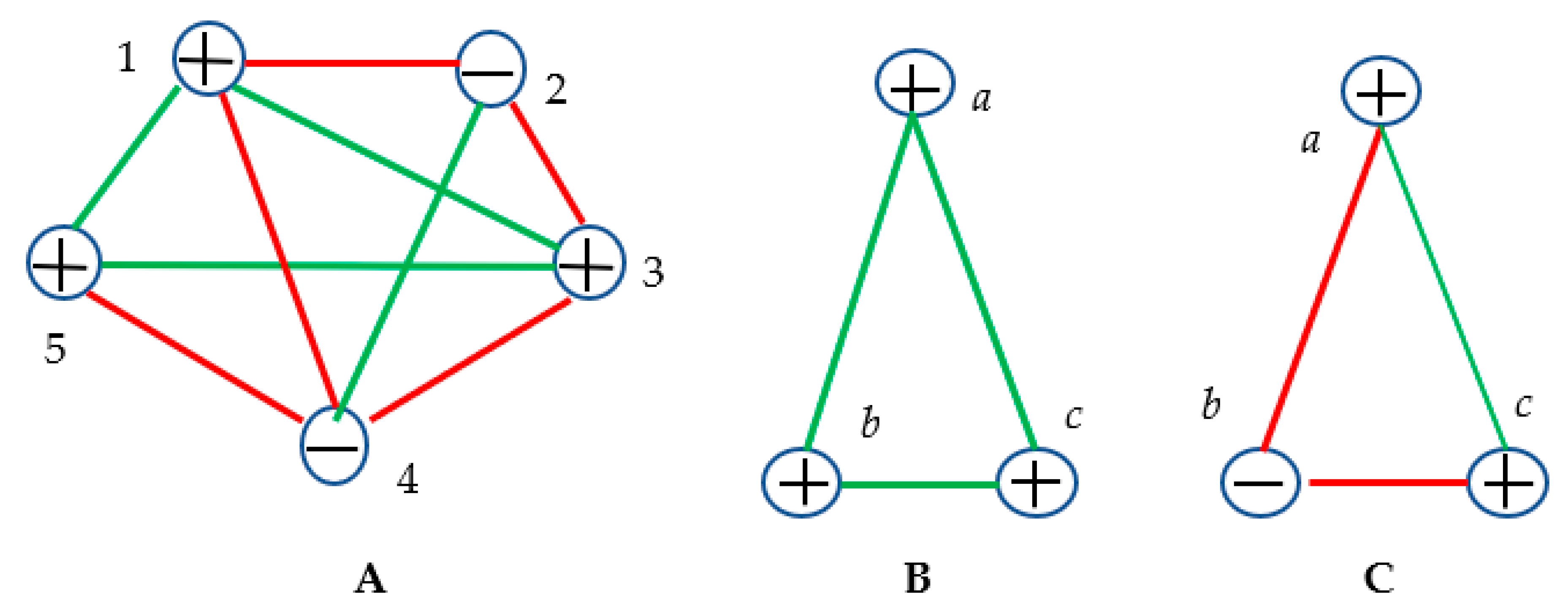
Now, let us specify the exact kind of these interactions. It seems natural to consider the Coulomb forces acting between the point electrical charges as attractive/repulsive interactions. It also seems from the first glance, that the Coulomb interactions represent the particular case of the aforementioned case, shown in Figure 1, and R 3,3 = 6 is kept. However, this answer is wrong, due to the fact that the Coulomb forces represent physical interactions, which may be transitive or intransitive in their physical nature. Consider the system of five point electrical charges, depicted in Figure 2A. It is immediately recognized from Figure 2A that in the sub-system labeled “135”, only repulsive Coulomb interactions are present. Moreover, in any system of five point charges (whatever are their signs) we will find at least one sub-system built of three point charges interacting via repulsive forces. No triangle built of attractions (red links) is recognized. Let us understand this observation.
When charges “a”, “b” and “c” are of the same sign, interactions a ⟷ b ,   b ⟷ c   a n d   a ⟷ c are necessarily repulsive, in other words, when a positive charge “a” repulses a positive point charge “b”, and a positive charge “b” repulses a positive charge “c”, necessarily, charge “a” repulses charge “c” (see Figure 2B). Thus, when the signs of the point charges are the same, the Coulomb interactions are transitive [13].
Now, consider the situation when the signs of the point charges are different, as illustrated with Figure 2C. In this case, when a positive charge “a” attracts a negative point charge “b”, and negative charge “b” attracts positive charge “c”, necessarily charge “a” repulses charge “c”. This kind of relations is called in mathematical logic “intransitivity”. Let us illustrate this property with the following logical example, involving three groups of experts, labeled “A”, “B” and “C” correspondingly. Consider the situation when group of experts “A” recognizes group “B”, and group “B” recognizes group “C”, but group “A” does not recognize group “C”. In this case, the recognition relation among the expert groups is defined as “intransitive”. This is exactly the situation inherent for the Coulomb interaction of three point charges of different signs, shown in Figure 2C. It should be emphasized that no monochromatic triangle will appear when the point charges of various signs are located in its vertices; however, the clique built of two monochromic edges will be necessarily present, as shown in Figure 2C. On the other hand, the monochromatic triangle will necessarily appear when the three point charges of the same sign are placed in the vertices, as depicted in Figure 2B. Using the notions of the Ramsey theory, we conclude that R t r a n s , i n t r a n s 2,3 = 3   is true for the Coulomb interactions acting between the point charges.
In other words, when interactions between charges “a” and “b”, and “b” and “c” are known, the kind of interaction between charges “a” and “c” is pre-scribed unequivocally, irrespectively of the spatial location of the charges. However, these interactions may be transitive, giving rise to monochromatic triangles, and intransitive, which do not enable monochromatic triangles. It is easily seen that in any system built of five point charges, at least one monochromatic triangle will necessarily appear. This is true for any odd number of point electrical charges.
The transitivity/intransitivity of the Coulomb force immediately follows from the expression for the potential energy of interaction U r between two point charges q 1 and q 2 separated by the distance r:
U r = k q 1 q 2 r ,
where k is a constant depending on the adopted system of units. It is seen from Eq. 3 that the energy is increased with the decrease of the separation between the charges of the same sign (which corresponds to repulsion); whereas the energy is decreased with the decrease of the separation between the charges of the different signs (which corresponds to attraction). Thus, the Coulomb interaction within a triad of electrical charges is transitive/intransitive, depending on the signs of charges, as shown in Figure 2B-C. This will be true for a general Coulomb-like interaction, described by Eq. 4:
U r = ζ Φ 1 Φ 2 r n
where ζ is a coefficient depending on the system of units, Φ 1 and Φ 2 are “effective charges”, which may be of the different signs. Thus, the Ramsey theory may be also applied for the analysis of the physical situation, in which the “Coulomb-like” interactions between the effective charges, described by Eq. 4, are involved.
Finally, when the notions of the Ramsey theory are used, we formulate the obtained result as follows: the transitive/intransitive Ramsey number, describing Coulomb (or Coulomb-like) interactions between points charges/effective charges equals three, i.e. R t r a n s , i n t r a n s 2,3 = 3 , whereas R t r a n s , i n t r a n s 3,3 does not exist.

2.3. Non-transitive electro- and magneto-static interactions: why nature prefers cubic dipole lattices over hexagonal ones?

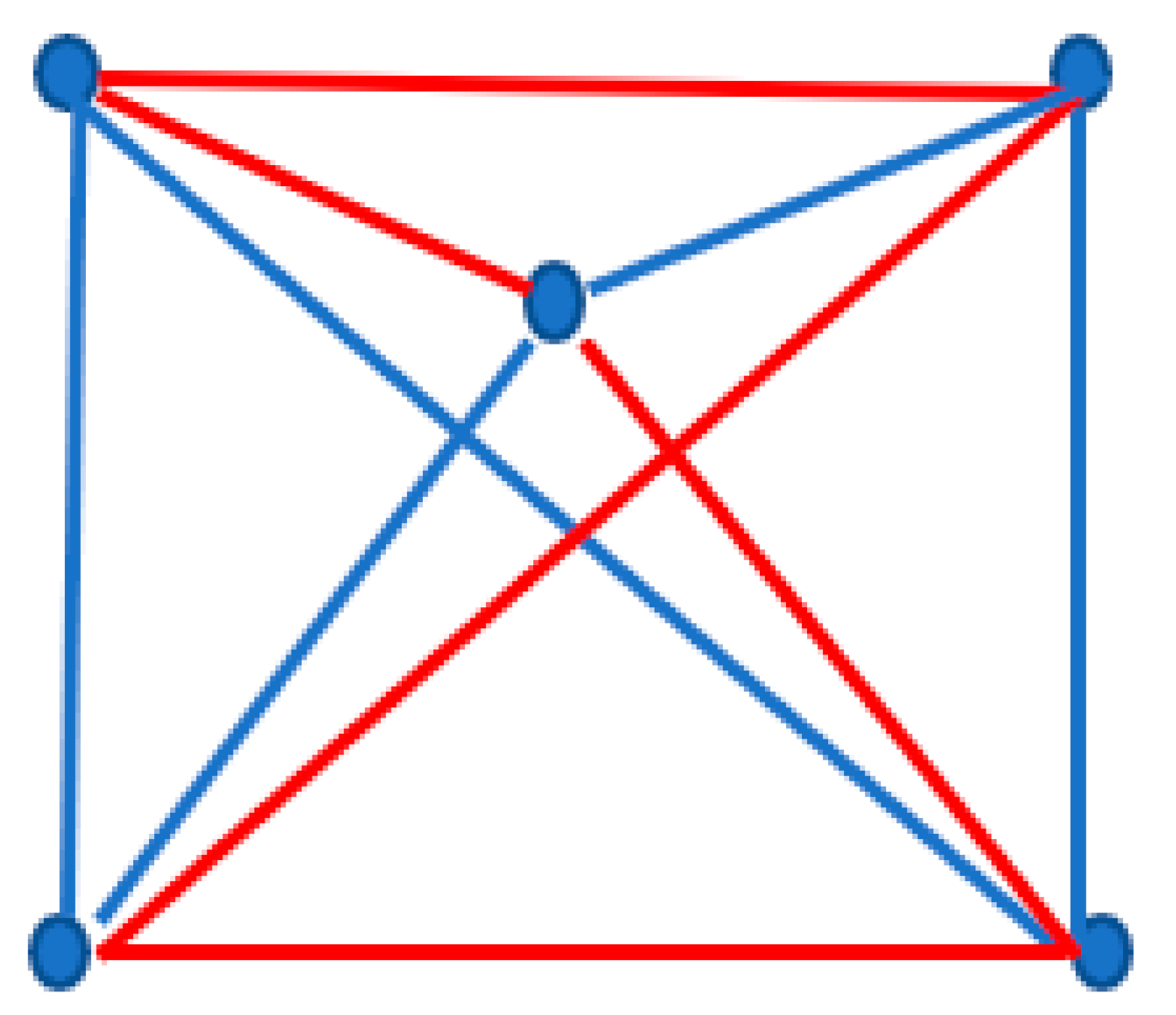
It should be emphasized that electrostatic interactions may be non-transitive. For example, interactions between electrical dipoles are non-transitive. Energy of interaction between two dipoles, illustrated with Figure 3, is described by Eq. 5 [14,15]:
U e l r = − k p 1 p 2 r 3 2 c o s θ 1 c o s θ 2 − s i n θ 1 s i n θ 2 c o s φ ,
where p 1 and p 2 are permanent dipole moments, r is the separation between the dipoles and the angles θ 1 , θ 2 and φ are shown in Figure 3.
Electric dipoles may attract or repel each other; when θ 1 = π 2 ; θ 2 = π 2   a n d   φ = 0   corresponding to the p → 1 ↑ ↑ p → 2 parallel configuration; the energy of the repulsive interaction stems from Eq. 5 and it is given by Eq. 6:
U e l r = k p 1 p 2 r 3
In turn, when θ 1 = π 2 ; θ 2 = − π 2   a n d   φ = 0   corresponding to the p → 1 ↑ ↓ p → 2 anti-parallel configuration, we derive for the energy of the attractive interaction (see Eq. 7):
U e l r = − k p 1 p 2 r 3
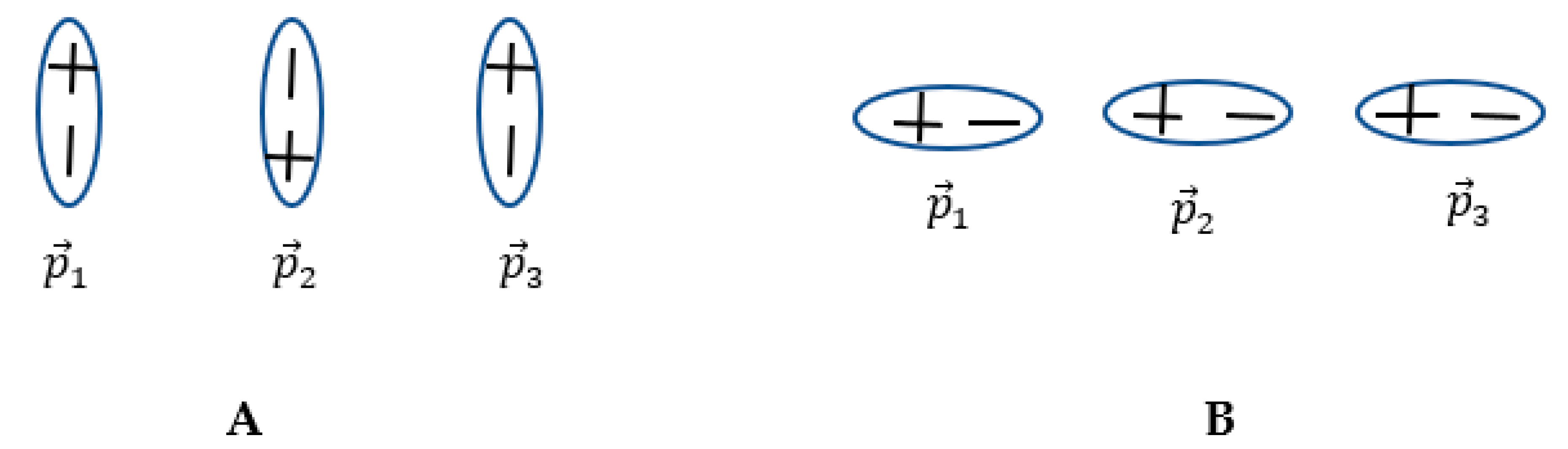
And it is noteworthy that the dipole-dipole interactions may by non-transitive as illustrated in Figure 4A.
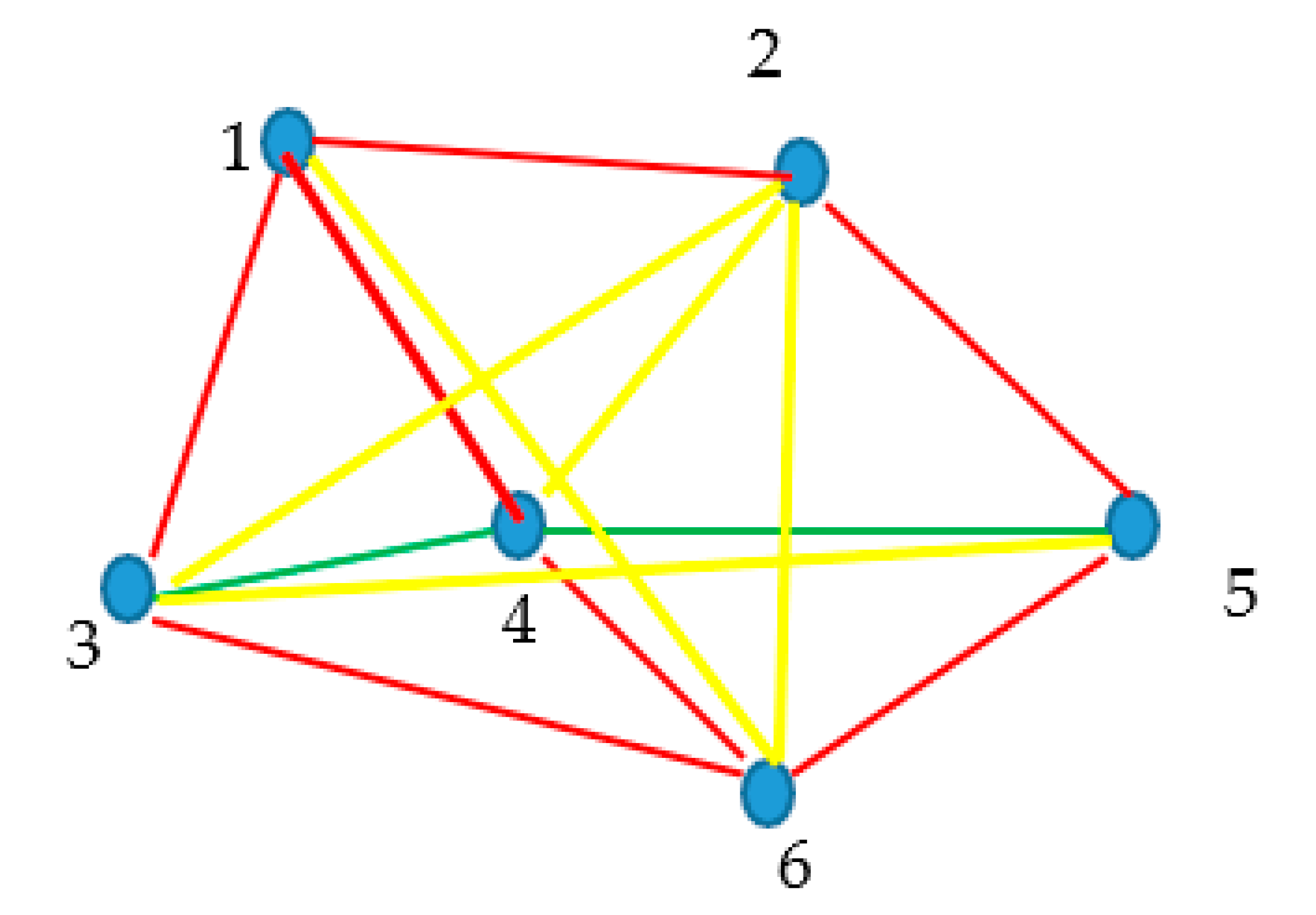
Indeed, in the scheme depicted in Figure 4A dipole p → 1 attracts dipole p → 2 and dipole p → 2 attracts dipole p → 3 , whereas dipole p → 1 repels dipole p → 3 . Thus, in this case the dipole-dipole interaction is non-transitive. However, in the scheme depicted in Figure 4B, all of the dipoles attract one another; consequently, the interaction is transitive. Thus, the kind of dipole-dipole interaction depends on their mutual spatial orientation, in contrast to the situation with the interaction of point charges. Consider the system of electrical dipoles depicted in Figure 5, in which red lines depict attractive dipole-dipole interaction, and green lines, in turn, depict repulsive dipole-dipole interactions; now, the nature of interaction depends on the spatial orientation between the dipoles, as follows from Eq. 5. For dipoles monochromatic triangles built of red links, corresponding to attraction become possible, and this is again in contrast to graphs, emerging from the interaction of point charges. Thus, we return to the situation described in Figure 1, when the transitivity of interaction is not unambiguously prescribed within the triad of interacting bodies. It brings us back to the complete non-transitive graphs, such as that depicted in Figure 1.
Recall that R 3,3 = 6 for complete non-transitive graphs. Indeed, triple sub-systems of dipoles labeled “125”, “135”, “124”, “235”, “265” and “146”, in which only attractive interactions act are recognized in Figure 5. No subsystem in which only repulsive interactions appear is present in the complete graph of interactions, shown in Figure 5.
Magneto-static interaction between two magnetic dipoles is also of the non-transitive nature. This becomes clear when the energies of electrical U e l r and magnetic interaction U m a g n r between dipoles are written in the symmetrized form [16]:
U e l r = 1 4 π ε 0 p → 1 · p → 2 − 3 p → 1 · r ^ p → 2 · r ^ r 3 ,
U m a g n r = μ 0 4 π μ → 1 · μ → 2 − 3 μ → 1 · r ^ μ → 2 · r ^ r 3
where μ → 1 and μ → 2 are the magnetic moments and r ^ is a unit vector parallel to the line joining the centers of the two dipoles.
The energy of interaction of two magnetic dipoles depends on the mutual orientation, and it may give rise to attractive and repulsive forces, which are non-transitive, as shown in Figure 6. Again, sub-systems of magnetic dipoles labeled “125”, “135”, “124”, “235”, “265” and “146”, in which only attractive interactions act, are recognized in Figure 5. There is no subsystem in which only repulsive interactions appearin the complete graph of interactions, shown in Figure 6. Thus, the Ramsey theory may supply additional insights to the Ising problem[17]. Consider artificial hexagonal honeycomb spin ice systems addressed in refs. 18-20. A spin ice is a magnetic substance that does not have a single minimal-energy state [18,19,20]. It has magnetic moments as elementary degrees of freedom, which are subject to frustrated interactions [18,19,20]. Frustrated interactions arise when a system cannot, due to local geometric constraints, minimize all the pairwise interactions simultaneously [18,19,20]. By their nature, these interactions prevent the moments from exhibiting a periodic pattern in their orientation down to a temperature much below the energy scale set by the said interactions [18,19,20]. The Ramsey theory predicts that for any hexagon built of spins, we will find the non-equilibrium triangle in which attractive or repulsive interactions will act between spins.
It should be emphasized, that nature “prefers” FCC spin ice systems (such as those observed in K2I2 Cl 6 and R 2Ti2O7, where R – is rare earth element) over artificial hexagonal lattices, as demonstrated in refs. 21-25. The reasonable and fundamental question is: why are the cubic Bravais systems preferred over hexagonal ones? We have a similar situation for the electrical dipole-dipole interactions, where FCC lattices were reported [26,27].
It is well-known that neon, argon, krypton, and xenon crystallize in the face-centered cubic (FCC) lattice, one of the two closest-packed structures; the other being the hexagonal lattice with axis ratio 1.633 [26,27]. The preference for the cubic over the hexagonal structure, however, cannot be explained on the basis of differences in the dipole-dipole, dipole-quadrupole, or higher pole interactions for the two crystals [26,27]. Nor does the repulsive energy, as usually calculated, account for the structure [26,27]. The Ramsey approach illustrated with Figure 7 suggests the possible explanation as to why nature prefers cubic lattices over hexagonal ones for a dipole/dipole system. Figure 7 represents the scheme of non-transitive dipole-dipole interactions acting in the (100) plane of the FCC system, in which no monochromatic triangle is present. This is possible due to the fact, that the (100) plane of the FCC system contains five dipoles, and R 3,3 = 6 > 5 . Hence, the stable arrangement of dipoles in which attraction is balanced by repulsion becomes possible, as depicted in Figure 7. Thus, the Ramsey approach explains abundance of FCC lattices over hexagonal ones for dipole-dipole systems, whether the dipoles are magnetic or electric ones [21,22,23,24,25,26,27].
We conclude that for the complete graphs depicting non-transitive repulsive and attractive interactions between electric and magnetic dipoles, R(3,3)=6 is true, and monochromatic triangles corresponding to attractive and repulsive interactions are inevitable. These triangles are statically unstable; indeed, the only equilibrium static configuration of three bodies attracting or repulsing one another by a central force is possible when the entire triad is located on the same straight line, which is not the case for HCP lattices (this becomes clear from the simple vector considerations). And this is in contrast to the Coulomb interaction between point electrical charges, where monochromatic triangles representing attraction are forbidden, by the logical structure of interaction between point electrical charges, as discussed in Section 2.2. This does not mean that hexagonal lattices built of dipoles are forbidden; the balance of attraction and repulsion make them possible [18,19,20] (moreover, the entropy considerations should be considered, and they may justify formation of hexagonal lattices). However, hexagonal lattice have to withstand inherent static instability of monochromatic triangles, corresponding to pure attraction or repulsion, and it is plausible to suggest that this is just the reason that hexagonal lattices are rare in their occurrence.

2.4. Non-transitive interactions of electrically charged particles

Electron-electron electrostatic interactions are necessarily transitive, as discussed in Section 2.2. However, dynamic quantum electron-electron interactions in crystals are not necessarily transitive. The well-known example of such interactions is the formation of Bardeen–Cooper–Schrieffer pair, emerging from phonons exchange [28,29]. Other kinds of electron-electron interactions in Fermi liquid were considered, including the Kohn-Luttinger mechanism, which is not related to electron-phonon attractive interaction in metals, [30]. The Kohn-Luttinger mechanism is based upon the following fundamental result, namely, it was discovered that the screened Coulomb potential in a Fermi liquid has a long-range oscillatory tail, hence, at some large enough distance between electrons, the screened Coulomb interaction gets overscreened and becomes attractive [31]. Landau and Pitaevskii addressed the pairing in an isotropic Fermi liquid at nonzero orbital momentum l of the pair, and found that the pairing problem decouples between different l. Because of this decoupling, if only one partial component of the interaction is attractive and all others are repulsive, the system already undergoes a pairing instability into a state with l, for which the interaction is attractive [32]. The aforementioned electron-electron quantum interactions are not transitive in their physical nature. These interactions acting between electrons in the hexagonal lattice were treated in refs. 33-34. The Ramsey analysis of the non-transitive attractive/repulsive interactions in the hexagonal lattice, performed in Section 2.1, leads to the non-trivial conclusion, that the monochromatic triangles built only of attractive or repulsive interactions will be necessarily present in the hexagonal lattice due to the fact that R 3,3 = 6 .

2.5. Triple interacting systems: the Ramsey approach

The Ramsey Theory supplies the general framework for more complicated systems in which arbitrary number of interactions are possible. For example, consider the system in which three kinds of interactions are possible, namely: attraction, repulsion and zero interaction, which are supposed to be non-transitive. Consider the system depicted in Figure 8. Red lines in Figure 8 correspond to the attractive interaction between the bodies, green lines depict repulsive interactions, and yellow lines connect the bodies, which do not interact. It is easily seen from Figure 8 that no monochromatic triangles appear in Figure 8.
Let us address the following question: what is the minimal number of bodies, giving rise to appearance of sub-systems, in which monochromatic triangles will necessarily appear? In other words, sub-systems including only attracting or repulsing or non-interacting bodies are present. From the point of view of the Ramsey theory, the question is formulated as follows: what is the value of R ( 3,3 , 3 ) number? The problem was solved by mathematicians: R 3,3 , 3 = 17 16 . It is noteworthy that a restricted set of Ramsey numbers is known until now [11,35].

2.6. Ramsey theory and dynamics of mechanical system

Consider now the Ramsey re-interpretation of the classical mechanics. The dynamics of mechanical systems is determined by the Hamiltonian principle, stating that the true evolution q t of a system described by N generalized coordinates q = q 1 , q 2 … q n between two specified states q t 1 = q 1 ( t 1 ) , q 2 ( t 1 ) … q n t 1 and q t 2 = q 1 ( t 2 ) , q 2 ( t 2 ) … q n t 2 at two specified times t1 and t2 is a stationary point (a point where the variation δ S is zero) of the action functional S, defined by Eq. 10:
S = ∫ t 1 t 2 L q t , q ˙ ( t ) d t
Consider that the motion of the system may be pictured as that of the single point (usually labeled C-point) in the extended configurational space comprising the generalized coordinates and time as independent variables [36,37]. In this space the successive phases of the motion show up as successive points of a curve. This curve, the “world-line” of the C–point, contains in geometrical form the entire physical history of the mechanical system [36,37]. The Hamilton principle states that the motion of the system between the initial time t 1 and final time t 2 follows a path that minimizes the scalar action integral, defined as the time integral of the Lagrangian, provided the initial and final configurations of the system are prescribed. Thus, from the point of view of a pure logic, two kinds of pathways are possible in the configurational space, namely: i) pathways which minimize the action integral (at these pathways δ S = 0 takes place), we call these paths the “actual paths”; and ii) paths which do not minimize the action functional, given by Eq. 10. 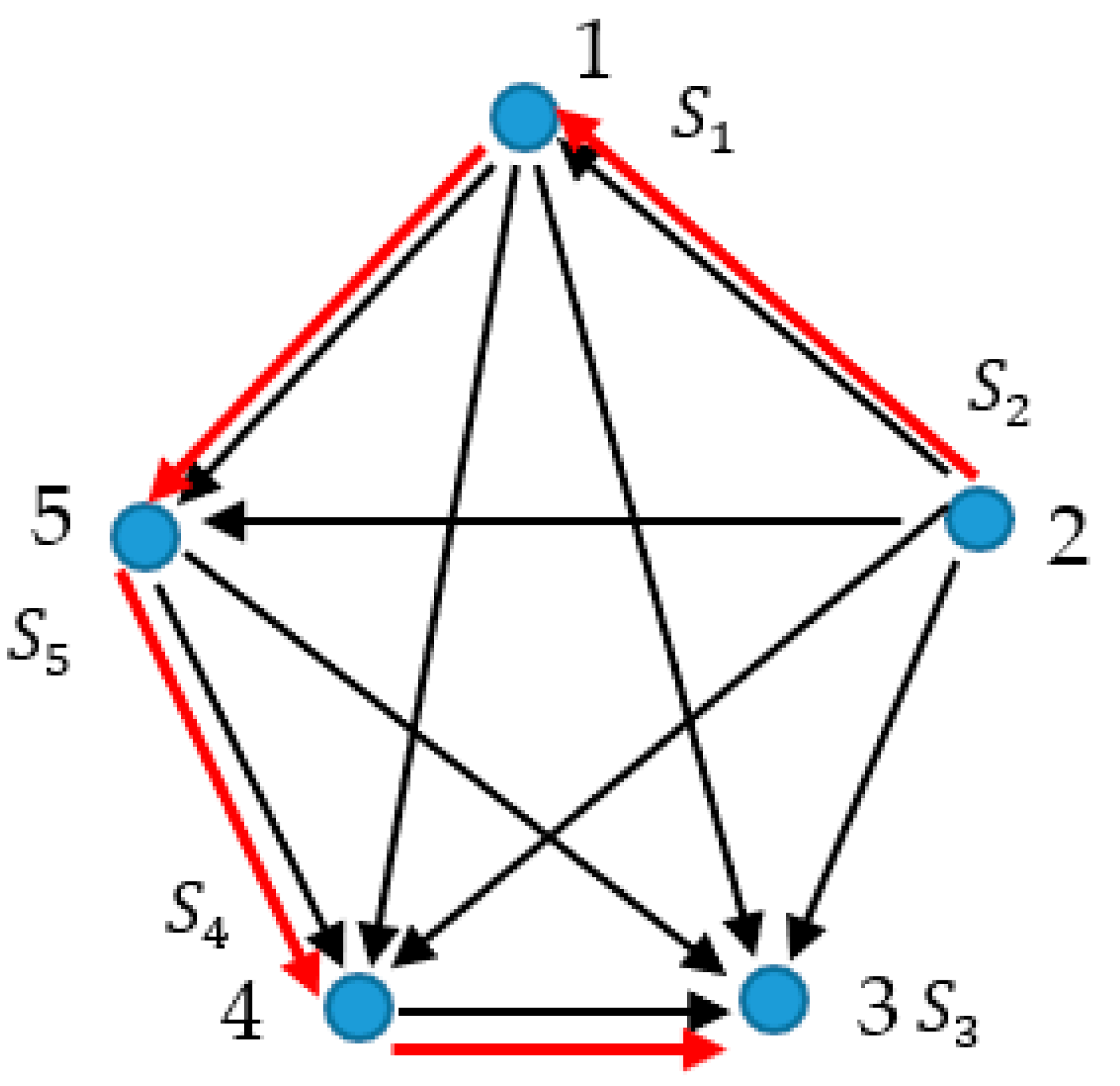Below we call these paths the “virtual paths” and δ S ≠ 0 holds along these paths. Thus, premises for application of the Ramsey approach are created, as illustrated with Figure 9.
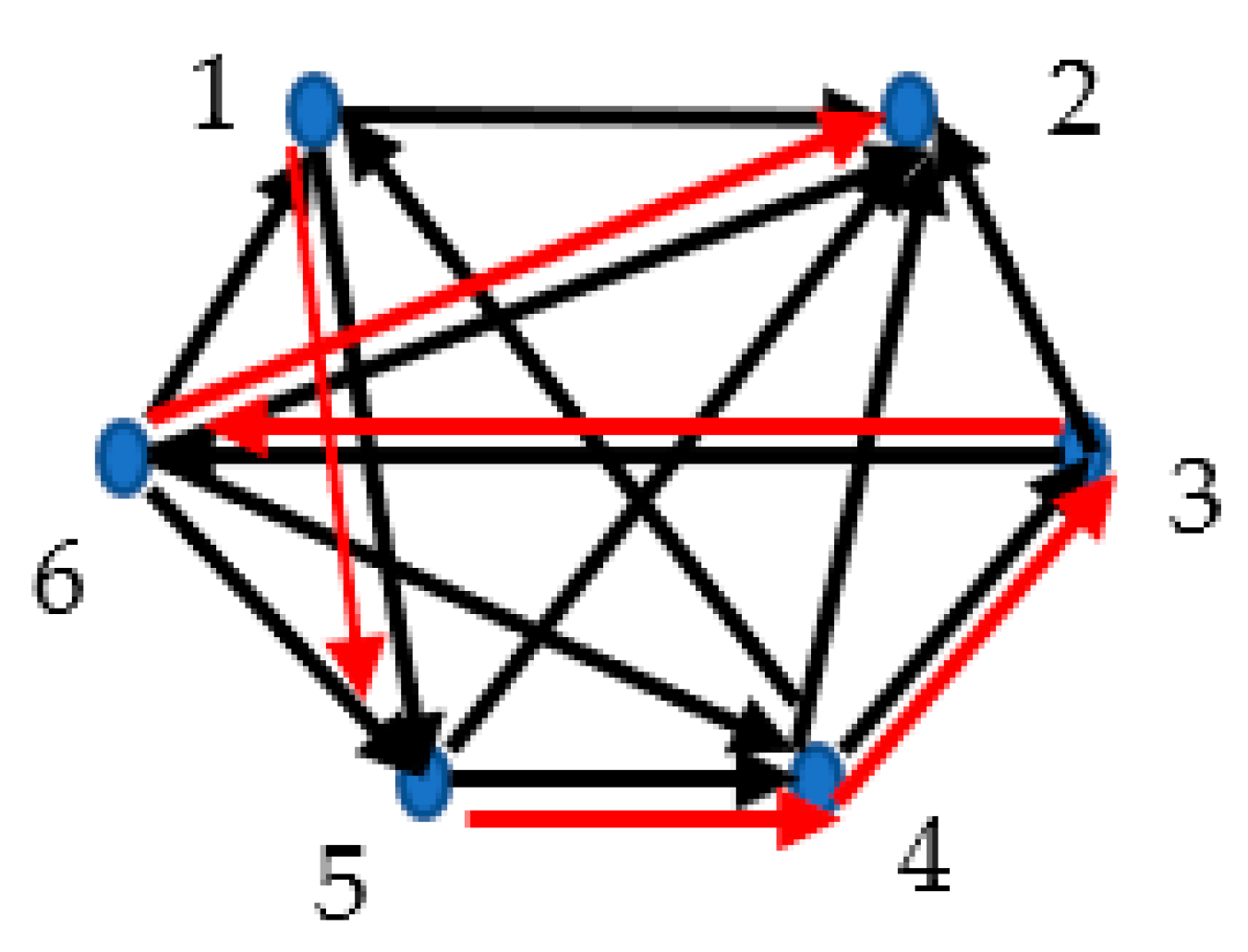
Consider the map of the states, available for the system in the configurational space. The map emerges from five points in the configurational space of the mechanical system. The points are interconnected by paths corresponding to the actual paths, corresponding to the actual motions of the mechanical system ( δ S = 0 ), and virtual paths ( δ S ≠ 0 ) which were not chosen by nature for actual motions of the system. Actual paths are shown with red links, whereas virtual motions are shown with black links. These paths form the complete graph. It is recognized from the map supplied in Figure 9, that it is possible to create a graph in which no monochrome triangle is present. However, this would be impossible for a map comprising six points, due to the fact that R 3,3 = 6 .
Thus, in the graph built of the six vertices representing C-points in the configurational space and interconnected by actual and virtual paths, cycles will necessarily appear. These cycles (“red cycles” or alternatively “black” ones) may correspond to actual or virtual (motions) of the C-point in the configurational space. Therefore, any evolution of any mechanical system may be represented with the corresponding Ramsey graph, enabling identification of periodic (cyclic) orbits of C-points. Why identification of periodic orbits is important? It was stated (we quote ref. 38): “that the periodic orbit theory of classical and quantum chaos is one of the major advances in the study of long-time behavior of chaotic dynamical systems. The theory expresses all long-time averages over chaotic dynamics in terms of cycle expansions [39], sums over periodic orbits (cycles) ordered hierarchically according to the orbit length, stability, or action. If the symbolic dynamics is known, and the flow is hyperbolic, longer cycles are shadowed by shorter ones, and cycle expansions converge exponentially or even superexponentially with the cycle length” [40].Thus, the Ramsey approach supplies an additional insight for the analysis of dynamics of chaotic systems.

2.7. Irreversible processes and graph theory

Until now, we did not address reversibility of the addressed mechanical processes. Now, consider the physical system in which only irreversible processes are possible (as a matter of fact, in any macro scale mechanical system friction is inevitable, and the processes are irreversible to a greater or lesser extent). Again, we consider the map of the states in the configurational space available to the system, shown in Figure 10.
Black arrows indicate directions of the irreversible processes. We assume that irreversible transitions between all of the states, corresponding to the points in the configurational space are possible, as shown in Figure 10. Thus, a tournament which is a directed graph (digraph) is obtained by assigning a direction for each edge emerges [1]. We assume that the emerging tournament is transitive, namely a → b   a n d   b → c ⇒ a → c takes place in such a tournament (for example: 6 → 1   a n d   1 → 2 ⇒ 6 → 2 is true for the discussed tournament). If the tournament is transitive, the theory of graphs predicts three consequences: i) the tournament is acyclic, i.e. it is a directed graph with no directed cycles; in particular, the tournament does not contain a cycle of length 3. Indeed, we recognize from Figure 10, that no cyclic process is possible for the presented tournament; ii) the tournament contains the Hamiltonian path. Hamiltonian path is the directed path on all n vertices of the graph, which is shown with red arrows in Figure 10. It should be emphasized that the transitive directed graph has only one Hamiltonian path. Thus, an irreversible process which passes over all available states in the configurational space of the system is possible.
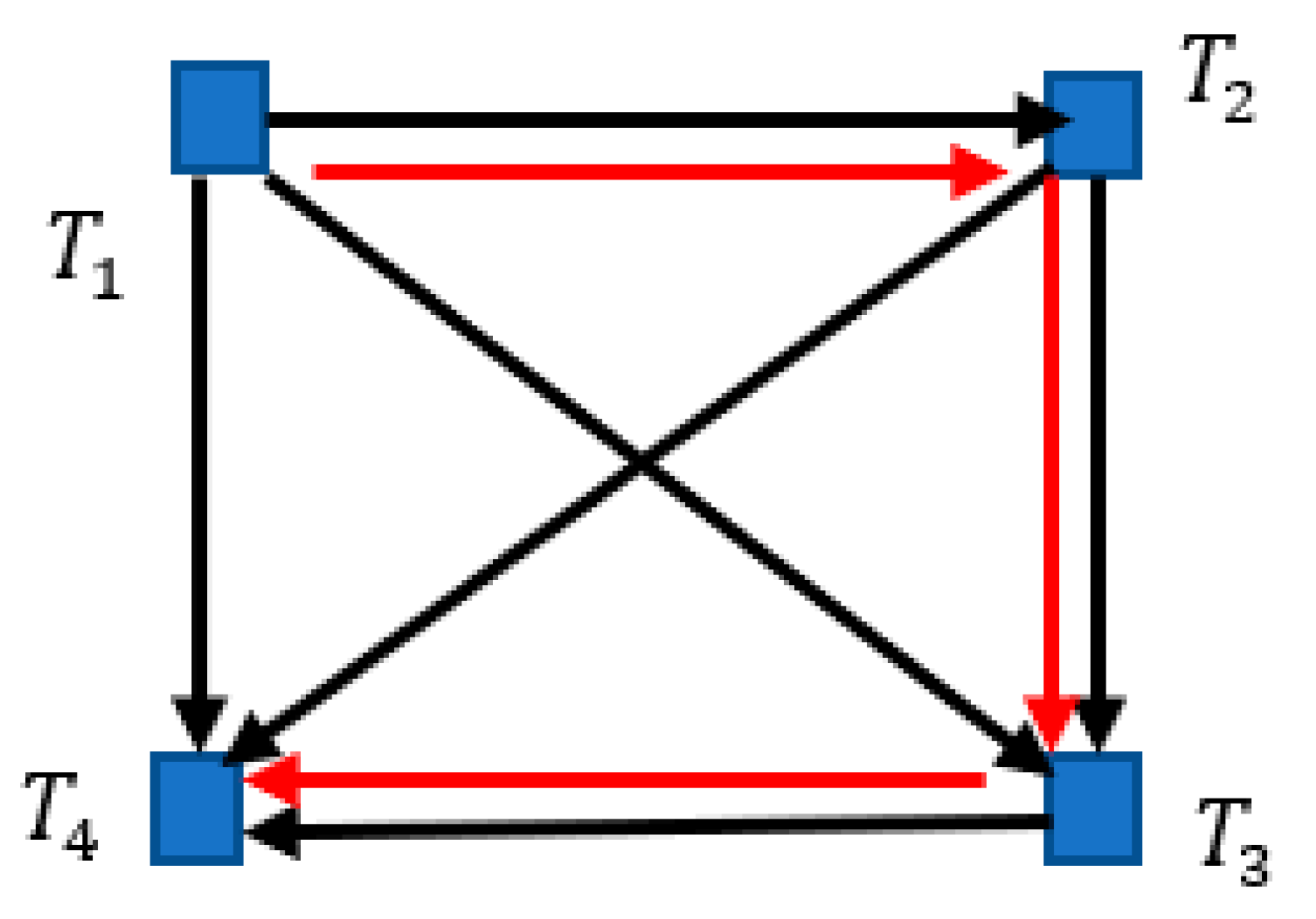
Now consider the graph theory interpretation of thermodynamic processes. Consider n bodies which are in a thermal contact, the temperatures of the bodies are labeled T i i = 1,2 … n . We accept that no pair of bodies is in thermal equilibrium, in other words, T i ≠ T k , when i ≠ k . According to the Clausius statement “heat can never pass from a colder to a warmer body without some other change connected therewith, occurring at the same time” [41]. Thus, directions of the heat transfer give rise to the tournament; we assume that all of the bodies are in thermal contact one with another. For a sake of simplicity consider the system built of four bodies, T 1 > T 2 > T 3 > T 4 as shown in Figure 11.
The graph shown in Figure 10 is a transitive tournament; no cycles of length 3 are recognized in the graph, and the single Hamiltonian path (shown with the red arrows) is inherent for this graph. The generalization for n bodies in thermal contact is straightforward. Thus, re-shaping of the Second Law of Thermodynamics with the graph theory becomes possible as follows: the heat transfer in the system of n bodies T i i = 1,2 … n , T i ≠ T k , when i ≠ k generates a transitive tournament. No cycles with a length of 3 are present in this graph. Thus, no cyclic processes are possible in the system. A single Hamiltonian path is possible in the graph.

2.8. Ramsey theory and general relativity

The Ramsey theory enables a new interpretation of the general relativity. An interval ds between two events in the general relativity is given by Eq. 11:
− d s 2 = g i k d x i d x k
where g i k is the metric tensor (we use the definition of interval adopted in the classical textbook by Landau and Lifshitz [42]). Generally speaking, g i k is the continuous function of the space coordinates and time [42]. We consider the situation of the discrete change in the metric tensor, in other words, the situation when the interval between two events is given by Eqs. 12-13 (discrete Riemann geometry was addressed recently in refs. 43-44):
− d s 2 = g i k ( 1 ) d x i d x k
− d s 2 = g i k ( 2 ) d x i d x k ,
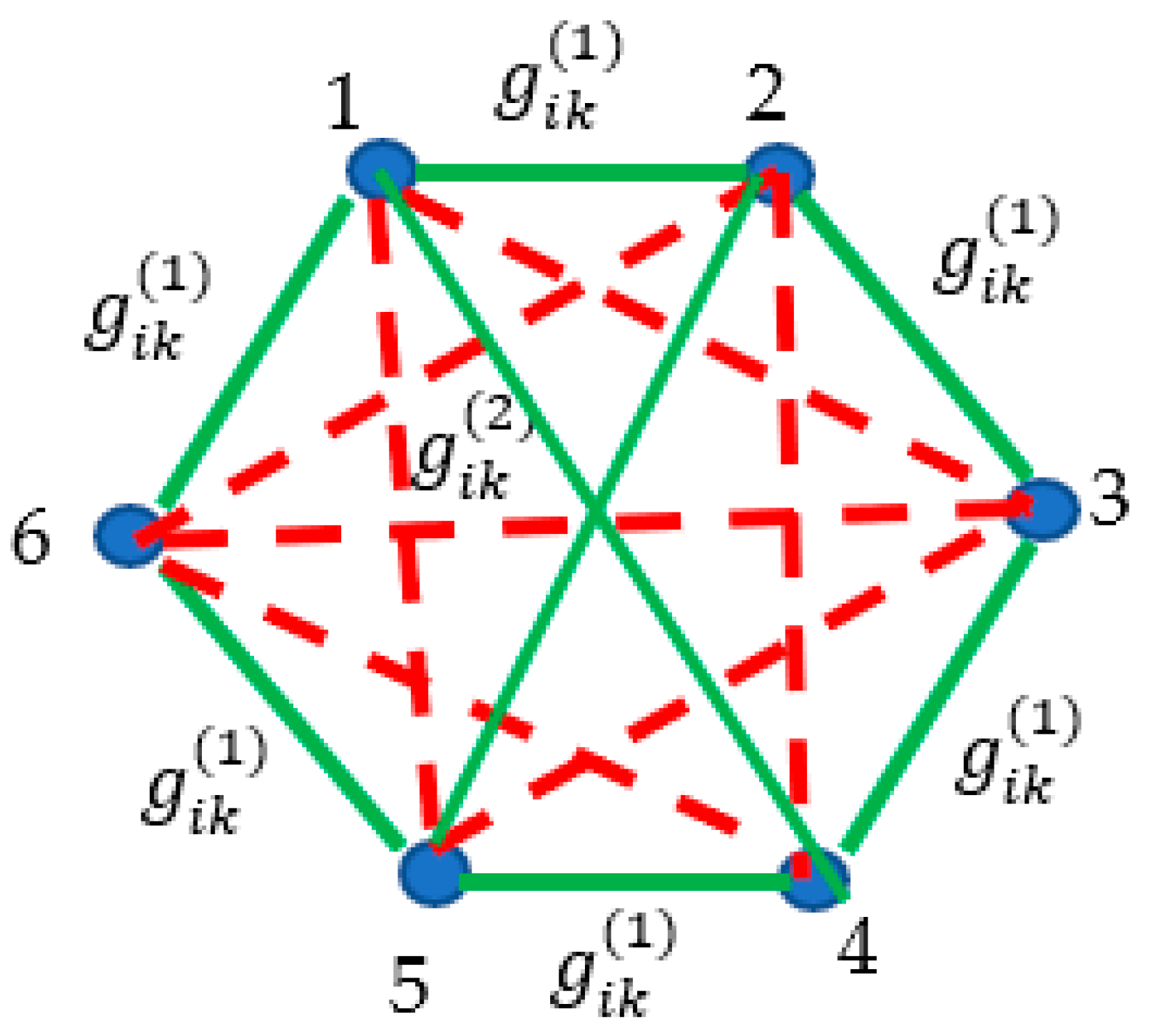
where g i k ( 1 ) and g i k ( 2 ) , are the metric tensors, which are not-equal each to another. For the sake of simplicity, the components of the tensors may be taken as constant. This situation is depicted in Figure 12, in which six events separated by different metric tensors g i k ( 1 ) and g i k ( 2 ) are depicted.
The events form a complete, non-transitive, non-directed graph, shown in Figure 12.Let us pose the following fundamental question: what is the minimal number of physical events providing the appearance of triangles within the events’ map, interconnected by the same metric tensor ( g i k ( 1 ) or g i k ( 2 ) ) ? The answer to this question is again supplied by the Ramsey theory: R 3,3 = 6 . Indeed, in the events’ map presented in Figure 12, red triangles “135” and “246” corresponding to the events connected by the metric tensor g i k ( 2 ) are recognized.

2.9. Graph theory and simultaneous events in classical physics and relativity: the Ramsey theory and causality

We address now the Ramsey interpretation of the notion of simultaneity. Consider five events which occurred in the given frame of references. Two kinds of time relationship between the events are possible: the first relationship occurs when the events occurred non-simultaneously, i.e. Δ τ ≠ 0 takes place, where Δ τ is the time span between the events (we consider now the classical meaning of simultaneity of events; the relativistic extension of the Ramsey approach to simultaneity of events will be treated immediately below). These events are connected in Figure 13 with the red line. The second situation takes place when the events are simultaneous, i.e. Δ τ = 0 .These events are connected with the green line (as shown in Figure 13). Let us address the following question: what is the minimal set of events in which three events took place simultaneously ( Δ τ = 0 ) or three events occurred non-simultaneously ( Δ τ ≠ 0 ) ? Simultaneity of events is the transitive property in classical physics (the relativistic extension of the problem is more complicated and it will be treated below). The answer to this question again is supplied by the Ramsey theory, and it is formulated as follows: what is the minimal transitive Ramsey R t r 3,3 ? The answer to this question was addressed in Section 2.1 and it is R t r 3,3 = 5 (see ref. 11). Indeed, we recognize in the example illustrated with Figure 13, that in the set built of five events, in which the relationships “to be simultaneous” and “to be non-simultaneous” are necessarily present, we find a triad of simultaneous events connected with green lines. The triad of simultaneous events appears as a green triangle in Figure 13.
This fact imposes the restrictions on the causality of the aforementioned events. The events forming the green triangle in Figure 13 cannot influence one another.
Let us consider the relativistic extension of the aforementioned approach. The special relativity-based generalization is trivial: the synchronization of clocks with a light beam. should be carried out [42,45]. This will reduce the situation to that presented in Figure 13. Synchronization of clocks in the general relativity is a more complicated problem [42,45]. In the general theory of relativity, proper time elapses differently even at different points of space in the same reference system [45]. This means that the interval of proper time between two events occurring at some point in space, and the interval of time between two events simultaneous with these at another point in space, are in general different from one another. The time difference between two events, occurring at infinitely near points is given by:
Δ τ = − g 0 i d x i g 00 , i = 1,2 , 3 ,  
where g i k is the metric tensor. Eq. 14 enables synchronization of clocks in any infinitesimal region of space. Carrying out a similar synchronization from the given point, we can synchronize clocks, i.e. we can define simultaneity of events, along any open curve. However, synchronization of clocks along a closed contour turns out to be impossible in general; indeed, starting out along the contour and returning to the initial point, we would obtain for Δ τ a value different from zero [45,46]. Thus, it is impossible to synchronize clocks over all space. The exceptional cases are those reference systems in which all the components of the metric tensor g o i are equal to zero (i.e. so called the time-orthogonal coordinate systems). However, in any gravitational field it is possible to choose the reference system so that the three components of the metric tensor g o i are equal to zero [45,46]; thus, making a complete synchronization of clocks possible. Simultaneity is transitive if, and only if, a space-time is time-orthogonal. Thus, the graph analysis supplied in Figure 13 will apply only to the time-orthogonal coordinate systems. In these systems, the aforementioned conclusions arising from the Ramsey-theory-based analysis remain true.

2.10. Irreversible processes in the relativity: the graph theory analysis

Now consider the relativistic generalization of the thermodynamic processes already considered in Section 2.7. Consider the chain of the irreversible thermodynamic processes, depicted in Figure 14. We define now the processes as “irreversible” when they create new entropy, denoted S [46,47]. The hierarchy of entropies, supplied by Eq. 15 is assumed:
S 3 > S 4 > S 5 > S 1 > S 2
In this case, we obviously deal with the directed transitive tournament (see Section 2.6). Therefore no cycles are present in the graph. The Hamiltonian path inherent for this tournament is shown with red arrows. Now we are interested in the relativistic analysis of this graph. Entropy of the physical system is relativistic invariant [48]. Thus, the ordering of the graph with entropy is also relativistic invariant, hence the Hamiltonian path is relativistic invariant. Thus, an important theorem is proved for any set of states in the phase space of a physical system, between which irreversible processes are possible, namely: the Hamiltonian path of the tournament emerging from the graph uniting these states is a relativistic invariant.

4. Discussion

The concepts of modern mathematics turn out to be extremely useful for understanding the physical reality [49,50]. Galileo Galilei stated that the book of nature is “written in the language of mathematics” and Eugene Wigner stressed the “unreasonable effectiveness of mathematics in physical sciences” [50]. Tegmark suggested that our physical reality is a pure mathematical structure [49]. That is, the physical universe is not merely described by mathematics, but is mathematics itself [49]. As an example, the physical Universe may be seen as a hologram [51]. The classical example of this kind of physical thinking is the identification of gravity with the geometry of time-space continuum in the general relativity. We propose to view the physical reality as a graph and suggest the application of the graph theory to physical problems. Thus, notions of mathematical logic, such as transitivity and intransitivity, start to play a decisive role in the treatment of physical problems.
In a majority of physical problems, various kinds of fundamental relationships between physical bodies are present; these relationships may be: attraction and repulsion between physical objects, simultaneous and non-simultaneous events in the special and general relativity, etc. This fact makes possible the implementation of the Ramsey theory to the analysis of physical systems. The Ramsey theory, named after the British mathematician and philosopher Frank P. Ramsey, is a branch of combinatorics that focuses on the appearance of order in a substructure, given a structure of a known size [8,9,10]. Thus, the problem may be formulated as follows: consider a physical system in which repulsions and attractions between the bodies are present. How large must the addressed system be to guarantee the appearance of triads of bodies interconnected by attractive and repulsive force? The answer supplied by the Ramsey theory is R 3,3 = 6 . However, when the kind of interactions is specified, the possible transitivity/intransitivity of these interactions should be considered. And this is the case when Coulomb electrostatic interactions between point electrical charges are addressed. When electrical charges of various signs are involved in these interactions, they are intransitive, and no monochromatic triangle corresponding to attractions will appear in the complete graph representing Coulomb interactions between point charges. Dynamic quantum interactions between electrons may be non-transitive, this is the case when the Cooper pairing of electrons is treated. We addressed several examples in which the Ramsey analysis of the physical system is useful, including the relativity and thermodynamics problems.
The notions of mathematical logic occupy a central place in the Ramsey theory, thus these notions also are of primary importance for the Ramsey-based analysis of physical problems. In particular, consideration of the physical properties becomes extremely important for the analysis of physical problems. The deep treatment of the analogy between transitivity of the heat transfer and the simultaneity of events in the general relativity was carried out in ref. 45. It becomes extremely important for the Ramsey analysis of transitive and non-transitive graphs, representing physical problems; the transitive and non-transitive Ramsey numbers are different [11]. Applications of the Ramsey theory to the analysis physical problems are rare [52,53]; we demonstrate the possibility of these applications in the various sub-fields of fundamental physics.

5. Conclusions

The ideas of discrete mathematics become ubiquitous in the analysis of physical systems. We demonstrate that methods supplied by the graph theory are applicable for the analysis of fundamental physical problems, in particular we focus on the application of the Ramsey theory to discrete physical systems and processes. Interactions between physical bodies may be very generally classified as repulsive and attractive. This makes possible the formulation of the typical Ramsey-shaped question: how large should a physical system be in order to provide the appearance of triads of bodies/particles interconnected by repulsion or attraction? An answer to this question has a fine structure: the interactions may be transitive and non-transitive (and it is also possible that bodies/particles do not interact). Coulomb interactions between point charges may be transitive or intransitive, depending on the signs of electric charges, irrespective of the spatial location of the charges. On the other hand, static interactions between electrical and magnetic dipoles may be transitive and non-transitive, depending on their mutual spatial orientation. The transitive/intransitive Ramsey number, describing Coulomb (or Coulomb-like) interactions between points charges/effective charges equals three, i.e. R t r a n s , i n t r a n s 2,3 = 3 , whereas R t r a n s , i n t r a n s 3,3 does not exist. Thus, no monochromatic triangle corresponding to attractions will appear in the complete graph representing Coulomb interactions between point electrical charges. The quantum interactions between electrons may be non-transitive and this is the case when the Cooper or Kohn-Luttinger pairing of electrons is considered.
The non-transitive Ramsey number R 3,3 = 6 is applicable for the graph describing static interactions between electric and magnetic dipoles. This result supplies an additional insight into the Ising problem, when interaction between magnetic dipoles is considered, and suggests an explanation to the abundance of cubic FCC lattices among the physical systems built of electric or magnetic dipoles. FCC lattices in this case do not necessarily contain monochromatic triangles, in which only attractive or repulsive interactions are present; whereas, hexagonal lattices necessarily contain such statically non-equilibrium triangles. It should be mentioned that dynamically stable three-body systems, in which only attractive (gravitational) interactions are present, are well-known in astrophysics and should be clearly distinguished from the static ones [54]
Considering the triple interaction problem, i.e. allowing for the bodies/particles attraction, repulsion and zero interaction, gives rise to the three-color Ramsey problem, the Ramsey number for this problem is R 3,3 , 3 = 17 .
The Ramsey approach may be applied to the analysis of mechanical systems, when actual (i. e. emerging from the Hamilton principle) and virtual paths between the states in the configurational space are taken into account. In this case the Ramsey number is R 3,3 = 6 . Thus, in the graph built of the six vertices, representing C-points in the configurational space and interconnected by actual and virtual paths, cycles of actual or virtual paths will necessarily appear. These cycles may correspond to actual or virtual motions of the C-point in the configurational space. Thus, the evolution of any mechanical system may be represented with the Ramsey graph. The Ramsey theory enables reconsideration of the concept of “simultaneity” in classical mechanics and relativity. In classical mechanics, simultaneity is transitive; thus, in the set built of five events, in which the relationships “to be simultaneous” and “to be non-simultaneous” are present, we necessarily find the triad of simultaneous or non-simultaneous ones. This stems from the fact that the transitive Ramsey number R t r 3,3 = 5 . Triads of “simultaneous graph vertices” in this case represent events which cannot influence each other. In turn, simultaneity is transitive in the general relativity only if a space-time is time-orthogonal (i.e. we mean the reference systems in which all the components of the metric tensor g 0 i i = 1,2 , 3 are equal to zero). In these systems, again in the set built of five events, we necessarily find the triad of simultaneous or non-simultaneous ones. Graph theory is extremely useful for the analysis of the chains of irreversible processes (whether mechanical or thermodynamic). These chains form transitive tournaments; thus, no cycles of length 3 are possible in these directed graphs. Only one Hamiltonian path is possible in these graphs, and this path is a relativistic invariant for the directed graphs ordered according to the entropies of discrete thermodynamic states. Restrictions inherent to the Ramsey theory should be considered. Firstly, the results supplied by the Ramsey theory are non-constructive: they may show that some sub-structure exists, but they give no process for finding this structure (other than brute-force search). Secondly, the Ramsey theory states that sufficiently large objects must necessarily contain a given sub-structure, often the proof of these results requires these objects to be enormously large, giving rise to bounds that grow exponentially. Anyway, the Ramsey approach enables a fresh glance on the physical systems and processes seen as discrete entities and reshaping of fundamental physical problems with the notions of mathematical logic.

Author Contributions

Conceptualization, E. B. and N.S.; methodology, E. B.; N. S.; M. F. and S. S.; formal analysis, E. B.; N. S.; M. F. and S. S; investigation, E. B.; N. S.; M. F. and S. S.; writing—original draft preparation, E. B.

Funding

This research received no external funding.

Data Availability Statement

Not applicable.

Acknowledgments

The authors are thankful to Yelena Bormashenko for her kind help in preparing this paper. The Authors are thankful to Professor O. Gendelman for extremely useful discussions.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Bondy, J. A.; Murty, U. S. R. Graph Theory with Applications, North Holland, New York, USA, 1976.
  2. Trudeau, R. Introduction to graph theory, Dover Publications, New York, 1993, USA.
  3. Nowotny, T.; Requardt, M. J. Dimension theory of graphs and networks. J. Phys. A: Math. Gen. 1998, 31, 2447.
  4. Nowotny, T.; Requardt, M. Pregeometric concepts on graphs and cellular networks as possible models of space-time at the Planck-scale. Chaos, Solitons & Fractals 1999, 10 (2–3), 469-481.
  5. Wouters, J.; Giotis, A.; Kang, R.; Schuricht, D.; Fritz, L. Lower bounds for Ramsey numbers as a statistical physics problem. J. Stat. Mech. 2022, 2022, 0332[6] F. P. Ramsey, On a Problem of Formal Logic. In: Gessel, I., Rota, GC. (eds) Classic Papers in Combinatorics. Modern Birkhäuser Classics. Birkhäuser Boston 2009, pp. 264-286. [CrossRef]
  6. Katz, M.; Reimann, J. An Introduction to Ramsey Theory: Fast Functions, Infinity, and Metamathematics, Student Mathematical Library Volume: 87; 2018; pp. 1-34.
  7. Fujita S., C. Magnant, K. Ozeki, Rainbow Generalizations of Ramsey Theory: A Survey. Graphs and Combinatorics 26 (2010) 1–30.
  8. Graham, R. L.; Spencer, J. H. Ramsey Theory, Scientific American, 7 (1990) 112-117.
  9. Graham, R.; Butler, S. Rudiments of Ramsey Theory (2nd ed.). American Mathematical Society, Providence, Rhode Island, USA, 2015, pp. 7-46.
  10. Graham, R, L.; Rothschild, B. L.; Spencer, J. H.Ramsey theory, 2nd ed., Wiley-Interscience Series in Discrete Mathematics and Optimization, John Wiley & Sons, Inc., New York, A Wiley-Interscience Publication, 1990, pp. 10-110.11.
  11. Kotov, V. N.; Uchoa, B.; Pereira, V.M., Guinea, F.; Castro Neto, A, H. Electron-Electron Interactions in Graphene: Current Status and Perspectives, Rev. Mod. Phys. 2012, 84, 1067.
  12. Weeks, J. D.; Chandler, D.; Andersen, H. C. Role of Repulsive Forces in Determining the Equilibrium Structure of Simple Liquids, J. Chem. Phys. 1971, 54, 5237.
  13. Choudum, S. A.; Ponnusamy, B. Ramsey numbers for transitive tournaments, Discrete Mathematics 1999, 206, 119–129.
  14. Erbil, H. Y. Solid and Liquid Interfaces, Blackwell Publishing, Oxford, UK, 2006.
  15. Israelachvili, J. Intermolecular and Surface Forces, 3rd Ed., Elsevier, Amsterdam, 2011.
  16. Jackson, D. Classical Electrodynamics Third Edition, 3rd ed. Wiley, New York, 1998.
  17. Brush, S. G. History of the Lenz-Ising Model, Rev. Mod. Phys. 1967, 39, 883.
  18. Bramwell, S. T.; Gingras, M. J. P. Spin Ice State in Frustrated Magnetic Pyrochlore Materials, Science 2001, 294 (5546): 1495–1501.
  19. Zhang, S.; Li, J.; Gilbert, I.; Bartell, J.; Erickson, M. J.; Pan, Y.; Lammert, P. E.; Nisoli, C.; Kohli, K. K.; Misra, R.; Crespi, V. H.; Samarth, N.; Leighton, C.; Schiffer, P. Perpendicular Magnetization and Generic Realization of the Ising Model in Artificial Spin Ice, Phys. Rev. Lett. 2012, 109, 087201.
  20. Zhang, S.; Gilbert, I.; Nisoli, C.; Chern, G-W.; Erickson, M. J.; O’Brien, L.; Leighton, C.; Lammert, P.E.; Crespi, V. H.; Schiffer, P. Crystallites of magnetic charges in artificial spin ice, Nature 2013, 500, 553-557.
  21. Janssen, T. The Magnetic Structure of an FCC. Spin Lattice System with Exchange and Dipolar Interactions. Phys. kondens. Materie 1972, 15, 142-157.
  22. Siddharthan, R.; Shastry, B. S.; Ramirez, A. P.; Hayashi, A.; Cava, R. J.; Rosenkranz, S. Ising Pyrochlore Magnets: Low-Temperature Properties, “Ice Rules,” and Beyond, Phys. Rev. Lett. 1999, 83, 1854.
  23. Melko, R. G.; den Hertog, B. C.; Gingras, M. J.P. Long-Range Order at Low Temperatures in Dipolar Spin Ice. Phys. Rev. Lett. 2001, 87, 067203.
  24. Ruff, J. P.C; Melko, R. G.; Gingras, M, J, P. Finite-Temperature Transitions in Dipolar Spin Ice in a Large Magnetic Field, Phys. Rev. Lett. 2005, 95, 097202.
  25. Khan, N.; Prishchenko, D.; Skourski, Y.; Mazurenko, V. G.; Tsirlin, A. A. Cubic symmetry and magnetic frustration on the fcc spin lattice in K2IrCl6, Phys. Rev. B, 2019, 99, 144425.
  26. Axilrod, B. M. Triple-Dipole Interaction. II. Cohesion in Crystals of the Rare Gases, J. Chem. Phys. 1951, 19, 724.
  27. Singh, A. N.; Dyre, J. C.; Pedersen U. R. Solid–liquid coexistence of neon, argon, krypton, and xenon studied by simulations. J. Chem. Phys. 2021, 154, 134501.
  28. Cooper, L. N. Bound electron pairs in a degenerate Fermi gas. Phys. Rev. 1956, 104 (4), 1189–1190.
  29. Fujita, S.; Ito, K.; Godoy, S.Quantum Theory of Conducting Matter. 2009, Springer Publ. Berlin, Ge., pp. 15–27.
  30. Kohn, W.; Luttinger, J. M. New Mechanism for Supeconductivity, Phys. Rev. Lett. 1965, 15, 524 .
  31. Friedel, J. The distribution of electrons round impurities in monovalent metals. Philos. Mag. 1952, 43, 153-189.
  32. Lifshitz E. M.; Pitaevskii, L. P. Statistical Physics (Part 2), Ch. 5, pp. 153-219, Pergamon Press, Oxford, 2002.
  33. Nandkishore, R.; Thomale, R.; Chubukov, A.V. Superconductivity from weak repulsion in hexagonal lattice systems. Phys. Rev. B 2014, 89, 144501.
  34. Herbut, I. F.; Juričić, V.; Roy, B. Theory of interacting electrons on the honeycomb lattice. Phys. Rev. B 2009, 79, 085116.
  35. Radziszowski, S. Small Ramsey numbers, The Electronic Journal of Combinatorics, 2021, 1000, MR1670625.
  36. Lanczoc C. The Variational Principles of Mechanics, 4th Ed. Dover Publications, University of Toronto Press, Canada, 1970.
  37. Cline, D. Variational Principles in Classical Mechanics, University of Rochester River Campus Libraries, Rochester, USA, 2018.
  38. Lan, Y.; Cvitanovic, P. Variational method for finding periodic orbits in a general flow. Phys. Rev. E. 2004, 69, 016217.
  39. Artuso, R.; Aurell, E.; Cvitanovic, P. Recycling of strange sets: I. Cycle expansions, Nonlinearity 1990, 3, 325.
  40. H. Rugh, The correlation spectrum for hyperbolic analytic maps, Nonlinearity 1992, 5, 1237. 41. Clausius, R. Über eine veränderte Form des zweiten Hauptsatzes der mechanischen Wärmetheorie. Annalen der Physik. 1854, 93 (12), 481–506.
  41. Landau, L. D.; Lifshitz, E. M. The Classical Theory of Fields. Vol. 2 (4th ed.). Butterworth-Heinemann, Oxford, UK, 1975.
  42. Dimakis, A.; Müller-Hoissen, F. Discrete Riemannian geometry. J. Math. Phys. 1999, 40, 1518.
  43. Bochniak A.; Sitarz, A.; Zalecki, P. Riemannian geometry of a discretized circle and torus. Symmetry, Integrability, Geometry: Methods & Appl. 2020, 16, 143.
  44. Zheng, Z.; Chen, P. Zeroth Law of Thermodynamics and Transitivity of Simultaneity, Int. J. Theor. Physics 1997, 36 (10), 2153-2159.
  45. Landau, L. D. Lifshitz, E.M. Statistical Physics, 3rd ed.; Course of Theoretical Physics; Elsevier: Oxford, UK, 2011; Volume 5.
  46. Shroeder, D. V. Thermal Physics, Addison Wesley – Longman, San Francisco, pp. 125-129.
  47. Tolman, R.C. Relativity, Thermodynamics and Cosmology; Oxford University Press: Oxford, 1934.
  48. Tegmark, M. Our Mathematical Universe, Alfred A. Knopf, New York, USA, 2014.
  49. Wigner, E. Symmetries and Reflections: Scientific Essays. Indiana University Press, Bloomington, USA, 1970.
  50. Bekenstein, J.D. Information in the holographic universe. Sci. Am. 2003, 289, 58–65.
  51. Wouters, J.; Giotis, A.; Kang, R.; Schuricht, D.; Fritz, L. Lower bounds for Ramseynumbers as a statistical physics problem. J. Stat. Mech. 2022, 2022, 0332.
  52. Shvalb, N.; Frenkel, M. Shoval, S.; Bormashenko, Ed. Dynamic Ramsey Theory of Mechanical Systems Forming a Complete Graph and Vibrations of Cyclic Compounds, preprints, 2022. [CrossRef]
  53. Mikkola, S. (2008). Dynamics and Stability of Triple Stars. In: Hubrig, S., Petr-Gotzens, M., Tokovinin, A. (eds) Multiple Stars Across the H-R Diagram. ESO Astrophysics Symposia. Springer, Berlin, Heidelberg.
Preprints 67612 g001
Figure 1. System built of six interacting bodies is represented. Red lines depict attractive interaction between the bodies; green lines depict repulsive interactions between the bodies.
Figure 1. System built of six interacting bodies is represented. Red lines depict attractive interaction between the bodies; green lines depict repulsive interactions between the bodies.
Preprints 67612 g001
Preprints 67612 g002
Figure 2. A. System built of five point electrical charges is represented. Red lines depict attractive Coulomb interaction between the bodies; green lines depict repulsive Coulomb interactions between the point charges. B. Coulomb interactions in the system of the three point charges of the same sign are shown. C. Coulomb interactions in the system of the three point charges of the different signs are shown.
Figure 2. A. System built of five point electrical charges is represented. Red lines depict attractive Coulomb interaction between the bodies; green lines depict repulsive Coulomb interactions between the point charges. B. Coulomb interactions in the system of the three point charges of the same sign are shown. C. Coulomb interactions in the system of the three point charges of the different signs are shown.
Preprints 67612 g002
Preprints 67612 g003
Figure 3. Geometric relations in a schematic dipole-dipole interaction are shown; p → 1 and p → 2 are permanent dipole moments, r is the separation between the dipoles, θ 1 and θ 2 are the angles of each dipole in polar coordinates, and φ is the rotation angle around the axis; all three angles describe the orientation of the two dipoles to each other.
Figure 3. Geometric relations in a schematic dipole-dipole interaction are shown; p → 1 and p → 2 are permanent dipole moments, r is the separation between the dipoles, θ 1 and θ 2 are the angles of each dipole in polar coordinates, and φ is the rotation angle around the axis; all three angles describe the orientation of the two dipoles to each other.
Preprints 67612 g003
Preprints 67612 g004
Figure 4. Sketch illustrating the non-transitive nature of interaction between electric dipoles is shown. A. Dipole p → 1 , attracts dipole p → 2 , dipole p → 2 attracts dipole p → 3 , whereas dipole p → 1 repels dipole p → 3 . B. All of the dipoles attract one another.
Figure 4. Sketch illustrating the non-transitive nature of interaction between electric dipoles is shown. A. Dipole p → 1 , attracts dipole p → 2 , dipole p → 2 attracts dipole p → 3 , whereas dipole p → 1 repels dipole p → 3 . B. All of the dipoles attract one another.
Preprints 67612 g004
Preprints 67612 g005
Figure 5. System of dipoles is shown. Red lines depict attractive interactions; green lines depict repulsive interactions between the dipoles (see Eq. 5). The spatial orientation of the dipoles is not represented exactly in the scheme; the value of the rotational angle φ is neglected.
Figure 5. System of dipoles is shown. Red lines depict attractive interactions; green lines depict repulsive interactions between the dipoles (see Eq. 5). The spatial orientation of the dipoles is not represented exactly in the scheme; the value of the rotational angle φ is neglected.
Preprints 67612 g005
Preprints 67612 g006
Figure 6. System of magnetic dipoles μ → resembling the system of electric dipoles shown in Figure 5 is shown (see Eq. 6 and Eq. 7). Red lines depict attractive interactions; green lines depict repulsive interactions between the dipoles. The nature of the interaction depends on the mutual orientation of magnetic dipoles (see Eq. 7). The spatial orientation of magnetic dipoles is not represented exactly in the scheme; the value of the rotational angle φ is neglected.
Figure 6. System of magnetic dipoles μ → resembling the system of electric dipoles shown in Figure 5 is shown (see Eq. 6 and Eq. 7). Red lines depict attractive interactions; green lines depict repulsive interactions between the dipoles. The nature of the interaction depends on the mutual orientation of magnetic dipoles (see Eq. 7). The spatial orientation of magnetic dipoles is not represented exactly in the scheme; the value of the rotational angle φ is neglected.
Preprints 67612 g006
Preprints 67612 g007
Figure 7. Scheme of interactions of dipoles in the (100) plane of the FCC cubic system. Dipoles are shown with blue circles; the central dipole is displaced from its true location for the sake of clarity. Red lines depict attractive interactions; green lines depict repulsive interactions between the dipoles. No monochromatic triangle is recognized.
Figure 7. Scheme of interactions of dipoles in the (100) plane of the FCC cubic system. Dipoles are shown with blue circles; the central dipole is displaced from its true location for the sake of clarity. Red lines depict attractive interactions; green lines depict repulsive interactions between the dipoles. No monochromatic triangle is recognized.
Preprints 67612 g007
Preprints 67612 g008
Figure 8. System built of six bodies is represented. Red lines depict attractive interaction between the bodies; green lines depict repulsive interactions; yellow lines correspond to the zero interaction between the bodies (the bodies do not interact).
Figure 8. System built of six bodies is represented. Red lines depict attractive interaction between the bodies; green lines depict repulsive interactions; yellow lines correspond to the zero interaction between the bodies (the bodies do not interact).
Preprints 67612 g008
Preprints 67612 g009
Figure 9. Map depicting five states in the configuration space is shown. Red lines correspond to the true evolution of the system, i.e. providing δ S = 0 ( a c t u a l   p a t h s ) ; black lines illustrate virtual pathways in the configurational space, δ S ≠ 0 along black pathways (virtual paths).
Figure 9. Map depicting five states in the configuration space is shown. Red lines correspond to the true evolution of the system, i.e. providing δ S = 0 ( a c t u a l   p a t h s ) ; black lines illustrate virtual pathways in the configurational space, δ S ≠ 0 along black pathways (virtual paths).
Preprints 67612 g009
Preprints 67612 g010
Figure 10. Map depicting six states in the configurational space is depicted. Only irreversible transitions between the states are possible. The transitive tournament is shown with black arrows. Red arrows indicate the Hamiltonian path.
Figure 10. Map depicting six states in the configurational space is depicted. Only irreversible transitions between the states are possible. The transitive tournament is shown with black arrows. Red arrows indicate the Hamiltonian path.
Preprints 67612 g010
Preprints 67612 g011
Figure 11. Graph illustrating thermal contact of four bodies is depicted, T 1 > T 2 > T 3 > T 4 is assumed. Black arrows depict the direction of the heat transfer. The graph represents the transitive tournament. Red arrows depict the Hamiltonian path.
Figure 11. Graph illustrating thermal contact of four bodies is depicted, T 1 > T 2 > T 3 > T 4 is assumed. Black arrows depict the direction of the heat transfer. The graph represents the transitive tournament. Red arrows depict the Hamiltonian path.
Preprints 67612 g011
Preprints 67612 g012
Figure 12. The map representing six events is depicted. The events are separated by the intervals supplied by Eqs. 12-13. Green lines correspond to the events separated by the interval, defined by the metric tensor g i k ( 1 ) ; red lines, in turn, correspond to the events separated by the interval, defined by the metric tensor g i k ( 2 ) . Red triangles “135” and “246” are recognized in the map.
Figure 12. The map representing six events is depicted. The events are separated by the intervals supplied by Eqs. 12-13. Green lines correspond to the events separated by the interval, defined by the metric tensor g i k ( 1 ) ; red lines, in turn, correspond to the events separated by the interval, defined by the metric tensor g i k ( 2 ) . Red triangles “135” and “246” are recognized in the map.
Preprints 67612 g012
Preprints 67612 g013
Figure 13. Graph representing five events which took place in the same frame of references is presented. Red lines link events which are non-simultaneous Δ τ ≠ 0 ; green lines link simultaneous events ( Δ τ = 0 ).
Figure 13. Graph representing five events which took place in the same frame of references is presented. Red lines link events which are non-simultaneous Δ τ ≠ 0 ; green lines link simultaneous events ( Δ τ = 0 ).
Preprints 67612 g013
Preprints 67612 g014
Figure 14. Graph representing the chain built of five irreversible processes is shown. Hierarchy of entropies is given by: S 3 > S 4 > S 5 > S 1 > S 2 . Black arrows show the direction of the processes; red arrows demonstrate the Hamiltonian path.
Figure 14. Graph representing the chain built of five irreversible processes is shown. Hierarchy of entropies is given by: S 3 > S 4 > S 5 > S 1 > S 2 . Black arrows show the direction of the processes; red arrows demonstrate the Hamiltonian path.
Preprints 67612 g014
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated