Preprint

Article

Dirac Fermion of a Monopole Pair (MP) Model

Altmetrics

Downloads

801

Views

223

Comments

Samuel Yuguru^*

This version is not peer-reviewed

This preprints belongs to the Topic

Applications of Photonics, Laser, Plasma and Radiation Physics

Abstract

The electron of spin −1/2 is a Dirac fermion of a complex four-component spinor field. Though it is effectively addressed by relativistic quantum field theory (QFT), an intuitive form of the fermion still remains lacking and it is often speculated by Dirac belt trick or its related analogies. In a similar fashion, the interpretation of Dirac fermion by QFT is examined within a recently proposed MP model of a hydrogen atom into 4D space-time. The model consists of clockwise precession of an elliptical MP field mimicking Dirac string and an electron of physical entity in orbit of time reversal. Such dynamics sustains charge conjugate, parity inversion and time reversal symmetry with the transition of the electron to Dirac fermion being consistent with Dirac belt trick, quantum mechanics and Lie group. The electron path is solenoidal to on-shell momentum of circular Bohr obit (BO), and by disturbance, this levitates and dissects the MP field into n-dimensions of Minkowski space-time. Contraction of BOs towards the vertices generates Euclidean space-time to a spherical MP model. These outcomes are compatible with QFT such as Dirac field theory and its related components like wave function collapse, quantized Hamiltonian, non-relativistic wave function, Weyl spinor, Lorentz transformation and electroweak symmetry breaking mechanism. The model though speculative, it could become important towards defining the fundamental state of matter subject to further examinations by conventional methods in both experiment and theoretical applications.

Keywords:

Submitted:

13 July 2024

Posted:

15 July 2024

Read the latest preprint version here

Alerts

Abstract

Keywords:

Subject: Physical Sciences - Theoretical Physics

1. Introduction

At the fundamental level of matter, particles are described by wave-particle duality, charges and their spin property. These properties are revealed from light interactions and are pursued by the application of relativistic QFT [1,2]. The theory of special relativity defines lightspeed, c to be constant in a vacuum and its particle-like property consist of massless photon of spin 1 with a neutral charge. Any differences to photon’s spin, charge and mass-energy equivalence by,

m = E / c^{2}

provide the inherent properties of matter particles such as fermions of spin ±1/2 and this is termed causality [3,4]. Based on QFT, particles appear as excitation of fields permeating space at less than lightspeed. Within the atom, the electron is a fermion and its position is defined by non-relativistic Schrödinger’s wave function,

ψ

of probabilistic distribution [5]. A level of indetermination is associated with the observation of its spin-charge property, whereas the wave-particle duality is depended on the instrumental set-up [6,7]. Based on quantum mechanics interpretation, the atom radiates energy in quantized form,

n h v

of infinitesimal steps. When this is incorporated into QFT, it becomes difficult to imagine wavy form of particles such as electrons freely permeating space without interactions and this somehow collapses to a point at observation [8]. Similarly, the resistive nature of proton decay [9] somehow suggests the preservation of the electron and hence, atom to balance out the charges. While proton decay is an active topic of research, in the meantime, the preferred quest is to make non-relativistic equations become relativistic due to the shared properties of both matter and light at the fundamental level as mentioned above.

Beginning with Klein-Gordon equation [10], the energy and momentum operators of Schrödinger equation,

\hat{E} = i ℏ \frac{\partial}{\partial t}, \hat{p} = - i ℏ \nabla,

(1)

are adapted in the expression,

(ℏ^{2} \frac{\partial^{2}}{\partial t^{2}} - c^{2} ℏ^{2} \nabla^{2} + m^{2} c^{4}) ψ (t, \bar{x}) = 0 .

(2)

Equation (2) incorporates special relativity;

E^{2} = p^{2} c^{2} + m^{2} c^{4}

for mass-energy equivalence;

\nabla

is the del operator in 3D space; ℏ is reduced Planck constant and

i

is an imaginary number;

i = \sqrt{- 1}

. Only one component is considered in Equation (2) and it does not take into account the negative energy contribution from antimatter. In contrast; the Hamiltonian operator;

\hat{H}

of Dirac equation [11] for a free particle is,

\hat{H} ψ = (- i \nabla . a + m β) ψ .

(3)

The

ψ

has four-components of fields,

i

with vectors of momentum,

\nabla

and gamma matrices, α, β represent Pauli matrices and unitarity. The concept is akin to, e⁺ e^– ⟶ 2γ, where the electron annihilates with its antimatter to produce two gamma rays. Antimatter existence is readily observed in both Stern-Gerlach experiment and positron from cosmic rays. The relationship between matter and antimatter at the subatomic level is described by charge conjugation (C), parity inversion (P) and time reversal (T) symmetry. Charge conjugation reverses the charge without changing the direction of the spin vector or momentum of the particle. Only time reversal accounts for changes in the spin direction. Parity is discreet space-time symmetry offered by spatial coordinates and these are invariant under inversion when the charge is reversed. Based on QFT, numerous literatures explore these parameters in order to explain the anomaly of the dominance of matter over antimatter and space-time quantization. The electron dominance over its conjugate pair is explained by 360° rotation, where a positron is generated. Another 360° rotation for a total of 720° rotation and the electron is restored to its original state. The process offers the helical property of the electron as a fermion of fractional spin and is described by so-called Dirac belt trick [13] in an attempt to capture the CPT symmetry. Other related descriptions include Balinese cup trick [14] or Dirac scissors problem [15]. The notion of space-time at singularity, where the electron translates to positron and vice versa is not well defined with respect to CPT symmetry. One way to visualize space-time in 4D is from Klein bottle topology of 2D manifold [16], where spin vector varies within the manifold without a reference point-boundary akin to a sphere. Quantum gravity at singularity is expected to define space-time boundary, where CPT symmetry becomes prominent such as for particles assuming its own antimatter like the electron. Quantization of gravitational field with respect to quantum gravity is predicted by the existence of graviton, a spin 2 particle and it is yet to be positively identified in both high energy physics experiments and gravitational waves emanating from astronomical sources.

In this study, how Dirac fermion is interpretable within a MP model mimicking hydrogen atom of 4D space-time is examined. The orbit of the electron of a charged particle is of time reversal imposed on a clockwise precession of elliptical MP field mimicking Dirac string. These connotations of matter and space-time dynamics somehow transforms the electron into a Dirac fermion of a complex spinor consistent with Dirac belt trick, quantum mechanics and Lie group. The orbit is solenoidal into n-dimensions of both Minkowski and Euclidean space-times by disturbance and this is relevant to the emergence of monopole at the vertex of the MP field. These outcomes appear compatible with Dirac field theory and its associated components like wave function collapse, quantized Hamiltonian, non-relativistic wave function, Weyl spinor, Lorentz transformation and electroweak symmetry breaking mechanism. Though the model is a speculative tool, it is can become important towards defining the fundamental state of matter subject to further examinations by conventional methods.

2. An electron Conversion to a Fermion by Dirac Process

In this section, the transformation of an electron of hydrogen atom type of 4D space to a fermion by Dirac process is examined within a spherical MP model (Figure 1a–d). First the process of Dirac belt trick is demonstrated, where the electron or its particle-hole by ionization balances out the proton charge with conservation assumed. Second, the relevance of the model to basic interpretations of quantum mechanics, QFT and Lie Group are incorporated with a summary offered at the end.

2a. Unveiling Dirac Belt Trick within the Spherical MP Model

The electron’s orbit of time reversal in discrete continuum form of sinusoidal wave is defined by Planck radiation, h. In forward time, the orbit is transformed into an elliptical shape of a MP pair field somewhat mimicking Dirac string (Figure 1a). With clockwise precession, the torque or right-handedness exerted on the MP field shifts the electron of spin up from positions 0 to 4 to assume 360° rotation. Time reversal orbit against clockwise precession allows for maximum twist at the point-boundary or vertex of the MP field at position 4. The electron then flips to spin down mimicking a positron to begin the unfolding process and emits radiation by,

E = n h v

. The positron is short-lived from possible repulsion of the proton and by another 360° rotation from positions 5 to 8, the electron is restored to its original state. These intuitions are relatable to Dirac belt trick at 720° rotation, where the Dirac four-component spinor,

ψ = (\binom{ψ_{0}}{\begin{matrix} ψ_{1} \\ \binom{ψ_{2}}{ψ_{3}} \end{matrix}})

is assigned to positions 0 to 3 and its transposition to positions 4 to 8 at spherical lightspeed. The conjugate pairs of positions, 1, 3 and 5,7 cancels out the charges to form loops of Bohr orbits (BOs). These levitates and translates into n-dimensions of energy levels by disturbance to generate Minkowski space-time (Figure 1b). The emergence of light-cones depict Weyl spinor and singularity at the center is evaded by the electron’s shift at positions, 2 and 6 and is breached by the z-axis of the MP field. For an irreducible spinor field (centered image of Figure 1a–d), gravity is considered a classical force. Additional details on the conceptualization path of the model from electron wave-diffraction is offered elsewhere [17]. Clockwise precession by spherical lightspeed presents an inertia reference frame, λ (Figure 1a) under the conditions,

λ_{\pm}^{2} = λ_{\pm} T r λ_{\pm} = 2 λ_{+} + λ_{-} = 1,

(4)

where the trace function, Tr is the sum of all elements within the model. These elements are pertinent to quantum mechanics, QFT and the Lie group as presented next.

Figure 1. The MP model [17]. (a) In flat space, a spinning electron (green dot) in orbit of sinusoidal form (green curve) is of time reversal. It is normalized to an elliptical MP field (black area) of a magnetic field, B mimicking Dirac string. By clockwise precession (black arrows), an electric field, E of inertia frame, λ is generated. The shift in the electron’s position from positions 0 to 4 at 360° rotation against clockwise precession offers maximum twist. At position 4, the electron flips to a positron to begin the unfolding process from positions 5 to 8 for another 360° rotation to restore the electron to its original state analogous to Dirac belt trick. For the total of 720° rotation, a dipole moment (±) is generated for the spherical model with CPT symmetry sustained for the electron. (b) The BOs are defined by conjugate numbered pairs, 1,3 and 5,7, where cancellation of charges allows for the emergence of angular momentum (purple dotted lines) of spin ±1/2 (navy colored light cones) with vectors aligned to the vertices of the MP field at positions 0 and 4. Levitation of BOs into n-dimensions of Minkowski space-time is by disturbance. These are projected in degeneracy towards the center and by contraction to the vertices of the spherical model as Euclidean space-time. (c) The electron in orbit is tangential to smooth manifold of BO intersecting the MP field and this is relevant to Lie group. With precession stages,

Ω

, at spherical lightspeed the model is polarized to qubits, 0 and ±1 at the vertices of the MP field. The polar coordinates (r, θ, Φ) are attributed to Schrödinger wave function with respect to the electron’s position in space. (d) Topological torus emerges from BO defined by

ϕ

(white loops) and its dissection perpendicularly by

θ

(yellow circles) from intermittent clockwise precession stages of the MP field. Any light-matter interactions are tangential to the electron’s position at the base point of BOs. Levitation of manifolds of BOs into n-dimensions of Minkowski space-time is solenoidal by linearization along the principle axis of the MP field as time axis in asymmetry. Singularity at the center for the light-cone is constrained by electron’s shift at positions, 2 and 6 along horizontal x-y plane of an irreducible spinor field (insert centered image). The embedded terms and equations are explained in the text.

Ω

ϕ

(white loops) and its dissection perpendicularly by

θ

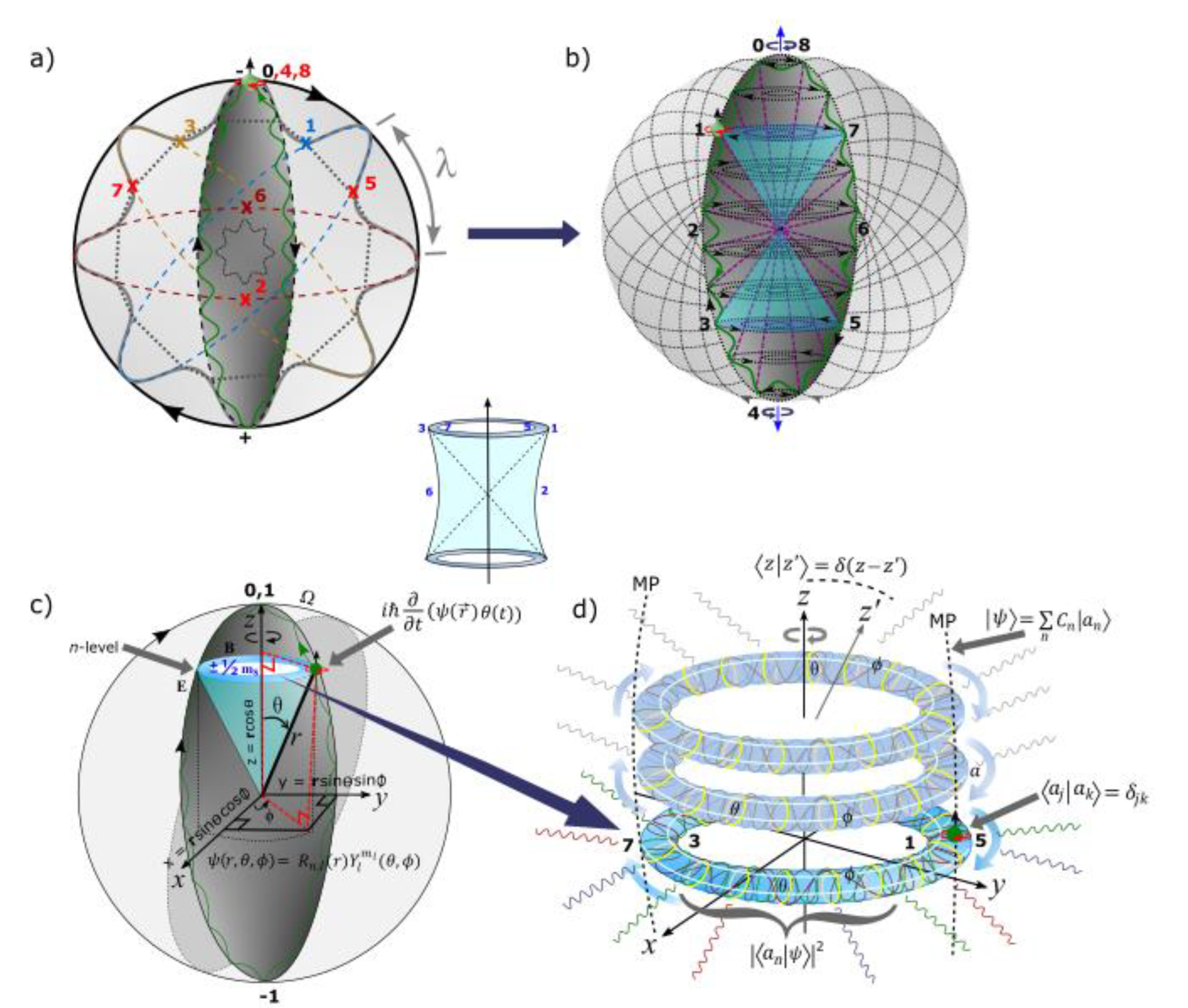
2b. Quantum Mechanics and Dirac Notations

The transformation of the electron to a Dirac fermion within the MP model can further accommodate some basic concepts in quantum mechanics and QFT (Figure 1c,d). Some of them are outlined below in bullet points based on ref. [18].

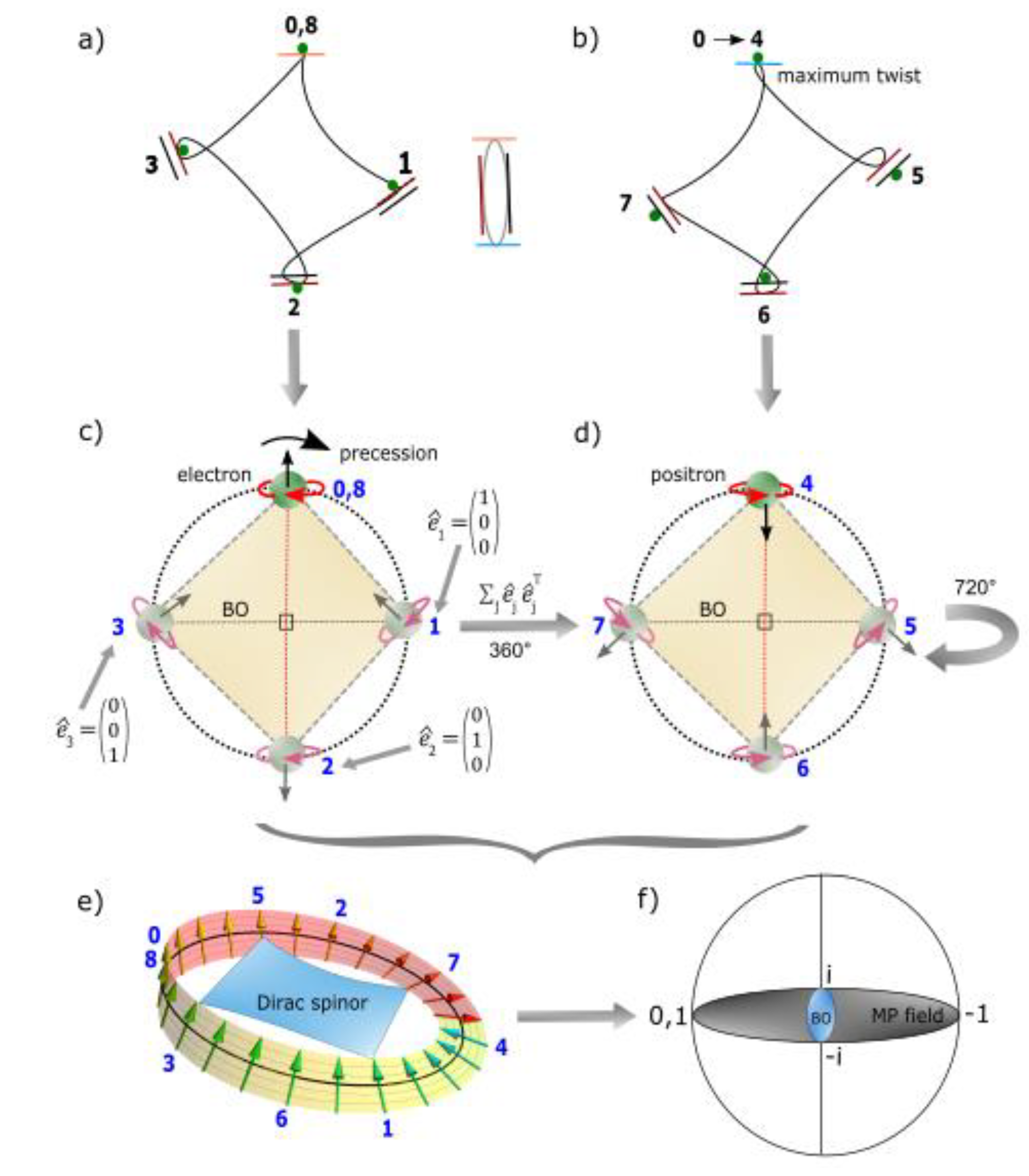
The electron of wave-particle duality obeys de Broglie relationship, $λ = h / m v$ with h assigned to its sinusoidal orbit and mv to BO. It is defined by the wave function, $ψ$ and its orbit of time reversal adheres to the Schrödinger equation, $i ℏ \frac{\partial}{\partial t} (ψ (\vec{r}) θ (t))$ in space-time (Figure 1c) (see also Appendix A for further explanations). Its superposition state (electron-positron pair) in space is linked to BO defined by $ϕ$ and thus, its inner product is, ${⟨ψ| ϕ⟩}^{*} = ⟨ψ| ϕ⟩$ with respect to z-axis. Conjugate charges at positions, 1, 3 and 5 and 7 cancels each other out at spherical lightspeed to form close loops, where the electron is stabilized to generate only either spin up or spin down in its orbit at an energy n-level in accordance with Pauli exclusion principle. At 360° rotation, an electron of spin up is produced and at 720° rotation, a positron of spin down is formed. The loops of BOs are topology construct of differential manifolds into n-levels or n-dimensions by levitation due to disturbance (Figure 1d). In this way, the electron forms a weak isospin, whereas the z-axis mimicking spin up and spin down resembles nuclear isospin.
Both radial and angular wave functions are applicable to the electron, $ψ (r, θ, ϕ) = R_{n, l} (r) Y_{l}^{m_{l}} (θ, ϕ)$ . The radial part, $R_{n, l}$ is attributed to the principal quantum number, n and angular momentum, l of a light-cone with respect to r (Figure 1c). The angular part, $Y_{l}^{m_{l}}$ in degenerate states, ${\pm m}_{l}$ with respect to the z-axis is assigned to the BO defined by both $θ$ and $ϕ$ (Figure 1d).
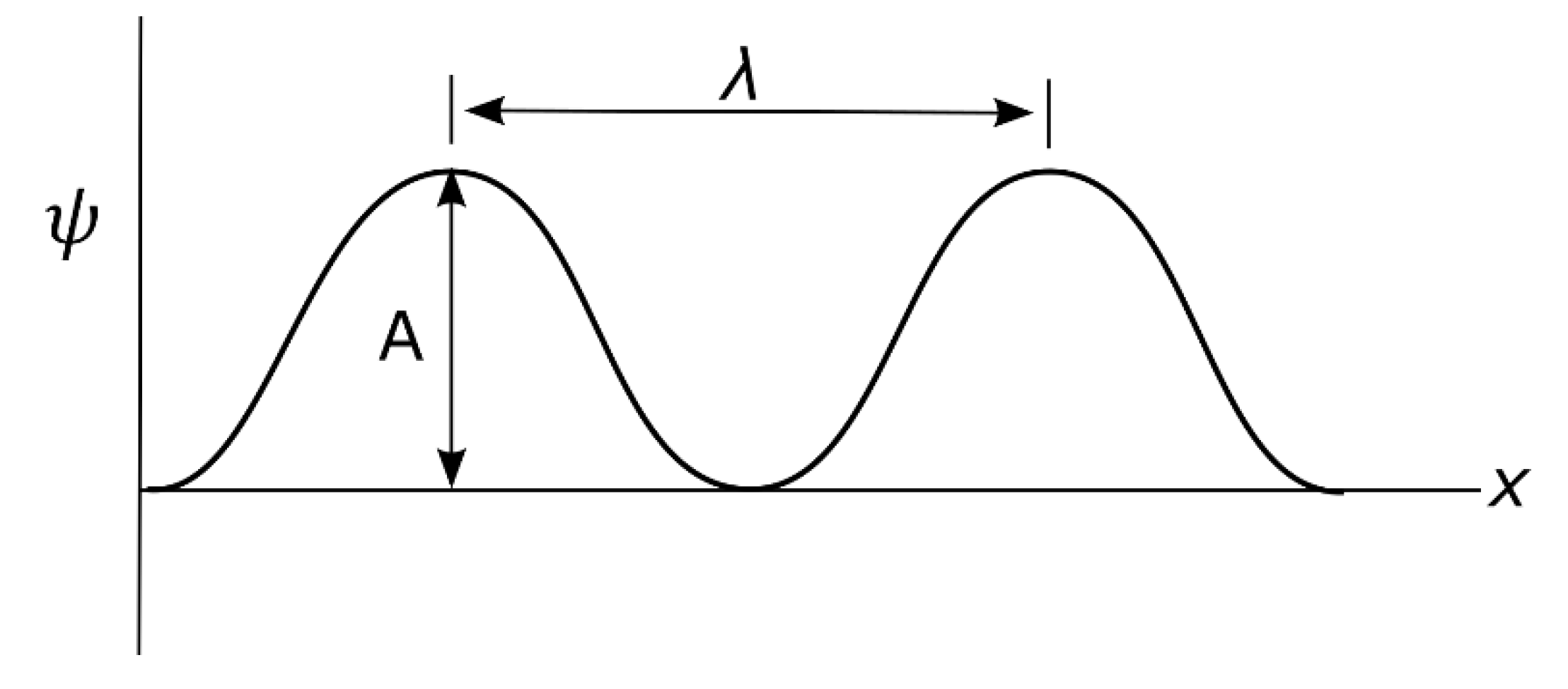
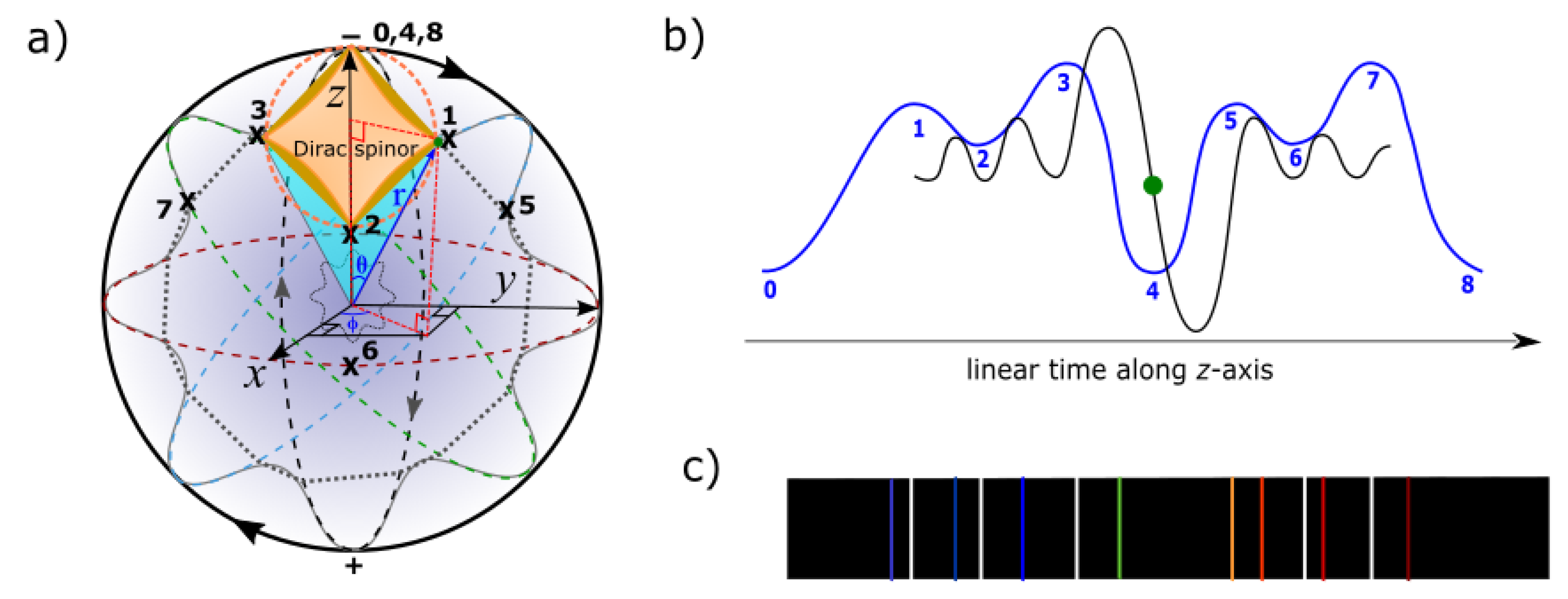
The BO is defined by a constant structure, ɑ and its orthogonal (perpendicular) to z-axis by linearization (Figure 1d). Its link to electron-positron pair is, $⟨a_{j}| a_{k}⟩ = \int d x ψ_{a_{j}}^{*} (x) ψ_{a_{k}} (x) = δ_{j k}$ for continuous derivation by rotation and is relevant to Fourier transform (see also Appendix B). Linear translation for the n-levels along z-axis can relate to the sum of expansion coefficients, $C_{n}$ , where the electron’s position offers an expectant value, $|ψ⟩ = \sum_{n} C_{n} / a_{n}⟩$ . Its probability is of the type, ${⟨a_{n}| ψ⟩}^{2}$ .
The shift in the electron’s position of hermitian conjugates by Dirac process, P(0→8) = $\int_{τ} ψ^{*} \hat{H} ψ d τ$ assumes Hamiltonian space with $τ$ by precession (Appendix B). The complete spherical rotation towards the point-boundary for the polarization states, 0, 1 assumes U(1) symmetry and incorporates Euler’s formula, $e^{i π}$ + 1 = 0 in real space.
Singularity at Planck’s length is assigned to the point-boundary at position 0 and this promotes radiation of the type, $E = n h v$ by the electron-positron transition. Somehow it sustains the principle axis of the MP field as z-axis or nuclear isospin in asymmetry and this sustains ±h at spherical lightspeed.

2c. Lie Group

The geometry of the MP model is relevant to Lie group of differential smooth manifolds and this is attributed to both BO of a circle and the spherical model (Figure 1c). The BO in degeneracy is topological into n-dimensions by levitation due to disturbance. Electron-light interaction appears tangential to the manifolds of BOs of non-abelian and this generates a solenoid with

\nabla . B = μ_{0} ρ

(Figure 1d). At the vertices of the MP field at positions 0 and 4 (Figure 1c), the solenoid is reduced to singularity with

\nabla . B = 0

and the electron is transformed to a monopole. Rotation matrices of the type,

{R r}_{y z} (θ)

and

R_{z x} (θ)

is attributed to the MP field by precession with any shift in z-axis of nuclear isospin trivial,

⟨z| z'⟩ = δ (z - z^{'})

(Figure 1d). The rotation matrix,

R_{x y} (θ)

is assigned to the BO into n-dimensions. These are relevant to describe both integer and half-integer spins such as, 0, 1/2 and 1 towards complete rotation at position 0 at the point-boundary. These attributes are presented in Figure A2 of Appendix B with some examples are explored in here based on refs. [19,20].

Chirality of the electron is described by,

g \in G,

(5)

where g is the electron’s position as subset of the space tangential to the manifolds and G represents the Lie group. For the conjugate numbered pairs, 1, 3 and 5, 7 of BO (Figure 1d), Equation (5) validates the operations,

g_{1,5} + g_{3,7} \in G

(6a)

and

g + (- g) = i,

(6b)

where

i

is spin matrix for both spin ±1/2 (Figure A2). The form,

g_{1} + g_{3} \neq g_{5} + g_{7}

due to electron-positron (±

g

) transition and radiation loss,

E = n h v

tangential to the manifolds. For linear transformation along z-axis in 1D space, the BOs are isomorphic with respect to the particle position,

|ψ⟩ = \sum_{n} C_{n} / a_{n}⟩

(Figures 1d and 2A). By intermittent precession, the inner product of r is a scalar and relates to the boundary of the MP field in the form,

{\vec{r}}_{1} {. \vec{r}}_{2} = |{\vec{r}}_{1}| |{\vec{r}}_{2}| c o s θ

(7)

where rotation of both vectors preserve the lengths and relative angles (e.g., Figure 1c). By assigning rotation matrix, R to Equation (7), its transposition is,

{(R r_{1})}^{T} (R r_{2}) = r_{1}^{T} r_{2} I,

(8)

where the identity matrix,

I = R^{T} \times R

by reduction (Figure A2). The orthogonal relationship of BO to clockwise precession along z-axis at 90° for all rotations suggests,

R \in S O (3)

. The SO(3) group rotation for integer spin 1 in 3D space is,

R_{y z} (θ) = (\begin{matrix} 1 & 0 & 0 \\ 0 & c o s θ & - s i n θ \\ 0 & s i n θ & c o s θ \end{matrix}) (\begin{matrix} x \\ y \\ z \end{matrix}) .

(9)

Equation (9) can also be pursued for integer spin 0 and higher spin particles. When rotating as 2 x 2 Pauli vector for SU(2) symmetry with respect to a light-cone of half-integer spin (Figure 1d), Equation (9) translates to the form,

\pm (\begin{matrix} c o s \frac{θ}{2} & i s i n \frac{θ}{2} \\ i s i n \frac{θ}{2} & c o s \frac{θ}{2} \end{matrix}) = (\begin{matrix} z & x - y_{i} \\ x + y_{i} & - z \end{matrix}) = |\begin{matrix} ξ_{1} \\ ξ_{2} \end{matrix}| |\begin{matrix} - ξ_{2} & ξ_{1} \end{matrix}|,

(10)

where

ξ_{1}

and

ξ_{2}

are Pauli spinors of rank 1 to rank 1/2 tensor relevant for Dirac matrices (Figure A2). By orthogonal geometry, the column is attributed θ at n-levels along z-axis and the row to BO defined by ϕ in degeneracy. For ladder operators at n-dimension along z-axis, SU(2) is irreducible for the shift in θ and ϕ such as,

(\begin{matrix} S U (2) \\ n \times n \end{matrix}) \neq (\begin{matrix} S U (2) \\ l \times l \end{matrix}) ⨁ (\begin{matrix} S U (2) \\ m \times m \end{matrix})

. Translation of SU(2) by accentuating precession at high energy like,

(\begin{matrix} S U (2) \\ 2 \times 2 \end{matrix}) ⨁ (\begin{matrix} S U (2) \\ 2 \times 2 \end{matrix})

matrices is reduced to the upright MP field position (e.g., Figure 1b). For the particle’s position, when y = 0, z = x is a real number. At x = 0,

z = y

becomes an imaginary number. The BO linked to the electron’s position can be assigned to SO(2) group in 2D such as,

(\begin{matrix} c o s θ & s i n θ \\ - s i n θ & c o s θ \end{matrix}) ≅ (\begin{matrix} 1 & θ \\ - θ & 1 \end{matrix}) = I + θ (\begin{matrix} 0 & 1 \\ - 1 & 0 \end{matrix}),

(11)

where,

θ \in [0,2 π]

incorporates Dirac process at 720° rotation (e.g., Figure 1a). Similar relationships can be forged for

R_{x y} (ϕ)

with respect to the BO along x-y plane with respect to Equation (9) in the form,

R_{x y} (ϕ) = (\begin{matrix} c o s ϕ & - s i n ϕ & 0 \\ s i n ϕ & c o s ϕ & 0 \\ 0 & 0 & 1 \end{matrix}) (\begin{matrix} x \\ y \\ z \end{matrix}) = \pm (\begin{matrix} e^{i \frac{ϕ}{2}} & 0 \\ 0 & e^{- i \frac{ϕ}{2}} \end{matrix}) .

(12)

Substitution of Equation (12) with

R_{x y} (ϕ) = e^{θ}

can relate to polarization states, -1, 1 and 0 at the vertices of the MP field (Figure 1c) from the electron-positron transition such as,

e^{θ} [\begin{matrix} 0 & - 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{matrix}] = [\begin{matrix} c o s θ & - s i n θ & 0 \\ s i n θ & c o s θ & 0 \\ 0 & 0 & 1 \end{matrix}] .

(13)

The matrices described by Equation (13) is relevant to Figure A2. These explanations offer the basics to the complexities of compact Lie group similar to those demonstrated for quantum mechanics and Dirac notations in the preceding subsection.

2d. Summary

The electron of a charged particle and its transition to positron within the MP model in space-time sustains CPT symmetry (e.g., Figure 1a,b) and accommodates both fermion and monopole. The former by Dirac process with the electron dominance over its conjugate pair to balance out positive charge of the proton. Polarization of the model by the electron in transition generates electric dipole moment for quantization of electric charge with

\nabla . E = ρ / ε_{0}

. The electron tangential to the vertex of the MP field at position 0 reduces the solenoidal coil of n-dimensions of BOs by levitation (Figure 1d) to a point and this mimics a monopole. The monopole is not transferrable by linearization possibly due to coupling of the vertices with decompression of the MP field of Dirac string expected comparable to a bar of magnet. These descriptions are compatible with quantum mechanics, QFT and Lie group (Sections 2b and 2c). In this case, center of mass (COM) at the point-boundary for the electron-positron transition is applicable to Coulomb’s law of electric force,

F = \frac{1}{4 π ε_{0}} . \frac{q_{1} . q_{2}}{r^{2}}

between two charged bodies in a vacuum. The radius, r is assigned to the principle axis of the MP field (Figure 1a) and it links COM with the nucleus akin to nuclear isospin. The inertia frame of the model by precession at a constant velocity can accommodate centripetal force for light-matter interaction limited to COM at the point-boundary. When zooming in towards position 0, the particle property is constrained but the potential well becomes infinite at positions 1 and 3 with momentum undefined in accordance with the uncertainty principle.

3. Dirac Field Theory and Its Related Components

Further exposition of the helical property of the MP model to induce Dirac belt-trick is offered in Figure 2a–f. CPT symmetry is sustained for the electron-positron transition at the point-boundary, where COM is assumed. The electron’s time reversal orbit of a MP field mimics Dirac string and it is subjected to both twisting and unfolding process by clockwise precession. Cancellation of charges at conjugate positions 1, 3 and 5, 7 allows for the emergence of BO to accommodate either spin up or spin down states. The BOs of manifolds into n-dimensions by levitation are relevant to disturbance of the model (e.g., Figure 1d). How all these become compatible with the basics of Dirac theory and its associated components [1,2,10,11] are succinctly described here in bullet points in order to plot the path for further undertakings.

⇒: Dirac theory and helical property. The fermion field is defined by the famous Dirac equation of the generic form,

i ℏ γ^{u} \partial_{u} ψ (x) - m c ψ (x) = 0,

(14)

where

γ^{u}

are gamma matrices. The exponentials of the matrices,

\{γ^{o} γ^{1} γ^{2} γ^{3}\}

are attributed to the electron’s position by clockwise precession acting on its time reversal orbit. For example,

γ^{o}

is assigned to the vertex of the MP field and by electron-positron transition at position 0, it sustains z-axis as arrow of time in asymmetry. Thus, arrow of time for a pair of vertices for spin up and spin down incorporates time reversal symmetry. The

γ^{1} γ^{2} γ^{3}

variables of Dirac matrices are assumed by the electron shift in its positions (Figure 2a–f). Orthogonal projections of the space-time variables,

\frac{1}{2} (1 \pm i γ^{0} γ^{1} γ^{2} γ^{3})

are confined to a hemisphere and assigned to a light cone to generate spin-charge of the electron (e.g., Figure 1c). These descriptions uphold CPT symmetry and are indirectly incorporated into the famous Dirac equation,

(i γ^{0} \frac{\partial}{\partial t} + c A \frac{\partial}{\partial x} + c B \frac{\partial}{\partial y} + c C \frac{\partial}{\partial z} - \frac{{m c}^{2}}{ℏ}) ψ (t, \vec{x}),

(15)

where c acts on the coefficients A, B and C and transforms them to

γ^{1} {, γ}^{2}

and

γ^{3}

. The exponentials of

γ

are denoted i for off-diagonal Pauli matrices for the light-cone (Figure 1d) and is defined by,

γ^{i} = (\begin{matrix} 0 & σ^{i} \\ {- σ}^{i} & 0 \end{matrix}),

(16a)

and zero exponential,

γ^{o}

is,

γ^{0} = (\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix}) .

(16b)

σ^{i}

is relevant to oscillations assumed at the BOs (Figure 1d) with anticommutation relationship,

e^{+} (ψ) \neq e^{-} (\bar{ψ})

of chiral symmetry (Figure 2c,d). The associated vector gauge invariance for the electron-positron transition exhibits the following relationships,

ψ_{L} \to e^{i θ L} ψ_{L}

(17a)

and

ψ_{R} \to e^{i θ L} ψ_{R} .

(17b)

The exponential factor, iθ refers to the position, i of the electron of a complex number and θ, is its angular momentum (e.g., Figure 1c). The unitary rotations of right-handedness (R) or positive helicity and left-handedness (L) or negative helicity are applicable to the electron transformation to Dirac fermion (e.g., Figure A2 in Appendix B). The process is confined to a hemisphere and this equates to spin 1/2 property of a complex spinor. Two successive rotations of the electron in orbit by clockwise precession of the MP field is identified by

i ћ

. The chirality or vector axial current at the point-boundary is assigned to polarized states, ±1 of the model (Figure 1c). The helical symmetry from projections operators or nuclear isospin of z-axis acting on the spinors (Figure 2e) is,

P_{L} = \frac{1}{2} (1 - γ_{5})

(18a)

and

P_{R} = \frac{1}{2} (1 - γ_{5}),

(18b)

where

γ_{5}

is likened to thermal radiation of a black body. The usual properties of projection operators are: L + R = 1; RL = LR = 0; L² = L and R² = R (e.g., Figure 2a–d) consistent with CPT symmetry.

⇒: Wave function collapse. Dirac fermion or spinor is denoted ψ(x) in 3D Euclidean space and it is superimposed onto the MP model of 4D space-time, ψ(x,t) by clockwise precession (Figure 3a). The latter resembles Minkowski space-time and consists of a light-cone dissected by z-axis as arrow of time into asymmetry (Figure 1b). The former includes both positive and negative curvatures of non-Euclidean space (e.g., Figure 2a,b) normalized to straight paths of Euclidean space (Figure 2c,d). These are of non-abelian Lie group (see Section 2c) imposed on the surface of the spherical MP model somewhat mimicking Poincaré sphere. The Dirac four-component spinor, $ψ = (\binom{ψ_{0}}{\begin{matrix} ψ_{1} \\ \binom{ψ_{2}}{ψ_{3}} \end{matrix}})$ is attributed to positions 0 to 3 of conjugate pairs in 3D space. Convergence of positions 1 and 3 at either position 0 or 2 is relevant to the equivalence principle based on general relativity and is relevant to Euclidean geometry. The quantum aspect of de Sitter space by geodetic clockwise precession is balanced out by anti-de Sitter form of the electron transition in its orbit of time reversal due to gravity. For the irreducible spinor represented by the MP model, gravity becomes a classical force as implied earlier (see also Section 2d). Any light paths tangential to the point-boundary of BOs into n-energy manifolds is expected to mimic Fourier transform along the principle axis or z-axis of the MP field as time axis in asymmetry and this is equivalent to wave function collapse (Figure 3b). Constraining the electron’s position along the z-axis offers the uncertainty principle with on-shell momentum linked to BO. The generated wave amplitudes from BOs levitation into n-dimensions can relate to a typical hydrogen emission spectrum for external light-matter coupling with the electron in orbit (Figure 3c). In this case, wave function collapse of probabilistic distribution by Born’s rule, ${|ψ|}^{2}$ , is applicable to excitation of the model.

⇒: Quantized Hamiltonian. Two ansatzes adapted from Equation (14) are given by,

ψ = u (p) e^{- i p . x},

(19a)

and

ψ = v (p) e^{i p . x},

(19b)

where outward project of spin at positions 5, 7 is represented by

v

and inward projection at positions 1, 3 by

u

(e.g., Figure 2c,d). By linear transformation, the hermitian plane wave solutions form the basis for Fourier components in 3D space (Figure 1d and Figure 3b). Decomposition of quantized Hamiltonian [22] ensues as,

ψ (x) = \frac{1}{{(2 π)}^{3 / 2}} \int \frac{d^{3}}{2 E_{p}} \sum_{s} (a_{P}^{s} u^{s} (p) e^{- i p . x} + b_{P}^{s †} v^{s} (p) e^{i p . x}),

(20a)

where the constant,

\frac{1}{{(2 π)}^{3 / 2}}

is attributed to the dissection of BOs along z-axis. Its conjugate form is by,

\bar{ψ} (x) = \frac{1}{{(2 π)}^{3 / 2}} \int \frac{d^{3}}{2 E_{p}} \sum_{s} (a_{P}^{s †} {\bar{u}}^{s} (p) e^{i p . x} + {b_{P}^{s} \bar{v}}^{s} (p) e^{- i p . x}) .

(20b)

The coefficients

a_{P}^{s}

and

a_{P}^{s †}

are ladder operators for u-type spinor and

b_{P}^{s}

and

b_{P}^{s †}

for v-type spinor at n-dimensions of BOs by levitation (e.g., Figure 1d). These are related to Dirac spinors of two spin states, ±1/2 with

{\bar{v}}^{s}

and

{\bar{u}}^{s}

as their antiparticles. Dirac Hamiltonian of one-particle quantum mechanics relevant to the MP model of hydrogen atom type is,

H = \int d^{3} x ψ^{†} (x) [- i γ^{0} γ . \nabla + m γ^{0}] ψ (x) .

(21)

The quantity in the bracket is provided in Equation (3). By parity transformation, the observable and holographic oscillators are canonically conjugates (e.g., Figure 2c,d). The associated momentum is,

π = \frac{\partial L}{\partial ψ} - \bar{ψ} i γ^{0} = i ψ^{†} .

(22)

With z-axis of the MP field assuming time axis in asymmetry (Figure 1c), V-A currents are projected in either x or y directions in 3D space comparable to Fourier transform (e.g., Figure 3b). These assume the relationships,

[ψ_{α} (x, t), ψ_{β} (y, t)] = [ψ_{α}^{†} (x, t), ψ_{β}^{†} (y, t)] = 0,

(23a)

and its matrix form,

[ψ_{α} (x, t), ψ_{β}^{†} (y, t)] = δ_{α β} δ^{3} (x - y),

(23b)

where α and β denote the spinor components of

ψ

. Equations (23a) refers to unitarity of the model and Equation (23b) is assumed by the electron-positron transition about the manifolds of BOs in 3D space (Figure 1d). The

ψ

independent of time in 3D space obeys the uncertainty principle with respect to the electron’s position, p and momentum, q, as conjugate operators (Figure 1c). The commutation relationship of p and q is,

\{a_{P}^{r}, a_{q}^{s †}\} = \{b_{p}^{r}, b_{q}^{s †}\} = {(2 π)}^{3} δ^{r s} δ^{3} (p - q) .

(24)

Equation (24) incorporates both matter and antimatter and their translation to linear time (Figure 3b). The electron as a physical entity generates a positive-frequency such as,

⟨0| ψ (x) \bar{ψ} (y)| 0⟩ = ⟨0 │ \int \frac{d^{3} p}{{(2 π)}^{3}} \frac{1}{\sqrt{{2 E}_{p}}} \sum_{r} a_{p}^{r} u^{r} (p) e^{- i p x} \times \int \frac{d^{3} q}{{(2 π)}^{3}} \frac{1}{\sqrt{{2 E}_{q}}} \sum_{s} a_{q}^{s †} {\bar{u}}^{s} (q) e^{i q y} │ 0⟩ .

(25)

Equation (25) could explain the dominance of matter (electron) over antimatter if the latter is accorded to the conceptualization process of Dirac fermion provided by the model (e.g., Figure 2a,b).

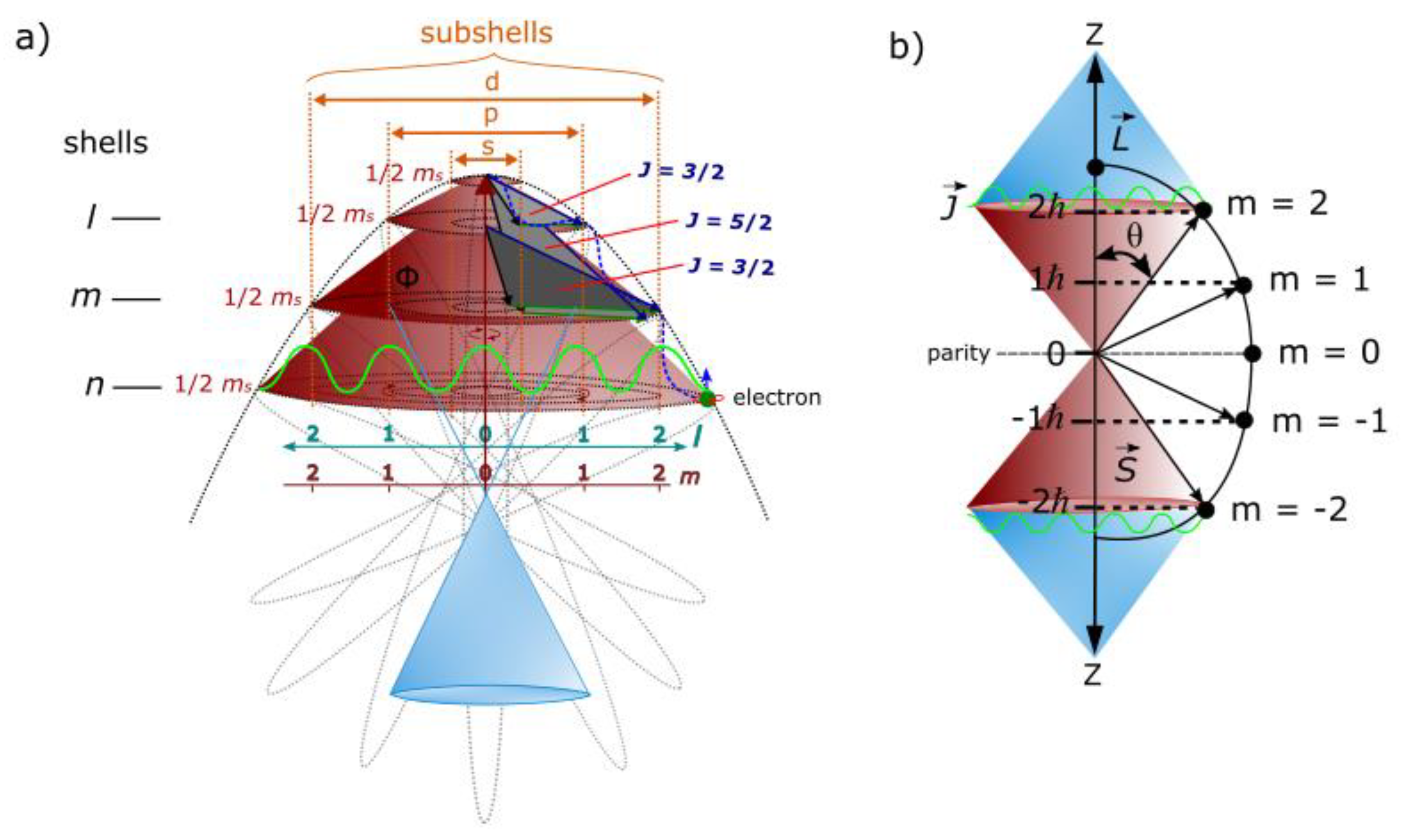
⇒: Non-relativistic wave function. Observation by light-matter interaction allows for the emergence of the model from the point-boundary at Planck length. Subsequent energy shells of BOs at the n-levels by excitation accommodates complex fermions, ±1/2, ±3/2, ±5/2 and so forth (Figure 4a). The orbitals of 3D are defined by total angular momentum,

\vec{J} = \vec{l} + \vec{s}

and this incorporates both orbital angular momentum, l and spin angular momentum, s (Figure 4b). These are aligned with Schrödinger wave function (e.g., Figure 1c). The reader is also referred to Appendix A, Appendix B and Appendix C. Within a hemisphere, the model is transformed to a classical oscillator. By clockwise precession, a holographic oscillator from the other hemisphere of the MP field remains hidden. One oscillator levitates about the other (Figure 4b) and both are not simultaneously accessible to observation by Fourier transform (e.g., Figure 3b). Levitation of on-shell momentum of BO into n-levels by disturbance can be pursued for Fermi-Dirac statistics if these equate to fermions. The point-boundary at the vertex of MP field at position 0 is assigned to zero-point energy (ZPE) and both vertices constrain vacuum energy with its excitation by precession. The

\pm \vec{J}

splitting (Figure 4a) applies to Landé interval rule for the electron of weak isospin and this can somehow accommodate lamb shift and thus, hyperfine structure constant from levitation of BOs into n-dimensions (e.g., Figure 1d). Such a scenario is similar to how vibrational spectra of a harmonic oscillator for diatoms like hydrogen molecule incorporates rotational energy levels (Figure 4a). The difference of the classical oscillator to the quantum scale is the application of Schrödinger wave equation (e.g., Figure 1c).

⇒: Weyl spinor. The light cone within a hemisphere accommodates both matter and antimatter by parity transformation (Figure 4a,b). It is described in the form,

ψ = (\begin{matrix} \begin{matrix} ψ_{0} \\ ψ_{1} \\ ψ_{2} \end{matrix} \\ ψ_{3} \end{matrix}) .

(26)

Equation (26) corresponds to spin up fermion, a spin down fermion, a spin up antifermion and a spin down antifermion (e.g., Figure 2c,d). By forming its own antimatter, Dirac fermion somewhat resembles Majorana fermions. It is difficult to observe them simultaneously due to wave function collapse long z-axis of linear time (e.g., Figure 3b). Non-relativistic Weyl spinor of a pair of light cones in 4D space-time are relevant to Schrödinger wave equation in 3D space (Figure 1c, Figure 3a and Figure 4a). These are defined by reduction of Equation (26) to a bispinor in the form,

ψ = (\begin{matrix} u_{+} \\ u_{-} \end{matrix}),

(27)

where

u_{\pm}

are Weyl spinors of chirality with respect to the electron position. By parity operation, x → x’ = (t, ‒ x), qubits 1 and −1 are generated at the vertices of the MP field (e.g., Figure 1c). Depending on the reference point-boundary of the BO (Figure 1d), the exchanges of left- and right-handed Weyl spinor assumed the process,

(\begin{matrix} ψ_{L}^{'} \\ ψ_{R}^{'} \end{matrix}) = (\begin{matrix} ψ_{R} (x) \\ ψ_{L} (x) \end{matrix}) \Rightarrow \begin{matrix} ψ^{'} (x^{'}) = γ^{0} ψ (x) \\ {\bar{ψ}}^{'} (x^{'}) = \bar{ψ} (x) γ^{0} . \end{matrix}

(28)

Conversion of Weyl spinors to Dirac bispinor,

ξ^{1}

ξ^{2}

are of transposition state (e.g., Figure 2d,d)). The two-component spinor,

ξ^{1}

ξ^{2}

= 1 are normalized at the point-boundary at position 0 of the spherical model (Figure 1a).

⇒: Lorentz transformation. The Hermitian pair, $ψ^{†} ψ$ of Dirac fermion based on Equation (27) undergo Lorentz boost and translate the BOs into n-levels (Figure 1d) of the form,

$u^{†} u = (ξ^{†} \sqrt{p . σ,} ξ \sqrt{p . \bar{σ}} . (\begin{matrix} \sqrt{p . σ} ξ \\ \sqrt{p . \bar{σ}} ξ \end{matrix}), = 2 E_{P} ξ^{†} ξ .$

(29)

The corresponding Lorentz scalar applicable to scattering from on-shell momentum tangential to the BOs (Figure 1d) is,

\bar{u} (p) = u^{†} (p) γ^{0} .

(30)

Equation (30) is referenced to z-axis of the MP field as time axis and is relevant to Fourier transform into linear time. By identical calculation to Equation (29), the Weyl spinor is,

\bar{u} u = 2 m ξ^{†} ξ,

(31)

Both Weyl spinor of a light-cone (Figure 4a) and Majorana fermion are indistinguishable from Dirac spinor for light-matter interaction confined to position 0 (e.g., Figure 1a).

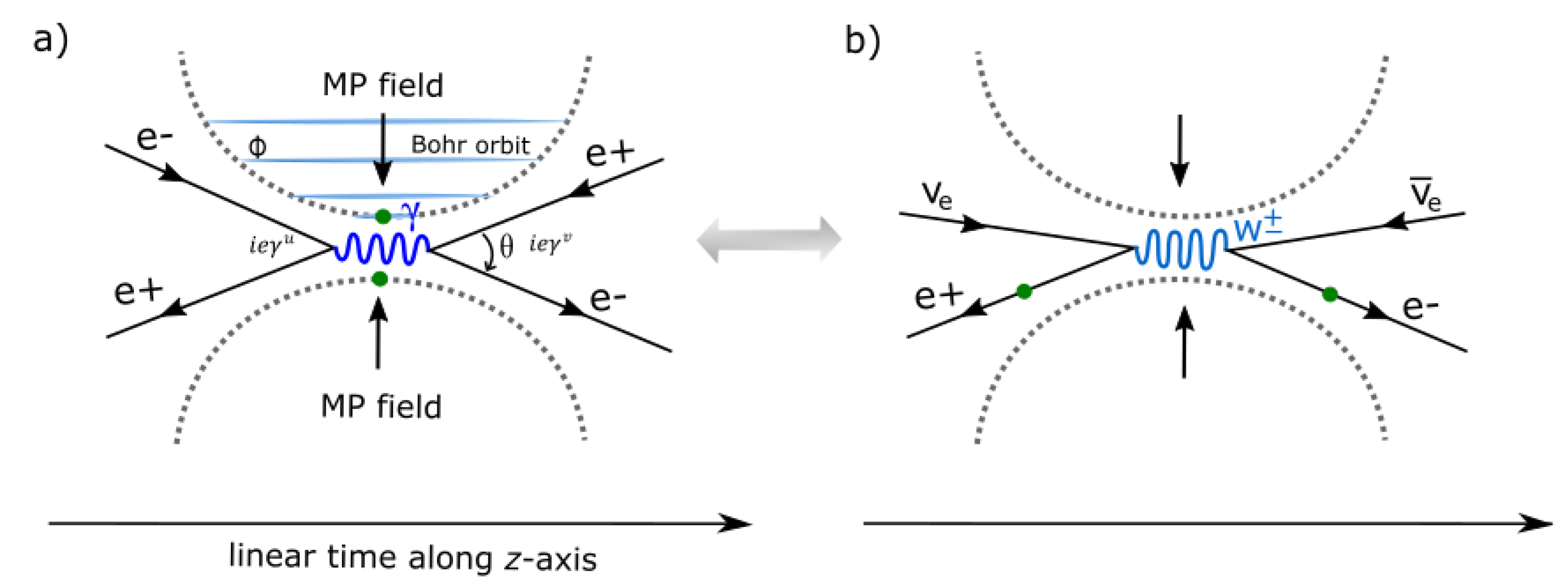
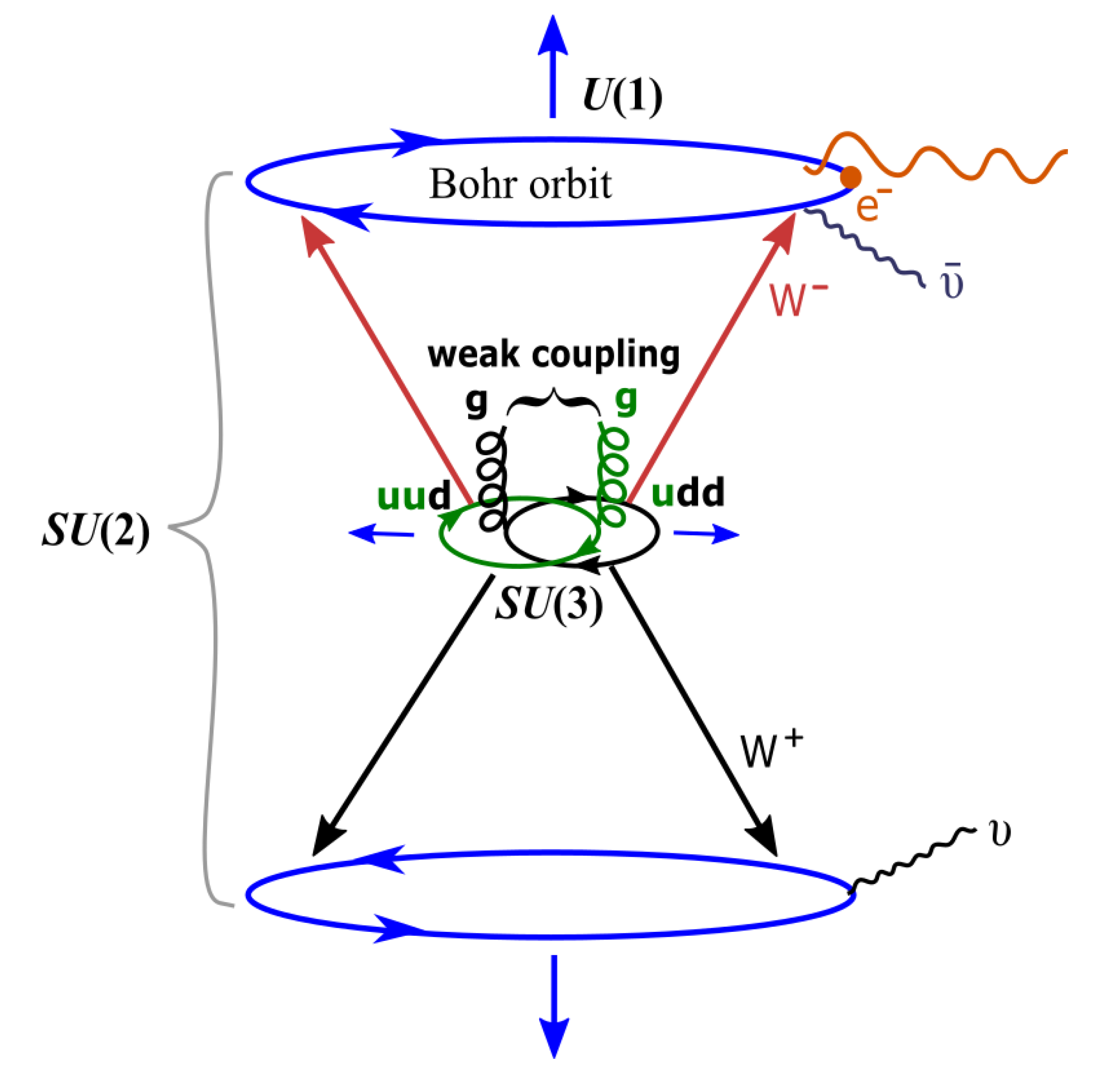
⇒: Electroweak symmetry breaking. Coupling of the MP models and ejection of particles of weak isospin to hypercharge of ±1 is assumed at the COM at position 0 (Figure 5a,b) (see also Section 2d). The emergence of particle-hole symmetry mimicking the ELECTRON may exhibit variation in the electrostatic force with the proton. Thus, any adjustments by the proton to accommodate changes in charge and mass along the z-axis towards the point-boundary breaks CPT symmetry such as for electroweak symmetry breaking like beta decay, $n^{0} \to p^{+} + W^{-} \to u u d + e^{-} + \bar{ν}$ (Figure 6). Observation is deterministic tangential to BOs into n-dimensions for on-shell momentum. If neutrino types (e.g., $\bar{ν}$ ) of helical property mimic the electron-positron transition, these can be generated at positions 1 and 3 with trivial shift in z-axis, $⟨z| z'⟩ = δ (z - z^{'})$ by precession (Figure 1d). and are not expected to violate CPT symmetry. The particles acquire energy, $γ$ or $\frac{{- i g}_{u v}}{p^{2}}$ from on-shell momentum ( $p^{2} = m^{2}$ ) tangential to the BO and sustain Einstein mass-energy equivalence of the form,

$E^{2} - {|\vec{p}|}^{2} c^{2} = m^{2} c^{2} .$

(32)

Translation to linear time by wave function collapse is normalized to the z-axis (Figure 3b) for particles possessing angular momenta,

{i e γ}^{u}

{i e γ}^{v}

such as vector bosons,

W^{\pm}

at short range within the vicinity of the model (Figure 6) during coupling process (Figure 5b). If spin 1 and spin 0 particles are assigned to the COM of ZPE at the point-boundary of a classical oscillator (Figure 4a), hypercharge BOs by levitation into n-dimensions of Minkowski space-time (Figure 1d) are relevant to the emergence of leptons. Higgs boson,

H °

assigned to COM is included in the first term of its field of a scalar quantity,

V (ϕ) = m_{H}^{2} ϕ^{2} + {λ ϕ}^{4}

. The second term is applicable to positions 1 and 3 by precession into space-time for the emergence of measureable quantity,

ϕ

along horizontal x-axis (Figure 1a). The y-axis consists of imaginary potential,

ϕ

and both axes are normalized to z-axis of the MP field as time axis and both are relevant to generation of V-A currents (e.g., Equations (23a and 23b)). By constriction of the model,

H °

can translate to massive Nambu-Goldstone boson for combined COMs from the vertices of the MP field. Comparable to monopole (Section 2d), such boson is not transferrable to observation with decompression of vertices for the MP field of Dirac string expected instead. Light-matter interaction restricted to the point-boundary of COM allows for confinement of quark flavor and color charge of ±1/3 spin within the model. These would mimic the electron-positron transition (Figure 6) when translated along the z-axis of the MP field as time axis in asymmetry akin to nuclear isospin. The generated wave amplitudes are expected to be engulfed by those of electron-positron transition into linear time by Fourier transform (e.g., Figure 3b). Such explanations offer an alternative interpretation of electroweak symmetry breaking with variations in mass and charge for a plethora of particles from on-shell momentum of BO by levitation into n-dimensions (e.g., Figure 1d). The particles’ relationships to vectors, matrices and tensors with respect to QFT are provided in the text and also demonstrated in Figure A2 (Appendix B). This looks promising to link nuclear physics, high and low energies physics for electroweak breaking of SU(3) x SU(2) x U(1) symmetry (Figure 6). For example, U(1) is assigned to COM at position 0 of the point-boundary (Section 2b). SU(2) is described by Lie group (Section 2c) and Dirac field theory within this section. SU(3) is linked to the z-axis of the MP field as nuclear isospin and it possibly dissects miniature doublet MP models of 4D to form 8D for the quark model (Figure 6). Any deviations in the magnetic moment of the electron from BO by levitation into n-dimensions can account for the fine-structure constant,

a = \frac{e^{2}}{ℏ c} = \frac{e^{2}}{4 π} \approx \frac{1}{137}

such as lamb shift when translated along the z-axis of the MP field into linear time (e.g., Figure 3b) and this is relevant to pursuits in quantum electrodynamics.

4. Conclusions

The dynamics of the MP model of 4D space-time offered in this study allows for the transformation of the electron of hydrogen atom type to Dirac fermion of a complex four-component spinor. It consists of an electron in orbit of time reversal in an elliptical MP field of Dirac string undergoing clockwise precession and this generates a spherical model applicable to both Minkowski and Euclidean space-times. Such intuition upholds CPT symmetry and appears consistent with Dirac belt trick and basic interpretations of quantum mechanics and Lie group. Its application to QFT is shown to be relevant to describe Dirac field theory and its related components like wave function collapse, quantized Hamiltonian, non-relativistic wave function, Weyl spinor, Lorentz transformation and electroweak symmetry breaking mechanism. Though the model remains a speculative tool, it can become important towards defining the fundamental state of matter and its field theory subject to further investigations by conventional methods in both experiment and theoretical applications.

Data Availability Statement

The modeling data attempted for the current study are available from the corresponding author upon reasonable request.

Competing Financial Interests

The author declares no competing financial interests.

Appendix A. Mathematical Property of Schrödinger Wave Equation

The Schrödinger equation cannot be derived similar to Newton’s law of gravity. Its mathematical property can be plotted [23] beginning with the normalized sine wave function,

ψ = A s i n \frac{2 π x}{λ},

(1A)

where A is the amplitude shown in Figure A1. Its second derivation is,

Figure A1. Translation of a sine wave function along x-axis.

\frac{d^{2} ψ (x)}{{d x}^{2}} = = \frac{{- 4 π}^{2}}{λ^{2}} ψ (x) .

(2A)

Velocity,

v

can be calculated from total energy in the form,

v^{2} = \frac{2 (E - V)}{m},

(3A)

where V is potential energy and kinetic energy is,

\frac{1}{2} m v^{2}

. Taking the squared function of de Broglie relationship becomes,

λ^{2} = \frac{h^{2}}{m^{2} v^{2}} .

(4A(i))

By substitution from Equation (3A), Equation (4A(i)) can be rewritten as,

λ^{2} = \frac{h^{2}}{2 m (E - V)} .

(4A(ii))

By substitution into Equation (2A), this becomes,

\frac{d^{2} ψ (x)}{{d x}^{2}} = = \frac{{- 8 m π}^{2}}{h^{2}} (E - V) ψ (x) .

(5A(i))

An alternative form of Equation (5A(i)) is,

- \frac{ℏ}{2 m} \frac{\partial^{2}}{{\partial x}^{2}} + V ψ (x) = \frac{p^{2}}{2 m} ψ (x) = E ψ (x) .

(5A(ii))

By first derivation of space-time due to clockwise precession of the MP model (Figure 1c), Equation (5A(ii)) is given by,

i ℏ \frac{\partial}{\partial t} (ψ (\vec{r}) θ (t) = E ψ .

(5A(iii))

In this way, the model offers physical meaning to Schrödinger wave equation as an eigenvalue of

ψ

similar to Newton’s law of gravity with the electron of isospin represented by, i or 2m.

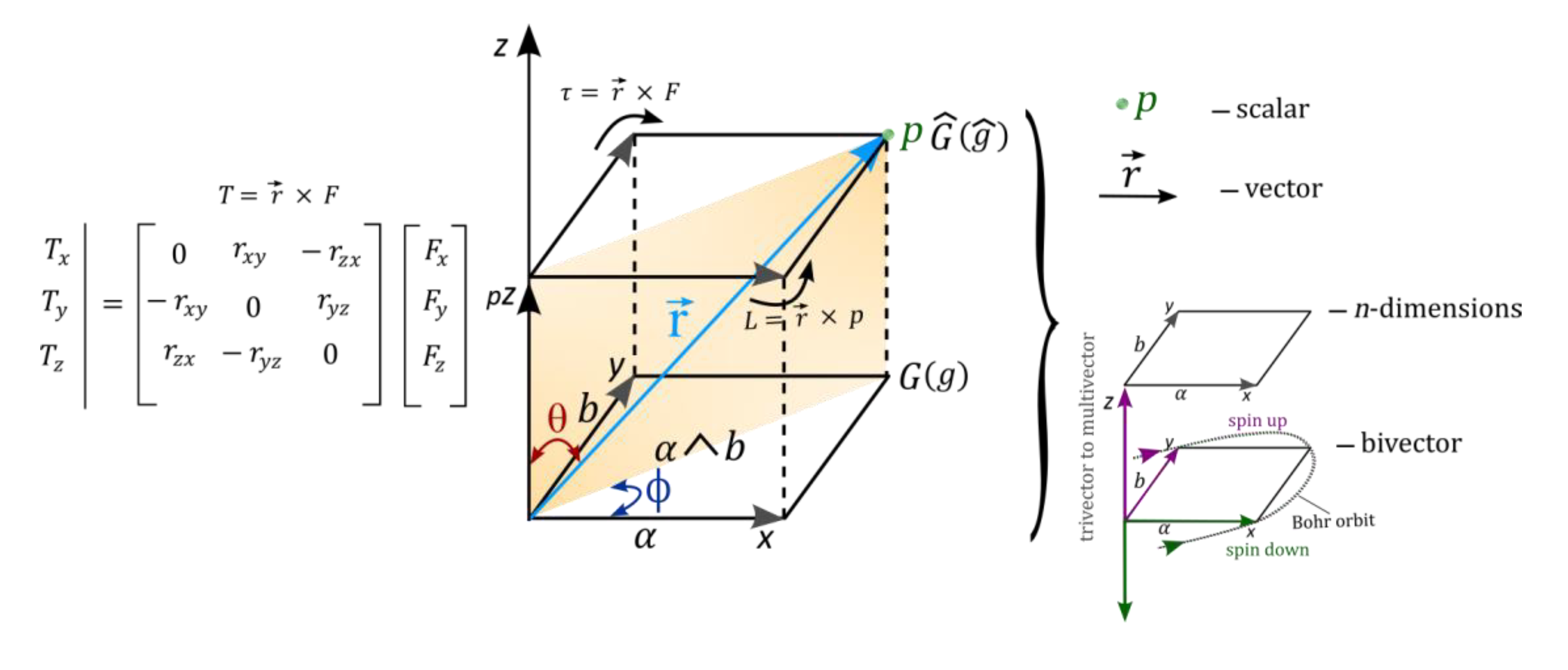
Appendix B. Basis of Vectors, Matrices, Tensors and Fourier Transform

The physicality of the complexity of Dirac four-component spinor can somehow relate to the geometric MP model. The BOs provide the basis for vector to multivector by levitation into n-dimensions or n-energy levels along the z-axis (Figure A2). By rotation, the BOs generate both spin up and spin down in correspondence to the principle axis of the MP field as time axis in asymmetry. The manifold of BOs can be assigned to a box (Figure A2). The rotation by

\vec{r}

is a four 3-fold axis in 3D and its matrices are defined by Cartesian coordinates, x, y and z. These are related to shift in both

θ

and

Φ

as double cover of SU(2) for vector to multivectors assumed within the BOs. They are applicable to the Lie group ladder operators,

G (g)

and

\hat{G} (\hat{g})

of 3D space and 4D space-time. By linearization akin to Fourier transform (e.g., Figure 3b), the boxes of isomorphism consisting of BOs by levitation and these are translated along the z-axis of the MP field (Figure A2). The BO of bivector field is related to

z / p z

of integers modulo p of prime. The shift along z-axis of isospin from vertices of the MP field of Dirac string is commutative (Figure A2) and any changes by precession is trivial. The MP model of irreducible representation,

Π

is given by [21],

Figure A2. The basis of vectors to multivectors, matrices, tensors and Fourier transform. The vectors are aligned with either spin up or spin down by rotation of the BO. Translation along z-axis of nuclear isospin provides trivectors to multivector into n-dimensions by levitation of BOs of unidirectional. The matrices are related to tensors along z-axis by Fourier transform for the commutation,

p Z

Z

(see text for details). The

\vec{r}

is a four 3-fold rotational axis (shaded orange plane) in 3D of the box and is applicable to Fourier transform (e.g., Figure 3b). It mimics a 4-gradient Dirac operator,

\nabla

for vectors to multivector into n-dimensions of the box (see also red rectangle in Figure 1c). Rotation into forward time,

τ = \vec{r} \times F

is by clockwise precession and this insinuates spin up with the unfolding process for spin down by,

L = \vec{r} \times p

. The spin rotation matrices applicable to Clifford algebra are shown to the left. The half-integer spins of SU(2) group provide double cover (bivector) with shift in both

θ

and

ϕ

into n-dimensions by levitation of BOs. This is relevant to the Lie group ladder operators,

G (g)

and

\hat{G} (\hat{g})

. Some key features of the dimensional box are expounded to the right.

p Z

Z

(see text for details). The

\vec{r}

is a four 3-fold rotational axis (shaded orange plane) in 3D of the box and is applicable to Fourier transform (e.g., Figure 3b). It mimics a 4-gradient Dirac operator,

\nabla

for vectors to multivector into n-dimensions of the box (see also red rectangle in Figure 1c). Rotation into forward time,

τ = \vec{r} \times F

is by clockwise precession and this insinuates spin up with the unfolding process for spin down by,

L = \vec{r} \times p

. The spin rotation matrices applicable to Clifford algebra are shown to the left. The half-integer spins of SU(2) group provide double cover (bivector) with shift in both

θ

and

ϕ

into n-dimensions by levitation of BOs. This is relevant to the Lie group ladder operators,

G (g)

and

\hat{G} (\hat{g})

. Some key features of the dimensional box are expounded to the right.

ρ (g) = [Π (\hat{g})],

(6A)

where

ρ

is composed of algebraic structure (

p z

+ p

and

x p

) for vectorization, V into p-dimensional space defined by

α \land b

(Figure A2). The two operators,

T_{a}

and

S_{a}

acting on V are

(T_{a} f) (b) = f (b - a)

(7A(i))

and

(S_{a} f) (b) = e^{2 π i a b} f (b),

(7A(ii))

where T is identified by the rotational matrices,

T = \vec{r} \times F

(Figure A2) and

S_{a}

is the shift in frequency in space along z-axis (e.g., Figure 3b). These intuitive demonstrations somehow provide a geometry perspective to the MP model with its relevance to the Lie group and QFT in terms of Dirac field theory elaborated in the article (see Section 2c and Section 3).

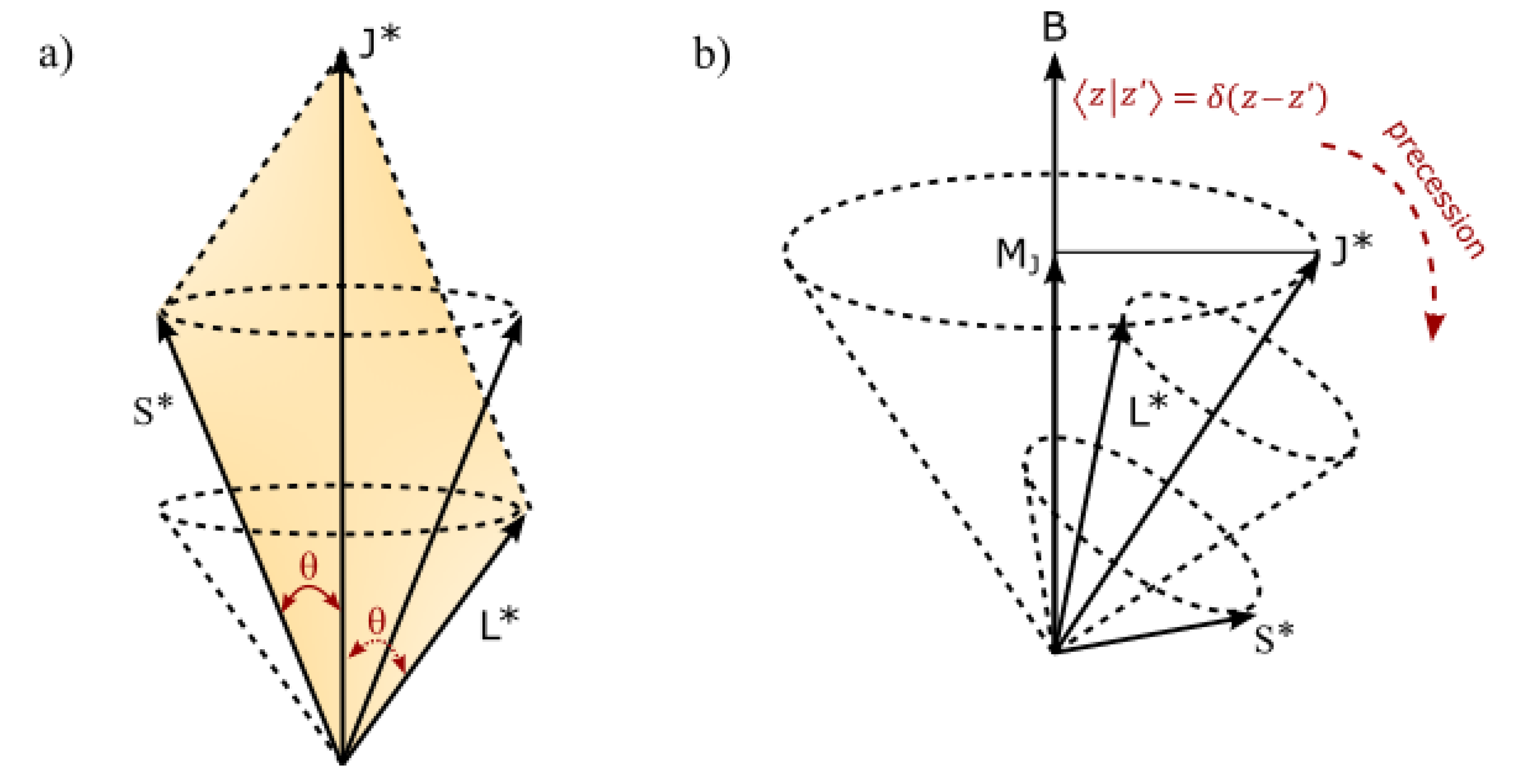
Appendix C. Vector Modelling of the MP Model

Schrödinger wave equation forms the basis of quantum mechanics and offers satisfactory explanations to account for probability distribution or orbitals of subatomic particles like electrons in the atom. However, quantum mechanics cannot account for the combination of orbital angular momenta, spin angular momenta and magnetic moments of valence electrons observed in atomic spectra. Russell-Saunders orbital-spin (L-S) coupling ensues by Clebsch-Gordon series such as for the eigenvalue of total angular momentum,

\vec{J} = \vec{l} + \vec{s}

, and this incorporates eigenvalues of both orbital angular momentum, l and spin angular momentum, s.

Figure A3. Vectors of orbital angular momentum. (a) Vectors L and S precess about this resultant J. In other words, any precession affecting L and S in the form,

⟨z| z'⟩ = δ (z - z^{'})

is reduced to the MP field of magnetic property such as Dirac string along z-axis. The shaded area of bivector from Figure A2 is extended to the point-boundary of the MP model (see also Figure 4a). (b) Vector J of the MP field precesses in correspondence to applied external magnetic field B. Both images are adapted from ref. [24].

Figure A3. Vectors of orbital angular momentum. (a) Vectors L and S precess about this resultant J. In other words, any precession affecting L and S in the form,

⟨z| z'⟩ = δ (z - z^{'})

From the emergence of the oscillator at the point-boundary (Figure 4a), levitation of BOs into n-dimensions can cater for both the resultant orbital angular momentum, L and resultant spin angular momentum, S, where spin-orbit interaction is related to constant shift in the electron position. Complete rotation towards the point-boundary by Dirac process is twice, 2π and the positron-electron transition is related to h. The lone valence electron of the MP model akin to hydrogen atom by precession takes the form,

|l| = \sqrt{l_{i} (l_{i} + 1)} ℏ,

(8A(i))

where i is equal to the subshells (Figure 4a). For example, n = 2 is split into s and p orbitals with each one accommodating spin 1/2 and from electron-positron transition of Dirac process at spherical lightspeed (Figure 1a), this equates to ±1/2 spin in accordance with Pauli exclusion principle. The total angular momentum,

\vec{J} = l \pm \frac{1}{2}

, is

\frac{3}{2}

and

\frac{1}{2}

at n = 2, l = 1. The former is assumed from the summation of spin, 1/2 + 1/2 + 1/2 from combined s and p subshells by

n_{2}

n_{1}

\frac{3}{2}

, when both orbital and spin angular momenta are aligned in the same direction (Figure 4b). It also provides the magnitude of S. The latter of low energy from

n_{2} -

n_{1}

\frac{1}{2}

in the form, 1/2 + 1/2 − 1/2 and is assigned to p orbital by cancelling out 1s orbital. This does not consider the orientation such as of the p subshells by levitation into n-dimensions (e.g., Figure 4a). The corresponding L from the combination of

\sum l_{i}

in a complete loop of BO at n-dimension is,

|L| = \sqrt{L_{n} (L_{n} + 1)} ℏ,

(8A(ii))

where the values of 0,

\sqrt{2} ℏ

and

\sqrt{6} ℏ

are generated at n = 0 to n = 2. Their projection with respect to z-axis for the irreducible MP field is,

|L_{Z}| = M_{L} ℏ .

(8A(iii))

Equation (8A(iii)) is applicable to the light cone and the same is projected for

\vec{J}

such as,

J_{Z} = m_{l} ℏ,

(9A(i))

where

m_{l}

can take (2l + 1) values in both equations as eigenfunciton of

M_{L}

. Both S and L combine to generate J in the form,

J = L + S .

(9A(ii))

Distinction of L and S are provided in Figure 4b and the orientations by precession are applicable to

M_{L}

. These explanations can possibly account for odd fermion spin types such as,

\frac{1}{2}, \frac{3}{2}, \frac{5}{2}

noted for Zeeman effect (e.g., Figure 4a) and also lamb shift from the electron-positron transition in discreet form (e.g., Figure 3c). In this case, the electron is of weak isospin and z-axis is applicable to nuclear isospin. Both are linked to BOs into n-dimensions by levitation and these are subjected to the twisting and unfolding process by Dirac process (Figure 1a,b).

References

Peskin, M. E. & Schroeder, D. V. An introduction to quantum field theory. Addison-Wesley, Massachusetts, USA (1995). pp 13–25, 40–62.
Alvarez-Gaumé, L. & Vazquez-Mozo, M. A. Introductory lectures on quantum field theory. arXiv preprint hep-th/0510040 (2005).
Pawłowski, M.; et al. Information causality as a physical principle. Nature 2009, 461, 1101–1104. [Google Scholar] [CrossRef] [PubMed]
Henson, J. Comparing causality principles. Stud. Hist. Philos M. P 2005, 36, 519–543. [Google Scholar] [CrossRef]
Nelson, E. Derivation of the Schrödinger equation from Newtonian mechanics. Phys. Rev. 1966, 150, 1079. [Google Scholar] [CrossRef]
Li, Z. Y. Elementary analysis of interferometers for wave—particle duality test and the prospect of going beyond the complementarity principle. Chin. Phys. B 2014, 23, 110309. [Google Scholar] [CrossRef]
Rabinowitz, M. Examination of wave-particle duality via two-slit interference. Mod. Phys. Lett. B 1995, 9, 763–789. [Google Scholar] [CrossRef]
Rovelli, C. Space is blue and birds fly through it. Philos. Trans. Royal Soc. Proc. Math. Phys. Eng. 2018, 376, 20170312. [Google Scholar] [CrossRef] [PubMed]
Perkins, D. H. Proton decay experiments. Ann. Rev. Nucl. Part. Sci. 1984, 34, 1–50. [Google Scholar] [CrossRef]
Sun, H. Solutions of nonrelativistic Schrödinger equation from relativistic Klein–Gordon equation. Phys. Lett. A 2009, 374, 116–122. [Google Scholar] [CrossRef]
Oshima, S. , Kanemaki, S. & Fujita, T. Problems of Real Scalar Klein-Gordon Field. arXiv preprint hep-th/0512156 (2005).
Bass, S. D. , De Roeck, A. & Kado, M. The Higgs boson implications and prospects for future discoveries. Nat. Rev. Phys. 2021, 3, 608–624. [Google Scholar]
Weiss, L. S.; et al. Controlled creation of a singular spinor vortex by circumventing the Dirac belt trick. Nat. Commun. 2019, 10, 1–8. [Google Scholar] [CrossRef] [PubMed]
Silagadze, Z. K. Mirror objects in the solar system?. arXiv preprint astro-ph/0110161 (2001).
Rieflin, E. Some mechanisms related to Dirac’s strings. Am. J. Phys. 1979, 47, 379–380. [Google Scholar] [CrossRef]
Yuguru, S. P. Unconventional reconciliation path for quantum mechanics and general relativity. IET Quant. Comm. 2022, 3, 99–111. [Google Scholar] [CrossRef]
Jaffe. R. L. Supplementary notes on Dirac notation, quantum states, etc. https://web.mit.edu/8.05/handouts/jaffe1.pdf (September, 2007).
Eigen, C. Eigen, C. Spinors for beginners. https://www.youtube.com/@eigenchris (November, 2012).
Zhelobenko, D. P. Compact Lie groups and their representations. J. Amer. Math. Soc. 1973, 40, 26–49. [Google Scholar]
https://en.wikipedia.org/wiki/Spinor (updated February 2024).
Burdman, G. Quantum field theory I_Lectures. http://fma.if.usp.br/~burdman (October, 2023).
Das, I.; et al. An introduction to physical chemistry. New Age International (P) Limited, New Delhi, India (2005) 2nd Ed. pp 16-20.
Singh, R. B. Introduction to modern physics. New Age International (P) Limited, New Delhi, India (2009) 2nd Ed. Vol. 1, pp 420-425.

Figure 2. Exposition of Dirac belt trick. (a) An irreducible spinor field of close loop within a hemisphere is generated at spherical lightspeed with the electron’s (green dot) shift in position of time reversal against clockwise precession of the MP model (Figure 1a). The position of the particle on a straight path (colored lines) is referenced to the MP field of elliptical shape (centered image). (b) Maximum twist is attained at position 4 as detectable energy and the unfolding process by another 360° rotation for a total of 720° rotation restores the electron at position 8 or 0 akin to Dirac belt trick. (c) Precession normalizes the loop to generate an electron of positive helicity or right-handedness. Spin up vector at the point-boundary correlates with the direction of precession. (d) At position 4, the electron flips to a positron of negative helicity or left-handedness. The spin down vector is in opposite direction to the direction of precession to begin the unfolding process. Transposition is attained at 720° rotation,

\sum_{j} {\hat{e}}_{j} {\hat{e}}_{j}^{T} = [e_{i} e_{j}] = c_{i j}^{k} e_{k}

with

c_{i j}^{k}

is expansion coefficients,

{\hat{e}}_{k}

is unit matrices and

i j

is electron-positron transition. (e) Irreducible spinor field at spherical lightspeed. Cancelation of charges at conjugate positions, 1, 3 and 5, 7 from on-shell momentum offers close loops of BOs to stabilize the electron to only generate either spin up or spin down states respectively at position 0 and 4. The point of singularity at the center is evaded due to shift in the electron’s position at 2 and 6. The slight tilt at position 4 compared to position 0 is attributed to energy loss from the electron-positron transition in the form,

E = h v = g β B

. (f) Polarization of the model either horizontally or vertically with respect to the electron-positron pair, ±i at position 0 by 720° rotation generates qubits 0 and 1 by hypercharge with qubit –1 at position 4. Image (e) adapted from ref. [21].

\sum_{j} {\hat{e}}_{j} {\hat{e}}_{j}^{T} = [e_{i} e_{j}] = c_{i j}^{k} e_{k}

with

c_{i j}^{k}

is expansion coefficients,

{\hat{e}}_{k}

is unit matrices and

i j

E = h v = g β B

Figure 3. Wave function collapse. (a) Irreducible Dirac spinor is defined by vector space superimposed on Poincaré sphere. It consists of both Euclidean (straight paths) and non-Euclidean (negative and positive curves) spaces. Clockwise precession by geodesic motion induces a circle at 360° rotation to the negative curves at positions 0 to 3 (e.g., Figure 2c). The polar coordinates (r, θ, Φ) are linked to a light cone (navy colored). Position 6 is projected inwards from position 2. (b) By on-shell momentum of BO with respect to the electron position in transition is applicable to Fourier transform (blue wavy curve) into linear time. Positions 2 and 6 constrains the reach of singularity. Zooming in towards real particle emergence at position 0 presents the Heisenberg uncertainty principle (black wavy curve) of superposition states. (c) The particle shifts in position and levitation of BOs into n-dimensions (Figure 1d) can somehow translate to a typical hydrogen emission spectrum. The amplitudes by Fourier transform are shown by white spectral lines and the uncertainty principle with respect to the particle property by colored spectral lines. .

Figure 4. Light-MP model coupling. (a) To an external observer, the topological point-boundary provides the origin for the emergence of the oscillator (maroon light cones). Total angular momentum,

J_{z} = S + L

is minimal with S and L in opposite directions. Levitation of BOs into n-dimensions from k to l offers asymptotic boundary to the energy shells and subshells inclusive of the hidden oscillator. The BOs in degeneracy, Φ_i (see also Figure 1d) can accommodate Fermi-Dirac statistics (green wavy curve) and possibly Fock space for non-relativistic many-particle systems if multielectron are assigned to multiple MP fields. The observable oscillator is partitioned at an infinite boundary towards the center of the MP field and is equivalent to classical limit, and defines asymptotic freedom. The blue light cone is from the perspective of the observer at the center and is relevant to Schrödinger wave function (e.g., Figure 1c). (b) The emergence of quantized magnetic moment,

{\pm J}_{z} = m_{j} ℏ

from the point-boundary (maroon light cones) levitates about the internal frame of the model (blue light cones). Parity transformation for the conjugate pairs is confined to a hemisphere (e.g., Figure 2a,b) and it is related to z-axis of nuclear isospin. Minimal scatterings (green wavy curves) are applicable to light-MP model interactions along the BOs for the eigenfunction,

\vec{J} = \vec{L} + \vec{S}

J_{z} = S + L

{\pm J}_{z} = m_{j} ℏ

\vec{J} = \vec{L} + \vec{S}

Figure 5. Feynman diagrams of MP models coupling. (a) Two electrons (green dots) or their particle-hole symmetries at the vertices of the MP models may undergo either repulsion or attraction when approaching each other. (b) Ejection of the electron/positron would induce weak particle-hole isospin. COM assumed at the vertices are related to ZPE of classical oscillator (e.g., Fig 4a) and these can generate both bosons and others like neutrinos and antineutrinos of helical property mimicking the electron-positron pair (e.g., Figure 2c,d).

Figure 6. A hypothetical scenario of beta decay from an energized MP model during coupling process. The proton and neutron are assumed to mimic the MP field. The charge and color flavor of quarks from exchanges by gluons are short range from on-shell momentum tangential to the BO. The symbols, u = up quark, d = quark and ɡ = gluon. Note,

W^{\pm}

bosons can align with z-axis of the MP model (blue arrows) as nuclear isospin during precession.

W^{\pm}

bosons can align with z-axis of the MP model (blue arrows) as nuclear isospin during precession.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Dirac Fermion of a Monopole Pair (MP) Model

Abstract

Abstract

1. Introduction

2. An electron Conversion to a Fermion by Dirac Process

2a. Unveiling Dirac Belt Trick within the Spherical MP Model

2b. Quantum Mechanics and Dirac Notations

2c. Lie Group

2d. Summary

3. Dirac Field Theory and Its Related Components

4. Conclusions

Data Availability Statement

Competing Financial Interests

Appendix A. Mathematical Property of Schrödinger Wave Equation

Appendix B. Basis of Vectors, Matrices, Tensors and Fourier Transform

Appendix C. Vector Modelling of the MP Model

References

MDPI Initiatives

Important Links

Subscribe