Submitted:
13 June 2023
Posted:
14 June 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Problem Formulation
2.1. Ant Lion Optimizer
2.1.1. Operators for ALO
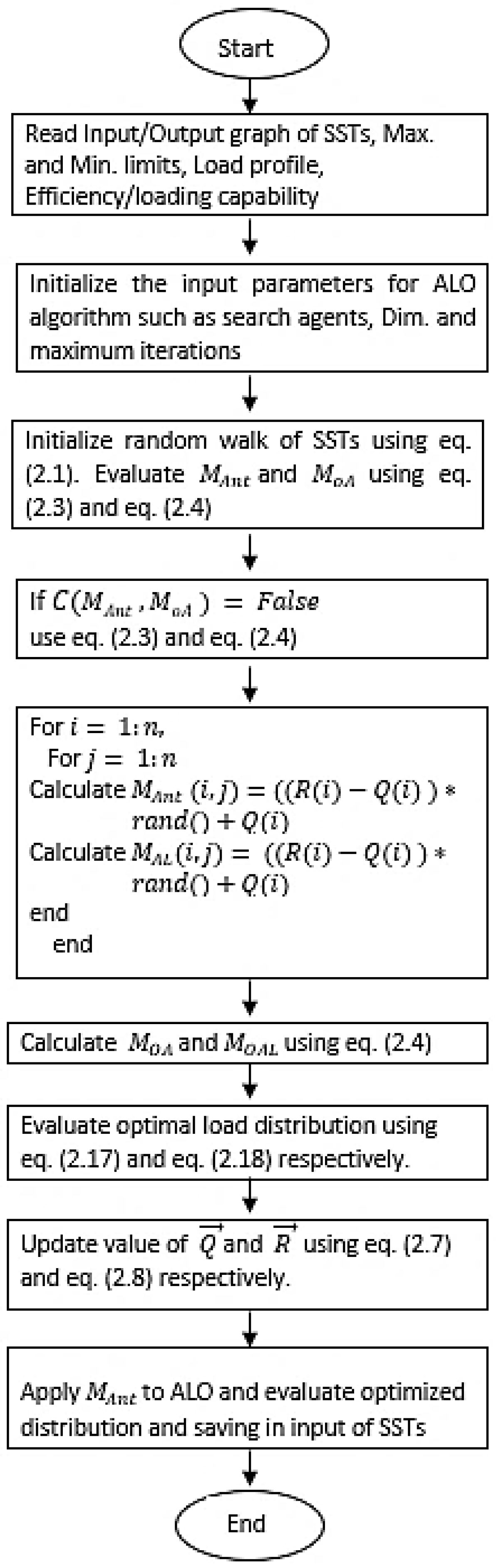
2.2. Objective Function
3. Simulation and Results
4. Conclusions and Future Recommendations
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| DER | Distributed energy resources |
| LFT | Low frequency transformer |
| cumSm | Cumulative sum |
| r(t) | Stochastic function |
| t | Step of random walk |
| Rand | Random number generator |
| Mant | Parameters of each solution |
| Minimum of random walks in ith variable | |
| Maximum of random walks in ith variable | |
| Maximum ith variable in tth iteration. | |
| Minimum ith variable in tth iteration . | |
| WAt | Random walk around the antlion selected by the roulette wheel |
| WEt | Random walk around elite at the tth iteration |
| Pjn | Input of SST |
| Poj | Output of each SST |
| (a, b & c ) | Constants from Input/output quadratic equation |
| PD | Load demand |
| Minimum and maximum output power limitations | |
| Maximum output power limitations. | |
| Lagrangian constant | |
| Total input power of all SSTs | |
| Efficiency of jth SST | |
| Coefficients for efficiency and loading graph | |
| Loj | Loading capability of the graph |
| pin | Input power of SST |
| Pmin | Minimum power handling capability of SST. |
| Pmax | Maximum power handling capability of SST. |
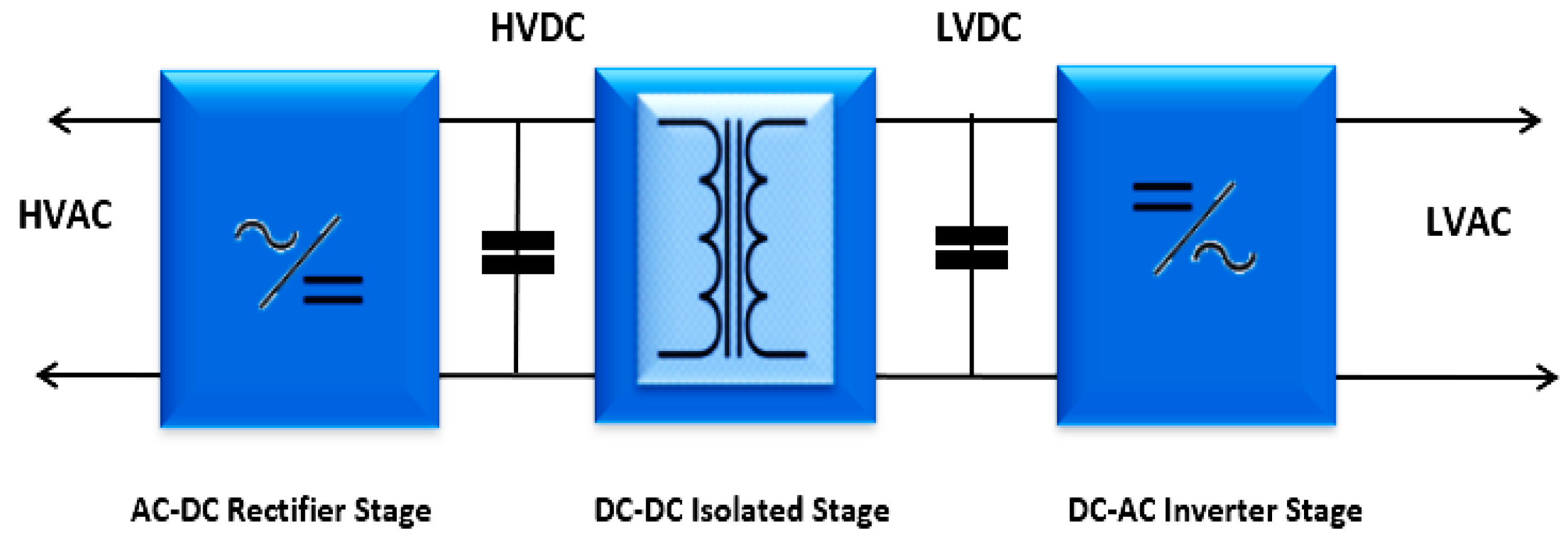
| HFT | High frequency transformer |
| DER | Distributed energy resources |
| LFT | Low frequency transformer |
References
- McPherson (Ed). (2012)., S.S. War of the Currents: Thomas Edison vs Nikola Tesla; Twenty-First Century. U.S.A. 2012.
- Davidson, C. Thomas Edison vindicated—The resurgence of DC in MV and HV power grids. In Proceedings of the22nd European Conference on Power Electronics and Applications (EPE’20 ECCE Europe), Virtual, 7–11 September 2020.
- Tahir, H.; Lee, J.S.; Kim, R.Y. Efficiency evaluation of the microgrid for selection of common bus using copula function-based efficiency curves of the converters. Sustain. Energy Technol. Assess. 2021, 48, 101621. [CrossRef]
- Gomez-Exposito, A. The Unstoppable Changing of the Electricity Guard [Commentary]. IEEE Technol. Soc. Mag. 2017, 36, 30–33. [CrossRef]
- Zhang, G.; Zhang, B.; Li, Z. A Brief History of Power Electronics Converters. In Designing Impedance Networks Converters (Stud. Syst. Decis. Control); Springer International Publishing AG. Switzerland, 2018; pp. 1–6. [CrossRef]
- Zhang, G.; Li, Z.; Zhang, B.; Halang, W.A. Power electronics converters: Past, present and future. Renew. Sust. Energy Rev. 2018, 81, 2028–2044. [CrossRef]
- Korytowski, M. Uno Lamm: The Father of HVdc Transmission [History]. IEEE Power Energy Mag. 2017, 15, 92–102.
- Chinnathambi, N.D.; Nagappan, K.; Samuel, C.R.; Tamilarasu, K. Internet of things-based smart residential building energy management system for a grid-connected solar photovoltaic-powered DC residential building. Int. J. Energy Res. 2022, 46, 1497–1517. [CrossRef]
- Gelani, H.E.; Dastgeer, F.; Siraj, K.; Nasir, M.; Niazi, K.A.K.; Yang, Y. Efficiency Comparison of AC and DC Distribution Networks for Modern Residential Localities. Appl. Sci. 2019, 9, 582. [CrossRef]
- Gelani, H.E.; Nasir, M.; Dastgeer, F.; Hussain, H. Efficiency comparison of alternating current (AC) and direct current (DC) distribution system at residential level with load characterization and daily load variation. Proc. Pak. Acad. Sci. 2017, 54, 111–118.
- Ahmad, F.; Dastgeer, F.; Gelani, H.E.; Khan, S.; Nasir, M. Comparative analyses of residential building efficiency for AC and DC distribution networks. J. Bull. Pol. Acad. Sci. 2021, 69. [CrossRef]
- Rasheed, A.; Khan, S.; Gelani, H.E.; Dastgeer, F. AC vs. DC Home: An Efficiency Comparison. In Proceedings of the International Symposium on Recent Advances in Electrical Engineering (RAEE), Islamabad, Pakistan, 28–29 August 2019; Volume 4, pp. 1–6.
- Gerber, DL;Vossos, V; Feng, W; Marnay, C; Nordman, B; Brown, R. A simulation-based efficiency comparison of AC and DC power distribution networks in commercial buildings. Applied Energy, 210(C), 2018, 1167-1187. [CrossRef]
- Gelani, H.E.; Dastgeer, F. Efficiency Analyses of a DC Residential Power Distribution System for the Modern Home. J. Adv. Electr. Comput. Eng. 2015, 15, 135–142. [CrossRef]
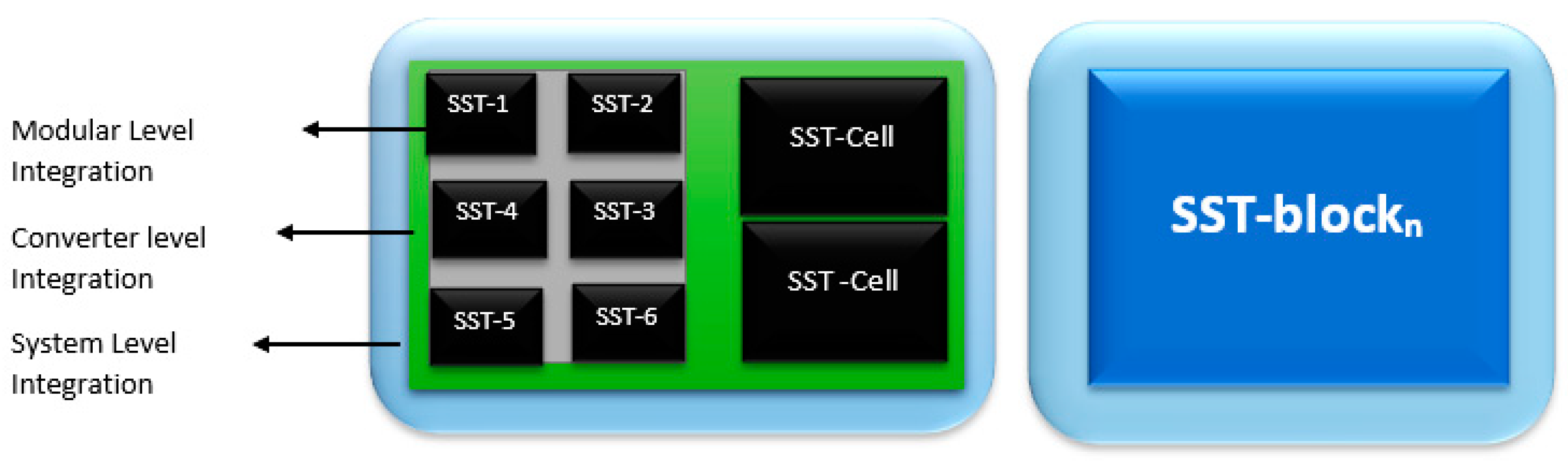
- Mishra, D.K.; Ghadi, M.J.; Li, L.; Hossain, M.J.; Zhang, J.; Ray, P.K.; Mohanty, A. A review on solid-state transformer: A breakthrough technology for future smart distribution grids. Int. J. Electr. Power Ener. 2021, 133, 107255. [CrossRef]
- Hunziker, C.; Lehmann, J.; Keller, T.; Heim, T.; Schulz, N. Networks, Sustainability assessment of novel transformer technologies in distribution grid applications. J. Sust. Energy Grids Netw. 2020, 21, 100314. [CrossRef]
- Rødal, G.L.; Pushpalatha, Y.V.; Peftitsis, D. Design Evaluation of Medium-Voltage and High-Power Modularized DC/DC Converters with SiC MOSFETs. In Proceedings of the 23rd European Conference on Power Electronics and Applications (EPE’21 ECCE Europe), Ghent, Belgium, 6–10 September 2021.
- Sanchez, S.; Molinas, M. Degree of influence of system states transition on the stability of a DC microgrid. J. IEEE Trans. Smart Grid. 2014, 5, 2535–2542. [CrossRef]
- Baliga, B.J. Chapter 7—Gate Drive Circuit Design. In The IGBT Device; Baliga, B.J., Ed.; William Andrew Publishing: Amsterdam, The Netherlands, 2015; pp. 193–203.
- Shair, J.; Li, H.; Hu, J.; Xie, X. Power system stability issues, classifications and research prospects in the context of high-penetration of renewables and power electronics. J. Renew. Sust. Energy Rev. 2021, 145, 111111. [CrossRef]
- Dastgeer, F.; Gelani, H.; Ali, F.; Javed, Z. Enhancing the Energy/Power Efficiency of a DC Distribution Grid for Residential Buildings via Modular Architecture of DC/DC Solid State Transformers. J. Adv. Sci. Technol. Eng. Syst. 2018, 3, 288–297. DOI: 10.25046/aj030534.
- Tingfang, Y.; Ting, T.O. Methodological Priority List for Unit Commitment Problem. In the Proceedings of the 2008 International Conference on Computer Science and Software Engineering, Wuhan, China, 12–14 December 2008; Volume 1, pp. 176–179.
- Raj, V.M.; Chanana, S. Analysis of unit commitment problem through Lagrange relaxation and priority listing method. In Proceedings of the 6th IEEE Power India International Conference (PIICON), Delhi, India, 5–7 December 2014; pp. 1–6.
- Skolfield, J.K.; Escobedo, A.R. Operations research in optimal power flow: A guide to recent and emerging methodologies and applications. Eur. J. Oper. Res. 2022, 300, 387–404. [CrossRef]
- Travers, D.L.; Kaye, R.J. Dynamic dispatch by constructive dynamic programming. IEEE Trans. Power Syst. 1998, 13, 72–78. [CrossRef]
- Chaitanya, S.N.V.S.K.; Ashok Bakkiyaraj, R.; Venkateswara Rao, B. Technical Review on Optimal Reactive Power Dispatch with FACTS Devices and Renewable Energy Sources. In Lecture Notes in Electrical Engineering; Springer: Singapore, 2022; pp. 185–194.
- Naderi, E.; Narimani, H.; Pourakbari-Kasmaei, M.; Cerna, F.V.; Marzband, M.; Lehtonen, M. State-of-the-Art of Optimal Active and Reactive Power Flow: A Comprehensive Review from Various Standpoints. Processes 2021, 9, 1319. [CrossRef]
- Rugthaicharoencheep, N.; Boonthienthong, M.; Charlangsut, A. Optimal Reactive Power Control in Power System with Particle Swarm Optimization Technique. Appl. Mech. Mater. 2019, 891, 246–252.
- Mouassa, S.; Bouktir, T. Artificial Bee Colony Algorithm for Discrete Optimal Reactive Power Dispatch. In Proceedings of the International Conference on Industrial Engineering and Systems Management (IESM), Seville, Spain, 21–23 October 2015; pp. 654–662.
- Boussaïd, I.; Lepagnot, J.; Siarry, P. A survey on optimization metaheuristics. Inf. Sci. 2013, 237, 82–117. [CrossRef]
- Zedadra, O.; Guerrieri, A.; Jouandeau, N.; Spezzano, G.; Seridi, H.; Fortino, G. Swarm intelligence-based algorithms within IoT-based systems: A review. J. Parallel Distrib. Comput. 2018, 122, 173–187. [CrossRef]
- Dokeroglu, T.; Sevinc, E.; Kucukyilmaz, T.; Cosar, A. A survey on new generation metaheuristic algorithms. Comput. Ind. Eng. 2019, 137, 106040. [CrossRef]
- Reddy, A.V.S.; Reddy, Y.P.K.; Reddy, B.B.R. Application of ALO to Economic Load Dispatch Without Network Losses for Different Conditions. In Proceedings of the 2nd IEEE International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), New Delhi, India, 22 October 2018; pp. 244–248.
- Faseela, C.K.; Vennila, H. Economic and Emission Dispatch using Whale Optimization Algorithm (WOA). Int. J. Electr. Comput. Eng. 2018, 8, 1297. [CrossRef]
- Pulluri, H.; Kumar, N.G.; Rao, U.M.; Preeti; Kumar, M.G. Krill Herd Algorithm for Solution of Economic Dispatch with Valve-Point Loading Effect; Springer: Singapore, 2019; pp. 383–392. [CrossRef]
- Karakonstantis, I.; Vlachos, A. Bat algorithm applied to continuous constrained optimization problems. J. Inf. Optim. Sci. 2021, 42, 57–75. [CrossRef]
- Kumar, A.; Singhi, R.; Das, S.; Malakar, T.; Prakash, O.; Das, P. Economic Load Dispatch Using Salp Swarm Algorithm. In Proceedings of the IEEE 9th Power India International Conference (PIICON), Sonepat, India, 28 February–1 March 2020.
- Mirjalili, S. The Ant Lion Optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [CrossRef]
- Kamboj, V.; Bhadoria, A.; Bath, S.K. Solution of non-convex economic load dispatch problem for small-scale power systems using ant lion optimizer. Neural. Comput. Appl. 2017, 28, 2181–2192. [CrossRef]
- Dastgeer, F.; Gelani, H.E. A Comparative analysis of system efficiency for AC and DC residential power distribution paradigms. Energy Build. 2017, 138, 648–654. [CrossRef]
- Ryu, M.-H.; Kim, H.-S.; Baek, J.-W.; Kim, H.-G.; Jung, J.-H. Effective Test Bed of 380-V DC Distribution System Using Isolated Power Converters. IEEE Trans. Ind. Electron. 2015, 62, 4525–4536. [CrossRef]
- Sha, D.; Wang, X.; Chen, D. High Efficiency Current-Fed Dual Active Bridge DC–DC Converter with ZVS Achievement Throughout Full Range of Load Using Optimized Switching Patterns. IEEE Trans. Power Elect. 2018, 33, 1347–1357. [CrossRef]
- Powerstax Europe. Powerstax F351 Datasheet—Full Brick 350W DC/DC Converter; Powerstax Ltd UK. 22 July 2017.
- Fan, H.; Li, H. High-Frequency Transformer Isolated Bidirectional DC–DC Converter Modules with High Efficiency Over Wide Load Range for 20 kVA Solid-State Transformer. IEEE Trans. Power Elect. 2011, 26, 3599–3608. [CrossRef]
- COSEL. Cosel DBS700B28—700W DC/DC Converter. Available online: https://www.digikey.com/en/products/detail/cosel-usa-inc/DBS700B28/7046342 (accessed on 21 June 2022).
- Kim, H.-S.; Ryu, M.-H.; Baek, J.-W.; Jung, J.-H. High-Efficiency Isolated Bidirectional AC–DC Converter for a DC Distribution System. IEEE Trans. Power Electron. 2013, 28, 1642–1654. [CrossRef]
- Kelishami, M.K.; Lakzian, E. Optimization of the blowing ratio for film cooling on a flat plate. Int. J. Numer. Method H 2017, 27, 104–119. [CrossRef]
- Hosseini, R.; Lakzian, E. Optimization volumetric heating in condensing steam flow by a novel method. J. Therm. Anal. Calorim. 2020, 140, 2421–2433. [CrossRef]
- Hoseinzade, D.; Lakzian, E.; Hashemian, A. A blackbox optimization of volumetric heating rate for reducing the wetness of the steam flow through turbine blades. Energy 2021, 220, 119751. [CrossRef]
- Kiehbadroudinezhad, M.; Merabet, A.; Rajabipour, A.; Cada, M.; Kiehbadroudinezhad, S.; Khanali, M.; Hosseinzadeh-Bandbafha, H. Optimization of wind/solar energy microgrid by division algorithm considering human health and environmental impacts for power-water cogeneration. Energy Convers. Manag. 2022, 252, 115064. [CrossRef]
- Gelani, H.; Dastgeer, F.; Nasir, M.; Khan, S.; Guerrero, J. AC vs. DC Distribution Efficiency: Are We on the Right Path? Energies 2021, 14, 4039. [CrossRef]
- Dastgeer, F.; Gelani, H.E.; Anees, H.M.; Paracha, Z.J.; Kalam, A. Analyses of efficiency/energy-savings of DC power distribution systems/microgrids: Past, present and future. Int. J. Electr. Power Energy Syst. 2019, 104, 89–100. [CrossRef]
- Kadandani, N.; Dahidah, M.; Ethni, S.; Yu, J. Solid state transformer: An overview of circuit configurations and applications. In Proceedings of the 15th IET International Conference on AC and DC Power Transmission (ACDC 2019), Coventry, UK, 5–7 February 2019; p. 6. [CrossRef]
- Shadfar, H.; Pashakolaei, M.G.; Foroud A.A. Solid-state transformers: An overview of the concept, topology, and its applications in the smart grid. Int. Trans. Electr. Energy Syst. 2021, 31, e12996. [CrossRef]
- Smart Cities and Smart Spaces: Concepts, Methodologies, Tools, and Applications; Ed. Information Resources Management Association (USA), IGI Global: 2019. [CrossRef]
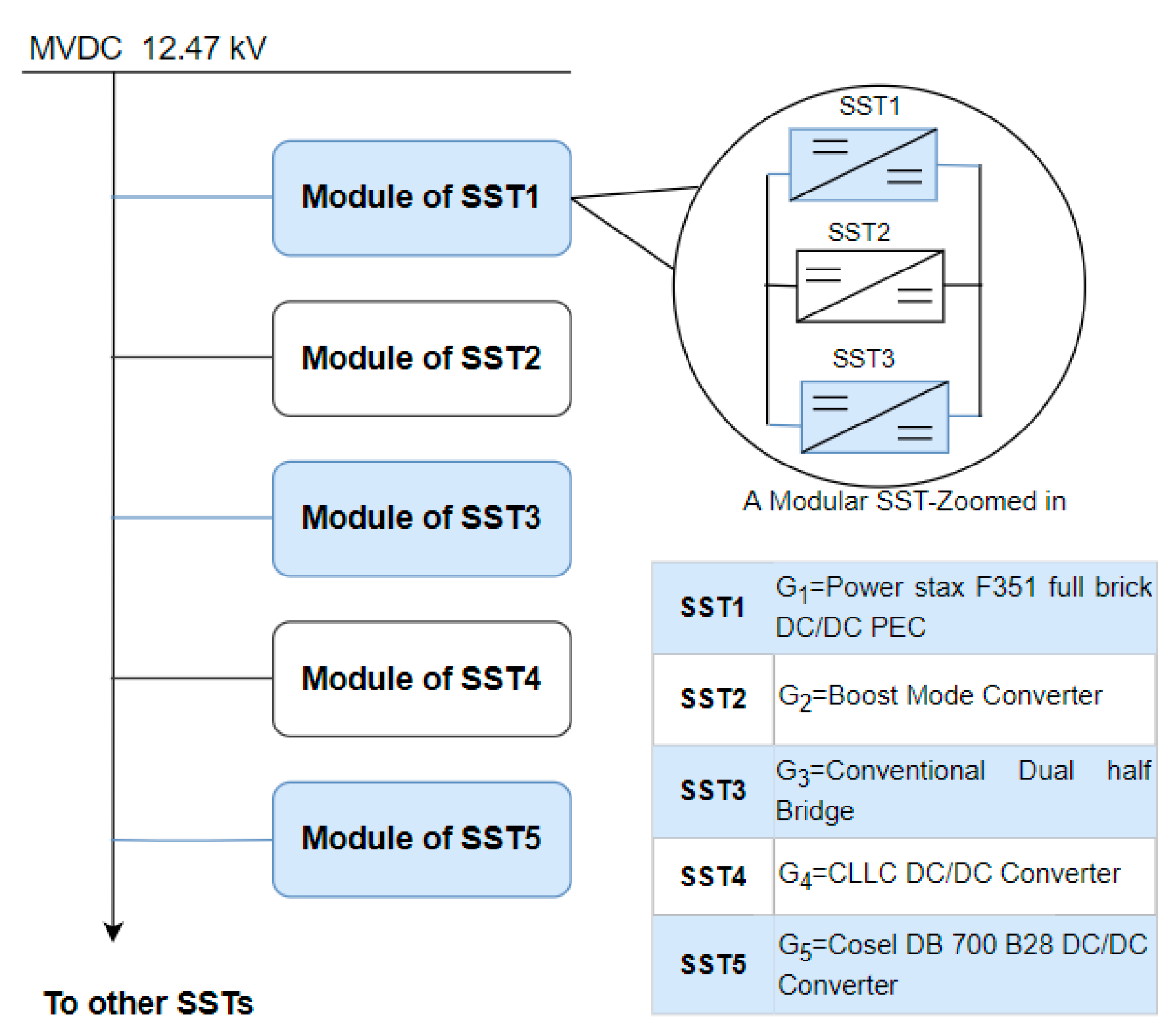
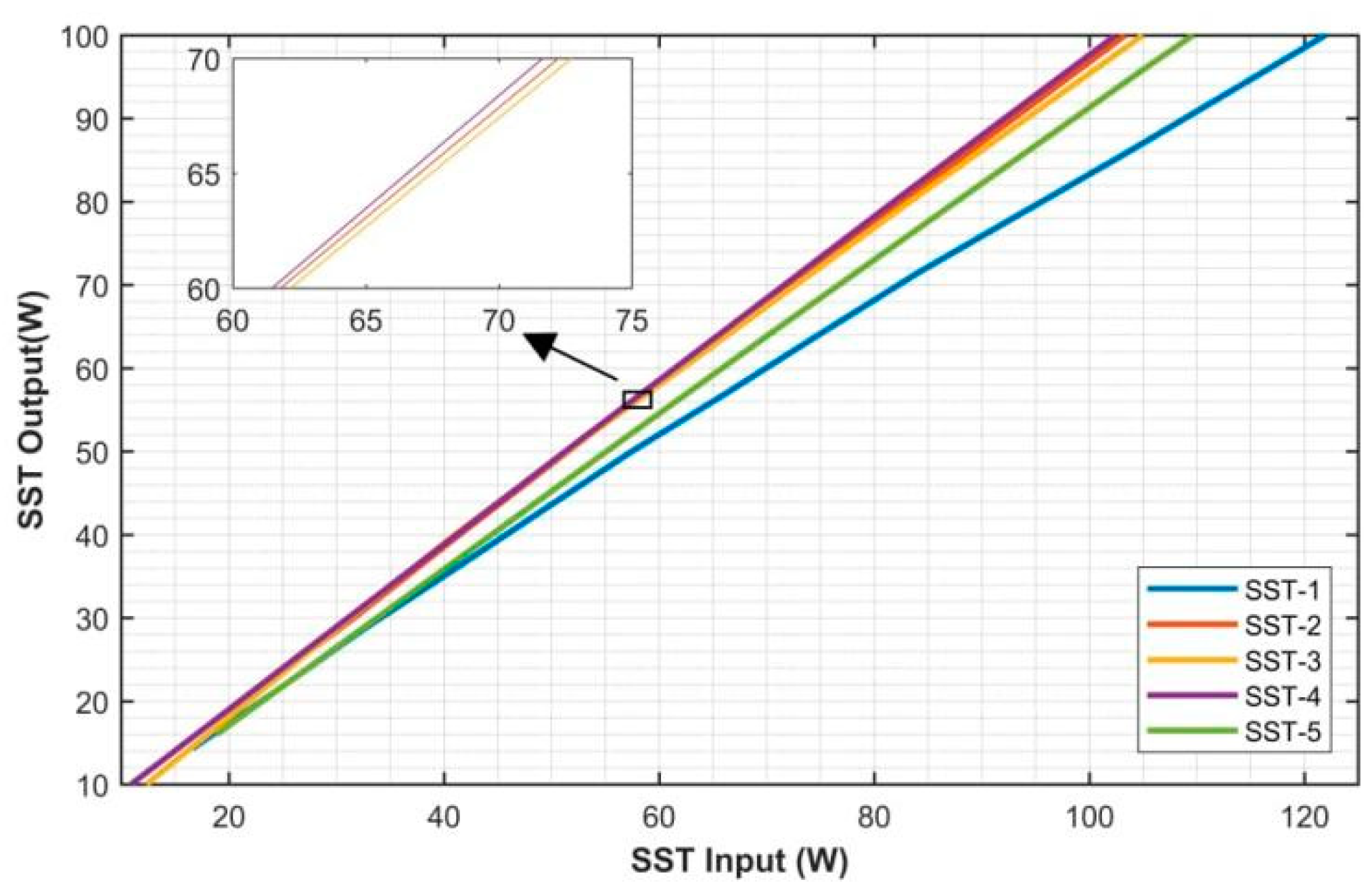
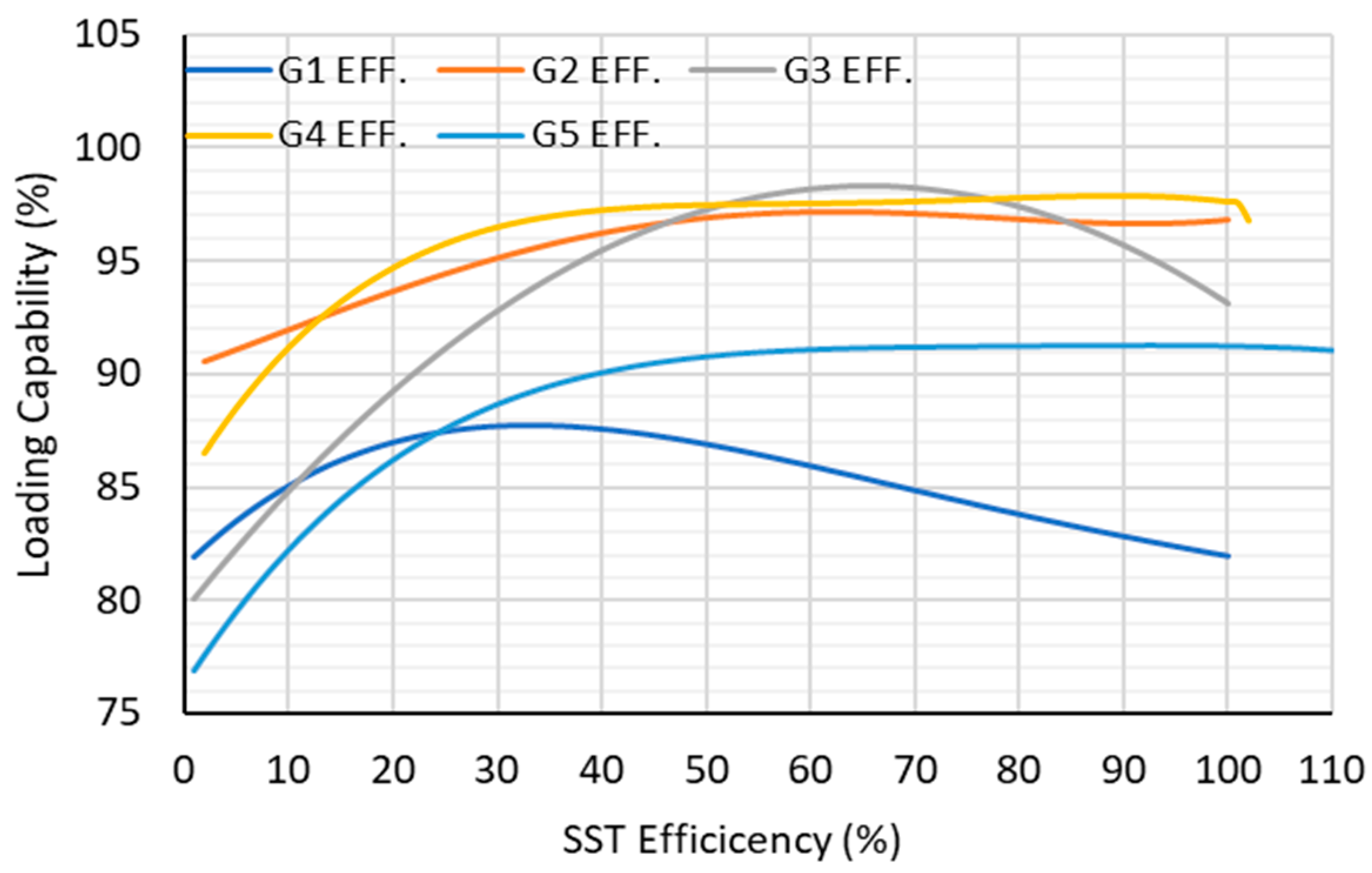
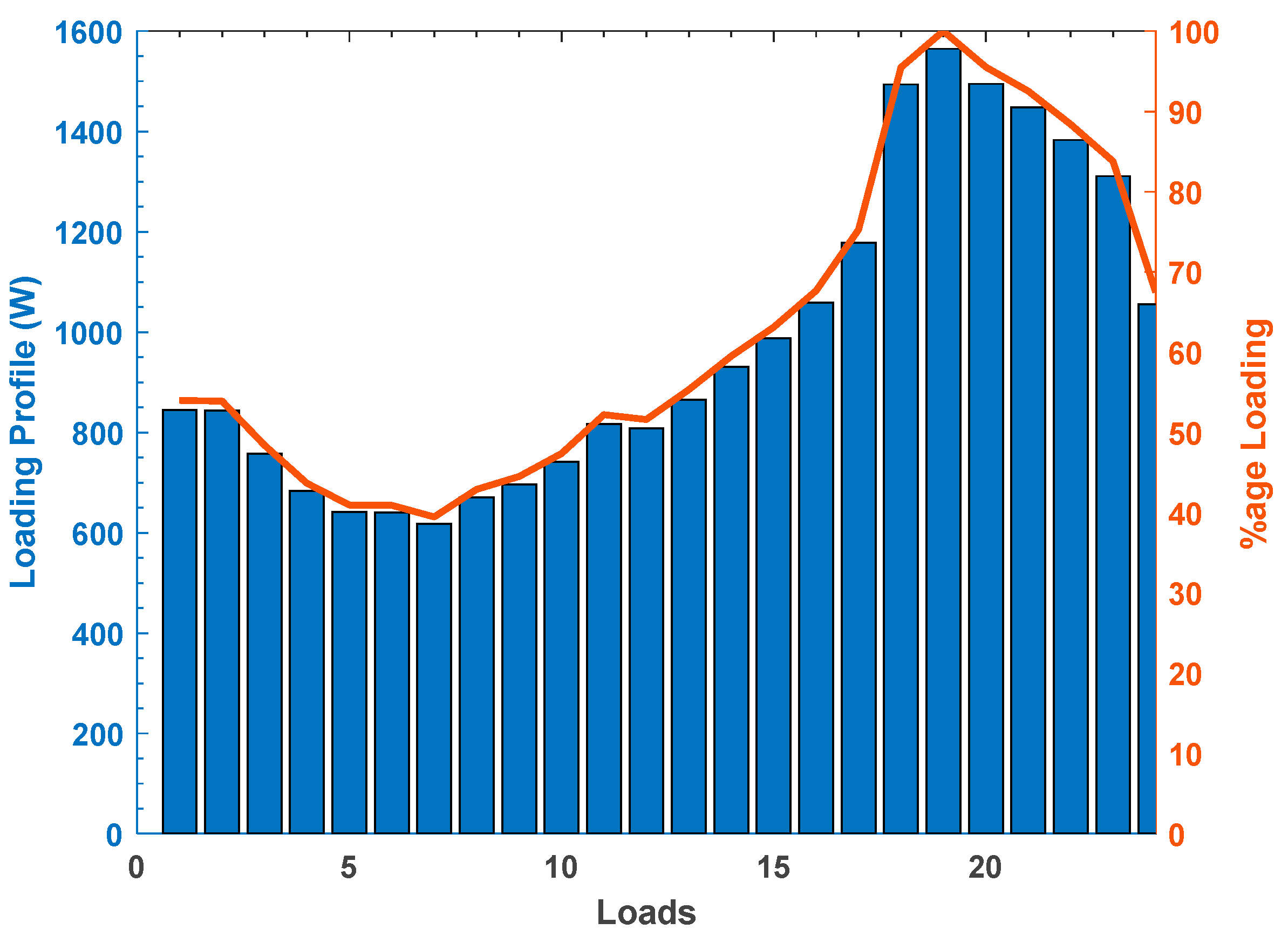
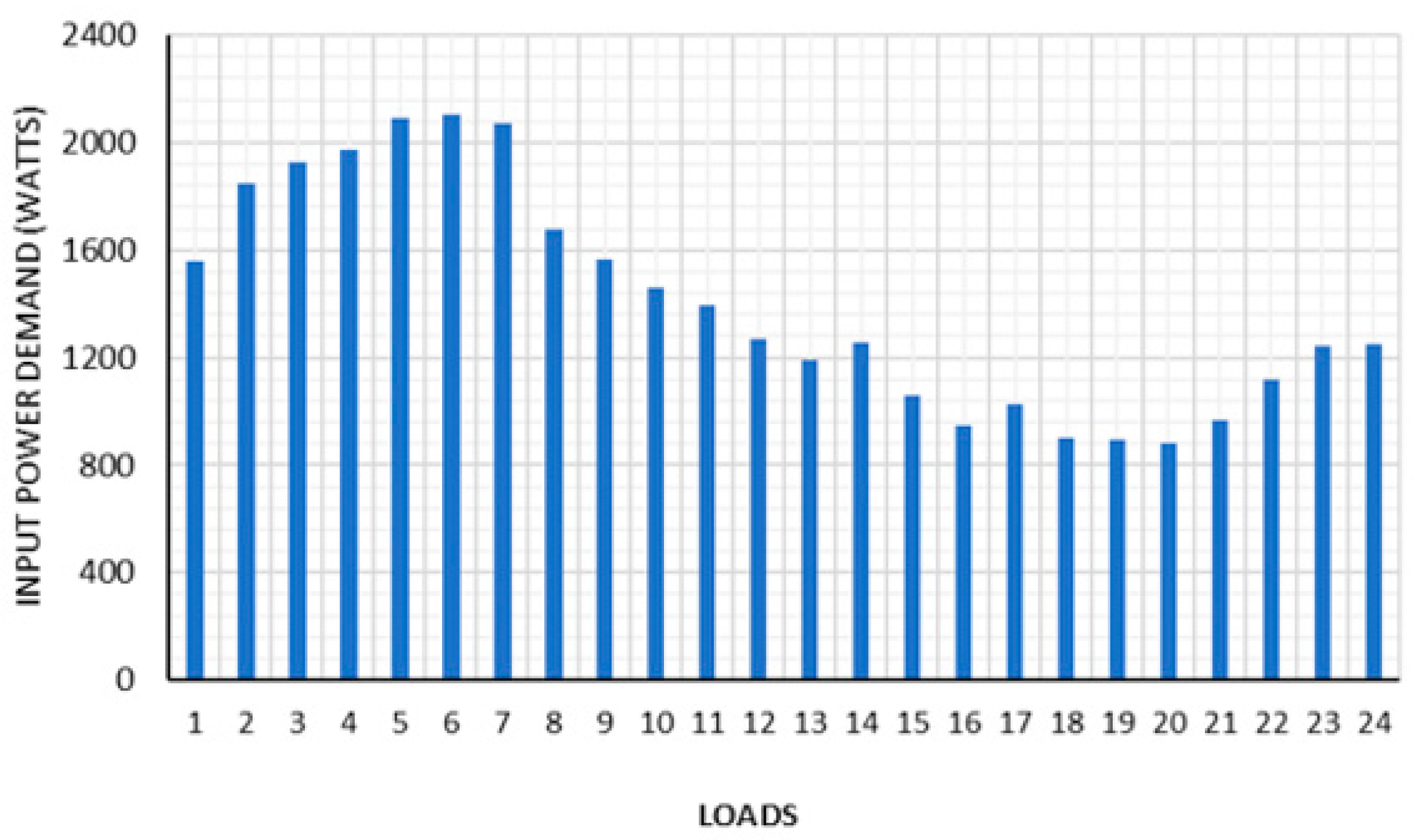
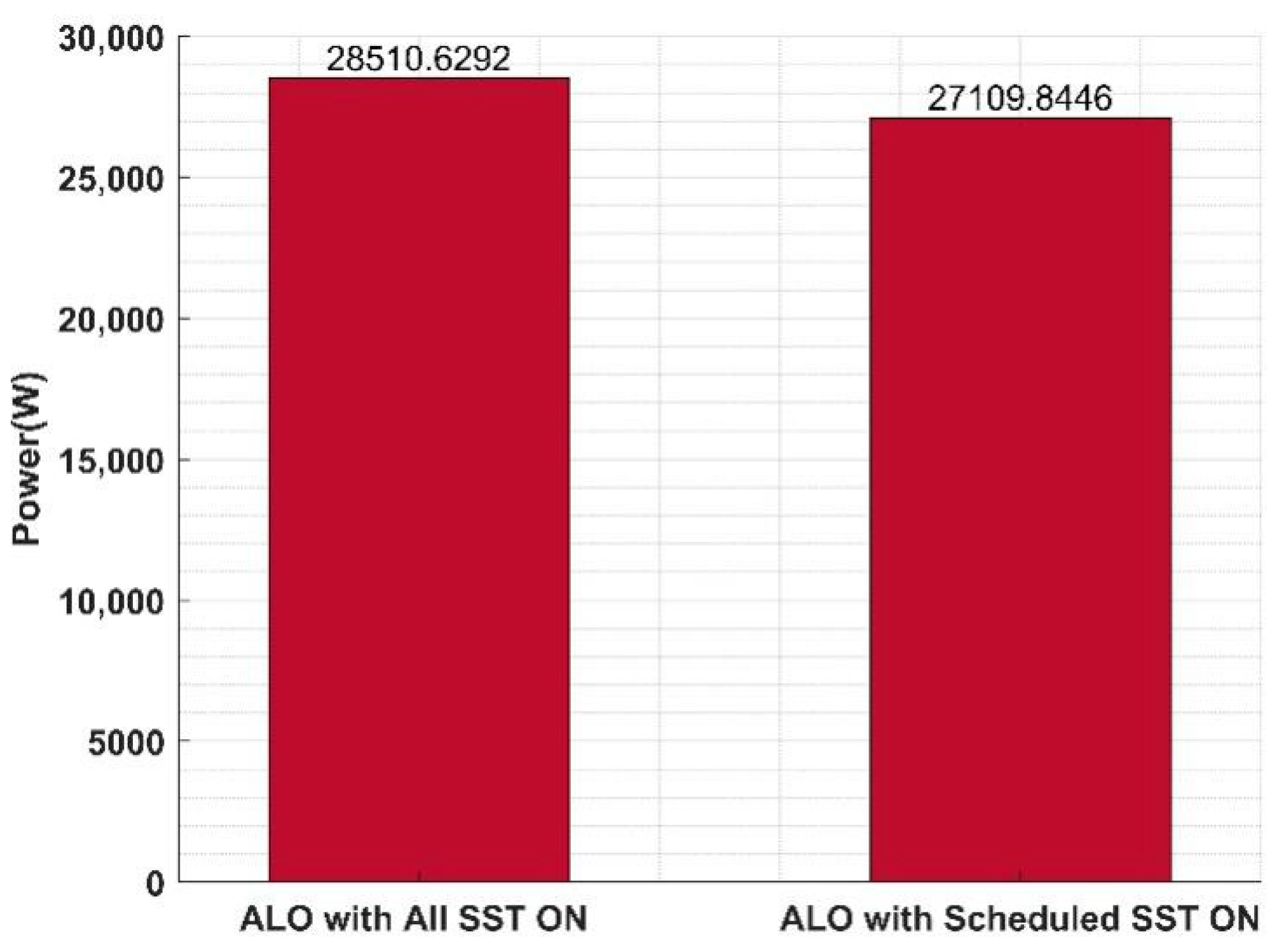
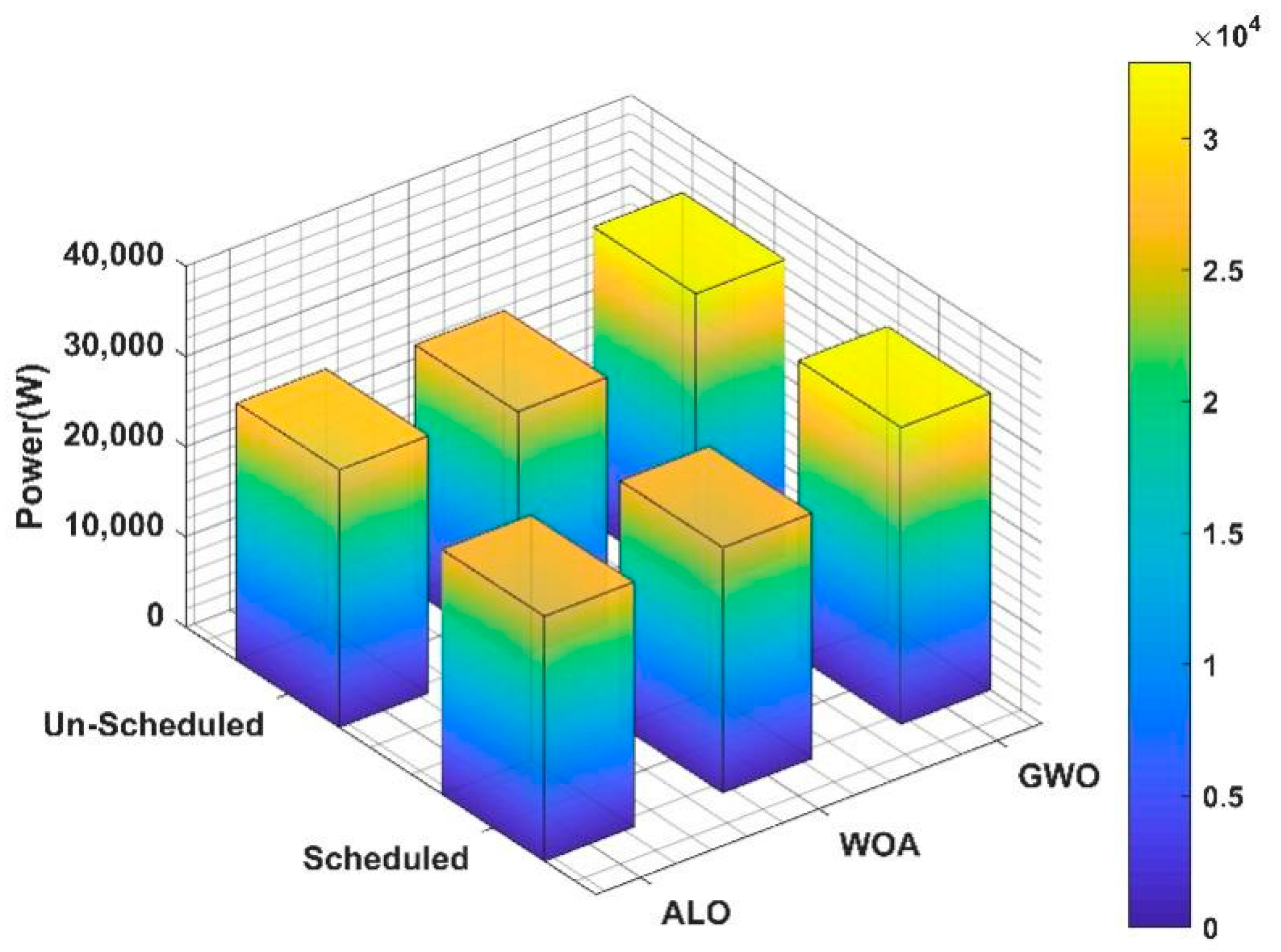
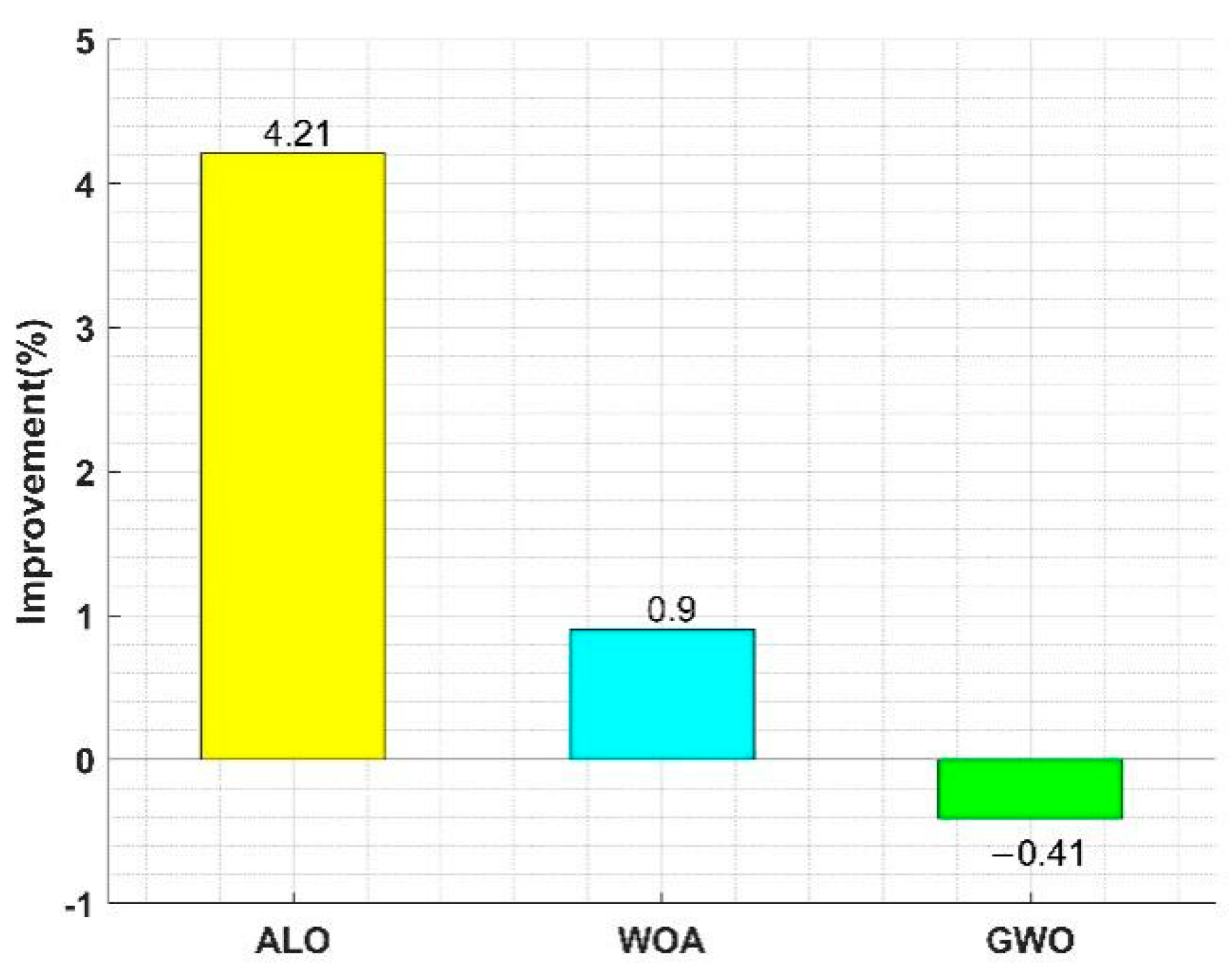
| SST Configuration Input/Output | α | β | γ | Pmin | Pmax |
|---|---|---|---|---|---|
| SST1-set of 3 | 0.0017 | 1.0409 | 1.4481 | 14.28 | 100 |
| SST2-set of 3 | 0.003 | 0.9845 | 1.5944 | 20 | 100 |
| SST3-set of 3 | 0.0010 | 0.9268 | 2.8204 | 10 | 100 |
| SST4-set of 3 | 0.0002 | 0.9991 | 0.9542 | 10 | 100 |
| SST5-set of 4 | 0.003 | 1.0438 | 2.1322 | 16 | 110 |
| Loading/Efficiency | a | b | c |
|---|---|---|---|
| SST1 | −0.0012 | 0.0780 | 85.9195 |
| SST2 | −0.0015 | 0.2206 | 89.5267 |
| SST3 | −0.0044 | 0.5768 | 79.4532 |
| SST4 | −0.0015 | 0.2108 | 90.6773 |
| SST5 | −0.0015 | 0.2444 | 81.9398 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





