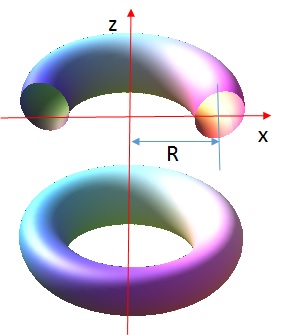
For a given material, different shapes correspond to different rigidities. In this paper, the radii of the oblique elliptic torus are formulated, a nonlinear displacement formulation is presented and numerical simulations are carried out for circular, normal elliptic, and oblique tori, respectively. Our investigation shows that both the deformation and the stress response of an elastic torus are sensitive to the radius ratio, and indicate that the analysis of a torus should be done by using the bending theory of shells rather than membrance theory. A numerical study demonstrates that the inner region of the torus is stiffer than the outer region due to the Gauss curvature. The study also shows that an elastic torus deforms in a very specific manner, as the strain and stress concentration in two very narrow regions around the top and bottom crowns. The desired rigidity can be achieved by adjusting the ratio of minor and major radii and the oblique angle.