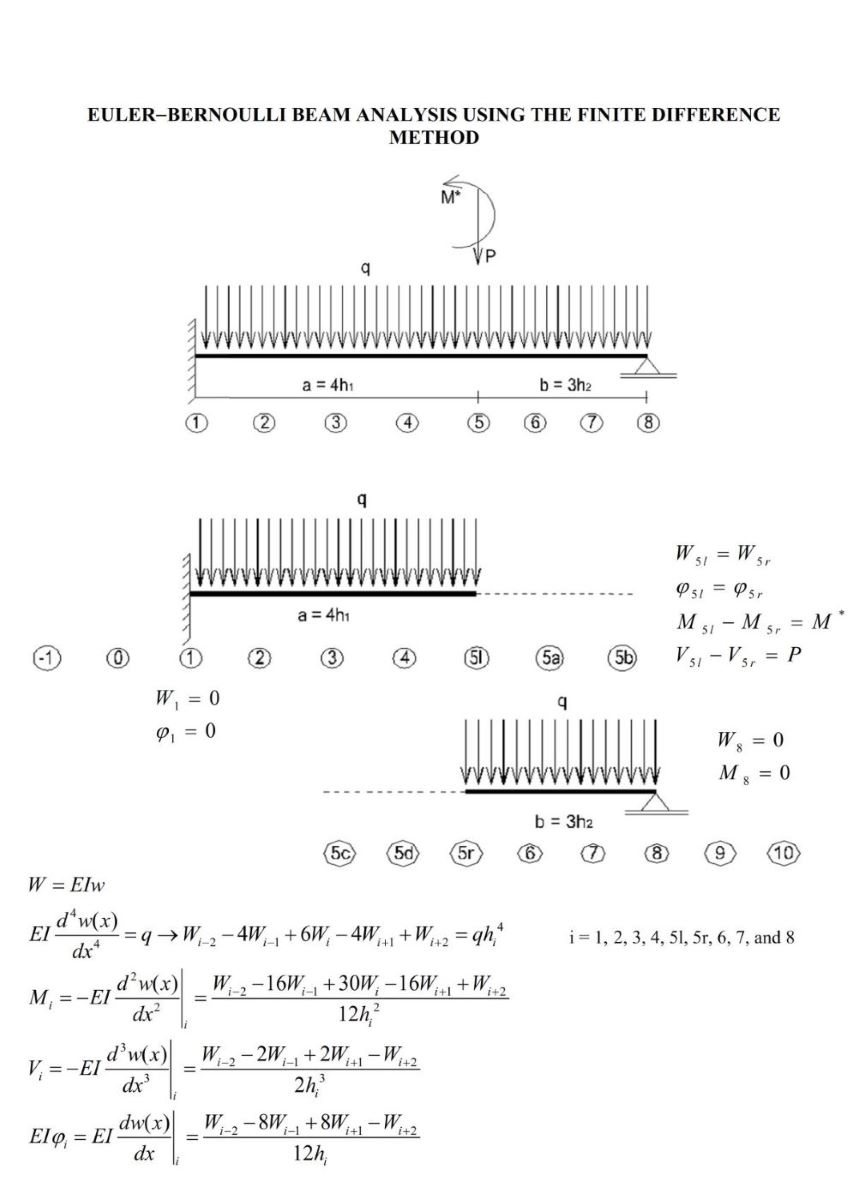
This paper presents an approach to the Euler-Bernoulli beam theory (EBBT) using the finite difference method (FDM). The EBBT covers the case of small deflections, and shear deformations are not considered. The FDM is an approximate method for solving problems described with differential equations (or partial differential equations). The FDM does not involve solving differential equations; equations are formulated with values at selected points of the structure. The model developed in this paper consists of formulating partial differential equations with finite differences and introducing new points (additional points or imaginary points) at boundaries and positions of discontinuity (concentrated loads or moments, supports, hinges, springs, brutal change of stiffness, etc.). The introduction of additional points permits us to satisfy boundary conditions and continuity conditions. First-order analysis, second-order analysis, and vibration analysis of structures were conducted with this model. Efforts, displacements, stiffness matrices, buckling loads, and vibration frequencies were determined. Tapered beams were analyzed (e.g., element stiffness matrix, second-order analysis). Finally, a direct time integration method (DTIM) was presented. The FDM-based DTIM enabled the analysis of forced vibration of structures, the damping being considered. The efforts and displacements could be determined at any time.