Kullback–Leibler Divergence of a Freely Cooling Granular Gas

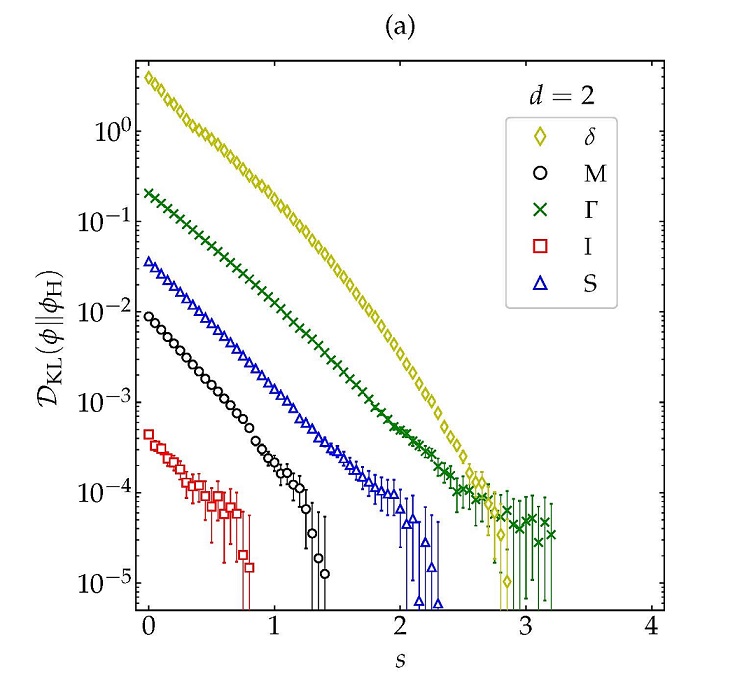
Finding the proper entropy functional associated with the inelastic Boltzmann equation for a granular gas is a yet unsolved challenge. The original H-theorem hypotheses do not fit here and the H-functional presents some additional measure problems that are solved by the Kullback–Leibler divergence (KLD) of a reference velocity distribution function from the actual distribution. The right choice of the reference distribution in the KLD is crucial for the latter to qualify or not as a Lyapunov functional, the “homogeneous cooling state” (HCS) distribution of the freely cooling system being a potential candidate. Due to the lack of a formal proof, the aim of this work is to support this conjecture aided by molecular dynamics simulations of inelastic hard disks and spheres in a wide range of values for the coefficient of restitution (α). Our results reject the Maxwellian distribution as a possible reference, whereas reinforce the HCS one. Moreover, the KLD is used to measure the amount of information lost on using the former rather than the latter, and reveals a nonmonotonic dependence with α. Additionally, a Maxwell-demon-like velocity-inversion experiment highlights the microscopic irreversibility of the granular gas dynamics.