An Alternative Model of Gravitational Forces in Nature Using the Combined Effects of Repulsion and Attraction Forces on Gaseous Molecules

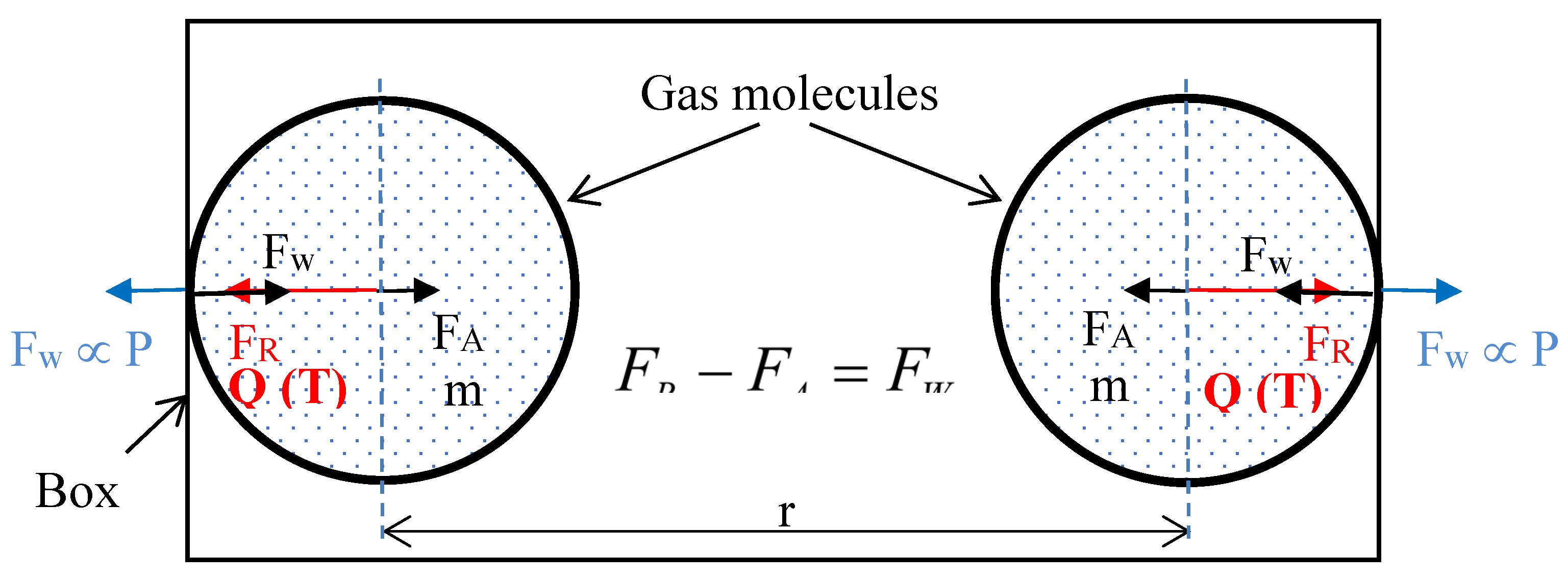
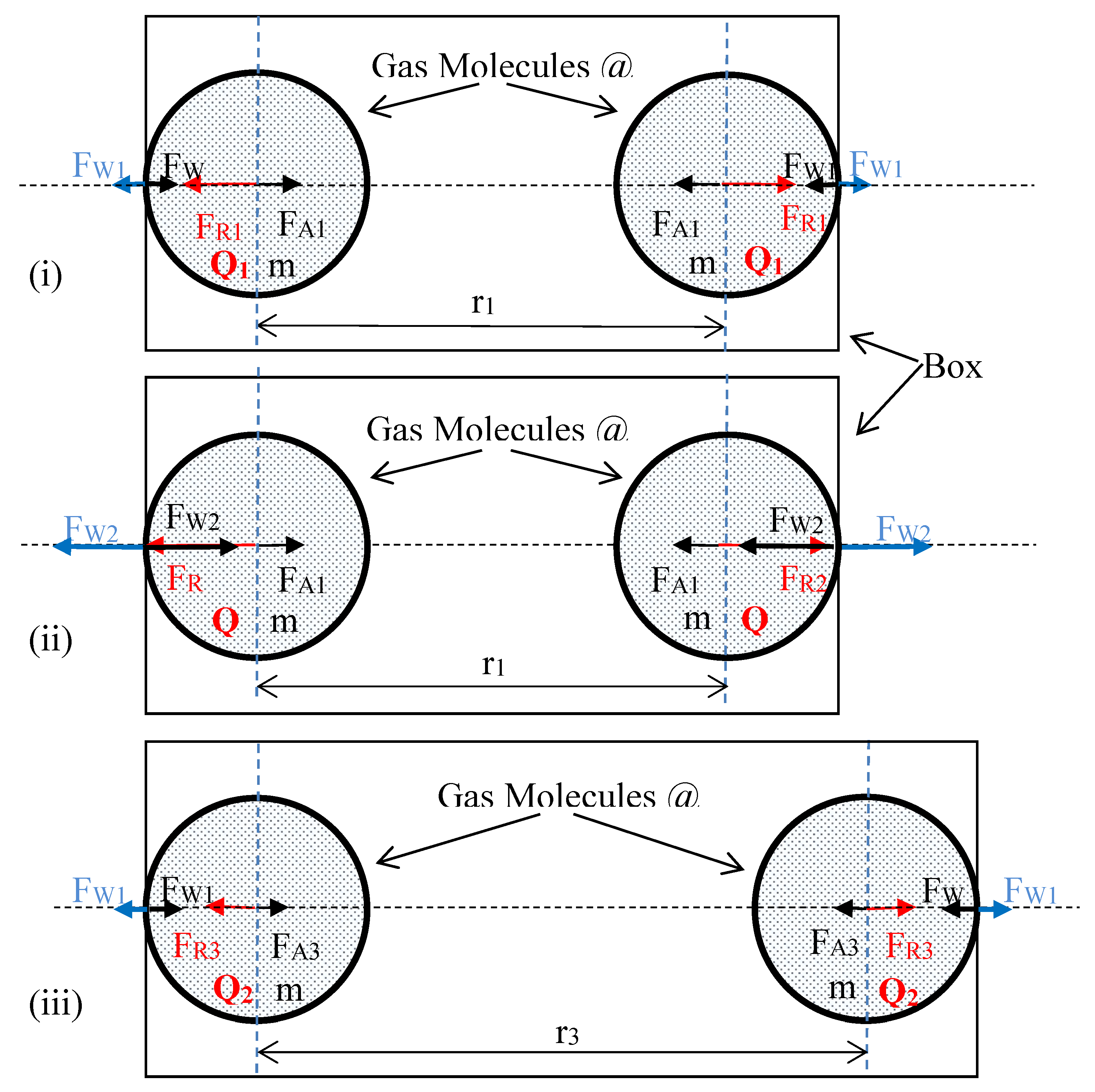
1. Introduction

An alternative mathematical model of the gravitational repulsion force and the gravitational attraction force has been developed herein, considering them as two distinct forces acting on gaseous matter. The model has been validated using experimentally determined and established data utilized in practical thermodynamic applications of mechanical engineering industries. It is a self-standing model, which requires no fitting into existing models. The presented alternative model could more effectively describe the nature of the universe at both micro and macro levels. The gravitational repulsion concept presented in the series of publications [1,2,4,5] emanating from this research program, are based on experimental observations and natural phenomena; making neither abstruse assumptions nor explanations.

The present understanding of the universe is that there are four fundamental interactions (also known as fundamental forces in classical theory): weak (subatomic), strong (subatomic), electromagnetic and gravitational. None of these fundamental forces are so far defined to be temperature (hence energy) dependent. There are, nevertheless, phenomena observed in the nature/universe (e.g.: pressure, expansion, and so on) that are dependent on temperature which is a manifestation of the thermal energy content. Both gravitational repulsion and attraction forces analytically and experimentally proved, in this research, to be dependent on the thermal energy content, thus fills the critical gap between energy and fundamental forces!

In some literature [6,7,8,9], the gravitational repulsion force is referred to as the antigravitational force. Therefore, we use both these words in our text to mean the same concept.

Presenting a new scientific revelation that fundamentally challenges our understanding of the universe, requires examining the foundations of our present understanding, viz., Newtonian and Einsteinian gravity concepts, and the kinetic theory of ideal gas. The Author would, hence briefly note:

• Newtonian and Einsteinian gravity concepts, highlighting foundations of our present understanding
• Early notions of the gravitational repulsion force and its recent revelations
• The challenges of a major assumption in the kinetic theory of ideal gas, used in the derivation of the ideal gas equation

1.1. Brief note on Newtonian and Einsteinian Gravity Concepts:

The concept of gravity, the ‘Law of Universal Gravity’, was first proposed and mathematically derived as a relationship based on inductive reasoning of empirical observations by Newton in 1687 [10]. This empirical solution for the gravitational force between two masses m₁ and m₂, which are distance r apart, is given in the following mathematical form (Equation (1)):

$$Gravitational Force=G\frac{m_1{m}_2}{r^2}$$

(1)

where, G is the universal gravitational constant.

Secondly, another major interpretation of gravity was given by Einstein in 1907 as General Relativity [11], which is the theory of gravitation where the observed gravitational effect between masses results from their warping of space-time. Therein, gravity is not considered as a force, it is a consequence of the curvature of spacetime caused by the presence of mass energy. See ‘Einstein Field Equations’ (EFE) in theory of general relativity.

The general form of EFE is given as (Equation (2)):

$$R_{\mu \nu }-\frac{1}{2}R{g}_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }=\frac{8\pi G}{c^4}{T}_{\mu \nu }$$

(2)

where, $R_{\mu \nu }$ is the Ricci curvature tensor, $R$ is the scalar curvature, $g_{\mu \nu }$ is the metric tensor, $\mathsf{\Lambda }$ is the cosmological constant, $G$ is Newton's gravitational constant, $c$ is the speed of light in vacuum, and $T_{\mu \nu }$ is the stress–energy tensor.

Experiments and observations show that Einstein's description of gravitation accounts for several effects that are unexplained by Newton's laws, such as minute anomalies in the orbits of Mercury and other planets [12]. General relativity also predicts novel effects of gravity, such as gravitational waves [13], gravitational lensing [14] and an effect of gravity on time known as gravitational time dilation [15]. While some of the astronomical anomalies have been explained by the Einstein’s theory of general relativity, almost all the practical applications (for example all engineering applications) to date are still based precisely on the Newtonian model of gravitation.

The cosmological constant $\mathsf{\Lambda }$, the energy density of space, that arises in the Albert Einstein's field equations could be closely associated with the concepts of dark energy and quintessence (hypothetical form of dark energy, postulated in explaining the accelerating expansion of the universe) [16,17]. However, some doubts have been raised lately on the accuracy of the cosmological constant [18,19,20].

It has also been shown that by obeying local energy–momentum conservation, the EFE converges to the Newton’s law of gravitation where the gravitational field is considered weak and velocities are much less than the speed of light [21]. It is worth noting that the empirically derived gravitational constant $G$ in EFE is borrowed from the Newton’s universal gravitation relation; not a constant derived independently by Einstein. It could, hence, be observed that the EFE is, to some extent, related to the Newton’s law of gravity. This aspect, however, is out of the scope of this paper, thus to be discussed separately.

It also has to be noted that, under existing (Newtonian and Einsteinian) models, the gravitational force has been reckoned as a “weak force”. According to Table 1, the gravitational force is 10 ^–36 weak compared to the electromagnetic force; accordingly, a negligible force.

1.2. Early Notions of Gravitational Repulsion Force:

The above discussion compares Newtonian and Einsteinian gravity concepts, highlighting foundations of our present understanding. Newton’s model describes gravitation as an attractive force, and the repulsive nature of gravity has never been entertained. It has, however, been shown that a repulsive gravitational force could manifest itself within the theory of general relativity [23,24,25,26,27,28].

Albert Einstein, subsequently, attempted to form a generalized theory of gravitation that would unify the gravitational and electromagnetic forces (and perhaps others), guided by a belief in a single origin for the entire set of physical laws. Models of electromagnetism and gravity were pursued by Einstein in his attempts at a unified field theory (UFT) [29]. There was an attempt at harnessing electromagnetic interactions with gravitational interactions to induce torsion, which in turn could null out gravity. Thus, a sort of counteraction to gravity or an “antigravity” field would be the result [30]. UFT could be a point in the history of science that the idea of antigravity surfaced.

In Newtonian and Einsteinian mechanics, what has been observed as a gravitational effect between two bodies is nothing but the resultant effect of both gravitational repulsion and attraction forces acting simultaneously [2]. If gravitation attraction is the only force, the universe must see a contraction instead of expansion with an acceleration [31,32], and would eventually collapse. To explain the accelerating expansion of the Universe there have developed numerous modified Einsteinian models, modified Poissonian models [33] and cosmological models [34] assuming hypothetical ‘dark energy’ [35], and a repulsive force of the cosmological scale [28] relating to ideas of dark matter and dark energy [6,7,36]. Although cosmologists have brought in such ideas as possible reasons for expansion of the universe, they are still speculative and incomplete in explaining the observations in processes occurring/happening in the universe.

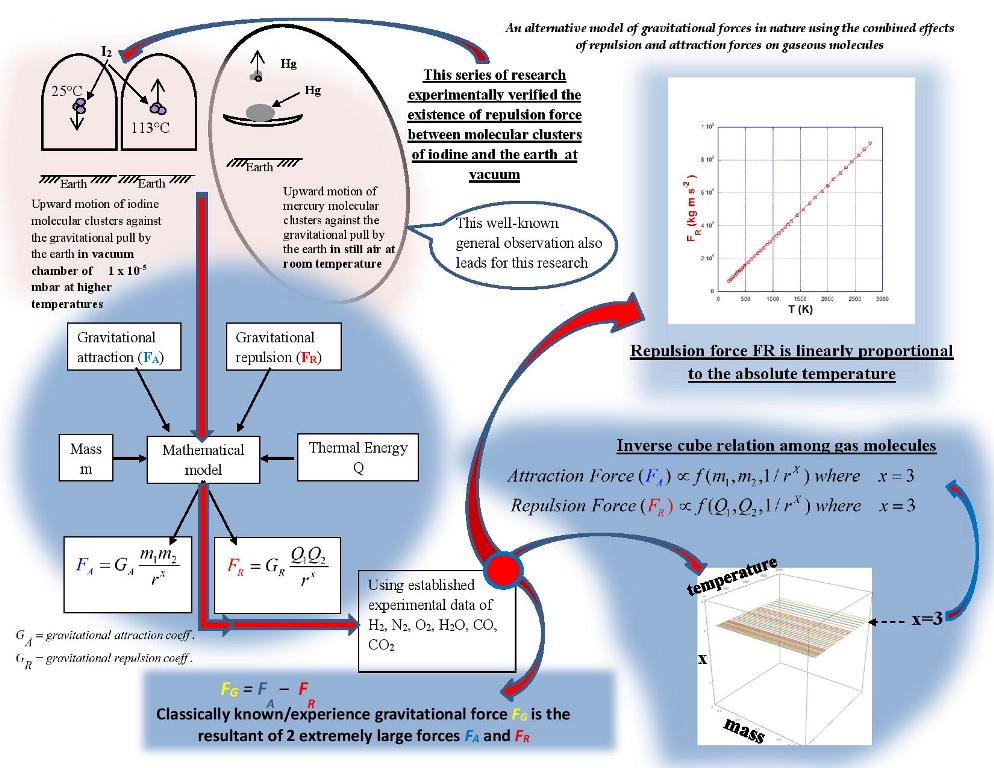
The present research makes an independent approach using of an alternative mathematical model of the gravitational repulsion force and the gravitational attraction force. No used hypothetical assumptions made. The model is validated using experimentally determined and established data utilized in practical thermodynamic applications of mechanical engineering industries.

1.3. Recent Revelation of the Gravitational Repulsion Force:

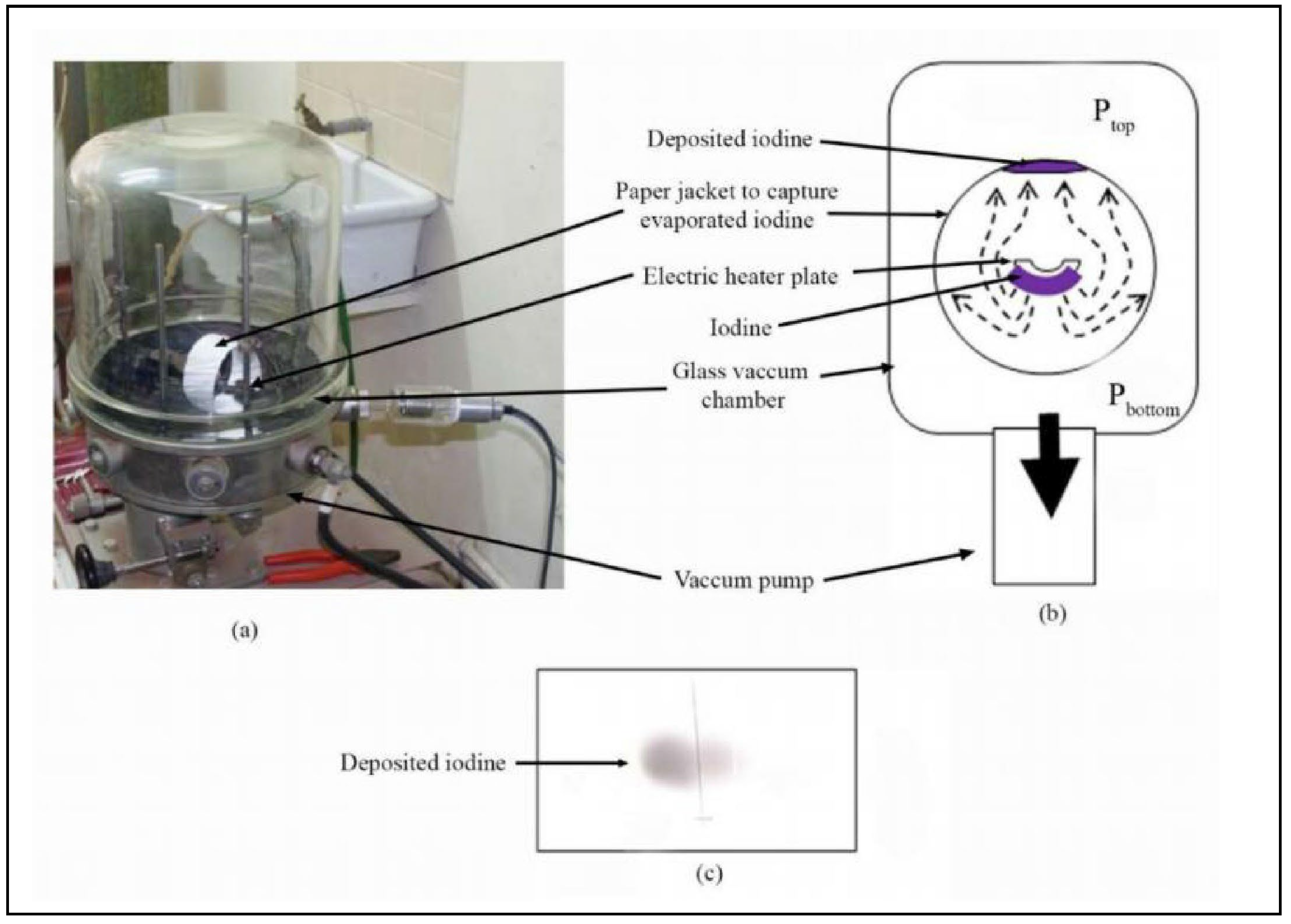
A series of experiments involving mechanistic laboratory studies [1,2,4,5] by the author, have shown that upward motion of matter against the gravitational attraction of the Earth happens due to a “cryptic” upward force; e.g., the upward movement of iodine in a vacuum[4] and upward movement water droplets in the air [2,5]. A series of studies [2,5] on water droplets confirmed that this cryptic force is proportional to the internal thermal energy of the droplets. The said tangible experiments, lead to the understanding of gravitational repulsion or antigravity force which persists against the gravitational attraction force. The iodine experiment is discussed in brief, later in this paper. It has further been extended that both gravitational repulsion and attraction forces pervade our surroundings both microscopically and macroscopically [1].

The discussion so far has briefly indicated why we need a deviation from the existing gravitational models; Newtonian ‘Law of Universal Gravity’ and Einsteinian ‘EFE’. Also, we need to deviate from a major idealistic assumption made in the kinetic theory of ideal gas. Now, our attempt is to develop a relationship to better understand the behavior of gas molecules with the force of repulsive nature on matter; antigravity.

1.4. Challenges of a Major Assumption in the Derivation of the Kinetic Theory of Ideal Gas:

As reasoned above, in application of the kinetic theory of ideal gas in derivation of the ideal gas equation, we are skeptical mainly about one major idealistic assumption [37]:

The intermolecular force in gaseous state is zero and as such molecules exhibit no force among themselves

In deriving the ideal gas equation, one of the most fundamental forces, the gravitational attraction among matter has been overlooked, both among air molecules themselves and with the Earth. Such steep assumption does not do justice to principles of fundamental science. Even though a gas molecule has minute quantity of matter, it is susceptible to gravitational forces with all entities of matter around. Therefore, it may not be prudent to make an assumption to neglect the gravitational forces on gas molecules with entities small or large. It is accepted that the atmosphere around the Earth exists because of the gravitational force of the Earth and this is a major force between the Earth and air molecules. Even Mars with a lower gravitational attraction accommodates an atmosphere of pressure ~ 0.6% (610 Pa) of the Earth atmosphere [38]. Also, denser atmospheres are found in planets with higher gravity such as Jupiter and Saturn, which hold even light gases such as hydrogen and helium in their atmospheres [39].

Further, the postulates of the kinetic molecular theory of ideal gases ignore the volume occupied by the molecules of a gas. Real gases, however, show significant deviations from the behavior expected for an ideal gas [40], e.g., Van Der Waals Equation.

1.5. Behavior of Real gas – the Van Der Waals Equation

Van der Waals modified [41] the ideal gas equation to describe the behavior of real gases by explicitly including the effects of molecular size and intermolecular attractive forces. The modified ideal gas equation, the so-called van der Waals equation:

$$(P+\frac{a{n}^2}{V^2})(V-nb)=nRT$$

(3)

where a and b are empirical constants that are dependent on the type of gas. an²/V² is added to compensate intermolecular attractive forces and nb corrects the volume term in the ideal gas equation by subtracting volume taken by the molecules in the space.

The anomalies addressed in the real gas behavior by the Van der Waals equation are only the attraction force and the volume taken by the gas molecules. The attraction force discussed by Van der Waals is considered as a week electrostatic force, and not a gravitational force.

The concept of gravitational repulsion or antigravity or matter moving against the gravitational field, is not a novel concept but one which has been under speculation over the years [6,7,8,9]. The repulsion between atoms at short distance (within the eigenvolume) has been modeled in Lennard-Jones potential [42,43]. This repulsion force, however, acts at very short range (~3-6 A°) usually between diatomic molecules. Van der Waals forces, nevertheless, are attractive interactions between atoms resulting from induced dipoles, and repulsive interactions resulting from overlap of the electron clouds of two atoms (electrostatic repulsion) when they get too close to each other [44]. The total energy of Van der Waals interactions could be approximated by the Lennard-Jones expression. They, however, did not consider gravitational repulsion and gravitational attraction forces among gaseous atoms/molecules.

Recently published experiments by the author [1,2,4,5] show that there exists not only gravitational attraction forces acting on matter but also gravitational repulsion forces between them. The following section briefly recalls a groundbreaking laboratory experiment [4] as it makes a landmark revelation of the effect of gravitational repulsion.

2. Groundbreaking Experiment on Gravitational Repulsion:

The very first information [1] on gravitational repulsion by the Author has shown the upward movement of heavy particles (iodine) in a vacuum (Figure 1, repeated here for clarity), in a situation where all factors which are believed to be causing the upward movement of particles against the gravitational pull in air, viz., buoyancy and convective forces, are eliminated by experimental design. Initially, at the room temperature (~25°C), the iodine particles detached from the iodine sample moved downward under gravitational attraction force with the Earth, and deposited in the bottom part of the paper jacket. When the iodine sample was heated, the experiment revealed that iodine particles move against gravitational pull in the vacuum as shown in the Figure 1 [1]. It also cites an example from electronic vacuum tubes (also called electronic valves) where evaporated tungsten and thorium particles (heavy metal particles) from the filaments move upwards despite the gravitational pull and the strong radial electric fields, and deposit at the top of the glass tube. These findings substantiate that the gravitational repulsion force acts on matter, similar to the gravitational attraction force.

(a)

Vacuum deposition chamber

(b)

A layer of iodine was gradually heat evaporated (ejected in the downward direction) inside the vacuum chamber. The electrical heater plate itself covers the iodine particles from moving directly in the upward direction. The iodine source was surrounded with a paper jacket in order to capture the deposition geometry of iodine. The paper was placed 50 mm radially away from the iodine source. Pressure in the chamber was ~ 1x10 ^–5 mbar, average mean free path is greater than 6.6 m and air density was approximately 12.6 ng m ^–3. Pressure at the top ($P_{top}$) of the chamber was higher than the bottom ($P_{bottom}$); $P_{top}$>$P_{bottom}$

(c)

Photograph of deposited iodine on inner top part of the paper.

2.1. Takeaways from the Above Iodine Experiment:

In the gravitational repulsion force experimentally observed as described above, the two entities of matter are iodine particles and the Earth. The findings of the said experiment could be summarized as:

1)

There is a repulsive force acting on iodine particles, in the direction opposite to the Earth’s gravitational force.

2)

The repulsive force is dependent on the thermal energy of the particle (as observed by the temperature T, which is a manifestation of the thermal energy Q).

Note: Heat is thermal energy. According to the existing definition, thermal energy is the net potential energy of the system. The internal energy is the net potential energy + the net kinetic energy of the system. The total kinetic energy of particles bounded by potential forces over time in virial theorem [44] assuming that average kinetic energy of a system is proportional to the average potential energy is another concept of energy in a system. Virial theorem also discusses some possible mechanisms [45] dominating stellar contraction due to the gravitational attraction. Our discussion, however, is grounded on a repulsive force dependent on thermal energy which is based only on its potential energy and therefore further engagement with kinetic energy is disregarded in this paper.

Further, other stages in this research program have experimentally demonstrated the existence repulsion force between water droplets and the Earth, and that the time-of-fall of a water-droplet in still air increases with the temperature of the droplet [1,2]. A similar idea has been predicted for a hypothetical quantum fluid: “that the temperature difference creates a direction in space in which quantum liquids can flow, even against the force of gravity” [45] p1950184-1.

2.2. Forces Between Two Entities of Matter:

The above summarized points are illustrated in Figure 2, generalized for any two entities of matter.

Reference the arrangement presented in Figure 2, relationships between two arbitrary entities of matter, with masses m₁, m₂, at absolute temperatures T₁, T₂ and thermal energy contents Q₁, Q₂ are:

1)

Based on the conventional gravitational law:

$$attraction force\propto mass(m_1,m_2)$$

(4)

2)

Experimental findings presented in author’s publication [2] show that:

$$repulsion force\propto thermal energy(Q_1,Q_2)$$

(5)

Thermal energy, Q is expressed by definition [41] as:

$$Q=mcT$$

(6)

where c is the specific heat capacity and T is the absolute temperature.

These mathematical relationships on gravitational repulsion and attraction forces would enable us study behavior of gases. The reason for focusing on the behavior gases is:

1)

The model could be applied to explain certain natural phenomena observed in the atmosphere, some of which have been studied in the previous experiments in this research program [1].

2)

Forces at the micro level (between gas molecules) may be generalized to the macro level to explain the behavior of the universe.

3. Alternative Mathematical Model for the Gravitational Repulsion and Attraction Forces, Yielding Behavior of Gases:

3.1. Introduction to the Analysis:

A model of the gravitational repulsion force and the gravitational attraction force (Figure 2) is developed herein, considering them as two distinct forces acting between two gas molecules (strictly for gases). Established experimental data on thermodynamic properties of gases are then applied to obtain:

a)

A mathematical model for the gravitational repulsion force

b)

A revised mathematical model for the gravitational attraction force

c)

Orders of magnitude of both gravitational repulsion coefficient and gravitational attraction coefficient

d)

Orders of magnitude of both gravitational repulsion and gravitational attraction forces

The analysis is conducted without using idealistic assumptions (such as discussed above) used in classical thermodynamics. The mathematical relationship is then applied to explain the behavior of gases. These relationships further suggest that natural phenomena such as the existence of clouds [1] and the accelerating expansion of the universe [32,46,47,48] could be explained more precisely by considering together both the gravitational repulsion [1,6] and gravitational attraction.

If these forces (gravitational repulsion and attraction) exist together in the universe, their effects must be the same everywhere: both at the microscopic level and the macroscopic level. The effect of increasing thermal energy on (a) expanding gas, i.e., at the microscopic level, and (b) expanding universe [1], i.e., at the macroscopic level, should be similar. Although alternative explanations focusing only on the expanding universe have been presented elsewhere [49,50], they are, however, they are still speculative and incomplete in explaining as mentioned above. The analysis presented in this paper, by way of mathematical model validated using experimentally determined and established data utilized in practical thermodynamic applications of mechanical engineering industries, rigorously reveals that, gravitational repulsion is a significant force between gas molecules (microscopic level), that could be generalized to the universe (macroscopic level).

3.2. Forces Between Two Gas Molecules:

To consider the gravitational repulsion force and the gravitational attraction force, strictly for gases, a simple diagram (Figure 3) could be drawn depicting two gas molecules in free space; each with mass m, thermal energy content Q, and distance r apart. There exist, gravitational repulsion forces F_R proportionate to their thermal energy contents Q and gravitational attraction forces F_A proportionate to their masses m. Both forces F_R and F_A are inversely proportionate to r.

Although some phenomena observed in the nature/universe, e.g., pressure and expansion, are dependent on temperature which is a manifestation of the thermal energy content, none of the four fundamental forces in Classical Theory are considered dependent on thermal energy content/temperature. As presented below, proven both analytically and experimentally, the thermal energy content dependent gravitational repulsion force, would fill the critical gap between energy and fundamental forces!

3.3. Mathematical Model for Gravitational Repulsion and Attraction Coefficient:

For the mathematical analysis, consider only these two molecules exist confined within a box at a distance r apart (Figure 4), at a certain pressure (i.e., outward force F_W exists). The two molecules, hence, are at rest touching the walls of the box, under the gravitational repulsion force (F_R), the gravitational attraction (F_A) and the F_W exerted by the wall. Existence of pressure on the box walls imply that the repulsion force between molecules is greater than the attraction force (F_R > F_A).

For equilibrium of forces on gas molecules depicted in Figure 4:

$$F_R-F_A=F_W$$

(7)

In this situation, Pressure P on the wall (by the two gas molecules) results from the outward force F_W of the system on a unit area; thus: P ∝ F_W

In reality, any small quantity of gas molecules exhibits same pressure regardless of the number of molecules enclosed. This implies that pressure at any point in the gas is caused by the very basic building block; intermolecular forces.

The intensity of the gravitational attraction force is proportional to the mass m (Equation 4). Under the proposed concept [2], the intensity of the gravitational repulsion force is proportional to the thermal energy Q (Equation 5).

Isotropic distribution of the force field from an entity of matter could be considered same irrespective of the type of force; whether gravitational repulsion force or gravitational attraction force. The distance r between the two entities of matter is in the denominator of the relationships for both the intensity of the gravitational repulsion force, as well as the intensity of the gravitational attraction force. In the denominator, the power of r is denoted by x, because the distribution of force field around the molecule with the distance is assumed unknown in the context of antigravity. The value of the exponent x is to be derived with empirical data.

For the two identical molecules with mass m given in Figure 4, gravitational attraction force F_A is defined (Equation 1 is modified) as:

$$F_A=G_A\frac{mm}{r^x}=G_A\frac{m^2}{r^x}$$

(8)

where, G_A is the ‘Gravitational Attraction Coefficient’.

For the two identical molecules with thermal energy Q in given Figure 4, gravitational repulsion force, F_R is also defined as:

$$F_R=G_R\frac{QQ}{r^x}=G_R\frac{Q{ }^2}{r^x}$$

(9)

where, G_R is the ‘Gravitational Repulsion Coefficient’.

Thermal energy Q (which contributes to the repulsion force) is defined (Equation (6) is modified) for the calculation of F_R as:

$$Q=mc{T}^y$$

(10)

where, c (Note 1 below) is the Specific Heat Capacity, T (Note 2 below) is the absolute temperature and y is the exponent of T. The parameter y as the exponent of T is introduced because the effect of absolute temperature on the thermal energy of an entity is not known in the context of gravitational repulsion. For example, radiant heat energy is proportional to the power 4 of T in the Stefan–Boltzmann Law [51]. Similarly, radiant field of antigravity is assumed proportional to the power y of T. The value of the exponent y is to be derived with empirical data.

Note 1: c is further defined for gases [41] as: c_v (Specific Heat Capacity at constant volume) and c_p (Specific Heat Capacity at constant pressure).

Note 2: In the existing theories, the thermal energy of a single molecule is considered as its kinetic energy (translational, vibrational, rotational etc.), and no temperature term is associated. Nevertheless, any matter, regardless of its size, absorbs and emits energy (infrared radiation in the case of thermal energy); Stefan–Boltzmann Law [51]. Gas molecule in the space is also an individual entity having its own characteristic mass and temperature, thus absorbs and emits radiation corresponding to its temperature regardless of its size[52].

Substituting values from Equations 8 and 9 to Equation 7:

$$F_W=F_R-F_A=G_R\frac{Q^2}{r^x}-G_A\frac{m^2}{r^x}$$

(11)

Application of the relationship in Equation 11 to the two gas molecules in the box (Figure 4), in the 3 situations given below, is used to derive:

1

The value of x

2

The value of y

3

The orders of magnitude of the relevant coefficients:

a.

G_R – Gravitational Repulsion Coefficient

b.

G_A – Gravitational Attraction Coefficient

4

The orders of magnitude of the forces:

a.

F_R – Gravitational Repulsion Force

b.

F_A – Gravitational Attraction Force

3.4. Building Relationships to Derive x, y, G_R, G_A, F_R and F_A:

Three situations defined as illustrated in Figure 5, where two gas molecules are in equilibrium in a box, are considered to derive x, y, G_R, G_A, F_R, and F_A.

Situation i.

Figure 5(i). Two gas molecules, each having mass m, and thermal energy content Q₁ (corresponding temperature is T₁), are at a distance r₁ apart, in a box. Molecules are pressing the opposite walls of the box by the force (using Equation 7):

$$F_{W1}=F_{R1}-F_{A1}$$

(12)

In this situation, pressure P₁ of the gas results from the force F_W1 (on the wall) of the system. Hence, P₁ ∝ F_W1

Situation ii.

Figure 5(ii). Thermal energy content of each molecule is Q₂ (Q₂ > Q₁). Corresponding temperature is T₂ (T₂ > T₁). The distance between molecules is r₁ (i.e., box dimensions are same as Situation i). Resultant force on the wall increases to F_W2 (F_W2 > F_W1). Hence, using Equation 7:

$$F_{W2}=F_{R2}-F_{A1}$$

(13)

In this situation, pressure P₂ of the gas (on the wall) results from the force F_W2 of the system. Hence, P₂∝ F_W2

Situation iii.

Figure 5(iii). Thermal energy content of each molecule is Q₂ (corresponding temperature is T₂). The distance between the two molecules is r₃, in order that, the resulting force applying on the wall is equal to F_W1. Hence, using Equation 7:

$$F_{W1}=F_{R3}-F_{A3}$$

(14)

In this situation, pressure P₁ of the gas (on the wall) results from the force F_W1 of the system. Hence, P₁ ∝ F_W1

(i)

Thermal energy of each molecule is Q₁ (corresponding temperature is T₁) and the distance between them is r₁. The molecules apply the force F_W1 on the wall.

(ii)

Thermal energy of each molecule is Q₂, Q₂ > Q₁ (corresponding temperature is T₂, T₂ > T₁). Both molecules are at the temperature T₂, and the distance r₁ between them is kept unchanged, hence, applying the force F_W2, F_W2> F_W1 on the wall.

(iii)

Thermal energy of each molecule is Q₂ (corresponding temperature is T₂). The distance between the two molecules is r₃, in order that, the resulting force applying on the wall is equal to F_W1.

Force diagram (Figure 6) shows the graphical representation of the magnitudes (not drawn to scale) of the forces on the two gas molecules when the temperature and the distance between them are as described in Situations i, ii and iii (also see Figure 5).

(i)

The two molecules at temperature T₁ and distance r₁ apart. Force on the wall is F_W1. Sum of forces F_A1 and F_W1 is equal to F_R1 (indicated as the distance d₁).

(ii)

The two molecules at temperature T₂ and distance r₁ apart. Force on the wall is F_W2. Sum of forces F_A1 and F_W2 is equal to F_R2 (indicated as the distance d₂).

(iii)

The two molecules at temperature T₂ and distance r₃ apart. Force on the wall is F_W1. Sum of forces F_A3 and F_W1 is equal to F_R3 (indicated as the distance d₃).

Situation i.

Forces act on the two air molecules, each with mass m and thermal energy Q₁ separated by a distance r₁. Substituting Situation i values in Equation 11:

$$F_{W1}=F_{R1}-F_{A1}=G_R\frac{Q_1^2}{r_1^x}-G_A\frac{m^2}{r_1^x}$$

(15)

The magnitude of forces in each direction at equilibrium, are depicted in Figure 6 by the distance d₁.

Situation ii.

At distance r₁ between the two molecules, the temperature is T₂. The force on the wall is F_W2. Substituting the Situation ii values in Equation 11:

$$F_{W2}=F_{R2}-F_{A1}=G_R\frac{Q_2^2}{r_1^x}-G_A\frac{m^2}{r_1^x}$$

(16)

The magnitude of forces in each direction at equilibrium, are depicted in Figure 6 by the distance d₂.

Situation iii.

The distance between the two molecules is r₃, r₃ > r₁ in order that the force on the wall is F_W1. The corresponding temperature is T₂ as the thermal energy of the molecule is Q₂ (Equation 6). Substituting Situation iii values in Equation 11:

$$F_{W1}=F_{R3}-F_{A3}=G_R\frac{Q_2^2}{r_3^x}-G_A\frac{m^2}{r_3^x}$$

(17)

The magnitude of forces in each direction at equilibrium, are depicted in Figure 6 by distance the d₃.

3.5. Translating Intermolecular Force to Pressure:

According to the definition, pressure is the force (or sum of the forces) on a unit area. Considering Figure 4:

$$F_W=\frac{P}{N_f}$$

(18)

where, N_f is the number of molecules on a unit area.

N_f is calculated from very general considerations. The number of molecules present at any given unit surface area within a gas volume (that contains evenly distributed n number of gas molecules per unit volume) at varying pressures and temperatures is considered with nearest image convention under periodic boundary conditions [43]. So, N_f is calculated by;

$$N_f=\frac{1}{6}(n-{(\sqrt[3]{n}-2)}^3)$$

(19)

3.6. Solving for Parameters x, G_R, G_A, F_R and F_A:

Equations 10, 15, 16, 17, 18 and 19 gives the solution for x as follows:

$$x=Log\left(\frac{\alpha m^2-\beta Q_1^2}{\alpha m^2-\beta Q_2^2}\right)/Log\left(\frac{r_1}{r_3}\right)$$

(20)

where: $\alpha =\frac{\beta Q_1^2-(P_1/N_f)}{m^2}$ and $\beta =\frac{P_2-P_1}{N_f(Q_2^2-Q_1^2)}$

General solutions for G_R, G_A, F_R and F_A are given as:

$$G_R=\beta r^x$$

(21)

$$G_A=\alpha r^x$$

(22)

$$F_R=\frac{G_R{Q}^2}{r^x}$$

(23)

$$F_A=\frac{G_A{m}^2}{r^x}$$

(24)

To determine numerical values for x, y, G_R, G_A, F_R and F_A it is necessary to consider experimental values of mass, specific heat capacity (either c_v or c_p discussed later in this paper), molecular distance, and pressure of gases at different temperatures. Therefore, as a sample calculation of the said analysis, to be presented in this paper, established experimental data on thermodynamic properties [3] of nitrogen N₂ gas are utilized. Analysis was repeated utilizing established experimental data on thermodynamic properties [3] of hydrogen, oxygen, water vapor, carbon monoxide and carbon dioxide as well, and all information is available on request.

Values of x, G_R, G_A, F_R and F_A are dependent on T and y. The value of y is taken as an independent parameter similar to the temperature T for all the calculations, and the value of y is to be derived with empirical data.

4. Calculation of x, y, G_R, G_A, F_R and F_A Based on Thermodynamic Properties of Gas:

The focus of this section is to engender a reasonable qualitative and quantitative picture of the combined effect of gravitational repulsion and attraction forces on matter in the gaseous state. Results would be considered and compared with conditions and observations encountered in the nature. Thermodynamic properties of gaseous nitrogen are used in the following sample calculation to elucidate the effect. (Calculations using Thermodynamic properties of hydrogen, oxygen, water vapor, carbon monoxide and carbon dioxide are also available on request). Established experimental data [3] (published in 1948) on gas properties of nitrogen (see Supplementary File 1) were applied to Equations 18–24, to calculate values for x, G_R, G_A, F_R and F_A. From the said table of properties of nitrogen with average molecular mass $28.016\times 1.66054\times {10}^{-27}$ kg/molecule, c_v and c_p at varying temperatures (from 146.65 K to 2888.9 K), were extracted. Molecular distance and pressure were calculated as given below.

4.1. Determining Values of P and r as T Varies:

Pressure P: Guillaume Amontons was the first to empirically establish the relationship between the pressure and the temperature of a gas (~1700 CE), and Joseph Louis Gay-Lussac determined the relationship more precisely (~1800 CE). Because of this, the P–T relationship of gases is known as either Amontons’ Law or Gay-Lussac’s Law. It states that: the pressure of a given amount of gas is directly proportional to its temperature on the absolute scale when the volume is held constant [53]. This empirically established relationship is used to obtain the pressure of a given mass of gas held within a unit volume, as temperature is varied; with reference to the temperature 305.54 K and pressure 101.325 kPa (see Supplementary File 1).

From the list of values in data [3], the temperature 305.54 K was chosen, because that is the value closest to the naturally existing livable temperatures. At that temperature, it was assumed that a unit volume of the gas exists at the pressure of 1 atm (standard atmosphere), i.e., 101.325 kPa. Amontons’ Law/Gay-Lussac’s Law was used to obtain the pressure of the given mass of gas held within a unit volume, at other temperatures listed in data tables.

Mean intermolecular distance r: Distances r₁ and r₃ between adjacent nitrogen gas molecules in a unit volume having total number of molecules n, at varying pressures relative to temperatures were calculated using the Avogadro number, provided that that the molecules are evenly distributed in the space. So, the r is given by $r\approx 1/\sqrt[3]{n}$ [54].

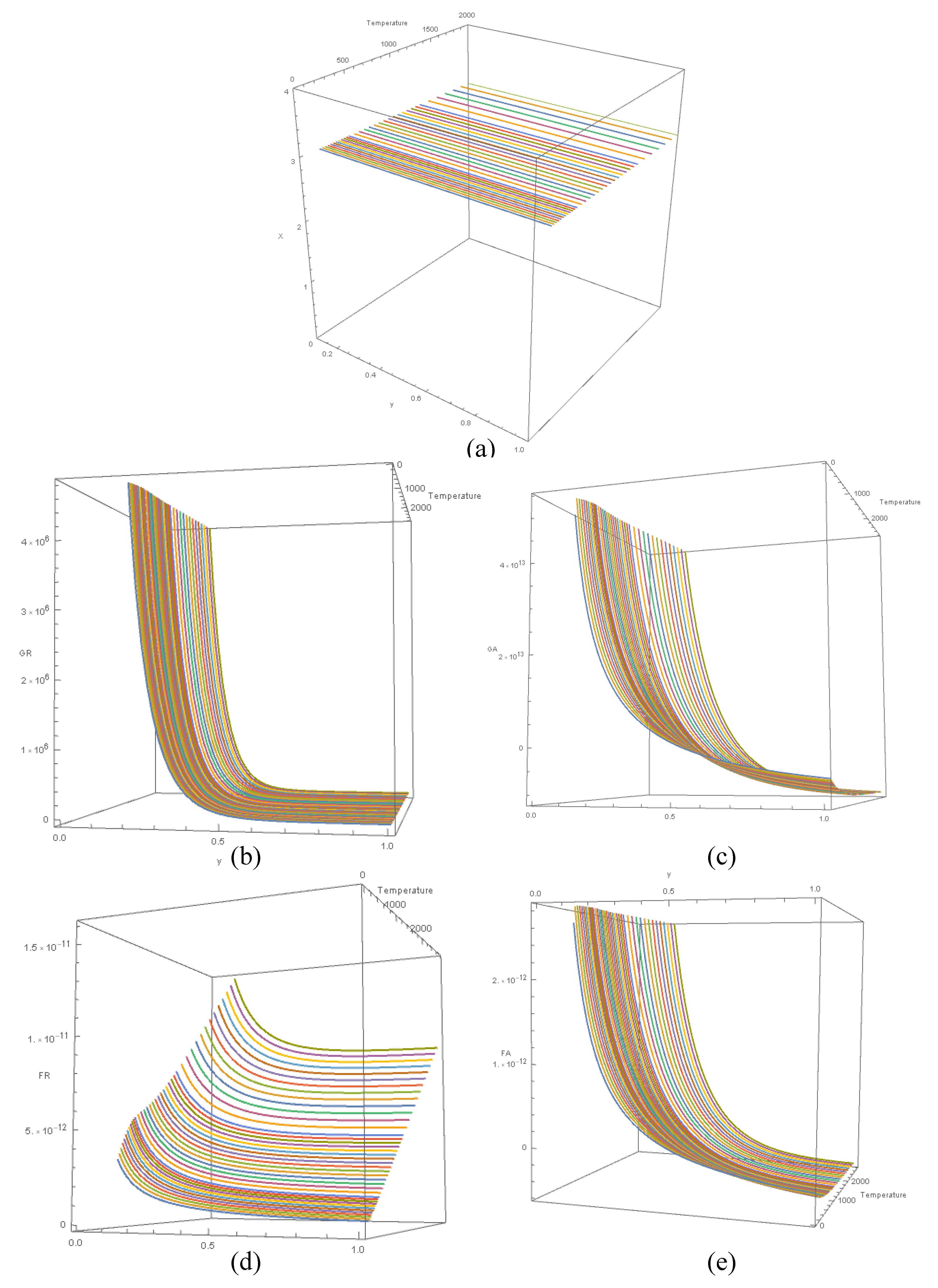
4.2. Observations of Characteristic Behaviors of x, G_R, G_A, F_R and F_A:

Characteristic behavior of x, G_R, G_A, F_R and F_A for temperatures ranging from 194.43 K to 2888.9 K (data availability) relative to y ranging from 0.1 to 1 (suitable range of y was determined as 0.1 to 1 by repeated calculations) was determined based on Equations 18–22. Calculations were conducted applying established experimental data [3], using Wolfram Mathematica 11.2, and the complete set of results is presented in Supplementary Files 2 and 3. For readers’ convenience, 3D graphs on behavior of x, G_R, G_A, F_R and F_A with respect to T and y are presented in Figure 7 Graphs (a), (b), (c), (d) and (e).

(a)

Variation of x relative to T and y. Value of x remains constant at 3 regardless of T and y.

(b)

Variation of G_R relative to T and y. G_R remains positive over the entire range of T and y. For any given value T:

i.

When y < 0.5, as y decreases, the rate of change of G_R is very high.

ii.

When y > 0.5, as y increases, G_R is much stable, compared when y values are low.

For any given value of y, variation of G_R vs. T is comparatively low.

(c)

Variation of G_A relative to T and y. For any given value T:

i.

When y < 0.5, G_A is positive, and the rate of change of G_A vs. y is high.

ii.

When y > 0.5, G_A is negative, and the rate of change of G_A vs. y is comparatively low.

For any given value y: variation of G_A vs. T appears significant; comparatively more than G_R.

(d)

Variation of F_R relative to T and y. F_R is linearly proportionate to T at any given value of y. Gradient of the linear relationship F_R vs. T is greater when y < 0.5 compared to when y > 0.5. Further, in the linear relationship F_R vs. T:

i.

When y < 0.5, intercept > 0

ii.

When y ≈ 0.5, intercept ≈ 0

iii.

When y > 0.5, intercept < 0

(e)

Variation of F_A relative to T and y.

i.

When y < 0.5, F_A is positive, and the rate of change of F_A vs. y is high.

ii.

When y > 0.5, F_A is negative, and the rate of change of F_A vs. y is comparatively low.

iii.

Hence, when y ≈ 0.5, F_A changes polarity.

The above analysis of Figure 7 shows that, for the gases investigated:

• x is a constant = 3, regardless of T and y (Figure 7(a)). The significance of this finding will be discussed below.
• Behaviors of G_R and G_A (Figure 7(b) and (c)) show that y = 0.5 is a significant point in this analysis.

At y = 0.5, G_A changes polarity, hence, F_A (Figure 7(e)) also changes polarity at y = 0.5. G_R remains positive over the entire range of T and y.

-

When y < 0.5, the rate of change of both G_R and G_A vs. y is high as y decreases.

-

When y > 0.5, both G_R and G_A are comparatively stable as y increases.

-

For any given value y, variation of G_A vs. T appears significant; comparatively more than G_R. In classical models of gravitational forces on matter, the dependency of G_A on temperature has not been known; Equation 1 is not dependent on temperature. However, the above analysis for gaseous form of matter shows otherwise. Therefore, F_A also depends on T (Equation 24).

• F_R is linearly proportionate to T at any given value of y (Figure 7(d)); thus, vindicating the mathematical model Equation 5. Significantly, this result confirms the findings presented in a previous paper [2] of the series of publications emanating from this research program (see Supplementary Figure S1). It states therein, [2] p148:

In experiment 2, t_f (time-of-fall) of a water-droplet in still air increases with the temperature of the droplet. That is: “The hotter the water-droplet, the slower it falls”.

A significant finding is that, in the linear relationship F_R vs. T extrapolated graph intercept ≈ 0 when y ≈ 0.5, while intercept > 0 when y < 0.5, and intercept < 0 when y > 0.5.

4.3. The Significance x = 3.0, Inverse Proportionality to the Cube of the Distance:

Results presented in Figure 7(a) and Supplementary Files 1-3, show that, at the length scale of intermolecular distances for gas molecules, x = 3.0 with a very low variance of 8.4233 x 10 ^–9 for both c_v and c_p. Calculations show that the x is constant, independent of the atomic mass m (analysis was repeated for hydrogen, oxygen, water vapor, carbon monoxide and carbon dioxide yielding the same result; information available on request), the Specific Heat Capacity c and y, over a wide range of temperature data. It is, hence, concluded that x = 3.0; a significant finding of this research. This delivers r³ in the denominators of expressions for both the gravitational repulsion force and the gravitational attraction force. In other words, both gravitational repulsion force and gravitational attraction force, at the length scale of intermolecular distances for gas molecules, are inversely proportional to the cube of the distance between them. The very low variance of the result x = 3.0 shows that the inverse cube relationship is dominant.

Until now, under the Newtonian model, it has been considered that the classically known gravitational force between two entities is inversely proportional to the square of the distance between them [10] (Equation (1)). Such classically known gravitational force is the resultant of the two distinct forces, viz., gravitational repulsion and attraction forces revealed in this research program. The inverse square concept is also seen in the Coulomb’s Law [55] for the electromagnetic force between two charged particles. Inverse proportionality to the cube of the distance is applicable to gravitational repulsion and attraction forces, determined at the length scale of intermolecular distances for gas molecules, is a significant deviation from the classical acceptance.

Value x = 3.0 gives that gravitational repulsion and attraction field/flux flow is closer to the volumetric or solid spherical distribution (4/3 πr³) rather than the area or surface distribution (4πr²) considered in the classical model. With the interpretation of the antigravity effect, we have come up with a volumetric or solid spherical (r³) model which is more relevant to gases in 3-dimensional space. Such volumetric or solid spherical model maybe more relevant to other contexts in the universe in general. Furthermore, this alternative model is a more appropriate application on a force field that fills up free space. This is a significant departure from the Inverse-Square Law. Inverse proportionality to the cube of the distance, revealed in this experiment, is one most important revelation/result in fundamental sciences.

4.4. The Significance of y = 0.5:

As stated, when presenting Equation 10, the parameter y as the exponent of T was introduced because the effect of absolute temperature on the thermal energy of an entity is not known in the context of gravitational repulsion. The above analysis (Figure 7) elaborated that y = 0.5 is a very noteworthy value when considering behaviors of G_R, G_A, F_R and F_A.

It is very significant that, for both c_v and c_p, when y ≈ 0.5:

• Extrapolation of graph F_R vs. T crosses (0,0) (Supplementary Figure S2).
• Negative F_A tends to become positive as T approaches 0 K (Supplementary Figure S3).

Hence, F_W [= F_R - F_A] may become negative and the gas may condense, when y ≈ 0.5 and T → 0; see Equation 11. The analysis was repeated for hydrogen, oxygen, water vapor, carbon monoxide and carbon dioxide, yielding the same result irrespective of atomic mass m; information available on request. This happens only when y ≈ 0.5, although P ∝ T concept of the Amontons’ Law/Gay-Lussac’s Law was applied across all calculations irrespective of the value of y. Therefore, y = 0.5 is observed as the value that satisfies existing empirical observations of the Amontons’ Law/Gay-Lussac’s Law, hence, chosen to conduct subsequent analysis in this paper.

4.5. Units of G_R, G_A, F_R and F_A:

When y = 0.5, units of G_R and G_A would be as follows:

G_R: s² K kg^-1

G_A: m⁴ kg^-1 s^-2

Newtonian Universal Gravitation Constant G has m³ kg^-1 s^-2 as units; note m³ in the numerator. Units of G_A have m⁴ in the numerator. This difference of one in the power of the unit of length is because the Newtonian model is based on the Inverse Square Law, whereas the model presented above is based on the Inverse Cube Law. The units of the finally calculated forces F_R and F_A are found to be kg m s^-2, i.e., Newton, as expected, thus vindicating the model.

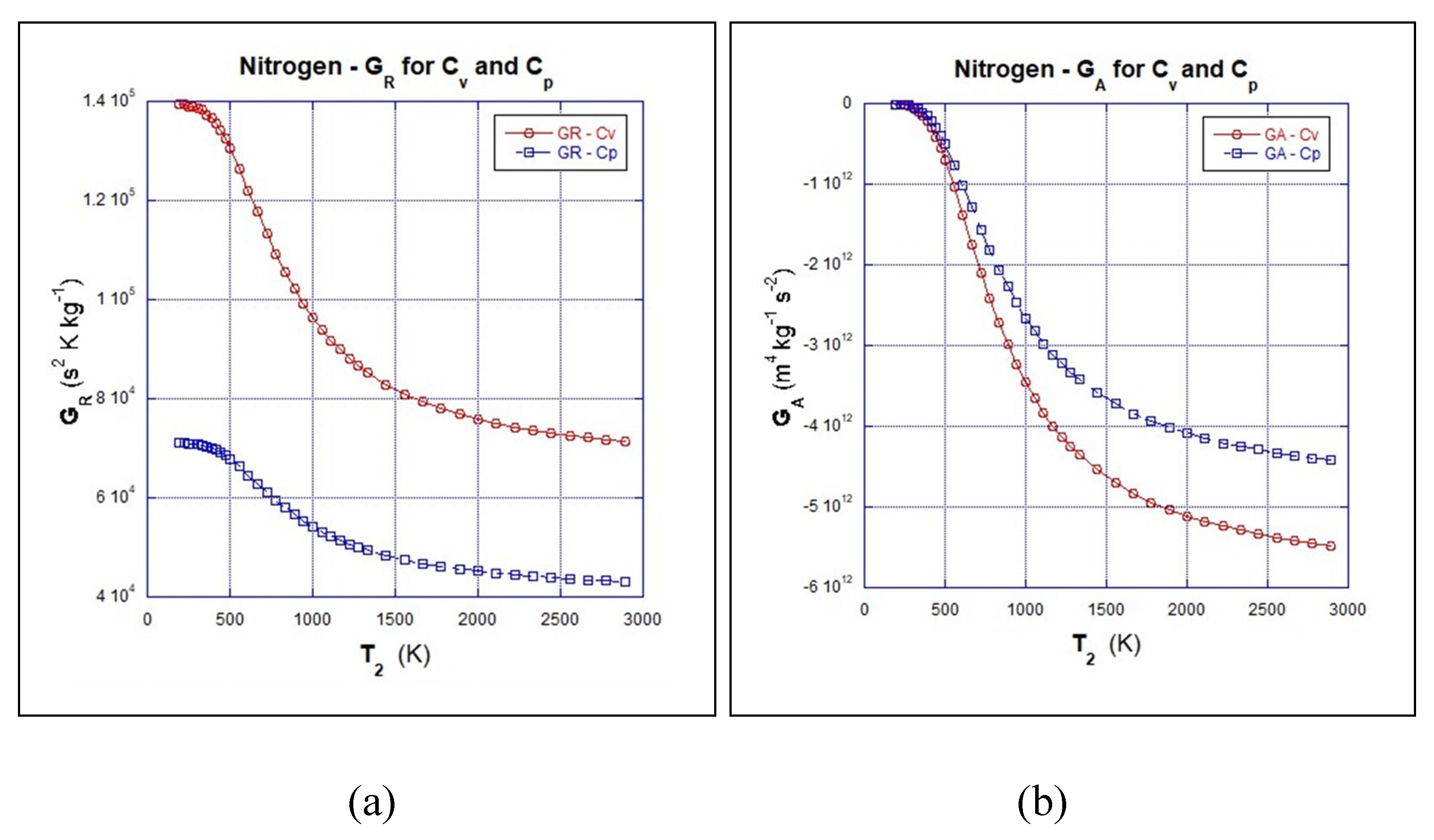
4.6. Orders of the Magnitude of G_R and G_A:

Figure 8 presents variations of G_R and G_A against T for gaseous nitrogen; thus, depicts their orders of magnitude. The values were calculated applying the empirical data and the value y = 0.5 to Equations 21–22 (Supplementary File 1).

Gravitational attraction was initially, expected to be independent of T. Results presented in Figure 8(b), nevertheless, show that G_A is dependent of T, and this would be discussed later together with F_A.

Results pertaining to both c_p and c_v are presented for comparison in Figure 8. The variance of G_R and G_A are smaller for c_p compared to c_v. It could be noted that, the model developed herein is where starting (Situation i) and ending (Situation iii) pressures are equal (over all under constant pressure). Hence, data pertaining to c_p is more appropriate to the analysis. Substituting c_p values to Equations 21–22, therefore, shows lesser variations of both G_R and G_A.

(a)

Results of G_R from calculations using c_v and c_p

(b)

Results of G_A from calculations using c_v and c_p

The variance of G_R and G_A are smaller for c_p compared to c_v.

The orders of the magnitude of G_R and G_A yielded by the gravitational repulsion and attraction model, as presented above, are very large compared to the Newtonian Universal Gravitation Constant G, which is 6.674 x 10^-11 m³ kg^-1 s^-2. Considering equilibria in the infinite universe with infinite distances, such large values of G_R and G_A are not impractical. The very small value Newtonian constant has been deduced to represent a very small gravity force observed by the scientists at that time [56]. The present program of research has shown that the so called ‘weak’ gravitational force is actually the resultant of two extremely large forces, i.e., gravitational repulsion and gravitational attraction, which distinctly act on matter. This would be discussed in more details in the subsequent section that deals with the orders of the magnitude of the forces.

The analysis was repeated for hydrogen, oxygen, water vapor, carbon monoxide and carbon dioxide as well, yielding the similar result; information available on request. Magnitudes of G_R and G_A for the above gases were also in the similar order.

4.7. Orders of the Magnitude of F_R and F_A:

Values of F_R and F_A for nitrogen gas are calculated applying the empirical data and the value y = 0.5 to Equations 23–24 (Supplementary File 1). The analysis was repeated for hydrogen, oxygen, water vapor, carbon monoxide and carbon dioxide as well, yielding similar results; information available on request.

To give an example for the convenience of readers, the values of F_R and F_A between two nitrogen gas molecules, at the temperature T₂ 333.32 K (≈ 60 °C) and pertaining to c_p are, respectively, 1.324 × 10^-12 N and -3.587 × 10^-15 N. (Note: F_R >>> F_A). The resultant of F_R and F_A between two nitrogen gas molecules = F_W = F_R - F_A = 1.328 × 10^-12 N. [Note: As defined in the mathematical model presented herein, F_W acts in the direction of repulsion]. F_W exerted by nitrogen gas molecules, was translated to Pressure P, in the unit Pa by applying Equations 18 and 19. The result is: 110.537 N on an area of 1 m² (110.537 kPa = 1.091 standard atmosphere), which is equal to the value obtained by applying Amontons’ Law/Gay-Lussac’s Law. See Supplementary File 1 for the full set of results.

Further in the Supplementary File 1, when F_W values obtained based on c_p and c_v (corresponding to any given temperature) are compared, the difference is in the order of a millionth of the F_W values. It shows that difference in F_W caused by the difference of applying either c_p or c_v is very small.

It is useful to compare F_R and F_A with the gravitational force between gas molecules calculated according to the classical theory as defined in Equation 1. When two nitrogen molecules are 4.557 x 10^-9 m apart [which does occur at around 333 K (≈ 60 °C) and 1 atm], the classical theory calculated gravitational force between the two molecules is equal to 1.202 x 10^-44 N. [Note: As defined in the classical theory, this gravitational force acts in the direction of attraction]. It is, nevertheless, interesting to note that: F_R and F_A in nitrogen [at around 333 K (≈ 60 °C) and 1 atm] are respectively 1.101 x 10³² and 2.984 x 10²⁹ times greater than the gravitational force between gas molecules calculated according to the classical theory as defined in Equation 1.

Above pressure calculations were conducted using the mere two molecular system introduced in this paper. It could thus be justified that any two neighboring molecules of gas produces the same force at any given point throughout a gas; provided that the temperature and the molecular distance (volume) are the same. In reality, any small quantity of gas molecules exhibits the same pressure regardless of the number of molecules enclosed. Significance of this analysis is the absence of idealistic assumptions such as: large number of molecules making perfectly elastic collisions in deriving the ideal gas equation.

Gravitational attraction was, as pointed out before, initially expected to be independent of T. Results, nevertheless, show that G_R, G_A, F_R and F_A are dependent of T. Four fundamental interactions were not so far defined to be temperature dependent. Nevertheless, phenomena are observed in the nature/universe (e.g.: pressure, expansion, and so on) that are dependent on temperature/thermal energy content. With this research revealing that both F_R and F_A are temperature dependent, it appears that the critical gap between energy and fundamental forces has been filled.

4.8. Negative Gravitational Attraction Forces Among Gas Molecules:

Applying empirical data to Equation 24 shows that, F_A (the attraction force among gas molecules) is negative at elevated temperatures (Figure 7(e) and Supplementary Figure S3), implying that it acts as a repulsive force together with F_R. This negative F_A tends to become positive at lower temperatures where gases are expected to condense. For example, the value calculated for F_A between gaseous nitrogen molecules is -7.118 10^-16 N at 194.43 K and 64.478 kPa, and -2.299 10^-13 N at 2,888.9 K and 958.029 kPa (Supplementary File 1).

Negative values of F_A at elevated temperatures, together with F_R, cause the gas to have only repulsive forces among molecules. This gives rise to the property that real gases expand infinitely as the available space increases. Such circumstances of all repulsive forces were observed in other gases studied (hydrogen, oxygen, water vapor, carbon monoxide and carbon dioxide) as well. Further for all these gases, tendencies of negative F_A becoming positive at lower temperatures could also be observed from the results; suggesting that the gases are expected to condense. All these information on other gases studied are available on request.

The exact fundamental mechanism of condensation has so far not been explained by existing theories. It is presently believed that condensation is initiated by the formation of atomic/molecular clusters [57]. How such formation of clusters initiate has not been explained fundamentally. Both the kinetic theory and the ideal gas law predict that gases compressed to very high pressures and cooled to very low temperatures should still behave like gases. Concepts of thermodynamics, thus far, indicate only that decrease in temperature reduces kinetic energies of particles [41], but not how atoms/molecules form clusters or how/why aggregation occurs. Molecular vibrational distances are far smaller than intermolecular distances in gases. Reduction of molecular kinetic energy, hence, does not explain how intermolecular distances get smaller with the reduction of the temperature.

In real gases (obeying Van der Waals equation), it is conceptualized that [42] condensation occurs when the molecules of a gases are cooled to the point where they no longer possess sufficient kinetic energy to overcome intermolecular attractive forces [58]. Even in this explanation, it is not explained how kinetic energy and intermolecular force relates each other fundamentally.

Values of F_R and F_A calculated in the above analysis show that as temperature decreases, repulsion forces decrease and attraction forces increase (from negative at elevated temperatures to close to positive at lower temperatures) between gaseous molecules, thus causing aggregation of atoms/molecules together, i.e., causing condensation of the gas.

In other states of matter, different mechanisms pertaining to F_A could be observed. For example, as highlighted in the Author’s previous publication [1]: collections of water droplets suspended in midair are observed to flocculate as clouds. In such circumstances, gravitational attraction and repulsion forces among water droplets are equal thus in equilibrium (see ‘5.0 Discussion’).

4.9. The Gist of the Model and the Outcomes:

A perceptible alternative model of the gravitational repulsion force and the gravitational attraction force has been developed above, considering them as two distinct forces acting on gaseous matter. The development of this model has been presented in Section 3.0. When established experimental data on nitrogen, hydrogen, oxygen, water vapor, carbon monoxide and carbon dioxide were applied, the model performed, yielding significant outcomes. These outcomes have been presented in Section 4.0.

In view of the numerous details, equations, outcomes, etc., of the model presented above, the gist of them all is diagrammatically presented in Figure 9 for the convenience of the reader.

5. Discussion

It is observed that Newtonian and Einsteinian mechanics experience challenges in explaining certain phenomena seen in laboratory experiments (e.g.: upward motion of heated iodine particles in vacuum) and natural phenomena (e.g.: condensation of gases, accumulative (flocking together) nature of clouds and accelerating expansion of the universe) [1,2,4,5]. Under these existing models, the gravitational force has been reckoned as a “weak force”. Thus, in deriving the ideal gas equation, one of the most fundamental forces, the gravitational attraction among matter has been overlooked, both among air molecules themselves and with the Earth. Such lapses tempt deviation from the existing models, viz., Newtonian ‘Law of Universal Gravity’, Einsteinian ‘EFE’ and kinetic theory of ideal gases.

The alternative model considering both gravitational repulsion and attraction presented in this paper is self-standing, independent of existing idealistic models. This model has been built without idealistic assumptions such as: “intermolecular force in gaseous state is zero”, “perfectly elastic collisions”, “consists of a large number of molecules”, “volume of the molecules is negligibly small” and so on. In fact, there are no idealistic assumptions involved in this model; hence it is closer to reality.

The entire mathematical model presented in this paper was derived considering the forces of gravitational repulsion and attraction between just two gaseous molecules; the basic building blocks of the gas. Force (net repulsive) between individual gas molecules represents the pressure in the system; a significant deviation from the kinetic theory’s concept of momentum transfer. Hence, pressure does not depend on the number of molecules in a certain mass or volume of the gas, as assumed in the kinetic theory in the derivation of the ideal gas equation. The two gaseous molecule model justifies that any small quantity of gas molecules would exhibit same pressure as a large quantity at the same temperature and molecular number density; even a small quantity of gas could produce the same pressure as a large quantity.

It should be noted that the above relationships (Equations 18–24) are developed for the matter in the gaseous state, hence may not be valid for other states of matter (e.g., liquid, solid, plasma). It is, hence, recommended that future research should focus on analysis of matter in such other states.

The model has been validated using experimentally determined and established data [3]utilized in practical thermodynamic applications of mechanical engineering industries. The data has been published in 1948, by Joseph Henry Keenan and Joseph Kaye. Applying these data to Equations 18 24, behavior of x, G_R, G_A, F_R and F_A with respect to T and y are derived and presented in 3D graphs (a), (b), (c), (d) and (e) in Figure 7.

The result x = 3.0 as presented in the 3D graph Figure 7(a) contributes new scientific information on distribution of force fields that fill up the volume in free space, at the length scale of intermolecular distances for gas molecules. The relationship of gravitational repulsion and attraction forces being inversely proportional to the cube of the distance, interprets the gravitational force distributions as volumetric or solid spherical distributions (4/3 πr³) in free space, rather than the area or surface distributions (4πr²) considered in the classical model. This is a significant departure from the Inverse-Square Law. Inverse-Square Law describes wave front propagation of energy. In contrast, force fields fill up volume in the free space. The volumetric distribution or fill-up the free space by the force is more appropriate in understanding; as a force field always exists in a 3D space rather than on a 2D surface.

In forces among gravitational fields, the inverse proportionality to cube (Inverse-Cube Law) with the distance is not new. An extra force besides gravity, that is obeying the Inverse-Cube Law, has been mentioned in ‘Principia Mathematica’ [10] published by Isaac Newton in 1687; see Prepositions XLIII-XLV of Book 1, pp171-182. It has also been demonstrated [59] experimentally that, in magnetostatic fields where both poles geometrically coincide, attraction and repulsion forces obey the Inverse-Cube Law with the distance. Future research should focus on discerning where inverse proportionality to the cube of the distance is more appropriate in applications of fundamental physics.

The analysis presented in this paper signifies that y = 0.5 is a very special value when considering behaviors of G_R, G_A, F_R and F_A. Most noteworthy points were that, for both c_v and c_p, when y ≈ 0.5:

• extrapolation of graphs F_R vs. T crosses (0,0)
• negative F_A tends to become positive as T approaches 0 K

This was found to be true for all gases considered: nitrogen, hydrogen, oxygen, water vapor, carbon monoxide and carbon dioxide; yielding similar results irrespective of atomic mass m. How these results resonate with other empirically established models such as Boyle’s Law, Charles’ Law and Amontons’ Law/Gay-Lussac’s Law will be discussed in a future publication.

In the 3D graphs Figure 7(b) and (c), both Gravitational Repulsion Coefficient and Gravitational Attraction Coefficient appeared dependent on the temperature T. This result is unexpected, as temperature dependency of G_A is not previously known. Further to that, as presented in 3D graphs Figure 7(d) and (e), both F_R and F_A are temperature dependent; being gravitational forces, they are fundamental interactions in nature. Significant departure from the existing knowledge is that, the four fundamental interactions (fundamental forces) in classical theory are not defined to be temperature dependent. Existing theories, nevertheless, state that increase of thermal energy increases the potential energy of the gas molecules. Results showed that, increase of thermal energy increased repulsion (Eqs. 5 and 23) between gas molecules. See graphs of F_R vs. T and F_A vs. T, where, as T increases:

• positive value of F_R increases
• negative value of F_A increases

That implies that thermal energy is directly proportional to the resultant of F_R and F_A, confirming the relationship between energy and fundamental forces. With this revelation, the critical gap between energy and fundamental forces has been filled. Fundamental forces could be more readily linked with observable temperature dependent phenomena (e.g.: pressure, expansion, and so on) in the nature/universe; thus, enabling better explanations.

In the 3D graph Figure 7(d), gravitational repulsion force appeared linearly proportionate to the temperature. This vindicated the experiment conducted in this research program by the Author, presented in paper [2]. The said experiment demonstrated that the time-of-fall of water droplets is linearly proportionate to the temperature (Supplementary Figure S1). [Note: F_A also acts in this context. It was presented that F_R >>> F_A; see section ‘4.7 Orders of the Magnitude of F_R and F_A’].

Negative values of F_A at elevated temperatures [Figure 7(e)], together with F_R, cause the gas to have only repulsive forces among molecules. This gives rise to the property that real gases expand infinitely as the available space increases. Such circumstances of all repulsive forces were observed in other gases studied (hydrogen, oxygen, water vapor, carbon monoxide and carbon dioxide) as well (information available on request).

Analysis presented in this paper further shows that as temperature decreases, repulsion forces decrease and attraction forces increase (from negative at elevated temperatures to close to positive at lower temperatures) between gaseous molecules, thus causing aggregation of atoms/molecules together, i.e., causing condensation of the gas. This finding is significant in a context where exact fundamental mechanism of condensation has so far not been explained by existing theories.

The present program of research has shown that, the so called ‘weak’ gravitational force (Table 1), is actually the resultant of two extremely large forces, i.e., gravitational repulsion and gravitational attraction, which distinctly act on matter. Newly determined gravitational repulsion and attraction forces between two nitrogen molecules at 305 K are in the order of 10³⁰ times greater than the classically calculated gravitational attraction force. It thus reveals that gravitational repulsion and attraction forces in fact are of similar orders of magnitude as the other three forces in the nature.

Earlier in this paper, an experiment was described, where heated iodine particles moved upwards against the Earth’s gravitational pull. This is a groundbreaking experiment where the said phenomenon occurred in a situation where all factors which are believed to be causing the upward movement of particles against the gravitational pull in air, viz., buoyancy and convective forces, are eliminated by experimental design. Initially, at the room temperature (~25°C), the iodine particles detached from the iodine sample moved downward under gravitational attraction force with the Earth, and deposited in the bottom part of the paper jacket. When the iodine sample was heated, the experiment revealed that iodine particles move against gravitational pull in the vacuum and deposited in the top part of the paper jacket. In electronic vacuum tubes (also called electronic valves) also, evaporated tungsten and thorium particles from the filament moves upwards despite the gravitational pull and the strong radial electric fields, and deposit at the top of the glass tube.

The above was a laboratory experiment at a micro scale. The antigravity concept could also be extended to macro level phenomena in the nature such as clouds and the accelerating expansion of the universe. Review paper by the Author [1] on the previous papers in this research program states:

In addition to attractive and repulsive forces of water-droplets of a cloud with earth, there exist attractive and repulsive forces among water droplets within the cloud. These forces acting inside the cloud explain the accumulative (flocking together) nature of the cloud which has not been explained by the classical theories. The equilibrium of these two forces will confine the droplets to a certain area as a floccule. The repulsiveness does not allow shrinking and finally collapsing the cloud while the attractive force keeps the droplets together without dispersion. [1] p4

The above is an ideal example where there is no net outward force (no net pressure exerted outward) among water droplets. Water droplets behave as a flock under the equilibrium of gravitational attraction and gravitational repulsion forces. The paper [2] dispelled the classical belief that clouds float due to convection currents, and showed that the force that holds the water droplets up in the air is a cryptic force, known as “antigravity”.

Considering both gravitational attraction and gravitational repulsion on matter and filling the critical gap between energy and fundamental forces, opens the doors for more research enabling stronger scientific explanations of observable temperature dependent phenomena, e.g.:

• Heavy gas molecules (such as CFC) in the upper atmosphere
• Brownian Motion
• Condensation/evaporation/sublimation
• Expansion/contraction of gas/liquid/solid
• and more

The concept of gravitational repulsion and gravitational attraction forces could be further applied at macro level to explain the accelerating expansion of the universe. Even in our solar system:

… the distance of the Earth’s [sic] from the sun. Various measurements indicate that this distance (or at least the length of the Earth’s semimajor axis) is increasing at the rate of 15 cm per year (plus or minus 4 cm). [60,61]

Galaxies and other interstellar objects are not in a state of equilibrium as a result of increasing thermal energy content due to various reasons including atomic fission and fusion causing mass-energy conversion (E = mc²). Such mass-energy conversion has dual effects on equilibria in the universe: (1) increasing thermal energy increases gravitational repulsion forces, while (2) decreasing mass decreases gravitational attraction forces. Gravitational repulsion forces, hence, supersede gravitational attraction forces, thus causing outward expansion of the universe with acceleration [62].

This research has shown that, gravitational repulsion and gravitational attraction forces are colossal (larger in the order of 10³² and 10²⁹ times respectively at around 333 K and 1 atm) than the traditionally known gravitational force between gas molecules. What has been calculated as gravity force so far according to the classical theory is, the resultant of the two large forces gravitational repulsion and attraction, which are nearly equal thus nearly in equilibrium. These forces pervade our environments at both micro and macro levels. Once fully understood, such nearly in balance colossal forces offer the prospect of learning to control and manipulate to achieve hitherto unknown results, outcomes and developments. This is another direction for future research.

6. Conclusions

A self-standing alternative mathematical model on gravitational repulsion and attraction forces was built without idealistic assumptions. It was based on the forces between two gaseous molecules, i.e., the basic building blocks of the gas. The new mathematical model thus derived in this research performed successfully when established experimental data on gas properties of nitrogen, hydrogen, oxygen, water vapor, carbon monoxide and carbon dioxide were applied. Gravitational repulsion and attraction forces are inversely proportional to the cube of the distance between gaseous molecules; thus following an Inverse-Cube relationship; departing from the traditionally accepted Inverse-Square relationship. Gravitational repulsion force is linearly proportional to the thermal energy content (temperature, which is a manifestation of the thermal energy) of the entities of matter. The latter vindicated the previous experiment conducted in this research program. Gravitational attraction force too is found to be dependent on temperature. Mechanism between energy and fundamental forces being thus revealed, the critical gap between energy and fundamental forces has been filled; thus opening the doors for more research enabling better explanations of observable temperature dependent phenomena. The model could also be applied at macro level to explain the accelerating expansion of the universe. Also, the concept of dark-energy-an elusive idea, may also encompass antigravity while explicating it. The immediate need is to fully understand the gravitational repulsion and attraction forces, where both are found to be colossal; larger in the order of 10³⁰ times compared to the traditionally known gravitational force between gas molecules. Once these two colossal forces are fully understood, we could control and manipulate them to achieve hitherto unknown outcomes and developments. Such endeavors are where future research should focus.