PreprintArticleVersion 1Preserved in Portico This version is not peer-reviewed
Shannon Entropy of Epithelium and Five-Fold Morphology: A Fundamental Model to Explain Geometrical Organizations as a Source of Information in Biological Systems
Version 1
: Received: 12 September 2019 / Approved: 14 September 2019 / Online: 14 September 2019 (18:49:00 CEST)
How to cite:
López-Sauceda, J.; Carrillo Gonzalez, J.G.; Ortega Laurel, C.; von Bülow, P.; Mejia, C. Shannon Entropy of Epithelium and Five-Fold Morphology: A Fundamental Model to Explain Geometrical Organizations as a Source of Information in Biological Systems. Preprints2019, 2019090141. https://doi.org/10.20944/preprints201909.0141.v1
López-Sauceda, J.; Carrillo Gonzalez, J.G.; Ortega Laurel, C.; von Bülow, P.; Mejia, C. Shannon Entropy of Epithelium and Five-Fold Morphology: A Fundamental Model to Explain Geometrical Organizations as a Source of Information in Biological Systems. Preprints 2019, 2019090141. https://doi.org/10.20944/preprints201909.0141.v1
López-Sauceda, J.; Carrillo Gonzalez, J.G.; Ortega Laurel, C.; von Bülow, P.; Mejia, C. Shannon Entropy of Epithelium and Five-Fold Morphology: A Fundamental Model to Explain Geometrical Organizations as a Source of Information in Biological Systems. Preprints2019, 2019090141. https://doi.org/10.20944/preprints201909.0141.v1
APA Style
López-Sauceda, J., Carrillo Gonzalez, J.G., Ortega Laurel, C., von Bülow, P., & Mejia, C. (2019). Shannon Entropy of Epithelium and Five-Fold Morphology: A Fundamental Model to Explain Geometrical Organizations as a Source of Information in Biological Systems. Preprints. https://doi.org/10.20944/preprints201909.0141.v1
Chicago/Turabian Style
López-Sauceda, J., Philipp von Bülow and Carmen Mejia. 2019 "Shannon Entropy of Epithelium and Five-Fold Morphology: A Fundamental Model to Explain Geometrical Organizations as a Source of Information in Biological Systems" Preprints. https://doi.org/10.20944/preprints201909.0141.v1
Abstract
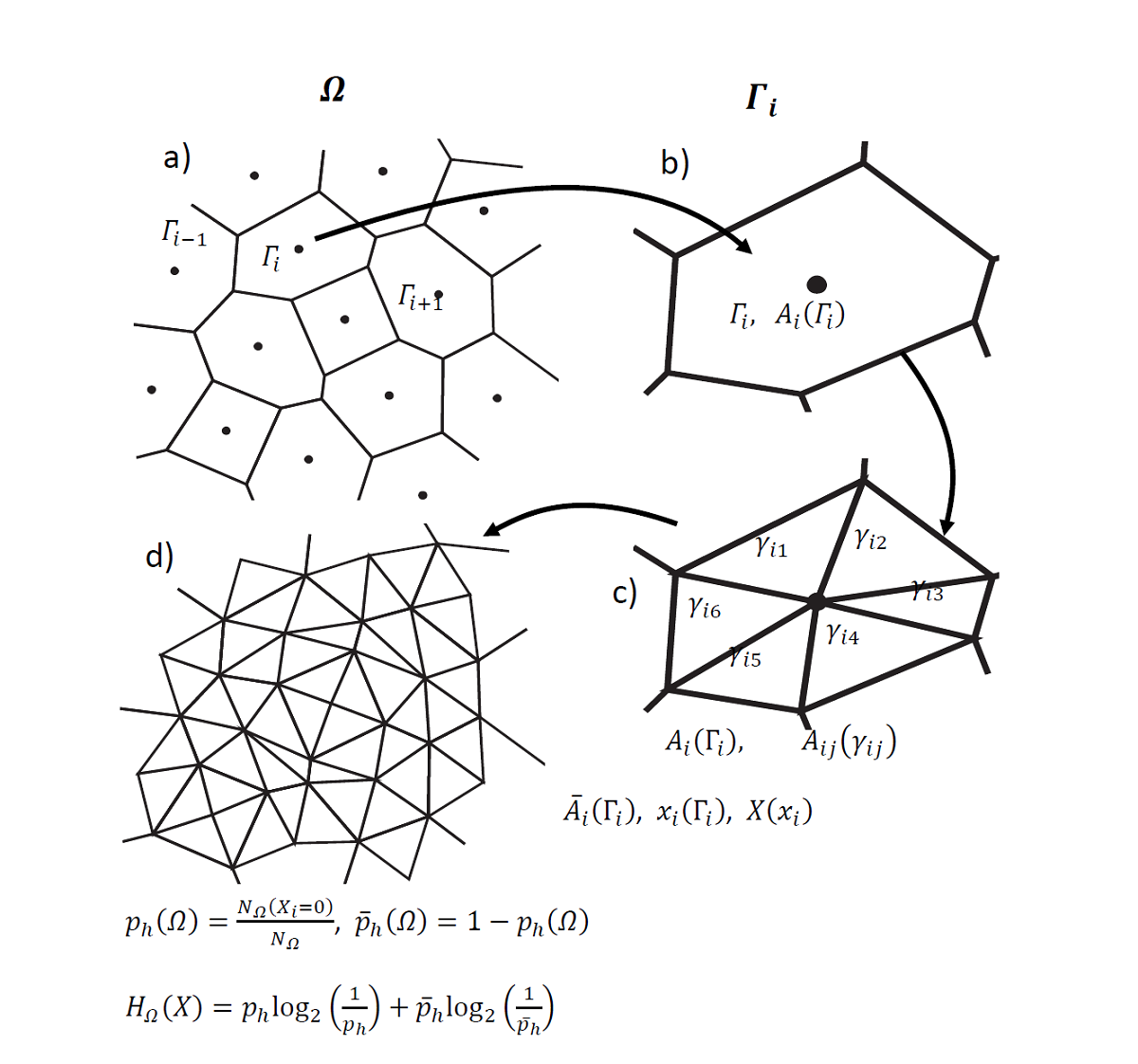
Based on a measuring system to determine levels of spatial organization in 2D polygons (homogeneous or heterogeneous partition of defined areas) lying on principles of regularity, we propose the entropy term linked to the concept of “information”, from the “information theory field”, in order to obtain an information measurement regarding a quantity of or amount of information in the architecture of complex 2D biological organizations. The term “quantity” does not refer to the amount of data (size), but to the probability of a geometrical basic pattern within a set of possible statistical configurations regarding levels of homogeneity and heterogeneity. It is this notion of information that is important in information theory, and measures of information in units of bits, what we propose to use for measuring quantities of organization in the architecture of complex geometrical systems. Two complex systems are tested, biological and non biological in order to obtain experimental results, which are verified with the evaluation criteria “entropy”. Experimental results show that the lowest levels of information and entropy, in addition with low rates of heterogeneity and high rates of homogeneity are particular features of geometrical organizations in biological systems.
Keywords
biocomplexity; self-organization; spatial organization; geometrical shape; information theory; entropy
Subject
Biology and Life Sciences, Anatomy and Physiology
Copyright:
This is an open access article distributed under the Creative Commons Attribution License which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
,
,
,
,
