Müser, M.H.; Wang, A. Contact-Patch-Size Distribution and Limits of Self-Affinity in Contacts between Randomly Rough Surfaces. Lubricants2018, 6, 85.
Müser, M.H.; Wang, A. Contact-Patch-Size Distribution and Limits of Self-Affinity in Contacts between Randomly Rough Surfaces. Lubricants 2018, 6, 85.
Müser, M.H.; Wang, A. Contact-Patch-Size Distribution and Limits of Self-Affinity in Contacts between Randomly Rough Surfaces. Lubricants2018, 6, 85.
Müser, M.H.; Wang, A. Contact-Patch-Size Distribution and Limits of Self-Affinity in Contacts between Randomly Rough Surfaces. Lubricants 2018, 6, 85.
Abstract
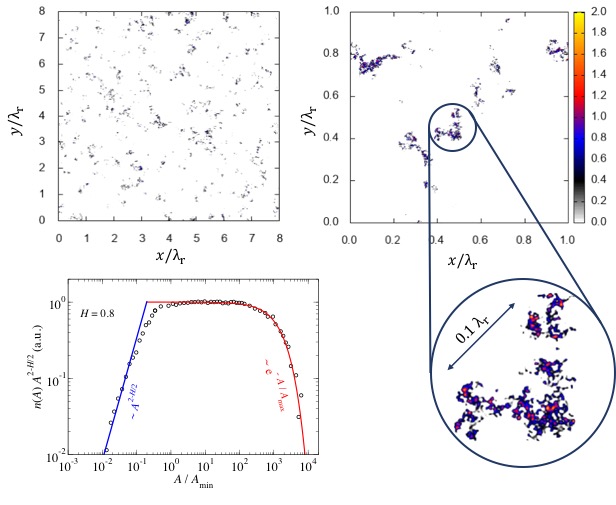
True contact between solids with randomly rough surfaces tends to occur at a large number of microscopic contact patches. So far, two scaling regimes have been identified for the number density n(A) of contact-patch sizes A in elastic, non-adhesive, self-affine contacts. At small A, n(A) is approximately constant, while n(A) decreases as a power law at large A. Using Green’s function molecular dynamics, we identify a characteristic (maximum) contact area Ac above which a superexponential decay of n(A) becomes apparent if the contact pressure is below the pressure pcp at which contact percolates. We also find that Ac increases with load relatively slowly far away from contact percolation. Results for Ac can be estimated from the stress autocorrelation function Gσσ (r) with the following argument: the radius of characteristic contact patches, rc, cannot be so large that Gσσ (rc) is much less than pc2. Our findings provide a possible mechanism for the breakdown of the proportionality between friction and wear with load at large contact pressures and/or for surfaces with a large roll-off wavelength.
Keywords
surface roughness; contact mechanics; friction; wear; Amontons' law; Archard's law
Subject
Chemistry and Materials Science, Materials Science and Technology
Copyright:
This is an open access article distributed under the Creative Commons Attribution License which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
