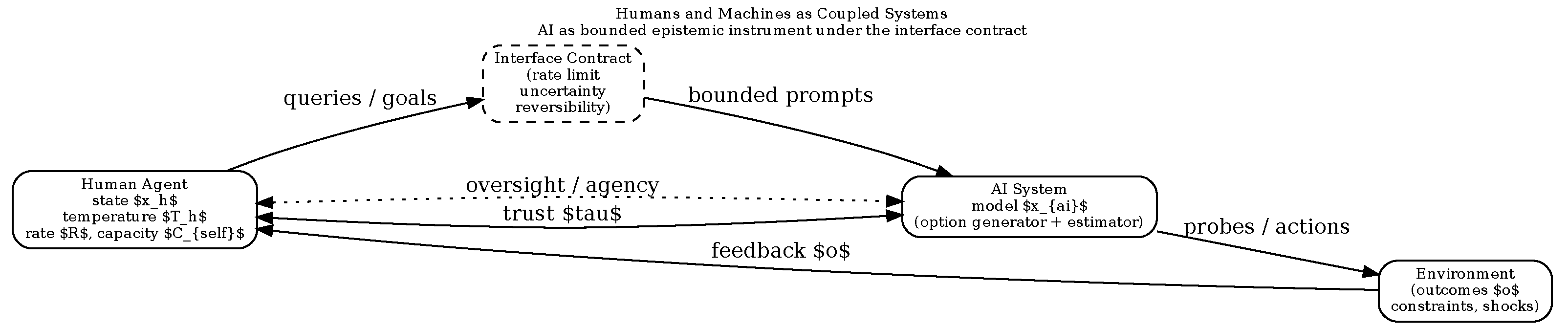
1. Introduction
Artificial intelligence is rapidly transforming the informational, economic, and cognitive environments in which human systems operate. Tasks once considered stable and professionalized are increasingly automated, augmented, or restructured, producing steep gradients that require continuous adaptation rather than one-time optimization. Task-based accounts of technological change emphasize that automation reallocates work by reshaping task compositions and skill demands, creating both displacement and continual reinvention pressures across the labor market [
1,
2]. In this emerging landscape, the most practically relevant example of a complex adaptive system interacting with artificial intelligence is not an organization or a market in the abstract, but the coupled human–AI system itself.
Historically, many individuals in professional societies have followed what may be called a
blueprint philosophy: one studies early, qualifies into a profession, stabilizes into an identity, and then exploits that competence over decades. This model presumes a relatively stationary environment in which early optimization confers long-term robustness. However, AI-driven change undermines this stability, particularly in traditionally professionalized domains where specialization and credentialing are strongest. In the blueprint regime, retraining was episodic and optional; in the AI regime, retraining becomes continuous and often unavoidable [
1,
2]. This shift creates a structural vulnerability: systems that cooled early into narrow roles and identities can become brittle when gradients steepen later under irreversible constraints.
A parallel literature in human–automation interaction shows that intelligent assistance fails as often through
relational and
epistemic breakdowns as through technical limitations. Classic results describe misuse, disuse, and abuse of automation as recurrent failure modes when uncertainty and responsibility are poorly calibrated [
3,
4]. Trust is likewise central: appropriate reliance depends on how competence, intent, and uncertainty are communicated [
5,
6]. More recent work emphasizes calibration in modern predictive systems and highlights the risk of both overconfidence and underuse in AI-supported decisions [
7,
8]. These results motivate our focus on
agency as a structural property of the coupled system, not a matter of willpower.
The present work also draws on three mature technical foundations. First, nonequilibrium thermodynamics explains how structured systems arise and persist far from equilibrium while dissipating gradients and producing entropy [
9,
10]. Stochastic thermodynamics extends these ideas to fluctuating systems and provides modern fluctuation relations that sharpen the connection between irreversibility, work, and entropy production [
11,
12,
13]. Second, information theory formalizes uncertainty, rate limits, and channel capacity, establishing hard constraints on reliable information integration [
14,
15]. Landauer’s principle makes the bridge explicit by relating logical irreversibility (e.g., erasure) to minimal thermodynamic dissipation [
16]. Third, stochastic optimization provides constructive methods for escaping local optima in rugged landscapes. Simulated annealing and related Markov chain methods show how controlled noise and cooling schedules can discover globally viable configurations without assuming a known blueprint of the optimum [
17,
18,
19,
20]. Closely related “deterministic annealing” approaches make the same exploration–commitment trade-off explicit as a variational free-energy balance [
21,
22]. At a foundational level, these methods connect directly to Langevin dynamics and diffusion-based sampling [
23,
24] and to Bayesian learning dynamics [
25,
26].
The novelty of this paper lies in making these connections
domain-agnostic and inspectable while extending them to the self and to human–AI coupling. Prior frameworks already share family resemblance with this ambition. In particular, Friston’s Free Energy Principle and active inference formalize adaptive biological systems as minimizing variational free energy (reducing surprise) under generative models [
27,
28]. Interpretive and critical discussions emphasize that the principle is best read as a constrained dynamical account rather than a teleological claim [
29]. Separately, work on “psychological entropy” treats uncertainty and prediction error as central drivers of affect and motivation [
30]. However, these literatures typically do not connect (i) controlled
reheating as a proactive mechanism (ambition as temperature control), (ii) explicit
capacity bounds from Shannon theory as a failure condition for agency, and (iii) practical decision protocols for high-stakes human life choices and professional adaptation under AI.
At the cognitive and behavioral level, evidence supports the relevance of explicit capacity constraints. Cognitive load theory shows that learning and performance degrade when processing demands exceed working-memory and integration limits [
31]. Information overload is a well-studied organizational failure mode [
32,
33], and choice overload can reduce decision quality and motivation even as the option set grows [
34]. These findings align with a central diagnosis of the AI age: AI can increase the effective
option velocity and information rate faster than human systems can reliably integrate, thereby destabilizing agency.
This paper addresses these gaps by proposing a unified annealing-based framework linking thermodynamic entropy, information entropy, and a formally defined self-entropy. Within this framework, ambition is reinterpreted not as goal pursuit but as temperature control: the capacity to sustain stochastic exploration in the absence of immediate external pressure. Premature stabilization—cooling too early in environments of safety or abundance—produces locally coherent but globally brittle configurations. AI steepens gradients and accelerates information flow, making premature cooling increasingly costly in professional societies where the blueprint trajectory has historically been rewarded.
A particularly relevant instance of such complex adaptive systems is the human–AI dyad itself. As AI systems increasingly mediate professional work, learning, and decision-making, they function not merely as tools but as gradient multipliers—accelerating rates of change while leaving human adaptive capacity largely unchanged. Understanding adaptation in this setting therefore requires a framework that treats humans and AI as coupled dynamical systems, rather than as independent optimizers.
The main aim of this work is threefold. First, we formalize a unified stochastic dynamical model that governs adaptation across physical systems, learning systems, and human lives. Second, we apply this model to human–AI systems, explaining why blueprint-based career and identity formation fail under accelerating informational change and task displacement [
1,
2]. Third, we derive practical implications for decision-making, education, and lifelong learning, emphasizing that capacity and exploration tolerance must be trained early—before external AI gradients force abrupt reheating that exceeds integration limits.
Existing approaches to human–AI adaptation emphasize static optimization, equilibrium notions of rationality, or the minimization of surprise and error. While effective in slowly varying environments, these models implicitly assume that identity, skill sets, and goals can stabilize before external conditions shift. We advance the alternative hypothesis that adaptation under accelerating AI-driven change is fundamentally annealing-limited: failure arises not from suboptimal goals, but from premature entropy collapse and rate–capacity mismatch.
The principal conclusion is that adaptation in the AI age cannot be achieved by optimizing static targets such as happiness, certainty, or professional success. Instead, viable human–AI systems must optimize for the continuity of agency: the maintained ability to explore, commit, and reconfigure in response to changing gradients. Entropy-aware annealing is not merely a metaphor for this process; it is its governing structure.
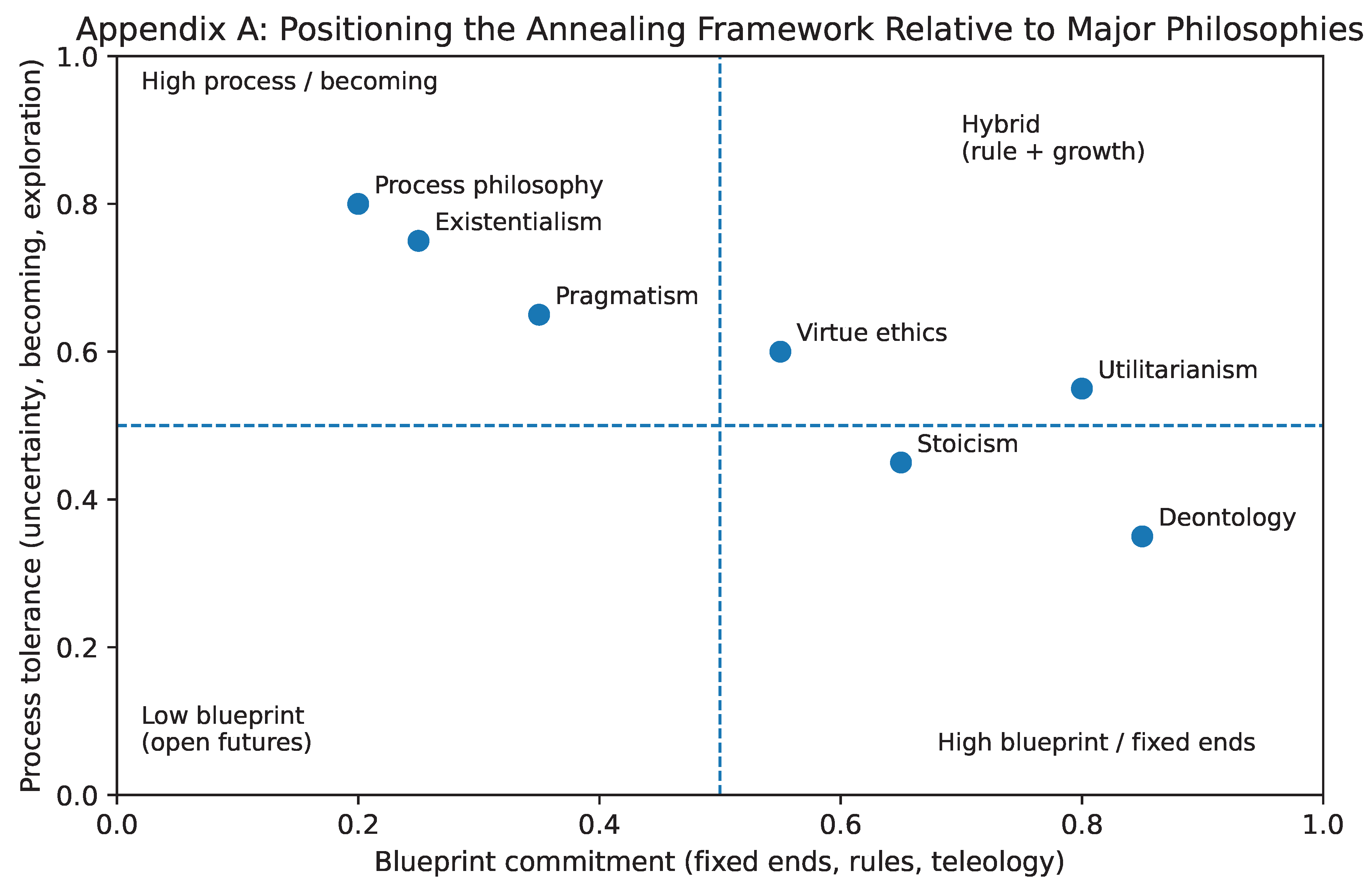
For readers interested in how this framework relates to existing philosophical traditions—including Stoicism, utilitarianism, existentialism, and process philosophies—a concise comparative positioning is provided in Appendix A.
2. Life as a Consequence of Nature
Life did not arise as the execution of a plan. It emerged as a consequence of physical law: matter driven far from equilibrium by persistent gradients can form, maintain, and reproduce structured states while exporting entropy to the environment. This is the central thermodynamic insight behind the classic view of organisms as “order” maintained through dissipation rather than equilibrium [
9,
10]. In modern terms, living systems are best understood as open, nonequilibrium processes whose stability depends on sustained flows and on the continual processing of gradients [
11].
This framing matters for the aims of this paper. If life is a consequence of how systems behave under gradients and constraints, then it is legitimate—and often necessary—to use the same structural language (gradients, entropy, capacity, exploration, stabilization) when reasoning about biological, cognitive, and social adaptation. The claim is not that humans are reducible to physics, but that humans are part of nature, and therefore subject to the same constraint logic that governs other complex adaptive systems.
2.1. Gradients as the Universal Change Catalyst
A gradient is a spatial or temporal difference in a quantity that can drive flux and enable work. Physical examples include temperature differences, chemical potential differences, and concentration gradients; when such gradients exist, systems can extract work and undergo irreversible change. When gradients vanish, systems relax toward equilibrium and dynamics slow or cease.
The crucial point is that gradients do not encode outcomes. A gradient specifies an opportunity for change, not a blueprint for what the system should become. As a result, the structures that emerge under gradients are not designed from above. They are discovered through local interactions and constrained by what is dynamically accessible.
2.2. Bottom-Up Emergence and the Failure of Blueprints
Blueprint thinking treats complex outcomes as if they were specified in advance: one chooses a goal, commits to a plan, and executes. This intuition is powerful in engineering and institutions, but it is not how natural complex systems operate. In bottom-up systems, components respond locally to constraints and signals; global organization emerges from interaction, feedback, and selection among viable configurations.
This distinction becomes practically important under changing environments. Blueprint strategies perform well when the landscape is stable: early specialization and early commitment can be optimal if gradients and demands remain predictable. But when the landscape shifts, early commitment can create brittleness. In the language developed later, blueprints correspond to premature stabilization: the system “cools” into a narrow set of configurations before it has sampled enough of the space to remain robust to future gradients.
2.3. Stability Is Contingent, Not Guaranteed
From an entropy-based perspective, stability is not the default state of nature; it is a transient achievement under continuing flux. Ordered structures persist only so long as (i) gradients continue to supply usable free energy, and (ii) the structure remains an effective pathway for dissipating those gradients. When gradients change or constraints tighten, previously stable configurations can become maladaptive or collapse.
This reframes “success” as conditional. A configuration can be locally optimal under yesterday’s gradients and fragile under tomorrow’s. This is not a moral claim; it is a structural one. Nature rewards neither comfort nor ambition. It simply enforces constraints and selects what remains viable under shifting conditions.
2.4. Implications for Professional Life in the AI Age
The AI age makes this natural-law framing operational. Task-based accounts of automation emphasize that technological change reallocates work by reshaping task compositions, often requiring continual reconfiguration rather than once-off qualification [
1,
2]. This introduces a steep external gradient for individuals and organizations: the need to retrain, respecialize, and redefine roles at a rate that can exceed historical norms.
The most exposed populations are often those whose careers were built as blueprints. Traditionally professional societies reward early specialization, credentialing, and identity locking (medicine, law, engineering, actuarial science). Under slow change, that strategy is robust. Under rapid AI-driven change, it can become a liability: the system has cooled early into a deep local minimum, with high irreversibility and reduced optionality. When displacement and retraining pressures arrive late, adaptation is required under tighter constraints and with less reversibility.
This motivates a central thesis of the paper: in nonstationary environments, the key variable is not whether one has chosen the “right” blueprint, but whether one has preserved and trained the capacity for exploration and reconfiguration before gradients become unavoidable. The next section formalizes these intuitions in thermodynamic terms by defining entropy, gradients, and free energy precisely, establishing the mathematical substrate for the later move to information, capacity, and self-entropy.
3. Thermodynamic Entropy and the Role of Gradients
Thermodynamic entropy provides the first and most fundamental setting in which the logic of this work can be stated precisely. Long before concepts such as information, learning, or agency arise, physical systems already exhibit a universal pattern: when gradients exist, structure forms; when gradients vanish, dynamics stagnate. Life itself emerges not as an exception to thermodynamic law, but as a consequence of it [
9,
10].
3.1. Entropy as a State Variable
In classical thermodynamics, entropy
S is a state function that quantifies the number of microscopic configurations compatible with a macroscopic description. For a system with internal energy
U, volume
V, and particle number
N, entropy is defined (up to an additive constant) by
where
is the reversible heat absorbed and
T the absolute temperature. The second law of thermodynamics states that entropy increases in isolated systems.
However, entropy alone does not explain the emergence of structure. A homogeneous equilibrium state has maximal entropy but is dynamically inert. What matters is not entropy as a scalar quantity, but entropy production driven by gradients.
3.2. Gradients as Drivers of Irreversible Dynamics
A gradient is a spatial or temporal variation in an intensive quantity such as temperature, chemical potential, or pressure. Formally, gradients appear as derivatives of thermodynamic potentials, for example
Gradients break symmetry and generate fluxes. Heat flows down temperature gradients, particles diffuse down chemical potential gradients, and mechanical work is extracted from pressure gradients.
The local rate of entropy production
can be written schematically as
where
are fluxes and
the corresponding thermodynamic forces [
10,
11]. Without gradients (
), fluxes vanish and the system ceases to evolve.
3.3. Open Systems and the Emergence of Structure
Living systems are open systems maintained far from equilibrium by sustained gradients—solar radiation, redox potentials, and nutrient flows. Under these conditions, entropy production does not destroy structure; it enables it. Dissipative structures such as convection cells, chemical oscillations, and metabolic networks arise precisely because they process gradients efficiently [
10].
This observation is foundational: order does not arise despite entropy, but because entropy production is constrained by structure. Systems that process gradients more effectively persist longer.
3.4. Cooling, Trapping, and Metastability
As gradients weaken or are exhausted, systems relax toward equilibrium. In rugged energy landscapes, this relaxation often leads to metastable states—local minima separated by barriers. Rapid cooling suppresses fluctuations and prevents exploration of alternative configurations, while slow cooling allows broader sampling before stabilization.
This physical insight foreshadows simulated annealing, where controlled stochasticity enables systems to escape local optima before committing to stable configurations.
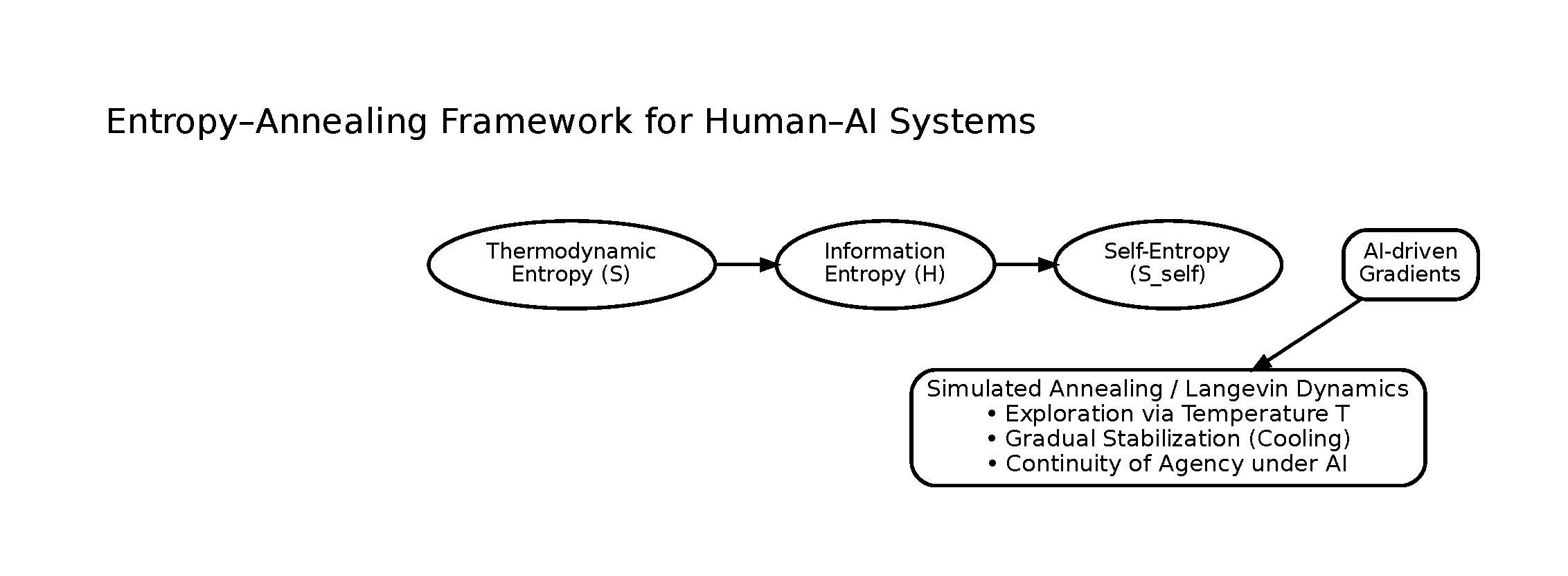
Figure 1.
Gradients drive dissipation in a minimal toy model: as a temperature gradient increases, the associated entropy production rate increases. This figure is schematic and intended to build intuition for the role of gradients as the driver of irreversible change.
Figure 1.
Gradients drive dissipation in a minimal toy model: as a temperature gradient increases, the associated entropy production rate increases. This figure is schematic and intended to build intuition for the role of gradients as the driver of irreversible change.
3.5. Why Gradients Matter Beyond Physics
The role of gradients generalizes beyond thermodynamics. In later sections, we show that informational uncertainty, learning dynamics, and human identity evolution follow the same structural logic. Change occurs only when gradients are encountered; stagnation occurs when systems cool too early.
This distinction becomes practically important under changing environments. When gradients steepen—whether due to environmental shocks or technological change—systems that have prematurely stabilized struggle to adapt. Those that have preserved exploratory capacity respond more robustly.
The next section makes the thermodynamic–informational bridge explicit, showing how entropy, free energy, and gradients reappear in the mathematics of inference and learning.
4. From Thermodynamics to Information
Section 3 established the core physical logic: gradients generate fluxes; fluxes generate entropy production; and far-from-equilibrium conditions can support persistent structure. The purpose of this section is to make explicit why it is valid to move from thermodynamic entropy to information-theoretic entropy without changing the underlying constraint logic. The bridge is not metaphorical. It is structural: both domains are governed by probability distributions over accessible states, and both admit variational principles in which uncertainty (entropy) trades off against cost.
4.1. Entropy as Uncertainty over Accessible States
In statistical physics, a macroscopic description of a system corresponds to a probability distribution over microscopic configurations. The Gibbs entropy for a discrete state space
with probabilities
is
where
converts dimensionless uncertainty into physical units. In information theory, Shannon introduced the analogous quantity for a random variable
X,
measured in bits (log base 2) or nats (natural log) [
14,
15]. The functional identity between is not accidental. In both cases entropy measures the effective breadth of the distribution: how many states are meaningfully accessible under the constraints that define
p.
The difference is interpretive and dimensional. Thermodynamic entropy is uncertainty over microstates consistent with a macroscopic description; Shannon entropy is uncertainty over symbols, hypotheses, or messages. But in both cases, entropy quantifies uncertainty under constraint. This shared structure is precisely what allows the thermodynamic language of gradients and dissipation to be carried into informational settings.
4.2. Free Energy and the Cost–Uncertainty Trade-Off
Thermodynamic equilibrium at temperature
T is characterized by the Boltzmann distribution
where
is the physical energy. A central result is that Equation (
6) can be derived variationally:
minimizes the Helmholtz free-energy functional
over distributions
q [
25]. The structure is explicit: expected energy is traded against entropy. High temperature weights entropy and yields broad exploration; low temperature weights energy and concentrates probability mass into low-energy regions.
In learning and inference, the same mathematics reappears when we interpret
x as a hypothesis or parameter vector and define an informational energy by negative log probability. For observed data
D,
Low energy corresponds to high posterior plausibility. Substituting Equation (
8) into Equation (
7) yields the same cost–uncertainty trade-off, now interpreted as balancing explanatory fit against uncertainty over explanations. This variational viewpoint underlies deterministic annealing and related methods in which optimization proceeds via controlled entropy reduction [
21,
22].
4.3. Information Is Physical
The thermodynamics→information bridge is further strengthened by the fact that information processing has irreducible physical costs. Landauer’s principle shows that logically irreversible operations (such as bit erasure) require a minimal dissipation of heat [
16]. In modern stochastic thermodynamics, irreversibility along trajectories is quantified directly through entropy production [
11]. Taken together, these results justify treating information as a constrained physical resource rather than an abstract bookkeeping device.
This point becomes important when we later discuss capacity limits and agency collapse. If uncertainty reduction and information integration are constrained processes, then the ability of a system to remain adaptive is bounded not only by preferences or motivation, but by hard rate limits on what can be processed reliably over time.
4.4. Why This Bridge Matters for the AI Age
AI systems increase the volume, velocity, and availability of information. They can generate predictions, counterfactuals, and options at rates that exceed the integration capacity of individuals and organizations. Empirical work on cognitive load and information overload is consistent with a simple structural diagnosis: performance and learning degrade when processing demands exceed integrative capacity [
31,
33], and expanding choice sets can reduce decision quality and motivation [
34].
The implication is that informational gradients can destabilize agency in the same way that steep physical gradients can destabilize fragile structures. This motivates the next section, where we define information entropy, informational gradients, and channel capacity explicitly. The thesis is that the AI age changes human outcomes not merely by adding tools, but by steepening the informational landscape in which coupled human–AI systems must adapt.
5. Information Entropy and Informational Gradients
Section 4 established the formal continuity between thermodynamic and informational entropy: both quantify uncertainty over accessible states, and both support a variational interpretation in which uncertainty trades off against cost. We now develop the information-theoretic side explicitly. The purpose is twofold: (i) to define the quantities that will later serve as primitives for “self-entropy”; and (ii) to introduce
rate limits—hard constraints on reliable integration—that become decisive in the AI age.
5.1. Shannon Entropy, Conditional Entropy, and Mutual Information
Let
X be a discrete random variable with distribution
. Shannon entropy is
measuring uncertainty in bits (log base 2) or nats (natural log) [
14,
15].
For two random variables
with joint distribution
, the conditional entropy
quantifies residual uncertainty about
X after observing
Y. The mutual information
measures the expected reduction in uncertainty about one variable gained by observing the other [
15]. These quantities provide a precise language for “how much the system learns” when it receives a signal.
5.2. Informational Gradients as Uncertainty Reduction Under Interaction
In physical systems, gradients in intensive variables drive fluxes. In informational systems, the analogous drivers are
differences in uncertainty over outcomes, states, or explanations. A simple representation is to treat negative log probability as an informational “energy” [
25]:
so that high-probability states have low informational energy. Changes in evidence, context, or interaction reshape
and therefore reshape the energy landscape.
An
informational gradient can then be operationalized as a local sensitivity of uncertainty (or surprise) to controllable variables (actions, queries, attention allocation). For example, suppose an agent selects an action
a that influences an observation
Y. A natural objective of exploration is to maximize expected information gain,
i.e., choose actions that are expected to reduce uncertainty most. This is the informational analogue of following a gradient: the system moves toward actions that produce the steepest expected reduction in uncertainty [
15].
This idea also clarifies why “more information” is not always beneficial. Information gain is only valuable to the extent that it can be integrated and used to update beliefs, policies, and commitments. That constraint is formalized by channel capacity.
5.3. Rate, Capacity, and the Reliability of Integration
Shannon’s channel coding theorem establishes that reliable communication over a noisy channel is possible only when the information rate
R does not exceed channel capacity
C:
where
C is the maximum achievable mutual information per channel use under the channel constraints [
14,
15]. When
, error rates cannot be driven arbitrarily low by any coding scheme.
This inequality will later become the central formal constraint on agency. The key move is to treat human adaptation and decision-making as an integration process operating under limited cognitive, emotional, and temporal bandwidth. If incoming options, signals, and counterfactuals arrive at an effective rate R that exceeds the system’s integrative capacity, then reliable updating fails: decisions become unstable, learning becomes noisy, and commitment collapses into either paralysis or premature closure.
Empirical literatures in cognitive load and information overload are consistent with this structural diagnosis: performance and learning degrade when processing demands exceed integrative limits [
31,
33], and expanding choice sets can reduce decision quality and motivation [
34]. Information theory provides the hard bound underlying these observed phenomena.
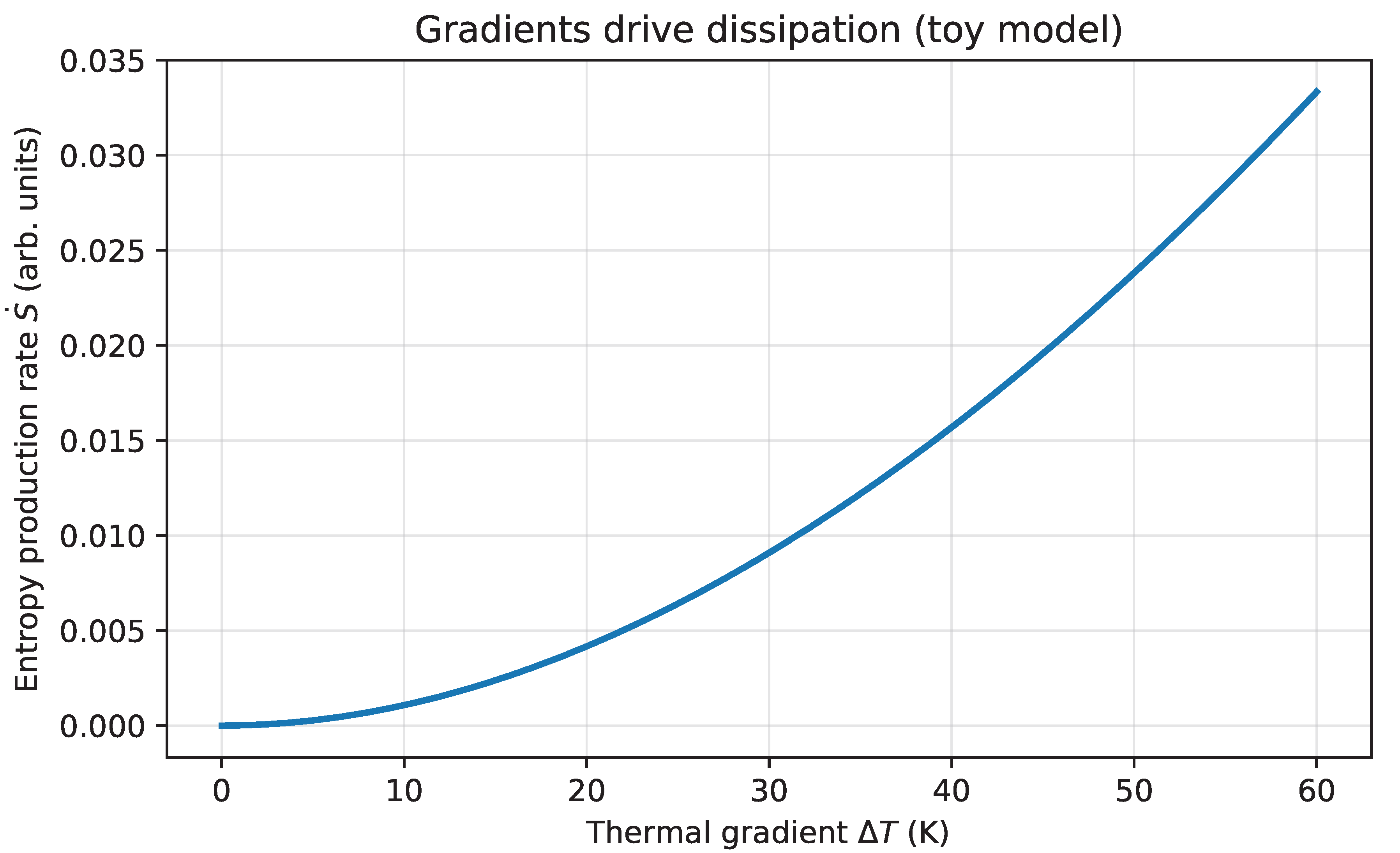
Figure 2.
Informational gradients reduce uncertainty: a simple Bayesian toy model illustrates how evidence concentrates the posterior distribution and reduces entropy. Stronger evidence produces faster entropy collapse than weaker evidence.
Figure 2.
Informational gradients reduce uncertainty: a simple Bayesian toy model illustrates how evidence concentrates the posterior distribution and reduces entropy. Stronger evidence produces faster entropy collapse than weaker evidence.
5.4. Implications for the AI Age
AI steepens informational gradients by increasing the volume and velocity of predictions, options, and comparisons. It can also reduce the marginal cost of generating new hypotheses and plans, encouraging constant exploration. This changes the landscape in which individuals and institutions must operate: the effective rate R of actionable information can rise faster than human integrative capacity, pushing coupled human–AI systems toward the regime .
The next section extends these concepts into the existential domain by defining a state space of the self and a corresponding self-entropy. The goal is to show that the same structural objects—entropy, gradients, rate limits, and controlled exploration—govern adaptation not only in physics and learning, but in the evolution of identity and agency under accelerating AI-driven change.
6. Self-Entropy and Capacity
Section 3,
Section 4 and
Section 5 established two domains in which the same structural logic repeats: (i) gradients create pressure for change; (ii) entropy quantifies the breadth of accessible states; and (iii) stabilization is a regulated reduction of that breadth under constraint. We now extend this logic to the existential domain by defining a state space for the self and a corresponding self-entropy. The purpose is not to reduce lived experience to a scalar, but to introduce an
inspectable object that can later be coupled to informational gradients and capacity limits in the AI age.
6.1. State Space of the Self
Let denote a set of possible self-states available to an individual at time t. Each represents a coherent configuration of identity: roles, values, commitments, skills, relationships, and narrative stance. The precise content of a state is application dependent; what matters is that represents plausible ways of being that the individual experiences as accessible.
At any moment, the individual implicitly assigns a probability distribution over this space,
shaped by prior experience, culture, biology, environment, and accumulated commitments. In practice
need not be explicit; it is encoded in preference, affect, perceived feasibility, and habitual action.
6.2. Definition of Self-Entropy
We define self-entropy as the Shannon entropy of the distribution over self-states:
Self-entropy measures the breadth of identity space experienced as available. High corresponds to a wide sense of possibility: multiple futures feel live and reachable. Low corresponds to a narrow identity distribution: a small number of futures dominate, and alternatives feel remote or impossible.
This definition is descriptive, not normative. High self-entropy is not inherently good, nor is low self-entropy inherently bad. As in thermodynamics and information theory, what matters is how entropy changes under constraint, and whether reduction is regulated or premature.
6.3. Self-Entropy Is Not Chaos
It is tempting to equate high self-entropy with confusion or instability. This is a mistake. Entropy measures uncertainty over accessible states, not dysfunction. In physical systems, high entropy does not imply random motion; it implies many accessible microstates. In inference, high entropy does not imply ignorance; it implies openness to revision. Likewise, high self-entropy does not imply lack of identity; it implies that identity has not collapsed into a single narrow narrative.
Conversely, low self-entropy may reflect coherence, commitment, and purpose. But it may also reflect premature closure: a collapse of possibility induced by safety, external expectations, or institutional reinforcement. The mathematics does not judge; it clarifies the structural regime.
6.4. Experiential Gradients and Pressure to Change
As in the physical and informational domains, self-entropy does not change spontaneously. It changes under gradients. In the existential domain, gradients appear as experienced discrepancies between (i) current self-states and environmental demands, (ii) current identity and internal drives, or (iii) current life and perceived alternatives. These gradients may be felt as boredom, restlessness, dissatisfaction, ambition, attraction, or crisis.
A useful formal correspondence is to define an “energy” over self-states using negative log plausibility:
so that highly plausible identities have low energy and implausible identities have high energy. Experiences that introduce new information, new exemplars, or new constraints reshape
and therefore reshape
. When a previously unlikely identity becomes salient—through exposure, success, failure, or encounter—a gradient is introduced that pressures the distribution to shift.
Importantly, gradients create necessity. Without gradients, the distribution remains static: the system “cools” into a stable basin and self-entropy collapses through routine reinforcement.
6.5. Capacity as a Hard Constraint on Integration
Self-entropy describes
how many futures feel available. Capacity describes
how fast the system can integrate change. Information theory provides the relevant concept: a rate limit on reliable integration. For a noisy channel, Shannon’s theorem implies that reliable transmission is possible only when the information rate does not exceed channel capacity [
14,
15]:
We interpret
as the effective capacity of the human system to integrate information into stable updates of belief, behavior, and commitment. This capacity is constrained by cognitive resources, time, emotional regulation, social context, and physiological state. Empirical work supports the general form of this constraint: performance and learning degrade when processing demands exceed integrative limits [
31,
33], and expanding option sets can reduce decision quality and motivation [
34].
When , updating becomes unreliable. The subjective signature is familiar: overwhelm, fragmentation, paralysis, impulsive commitment, or oscillation. This is not primarily a failure of willpower. It is a violation of a rate constraint.
6.6. AI as an Amplifier of Informational Gradients
AI systems can dramatically increase the effective rate by producing more options, faster feedback, more counterfactuals, and more comparisons. In coupled human–AI systems, this can push individuals and organizations into the regime , causing a collapse of agency even as the system appears to be “more informed”. This mechanism will be developed explicitly in later sections; here we emphasize the structural implication: in the AI age, preserving agency requires managing rate as much as managing choice.
6.7. Meaning as Regulated Entropy Reduction
A final point is critical for the arc of the paper. Self-entropy must eventually decrease if the self is to become coherent. Commitment is, in a precise sense, entropy reduction: probability mass concentrates into a narrower set of identities and trajectories. The question is not whether entropy should decrease, but whether the reduction is regulated—supported by sufficient exploration and integration capacity—or premature, producing a brittle local optimum that later destabilizes under steep gradients. This is the basis for the annealing dynamics introduced next.
The next section will unify the physical, informational, and existential domains under a single stochastic dynamical form and interpret simulated annealing as the general mechanism by which complex systems without foresight discover order under constraint.
7. Unified Dynamics and Simulated Annealing
Section 3,
Section 4,
Section 5 and
Section 6 developed three parallel domains: thermodynamic entropy (structure under physical gradients), information entropy (uncertainty under informational gradients), and self-entropy (possibility under existential gradients) subject to capacity constraints. We now unify these domains under a single dynamical form. The purpose of this section is to state, clearly and formally, the process that connects gradients to exploration and exploration to stabilization:
controlled stochastic gradient flow. This is the common mechanism by which complex systems without foresight discover viable structure under constraint.
7.1. A Single Dynamical Form Across Domains
Let
denote a system state evolving in time. The interpretation of
x depends on domain: a physical configuration, a hypothesis or parameter vector, or a self-state in identity space. Let
be an effective energy (or cost) landscape, capturing what is locally stable or costly under the system’s constraints at time
t. We consider the canonical continuous-time model of overdamped Langevin dynamics:
where
is standard Brownian motion and
is an effective temperature controlling stochastic exploration [
23,
24]. The first term drives descent along local gradients; the second injects fluctuations that enable exploration and barrier crossing.
At fixed temperature
T, the stationary distribution of Equation (
19) under appropriate conditions is a Gibbs distribution,
making explicit the role of temperature as a knob controlling distributional breadth: higher
T spreads probability mass across more states; lower
T concentrates it into lower-energy basins [
24].
7.2. Domain Instantiations
Thermodynamics.
In thermodynamics,
x represents a physical configuration,
is physical energy, and
T is temperature. Cooling reduces entropy by confining the distribution to lower-energy regions, but only if sufficient thermal exploration occurs first; otherwise the system becomes trapped in metastable local minima. This is the physical origin of annealing logic [
10,
11].
Learning and inference.
In learning,
x represents hypotheses or model parameters, and a natural energy is negative log posterior,
so that low energy corresponds to high posterior plausibility. Temperature corresponds to the degree of exploration in hypothesis space: high
T tolerates unlikely explanations; low
T concentrates around dominant models. This connects directly to Bayesian learning dynamics and stochastic-gradient sampling [
25,
26]. Deterministic annealing makes the trade-off explicit by minimizing a free-energy functional that balances expected cost against entropy [
21,
22].
The self.
In the existential domain, x denotes a configuration of identity and commitments (a point in self-state space). The energy encodes misfit, fragility, ethical load, irreversible loss, and loss of agency. Temperature corresponds to tolerance for uncertainty and the capacity to explore: trying new roles, projects, relationships, or ways of being. Premature cooling traps the individual in locally stable but potentially misaligned identities; failure to cool at all yields fragmentation and incoherence. A viable self is one that anneals.
7.3. Simulated Annealing as Controlled Entropy Reduction
Simulated annealing is the strategy of controlling
to discover low-energy configurations in rugged landscapes [
17,
18,
19,
20]. High initial temperature enables barrier crossing and broad exploration; gradual cooling concentrates probability mass into stable basins. Crucially, simulated annealing does not assume that the global optimum is known in advance. It assumes only that local gradients are observable, exploration is costly but informative, and constraints tighten over time.
The structural lesson generalizes: exploration is not the opposite of optimization; it is the precondition for meaningful optimization in rugged, nonconvex landscapes. Without stochastic sampling, systems converge reliably—but locally. They settle into configurations that are stable relative to their immediate surroundings, not necessarily those that are globally viable or future-robust.
7.4. Ambition as Temperature Control
Within this framework, ambition can be reinterpreted as the ability to sustain non-zero effective temperature in the absence of external pressure. In environments of abundance and safety, gradients are muted and natural cooling dominates; decays, exploration collapses, and the system stabilizes early. Ambition counteracts this decay by injecting controlled randomness: the deliberate sampling of new regions of state space before external gradients force abrupt reheating.
This interpretation has a practical implication that will recur throughout the paper: in nonstationary environments, robustness is achieved not by early convergence, but by maintaining the capacity to explore and reconfigure at a rate that remains within integration bounds (
Section 6).
7.5. A Phase Portrait as Intuition for the Unified Dynamics
Although Equation (
19) is high-dimensional in most realistic settings, its qualitative behavior can be visualized in low-dimensional projections. In later sections we will project the self-state dynamics onto a reduced coordinate
u (along the dominant self-gradient) and the effective temperature
T, yielding a phase portrait that distinguishes regimes of (i) premature cooling and entropic collapse, (ii) healthy exploration and gradual stabilization, and (iii) overheating and fragmentation.
This phase-portrait view is not merely illustrative: it provides a geometric language for decision protocols. If identity evolution is an annealing process, then guidance consists of controlling temperature schedules, preserving reversibility when possible, and ensuring that exploration proceeds at a rate the system can integrate.
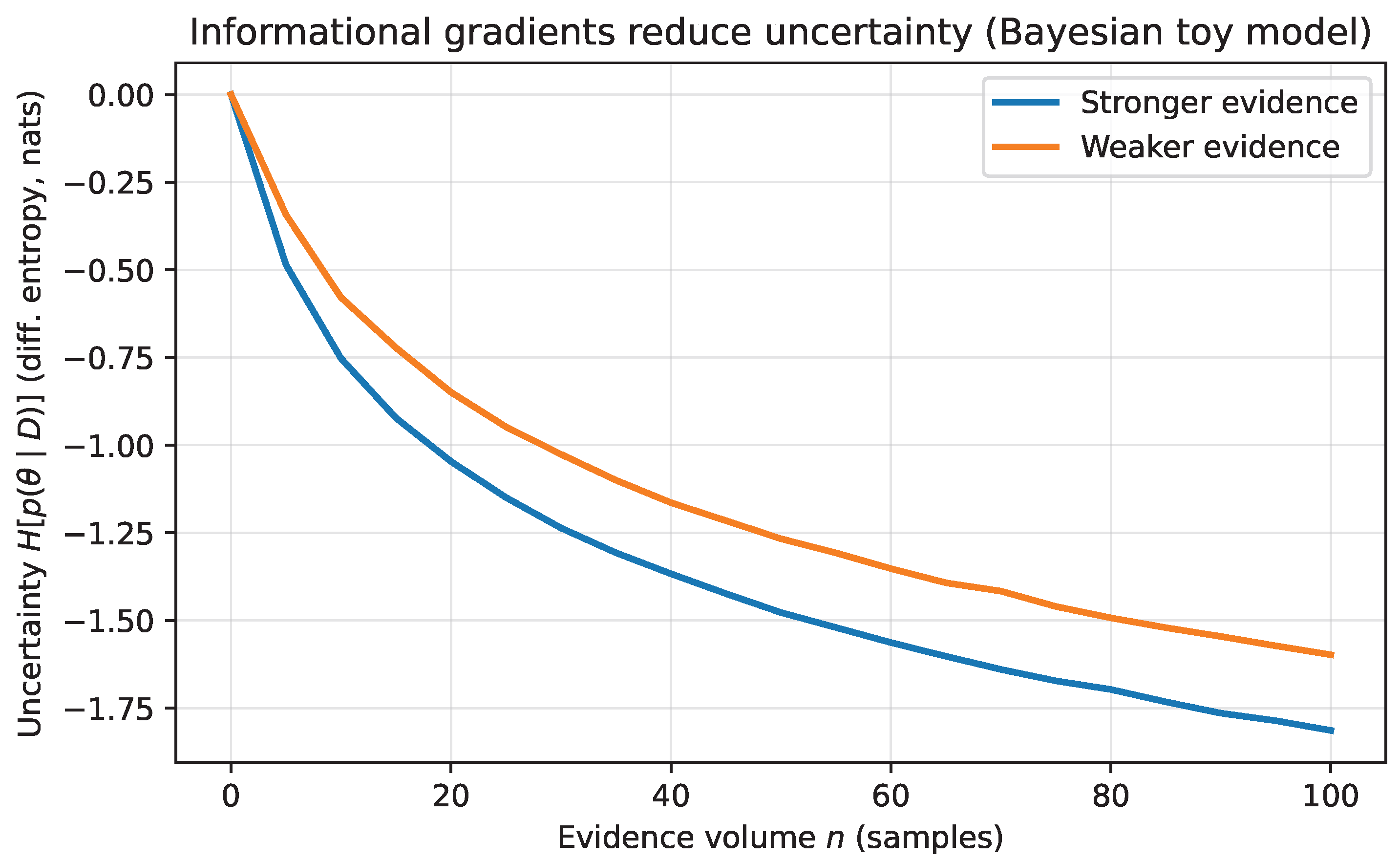
Figure 3.
Annealing schedules in a rugged landscape: slower cooling permits exploration and escape from local minima; faster cooling tends to trap the trajectory. This is a schematic illustration of why stochastic sampling is a precondition for robust optimization in rugged landscapes.
Figure 3.
Annealing schedules in a rugged landscape: slower cooling permits exploration and escape from local minima; faster cooling tends to trap the trajectory. This is a schematic illustration of why stochastic sampling is a precondition for robust optimization in rugged landscapes.
7.6. Relation to Active Inference
The annealing dynamics used here are closely related to the variational formulations of active inference, where biological agents minimize a free-energy functional balancing expected cost against entropy [
28,
35]. In that framework, adaptive behavior emerges through inference over hidden states under a generative model of the world. The present work adopts the same mathematical structure, but treats temperature as an explicit, time-dependent control parameter rather than an implicit constant. This distinction becomes critical in non-stationary environments, where gradients steepen faster than inference alone can stabilize identity or policy. Under such conditions, premature entropy reduction leads to brittle commitments, even when prediction error is locally minimized.
Unlike standard active inference formulations, which emphasize surprise minimization, the annealing perspective foregrounds controlled exploration under constraint as the prerequisite for meaningful stabilization. This shift is essential in environments shaped by artificial intelligence, where option generation and informational gradients accelerate beyond biological integration limits.
Section 9 introduces a concrete instantiation of premature cooling under abundance—Anna—as a worked example. Her case illustrates how late reheating under tight constraints produces oscillation and paralysis, and why this pattern becomes increasingly common in the AI age.
8. Materials and Methods
This study is theoretical and computational in nature. No human or animal subjects were involved, and no empirical data were collected. The methods consist of analytical modeling, numerical illustration, and qualitative synthesis grounded in established principles from statistical physics, information theory, and dynamical systems.
8.1. Unified Stochastic Dynamics
The central modeling framework is based on overdamped Langevin dynamics and simulated annealing. System evolution is described by stochastic differential equations of the form
where
denotes the system state,
an effective energy or cost functional,
a time-dependent temperature controlling exploration, and
a Wiener process. This formalism is applied consistently across physical, informational, and existential domains by appropriate interpretation of the state variables and energy functions.
Phase portraits and reduced-order models are constructed by projecting high-dimensional dynamics onto dominant order parameters, such as identity alignment and effective exploration capacity. Analytical results are supported by schematic simulations illustrating qualitative system behavior under varying temperature schedules and rate constraints.
8.2. Information-Theoretic Capacity Constraints
Agency is formalized as a rate-limited process using Shannon’s channel capacity framework. The relationship between environmental change rate R and individual capacity is expressed through inequalities of the form , with qualitative failure modes analyzed when this bound is violated. These formulations are analytical and conceptual rather than empirical.
8.3. Computational Tools
All figures and simulations were generated using Python (version 3.11). Visualization employed Matplotlib (version 3.8) for continuous plots and Graphviz (version 9.0) for block diagrams and system schematics. Numerical examples are illustrative and intended to clarify structural dynamics rather than provide quantitative prediction. Source code used to generate figures is available from the author upon reasonable request.
8.4. Use of Generative Artificial Intelligence
Generative artificial intelligence tools were used to assist with drafting, code generation for figures, and iterative refinement of mathematical exposition. All theoretical formulations, interpretations, and conclusions were developed and verified by the author.
9. Premature Cooling Under Abundance: Anna as a Professional Shock Case
We now introduce Anna as a concrete instantiation of the dynamics developed in
Section 6Section 7. The purpose is not biographical detail for its own sake, but clarification: to show how a common professional trajectory becomes brittle under AI-driven gradients. Anna is representative of a class of highly successful professionals whose lives followed a stable blueprint: early specialization, credentialing, steady promotion, and identity consolidation in a buffered environment [
1,
2].
Anna grew up in an environment of exceptional stability and expectation. Both of her parents are medical professionals. On her father’s side, the family is well established, respected, and embedded in public institutions. On her mother’s side, there is a strong narrative of upward mobility: her maternal grandfather was an entrepreneur, and her mother was the first in her family to study medicine. Together, these forces created a world that was materially secure, intellectually demanding, and ethically coherent.
From early on, the signal Anna received was clear: safety was abundant, and excellence— particularly intellectual excellence—was expected. Achievement was rewarded not as exploration, but as confirmation of competence and worth. Anna responded optimally to this landscape. She performed at the top of her class, excelled at university, and qualified as an actuary. Her professional career progressed rapidly. Promotions followed. External validation accumulated. By conventional standards, Anna’s life is a success.
Anna is married to a lawyer whose career followed a similar blueprint. His professional path was likewise defined by early specialization, credentialing, and institutional stability. Together, they form a household whose financial risk is buffered and whose social standing is secure. Their world is small, but stable. Even in the face of disruption, their immediate economic survival is unlikely to be threatened.
Structurally, however, this environment suppressed gradients. Financial risk was absorbed. Career paths were predictable. Identity and self-worth were tightly coupled to professional competence and institutional recognition. In annealing terms, Anna’s life cooled early. Her effective temperature declined not because of fear or constraint, but because nothing in her environment required continued stochastic exploration. Local minima were deep, comfortable, and continuously reinforced.
This is abundance at its most effective—and its most dangerous.
The AI age introduces the missing gradient. As automation, model-driven decision systems, and task decomposition accelerate, roles that once appeared stable are restructured or eliminated [
1,
2]. Suppose Anna’s actuarial role is significantly altered or displaced. New tools, new workflows, and new expectations appear. The volume and velocity of information required to remain professionally viable increase rapidly. Retraining is no longer episodic; it becomes continuous.
Crucially, the dominant loss in this scenario is not financial fragility. Household resources and family support buffer economic shock. The primary loss is a loss of identity-based self-worth and perceived agency. Anna’s stabilizing basin was built on competence-signaling: being needed, being relied upon, being correct. When the role collapses, the system loses its main source of coherence. This produces a sharp increase in an effective loss term associated with narrative continuity and status, and an even sharper increase in an agency penalty: the felt inability to steer outcomes despite sustained effort.
In the language of
Section 6, AI-driven restructuring also increases the effective information rate
: tool churn, retraining demands, and option velocity rise sharply. Even when economic fragility remains low, an agency collapse occurs when
exceeds the system’s integrative capacity
. Learning becomes noisy, decisions destabilize, and commitment oscillates.
The situation is compounded by coupling. Anna’s husband faces similar pressures in the legal profession, where AI-assisted research, document generation, and case analysis restructure traditional roles. The household therefore experiences correlated gradients. Two early-cooled systems are reheated simultaneously. Mutual reinforcement that once stabilized the system now amplifies uncertainty.
Anna’s subjective experience is therefore not mysterious. She may feel overwhelmed, fragmented, or paralyzed despite being intelligent, disciplined, and historically successful. This is exactly what one expects from a system that cooled early in a buffered landscape and is now reheated abruptly under tight constraints.
Importantly, this analysis is not moral. It does not claim that Anna lacks resilience or courage. It identifies a structural regime: premature stabilization under abundance, followed by late gradient exposure. The relevant question is no longer “What is the right blueprint?” but:
How can exploration be reintroduced at a rate the system can integrate, while preserving reversibility and minimizing irreversible loss?
This question admits of principled answers. It requires pacing, temperature control, and capacity-aware exploration rather than binary decisions.
9.1. Why Professionals Are Uniquely Vulnerable
A distinctive feature of the AI transition is that it targets occupations historically treated as protected by credentials. Medicine, law, actuarial science, accounting, and related professions have long operated as “blueprint careers”: a front-loaded investment in education followed by decades of relatively stable identity and practice. This structure encourages early cooling. Competence becomes narrowly defined by a fixed corpus of knowledge, institutional signaling substitutes for continued exploration, and long time horizons reinforce commitment to a single basin of expertise.
AI steepens gradients precisely where this model is most rigid. The relevant shift is task-based: professional work is decomposed into smaller units, many of which are automatable or re-allocatable between humans and machines [
1,
2]. Even when entire occupations persist, the internal task composition changes rapidly, and the rate at which tools, standards, and competitive baselines update increases. For the individual professional, this manifests as a rise in effective information rate
and an increase in volatility of the local energy landscape
: what counted as competence last year may not count next year.
The result is a specific fragility of early-cooled systems. Professionals often have high general intelligence but low practiced exploration: their training optimized for convergence on a single validated pathway. When AI imposes abrupt retraining demands, the dominant loss is frequently not economic survival but agency and self-worth, because competence-signaling is the core stabilizer of identity. In the terms of
Section 6, agency failure emerges when the option and retraining rate exceeds integration capacity,
. In such regimes, more information and more options do not increase freedom; they increase error, oscillation, and premature closure.
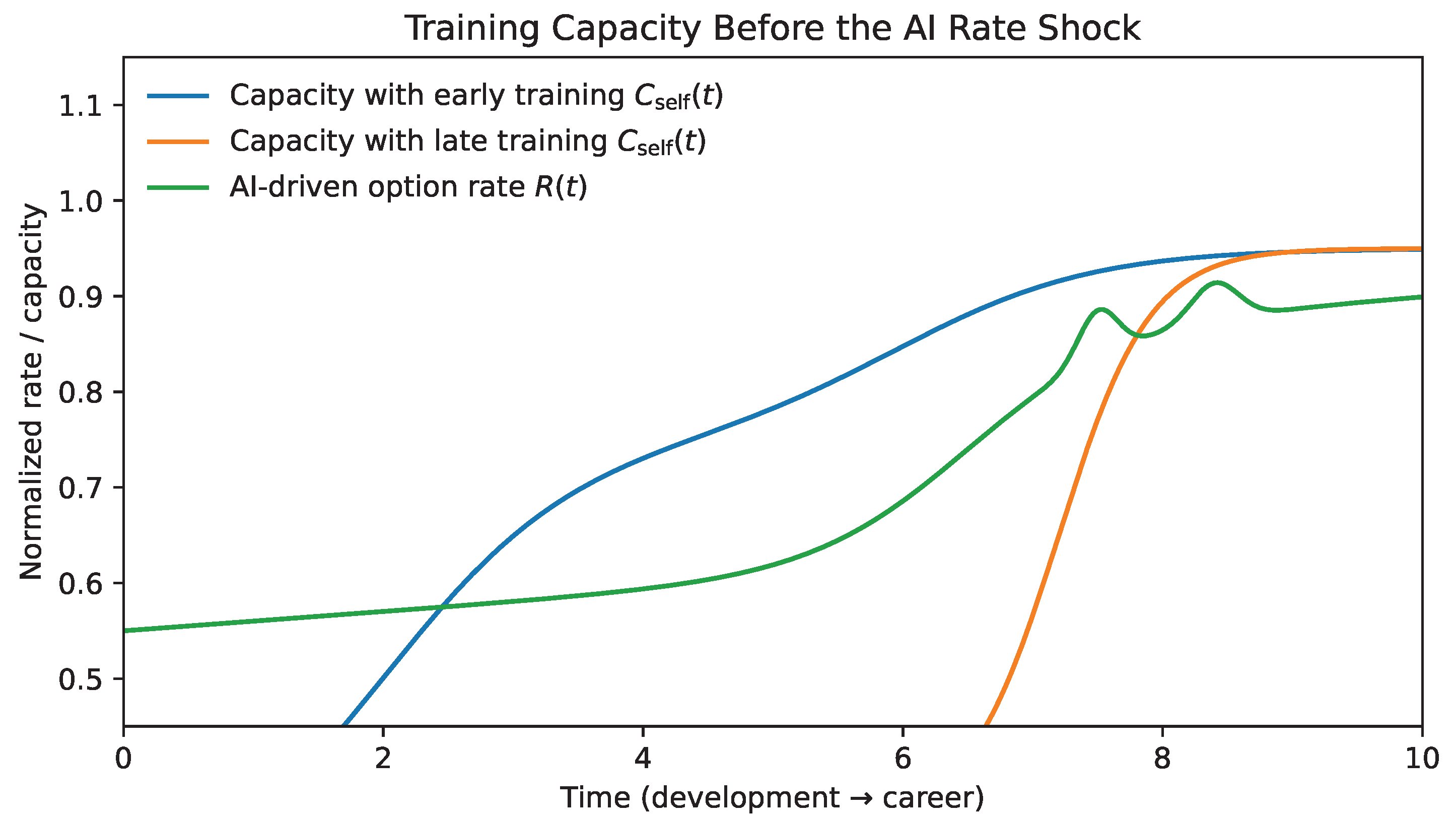
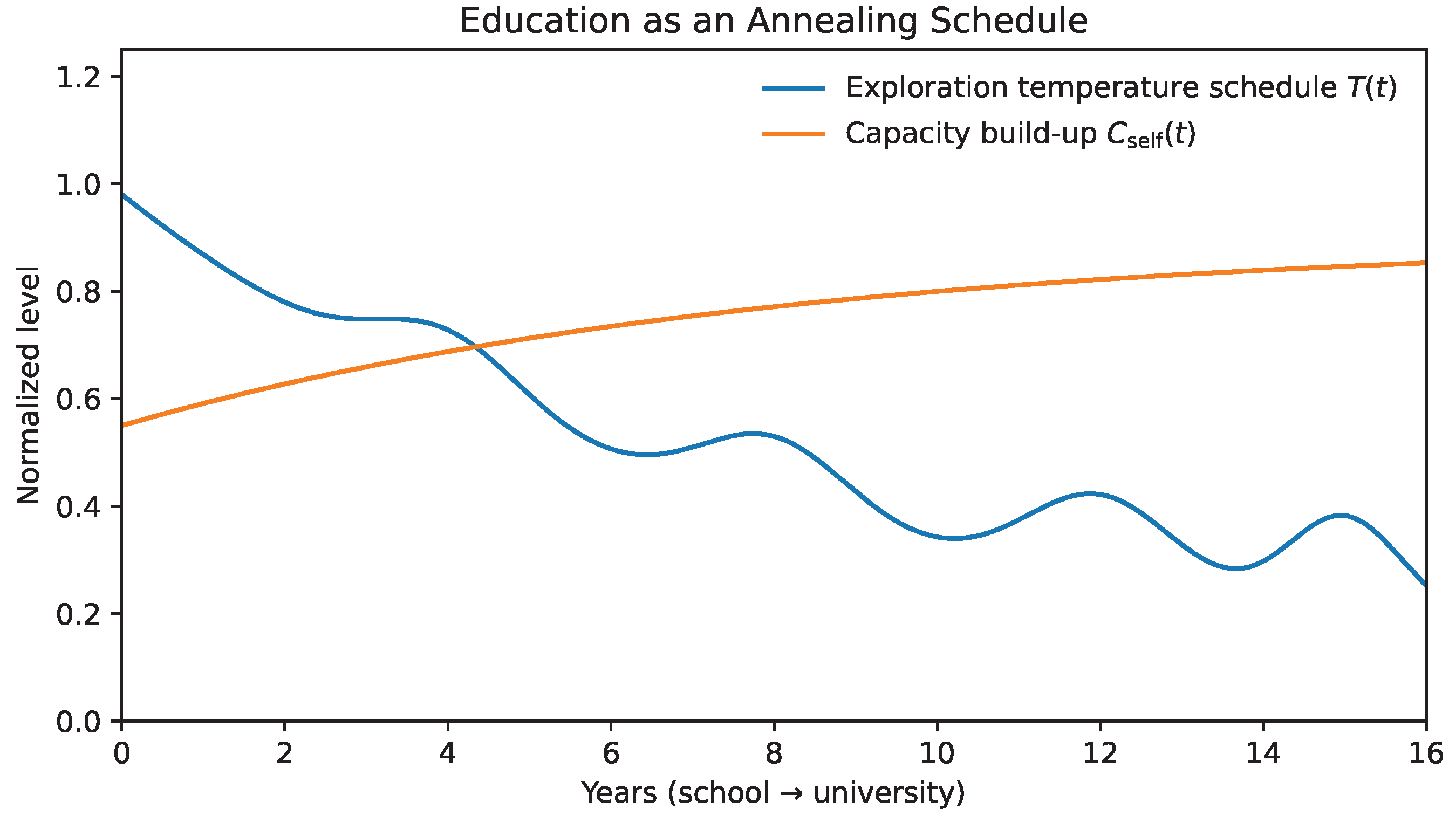
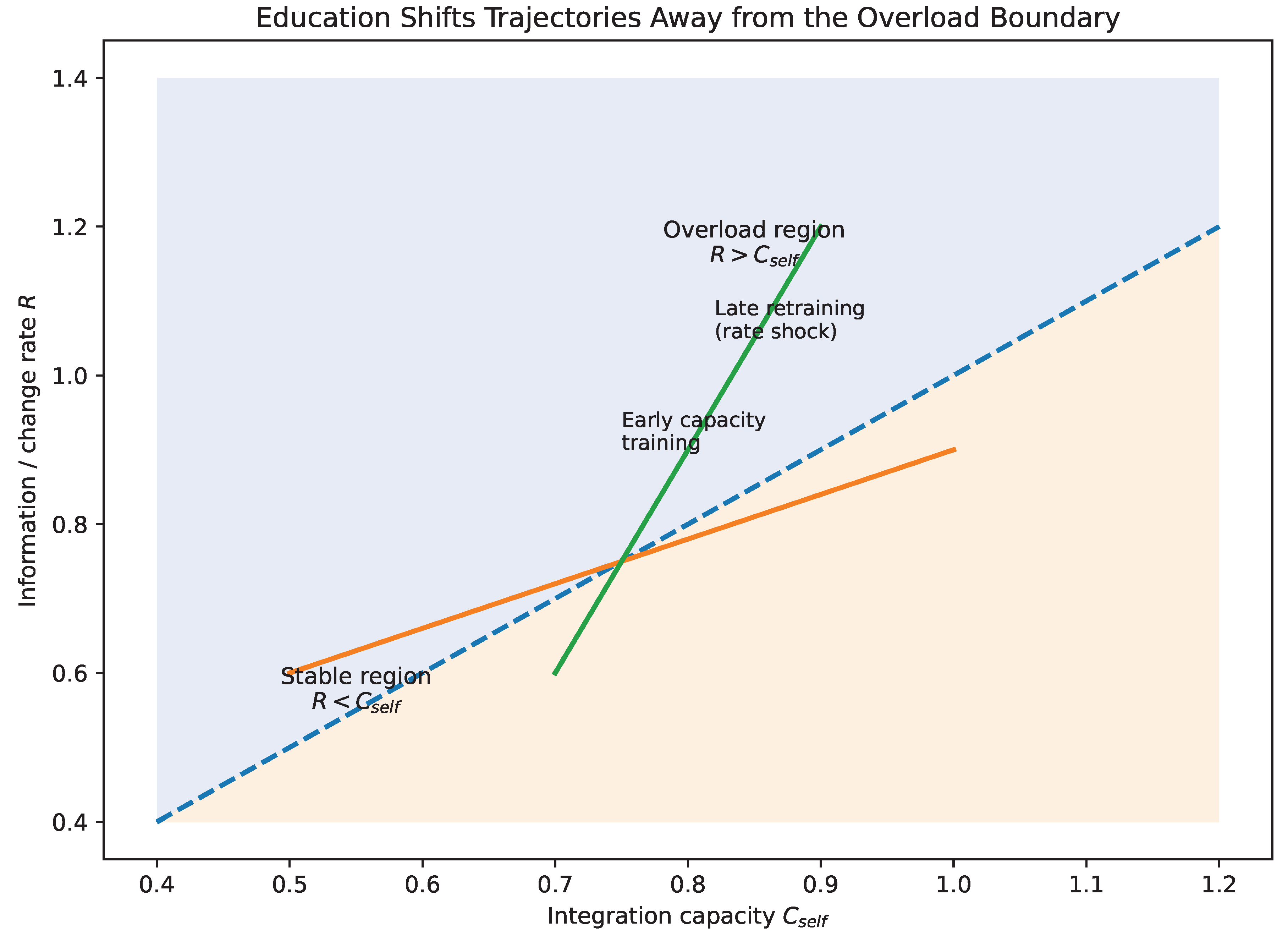
This observation has direct implications for policy and education. If AI-driven gradients make continuous reskilling structurally necessary, then capacity must be trained early, before steep gradients arrive. A schooling system designed around one-time specialization is optimized for a world with slow-changing landscapes. In the AI age, education must explicitly cultivate controlled exploration: the ability to sample new domains, update priors, and rehearse transition moves without catastrophic loss. In later sections we return to this implication and argue that “learning how to learn” is not an aspirational slogan but an annealing requirement: systems that do not practice exploration while constraints are loose become brittle when constraints tighten.
The next section formalizes Anna’s situation using the unified annealing dynamics and introduces a phase-portrait representation that will later support an explicit decision protocol for AI-driven professional adaptation.
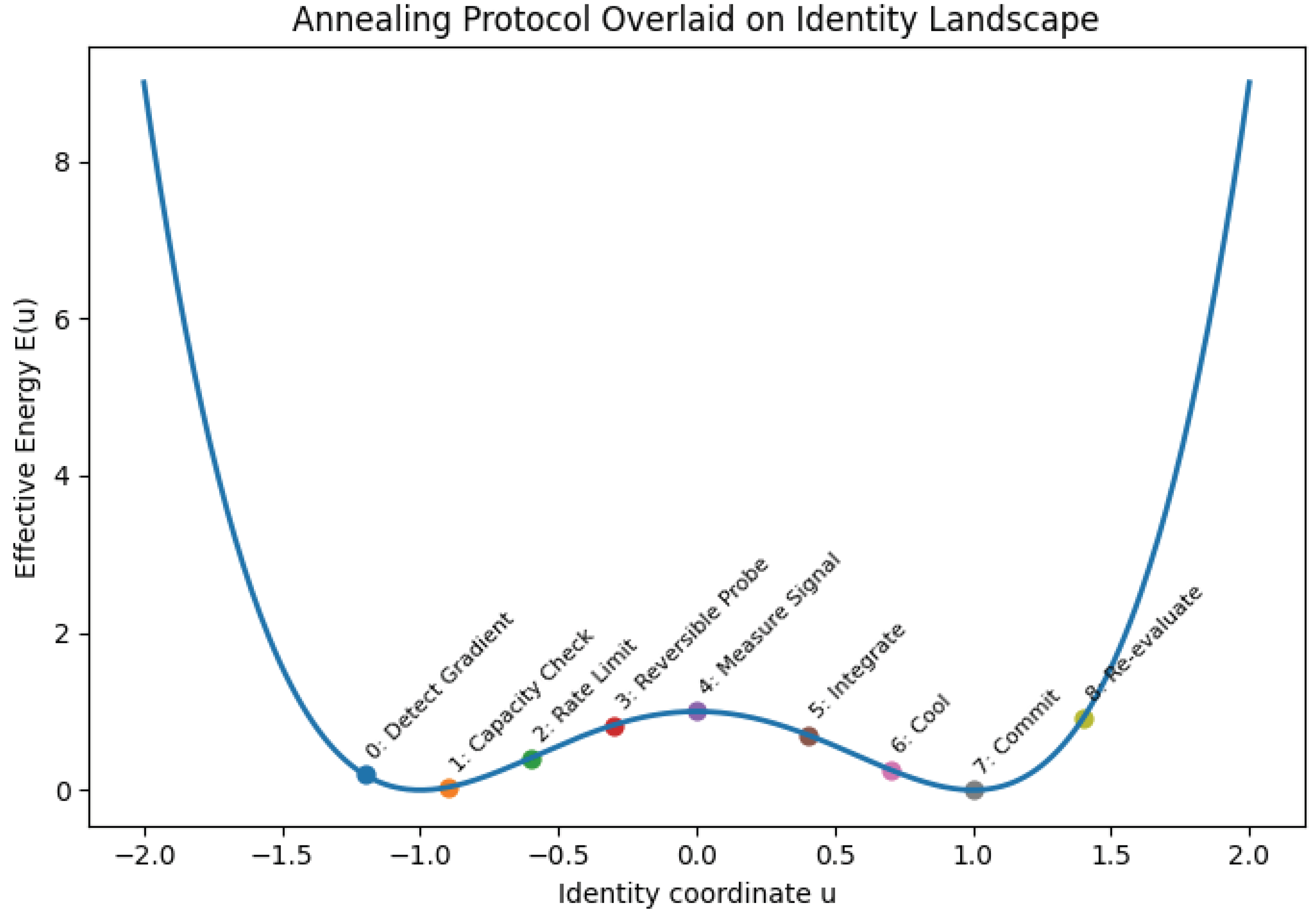
10. Phase Portrait: Identity, Agency, and Rate
The unified dynamics in
Section 7 describe high-dimensional stochastic gradient flow. For interpretability and for protocol design, we now reduce the self-dynamics to a low-dimensional phase portrait that makes three quantities explicit:
identity (where the system is in self-space),
agency (whether the system can reliably update), and
rate (how fast information and demands arrive).
10.1. A Reduced Coordinate for Identity
Let denote a reduced coordinate along the dominant axis of identity change. The left side () corresponds to the inherited/stabilized professional identity (legacy basin), while the right side () corresponds to a reconfigured, self-authored, and exploratory identity (novel basin). This projection does not claim that the self is one-dimensional; it claims only that in many high-stakes transitions, a single axis dominates decision-relevant motion.
We represent stability and misalignment by an effective potential
with (typically) multiple basins. A canonical choice is a double-well landscape whose relative depths can shift with time, representing a moving professional environment:
where
controls barrier height and
tilts the landscape as the environment changes.
10.2. Temperature as Controlled Exploration
Let
denote the effective self-temperature introduced in
Section 7. In the reduced model,
T governs how much stochastic exploration is possible in identity space. High
T enables barrier crossing and sampling of alternative selves; low
T collapses exploration and produces early stabilization.
A minimal mean-field dynamics consistent with the unified Langevin form is:
where
is the natural cooling rate (routine, reinforcement, comfort),
is the experienced gradient magnitude (pressure to change), and
captures sensitivity to gradients.
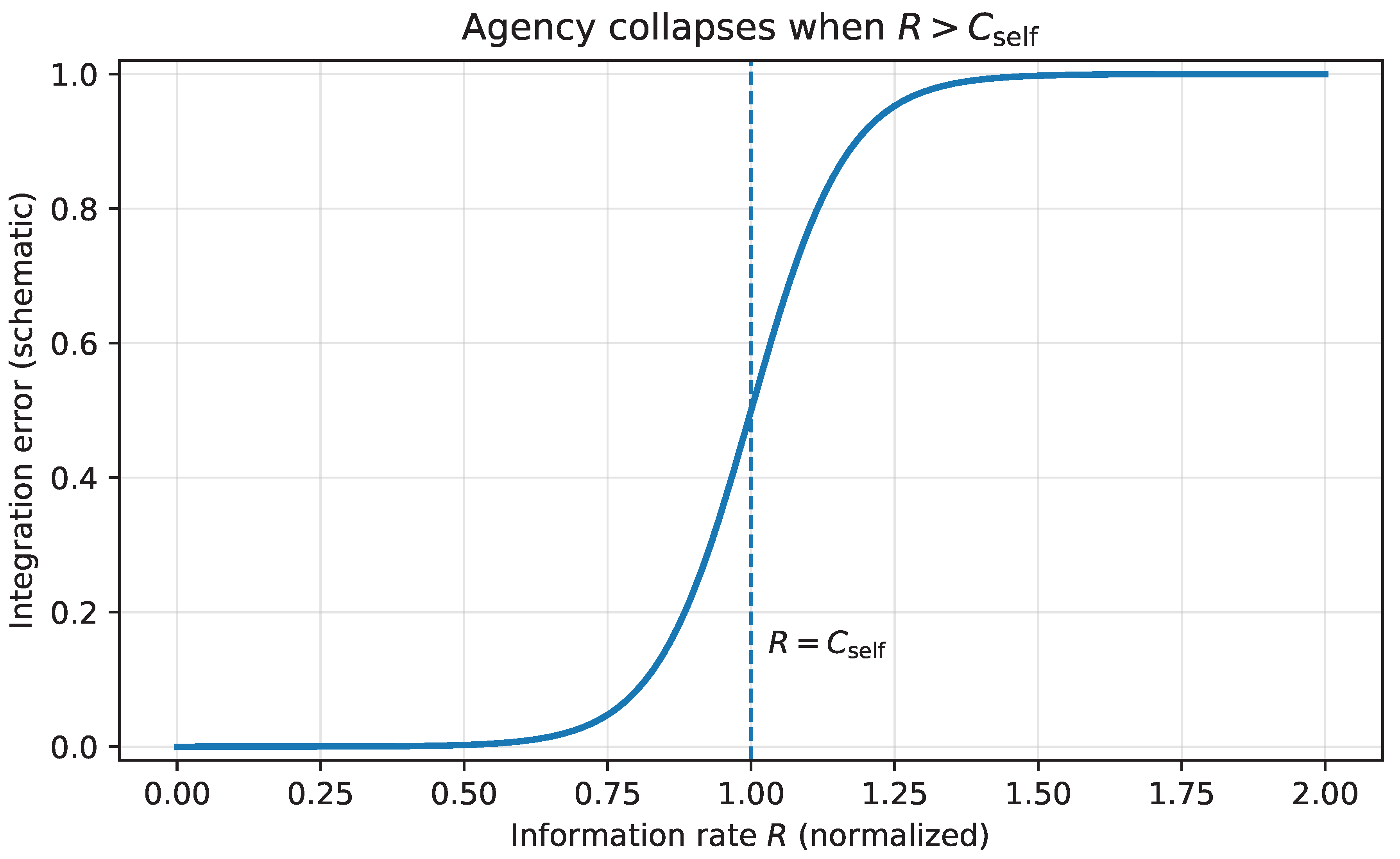
10.3. Rate and Capacity as the Agency Constraint
To make agency explicit, we introduce the information-rate constraint from
Section 6. Let
denote the effective rate at which the individual must integrate actionable information to adapt: tool churn, retraining demands, options, and evaluation updates. Let
denote integrative capacity.
Agency fails when
exceeds capacity:
For phase-portrait purposes, define an
agency margin (positive when stable, negative when overloaded):
When , updates become unreliable and the system exhibits oscillation, impulsive closure, or paralysis even if motivation is high. This makes “loss of agency” a structural condition rather than a moral interpretation.
To couple agency back into the identity landscape, we can include an agency penalty term in the effective energy:
where
is a nonnegative increasing function for
(e.g.,
) and
sets the strength of agency loss in the landscape. Intuitively, overload makes all moves feel more costly: exploration is punished by error and exhaustion.
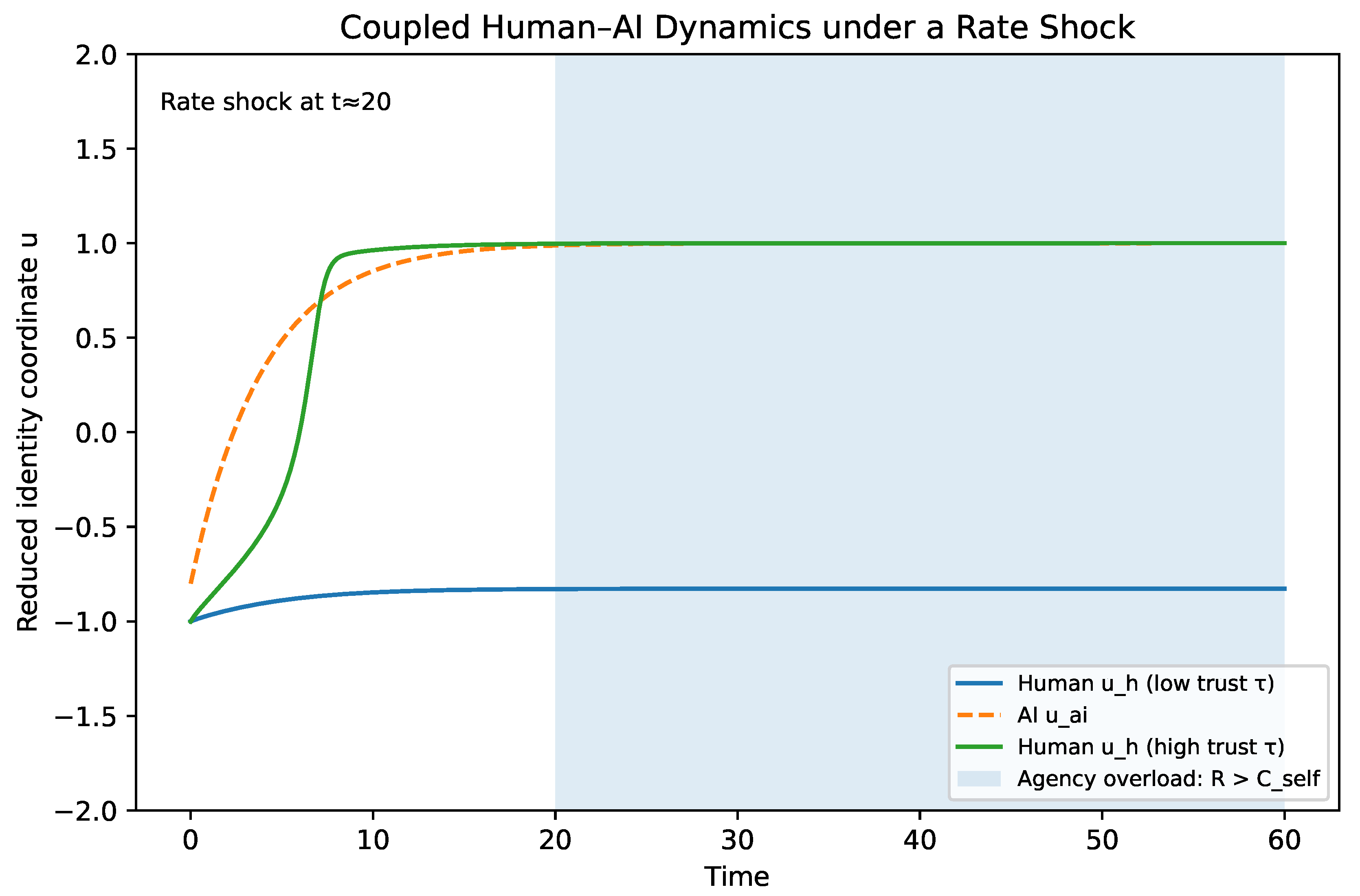
10.4. Interpreting Anna’s Trajectory Under AI Shock
Anna’s situation (
Section 9) is a textbook case of a system that cooled early in a buffered professional environment and then encountered a late, steep gradient under AI-driven task restructuring. In this phase portrait:
Identity (u): Anna begins deep in the legacy basin (), because her professional blueprint encouraged early convergence.
Exploration (T): Natural cooling dominated for years, driving , collapsing self-entropy.
Rate (R): AI increases abruptly (tool churn and reskilling velocity), while cannot increase instantly.
Agency (): When , the agency margin becomes negative and the system enters an overload regime in which motion is noisy but integration is poor.
The critical point is that Anna can remain financially safe while still losing agency: the dominant loss is not economic fragility but identity coherence and self-worth (competence-signaling). This is why credentialed professionals are uniquely vulnerable: their stability is often built on narrow identity basins that are disrupted by task-level AI gradients.
10.5. The Phase Portrait Figure
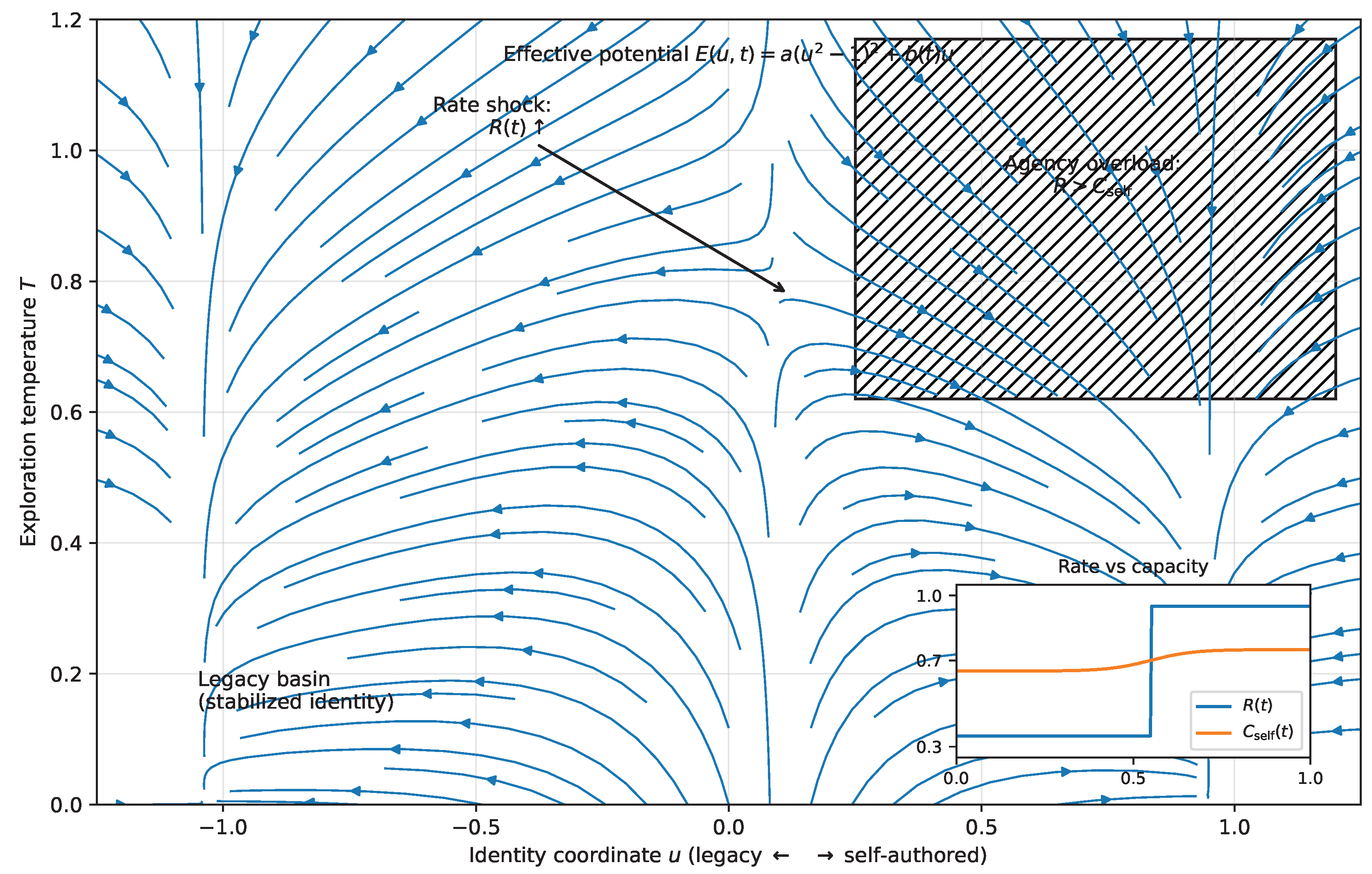
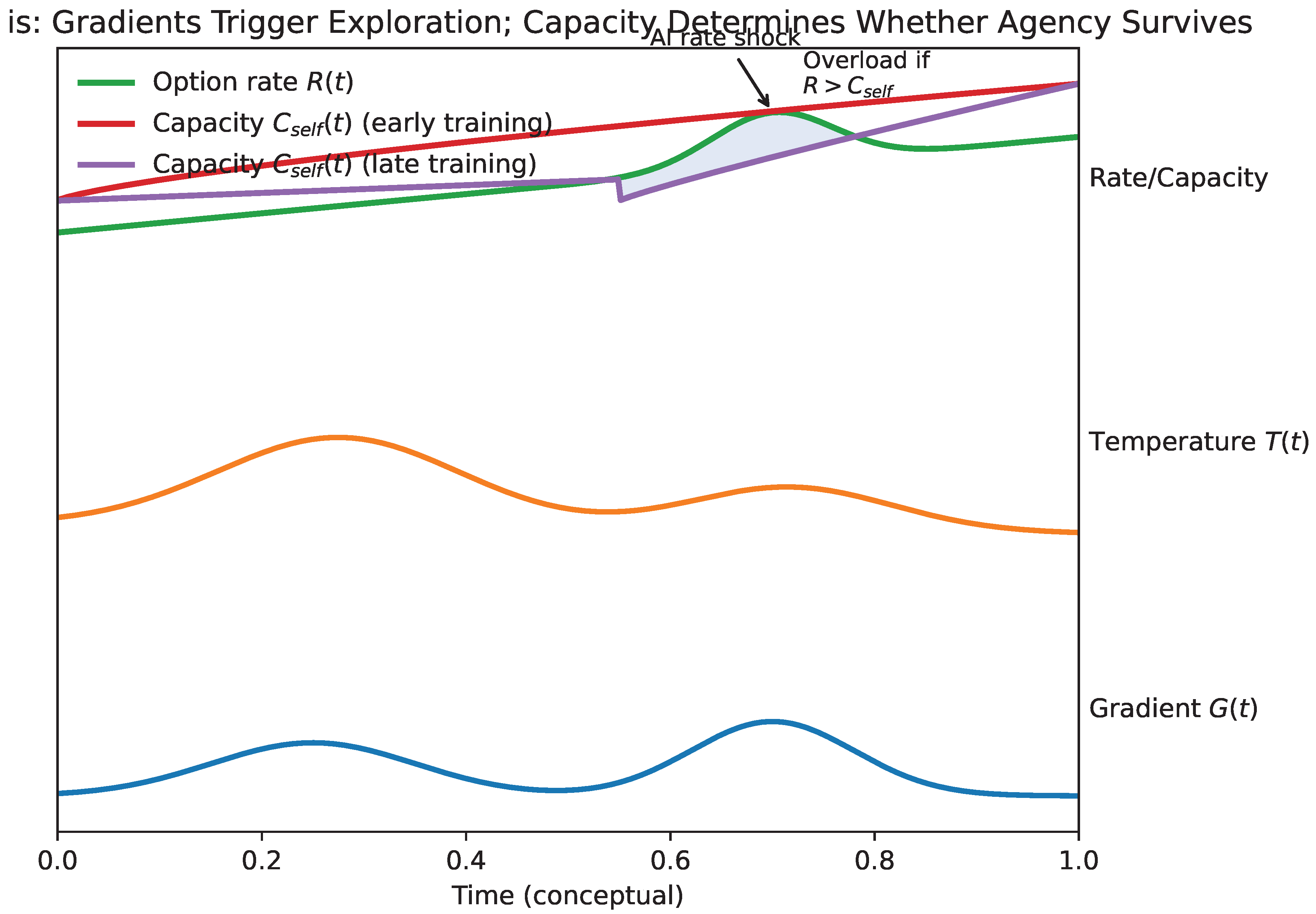
Figure 4 visualizes the reduced dynamics. The horizontal axis is identity (
u), the vertical axis is temperature (
T), and the shaded/annotated region indicates the
agency overload regime where
and updates become unreliable. The schematic trajectory illustrates premature cooling (drift toward low
T in the left basin), followed by AI-induced reheating (increased
T from steepened gradients), and then oscillation when reheating occurs under tight constraints and high rate.
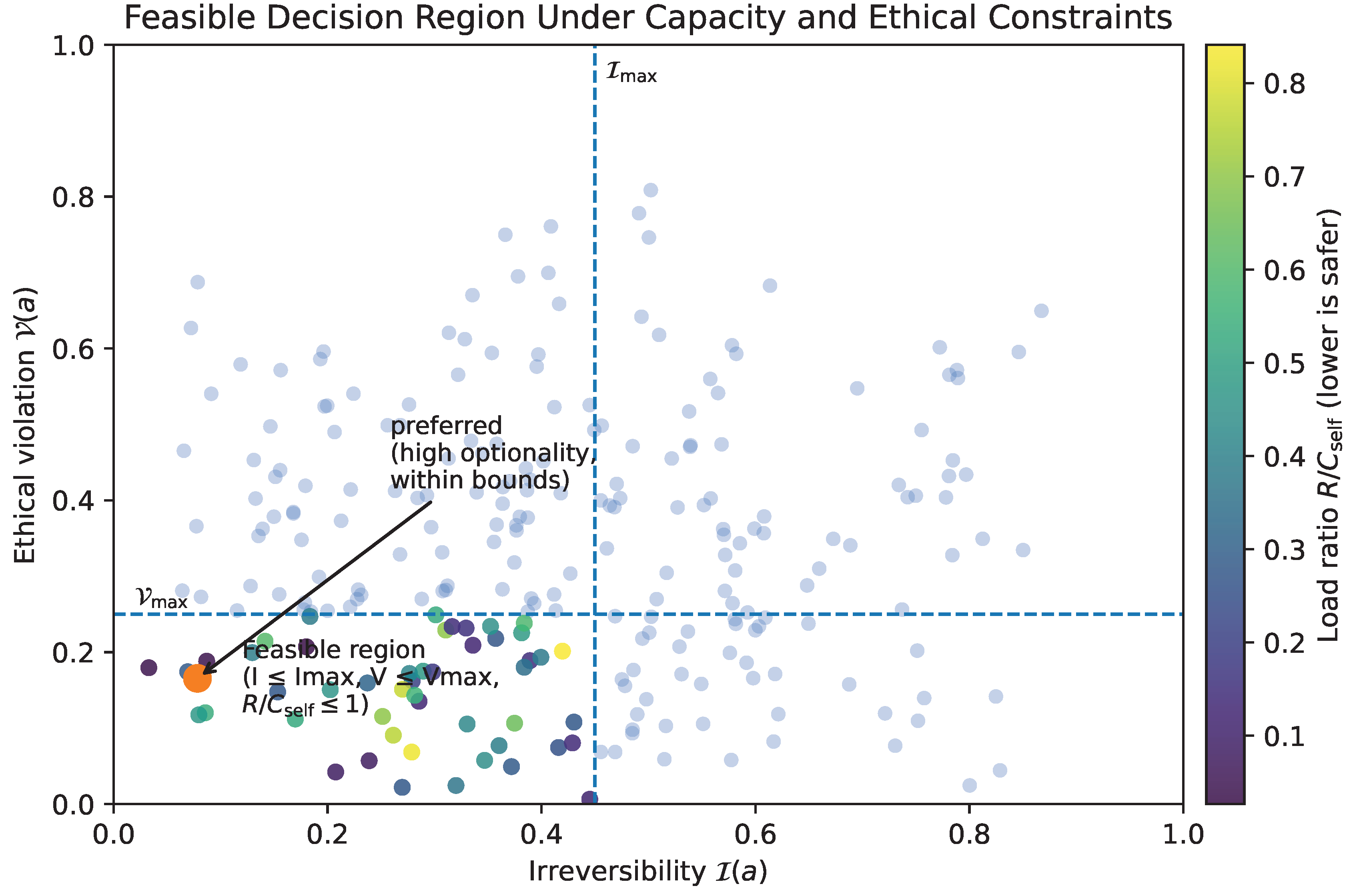
This phase portrait is more than illustration: it provides an operational geometry for intervention. The decision protocol developed later will be derived from controlling and so that exploration remains possible without pushing the system into sustained overload (), enabling regulated entropy reduction rather than premature closure or fragmentation.
11. AI as a Gradient Multiplier in Professional Landscapes
The preceding sections establish a single structural claim: complex systems that cool early in buffered environments become brittle when gradients steepen, and agency collapses when the effective information rate exceeds integration capacity (). The AI age intensifies both mechanisms simultaneously. It steepens gradients in the environment and increases the rate at which actionable information arrives. This section formalizes these effects and explains why AI is not merely a new tool but a regime change in the annealing conditions of professional life.
11.1. Why AI Steepens Gradients
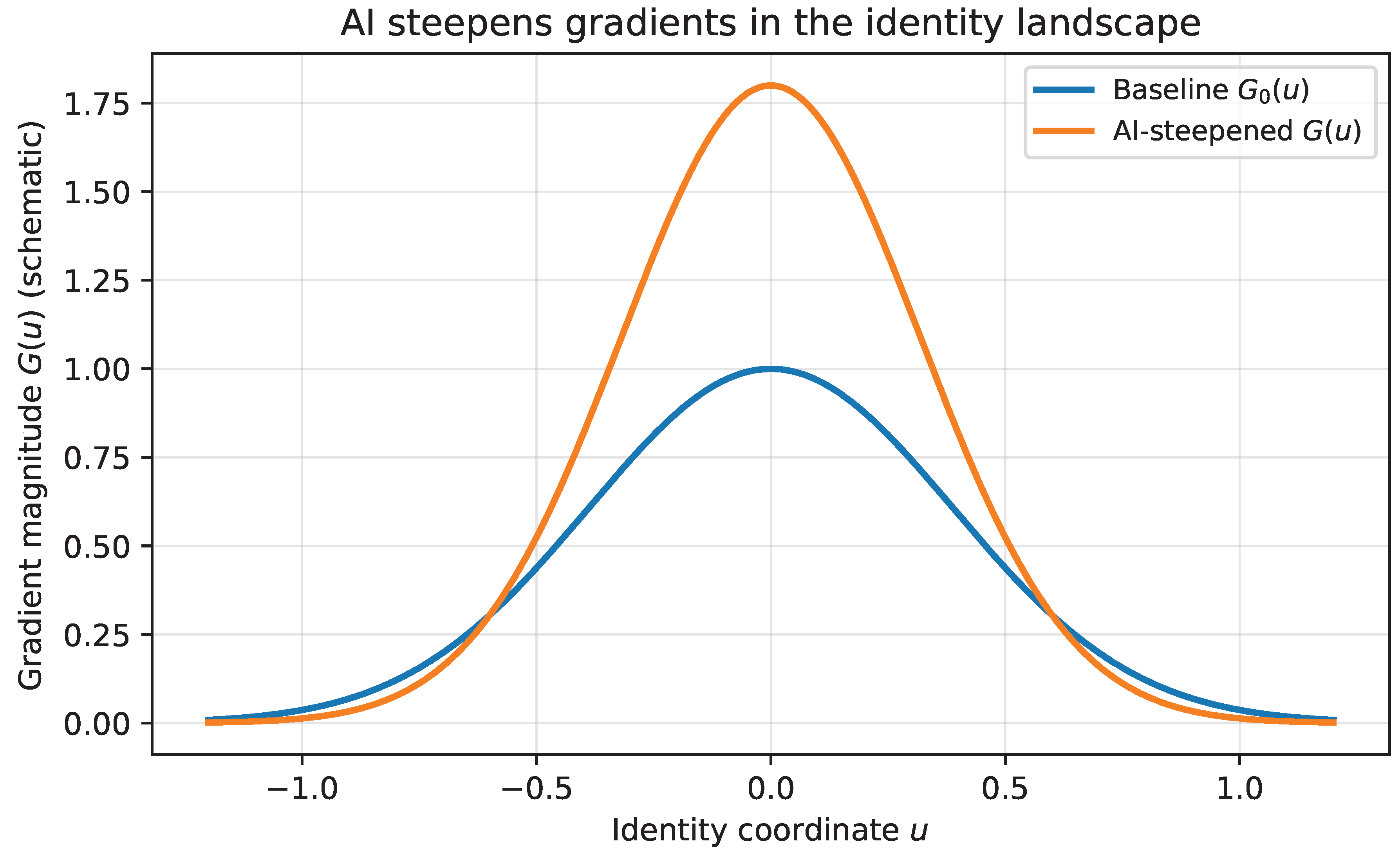
A gradient is any systematic pressure that changes the relative viability of states in the landscape. In the professional domain, the landscape is the set of roles, skills, reputations, and institutional niches that constitute employability and status. AI steepens gradients in at least three ways.
First, AI reduces the cost of producing high-quality cognitive outputs (drafts, code, analyses, summaries), compressing the advantage historically conferred by expertise and time. This changes the slope of the competitive landscape: what was previously scarce becomes abundant, and differences between agents are reweighted toward those who can define problems, validate outputs, and adapt quickly [
1,
36].
Second, AI accelerates task decomposition. Occupations persist, but the internal task composition shifts rapidly as specific tasks are automated, rearranged, or recombined [
1,
2]. From the perspective of the energy function, this means that the effective potential
becomes time-dependent and nonstationary: basins that were deep can become shallow, and barriers that maintained stability can erode.
Third, AI increases the rate at which new tools, workflows, and evaluation criteria appear. Even when an individual remains in the same occupation, the mapping from skill to value changes faster than traditional training pipelines can accommodate. This steepens the experienced gradient not only at moments of job displacement but continuously during ordinary work.
This effect is illustrated schematically in
Figure 5, where AI increases the effective gradient magnitude
and thereby raises the pressure to move across the landscape.
This mechanism is illustrated schematically in
Figure 5, where AI acts to amplify the effective gradient
, increasing the pressure on the system to move across identity and capability space.
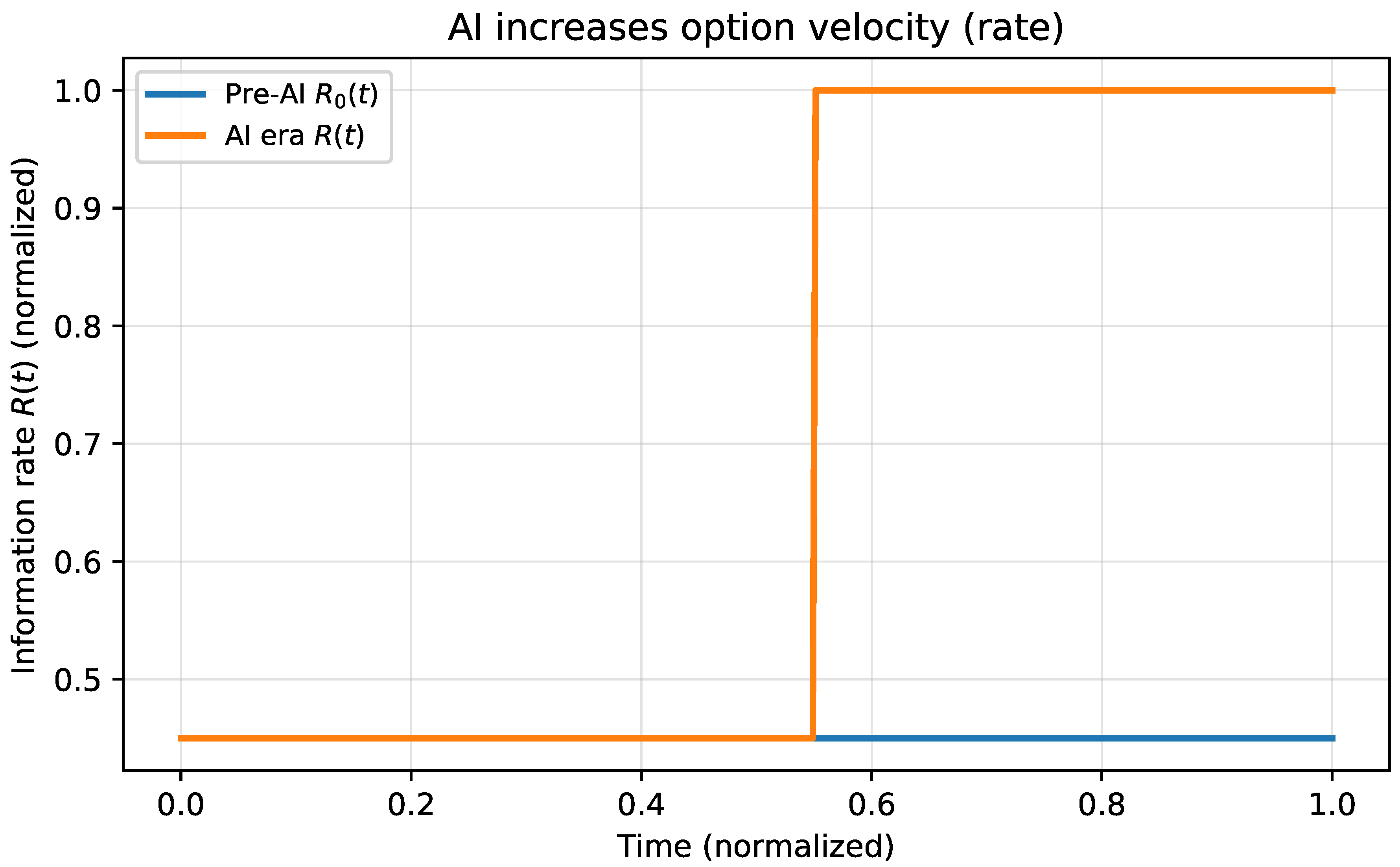
11.2. AI Increases Effective Information Rate
Steep gradients are necessary but not sufficient for agency collapse. The second effect is a rate effect: AI increases the option velocity of the environment. Let denote the effective information rate an individual must integrate to remain adaptive. In AI-mediated settings, increases because:
the number of plausible actions expands (more options),
feedback loops tighten (faster updates),
social comparison accelerates (more visible counterfactuals),
and tool ecosystems churn (continuous onboarding).
Figure 6 shows this rate effect schematically as a discontinuous increase in
(option velocity) under an AI-driven shock.
Figure 6 visualizes this effect as a sharp increase in the rate
induced by AI-mediated option proliferation.
Rate matters because integration is bounded.
Section 6 defined an integration capacity
(a channel-capacity analogue) and
Section 10 introduced the agency margin
. When
, additional information does not increase effective choice; it increases error. This reframes a central experience of modern professional life: overload is not a character flaw but a rate-limit violation.
11.3. A Minimal Coupling Model: AI as Gradient and Rate Amplifier
We can express AI as a multiplier on gradients and rates in the reduced phase portrait. Let
denote the intensity of AI-mediated change in the individual’s environment (tool adoption, organizational restructuring, market pressure). A minimal coupling is:
where
and
are baseline (pre-AI) gradient and rate, and
quantify AI-induced amplification. Substituting into the temperature dynamics and agency margin makes the mechanism explicit:
while agency becomes fragile when:
Equation (
32) captures a practical asymmetry:
can increase rapidly via external change, while
can increase only through training and time. This makes early-cooled systems vulnerable. When exploration was deferred for decades, the system has not practiced the transition dynamics required to keep
under shocks.
11.4. Why Job Loss Is a Special Case of the Same Mechanism
Job displacement is the most visible gradient encounter, but it is not the only one. It is best interpreted as a discontinuity in the landscape: a basin disappears or becomes inaccessible. In that case, both and spike, and the system must traverse state space under high irreversibility. This is the worst case for prematurely cooled identities, because exploration must be reintroduced late, when constraints are tight and errors are costly.
This is why professionals who appear safe and successful can be uniquely destabilized by AI change. When income is buffered, the dominant loss is agency and self-worth: the collapse of competence-signaling as the primary stabilizer of identity. The framework predicts this outcome directly, without assuming pathology.
11.5. Implication
AI changes the annealing conditions of professional life. It steepens gradients and increases rates. In such a regime, the central practical task is not accumulating more options but managing exploration so that it remains within capacity. The next section formalizes the failure mode: how information overload produces the collapse of agency and why “more willpower” is the wrong response.
When gradients steepen faster than the system’s capacity to integrate them, agency does not expand but collapses—a dynamic examined formally in
Section 12.
12. Information Overload and the Collapse of Agency
The AI age does not merely change what is possible; it changes the
rate at which possibility arrives. The preceding section formalized this as a rate amplification
and showed how rate interacts with exploration via the phase portrait in
Section 10. We now make explicit the central failure mode for human–AI systems:
agency collapses when the environment demands adaptation faster than the self can integrate. This section formalizes that failure mode and clarifies why “more willpower” is often counterproductive under overload.
12.1. Capacity as a Hard Constraint
Let
denote the effective information rate the individual must integrate to remain adaptive: tool churn, reskilling demands, option velocity, feedback loop speed, and organizational update rate. Let
denote the effective integration capacity of the self, introduced in
Section 6. The structural condition for reliable adaptation is:
When Equation (
33) is violated, behavior may remain energetic and even hyperactive, but it becomes poorly integrated. The system produces actions without consolidation. Decision making becomes noisy. Commitments are made impulsively and then reversed. Alternatively, the system freezes, experiencing a subjective paralysis: many options are visible but none can be stably selected.
This transition is illustrated schematically in
Figure 7. As the incoming rate
R approaches capacity, performance degrades smoothly. Once
R exceeds
, error grows superlinearly. Beyond this threshold, additional effort cannot restore agency; it only amplifies noise and fragmentation.
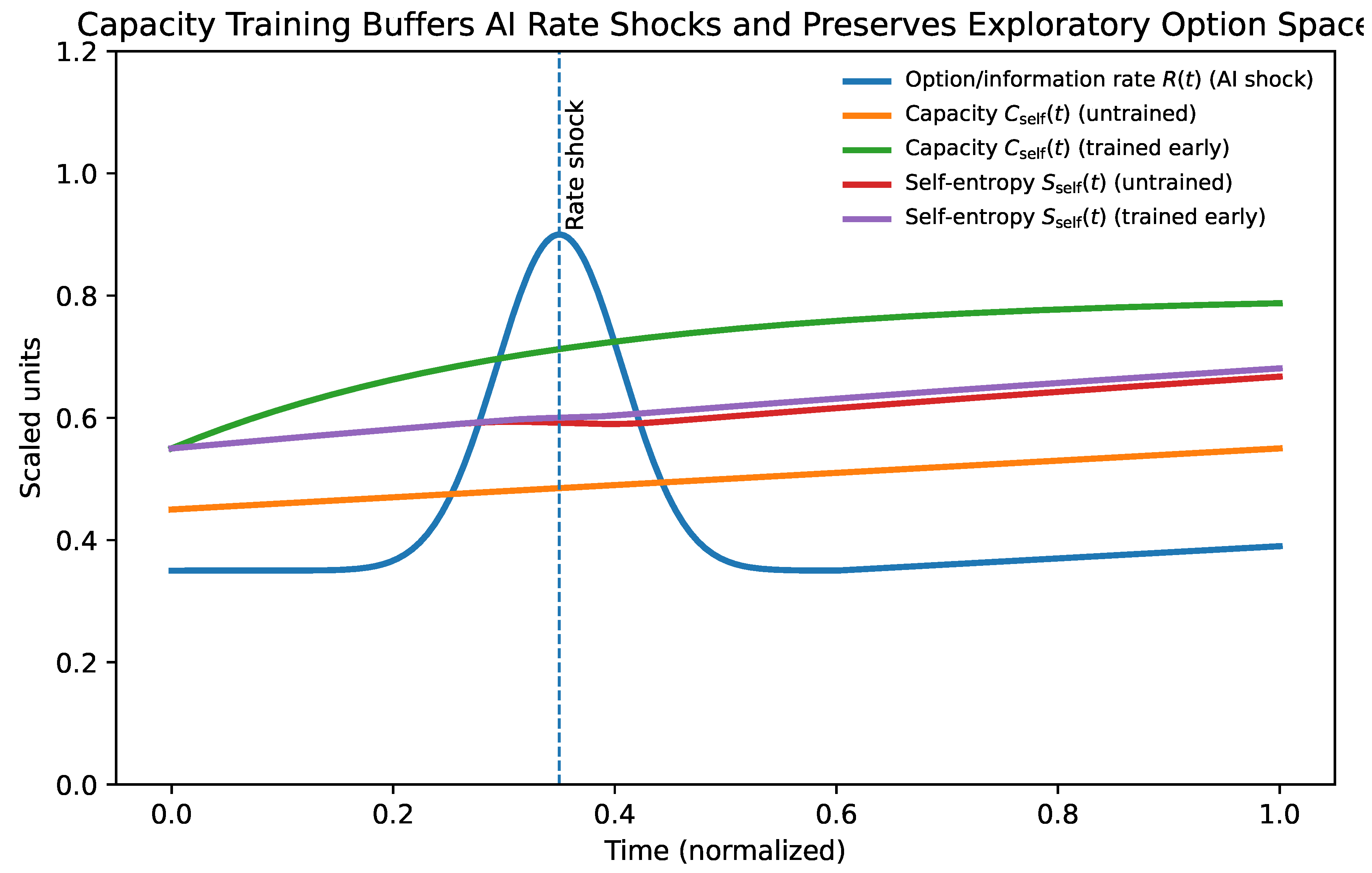
Figure 8 contrasts two trajectories under an identical external rate shock. In the untrained system, capacity is exceeded immediately, leading to collapse. In the trained system, prior exposure to manageable gradients has expanded
, allowing the same shock to be integrated without loss of coherence.
To express this compactly we reuse the agency margin from
Section 10:
Agency is robust when and degrades when .
12.2. Why Overload Increases Error Rather than Freedom
A common intuition is that more options increase freedom. Under capacity constraints the opposite can occur. When rises, an individual can attempt to “keep up” by increasing effort. However, effort does not increase capacity instantaneously. In rate-limited regimes, pushing more information through a fixed channel increases error. The practical signature is not ignorance but mis-integration: learning fragments into uncoordinated pieces, and choices cannot be maintained long enough to yield evidence.
This mechanism explains a characteristic pattern in AI-mediated work. Generative systems increase the number of plausible next actions and accelerate iteration. If the human attempt to evaluate all outputs, track all options, and respond to all signals, can exceed even when the human is competent. The result is a paradoxical reduction of agency: the system sees more but chooses less.
12.3. Overload Couples Back into the Energy Landscape
Overload is not only a rate issue; it reshapes the experienced landscape
. When
, exploration becomes costly. Errors accumulate. Confidence degrades. The subjective cost of change rises, and the system is pulled toward premature closure as a defense. A minimal way to express this feedback is an agency penalty term:
where
is increasing for
(e.g.,
) and
sets the strength of the overload penalty. In words: when the world is arriving too fast, every move feels more expensive.
This feedback produces two common failure modes that can be misread as personality.
Premature freezing: the system drives to reduce decision load, collapsing self-entropy rapidly into an available “safe” basin. This may restore short-term stability while increasing long-term brittleness.
Unstable reheating: the system remains hot because gradients are steep, but cannot cool into a stable basin because integration is failing. The result is oscillation: activity without settlement.
Both are predictable consequences of Equation (
33); neither requires a moral explanation.
12.4. Capacity Can Be Trained, but Not Instantly
A central implication follows. Capacity is plastic over long time scales but constrained over short ones. Increases in require repeated practice of integration under bounded load: learning-to-learn, tool onboarding, and the deliberate rehearsal of transitions. This is why the timing matters. If exploration and reskilling are deferred until the AI gradient arrives, can jump faster than can grow, making collapse likely. Conversely, systems that maintain non-zero exploration under low stakes gradually expand capacity and can absorb higher later.
This observation reframes a basic claim about education and professional development. Training is not only the acquisition of content; it is the expansion of integration capacity and the acquisition of rate management skills (how to reduce by selecting, batching, and constraining inputs). This will be returned to explicitly in the decision protocol.
12.5. Implication for Intervention
The immediate intervention target under overload is not motivation but rate control. When , the system must reduce (triage, constraints, batching, deliberate narrowing) and/or temporarily increase effective capacity (sleep, recovery, social support, scaffolding) before attempting high-stakes exploration. Without this step, advice to “explore more” is destabilizing: it increases further and deepens overload.
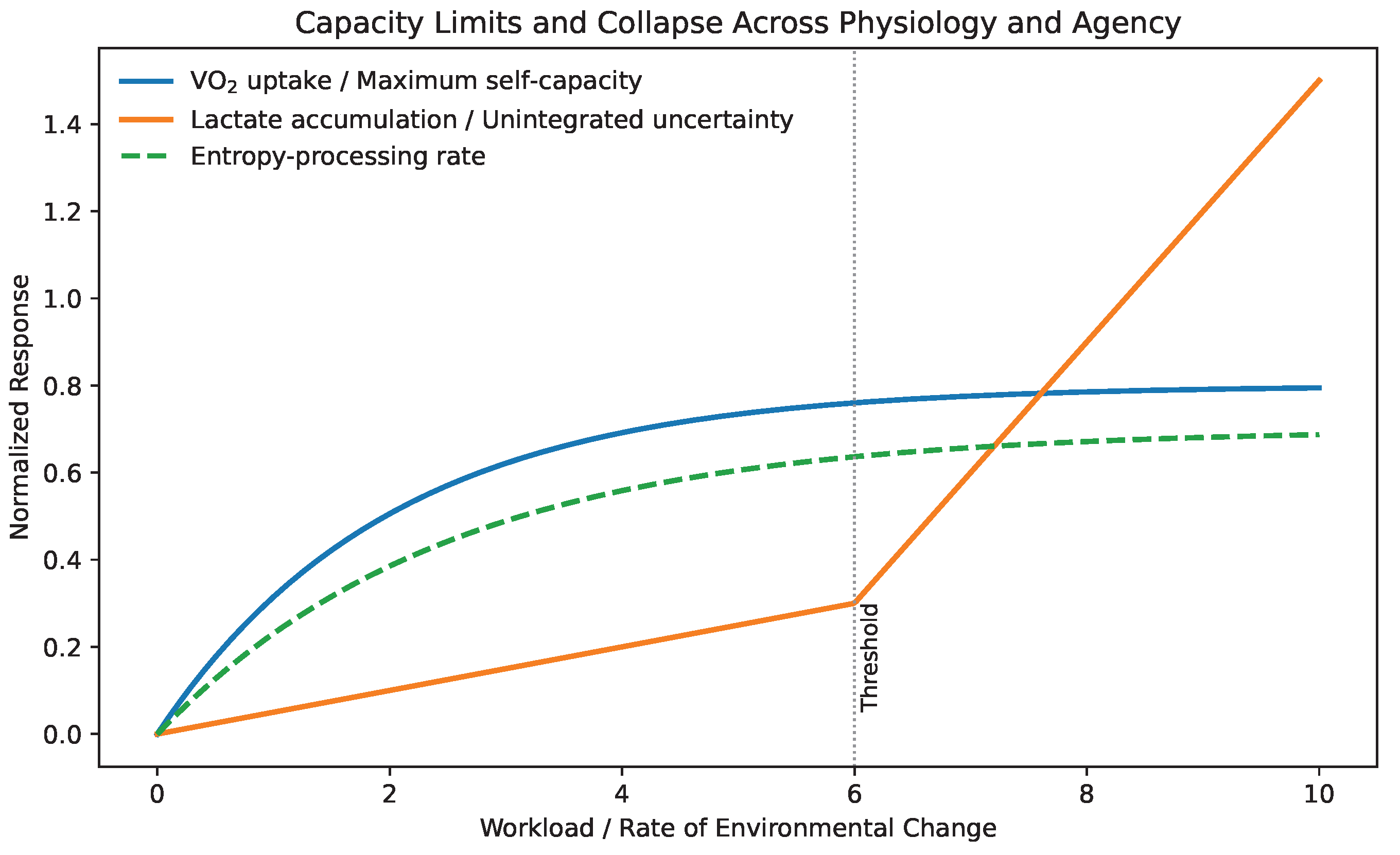
12.6. Capacity as a Physiological Analogue: VO2max Lactate Threshold, and Entropy Rate
In human physiology, maximal oxygen uptake (
max) is widely regarded as one of the strongest integrative indicators of health, resilience, and longevity, as it reflects the upper bound on sustainable metabolic energy production under load [
37,
38]. Crucially,
max does not describe typical performance, but rather the maximum rate at which energy can be mobilized when required.
We argue that an analogous quantity exists for adaptive cognition and agency: a self-capacity , representing the maximum sustainable rate at which an individual can absorb novelty, update internal models, and reorganize identity under changing conditions. As with max, this capacity is shaped jointly by genetics, developmental history, training, and environment, and it is not directly observable through behavior alone.
Physiology further distinguishes between absolute capacity and
thresholds. In endurance sports, the lactate threshold marks the transition beyond which metabolic demand exceeds clearance capacity, leading to rapid fatigue and loss of performance [
39]. Operating persistently above this threshold results in accumulation rather than integration.
The same distinction applies to adaptive systems. When the externally imposed rate of change exceeds an individual’s effective capacity , unintegrated informational load accumulates. In the present framework, this manifests as entropy accumulation without consolidation, producing stress, indecision, identity fragmentation, or collapse of agency. Below this threshold, exploration remains metabolizable; above it, adaptation degrades.
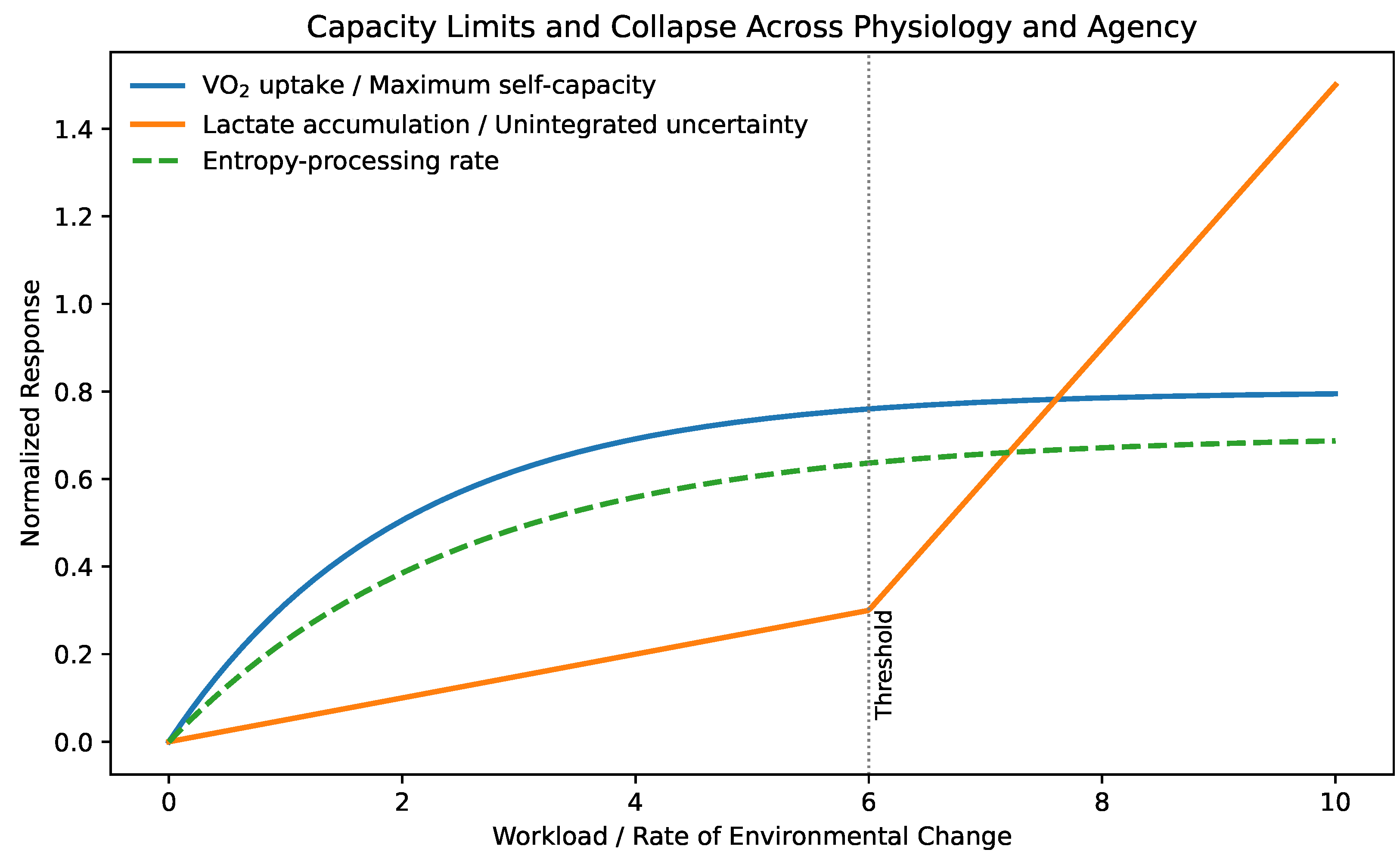
Figure 9 illustrates this analogy explicitly, mapping physiological capacity and thresholds onto cognitive–existential dynamics. Capacity determines what is possible; thresholds determine what is sustainable.
This distinction has immediate implications for the AI age. Artificial intelligence increases the rate of environmental change without regard for individual capacity. Systems optimized solely for efficiency or output risk pushing humans chronically above their adaptive threshold. Preserving agency therefore requires active regulation of rate, not merely expansion of choice.
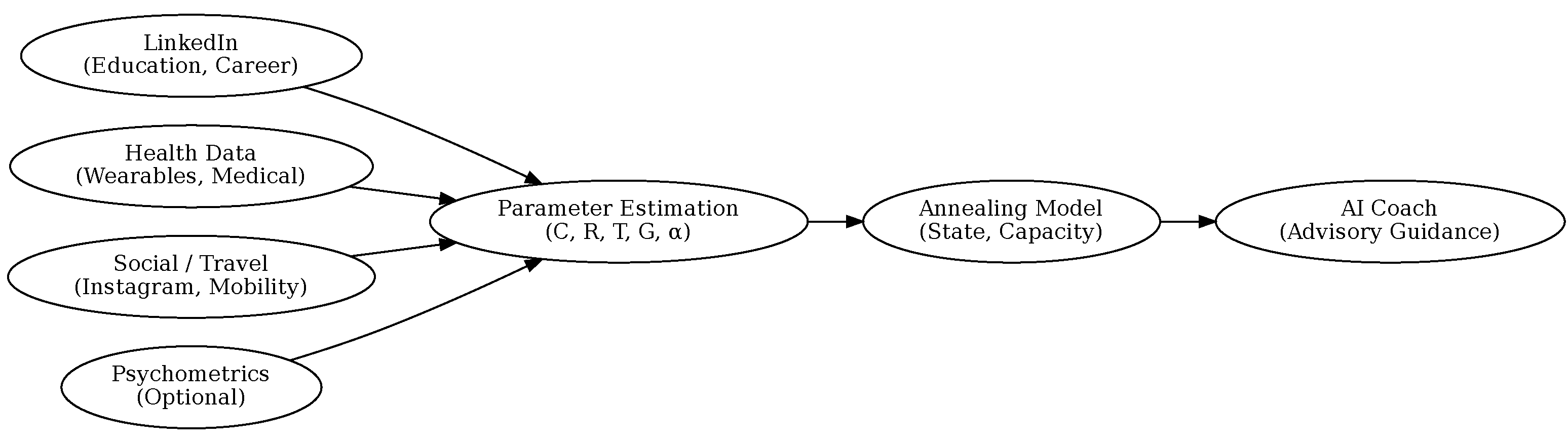
Operationally, while max can be measured through graded exercise testing, must be inferred indirectly. In Appendix H, we outline a protocol for estimating adaptive capacity using longitudinal multimodal data, including wearable physiology, cognitive load proxies, work-pattern variability, and recovery dynamics. This enables capacity-aware guidance analogous to modern endurance training, where load is modulated relative to physiological thresholds rather than absolute demand.
Table 1 highlights a close structural analogy between well-established concepts in exercise physiology and the dynamics of self-capacity introduced here. In physiology,
max provides a robust, integrative measure of an individual’s maximal aerobic capacity and is among the strongest predictors of long-term health and mortality. Analogously, maximum self-capacity characterizes the upper bound on the rate at which an individual can process uncertainty, novelty, and adaptive demands without loss of coherence.
The lactate threshold is particularly instructive. Below this threshold, metabolic byproducts are cleared and integrated; above it, lactate accumulates and performance degrades despite adequate raw capacity. In the present framework, this corresponds to a sustainable entropy-processing rate. When environmental or informational change exceeds this rate, unintegrated uncertainty accumulates, eventually producing agency collapse. Importantly, failure arises not from insufficient capacity per se, but from a mismatch between imposed rate and adaptive bandwidth.
This analogy clarifies why resilience depends critically on pacing. Just as physiological capacity is expanded through controlled threshold training rather than maximal exertion, self-capacity is increased through regulated exploration and gradual reheating. Conversely, sustained overload leads to burnout or premature cooling, mirroring the effects of overtraining in biological systems.
In the next section, we translate these constraints into an explicit optimality criterion that avoids subjective collapse and then derive a practical annealing protocol for AI-assisted decision making.
13. What Should We Optimize For?
Section 11 and
Section 12 establish a constraint-driven diagnosis: AI steepens gradients and increases the effective information rate
, while the self has finite integration capacity
. When
, agency collapses. The remaining question is normative but can be stated structurally:
what objective function can be defended without collapsing into subjective targets (e.g., happiness, certainty, success), yet remains actionable under capacity constraints?
13.1. Why Naive Objectives Fail Under Gradients
Classical “blueprint” objectives implicitly assume a stationary landscape: pick a target (career identity, lifestyle, value set), then optimize toward it. In nonstationary, gradient-driven environments, this approach is brittle for two reasons. First, the energy landscape
moves: what is locally optimal today may become unstable tomorrow. Second, the process is capacity-limited: even if a target were well-defined, the rate at which the target must be revised may exceed
, producing error and fragmentation instead of control (
Section 12).
The annealing framework suggests that the correct objective is not a final state, but a property of the process that keeps a system viable under change.
13.2. A Structural Objective: Preserve Future Feasibility of Controlled Annealing
Recall the unified dynamics (
Section 7), in which adaptation requires both (i) exploration (stochastic sampling) and (ii) stabilization (cooling/commitment). The failure modes are: premature cooling (brittle local minima) and perpetual reheating (fragmentation). A defensible objective should therefore reward neither maximal exploration nor maximal stability, but the ability to
regulate the transition between them.
We formalize this as the preservation of future feasibility of controlled annealing. Informally: the system should act so that, at future times, it can still (a) explore when needed, (b) commit when appropriate, and (c) remain within capacity constraints.
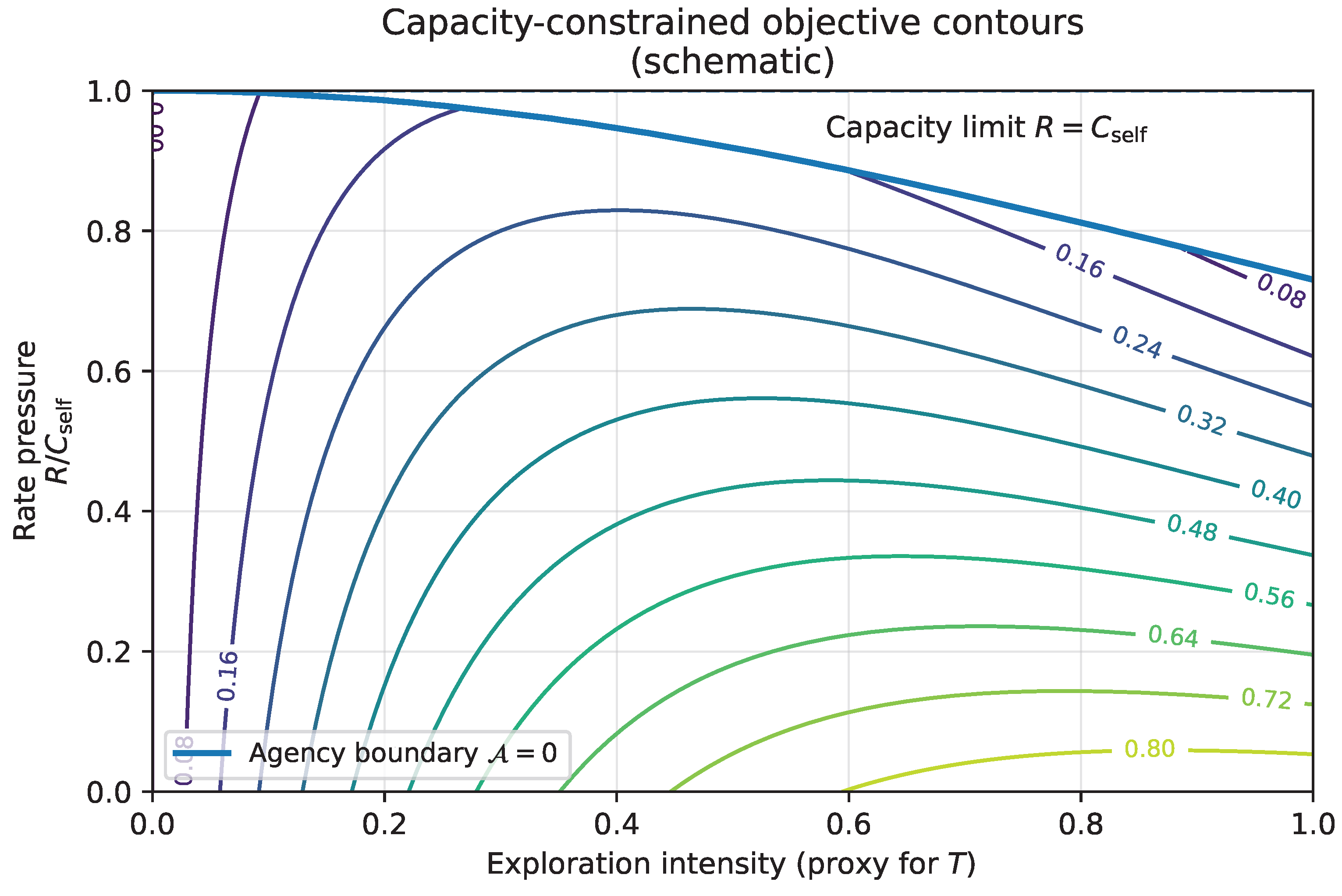
One convenient way to express this is as a margin condition:
where
indicates that the system can integrate the rate of change without losing coherence, and
indicates overload. A structural optimization criterion is then:
where
is a discount/priority weight and
is a planning horizon. This objective does not specify what to value. Instead, it preserves the precondition for coherent valuation under change: continued agency.
13.3. Meaning as Regulated Reduction, Not Maximization
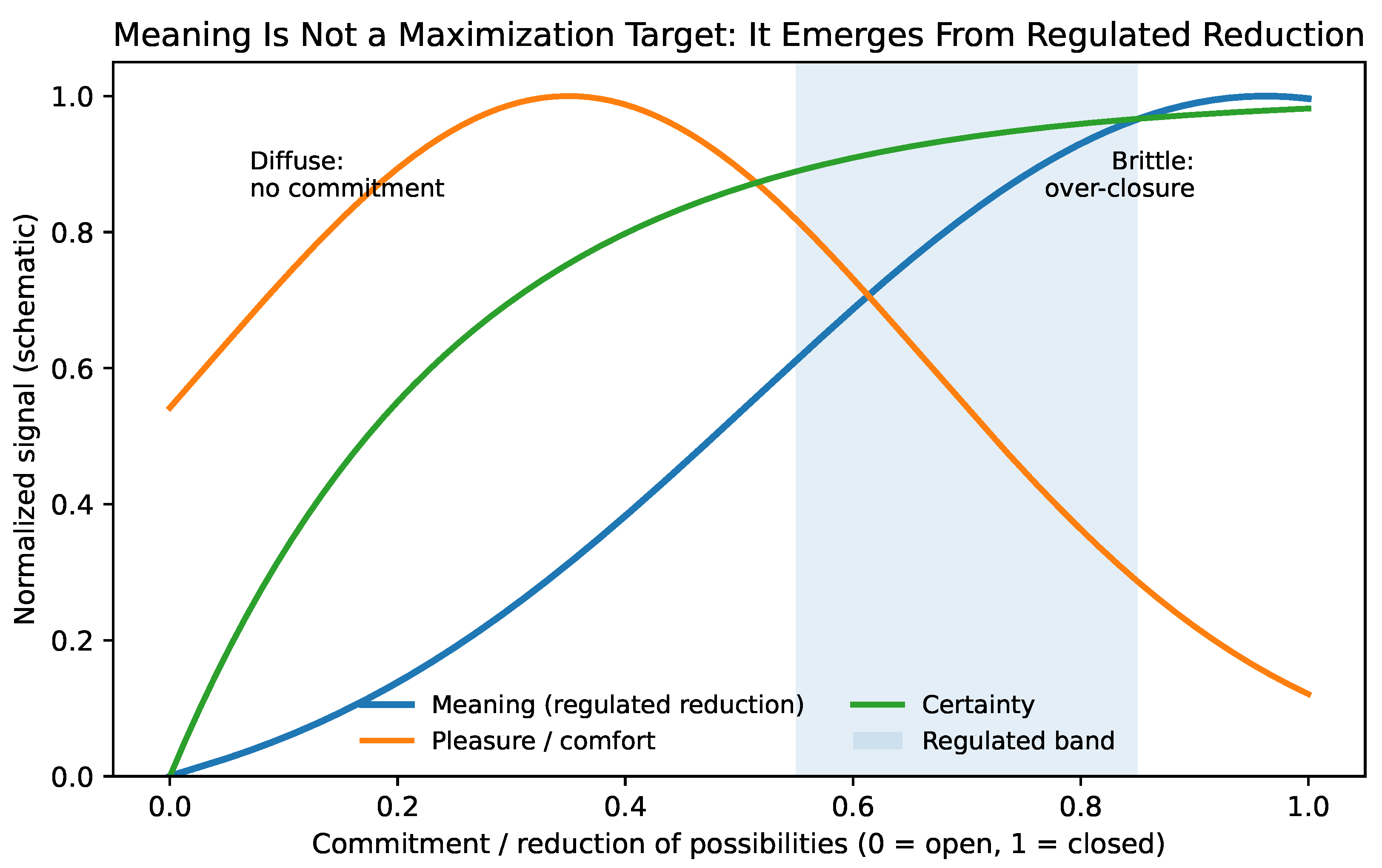
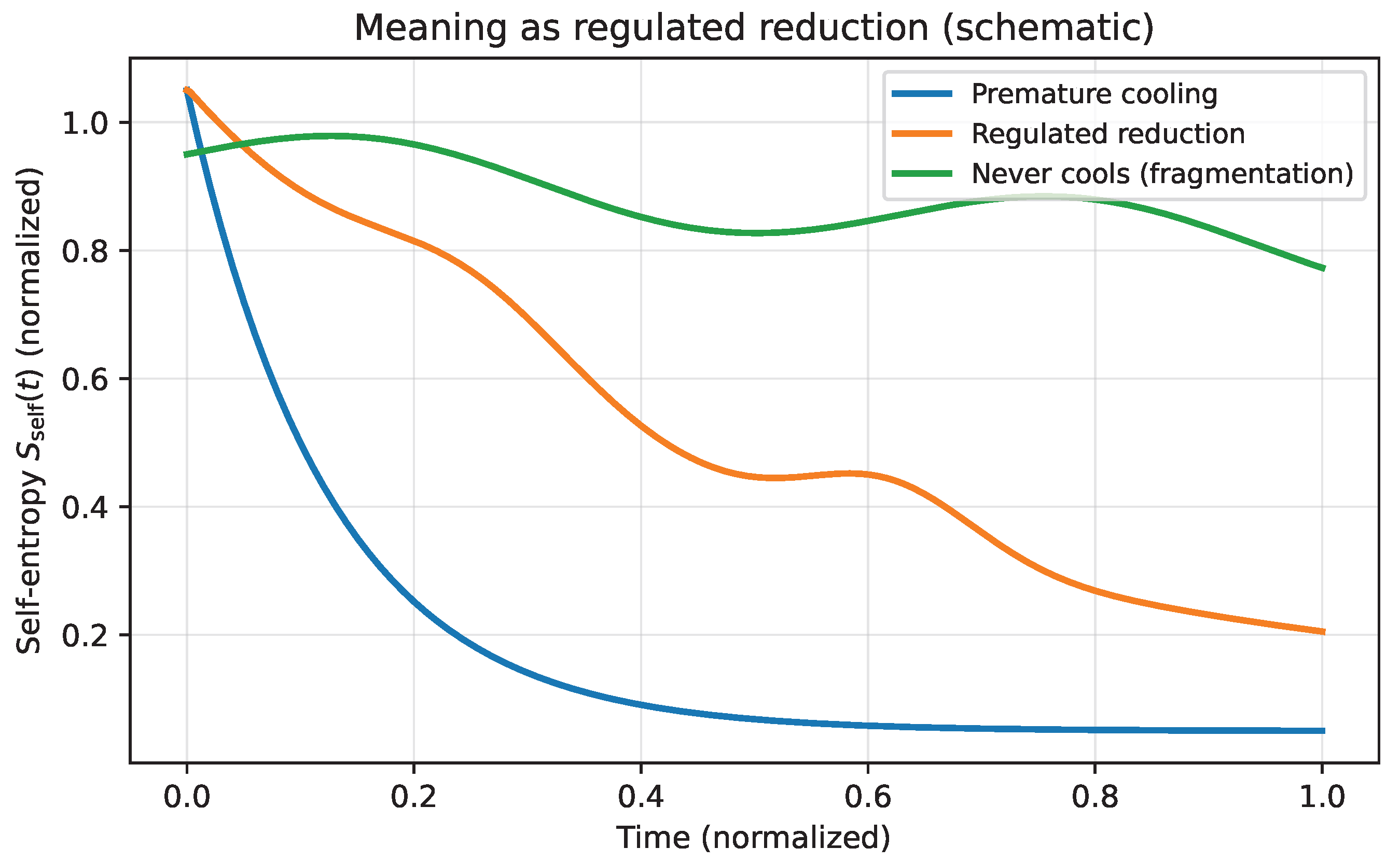
The framework developed here supports a precise claim that is often misunderstood: meaning does not arise from maximizing self-entropy nor from minimizing it, but from its regulated reduction under constraint. Exploration increases accessible possibility; stabilization compresses possibility into commitment. Meaning is the subjective signature of committing after sufficient sampling, and then bearing the irreversibility of the commitment.
Figure 10 illustrates three schematic regimes in terms of
. Premature cooling produces an early collapse of possibility and later brittleness. Perpetual reheating preserves possibility but prevents consolidation. Regulated reduction maintains exploration early and gradually concentrates into stable commitments, with occasional reheating events when gradients change.
This view also clarifies what meaning is not. Meaning is not identical to happiness, pleasure, certainty, moral correctness, or external achievement. Those may correlate with meaning in some regimes, but they do not define it. Under accelerating gradients, equating meaning with any one of these collapses the objective function and produces maladaptive behavior (e.g., optimizing comfort at the expense of future feasibility).
13.4. A Capacity-Constrained Decision Criterion: Information Gain per Irreversibility
A practical criterion consistent with (
37) is to select actions that maximize
information gain per unit irreversibility while maintaining positive agency margin. Let a proposed move
(new project, role, tool adoption, reskilling path) have: (i) expected information gain
about the landscape, (ii) irreversibility cost
(time sunk, reputational lock-in, relationship loss), and (iii) induced rate load
.
A structurally safe class of moves satisfies:
and among feasible moves we prefer those that maximize:
with
to avoid degeneracy. The objective is not to avoid irreversibility; it is to
spend irreversibility efficiently in order to locate robust basins before committing.
Figure 11 provides a schematic visualization of this logic. As rate pressure
increases, the feasible region for exploration contracts. The optimal exploration intensity (proxy for temperature) shifts: high exploration becomes unsafe near capacity, even if it would be valuable in a low-rate environment.
13.5. Implication
Under AI-driven nonstationarity, the appropriate optimization target is not a blueprint endpoint. It is the preservation of the system’s ability to anneal: to explore, to commit, and to remain within capacity limits as gradients change. The next section operationalizes this claim into a decision protocol that regulates rate, reversibility, and temperature in a stepwise workflow.
14. The Annealing Decision Protocol
Section 12 and
Section 13 argue that the core problem in the AI age is not a lack of options but the loss of agency under rate pressure: when the effective decision/learning rate
exceeds integration capacity
, the system fragments. This section turns the framework into a practical protocol: a computable workflow for navigating high-stakes decisions in nonstationary landscapes while remaining within capacity constraints.
14.1. Protocol Overview
The protocol is organized as eight steps with an explicit feedback loop (
Figure 12). It is not a blueprint for what to choose. It is a method for regulating
how choices are made under gradients, by controlling three quantities:
14.2. Step 0: Define the Decision and Hard Constraints
Let the decision be a choice among actions (job transition, retraining path, tool adoption, restructuring, relocation). Specify non-negotiable constraints: dependents and duty-of-care obligations, contractual or legal constraints, financial floors, and ethical boundaries. Formally, define a feasible set .
14.3. Step 1: Measure Load—Estimate R and
Estimate the current effective information/decision rate : incoming demands, tool churn, managerial pressure, retraining requirements, and option velocity. Estimate : available cognitive time, emotional bandwidth, and recovery capacity.
The single most important diagnostic is whether the system is already near the boundary:
If overloaded, the protocol prioritizes rate reduction before major exploration.
14.4. Step 2: Diagnose Gradients—Misfit Versus Novelty
Not all gradients are equal. Define two common components: (i) a
misfit gradient (persistent mismatch between current basin and underlying capability/values), and (ii) a
novelty excitation (short-lived salience without durable structure). The protocol requires explicit evidence for misfit: persistence over time, cross-context recurrence, and measurable degradation in agency margin (Equation (
34)).
14.5. Step 3: Set Temperature as an Exploration Budget
Choose an exploration intensity (temperature proxy) consistent with capacity:
Here is the additional rate load induced by exploration (e.g., learning demands, social volatility, logistical complexity). The goal is not maximal heat, but controlled reheating.
14.6. Step 4: Generate Reversible Moves That Maximize Information per Irreversibility
Construct a short list of reversible moves
that increase information about the landscape while minimizing irreversible costs. Operationally, prefer actions that score high on the ratio
where
is information gain and
is irreversibility cost (time sunk, reputational lock-in, relationship damage), with
.
14.7. Steps 5–6: Run Bounded Experiments and Update
Run trials with explicit boundaries: time-boxed, scope-limited, and reversible where possible (pilot projects, shadowing, short courses, internal transfers, limited consulting engagements). After each trial, update beliefs about the landscape: revise the posterior over options, update and , and re-estimate misfit versus novelty.
14.8. Step 7: Commit Gradually (Cool Only After Sampling)
Cooling is commitment: narrowing the distribution over futures. The protocol requires that commitment be delayed until trials have produced sufficient evidence of robustness and the agency margin is stable. Premature cooling reintroduces brittleness; delayed cooling risks fragmentation. The criterion is structural: commit when the selected basin remains viable under plausible shocks and does not push above capacity.
14.9. Step 8: Monitor Drift and Reheat When Gradients Change
Landscapes move. AI systems, organizational policies, and labor markets introduce nonstationarity. The protocol therefore ends with monitoring: detect changes in gradients and rate; reintroduce exploration when increases or when the margin shrinks.
14.10. Where AI Sits in the Loop
AI is not only a tool; it is part of the environment that generates both gradients and rate pressure. It can either (i) steepen gradients and increase
indiscriminately (breaking agency), or (ii) support controlled exploration by reducing waste and compressing complexity into digestible proposals.
Figure 13 locates AI within the feedback loop: it shapes
G and
R, while the protocol constrains how the system responds through
and reversibility.
14.11. Implications for Education and Training
Because capacity can be expanded only gradually, the protocol implies a timing asymmetry: training exploration skill after an AI-driven rate shock is inferior to training it before shocks arrive. Educational systems built on blueprint trajectories (front-loaded training followed by long exploitation) will tend to produce early-cooled professionals with low adaptive bandwidth. A capacity-first curriculum emphasizes repeated, bounded exploration cycles: sampling new domains, integrating feedback, and consolidating skills without exceeding rate limits. This is not “teaching risk” for its own sake; it is training the control of temperature and rate in a world where gradients will not remain gentle.
The following protocol operationalizes the annealing dynamics of
Section 7 and aligns directly with active inference formulations of controlled uncertainty regulation.
Annealing-Aligned Decision Protocol for Human–AI Systems
- 1:
Input: Current self-state , perceived options , constraints
- 2:
Step 0: Diagnose Regime - 3:
Estimate decision rate R and self-channel capacity
- 4:
Ifthen enter overload mitigation mode - 5:
Step 1: Identify Dominant Gradient - 6:
Decompose dissatisfaction into misfit, novelty, and external pressure components - 7:
Step 2: Estimate Energy Landscape - 8:
Evaluate effective self-energy
- 9:
Step 3: Set Temperature - 10:
Choose exploration temperature within capacity bounds - 11:
Avoid forced cooling () under uncertainty - 12:
Step 4: Propose Reversible Moves - 13:
Generate candidate actions maximizing information gain - 14:
Prefer moves with low irreversible loss - 15:
Step 5: Sample - 16:
Execute stochastic exploration:
- 17:
Step 6: Update Beliefs - 18:
Update plausibility distribution and self-entropy
- 19:
Step 7: Monitor Stability - 20:
Check for coherence, ethical load, and agency margin - 21:
If instability detected then reduce
- 22:
Step 8: Gradual Cooling - 23:
Anneal temperature slowly only after sufficient sampling - 24:
Commit when variance collapses naturally - 25:
Output: Updated self-state with preserved agency
|
Interpretation. The protocol does not prescribe choices or outcomes. It constrains how decisions are made under steep gradients. Agency is preserved by rate control, reversibility, and delayed commitment. Failure modes arise not from exploration itself, but from unmanaged temperature schedules.
Figure 14.
Annealing protocol overlaid on the reduced identity energy landscape. Steps 0–8 correspond to sequential phases of controlled exploration and stabilization. Premature cooling traps the system in local minima, while regulated reduction enables coherent commitment.
Figure 14.
Annealing protocol overlaid on the reduced identity energy landscape. Steps 0–8 correspond to sequential phases of controlled exploration and stabilization. Premature cooling traps the system in local minima, while regulated reduction enables coherent commitment.
14.12. Active Inference Alignment
To anticipate active-inference interpretations, we make the correspondence between the annealing protocol and standard free-energy terms explicit. In active inference, agents maintain adaptive coherence by selecting policies
that minimize expected free energy
, with inference driven by prediction errors weighted by precision [
28,
35,
40].
Notation.
Let observations be
o, latent states be
s, and actions/policies be
. Let
denote sensory (outcome) prediction error and
its precision (roughly, inverse noise variance). Policy selection is performed by minimizing expected free energy
, which can be written in a standard decomposition into
risk (expected negative utility) and
ambiguity (expected uncertainty), plus epistemic terms corresponding to expected information gain [
40,
41]. Within our decision protocol, the effective self-energy
plays the role of a task- and constraint-weighted cost landscape (
Section 7).
Step-by-step mapping.
Each protocol step corresponds to a recognizable component in active inference:
Step 0 (Detect gradient) ↔ sustained prediction error. A “gradient” corresponds to persistent, structured prediction error: remains elevated across contexts and time. In active inference language, the agent is outside a preferred set (a violation of prior preferences over outcomes), producing sustained “surprise” that cannot be quenched by local action.
Step 1 (Capacity check) ↔ precision budgeting / gain control. When , the system is in an overload regime where prediction errors cannot be integrated without instability. In active inference terms, this corresponds to pathological precision allocation: either overly high precision on noisy errors (hypervigilance) or precision collapse (learned helplessness). The protocol’s first move is to restore a stable precision budget by reducing effective rate (downsampling the stream of error signals and decisions).
Step 2 (Diagnose gradients) ↔ model comparison: epistemic vs hedonic drive. Distinguishing misfit from novelty maps to separating (i) persistent model evidence deficits (systematic prediction error under the current generative model) from (ii) transient salience spikes (short-lived changes in precision or attentional gain). This corresponds to evaluating whether exploratory behavior is justified by expected epistemic value (information gain) versus mere arousal.
Step 3 (Set temperature T) ↔ controlled stochasticity / precision tempering. In active inference, exploration can be induced by reducing precision (increasing effective uncertainty) or by policies with high epistemic value (information-seeking). Our temperature parameter plays the role of an explicit precision-tempering schedule: higher T broadens the posterior over self-states (or policies), lower T concentrates it. Thus, “ambition” corresponds to maintaining non-zero exploratory variance even when local prediction errors are not externally enforced.
Step 4 (Reversible probing) ↔ epistemic action under low irreversibility. Selecting reversible moves corresponds to choosing policies whose expected free energy is dominated by epistemic value (expected information gain) while keeping risk (irreversible loss) bounded. Operationally, this approximates: choose that maximizes information gain per unit risk, i.e., high epistemic value with constrained expected cost.
Step 5 (Sample / experiments) ↔ active data acquisition. Bounded experiments are active sampling: actions are chosen to produce observations o that discriminate hypotheses or identity basins. In active inference, this is the canonical role of epistemic foraging: minimizing expected free energy by acquiring evidence that reduces posterior uncertainty over s (and thus over viable policies).
Step 6 (Update beliefs) ↔ variational belief updating. Posterior updating over self-states corresponds directly to variational inference . The protocol makes explicit that “learning” is a regulated reduction of uncertainty: self-entropy decreases only after new evidence arrives and is integrated.
Step 7 (Monitor stability) ↔ precision and policy stability diagnostics. Stability checks correspond to monitoring whether inferred states/policies remain coherent under prediction error, and whether precision has become either rigid (brittle commitment) or diffuse (fragmentation). In active inference terms, this is monitoring for maladaptive attractors in belief dynamics: overconfident posteriors that resist evidence, or unstable posteriors that fail to settle.
Step 8 (Gradual cooling) ↔ commitment via precision increase / policy consolidation. Cooling corresponds to raising effective precision (reducing posterior variance) and consolidating a policy/identity basin when evidence supports it. This is policy selection under stabilized beliefs: the system commits by concentrating probability mass on a narrow region of the state (or policy) space. The critical constraint is that cooling must follow sufficient epistemic sampling; otherwise the system selects a locally plausible but globally brittle policy.
Summary.
In active inference terms, the protocol is an explicit control law over (i) the rate at which prediction errors arrive, (ii) the precision with which they are weighted, and (iii) the balance between epistemic and pragmatic value in policy selection. The novelty of the present formulation is to surface these controls as operational levers for human decision-making under accelerated, nonstationary gradients (e.g., AI-driven rate shocks), rather than leaving them implicit in the inferential machinery.
AI Interface Contract (Annealing-Aligned Assistance) The AI system operates under the following non-negotiable constraints when assisting a human decision-maker:
No direct policy selection. The AI does not recommend or select actions, identities, or commitments on behalf of the human agent.
Gradient exposure only. The AI may surface latent gradients (misfit, opportunity, rate shocks) by highlighting where prediction errors persist, but it must not amplify them beyond the user’s declared capacity.
Capacity-respecting rate control. The AI must ensure that the rate of options, scenarios, or counterfactuals presented satisfies
where is the estimated integrative capacity of the user.
Reversibility prioritization. The AI should preferentially suggest exploratory probes that preserve optionality and minimize irreversible loss.
Explicit uncertainty signaling. All outputs must distinguish between epistemic uncertainty (lack of information) and aleatory uncertainty (inherent variability), preventing false confidence.
Cooling discipline. The AI must not encourage premature commitment. Consolidation is permitted only after sufficient exploration has occurred and when gradients have demonstrably stabilized. Interpretation. Under this contract, the AI functions as a bounded epistemic instrument within the human’s annealing loop: it clarifies landscapes, regulates informational rate, and supports belief updating—without substituting for agency or collapsing the space of possible futures. |
15. Humans and Machines as Coupled Systems
The preceding sections treated AI as an exogenous gradient multiplier: it steepens
and increases option rate
, thereby stressing the human channel capacity (
Section 12) and destabilizing early-cooled systems (
Section 9). In practice, however, AI rarely appears as a distant environmental force. It enters the loop as an
interactive component within the decision process itself. The relevant unit of analysis is therefore not the human alone or the AI alone, but the
human–AI dyad as a coupled adaptive system.
15.1. A Coupled-State View
Let
denote the human state (identity, commitments, affective state, and executive control), and let
denote the AI state (its internal model, context window, and policy for generating outputs). The coupled system evolves jointly under observations
and interactions
:
where
denotes exploratory noise in the human process, modulated by an effective temperature
(
Section 7,
Section 8,
Section 9,
Section 10,
Section 11,
Section 12,
Section 13 and
Section 14), and
controls exploratory variance. The AI is written deterministically for clarity; stochasticity can be included without changing the argument.
The critical point is that coupling introduces new control variables that do not exist in the uncoupled model:
trust,
oversight, and
rate regulation. We represent trust by
, which scales how strongly AI outputs update the human belief state. When
is high, AI suggestions act like high-precision prediction-error signals; when
is low, they are treated as low-precision hypotheses. This mirrors active inference language: coupling strength behaves like a precision term controlling belief updating [
28,
35,
40,
41].
15.2. The Interface Contract as a Stability Condition
Because AI can generate counterfactuals faster than humans can integrate them, a coupled system has a distinct failure mode:
agency collapse by rate violation. Formally, collapse occurs when
so that decision-relevant information arrives faster than the system can compress into stable commitments (
Section 12). The role of the AI interface contract (
Section 14) is therefore not primarily “ethical” in the abstract sense, but
dynamical: it constrains the interaction so that the coupled system remains in a regime where exploration is possible without fragmentation.
Figure 15 depicts this perspective: the AI is best understood as a bounded epistemic instrument situated inside the human annealing loop. Under the contract, AI assistance is restricted to: (i) surfacing gradients, (ii) proposing reversible probes, (iii) compressing option sets, and (iv) making uncertainty explicit. It is explicitly not permitted to select commitments on behalf of the human agent.
15.3. Trust, Precision, and Policy Selection
In active inference, policy selection minimizes expected free energy by trading off epistemic value (information gain) against pragmatic value (risk) [
40,
41]. In the coupled setting, AI systems disproportionately increase epistemic supply: they can produce explanations, plans, and counterfactuals at high rate. If trust is high and the AI stream is treated as high-precision, the human update dynamics can become over-driven, producing rapid oscillation among policies rather than stable selection. Conversely, low trust can blunt epistemic value and reduce the benefit of AI assistance.
Thus, trust should be treated as a control parameter, not a personality trait. In practice, should be bounded above when overload risk is high, and increased only after the system demonstrates integrative stability under the current decision tempo. This is an operational interpretation of precision control: the system should never assign more precision to AI-supplied prediction errors than it can integrate into coherent action.
15.4. A Minimal Demonstration Under a Rate Shock
To make the above dynamics concrete,
Figure 16 shows a stylized mean-field simulation in which a rate shock (representing AI-driven environmental change) pushes the system toward overload. Two trajectories are shown: low trust and high trust. The AI “suggestion” state drifts toward a novel basin (high exploration), while the human state is pulled by both the energy gradient and the coupling term. Under high trust, the coupling can accelerate movement but may also increase instability under overload; under low trust, movement is slower but may preserve coherence.
15.5. Design Principle
The coupled-systems view yields a practical design principle: AI should be evaluated not by the quantity of options it can generate, but by whether it maintains the coupled system in a stable annealing regime. This requires enforcing rate limits, prioritizing reversibility, and treating trust/precision as adjustable controls. In the next section, we formalize how overload collapses agency and why the failure mode is increasingly common in AI-mediated environments.
15.6. Limitations and Scope
This work is intentionally theoretical and conceptual in nature. Its primary contribution is not the empirical validation of specific behavioral predictions, but the introduction of a unifying dynamical framework that connects thermodynamic entropy, information theory, simulated annealing, and human agency under conditions of accelerating technological change.
Several limitations should be noted.
First, the models presented here operate at a coarse-grained level. Human self-states, identity configurations, and capacity limits are represented as abstract variables rather than directly observable quantities. While this abstraction is necessary to establish structural equivalence across physical, informational, and existential domains, it implies that quantitative parameter estimation remains an open challenge. Empirical instantiations will require domain-specific operationalizations and careful validation.
Second, the framework does not claim psychological completeness. It is not a replacement for established models of cognition, affect, or behavior, nor does it attempt to capture the full richness of human motivation or social dynamics. Instead, it addresses a narrower but increasingly critical question: under what structural conditions does agency remain viable when information rates and gradient steepness increase? Many phenomena traditionally treated as psychological—such as burnout, indecision, or loss of meaning—are interpreted here as emergent consequences of rate–capacity mismatch rather than as standalone pathologies.
Third, although the framework is compatible with active inference and free-energy-based accounts of cognition, it is not formally derived from them. The correspondence between prediction error, precision, and temperature is heuristic rather than exact. The present work emphasizes annealing schedules and capacity constraints—features that are often implicit or underdeveloped in existing formulations—without asserting formal equivalence.
Fourth, the human–AI coupling described here focuses on decision-support and informational systems rather than autonomous artificial agents. The analysis is therefore most directly applicable to settings such as professional work, education, retraining, and high-stakes decision-making. Extensions to multi-agent systems, collective dynamics, or fully autonomous AI governance are beyond the current scope.
Finally, the framework does not prescribe normative goals such as happiness, utility maximization, or moral correctness. Its objective is structural rather than teleological: to characterize the conditions under which adaptive exploration, stabilization, and future agency remain possible. Normative interpretation is deliberately left to downstream ethical, cultural, or institutional contexts.
Despite these limitations, the framework offers a compact and transferable lens for analyzing a wide class of human–AI interactions. Its value lies in providing a common language for phenomena that are often treated separately, and in making explicit the dynamical trade-offs that become unavoidable in the AI age.
16. Information Overload and Preparing for the AI Gradient
The central claim of this paper is that agency in rugged, fast-changing landscapes is a dynamical stability property rather than a moral trait. In the AI age, the dominant destabilizer is not a single shock but a persistent increase in the rate at which options, predictions, and counterfactuals are generated. This section translates that claim into a practical implication: education and workforce training must be redesigned around capacity formation and controlled exploration, not around one-time credentialing.
16.1. The AI Gradient as a Persistent Rate Shock
Let
denote the effective decision-relevant information rate impinging on an individual (e.g., new tool affordances, role alternatives, market signals, requirements to retrain). Let
denote the individual’s integration capacity as defined in
Section 6. A minimal stability condition for preserving coherent policy selection is
with sustained violations producing rising error, degraded coherence, and reversion to rigid or avoidant strategies (
Section 12).
In the pre-AI “blueprint” regime, the implicit social contract was that early training would amortize over decades: individuals specialized once and then exploited that specialization under relatively slow environmental drift. AI breaks this assumption by steepening gradients and accelerating option turnover (
Section 11). As a result, retraining is no longer exceptional; it becomes periodic. The practical consequence is that
must be treated as a trainable state variable rather than a fixed trait.
Figure 17.
Capacity formation before the AI rate shock. If capacity is trained early (deliberate exposure to novelty, uncertainty, and skill acquisition), the system remains below the overload boundary even as AI increases effective option rate. If training is deferred until the shock arrives, the same produces a prolonged overload regime, degrading agency precisely when adaptation is most needed.
Figure 17.
Capacity formation before the AI rate shock. If capacity is trained early (deliberate exposure to novelty, uncertainty, and skill acquisition), the system remains below the overload boundary even as AI increases effective option rate. If training is deferred until the shock arrives, the same produces a prolonged overload regime, degrading agency precisely when adaptation is most needed.
16.2. Education as an Annealing Schedule
Section 7,
Section 8 and
Section 9 model adaptation as regulated exploration followed by stabilization. In that language, education is an annealing schedule imposed by institutions. A robust curriculum should therefore specify (explicitly or implicitly) a time-varying exploration temperature
and an accompanying capacity-building program that increases
.
A compact design target is:
while ensuring that the exploration rate never forces persistent violations of (
45). This is not a call for constant novelty. Rather, it is the controlled alternation of (i) safe-to-fail sampling and (ii) consolidation into stable skills, habits, and professional identity.
Figure 18.
Education as an annealing schedule. A stylized exploration temperature decays over the training horizon but includes deliberate reheating episodes (projects, apprenticeships, role rotations) that force sampling without requiring irreversible commitment. Capacity is co-trained so that increasing autonomy does not produce overload under rising external rate pressure.
Figure 18.
Education as an annealing schedule. A stylized exploration temperature decays over the training horizon but includes deliberate reheating episodes (projects, apprenticeships, role rotations) that force sampling without requiring irreversible commitment. Capacity is co-trained so that increasing autonomy does not produce overload under rising external rate pressure.
Figure 19.
Phase-space view of rate–capacity stability. The diagonal boundary separates stable operation (below) from agency overload (above). Early capacity training shifts trajectories away from the overload region under increasing AI-driven option rate, whereas deferred training produces a prolonged overload regime triggered by a rate shock.
Figure 19.
Phase-space view of rate–capacity stability. The diagonal boundary separates stable operation (below) from agency overload (above). Early capacity training shifts trajectories away from the overload region under increasing AI-driven option rate, whereas deferred training produces a prolonged overload regime triggered by a rate shock.
16.3. Why Professionals Are Uniquely Vulnerable
Traditional professions (medicine, law, actuarial science, accounting) are optimized for blueprint stability: long training pipelines, strong credentialing, and high early commitment. These systems produce deep local minima in identity space: once stabilized, switching costs are high and exploration is discouraged. When AI compresses task boundaries and automates core competencies, the result is not merely job displacement. It is loss of locally stabilized identity, loss of perceived competence, and loss of agency—even when financial buffers exist.
In the framework of this paper, professional vulnerability is explained by the conjunction of: (i) early cooling into a narrow basin (low self-entropy), (ii) high irreversibility costs for switching, and (iii) an exogenous increase in that arrives faster than has been trained.
16.4. Design Principles for AI-Age Schooling and Retraining
We state concrete design principles implied by the model.
(P1) Train capacity as a first-class outcome.
Treat as a measurable and trainable construct. Curricula should include repeated practice of “learning how to learn”: decomposition, retrieval, transfer, and sustained effort under uncertainty.
(P2) Institutionalize reversible exploration.
Create structured opportunities for sampling (projects, internships, rotations) where reversibility is preserved and penalties for failure are bounded. This increases information gain while avoiding catastrophic loss.
(P3) Teach annealing control explicitly.
Students should be taught to modulate their own : how to reheat intentionally (explore) and how to cool intentionally (commit), and how to detect premature closure versus chronic fragmentation.
(P4) Rate-limit AI exposure.
Educational AI systems should enforce interface contracts that bound option-rate and cognitive load (see the AI interface contract box in the Appendices). More options are not inherently better if they force .
(P5) Make retraining periodic, not exceptional.
The default assumption should be periodic re-entry into exploration. Credentialing and professional norms must evolve accordingly.
16.5. Implications for Policy
At the policy level, the key variable is not only access to AI tools but access to training time and reversible experimentation. Societies that subsidize capacity formation early (and repeatedly) reduce the probability of large-scale agency collapse under rapid technological gradients. In this sense, education policy becomes a stability policy: it determines whether the human component of human–AI systems remains adaptive as external gradients steepen.
In the next section, we return from institutions to individuals and formalize ethics and responsibility without blueprint assumptions, focusing on how to preserve agency under unavoidable trade-offs.
17. Ethics and Responsibility Without Blueprints
Ethical discourse around AI often oscillates between two unsatisfactory poles: (i) rule-based prescriptions that assume stable environments and known outcomes (a blueprint ethic), and (ii) relativistic “do what feels right” narratives that collapse under uncertainty. The annealing framework developed in
Section 7,
Section 8,
Section 9,
Section 10,
Section 11 and
Section 12 suggests a third stance: ethics as a
stability constraint on exploration under rate limits.
The core structural tension is simple. Exploration is required to avoid premature closure in rugged landscapes, but exploration becomes reckless when it creates irreversible harm or commits the system to fragile basins. In the AI age, this tension becomes acute because external gradients steepen and the effective information rate
rises, increasing the frequency of high-stakes decisions (
Section 11,
Section 12,
Section 13,
Section 14,
Section 15 and
Section 16).
17.1. A Constrained Objective: Optionality Under Ethical and Capacity Bounds
Let a denote a candidate action (a career move, a reskilling program, a restructuring decision, or an AI-mediated policy). We treat ethical responsibility as a set of constraints on what actions are admissible, rather than as a single scalar target to optimize.
We therefore write a minimal decision criterion as a constrained maximization:
where:
is the maximum feasible increase in self-optionality enabled by action
a (Appendix B),
is the induced decision/learning rate under
a,
measures irreversibility (relationship damage, reputational loss, locked-in commitments), and
measures ethical violation (breach of duties, deception, exploitation, or unjust harm). This reframes “ethics” as the geometry of feasible moves in a landscape where exploration is necessary but bounded.
Two immediate implications follow.
First, ethics is not anti-entropy. It does not require low self-entropy or permanent stabilization. Instead, it prevents exploration from externalizing its costs onto others or into irreversible damage.
Second, ethics is not reducible to happiness, comfort, or agreement. A system may be comfortable yet brittle; it may be peaceful yet stagnant. Ethics in this framework is about preserving the conditions for ongoing, coherent agency for self and others under constraint.
17.2. Ethics–Entropy–Agency Regimes
Figure 20 summarizes the qualitative regimes. Low exploration with high conformity produces compliant stagnation (premature cooling). High exploration with low constraint produces reckless trajectories (unbounded irreversibility). The “annealing-aligned” region is neither: it is controlled reheating followed by gradual commitment, within explicit constraints.
17.3. Choosing Adventure Without Recklessness: A Pareto View
The sentence “choose adventure” becomes defensible only when it is made operational. In rugged landscapes, a useful operationalization is:
Prefer moves that maximize information gain and future optionality per unit irreversibility.
This is the decision-theoretic analogue of simulated annealing: propose moves that explore the landscape while retaining the option to reverse or reconfigure if the move samples a poor basin.
Figure 21 makes this explicit as a Pareto frontier. Candidate actions scatter across a trade-off surface between optionality gain and irreversible cost. The protocol preference is not “the riskiest move” but the move with high gain at low irreversibility—a locally rational exploration step rather than a final commitment.
Figure 22.
Feasible decision region under capacity and ethical constraints. Each point represents a candidate action a characterized by irreversibility and ethical violation , with color indicating load ratio . The dashed thresholds and define admissible moves; feasibility additionally requires . The highlighted point illustrates a “preferred” move: high optionality gain while remaining within the ethical and capacity bounds.
Figure 22.
Feasible decision region under capacity and ethical constraints. Each point represents a candidate action a characterized by irreversibility and ethical violation , with color indicating load ratio . The dashed thresholds and define admissible moves; feasibility additionally requires . The highlighted point illustrates a “preferred” move: high optionality gain while remaining within the ethical and capacity bounds.
17.4. Responsibility in Human–AI Systems
In coupled human–AI systems (
Section 15), responsibility must be allocated across the loop. An AI assistant can increase the rate
by proliferating options, counterfactuals, and plans. If it does so without enforcing interface constraints, it drives the system into the overload region
and degrades agency (
Section 12). Ethical alignment for AI, in this framework, therefore includes: (i) rate-limiting, (ii) reversible exploration defaults, and (iii) explicit constraint elicitation (what harms are unacceptable, what commitments are irreversible).
This motivates the “interface contract” (Appendix D): the system must not choose on behalf of the human, but it must shape the interaction so that human choice remains coherent under capacity limits.
17.5. Practical Synthesis
We summarize the ethics of annealing as a short set of operational commitments:
Preserve agency: avoid sustained by rate-limiting and pacing.
Prefer reversibility: sample with low irreversible cost; delay lock-in.
Bound harm: encode explicit constraints on deception, exploitation, and unjust externalized costs.
Commit gradually: cool only after sufficient sampling; do not force premature closure.
These are not moral slogans. They are stability conditions for complex adaptive systems under accelerating gradients.
18. Conclusion
This paper set out to address a practical failure mode in the AI age: the collapse of agency in systems that were optimized for stability under slow change. We argued that this failure is not primarily psychological or moral, but structural. When external gradients steepen and the information/option rate rises, many professional pathways that previously functioned as reliable blueprints become brittle. In this regime, the central problem is not the absence of choices but the inability to integrate them without error: sustained leads to decision noise, oscillation, and paralysis.
We developed a unified formalism in which thermodynamic, informational, and existential processes share a common stochastic gradient flow. Across these domains, complex order emerges not by executing a plan but by exploring state space under constraint and gradually stabilizing what is viable. The canonical continuous-time model—overdamped Langevin dynamics with a temperature schedule—served as the unifying mathematical object, linking entropy production, Bayesian learning, and identity formation through the same exploration–commitment trade-off.
Within this formalism, three claims follow.
(1) Gradients are the catalyst of change.
Across physics, inference, and the self, distributions remain static absent a gradient. In human systems, gradients manifest as mismatch, constraint, or opportunity; in the AI age, they are amplified by technological displacement and rapidly shifting skill landscapes. The framework therefore replaces blueprint narratives (“decide once, then execute”) with a gradient-aware stance (“track pressure, sample, then commit”).
(2) Ambition is temperature control, not goal fixation.
In rugged landscapes, deterministic optimization converges locally. Maintaining non-zero stochastic exploration—a non-zero effective temperature—is the structural prerequisite for accessing globally viable basins. This recasts “comfort” as premature cooling: a locally stable configuration that suppresses exploration and thereby makes latent potential structurally inaccessible.
(3) Agency has a rate limit.
By importing Shannon-style capacity constraints into the self-domain, we modeled modern overload as a rate violation rather than a moral deficiency. AI can increase by proliferating counterfactuals, plans, comparisons, and options. If is increased without pacing and filtering, the human–AI system fails even when intentions are good. The most useful contribution of an “aligned” AI, therefore, is not maximal assistance but controlled assistance: reducing effective rate, preserving reversibility, and maintaining coherent policy selection.
Figure 23 summarizes the synthesis. Gradients inject heat (exploration), but whether the system converts exploration into stable progress depends on capacity growth and annealing schedule. Early training increases
and prevents overload when rate shocks occur; late training forces adaptation under constraint, making oscillation and burnout more likely.
The practical implication is not that individuals should pursue maximal novelty or permanent instability. Rather, it is that modern environments demand deliberate annealing: pacing exploration, preferring reversible moves, cooling only after sufficient sampling, and explicitly respecting capacity constraints. This is also a policy implication. If schooling and professional development remain blueprint-shaped—front-loaded specialization followed by decades of exploitation—then technologically induced gradients will arrive as shocks that exceed capacity, producing avoidable agency collapse at scale. An education system designed for the AI age should instead train controlled exploration early and continuously, increasing the feasible set of futures before constraints tighten.
Finally, the framework provides a language for ethics without subjective collapse. Ethical responsibility appears here as feasibility: bounding irreversibility and harm while preserving the system’s ability to remain adaptive under changing gradients. In this sense, the most defensible long-horizon objective is not happiness, comfort, or certainty, but the continuity of coherent agency: the sustained capacity to sample, learn, and commit without fragmentation as the world accelerates.
Future work should test these claims empirically by operationalizing the proposed self-entropy and capacity measures in longitudinal cohorts, and by evaluating human–AI interface designs that explicitly enforce rate-limiting and reversibility as first-class constraints.
Author Contributions
Conceptualization, methodology, formal analysis, and writing were performed by P.v.R. (ORCID: 0009-0005-7708-8236). The author has read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No empirical datasets were generated or analyzed in this study. All analytical derivations are provided in the main text and appendices. Numerical simulations and figures are illustrative and were produced using standard computational tools as described in the Materials and Methods section. Source code used to generate figures can be made available by the author upon reasonable request.
Limitations and Scope
This work develops a theoretical and conceptual framework grounded in stochastic dynamics and information theory. While the model is mathematically well defined and internally consistent, it is not intended to provide quantitative predictions for individual behavior or organizational outcomes. The formulation abstracts over individual differences, cultural context, and institutional structure, and therefore should be interpreted as describing structural tendencies rather than deterministic trajectories. Empirical validation, parameter estimation in real-world populations, and longitudinal testing of the proposed annealing protocols are important directions for future research. The framework is intended as a lens for understanding adaptation under accelerating change, rather than as a prescriptive or exhaustive account of human decision-making.
Acknowledgments
The author thanks collaborators and reviewers for constructive feedback.
Conflicts of Interest
The author is an entrepreneur and inventor involved in the development of artificial intelligence and computational systems. These activities did not influence the theoretical analysis or conclusions presented in this work. The author declares no conflict of interest.
Appendix A Philosophical Positioning: From Blueprints to Annealing
This appendix positions the proposed annealing framework relative to major philosophical traditions that reviewers may invoke as implicit alternatives. The goal is not to “replace” philosophy with mathematics, but to clarify which philosophical intuitions the framework preserves, which it rejects, and why the AI age changes what is practically defensible.
Appendix A.1. What We Mean by “Blueprint” Versus “Annealing”
A blueprint philosophy assumes that the good life (or right action) can be specified as a relatively stable target in advance, and that rational execution is primarily a matter of applying rules, optimizing an objective, or following a known path. Blueprint ethics often works well in slow-changing environments with predictable institutions.
By contrast, the annealing view treats the agent as a complex adaptive system embedded in non-stationary landscapes. In such landscapes, the central problem is not “select the correct plan once,” but rather: (i) maintain exploration long enough to discover viable basins, (ii) commit gradually as constraints tighten, and (iii) preserve coherent agency under rate limits. This is a process metaphysics in the minimal sense: identity and policy are formed through regulated exploration under constraints, not read off from a prior design.
Appendix A.2. Why This Matters in the AI Age
As argued in
Section 11 and
Section 12, AI steepens gradients and increases the option/ information rate
. This changes the failure mode of blueprint approaches: even if the “right” plan exists, the agent may be unable to integrate the proliferating counterfactuals without violating
. In practice, many failures are rate failures (agency collapse), not moral failures.
Appendix A.3. Relative Positioning of Major Traditions
Figure A1 is a coarse map (for reviewer orientation, not as a claim of historical precision). The horizontal axis indicates
blueprint commitment (fixed ends, rule primacy, teleology). The vertical axis indicates
process tolerance (uncertainty, becoming, openness to exploration). The annealing framework sits naturally in the high-process / low-blueprint quadrant, while still permitting strong constraints on harm and irreversibility (
Section 17).
Figure A1.
Positioning the annealing framework relative to major philosophical traditions. High blueprint commitment emphasizes fixed ends and stable prescriptions; high process tolerance emphasizes identity and policy as emergent through exploration under constraint.
Figure A1.
Positioning the annealing framework relative to major philosophical traditions. High blueprint commitment emphasizes fixed ends and stable prescriptions; high process tolerance emphasizes identity and policy as emergent through exploration under constraint.
Appendix A.4. Stress-Test: Where Each Tradition Aligns or Conflicts with Annealing
It is useful to anticipate the most likely reviewer objections and show how the framework relates to established ideas:
Stoicism.
Stoic philosophy emphasizes the distinction between what lies within an individual’s control and what does not. External events are treated as constraints rather than objectives, while agency is exercised through internal regulation of response. This aligns closely with the annealing framework’s emphasis on constraint-respecting dynamics and internal temperature control. In annealing terms, Stoicism promotes stabilization within known basins under fixed constraints, prioritizing robustness over exploration [
42,
43].
Deontology.
Deontological traditions align with explicit ethical constraints: duties and prohibitions act as hard feasibility bounds (e.g., deception, exploitation). This maps naturally to constraints such as
and
(
Section 17). Potential tension arises if rules are treated as complete action selectors in contexts where the landscape is novel and consequences are uncertain; annealing treats rules as constraints, not complete policies [
44].
Utilitarianism.
Utilitarian approaches align with optimization language and provide a disciplined framework for trade-offs. Their main mismatch with the present framework is practical: maximizing an external aggregate objective can be undefined or unstable in non-stationary environments, and it can ignore the agent’s internal rate limit. Annealing foregrounds feasibility of coherent choice under
before any higher-level optimization is meaningful [
45].
Existentialism.
Existentialist traditions align strongly with self-authorship, freedom under uncertainty, and the inevitability of choice. This is compatible with the exploration requirement (non-zero temperature). The main tension is that existentialism can under-specify stabilizing constraints and rate limits; annealing adds precisely the structural constraints that prevent freedom from collapsing into oscillation [
46].
These alignments can be summarized by asking which components of the annealing protocol each tradition emphasizes.
Figure A2 provides a compact qualitative mapping.
Figure A2.
How different traditions emphasize elements of the annealing protocol. Values are qualitative (for reviewer orientation) and indicate relative emphasis on: exploration control (T), explicit constraints (harm/irreversibility), rate-limiting (), and commitment (cooling).
Figure A2.
How different traditions emphasize elements of the annealing protocol. Values are qualitative (for reviewer orientation) and indicate relative emphasis on: exploration control (T), explicit constraints (harm/irreversibility), rate-limiting (), and commitment (cooling).
Process and Pragmatist Philosophies
Process-oriented philosophies reject static conceptions of identity or value, emphasizing becoming over being. Whitehead’s process metaphysics and Dewey’s pragmatism both view order as emergent from interaction rather than execution of a fixed plan. This closely parallels the annealing framework’s rejection of blueprint optimization in favor of adaptive exploration under constraint, where structure arises through regulated entropy reduction [
47,
48].
Summary
Across these traditions, differences arise not primarily from conflicting values, but from differing assumptions about exploration, constraint, and stabilization. The annealing framework does not adjudicate between ethical doctrines; instead, it clarifies the structural conditions under which agency, meaning, and coherence can emerge. In doing so, it provides a unifying formal language capable of accommodating diverse philosophical intuitions while remaining grounded in thermodynamic and informational principles.
Appendix A.5. Takeaway for Reviewers
The annealing framework is compatible with many philosophical intuitions, but it changes the order of operations for the AI age:
Preserve coherent agency first (respect capacity and rate limits).
Explore second (reheat in a controlled, reversible way).
Commit third (cool gradually once sufficient sampling has occurred).
Treat ethics as feasibility constraints, not as a single subjective scalar target.
This is the minimal philosophical shift required by accelerating gradients: from “follow the plan” to “remain adaptive without collapsing agency.”
Appendix B. Maximum Feasible Self-Entropy and a Decision Criterion
This appendix derives a practical decision criterion based on a maximum feasible increase in self-entropy. The purpose is to formalize a concept that appears repeatedly in the main text: in rugged landscapes, the most useful choices are those that increase future option space (self-entropy) without violating irreversibility, ethical, and capacity constraints.
Appendix B.1. Setup: Self-State Distribution and Entropy
Let the self-state be a discrete or continuous variable
. At time
t, the agent maintains an implicit distribution
over feasible self-states. Define self-entropy as the Shannon entropy
with the discrete analogue
[
14,
15].
Appendix B.2. Feasibility Constraints
We model “feasible” self-states via constraint functionals that encode the dominant irreversibilities discussed in the paper. Let denote irreversibility cost (e.g., locked-in commitments, lost options), denote ethical-violation cost, and denote fragility/loss exposure. Let denote the effective option-rate load induced by occupying or moving toward x (the informational “rate” pressure).
We define a feasible set
and impose an explicit capacity constraint at the distribution level:
where
is the effective integrated option/information rate induced by the distribution
q (as used in the main text), and
is the agent’s integration capacity [
15].
Appendix B.3. Maximum-Entropy Principle Under Constraints
Among all distributions supported on the feasible set, the
maximum feasible self-entropy is
If we ignore the rate constraint (or treat it as non-binding), then the entropy-maximizing distribution subject only to support on
is the uniform distribution on
(discrete or continuous), yielding
i.e., maximum feasible self-entropy is the log-size of the feasible identity region [
14].
When additional
moment constraints are present (e.g., bounded expected irreversibility), the maximum-entropy distribution takes the exponential-family form
where
are Lagrange multipliers and
is the normalizer. This is the classical maximum-entropy result (Jaynes) applied to the self-domain [
25].
Appendix B.4. A Decision-Relevant Quantity: Maximum Feasible Gain in Self-Entropy
Let
be the current self-distribution at time
. Define the maximum feasible
increase in self-entropy achievable over a decision horizon
as
where
denotes distributions that respect the feasibility and capacity constraints (Eqs. (
A2)–(
A3)).
Interpreted operationally: measures how much future option space can be expanded without crossing irreversibility/ethics bounds or exceeding integration capacity. It is therefore a structural “room-to-move” metric.
Appendix B.5. A Constrained Optimality Criterion
For a candidate action
a (e.g., a retraining program, an internal transfer, a reversible experiment), let the post-action feasible set be
and the corresponding maximum feasible gain be
. We propose the following criterion for
entropy-aware, non-reckless action selection:
This objective does not optimize happiness, pleasure, certainty, or moral righteousness; it optimizes feasible expansion of future agency under explicit constraints.
Appendix B.6. Intuition and a Schematic
Figure A3 provides an intuition: loosening constraints expands the feasible region and increases
, while a binding rate/capacity constraint suppresses achievable expansion even when other constraints loosen. This matches the main claim of the paper: in the AI age, the limiting factor is often not opportunity but integration capacity.
Figure A3.
Schematic behavior of maximum feasible self-entropy gain as constraints loosen. When rate limits bind, achievable expansion is reduced even if other constraints loosen.
Figure A3.
Schematic behavior of maximum feasible self-entropy gain as constraints loosen. When rate limits bind, achievable expansion is reduced even if other constraints loosen.
Appendix B.7. Notes for Implementation
In practice, can be approximated by: (i) enumerating a finite set of candidate future states, (ii) filtering by feasibility constraints, (iii) estimating the log-size (or entropy) of the remaining set, and (iv) applying a rate-limiter that enforces (Appendix D/E). This estimation can be performed by an AI assistant without choosing on behalf of the human, provided the assistant respects an explicit interface contract (Appendix D).
Appendix C. Worked Example—Anna Under AI-Driven Job Displacement
This appendix illustrates how the maximum feasible self-entropy criterion from Appendix B behaves in a concrete, professionally relevant scenario: Anna, an actuary in a historically “blueprint” profession, experiences AI-driven displacement (or rapid task-automation) that abruptly increases the option/information rate while destabilizing her identity basin. The purpose is not to numerically predict Anna’s life, but to show how the criterion produces an actionable ranking of interventions under explicit constraints.
Appendix C.1. Scenario and Assumptions
Anna has high external stability (family and marriage) but derives a large fraction of self-worth and agency from professional competence and status. An AI-induced shock reduces the stability of her incumbent career basin. As described in the main text, the dominant near-term loss is not material survival but agency: loss of perceived competence, narrative coherence, and control.
We evaluate candidate actions over a horizon (months to a year), comparing their ability to expand Anna’s feasible future option space while respecting: (i) irreversibility bounds, (ii) ethical constraints, and (iii) the capacity constraint .
Appendix C.2. Candidate Actions
Consider five stylized action families:
A0: Do nothing (wait, deny, or attempt to preserve the prior basin without adaptation).
A1: Narrow upskill (incremental skills in the same domain, e.g., actuarial automation oversight).
A2: Broad reskill (adjacent field, e.g., data science, risk engineering, applied ML governance).
A3: Portfolio strategy (two-track exploration: one stabilizing track plus one exploratory track).
A4: Radical pivot (new identity basin: entrepreneurship, a different profession, or a new role family).
Each action changes the feasible identity region
(Appendix B, Eq. (B.
A2)) and changes the induced option rate
. The maximum feasible entropy-gain criterion is:
where
is defined in Appendix B (Eq. (B.
A7)).
Appendix C.3. Two Effects: Constraint Expansion Versus Rate Penalties
Actions typically increase feasible option space (they expand ), but they also increase the rate at which Anna must evaluate and integrate new possibilities. Thus, the criterion separates two quantities:
Figure A4 illustrates this separation schematically. Actions that look best under constraints-only reasoning can become infeasible or counterproductive once the rate constraint binds.
Figure A4.
Anna under AI-driven job displacement: schematic comparison of maximum feasible self-entropy gain across action families. The right bar in each pair enforces the rate constraint , showing how capacity limits suppress what is achievable even when opportunities exist.
Figure A4.
Anna under AI-driven job displacement: schematic comparison of maximum feasible self-entropy gain across action families. The right bar in each pair enforces the rate constraint , showing how capacity limits suppress what is achievable even when opportunities exist.
Appendix C.4. Interpretation for Anna
The criterion yields three practically important conclusions:
Appendix C.5.5.19. (i) “Do nothing” minimizes overload but collapses option space.
A0 may keep R low, but it fails to expand ; remains small. Under AI shocks, this strategy tends toward brittle stabilization: Anna stays coherent until the basin fails, after which recovery is harder.
Appendix C.5.5.20. (ii) Portfolio strategies dominate under capacity limits.
A3 performs well because it expands option space while controlling rate. It corresponds to controlled reheating: a stabilizing track (cooling) plus a bounded exploratory track (temperature control).
Appendix C.5.5.21. (iii) Radical pivots are often rate-infeasible in early-cooled systems.
A4 can maximize constraints-only expansion but typically imposes high option rate and identity instability. In early-cooled systems like Anna’s, capacity and integration lags can make A4 locally non-viable even if it is globally attractive.
Figure A5.
Horizon dependence of the maximum feasible self-entropy gain for actions A1–A4 under a rate limit. Short horizons favor bounded moves; longer horizons allow larger feasible expansion as capacity and integration catch up.
Figure A5.
Horizon dependence of the maximum feasible self-entropy gain for actions A1–A4 under a rate limit. Short horizons favor bounded moves; longer horizons allow larger feasible expansion as capacity and integration catch up.
Appendix C.5. Why Early Capacity Training Changes the Outcome
Figure A6 shows the same logic dynamically: a rate shock
(from AI displacement) can push the system into overload (
), which precipitates entropy collapse (panic stabilization, premature closure, or oscillation). By contrast, early training increases
, allowing exploration to remain feasible under shock, thereby preserving
.
Figure A6.
Schematic dynamics: AI rate shocks can drive , causing self-entropy collapse and loss of agency. Early capacity training increases and preserves exploratory option space under shock.
Figure A6.
Schematic dynamics: AI rate shocks can drive , causing self-entropy collapse and loss of agency. Early capacity training increases and preserves exploratory option space under shock.
Appendix C.6. Practical Takeaway
For Anna, the criterion does not say “choose the biggest change” or “choose safety.” It says: choose the action sequence that maximizes feasible expansion of future identity and agency, given explicit irreversibility and ethical constraints and the hard rate limit . In many AI-displacement cases, this will favor portfolio reheating (bounded exploration plus stabilizing commitment) rather than either denial (A0) or abrupt pivots (A4).
This provides a formal basis for the paper’s educational claim: capacity must be trained early. If training is delayed until after AI shocks, the system is forced into overload regimes where exploration becomes structurally infeasible.
Appendix D. How an AI System Can Estimate Without Choosing for the Human
This appendix specifies how an AI assistant can estimate the maximum feasible self-entropy gain (Appendix B) and present decision-relevant structure without selecting actions on the user’s behalf. The aim is to make the human–AI system legible: the AI provides estimates, constraints, and uncertainty, while the human retains authority, commitment, and ethics.
Appendix D.1. Design Goal
Given a human state distribution
over self-states, and a set of candidate action families
(e.g., training paths, role changes, portfolio strategies), the assistant should estimate
subject to feasibility constraints and a rate/capacity constraint (Appendix B). Crucially, the assistant must
not optimize a hidden value function for the user; it should optimize
epistemic quality of the report and
respect the constraints.
Appendix D.2. Operational Decomposition
We represent each candidate action a as inducing: (i) a set of plausible future self-states and (ii) a constraint mask that filters to a feasible subset . A practical decomposition is:
Generate counterfactuals. Propose a finite set of candidate future states and trajectories over horizon . This is a structured search step (akin to proposal moves in simulated annealing).
Score constraints and irreversibility. For each
, estimate:
Apply feasibility filter. Define .
-
Apply rate limiter. Estimate the induced option/information rate
and enforce a capacity bound:
If , the assistant must either (i) downshift the action into smaller reversible sub-moves (portfolio / staged annealing), or (ii) flag the action as overload-prone.
Estimate entropy gain. Approximate
by (a) an entropy estimate over the feasible set (log-volume / log-count) or (b) a maximum-entropy distribution under moment constraints [
14,
15,
25].
Appendix D.3. What the AI May and May Not Do
The assistant may:
Enumerate options and counterfactuals, with uncertainty bounds.
Compute and report feasibility, irreversibility, and rate-load proxies.
Rank actions by given explicitly stated constraints.
The assistant must not:
Choose the action or coerce commitment.
Hide objective functions or optimize for proxy goals (e.g., engagement).
Collapse ethical constraints into utility unless the user explicitly specifies them.
Appendix D.4. Why Most AI Breaks Agency
Most AI assistants implicitly optimize for
throughput and convenience: they generate many options quickly, compress ambiguity into confident recommendations, and push the user toward commitment. In this framework, that behavior increases
R (option velocity) faster than the human can integrate, violating the hard constraint
. The result is predictable: overload, decision error, and a subjective collapse of agency (
Section 10–12).
Appendix D.5. Contrast Table: Typical Assistant vs Annealing-Aligned Assistant
Table A1.
Typical AI assistant versus annealing-aligned AI (this framework).
Table A1.
Typical AI assistant versus annealing-aligned AI (this framework).
| Dimension |
Typical AI assistant |
Annealing-aligned AI (this work) |
| Primary optimization |
Convenience / speed / “best answer” |
Preserve agency under constraints |
| Option generation |
Maximizes number of options |
Controls option rate R relative to
|
| Uncertainty handling |
Often collapsed into confidence |
Explicit uncertainty + reversible probes |
| User model |
Preferences inferred / assumed |
Constraints elicited explicitly |
| Action style |
Recommend and converge |
Stage, probe, and anneal (reheating schedule) |
| Failure mode |
Overload + dependence |
Optionality preserved + user sovereignty |
Appendix D.6. AI Interface Contract (Non-Negotiable)
|
Interface Contract (Human Sovereignty). The AI may propose actions, estimate feasibility, irreversibility, uncertainty, and rate-load, and compute under stated constraints. The AI may not select the user’s objective, override ethical constraints, pressure commitment, or optimize engagement. All recommendations must be accompanied by: (i) the constraints assumed, (ii) the uncertainty of key estimates, and (iii) at least one lower-irreversibility probe option.
|
Appendix D.7. Where the AI Sits in the Annealing Loop
Figure A7 summarizes the assistant’s role as an estimator and rate limiter embedded in a feedback loop. The loop is explicitly designed so that the AI increases
information gain per unit irreversibility while preventing overload (
Section 10–12).
Figure A7.
AI estimation of without choosing for the human. The assistant generates counterfactuals, filters by feasibility, enforces a rate limit, computes entropy-gain estimates, and reports ranked options with uncertainty, while the human provides constraint updates and retains authority.
Figure A7.
AI estimation of without choosing for the human. The assistant generates counterfactuals, filters by feasibility, enforces a rate limit, computes entropy-gain estimates, and reports ranked options with uncertainty, while the human provides constraint updates and retains authority.
Appendix D.8. Notes on Implementation and Reviewer-Facing Scope
This appendix specifies a contract and an estimation workflow, not a claim that the AI can measure the self with precision. All quantities (, , , R, ) are operational proxies that can be elicited via questionnaires (Appendix E) and refined through iterative feedback. The scientific contribution is the structural decomposition: estimate option-space expansion while enforcing rate and irreversibility bounds.
Appendix E: Diagnostic Questionnaire, Scoring Rubric, and Report Template
This appendix provides a practical instrument that operationalizes the paper’s variables for real-world use. It includes: (i) a 2–3 page questionnaire form, (ii) a scoring rubric that maps subscales to and constraint terms, and (iii) a one-page crisp report template suitable for AI-assisted feedback under the interface contract (Appendix D).
Appendix E.1. Instructions (for Respondents)
Time: 8–12 minutes. Frame: answer for the last 30 days unless otherwise specified.
Use the 1–7 scale: 1 = strongly disagree, 4 = neutral, 7 = strongly agree.
Answer quickly. Precision is less important than honesty.
If you are in acute crisis, treat this as a baseline snapshot, not a verdict.
Appendix E.2. Questionnaire (2–3 Pages)
Participant:_________________
Date:_________________
Context (career / relationship / both):
Scale: 1234567 (circle one number per statement)
A. Integration capacity (maps to C self )
I can hold multiple priorities in mind without feeling scattered. 1 2 3 4 5 6 7
When new tasks arrive, I can triage calmly rather than panic. 1 2 3 4 5 6 7
I can sustain focused work for 45–90 minutes when needed. 1 2 3 4 5 6 7
My sleep / recovery is sufficient for the demands I face. 1 2 3 4 5 6 7
I regularly finish what I start (low “open loops”). 1 2 3 4 5 6 7
B. Option-Rate Pressure (Maps to R)
I receive more inputs (messages, tasks, prompts, ideas) than I can process. 1 2 3 4 5 6 7
Decisions arrive faster than I can integrate their consequences. 1 2 3 4 5 6 7
AI/tools have increased the number of options I feel I must consider. 1 2 3 4 5 6 7
I frequently switch context due to incoming demands. 1 2 3 4 5 6 7
I feel pressure to respond quickly rather than think well. 1 2 3 4 5 6 7
C. Exploration Tolerance (Maps to Temperature T)
I can try unfamiliar paths without immediate certainty. 1 2 3 4 5 6 7
I tolerate ambiguity without rushing to closure. 1 2 3 4 5 6 7
I actively seek feedback that might change my mind. 1 2 3 4 5 6 7
I can take small risks repeatedly (not one big gamble). 1 2 3 4 5 6 7
Novelty excites me more than it threatens me. 1 2 3 4 5 6 7
D. Gradient Intensity (Maps to G)
My environment is changing in ways that force adaptation. 1 2 3 4 5 6 7
My current skills are becoming less valuable (or less differentiated). 1 2 3 4 5 6 7
My role/career stability has decreased in the last year. 1 2 3 4 5 6 7
Competitive pressure is increasing (faster cycles, tighter margins). 1 2 3 4 5 6 7
I feel “pulled” by a concrete external gradient (deadline, disruption, opportunity). 1 2 3 4 5 6 7
E. Cooling Forces (Maps to α)
My routines strongly reinforce the status quo. 1 2 3 4 5 6 7
I avoid changing course because it would disrupt comfort or identity. 1 2 3 4 5 6 7
The people around me subtly punish risk-taking. 1 2 3 4 5 6 7
I default to stability even when it costs growth. 1 2 3 4 5 6 7
I often tell myself “this is fine” even when I feel misfit. 1 2 3 4 5 6 7
F. Ethical Load / Boundaries (Constraint Term V)
I have clear boundaries about what I will not do to win. 1 2 3 4 5 6 7
I can tell the truth about trade-offs without self-deception. 1 2 3 4 5 6 7
I feel guilt that is proportional and informative (not flooding). 1 2 3 4 5 6 7
I can repair trust when I cause harm. 1 2 3 4 5 6 7
My values are stable under stress. 1 2 3 4 5 6 7
G. Irreversibility Exposure (Constraint Term I)
I have dependents or obligations that make failure costly. 1 2 3 4 5 6 7
I carry financial commitments that reduce my ability to pivot. 1 2 3 4 5 6 7
My reputation is tightly coupled to my current role/identity. 1 2 3 4 5 6 7
A wrong move would be hard to reverse within 12 months. 1 2 3 4 5 6 7
My support network would weaken if I changed direction. 1 2 3 4 5 6 7
H. Meaning Signal (Report-Only; Not an Optimization Target)
My current work/role feels intrinsically worth doing. 1 2 3 4 5 6 7
I experience “voluntary difficulty” (effort I would choose again). 1 2 3 4 5 6 7
I can name what I am sacrificing and why it is worth it. 1 2 3 4 5 6 7
I feel my commitments reduce possibilities in a way that makes my life clearer. 1 2 3 4 5 6 7
I feel alive to the future (not resigned, not frantic). 1 2 3 4 5 6 7
Appendix E.3. Scoring Rubric (Maps Subscales to Model Parameters)
Let
denote the mean score of items in section
A (range 1–7). Define a normalized score
We define operational proxies:
Appendix E.5.5.30. Agency overload flag (hard constraint).
Define the overload index
Interpretation: if
, the system is in a rate-violation regime where agency errors increase (
Section 10–12). The first intervention is
rate reduction or capacity building, not more options.
Appendix E.5.5.31. Cooling-trap flag (premature closure).
Define a premature cooling index
where high
indicates strong status-quo reinforcement (high
), low exploration tolerance (low
T), and muted gradients (low
G).
Appendix E.5.5.32. Meaning signal (report-only).
Define
used to contextualize whether current commitments are experiencing “regulated reduction” (
Section 11; Appendix F).
It is not the objective to be maximized.
Appendix E.6. Notes on References
This appendix is primarily operational; it instantiates variables already defined in the main text. If you want a reviewer-facing citation for “capacity” as an empirical cognitive construct (distinct from Shannon capacity), we can optionally cite classic working-memory/cognitive-load sources, but it is not required for the mathematical role of the rate constraint in the paper.
Appendix F: Why Meaning Cannot Be Optimized (and Why Meaning ≠ Happiness)
This appendix formalizes a point used throughout the paper but easy for reviewers (and readers) to misinterpret:
meaning is not an objective function to be maximized. Meaning is an emergent signal that arises during
regulated reduction of self-entropy under constraint (
Section 11), not a scalar reward that can safely drive optimization.
Appendix F.1. What Meaning Is Not
In this framework, meaning does not mean:
happiness (a valence state);
satisfaction (a local evaluation);
pleasure (a hedonic reward);
certainty (low uncertainty / closure);
moral correctness (norm compliance);
success or achievement (external validation).
These quantities can correlate with meaning in particular regimes, but they are not equivalent. A key failure mode of the “blueprint” worldview is treating one of these as the target and then optimizing it directly, which tends to create brittle or self-deceptive equilibria.
This identification is explicitly rejected in existential psychology. Frankl argues that meaning arises not from comfort or pleasure, but from engagement with responsibility, tension, and commitment under constraint [
49]. In this view, meaning often increases
despite discomfort and uncertainty.
Importantly, this does not make meaning irrational or subjective. It makes it non-optimizable as a scalar reward.
Appendix F.2 Structural Argument: Why Optimization Collapses Meaning
From a systems perspective, optimizing meaning as a terminal objective produces a collapse analogous to premature cooling in simulated annealing.
Any scalar objective function, once optimized, eliminates exploration. However, meaning—like learning and agency—emerges from regulated reduction of possibility, not its elimination.
This is consistent with formal treatments of adaptive systems. Active inference frameworks show that viable agents do not converge to a final optimum, but continuously regulate prediction error and uncertainty under changing constraints [
35]. A system that reaches a terminal optimum ceases to adapt.
Thus, meaning cannot be a maximand without destroying the very dynamics that allow it to arise.
Appendix F.3 Meaning as a Byproduct of Regulated Reduction
Within the framework developed in this work, meaning appears when:
a system explores a sufficiently rich space of possibilities,
constraints progressively reduce that space,
commitments are made under irreversibility,
agency remains intact throughout the process.
Meaning is therefore not an objective to be optimized, but a structural byproduct of annealing carried out within capacity limits.
Attempts to optimize meaning directly—whether through happiness maximization, certainty seeking, or moral absolutism—produce the same failure mode: premature closure.
Appendix F.4. A Reviewer-Proof Intuition: Meaning Versus Nearby Quantities
Figure A9 illustrates schematically why meaning behaves differently from pleasure or certainty. Pleasure can peak early (comfort/novelty), certainty rises monotonically with closure, but meaning peaks in a
regulated band where commitment is strong enough to reduce entropy yet not so total that the system becomes brittle. This is consistent with the paper’s central thesis: meaning emerges when exploration is followed by stabilization at a pace the system can integrate.
Figure A9.
Schematic separation of meaning from nearby psychological quantities. Meaning peaks in a regulated band of commitment (regulated reduction), while pleasure and certainty follow different shapes. The figure is illustrative, not empirical.
Figure A9.
Schematic separation of meaning from nearby psychological quantities. Meaning peaks in a regulated band of commitment (regulated reduction), while pleasure and certainty follow different shapes. The figure is illustrative, not empirical.
Appendix F.5. Practical Implication for the Diagnostic Report (Appendix E)
The diagnostic “meaning signal” subscale in Appendix E is included to contextualize a person’s current commitments: is their current reduction of possibilities experienced as voluntary, integrable, and constraint-respecting? It is explicitly not used as the objective to be maximized. The report should therefore phrase meaning as:
“Meaning is a lagging indicator of regulated reduction. We do not chase it; we shape the annealing schedule and constraints, and meaning either appears or it does not.”
Appendix G. Multimodal Estimation of Annealing State and Capacity in the AI Age
Appendix G.1. Motivation
The annealing framework developed in the main text relies on a small set of latent parameters— capacity (C), experienced rate of change (R), exploration temperature (T), gradient strength (G), and cooling coefficient ()—that jointly determine an individual’s adaptive regime. In Appendix E, these parameters were estimated using a structured self-report questionnaire. While valuable in low-data or cold-start settings, questionnaire-based estimation is inherently episodic and subjective.
In contemporary AI-mediated environments, however, individuals continuously generate rich behavioral, physiological, and contextual data. From an information-theoretic perspective, these data streams provide ongoing, noisy observations of the underlying adaptive state of the self. This appendix formalizes how such multimodal signals can be integrated by an AI system to estimate annealing parameters continuously, while preserving human agency and ethical constraints.
Appendix G.2. Multimodal Observations
Let denote the vector of annealing parameters. We assume access to a set of heterogeneous observation streams , each providing partial information about .
Representative examples include:
Professional and educational trajectories (e.g., employment history, retraining frequency, role transitions), which inform long-term cooling dynamics and identity rigidity.
Physiological and health signals (e.g., heart rate variability, sleep regularity, stress markers), which constrain momentary capacity and tolerable temperature .
Behavioral and mobility traces (e.g., travel, novelty exposure, social diversity), which proxy exploratory sampling and gradient encounters.
Interaction patterns with AI systems (e.g., prompt frequency, task switching, reliance on automation), which reflect experienced rate R and precision allocation.
No single data stream is sufficient; identifiability arises only through integration.
Appendix G.3. Estimation as Inference Over Annealing Parameters
Formally, the AI system maintains a posterior distribution
updated sequentially as new observations arrive. This framing aligns directly with Bayesian filtering and variational inference, where annealing parameters play the role of slowly varying latent states.
Importantly, the AI system does not infer or represent specific actions, goals, or life choices. It estimates only structural properties of the adaptive process itself. The output of inference is therefore a region of feasible dynamics rather than a recommended trajectory.
Appendix G.4. Connection to Active Inference and Precision Control
This estimation architecture can be interpreted through the lens of active inference. In that framework, adaptation depends on the regulation of precision—the confidence assigned to prediction errors at different hierarchical levels.
Within the present model:
Temperature T corresponds to precision modulation over exploratory policies. Higher T reduces precision, enabling stochastic sampling; lower T increases precision, favoring commitment.
Capacity C bounds the maximum sustainable precision-weighted prediction error that can be integrated without collapse.
Rate R reflects the velocity of incoming prediction error imposed by the environment, including AI-mediated task acceleration.
From this perspective, agency collapse occurs when precision-weighted error accumulation exceeds capacity (), forcing pathological down-weighting, disengagement, or rigid overconfidence. The AI system’s role is to estimate these quantities, not to optimize behavior directly.
Appendix G.5. The AI Coach as a Constrained Advisory System
Downstream of parameter estimation, an AI coach may provide guidance to the human user. Crucially, this guidance is constrained by an explicit interface contract:
The AI may report inferred parameter ranges and risk regimes (e.g., overload, premature cooling, unsafe reheating).
The AI may suggest classes of reversible experiments consistent with capacity constraints.
The AI must not select actions, rank life choices, or optimize outcomes on behalf of the user.
This separation ensures that the AI functions as a regulator of precision and information flow, not as a substitute decision-maker.
Appendix G.6. Privacy, Consent, and Ethical Constraints
Because multimodal estimation relies on sensitive personal data, strict constraints are required for ethical deployment:
Explicit informed consent: each data modality must be opt-in, with clear articulation of its role in parameter estimation.
Local or federated processing: wherever possible, inference should be performed on-device or via privacy-preserving aggregation to minimize data exposure.
Parameter-level storage: raw data should not be retained; only inferred parameter distributions and uncertainty bounds are persisted.
Right to opacity: users may choose to disable estimation entirely or restrict specific modalities without penalty.
These constraints are not ancillary. They are structurally required to preserve agency under AI mediation and to prevent the annealing framework itself from becoming a source of coercive optimization.
Figure A10.
Multimodal estimation of annealing state and capacity in a human–AI system. Heterogeneous data streams—including educational and professional history (e.g., LinkedIn), physiological and health signals (wearables and medical data), and behavioral or mobility traces (e.g., travel and social activity)—are integrated to estimate the parameters of the annealing model: capacity (C), rate (R), temperature (T), gradient strength (G), and cooling coefficient (). These parameters define the individual’s current annealed state and feasible adaptation region. An AI coach operates downstream of this estimation, providing guidance that is advisory rather than prescriptive, explicitly constrained to preserve human agency and continuity of self.
Figure A10.
Multimodal estimation of annealing state and capacity in a human–AI system. Heterogeneous data streams—including educational and professional history (e.g., LinkedIn), physiological and health signals (wearables and medical data), and behavioral or mobility traces (e.g., travel and social activity)—are integrated to estimate the parameters of the annealing model: capacity (C), rate (R), temperature (T), gradient strength (G), and cooling coefficient (). These parameters define the individual’s current annealed state and feasible adaptation region. An AI coach operates downstream of this estimation, providing guidance that is advisory rather than prescriptive, explicitly constrained to preserve human agency and continuity of self.
Appendix G.7. Summary
This appendix demonstrates that annealing state and capacity need not be inferred through introspection alone. In AI-saturated environments, they can be estimated continuously from multimodal data—provided that inference is strictly limited to structural parameters and that precision control remains human-directed. In this sense, the framework extends active inference from a theory of biological regulation to a practical scaffold for agency preservation in human–AI systems.
Appendix H. A Protocol for Estimating Self-Capacity
Appendix H.1. Motivation and Scope
In physiology, maximal oxygen uptake (
max) and lactate threshold are among the most reliable integrative indicators of cardiovascular fitness, resilience, and long-term health outcomes [
37,
38]. Crucially, these metrics do not measure strength, endurance, or performance directly; rather, they quantify the
maximum sustainable rate at which the organism can process metabolic demand without collapse.
In this work, we propose an explicit analogy: self-capacity plays an equivalent role for adaptive cognition and agency. It characterizes the maximum sustainable rate at which an individual can process uncertainty, novelty, and informational gradients while maintaining coherence and agency. Appendix H formalizes a practical protocol for estimating this capacity in a manner consistent with the annealing framework developed in the main text.
This protocol is descriptive rather than diagnostic and is intended to support guidance, pacing, and early intervention rather than categorical labeling.
Appendix H.2. Conceptual Analogy to Physiological Stress Testing
Figure A11 illustrates the correspondence between physiological fitness metrics and their counterparts in the present framework.
Figure A11.
Analogy between physiological fitness metrics and self-capacity in the annealing framework. max corresponds to maximum self-capacity, while lactate threshold corresponds to the sustainable entropy-processing rate. Beyond this threshold, unintegrated uncertainty accumulates, leading to fatigue analogues such as agency collapse.
Figure A11.
Analogy between physiological fitness metrics and self-capacity in the annealing framework. max corresponds to maximum self-capacity, while lactate threshold corresponds to the sustainable entropy-processing rate. Beyond this threshold, unintegrated uncertainty accumulates, leading to fatigue analogues such as agency collapse.
The key insight is that failure often arises not from insufficient capacity per se, but from a mismatch between imposed rate and sustainable rate. Individuals may appear highly capable while nonetheless failing under inappropriate pacing, analogous to elite athletes experiencing metabolic collapse beyond lactate threshold.
Appendix H.3. Observable Signals of Capacity
Unlike max, self-capacity cannot be measured through a single direct assay. Instead, it is inferred from convergent signals across behavioral, physiological, and contextual domains. In this protocol, capacity estimation relies on the following classes of observables:
Physiological proxies: heart-rate variability, sleep regularity, recovery dynamics, and stress markers derived from wearable devices.
Cognitive load indicators: task-switching frequency, error rates under time pressure, and sustained attention measures.
Behavioral pacing: frequency of abandonment, oscillatory decision patterns, and recovery time after setbacks.
Contextual gradients: rate of environmental change, role turnover, and externally imposed retraining demands.
These signals are integrated longitudinally rather than cross-sectionally, emphasizing trends and recovery dynamics over point estimates.
Appendix H.4. Capacity Stress Test via Controlled Reheating
Analogous to graded exercise testing, self-capacity is estimated through controlled increases in exploratory demand. Within the annealing framework, this corresponds to a temporary and reversible increase in effective temperature , while monitoring integration quality.
Formally, let
denote the experienced rate of informational change and
the inferred capacity. Capacity stress manifests when:
leading to accumulation of unintegrated uncertainty, behavioral noise, or collapse of commitment.
The protocol increases incrementally through reversible challenges (e.g., bounded novelty, short-term role variation) and observes the point at which recovery time diverges or coherence degrades. This threshold provides an operational estimate of sustainable capacity.
Appendix H.5. Integration with Multimodal AI Estimation
In practice, this protocol is implemented through the multimodal estimation pipeline described in Appendix G. Wearable data, professional trajectory signals, and self-report instruments are fused by an AI system that estimates latent parameters governing annealing dynamics, including capacity, cooling rate, and gradient sensitivity.
Importantly, the AI system does not select actions or make decisions on behalf of the individual. Its role is limited to estimation, visualization, and pacing recommendations consistent with agency preservation.
Appendix H.6. Privacy, Consent, and Non-Diagnostic Framing
All capacity estimation must operate under explicit informed consent, strict data minimization, and local-first processing where possible. Capacity estimates are probabilistic and context-dependent; they are not clinical diagnoses, performance ratings, or indicators of worth.
The purpose of this protocol is to prevent late-stage overload by identifying sustainable rates early, enabling gradual capacity expansion through controlled reheating rather than crisis-driven adaptation.
Appendix H.7. Summary
Self-capacity plays a role for adaptive agency analogous to max in physiology: it is a unifying, predictive, and trainable variable that governs resilience under stress. By formalizing its estimation, this framework provides a practical bridge between entropy-based theory and real-world human–AI adaptation.
References
- Autor, D.H. Why Are There Still So Many Jobs? The History and Future of Workplace Automation. Journal of Economic Perspectives 2015, 29, 3–30. [Google Scholar] [CrossRef]
- Acemoglu, D.; Restrepo, P. Automation and New Tasks: How Technology Displaces and Reinstates Labor. Journal of Economic Perspectives 2019, 33, 3–30. [Google Scholar] [CrossRef]
- Parasuraman, R.; Riley, V. Humans and Automation: Use, Misuse, Disuse, Abuse. Human Factors 1997, 39, 230–253. [Google Scholar] [CrossRef]
- Parasuraman, R.; Riley, V. Humans and Automation: Use, Misuse, Disuse, Abuse. Human Factors 1997, 39, 230–253. [Google Scholar] [CrossRef]
- Lee, J.D.; See, K.A. Trust in Automation: Designing for Appropriate Reliance. Human Factors 2004, 46, 50–80. [Google Scholar] [CrossRef]
- Hoff, K.A.; Bashir, M. Trust in Automation: Integrating Empirical Evidence on Factors That Influence Trust. Human Factors 2015, 57, 407–434. [Google Scholar] [CrossRef]
- Bansal, G.; Wu, T.; Zhou, J.; et al. Does the Whole Exceed Its Parts? The Effect of AI Explanations on Human Decision-Making. Proceedings of the ACM on Human-Computer Interaction 2021, 5, 1–23. [Google Scholar] [CrossRef]
- Lai, V.; Tan, C. On Human Predictions with Explanations and Predictions of Machine Learning Models. Proceedings of the ACM on Human-Computer Interaction 2019, 3, 1–21. [Google Scholar] [CrossRef]
- Schr"odinger, E. What Is Life? The Physical Aspect of the Living Cell; Cambridge University Press: Cambridge, UK, 1944. [Google Scholar]
- Prigogine, I.; Stengers, I. Order Out of Chaos: Man’s New Dialogue with Nature; Bantam Books: New York, NY, USA, 1984. [Google Scholar]
- Seifert, U. Stochastic Thermodynamics, Fluctuation Theorems and Molecular Machines. Reports on Progress in Physics 2012, 75, 126001. [Google Scholar] [CrossRef]
- Jarzynski, C. Nonequilibrium Equality for Free Energy Differences. Physical Review Letters 1997, 78, 2690–2693. [Google Scholar] [CrossRef]
- Crooks, G.E. Entropy Production Fluctuation Theorem and the Nonequilibrium Work Relation for Free Energy Differences. Physical Review E 1999, 60, 2721–2726. [Google Scholar] [CrossRef] [PubMed]
- Shannon, C.E. A Mathematical Theory of Communication. The Bell System Technical Journal 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2 ed.; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Landauer, R. Irreversibility and Heat Generation in the Computing Process. IBM Journal of Research and Development 1961, 5, 183–191. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Geman, S.; Geman, D. Stochastic Relaxation, Gibbs Distributions, and the Bayesian Restoration of Images. IEEE Transactions on Pattern Analysis and Machine Intelligence 1984, PAMI-6, 721–741. [Google Scholar] [CrossRef]
- Hajek, B. Cooling Schedules for Optimal Annealing. Mathematics of Operations Research 1988, 13, 311–329. [Google Scholar] [CrossRef]
- van Laarhoven, P.J.M.; Aarts, E.H.L. Simulated Annealing: Theory and Applications; Springer, 1987. [Google Scholar]
- Rose, K.; Gurewitz, E.; Fox, G.C. Statistical Mechanics and Phase Transitions in Clustering. Physical Review Letters 1990, 65, 945–948. [Google Scholar] [CrossRef]
- Rose, K. Deterministic Annealing for Clustering, Compression, Classification, Regression, and Related Optimization Problems. Proceedings of the IEEE 1998, 86, 2210–2239. [Google Scholar] [CrossRef]
- Langevin, P. Sur la th’eorie du mouvement brownien. Comptes Rendus de l’Acad’emie des Sciences (Paris) 1908, 146, 530–533. [Google Scholar]
- Gardiner, C.W. Stochastic Methods: A Handbook for the Natural and Social Sciences, 4 ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Jaynes, E.T. Information Theory and Statistical Mechanics. Physical Review 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Welling, M.; Teh, Y.W. Bayesian Learning via Stochastic Gradient Langevin Dynamics. In Proceedings of the Proceedings of the 28th International Conference on Machine Learning (ICML-11), 2011; pp. 681–688. [Google Scholar]
- Friston, K. The Free-Energy Principle: A Rough Guide to the Brain? Trends in Cognitive Sciences 2009, 13, 293–301. [Google Scholar] [CrossRef] [PubMed]
- Friston, K. The Free-Energy Principle: A Unified Brain Theory? Nature Reviews Neuroscience 2010, 11, 127–138. [Google Scholar] [CrossRef] [PubMed]
- Bruineberg, J.; Kiverstein, J.; Rietveld, E. The Free-Energy Principle: A Critical Review. Philosophy and the Mind Sciences 2018, 1, 1–33. [Google Scholar] [CrossRef]
- Hirsh, J.B.; Mar, R.A.; Peterson, J.B. Psychological Entropy: A Framework for Understanding Uncertainty-Related Anxiety. Psychological Review 2012, 119, 304–320. [Google Scholar] [CrossRef]
- Sweller, J. Cognitive Load during Problem Solving: Effects on Learning. Cognitive Science 1988, 12, 257–285. [Google Scholar] [CrossRef]
- Eppler, M.J.; Mengis, J. The Concept of Information Overload: A Review of Literature from Organization Science, Accounting, Marketing, MIS, and Related Disciplines. The Information Society 2004, 20, 325–344. [Google Scholar] [CrossRef]
- Eppler, M.J.; Mengis, J. The Concept of Information Overload: A Review of Literature from Organization Science, Accounting, Marketing, MIS, and Related Disciplines. The Information Society 2004, 20, 325–344. [Google Scholar] [CrossRef]
- Iyengar, S.S.; Lepper, M.R. When Choice Is Demotivating: Can One Desire Too Much of a Good Thing? Journal of Personality and Social Psychology 2000, 79, 995–1006. [Google Scholar] [CrossRef]
- Friston, K.; FitzGerald, T.; Rigoli, F.; Schwartenbeck, P.; Pezzulo, G. Active inference: A process theory. Nature Reviews Neuroscience 2017, 18, 151–162. [Google Scholar] [CrossRef]
- Brynjolfsson, E.; Rock, D.; Syverson, C. Artificial Intelligence and the Modern Productivity Paradox: A Clash of Expectations and Statistics. Working Paper 24001, 2017; National Bureau of Economic Research. [Google Scholar]
- Bassett, D.R.; Howley, E.T. Limiting factors for maximum oxygen uptake and determinants of endurance performance. Medicine & Science in Sports & Exercise 2000, 32, 70–84. [Google Scholar] [CrossRef]
- Blair, S.N.; Horton, E.; Leon, A.S.; Lee, I.M.; Drinkwater, B.L.; Dishman, R.K.; Mackey, M. Physical Activity, Nutrition, and Chronic Disease. Medicine and Science in Sports and Exercise 1996, 28, 335–349. [Google Scholar] [CrossRef]
- Faude, O.; Kindermann, W.; Meyer, T. Lactate threshold concepts: how valid are they? Sports Medicine 2009, 39, 469–490. [Google Scholar] [CrossRef]
- Da Costa, L.; Parr, T.; Sajid, N.; Veselic, S.; Neacsu, V.; Friston, K. Active inference on discrete state-spaces: A synthesis. Journal of Mathematical Psychology 2020, 99, 102447. [Google Scholar] [CrossRef]
- Friston, K.; Rigoli, F.; Ognibene, D.; Mathys, C.; Fitzgerald, T.; Pezzulo, G. Active inference and epistemic value. Cognitive Neuroscience 2015, 6, 187–214. [Google Scholar] [CrossRef]
- Aurelius, M. Meditations; Modern Library, 2002. [Google Scholar]
- Epictetus. The Enchiridion; Dover Publications, 1997. [Google Scholar]
- Kant, I. Groundwork of the Metaphysics of Morals; Cambridge University Press, 1998. [Google Scholar]
- Mill, J.S. Utilitarianism; Hackett Publishing, 2001. [Google Scholar]
- Sartre, J.P. Being and Nothingness; Washington Square Press, 1993. [Google Scholar]
- Whitehead, A.N. Process and Reality; Free Press, 1978. [Google Scholar]
- Dewey, J. Experience and Nature; Open Court, 1925. [Google Scholar]
- Frankl, V.E. Man’s Search for Meaning; Beacon Press: Boston, MA, 1959. [Google Scholar]
Figure 4.
Phase portrait of the reduced annealing dynamics with explicit labels for identity u, exploration temperature T, and agency overload. The shaded/marked region denotes regimes where the effective information rate R exceeds integrative capacity , i.e., . In this regime, additional options and information increase error and oscillation rather than improving choice. The trajectory illustrates premature cooling in a stable professional basin, followed by AI-driven reheating and destabilization under rate pressure.
Figure 4.
Phase portrait of the reduced annealing dynamics with explicit labels for identity u, exploration temperature T, and agency overload. The shaded/marked region denotes regimes where the effective information rate R exceeds integrative capacity , i.e., . In this regime, additional options and information increase error and oscillation rather than improving choice. The trajectory illustrates premature cooling in a stable professional basin, followed by AI-driven reheating and destabilization under rate pressure.
Figure 5.
Schematic illustration of AI as a gradient multiplier: the effective gradient in the identity/professional landscape becomes steeper, increasing pressure to change and reheating the system.
Figure 5.
Schematic illustration of AI as a gradient multiplier: the effective gradient in the identity/professional landscape becomes steeper, increasing pressure to change and reheating the system.
Figure 6.
Schematic illustration of AI as a rate multiplier: the effective information rate (option velocity) can increase discontinuously, stressing integration capacity.
Figure 6.
Schematic illustration of AI as a rate multiplier: the effective information rate (option velocity) can increase discontinuously, stressing integration capacity.
Figure 7.
Schematic integration error as a function of information rate R relative to capacity . When , additional information increases error rather than effective agency.
Figure 7.
Schematic integration error as a function of information rate R relative to capacity . When , additional information increases error rather than effective agency.
Figure 8.
Rate shock vs slow capacity adaptation: AI can increase the effective rate of required adaptation faster than can adjust. The shaded region indicates overload ().
Figure 8.
Rate shock vs slow capacity adaptation: AI can increase the effective rate of required adaptation faster than can adjust. The shaded region indicates overload ().
Figure 9.
Analogy between physiological capacity and adaptive self-capacity. max corresponds to the maximum achievable adaptive capacity , while the lactate threshold corresponds to a critical rate beyond which informational load accumulates rather than integrates. Sustainable adaptation occurs when the rate of environmental change remains below capacity-derived thresholds.
Figure 9.
Analogy between physiological capacity and adaptive self-capacity. max corresponds to the maximum achievable adaptive capacity , while the lactate threshold corresponds to a critical rate beyond which informational load accumulates rather than integrates. Sustainable adaptation occurs when the rate of environmental change remains below capacity-derived thresholds.
Figure 10.
Meaning as regulated reduction (schematic). Premature cooling collapses self-entropy too early and tends to produce brittleness under change. Never cooling preserves options but erodes coherence. Regulated reduction combines early exploration with gradual commitment, with episodic reheating when gradients shift.
Figure 10.
Meaning as regulated reduction (schematic). Premature cooling collapses self-entropy too early and tends to produce brittleness under change. Never cooling preserves options but erodes coherence. Regulated reduction combines early exploration with gradual commitment, with episodic reheating when gradients shift.
Figure 11.
Capacity-constrained objective contours (schematic). Contours represent a generic exploration–stabilization tradeoff objective. As rate pressure approaches one, the feasible region shrinks; beyond the agency boundary, coherent adaptation fails. This visualizes why “more exploration” is not always better and why pacing matters under AI-driven rate shocks.
Figure 11.
Capacity-constrained objective contours (schematic). Contours represent a generic exploration–stabilization tradeoff objective. As rate pressure approaches one, the feasible region shrinks; beyond the agency boundary, coherent adaptation fails. This visualizes why “more exploration” is not always better and why pacing matters under AI-driven rate shocks.
Figure 12.
Annealing decision protocol (schematic). Steps 0–8 define a capacity-aware workflow: clarify constraints, estimate rate and capacity, diagnose gradients, allocate exploration temperature, run bounded trials, update beliefs, and commit gradually. A feedback loop reintroduces exploration when gradients shift or overload appears.
Figure 12.
Annealing decision protocol (schematic). Steps 0–8 define a capacity-aware workflow: clarify constraints, estimate rate and capacity, diagnose gradients, allocate exploration temperature, run bounded trials, update beliefs, and commit gradually. A feedback loop reintroduces exploration when gradients shift or overload appears.
Figure 13.
Where AI sits in the annealing loop (schematic). AI influences the experienced gradients and the effective rate . The protocol regulates exploration temperature and reversibility to keep adaptation within capacity constraints.
Figure 13.
Where AI sits in the annealing loop (schematic). AI influences the experienced gradients and the effective rate . The protocol regulates exploration temperature and reversibility to keep adaptation within capacity constraints.
Figure 15.
Human–AI decision-making as a coupled system. Trust modulates the strength of belief updates induced by AI outputs, while the interface contract enforces rate and reversibility constraints (e.g., ).
Figure 15.
Human–AI decision-making as a coupled system. Trust modulates the strength of belief updates induced by AI outputs, while the interface contract enforces rate and reversibility constraints (e.g., ).
Figure 16.
Stylized coupled dynamics under a rate shock. The shaded region indicates agency overload (). Trust controls the strength of coupling between AI suggestions and human state evolution, analogous to precision weighting in active inference.
Figure 16.
Stylized coupled dynamics under a rate shock. The shaded region indicates agency overload (). Trust controls the strength of coupling between AI suggestions and human state evolution, analogous to precision weighting in active inference.
Figure 20.
Ethics–entropy–agency regimes. The viable region is not maximized novelty nor rigid stability, but controlled exploration (temperature) under binding ethical constraints. This corresponds to annealing: reheating to sample, then cooling to commit, while keeping irreversibility and harm bounded.
Figure 20.
Ethics–entropy–agency regimes. The viable region is not maximized novelty nor rigid stability, but controlled exploration (temperature) under binding ethical constraints. This corresponds to annealing: reheating to sample, then cooling to commit, while keeping irreversibility and harm bounded.
Figure 21.
Gain vs irreversibility. Candidate actions trade off optionality gain (proxy: ) against irreversible cost (ethical, relational, reputational). Annealing-aligned decisions prioritize high gain per unit irreversibility, preserving reversibility while sampling the landscape.
Figure 21.
Gain vs irreversibility. Candidate actions trade off optionality gain (proxy: ) against irreversible cost (ethical, relational, reputational). Annealing-aligned decisions prioritize high gain per unit irreversibility, preserving reversibility while sampling the landscape.
Figure 23.
Synthesis across the paper. Gradients trigger exploration via increased temperature . In the AI age, the option/information rate trends upward and may exhibit shocks. Whether agency remains coherent depends on whether integration capacity is trained early enough to avoid sustained overload ().
Figure 23.
Synthesis across the paper. Gradients trigger exploration via increased temperature . In the AI age, the option/information rate trends upward and may exhibit shocks. Whether agency remains coherent depends on whether integration capacity is trained early enough to avoid sustained overload ().
Table 1.
Physiological analogues for self-capacity and agency dynamics.
Table 1.
Physiological analogues for self-capacity and agency dynamics.
| Physiology |
This Framework |
|
max |
Maximum self-capacity |
| Lactate threshold |
Sustainable entropy-processing rate |
| Lactate accumulation |
Unintegrated uncertainty |
| Fatigue |
Agency collapse |
| Threshold training |
Controlled reheating |
| Overtraining |
Premature cooling or burnout |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2026 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).