Seamlessly Natural: Image Stitching with Natural Appearance Preservation

1. Related Work

Research in image stitching has explored a wide range of strategies, from feature-based methods to deep learning approaches, yet three major limitations persist across the state-of-the-art.

• Geometric Distortion from Global Warps: The dominant homography model [11,12,30] is frequently used because its 8 degrees of freedom allow it to model full perspective effects. However, when applied to real-world scenes with parallax and depth variation, the homography is forced to reconcile conflicting motions, which often results in non-uniform distortions like spindle-shaped warps, unnatural stretching, or spherical bulging. Advanced hybrid warps, such as the "as-projective-as-possible" (APAP) [9], and elastic warping improve flexibility but risk overfitting or over-flexibility, which can produce local stretching artifacts.
• Reliance on Complex Preprocessing: Many seamline optimization methods( [15,26,27]) formulate a cost function over the overlapping region and search for a seam that minimizes this cost, ideally passing through visually consistent areas. However, these approaches often depend on complex preprocessing steps, such as semantic segmentation or depth estimation, to guide the cost map, increasing computational cost and sensitivity to errors and inaccuracies.
• Structural Assumptions and Computational Overhead:

  –

  Plane or Multi-Homography Models [12,18] attempt to reduce single homography distortion by fitting local projective models per plane or blending dual homographies. These methods, however, rely on strong assumptions about scene structure (e.g., two planes or projective-consistent regions) and can become brittle in complex or irregular depth geometries.

  –

  Structure-Preserving Warps successfully reduce distortions and preserve salient structures by incorporating complex optimization frameworks and constraints (e.g., collinearity constraints). These methods, however, are often computationally demanding and remain sensitive to poor feature distribution.

  –

  Learning-Based Approaches use deep learning for tasks like transformer-based warping and optical flow with inpainting [2,13,19,25]. While they generalize well and show strong performance, they demand heavy training requirements, reliance on large datasets, and risk hallucinating content or propagating errors, reducing interpretability compared to geometric models.

Overall, prior methods still face three major challenges: (1) global or overly flexible warps compromise structural fidelity and introduce geometric distortions; (2) seam selection strategies based on cost-function minimization often rely on complex preprocessing steps (like semantic segmentation or feature classification), increasing sensitivity to inaccuracies that reduce the visual realism of the stitched panorama; and (3) dependence on strong scene assumptions (planarity, dual planes, or consistent surface normals).

2. Seamless and Structurally Consistent Image Stitching

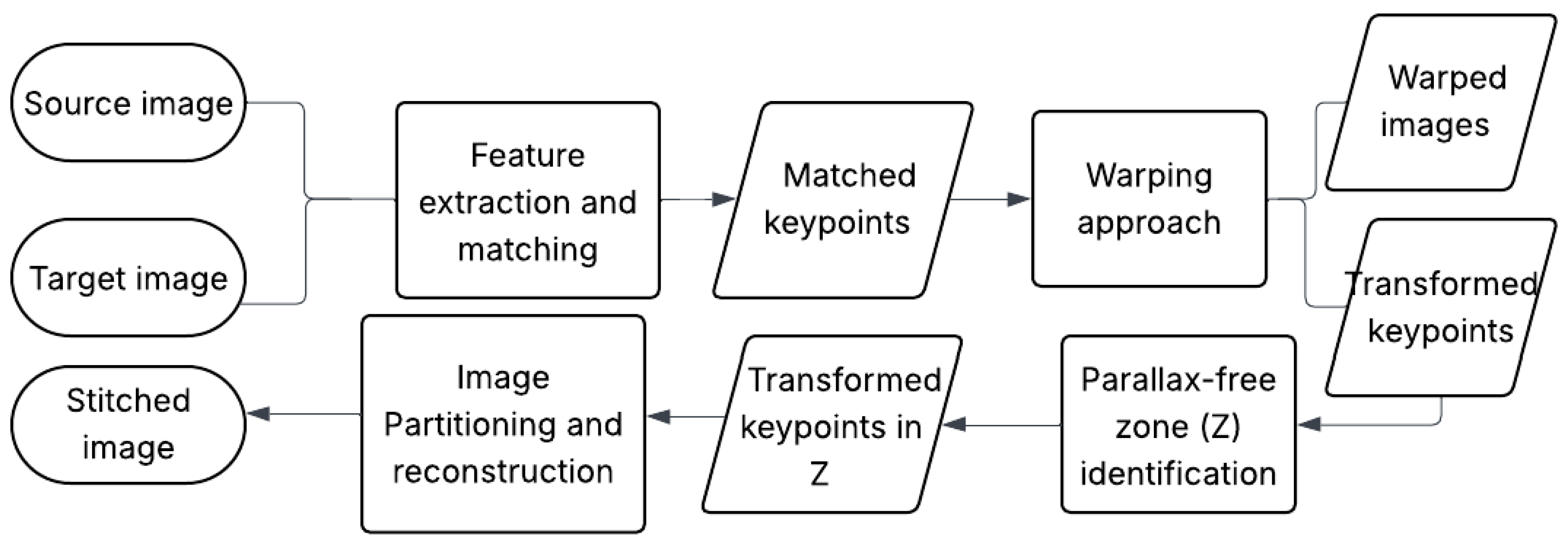
To overcome the excessive distortion and misalignment common in image stitching, we propose a three-stage framework that emphasizes local adaptability, geometry-driven parallax handling, and structurally consistent reconstruction. The method transforms the source image into the domain of the target image while rigorously preserving geometric structure.

2.1. The Three Stage Framework

• Local Image Warping: We deliberately move beyond global homographies and spline-based deformations. The source image is coarsely aligned using a global affine transformation (estimated via RANSAC). This is followed by a refinement stage where the overlap is subdivided into local grids, and distinct affine models are fitted to local feature correspondences. This process generates a Smooth Free-Form Deformation (FFD) field, which is blended and adaptively smoothed using a seamguard strategy that utilizes a ramp mask and match density weighting to prevent discontinuities at boundaries. This preserves overall structural fidelity while reducing geometric distortion.
• Adequate Parallax Minimized Zone Identification: In contrast to seam selection methods relying on semantic segmentation, we introduce a model free strategy. This method analyzes disparity variations and geometric consistency among matched features to isolate a stable stitching zone that inherently minimizes parallax artifacts.
• Image Partitioning and Reconstruction: Within the identified stable zone, an ordered chain of refined keypoints defines the optimal stitching line. Both images are then partitioned into corresponding vertical slices anchored by these keypoints. This anchor-based segmentation enforces structural consistency between the two images by construction: every vertical slice in one image has a direct, aligned counterpart in the other. By tying the seamline to these geometric anchors, our method eliminates the duplication, ghosting, and misalignment issues often associated with blending.

The overall flow of the proposed method is provided in Figure 2.

2.2. Locally Adaptive Image Warping

Our approach generates a content-aware, seam-guarded deformation field to precisely align a source image ($I_s$) to a target image ($I_t$) using only sparse feature matches. The pipeline is structured in six sequential steps, strategically combining global alignment with local adaptivity. This methodology ensures both structural fidelity and robustness through confidence-weighted blending and specific gating mechanisms.

Step 1: Global Affine Estimation via RANSAC

We begin by detecting, extracting, and matching features using the XFeat algorithm [23], which is selected for its effective balance between computational efficiency and matching accuracy. From the resulting set of matched keypoints $\left\{(p_{s_i},p_{t_i})\right\}$, we compute a robust global affine transformation $A_{\mathrm{glob}}\in {\mathbb{R}}^{3\times 3}$ using the RANSAC algorithm. This initial step serves two critical functions: establishing a coarse alignment and filtering outliers. Only the inlier matches, as determined by RANSAC, are retained for all subsequent local refinement steps.

Step 2: Overlap Region and Local Grid Cell Generation

This step defines the area of alignment and prepares it for localized warping.

Using the global affine transformation $A_{\mathrm{glob}}$, the four corners of the source image ($I_s$) are projected into the coordinate space of the target image ($I_t$), creating a quadrilateral. This quadrilateral is then clipped to the bounds of $I_t$ using the Sutherland-Hodgman algorithm to precisely define the polygonal overlap region. A binary mask, $M_{\mathrm{tgt}}^{\mathrm{overlap}}$, is generated from this resulting polygon.

Next, a uniform $G_x\times G_y$ grid is overlaid onto the bounding box of this overlap region. For each resulting grid cell ($c_j$), the following parameters are computed:

• A binary mask $M_{c_j}$, derived from the intersection of the grid cell with $M_{\mathrm{tgt}}^{\mathrm{overlap}}$.
• A centroid ${\mathbf{c}}_j=(c_{x_j},c_{y_j})$, calculated using image moments.
• A bounding box ($(x_0^{\left(j\right)},x_1^{\left(j\right)},y_0^{\left(j\right)},y_1^{\left(j\right)})$), utilized for subsequent spatial weighting and diagnostics.

Step 3: Local Affine Refinement with Adaptive Transformation Selection & Confidence Scoring

For each grid cell $c_j$, a local affine transformation $T_j$ is fitted using the feature matches that fall within the cell and its immediate neighbors. This fitting employs ridge regression with a regularization ${\lambda }_1$, which biases the local solution toward the initial global transformation $A_{\mathrm{glob}}$ to ensure stability.

Spatial Confidence Metric

Instead of relying on statistical residuals or covariance, a novel confidence score is defined for each local affine transformation based on the density and spatial distribution of its supporting feature points. The Gaussian weight $w_i^{\left(j\right)}$ of a feature point i relative to the cell center $\left(c_j\right)$, is computed as:

$w_i^{\left(j\right)}=exp\left(-{\displaystyle \frac{\parallel {\mathbf{p}}_{t_i}-{\mathbf{c}}_j{\parallel }^2}{2{\sigma }_j^2}}\right)$

Here, the Gaussian standard deviation is defined by the scaling factor $\alpha$ applied to the diagonal length of the cell’s bounding box $\mathrm{diag}\left(c_j\right)$, where ${\sigma }_j=\alpha ·\mathrm{diag}\left(c_j\right)$. The overall confidence score is then computed based on this weighted density.

The confidence score is computed as:

$${\mathrm{conf}}_j=max\left({\kappa }_{min},min\left({\kappa }_{max},{\displaystyle \frac{{\sum }_i{w}_i^{\left(j\right)}}{\beta ·{max}_i{w}_i^{\left(j\right)}}}\right)\right)$$

(1)

where ${\kappa }_{min},{\kappa }_{max},\beta$ are clamping and normalization constants. This score reflects the “weight mass” of matches in the cell — a heuristic robust to sparsity and uneven distributions.

Adaptive Transformation Selection via Composite Diagnostic Score

The system employs an adaptive strategy to maintain geometric stability. If the initial local affine transformation $T_j$ produces unstable geometry—diagnosed using metrics such as Root Mean Square Error (RMSE), the determinant, the condition number, or the displacement from the global affine $A_{glob}$—the transformation is refitted using a stronger regularization parameter ${\lambda }_2>{\lambda }_1$. The superior version of the transformation is then selected based on a composite instability score.

$$\mathrm{score}\left(T\right)=\mathrm{RMSE}+{\omega }_{\mathrm{cond}}·\mathrm{cond}+{\omega }_{det}·max(0,{\tau }_{det}-|det|)+{\omega }_{\delta }·{\delta }_{\mathrm{mean}}$$

(2)

where ${\omega }_{\mathrm{cond}},{\omega }_{det},{\omega }_{\delta },{\tau }_{det}$ are weighting and threshold parameters, and ${\delta }_{\mathrm{mean}}$ is the mean displacement between the outputs of the local affine transformation and the global affine transformation, computed over an $N_g\times N_g$ evaluation grid uniformly sampled within the cell’s bounding box. This embedded selection mechanism ensures geometric stability without manual intervention.

Step 4: Free-Form Deformation Field via Confidence-Weighted Local Transformation Blending

We construct a deformation field on an $N_y\times N_x$ lattice over the output canvas. For each lattice point $\mathbf{u}=(u,v)$, we compute its corresponding coordinate in target space ${\mathbf{p}}_t=(u-o_x,v-o_y)$, and its base source coordinate via global affine: ${\mathbf{p}}_{\mathrm{base}}=\Pi (A_{\mathrm{glob}}^{-1}·{[{\mathbf{p}}_t,1]}^T)$, where $\Pi \left(\mathbf{x}\right)=(x/z,y/z)$ is perspective division. For each local transformation $T_j$, we compute its mapped source coordinate ${\mathbf{p}}_{\mathrm{local}}^{\left(j\right)}=\Pi (T_j^{-1}·{[{\mathbf{p}}_t,1]}^T)$, and the displacement $\Delta {\mathbf{p}}^{\left(j\right)}={\mathbf{p}}_{\mathrm{local}}^{\left(j\right)}-{\mathbf{p}}_{\mathrm{base}}$.

Confidence-Weighted Spatial Blending

The final displacement $\Delta \mathbf{p}$ is a normalized blend of all local transformation displacements, weighted by both spatial proximity and transformation confidence:

$$\Delta \mathbf{p}=\sum _{j=1}^J{w}_j\left({\mathbf{p}}_t\right)·\Delta {\mathbf{p}}^{\left(j\right)}\mathrm{where}{w}_j\left({\mathbf{p}}_t\right)={\displaystyle \frac{{\mathrm{conf}}_j·exp\left(-\frac{\parallel {\mathbf{p}}_t-{\mathbf{c}}_j{\parallel }^2}{2{\sigma }_f^2}\right)}{{\sum }_{k=1}^J{\mathrm{conf}}_k·exp\left(-\frac{\parallel {\mathbf{p}}_t-{\mathbf{c}}_k{\parallel }^2}{2{\sigma }_f^2}\right)}}$$

(3)

where ${\sigma }_f={\alpha }_f·\mathrm{mean}\left(\mathrm{cell}\mathrm{diagonals}\right)$, and ${\alpha }_f$ is a spatial decay factor. Displacements are clipped to $[-d_{max},d_{max}]$ and lightly smoothed with Gaussian blur (${\sigma }_l$) before upsampling to full canvas resolution via bicubic interpolation.

Step 5: Seam Guarding via Dual-Channel Gating

The final step in suppressing artifacts near boundaries or in sparse regions is the modulation of the full-resolution deformation field $\Delta \mathbf{p}$ using a multiplicative gate ($\mathbf{G}$) derived from two primary signals:

• Geometric Ramp (${\mathbf{R}}_{\mathrm{canvas}}$): A smootherstep function applied to the signed distance field of the overlap region, with bandwidth proportional to image diagonal ($b=\rho ·{\mathrm{diag}}_{\mathrm{img}}$).
• Match Density Map (${\mathbf{D}}_{\mathrm{canvas}}$): A Gaussian-blurred heatmap of inlier keypoint locations, normalized to $[0,1]$, with kernel standard deviation (${\sigma }_d$).

Dual-Gated Seam Suppression

The final gating mask combines both signals multiplicatively:

$$G\left(\mathbf{u}\right)=\underset{\mathrm{geometric}\mathrm{falloff}}{\underbrace{{\left[S\left(R_{\mathrm{canvas}}\left(\mathbf{u}\right)\right)\right]}^{{\gamma }_p}}}·\underset{\mathrm{density}-\mathrm{aware}\mathrm{modulation}}{\underbrace{\left({\gamma }_{min}+(1-{\gamma }_{min})·S\left(D_{\mathrm{canvas}}\left(\mathbf{u}\right)\right)\right)}}$$

(4)

where $S\left(t\right)=6t^5-15t^4+10t^3$ is the smootherstep function, ${\gamma }_p$ controls ramp steepness, and ${\gamma }_{min}$ is the minimum gate value. The guarded deformation field is then smoothed:

$$\Delta {\mathbf{p}}_{\mathrm{guarded}}\left(\mathbf{u}\right)={\mathrm{GaussianBlur}}_{{\sigma }_g}\left(\Delta \mathbf{p}\left(\mathbf{u}\right)·G\left(\mathbf{u}\right)\right)$$

This is not post-warp blending; rather, it is a mechanism for pre-warp suppression of unreliable deformations. The final displacement field ${\Delta }_p$ is modulated by the gate G:

$$\Delta {\mathbf{p}}_{\mathrm{gated}}=\mathbf{G}\odot \Delta \mathbf{p}$$

This multiplicative gating ensures that the full-resolution displacement is only applied in geometrically stable and feature-supported areas. The combination of geometric and photometric (match-density based) gating for Free-Form Deformation (FFD) fields is, to our knowledge, unprecedented in the image stitching literature.

Step 6: Final Warping and Output

The final source-to-canvas mapping is computed by combining the inverse global affine transformation with the gated deformation field. The source image $I_s$ is then warped into the final canvas space using bilinear interpolation. Concurrently, the target image $I_t$ is pasted onto the output canvas using the pre-computed offset $(o_x,o_y)$.

For evaluation purposes, the final transformed coordinates of the original inlier matches are computed. This involves a simple translation to canvas coordinates for target points and applying the full warp (global affine + FFD + multiplicative gate) with bilinear interpolation of the displacement field for source points.

These collective innovations enable our method to produce seamless, artifact-free alignments even when operating with sparse, uneven, or noisy feature matches.

2.3. Optimal Stitching Line

2.3.1. Determination of an Adequate Parallax-Free Zone

Identifying an adequate stitching area relies on finding a region containing a high density of reliable feature correspondences governed by a dominant geometric transformation. Initially, regions with low information content, which are quantifiable by low local image variance, are systematically excluded as they produce unstable matches. However, scenes with significant depth often exhibit motion parallax, resulting in a multi-modal distribution of disparity vectors that complicates the search for a consistent seam.

To robustly handle this parallax, our method focuses on isolating the most extensive and stable surface. This is achieved by identifying the dominant motion group, which corresponds to the true inliers for a stable stitch. Specifically, the algorithm locates regions where keypoint disparities are statistically consistent (exhibiting low local variance) and where their local mean converges to the global mean $\mu$ of the primary motion mode. This approach allows the algorithm to robustly handle parallax by isolating the most extensive and stable surface.

Given a set of matched keypoint pairs (($x_S,y_S$),($x_T,y_T$)), where $x_S$ and $y_S$ denote the coordinates in the source image and $x_T$ and $y_T$ denote the coordinates in the target image, respectively, keypoints are initially sorted using two primary spatial criteria to account for the camera geometry.

• First, $x_S>x_T$, reflecting the relative frontal position of the camera of the source image.
• $(y_S>y_T)\vee (y_T>y_S)$, for one camera physically positioned above the other in most cases.

The matched keypoints are partitioned into classes $C_i$ based on their abscissa values (x-coordinates). Each class corresponds to a spatial range, R, which is defined as R=width/20. For every keypoint within a class, we compute its disparity as ($x_S-x_T$) and subsequently calculate the mean disparity for that class.

We then iterate through the resulting list of mean disparities (one value per class) and group the corresponding classes into clusters based on the statistical consistency of these mean disparity values. This clustering process isolates the most dominant motion groups, enabling the identification of the parallax-minimized "adequate zone."

Algorithm 1: Threshold-Based Disparity Clustering.

Require:  D: A list of mean disparities $d_1,d_2,\dots ,d_n$, where $d_i$ corresponds to the mean disparity of class i. Require:  v: A positive, user-defined threshold value for disparity difference. Ensure:  C: A set of clusters, where each cluster is a list of consecutive classes from D.   1: Initialize an empty list of clusters C   2: Initialize the current cluster $C_{\mathrm{current}}$ with the first class $d_1$   3: for$i=2$ to n do   4:    if $|d_i-d_{i-1}|\le v$ then   5:      Add class i to $C_{\mathrm{current}}$   6:    else   7:      if $C_{\mathrm{current}}$ contains at least two classes then   8:         Add $C_{\mathrm{current}}$ to the list of clusters C   9:      end if 10:      Start a new cluster with class i: $C_{\mathrm{current}}\leftarrow \left\{d_i\right\}$ 11:    end if 12: end for 13: if$C_{\mathrm{current}}$ contains at least two classes then 14:    Add $C_{\mathrm{current}}$ to the list of clusters C 15: end if 16: returnC

The optimal stitching cluster is selected based on a scoring metric that evaluates the consistency and reliability of each cluster against three key parameters:

• Standard Deviation (${\sigma }_k$): This measures the internal coherence of the cluster. A smaller standard deviation indicates that the individual class mean disparities are tightly grouped around the cluster mean, suggesting a more consistent depth plane.
• Cardinality ($C_k$): This is the total number of keypoints contained within all classes of the cluster. High cardinality indicates that the cluster is supported by a large amount of data, which directly increases the reliability and robustness of its mean disparity calculation.
• Disparity Deviation ($\Delta {\mu }_k$): This is defined as the absolute difference between the mean disparity of the cluster (${\mu }_{c,k}$) and the global mean disparity of all classes (${\mu }_g$).

To prevent the selection of clusters with low reliability (low cardinality), high incoherence (high standard deviation), or minimal deviation from the global mean (low significance), we define a weighted score, $w_k$ , for each cluster k given by Equation 5.

$$w={\displaystyle \frac{C}{(\sigma +\lambda ·\Delta \mu )+ϵ}}$$

(5)

where:

• $\sigma$: standard deviation of the disparities within the cluster,
• C: cardinality (number of keypoints in the cluster),
• $\lambda$: weighting factor controlling the influence of the disparity deviation,
• $\Delta \mu =|{\mu }_c-{\mu }_g|$: absolute difference between the mean disparity of the cluster ${\mu }_c$ and the global mean disparity ${\mu }_g$,
• $ϵ$: a small constant added to avoid division by zero.

The cluster with the highest calculated score, $w_{max}$, is selected as the optimal cluster. The "adequate zone" is then defined as the combination of all the classes within this selected cluster.

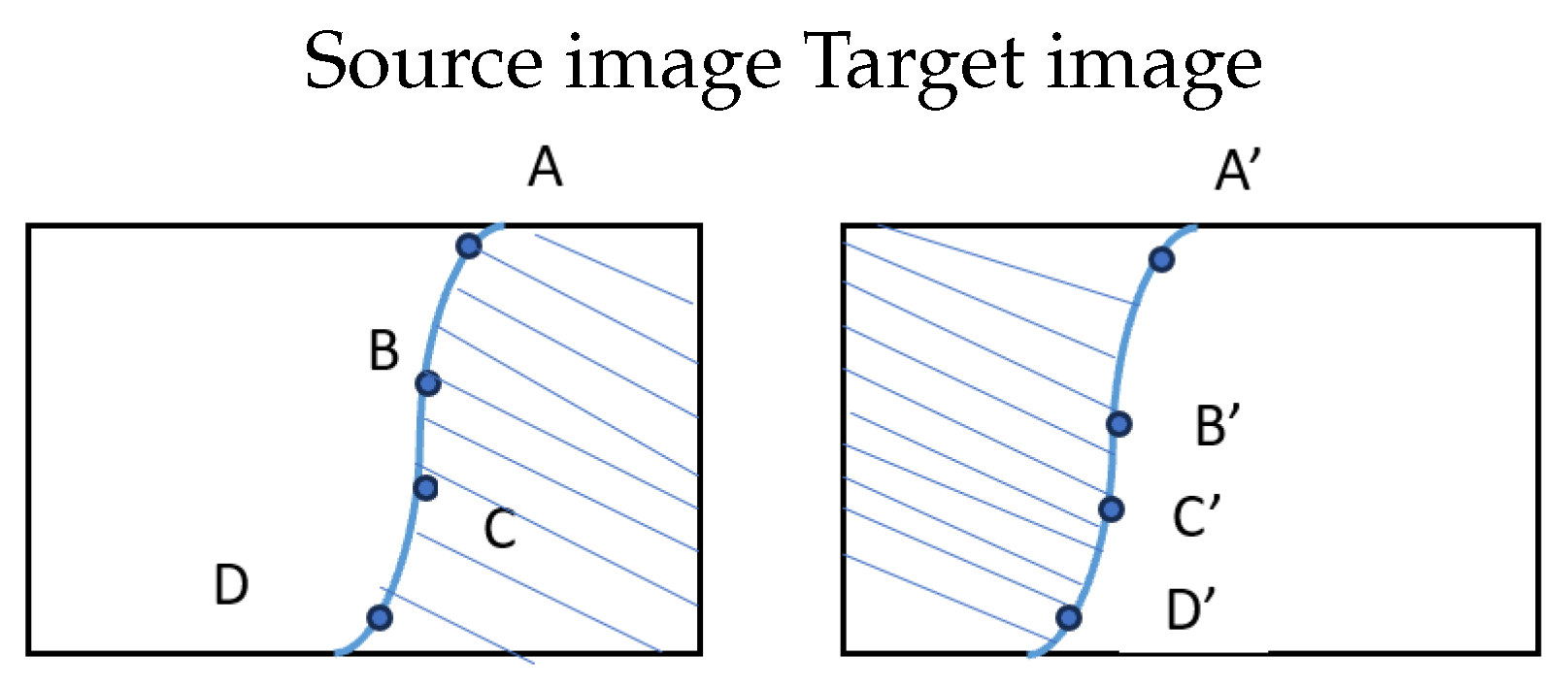
2.3.2. Keypoint Chain Refinement

Once an adequate overlapping area is identified, the initial set of keypoint correspondences cannot be used directly, as this raw data is inherently unreliable and contains significant outliers or misaligned matches. Using these erroneous points to guide partitioning would create inconsistent divisions between the two images, leading directly to visible stitching artifacts such as ghosting and duplications. Therefore, refining this initial set of keypoints is a critical prerequisite.

A dedicated algorithm is employed to generate two clean, synchronized, and ordered lists of keypoints, forming a coherent "keypoint chain". For brightness consistency, a selection step is performed, determining each keypoint’s intensity and retaining only those with similar levels. An initial anchor is established at the keypoint closest to the image edge. From there, the algorithm iteratively matches each point in the first image with its closest corresponding point in the second based on Euclidean distance. A crucial constraint is applied during this process: each match must be unique in its horizontal (x) position. This filtering step prunes the ambiguous or conflicting matches that cause structural inconsistencies, yielding a refined set of high-confidence pairs.

The optimal stitching line in each image is defined by the path connecting the first element to the last element of the refined set in the corresponding pair.

2.4. Partitioning and Reconstruction

2.4.1. Image Partitioning

The image partitioning process begins with the optimal stitching line, which is defined by an ordered set of n reliable keypoint pairs (see Figure 3. These points function as anchors for segmenting each image into $S=n+1$ vertical slices.

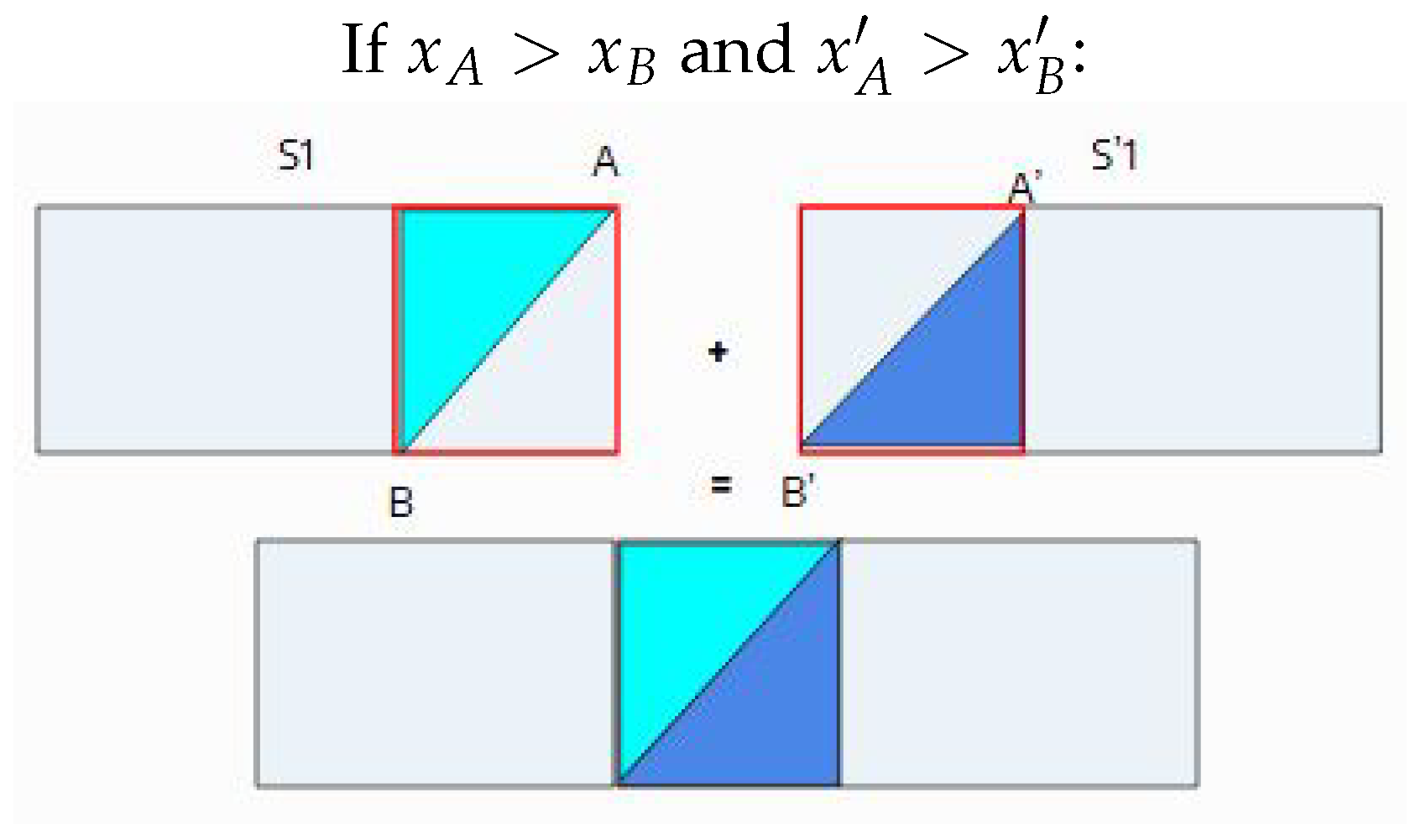
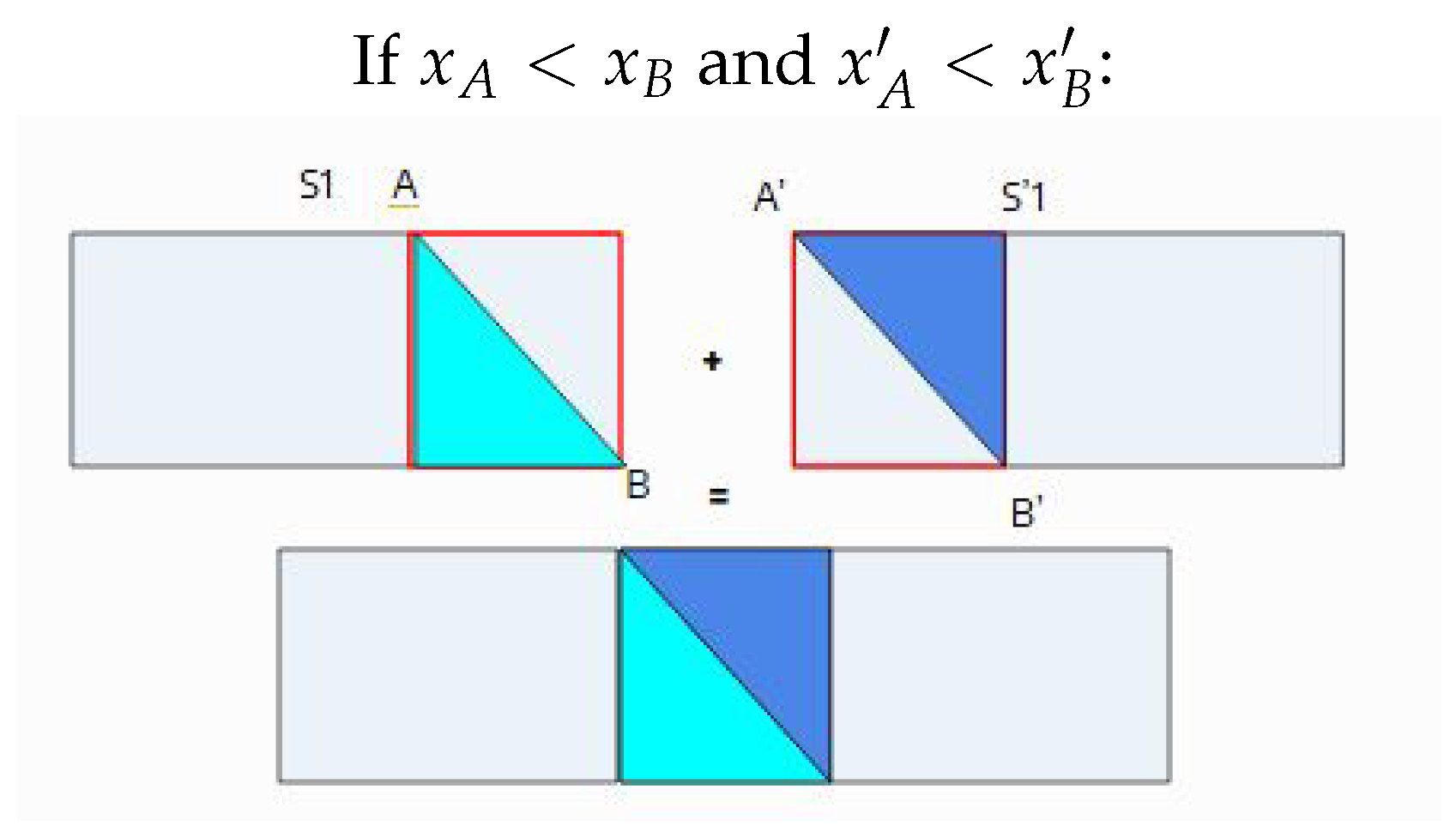
To ensure the resulting vertical slices are structurally complementary (meaning they maintain consistent relative order and direction between the two images), a directional validation is performed on each consecutive pair of anchors $(A,B)$ and their corresponding pair ($A^{\prime },B^{\prime }$) from the second image:

• Valid Segments (Consistent Direction):

  –

  If the x-coordinate of A is greater than B ($x_A>x_B$) AND $A’$ is greater than $B’$ ($x_A’>x_B’$): The segments are valid, as both pairs move from right-to-left (see Figure 4).

  –

  If $x_A<x_B$ and $x_A’<x_B’$: The segments are valid, as both pairs move from left-to-right (see Figure 5).

• Invalid Segments (Inconsistent Direction): If the direction is inconsistent between the two images (e.g., $x_A>x_B$ and $x_A’<x_B’$ or vice versa), the segments are rejected as they are not complementary (see Figure 6). This prevents structural inconsistencies from being introduced during the final reconstruction

2.4.2. Reconstruction

After the segments have been validated, the process moves to the concatenation phase. Because both input images share the identical partitioning pattern, each segment of the first image corresponds directly to a segment of the second image. Corresponding segments are merged using a simple linear alpha transition: the contribution of the left segment decreases linearly from left to right, while the contribution of the right segment increases symmetrically. A final, light Gaussian smoothing is then applied across the seam area to suppress any residual visible artifacts. The resulting blended composites are concatenated horizontally, and the constructed rows are subsequently stacked vertically to form the final stitched image.

Figure 7 summarizes all the described processes.

3. Experimentation and Results

The experiments were conducted within a Google Colaboratory environment, leveraging 12.67GB of RAM and 107.72 GB of storage. We utilized publicly available and widely recognized datasets provided by [4,5,19]. The code is available on GitHub.

3.1. Quantitative Evaluation

Table 1 This section summarizes quantitative results for recent algorithms on the UDIS-D dataset (1,106 images grouped by difficulty: easy, moderate, and hard). Alignment accuracy in the overlap region between stitched images is evaluated using Peak Signal-to-Noise Ratio (PSNR) and the Structural Similarity Index Measure (SSIM).

As shown in the Table 1, our method achieves the highest PSNR and SSIM values among all compared approaches, indicating superior stitching quality. This confirms that our geometry-driven strategy consistently reflects better structural preservation and visual fidelity across diverse scenes.

3.2. Qualitative evaluation

We compare our approach against several state-of-the-art methods, including APAP [9], ELA [29], UDIS [19], UDIS++ [13] and SEAMLESS [25]. Please feel free to zoom in on the images to better observe the highlighted elements. Additional data is given in the online resource and comprehensive visuals comparisons are provided on Google Drive.

Figure 8. APAP [9], ELA [29], and UDIS++ [13] exhibit pronounced ghosting artifacts, while UDIS [19] produces noticeable blurring and SEAMLESS [25] introduces stretching in certain regions. Moreover, most of these approaches display a generally blurred texture across the stitched image. In contrast, our method eliminates duplication and preserves the original sharp texture of the input images.

Figure 8. APAP [9], ELA [29], and UDIS++ [13] exhibit pronounced ghosting artifacts, while UDIS [19] produces noticeable blurring and SEAMLESS [25] introduces stretching in certain regions. Moreover, most of these approaches display a generally blurred texture across the stitched image. In contrast, our method eliminates duplication and preserves the original sharp texture of the input images.

Figure 9. We observe ghosting artifacts in APAP, ELA, UDIS, UDIS++ and a blurred texture in SEAMLESS. Our result is free of these artifacts.

Figure 9. We observe ghosting artifacts in APAP, ELA, UDIS, UDIS++ and a blurred texture in SEAMLESS. Our result is free of these artifacts.

Figure 10. Ghosting and blurring artifacts observed in state-of-the-art methods. Our approach produces seamless and visually consistent stitching results.

Figure 10. Ghosting and blurring artifacts observed in state-of-the-art methods. Our approach produces seamless and visually consistent stitching results.

Figure 11. Similar artifacts as in Figure 9 for the state of the art.

Figure 11. Similar artifacts as in Figure 9 for the state of the art.

Figure 12. Similar artifacts as in Figure 9 for the state of the art.

Figure 12. Similar artifacts as in Figure 9 for the state of the art.

Figure 13. Similar artifacts as in Figure 9 for the state of the art.

Figure 13. Similar artifacts as in Figure 9 for the state of the art.

Figure 14. Misalignments (tiles in the floor) in APAP, LPC, SPW, and correct alignment in SENA.

Figure 14. Misalignments (tiles in the floor) in APAP, LPC, SPW, and correct alignment in SENA.

Figure 15. UDIS++ [13] and SEAMLESS [25] present undistinguishable writings due to the blurred texture of the image, and misalignments. In SENA, the writings are clear as in the input images and a single slight misalignment is observed.

Figure 15. UDIS++ [13] and SEAMLESS [25] present undistinguishable writings due to the blurred texture of the image, and misalignments. In SENA, the writings are clear as in the input images and a single slight misalignment is observed.

Qualitative results show that state-of-the-art methods often produce noticeable artifacts, including duplication, texture loss, and stretching of image structures. In contrast, SENA generates sharper, higher-resolution stitched images, while preserving structural integrity and visual realism.

3.3. Ablation Studies

We evaluate here the effectiveness of our three main components — the locally adaptive image warping, the adequate parallax-free zone identification, and the segment-based reconstruction — in improving alignment and removing artifacts.

Figure 16. Without our warping strategy. This leads to alignment errors and geometric distortions.

Figure 16. Without our warping strategy. This leads to alignment errors and geometric distortions.

Figure 17. With our locally-adaptive image warping.

Figure 17. With our locally-adaptive image warping.

Figure 18. Without the identification of a parallax-free zone, the stitching might be performed in an unstable region, leading to visual artifacts in the result.

Figure 18. Without the identification of a parallax-free zone, the stitching might be performed in an unstable region, leading to visual artifacts in the result.

Figure 19. When identifying a parallax-free zone, the stitching is performed in a more stable region with consistent keypoints, resulting to an improved alignment.

Figure 19. When identifying a parallax-free zone, the stitching is performed in a more stable region with consistent keypoints, resulting to an improved alignment.

Figure 20. Without blending.

Figure 20. Without blending.

Figure 21. with our blending (linear alpha transition + light Gaussian smoothing).

Figure 21. with our blending (linear alpha transition + light Gaussian smoothing).

3.4. Limitations

As demonstrated earlier, SENA effectively stitches images while preserving their natural appearance and geometric structure. However, certain limitations remain. The alignment between images is achieved through a multi-stage local deformation process: a global affine transformation estimated via RANSAC provides coarse alignment, which is then refined within the overlap region using locally adaptive affine models interpolated into a smooth Free-Form Deformation (FFD) field. This design allows accurate alignment while mitigating excessive distortion and maintaining shape and texture consistency. Nevertheless, in scenes with complex depth variations, the estimation of local models may become unstable, leading to locally inconsistent deformations or slight geometric discontinuities. Furthermore, the quality of the detected keypoints directly influences the identification of the adequate parallax-minimized zone and the subsequent stitching line extraction. When feature detection or matching is unreliable, artifacts such as minor ghosting, blurring, or local misalignment may still appear in the final panorama.

Figure 22. Some failure cases

Figure 22. Some failure cases

4. Conclusion

This work introduced SENA, a structure-preserving image stitching framework explicitly designed to address the geometric limitations of homography-based and over-flexible warping models. Rather than compensating for depth induced parallax through non-physical distortions, SENA adopts a hierarchical affine deformation strategy, combining global affine initialization, local affine refinement within the overlap region, and a smoothly regularized free-form deformation field. This multi-scale design preserves local shape, parallelism, and aspect ratios while providing sufficient flexibility to ensure accurate alignment. To further mitigate parallax-related artifacts, SENA incorporates a geometry-driven stitching mechanism that identifies a parallax minimized adequate zone directly from the consistency of RANSAC filtered correspondences, avoiding reliance on semantic segmentation or learning-based preprocessing. Based on this zone, an anchor-based segmentation strategy is applied, partitioning the overlapping images into corresponding vertical slices aligned by refined keypoints. This guarantees one-to-one geometric correspondence across segments and enforces structural continuity across the stitching boundary, effectively reducing ghosting, duplication, and texture stretching.

Extensive experiments demonstrate that SENA consistently achieves visually coherent panoramas with improved structural fidelity and reduced distortion compared to representative homography-based and spline-based methods. While the method remains robust across a wide range of scenes, performance may degrade under extreme viewpoint changes or in severely texture-deprived environments, where feature extraction becomes unreliable. Future work will explore adaptive local deformation models and hybrid learning-based components to further enhance robustness under such challenging conditions.