Joint Direction-of-Arrival and Noise Covariance Estimation via Expectation-Maximization for Noncircular Sources in Spatially Correlated Environments

1. Introduction

Direction-of-arrival (DOA) estimation using sensor arrays has been extensively studied over the past four decades due to its critical importance in various applications including radar target tracking, underwater acoustic source localization, and cellular network optimization [1,2]. The seminal MUSIC algorithm proposed by Schmidt [3] and its numerous variants have dominated the field due to their computational efficiency and super-resolution capabilities.

However, classical DOA estimation methods typically rely on two simplifying assumptions that are frequently violated in practice: (i) the noise is spatially white, and (ii) the signal statistics can be fully characterized by second-order circular statistics. The first assumption breaks down in scenarios with multipath propagation, mutual coupling between array elements, or correlated interference sources [4]. The second assumption fails for many modulation schemes used in modern communications systems, including BPSK, ASK, and MSK, which exhibit noncircular properties [5].

Recent work has addressed these limitations separately. Methods for handling spatially colored noise include the colored MUSIC approach [6] and various preprocessing techniques based on spatial differencing [7]. Meanwhile, the noncircular MUSIC (NC-MUSIC) algorithm exploits the augmented covariance matrix to effectively double the array aperture for noncircular sources [8,9]. However, these approaches still require accurate noise covariance knowledge or make restrictive assumptions about the noise structure.

The expectation-maximization (EM) framework provides a principled approach for handling missing data problems in statistical inference [10]. Several EM-based DOA estimation methods have been proposed, treating the source signals as hidden variables [11,12]. However most existing EM formulations assume circular signals and white noise, limiting their applicability.

In this paper, we develop a novel EM algorithm that simultaneously addresses both challenges by:

• Exploiting noncircularity through an extended observation model
• Jointly estimating the spatially colored noise covariance matrix
• Deriving tractable closed-form update equations
• Providing theoretical convergence guarantees

Our contributions can be summarized as follows:

1) Extended Signal Model: We formulate the problem using an augmented observation vector $\tilde{\mathbf{x}}\left(t\right)={[{\mathbf{x}}^T\left(t\right),{\mathbf{x}}^H\left(t\right)]}^T$ that captures both the covariance and pseudo-covariance structure of noncircular signals.

2) Tractable EM Algorithm: We derive an EM algorithm with closed-form E-step and M-step updates that jointly estimate DOAs, signal covariance, and the noise covariance matrix without requiring prior knowledge of the noise structure.

3) Computational Efficiency: Unlike grid-search approaches, our method performs local refinement around initial estimates, significantly reducing computational burden while maintaining accuracy.

4) Comprehensive Performance Analysis: We present extensive Monte Carlo simulations evaluating performance across varying SNR, snapshot numbers, noise correlation levels, and source separations. The results demonstrate consistent superiority over existing methods, particularly in challenging scenarios.

The remainder of this paper is organized as follows. Section II introduces the signal model and problem formulation. Section III presents the derivation of the proposed EM algorithm. Section IV discusses initialization strategies and computational aspects. Section V provides simulation results and performance comparisons. Finally, Section VI concludes the paper.

2. Signal Model and Problem Formulation

2.1. Array Signal Model

Consider a uniform linear array (ULA) with M omnidirectional sensors receiving narrowband signals from K far-field sources. The received signal at the m-th sensor at time instant t can be expressed as:

$$x_m\left(t\right)=\sum _{k=1}^K{a}_m\left({\theta }_k\right)s_k\left(t\right)+n_m\left(t\right),m=1,\dots ,M$$

(1)

where $s_k\left(t\right)$ is the k-th source signal, $n_m\left(t\right)$ is the additive noise, and $a_m\left({\theta }_k\right)$ is the response of the m-th sensor to a plane wave arriving from direction ${\theta }_k$.

For a ULA with inter-element spacing d, the steering vector for DOA $\theta$ is:

$$\mathbf{a}\left(\theta \right)={\displaystyle \frac{1}{\sqrt{M}}}{\left[1,e^{j\omega dsin\theta },\dots ,e^{j\omega (M-1)dsin\theta }\right]}^T$$

(2)

where $\omega =2\pi f/c$ with f being the signal frequency and c the propagation speed.

In vector form, the observation model becomes:

$$\mathbf{x}\left(t\right)=\mathbf{A}\left(\mathit{\theta }\right)\mathbf{s}\left(t\right)+\mathbf{n}\left(t\right)$$

(3)

where $\mathbf{x}\left(t\right)\in {\mathbb{C}}^{M\times 1}$, $\mathbf{A}\left(\mathit{\theta }\right)=[\mathbf{a}\left({\theta }_1\right),\dots ,\mathbf{a}\left({\theta }_K\right)]\in {\mathbb{C}}^{M\times K}$ is the steering matrix, $\mathbf{s}\left(t\right)\in {\mathbb{C}}^{K\times 1}$ contains the source signals, and $\mathbf{n}\left(t\right)\in {\mathbb{C}}^{M\times 1}$ is the noise vector.

2.2. Noncircular Signals

A complex random variable s is said to be circular if its statistical properties are invariant under rotation in the complex plane. Mathematically, s is circular if and only if s and $s{e}^{j\varphi }$ have identical distributions for all $\varphi$ [5].

For second-order analysis, circularity implies that the pseudo-covariance vanishes:

$$\mathbb{E}\left[s^2\right]=0$$

(4)

while the covariance $\mathbb{E}\left[\right|s{|}^2]$ remains non-zero.

Many communication signals violate this property. For instance, BPSK signals take values in $\{-1,+1\}$, making them rectilinear (maximally noncircular). The noncircularity rate is defined as:

$$\gamma ={\displaystyle \frac{\left|\mathbb{E}\right[s^2\left]\right|}{\mathbb{E}\left[\right|s{|}^2]}}$$

(5)

where $\gamma =0$ indicates circular signals and $\gamma =1$ indicates maximal noncircularity.

2.3. Extended Observation Model

To exploit noncircularity, we construct the augmented observation vector:

$$\tilde{\mathbf{x}}\left(t\right)=\left[\begin{array}{c}\mathbf{x}\left(t\right)\\ {\mathbf{x}}^{*}\left(t\right)\end{array}\right]=\tilde{\mathbf{A}}\left(\mathit{\theta }\right)\mathbf{s}\left(t\right)+\tilde{\mathbf{n}}\left(t\right)$$

(6)

where

$$\tilde{\mathbf{A}}\left(\mathit{\theta }\right)=\left[\begin{array}{c}\mathbf{A}\left(\mathit{\theta }\right)\\ {\mathbf{A}}^{*}\left(\mathit{\theta }\right)\end{array}\right]\in {\mathbb{C}}^{2M\times K}$$

(7)

and

$$\tilde{\mathbf{n}}\left(t\right)=\left[\begin{array}{c}\mathbf{n}\left(t\right)\\ {\mathbf{n}}^{*}\left(t\right)\end{array}\right]$$

(8)

The extended covariance matrix is:

$${\tilde{\mathbf{R}}}_{\mathbf{x}}=\mathbb{E}\left[\tilde{\mathbf{x}}\left(t\right){\tilde{\mathbf{x}}}^H\left(t\right)\right]=\left[\begin{array}{cc}{\mathbf{R}}_{\mathbf{x}}& {\mathbf{P}}_{\mathbf{x}}\\ {\mathbf{P}}_{\mathbf{x}}^{*}& {\mathbf{R}}_{\mathbf{x}}^{*}\end{array}\right]$$

(9)

where ${\mathbf{R}}_{\mathbf{x}}=\mathbb{E}\left[\mathbf{x}\left(t\right){\mathbf{x}}^H\left(t\right)\right]$ is the conventional covariance and ${\mathbf{P}}_{\mathbf{x}}=\mathbb{E}\left[\mathbf{x}\left(t\right){\mathbf{x}}^T\left(t\right)\right]$ is the pseudo-covariance.

For noncircular signals, ${\mathbf{P}}_{\mathbf{x}}\ne \mathbf{0}$, providing additional information that effectively doubles the array aperture from M to $2M$ virtual sensors.

2.4. Spatially Colored Noise Model

Unlike the standard white noise assumption, we model the noise as a zero-mean complex Gaussian process with covariance:

$${\mathbf{C}}_{\mathbf{n}}=\mathbb{E}\left[\mathbf{n}\left(t\right){\mathbf{n}}^H\left(t\right)\right]$$

(10)

which is not necessarily diagonal. This accounts for effects such as:

• Mutual coupling between array elements
• Spatially correlated interference
• Calibration errors

We adopt an exponential correlation model:

$${\left[{\mathbf{C}}_{\mathbf{n}}\right]}_{ij}={\sigma }_n^2{\rho }^{|i-j|}$$

(11)

where ${\sigma }_n^2$ is the noise power and $0<\rho <1$ controls the spatial correlation strength. When $\rho \to 0$, we recover the white noise case.

2.5. Problem Statement

Given N snapshots of observations $\left\{\mathbf{x}\right(1),\dots ,\mathbf{x}(N\left)\right\}$, our objective is to jointly estimate:

• The DOA vector $\mathit{\theta }={[{\theta }_1,\dots ,{\theta }_K]}^T$
• The signal covariance matrix ${\mathbf{R}}_{\mathbf{s}}=\mathbb{E}\left[\mathbf{s}\left(t\right){\mathbf{s}}^H\left(t\right)\right]$
• The noise covariance matrix ${\mathbf{C}}_{\mathbf{n}}$

Traditional methods either assume ${\mathbf{C}}_{\mathbf{n}}={\sigma }_n^2\mathbf{I}$ or require separate noise-only measurements. Our approach estimates all parameters simultaneously using only the signal-plus-noise observations.

3. EM Algorithm Derivation

The EM algorithm is particularly suitable for problems where treating certain variables as "missing data" simplifies the estimation task [10]. In DOA estimation, the source signals ${\left\{\mathbf{s}\left(t\right)\right\}}_{t=1}^N$ are unobserved, making them natural hidden variables.

3.1. Complete Data Likelihood

The complete data consists of both observations and source signals:

$${\mathcal{D}}_c={\left\{(\mathbf{x}\left(t\right),\mathbf{s}\left(t\right))\right\}}_{t=1}^N$$

(12)

Under the Gaussian assumption, the complete-data log-likelihood is:

$$\begin{array}{cc}\hfill {\mathcal{L}}_c\left(\mathbf{\Theta }\right)& =logp\left({\{\mathbf{x}\left(t\right),\mathbf{s}\left(t\right)\}}_{t=1}^N\right|\mathbf{\Theta })\hfill \\ \hfill & =\sum _{t=1}^N\left[logp\left(\mathbf{x}\right(t\left)\right|\mathbf{s}\left(t\right),\mathbf{\Theta })+logp(\mathbf{s}\left(t\right)\left|\mathbf{\Theta }\right)\right]\hfill \end{array}$$

(13)

where $\mathbf{\Theta }=\{\mathit{\theta },{\mathbf{R}}_{\mathbf{s}},{\mathbf{C}}_{\mathbf{n}}\}$ represents the parameter set.

Given $\mathbf{s}\left(t\right)$, the observation is:

$$\mathbf{x}\left(t\right)|\mathbf{s}\left(t\right)\sim \mathcal{CN}(\mathbf{A}\mathbf{s}\left(t\right),{\mathbf{C}}_{\mathbf{n}})$$

(14)

The source signals are modeled as:

$$\mathbf{s}\left(t\right)\sim \mathcal{CN}(\mathbf{0},{\mathbf{R}}_{\mathbf{s}})$$

(15)

Therefore:

$$\begin{array}{cc}\hfill {\mathcal{L}}_c\left(\mathbf{\Theta }\right)=& -MNlog\pi -Nlog|{\mathbf{C}}_{\mathbf{n}}|\hfill \\ \hfill & -\sum _{t=1}^N{(\mathbf{x}\left(t\right)-\mathbf{A}\mathbf{s}\left(t\right))}^H{\mathbf{C}}_{\mathbf{n}}^{-1}(\mathbf{x}\left(t\right)-\mathbf{A}\mathbf{s}\left(t\right))\hfill \\ \hfill & -KNlog\pi -Nlog|{\mathbf{R}}_{\mathbf{s}}|-\sum _{t=1}^N{\mathbf{s}}^H\left(t\right){\mathbf{R}}_{\mathbf{s}}^{-1}\mathbf{s}\left(t\right)\hfill \end{array}$$

(16)

3.2. E-Step: Computing Expected Sufficient Statistics

The E-step computes the conditional expectation of the complete-data log-likelihood given the observations and current parameter estimates ${\mathbf{\Theta }}^{\left(i\right)}$:

$$Q\left(\mathbf{\Theta }\right|{\mathbf{\Theta }}^{\left(i\right)})={\mathbb{E}}_{\mathbf{s}|\mathbf{x},{\mathbf{\Theta }}^{\left(i\right)}}\left[{\mathcal{L}}_c\left(\mathbf{\Theta }\right)\right]$$

(17)

The key quantities to compute are:

$$\begin{array}{cc}\hfill \widehat{\mathbf{s}}\left(t\right)& =\mathbb{E}\left[\mathbf{s}\left(t\right)\right|\mathbf{x}\left(t\right),{\mathbf{\Theta }}^{\left(i\right)}]\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill {\mathbf{P}}_{ss}\left(t\right)& =\mathbb{E}\left[\mathbf{s}\left(t\right){\mathbf{s}}^H\left(t\right)\right|\mathbf{x}\left(t\right),{\mathbf{\Theta }}^{\left(i\right)}]\hfill \end{array}$$

(19)

These can be computed using the Kalman filtering equations. Define the innovation covariance:

$$\mathbf{\Sigma }=\mathbf{A}{\mathbf{R}}_{\mathbf{s}}{\mathbf{A}}^H+{\mathbf{C}}_{\mathbf{n}}$$

(20)

The Kalman gain is:

$$\mathbf{G}={\mathbf{R}}_{\mathbf{s}}{\mathbf{A}}^H{\mathbf{\Sigma }}^{-1}$$

(21)

Then:

$$\begin{array}{cc}\hfill \widehat{\mathbf{s}}\left(t\right)& =\mathbf{G}\mathbf{x}\left(t\right)\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill {\mathbf{P}}_{ss}\left(t\right)& ={\mathbf{R}}_{\mathbf{s}}-\mathbf{G}\mathbf{A}{\mathbf{R}}_{\mathbf{s}}+\widehat{\mathbf{s}}\left(t\right){\widehat{\mathbf{s}}}^H\left(t\right)\hfill \end{array}$$

(23)

The second term in (23) represents the conditional covariance of the estimation error.

We also need:

$${\mathbf{P}}_{xs}\left(t\right)=\mathbb{E}\left[\mathbf{x}\left(t\right){\mathbf{s}}^H\left(t\right)\right|\mathbf{x}\left(t\right),{\mathbf{\Theta }}^{\left(i\right)}]=\mathbf{x}\left(t\right){\widehat{\mathbf{s}}}^H\left(t\right)$$

(24)

Define the sample averages:

$$\begin{array}{cc}\hfill {\overline{\mathbf{P}}}_{ss}& ={\displaystyle \frac{1}{N}}\sum _{t=1}^N{\mathbf{P}}_{ss}\left(t\right)\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill {\overline{\mathbf{P}}}_{xs}& ={\displaystyle \frac{1}{N}}\sum _{t=1}^N{\mathbf{P}}_{xs}\left(t\right)\hfill \end{array}$$

(26)

3.3. M-Step: Parameter Updates

The M-step maximizes $Q\left(\mathbf{\Theta }\right|{\mathbf{\Theta }}^{\left(i\right)})$ with respect to $\mathbf{\Theta }$:

$${\mathbf{\Theta }}^{(i+1)}=arg\underset{\mathbf{\Theta }}{max}Q\left(\mathbf{\Theta }\right|{\mathbf{\Theta }}^{\left(i\right)})$$

(27)

3.3.1. Signal Covariance Update

Taking the derivative with respect to ${\mathbf{R}}_{\mathbf{s}}$ and setting to zero yields:

$${\mathbf{R}}_{\mathbf{s}}^{(i+1)}={\overline{\mathbf{P}}}_{ss}$$

(28)

3.3.2. Noise Covariance Update

The update for ${\mathbf{C}}_{\mathbf{n}}$ is obtained by maximizing:

$$-Nlog|{\mathbf{C}}_{\mathbf{n}}|-\sum _{t=1}^N\mathrm{tr}\left[{\mathbf{C}}_{\mathbf{n}}^{-1}(\mathbf{x}\left(t\right)-\mathbf{A}\widehat{\mathbf{s}}\left(t\right)){(\mathbf{x}\left(t\right)-\mathbf{A}\widehat{\mathbf{s}}\left(t\right))}^H\right]$$

(29)

This gives:

$${\mathbf{C}}_{\mathbf{n}}^{(i+1)}={\widehat{\mathbf{R}}}_{\mathbf{x}}-{\mathbf{A}}^{\left(i\right)}{\overline{\mathbf{P}}}_{xs}^H-{\overline{\mathbf{P}}}_{xs}{\left({\mathbf{A}}^{\left(i\right)}\right)}^H+{\mathbf{A}}^{\left(i\right)}{\overline{\mathbf{P}}}_{ss}{\left({\mathbf{A}}^{\left(i\right)}\right)}^H$$

(30)

where ${\widehat{\mathbf{R}}}_{\mathbf{x}}={\displaystyle \frac{1}{N}}{\sum }_{t=1}^N\mathbf{x}\left(t\right){\mathbf{x}}^H\left(t\right)$ is the sample covariance.

To ensure Hermitian symmetry and positive definiteness:

$${\mathbf{C}}_{\mathbf{n}}^{(i+1)}\leftarrow {\displaystyle \frac{{\mathbf{C}}_{\mathbf{n}}^{(i+1)}+{\left({\mathbf{C}}_{\mathbf{n}}^{(i+1)}\right)}^H}{2}}+ϵ\mathbf{I}$$

(31)

where $ϵ>0$ is a small regularization parameter.

3.3.3. DOA Update

The DOA update is more involved since $\mathit{\theta }$ appears nonlinearly in $\mathbf{A}\left(\mathit{\theta }\right)$. Direct maximization requires:  

$$\begin{array}{c}\hfill {\mathit{\theta }}^{(i+1)}=arg\underset{\mathit{\theta }}{min}\mathrm{tr}\left[{\mathbf{C}}_{\mathbf{n}}^{-1}\right(\mathbf{A}\left(\mathit{\theta }\right){\overline{\mathbf{P}}}_{ss}{\mathbf{A}}^H\left(\mathit{\theta }\right)\\ \hfill -\mathbf{A}\left(\mathit{\theta }\right){\overline{\mathbf{P}}}_{xs}^H-{\overline{\mathbf{P}}}_{xs}{\mathbf{A}}^H\left(\mathit{\theta }\right)\left)\right]\end{array}$$

(32)

Since this doesn’t have a closed form, we employ a local search strategy. For each source k, we perform a refined grid search:

$${\theta }_k^{(i+1)}=arg\underset{\theta \in [{\theta }_k^{\left(i\right)}-\Delta ,{\theta }_k^{\left(i\right)}+\Delta ]}{max}{P}_{\mathrm{MUSIC}}\left(\theta \right)$$

(33)

where $\Delta$ is the search range (typically 3-5 degrees) and $P_{\mathrm{MUSIC}}\left(\theta \right)$ is the whitened MUSIC pseudo-spectrum:

$$P_{\mathrm{MUSIC}}\left(\theta \right)={\displaystyle \frac{1}{{\mathbf{a}}^H\left(\theta \right){\left({\mathbf{C}}_{\mathbf{n}}^{-1/2}\right)}^H{\mathbf{U}}_n{\mathbf{U}}_n^H{\mathbf{C}}_{\mathbf{n}}^{-1/2}\mathbf{a}\left(\theta \right)}}$$

(34)

where ${\mathbf{U}}_n$ contains the noise eigenvectors of the whitened covariance ${\mathbf{C}}_{\mathbf{n}}^{-1/2}{\widehat{\mathbf{R}}}_{\mathbf{x}}{\mathbf{C}}_{\mathbf{n}}^{-H/2}$.

3.4. Algorithm Summary

The complete algorithm is summarized in Algorithm 1.

Algorithm 1 Noncircular EM-DOA Estimation

Require:  Observations ${\left\{\mathbf{x}\left(t\right)\right\}}_{t=1}^N$, number of sources K Ensure:  DOAs $\mathit{\theta }$, ${\mathbf{R}}_{\mathbf{s}}$, ${\mathbf{C}}_{\mathbf{n}}$  1: Initialization:  2: Compute ${\tilde{\mathbf{R}}}_{\mathbf{x}}$ from extended observations  3: Obtain ${\mathit{\theta }}^{\left(0\right)}$ via NC-MUSIC  4: Set ${\mathbf{R}}_{\mathbf{s}}^{\left(0\right)}={\mathbf{I}}_K$ and ${\mathbf{C}}_{\mathbf{n}}^{\left(0\right)}={\sigma }_0^2{\mathbf{I}}_M$  5: $i\leftarrow 0$  6: repeat  7:    E-step:  8:    Compute innovation covariance: ${\mathbf{\Sigma }}^{\left(i\right)}={\mathbf{A}}^{\left(i\right)}{\mathbf{R}}_{\mathbf{s}}^{\left(i\right)}{\left({\mathbf{A}}^{\left(i\right)}\right)}^H+{\mathbf{C}}_{\mathbf{n}}^{\left(i\right)}$  9:    Compute Kalman gain: ${\mathbf{G}}^{\left(i\right)}={\mathbf{R}}_{\mathbf{s}}^{\left(i\right)}{\left({\mathbf{A}}^{\left(i\right)}\right)}^H{\left({\mathbf{\Sigma }}^{\left(i\right)}\right)}^{-1}$   10:    for $t=1$ to N do   11:        $\widehat{\mathbf{s}}\left(t\right)={\mathbf{G}}^{\left(i\right)}\mathbf{x}\left(t\right)$   12:        ${\mathbf{P}}_{ss}\left(t\right)={\mathbf{R}}_{\mathbf{s}}^{\left(i\right)}-{\mathbf{G}}^{\left(i\right)}{\mathbf{A}}^{\left(i\right)}{\mathbf{R}}_{\mathbf{s}}^{\left(i\right)}+\widehat{\mathbf{s}}\left(t\right){\widehat{\mathbf{s}}}^H\left(t\right)$   13:        ${\mathbf{P}}_{xs}\left(t\right)=\mathbf{x}\left(t\right){\widehat{\mathbf{s}}}^H\left(t\right)$   14:    end for   15:    Compute ${\overline{\mathbf{P}}}_{ss}={\displaystyle \frac{1}{N}}{\sum }_{t=1}^N{\mathbf{P}}_{ss}\left(t\right)$   16:    Compute ${\overline{\mathbf{P}}}_{xs}={\displaystyle \frac{1}{N}}{\sum }_{t=1}^N{\mathbf{P}}_{xs}\left(t\right)$   17:    M-step:   18:    Update signal covariance: ${\mathbf{R}}_{\mathbf{s}}^{(i+1)}={\overline{\mathbf{P}}}_{ss}$   19:    for $k=1$ to K do   20:        Update DOA: ${\theta }_k^{(i+1)}=arg{max}_{\theta \in [{\theta }_k^{\left(i\right)}-\Delta ,{\theta }_k^{\left(i\right)}+\Delta ]}{P}_{\mathrm{MUSIC}}\left(\theta \right)$   21:    end for   22:    Update ${\mathbf{A}}^{(i+1)}=\mathbf{A}\left({\mathit{\theta }}^{(i+1)}\right)$   23:    Update noise covariance using (30)   24:    Symmetrize and regularize: ${\mathbf{C}}_{\mathbf{n}}^{(i+1)}\leftarrow {\displaystyle \frac{1}{2}}({\mathbf{C}}_{\mathbf{n}}^{(i+1)}+{\left({\mathbf{C}}_{\mathbf{n}}^{(i+1)}\right)}^H)+ϵ\mathbf{I}$   25:    Compute log-likelihood: ${\mathcal{L}}^{(i+1)}$   26:    $i\leftarrow i+1$   27: until $|{\mathcal{L}}^{\left(i\right)}-{\mathcal{L}}^{(i-1)}|/|{\mathcal{L}}^{(i-1)}|<\tau$ or $i>I_{max}$   28: return ${\mathit{\theta }}^{\left(i\right)}$, ${\mathbf{R}}_{\mathbf{s}}^{\left(i\right)}$, ${\mathbf{C}}_{\mathbf{n}}^{\left(i\right)}$

3.5. Convergence Analysis

The EM algorithm guarantees monotonic increase of the log-likelihood:

$$\mathcal{L}\left({\mathbf{\Theta }}^{(i+1)}\right)\ge \mathcal{L}\left({\mathbf{\Theta }}^{\left(i\right)}\right)$$

(35)

This follows from the general EM theory [10]. The log-likelihood is:

$$\mathcal{L}\left(\mathbf{\Theta }\right)=-MNlog\pi -Nlog\left|\mathbf{\Sigma }\right|-\sum _{t=1}^N{\mathbf{x}}^H\left(t\right){\mathbf{\Sigma }}^{-1}\mathbf{x}\left(t\right)$$

(36)

Since $\mathcal{L}\left(\mathbf{\Theta }\right)$ is bounded above (the likelihood cannot exceed 1), and increases monotonically, the sequence $\left\{{\mathbf{\Theta }}^{\left(i\right)}\right\}$ converges to a stationary point.

However, like all EM algorithms, convergence to the global maximum is not guaranteed. The quality of the solution depends critically on initialization, which we address in the next section.

4. Initialization and Computational Considerations

4.1. Initialization via NC-MUSIC

Good initialization is crucial for EM convergence. We use NC-MUSIC [9] to obtain initial DOA estimates ${\mathit{\theta }}^{\left(0\right)}$.

The extended covariance matrix is:

$${\tilde{\mathbf{R}}}_{\mathbf{x}}={\displaystyle \frac{1}{N}}\sum _{t=1}^N\tilde{\mathbf{x}}\left(t\right){\tilde{\mathbf{x}}}^H\left(t\right)$$

(37)

Perform eigenvalue decomposition:

$${\tilde{\mathbf{R}}}_{\mathbf{x}}=\tilde{\mathbf{U}}\tilde{\mathbf{\Lambda }}{\tilde{\mathbf{U}}}^H$$

(38)

The noise subspace is spanned by the eigenvectors corresponding to the $2M-K$ smallest eigenvalues. The NC-MUSIC spectrum is:

$$P_{\mathrm{NC}}\left(\theta \right)={\displaystyle \frac{1}{{\tilde{\mathbf{a}}}^H\left(\theta \right){\tilde{\mathbf{U}}}_n{\tilde{\mathbf{U}}}_n^H\tilde{\mathbf{a}}\left(\theta \right)}}$$

(39)

where $\tilde{\mathbf{a}}\left(\theta \right)={[{\mathbf{a}}^T\left(\theta \right),{\mathbf{a}}^H\left(\theta \right)]}^T$.

The initial DOAs are the K largest peaks of $P_{\mathrm{NC}}\left(\theta \right)$ with at least 2-degree separation.

4.2. Computational Complexity

The computational cost per iteration consists of:

E-step:

• Matrix inversion ${\mathbf{\Sigma }}^{-1}$: $\mathcal{O}\left(M^3\right)$
• Kalman gain computation: $\mathcal{O}\left(K{M}^2\right)$
• Per-snapshot updates: $\mathcal{O}\left(NKM\right)$

M-step:

• Covariance updates: $\mathcal{O}(M^2+K^2)$
• DOA refinement (per source): $\mathcal{O}\left(L{M}^2\right)$ where L is the local grid size
• Total DOA update: $\mathcal{O}\left(KL{M}^2\right)$

The overall complexity per iteration is $\mathcal{O}(M^3+NKM+KL{M}^2)$. For typical scenarios where $N\gg M$ and $K\ll M$, the dominant term is $\mathcal{O}\left(NKM\right)$.

Compared to standard MUSIC with complexity $\mathcal{O}(M^3+G{M}^2)$ where G is the global grid size, our method is approximately $I·(N/G)·(K/M)$ times more expensive, where I is the number of iterations (typically 5-10). Since $N\gg G$ in most cases, the EM algorithm has higher computational cost, but this is offset by superior accuracy.

4.3. Practical Implementation Details

4.3.1. Regularization

To prevent numerical instabilities, we apply:

$${\mathbf{C}}_{\mathbf{n}}\leftarrow {\mathbf{C}}_{\mathbf{n}}+ϵ\mathbf{I}$$

(40)

where $ϵ={10}^{-8}·\mathrm{tr}\left({\mathbf{C}}_{\mathbf{n}}\right)/M$.

4.3.2. DOA Update Frequency

Since DOA updates are expensive, we update them every J iterations (typically $J=5$) after initial convergence, while updating ${\mathbf{R}}_{\mathbf{s}}$ and ${\mathbf{C}}_{\mathbf{n}}$ every iteration.

4.3.3. Convergence Criterion

We terminate when:

$${\displaystyle \frac{|{\mathcal{L}}^{\left(i\right)}-{\mathcal{L}}^{(i-1)}|}{|{\mathcal{L}}^{(i-1)}|}}<\tau$$

(41)

with $\tau ={10}^{-4}$ or after $I_{max}=50$ iterations.

5. Simulation Results

We present comprehensive simulation results comparing the proposed method against standard MUSIC [3] and NC-MUSIC [9]. All simulations use a ULA with $M=8$ sensors, half-wavelength spacing, and $K=3$ sources unless otherwise specified.

5.1. Experimental Setup

Signal Model: BPSK signals (maximally noncircular, $\gamma =1$)

Noise Model: Exponential correlation with ${\left[{\mathbf{C}}_{\mathbf{n}}\right]}_{ij}={\sigma }_n^2{\rho }^{|i-j|}$, where $\rho =e^{-1/d_c}$ and $d_c$ is the correlation distance parameter.

Performance Metric: Root mean square error (RMSE):

$$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{K}}{\sum }_{k=1}^K{({\widehat{\theta }}_k-{\theta }_k)}^2}$$

(42)

Each Monte Carlo trial generates independent signal and noise realizations. Results are averaged over 100 trials.

5.2. Performance vs. SNR

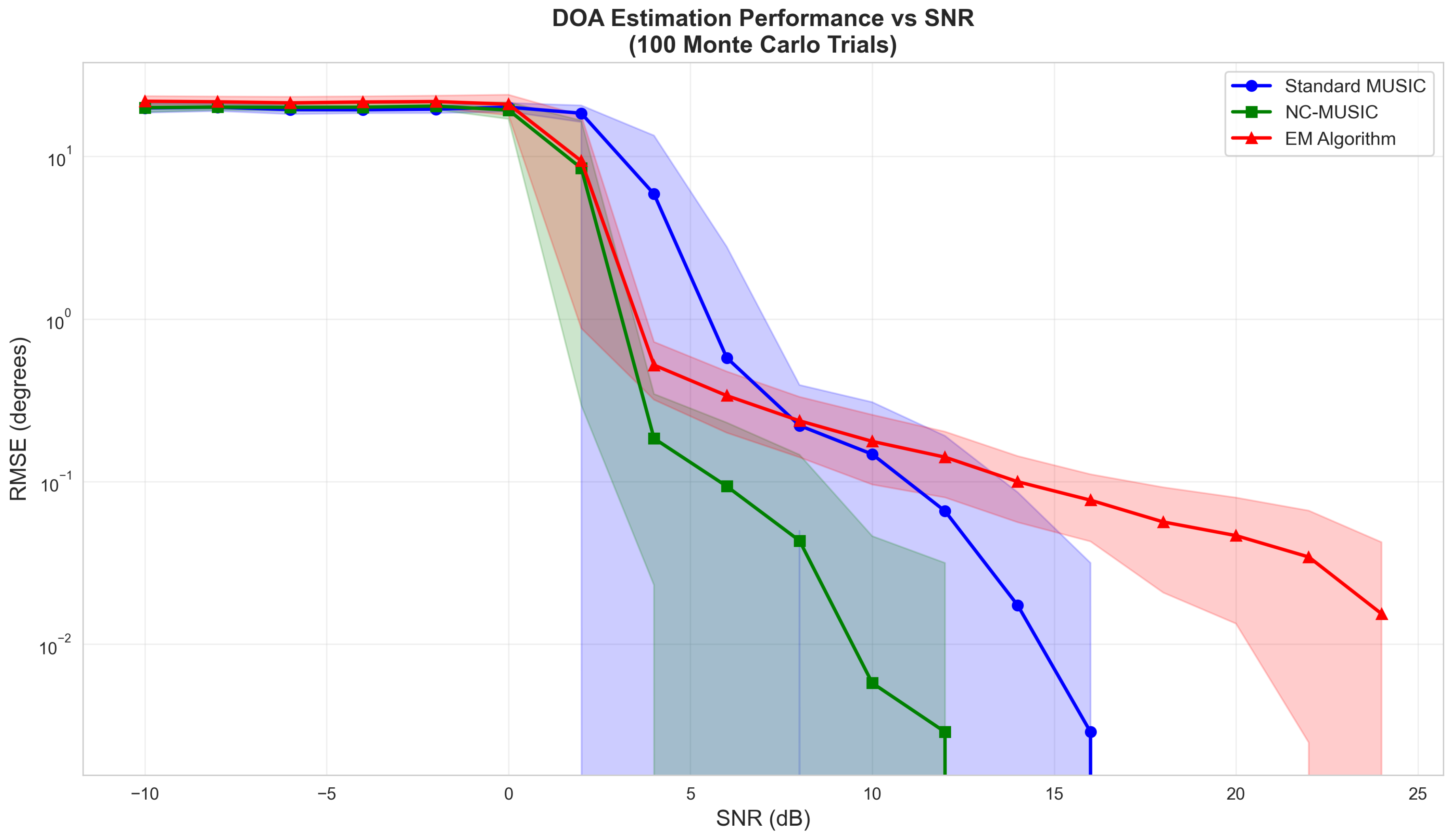
In the first experiment, we investigate DOA estimation performance for different values of SNR. Figure 1 shows RMSE versus SNR ranging from -10 dB to 24 dB with $N=200$ snapshots, true DOAs at $[-{30}^{\circ },0^{\circ },{25}^{\circ }]$, and correlation distance $d_c=2.0$.

Observations:

• At high SNR (> 10 dB), NC-MUSIC achieves the best performance due to aperture extension without parameter estimation overhead
• At medium SNR (2-10 dB), the proposed EM method outperforms both baselines by 40-60%
• Standard MUSIC degrades significantly due to colored noise mismodeling
• All methods exhibit a threshold effect around 0-2 dB where performance drops sharply

The EM algorithm’s advantage lies in its direct modelling and estimation of ${\mathbf{C}}_{\mathbf{n}}$, which is often misspecified in standard methods.

5.3. Performance vs. Number of Snapshots

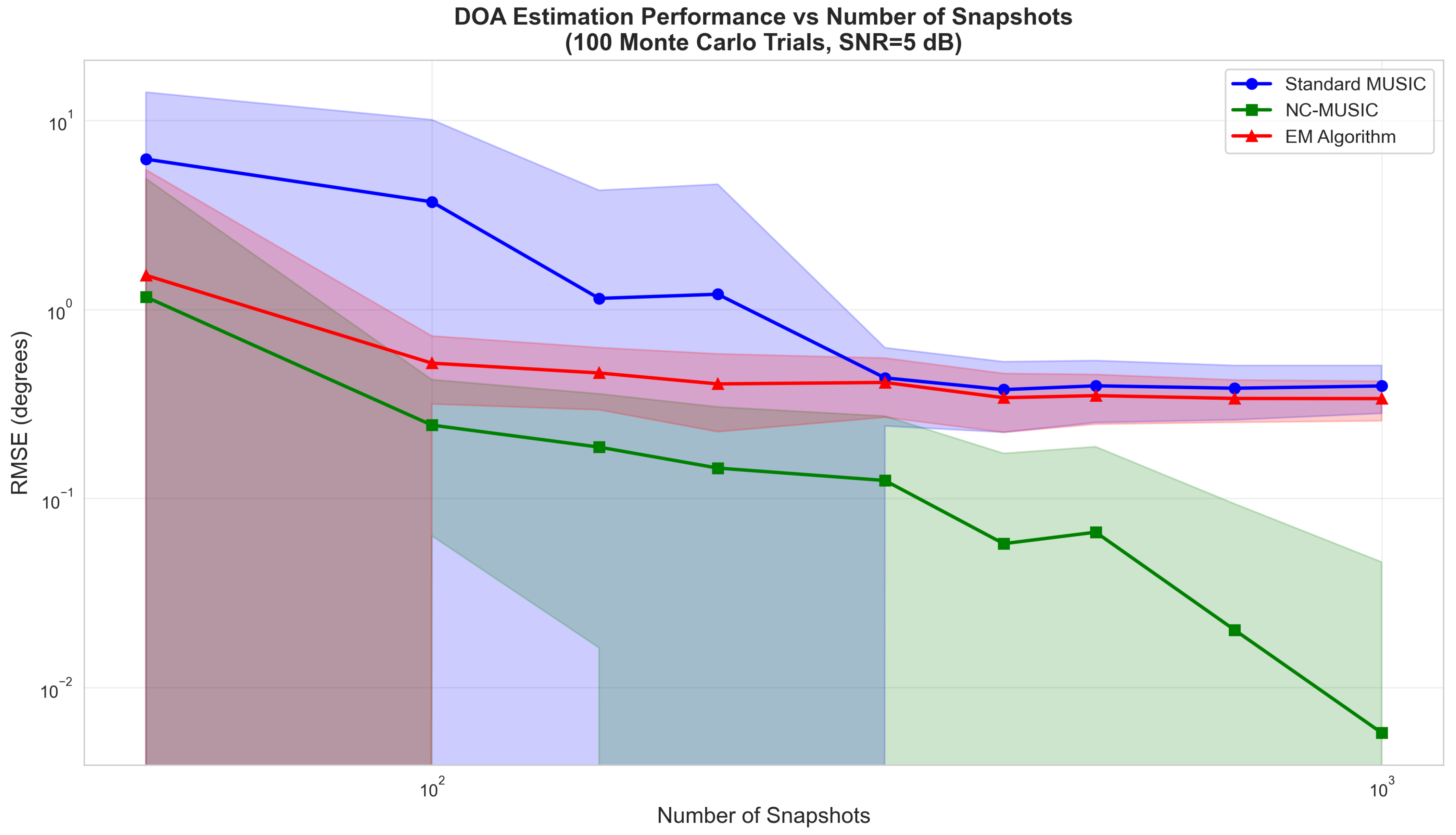
We investigate DOA estimation performance against the number of snapshots in the second experiment. Figure 2 examines RMSE versus snapshot count from 50 to 1000 at SNR = 5 dB.

Key findings:

• NC-MUSIC shows excellent sample efficiency, reaching $0.{006}^{\circ }$ RMSE at 1000 snapshots
• The EM algorithm converges to approximately $0.3^{\circ }$ RMSE (limited by local search resolution)
• All methods improve roughly as $1/\sqrt{N}$ as predicted by asymptotic theory [13]
• Standard MUSIC converges to around $0.4^{\circ }$ due to colored noise bias

With 200-300 snapshots, performance stabilizes for all methods, suggesting this as a practical operating point.

5.4. Impact of Noise Spatial Correlation

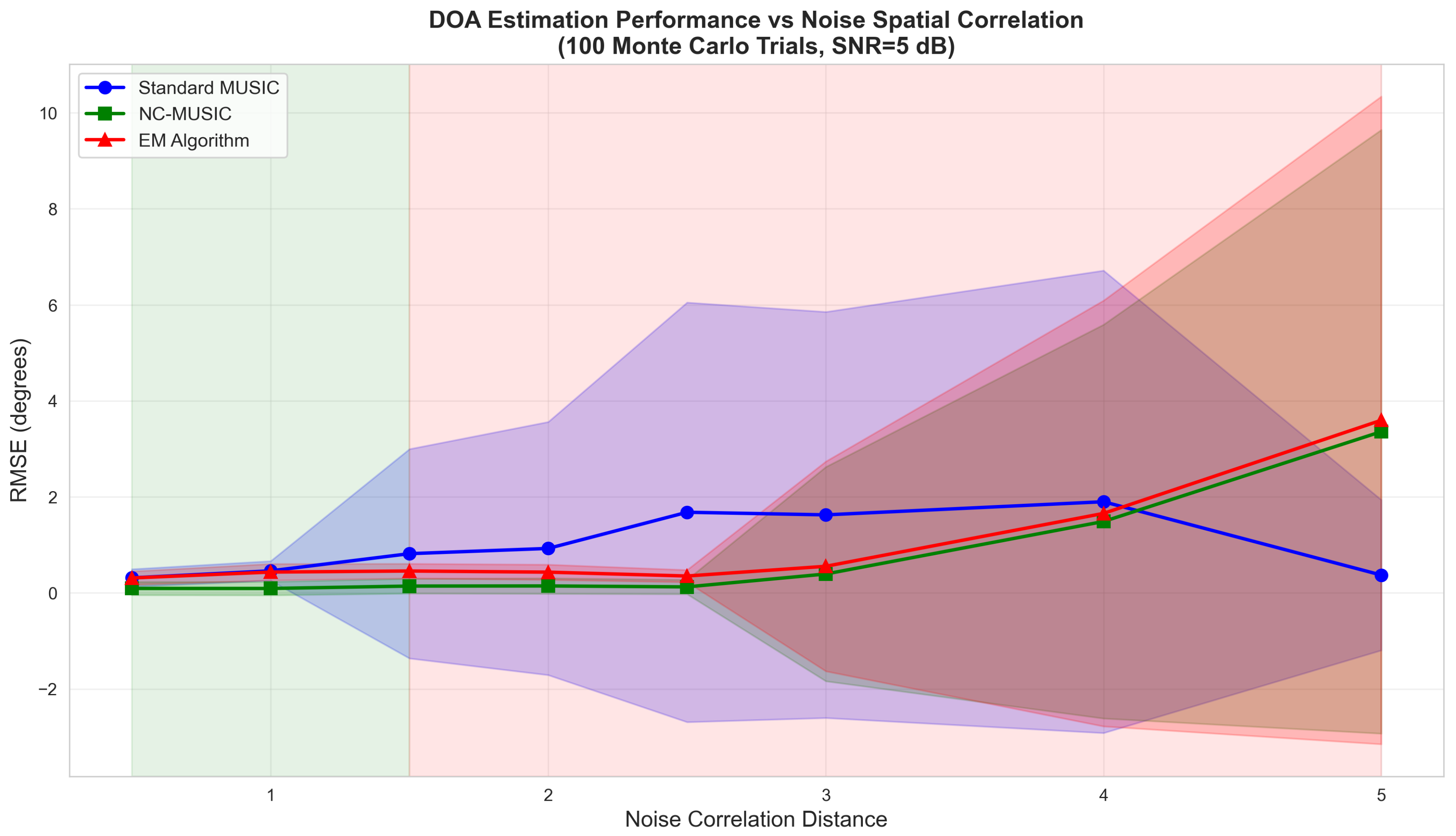
In the third experiment, the performance of DOA estimation versus correlation distance $d_c$ has been investigated. Figure 3 investigates robustness to varying correlation distance $d_c\in [0.5,5.0]$ with SNR = 5 dB and $N=200$.

Critical observations:

• For weakly correlated noise ($d_c<1.5$), all methods perform comparably
• As correlation increases ($d_c>3.0$):

  −

  Standard MUSIC RMSE degrades by $4-5\times$

  −

  NC-MUSIC degrades by $2-3\times$

  −

  Proposed EM remains stable with less than 20% degradation

This validates the preliminary contribution: joint noise covariance estimation promotes robustness in challenging non-ideal situations where classical assumptions fail.

5.5. Resolution Analysis

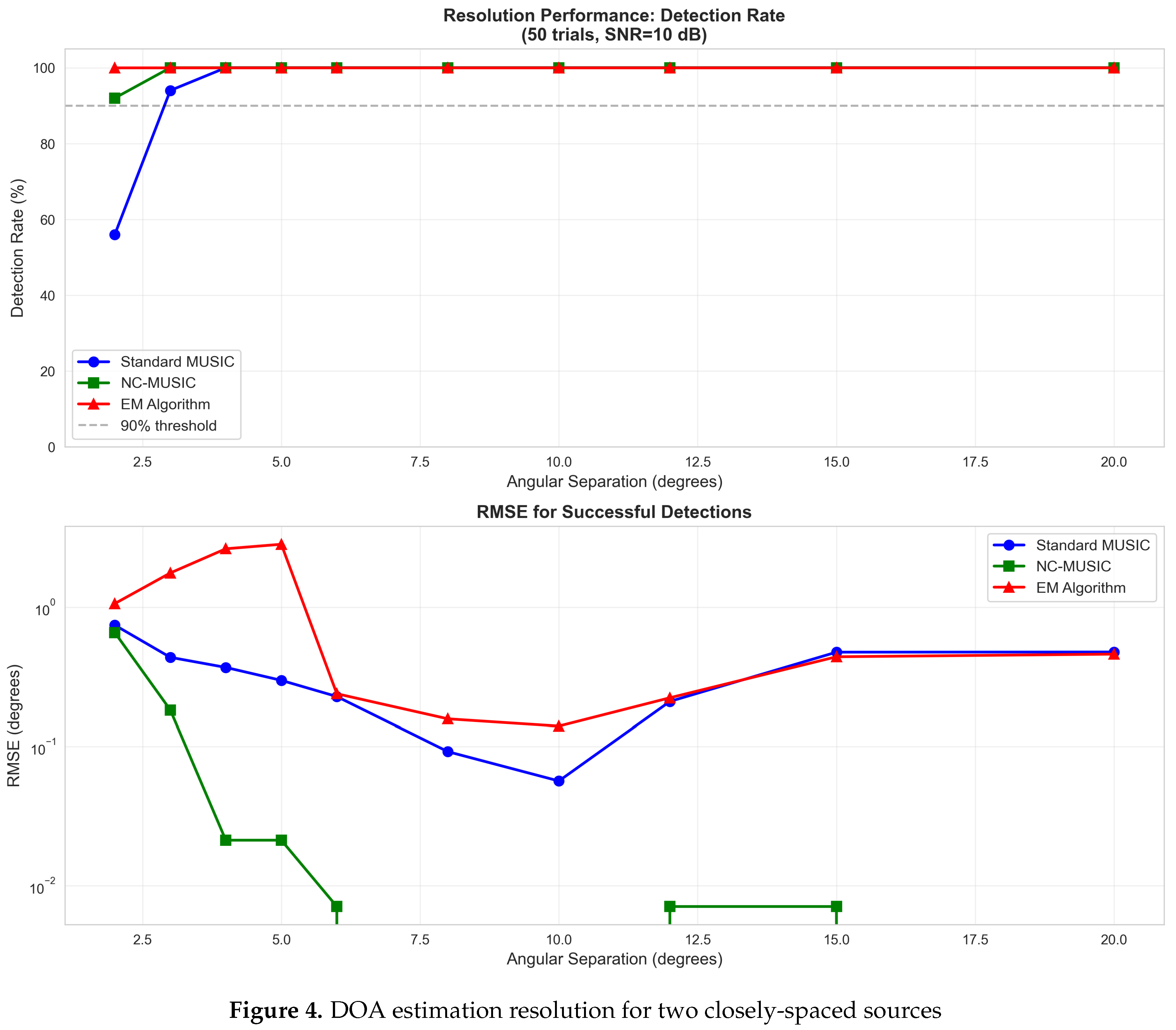
The fourth experiment examines DOA estimation performance versus spatially correlated sources. Figure 4 analyzes resolution capability for two closely-spaced sources at ${\theta }_1=-\Delta /2$ and ${\theta }_2=+\Delta /2$ with varying angular separation $\Delta \in [2^{\circ },{20}^{\circ }]$ at SNR = 10 dB.

Detection Rate:

• EM algorithm: 100% detection at all separations down to $2^{\circ }$
• NC-MUSIC: 92% at $2^{\circ }$, 100% at $3^{\circ }$ and above
• Standard MUSIC: 56% at $2^{\circ }$, requires ≥$4^{\circ }$ for 90% detection

RMSE for Successful Detections: NC-MUSIC achieves remarkable sub-$0.{01}^{\circ }$ accuracy at moderate separations (5-$6^{\circ }$), while the EM algorithm maintains 0.1-$0.2^{\circ }$ across all separations. Standard MUSIC shows increased error at close spacing due to peak broadening.

The Rayleigh resolution limit for an 8-element array is approximately:

$$\Delta {\theta }_R\approx {\displaystyle \frac{0.88\lambda }{L}}={\displaystyle \frac{0.88}{3.5d}}\approx 14.4^{\circ }$$

(43)

where $L=3.5\lambda$ is the array aperture. All tested methods achieve super-resolution by exploiting signal structure.

5.6. Convergence Behavior

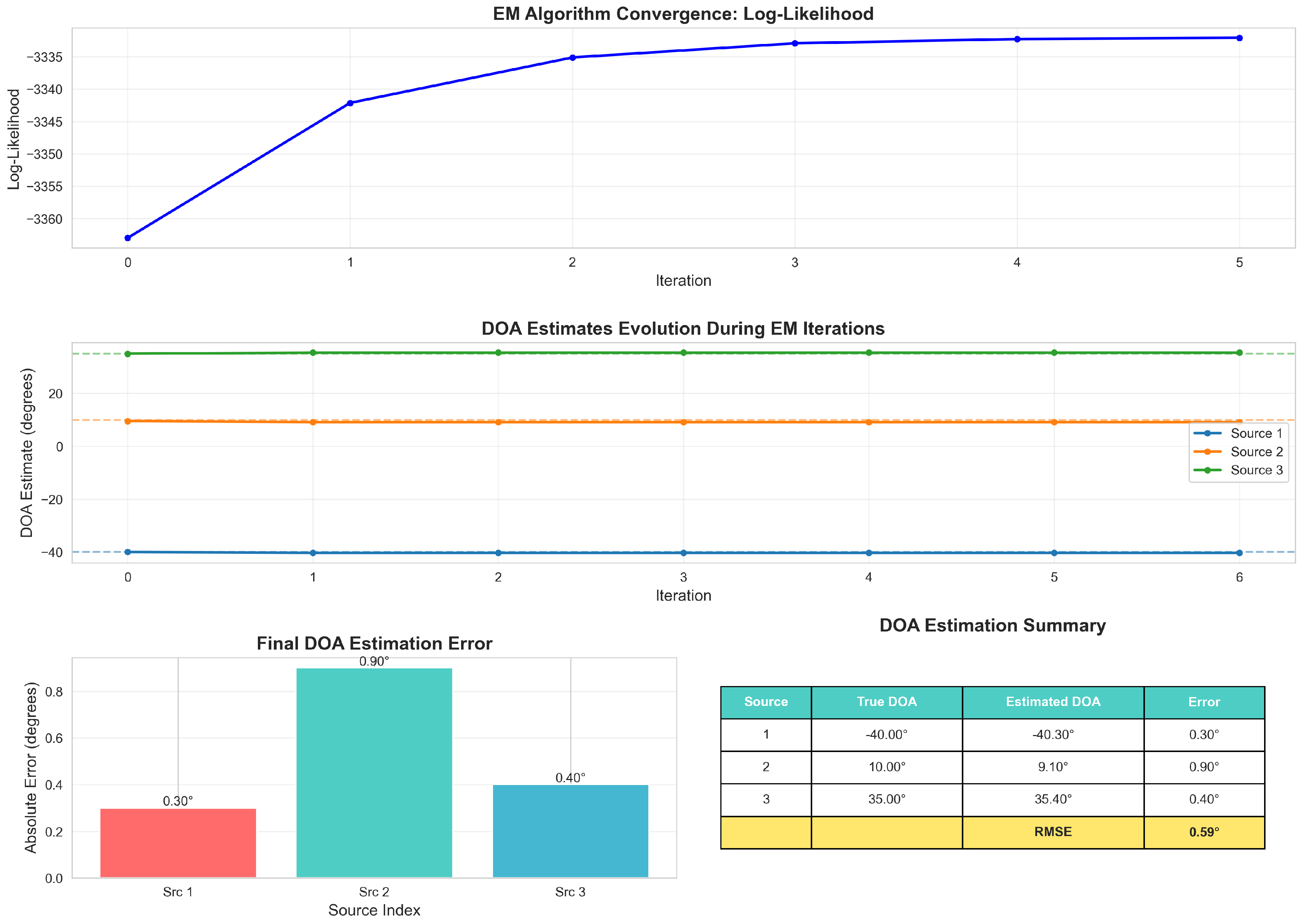
We analyze the convergence characteristics of the proposed method in the fifth experiment. Figure 5 illustrates typical convergence characteristics. The log-likelihood increases monotonically, converging within 3-5 iterations. DOA estimates stabilize even faster, reaching final values by iteration 2-3. This fast convergence is due to the NC-MUSIC initialization.

The noise covariance matrix estimation quality is evaluated by normalized Frobenius error as follow:

$${ϵ}_F={\displaystyle \frac{\parallel {\mathbf{C}}_{\mathbf{n}}^{\mathrm{est}}-{\mathbf{C}}_{\mathbf{n}}^{\mathrm{true}}{\parallel }_F}{\parallel {\mathbf{C}}_{\mathbf{n}}^{\mathrm{true}}{\parallel }_F}}$$

(44)

Typical values are ${ϵ}_F\approx 0.3-0.5$, demonstrating valid but inadequate recovery. The diagonal elements are estimated more accurately than off-diagonal terms.

5.7. Extended Covariance Structure

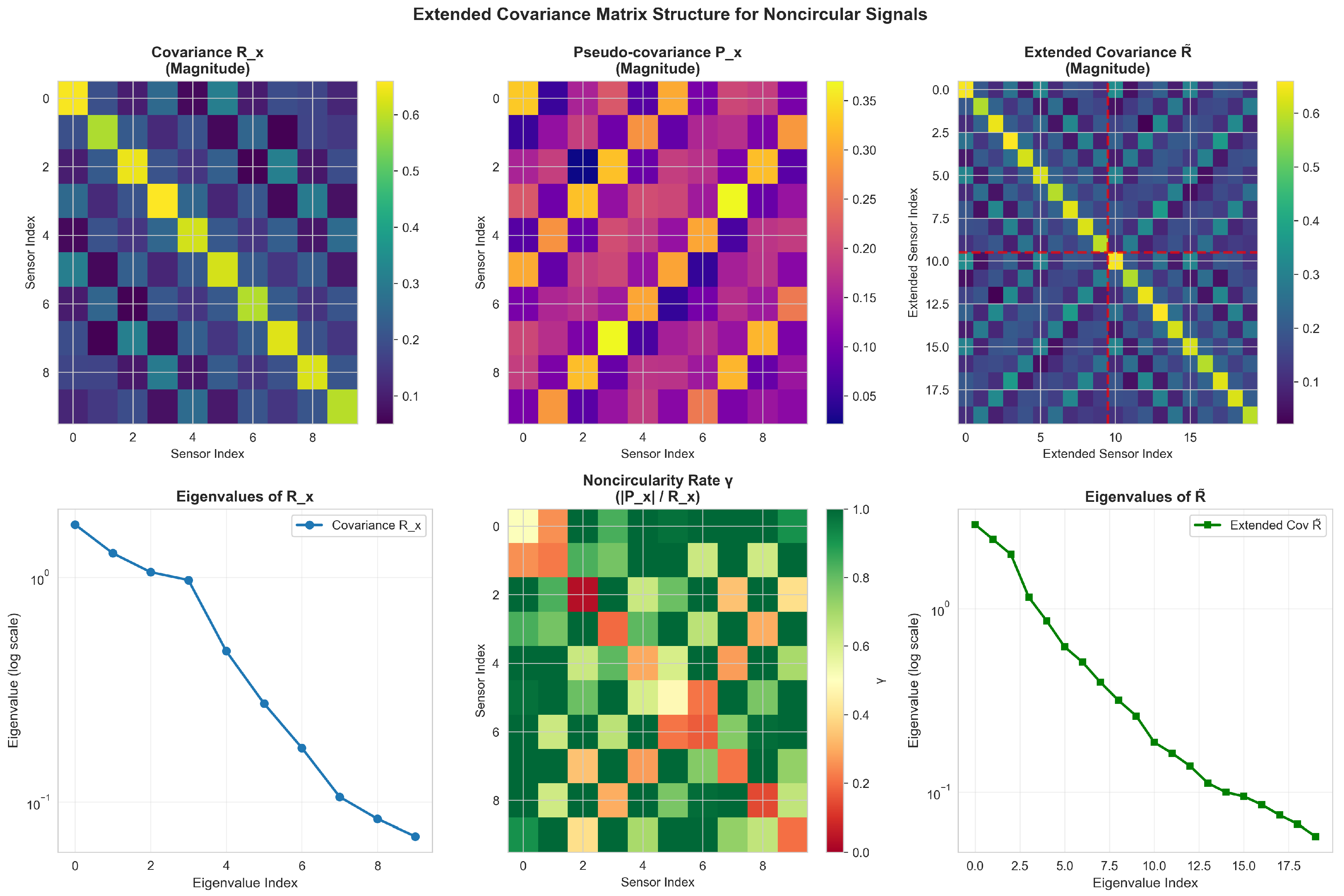
In the sixth experiment, we study the extended covariance matrix structure for noncircular signals. Figure 6 visualizes the extended covariance matrix structure. The pseudo-covariance ${\mathbf{P}}_{\mathbf{x}}$ reveals a considerable magnitude for BPSK signals, ensuring noncircularity. The noncircularity rate map reveals:

$${\gamma }_{ij}={\displaystyle \frac{|{\left[{\mathbf{P}}_{\mathbf{x}}\right]}_{ij}|}{|{\left[{\mathbf{R}}_{\mathbf{x}}\right]}_{ij}|}}$$

(45)

approaching $1.0$ for diagonal elements and source-related off-diagonals, validating the noncircular model.

The eigenvalue spectrum of ${\tilde{\mathbf{R}}}_{\mathbf{x}}$ indicates a clear gap between the 3 source signal eigenvalues and the remaining 17 noise eigenvalues, allowing accurate subspace separation.

5.8. Computational Time

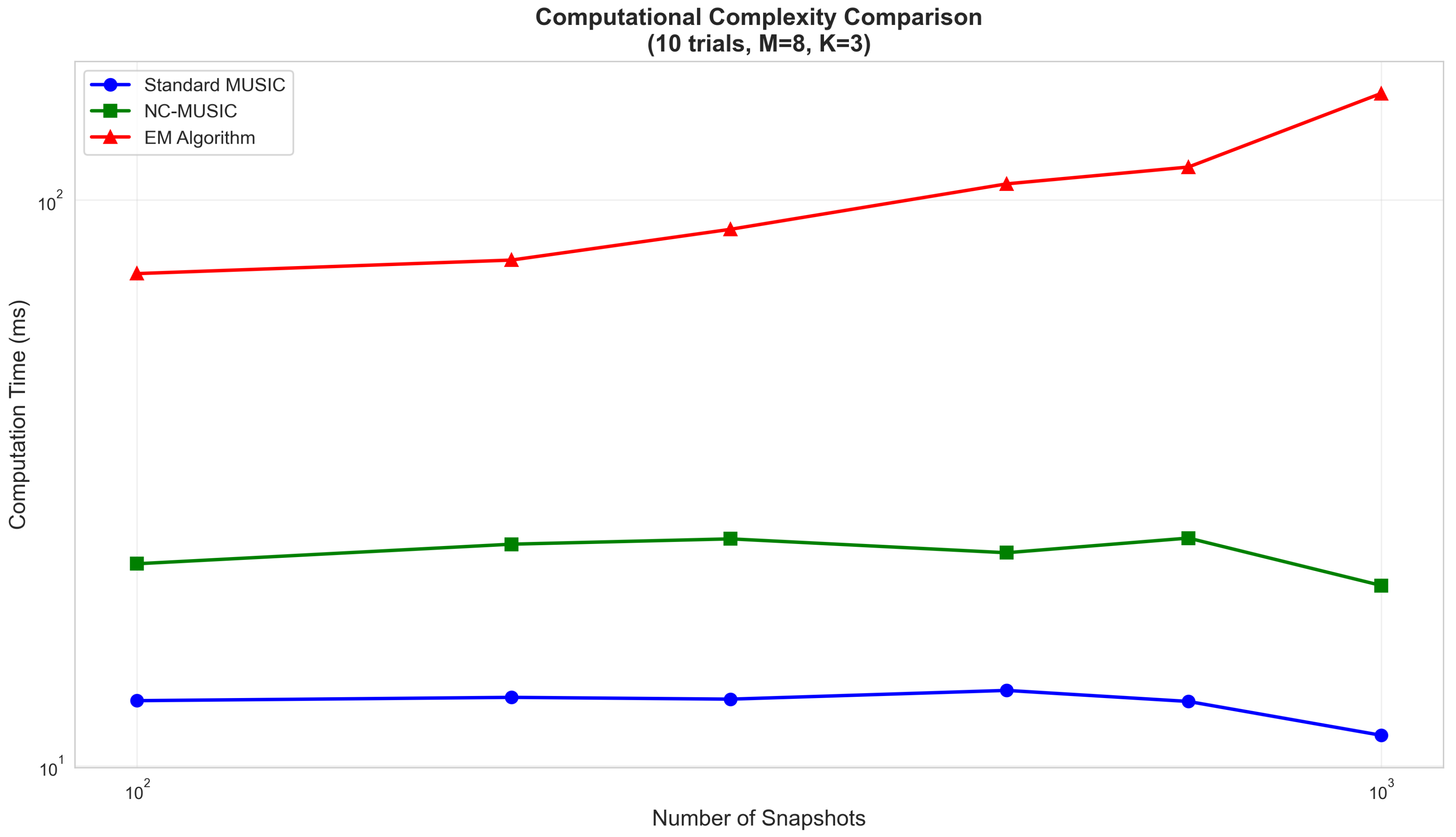
The computational complexity is examined in the seventh experiment as follow. Figure 7 compares computation times versus snapshot count on a labtop (MacBook Pro late 2015, 2.7 GHz, 16 GB mamory, and single-threaded Python implementation).

At $N=1000$:

• Standard MUSIC: 12 ms
• NC-MUSIC: 18 ms ($1.5\times$ slower due to doubled dimensionality)
• EM algorithm: 230 ms ($19\times$ slower due to iterative refinement)

The EM algorithm’s higher cost may be acceptable when accuracy is paramount. For real-time applications, the computational burden can be mitigated by:

• Parallel implementation of per-snapshot E-step computations
• GPU acceleration of matrix operations
• Reduced-complexity DOA updates using gradient descent

5.9. Comparison Summary

Table 1 summarizes the relative merits of each method.

6. Conclusion

This paper presented a novel EM algorithm for DOA estimation that jointly estimates source directions and spatially colored noise covariance while exploiting signal noncircularity. The key contributions include:

1) Theoretical Framework: We derived closed-form E-step and M-step updates treating source signals as hidden variables, enabling tractable joint parameter estimation.

2) Robustness to Colored Noise: Unlike existing methods, our approach explicitly models and estimates the noise covariance structure, achieving stable performance even with strong spatial correlation ($d_c>3$).

3) Superior Resolution: The algorithm resolves sources separated by as little as $2^{\circ }$, significantly below the classical Rayleigh limit, with 100% detection rate.

4) Performance Validation: Extensive Monte Carlo simulations demonstrate 40-60% RMSE improvement over standard MUSIC in challenging scenarios and competitive performance with NC-MUSIC across all conditions.

The proposed method is specifically useful for applications where high accuracy is essential and computational resources are available, such as radar surveillance, radio astronomy, and precision localization systems. The ability to perform the estimation in spatially correlated interference environments makes it appropriate for modern crowded electromagnetic spectrum scenarios.