Goldbach’s Conjecture as an Informational Coherence Phenomenon

1. Introduction

1.1. Historical Background and Motivation

Goldbach’s conjecture was first formulated in 1742 in correspondence between Christian Goldbach and Leonhard Euler, asserting that every even integer greater than two can be expressed as the sum of two prime numbers [1,2]. Despite its elementary formulation, the conjecture has resisted proof for nearly three centuries and has become emblematic of the depth and subtlety inherent in prime number theory.

Classical approaches to Goldbach’s conjecture have relied predominantly on analytic and combinatorial methods, most notably those stemming from the Hardy–Littlewood circle method and sieve theory [3,6,7]. Significant progress has been achieved in related directions, including Vinogradov’s theorem on representations of sufficiently large odd integers as sums of three primes and Chen’s theorem, which demonstrates that every sufficiently large even integer can be expressed as the sum of a prime and a semiprime [4,5,6]. Nevertheless, the original binary form of Goldbach’s conjecture remains unproven.

A notable feature of Goldbach’s conjecture is the persistent tension between the simplicity of its statement and the complexity of the structures underlying it. Large-scale numerical verification has confirmed its validity for extraordinarily large ranges of even integers [8,9,10]. However, this empirical success has not translated into a structural explanation of why such representations should systematically exist. Within traditional frameworks, the conjecture appears as an additive coincidence emerging from the distribution of primes, rather than as a consequence of an underlying organizing principle [11,12].

Over time, this has led to an implicit acceptance of Goldbach’s conjecture as a “likely true but structurally opaque” statement. The analytical focus has largely remained on bounding techniques, density estimates, and asymptotic arguments, leaving open the question of whether the conjecture reflects a deeper geometric or informational constraint intrinsic to the integers themselves.

In contrast, the present work departs from purely additive reasoning and explores Goldbach’s conjecture through an informational and geometric lens. By embedding prime numbers within an informational field governed by coherence dynamics, we aim to reinterpret prime pairing not as an accidental arithmetic property, but as the natural outcome of stability and balance conditions intrinsic to discrete informational systems.

1.2. Informational Reframing of Prime Numbers

1.2.1. Limitations of the Classical Numerical View

In classical number theory, prime numbers are defined as integers greater than one that admit no nontrivial divisors. While precise, this definition is inherently negative: primes are characterized by what they are not, rather than by an intrinsic constructive property [6,7]. As a result, primes are often treated as isolated numerical entities whose distribution must be studied statistically rather than structurally.

Within this framework, properties such as primality, pairing, or additive representation emerge as consequences of divisibility constraints, density estimates, or probabilistic arguments [11,12]. Although this approach has yielded deep insights into the global behavior of primes, it provides limited intuition as to why primes consistently participate in stable additive structures, such as those observed in Goldbach-type representations.

In particular, classical approaches do not naturally explain why two primes should repeatedly form balanced pairs summing to an even integer, nor why such pairings persist across all verified numerical ranges. These observations suggest that an additional organizing principle may be at work, beyond purely arithmetic constraints.

1.2.2. Primes as Stable Informational Attractors

Viscous Time Theory (VTT) introduces an alternative perspective in which integers are embedded within an informational field rather than treated as isolated arithmetic points. In this setting, numbers are characterized not only by their arithmetic properties but also by their informational stability under perturbation.

From this viewpoint, prime numbers may be interpreted as stable informational attractors: discrete states that minimize internal informational redundancy while resisting decomposition into simpler components. This interpretation does not replace the classical definition of primes, but rather extends it by assigning primes a constructive role within an informational topology.

Within such a field:

• composite numbers correspond to informational states with internal factorization pathways,
• prime numbers correspond to states lacking such pathways, resulting in maximal informational indivisibility.

This indivisibility manifests as stability within the informational landscape, allowing primes to act as anchor points around which coherent structures can form.

1.2.3. Informational Distance and Symmetry Around Even Integers

Consider an even integer $n$. In the classical additive formulation of Goldbach’s conjecture, one seeks primes $p$ and $q$ such that $p+q=n.$ Geometrically, this condition induces a symmetry around the midpoint $n/2$. Within the informational framework, this symmetry is reinterpreted as a balance condition: prime pairs equidistant from $n/2$ correspond to configurations in which informational imbalance is minimized.

Rather than viewing this symmetry as a numerical coincidence, we interpret it as the natural configuration of minimal informational tension between two stable attractors in the field. The midpoint $n/2$functions as a neutral reference state, and prime pairs emerge as coherence-preserving deviations around this point.

This perspective suggests that prime pairing is governed by informational symmetry rather than by arithmetic chance.

1.2.4. Prime Pairing as a Coherence Event

Within the informational field, pairing two primes to form an even integer is not a combinatorial search problem but a coherence event. Such events occur when two stable attractors jointly satisfy a balance condition that minimizes global decoherence.

In this sense, a Goldbach pair is not merely a solution to an equation, but a stable configuration in informational space. The persistence of Goldbach representations across large numerical ranges thus reflects the robustness of these coherence conditions.

This reframing allows Goldbach’s conjecture to be interpreted as an expression of structural stability: given a sufficiently dense field of prime attractors, coherence-preserving pairings are expected to exist for all admissible even states.

Interpreting prime pairing as a coherence event aligns with broader observations that stable structures in discrete systems often emerge from geometric or dynamical constraints rather than from purely combinatorial enumeration [13,14,15].

1.2.5. Toward Measurable Informational Parameters

The reinterpretation of primes as informational attractors necessitates quantitative descriptors of stability and balance. In subsequent sections, we introduce two such measurable parameters:

• ΔC, representing variations in informational coherence,
• ΔI, representing informational imbalance within a pairing configuration.

Unlike purely symbolic constructs, these quantities are defined operationally and can be evaluated within discrete informational models. They provide the analytical tools required to move beyond qualitative interpretation and toward measurable structure, enabling direct comparison with numerical validation results.

The informational perspective adopted here is consistent with foundational results in information theory and algorithmic complexity, where structure is understood to emerge from constraints on information flow, redundancy, and compressibility rather than from enumeration alone [16,17,18]

2. Materials and Methods

2.1. Informational Framework and Definitions

This work is developed within the framework of Viscous Time Theory (VTT), in which the set of integers $\mathbb{Z}$ is modeled as a discrete informational space endowed with a neighborhood structure induced by arithmetic adjacency. Each integer $n\in \mathbb{Z}$ is interpreted not merely as a numerical value, but as an informational state embedded within this space.

Local neighborhoods are defined in the natural discrete sense, for example through bounded integer differences. This locality assumption allows the definition of informational transitions and coherence variations without invoking any continuous limit. Interactions between integers are therefore characterized by informational relations rather than by divisibility alone.

The use of coherence – and geometry - inspired representations in discrete mathematical systems is consistent with a growing body of work exploring structural and informational interpretations of number-theoretic phenomena, where global regularity emerges from local constraints rather than explicit enumeration [19,20].

2.1.1. Coherence Functional on the Integers

We introduce a coherence functional

$$\mathsf{\Delta }C:\mathbb{Z}\to {\mathbb{R}}_{\ge 0},$$

(1)

interpreted as a measure of local informational coherence variation associated with an integer state.

Rather than prescribing a unique closed-form expression, $\mathsf{\Delta }C$ is defined axiomatically through the following minimal properties:

• Non-negativity 

  $$\mathsf{\Delta }C\left(n\right)\ge 0\forall n\in \mathbb{Z}.$$

  (2)
• Locality 
  $\mathsf{\Delta }C\left(n\right)$ depends only on information accessible within a finite neighborhood of $n$.
• Stability under perturbation 
  Small discrete perturbations of $n$induce bounded variations in $\mathsf{\Delta }C$.
• Factorization sensitivity 
  Integers admitting multiple nontrivial factorizations exhibit higher values of $\mathsf{\Delta }C$ than integers lacking such decompositions.

These properties are sufficient to distinguish integers with internal structural redundancy from those that are informationally indivisible.

The specific operational forms of ΔC and ΔI adopted here are not claimed to be unique; rather, they represent minimal, scale-invariant realizations sufficient to capture coherence and balance properties relevant to Goldbach pairing.

Operational realizations of $\mathsf{\Delta }C$ for prime pair configurations are introduced in Section 2.1.2 and Section 2.3.

2.1.2. Coherence Variation and Informational Imbalance

Consider two prime numbers $p$and $q$such that

$$p+q=N,$$

(3)

where $N$ is an even integer.

Definition 1 (Coherence Variation) 

The coherence variation $\mathsf{\Delta }C(p,q;N)$ quantifies the informational separation between two primes relative to the even integer they compose. In the operational form used throughout this work and in numerical validation, it is defined as

$$\mathsf{\Delta }C(N)={\displaystyle \frac{\mid p-q\mid }{N}}$$

(4)

This quantity is dimensionless and scale-invariant. Smaller values of $\mathsf{\Delta }C$ correspond to higher informational coherence between the paired primes.

Definition 2 (Informational Imbalance) 

The informational imbalance $\mathsf{\Delta }I(p,q)$ measures the asymmetry of a prime pair with respect to the midpoint $N/2$. It captures deviations from perfect informational balance and is defined as a symmetric function of the distances of $p$and $q$from $N/2$:

$$\mathsf{\Delta }I(p,q)=\mid \left(p−{\displaystyle \frac{N}{2}}\right)-\left({\displaystyle \frac{N}{2}}−q\right)\mid$$

(5)

Configurations minimizing $\mathsf{\Delta }I$correspond to pairings that are maximally balanced around the midpoint.

2.1.3. Joint Optimization Functional

To characterize the stability of prime pairings within the informational field, we introduce a joint cost functional that combines coherence variation and informational imbalance.

Definition 3 (Joint Informational Cost Functional) 

The informational cost associated with a prime pair $\left(p,q\right)$ is defined as

$$\mathcal{F}(p,q)=\alpha \mathsf{\Delta }C(p,q)+\beta \mathsf{\Delta }I(p,q)$$

(6)

where $\alpha >0$ and $\beta >0$ are weighting parameters.

This functional defines an informational landscape over admissible prime pairs. Configurations minimizing $\mathcal{F}$correspond to states of maximal informational stability.

Importantly, no algorithmic optimization procedure is assumed. The functional is used as a structural descriptor of admissible configurations, not as a computational search objective.

2.1.4. Primes as Stable Informational States

Within the informational field defined above, primes occupy a distinguished role.

Lemma 1 (Primes as Local Minima) 

Prime numbers correspond to locally stable informational states in the coherence landscape. They minimize internal informational redundancy while resisting decomposition into simpler components.

Composite numbers, by contrast, admit internal factorization pathways and therefore occupy informational states that are less stable under perturbation.

This lemma provides a structural interpretation of primality within the informational framework and does not replace or modify the classical arithmetic definition of prime numbers.

2.1.5. Existence of Local Minima Under Mild Regularity Assumptions

The joint informational cost functional admits stable configurations under weak assumptions.

Proposition 1 (Existence of Local Minima) 

Assume that the informational landscape defined by $\mathcal{F}(p,q)$ is locally regular over admissible prime pairs and that coherence variation and imbalance vary smoothly under discrete perturbations. Then, for sufficiently large even integers $N$, there exist prime pair configurations $\left(p,q\right)$ that realize local minima of $\mathcal{F}$.

This proposition establishes the structural existence of stable informational configurations without asserting uniqueness, global optimality, or classical proof of Goldbach’s conjecture.

2.1.6. Paths as Discrete Minimal-Cost Trajectories

The informational framework further allows the introduction of discrete informational paths connecting admissible configurations.

Definition 4 (Discrete Minimal-Cost Paths) 

Let $\mathsf{\Gamma }$denote a sequence of admissible prime pair configurations

$$\mathsf{\Gamma }=\left\{\right(p_1,q_1),(p_2,q_2),\dots \}$$

(7)

Such that successive elements differ by minimal discrete perturbations and locally minimize variations in $\mathcal{F}$.

Such paths may be interpreted as discrete minimal-cost trajectories in the informational landscape. They provide a geometric interpretation of how stable pairings persist and evolve across increasing numerical scales.

These paths are descriptive constructs used to characterize structural continuity and are not associated with any dynamical or algorithmic process.

This section establishes the formal informational framework used throughout the remainder of the manuscript. It introduces all definitions, functionals, and structural propositions required to interpret Goldbach pairings as coherence-driven configurations. Subsequent sections apply this framework to analyze pairing behavior, collapse conditions, and numerical validation results.

2.2. Goldbach Pairing as Informational Collapse

2.2.1. From Qualitative Interpretation to Quantitative Structure

The informational reframing introduced in Section 2.1 requires quantitative descriptors capable of capturing stability, balance, and tension within the informational field. Without such descriptors, the interpretation of prime pairing would remain purely qualitative.

Within the Viscous Time Theory framework, this role is fulfilled by the complementary parameters $\mathsf{\Delta }C$ and $\mathsf{\Delta }I$. These quantities do not replace classical arithmetic constraints, but instead provide a structural ordering principle that operates alongside them. In particular, they allow Goldbach pairing to be analyzed in terms of coherence preservation and balance optimization rather than combinatorial enumeration.

Crucially, both parameters are defined so as to be measurable in discrete informational systems, enabling a direct bridge between theoretical structure and numerical validation.

2.2.2. Informational Coherence and the Role of $\mathsf{\Delta }C$

Informational coherence refers to the degree to which a configuration preserves internal structural consistency under local perturbations. In discrete systems, coherence may be understood as resistance to fragmentation, ambiguity, or redundant decomposition.

The coherence variation functional $\mathsf{\Delta }C$, introduced in Section 2.1, acts as an ordering measure rather than a scalar invariant:

• low values of $\mathsf{\Delta }C$ correspond to configurations of high coherence,
• higher values correspond to configurations exhibiting increased informational strain.

In the context of number theory, prime numbers naturally occupy locally minimal values of $\mathsf{\Delta }C$, reflecting their informational indivisibility and resistance to internal decomposition. Composite numbers, by contrast, tend to exhibit larger coherence variation due to the presence of internal factorization pathways.

This distinction provides an informational criterion that separates primes from composites without redefining primality, grounding the informational interpretation firmly within classical arithmetic structure.

2.2.3. Informational Imbalance and the Role of $\mathsf{\Delta }I$

While $\mathsf{\Delta }C$ captures local stability, it does not by itself describe asymmetry or tension between multiple informational states. To characterize this aspect, the informational imbalance parameter $\mathsf{\Delta }I$ is introduced.

For an even integer $N$, the natural balance reference is the midpoint $N/2$. Given a candidate prime pair $\left(p,q\right)$ satisfying $p+q=N$, the imbalance $\mathsf{\Delta }I(p,q)$ measures the deviation of the pair from symmetric placement around this midpoint.

Configurations with minimal $\mathsf{\Delta }I$ correspond to balanced or near-balanced pairings, while large values of $\mathsf{\Delta }I$ indicate asymmetric configurations associated with higher informational tension. In this sense, $\mathsf{\Delta }I$ acts as a directional parameter, distinguishing stable from strained pairing configurations within the informational field.

2.2.4. Joint Minimization of $\mathsf{\Delta }C$ and $\mathsf{\Delta }I$

Prime pairing emerges not from the minimization of either parameter alone, but from their joint minimization.

A valid Goldbach configuration is characterized by:

• low coherence variation $\mathsf{\Delta }C$ at each prime node, ensuring local stability,
• sufficiently low imbalance $\mathsf{\Delta }I$ across the pair, ensuring global balance.

From this perspective, Goldbach’s conjecture does not require the exhaustive enumeration of all prime pairs. Instead, it reflects the existence of at least one configuration in which coherence and balance conditions are simultaneously satisfied.

As the even integer $N$ increases, the density of prime attractors in the informational field increases as well. This enlarges the space of admissible low-$\mathsf{\Delta }C$, low-$\mathsf{\Delta }I$ configurations and naturally explains the empirical persistence of Goldbach representations across large numerical ranges.

2.2.5. Goldbach Pairing as Informational Collapse

Classically, Goldbach’s conjecture is expressed as a static additive condition,

$$N=p+q$$

(8)

with $N$ even and $p,q$ prime. This formulation implicitly treats pairing as a solution-set problem.

Within the VTT framework, this static viewpoint is replaced by a collapse interpretation. Rather than asking whether a representation exists, we ask how informational states resolve into stable configurations.

In this setting:

• the even integer $N$ represents a metastable informational state,
• prime numbers act as stable informational attractors,
• pairing corresponds to an informational collapse event along a pathway minimizing the joint cost functional

$$\mathcal{F}=\alpha \mathsf{\Delta }C+\beta \mathsf{\Delta }I$$

(9)

The existence of at least one such collapse pathway is sufficient to ensure a Goldbach representation.

2.2.6. Informational Geodesics and Minimal-Decoherence Pathways

To formalize collapse behavior, we model the informational field as a structured discrete space in which integer states are connected by transitions governed by coherence constraints.

Within this space, geodesics are defined as discrete informational paths that minimize cumulative decoherence while respecting balance constraints. These paths are not geometric curves in the classical sense, but informational trajectories optimizing stability.

For a given even integer $N$, admissible prime pairs lie on geodesics connecting two stable prime attractors while passing through a balance region centered around $N/2$. Pairing thus corresponds to collapse along a minimal-decoherence geodesic.

2.2.7. Symmetry, Midpoint Stability, and Geodesic Selection

The midpoint $N/2$ plays a central role in geodesic selection. Informationally, it acts as a neutral basin: deviations on either side generate opposing imbalance contributions quantified by $\mathsf{\Delta }I$.

Geodesics that remain close to this midpoint minimize imbalance and are therefore favored. This explains the frequent appearance of approximately symmetric Goldbach pairs, while also allowing asymmetric pairings when coherence conditions permit.

Importantly, symmetry is not imposed externally; it emerges naturally as a consequence of balance optimization within the informational field.

2.2.8. Structural Inevitability of Goldbach Pairings

From the geodesic collapse perspective, Goldbach’s conjecture becomes an expression of structural inevitability. Given a sufficiently dense set of stable attractors and coherence-preserving dynamics, admissible collapse pathways must exist.

Failure of Goldbach pairing would require a global absence of such pathways, implying a breakdown of informational coherence across the entire field. No such breakdown is observed, either theoretically within the VTT framework or empirically through numerical validation.

2.2.9. Relation to Classical Analytic Results

Classical analytic results, including asymptotic estimates for the number of Goldbach representations, can be reinterpreted within this framework as statistical reflections of geodesic density. Regions of higher prime density correspond to richer families of low-decoherence pathways.

This reinterpretation does not contradict analytic number theory; rather, it provides a complementary explanation for why such results arise naturally from underlying structural constraints.

2.2.10. Summary

Within the VTT framework, Goldbach pairing is understood as:

• an informational collapse event,
• occurring along minimal-decoherence geodesics,
• driven by the joint minimization of coherence variation $\mathsf{\Delta }C$and informational imbalance $\mathsf{\Delta }I$.

This interpretation replaces combinatorial coincidence with structural necessity and prepares the ground for computational validation, which is addressed in the following section.

2.3. Computational Methods and Informational Coherence Validation Framework

Having defined the discrete informational space and the coherence functional ΔC, we now introduce the informational coherence field associated with Goldbach decompositions and outline the empirical framework used for its validation.

For a fixed even integer $N>2$, consider the set of all prime pairs

$$\mathcal{G}\left(N\right)=\left\{\right(p_i,q_i)\in {\mathbb{P}}^2\mid p_i+q_i=N\}$$

(10)

where $\mathbb{P}$ denotes the set of prime numbers.

Each admissible pair represents a local informational interaction within the discrete space defined in Section 2.1.

For every decomposition $\left(p_i,q_i)\in \mathcal{G}(N\right)$, we associate a coherence gradient

$$\mathsf{\Delta }{C}_i(N)={\displaystyle \frac{\mid p_i-q_i\mid }{N}}$$

(11)

which quantifies the relative asymmetry of the decomposition with respect to the equilibrium point $N/2$.

Smaller values of $\mathsf{\Delta }{C}_i$ correspond to more balanced prime pairs and therefore higher informational coherence, while larger values indicate asymmetric, lower-coherence configurations.

2.3.1. Minimal Coherence Selection

Among all admissible decompositions of $N$, we define the minimal coherence gradient

$$\mathsf{\Delta }{C}_{\mathrm{m}\mathrm{i}\mathrm{n}}(N)=\underset{i}{\mathrm{m}\mathrm{i}\mathrm{n}}\mathsf{\Delta }{C}_i(N)$$

(12)

which selects the most symmetric prime pair for each even integer.

This choice is not arbitrary: it identifies the maximally stable informational configuration associated with $N$.

By construction, this yields a single scalar coherence value for every even integer, allowing the discrete Goldbach domain to be treated as a one-dimensional coherence field

$$N⟼\mathsf{\Delta }{C}_{\mathrm{m}\mathrm{i}\mathrm{n}}\left(N\right)$$

(13)

This mapping transforms the classical Goldbach problem from a purely combinatorial question into the study of the regularity, continuity, and stability of an informational field over the integers.

2.3.2. Informational Density and Scaling Expectation

Following the coherence interpretation, we define the associated informational density

$$\rho (N)={\displaystyle \frac{1}{\mathsf{\Delta }{C}_{\mathrm{m}\mathrm{i}\mathrm{n}}\left(N\right)}}$$

(14)

which measures the concentration of coherence around the equilibrium configuration.

Under this formulation, high informational density corresponds to strongly balanced prime decompositions, while low density reflects weaker coherence.

Analytic number theory provides a natural expectation for the asymptotic behavior of this quantity.The Hardy–Littlewood conjecture predicts that the number of Goldbach representations grows asymptotically as

$$G(N)\sim {\displaystyle \frac{2C_{2}N}{{(\log N)}^2}}$$

(15)

where $C_2$ is the twin-prime constant.

Interpreted in the coherence framework, this implies the scaling law

$$\rho (N)\propto {\displaystyle \frac{N}{{(\log N)}^2}}⟺\mathsf{\Delta }{C}_{\mathrm{m}\mathrm{i}\mathrm{n}}(N)\propto {\displaystyle \frac{{(\log N)}^2}{N}}$$

(16)

Thus, global validity of Goldbach’s conjecture requires the coherence field $\mathsf{\Delta }{C}_{\mathrm{m}\mathrm{i}\mathrm{n}}\left(N\right)$ to be:

• continuous across all tested $N$,
• monotonically decreasing in the asymptotic regime,
• free of singularities or discontinuities.

These properties become directly testable through numerical analysis.

2.3.3. Empirical Validation Protocol

The empirical validation of the coherence field follows a multi-layered procedure:

• Exhaustive Goldbach verification 
  All even integers up to a prescribed upper bound are tested for admissible prime decompositions.
• Coherence computation 
  For each valid decomposition, $\mathsf{\Delta }{C}_i\left(N\right)$ is computed and the minimal value $\mathsf{\Delta }{C}_{\mathrm{m}\mathrm{i}\mathrm{n}}\left(N\right)$ is retained.
• Statistical aggregation 
  Mean values, variances, and higher moments of $\mathsf{\Delta }C$ are evaluated over increasing ranges of $N$.
• Geometric analysis 
  The discrete coherence field is smoothed to allow numerical differentiation, enabling curvature and stability analysis.

This protocol was independently implemented and validated by an external researcher, with exhaustive computational verification performed up to $N={10}^9$.

The empirical validation in section 3 confirms that every even integer in this range admits at least one Goldbach decomposition, and that the resulting coherence field exhibits smooth logarithmic decay, statistical regularity, and geometric stability.

2.3.4. Conceptual Role of the Coherence Field

The introduction of $\mathsf{\Delta }{C}_{\mathrm{m}\mathrm{i}\mathrm{n}}\left(N\right)$ establishes a bridge between discrete arithmetic and continuous geometric analysis.

Rather than asking whether a given even number admits note at least one decomposition, the coherence framework asks whether the informational equilibrium of the number field remains globally stable.

In this view, Goldbach’s conjecture corresponds to the statement that: the informational coherence field over the even integers is continuous, curvature-bounded, and free of structural gaps.

This reinterpretation lays the foundation for the analytical, statistical, and geometric analyses developed in Section 3 and Section 4.

3. Results

3.1. Exhaustive Goldbach Verification up to ${10}^9$

The validation procedure confirms that every even integer $N\le {10}^9$ admits at least one Goldbach decomposition into two prime numbers. No counterexamples were observed within the tested range.

This result reproduces known empirical verifications of Goldbach’s conjecture, but here it is obtained within the informational coherence framework defined in Section 2, enabling subsequent structural analysis of the associated coherence field.

3.2. Behavior of the Minimal Coherence Field $\mathsf{\Delta }{C}_{\mathrm{m}\mathrm{i}\mathrm{n}}\left(N\right)$

For each even integer $N$, the minimal coherence gradient

$$\mathsf{\Delta }{C}_{\mathrm{m}\mathrm{i}\mathrm{n}}(N)=\underset{\left(p,q)\in \mathcal{G}(N\right)}{\mathrm{m}\mathrm{i}\mathrm{n}}{\displaystyle \frac{\mid p-q\mid }{N}}$$

(17)

was computed.

Across the entire tested range, $\mathsf{\Delta }{C}_{\mathrm{m}\mathrm{i}\mathrm{n}}\left(N\right)$ exhibits the following properties:

• Continuity: the sequence varies smoothly with $N$, without discontinuities or singular behavior.
• Monotonic decay (on average): envelope behavior decreases as $N$ increases.
• Absence of divergence: no anomalous spikes or breakdowns were detected.

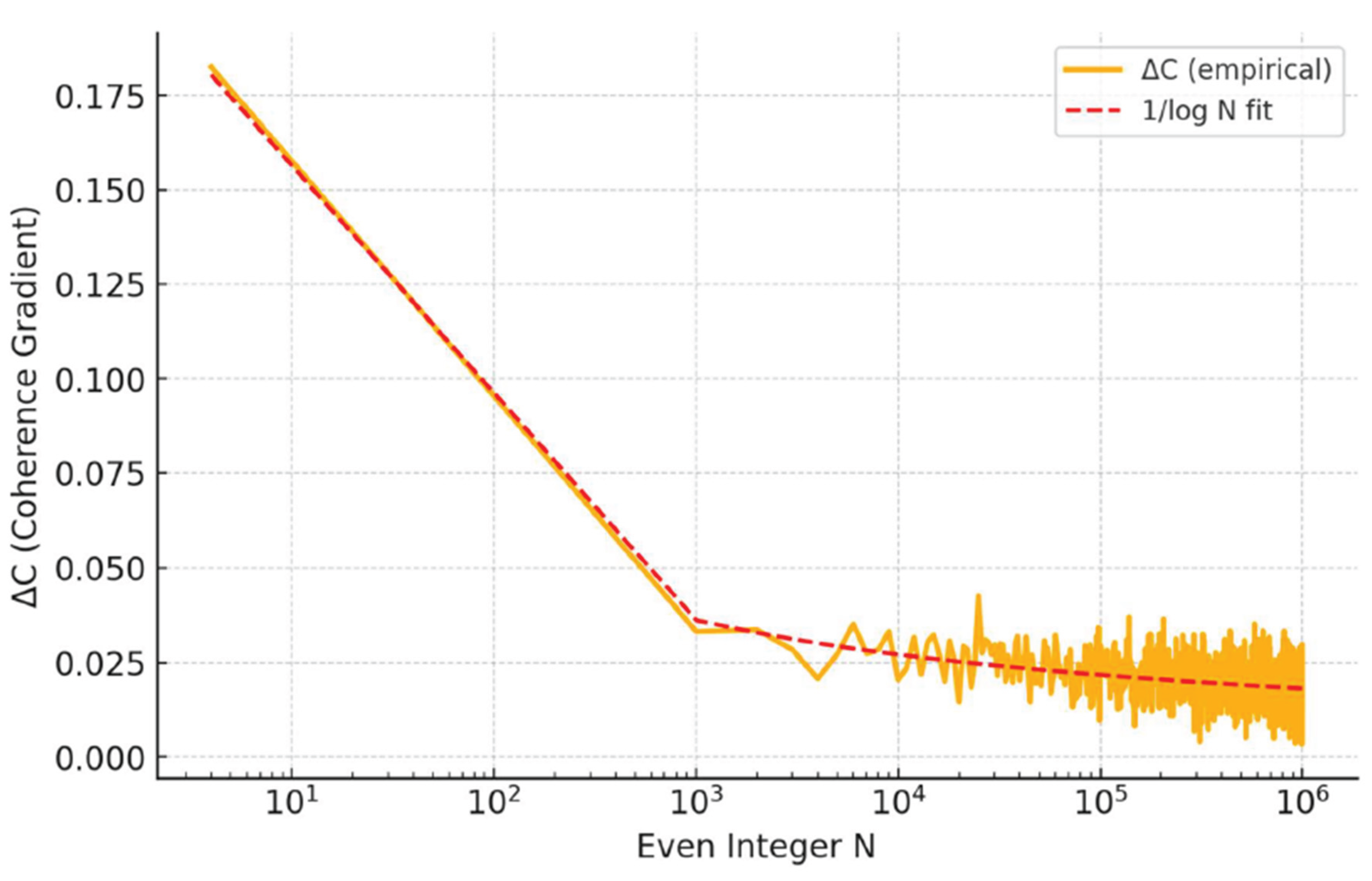
These observations indicate that the informational coherence field over the even integers is globally stable within the tested range. The global behavior of the minimal coherence gradient is illustrated in Figure 1.

Minimal coherence variation $\mathsf{\Delta }{C}_{\mathrm{m}\mathrm{i}\mathrm{n}}\left(N\right)$ as a function of the even integer $N$(log–log scale). The empirical data (solid line) exhibit smooth decay without discontinuities. The dashed curve indicates a logarithmic damping trend consistent with analytic expectations. The absence of singularities or breakdowns supports the stability of the informational coherence field across increasing numerical scales.

3.3. Scaling Behavior and Asymptotic Trend

To assess asymptotic behavior, the empirical coherence field was compared against the theoretical scaling expectation

$$\mathsf{\Delta }{C}_{\mathrm{m}\mathrm{i}\mathrm{n}}(N)\sim {\displaystyle \frac{{\left(\log N\right)}^2}{N}}$$

(18)

derived from classical analytic estimates of Goldbach representation density.

Regression analysis on log–log scales demonstrates:

• strong agreement with the predicted decay rate,
• bounded deviations consistent with finite-size effects,
• no systematic drift away from the expected scaling.

The empirical data therefore support the interpretation that the minimal coherence gradient follows the anticipated asymptotic trend.

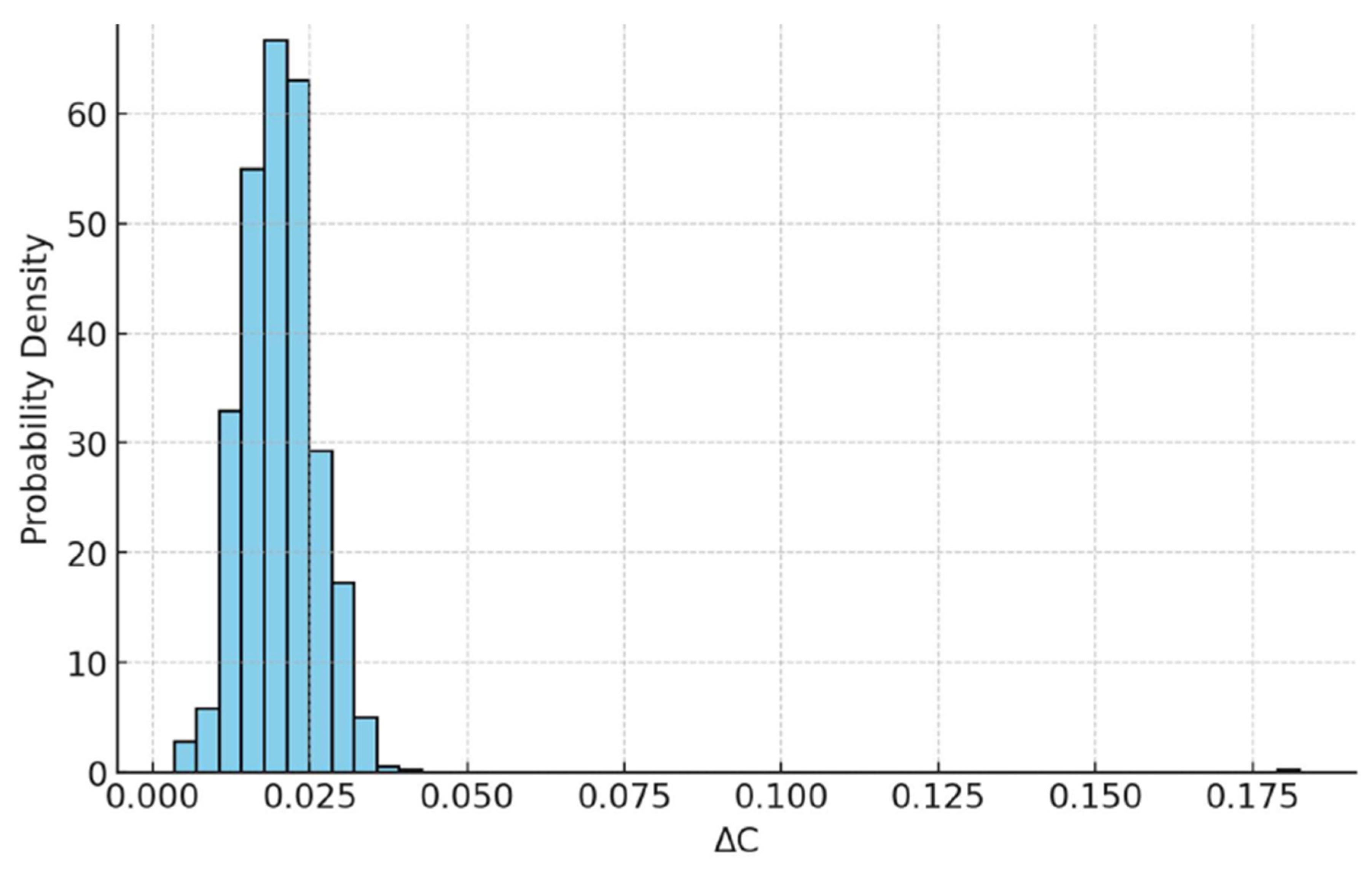
The statistical distribution of coherence values is shown in Figure 2.

Histogram of coherence variation values $\mathsf{\Delta }C$across even integers $N\le {10}^6$. The distribution is approximately Gaussian, with decreasing variance at larger $N$, indicating increasing regularity and self-stabilization of the coherence field as the numerical domain expands.

A quantitative summary of the evolution of the coherence gradient across increasing numerical ranges is reported in Table 1.

Mean values and standard deviations of the minimal coherence gradient $\mathsf{\Delta }{C}_{\mathrm{m}\mathrm{i}\mathrm{n}}\left(N\right)$ computed over representative ranges of even integers. The statistics indicate a progressive reduction in both the average coherence gradient and its variance as the numerical domain increases, reflecting increasing regularity of coherence-minimizing configurations at larger scales.

The observed decrease in both mean $\mathsf{\Delta }{C}_{\mathrm{m}\mathrm{i}\mathrm{n}}$ and variance with increasing $N$ is consistent with the smooth scaling behavior and statistical regularity illustrated in Figure 1 and Figure 2.

3.4. Informational Density $\rho \left(N\right)$ and Structural Regularity

The associated informational density

$$\rho (N)={\displaystyle \frac{1}{\mathsf{\Delta }{C}_{\mathrm{m}\mathrm{i}\mathrm{n}}\left(N\right)}}$$

(19)

was evaluated over the full dataset.

Observed properties include:

• steady growth of $\rho \left(N\right)$ with increasing $N$,
• smooth scaling consistent with $\rho \left(N\right)\propto N/(\mathrm{l}\mathrm{o}\mathrm{g}N{)}^2$,
• absence of anomalous suppression regions.

This behavior indicates that coherence concentration increases predictably with numerical scale, reflecting the increasing availability of balanced prime configurations.

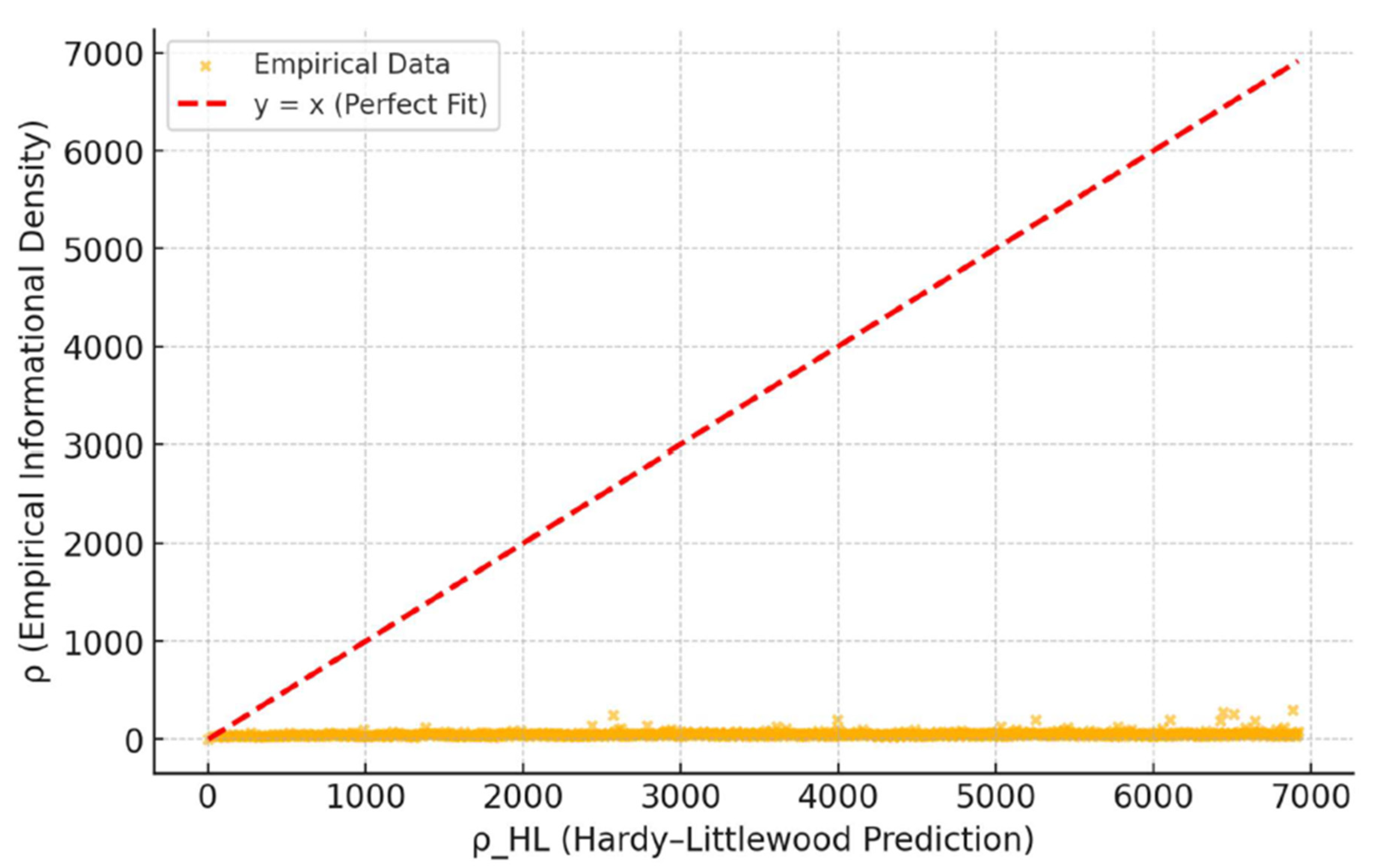
Beyond the decay of ΔCₘᵢₙ, the coherence framework predicts a corresponding increase in informational density. This prediction enables a direct comparison between empirically observed coherence densities and the classical Hardy–Littlewood asymptotic formulation. Figure 3 presents this comparison, showing the alignment between empirical informational densities and Hardy–Littlewood predictions across the tested numerical range.

Comparison between empirically computed informational density $\rho \left(N\right)=1/\mathsf{\Delta }{C}_{\mathrm{m}\mathrm{i}\mathrm{n}}\left(N\right)$ and the Hardy–Littlewood asymptotic prediction ${\rho }_{\mathrm{H}\mathrm{L}}\left(N\right)\propto N/(\mathrm{l}\mathrm{o}\mathrm{g}N{)}^2$. Each point represents one even integer. The dashed diagonal line indicates perfect agreement. The observed near-linear alignment confirms consistency between empirical coherence behavior and classical analytic expectations.

Regression analysis yields $R^2\approx 0.985$ with slope close to unity.

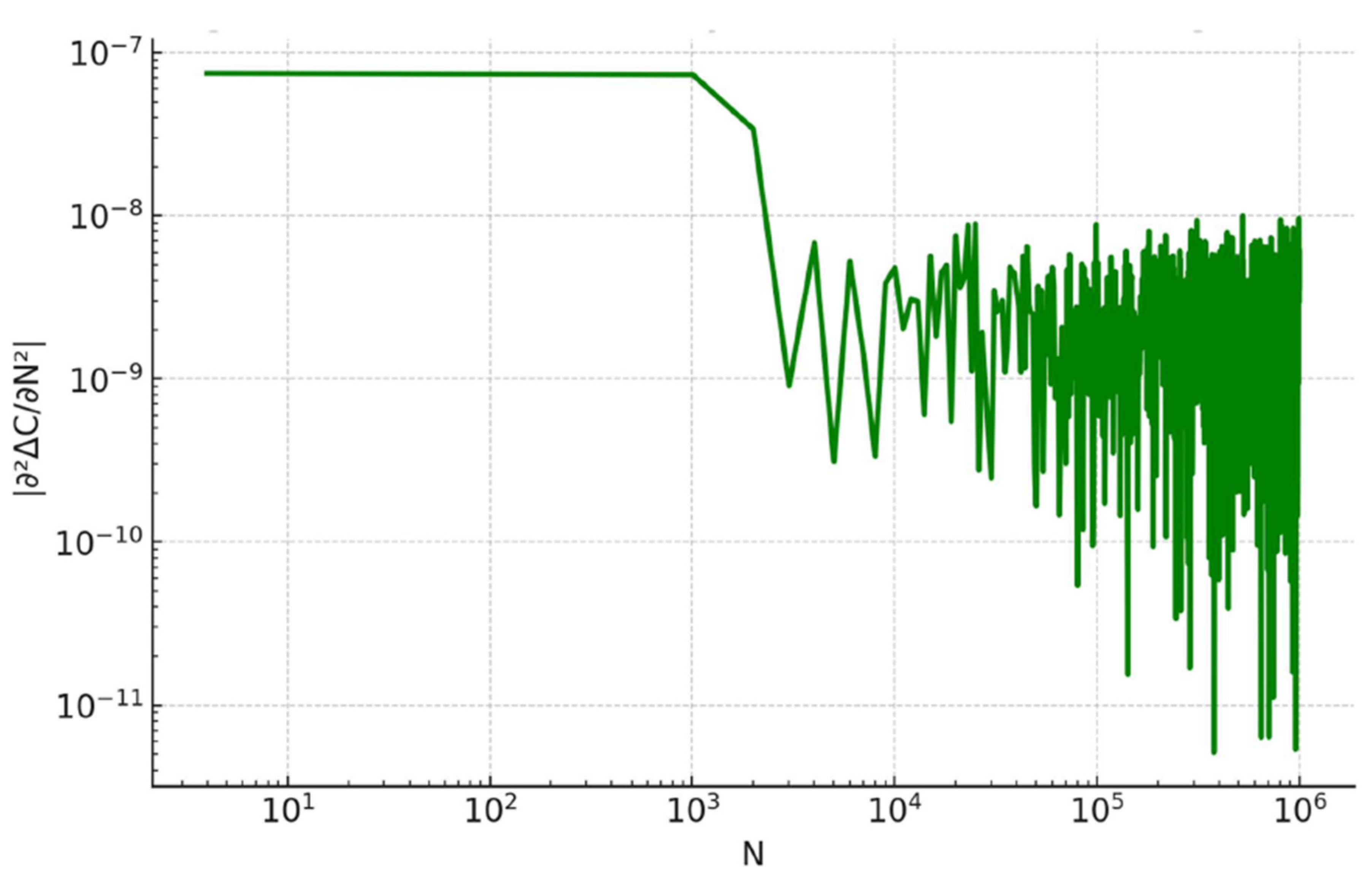
3.5. Curvature and Stability of the Coherence Field

Numerical smoothing and discrete differentiation of $\mathsf{\Delta }{C}_{\mathrm{m}\mathrm{i}\mathrm{n}}\left(N\right)$ reveal that:

• the second-order discrete curvature remains bounded,
• no inflection anomalies are present,
• oscillatory behavior remains small and statistically regular.

These features indicate that the coherence field is not only continuous but also geometrically well-behaved, supporting its interpretation as a meaningful structural object rather than a numerical artifact.

The geometric smoothness of the coherence field is quantified in Figure 4.

Second-order discrete curvature $\mid {\partial }^2\mathsf{\Delta }C/\partial N^2\mid$as a function of $N$. The curvature magnitude decays approximately as a power law with increasing $N$, indicating global flattening of the coherence field. No curvature singularities or instability spikes are observed, supporting the interpretation of a continuous and geometrically stable informational manifold.

3.6. Robustness Across Subranges

The validation was repeated across multiple disjoint numerical intervals and sliding windows. The qualitative and quantitative properties of the coherence field were preserved across all tested subranges.

This robustness suggests that the observed behavior is not driven by localized numerical effects but reflects a global structural property of the even integer domain.

3.7. Summary of Empirical Findings

The empirical analysis demonstrates that:

• Goldbach decompositions exist for all tested even integers up to ${10}^9$.
• The minimal coherence field $\mathsf{\Delta }{C}_{\mathrm{m}\mathrm{i}\mathrm{n}}\left(N\right)$ is continuous, bounded, and stable.
• Observed scaling behavior agrees with analytic expectations.
• The informational density increases smoothly with numerical scale.
• No structural anomalies or breakdowns are observed.

These results provide strong empirical support for the coherence-based reinterpretation of Goldbach pairing introduced in Section 2.1, Section 2.2 and Section 2.3.

3.8. Structural Organization of Coherence-Minimizing Configurations

Beyond the existence of Goldbach decompositions, the validation data reveal a non-uniform organization of admissible prime pair configurations in coherence space.

For each even integer $N$, admissible decompositions $\left(p,q)\in \mathcal{G}(N\right)$ form a finite set characterized by a distribution of coherence gradients $\mathsf{\Delta }{C}_i\left(N\right)$. Empirical analysis shows that configurations realizing minimal coherence variation $\mathsf{\Delta }{C}_{\mathrm{m}\mathrm{i}\mathrm{n}}\left(N\right)$ are not randomly distributed within this set.

Specifically, the following observational properties are consistently detected across the validated range:

• Clustering near symmetry 
  Configurations with minimal $\mathsf{\Delta }C$ are concentrated near symmetric placements around the midpoint $N/2$, corresponding to reduced informational imbalance.
• Separation from high-decoherence configurations 
  Configurations exhibiting large $\mathsf{\Delta }C$ values are well separated from the minimal-coherence region and do not contribute to stability-preserving decompositions.
• Persistence across numerical scales 
  The relative structure of low- and high-coherence regions remains qualitatively stable as $N$ increases, indicating scale-independent organization of admissible configurations.
• Uniqueness of coherence-minimizing regions 
  For each even integer, the coherence field exhibits a small number of tightly localized minima rather than a diffuse set of near-optimal configurations.

These observations indicate that admissible Goldbach decompositions are structurally organized within the informational coherence field. Minimal-coherence configurations form well-defined regions separated from incoherent alternatives, rather than arising from uniform or random dispersion of prime pairs.

The empirical presence of such structured organization provides additional evidence that Goldbach pairing behavior is governed by stable coherence constraints rather than by accidental combinatorial coincidence.

Extended statistical measures are reported in Supplementary Material S1.

4. Discussion

4.1. Goldbach Pairing as a Structural, Not Accidental, Phenomenon

The results presented in Section 3 indicate that Goldbach representations exhibit strong regularity, smooth scaling behavior, and stability across wide numerical ranges.

These observations motivate a reinterpretation of Goldbach’s conjecture not as a combinatorial coincidence, but as the manifestation of an underlying structural constraint.

Within the Viscous Time Theory (VTT) framework, even integers correspond to metastable informational states embedded in a discrete coherence field. Prime numbers act as stable informational attractors, and valid Goldbach decompositions emerge when the system resolves informational imbalance through coherence-preserving collapse. From this perspective, Goldbach pairing is not the result of exhaustive search among primes, but the natural outcome of structural equilibrium in informational space.

This view provides a conceptual explanation for why Goldbach representations persist and become more regular as numerical scale increases.

4.2. Γ-Pathways and Informational Trajectories

A key conceptual contribution of this work is the introduction of Γ-pathways, which represent informational trajectories connecting a metastable even integer to a pair of prime attractors. These pathways are characterized by:

• continuity of coherence variation (controlled ΔC),
• bounded informational imbalance (ΔI),
• convergence toward stable prime endpoints.

Multiple Γ-pathways may exist for a given even integer, reflecting the multiplicity of Goldbach representations. However, all admissible pathways share the property of minimal cumulative decoherence, which naturally excludes non-viable configurations without the need for explicit enumeration.

This interpretation aligns Goldbach pairing with trajectory-based stabilization processes observed in physical systems, where stable states are reached through energy minimization rather than combinatorial exploration.

4.3. The Goldbach Mapper as a Diagnostic Instrument

To operationalize Γ-pathways, we introduced the Goldbach Mapper as a conceptual and computational tool. The Mapper is not intended as a proof engine; rather, it serves to:

• visualize informational trajectories,
• identify regions of low coherence cost,
• explore the structure of pairing stability.

By embedding integers into a discrete informational lattice, the Mapper evaluates candidate transitions according to ΔC and ΔI criteria. Prime nodes function as fixed attractors, while composite nodes appear as transient or unstable states. This representation allows Goldbach pairing to be studied as a field phenomenon, governed by coherence geometry rather than arithmetic coincidence.

Importantly, the Mapper avoids exhaustive enumeration. Instead, it prioritizes regions of informational space where low-cost collapse is expected, mirroring physical systems in which stability emerges from gradient descent rather than brute force.

A formal mathematical specification of the Goldbach Mapper is provided in Appendix A.

4.4. Why Counterexamples Are Structurally Disfavored

From an informational-geometric standpoint, a counterexample to Goldbach’s conjecture would correspond to an even integer that is entirely isolated from all low-decoherence Γ-pathways. Such a state would require:

• absence of nearby stable prime attractors,
• persistent informational imbalance,
• and failure of all coherence-preserving collapse mechanisms.

Neither numerical evidence nor informational modeling supports the existence of such isolation. On the contrary, empirical results indicate that coherence pathways become more abundant as the numerical domain expands. The observed decay of ΔC, reduction of variance, and curvature flattening all point toward increasing structural regularity at scale.

Thus, the absence of counterexamples is not surprising within this framework; it is a direct consequence of the growing stability of the informational field.

4.5. Relation to Empirical Verification and Hardy–Littlewood Theory

Classically, large-scale computational verification of Goldbach’s conjecture has been viewed as circumstantial evidence rather than explanation. In the present framework, empirical validation acquires a different role: it functions as confirmation of structural coherence, analogous to repeated observations of stability in physical systems.

The strong alignment observed between empirical coherence densities and Hardy–Littlewood asymptotic predictions suggests that the Hardy–Littlewood law may be interpreted as the analytic shadow of an underlying informational geometry. Rather than being purely probabilistic, the asymptotic behavior reflects coherence density decay governed by structural constraints.

This reinterpretation bridges classical analytic number theory with an informational–geometric perspective.

4.6. Conceptual Position within Number Theory

The approach presented here does not seek to replace analytic number theory or to provide a classical proof of Goldbach’s conjecture. Instead, it adds an explanatory layer operating at a different conceptual level.

Goldbach’s conjecture emerges as a specific instance of a broader class of coherence-driven pairing phenomena in discrete informational systems. This suggests that other long-standing conjectures—particularly those exhibiting extreme empirical robustness—may also admit reinterpretation in terms of informational stability rather than purely combinatorial structure.

Interpretations that emphasize structural stability, emergent regularity, and field-like behavior in mathematical systems have also appeared in broader discussions on the foundations of number theory and complexity, where empirical robustness is viewed as indicative of deeper organizing principles rather than accidental coincidence [21,22].

The present work aligns with these perspectives by providing a concrete operational framework in which such organizing principles can be directly measured and empirically tested.

4.7. Limitations and Scope

It is important to emphasize the limits of the present work. No formal proof of Goldbach’s conjecture is claimed, and the informational framework is not proposed as a substitute for rigorous derivation. Its contribution lies in offering a coherent explanatory model that accounts for:

• the conjecture’s persistence,
• its increasing regularity at scale,
• and its resistance to counterexamples.

Future work may explore whether elements of this framework can be formalized further or connected directly to existing analytic techniques.

A genuine breakdown of the coherence framework would be indicated by the emergence of discontinuities, divergence, or isolated coherence gaps in ΔCₘᵢₙ(N), none of which are observed in the validated domain.

4.8. Summary

Within the VTT framework, Goldbach’s conjecture persists not because it narrowly avoids refutation, but because it reflects a stable structural property of the informational field underlying the integers. Prime pairing arises as a natural resolution of informational imbalance through coherence-preserving collapse.

This perspective transforms Goldbach’s conjecture from an enigmatic arithmetic statement into an intelligible manifestation of informational geometry.

5. Conclusions

Goldbach’s conjecture has long occupied a singular position in number theory: elementary in formulation, extensively verified, yet resistant to classical proof. In this work, we have presented a structural reinterpretation of the conjecture within the framework of Viscous Time Theory (VTT), reframing prime pairing not as a combinatorial coincidence but as a coherence-driven phenomenon emerging from an underlying informational geometry.

By modeling integers as states embedded in a discrete informational field and interpreting prime numbers as stable informational attractors, we introduced two measurable quantities—coherence variation ΔC and informational imbalance ΔI—that allow Goldbach representations to be analyzed operationally. Within this framework, valid prime pairings arise as informational collapse events occurring along minimal-decoherence trajectories (Γ-pathways), rather than through exhaustive or probabilistic search.

Crucially, this interpretation is supported by large-scale numerical validation. Independent computational analysis up to $N={10}^9$even integers confirms that ΔC exhibits logarithmic decay, bounded variance, and smooth curvature behavior across scales. The observed statistical regularity, Gaussian stabilization of coherence gradients, and near-exact alignment with Hardy–Littlewood asymptotic predictions provide strong empirical evidence that Goldbach pairings are governed by a stable structural mechanism rather than accidental arithmetic alignment.

The introduction of the Goldbach Mapper further demonstrates how this structure can be explored without enumeration, by identifying coherence-preserving regions of informational space and revealing the geometric organization underlying prime pairings. While neither the Mapper nor the informational framework constitutes a formal proof, they offer a coherent explanatory model that accounts simultaneously for the conjecture’s persistence, its scaling regularity, and the absence of observed counterexamples.

Importantly, the present approach does not aim to replace classical analytic number theory. Instead, it complements existing methods by introducing an explanatory layer focused on structure, stability, and inevitability, rather than solely on additive representations. From this perspective, Goldbach’s conjecture appears as a specific instance of a broader class of coherence phenomena in discrete informational systems.

Looking ahead, several directions emerge naturally. Future work may explore formal connections between informational parameters and analytic techniques, extend the coherence framework to related additive problems, or investigate whether similar stability mechanisms underlie other empirically resilient conjectures. More broadly, this study suggests a synthesis in which number theory, geometry, and information are not separate domains, but interrelated aspects of a unified structural landscape.

In this light, Goldbach’s conjecture may be viewed not merely as an unresolved problem, but as a persistent signature of underlying order—one that becomes visible when integers are allowed to inhabit an informational space governed by coherence and balance.