Rupture Velocity Acceleration and Slip Partitioning along an Oceanic Transform Fault: The 2025 Mw 7.6 Cayman Trough Earthquake

1. Introduction

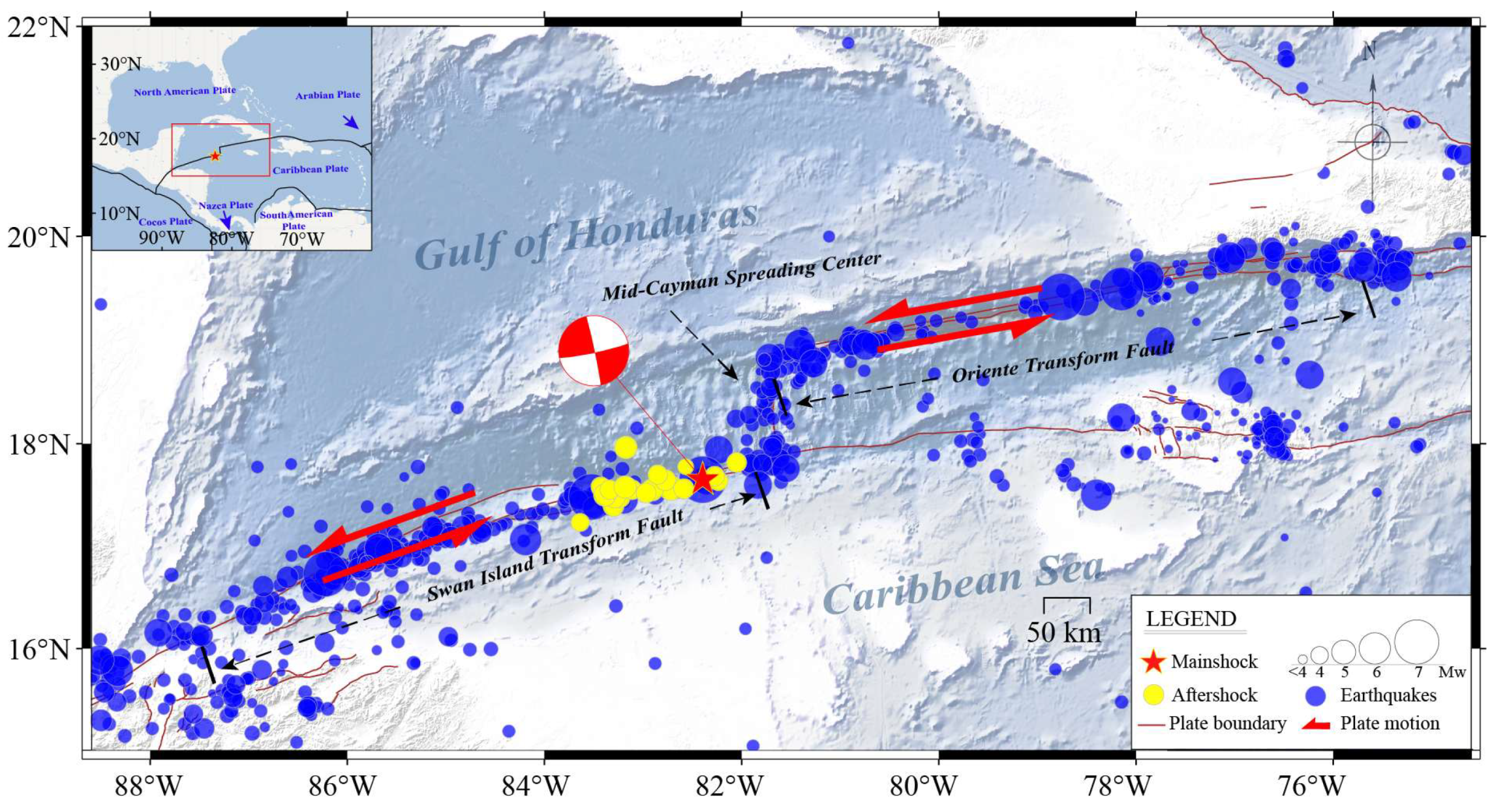
On 8 February 2025, a large Mw 7.6 strike-slip earthquake occurred in the northern Caribbean, with its epicenter located within the Cayman Trough transform fault system, the primary plate boundary between the North American and Caribbean plates (Figure 1). Geodetic and geological studies indicate that the two plates undergo left-lateral relative motion at a rate of approximately 15–20 mm/y [1,2]. Against this long-term tectonic background, the plate boundary has historically hosted multiple large strike-slip earthquakes, including the 1976 Mw 7.5 Guatemala earthquake, the 2020 Mw 7.7 Jamaica–Cuba earthquake, and other major events along adjacent fault segments [3,4], highlighting its substantial seismic hazard.

The northern Caribbean plate boundary consists of several key tectonic units, including the Swan Islands Transform Fault, the Mid-Cayman Spreading Center, and the Oriente Transform Fault (Figure 1). The Mid-Cayman Spreading Center connects the two strike-slip faults, featuring predominantly normal faulting nearly perpendicular to the transform fault trend, with an ultra-slow seafloor spreading rate of ~15 mm/yr, forming one of the world’s deepest oceanic basins [5,6,7,8]. Collectively, these structures create a geometrically complex and kinematically diverse plate boundary system, accommodating relative motion through strike-slip, extension, and localized compression.

The 2025 Mw 7.6 earthquake occurred on the eastern segment of the Swan Islands Transform Fault, near its junction with the Mid-Cayman Spreading Center (Figure 1). Although the Cayman Trough is often interpreted as a large releasing step or pull-apart basin, geological and geophysical studies indicate that the transform fault system is highly segmented, with pronounced releasing and restraining bends along the Swan Islands fault [5,9,10]. In left-lateral strike-slip systems, restraining bends typically correspond to localized compressional deformation and elevated stress accumulation, with mechanical strength significantly higher than surrounding segments, making them potential nucleation or rupture-arrest zones for large earthquakes [10,11].

Compared with continental strike-slip faults such as Saging Fault [12], earthquake-related deformation can be effectively measured and extensively investigated through earthquake geological surveys and spaceborne geodetic observation techniques [13,14], large earthquakes on oceanic transform faults remain relatively understudied, largely due to their offshore location and sparse near-field observations. Consequently, key scientific questions remain regarding the rupture duration, rupture speed, and the influence of fault geometric complexity on rupture propagation. In this context, teleseismic imaging techniques provide an essential approach for investigating the rupture process of such events.

In this study, we combine high-frequency teleseismic back-projection with low-frequency finite-fault inversion to systematically investigate the rupture process of the 2025 Mw 7.6 Cayman Trough earthquake. Back-projection is employed to resolve the spatiotemporal evolution of high-frequency seismic radiation and rupture propagation, while finite-fault inversion constrains the low-frequency coseismic slip distribution and moment release. By jointly analyzing rupture duration, rupture speed, and slip characteristics, we aim to elucidate how the geometric complexity of the Swan Islands Transform Fault and its proximity to the Mid-Cayman Spreading Center control rupture behavior, providing new insights into the seismogenic mechanisms and associated hazard of oceanic transform faults.

2. Back-Projection Analysis

2.1. Data and Processing

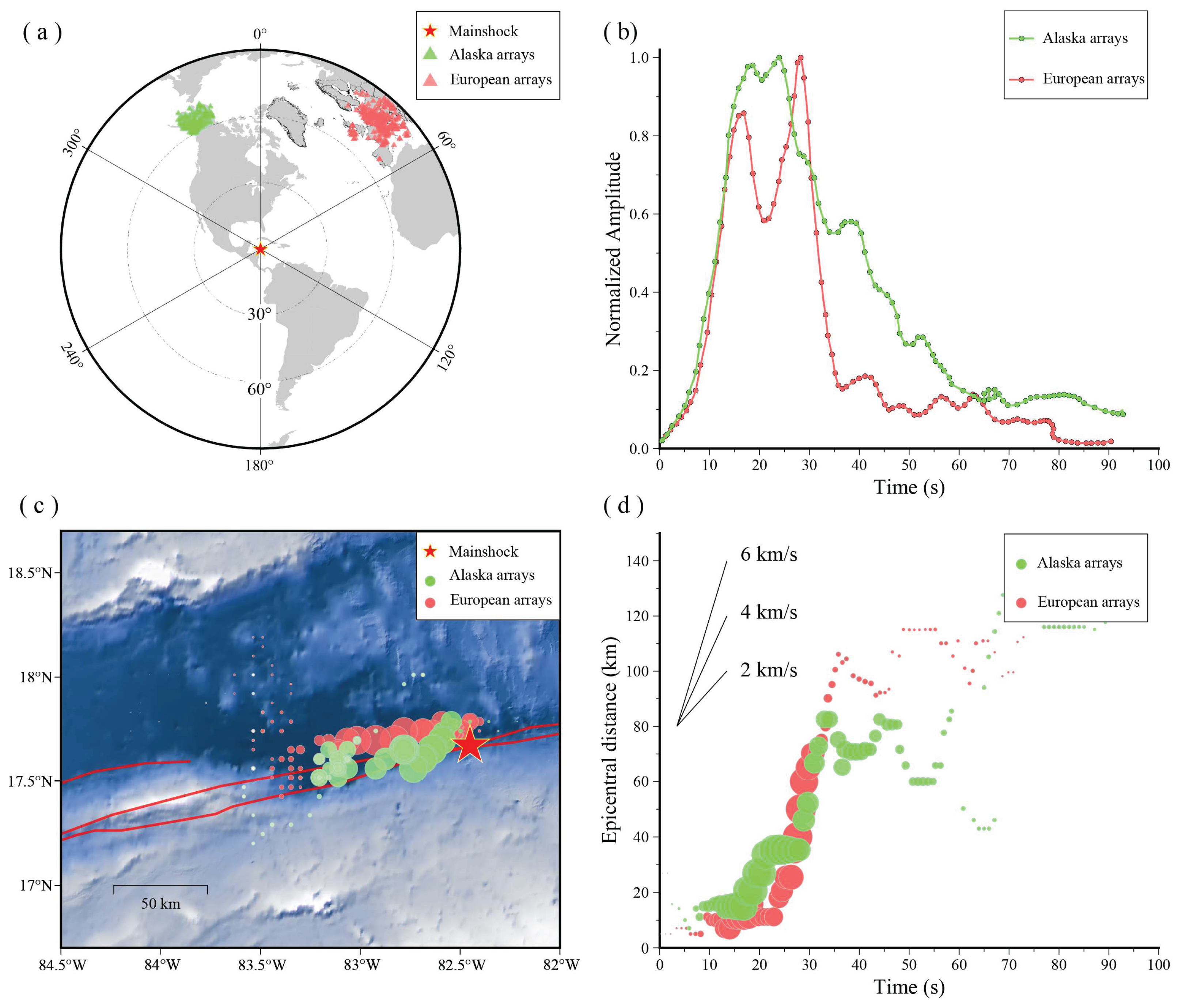
We applied teleseismic back-projection (BP) to investigate the rupture process of the 8 February 2025 Mw 7.6 Cayman Trough earthquake [15]. Waveforms from the European and Alaska seismic arrays were used, providing complementary azimuthal coverage and dense station distribution (epicentral distances and azimuths: Alaska array 60°–75°, −36°–17°; European array 60°–85°, 21°–64°). This setup enables robust imaging of high-frequency radiation emitted from the rupture front, and thus achieves detailed imaging of the earthquake rupture process, leading to new insights from case studies of a series of recent earthquakes. [16,17,18,19,20].

2.2. Back-Projection Method

The back-projection method maps high-frequency seismic energy by summing time-shifted waveforms on a predefined source grid.

Following Wang et al. (2016), waveforms were preprocessed by removing the instrument response and applying a 0.5–2.0 Hz bandpass filter, which is sensitive to high-frequency radiation near the rupture front. For teleseismic observations, direct P-wave arrivals were used to compute theoretical travel times from each grid point to each station [21]. To correct for travel-time errors induced by local heterogeneities beneath each station, we computed station corrections via cross-correlation using the first 6 s of the direct P-wave. Stations with low correlation coefficients were excluded to ensure coherent stacking of the waveforms. After applying station corrections and theoretical travel times, waveforms were stacked within sliding time windows.

In this study, we used a 10 s time window with a 1 s sliding step, resulting in 100 consecutive windows. The stacking amplitude for each window was defined as the squared sum of the stacked waveforms, enhancing coherent energy while suppressing noise. The resulting amplitudes were projected onto the source grid to determine the spatiotemporal distribution of high-frequency radiation. To account for apparent time shifts caused by rupture directivity, we applied corrections following Krüger and Ohrnberger (2005) [17], ensuring consistency of rupture evolution across different arrays.

2.3. Back-Projection Results

As shown in Figure 2, back-projection results from the European and Alaska arrays are highly consistent, indicating robust imaging. Both arrays reveal that the rupture propagated predominantly westward along the Swan Islands Transform Fault, with a total duration of ~40–50 s and a rupture length of 80–100 km.

The rupture evolution exhibits a clear two-stage pattern:

• The initial ~20 s corresponds to a sub-shear phase, with an average rupture speed of ~1 km/s.
• In the subsequent stage, the rupture accelerates significantly, reaching supershear speeds of ~5–6 km/s.

According to the CRUST1.0 model [22], the S-wave velocity at the source depth (~10 km) is ~2.55 km/s. The later-stage rupture clearly exceeds this shear-wave velocity, satisfying the classical supershear rupture criterion, where the rupture front velocity exceeds the local S-wave speed [23,24]. Therefore, the 2025 Cayman Trough earthquake underwent a transition from an initial sub-shear phase to a subsequent supershear stage, highlighting significant temporal variation in the rupture dynamics along the Swan Islands Transform Fault.

3. Finite-Fault Inversion

To further constrain the low-frequency co-seismic slip distribution and moment release of the 8 February 2025 Mw 7.6 Honduras earthquake, we conducted finite-fault inversion (FFI) using broadband teleseismic P-waveforms from the Global Seismographic Network (GSN) based on the MuDpy framework [25]. MuDpy, developed as an improvement on classical finite-fault inversion, introduces regularization constraints, time-window segmentation, and moment tensor parameterization to enhance stability and reproducibility.

Guided by the back-projection results, we constructed a finite-fault model along the strike of the Swan Islands Transform Fault, discretized into 27 × 4 subfaults (5 km × 4 km each). The source-time function (STF) for each subfault was represented by a triangular function with a half-duration of 1.5 s, and slip variations over time were constrained using four consecutive time windows to improve temporal resolution. To increase inversion robustness, we applied a priori rupture speed constraints informed by back-projection: an initial maximum Vr of 1 km/s for the first ~20 s within ~20 km of the rupture front, and another higher maximum Vr of 6 km/s in later stages [26].

3.1. Data and Method

Teleseismic P-waveforms at epicentral distances of 30°–90° were used for waveform fitting. Each waveform was corrected for instrument response, filtered, and time-aligned. Slip and rupture initiation times for each subfault were solved via least-squares fitting of observed waveforms to synthetic waveforms generated for each subfault using the corresponding moment tensor [21,27,28].

3.2. Inversion Results

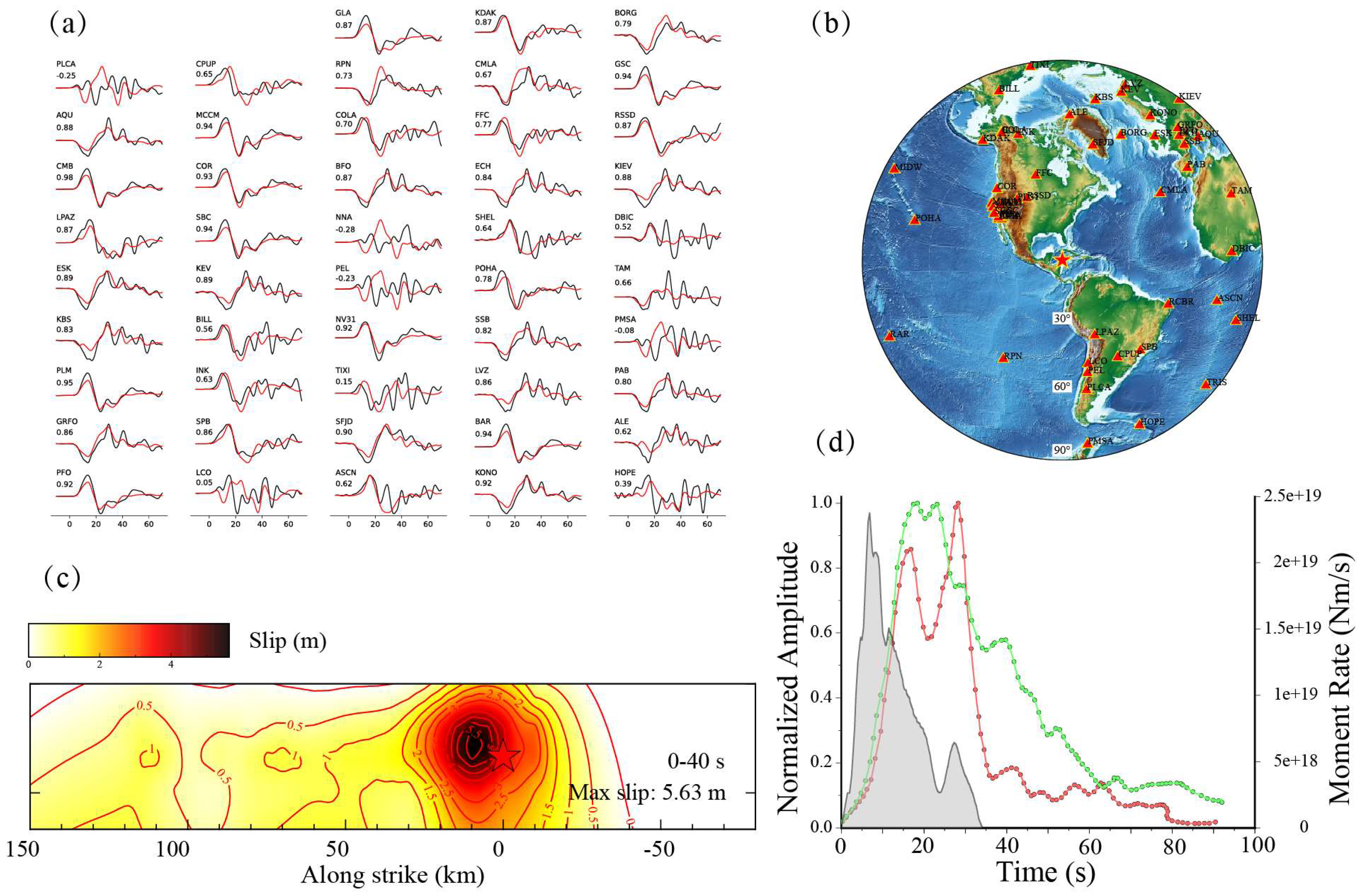
The FFI successfully reproduces the observed teleseismic P-waveforms (Figure 3a–b). The final slip distribution (Figure 3c) shows a maximum slip of ~5.6 m, concentrated within ~20 km west of the epicenter, indicating that the seismic moment release occurred primarily in the shallow main fault segment. The STF derived from FFI (Figure 3d, gray curve) peaks at ~10 s, with an overall rupture duration of ~40 s. Comparison with the back-projection results (red and green curves, European and Alaska arrays, respectively) indicates that high-frequency energy peaks later (~20 s), suggesting that low-frequency slip dominates the early rupture stage.

3.3. Spatiotemporal Rupture Evolution

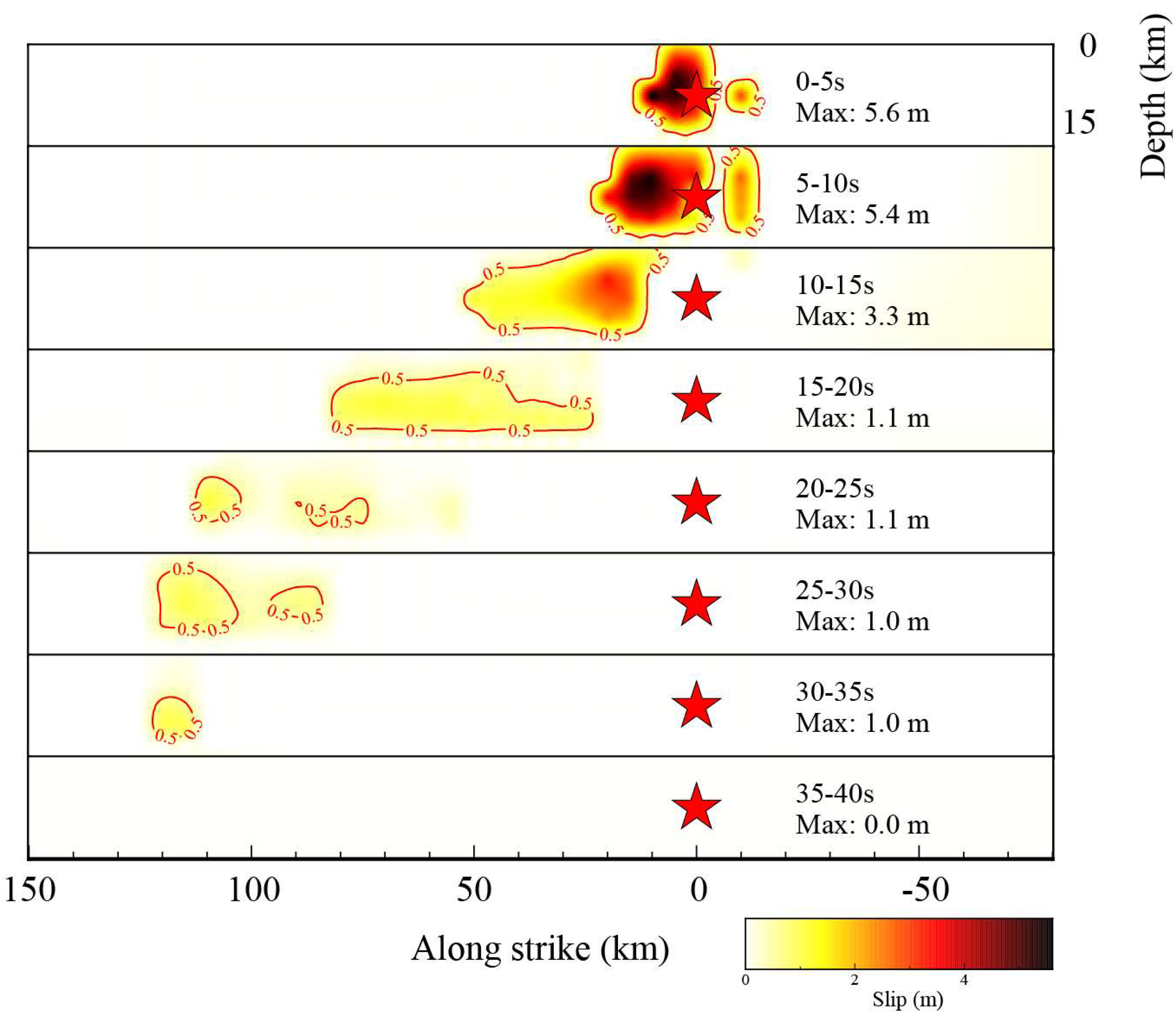
Figure 4 presents rupture snapshots at successive 5-s intervals. During 0–5 s, rupture initiates near the epicenter with maximum slip 5.6 m and propagates ~10 km westward. Between 5–10 s, the rupture advances another ~10 km with peak slip 5.4 m. From 10–15 s, maximum slip decreases to 3.3 m while the rupture front reaches ~50 km west. Between 15–20 s, slip further reduces (~1.1 m), and the rupture front extends to ~80 km. During 20–30 s, rupture propagation slows, with maximum slip decreasing from ~1.1 m to ~1.00 m and the rupture front reaching ~110 km west. After 30 s, maximum slip amplitudes drop below ~1 m, and rupture arrests at ~120 km west of the epicenter. The inferred rupture speed ranges from ~1 km/s for the initial stage to ~6 km/s of the later stage, indicating similar accelerating process as shown in the back-projection results.

4. Discussion

Our finite-fault inversion reveals a pronounced along-strike trade-off between slip amplitude and rupture speed. The largest slip concentrates around the hypocentral area and within ~20 km, where the peak slip reaches ~5 m but the inferred rupture speed is only ~1 km/s. In contrast, the rupture propagates much faster (5–6 km/s) from ~20 km west of the hypocenter to ~120 km west, yet this segment is characterized by comparatively small slip. Such spatial anti-correlation is not unusual: a global catalog of rupture velocities suggests that rupture speed can be inversely related to source strength/stress-drop–related measures, with slow ruptures often associated with large slip in some settings [29,30] , whereas faster ruptures tend to occur where the dynamic conditions favor efficient propagation [31].

A useful physical framing is energy balance at the rupture front. The rupture speed is controlled by the ratio between the energy available to drive rupture (energy release rate, linked to prestress and elastic properties) and the energy consumed by the rupture process (fracture energy, including breakdown work and off-fault damage). Recent synthesis modeling argues that the full spectrum of rupture speeds can be explained by variations in this ratio: lower effective fracture energy or higher driving stress promotes faster propagation, while higher fracture energy (or lower driving stress) slows rupture [32]. In this context, the hypocentral/high-slip patch may represent a mechanically “tough” nucleation/asperity region where rupture must spend substantial energy to overcome local strength (high breakdown work, elevated normal stress, strong heterogeneity, geometric complexity, or enhanced off-fault damage). These factors can reduce the net energy available for advancing the crack tip, yielding a slow initial rupture even though slip eventually becomes large once weakening mechanisms fully develop. Accurate sub-seafloor velocity models will facilitate more in-depth investigation and discussion of this topic [33].

Why, then, does the far-west segment exhibit fast rupture but small slip? One explanation is a transition from a crack-like rupture (large slip, long local slip duration) near the hypocenter to a pulse-like rupture (short slip duration, limited final slip) during rapid propagation. Self-healing slip pulses arise naturally in frictional models and can sustain high rupture speeds while limiting accumulated slip because the fault heals quickly behind the front [34]. Laboratory and theoretical work also shows that pulse-like or localized rupture modes can be dynamically stable and can propagate rapidly, with slip concentrated in a narrow zone near the tip rather than building large final slip everywhere [35]. In such a regime, high rupture speed is compatible with small slip because the local rise time (or effective slip duration) is short; the fault does not remain weak long enough to accumulate meters of slip before restrengthening.

The observed pattern can be interpreted as a cascading rupture in which the initial slow, high-slip zone “primes” the system (through stress redistribution and dynamic stressing) and then the rupture transitions into a dynamically favorable corridor where propagation is easy but slip is constrained by rapid restrengthening. This highlights that “large slip” and “fast rupture” need not coincide spatially: slip reflects the integrated history of stress and weakening at a point, while rupture speed reflects the instantaneous ability of the front to advance. Future work that jointly inverts for spatially variable rise time (or slip-rate function) and tests crack- versus pulse-like models would directly evaluate whether the fast segment is characterized by shorter durations and stronger healing, as predicted by pulse-like dynamics [36].

Our finite-fault inversion reveals a clear along-strike trade-off between slip amplitude and rupture speed, highlighting a fundamental aspect of rupture dynamics. The largest slip is concentrated around the hypocentral region and within ~20 km of it, where peak slip reaches ~5 m but the inferred rupture speed is remarkably low, on the order of ~1 km/s. In contrast, the rupture accelerates dramatically west of this zone, propagating at 5–6 km/s from ~20 km to ~120 km west of the hypocenter, while producing comparatively small slip. This pronounced spatial anti-correlation between slip magnitude and rupture speed is not anomalous. A global compilation of rupture velocities indicates that rupture speed can be inversely related to stress-drop–related source properties: slow ruptures are often associated with large slip in certain environments (e.g., tsunami earthquakes), whereas fast ruptures tend to occur where dynamic conditions favor efficient rupture propagation [31].

This behavior can be naturally interpreted within the framework of energy balance at the rupture front. Rupture speed is governed by the competition between the energy available to drive rupture—controlled by prestress and elastic properties—and the energy dissipated during rupture, commonly referred to as fracture energy, which includes breakdown work and off-fault damage. Recent theoretical synthesis demonstrates that the full spectrum of observed rupture velocities can be explained by variations in this energy ratio: higher driving stress or lower effective fracture energy promotes fast rupture, whereas higher fracture energy or reduced driving stress leads to slower rupture [32]. From this perspective, the hypocentral high-slip region may represent a mechanically “tough” asperity or nucleation zone, where rupture must overcome elevated strength and dissipate substantial energy. Factors such as high normal stress, strong material heterogeneity, geometric complexity, or intense off-fault damage can significantly increase breakdown work, thereby limiting the energy available to advance the rupture front. As a result, rupture propagates slowly in this region despite ultimately producing large slip once weakening mechanisms are fully activated.

A key scientific question, then, is why the western segment exhibits rapid rupture propagation while accommodating only modest slip. One plausible explanation is a transition in rupture mode from crack-like behavior near the hypocenter to pulse-like behavior during fast propagation. Crack-like rupture is characterized by long slip durations and large final slip, whereas pulse-like rupture involves short slip durations and self-healing behavior that limits total slip. Self-healing slip pulses arise naturally in rate-and-state friction models and allow ruptures to propagate rapidly while restricting slip accumulation, because the fault restrengthens quickly behind the rupture front [34]. Laboratory and theoretical studies further demonstrate that pulse-like rupture modes can be dynamically stable and propagate efficiently, with slip localized near the rupture tip rather than accumulating uniformly along the fault [35]. In such a regime, fast rupture speed is fully compatible with small slip, as the short rise time prevents the fault from remaining weak long enough to accumulate meters of displacement.

More broadly, the observed rupture pattern suggests a cascading rupture process. The initial slow, high-slip nucleation zone may act as an energy-intensive “starter,”redistributing stress and dynamically loading adjacent fault segments. Once rupture enters a mechanically favorable corridor—characterized by lower fracture energy or more efficient weakening—it accelerates dramatically, while rapid restrengthening limits local slip. This interpretation underscores a critical conceptual point: large slip and fast rupture need not be spatially coincident. Slip reflects the time-integrated history of stress release and weakening at a given location, whereas rupture speed reflects the instantaneous ability of the rupture front to propagate. Disentangling these two aspects is essential for understanding earthquake dynamics, seismic radiation, and associated hazards. Future studies that jointly invert for spatially variable rise time or slip-rate functions, and explicitly test crack-like versus pulse-like rupture models, will be crucial for evaluating whether the fast-propagating segment is indeed governed by short-duration, strongly self-healing slip, as predicted by pulse-like rupture theory [37].

5. Conclusions

We investigated the rupture characteristics of the 8 February 2025 Mw 7.6 Cayman Trough earthquake through a joint analysis of teleseismic back-projection and finite-fault inversion. The rupture advanced predominantly westward along the Swan Islands Transform Fault and exhibited clear changes in propagation behavior over the course of the event. An initially slow rupture phase, lasting approximately 20 s with a velocity of ~1 km/s, transitioned into a rapidly propagating segment that reached velocities of 5–6 km/s, exceeding the local shear-wave speed. Slip distribution inferred from waveform inversion indicates that deformation was strongly localized near the hypocentral region, with the largest slip (~5.6 m) confined to a narrow zone within ~20 km west of the epicenter. In contrast, the later portion of the rupture extended farther along strike but was associated with much smaller slip. The temporal correspondence between rupture kinematics and frequency-dependent radiation shows that the majority of seismic moment was released during the early, slower phase, whereas the acceleration stage was marked by enhanced high-frequency energy despite limited additional slip.

These observations document a clear along-strike complementarity between rupture speed and slip amplitude, reflecting systematic changes in rupture behavior along the fault. Such contrasts likely arise from spatial variations in fault properties, including strength, fracture energy, and geometric or structural complexity. By integrating high-frequency and low-frequency seismic constraints, this study provides a refined depiction of rupture evolution for an offshore strike-slip earthquake and contributes to a better understanding of supershear rupture processes along oceanic transform faults.